https://ebookmass.com/product/complexity-and-complex-thermo-
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Complexity and Complex Chemo-Electric Systems Stanislaw Sieniutycz
https://ebookmass.com/product/complexity-and-complex-chemo-electricsystems-stanislaw-sieniutycz/
ebookmass.com
Thermodynamic Approaches in Engineering Systems 1st Edition Stanislaw Sieniutycz
https://ebookmass.com/product/thermodynamic-approaches-in-engineeringsystems-1st-edition-stanislaw-sieniutycz/
ebookmass.com
A Thermo-Economic Approach to Energy from Waste Anand Ramanathan
https://ebookmass.com/product/a-thermo-economic-approach-to-energyfrom-waste-anand-ramanathan/
ebookmass.com
The Tickler's Jam Murders 1st eBook Ed. Edition Peter Tickler
https://ebookmass.com/product/the-ticklers-jam-murders-1st-ebook-ededition-peter-tickler/
ebookmass.com
Ancient and Medieval Thought on Greek Enclitics Stephanie Roussou
https://ebookmass.com/product/ancient-and-medieval-thought-on-greekenclitics-stephanie-roussou-2/
ebookmass.com
Fair Catch (Vegas Aces: The Playbook Book 3) Lisa Suzanne
https://ebookmass.com/product/fair-catch-vegas-aces-the-playbookbook-3-lisa-suzanne/
ebookmass.com
The Art of Game Design: A Book of Lenses, Second Edition
https://ebookmass.com/product/the-art-of-game-design-a-book-of-lensessecond-edition/
ebookmass.com
A Treatise on Northern Ireland, Volume 3: Consociation and Confederation Brendan O'Leary
https://ebookmass.com/product/a-treatise-on-northern-irelandvolume-3-consociation-and-confederation-brendan-oleary/
ebookmass.com
ISE Data Analytics for Accounting 2nd Edition Vernon Richardson Professor
https://ebookmass.com/product/ise-data-analytics-for-accounting-2ndedition-vernon-richardson-professor/
ebookmass.com
Mass-Produced Original Paintings, the Psychology of Art, and an Everyday Aesthetics 1st ed. Edition Martin S. Lindauer
https://ebookmass.com/product/mass-produced-original-paintings-thepsychology-of-art-and-an-everyday-aesthetics-1st-ed-edition-martin-slindauer/ ebookmass.com
ComplexityandComplex Thermo-EconomicSystems
StanisławSieniutycz
WarsawUniversityofTechnology, FacultyofChemicalandProcessEngineering, Warsaw,Poland
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
©2020ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicormechanical, includingphotocopying,recording,oranyinformationstorageandretrievalsystem,withoutpermissioninwritingfromthe publisher.Detailsonhowtoseekpermission,furtherinformationaboutthePublisher’spermissionspoliciesandour arrangementswithorganizationssuchastheCopyrightClearanceCenterandtheCopyrightLicensingAgency,canbefound atourwebsite: www.elsevier.com/permissions.
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher(otherthanas maybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperiencebroadenour understanding,changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusinganyinformation, methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationormethodstheyshouldbemindfulof theirownsafetyandthesafetyofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliabilityfor anyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,orfromanyuse oroperationofanymethods,products,instructions,orideascontainedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-12-818594-0
ForinformationonallElsevierpublicationsvisit ourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: SusanDennis
AcquisitionEditor: AnitaKoch
EditorialProjectManager: EmeraldLi
ProductionProjectManager: PremKumarKaliamoorthi
CoverDesigner: MilesHitchen
TypesetbySPiGlobal,India
Preface
Thetitleofthisbookatthetimewhenitwasplannedwas ComplexityandComplex ThermodynamicSystems,i.e.,anarrowedtreatisewasintended,associatedonlywith thermodynamicaspectsofcomplexity.However,asstressedbyReynoldsandHolwellintheir book SystemApproachestoManagingChange (Springer2010;ISBN978-1-84882-808-7) weliveandworkinahighlycomplexandinterconnectedworld,thusevensmallenlargementof thedecisionmanifoldmayhaveanimpactonorganizations,societies,environment,etc. Therefore,itwasnaturaltoextendinthepresentvolumetheclassofcomplexthermodynamic systemstotheclassofcomplexthermoeconomicsystems,thusincreasingtheapplicative contentsofthebook(evenatthecostofoccasionalviolationofthebookcoherence).Keeping thischangeinmindwewill,nevertheless,preservethepriorityofthermodynamics,“aqueenof macroscopicscienceswhichwillneverbeoverthrown.”Infact,thermodynamicsisinvariably thebasisandtheinevitablecomponentinmodeling,analysis,synthesis,andoptimization ofmostpracticalandindustrialsystems,inparticularthoseconsideredinthisbook.
Thermodynamicmodelsconsiderenergyandmatterbalances,theresultsofinvarianceprinciples ofphysics.Thesebalancesincorporatelimitationsonworkingparametersofrealprocesses, whichshouldbeconsideredwhenformulatingconstraintsontheperformanceofpracticaland industrialsystems.Thermodynamicsandkinetictheoryprovidedataofstaticandtransport propertiesneededincalculations.Thesedataarenecessarytoexpressbalanceorconservation lawsforenergyandsubstancesintermsofvariablesusedinsystemsmodeling,analysis, synthesis,thestagesterminatingsometimesatanoptimizationproblem(aftermakingaselection ofstatevariables,controls,andparameters).Infact,thermodynamicvariablesarefrequently stateand/orcontrolcoordinatesinsystemicoptimizations;moreover,somethermodynamic variablesortheirfunctionsmayconstituteperformancecriteriaofoptimization. Thermodynamicsmayalsohelptosetsellingpricesofchemicalsubstancesandthusinfluencethe formulationofparaeconomicoptimizationcriteria(thermoeconomicoptimizationofsystems).
Briefly,thebasicpurposeofthisbookistoachieveandinvestigateformulations,solvingtools, andsolutionsdescribingtheperformanceofselectedcomplexsystems,includingthose consideredfromthestandpointofapreassignedoptimizationcriterion(chemicalconversion, thermoeconomicaloreconomicalprofit,oratechnicalindex).
In Chapters1–3,cyberneticsandsystemtheoryaredefinedastwosisterdisciplines governedbygeneralsystemmethodology,andintroducecyberneticiansandsystemexperts: researchersworkinginsystemstheory,scientistswhobyassumptionapplytheirbasicobjective ofbuildinggeneral,domain-independentsystemicmodels,inoppositiontotraditional scientistswhofocusonapplicationscomingfromvariousspecificdisciplines(chemistry, economics,thermodynamics,patternrecognition,etc.).
Furtherchaptersinvestigatevariouscomplexsystemsastheydifferintheirstructureand properties. Chapter4 isdevotedtosystemsofneuralnetworksandtheirapplicationfor emissionpredictionofpollutants. Chapter5 characterizesindetailcomponentsofsystem designwhichinvolves,insequence,modeling,analysis,synthesis,andoptimization,oftenwith adaptivecontrols. Chapter6 focusesonsystemsofenergyengineeringwithafewexcursionsto ecology. Chapter7 offersarigorousmathematicaltreatmentofoptimaldynamicsinboth continuousanddiscretesystemsgovernedbyordinarydifferentialequations,anddiscusses nonclassicaloptimalsolutionsstemmingfromtheuseofthedynamicprogrammingmethod. Chapter8 focusesonoptimizationofchemicallycomplexsystemswithcatalystdecayand regeneration. Chapter9 dealswithdiversecasesofcomplexdynamicsandthermodynamics, andincludesdecision-makingprocesseswithineconomicsystemsanalyzedintermsofSimon’s conceptionofrationalityandMorecroft’sboundedrationality,bothcasesportrayingsituations whendecisionsaremadebyindividuals.
Systemoptimization,describedbrieflywithmathematicsin Chapters3–6and8,offersaformal wayofassuringthebestinterventionintoacomplicatedreality,eitherbyprovidinglimiting valuesofcertainquantities(extremumpower,minimumcost,maximumyield,etc.)orby findingeconomicallyoptimalsolutions(optimaltrajectoriesandoptimalcontrols).These solutionsensureoptimalfeasibleprofitsorcostsattributedtoeconomicalorexergy-economical models.Optimalsolutions,alsocalled“bestsolutions,”areobtainedbycalculations applyingsuitablecomputationalalgorithms.Thecorrespondingcomputerprogramsusethese algorithms,eachleadingtooptimalsolutioninitsownway.Resultsofoptimization calculationsincludeoptimaltrajectoriesandcontrolsusuallyindiscreteforms(discrete representationoftheoptimizationsolution).
ThisbookisintendedtosupplementthevolumewrittenbySieniutyczandJezowskititled Energy OptimizationinProcessSystems,Elsevier,Oxford,2009anditssecondandthirdeditions bothtitled EnergyOptimizationinProcessSystemsandFuelCells,Elsevier,Oxford,2013and 2018.Inthesebooks,theauthorsdefinedandinvestigatedlimitsofenergyandpowerforvarious deterministic,power-yieldandmechanical-energy-yieldsystems,importantinchemicaland mechanicalengineering.
Thecontentsofthebookextendthepreviouslytreatedcontentsbyinclusionofselforganizationissues,emergentproperties,economicandthermoeconomicsolutions, deactivationandregenerationofcatalysts,hierarchicaldecisionmodels,andotherfactors
characteristicofcomplexsystems.Ofspecialinterestsarelimitingsolutionsobtainedwith performancecriteriainvolvingthermoeconomic,environmental,and,occasionally,ecological terms.Thermodynamicbehaviorofsystemsisinvestigatedintermsoffinite-rateprocesses withheat,work,andmasstransfer,occurringinapparatusesoffinitedimension.Analysesof complexchemicalsystemsfocusonheterogeneouscatalyticreactors,deactivatingcatalysts andcatalystregenerators.Optimizationapproaches,occasionallyinthespiritoffinite-rate thermodynamics,arebasedontheconditionthatinordertomaketheresultsofthermodynamic analysesusableinengineeringitisthethermodynamiclimitorathermoeconomiclimit,notthe maximumofthermodynamicefficiency,whichmustbeovercomeforprescribedprocess requirements.
Notsurprisingly,systemsrequiringdeterminationofpowerorenergylimits,i.e.,practical powergenerators,treatedindetailinthepreviousbooksofthepresentauthor,areonlybriefly mentionedhereassystemsinwhichtheoptimalcontroltheoryservestodetermineoptimal inputsofdrivingenergyordrivingsubstance.Theyarecontrolsystemsofheatpumptype, enginetype,oraseparatortypewhichareassumedtoutilizethelow-gradeheatorexergyof transferredheatandmass.Linkswithexergydefinitioninreversiblesystemsandclassical problemsofextremumworkarerediscoveredinthesesystemsinthecontextofreversible problemsofmaximumpower.Ontheotherhand,moreattentionisdevotedinthebookto optimizationofmultilevelcontrolsystemswithdecayingcatalystsandcatalystregenerators.
Thebookhassomeuniquefeaturesofrelatedbenefittothereader,inviewofstilldemanded literatureinformationonsolutionsofpracticaloptimizationproblems.Thebookextendsthe familyofpreviouslytreatedoptimizationproblemsbyinclusionofeconomicand environmentalissues,deactivationandregenerationofcatalysts,andotherfactorsappropriate forusingthermodynamicmodelsandmethodsofthermoeconomicoptimization.
Theliteratureofoptimizationsinchemicalandeconomicalworldskeepsgrowing,sothat efficientliteraturesearchesarestillnecessary.Thebookisintendedasacollectionofchapters addressedtoactivelyworkingscientistsandstudents(bothundergraduatesandgraduates).
Associatedprofessionalsare:chemicalengineers,economists,environmentalengineers, controlengineers,thermalengineers,solarsystemengineers,andsomeothers.Theauthors offerbasicallyatextbookequippedinthefeatureofareferencebook.Becauseofabundanceof literaturediscussionandcitationofnumerousreferences,thebookshouldconstituteavaluable andhelpfulreferencevolumeforanyreader,includingreadersemployedinindustriesand universities.Becauseofthetextbookpropertyoftheproposedvolume,namesandlevelsof appropriatecoursesarelistedbelow.Thebookcanbeusedinschools,libraries,industries,and internetcentersasadirectoryofguidedtourdescribedinthebookchapters,eachtour representingaresearchproblem.
Onecanask:Whattypeofknowledgedoreadersneedbeforereadingthebook?Thebookapplies analyticalreasoning,andtransferstothereaderareasonableamountofanalyticalmathematics.
Therefore,theknowledgeofelementaryanddifferentialcalculusismandatory.Basic equationsofoptimalcontrol(Pontryagin’smaximumprincipleandthecorresponding optimizationtheory)shouldbetherequirementonlywhenreading Chapters7and8. Since,however,thesatisfactionofthisconditionmightbedifficulttothegeneralreader, Chapter12ofSieniutycz’sandSzwast’s2018book OptimizingThermal,Chemicaland EnvironmentalSystems offersasimple,synthesizingtextonPontryagin’smaximumprinciple andrelatedcriteriaofdynamicoptimization.Becauseofthepresenceoftheabovetheoretical information,itisnotassumedthatusingothersourceswillbenecessary.Inthemostadvanced examples,completeanalysesaredevelopedtoachievesolutionsenablingverbaldescriptions andsubsumingofthediscussedproblems.
Anotherquestionis:Whatshouldthereadersgain(academically/professionally)fromthereading ofthebook?Whenthevolumeisusedasatextbook,itcanconstituteabasicorsupplementary textinthefollowingcoursesconductedinengineeringdepartmentsoftechnicaluniversities:
• Technicalthermodynamicsandindustrialenergetics(undergraduate)
• Chemicalreactionengineering(undergraduate)
• Alternativeandunconventionalenergysources(graduate)
• Catalystdecayandoptimalcatalystregeneration(graduate)
• Complexityandcomplexsystemstheory(graduate)
• Economicmodelsinengineering(graduate)
Havingreadthebook,thereaderswillgainthenecessaryinformationonwhathasbeen achievedtodateinthefieldofcomplexityandcomplexsystems;whatnewresearchproblems couldbestated;orwhatkindoffurtherstudiesshouldbedevelopedwithinspecialized optimizationsofthediscussedcases.Itisexpectedthattheinformationcontainedinthebook willhelptoimprovetechnicalskillsofthereader.Thisbookisespeciallyintendedtoattract graduatestudentsandresearchersinengineeringdepartments(especiallyinchemical, mechanical,material,andenvironmentalengineering).Theauthorhopesthatthebookwillalso beahelpfulsourcetoactivelyworkingeconomists,engineers,andstudents.
Finally,weliketolistotherrelatedbooksthatcantargetasimilaraudiencewiththistypeof content.Elsevierhasrecentlypublishedthefollowingthermodynamicallyorientedbooks:
VariationalandExtremumPrinciplesinMacroscopicSystems (Ed.byS.Sieniutycz andH.Farkas,Elsevier,Oxford,2000).
EnergyOptimizationinProcessSystems (byS.SieniutyczandJ.Jez ˙ owski,Elsevier, Oxford,2009).
EnergyOptimizationinProcessSystemsandFuelCells (byS.SieniutyczandJ.Jezowski, Elsevier,Oxford,2013(2nded.)).
ThermodynamicApproachesinEngineeringSystems (byS.Sieniutycz,Elsevier, Oxford,2016).
OptimizingThermal,ChemicalandEnvironmentalSystems (byS.SieniutyczandZ. Szwast,Elsevier,Oxford2018).
EnergyOptimizationinProcessSystemsandFuelCells (byS.SieniutyczandJ.Jezowski, Elsevier,Oxford,2018(3rded.)).
Readingthisbookon ComplexityandComplexThermoeconomicSystems willprovidethe opportunityfortreatingalltheabove-mentionedbooksbecauseoftheirunityofteachingstyle asateachingcluster.
Ourfutureplansinvolvethepublicationofthenewtitle: ComplexityandComplex ChemoelectricSystems,themanuscriptsubmissionpredictedinDecember2021.
Acknowledgments
Theauthorstartedhisresearchandcollectingscientificmaterialsonsystemtheoryand complexityprinciplesduringhis2001stayattheChemistryDepartmentofTheUniversity ofChicagoandthenwhilelecturingonacourseonthesystemstheoryforstudentsofFaculty ofChemicalEngineeringattheWarsawUniversityofTechnology(WarsawTU).Apartof suitablematerialswasobtainedintheframeworkoftwonationalgrants,namelyGrant3T09C 02426fromthePolishCommitteeofNationalResearch(KBN)andtheHungarianOTKA GrantT-42708,thelatterincooperationwithHenrikFarkasoftheDepartmentofPhysicsatthe BudapestUniversityofTechnologyandEconomics.Inpreparingthisvolume,theauthor receivedhelpandguidancefromMarekBerezowski(FacultyofEngineeringandChemical Technology,CracowUniversityofTechnology),AndrzejZiębik,(SilesianUniversityof Technology,Gliwice),AndrzejB.Jarzębski(InstituteofChemicalEngineeringofPolish AcademyofScienceandFacultyofChemistryattheSilesianTU,Gliwice),Elz ˙ bietaSieniutycz (UniversityofWarsaw),LingenChen(NavalUniversityofEngineering,Wuhan,PRChina), ZbigniewSzwast,andPiotrKuran(FacultyofChemicalandProcessEngineeringatthe WarsawUniversityofTechnology).TheauthorisalsosincerelygratefultoPiotrJuszczyk (WarsawTU)forhiscarefulandcreativeworkinmakingallnecessaryartworksforthisbook. Animportantpartofpreparinganybookistheprocessofreviewing,thustheauthorisvery muchobligedtoallresearcherswhopatientlyhelpedhimtoreadthroughsubsequentchapters andwhomadevaluablesuggestions.Theauthor,furthermore,owesadebtofgratitudetohis studentswhoparticipatedandlistenedtohislecturesonsystemsengineeringintheperiod 2010–16.Finally,appreciationsalsogotoAnitaKoch,Elsevier’sAcquisitionEditor,and thewholebook’sproductionteaminElsevierfortheircooperation,help,patience,and courtesy.
Systemssciencevscybernetics
1.1Generalsystemstheory
Generalsystemstheory(GST)isascienceinvestigatinggenerallawsforarbitrarily complexarrangements—“systems”—whichconstitutefunctionalintegrities.Theoriginof thegeneralsystemstheoryisassociatedwiththepublicationin1928ofaseminalbook (VonBertalanffy,1928,1968)titled KritischeTheoriederFormbildung,authoredbyeminent AustrianbiologistandphilosopherLudwigvonBertalanffy(1901–71).
Generalsystemstheory(GST)islinkedwithcyberneticsandinformationtheory.Rigorous (axiomatic)mathematicalformulationforGSTwasprovidedbyMesarovicandhis collaborators(Mesarovic,1964; MesarovicandMacko,1970; MesarovicandTakahara,1975, 1988),whereasimportantcontributionstodevelopmentsofsystemstheoryweremadebyG.J. Klirinthefieldofcomputermethodsofsolvingvarioussystemicproblems(Klir,1969,1972, 1981,1985,1992; KlirandFolger,1987)andJ.G.Millerinthefieldoflivingsystemstheory (Miller,1978).
Themosttypicalingredients(components)ofthesystemstheoryinclude:basicdefinitions, systemthinking,systemtopologies,lifecycles,systemperformance,conceptualdesign,current stateevaluations,relatedsciences,solvingmethods,creativesolutions,systemsynthesis, systemanalysis,optimization,solutionassessment,virtualoptimizing,systemengineering,and evaluationofknowledgeineconomyandsociety.Contentsofuniversitycoursesusually involve:thesignificanceofpropermodelingandtheroleofidentificationandcontrolaspects forsystemsofvariousstructure.Theseissuesareanalyzedandtheimportanceofcomputersin applicationsisevaluated.
1.2Cyberneticsandsystemsscienceinacademics
Thebasicconceptsofcyberneticshaveproventobeverypowerfulinavarietyofdisciplines: computerscience,management,sociology,biology,thermodynamics,etc.Cyberneticsand systemssciencelinktheabstractionofphilosophyandmathematicswiththeconcretenessof (dealingwith)thetheoryandmodelingofrealworldsystems.Asexemplarilyinterdisciplinary sciences,cyberneticsandsystemsscienceworkbetweenandamongrudimentarydisciplines, usuallypairwise,butoccasionallyacrossmorethantwokindsofsystems.
ComplexityandComplexThermo-EconomicSystems. https://doi.org/10.1016/B978-0-12-818594-0.00001-5 # 2020ElsevierInc.Allrightsreserved. 1
Somerecentapproacheshavetheiroriginsinideasandconceptsproposedbyscientistsmany yearsago:forexample,neuralnetworks,artificialintelligence,human-machineinterfaces, organizedtherapies,etc.Intheseapproaches,themajorityofbasicconceptsandproblemshave alreadybeenformulated,mainlyintheperiodofyears1940–80,bycyberneticianssuchas Von Bertalanffy(1928,1968), Wiener(1948), Ashby(1952), Boulding(1978),Forrester(1961), VonFoerster(1979), VonNeumann(1958), McCulloch(1965),and Pattee(1973).
Sincetheirfounding,cyberneticsandsystemssciencehavestruggledtoachievealevelof respectabilityintheacademicsociety.Cyberneticiansespeciallyhavefounditdifficulttofind theirhomesinacademicinstitutionsortocreatetheirown.Presently,anumber,perhapsstill insufficient,ofacademicprogramsincyberneticsandsystemsscience(CSS)exist,andthose workinginthenewdisciplinesdescribedseemnottoalwaysremembertheircybernetic predecessors.
Whatisthereasonthattheprogressinthepopularityofcyberneticsissoslow?Thedifference betweencyberneticiansandresearchersinthepreviouslymentionedareasisthat“theformer stubbornlysticktotheirobjectiveofbuildinggeneral,domainindependenttheories,whereas thelatterfocusonveryspecificapplications,suchas:expertsystems,psychotherapy, thermodynamics,patternrecognition,etc. Generalintegrationoftheformerresearchersis quiteabstract,henceitisnotsufficientlyeasytobereallyappreciated”(Joslynand Heylighen,1992).
Asacommoninterdisciplinaryfield,cyberneticsandsystemsscience(CSS)offerscommon conceptsusedinmultipletraditionaldisciplinesandattemptstoachievealogicallyconsistent unificationbyfindingcommontermsforsimilarconceptsinthesemultipledisciplines.Thus, CSSunifiesindividualconcepts,theories,andterminologiesinaspecificdisciplinedirected towardgeneral,andperhapsidiosyncratictools(usages).Thesenewconceptualcategoriesmay notberecognizabletothetraditionalresearchers,ortheymayfindnoreasonintheuseofthe generalconcepts(JoslynandHeylighen,1992).
Clearly,theproblemofbuildingaglobaltheoryismuchmorecomplexthananyofthemore down-to-earthgoalsofthefashionableapproaches(JoslynandHeylighen,1992).Butwemay alsosaythatthegeneralityoftheproblemisdangerousinitselfifitleadstobeing“stuck”in abstractionswhicharesofarremovedfromeverydayworldthatitisdifficulttousethem, interactwiththem,ortestthemonconcreteproblems;inotherwords,“togetafeelforhowthey behaveandwhattheirstrengthsandweaknessesare”(JoslynandHeylighen,1992).
Althoughtherearemanyexceptions,researchersincyberneticsandsystemssciencetendtobe trainedinatraditionalspecialty(likebiology,management,orpsychology)andthencometo applythemselvestoproblemsinotherareas,perhapsasingleotherarea.Thus,theirexposureto cyberneticsandsystemsscienceconceptsandtheorytendstobesomewhat adhoc andspecific tothetwoorthreefieldstheyapplythemselvesto(JoslynandHeylighen,1992).However,this
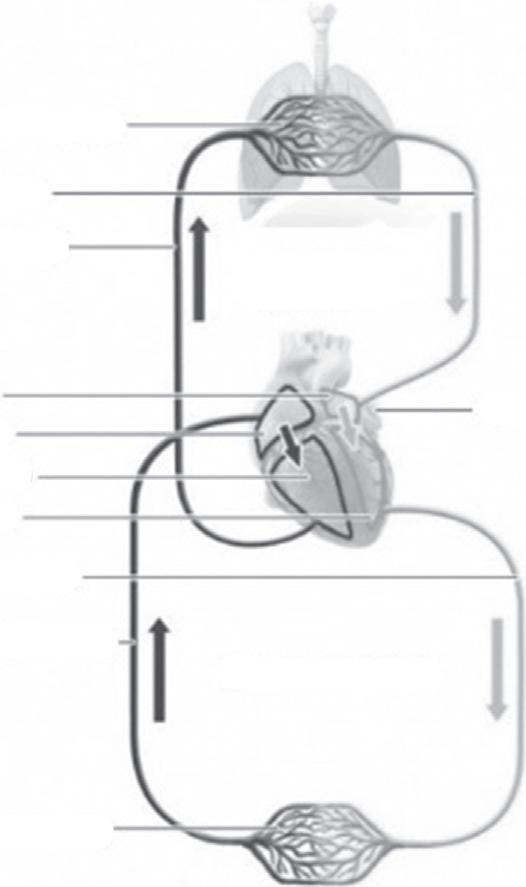
Capillaries in the lungs
Pulmonary vein
Pulmonary artery
Left atrium
Right atrium
Right ventricle
Left ventricle
Aorta (main artery)
Vena cava (main vein)
circulation
Capillaries in the body
Red: Oxygen-rich blood
Blue: Oxygen-poor blood
Thehumancardiovascularsystem.
doesn’tmeanthatthetremendousresearchrecordandgreatachievementsoflastyears (especiallythoseinbiologyafterthediscoveryofDNA)arenotappreciatedenough.Rather,a muchlongerperiodisexpectedforinclusionofbasicbiologicalandbiochemicalsystemsinto thegeneralschemeofcyberneticsandsystemsscience(VoetandVoet,1995; Menche,2016; Schmidtetal.,2017). Fig.1.1,whichschematizesthehumancardiovascularsystem,isan exampleofaverylargenumberofcomplexbiologicalsubsystemsfoundinlivingorganisms.
Thebloodcirculatorysystem(cardiovascularsystem)consistsoftheheartandthebloodvessels runningthroughtheentirebody.Thearteriescarrybloodawayfromtheheart;theveinscarryit backtotheheart.Thereisn’tonlyonebloodcirculatorysysteminthehumanbody,buttwo, whichareconnected:Thesystemiccirculationprovidesorgans,tissues,andcellswithbloodso thattheygetoxygenandothervitalsubstances.Thepulmonarycirculationiswherethefresh oxygenwebreatheinenterstheblood.Atthesametime,carbondioxideisreleasedfromthe blood(Menche,2016; Schmidtetal.,2017).
1.3Relationtootherdisciplines
Ideasrelatedtothedomainofcyberneticsandsystemsarefirstlyusedintheemerging“sciences ofcomplexity,”alsocalled“complexadaptivesystems,”studyingselforganizationand heterogeneousnetworksofinteractingentities(e.g.,theworkoftheSantaFeInstitute,
Fig.1.1
JoslynandHeylighen,1992),and,secondly,inanassociatedresearchinthenaturalsciences suchasfar-fromequilibriumthermodynamics,stabilitytheory,catastrophetheory,chaos,and dynamicalsystems.Anexampleisabifurcationdiagramofthestabilitytheory, Fig.1.2,which showshowthechangeofthecontrolparameterCinfluencesthechangeofthestability propertiesofthesystem.
Athirdstrandisconstitutedbydifferenthigh-levelcomputingapplicationssuchasartificial intelligence,neuralnetworks,man-machineinteraction,andcomputermodelingand simulation.
Unfortunately,fewpractitionersintheserecentdisciplinesseemtobeawarethatmanyoftheir conceptsandmethodshavebeenproposedandusedbycyberneticiansformanyyears(Joslyn andHeylighen,1992).Subjectslikecomplexity,selforganization,connectionism,and
Bifurcationdiagramshowinghowthestatevariable X isaffectedwhenanarbitrarycontrolparameter variesalongthehorizontaldirection:theuniquesolution(a),thethermodynamicbranchlosesits stabilityatthepointwherethecurvilinearboundarylinetouchestheverticalstraightlineseparatinga uniquesolutionandmultiplesolutions.Atthisvalueofcontrolparameter,newbranchesofsolutions (b1, b2),whicharestableasimpliedbythisexample,aregenerated. BasedonNicolis,G.,Prigogine,I., 1989.ExploringComplexity.W.H.Freeman.p.72.
adaptivesystemshavealreadybeenextensivelystudied,inthe1940sand1950s,byresearchers likeWiener,Ashby,vonNeumann,andvonFoerster,andindiscussionforumslikethefamous JosiahMacymeetingsoncybernetics(Heims,1991).Somepopularizingbookson“thesciences ofcomplexity,”e.g., Waldroop(1993),seemtoignorethefact,creatingthefalseimpression thatworkoncomplexadaptivesystemsonlystartedinearnestwiththecreationoftheSantaFe Instituteinthe1980s(JoslynandHeylighen,1992).
1.4Whatarecyberneticsandsystemsscience?
Cyberneticsandsystemsscience(also“generalsystemtheory”or“system’sresearch”) constitutesasomewhatfuzzilydefinedacademicdomainwhichtouchesuponvirtuallyall traditionaldisciplines,frommathematics,technology,andbiologytophilosophyandsocial sciences.Itismorespecificallyrelatedtotherecentlydeveloping“sciencesofcomplexity,” includingartificialintelligence(AI),neuralnetworks(NN),dynamicalsystems,chaos,and complexadaptivesystems.Thehistoryof“sciencesofcomplexity”datesbacktothe1940sand 1950swhenthinkerssuchasWiener,vonBertalanffy,Ashby,andvonFoersterfoundedthe domainthroughaseriesofinterdisciplinarymeetings.
Systemstheoryorsystemsciencearguesthathowevercomplexordiversetheworldthatwe experienceis,wewillalwaysfinddifferenttypesoforganizationsinit,andsuchorganizations canbedescribedbyconceptsandprincipleswhichare independentfromthespecificdomain at whichwearelooking.Hence,ifweweretouncoverthesegenerallaws,wewouldbeableto analyzeandsolveproblemsinanydomain,pertainingtoanytypeofsystem.Thesystem approachdistinguishesitselffromthemoretraditionalanalyticalapproachbyemphasizingthe interactionsandconnectednessofdifferentcomponentsofasystem.
Althoughthesystemapproachinprincipleconsidersalltypesofsystems,inpractice,itfocuses onmorecomplexadaptive,self-regulatingsystemswhichwemightcall cybernetic (Heylighen etal.,1999).
Manyconceptsusedbysystemscientistscomefromcloselyrelatedapproachofcybernetics: information,control,feedback,communication,etc.Cybernetics,derivedfromtheGreek wordforsteersman(kybernetes ),wasfirstintroducedbythemathematicianWiener,asthe scienceofcommunicationandcontrolintheanimalandthemachine(towhichwenowmight add:insocialsocietyandinindividualhumanbeings).ItgrewoutofShannon’sinformation theory,whichwasdesignedtooptimizethetransmissionofinformationthrough communicationchannelsandthefeedbackconceptusedinengineeringcontrolsystems.See variousschemesofacommunicationchannelsin ShannonandWeaver(1949) orotherbooks ontheinformationtheory.Inthepresentincarnationof“secondordercybernetics,”the emphasisisonhowobserversconstructmodelsofthesystemswithwhichtheyinteract(c.f. constructivism).
Infact,cyberneticsandsystemstheorystudyessentiallythesameproblem.Theproblemis organizationindependentofthesubstrateinwhichitisembodied.Insofarasitismeaningful tomakeadistinction,systemstheoryisfocusedmoreonthestructureofsystemsandtheir models,whereascyberneticsisfocusedonhowsystemsfunction,thatistosayhowthey controltheiractionsandhowtheycommunicatewithothersystemsorwiththeirown components.Sincestructureandfunctionofasystemcannotbeunderstoodinseparation,itis clearthatcyberneticsandsystemstheoryshouldbeviewedastwofacetsofasingleapproach ( Heylighenetal.,1999 ).
Thisinsighthasresultedinthetwodomainsalmostmerginginpractice:many,ifnotmost,of thecentralassociations,journals,andconferencesinthefieldincludebothterms,systemsand cybernetics,intheirtitle.Inspiteoftheabsenceofstrictsubdivisions,though,thefieldisrather fragmentedwithmanydifferentapproaches,similarinsomerespects,differentinothers, existingside-by-side(Heylighenetal.,1999).
Many“schools,”suchasautopoieticsystems,anticipatorysystems,livingsystems,viable systems,orsoftsystems,areassociatedwithaparticulartheoristorthinker,respectively MaturanaandVarela(1987), Rosen(1970), Miller(1978), Beer(1975), Turchin(1997).Asa result,occasionally,thecyberneticsandsystemsdomainstilllacksclearfoundations.Yet,the authorsofthePrincipiaCyberneticaProject(Heylighenetal.,1999),believethat“the commonalitiesaremuchlargerthanthedifferences,”and,therefore,itisworthwhileattempting tointegratedifferentapproachesinacommonconceptualnetwork.
Whilethepresentchaptercitesmanystatementsdiscussedinthetextof Heylighenetal.(1999), someimportantissuescontainedthereinwereomittedforbrevity.Thispertains,inparticular,to informationaboutoutsideinternetlinks.Someverygood,readableintroductorybookson cyberneticsandsystemscanbedownloadedfromthePrincipiaCyberneticaLibrary(Heylighen etal.,1999).Togetherwithadictionaryandbibliographyofbasicbooksandpapers,thisshould besufficientforatleastanintroductorycourseinthedomain.
Optimizationofenergysystemsiscoveredinthreeeditionsofthebookwrittenbythepresent authorwithJacekJez ˙ owski(SieniutyczandJez ˙ owski,2009,2013,2018);forabroader perspective,acomprehensivereviewofvariousthermodynamicapproachestopractical systemsshouldbehelpful(Sieniutycz,2016).Occasionallyusefularesourcesandlinksto diversearticles,books,andwebsites,whichprovidefurtherinformationandreferences.In particular,diversesourcesareessentialforunderstandingbasicproblemsofselforganization.
Summingup,inthisintroduction,typicalingredientsofthesystemstheoryarespecifiedandits linkwithcyberneticsispointedout.Generalsystemstheory(GST)isdefinedasascience investigatinggenerallawsfortopologicallycomplicatedarrangements—“systems”—which constitutethefunctionalintegrities.Thisintroductorychapterprovidesthereaderwithbotha historicaloutlineandbriefstate-of-artoftheGSTawellasthelistofthescientistswho
contributedtothebirthofthefieldandtothedevelopmentofitsmathematicalbackgrounds(in particulartothedevelopmentofcomputermethodsandindicationoftheirapplicativepotential).
References
Ashby,R.,1952.DesignforaBrain.Wiley,NewYork. Beer,S.,1975.PlatformforChange.Wiley,Chichester. Boulding,K.,1978.Ecodynamics.Sage,BeverlyHills. Forrester,J.W.,1961.IndustrialDynamics.AppendixE.MITPress,Cambridge,MA. Heims,S.,1991.TheCyberneticsGroup.MITPress,Cambridge,MA.
Heylighen,F.,Joslyn,C.,Turchin,1999.WhatareCyberneticsandSystemsScience? http://pespmc1.vub.ac.be/ CYBSWHAT.html
Joslyn,C.,Heylighen,F.,1992.CyberneticsandSystemsScienceinAcademics. http://pespmc1.vub.ac.be/ CYBSACAD.html.
Klir,G.,1969.AnApproachtoGeneralSystemsTheory.VanNostrand,NewYork. Klir,G.(Ed.),1972.TrendsinGeneralSystemsTheory.Wiley,NewYork. Klir,G.,1981.Specialissueonreconstructibilityanalysis.Int.J.Gen.Syst.7(1),1–107. Klir,G.,1985.ArchitectureofSystemsProblemSolving.Plenum,NewYork. Klir,G.,1992.FacetsofSystemsScience.Plenum,NewYork.
Klir,G.,Folger,T.,1987.FuzzySets,Uncertainty,andInformation.PrenticeHall,EnglewoodCliffs. Maturana,H.R.,Varela,F.,1987.TheTreeofKnowledge—TheBiologicalRootsofHumanUnderstanding. ShambalaPublications,Boston. McCulloch,W.,1965.EmbodimentsofMind.MITPress,Cambridge,MA. Menche,N.,2016.BiologieAnatomiePhysiologie.UrbanundFischer,Munich(refertoFig.1.1).
Mesarovic,M.D.,1964.ViewsofGeneralSystemsTheory.Wiley,NewYork.
Mesarovic,M.D.,Macko,D.,1970.TheoryofHierarchicalMulti-LevelSystems.AcademicPress,NewYork. Mesarovic,M.D.,Takahara,Y.,1975.GeneralSystemsTheory:MathematicalFoundations.AcademicPress,New York.
Mesarovic,M.D.,Takahara,Y.,1988.AbstractSystemsTheory.Springer-Verlag,Berlin.
Miller,J.G.,1978.LivingSystems.McGrawHill,NewYork.
Pattee,H.(Ed.),1973.HierarchyTheory.GeorgeBraziller,NewYork. Rosen,R.,1970.DynamicalSystemsTheoryinBiology.Wiley,NewYork. Schmidt,R.,Lang,F.,Heckmann,M.,2017.PhysiologiedesMenschen:MitPathophysiologie.Springer,Berlin (refertoFig.1.1).
Shannon,C.E.,Weaver,W.,1949.TheMathematicalTheoryofCommunication.TheUniversityofIllinoisPress, Urbana.
Sieniutycz,S.,2016.ThermodynamicApproachesinEngineeringSystems.Elsevier,Oxford.
Sieniutycz,S.,Jez ˙ owski,J.,2009.EnergyOptimizationinProcessSystems,firsted.Elsevier,Oxford. Sieniutycz,S.,Jezowski,J.,2013.EnergyOptimizationinProcessSystemsandFuelcells,seconded.Elsevier, Oxford.
Sieniutycz,S.,Jezowski,J.,2018.EnergyOptimizationinProcessSystems,thirded.Elsevier,Oxford. Turchin,V.,1997.PhenomenonofScience.ColumbiaUniversity,NewYork. Voet,D.,Voet,J.G.,1995.Biochemistry,seconded.Wiley,NewYork. VonBertalanffy,L.,1928.KritischeTheoriederFormbildung.Gebr€ uderBorntraeger,Berlin. VonBertalanffy,L.,1968.GeneralSystemsTheory.GeorgeBraziller,NewYork. VonFoerster,H.,1979.In:Kripendorf,K.(Ed.),CyberneticsofCybernetics.GordonandBreach,NewYork. VonNeumann,J.,1958.ComputerandtheBrain.YaleUniversity,NewHaven. Waldroop,M.M.,1993.Complexity:TheEmergingScienceattheEdgeofOrderandChaos.(APopularizingBook on“TheSciencesofComplexity”).VikingBooks,London. Wiener,N.,1948.CyberneticsorControlandCommunicationintheAnimalandMachine.MassachusettsInstitute ofTechnologyPress,Cambridge,MA.
Furtherreading
Mittleton-Kelly,E.,2003.Tenprinciplesofcomplexity.In:ComplexSystemsandEvolutionaryPerspectiveson Organizations.Elsevier,Oxford,ISBN:0-08-043957-8.
Nicolis,G.,Prigogine,I.,1989.ExploringComplexity.W.H.Freeman.p.72. Pschyrembel,2017.KlinischesW€ orterbuch.DeGruyter,Berlin.
Selforganizationandcomplexity
2.1Whatisselforganization
Selforganizationisaparticularprocessinwhichtheorganizationofasystem,orits susceptibilitytoaconstrainingaction,spontaneouslyincreases,andthisincreasefollows withoutcontrolofanyexternalforcesoftheenvironment.Onemayregardselforganizationasa sortofevolutionprocessinwhichtheeffectoftheexternalworld(environment)issosmallthat itmaybeignored.Thedevelopmentofnew,complexstructurestakesplaceprimarilyinand throughthesystemitself.Inthetextbelow,thefollowingproblemswhichaccompany selforganizationareconsidered:definitionofselforganization,significanceofselforganization andcomplexityinthenaturalsciences,selforganizationprincipleasapossiblefourthlawof thermodynamics,theroleofselforganizationintheemergenceandthearchitectureof complexity,andapossiblelinkwithmaximumpowerorenergydissipationprinciplesin thermodynamics.Currently,duetotheeffectiveuseofcomputers,itispossibletoobtainmany numericalsolutionstocomplexselforganizationproblems.However,inordertoensureexplicit selforganizationeffects,asuitableprocessrequiressubtleassumptionsforratefunctionsand constrainingsets.Nondifferentiablesolutionstotheequationsgoverningselforganizationmay occur.Ineffect,selforganizationcanbeunderstoodonthebasisofthesamevariationand naturalselectionprocessesasother,environmentallypropelledevolutionprocesses.Yet, selforganizationofacomplexsystemoftenrepresents“holisticdynamics”(Crossand Hohenberg,1993; Heylighen,1997; CempelandNatke,1996; Cempel,2008).RayleighBenardconvectionprovidesasimple,classicalexampleofselforganization.
Theincreaseofselforganizationcanbemeasuredmoreobjectivelybyadecreaseofthe system’sstatisticalentropy.Thispropertycanbebrieflysummedupbytheso-calledPrinciple ofAsymmetricTransitions(Heylighen,1992),whichstatesasfollows:Atransitionfroman unstableconfigurationtoastableoneispossible,buttheconverseisnot.Thisprincipleimplies afundamentalasymmetryinevolution:onedirectionofchange(fromunstabletostable)is morelikelythantheoppositedirection.Thegeneralized,“continuous”versionoftheprinciple isthefollowing:TheprobabilityoftransitionfromalessstableconfigurationAtoamorestable oneBislargerthantheprobabilityfortheinversetransition:P(A ! B) > P(B ! A)(holdsunder theconditionP(A ! B) 6¼ 0).
Asimilarprinciplewasproposedby Ashby(1962) inhis“principlesofself-organizing systems”:“Westartwiththefactthatsystemsingeneralgotoequilibrium.Now,mostofa system’sstatesarenonequilibria.Soingoingfromanystatetooneoftheequilibria,thesystem isgoingfromalargertoasmallernumberofstates.Inthisway,itisperformingaselection,in thepurelyobjectivesensethatitrejectssomestates,byleavingthem,andretainssomeother state,bystickingtoit.”
Selforganizationisusuallytriggeredbysmallperturbationsaccompanyinginternalvariation processes,usuallycalled“fluctuations”or“noise.”Thephenomenonoftheseprocesses yieldingaselectiveretainedorderedconfigurationiscalledthe“orderfromnoise”principleby vonFoerster(1949,1958,1961,2002), vonFoersterandPask(1961), vonFoersteretal.(1960), andby Prigogine(1947,1955) and GlansdorffandPrigogine(1971) the“orderthrough fluctuationsmechanism.”BoththesetermsmayberegardedasspecialcasesofwhatHeylighen proposestocallthe principleofselectivevariety (Heylighen,1997).
Thisreductioninthenumberofreachablestatessignifiesthatthevariety,andhencethe statisticalentropy,ofthesystemdiminishes.Itisbecauseofthisincreaseinneg-entropyor organizationthat Ashby(1962) callstheprocessselforganization.Buthowdoesthisfitinwith the2ndlawofthermodynamicswhichstatesthatentropyinclosedsystemscannotdecrease? Theeasywayoutistoconcludethatsuchaself-organizingsystemcannotbeclosedandmust loseentropytoitsenvironment(vonFoersteretal.,1960).
Adeeperunderstandingcanbereachedbygoingbackfromthestatisticaldefinitionofentropy tothethermodynamicone,intermsofenergyorheat.Energyisdefinedasthecapacitytodo work,andworkingmeansmakingchanges,thatistosayexertingvariation.Hence,energyinput canbeviewedaspotentialvariation.Astableconfigurationisnotsubjecttovariation.Inorder todestroyastableequilibrium,youneedtoaddenergy,andthemorestabletheconfiguration, themoreenergyyouwillneed.Therefore,stabilityistraditionallyequatedwithminimal energy.
The1stlawofthermodynamicsstatesthatenergyisconserved.Asimpleinterpretationofthat lawwouldconcludethattheprincipleofasymmetrictransitionscannotbevalid,sinceit postulatesatransitionfromanunstable(highenergy)toastable(lowenergy)configuration.If energyisabsolutelyconserved,thenanunstableconfigurationcanonlybefollowedbyanother unstableconfiguration.Thisisthepictureusedinclassicalmechanics,whereevolutionis reversible,thatistosaysymmetric.Incidentally,thisshowsthattheprincipleofasymmetric transitionsisnottautological—thoughitmayappearself-evident—sinceaperfectlyconsistent theory(classicalmechanics)canbebuiltonitsnegation(Heylighen,1997).
Thisprincipleisagainequivalenttoanincreaseinredundancy,information,orconstraint:after theprocessisself-organized,thereislessambiguityaboutwhichstatethesystemisin.Aselforganizingsystem,whichalsodecreasesitsthermodynamicentropy,mustnecessarily(because
ofthesecondlawofthermodynamics)export(“dissipate”)suchentropytoitssurroundings, e.g.,totheambient,asexplainedbyvonFoerster(2002)andPrigogineandothers. Prigogine (1947,1955) and GlansdorffandPrigogine(1971) usedtheterm“dissipativestructures”to namesystemswhichcontinuouslyexportentropyinordertomaintaintheirorganization.
2.2Selforganizationandcomplexityinthenaturalsciences
AccordingtoHeylingen,selforganizationisusuallyassociatedwithnonlinearphenomenaof increasedcomplexityratherthanwitharelativelysimpleprocessofstructuremaintenanceby diffusion(Heylighen,1997).Alltheintricatephenomenaassociatedwithnonlinearity(limit cycles,chaos,sensitivitytoinitialconditions,dissipativestructuration,etc.)canbeunderstood throughtheinterplayofpositiveandnegativefeedbackcyclesinwhichsomevariationsor perturbationstendtoreinforcethemselves.
Animportantstrandofworkleadingtotheanalysisofcomplexevolutionsislaiddownby thermodynamics.IlyaPrigoginereceivedtheNobelPrizeforhisworkincollaborationwithother membersof“BrusselsSchool”aftershowingthatphysicalandchemicalsystemsfarfrom thermodynamicequilibriumtendtoself-organizebyexportingentropyandtoformdisequilibrium systemscalleddissipativestructures.BothPrigogine’sphilosophicalconsiderationsaboutthe newworldviewimpliedbyselforganizationandirreversiblechange(PrigogineandStengers, 1984)andhisscientificresearch(NicolisandPrigogine,1977,1989;Prigogine,1980)on bifurcationsand orderthroughfluctuations remainclassics,citedinverydiversecontexts.
Lotka-Volterraoscillations(Fig.2.1),Lorentzattractor(Fig.2.2),andtherollstreamlinesin Rayleigh-Benardconvection(Fig.2.3),werecrucialforthedevelopmentofthetheoryofselforganizingsystems.Thesemodelsshowedthatthecompetitionofdissipationanddampingwith restoringforcesleadstooscillationsandlimitcycles.Theearlyhistoryandthedebate surroundingoscillatingreactionscanbefoundinnumerousreferencessuchas Glansdorffand Prigogine(1971),NicolisandPortnow(1973),GrayandScott(1975,1990), Nicolisand Prigogine(1977,1979), NicolisandRouvas-Nicolis(2007a,b),andmanyothers.
Thesamebasicapproachmaybeusedformolecularcollisions,hydrodynamics,andchemicalor electrochemicalprocesses.Nonlinearmolecularmechanismgivesrisetocriticalpoints, instabilities,bifurcations,oscillations,chaoticbehavior,andlimitcycles(Figs.2.1and2.2).It leads,ingeneral,tovariousformsoforganization(Ebeling,1985;EbelingandKlimontovich,1984; Klimontovich,1986,1991,1982; FeistelandEbeling,1989; EbelingandFeistel,1982,2011).
FeistelandEbeling(1989) write:Oneofthemost(oreventhemostatall)strikingfeaturesin natureisthephenomenonofnaturalevolution.Sincealongtime,ithasattractedtheinterestof peopleandespeciallyofscientists,anduptoourdays,ithasnotlostthisattractivity.Itis impressivetoobservehowinthecourseofscientifichistorytheevolutionconceptinfluenced
Lotka-Volterramodelisaclassicalschemedescribinginteractionsbetweenpopulationsofpredators andpreys.Thetimevariabilityofthepopulationsofpredators(foxes)andpreys(rabbits)providesthe ecologicalinterpretationofthemodel.TheLotkadiagramshowsthegeneralcharacterofintegral curvesofhisequationwhichdescribesratio dX2/dX1 intermsof X1 and X2.Inthepositivequadrantof X1X2,thecurvesareclosed,containedentirelywithinthequadrant,andintersectingtheaxesof x1x2 orthogonally.Nearorigincurvesareverynearlyelliptical(Lotka,1920).
practicallyallbranchesofscience,replacingfinallytheoldviewoftheworldasastatic(or strictlyperiodic)building.
Thebiologicalworldwithfixedandunchangeablespeciescouldnotstandtheoverwhelming numberoffactssupportingDarwin’spictureofaflexible,continuouslychangingandadapting
Fig.2.1
Fig.2.2 Lorentzattractor.
Selforganizationandcomplexity13
Fig.2.3
SchematicpictureofRayleigh-Benardconvectionwithstreamlinesinanidealrollstate. BasedonCross, M.C.,Hohenberg,P.C.,1993.Patternformationoutsideofequilibrium.Rev.Mod.Phys.65(3),851–1125.
biosphereundertheselectionpressureofcompetitionandchangingenvironmentalconditions. Thecrystalsphereofheavenwithtwinklingstarspinnedonitwasreplacedbyanexpanding universefilledwithevolvinggalaxiesandsolarsystems.Andeventheseeminglyrigidearth crustwithcontinentsandoceanshasnowadaystobeseenasacomplexsystemofdriftingplates withcontinuedexchangeofmatterbetweenthesolidearthsurfaceandthefluidmantle.
Interestinglyenough,themostfundamentalnaturalscience,physics,dealingwiththefirst principlesthatgovernthemotionoftheworld,wasforalongtimeuntouchedbytheevolution ideasthatoccupiedmanyothersciences.Thissituationischangingnow.Itwasabreakthrough tounderstandthatevolvingsystemsareessentiallysystemsbeingfarfromthermodynamic equilibrium(GlansdorffandPrigogine,1971;Haken,1984; FeistelandEbeling,1989)andthat, undertheseconditions,thesecondlawofthermodynamicsnotatallstatesthedestructionofany existingstructure.
Ebeling(1983,1985)corroboratesbyexperimentsthetheoryofhydrodynamicturbulenceof Klimontovich(1982),whichyieldseffectiveturbulentviscosityasalinearfunctionofthe Reynoldsnumber.Thistheoryseemstobeabletodescribetheobservedeffectiveviscosityof vorticesand,aftermodifications,thefluidflowintubesuptoveryhighReynoldsnumbers.
Klimontovich(1986,1991)evaluatestheentropiesoflaminarandturbulentmotionswith respecttothevelocityofthelaminarflowandthevelocityoftheaveragedturbulentflow,for thesamevaluesoftheaveragekineticenergies.Heshowsthat,whentransitionoccursfrom laminarflowtoturbulentflow,theentropyproductionandentropyitselfdecrease.This indicatesthatthedisequilibriumphasetransitionfromlaminarflowtoturbulentflowtransfers thesystemtoamoreorderedstate.Healsoprovesthattheturbulentmotionshouldbethought ashavingalowertemperaturethanlaminarmotion.Applyinghistheoryofturbulence, Klimontovich(1991)examinesthelinkbetweentheturbulentmotionandthestructure ofchaos.
Klimontovich(1999)considersentropy,information,andrelativecriteriaoforderforstatesof opensystems.Hepointsoutthattwodefinitionsofthe“information”conceptareknowninthe theoryofcommunication.ThefirstdefinitioncoincidesinformwiththeBoltzmannentropy.
Thesecondonereferstothedifferencebetweenunconditionalandconditionalentropies. Klimontovichinvestigatestwokindsofopensystems.Thesystemsofthefirstkind,withzero valueofacontrollingparameter,areintheequilibriumstate.Thoseofthesecondkindare disequilibriumsystems.Inselforganizationassociatedwiththeprocessofescapingfromthe equilibriumstate,theinformationisincreased.Foropensystemsandallvaluesofthe controllingparameter,aconservationlawisprovedforthesumofinformationandentropywith allvaluesofcontrollingparameter.Klimontovich’s(1999)treatmentiscarriedoutonanumber of(classicalandquantum)examplesofphysicalsystems.Anexampleofamedical-biological systemisalsointroduced.
Ebeling(1983,1985)compareswithexperimentsthetheoryofhydrodynamicturbulenceof Klimontovich(1982),whichyieldseffectiveturbulentviscosityasalinearfunctionofthe Reynoldsnumber.Thistheorydescribestheobservedeffectiveviscosityofvorticesand,after modifications,thefluidflowintubesuptoveryhighReynoldsnumbers.
Ebeling(1985,2002)studiesaspecialclassofnonequilibriumsystemswhichallowstodevelop anensembletheoryofsomegenerality.Fortheseso-calledcanonical-dissipativesystems,the drivingtermsaredeterminedonlybyinvariantsofmotion.First,Ebelingconstructssystems whichareergodiconcertainsurfacesofthephaseplane.Thesesystemsmaybedescribedbya nonequilibriummicrocanonicalensemble,correspondingtoanequaldistributiononthetarget surface.Next,heconstructsandsolvesFokker-Planckequations.Inthelastpart,hediscussesa specialrealization:systemsofactiveBrownianparticles.Inconclusion,hisworkisdevotedto thestudyof“canonical”dissipativesystemswhicharepumpedfromexternalsourceswithfree energy.EbelingstartedhisworkfromtheHamiltoniantheoryforconservativemechanical systems.Inordertoextendtheknownsolutionsforconservativesystemstodissipativesystems, heusedageneraltheoryofcanonical-dissipativesystems.Heconstructedspecialcanonicaldissipativesystemswhosesolutionconvergestothesolutionoftheconservativesystemwith givenenergy,orotherprescribedinvariantsofmotion.Inthisway,hewasabletogenerate nonequilibriumstatescharacterizedbycertainprescribedinvariantsofmechanicalmotion.He postulatedspecialdistributionswhichareanaloguesofthemicrocanonicalensemblein equilibrium.Furtheron,hefoundsolutionsoftheFokker-Planckequationwhichmaybe consideredasanaloguesofthecanonicalequilibriumensembles.Ebelingproposedcalling thesedistributionscanonical-dissipativeensembles.Withthehelpofexplicitnonequilibrium solutions,hewasabletoconstructforcanonical-dissipativesystemsacompletestatistical thermodynamicswhichincludesanevolutioncriterionforthenonequilibrium.
EbelingandFeistel’s(2011) updatedbookonselforganizationandevolutionincludesareview ofmorerecentliterature.Itretainstheoriginalfascinationsurroundingthermodynamicsystems farfromequilibrium,synergetics,andtheoriginoflife.Whilefocusingonthephysicaland theoreticalmodelingofnaturalselectionandevolutionprocesses,thebookcoversindetail experimentalandtheoreticalfundamentalsofself-organizingsystemsaswellassuchselected
featuresasrandomprocesses,structuralnetworks,andmultistablesystems.Theauthorstake examplesfromphysics,chemistry,biology,andsocialsciences.Theresultisaresourcesuitable forstudentsandscientistsinphysicsandrelatedinterdisciplinaryfields,including mathematicalphysics,biophysics,informationscience,andnanotechnology.
Ideasof NicolisandPrigogine(1977) diffusedquicklytotheecologyandsoonreceiveditsown characteristicpicture.Prigogine’snameisbestknownforextendingthesecondlawof thermodynamicstosystemsthatarefarfromequilibriumandimplyingthatnewformsof orderedstructurescouldexistundersuchconditions.Prigoginecalledtheseforms“dissipative structures,”pointingoutthattheycannotexistindependentlyoftheirenvironment. Nicolisand Prigogine(1977) showedthattheformationofdissipativestructuresallowsordertobecreated fromdisorderinnonequilibriumsystems.Thesestructureshavesincebeenusedtodescribe manyphenomenaofbiologyandecology.
Entropyandentropylowering,incomparisontotheirequilibriumvalues,aregoodindicatorsof disequilibrium.EbelingandEngel-Herbert(1986)provethatentropydecreaseswithexcitation undertheconditionoffixedenergy.Theyalsoshowthatentropyloweringreferstothe contractionoftheoccupiedpartofthephasespaceduetotheformationofattractors.Excitation ofoscillationsinsolidsandturbulenceinliquidflowsserveasexamples.Theentropystatement formulatedbyKlimontovichisdiscussedintheturbulencecontext.Twoexamplesaregiven: (1)selfoscillationsofnonlinearoscillators,and(2)laminarandturbulentflowsintubes.
InspiredbyPrigogine’stheories,ErichJantshmadeanambitiousattempttosynthesize everythingwhichwasknownatthetime( Jantsh,1979)aboutself-organizingprocesses,from theBigBangtotheevolutionofsociety,intoanencompassingworldview.Thephysicist HermanHakenhassuggestedin1978thelabelofsynergeticsforthefieldwhichinvestigates thecollectivepatternsemergingfrommanyinteractingcomponents,astheyarefoundin chemicalreactions,crystalformations,orlasers.ANobellaureate,Eigen(1992),hasfocused ontheoriginsoflife,thedomainwherechemicalselforganizationmeetsbiologicalevolution. Heintroducedtheconceptof hypercycle,whichisanautocatalyticcycleofchemicalreactions containingothercycles,andof quasispecies,thefuzzydistributionofgenotypescharacterizing apopulationofquicklymutatingorganismsormolecules(EigenandSchuster,1979).
Themodelingofnonlinearsystemsinphysicshasledtotheconceptof chaos,thebehaviorofa deterministicprocesscharacterizedbyextremesensitivitytotheinitialconditionsof trajectories(Crutchfieldetal.,1986).Althoughchaoticdynamicsisnotstrictlyaformof evolution,itisanimportantaspectofthebehaviorofcomplexsystems.ThesciencejournalistJ. Gleickhaswrittenapopularhistoryandevolutionofthefieldinthebookoncellularautomata. Mathematicalmodelsofdistributeddynamicalprocessescharacterizedbyadiscretespaceand timehavewidelybeenusedtostudyphenomenasuchaschaos,attractors,andtheanalogy betweendynamicsandcomputationthroughcomputersimulation.Wolfram(2017)hasmadea fundamentalclassificationofthecriticalbehaviorofcontinuousmappings.Catastrophetheory
wasdevelopedbyThom(1975).Hisresultsserved,inparticular,thepurposeofmodelingthe continuousdevelopmentofdiscontinuousformsoforganisms,thusextendingthemucholder workbythebiologistThompson(1917).
AnotherFrenchmathematician,Mandelbrot(1983),hasfoundedthefieldoffractalgeometry, whichmodelstherecurrenceofsimilarpatternsatdifferentscalescharacterizingmostnatural systems.Suchself-similarstructuresexhibitpowerlawslikethefamousZipf’slawgoverning thefrequencyofwords.Bystudyingprocessessuchasavalanchesandearthquakes,Bakand Chen(1989a,b)haveshownthatmanycomplexsystemswillfreelyevolvetothecriticaledge betweenstabilityandchaos,wherethesizeofdisturbancesobeysapowerlawandlarge disturbancesarelessfrequentthansmallones.Thephenomenon,whichhecalledselforganizedcriticality,mayalsoprovideanexplanationfortheso-calledpunctuatedequilibrium dynamicsobservedinbiologicalevolution.
2.3Selforganization:Thefourthlawofthermodynamics?
ThetextbelowfollowswithsmallchangestheopinionofCharlesGurtinandDrewKerkhoff expressedin1996attheEcologicalComplexitySeminar,heldintheDepartmentofBiologyat theUniversityofNewMexico.
Thefollowingcriteriaforevaluationofnewtheoreticalconstructsinecologyaresuggestedby O’Neilletal.(1986):
1. Thetheorymustbeinternallyconsistent
2. Thetheorymustnotbeadoptedsimplybecauseofsuccessinotherfields
3. Thetheorymustagreewithknownpropertiesofecosystems
4. Thetheorymustbecapableofproducingnewandtestablehypotheses
Theabovecriteriaareabasisfortheevaluationof“complexitytheory”aswehavecometo understanditoverthecourseofnumerousdiscussions.Itmaybearguedthatselforganization liesatthebasisofcomplexityaswehavecometointerpretit.Forexample,itistheselforganizedorderofBernardcells(Chapter10)whichrendersthesystemcomplex.Itiswellknownthat,belowacriticaltemperature,thesystemsexhibitonlyuniformconduction.The systembecomesmoreattractivewhenselforganizationoccurs,andselforganizationrequires thatasystembeawayfromthethermodynamicequilibrium.Morowitz(1992)providesthe followingintuitiveexplanation:
Indeed,thereisastatement,sometimescalledthefourthlawofthermodynamicswhich statesthattheflowofenergyfromasourcetoasinkthroughanintermediatesystemorders thatsystem.Herethewordordermustbetakenasincreasedcomplexity.
BakandChen(1989a,b)extendthisnotionofthefourthlawbysuggestionthat“slowlydriven systemsnaturallyself-organizeintoacriticalstate.”Thisimpliesthat,indisequilibrium systems,criticalityandcomplexitymaybearuleratherthananexception(BakandChen,