https://ebookmass.com/product/applications-of-hypothesis-
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Applied Statistics for Environmental Science With R 1st Edition Abbas F. M. Alkarkhi
https://ebookmass.com/product/applied-statistics-for-environmentalscience-with-r-1st-edition-abbas-f-m-alkarkhi/
ebookmass.com
Introduction to Robust Estimation and Hypothesis Testing
4th Edition Rand Wilcox
https://ebookmass.com/product/introduction-to-robust-estimation-andhypothesis-testing-4th-edition-rand-wilcox/
ebookmass.com
Introduction to Robust Estimation and Hypothesis Testing
5th Edition Rand R. Wilcox
https://ebookmass.com/product/introduction-to-robust-estimation-andhypothesis-testing-5th-edition-rand-r-wilcox/
ebookmass.com
Morrey’s The Elbow and Its Disorders 5th Edition Bernard F. Morrey
https://ebookmass.com/product/morreys-the-elbow-and-its-disorders-5thedition-bernard-f-morrey/
ebookmass.com
Spinoza and Biblical Philology in the Dutch Republic, 1660-1710 Jetze Touber
https://ebookmass.com/product/spinoza-and-biblical-philology-in-thedutch-republic-1660-1710-jetze-touber/
ebookmass.com
The Fall of the Roman Republic: Roman History, Books 36-40 (Oxford World's Classics) Dio
https://ebookmass.com/product/the-fall-of-the-roman-republic-romanhistory-books-36-40-oxford-worlds-classics-dio/
ebookmass.com
Good Governance: Concept and Context Henk Addink
https://ebookmass.com/product/good-governance-concept-and-contexthenk-addink/
ebookmass.com
The Mineral Fix: How to Optimize Your Mineral Intake for Energy, Longevity, Immunity, Sleep and More 1st Edition
James Dinicolantonio
https://ebookmass.com/product/the-mineral-fix-how-to-optimize-yourmineral-intake-for-energy-longevity-immunity-sleep-and-more-1stedition-james-dinicolantonio/ ebookmass.com
eTextbook 978-0133412130 Exploring Microsoft Office 2013, Brief: Microsoft Office 2013, Brief (Exploring for Office 2013)
https://ebookmass.com/product/etextbook-978-0133412130-exploringmicrosoft-office-2013-brief-microsoft-office-2013-brief-exploring-foroffice-2013/
ebookmass.com
AACN Essentials of Progressive Care Nursing, Third Edition (Chulay, AACN Essentials of Progressive Care Nursing) 3rd Edition, (Ebook PDF)
https://ebookmass.com/product/aacn-essentials-of-progressive-carenursing-third-edition-chulay-aacn-essentials-of-progressive-carenursing-3rd-edition-ebook-pdf/ ebookmass.com
Applicationsof HypothesisTestingfor EnvironmentalScience AbbasF.M.Alkarkhi
UniversityofKualaLumpur(Unikl)–Malaysia
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2021ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans, electronicormechanical,includingphotocopying,recording,oranyinformationstorageand retrievalsystem,withoutpermissioninwritingfromthepublisher.Detailsonhowtoseek permission,furtherinformationaboutthePublisher’spermissionspoliciesandour arrangementswithorganizationssuchastheCopyrightClearanceCenterandtheCopyright LicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions .
Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightby thePublisher(otherthanasmaybenotedherein).
Notices Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchand experiencebroadenourunderstanding,changesinresearchmethods,professionalpractices, ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgein evaluatingandusinganyinformation,methods,compounds,orexperimentsdescribed herein.Inusingsuchinformationormethodstheyshouldbemindfuloftheirownsafety andthesafetyofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,or editors,assumeanyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatter ofproductsliability,negligenceorotherwise,orfromanyuseoroperationofanymethods, products,instructions,orideascontainedinthematerialherein.
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
ISBN:978-0-12-824301-5
ForInformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: JosephHayton
AcquisitionsEditor: MarisaLaFleur
EditorialProjectManager: GraceLander
ProductionProjectManager: SruthiSatheesh
CoverDesigner: ChristianBilbow
TypesetbyMPSLimited,Chennai,India
Dedication Tothememoryofmyparents(deceased)
TomybelovedchildrenAtheer,Hibah,andFarah
Tomybelovedwife AbbasF.M.Alkarkhi
Prefacexi
1Introductiontostatisticalhypothesistesting1 Learningoutcomes1 1.1Introduction1 1.2Whatishypothesistesting?2
1.3Thegeneralprocedureforperformingstatistical hypothesistesting6
1.4Proceduresforperforminghypothesistesting10 1.5Typesoferrors11 Furtherreading12
2Z-testforone-samplemean13 Learningoutcomes13
2.1Introduction13
2.2Whatisnormaldistribution?14
2.3Whatisstandardnormaldistribution?15
2.4Findingtheareaunderthenormalcurve16
2.5Hypothesistestingforonesamplemean(Z-test)25 Furtherreading32
3t-testforone-samplemean33 Learningoutcomes33 3.1Introduction33
3.2Whatistdistribution?34
3.3Findingthetcriticalvalues35
3.4Hypothesistestingforaone-samplemean(t-test)39 Furtherreading46
4Z-testforonesampleproportion47 Learningoutcomes47 4.1Introduction47
4.2WhatisBernoullidistribution?48
4.3WhatisBinomialdistribution?48
4.4Hypothesistestingforonesampleproportion(Z-test)52 Furtherreading61
5Chi-squaretestforonesamplevariance63
Learningoutcomes63
5.1Introduction63
5.2Whatischi-squaredistribution?64
5.3Findingthechi-squarevalues(areaunderthechi-squarecurve)65
5.4Hypothesistestingforone-samplevarianceorstandarddeviation71
Furtherreading78
6Theobservedsignificancelevel(P-value)procedure79
Learningoutcomes79
6.1Introduction79
6.2Whatistheobservedsignificancelevel?80
6.3Computingthe P-valueforaZ-test80
6.4Testingonesamplemeanwhenthevariance isknown: P-value85
6.5Computingthe P-valueforat-test90
6.6Testingonesamplemeanwhenthevariance isunknown: P-value95
6.7Testingonesampleproportion: P-value101
6.8Computethe P-valueforachi-squaretest107
6.9Testingone-samplepopulationvarianceor standarddeviation: P-value112
Furtherreading118
7Intervalestimationforonepopulation121
Learningoutcomes121
7.1Introduction121
7.2Whatisintervalestimation?122
7.3Confidenceintervalforonepopulationmean123
7.4Confidenceintervalforonepopulationproportion128
7.5Confidenceintervalforonepopulationvariance131
Furtherreading133
8Theintervalestimationprocedure:hypothesistesting foronepopulation135
Learningoutcomes135
8.1Introduction135
8.2Thestepsfortheconfidenceintervalprocedure136
8.3Confidenceintervalfortestingonemeanvalue:Z-test136
8.4Confidenceintervalfortestingonemeanvalue:t-test140
8.5Confidenceintervalfortestingoneproportionvalue145
8.6Confidenceintervalfortestingonestandarddeviationvalue149
Furtherreading154
9Hypothesistestingforthedifferencebetweentwopopulations155 Learningoutcomes155 9.1Introduction155
9.2Thegeneralprocedurefortestingtwosamples156
9.3Testingthedifferencebetweentwomeanswhenthe samplesizeislarge161
9.4Testingthedifferencebetweentwomeanswhenthe samplesizeissmall169
9.5Testingtwodependentsamples179
9.6Testingthedifferencebetweentwoproportions189
9.7Testingtheratiooftwovariances199 Furtherreading208
10Intervalestimationforthedifferencebetweentwopopulations209 Learningoutcomes209 10.1Introduction209
10.2Thestepsfortheconfidenceintervalprocedurefor thedifferencebetweentwopopulations210
10.3Confidenceintervalforthedifferencebetweentwomeans whenthesamplesizeislarge210
10.4Confidenceintervalforthedifferencebetweentwomeans whenthesamplesizeissmall214
10.5Confidenceintervalfordependentsamples218
10.6Confidenceintervalforthedifferencebetweentwoproportions221
10.7Confidenceintervalfortheratiooftwovariances225 Furtherreading229
11Theintervalestimationprocedure:hypothesistestingfortwo populations231 Learningoutcomes231 11.1Introduction231
11.2Thestepsfortheconfidenceintervalprocedureforthe differencebetweentwopopulations232
11.3Confidenceintervalfortestingthedifferencebetween twomeanswhensamplesizeislarge232
11.4Confidenceintervalfortestingthedifferencebetween twomeanswhenthesamplesizeissmall238
11.5Confidenceintervalfortestingtwodependentsamples246
11.6Confidenceintervalfortestingthedifferencebetween twoproportions251
11.7Confidenceintervalfortestingtheratiooftwovariances257 Furtherreading263 Appendix265 Index275
Preface Inthisbookapplicationsofhypothesistestingforenvironmentalscienceare describedinaneasyandenjoyablestyletohelpandassistgraduateandpostgraduate studentsandresearchersworkinginthefieldsofenvironmentalscience,environmentalengineering,andrelatedfields.Thelackofknowledgeofmanyresearchersabout theconceptandapplicationofhypothesistestingintheenvironmentalfield,includinghowtostatethehypothesis,howtochoosethemostsuitabletest,andhowto interpretanddrawconclusionsmotivatedmetowritethisbookandintroduce hypothesistestingforoneandtwoparameterscoveringthreeproceduresforhypothesistesting(criticalvalue, P-value,andconfidenceinterval)andtoconnectthetheorytotheenvironmentalfieldtomeettheneedsofresearchersandenablethemto carryoutvarioustestingproceduresanddrawconclusions.
Theconceptofhypothesistesting,thetypeoftest,interpretationoftheresults, anddrawingconclusionsarecarriedoutinastep-by-step,easy,andclearmannerto enableresearcherstounderstanditclearlyanduseitintheirresearch.Thebook focusesontheapplicationofhypothesistestingforoneandtwopopulationparametersincluding Z-test, t-test,chi-squaretest,and F-test,whicharefrequentlyused byresearchersintheenvironmentalfield.Mostofthetutorialsinthebookusereal dataobtainedthroughover18yearsofresearchinthisarea.
Finally,Iwishtothankmybelovedfamilyfortheircontinuoussupport.Ialsowould liketoexpressmygratitudetoUniversityofKualaLumpur(Unikl)foritssupport.
AbbasF.M.Alkarkhi
June2020
Introductiontostatistical hypothesistesting Abstract Chapter1istheintroductorychapterthatpresentsthephilosophyofhypothesistesting andtheconceptofnullandalternativehypotheses,rejectionregion,nonrejectionregion, significancelevel,andcriticalvalues.Furthermore,thegeneralprocedureforperforming hypothesistestingisgivenalongwiththetwotypesoferrorsthatcouldoccurwhileperformingtheprocedure.Typesofhypothesistestingincludingone-tailed(right-tailedand left-tailed)andtwo-tailedtestsaredeliveredinasimpleandeasytounderstandway.This chapterincludesexamplesobtainedfromthefieldofenvironmentalsciencetoshowthe applicationofhypothesistestinginthefieldofenvironmentalscienceandengineering.
Keywords: Nullandalternativehypotheses;criticalvalue;rejectionandnonrejection regions;significancelevel;typesIandIIerrors
Learningoutcomes Aftercompletingthischapter,readerswillbeableto:
● Understandthephilosophybehindhypothesistestingidea;
● Knowthegeneralprocedureforperforminghypothesistesting;
● Knowhowtodefinethetwohypotheses(nullandalternative);
● Describethestepsonhowtosetupthenullandalternativehypothesesintermsofmathematicalforms;
● Understandthedifferencebetweenrejectionandnonrejectionregions;
● Knowhowtoobtaincriticalvaluesfromaprobabilitydistributiontable;
● Knowthelevelofsignificanceandhowtouseit;
● Knowhowtousethesampledataincalculatingtheteststatistic;
● Describethetwotypesorerrors(typeIandtypeIIerrors);
● Understandthedifferencebetweentwo-tailedandone-tailedtests;
● Understandtheprocedureforapplyinghypothesistestinginthefieldofenvironmental scienceorengineering;
● Explaintheoutputsandmatchtheresultstoenvironmentalissues;
● Knowhowtoextracthelpfulinferencesregardingtheproblemunderstudy.
1.1Introduction Researchersusuallycarryoutvariousexperimentsusingstatisticaltechniques forcollecting,analyzing,summarizing,anddrawconclusionstogather ApplicationsofHypothesisTestingforEnvironmentalScience.DOI: https://doi.org/10.1016/B978-0-12-824301-5.00006-X © 2021ElsevierInc.Allrightsreserved.
2ApplicationsofHypothesisTestingforEnvironmentalScience
informationregardingthebehaviorof populationsunderinvestigationandhelp inmakingjudgmentsregardingthepurpo seofstudy.Statisticalhypothesistestingisusedtomakejudgmentsregardin ganyclaimorissueusingthesample datatoobtainthecorrectdecisionthat guidesresearcherstoaccomplishthe researchandachievetheobjectives.Gat heringinformationcanbedoneusinga representativesamplechosenfromthes amepopulationunderinvestigation. Hypothesistestingisanimportantmeth odtoexaminevariousclaimsorstatementsregardingdifferentissuestosupportordenytheclaimsinordertoplan forthenextstep.
Hypothesistestingconcerningpopulationproportions,populationmeans,and populationvariancesisofthesubjectofthistext.A Z-testisusedtocarryout hypothesistestingregardingpopulationproportions.Furthermore,a Z-testcanbe usedforpopulationmeanswhenthesamplesizeislarge,anda t-testisusedwhen thesamplesizeissmall.Achi-squaretestand F-testareusedtotestahypothesis concerningoneandtwovariances.
Asanexample,consideraresearcherwhowantstotestaclaimregardingthe concentrationoftotalsuspendedsolids(TSSs)inthesurfacewaterofariver,the claimsaysthatthemeanconcentrationofTSSsis465(mg/L).Asampleshouldbe selectedfromtheriverandtestedfortheconcentrationofTSSsandthentheresults summarizedandanalyzedtofinallydecidewhethertosupporttheclaimorto rejectit.
1.2Whatishypothesistesting? Hypothesistestingisastatisticaltechniqueusedtomakejudgmentsregarding claimsorstatementsrelatedtopopulations.Theopinionanddefinitionofhypothesistestingwiththegeneralprocedureofconductingtheanalysisareclarifiedbefore beingappliedtoenvironmentaldata.
Anyclaimorstatementmadeonpopulationparameters(mean,standarddeviation,andproportion)iscalledahypothesis.Asampleshouldbechosenfromthe populationofinteresttounderstandthebehavioroftheissueunderinvestigation andmakeajudgmentbasedonthecollectedsampleinformation.
Wecanidentifytwotypesofhypotheses:thenullhypothesisandthealternative hypothesis.Thetwohypothesesaremutuallyexclusive(theycannotoccur together).
Thenullhypothesisisastatisticalhypothesisthatsaysnorealdifference existsbetweenapopulationparameter(s uchasproportion,average,andstandarddeviation)andsomeclaimedvalue(givenvalue).Thesymbolfornull hypothesisis H 0
Thealternativehypothesisisastatisticalhypothesisthatrepresentstheopposite ofthenullhypothesis.Analternativehypothesissaysthatarealdifferenceexists betweenapopulationparameterandagivenvalue.Thesymbolforalternative hypothesisis H1
Threestepscanbeemployedtospecifythenullandalternativehypothesesmathematicallyasgivenbelow.
1. Findoutthehypothesisconcerningtheissueunderinvestigation.
2. Translatethewordsofthenullhypothesisintoamathematicalexpression.
3. Translatethewordsofthealternativehypothesisintoamathematicalexpression.
Example1.1:Specifythetwohypothesesforthetwo-sidedtest: Anenvironmentalistwishestoinvestigateaclaimregardingthemeanconcentrationofcadmium (Cd)ofsurfacewater.Theenvironmentalistwantstoexaminetheclaimthatthe meanconcentrationofcadmiumofsurfacewateris0.17mg/L.
Thethreestepsforspecifyingthenullandalternativehypothesescanbeusedto writethetwohypothesesasshownbelow.
1. Findoutthehypothesisconcerningtheissueunderinvestigation
Onecanseethatthehypothesisisgiveninwords;thusweneedtofigureoutthe hypothesis.Thehypothesissays,“themeanconcentrationofcadmiumofsurfacewateris 0.17mg/L.”
2. Translatethewordsofthenullhypothesisintoamathematicalexpression
Thenextstepinspecifyingthenullandalternativehypothesesistotranslatethewords ofthenullhypothesisintoamathematicalform.Thenullhypothesisstatesthatthemean concentrationofcadmiumofsurfacewaterisexactly0.17mg/L.Thisstatementcanbe translatedintoamathematicalformasgivenbelow:
where μ referstothepopulationmean.
Onecanseethattheequalitysignisunderthenullhypothesis.
3. Translatethewordsofthealternativehypothesisintoamathematicalexpression
Thenullhypothesisstatesthatthemeanconcentrationofcadmiumofsurfacewater equals0.17mg/L.Theoppositeofthenullhypothesisrepresentsthealternativehypothesis,whichisnotequal.Thus,ifthemeanconcentrationofcadmiumofsurfacewateris notequalto0.17mg/L,thenthemeanconcentrationofcadmiumofsurfacewaterwillbe eithergreaterthanorlesserthan0.17mg/L.Wecanrecognizetwodirectionsforthe alternativehypothesis,thefirstdirectionisgreaterthan0.17mg/Landthesecond directionislessthan0.17mg/L.Thetwodirectionscanberepresentedinamathematical symbolas ¼ .Thealternativehypothesisintermsofamathematicalformis
17
Onecanseethatthenullandalternativehypothesesaremutuallyexclusive(theycannotoccuratthesametime).
Example1.2:Specifythetwohypothesesforaright-tailedtest: Anenvironmentalistwishestoinvestigateaclaimregardingthemeanconcentrationofcadmium (Cd)ofsurfacewater.Theenvironmentalistwantstoexaminetheclaimthatthe meanconcentrationofcadmiumofsurfacewaterisgreaterthan0.17mg/L.
H0 :μ 5 0:17ClaimðÞ
H1 :μ ¼ 0
Thethreestepsforspecifyingthenullandalternativehypothesescanbeusedto writethetwohypothesesasshownbelow.
1. Findoutthehypothesisconcerningtheissueunderinvestigation
Onecanseethatthehypothesisisgiveninwords;thusweneedtofigureoutthe hypothesis.Theclaimsays,“themeanconcentrationofcadmiumofsurfacewateris greaterthan0.17mg/L.”
2. Translatethewordsofthenullhypothesisintoamathematicalexpression
Thenextstepinspecifyingthenullandalternativehypothesesistotranslatethewords ofthenullhypothesisintoamathematicalform.Theclaimstatesthatthemeanconcentrationofcadmiumofsurfacewaterisgreaterthan0.17mg/L.Thus,ifthemeanconcentrationofcadmiumisnotgreaterthan0.17mg/L,thenthemeanconcentrationofcadmium ofsurfacewaterwillbeeitherequalto0.17mg/Lorlessthan0.17mg/L.Thuswecan usethetwodirectionstorepresentthenullhypothesisas # .Thisstatementcanbetranslatedintoamathematicalformasgivenbelow:
Onecanseethattheequalitysignisunderthenullhypothesis.
3. Translatethewordsofthealternativehypothesisintoamathematicalexpression
Thenullhypothesisstatesthatthemeanconcentrationofcadmiuminsurfacewater islessthanorequalto0.17mg/L.Theoppositeofthenullhypothesisrepresentsthe alternativehypothesis;thusifthemeanc oncentrationofcadmiumofsurfacewateris notlessthanorequalto0.17mg/L,thenthemeanconcentrationofcadmiumofsurface waterwillbegreaterthan0.17mg/L.Thuswecanrecognizeonedirectionforthealternativehypothesiswhichisgreaterthan0.17 mg/L.Thisdirectioncanberepresentedin amathematicalsymbolas . .Thealternativehypothesisintermsofamathematical formis:
Onecanseethatthenullandalternativehypothesesaremutuallyexclusive(theycannotoccuratthesametime).
Example1.3:Specifythetwohypothesesforaleft-tailedtest: Anenvironmentalistwishestoinvestigateaclaimregardingthemeanconcentrationofcadmium(Cd) ofsurfacewater.Theenvironmentalistwantstoexaminetheclaimthatthemean concentrationofcadmiumofsurfacewaterislessthan0.17mg/L.
Thethreestepsforspecifyingthenullandalternativehypothesescanbeusedto writethetwohypothesesasshownbelow.
1. Findoutthehypothesisconcerningtheissueunderinvestigation
Onecanseethatthehypothesisisgiveninwords;thusweneedtofigureoutthe hypothesis.Thehypothesissays,“themeanconcentrationofcadmiumofsurfacewateris lessthan0.17mg/L.”
2. Translatethewordsofthenullhypothesisintoamathematicalexpression
Thenextstepinspecifyingthenullandalternativehypothesesistotranslatethewords ofthenullhypothesisintoamathematicalform.Theclaimstatesthatthemean 4ApplicationsofHypothesisTestingforEnvironmentalScience
H0 :μ # 0 17
H1 :μ . 0 17
concentrationofcadmiumofsurfacewaterislessthan0.17mg/L.Thus,ifthemeanconcentrationofcadmiumisnotlessthan0.17mg/L,thenthemeanconcentrationofcadmiumofsurfacewaterwillbeeitherequalto0.17mg/Lorgreaterthan0.17mg/L.Thus wecanusethetwodirectionstorepresentthenullhypothesisas $ .Thisstatementcan betranslatedintoamathematicalformasgivenbelow:
0 :μ $ 0 17
Onecanseethattheequalitysignisunderthenullhypothesis.
3. Translatethewordsofthealternativehypothesisintoamathematicalexpression
Thenullhypothesisstatesthatthemeanconcentrationofcadmiuminsurfacewater isgreaterthanorequalto0.17mg/L.Theoppositeofthenullhypothesisrepresentsthe alternativehypothesis;thusifthemeanconcentrationofcadmiumofsurfacewateris notmorethanorequalto0.17mg/L,thenthemeanconcentrationofcadmiumofsurfacewaterwillbelessthan0.17mg/L.Thu swecanrecognizeonedirectionforthe alternativehypothesiswhichislessthan0.17mg/L.Thisdirectioncanberepresentedin amathematicalsymbolas , .Thealternativehypothesisintermsofamathematical formis:
H1 :μ , 0 17
Onecanseethatthenullandalternativehypothesesaremutuallyexclusive(theycannotoccuratthesametime).
Wecansummarizethethreesituationsofstatisticalhypothesesincludingonesituationforthetwo-tailedtestandtwosituationsfortheone-tailedtest.
1. Thetwo-tailedtestwillhavethetwohypothesesasgivenin Eq.(1.1).
H0 :μ 5 c H1 :μ ¼ c
2. Theright-tailedtestisaone-tailedtest,andthetwohypothesesfortheright-tailedtestare givenin Eq.(1.2).
0 :μ # c
H1 :μ . c (1.2)
3. Theleft-tailedtestisaone-tailedtest,andthetwohypothesesfortheleft-tailedtestare givenin Eq.(1.3).
H0 :μ $ c
H1 :μ , c (1.3) where c isagivenvalue.
Researchersusuallyemployoneofthehypothesesintheirresearchtomatchthe purposeofthestudy.
H
H
Note
● Onecanseethattheequalitysign 5 ; $ ; # ðÞ mustbeplacedwiththenullhypothesis H0
● Wealwaysinclude , , . ,or ¼ inthealternativehypothesis H1.
● Onecanseethatthetwohypothesesaremutuallyexclusive.
1.3Thegeneralprocedureforperformingstatistical hypothesistesting Thegeneralprocedureforconductinghypothesistestingcanbesummarizedbythe stepsgivenbelow.
Step1:Specifythenullandalternativehypotheses.
Step2:Selectthesignificancelevel(α)forthestudy.
Step3:Usethesampleinformationtocalculatetheteststatisticvalue.
Step4:Identifythecriticalandnoncriticalregionsforthestudy.
Step5:Makeadecisionandinterprettheresults.
Wewilldiscussthegeneralprocedurestep-by-stepsupportedbyexampleswhere necessary.
Step1:Specifythenullandalternativehypotheses
Wehavestudiedthisstepearlieronhowtowriteandspecifythenullandalternativehypotheses.
Step2:Selectthesignificancelevel(α)forthestudy
Thesignificancelevel,usuallycalledalpha(α),isalsocalledthelevelofsignificance.Considerthatthenullhypothesisistrue(H0),thentheprobabilityofrejectingthenullhypothesis(H0)iscalledthealphaorsignificancelevel.Thevalueof alphareferstothesignificanceoftheresults,andweusuallyselectthevalueof alpha(α)tobe0.05or0.01.
Step3:Usethesampleinformationtocalculatetheteststatisticvalue
Thesampleinformation(data)isusedtocalculateavaluecalledtheteststatistic. Thisvalueiscalculatedusingaspecificmathematicalformulaforeachdistribution. Researchersusetheteststatisticvaluetomakeadecisiontorejectthenullhypothesisornot.
Step4:Identifythecriticalandnoncriticalregionsforthestudy
Thecriticalandnoncriticalregionsarealsocalledrejectionandnonrejection regions;weshoulddelivertheconceptofcriticalvalues,andcriticalandnoncritical regions.
Therangeofvaluesoftheteststatisticthatwouldrejectthenullhypothesisis calledthecriticalregionortherejectionregionforahypothesistesting.
Therangeofvaluesoftheteststatisticthatwouldnotrejectthenullhypothesis iscalledthenoncriticalregionorthenonrejectionregionforahypothesistesting.
Thevaluethatiscalculatedfromaprobabilitydistributionrelatedtotheproblem understudyiscalledthecriticalvalue.Thisvalueisusedinhypothesistestingto 6ApplicationsofHypothesisTestingforEnvironmentalScience
differentiatethecriticalregion(where H0 shouldberejected)fromthenoncritical region.Wecancalculatecriticalvaluesforeachdistributionbasedonthesignificancelevel.
Wecanrecognizethecriticalandnoncriticalregionsbyemployingthreesimple stepsgivenbelow:
1. Specifythealternativehypothesis;
2. Selecttheappropriatesignificancelevel;
3. Extractthecorrectcriticalvalue.
Weshouldmakeadecisionregardingthenullhypothesisofthestudywhetherto reject H0 ornot.Thenweneedtointerpretthedecisionanddrawaconclusion regardingthestudyunderinvestigation.
Examplesaboutthemeanvaluewillbeshowntoidentifythecriticalandnoncriticalregions.Weconsiderthevariableunderstudytobenormallydistributed.
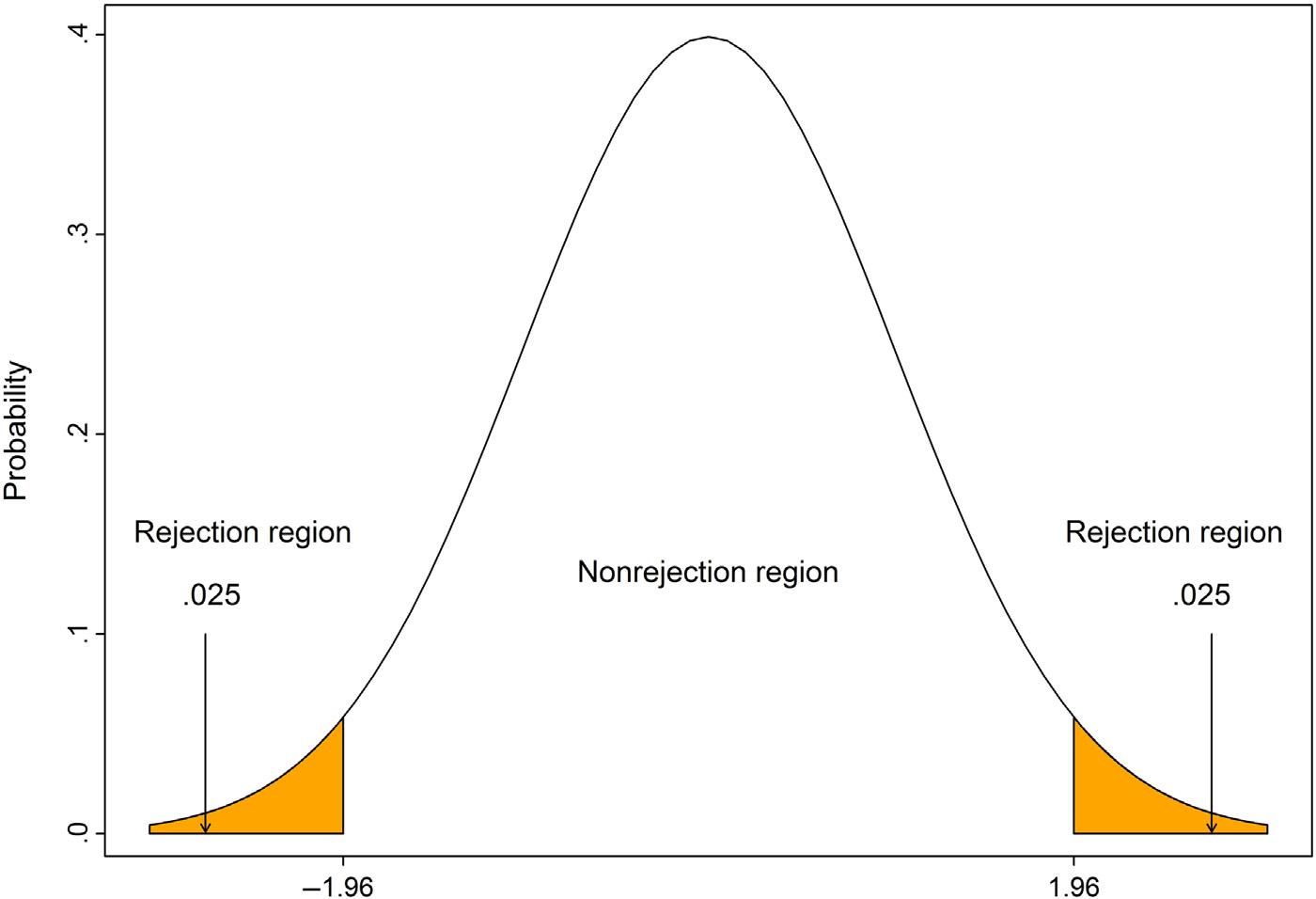
Example1.4:Identifythecriticalandnoncriticalregionsforthetwo-tailed test: Anenvironmentalistwishestoidentifythecriticalandnoncriticalregionsfor aclaimregardingthemeanconcentrationofcadmium(Cd)ofsurfacewater.The environmentalistwantstoexaminetheclaimthatthemeanconcentrationofcadmiumofsurfacewateris0.17mg/L.Useasignificancelevelof α 5 0.05toidentify thetworegions.Assumethatthedataarenormallydistributed.
Wecanusethethreestepspresentedearliertoidentifythecriticalandnoncriticalregionsforthetwo-tailedtest.
1. Specifythealternativehypothesis
Thekeytospecifyingthecriticalandnoncriticalregionsistoknowthealternative hypothesis.Thenullandalternativehypothesesare H0 :μ 5 0 17 H1 :μ ¼ 0:17
2. Selecttheappropriatesignificancelevel
Thesecondstepintheprocedureforidentifyingthecriticalandnoncriticalregionsis toselecttheappropriatesignificancelevel.Theappropriatesignificancelevelisselected tobe0.05(α 5 0.05).Becausethetestisatwo-tailedtest,weshoulddividealphaby2to identifytwoequallycriticalregionsonbothtails.
Anareaof0.025 α 2 willbeoneachtailtorepresentthecritical(rejection)region.
3. Extractthecorrectcriticalvalue
Theextractedcriticalvalue e forthetwo-tailedtestwith α 5 0.05is 6 1.96(seestandardnormalTableA).Thecriticalandnoncriticalregionsforthisstudywhichrepresent thetwo-tailedtestarepresentedin Fig.1.1.Theshadedareain Fig.1.1 iscalledthecritical(rejection)region.
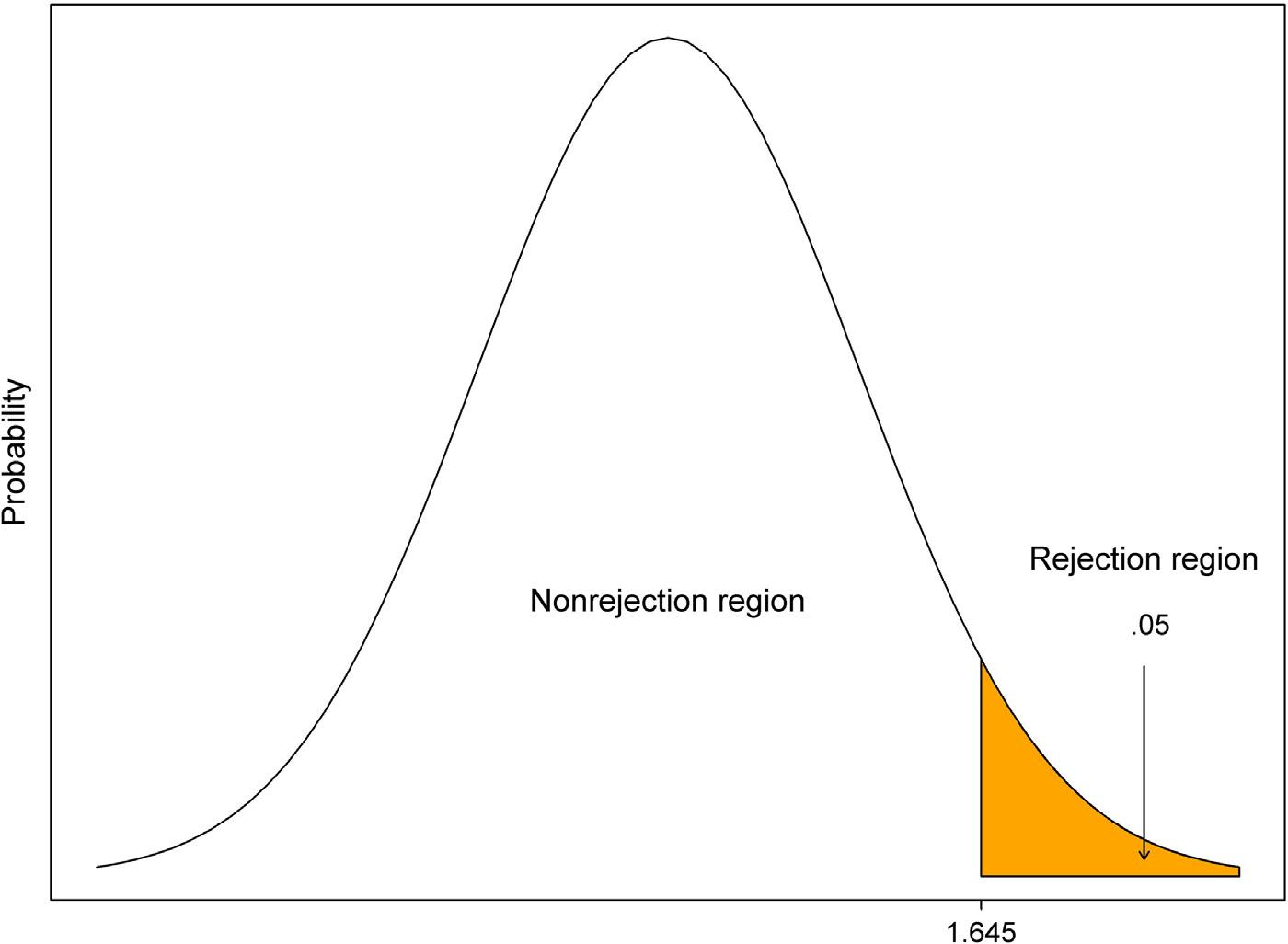
Example1.5:Identifythecriticalandnoncriticalregionsfortheright-tailed test: Anenvironmentalistwishestospecifythecriticalandnoncriticalregionsfora claimregardingthemeanconcentrationofcadmium(Cd)ofsurfacewater. Theenvironmentalistwantstoexaminetheclaimthatthemeanconcentration ofcadmiumofsurfacewaterisgreaterthan0.17mg/L.Useasignificancelevel of α 5 0.05tospecifythetworegions.Assumethatthedataarenormallydistributed.
Wecanusethethreestepspresentedearliertoidentifythecriticalandnoncriticalregionsfortheright-tailedtest.
1. Specifythealternativehypothesis
Thekeytospecifyingthecriticalandnoncriticalregionsistoknowthealternative hypothesis.Thenullandalternativehypothesesare
0 :μ # 0:17
H1 :μ . 0 17
2. Selecttheappropriatesignificancelevel
Thesecondstepintheprocedureforidentifyingthecriticalandnoncriticalregionsis toselecttheappropriatesignificancelevel.Theappropriatesignificancelevelisselected tobe0.05(α 5 0.05).Becausethetestisaone-tailedtest(right-tailed),weidentifythe criticalregion(rejection)of α 5 0.05ontherighttail.
3. Extractthecorrectcriticalvalue
Theextractedcriticalvaluefortheone-tailedtestwith α 5 0.05is 6 1.645(seestandard normalTableA).Thecriticalandnoncriticalregionsforthisstudywhichrepresentaone-tailed testarepresentedin Fig.1.2.Theshadedareain Fig.1.2 iscalledthecritical(rejection)region.
H
Figure1.1 Thecriticalandnoncriticalregionsfor H1 :μ ¼ 0 17.
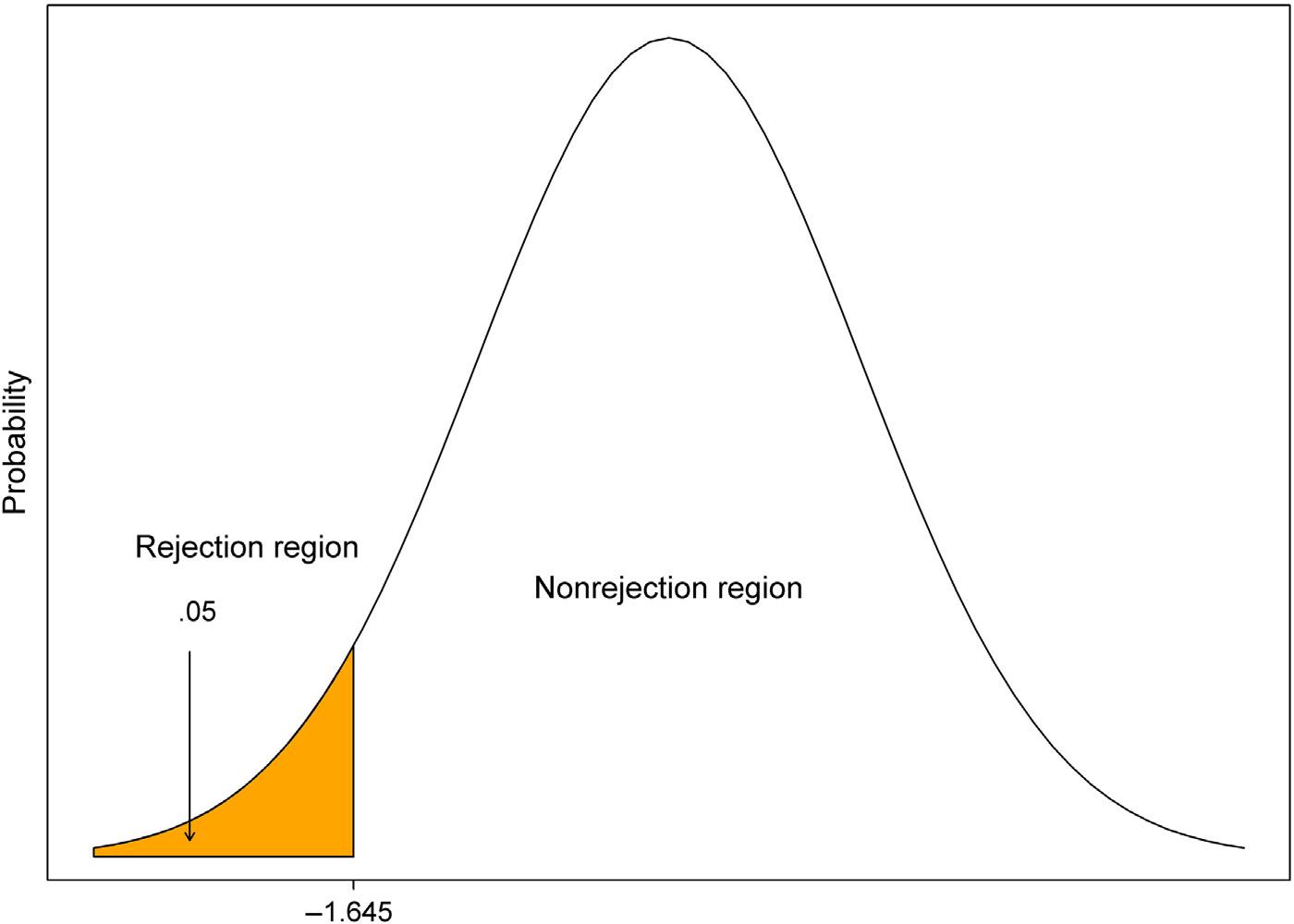
Example1.6:Identifythecriticalandnoncriticalregionsfortheright-tailed test: Anenvironmentalistwishestospecifythecriticalandnoncriticalregionsfora claimregardingthemeanconcentrationofcadmium(Cd)ofsurfacewater.The environmentalistwantstoexaminetheclaimthatthemeanconcentrationofcadmiumofsurfacewaterislessthan0.17mg/L.Useasignificancelevelof α 5 0.05 toidentifythetworegions.Assumethatthedataarenormallydistributed.
Wecanusethethreestepspresentedearliertospecifythecriticalandnoncritical regionsfortheright-tailedtest.
1. Specifythealternativehypothesis
Thekeytoidentifyingthecriticalandnoncriticalregionsistoknowthealternative hypothesis.Thenullandalternativehypothesesare
2. Selecttheappropriatesignificancelevel
Thesecondstepintheprocedureforidentifyingthecriticalandnoncriticalregionsis toselecttheappropriatesignificancelevel.Theappropriatesignificancelevelisselected tobe0.05(α 5 0.05).Becausethetestisaone-tailedtest(left-tailed),weidentifythecriticalregion(rejection)of α 5 0.05onthelefttail.
3. Extractthecorrectcriticalvalue
Theextractedcriticalvaluefortheone-tailedtestwith α 5 0.05is 6 1.645(seestandardnor-
malTableA).Thecriticalandnoncriticalregionsforthisstudywhichrepresenttheone-tailed testarepresentedin Fig.1.3.Theshadedareain Fig.1.3 iscalledthecritical(rejection)region.
H0 :μ $ 0 17
H1 :μ , 0:17
Figure1.2 Therejectionandnonrejectionregionsfor H1 :μ . 0:17.
Step5:Makeadecisionandinterprettheresults
Thelaststepinthegeneralprocedureforhypothesistestingistomakeadecisiontorejectthenullhypothesis(H0)ornot.Interpretationofthedecisionisneeded anditisimportanttodrawaconclusionregardingthestudyunderinvestigationand reachtheobjectiveofthestudy.
1.4Proceduresforperforminghypothesistesting Therearethreeproceduresformakingadecisioninstatisticalhypothesistesting, whicharethecriticalvalueprocedure, P-valueprocedure,andconfidenceinterval procedure.Wewillpresentthecriticalvalueprocedureinthischapter,whilethe PvalueandconfidenceintervalprocedureswillbegiveninChapter6,Theobserved significancelevel(P-value)procedure,andChapter7,Intervalestimationforone population,respectively.
1. Criticalvalueprocedure
Thecriticalvalueprocedureisusedtoguide researchersandhelpinmakingadecision instatisticalhypothesistesting.Thisprocedureisalsoknownasatraditionalprocedure. Wecanusethecriticalvalueproceduretomakeadecisionregardingthenullhypothesis usingtheteststatisticvalueandthecriticalvaluerelatedtothedistributionusedforsolvingtheproblem.Thedecisionismadebycomparingthetwovalues(teststatisticvalue
Figure1.3 Therejectionandnonrejectionregionsfor H1 :μ , 0 17.
andcriticalvalue).Iftheabsoluteteststatisticvalueisgreaterthanthecriticalvalue,the nullhypothesisisrejected;otherwisethenullhypothesisisnotrejected.Orusingtheprobabilitydistributioncurve,iftheteststatisticvaluefallsinthecriticalregion,thenull hypothesisisrejected;otherwisethenullhypothesisisnotrejected.
Wewillemploythecriticalvalueprocedureformakingadecisionregardingtheonesampletestforthemeanvalue,proportionvalue,andvariancevalue,whiletheothertwo procedures,the P-valueandconfidenceintervalprocedures,willbegiveninChapter6, Theobservedsignificancelevel(P-value)procedure,andChapter7,Intervalestimation foronepopulation,respectively,andthencomparetheresultsofvariousprocedures.
1.5Typesoferrors Twotypesoferrorsareassociatedwithhypothesistestingproceduresinmakinga decisionregardingthenullhypothesis.Adecisionisusuallymadebasedonthe sampleinformation,andthisdecisioncouldbecorrectorincorrect.Thetwotypes oferrorsaretypeIandtypeIIerrors.
Thefirsttypeoferroriscalleda typeIerror.Thiserroroccurswhenweincorrectlydecidetorejectatruenullhypothesis.AtypeIerroriscalledthesignificance level(α).
Thesecondtypeoferroriscalleda typeIIerror .Thiserroroccurswhenwe failtorejectafalsenullhypothesis.ThesymbolfortheprobabilityofatypeII erroris β . Note
● TypeIandtypeIIerrorsareinverselyproportional;decreasingtypeIerror(α)would increasetypeIIerror β ,andincreasingtypeIerror(α)woulddecreasetypeIIerror(β ).
Example1.7:SpecifytypeIandtypeIIerrors: SpecifytypeIandtypeIIerrors fortheclaimwhichstatesthatthemeanconcentrationofcadmium(Cd)is0.17mg/L.
Weneedtoidentifythenullandalternativehypothesesforthisclaim.Thetwo hypothesesaregivenbelow:
H0 :μ 5 0:17
H1 :μ ¼ 0 17
TypeIerror
AtypeIerrorwouldoccurwhenweincorrectlydecidetorejectatruenull hypothesis.Forthemeanconcentrationofcadmium,atypeIerrorwouldoccurif themeanconcentrationofcadmiumofsurfacewateris0.17mg/L(μ 5 0.17),but theinformationprovidedbytheselectedsampletellsustorejecttheclaimthatthe meanconcentrationofcadmiumofsurfacewateris0.17mg/Landconcludethat themeanconcentrationofcadmiumofsurfacewaterisnotequalto0.17mg/L μ ¼ 0 17 ðÞ
TypeIIerror
AtypeIIerrorwouldoccurwhenwefailtorejectafalsenullhypothesis.For themeanconcentrationofcadmiumofsurfacewater,atypeIIerrorwouldoccurif themeanconcentrationofcadmiumofsurfacewaterisnotequalto0.17mg/L μ ¼ 0 17 ðÞ,buttheinformationprovidedbytheselectedsampletellsusnotto rejectthenullhypothesisandconcludethatthemeanconcentrationofcadmiumof surfacewaterisequalto0.17mg/L(μ 5 0.17).
Correctdecision
Acorrectdecisioncanbeachievedintwocases:inthefirstcase,ifwedonot rejectthenullhypothesiswhenitistrue.Thecorrectdecisionforthisexampleis wedonotrejectthenullhypothesisifthemeanconcentrationofcadmiumofsurfacewaterisequalto0.17mg/L(μ 5 0.17).
Inthesecondcase,ifwerejectthenullhypothesiswhenitisfalse.Thecorrect decisionforthisexampleiswerejectthenullhypothesisifthemeanconcentration ofcadmiumofsurfacewaterisnotequalto0.17mg/L μ ¼ 0:17 ðÞ.
Furtherreading Alkarkhi,A.F.M.,&ALqaraghuli,W.A.A.(2020). Appliedstatisticsforenvironmental sciencewithR (1sted.).Elsevier. Alkarkhi,A.F.M.,&Chin,L.H.(2012). Elementarystatisticsfortechnologist (1sted.). Malaysia:UniversitiSainsMalaysia. Bluman,A.G.(1998). Elementarystatistics:Astepbystepapproach (3rded.).Boston: WCBMcGraw-Hill. Weiss,N.A.(2012). Introductorystatistics (9thed.).Pearson. 12ApplicationsofHypothesisTestingforEnvironmentalScience
Z-testforone-samplemean Abstract 2 Thischapterpresentshypothesistestingbasedonnormaldistributionincludingtheconceptofnormaldistribution,standardnormaldistribution,andrelatedterms.Thearea undernormaldistributioncurvewiththeconceptofrejectionandnonrejectionregionsis deliveredwithillustrationsbyexamplesforeachregionusinganormaldistributioncurve. Moreover,thegeneralprocedureforhypothesistestingusingZ-testforalargesampleis givenandexplainedclearly.Examplesfromthefieldofenvironmentalscienceare selectedandusedtoillustratethestepsofhypothesistestingusingZ-testandmakinga decisionregardingthestudywithsufficientexplanationforeachstep.
Keywords: Normaldistribution;standardnormaldistribution;criticalandcriticalregions; criticalvalue;areaunderthecurve;Z-test
Learningoutcomes Aftercompletingthischapter,readerswillbeableto:
● Understandtheimportanceofnormaldistribution
● Explaintheconceptofstandardnormaldistribution
● Computetheareaunderthestandardnormalcurve
● Determinetheprobabilitiesfornormaldistribution
● Describethecommonstepsforperforminghypothesistesting
● ComputetheZ-teststatisticvalueforasinglepopulationmean
● KnowtherejectionandnonrejectionregionsforZ-test
● Knowone-tailedandtwo-tailedtestsforZ-test
● Describethestepsforprovidingcorrectinterpretationoftheresults
● Writeusefulconclusions
2.1Introduction Z-testforone-samplemeanandotherstatisticaltestsemploystheconceptofnormal distributiontoperformhypothesistesting.ThustheconceptandpropertiesofnormaldistributionshouldbedeliveredbeforegivingtheprocedureofhypothesistestingforonesampleZ-test.
Theconceptandpropertiesofnormaldistributionandstandardnormaldistributionarecoveredinthischapter.Moreover,theprocedureforcalculatingthearea underthestandardnormalcurveiscoveredandthegeneralprocedureforperformingaZ-testforaone-samplemeanalsoisgiven.
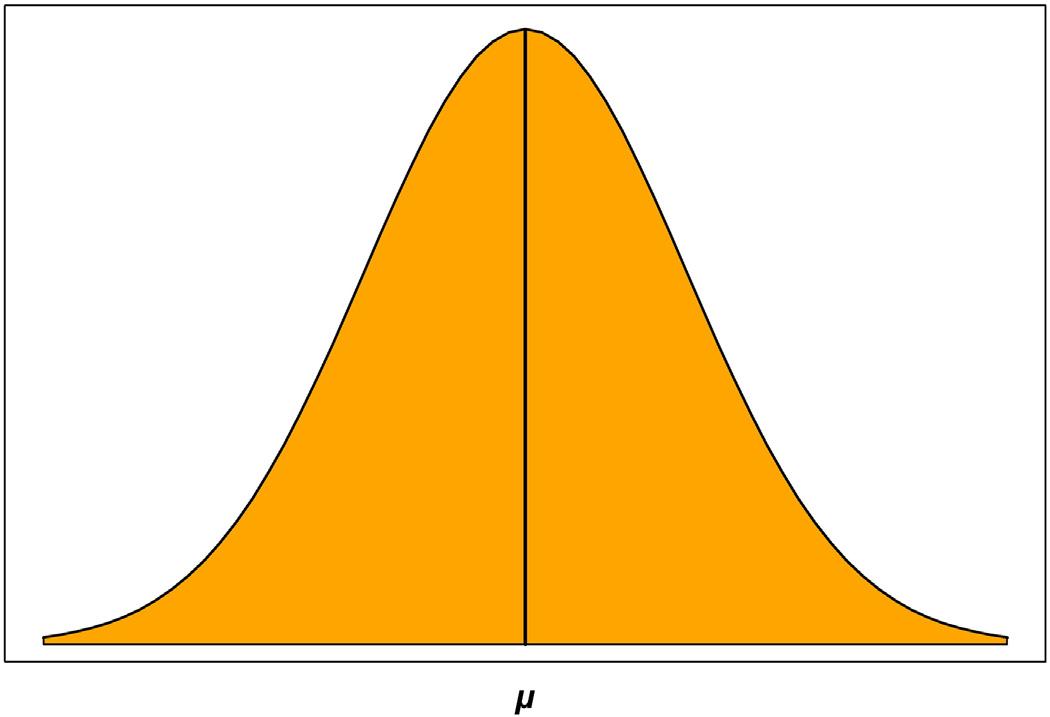
2.2Whatisnormaldistribution? Therearemanydistributionsinstatisticsusedtodescribethebehaviorofdifferent phenomena.Oneofthemostimportantdistributionsiscallednormaldistribution, orthebellcurveduetoitsshape(bell-shaped).AGaussiandistributionisanother namefornormaldistribution.Thenormaldistributioncurveispresentedin Fig.2.1
Figure2.1 Thenormaldistributioncurve.
Consider Y representsarandomvariablethatfollowsanormaldistributionwith mean μ ðÞ andvariance ðσ 2 Þ,thenthenormalprobabilitydistributionfunctionispresentedin Eq.(2.1)
where, Y representsarandomvariablethatisdistributednormally N ðμ; σ 2 Þ orsymbolizedas Y BN ðμ; σ 2 Þ, π 5 3:14,and eD2 71828
Thepropertiesofnormaldistributioncurveareasfollows:
1. Thenormaldistributioncurveisbell-shaped.
2. Theshapeofthenormaldistributioncurveissymmetricaboutthemean.
3. Themeanisatthecenteranddividestheareaintotwoequalparts.
4. Thetotalareaunderthenormaldistributioncurveisequalto1.
5. Mostoftheareaunderthecurvefallsbetweenthreestandarddeviationsofthemean.The percentageoftheareaunderone,two,andthreestandarddeviationsisgivenbelow.
● 68%ofthepointsfallbetweenonestandarddeviationofthemean;
● 95%ofthepointsfallbetweentwostandarddeviationsofthemean;
● 99.7%ofthepointsfallbetweenthreestandarddeviationsofthemean.
2.3Whatisstandardnormaldistribution? Considerthat Y representsarandomvariablethatfollowsanormaldistribution withmean(0)andvariance(1),thenthestandardnormaldistributionfunctionis presentedin Eq.(2.2)
Y representsarandomvariablethatisdistributednormally N 0; 1 ðÞ orsymbolized as Y BN 0; 1 ðÞ.Thestandardnormaldistributionhasthesamepropertiesofnormal distribution,thestandardnormaldistributioncurveispresentedin Fig.2.2 Figure2.2
16ApplicationsofHypothesisTestingforEnvironmentalScience
Wecanconvertanynormalrandomvariabletothestandardnormaldistribution employingtheformulagivenin Eq.(2.3).
Theformulain Eq.(2.3) iscalledthestandardscore.
2.4Findingtheareaunderthenormalcurve Theareaunderthestandardnormalcurvecanbecomputedusingthestandard score.TheZscoreprovidesinformationonthepositionofavaluecomparedtothe averagevalueusingthedistancetoexpressthepositionbyhowmanystandard deviationsthevaluefallsaboveorbelowtheaverage.Thestepsforfindingthearea underthestandardnormalcurverequiredescribingthestandardnormaltableand thenfollowafewstepstoextracttheareafromthetable.
WeuseTableAintheAppendixtoextracttheareaunderthecurveforZvalues from0to3.ThevalueofZshouldbedividedintotwoparts,thefirstpartoftheZ valueinTableAisrepresentedintheleft-hand(first)column,thevaluesofZin thetablestartfrom0to3(nearesttenth),whilethefirst(upper)rowprovidesthe secondpartoftheZvalue(seconddecimalplace).Wecanusethesametableto findtheareaunderthecurvefornegativeZvaluesbecauseofthesymmetrical propertyofnormaldistribution.
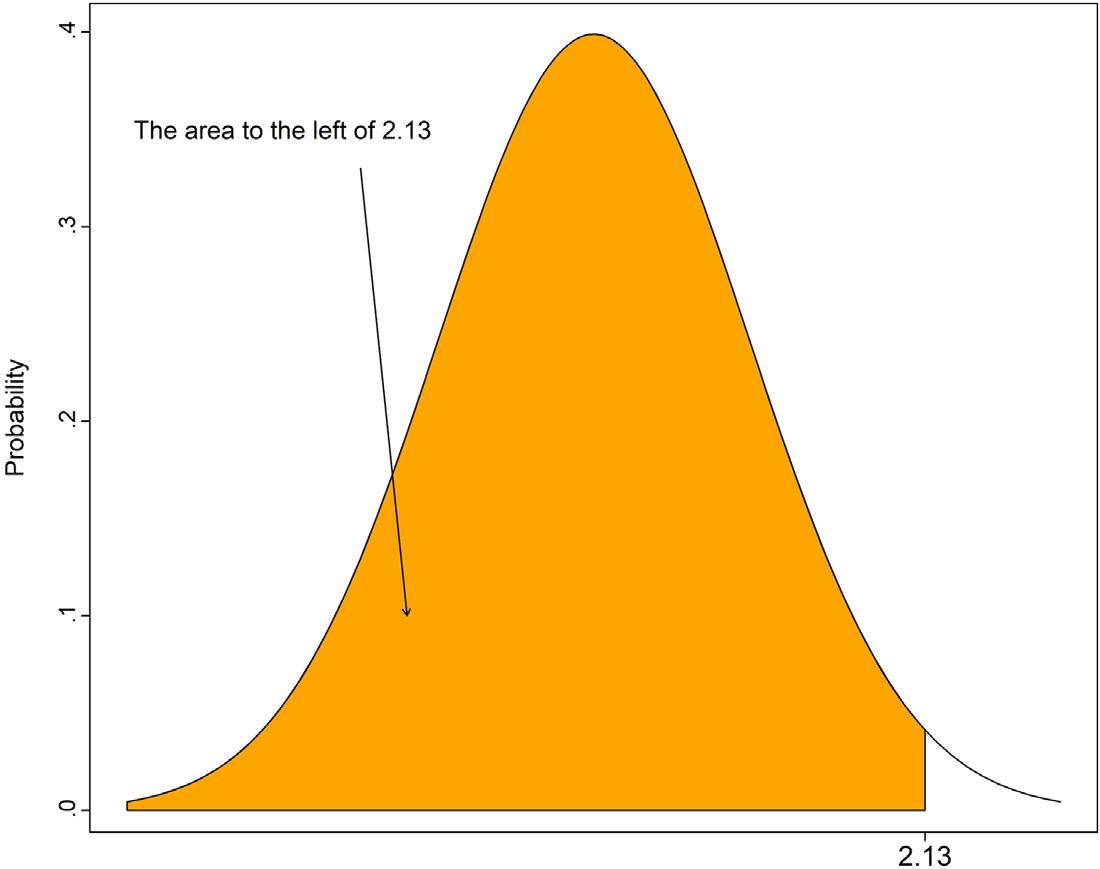
Example2.1:ComputetheareatotheleftofaZvalue: Computetheareaunder thestandardnormalcurvetotheleftofapositiveZvalueof2.13.
FindingtheareatotheleftofapositiveZvalueof2.13requiresusingTableAin theAppendixforthestandardnormal.Thevalue“2.13”shouldbedividedintotwo pieces,thefirstpieceis“2.1”andthesecondis“0.03.”Theexactareatotheleftof 2.13canbecomputedemployingthestepsbelow.
● Thefirststepistosearchforthepositionof“2.1”inthefirstverticalcolumnof Table2.1 labeledZtospecifythefirstpiece“2.1”ofthenumber2.13(highlightedrow)[Table2.1 isaportionofthestandardnormaltableintheAppendix(TableA)].
● Thesecondstepinfindingtheareaistomoveontherowof“2.1”tothecolumnlabeled “0.03”(highlightedcolumn),thepointofintersectionrepresentstherequiredvaluewhich is 0.9834 asshownin Table2.1 (boldvalue).
Theexactareatotheleftof2.13isshownin Fig.2.3 (shadedarea).
Table2.1 TheareatotheleftofaZvalueof2.13.
1.20.88490.88690.88880.89070.89250.89440.89620.8980.89970.9015 1.30.90320.90490.90660.90820.90990.91150.91310.91470.91620.9177
1.40.91920.92070.92220.92360.92510.92650.92790.92920.93060.9319
2.20.98610.98640.98680.98710.98750.98780.98810.98840.98870.989
Showingtheareatotheleftof2.13.
Example2.2:ComputetheareatotherightofaZvalue: Computethearea underthestandardnormalcurvetotherightofapositiveZvalueof2.03.
FindingtheareatotherightofapositiveZvalueof2.03requiresusingTableA intheAppendixforthestandardnormal.Thevalue“2.03”shouldbedividedinto twopieces,thefirstpieceis“2.0”andthesecondis“0.03.”Theexactareatothe rightof2.03canbecomputedemployingthestepsbelow.
● Thefirststepistosearchforthepositionof“2.0”inthefirstcolumnof Table2.2 labeled Ztospecifythefirstpiece“2.0”ofthenumber2.03(highlightedrow)[Table2.2 isaportionofthestandardnormaltableintheAppendix(TableA)].
● Thesecondstepinfindingtheareaistomoveontherowof“2.0”tothecolumnlabeled “0.03”(highlightedcolumn),thepointofintersectionrepresentstheareatotheleftof 2.03whichis“0.9788”asshownin Table2.1 (boldvalue).
Figure2.3