AFFINE ARITHMETICBASEDMETHODS FORUNCERTAIN POWERSYSTEM ANALYSIS
ALFREDOVACCARO
ANTONIOPEPICIELLO
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2022ElsevierInc.Allrightsreserved.
MATLAB® isatrademarkofTheMathWorks,Inc.andisusedwithpermission. TheMathWorksdoesnotwarranttheaccuracyofthetextorexercisesinthisbook. Thisbook’suseordiscussionofMATLAB® softwareorrelatedproductsdoesnotconstitute endorsementorsponsorshipbyTheMathWorksofaparticularpedagogicalapproachorparticular useoftheMATLAB® software.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans, electronicormechanical,includingphotocopying,recording,oranyinformationstorageand retrievalsystem,withoutpermissioninwritingfromthepublisher.Detailsonhowtoseek permission,furtherinformationaboutthePublisher’spermissionspoliciesandourarrangements withorganizationssuchastheCopyrightClearanceCenterandtheCopyrightLicensingAgency, canbefoundatourwebsite: www.elsevier.com/permissions
Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythe Publisher(otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperience broadenourunderstanding,changesinresearchmethods,professionalpractices,ormedical treatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgein evaluatingandusinganyinformation,methods,compounds,orexperimentsdescribedherein.In usingsuchinformationormethodstheyshouldbemindfuloftheirownsafetyandthesafetyof others,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors, assumeanyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterofproducts liability,negligenceorotherwise,orfromanyuseoroperationofanymethods,products, instructions,orideascontainedinthematerialherein.
ISBN:978-0-323-90502-2
ForinformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: CharlotteCockle
AcquisitionsEditor: GrahamNisbet
EditorialProjectManager: SaraValentino
ProductionProjectManager: ManjuThirumalaivasan
Designer: MarkRogers
TypesetbyVTeX
Preface xi Acknowledgmentsxiii
1.Uncertaintymanagementinpowersystems1
1.1. Samplingmethods2
1.2. Analyticalmethods3
1.3. Approximatemethods3
1.4. Non-probabilisticmethods4 References6
2.Elementsofreliablecomputing9
2.1. Intervalarithmetic9
2.2. Affinearithmetic10
2.3. SolvinguncertainequationsbyAA14
2.4. Reliablesolutionofnon-linearequations16
2.5. Reliablesolutionsofconstrainedoptimizationproblems18 References22
3.Uncertainpowerflowanalysis23
3.1. Problemformulation24
3.2. Affinearithmeticbasedsolutionofthepowerflowequations25
3.3. Numericalresults29
3.4. Robustformulationofthepowerflowequations39
3.5. Casestudy42 References47
4.Uncertainoptimalpowerflowanalysis49
4.1. Mathematicalbackground49
4.2. Numericalresults55
4.3. Robustformulationofoptimalpowerflowproblems58
4.4. Casestudy62
4.5. Remarks63 References63
5.UnifiedAA-basedsolutionofuncertainPFandOPFproblems65
5.1. Theoreticalframework65
5.2. Applications70
5.3. Numericalresults72
5.4. Computationalrequirements79
5.5. Remarks79 References79
6.Uncertainpowersystemreliabilityanalysis81
6.1. MarkovChains82
6.2. UncertainMarkovChainsanalysisbyAA85
6.3. Casestudies88 References91
7.Uncertainanalysisofmulti-energysystems93
7.1. Optimalschedulingofanenergyhub94
7.2. Casestudy98 References104
8.Enablingmethodologiesforreducingthecomputationalburden inAA-basedcomputing105
8.1. PFanalysis105
8.2. OPFanalysis106
8.3. AA-basedcomputing106
8.4. Numericalresults108
8.5. Remarks122 References122
9.Uncertainvoltagestabilityanalysisbyaffinearithmetic123
9.1. AA-basedcalculationofPVcurves128
9.2. Numericalresults129
9.3. Remarks133 References133
10.Reliablemicrogridsschedulinginthepresenceofdata uncertainties135
10.1. Deterministicoptimization136
10.2. Robustoptimization138
10.3. Affinearithmetic-basedoptimization138
10.4. Numericalresultsanddiscussion140 10.5. Remarks143
References143
Index 145
InmemoryofmyFather(AlfredoVaccaro)
Tomyfamily(AntonioPepiciello)
Preface
Reliablepowersystemoperationrequirescomplexnumericalanalyses aimedatstudyingandimprovingthesecurityandresiliencyofelectrical grids.Manymathematicaltoolscansupportpowersystemoperatorsinaddressingthischallengingissue,suchaspowerflowandoptimalpowerflow analyses,static/dynamicsecurityassessment,andpowersystemreliability analysis.Theconventionalformalizationoftheseproblemsisbasedonthe assumptionthattheinputdataarespecifiedbydeterministicparameters, whichshouldbedefinedbytheanalysteitherfromasnapshotofthepower systemorinferredonthebasisofsomeassumptionsontheanalyzedsystem.
Consequently,thesolutionscomputedbysolvingthesedeterministic problemsarerigorouslyvalidonlyfortheconsideredpowersystemstate, whichrepresentsalimitedsetofsystemconditions.Thus,whentheinput dataareuncertain,numerousscenariosneedtobeevaluatedinthetaskof computingrobustproblemsolutions.
Toaddressthisproblem,thisBookintroducesthebasicelementsof AffineArithmetic-basedcomputing,outliningitsimportantroleinuncertainpowersystemanalysis.
AffineArithmeticisanenhancedmodelforreliablecomputingin whichtheinputdataandtheproblemvariablesarerepresentedbyaffine combinationsofprimitivenoisesymbols,whicharesymbolicvariablesrepresentingtheindependentuncertaintysourcesaffectingtheinputdata(i.e. exogenousuncertainties),orapproximationerrorsgeneratedduringthe computations(i.e.endogenousuncertainties).
AfterintroducingthemathematicalfoundationsofAffineArithmetic, itsdeploymentinsolvingthemostfundamentalpowersystemoperation problemsispresentedanddiscussed.Inthesecontextstheadoptionof AffineArithmetic-basedcomputingallowsformalizingthepowersystem stateequationsinamoreconvenientformalismcomparedtotheconventionalandwidelyusedformulationadoptedininterval-basedNewton methods.Thankstothisfeatureareliableestimationofthesolutionshull canbereliablyestimatedbyconsideringtheparameteruncertaintycorrelationsandthecumulativeeffectofalltheuncertaintysources.
Theseresultscanbegeneralizedinthetaskofsolvingagenericmathematicalprogrammingproblemunderuncertainty,whichcanbeformalized byanequivalentdeterministicproblem,definingacoherentsetofminimization,equality,andinequalityaffinearithmetic-basedoperators.This
AffineArithmetic-basedformulationallowscomputingfeasibleandrobust solutionenclosuresofcomplexuncertainoptimizationproblems,reducing theapproximationerrors,andtheestimationover-conservatism.
Thedeploymentofthiscomputingparadigmisappliedforsolvinga widerangeofpowersystemoperationproblems,asfarasoptimalpower flow,voltagestabilityanalysis,equipmentreliabilityassessment,andmicrogridschedulingareconcerned.
Finally,toreducethecomputationalburdenofAffineArithmetic-based computing,thisBookanalyzestheroleofformalmethodsforknowledge discoveryfromhistoricalpowersystemoperationdata,whichcouldalso playanimportantroleinoptimallyidentifyingtheparametersoftheaffine formsdescribingtheuncertaininputparameters.
Tothisaim,adataprocessingtechnique-basedonPrincipalcomponent Analysisisintroducedforidentifyingcomplexfeaturesandhiddenrelationshipspotentiallydescribingregularitiesintheproblemsolutions,hence reducingtheproblemcardinalityandthealgorithmcomplexity.Thanksto thistechniqueitisalsopossibletodefineaformalconnectionbetween theprincipalcomponentsandthenoisesymbolsoftheuncertainvariables, whichfurnishaneffectivemethodfortheoptimalidentificationofthe affineforms.
AlfredoVaccaro
Acknowledgments
TheAuthorswishtothankProf.ClaudioA.Canizareswhoinspiredour researchwork.SpecialthanksgotoProf.KankarBhattacharyaandDr. JuanCarlosMunozfortheirvaluablecontributionsinapplyingAffine Arithmetic-basedcomputinginvoltagestabilityanalysis,andProf.Alberto Berizziforhisusefulinsightsabouttherelationsbetweenaffinearithmetic androbustoptimization.
Uncertaintymanagementin powersystems
Stateoftheartandenablingmethodologies
Powersystemoperatorsrequiresophisticatednumericaltoolsaimedatanalyzingthecurrentandtheexpectedoperationstates,guaranteeingsecure andreliablegridoperation.Inthiscontext,numericalprogrammingrepresentsthemathematicalbackbonesupportingthemostfundamentalpower engineeringtools,suchasPowerFlow(PF)andOptimalPowerFlow (OPF)analyses,stateestimation,voltageandfrequencyregulation,and contingencyanalysis.Thesestudiescouldalsosupportthedevelopmentof advancedoperationstoolsforintegratedsystemsmanagement,suchasreliabilityandresilienceassessmentofmulti-carrierenergysystems,oroptimal energyflowmanagementindistributedenergyhubs,whicharerelevant applicationsinthelightoftheevolutionofmodernpowergridstowards moreintegrated,smarter,andsustainablesystems.
Numericalprogrammingproblemsinpowersystemanalysisareconventionallyformalizedbydeterministicmodels,whoseparametersareassumed tobeexactlyknownonthebasisofseveralassumptionsonthecurrent powersystemstate.However,boththemodelsandtheirparametersareintrinsicallyaffectedbycomplexandcorrelateduncertaintysources,which canberoughlyclassifiedinaleatoryandepistemic.Theformerisirreducible,i.e.ithastobeacceptedandcannotbecontrolled,whereasthe latterisrelatedtotheaccuracyofmeasurements,models,andparameters characterizingthesystem.
Uncertaintysourcesaremostlyrelatedtothecomplexdynamicsof activeandreactivepowersupplyanddemand,whichmayvaryduetodifferentcauses[1]:
• Variablegenerationmixdependingonthemarketclearing.
• Theincreasingpenetrationofnon-dispatchablegeneratorsbasedon renewableenergysources.
• Theunpredictablefluctuationofloadsduetounexpectedevents.
• Theincreasinggeographicaldispersionofenergygeneration.
AffineArithmetic-BasedMethodsforUncertainPowerSystemAnalysis https://doi.org/10.1016/B978-0-32-390502-2.00008-9
Copyright©2022ElsevierInc. Allrightsreserved. 1
Thepresenceofuncertaintieshinderstheeffectivenessofdeterministic methods.Indeed,theycanaffecttheproblemsolutionstoaconsiderable extent.Hence,reliablesolutionparadigms,whichincorporateinformation aboutdatauncertaintyarerequired.Theseparadigmsallowtocharacterize theuncertaintyassociatedtoinputdata,andtoassessitspropagationover iterativecalculations,henceprovidingacertainlevelofconfidenceabout theproblemsolutions,andassessingtheirsensitivitytochangesininput datauncertainties.
Thescientificliteratureproposesawiderangeofmethodologiestohandleuncertaintyinpowersystemanalysis[2,3],andthemostpromisingare summarizedinthenextsections.
1.1Samplingmethods
Samplingmethodsconsistingeneratingasetofscenarios,givensome randomvariableswithadefinedprobabilitydistributionfunction.Monte Carloisthebestexampleofsuchmethods:althoughitcanprovideveryaccuratesolutions,itinvolvesalargecomputationalburden,whichisdueto thelargenumberofproblemsthathavetobesolved,oneforeachscenario [4].Thisconditionpreventsitseffectiveutilizationforlarge-scalepower systemanalysis,wherethecomputationalburdencouldbeprohibitively expensive[5,6].
Duetothisreason,muchresearchefforthasbeenputinproposingenhancementsofMonteCarlomethods,whichtrytoimprovethesampling processatthecostofacceptinganincreasinglevelofrisk.Forexample, [7]integratesLatinhypercubesamplingandCholeskydecompositioninthe MonteCarlomethod.In[8],ahybridsolutionalgorithmbasedondeterministicannealingexpectationmaximizationalgorithmandMarkovChain MonteCarloisproposed.Correlationbetweenwindvariablesthroughan extendedLatinhypercubesamplingispresentedin[9].Finally,chanceconstrainedprogrammingproblemscanbeemployedforsolvinguncertain OPFanalysis,inwhichMonteCarloanddeterministicoptimizationare combinedtohandlethestochasticfeaturesoftheinputvariables[10].
Aspreviouslyhighlighted,thesemethodsrequirethedefinitionofa propertrade-offbetweenaccuracyandcomputationalburden,hencethey areusefulonlywhenadefineddegreeofriskcanbeaccepted.
1.2Analyticalmethods
Analyticalmethodsrequireasimplificationoftherealproblemandacertain numberofassumptionsinordertomaketheproblemtractable[11].Some simplificationscanbeobtainedbycharacterizingtheoutputrandomvariablesthroughmulti-linearization[12],convolutiontechniquesorFourier Transform[13].
Anexampleofthesemethodsisthecumulantmethod[14,15]orits combinationwiththeGram-Charlierexpansion[15]ortheintegrationof VonMisesfunctions,tohandlediscretedistributions[16].Anotherformulationispresentedin[6],throughchance-constrainedprogrammingmodel. However,manyofthesetechniquesrequirethelinearizationofPFequations,whicharenon-linear,andthisprocessgeneratesadditionalinaccuracy.
Theshortcomingsofanalyticaltechniquesaremultiple,asdiscussedin [17–20].Oneexamplecouldbethecommonassumptionofstatisticalindependenceoftheinputdata,ortheapproximationoftherealprobability distributionwithanidealrandomvariable.Inthissense,thelackofdeterminism,whichischaracteristicofpowersystems,especiallyasanincreasing amountofdispersedgeneratorsisbeinginstalled,canbeaprobleminthe correctformulationoftheprobabilisticmodels.Furthermore,whenvalidationofthesetechniquesisperformed,theassumptionsmadeareoftennot supportedbyempiricalevidence.
1.3Approximatemethods
Approximatemethods,suchaspointestimatemethods,havebeenproposed aspossiblealternativestobothanalyticalandsamplingmethods[21].These methodsaimatapproximatingthestatisticalpropertiesofthevariablesresultingasoutputsofPFandOPFanalyses.Forexample,incaseoffirstor secondordermethod,themeanandthevariancearepropagatedthrough thecalculations,byusingTaylorseriesexpansion[22].
Incaseofthepointestimationmethods,acertainnumberofdeterministicproblems,inparticular m,whichisthenumberofuncertainvariables, hastobesolvedinordertoestimatethestatisticalmomentsoftheproblem solutions[23].Extensionsofthismethodare,forexample,Hong’spointestimatemethod[24],whicharemuchfasterbuttheiraccuracyisguaranteed onlyforlowuncertaintyranges,andthelinearizationisagoodapproximationonlyaroundthenominaloperationpoint.
Otherapproachesarebasedonprimal-dualinteriorpointmethod[25], whichallowscomputingthesensitivityoftheuncertainparameterswith
respecttotheproblemsolution.Robustdesigntheorycanalsobeusedto approximateOPFsolutionsinthepresenceofmultipleuncertaintysources [26].
Finally,approximatemethodshavetheirshortcomingsaswell.Forexampletwo-pointestimatemethodsarenotfeasibleforanalyzinglargescale systems,especiallyinthepresenceofalargenumberofrandomvariables.
1.4Non-probabilisticmethods
Thespectrumofavailablemethodsforcarryingoutreliableanalysesin powersystemsinthepresenceofuncertaintysourceshasenrichedoverthe lastdecades.Thetheoryofevidence[27]andthetheoryofpossibility[28] aretwoexamples.
Thesemathematicalformulationsareassociatedtotheimprecisehumanknowledgeaboutthesystem,whichallowsonlyimpreciseestimates ofvaluesandrelationsbetweenvariables[29].Anexampleinpowersystemsisrelatedtowindenergyproduction:indeed,windcanbemeasured onlylocally,butitsspatialdistributionoveralargeareaisdifficultusing probabilities.Additionally,weatherforecastsprovidequalitativeinformation,whichisdifficulttoberepresentedinaprobabilisticway.Therefore, non-probabilisticmodelingandsimulationscanbeusefultopowersystem engineers.
Theapplicationoffuzzy-settheorytopowersystemanalysishasbeen proposedinseveralpapers[30–32].Inthiscase,bothinputdataandconstraintsaremodeledthroughfuzzynumbers,whichareparticularinstances offuzzysets[33].
Self-validatedcomputingisanotherwayofrepresentinguncertainty.Its advantageisthepossibilityofkeepingtrackoftheuncertaintypropagation throughthecalculations.Thispropagationdoesnotrequiremuchinformationabouttheuncertaintysourcesaffectingtheproblemvariables[34].The firstexampleofself-validatedmodelsisIntervalArithmetic(IA),which representseachvariablethroughintervalofrealnumbers,withoutaprobabilitystructure[35].Asetofoperationscanbedefinedovertheseintervals, suchthatthefinalcomputedintervalisguaranteedtocontaintheuncertain valueoftheoutputvariablewhichitrepresents.
IAhasbeenproposedasatoolforhandlinguncertaintyinpowersystems bymanyauthors[18,19,36,37].However,thesolutionobtainedinthiscase isaffectedbythedependencyproblemandthewrappingeffect[34,38], whichcouldreducetheeffectivenessofthemethodintermsofresults
interpretation.ThisismainlyduetotheimpossibilityofIAtorepresent correlationsbetweenuncertainvariables.Theseproblemsrequirespecial structuresoftheJacobianmatrices(e.g.M-matrices,H-matrices,diagonallydominantmatrices,tri-diagonalmatrices)[39]inorderforIAtobe effectiveinsolvingpowersystemoperationproblems,whicharecommonly notfoundinrealsystems.
Toovercometheselimitations,AffineArithmetic-based(AA)methods foruncertainpowersystemanalysishavebeenproposed.Inthisparadigm, eachvariableisdefinedbyafirstdegreepolynomial,representedbya centralvalueandanumberofpartialdeviations,eachonerepresenting astatisticalindependentuncertaintysource.Inthisway,theequationsdescribingtheproblemunderstudycanbeexpressedmoreconvenientlyand thecorrelationbetweentheuncertaininputvariablescanbeeffectively takenintoaccount.
Themainadvantageofthisparadigmisthatitissuitableforsolvinglarge-scaleproblems,bothcomputationallyandintermsofaccuracy androbustnessoftheobtainedsolution.In[40]andin[41],AAmethods havebeenadoptedtosolveuncertainPFandOPFproblems,byrepresentingallthestateandcontrolvariablesbyaffineforms,withoutassuminga probabilitydensityfunctionforeachofthem.Thisrepresentsapromising alternativetostochasticinformationmanagementinsmartgrids[42].
Severalpaperexploredthisidea,startedin[43],oftheapplicationofAA topowersystemanalysis.In[44],theeffectofnetworkuncertaintieswas processedthroughAAforsolvingthestateestimationprobleminpresence ofbothsynchrophasorsandconventionalmeasurements.
In[45],thecomplementarityconditionswereusedtorepresentbus voltagecontrolthroughanAA-basedmodel,whichreturnedoperationintervalsforPFvariablesinthepresenceofuncertainty.In[46],anuncertain PFproblemissolved,byformalizingitthroughintervalPFandsolvinga quadraticprogrammingoptimization.
Additionalapplicationsandbenefitsderivingfromtheapplicationof AAinpowersystemshavebeenproposedin[40,41,47–49].Inparticular, someofthemareplanningandoperationinthepresenceofalargepenetrationofrenewableenergysources,electricvehiclesintegrationordemand response.ThemainadvantageofAAoverIAderivesbyitscapacityin narrowingthetoleranceintervaloftheproblemsolutions,whichIA-based computationstendtoover-estimate,especiallywhenintegratediniterative solutionschemes.
Inthisbook,solutionmethodologiesbasedonAAareintroducedto solvethemostfundamentalpowersystemoperationproblems.AAisan enhancedmodelofself-validatednumericalanalysis,whichrepresentsthe variablesofinterestasaffinecombinationsofprimitivevariablesdescribingstatisticalindependentuncertaintysources.Thesecombinationsallow describingtheeffectsofcomplexandcorrelatedsourcesofexogenousuncertainty,andapproximationerrorsinvolvedinthecomputations.
Thismethodologycanbeenhancedbycombiningitwithadvanced techniquesforinformationdiscoveryanddatacompression,suchasprincipalcomponentanalysis.Inthisway,theparametersoftheaffineforms describingtheinputdatauncertaintycanberigorouslyidentifiedonthe basisofhistoricalinformation,andthecardinalityoftheconsideredproblemcanbesensiblyreduced.
References
[1]G.Verbic,C.Cañizares,Probabilisticoptimalpowerflowinelectricitymarketsbased onatwo-pointestimatemethod,IEEETransactionsonPowerSystems21(4)(2006) 1883–1893.
[2]P.Chen,Z.Chen,B.Bak-Jensen,Probabilisticloadflow:Areview,in:Proceedings ofthe3rdInternationalConferenceonDeregulationandRestructuringandPower Technologies,DRPT2008,2008,pp.1586–1591.
[3]B.Zou,Q.Xiao,SolvingprobabilisticoptimalpowerflowproblemusingquasiMonte Carlomethodandninth-orderpolynomialnormaltransformation,IEEETransactions onPowerSystems29(1)(2014)300–306.
[4]M.Hajian,W.Rosehart,H.Zareipour,ProbabilisticpowerflowbyMonteCarlo simulationwithLatinsupercubesampling,IEEETransactionsonPowerSystems28(2) (2013)1550–1559.
[5]C.Su,Probabilisticload-flowcomputationusingpointestimatemethod,IEEETransactionsonPowerSystems20(4)(2005)1843–1851.
[6]H.Zhang,P.Li,Probabilisticanalysisforoptimalpowerflowunderuncertainty,IET Generation,Transmission&Distribution4(5)(2010)553–561.
[7]H.Yu,C.Chung,K.Wong,H.Lee,J.Zhang,Probabilisticloadflowevaluationwith hybridLatinhypercubesamplingandCholeskydecomposition,IEEETransactionson PowerSystems24(2)(2009)661–667.
[8]H.Mori,W.Jiang,AnewprobabilisticloadflowmethodusingMCMCinconsiderationofnodalloadcorrelation,in:Proceedingsofthe15thInternationalConference onIntelligentSystemApplicationstoPowerSystems,2009,pp.1–6.
[9]H.Yu,W.D.Rosehart,Probabilisticpowerflowconsideringwindspeedcorrelation ofwindfarms,in:Proceedingsofthe17thPowerSystemsComputationConference, 2011,pp.1–7.
[10]M.Hajian,W.D.Rosehart,H.Zareipour,ProbabilisticpowerflowbyMonteCarlo simulationwithLatinsupercubesampling,IEEETransactionsonPowerSystems28(2) (2012)1550–1559.
[11]A.Schellenberg,W.Rosehart,J.Aguado,Cumulant-basedprobabilisticoptimalpower flow(P-OPF)withGaussianandgammadistributions,IEEETransactionsonPower Systems20(2)(2005)773–781.
[12]A.S.Meliopoulos,G.J.Cokkinides,X.Y.Chao,Anewprobabilisticpowerflowanalysismethod,IEEETransactionsonPowerSystems5(1)(1990)182–190.
[13]R.Allan,A.daSilva,R.Burchett,Evaluationmethodsandaccuracyinprobabilistic loadflowsolutions,IEEETransactionsonPowerApparatusandSystemsPAS-100(5) (1981)2539–2546.
[14]R.Allan,M.Al-Shakarchi,Probabilistictechniquesinacload-flowanalysis,ProceedingsoftheInstitutionofElectricalEngineers124(2)(1977)154–160.
[15]P.Zhang,S.T.Lee,Probabilisticloadflowcomputationusingthemethodofcombined cumulantsandGram-Charlierexpansion,IEEETransactionsonPowerSystems19(1) (2004)676–682.
[16]L.Sanabria,T.Dillon,StochasticpowerflowusingcumulantsandVonMisesfunctions,InternationalJournalofElectricalPower&EnergySystems8(1)(1986)47–60.
[17]A.Dimitrovski,K.Tomsovic,Boundaryloadflowsolutions,IEEETransactionson PowerSystems19(1)(2004)348–355.
[18]F.Alvarado,Y.Hu,R.Adapa,Uncertaintyinpowersystemmodelingandcomputation,in:ProceedingsoftheIEEEInternationalConferenceonSystems,Manand Cybernetics,1992,pp.754–760.
[19]A.Vaccaro,D.Villacci,Radialpowerflowtoleranceanalysisbyintervalconstraint propagation,IEEETransactionsonPowerSystems24(1)(2009)28–39.
[20]Z.Wang,F.Alvarado,Intervalarithmeticinpowerflowanalysis,IEEETransactions onPowerSystems7(3)(1992)1341–1349.
[21]M.Madrigal,K.Ponnambalam,V.Quintana,Probabilisticoptimalpowerflow,in: ProceedingsoftheIEEECanadianConferenceonElectricalandComputerEngineering,vol.1,1998,pp.385–388.
[22]X.Li,Y.Li,S.Zhang,Analysisofprobabilisticoptimalpowerflowtakingaccount ofthevariationofloadpower,IEEETransactionsonPowerSystems23(3)(2008) 992–999.
[23]G.Verbic,C.Canizares,Probabilisticoptimalpowerflowinelectricitymarketsbased onatwo-pointestimatemethod,IEEETransactionsonPowerSystems21(4)(2006) 1883–1893.
[24]J.M.Morales,J.Perez-Ruiz,Pointestimateschemestosolvetheprobabilisticpower flow,IEEETransactionsonPowerSystems22(4)(2007)1594–1601.
[25]A.Mohapatra,P.Bijwe,B.Panigrahi,Optimalpowerflowwithmultipledatauncertainties,ElectricPowerSystemsResearch95(2013)160–167.
[26]C.Boonchuay,K.Tomsovic,F.Li,W.Ongsakul,Robustoptimization-basedDC optimalpowerflowformanagingwindgenerationuncertainty,AIPConferenceProceedings1499(1)(2012)31–35.
[27]G.Shafer,AMathematicalTheoryofEvidence,vol.1,PrincetonUniversityPress, Princeton,1976.
[28]L.A.Zadeh,Fuzzysets,InformationandControl8(3)(1965)338–353.
[29]P.Smets,Imperfectinformation:Imprecisionanduncertainty,in:UncertaintyManagementinInformationSystems,Springer,1997,pp.225–254.
[30]P.Bijwe,G.V.Raju,Fuzzydistributionpowerflowforweaklymeshedsystems,IEEE TransactionsonPowerSystems21(4)(2006)1645–1652.
[31]V.Miranda,J.Saraiva,Fuzzymodellingofpowersystemoptimalloadflow, in:ProceedingsofthePowerIndustryComputerApplicationConference,1991, pp.386–392.
[32]P.Bijwe,M.Hanmandlu,V.Pande,Fuzzypowerflowsolutionswithreactivelimits andmultipleuncertainties,ElectricPowerSystemsResearch76(1)(2005)145–152.
[33]X.Guan,W.E.Liu,A.D.Papalexopoulos,Applicationofafuzzysetmethodinan optimalpowerflow,ElectricPowerSystemsResearch34(1)(1995)11–18.
[34]J.Stolfi,L.H.DeFigueiredo,Self-validatednumericalmethodsandapplications,in: ProceedingsoftheMonographfor21stBrazilianMathematicsColloquium,Citeseer, 1997.
[35]R.Moore,MethodsandApplicationsofIntervalAnalysis,vol.2,SIAM,1979.
[36]S.Wang,Q.Xu,G.Zhang,L.Yu,Modelingofwindspeeduncertaintyandinterval powerflowanalysisforwindfarms,AutomationofElectricPowerSystems33(1) (2009)82–86.
[37]L.Pereira,V.DaCosta,A.Rosa,Intervalarithmeticincurrentinjectionpowerflow analysis,InternationalJournalofElectricalPower&EnergySystems43(1)(2012) 1106–1113.
[38]M.Neher,FromintervalanalysistoTaylormodels—Anoverview,in:Proceedingsof theInternationalAssociationforMathematicsandComputersinSimulation,2005.
[39]L.V.Barboza,G.P.Dimuro,R.H.Reiser,Towardsintervalanalysisoftheloaduncertaintyinpowerelectricsystems,in:ProceedingsoftheInternationalConferenceon ProbabilisticMethodsAppliedtoPowerSystems,2004,pp.538–544.
[40]A.Vaccaro,C.A.Cañizares,K.Bhattacharya,Arangearithmetic-basedoptimization modelforpowerflowanalysisunderintervaluncertainty,IEEETransactionsonPower Systems28(2)(2013)1179–1186.
[41]M.Pirnia,C.A.Cañizares,K.Bhattacharya,A.Vaccaro,Anaffinearithmeticmethod tosolvethestochasticpowerflowproblembasedonamixedcomplementarityformulation,IEEETransactionsonPowerSystems29(6)(2014)2775–2783.
[42]H.Liang,A.K.Tamang,W.Zhuang,X.Shen,Stochasticinformationmanagementin smartgrid,IEEECommunicationsSurveysandTutorials16(3)(2014)1746–1770.
[43]A.Vaccaro,C.A.Cañizares,D.Villacci,Anaffinearithmetic-basedmethodologyfor reliablepowerflowanalysisinthepresenceofdatauncertainty,IEEETransactionson PowerSystems25(2)(2010)624–632.
[44]C.Rakpenthai,S.Uatrongjit,S.Premrudeepreechacharn,Stateestimationofpower systemconsideringnetworkparameteruncertaintybasedonparametricintervallinear systems,IEEETransactionsonPowerSystems27(1)(2012)305–313.
[45]M.Pirnia,C.A.Cañizares,K.Bhattacharya,A.Vaccaro,Anovelaffinearithmetic methodtosolveoptimalpowerflowproblemswithuncertainties,in:Proceedingsof theIEEEPowerandEnergySocietyGeneralMeeting,2012,pp.1–7.
[46]R.Bo,Q.Guo,H.Sun,W.Wu,B.Zhang,Anon-iterativeaffinearithmeticmethodologyforintervalpowerflowanalysisoftransmissionnetwork,Proceedingsofthe ChineseSocietyforElectricalEngineering33(19)(2013)76–83.
[47]S.Wang,L.Han,P.Zhang,Affinearithmetic-baseddcpowerflowforautomatic contingencyselectionwithconsiderationofloadandgenerationuncertainties,Electric PowerComponentsandSystems42(8)(2014)852–860.
[48]G.Wei,L.Lizi,D.Tao,M.Xiaoli,S.Wanxing,Anaffinearithmetic-basedalgorithm forradialdistributionsystempowerflowwithuncertainties,InternationalJournalof ElectricalPower&EnergySystems58(2014)242–245.
[49]T.Ding,H.Z.Cui,W.Gu,Q.L.Wan,Anuncertaintypowerflowalgorithmbasedon intervalandaffinearithmetic,AutomationofElectricPowerSystems36(13)(2012) 51–55.
Elementsofreliablecomputing
Theoreticalfoundations
2.1Intervalarithmetic
InIA,eachvariable x isassumedtobe“unknownbutbounded”inan intervalofrealnumbers X =[xinf , xsup ],alsoknownasthetoleranceof x Thefollowingtheoremisofforemostimportancetodefineoperationson intervals[1]:
Theorem2.1 (FundamentalinvariantofrangeanalysisforIA). ∀ : p → q ,globallyLipschitzwithboundedslope.Thereexistsanintervalextension I : p → q suchthat:
Extendingelementaryoperations,suchassumsorproducts,tointervals istrivial.Forexample,giventwointervals X
[
],somebasicoperationsare: • Sum:
Difference:
Product:
• Division:
Morecomplexfunctionscanbeobtainedbycomposingtheseprimitive operators[1,2].ThankstoTheorem 2.1,theintervalresultingfromthese operationsisguaranteedtoenclosetherealrangeoffunctionvalues.
AffineArithmetic-BasedMethodsforUncertainPowerSystemAnalysis https://doi.org/10.1016/B978-0-32-390502-2.00009-0
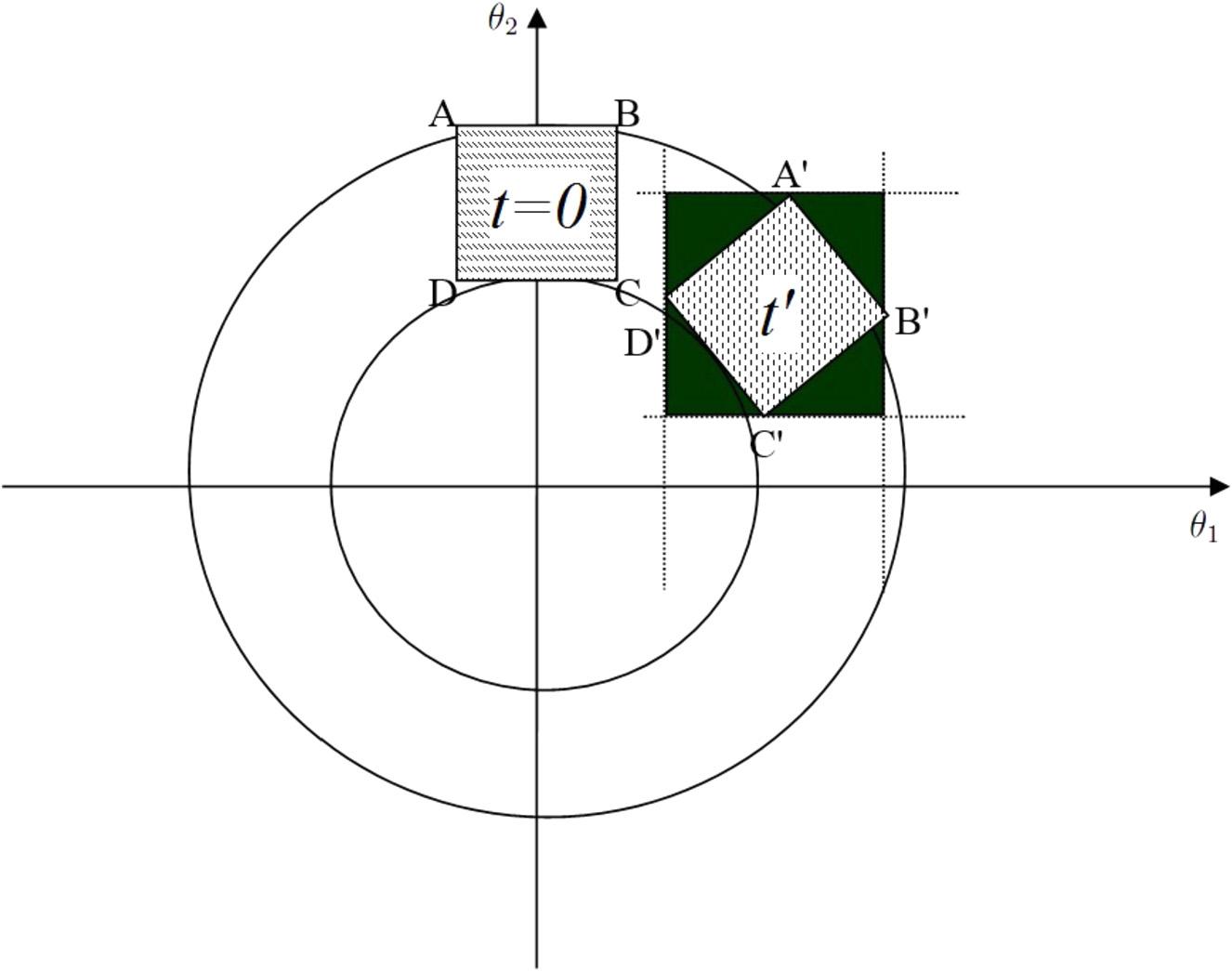
IAhasbeenappliedtosolvesystemsoflinear[3,4]andnon-linear equations[5],andoptimizationproblems[6,7].Theobtainedsolutions, however,canyieldunexpectedresults[8,9],duetothelackofIAin representingthecorrelationbetweenuncertainvariables,whichleadsto thewrappingproblem,asillustratedinFig. 2.1 [9].Thisproblemcanbe demonstratedbyconsideringanharmonicoscillatorevolvingthroughthe statespace ˙ x1 = x2 , ˙ x2 =−x1 .At t = 0,itisrepresentedasarectangle, whoselengthandheightareparalleltocartesianaxes.Sincetheevolution oftherectangleleadstoanotheronewhichisnotparalleltotheaxes,the evolutionoftheintervalat t requiresaddingaseriesofspuriousstates, representedbytheblackregion(rotatedrectangle) A B C D .Duetothis reason,theevolutionoftheinterval,inafewiterations,diverges,covering theentirephasespace.
Anotherexampleisgivenbythissimpleoperation:
Theresultingintervalismuchwiderthanthetruerange,andlongcomputationchainsmayleadtoaberrantsolutions.Thisphenomenonrequires adoptingspecialcomputingtechniques[10].
Finally,the“dependencyproblem”isanotherlimitingaspectofinterval computation,whichisaconsequenceofthedefinitionofthedifference operator(2.2): X X =[xinf , xsup
ThisproblemisaconsequenceoftheinabilityofIAindiscriminating relationsbetweenuncertaintysources,whicharealwaysassumedtobeindependent.Iftheintervalvariablesareindependent,thentheresultsare correct,suchasfor X1 =[1, 2] and X2 =[1, 2]:inthiscase,theirdifference X1 X2 =[−1, 3],leadstocorrectresults.Ontheotherhand,iftheinterval variablesarethesame,theoverestimationerrorisextremelylarge.
Toaddresstheselimitations,moreadvancedparadigms,basedonAA, willbediscussedinnextsection.
2.2Affinearithmetic
AA,whichhasbeenintroducedin[2],isaself-validatedcomputingmethod thatallowsmodelingerrors,imprecisedata,andtruncationerrors.The
Figure2.1 DynamicbehaviorofanoscillatoranalyzedthroughIA.
approachoriginatesfromIA,butitkeepstrackofcorrelationsbetweenthe uncertainvariables.Forthisreason,theresultingboundsaremuchtighter andthedivergenceofthesolutionintervalsobservedinIAcanbeavoided ormitigated[11].
InAA,anuncertainvariable x isrepresentedbyanaffineform,which isafirstdegreepolynomial:
where x0 and xk areknownrealcoefficientsrepresentingthecentralvalue andthepartialdeviationsoftheaffineform ˆ x,respectively.
Thevariables εk ,calledthenoisesymbols,aredefinedovertheinterval [−1, 1].Thenoisesymbolsrepresentindependentuncertaintysourcesaffectingtheproblemvariables,whichcanbeinducedbycomputationerrors orexogenousuncertainsources.
Givenanaffineform,itcanbeconvertedtoanintervalbydefiningthe radius rad ( ˆ x),theupperbound x,thelowerbound x,andtherange |X |
Operationsonaffineformsrequirethereplacementofrealoperators withtheirassociatedAA-basedversion.Anaffineoperator ( ˆ x, ˆ y) canbe definedtomapagenericfunction (x, y) totheaffinedomain.Thisallows computinganaffineformfor ζ = (x, y),whichiscoherentwiththeinput affineforms ( ˆ x, ˆ y)
Anusefulfeatureoflinearfunctionsofaffineforms,isthattheiraffine representationcanbeobtainedbyrearrangingalltheoriginalnoisesymbols intoanaffineform,asinthefollowingequations:
Unfortunately,non-linearfunctionsdonotallow ζ tobeexpressedonly intermsoftheoriginalnoisesymbols:
Inthiscase,aproperapproximatingaffinefunctionshouldbedefined:
thisnon-affineoperatorapproximatesthefunction ( ˆ x, ˆ y) reasonablywell overitsdomain:
wherethelasttermrepresentstheresidualorapproximationerror:
Inordertohandlethisapproximationerror,anadditionalnoisesymbol εp+1 isaddedin(2.17),inordertoproperlyboundthecorresponding approximationerrors:
Furthermore,affineapproximationsofdifferentfunctions,suchas a in(2.16),canbedifferentdependingontherequiredaccuracy,andthe maximumacceptablecomputationalburden.Thefollowingapproximation representsadecenttrade-offbetweentheserequirements:
wheretheunknowncoefficients α , β ,and ξ canbeidentifiedbythefollowingtheorem:
Theorem2.2 (Chebyshevapproximationtheoremforunivariatefunctions). Givenaboundedandtwicedifferentiablefunction ,definedinsome intervalxI =[xinf , xsup ],whosesecondderivativedoesnotchangesigninsidex. Let a ( ˆ x) = α ˆ x + ξ beitsChebyshevaffineapproximationinxI .Then:
= (xsup ) (xinf ) xsup xinf
andthemaximumabsoluteerroris:
Inthiscase,theoptimalcoefficients α and ξ canbeeasilycalculated. Indeed,byconsideringthelineinterpolatingthepoints (xinf , f (xinf )) and (xsup , f (xsup )),theslope d (u) dx = α canbeobtained.
Givenalltheseproperties,AAcanbedefinedasanintermediate paradigmbetweenTaylorformsandzonotopes,asdescribedin[12],which ischaracterizedbyasetofadvantages,lackingfromotherfirstorderapproximationparadigms.
2.3SolvinguncertainequationsbyAA
Aparticularclassofnon-linearoperationisthemultiplicationbetweentwo affineforms ˆ x and ˆ y:
Thisnon-affineoperationistraditionallyapproximatedbyboundingthe secondorderterms:
wherethe R (.) istheradiusoftheaffineform.Startingfromthisresult, anewnoisesymboldescribingtheapproximationerrorcanbedefinedas follows:
Asetofuncertainnon-linearequations,wherethenon-linearityderivesfromthemultiplicationofaffineforms,canbesolvedbyusingthe mathematicaloperatorsproposedin[13].
Inparticular,let’sconsiderthefollowingnon-linearequation:
Thesolutionofthisequationrequirescomputingthecentralvalue x0 and thepartialdeviations x1 and x2 oftheaffineform ˆ x,whichsharesthesame primitivenoisesymbolsoftheknownterm ˆ zF ,suchthat: ˆ x 2 = x 2 0 + 2x0 x1 ε1 + 2x0 x2 ε2 + R ( ˆ x)2 ε3 = 4 + 0.8ε1 + 0.4ε2 (2.25)