https://ebookmass.com/product/advances-in-heat-
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Advances in Nanofluid Heat Transfer Hafiz Muhammad Ali
https://ebookmass.com/product/advances-in-nanofluid-heat-transferhafiz-muhammad-ali/
ebookmass.com
Thermal
Radiation Heat Transfer, 5th Edition
https://ebookmass.com/product/thermal-radiation-heat-transfer-5thedition/
ebookmass.com
Heat Transfer 1 Michel Ledoux
https://ebookmass.com/product/heat-transfer-1-michel-ledoux/ ebookmass.com
In the Weeds B K Borison
https://ebookmass.com/product/in-the-weeds-b-k-borison/
ebookmass.com
The Skunk, the Tibetan Fox and Their Wolf Omega (Omegas of Animals: SD Book 6) Lorelei M. Hart & Wendy Rathbone
https://ebookmass.com/product/the-skunk-the-tibetan-fox-and-theirwolf-omega-omegas-of-animals-sd-book-6-lorelei-m-hart-wendy-rathbone/
ebookmass.com
The Cowboy Texas Ranger's Unexpected Love (The Cowboy Texas Rangers Series Book 3) Janalyn Knight
https://ebookmass.com/product/the-cowboy-texas-rangers-unexpectedlove-the-cowboy-texas-rangers-series-book-3-janalyn-knight/
ebookmass.com
Double-Edged Politics on Women’s Rights in the MENA Region 1st ed. 2020 Edition Hanane Darhour
https://ebookmass.com/product/double-edged-politics-on-womens-rightsin-the-mena-region-1st-ed-2020-edition-hanane-darhour/
ebookmass.com
The Little Book of the Occult Astrid Carvel
https://ebookmass.com/product/the-little-book-of-the-occult-astridcarvel/
ebookmass.com
Dosage Calculations (Jan 1, 2021)_(0176912266)_(Nelson Cengage Adapted) Gloria Pickar (Author)
https://ebookmass.com/product/dosage-calculationsjan-1-2021_0176912266_nelson-cengage-adapted-gloria-pickar-author/
ebookmass.com
https://ebookmass.com/product/tight-hold-vegas-aces-the-tight-endbook-2-lisa-suzanne/
ebookmass.com
AcademicPressisanimprintofElsevier
50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates 525BStreet,Suite1650,SanDiego,CA92101,UnitedStates TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 125LondonWall,London,EC2Y5AS,UnitedKingdom
Firstedition2020
Copyright©2020ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronic ormechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem, withoutpermissioninwritingfromthepublisher.Detailsonhowtoseekpermission,further informationaboutthePublisher’spermissionspoliciesandourarrangementswithorganizationssuch astheCopyrightClearanceCenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions.
Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythe Publisher (otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperience broadenourunderstanding,changesinresearchmethods,professionalpractices,ormedical treatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluating andusinganyinformation,methods,compounds,orexperimentsdescribedherein.Inusingsuch informationormethodstheyshouldbemindfuloftheirownsafetyandthesafetyofothers,including partiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assume anyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability, negligenceorotherwise,orfromanyuseoroperationofanymethods,products,instructions,orideas containedinthematerialherein.
ISBN:978-0-12-820737-6
ISSN:0065-2717
ForinformationonallAcademicPresspublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: Zoe Kruze
AcquisitionsEditor: AshlieJackman
EditorialProjectManager: ChrisHockaday
ProductionProjectManager: AbdullaSait
CoverDesigner: ChristianBilbow
TypesetbySPiGlobal,India
Analysesofbuoyancy-driven convection
TieWei*
DepartmentofMechanicalEngineering,NewMexicoInstituteofMiningandTechnology,Socorro, NM,UnitedStates
*Correspondingauthor:e-mailaddress:Tie.Wei@nmt.edu
Contents
1. Introduction2
2. PredictionofNusseltnumber6
2.1 Lessonsfromforcedconvection12
3. Governingequations14
3.1 Reynoldsaveragedequationsforthemeanflowandheattransport15
3.2 LaminarDHVCsolution18
4. Dimensionalanalysisofbuoyancy-drivenconvection20
4.1 DimensionalanalysisoflaminarDHVC21
4.2 DimensionalanalysisofturbulentDHVC23
5. Reviewofscalingpatchapproach27
5.1 Layerstructureofturbulentchannelflow31
5.2 Stepsinscalingpatchapproach33
6. ScalinganalysisoflaminarDHVC44
7. ScalinganalysisofthemeanmomentumequationinturbulentDHVC48
7.1 Layerstructureofthemeanmomentumbalanceequation48
7.2 PropertiesoftheReynoldsshearstress51
7.3 Outerscalingofthemeanmomentumequation53
7.4 Innerscalingofthemeanmomentumequation59
7.5Mesoscalingofthemeanmomentumequation62
8. Scalinganalysisofthemeanheatequation67
8.1 Layerstructureofthemeanheatequation68
8.2 Propertiesoftheturbulenttemperatureflux Rwθ 70
8.3 Outerscalingofthemeanheatequation71
8.4 Innerscalingofthemeanheatequation75
8.5 Scalingpatchesinthemeanheatequation78
9. NewpredictionofNusseltnumber82
10. Summaryandconclusions86 Acknowledgments89 References89
Abstract
Thisarticleinvestigatesthemultilayerstructureofturbulentflowandheattransportin buoyancy-drivenconvection,andinparticular,introducesarelativelynewscalingpatch approach.Adifferentiallyheatedverticalchannel(DHVC)isusedasanexampleof buoyancy-drivenconvection,anditsmultilayerstructureisfirstqualitativelyinvestigatedbydimensionalanalysis.Inthenear-wallregionofturbulentDHVC,flowandheat transportisstronglyinfluencedbythemoleculardiffusion,andthekinematicviscosity andthermaldiffusivityareimportantcontrolparametersinthedimensionalanalysis. Flowandheattransportintheinnerlayeriscontrolledbytwonondimensionalnumbers:thePrandtlnumberofthefluidandaninnerRichardsonnumber.Awayfromthe wall,flowandheattransportaredominatedbyeddymotions,largelyindependentof moleculardiffusion.ThecontrollingnondimensionalparameterintheouterlayerofturbulentDHVCisanouterRichardsonnumber.ThemultilayerstructureinturbulentDHVC isthenelucidatedquantitativelybythescalingpatchanalysis.Basedonthecharacteristicsofforcebalance,themeanmomentumequationisdividedintothreelayers:an innerlayer,amesolayer,andanouterlayer.TheinnerandouterRichardsonnumbers, derivedfromthedimensionalanalysis,appearnaturallyintheproperlyscaledmean momentumequation.Anothernondimensionalnumberthatappearsnaturallyfrom thescalingpatchanalysisisthefrictionReynoldsnumber.Thecharacteristiclengthscale intheinnerlayerisdirectlyinfluencedbythefrictionReynoldsnumber,distinctively differentfromthatinforcedconvection.Thecharacteristiclengthscaleinthemeso layerisanObukhov-stylelengthscale.Themeanheatequationcanalsobedividedinto multiplelayers.Infact,aninherenthierarchyoflayerstructure(scalingpatches)isrevealedthroughasimpletransformationoftheturbulenttemperatureflux.AnewpredictionoftheNusseltnumberisdevelopedbasedontheinsightgainedfromthe dimensionalanalysisandscalingpatchanalysis.ThenewpredictionisdirectlyconnectedtothemultilayerstructureofheattransportinturbulentDHVCandisfundamentallydifferentfromthetraditionalpower-lawcorrelations.
1.Introduction
Acornerstoneinthestudyofturbulenceistherecognitionthatthe dynamicsofturbulentflowandscalartransportoperateonagreatmany spaceandtimescales(see,e.g.,MoninandYaglom[1],Tennekesand Lumley[2]).Abetterunderstandingofthemultiscalestructureofturbulence iscriticalinimprovingourpredictivecapabilitiesofturbulence,i.e.,predictionofskinfrictionandheattransportrate.Twopowerfultoolstouncover themultiscalenatureofturbulencearedimensionalanalysisandscalinganalysis.Thisarticleappliesthesetoolstoelucidatethemultilayerstructureof turbulentbuoyancy-drivenconvection.Inparticular,oneaimofthisarticle istointroducearelativelynewscalingapproachtobuoyancy-drivenconvection.Thenewapproach,basedonthe“searchofscalingpatches,”was
originallydevelopedforforcedwall-boundedturbulencesuchassheardriventurbulentflowoveraflatplateorpressure-driventurbulentpipe andchannelflow,inaseriesofpapersbyFife,Klewicki,McMurtry, Wei,andcoworkers[3–17].Someconceptsandideasinthescalingpatch approacharesimilartopreviousscalingapproaches,however,thelogical trainsofthoughtinthenewapproacharedistinctlydifferent.
Generallyspeaking,afluidexpandswhenbeingheated,resultingina densitydecrease.Densityinhomogeneitycanalsobegeneratedfromthe mixingoffluidswithdifferentdensities.Inthepresenceofagravitational field,thereisanetforcethatpushesupwardalightfluidsurroundedbya heavierfluid,andthisupwardforceiscalledthebuoyancyforce.Thebuoyancyforcegivesrisetotheascendingofthelighterfluidanddescendingof theheavierfluid.Thebulkfluidmotioninducedbythebuoyancyforceis commonlycalledbuoyancy-drivenconvection.Ifthefluidmotionisdriven solelybybuoyancy,theconvectionisalsocallednaturalconvectionorfree convection.Ifthefluidmotionisdrivenbybothbuoyancyandshearor pressure,theconvectioniscalledmixedconvection.
Buoyancy-drivenconvectionsareencounteredinavarietyofnatural phenomenaandindustryapplications.Examplesincludeatmosphericand oceanicconvection,spaceheatingandcooling,smokeandfirespreading, nuclearreactorcontainment,andsolarcollectors.Therehavebeenanenormousamountofstudiesabouttheeffectsofbuoyancyonflowandheat(or mass)transport.Itisimpossibletogiveinonearticleanexhaustivereviewof buoyancy-drivenflowandheattransport,whichcanbefoundinbooks devotedtothesubject,e.g.byTurner[18],Jaluria[19],Gebhartetal. [20],Kakacetal.[21],MartynenkoandKhramtsov[22],andVerman[23].
Howbuoyancyaffectstheflowandheatormasstransportisofimportant practicalinterest,andisalsoofgreattheoreticalinterest.Tothisday,there arestillnoreliabletoolsforpredictingtheheatormasstransfercoefficientin buoyancy-driventurbulence[24].Oneoftheearlieststudiesofturbulent flowaffectedbybuoyancyisabouttheconvectiveatmosphericboundary layer(ABL)byTaylor[25]andSchmidt[26].AkeyquantityintheunderstandingandpredictionofstratifiedABListheverticaltransportofmomentum,watervapor,sensibleheat,orheatinlatentform[27].Oneofthe landmarksinthedevelopmentofourunderstandingofatmosphericturbulencewastheformationoftheconceptofthe Austausch coefficientby SchmidtandTaylor.Theideawasbuiltontheknowledgeofpressureorshear-drivenwallturbulencedevelopedbyPrandtletal.[27].Whilereasonableforsheardominatedturbulence,theconceptofeddyviscositybased
onlocalpropertiesbecomesmeaninglesswhenthebuoyancyeffectis strong,e.g.,inconvectiveatmosphericboundarylayer[28].Abetterunderstandingoftheunderlyingphysicsinbuoyancy-driventurbulenceiscritical indevelopingmorerobustmodels.
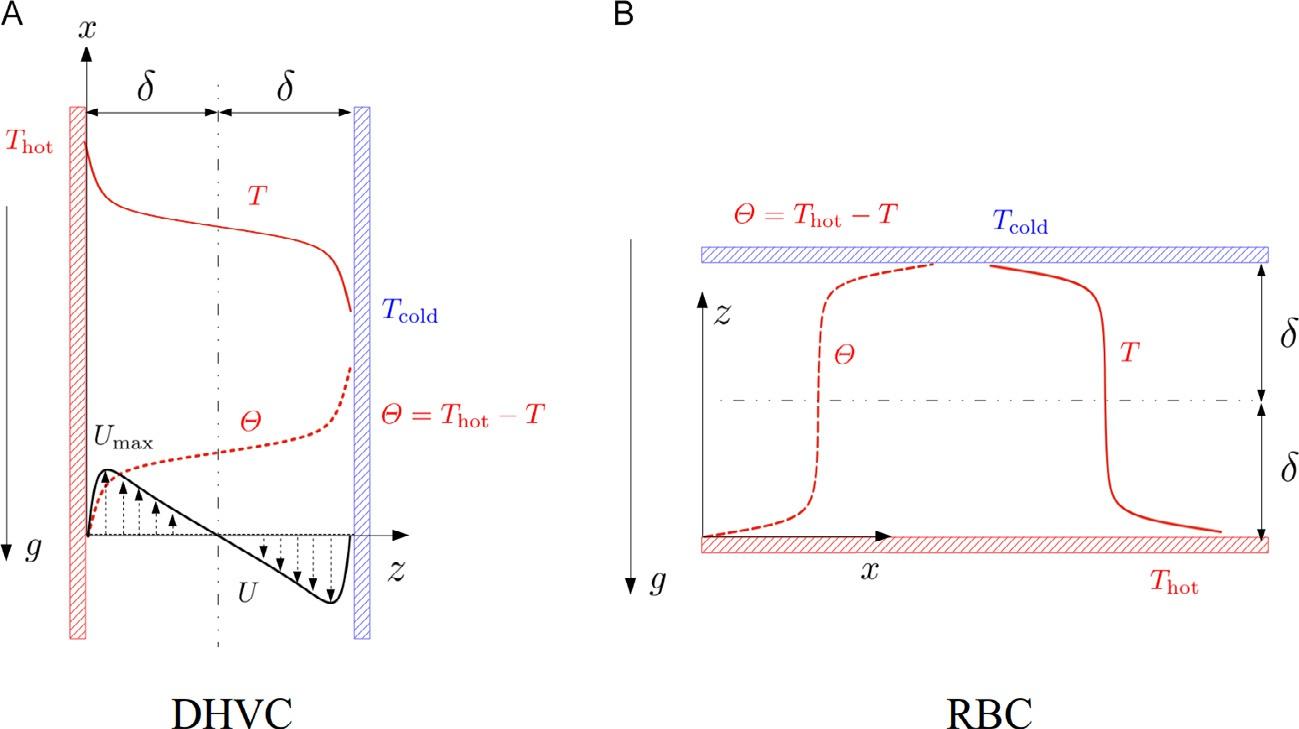
Tounderstandtheessentialphysicsofbuoyancy-driventurbulence, convectionwithsimplegeometryistypicallyusedinphysicalexperiments ornumericalsimulations.Twobuoyancy-drivenconvectionswithsimple geometryareillustratedin Fig1:differentiallyheatedverticalchannel (DHVC)andRayleigh-Benardconvection(RBC).Inbothcases,flow andheattransportoccursbetweentwoparallelplates,whicharemaintained atdifferenttemperatures.InDHVC,thetemperaturegradientisperpendiculartothegravity,butinRBC,thetemperaturegradientisalignedwiththe gravity.InDHVC,hotterfluidascendsalongthehotplateside,andatthe sametime,colderfluiddescendsalongthecoldplateside.Inturbulent RBC,aprominentfeatureistherisingupofhotfluidasplumesandfalling downofcoldfluidasinvertedplumes.
RBChasbeenextensivelystudiedinphysicallaboratoriesformorethan onehundredyears.Duringthepastthirtyyears,numericalsimulation,especiallydirectnumericalsimulation(DNS),hasbecomeanimportanttoolin thestudyofturbulentflows,includingbuoyancy-drivenconvection,RBC
Fig.1 Canonicalconfigurationsofbuoyancy-drivenconvection.(A)Differentially heatedverticalchannel(DHVC).Thehotterfluidrisesuponthe leftside,andthecolder fluiddescendsonthe rightside.(B)Rayleigh–Benardconvection.Themeanflowiszero andthemeantemperatureisantisymmetricaboutthemid-plane. Θ ¼ def T hot T isthe meantransformedtemperature.
andDHVC.Analysisofturbulentquantities,especiallythoseinvolved derivatives,areoftenonlyfeasiblewithDNSdata,duetotheaccuracy andresolutionrequirement.
Intheinterestsofsimplicityandclarity,buoyancy-drivenDHVCischosenasanexampletointroducethenewlydevelopedscalingpatchapproach, buttheapproachcanbereadilyadaptedtootherbuoyancy-drivenconvection.DHVCisaninterestingbuoyancy-drivenconvectiontotesttools andconceptsdevelopedoriginallyforforcedconvection.Inturbulent DHVC,flowisdrivenbybuoyancy,buttheturbulentkineticenergyis producedbytwomechanisms:shear-generationandbuoyancy-generation [29].Fromapracticalpointofview,abetterunderstandingofDHVCcan helpourpredictionofheattransferf romahotorcoldverticalwall,asinthe heatingorcoolingofbuildingspaces.Last,DHVCisselectedbecausethere havebeendirectnumericalsimulation(DNS)datafromthreeindependent studiesbyVersteegh[ 30],Kis ˇ [ 31],andNg[32].Asintheanalysisofforced wallturbulence[3],high-qualityDNSdataareessentialintheapplication andevaluationofthescalingpatchapproach.
MoredetailsonDHVCweregivenindissertationsbyVersteegh[30], Kis ˇ [31],andNg[32].Here,onlyabriefreviewofpreviousstudiesonturbulentDHVCisprovided.Oneoftheearlieststudiesofbuoyancy-driven turbulencenexttoaverticalplatewasbyGeorgeandCapp[33].Theyused classicalscalingargumentsandproposedathree-layerstructureofbuoyancydriventurbulence:aninnerlayeradjacenttothesolidwall,anouterlayer awayfromthewall,andabuoyantsublayerinbetween.Applyinganasymptoticmatchingapproach,theyproposedapower-lawvariationofthemean velocityprofileandmeantemperatureprofileinthebuoyantsublayer.Their scalinganalysisalsoleadstoanexplicitrelationshipbetweentheNusselt numberandtheRayleighnumber.
Someoftheearlynumericalsimulationsofbuoyancy-drivenconvectioninaverticalslotwerebyPhillips[ 34 ]andBoudjemadietal.[ 35].Due tothelimitofcomputingpower,earlyDNStypicallyusedasmallcomputationaldomain.ThefirstbenchmarkDNSstudyofDHVCwasbyVersteegh [30,36],whousedalargedomainof24 12 2(Lx Ly Lz).Usingthe simulationdata,theyinvestigatedthescalingbehaviorofthemeantemperature,themeanvelocityprofile,andtheprofilesofvariousturbulence statistics.
Kis ˇ [31,37]performeddirectnumericalsimulationsofDHVCovera widerrangeofRayleighnumberonalargecomputationdomainof24 12 2.Theeffectofdomainsize,spatialresolution,time-averagingperiod,
anderroranalysiswasexaminedindetail.BudgetsforReynoldsstressand turbulentheatfluxweredocumented,andentropygenerationwasalso investigated.
Ngandcoworkers[32,38–41]haveperformedthehighestRayleigh numbersimulationofDHVCsofar.Theyusedthesimulationdatato explorethescalingoftheflowandheattransport,thestructuresoftheflow field,andthespectralpropertiesoftheturbulence.
Therestofthearticleisorganizedasfollows.In Section2,thecurrent strategyinthepredictionofNusseltnumberisreviewed,anditsshortcomingispointedout.In Section3,governingequationsforflowandheat transportarepresented.In Section4, dimensionalanalysisisappliedtoboth thelaminarDHVCandturbulentDHVC.In Section5,thescalingpatch approachisreviewedanddemonstratedusingapressure-driventurbulent channelflow.In Section6,scalinganalysisisappliedtolaminarDHVC. In Section7,thescalingpatchanalysisisappliedtothemeanmomentum balanceequationinturbulentDHVC.In Section8,thescalingpatchanalysis isappliedtothemeanheatequationinturbulentDHVC.In Section9,a newpredictionofNusseltnumberisproposed. Section10 summarizes thearticle.
2.PredictionofNusseltnumber
Acenterpieceinmanystudiesofconvection,forcedorbuoyancydriven,isthepredictionofheattransportrate.Thepredictionofflow andheattransportoftenstartswithadimensionalanalysis[42].Thefirststep indimensionalanalysisistoidentifyparametersthataffectthequantitybeing predicted.Inbuoyancy-drivenconvection,DHVC,orRBC,theconventionallyusedcontrolparametersarelistedin Table1.
Thereareatotalofninecontrolparameters,andthreeprimarydimensionsareentailed:length L ,time t ,andtemperature T .Followingthe Buckingham-Pitheorem[ 43 ],flowandheattransportinDHVCor RBCaregovernedbysixnondime nsionalnumbers.Forexample, selecting ΔT , ν,and Lz (thedomainsizeinthedirectionoftemperature gradient)astherepeatingvariables,thefollowingsixnondimensional numbersarefoundaccordingly
Table1 Parametersthataffectflowandheattransportinbuoyancy-drivenconvection.
Material properties ν Kinematicviscosity[L2/t] α Thermaldiffusivity[L2/t] β Thermalexpansioncoefficient[1/T]
Force g ! Gravitationalacceleration[L/t2]
ThermalBC ΔT Temperaturedifference[T]
Geometry ∡ Anglebetweenthetemperaturegradientand g ! [1]
Lx, Ly, Lz Domainsize[L]
Thelastcolumnliststheprimarydimensionsoftheparameters:length L,time t,andtemperature T
where Π1 istheratiobetweenthekinematicviscosityandthermaldiffusivity,calledthePrandtlnumber.FortheidealconfigurationsofDHVCand RBCwithininfiniteparallelplates,theaspectratiosare Γx ≫ 1and Γy ≫ 1.
Theanglebetweenthetemperaturegradientandthegravitationalaccelerationis ∡ ¼ π =2forDHVCand ∡ ¼ 0forRBC.Thus,threenondimensionalcontrolparametersremainforDHVCorRBC: Π1 ¼ Pr, Π2 ¼
Intraditionalanalysesofbuoyancy-drivenconvection,thenondimensionalnumbers Π2 and Π3 arecombinedtoformaGrashofnumber (thejustificationisgivenin Section4).Inthisarticle,theGrashofnumber isdefinedusingthechannelhalf-width δ andthetemperaturedifference betweenthewallandchannelmid-plane Θmp ¼ 0.5ΔT as
Thereasonforusing δ and Θmp isthatthemultilayerstructuresofflowand heattransportinDHVCorRBCaresymmetricalaboutthechannel
mid-plane.SuchadefinedGrashofnumberiscompatiblewiththefriction Reynoldsnumberusedinpressure-drivenwall-boundedturbulence throughapipeorchannelReτ ¼ def δuτ =ν,where δ isthechannelhalf-width orpiperadiusand u τ isthefrictionvelocity[3 ].ThetraditionalGrashof numberisdefinedusingthechannelwholewidth Lz ¼ 2 δ andthetemperaturedifferenceacrossthewholechannel ΔT ¼ 2Θmp.Thus,thepresentlydefinedGrashofnumberis1/16ofthetraditionallydefinedGrashof number.
Traditionally,Grashofnumberisinterpretedasaratiobetweenthe buoyancyforceandtheviscousforce[44].However,Grashofnumber canalsoberelatedtotheratiooflengthscalesbyrearrangingasfollows
Thus,one-thirdpowerofGrashofnumbercanbeinterpretedastheratioof thechannelhalf-widthtoa“viscouslengthscale”definedas(ν2/gβ Θmp)1/3. Inthestudyofbuoyancy-drivenconvection,apopularnondimensional numberistheRayleighnumberdefinedas
Oneofthemostimportantquantitiesinthestudyofconvectionistheheat transportrate.Acommonlyusednondimensionalnumberforheattransport efficiencyistheNusseltnumber,whichisdefinedastheratiobetweenthe convectivetransportrateandconductivetransportrate:
where qt ¼ def
wall =ρref c p ¼
Θ=dzjwall isthetemperaturefluxatthewall, Qwall isthewallheatflux, ρref isthefluiddensity,and cp istheheatcapacity.
Mathematically,Nusseltnumbercanbeinterpretedasanormalizedsecond kindboundarycondition[44],i.e.,thetemperaturegradientatthewallnormalizedbyatemperaturescale Θmp andalengthscale δ. AccuratepredictionoftheNusseltnumberisofgreatimportancefor engineeringapplications.Basedonthedimensionalanalysis,itisobvious thatNusseltnumberinDHVCorRBCisafunctionofthePrandtlnumber ofthefluidandtheRayleighnumber:
Historically,power-lawisoftenusedtocorrelatetheNusseltnumberwith theRayleighnumberandPrandtlnumberas
WhileexperimentalmeasurementsofNusseltnumberforDHVCarescant, abundantexperimentalmeasurementsofNusseltnumberareavailablefor RBC.Hence,wewillusetheNusseltnumberpredictioninRBCtoillustratethecurrentstrategyofpredictingtheNusseltnumberforbuoyancydrivenconvection. Fig.2 presentstheNusseltnumberdataforRBCover awiderangeofRayleighnumbers.NumerouscorrelationshavebeenproposedfortheNusseltnumberinRBC,and Table2 listsjustafewofthem. Nearlyallthecorrelationsusedapower-lawfortheRayleighnumber dependenceasRam.However,along-standing,stillheateddebated,issue inthestudyofRBCisthevalueoftheexponent m
Inthe1950s,Malkus[45]analyzedturbulentRBCintermsofmarginal stabilityofthemeanflowandderivedanexponentof m ¼ 1/3.Thework wasfurtherdevelopedbyHoward[46].Inthe1960s,Kraichnan[47]refined
Fig.2 NusseltnumbervsRayleighnumberinRayleigh–Benardconvection. Inset shows thetrendatultra-highRayleighnumbers.Dataofhelium(U)arefromexperimental measurementUrbanetal.[50].Dataofhelium(N)arefromtheexperimentalmeasurementNiemelaandSreenivasan[51].DataofwaterandsiliconeoilAK3arefromexperimentalmeasurementofSilveston[52].
Nu C Pr n Ram :
Table2 ExamplesofcorrelationsforNusseltnumberinRBC.
YearResearchersFluidsCorrelations
1959GlobeandDropkin[53]AnyfluidsNu ¼ 0.069Ra0.33 Pr0.074
1969Rossby[54]MercuryNu ¼ 0.147Ra0.257
1975Threlfall[55]HeliumNu ¼ 0.173Ra0.28
1989Castaingetal.[48]HeliumNu ¼ 0.23Ra0.282
1996Takeshitaetal.[56]MercuryNu ¼ 0.155Ra0.27
TheapplicableRayleighnumberrangesofthecorrelationsarereferredtotheoriginalpapers. MorediscussionsonthecorrelationscanbefoundinAhlersetal.[57].
thesimilaritytheorytoincludeadoubleboundarylayer.Oneinteresting resultofhisanalysisisthatatultra-highRayleighnumber(sayRa ≳ 1018 ), theexponent m willbelargerthan1/3,becauseoftheinteractionofthe boundarylayerwithahorizontalfluctuatingwind.Basedoncryogenic heliumgasdataoverawiderangeofRayleighnumbers,Castaingetal. [48]observedthattheexponentissmallerthan m ¼ 1/3.Moreover,they developedanewscalingtheoryandsuggestedanexponentof m ¼ 2/7. Amorerecent,andcurrentlyverypopularmodelofRBChasbeendeveloped byGrossmannandLohse[49].Themodelisbuiltonatheoreticalanalysisof thedissipationrateinboththeboundarylayerandthewell-mixedcorelayer. Dependingontheratioofthedissipationrate,themodelprovidesasetofscalingrelationsbetweentheNusseltnumberandRayleighnumber,Prandtl number,andaspectratiooftheRBCcell.
Thedifferenceintheexponent,forexample, m ¼ 1/3vs m ¼ 2/7,can leadtosignificantdifferenceinthepredictionofNusseltnumber,uptoa factorof10atRa 1025,asshownintheinsetof Fig.2.Tobetterdiagnose theexistenceofapowerlaw,itiscommontoplottheso-calledcompensated NusseltnumberasNuRa m vstheRayleighnumber,asshownin Fig.3. ThecompensatedNusseltnumberwithanexponent m ¼ 2/7isshownin Fig.3A,andaconstantregionisobservedfortraditionalRayleighnumbers between105 and1010.However,thiscompensatedNusseltnumbermonotonicallyincreasesforRayleighnumberlargerthan1010.Fortheexponentof m ¼ 1/3,theconstantregionofthecompensatedNusseltnumberisathigher Rayleighnumbersbetween1010 and1014,asshownin Fig.3B.However, thetrendatultra-highRayleighnumber(> 1014)isnotclearpresently. Nevertheless, Fig.3 showsthatthedependenceofNusseltnumberonthe RayleighnumberinRBCcanbeapproximatedbyapower-law,butover
CompensatedNusseltnumbervsRayleighnumberinRBC.(A)NuRa
Fig.4 NusseltnumberinDHVC.(A)NusseltnumbervsRayleighnumber. (B)CompensatedNusseltnumbervsRayleighnumber.
alimitedrangeofRayleighnumber,andtheexponentvarieswiththe Rayleighnumber.Thenonconstancyoftheexponent m inthepowerlawpredictionofNusseltnumberisnotjustanuisanceinengineeringapplication,but,moreimportantly,itreflectsaninherentdrawbackofthe power-lawprediction:itlacksaconnectiontotheunderlyingphysicsin buoyancy-drivenconvection,i.e.,themultilayerstructureofturbulentflow andheattransport.
ForDHVC,theNusseltnumberdataaremainlyfromdirectnumerical simulations. Fig.4ApresentstheNusseltnumberdatavsRayleighnumberin theturbulentDHVCregime.Likeotherbuoyancy-drivenconvection, power-lawcorrelationsarealsopopularinpredictingtheNusseltnumber inDHVC,aslistedin Table3 .ComparedwiththeRBCcase,theRayleigh numberrangeofDHVCdataismuchmorelimited.Curve-fittingwithina limitedrangeofRayleighnumberscanalmostalwaysproduceapower-law
Fig.3
2/7 vsRa. (B)NuRa 1/3 vsRa.
Table3 CorrelationsforNusseltnumberinDHVC. YearResearchersCorrelations
1979GeorgeandCappNu ¼ 0.059(PrRa)1/3
1998VersteeghandNieuwstadtNu ¼ 0.071(PrRa)1/3
2007Balaji,HollingandHerwig Nu ¼ Ra1=3 ½0 101lnðRaÞ+6 3063 4=3
2012Kis ˇ andHerwigNu ¼ 0.186(PrRa)1/3.2
2014Ng,ChuangandOoiNu ¼ 0.046(PrRa)1/3
correlation,asshownin Fig.4 A.Thedeviationbetweenthedataand thepower-lawfunctionseemssmallin Fig.4A.However,whenthecompensatedNusseltnumberisplotted,asystematicdeviationisnoticeable in Fig.4 BastheRayleighincreases,similartotheRBCcaseshown in Fig.3
Onegoalofthisarticleistoadvocatethatitistimetomovebeyondthe power-lawpredictionofNusseltnumberinbuoyancy-drivenconvection usingEq.(7).Inforcedconvection,thepredictionofNusseltnumberwith power-lawcorrelationhaslongbeensupersededbymoreaccurateequations thatwerebuiltontheunderlyingphysicsofheattransfer.
2.1Lessonsfromforcedconvection
Power-lawcorrelationswithReynoldsnumberandPrandtlnumberwere popularinpredictingNusseltnumberinearlystudiesofforcedconvection. Forexample,forheattransfer(treatedaspassivescalar)throughaturbulent pipeflow,oneoftheearliestcorrelationsisthewell-knownDittus–Boelter equationdevelopedinthe1930s(see,e.g.,[58–62]) Nu 0:023Pr 0 4 Re0 8 b , (8)
whereReb isthebulkReynoldsnumberdefinedbythediameterofthepipe andthebulkmeanvelocity.TheDittus–Boelterequationcanbefoundin manytextbooksonheattransfer,e.g.,[44].Now,itisgenerallyagreedthat suchpower-lawpredictionisnotaccurateoverawiderangeofReynolds numbers,inparticularathighReynoldsnumbers.Moreaccuratepredictions thatarecommonlyusednowadaysarethePetukhovequation[63]andthe Gnielinskiequation[64]:
where f isthefrictioncoefficient.TheReynoldsnumberandPrandtlnumberrangesforthevalidityoftheseequationscanbefoundinstandardheat transfertextbooks,e.g.,Ref.[44].
Recently,Wei[65]andWeiandAbraham[66]showedthattheKader–Yaglomstyleequation[67]givesanexcellentpredictionofNusseltnumber, overawiderangeofPrandtlnumberandReynoldsnumbers.TheKader
Yaglomstyleequationispresentedas(see[65,66])
whereReτ isthefrictionReynoldsnumberdefinedusingthechannelhalfwidthorpiperadius, Θ+ mix isthemixedtemperaturescaledbythefriction temperature.
Itisknownthatthemeantemperatureinforcedwall-boundedturbulence canberobustlyapproximatedbyalogarithmicfunction,exceptinthenearwallregionandasmall,andbounded,deviationinthecoreofthepipe[1]. Thethermal“log-law”isanalogoustothewell-known“log-law”forthe meanvelocitythatwasfoundinthe1930s(see,e.g.,MoninandYaglom [1]).Moreimportantly,thelog-lawapproximationforthemeanvelocitydistributionhasbeenreliablyandrobustlyobservedinthehighReynoldsnumberexperimentssuchasPrincetonSuperpipeexperiments[68–70].
ThelogarithmicfunctionintheKader–YaglomstyleEq.(10)isdirectly relatedtothe“log-layer”forthemeantemperaturedistribution.Thefunction Bθ,m representsthetemperatureincrementsinthethermaldiffusion sublayer,andthedeviationinthecore(outerlayer)[65,66].Theeffectof thePrandtlnumberinthenear-wallregionisalsoaccountedforin Bθ,m Thus,theKader–Yaglomstyleequationisdirectlybuiltonthemultilayer structureofmean
In Section9,anewpredictionoftheNusseltnumberinbuoyancydrivenconvection,similartotheKader–Yaglomstyleequation,isdeveloped.Thenewpredictionequationisalsodirectlybuiltonthemultilayer structureofmeantemperatureinbuoyancy-driventurbulence.
3.Governingequations
Formostbuoyancy-drivenconvection,thevelocityofbulkmotionis sufficientlysmall,andthegoverningequationscanbeapproximatedbythe Boussinesq–Oberbeckequations[1].IntheBoussinesq–Oberbeckapproximation,thefluidisassumedtobeincompressible,andthedensityvariation isnegligibleexceptinthebuoyancyterm[1].Thegoverningequationsfor theinstantaneousflowandheattransferintheCartesiancoordinatesystems canbewrittenasfollows[1]
Inthisarticle,theinstantaneousflow orheatvariableisdenotedbyatilde. Forexample, e ui istheinstantaneousvelocityinthe i direction,and e θ isthe instantaneousmodifiedtemperaturedefinedasthedifferencebetweenthe meanwalltemperature T wall andtheinstantaneoustemperature e T : e θ ¼ def T wall e T g i isthecomponentofthebodyforceinthe i direction.
Eq.(11a)isthecontinuityequation,Eqs.(11b)arethewell-known Navier-Stokesequationforthemomentumsinthreedirections,andEq. (11c)istheenergyorheatequation.Onefluidproperty,thekinematicviscosity ν,appearsinthemomentumequations(11b),andanotherfluidproperty,thermaldiffusivity α appearsintheheatequation(11c).Inthisarticle,the materialpropertiesareassumedconstant,andthevariabilityofviscosity,thermaldiffusivity,ornon-Boussinesqeffectsarenotconsidered[71–74].
Thecoordinatesystemissetupthat z isinthewall-normaldirection.For wall-boundedflowandheattransport,no-slipboundaryconditionsare appliedfortheinstantaneousvelocityandtemperatureas e ui jz¼0 ¼ 0and e θ jz¼0 ¼ 0[1].
3.1Reynoldsaveragedequationsforthemeanflowandheat transport
GeneralsolutionstotheinstantaneousgoverningEq.(11)liebeyondthe scopeofexistingmethods.Moreover,inpracticalapplications,theknowledgeoftheinstantaneousflowfieldistoocumbersomeandisoftennotnecessary.Instead,wearemainlyinterestedinthemeanflowandscalartransport properties,forexample,themeanskinfriction,themeanheattransferrate, andsometimestheaverageofthefluctuationlevel.Reynoldsaveragingprovidesanextremelycommonframeworkforstudyingthemeanflowandscalartransport[1].Itisashortcutanderasesawealthofdetailsaboutthefluid motionsbeingstudied.
Conceptually,Reynoldsaveragingisensembleaveragingoveralarge numberofrealizationsoftheflowsundernominallythesameboundaryconditionsandinitialconditions[1].TheReynoldsaveragingdecomposesan instantaneousfloworheatvariableintoameancomponentandafluctuation component.Forexample,theinstantaneousvelocityisdecomposedas
Here,anuppercaseletterdenotesameanfloworheatvariable,andalower caseletterdenotesitsfluctuation.Similarlytheinstantaneoustemperatureis decomposedas e θ ¼ Θ + θ ,where Θ isthemeantemperatureand θ isthe temperaturefluctuation.
Inanexperimentalornumericalstudyofstatisticallysteadyturbulence,a morepracticalaveragingisobtainedbytimeaveraging.Moreover,forturbulencepossessingstatisticallyspatialhomogeneity,theaveragingisalso appliedspatiallyoverthehomogeneousplane.Forexample,inturbulent DHVC,meanflowandtemperaturevaryonlyinthewall-normal z direction, andarehomogeneousinthevertical x–y plane.Therefore,theexperimental orsimulationdataofturbulentDHVCarebothtime-averagedandspatial averagedinthe x–y plane.Theaveragedgoverningequationsforthemean heattransportandmeanflowinturbulentDHVCareasfollows[30,75]
where R wθ ¼ def hw θ i istheturbulenttemperaturefluxintheverticaldirection. R wu ¼ def hwui istheturbulentfluxofthestreamwisemomentumin theverticaldirection,commonlycalledthekinematicReynoldsshearstress.
Anglebrackets hi denotetheconceptualensembleaveraging. β isthethermalexpansioncoefficient,and Θmp isthemeantemperatureatthechannel mid-plane.
TheReynoldsshearstress Rwu arisesfromtheaveragingofthenonlinear inertialtermintheNavier-Stokesequations,representingaforceproduced byturbulentfluctuations.Theturbulenttemperatureflux Rwθ arisesfromthe averagingofthenonlinearadvectivetermintheinstantaneousheatequation. Therearefourunknowns Θ, U, Rwu,and Rwθ intwoEqs.(13a)and(13b). Thisisthewell-known“closure”probleminRANSmodeling.Being under-determined,theproblemcanyieldnouniquesolutionsbythemselves.Thisconflictswiththeusualimageofasymptoticmethods,which provideasequenceofmoreandmoreaccurateapproximationstoaunique exactsolution[5].Thescalingpatchapproachtackedthisbasicill-posed problembyaddingreasonableandminimalassumptionsaboutthequalitative natureofthesolutions[5].
Themeantemperature Θ inEq.(13a)andthemeanvelocity U inEq. (13b)aresecond-order,and Rwu and Rwθ arefirst-order.Thus,twoboundaryconditionsarerequiredfor U and Θ,andoneboundaryconditionis requiredfor Rwu and Rwθ.Thecommonlyusedboundaryconditionsin DHVCare
TheboundaryconditionsinEq.(14a)aretheno-slipconditionatthesolid surface.Notethatalltheseboundaryconditionsarethefirstkindboundary condition[44].However,asecondkindboundaryconditioncanalsobe appliedatthesolidsurfaceas
Here qu ¼ def τ wall =ρref denotesthekinematicmomentumfluxatthewall,where τwall isthewallshearstressand ρref isthefluiddensity. qt ¼ def Q wall =ρref c p denotes thetemperaturefluxatthewall.In Sections4 and 7, qu and qt areshowntoplay akeyroleinthemultiscalinganalysisofthemeanequationsusingthedimensionalanalysisapproachandthescalingpatchapproach.
Inthestudyofforcedwall-boundedturbulence,twoextremelyimportantwallvariablesarethefrictionvelocityandfrictiontemperature(see MoninandYaglom[1]andTennekesandLumley[2])definedbythewall shearstressandwallheatfluxas
IntegratingthemeanheatEq.(13a)andthemeanmomentumEq.(13b)in thewall-normal z directionandapplyingboundaryconditionsproducea relationforthetotaltemperaturefluxandtotalmomentumfluxas[75]
Thetotaltemperaturefluxconsistsofthemoleculardiffusion(firsttermon theleftofEq.(17a))andtheturbulenttransport(secondterm).Thephysical meaningofEq.(17a)isthatthetotaltemperatureflux(orheatfluxwhen multipliedby ρref c p)inafullydevelopedturbulentDHVCisaconstantacross thechannel,equaltothewalltemperature(orheat)flux.Thisconstancyof totaltemperaturefluxisanalogoustotheconstancyoftotalmomentumflux inturbulentplaneCouetteflow[76].
Thetotalmomentumfluxalsoconsistsoftwocomponents:aviscous transport(firsttermontheleftofEq.(17b))andaturbulenttransport(second term).ThephysicalmeaningofEq.(17b)isthatthetotalmomentumflux equalstothewallmomentumfluxminusaspatialintegralrelatedtothetemperaturedeficit.ThevariationoftotalmomentumfluxinDHVCisdistinctivelydifferentfromthatinforcedconvection[3].Forexample,inturbulent planeCouetteflow,thetotalmomentumfluxisaconstant,equaltothewall momentumflux[76].InturbulentDHVC,thetotalmomentumfluxis directlyrelatedtothebuoyancyeffect,whichplaysafundamentalrolein theshapeanddistributionofReynoldsshearstress,asshownin Section7.
Next,wepresenttheanalyticalsolutionsoflaminarDHVC.Theanalytic solutionsthemselvesaretrivial,buttheyprovideasimpleexampletoevaluatedimensionalanalysisandscalingpatchapproach.
3.2LaminarDHVCsolution
ThegoverningequationforlaminarDHVCcanbeobtainedbysettingturbulencetermstozerointhemeanheatEq.(13a)andthemeanmomentum Eq.(13b).Integratingalongthewall-normal z directionandapplying boundaryconditionsproducetheanalyticalsolutionforthetemperature andvelocitydistributioninlaminarDHVCas
Theanalyticalsolutionsforthetemperatureandvelocitydistributionsin laminarDHVCareshownin Fig.5A.Thetemperature Θ varieslinearly inthewall-normaldirection,likeapureconductiondistribution.Theverticalvelocityexhibitsamaximumvaluenearthehotterplate,thendecreases inthecoreofthechannel,andexhibitsaminimumnearthecolderplate. Theverticalvelocityisantisymmetricaboutthechannelmid-plane.For comparison,themeanvelocityandmeantemperaturedistributionsin
A B
Fig.5 TemperatureandverticalvelocityprofilesinaDHVC.(A)Laminarcase. (B)Turbulentcases.DataarefromtheDNSofKiš [31]attwoGrashofnumbers:Gr ¼ 4.75 104 (solidcurves)andGr ¼ 4.4 105 (dashedcurves).
turbulentDHVCarepresentedin Fig.5BattwoGrashofnumbers.InturbulentDHVC,themeantemperaturevariessharplyinthenear-wallregion, andthevariationoftemperatureinthecoreismuchsmaller.Ontheflow side,thevariationofthemeanvelocityisalsomuchsharperinthenear-wall region,andthepeaklocationofthemaximumvelocitymovesclosertothe wallwithincreasingGrashofnumber.
ThemaximumverticalvelocitylocationinlaminarDHVCcanbefound bysettingthevelocitygradienttozero.Themaximumlocationandvalue arefoundas
Inbuoyancy-drivenconvection,acommonlyusedvelocityscaleisthe so-calledfree-fallvelocitydefinedas
Hence,themaximumverticalvelocityinlaminarDHVCisrelatedthefreefallvelocityas
Thus,theso-called“free-fall”velocityisnotaproperor“natural”scalefor theverticalvelocityinlaminarDHVC,because Umax/Uff isnotaconstant, butincreasesas δUff/ν.In Section4,itisshownthatthis“free-fall”velocity isnotaproperscalefortheverticalvelocityinturbulentDHVCeither. Althoughfree-fallvelocityiseasytocomputefromtheinputsofthe buoyancy-drivenconvectionandiscommonlyusedtonormalizeequations ornumericalsimulationdata,suchscaledvariablesarenotappropriateand shouldbeavoidedinthescalingofbuoyancy-drivenconvection.
BasedonEq.(19b),abettervelocityscaleforlaminarDHVCisdefinedas
Asshownin Section4,thewalltemperatureandmomentumfluxes qt and qu arecriticalinunderstandingbuoyancy-drivenconvection.Forlaminar DHVC,thewalltemperaturefluxandthewallmomentumfluxcanbe obtainedfromtheanalyticalsolutionsas
Eq.(23a)indicatesthattheNusseltnumberinlaminarDHVCisNu ¼ 1.In otherwords,inlaminarDHVC,thereisbulkfluidmotioninthevertical direction,buttheflowdirectionisalongtheisothermalline,perpendicular tothetemperaturegradient.Thusthebulkfluidmotiondoesnotadvect heat,andtheheattransportfromthehotplatetothecoldplateisbypure moleculardiffusion.
FromEq.(23b),thefrictionvelocity uτ inlaminarDHVCis
ThefrictionReynoldsnumberforlaminarDHVCcanbeobtainedas
Theratiobetweenthe Umax and uτ inlaminarDHVCdependsonthe GrashofnumberandthefrictionReynoldsnumberas
4.Dimensionalanalysisofbuoyancy-drivenconvection
Dimensionalanalysisisapowerfultoolinthestudyoffluiddynamics andheattransfer(see,e.g.,Buckingham[43],Bridgman[77],Taylor[78], Townsend[79],Sedov[80],Barenblatt[81]).AccordingtoChurchill[60], thefundamentalbasisfordimensionalanalysiswasestablishedbyFourierin 1822.Rayleigh[82]demonstratedthepowerofdimensionalanalysisina shortpaperpublishedinthe Nature magazinein1915,givingexamplesfrom variousfields.Afascinatingexampleillustratingthepowerofdimensional analysisisthepredictionofthefirstatomicexplosionyieldbyG.I. Taylor[78],usingaseriesofpicturespublishedinamagazine.
WewillfirstpresentadimensionalanalysisoflaminarDHVC,followed byturbulentDHVC.InthedimensionalanalysisoflaminarDHVC,wepresenttwooptionsofselectingcontrolparametersanddiscussthecommonalityanddifference.
Table4 DimensionalanalysisoflaminarDHVC.
Option1Option2
Controlparameters
Repeatingvariables
Thegenericnondimensionalfunctions Ψ inthelastthreerowsare,ingeneral,differentfromeachother, andcannotbedeterminedbythedimensionalanalysisitself.
4.1DimensionalanalysisoflaminarDHVC
Properselectionofcontrolparametersisofutmostimportanceinasuccessfuldimensionalanalysisofanyfloworheattransportproblem.For laminarDHVC,twosetsofcontrolpa rameterscanbeselectedfordimensionalanalysis,aslistedin Table4 .Inbothoptions,onlythreeprimary dimensionsareentailed:length,tim e,andtemperature.However,there arefivecontrolparametersinoption 1,andsixinoption2.Hence,based ontheBuckinghamPitheorem,option1producestwonondimensional controlparameters,andoption2producesthree.
Thecommoncontrolparametersinoption1andoption2are gβ , ν, α, δ, whicharisefromthemomentumandheatequation,andthedomainsize (partoftheboundarycondition).Theparameter g and β aregrouped togetherbasedontheobservationofEq.(13b):theeffectofgravityon thebuoyancyforceisalwayscoupledwiththethermalexpansioncoefficient.Thereisnowhereinthegoverningequationsthat g and β appearseparately.Therefore, gβ shouldbetreatedasasingleparameter,insteadofas twoparametersasin Table1.
Thedifferencebetweenoption1andoption2in Table4 liesinthe parameter(s)relatedtoheat.Inoption1, Θmp isused.Notethat Θmp can beinterpretedasthetemperaturedifferencebetweenthewallandthechannelmid-plane.Inotherwords, Θmp isthedifferenceofthefirstkindthermal boundaryconditionsat z ¼ 0and z ¼ δ.Moreimportantly, Θmp ingeneral doesnotreflectanylocalrateoftemperaturechange,atthewall,ornearthe
channelmid-plane.Incontrast,thetwocontrolparameters qt and qu in option2representthelocalrateofchangeatthewall(asecondkindboundarycondition).
Applyingthestandarddimensionalanalysisprocedure[43],thetwocontrolparametersfromoption1in Table4 arethePrandtlnumberofthefluid andtheGrashofnumber.Forexample,basedonthedimensionalanalysis results,themaximumverticalvelocityinlaminarDHVCcanbepresentedas
where Ψ denotesagenericnondimensionalfunctionthatdependsonPrand Gr,whichhastobedeterminedfromanalyticalsolutionsorexperimental andnumericaldata.
Thethreenondimensionalparametersresultingfromoption2in Table4 arePr, Π2 ¼ gβ qtδ4/ν3,and Π3 ¼ quδ2/ν2.However,inlaminarDHVC,the boundaryconditionsof qu and qt arenotindependent,butdirectlyrelatedto eachotherasshowninEq.(23b):
Thus,thethirdnondimensionalnumber Π3 fromoption2in Table4 is redundant,andbothoptionsin Table4 produceidenticalnondimensional controlparameters.
Anadvantageofoption2in Table4 isthatitleadsdirectlytothedefinitionofafluxGrashofnumber.ThefluxGrashofnumberisdefinedusing thewalltemperatureflux qt as(e.g.,Bejan[42])
Similarly,afluxRayleighnumbercanbedefinedas
NotethatthisfluxRayleighnumberissimilartothe H numberdefinedby GeorgeandCapp[33]fornaturalconvectionalongaverticalplateunder constantheatflux.ForlaminarDHVC,Nu ¼ 1andthefluxGrashofnumberequalsthetraditionalGrashofnumberGr ¼ Grf andRa ¼ Raf
ThefluxGrashofnumberisrelatedtotheratiooftwolengthscales,as showinginthefollowingform
Thus,one-fourthpowerofthefluxGrashofnumbercanbeinterpretedas theratiobetweenthechannelhalf-width δ anda“viscouslengthscale” definedas(ν 2 α/gβ qt)1/4.Suchdefinedviscouslengthscaleissimilartothe innerlengthscaledefinedbyTownsend[79]forbuoyancy-drivenconvectionoverasinglehorizontalplaneorRayleigh–Benardconvection.
Torecap,laminarDHVCiscontrolledbytwonondimensionalnumbers.Twooptionsarevalidfortheselectionofcontrolparameters.Thedifferencebetweenthetwooptionsliesintheselectionofparameter(s)witha localrateoftemperaturechangeoraglobaltemperaturedifference.InlaminarDHVC,thetemperaturevarieslinearly,hence,theglobaltemperature difference Θmp isdirectlyrelatedtothelocalrateoftemperaturechange qt. Thus,thetwooptionsin Table4 areequivalent.However,inturbulent DHVC,themeantemperaturevariationisnotlinear,andtheselectionof Θmp becomesinappropriate.
4.2DimensionalanalysisofturbulentDHVC
Inpressure-orshear-drivenwall-boundedturbulence,itiswellknownthat theflowandheattransportcanbedividedintoseverallayers,andthecharacteristicscalesmayvarywithrespecttogivenlayers[1,2].Forexample,turbulentflowoveraflatplateistraditionallydividedintofourlayers:aviscous sublayer,abufferlayer,alog-layer,andanouterlayer(see,e.g.,Tennekes andLumley[2]).Intheviscoussublayer,thecharacteristiclengthscaleisthe viscouslengthscale ν/uτ.However,intheouterlayer,thecharacteristic lengthscaleistheboundarylayerthickness.
InturbulentDHVC,flowandheattransportcanalsobedividedinto severallayers,andthecontrolparametersineachlayermaybedifferent. Forexample,adjacenttothewall,thevelocityandtemperatureprofileshave largegradients(see Fig.5B).Asaresult,themoleculardiffusionisimportant, and ν and α shouldbeselectedasthecontrolparametersinthenear-wall region.Ontheotherhand,inthecoreofthechannel,flowandheattransportaredominatedbyeddymotions,andmoleculardiffusionisnegligible. Forexample,inthecoreofthechannelin Fig.5B,themeantemperature variationissmall,meaningthatthemoleculartemperatureflux αdΘ/dz is small.Therefore,thekinematicviscosity ν andthermaldiffusivity α should notbeselectedascontrolparametersfortheflowandheattransportinthe coreofthechannel.AtasufficientlyhighGrashofnumber,theseparation