ABOUT THE AUTHORS
KARA SEALOCK
Dr. Kara Sealock completed a Bachelor of Nursing in 2000, a Masters of Education in 2012, and a Doctorate of Education, specializing in adult learning, in 2019. Kara has been a nursing educator since 2008 and has worked in various roles such as a preceptor, clinical instructor, and theory instructor with a focus in medical/surgical care, critical care, and gerontology. Kara teaches pathophysiology, assessment, and pharmacology at the University of Calgary. She has considerable years of clinical experience in medical/surgical environments, research experience working with cardiology and endocrinology clients; however, the majority of her career has been positioned in critical care with an adult focus in intensive care and coronary care environments. Kara has substantive experience in preparing undergraduate nursing students for NCLEX-RN as she has facilitated preparation workshops and mock examination opportunities, and assumes an active role in preparing students for success. She currently sits on the Nursing Education Program Approval Committee at the College and Association of Registered Nurses (CARNA). Kara’s knowledge in adult learning, combined with her clinical and theoretical experience contributes to an enhanced foundation of learning bridging theory and practice for undergraduate nursing education. Kara is currently a senior instructor with a specific focus in teaching for the Faculty of Nursing at the University of Calgary.
CYDNEE SENEVIRATNE
Dr. Cydnee Seneviratne received a diploma in Nursing in 1991 and has dedicated her career to advancing neuroscience nursing, chronic stroke care, and gerontology. She received a BScN from the University of Victoria in 1995 and a Master of Nursing in 1997 from the University of Calgary. Cydnee received a FUTURE Program for Cardiovascular Nurse Scientists Fellowship (a CIHR Strategic Training Program in Health Research) while completing her PhD in 2007 at the University of Calgary and completed a post-doctoral fellowship in 2010 funded by the Heart and Stroke Foundation of Canada. Cydnee has been a nursing instructor in clinical, laboratory, and classroom settings (specifically pharmacology and pathophysiology) at the University of Calgary for 19 years and has remained closely linked to the clinical setting during her time as the Associate Dean of Undergraduate Practice Education. In the Associate Dean role, she was chair of the Nursing Education Program Approval Committee at the College and Association of Registered Nurses (CARNA) where she was instrumental in crafting undergraduate and nurse practitioner program approval processes. Cydnee is currently a senior instructor and is a leader in Interprofessional Simulation Education for the Faculty of Nursing.
LINDA LANE LILLEY
Dr. Linda Lilley received her diploma from Norfolk General School of Nursing, BSN from the University of Virginia, Master of Science (Nursing) from Old Dominion University, and PhD in Nursing from George Mason University. As an Associate Professor Emeritus and University Professor at Old Dominion University, her teaching experience in nursing education spans over 25 years, including almost 20 years at Old Dominion. Linda’s teaching expertise includes drug therapy and the nursing process, adult nursing, physical assessment, fundamentals in nursing, oncology nursing, nursing theory, and trends in health care. The awarding of the university’s most prestigious title of University Professor reflects her teaching excellence as a tenured faculty member. She has also been a two-time university nominee for the State Council of Higher Education in Virginia award for excellence in teaching, service, and scholarship. Linda received the 2012 Distinguished Nursing Alumni Award from Old Dominion University School of Nursing for her “continued work on the successful pharmacology textbook published by Elsevier” and to recognize her “extraordinary work and the impact [the book] has had on baccalaureate education.” While at Old Dominion University, Linda mentored and taught undergraduate and graduate students as well as registered nurses returning for their BSN. Linda authored the MED ERRORS column for the American Journal of Nursing between 1994 and 1999, as well as numerous other peer-reviewed, published articles in professional nursing journals. Since retiring in 2005, Linda continues to be active in nursing, serving as a member on dissertation committees with the College of Health Sciences and maintaining membership and involvement in numerous professional and academic organizations. Since January of 2014, Dr. Lilley continues to serve on the volunteer review panel for the monthly newsletter publication Nurse Advise-ERR (ISMP affiliated; the ISMP [Institute for Safe Medication Practices] is a nonprofit organization educating the healthcare community and consumers about safe medication practices). Linda has served as a consultant with school nurses in the city of Virginia Beach and as a member on the City of Virginia Beach’s Health Advisory Board. Linda also served as an appointed member on the national advisory panel on medication error prevention with the U.S. Pharmacopeia in Rockville, Maryland. She continues to educate nursing students and professional nurses about drug therapy and the nursing process and speaks on the topics of drug therapy, safe medication use, humor and healing, and grief and loss.
SHELLY RAINFORTH COLLINS
Shelly Rainforth Collins received her Doctor of Pharmacy degree from the University of Nebraska, College of Pharmacy in 1985, with High Distinction. She then completed a clinical pharmacy residency at Memorial Medical Center of Long Beach in Long Beach, California. She worked as a pediatric
clinical pharmacist (neonatal specialist) at Memorial Medical Center before moving to Mobile, Alabama, where she was the Assistant Director of Clinical Pharmacy Services at Mobile Infirmary Medical Center. After moving to Chesapeake, Virginia, she served as the Clinical Pharmacy Specialist/Coordinator of Clinical Pharmacy Services at Chesapeake Regional Medical Center in Chesapeake, Virginia for 19 years. Her practice focused on developing and implementing clinical pharmacy services as well as medication safety and Joint Commission medication management standards and national patient safety goals. She is president of Drug Information Consultants, a business offering consultation and expert witness review for attorneys on medical malpractice cases. She holds certifications in Medication Therapy Management, Anticoagulation Management, and Immunizations. Shelly was awarded the Clinical Pharmacist of the Year Award in 2007 from the Virginia Society of Healthsystem Pharmacists. She led a multidisciplinary team that won the Clinical Achievement of the Year Award from George Mason University School of Public Health in 2007 for promoting safety with narcotics in patients with sleep apnea; this program has also received national recognition. She was awarded the Service Excellence Award from Chesapeake Regional Medical Center. Shelly’s professional affiliations include the American Society of Healthsystem Pharmacists, the Virginia Society of Healthsystem Pharmacists, and the American Pharmacists Association.
JULIE S. SNYDER
Julie Snyder received her diploma from Norfolk General Hospital School of Nursing and her BSN and MSN from Old Dominion University. After working in medical-surgical nursing, she worked in nursing staff development and community education. Later, she transferred to the academic setting and taught fundamentals of nursing, pharmacology, physical assessment, and adult medical-surgical nursing at a university school of nursing. Julie has recently worked as a Quality Initiative Coordinator and a Clinical Nurse Educator in a local hospital. She is now a Lecturer at the School of Nursing of Regent University in Virginia Beach, Virginia. She has been certified by the ANCC in Nursing Continuing Education and Staff Development and currently holds ANCC certification in Medical-Surgical Nursing. She is a member of Sigma Theta Tau International and was inducted into Phi Kappa Phi as Outstanding Alumni for Old Dominion University. She has worked for Elsevier as a reviewer, ancillary writer, and author since 1997. Julie’s professional service has included serving on the Virginia Nurses’ Association Continuing Education Committee, serving as Educational Development Committee chair for the Epsilon Chi chapter of Sigma Theta Tau, serving as an item writer for the ANCC, working with a regional hospital educators’ group, and serving as a consultant on various projects for local hospital education departments. In addition, she has conducted pharmacology review classes for recent nursing graduates.
Paula Crawford-Dickinson, RN, BScN, BA, BHA, MN-ACNP, EdD
Professor
Sally Horsfall-Eaton School of Nursing George Brown College Toronto, Ontario
Kerry Lynn Durnford, RN, MN Instructor School of Health and Human Services Aurora College Yellowknife, Northwest Territories
Joanna Gallacher, RN, MN Professor
Practical Nursing Program School of Health & Community Services Durham College Oshawa, Ontario
Stacy E. Hunt, RN, BSN, MSN Nursing Faculty
Saskatchewan Collaborative Bachelor of Science in Nursing Program School of Nursing Saskatchewan Polytechnic Regina, Saskatchewan
Lindsay MacFarlane, HBScN, MEd, OCT, RN Professor, Practical Nursing School of Health and Community Services Confederation College Thunder Bay, Ontario
Wanda Pierson, RN, BSN, MSN, MA, PhD Faculty, Faculty of Nursing Langara College Vancouver, British Columbia
Kelly Marie Power-Kean, RN, BN, MHS, NP Nurse Educator, Nurse Practitioner Nursing Education Centre for Nursing Studies, and Memorial University of Newfoundland St. John’s, Newfoundland
Heather Scarlett-Ferguson, BSP, MEd, EdD, RPh Instructor Psychiatric Nursing MacEwan University Edmonton, Alberta
Joy Shewchuk, RN, BSc, BSN, MSN Professor, Nursing School of Health Sciences
Humber College Institute of Technology and Advanced Learning Toronto, Ontario
Ruth Swart, EdD, MHS, RN, BN, BSc
Senior Instructor Faculty of Nursing University of Calgary Calgary, Alberta
Nadia Torresan-Doodnaught, BScN, RNC, MN Professor of Nursing Faculty of Health Sciences Seneca College of Applied Arts and Technology King City, Ontario
Kari Dawn Ubels, CD, HBScN, RN Associate Chair of Practical Nurse Curriculum Faculty of Health and Community Studies NorQuest College Edmonton, Alberta
Jess White, RN, BN, ENC(C) Faculty, Practical Nursing Assiniboine College Winnipeg, Manitoba
Stephanie Zettel, RN, MN, BN, BSc (Honours) Associate Professor School of Health Sciences Department of Nursing School of Nursing and Midwifery Faculty of Health, Community and Education Mount Royal University Calgary, Alberta
PHARMD REVIEWERS
With special thanks to:
Grace Frankel, BSc Pharm, Pharm D, BCPS
Clinical Pharmacist
Primary Care/Hospital Practice, My Health Team, Southern Health Region
Steinbach, Manitoba
Thomas McFarlane, BSc Pharm, Pharm D Clinical Lecturer, Oncology School of Pharmacy, University of Waterloo Waterloo, Ontario
Karen Sutton, RN, BScN, MN, CNCC(C) Professor, Practical Nursing Program Coordinator, Critical Care Nursing Program Durham College Oshawa, Ontario
INTRODUCTION
The fourth edition of Lilley’s Pharmacology for Canadian Health Care Practice incorporates both the nursing process and evidence in practice as it is relevant to Canadian nursing. This text provides the most current and clinically relevant information in an appealing, understandable, and practical format. The clear writing style and full-colour design of Lilley’s Pharmacology for Canadian Health Care Practice are ideal for today’s busy nursing student. The book presents drug information that both RN and PN nursing students need to know for whatever exam they are preparing to take. It also provides information on what the professional nurse may encounter during drug administration in a variety of health care settings, including accounts of real-life medication errors and tips for avoiding those errors. Features that help set the book apart include:
• A focus on the role of prioritization in nursing care
• A strong focus on drug classes to help students acquire a better knowledge of how various drug classes work in the body, allowing them to apply this knowledge to individual drugs
• Canadian content relevant to Canadian students and educators that will strengthen their knowledge of the field
• Clinical practice guidelines produced or endorsed in Canada by national, provincial, or territorial medical or health organizations, or by professional societies, government agencies, or expert panels
• Ethnocultural examples that reflect the varied and complex ethnodemographic diversity of Canada
• Ease of readability to make this difficult content more understandable
For this edition, the author team has not only focused on providing the most “need-to-know” information but also the most up to date research related to pharmaceuticals while emphasizing the nursing process and prioritization. In addition, a brief discussion of pharmacology related to transgender men and women who may or may not be transitioning is included in this edition. In future editions a more fulsome discussion will be included in chapters 35 and 36. Many of the updates for this edition are in response to student and instructor feedback.
MARKET RESEARCH
To aid in the preparation of this text, nursing instructors from across Canada participated in extensive, detailed reviews of the Third Canadian Edition. These reviewers assessed changes that had occurred in the field of pharmacology since publication of the third edition and determined what was needed to better teach this subject to nursing students and how their evolving learning needs could be met.
This Canadian edition maintains the philosophy of making the challenging subject of pharmacology approachable and easy to understand. Additional concerns raised and enhancements suggested by educators and nursing students who served as
reviewers or consultants throughout the manuscript’s development, as well by the authors of this text, also have been addressed.
ORGANIZATION
This book includes 58 chapters presented in 10 parts, organized by body system. The 10 “concepts” chapters in Part 1 lay a solid foundation for the subsequent drug units and address the following topics:
• The nursing process and drug therapy
• Pharmacological principles
• Legal and ethical considerations
• Ethnocultural and lifespan considerations related to pharmacology
• Gene therapy and pharmacogenomics
• Preventing and responding to medication errors
• Patient education and drug therapy
• Over-the-counter drugs and natural health products
• Vitamins and minerals
• Drug administration techniques, including 100 drawings and photographs
Parts 2 through 10 present pharmacology and nursing management in a time-tested body systems and drug function framework. This approach facilitates learning by grouping functionally related drugs and drug groups. It provides an effective means of integrating the content into medical-surgical/adult health nursing courses or for teaching pharmacology in a separate course.
The 48 drug chapters in these 9 Parts constitute the main portion of the book. Drugs are presented in a consistent format with an emphasis on drug classes and key similarities and differences among the drugs in each class. Each chapter is subdivided into two discussions, beginning with (1) a brief overview of relevant anatomy, physiology, and pathophysiology and a complete discussion of pharmacology, followed by (2) a comprehensive yet succinct application of the nursing process.
Pharmacology is presented for each drug group in a consistent format:
• Mechanism of Action and Drug Effects
• Indications
• Contraindications
• Adverse Effects (often including Toxicity and Management of Overdose)
• Interactions
• Dosages
Drug class discussions conclude with specially highlighted Drug Profiles—brief narrative “capsules” of individual drugs in the class or group, including pharmacokinetics tables for each drug. Key drugs (prototypical drugs within a class) are identified throughout with a symbol for easy identification.
The pharmacology section is followed by a Nursing Process discussion that relates to the entire drug group. This nursing
content is covered in the following, familiar nursing process format:
• Assessment
• Nursing Diagnoses
• Planning (including Goals and Expected Patient Outcomes)
• Implementation
• Evaluation
At the end of each Nursing Process section is a Patient Teaching Tips box that summarizes key points for nursing students and practising nurses to include in the education of patients about their medications. These boxes focus on teaching how the drugs work, possible interactions, adverse effects, and other information related to the safe and effective use of the drug(s). The role of the nurse as patient educator and advocate continues to grow in importance in professional practice, so there is emphasis on this key content in each chapter in this edition.
Lilley’s Pharmacology for Canadian Health Care Practice also reflects the latest drug information and research through the following special boxes:
• Evidence in Practice
• Ethnocultural Implications
• Lab Values Related to Drug Therapy
• Legal and Ethical Principles
• Natural Health Products
• Preventing Medication Errors
• Special Populations: Adolescents
• Special Populations: Children
• Special Populations: The Older Adult
• Legal and Ethical Principles
• Pharmacokinetic Bridge to Nursing Process
NEW TO THIS EDITION
The hallmark readability and user-friendliness of Lilley’s Pharmacology for Canadian Health Care Practice helps students navigate easily through the textbook and thus the difficult subject of pharmacology and the nursing process.
This textbook continues to feature “need-to-know” content as well as up to date research related to pharmaceutical interventions and Canadian legislation. Information on drug adverse effects reflects only the most common and most serious adverse effects rather than listing all reported adverse effects. These adverse effects are listed in order of those most commonly seen. Another area continued from the previous addition is that of drug dosages; only those dosages that are seen in most common indications are included in the text and tables. (For other dosages, the student should refer to an up-to-date drug handbook or drug reference such as, Mosby’s Canadian Nursing Drug Reference.) This need-to-know approach to drug indications and adverse effects is crucial in helping the adult learner focus on the most essential content needed for safe drug administration.
Drugs included in the text are as up-to-date as possible and include related research to ensure students receive accurate information. The availability of drugs changes frequently because manufacturers discontinue production or as a result of shortages.
The use of abbreviations has been limited to the most common abbreviations. While the use of abbreviations is not encouraged overall, abbreviations are still approved and used by
agencies, and may also be part of the documentation method. The Institute of Safe Medication Practices (ISMP) Canada’s “Do Not Use List” of abbreviations, symbols, and dose designations has been adhered to within this text.
It is important to remember that although this textbook provides all of the need-to-know pharmacology content that students will need for an entry level of practice, it is first and foremost a nursing textbook rather than a pharmacology textbook, with a strong emphasis on the nursing process and professional nursing practice. The section on implementation also offers all of the most essential information, followed by a section on the evaluation of therapeutic and adverse effects. These changes highlight the significance of the nursing process as a foundation in drug therapy while helping the student to make strong cognitive connections among nursing diagnoses, goals, and expected patient outcomes.
The pharmacology and nursing content in each of the 58 chapters has been thoroughly revised and critically reviewed by nursing instructors, practising nurses, and PharmDs to reflect the latest drug information and nursing content. Key updates include:
• Updated population and incidence statistics in each chapter
• Summary of Canadian cannabis/marihuana regulations and the Cannabis Act in Chapter 3
• Revision of Chapters 4 and 7 include Indigenous health and healing practices, an explanation of the Indigenous medicine wheel, and alternative medicinal interventions in response to the Truth and Reconciliation Commission of Canada’s Calls to Action
• Revision of Chapter 11 includes an explanation of current practices when/if an opioid overdose occurs in the community, including a stepwise explanation of how to administer Naloxone
• Additional Examination Review Questions at the end of each chapter
ADDITIONAL TEACHING AND LEARNING FEATURES
The book also includes a variety of innovative teaching and learning features that prepare the student for important content to be covered in each chapter and encourage review and reinforcement of that content. Chapter-opener features include the following:
• Learning objectives
• Summary of Drug Profiles in the chapter, with page number references
• List of High-Alert Drugs in the chapter, with page number references
• Key terms with definitions and page number references (key terms being in bold type throughout the narrative to emphasize this essential terminology)
The following features appear at the end of each chapter:
• Patient Teaching Tips related to drug therapy
• Key Points boxes summarizing important chapter content
• Examination Review Questions, with answers provided at the end of the book for quick and easy review
• Critical Thinking activities
• List of Evolve Resources available to students
• References for works cited in the chapter
In addition to the special boxes listed previously, other special features that appear throughout the text include:
• Case Studies in every chapter, with answer guidelines provided on the Evolve website
• Dosages tables listing generic and trade names, pharmacological class, usual dosage ranges, and indications for the drugs
For a more comprehensive listing of the special features, please see the inside back cover of the book.
COLOUR
The use of colour continues to complement the text by making the book engaging for nursing students. Colour is used throughout to:
• Highlight important content
• Illustrate how drugs work in the body in numerous anatomical and drug process colour illustrations
• Improve the visual appearance of the content to make it more engaging and appealing to today’s more visually sophisticated reader
The use of colour and other visual engagement devices in these ways significantly improves students’ involvement and understanding of pharmacology.
SUPPLEMENTAL RESOURCES
A comprehensive ancillary package is available to students and instructors using Lilley’s Pharmacology for Canadian Health Care Practice. The following supplemental resources have been thoroughly revised for this edition and can significantly assist in the teaching and learning of pharmacology.
Study Guide
The student study guide—carefully aligned with the content and focus of the book—includes the following:
• Student Study Tips that reinforce the Study Skills available on the Evolve site and provide a “how to” guide to applying test-taking strategies
• Worksheets for each chapter, with Examination Review questions (with application-based, alternate-item, and dosage calculation questions), critical thinking and application questions, and other activities
• Case Studies followed by related critical thinking questions
• An updated Overview of Dosage Calculations with helpful tips for calculating doses, sample drug labels, practice problems, and a quiz
• Answers to all questions (provided in the back of the book) to facilitate self-study
Evolve Web Site
Located at http://evolve.elsevier.com/Canada/Lilley/pharmacology, the Evolve Web site for this book includes the following elements:
For Students
• More than 550 Review Questions for Exam Preparation
• Answers to Critical Thinking Activities from the book
• Printable Chapter Summaries for each chapter
• Answers to Case Studies from the book
• Audio Glossary
• Unfolding Case Studies
• Integrated Study Skills Tips present valuable study skills topics related to each Part within the text, including time management, note-taking, studying, test-taking and others. These tips help students learn the particularly demanding subject of pharmacology while also equipping them with tools that they can use in other courses and as lifelong learners who are building an evidence-based practice.
• Book-specific Next Generation NCLEX Case Studies (both single-episode and unfolding)
For Instructors
• TEACH for Nurses Lesson Plans that focus on the most important content from each chapter and provide innovative strategies for student engagement and learning. These new Lesson Plans include strategies for integrating nursing curriculum standards, links to all relevant student and instructor resources, and an original instructor-only Case Study in each chapter.
• ExamView® Test Bank that features more than 800 examination−format test questions (including alternate-item questions) with text page references, rationales, and answers coded for NCLEX® Client Needs category, nursing process step, and cognitive level (Bloom’s taxonomy). The robust ExamView® testing application, provided at no cost to faculty, allows instructors to create new tests; edit, add, and delete test questions; sort questions by NCLEX® Client Needs category, cognitive level, and nursing process step; and administer and grade tests online, with automated scoring and gradebook functionality.
• PowerPoint® Lecture Slides consisting of more than 2100 customizable text slides for instructors to use in lectures. The presentations include Unfolding Case Studies and applicable illustrations from the book’s Image Collection. Audience Response System Questions (three or more discussion-oriented questions per chapter for use with i>Clicker and other systems) are folded into these presentations.
• Generic Next Generation NCLEX Case Studies for Pharmacology (both single-episode and unfolding)
• An Image Collection with over 250 full-colour images from the book for instructors to use in lectures
• Access to all student resources listed above
Elsevier eBooks
More than just words on a screen, Elsevier eBooks on VitalSource come pre-loaded with interactive learning features that empower students to engage with course content in entirely new ways.
Ideal for use both inside the classroom and out, Elsevier eBooks on VitalSource gives students the ability to access textbook content any time, any place via desktop computer, laptop, tablet, or smartphone.
It includes study aids such as highlighting, e-note taking, and the ability to share notes with other students or with instructors. Even more importantly, it allows students and instructors to do a comprehensive search within the specific text or across a number of titles. Please check with your Elsevier sales representative for more information.
ICONS AT A GLANCE
ETHNOCULTURAL IMPLICATIONS
SPECIAL POPULATIONS: CHILDREN
NATURAL HEALTH PRODUCTS
SPECIAL POPULATIONS: OLDER ADULTS
DRUG PROFILES
HIGH-ALERT Drugs
LAB VALUES RELATED TO DRUG THERAPY
PREVENTING MEDICATION ERRORS
SPECIAL POPULATIONS: ADOLESCENTS
Key drug
NEXT GENERATION NCLEX
The National Council for the State Boards of Nursing (NCSBN) is a not-for-profit organization whose members include nursing regulatory bodies. In empowering and supporting nursing regulators in their mandate to protect the public, the NCSBN is involved in the development of nursing licensure examinations, such as the NCLEX-RN®. In Canada, the NCLEX-RN® was introduced in 2015 and is, as of the writing of this text, the recognized licensure exam required for practising RNs in Canada.
The NCLEX-RN® will, as of 2023, be changing in order to ensure that its item types adequately measure clinical judgement, critical thinking, and problem-solving skills on a consistent basis. The NCSBN will also be incorporating into the examination what they call the Clinical Judgement Measurement Model (CJMM), which is a framework that the NCSBN has created to measure a novice nurse’s ability to apply clinical judgement in practice.
These changes to the examination come as a result of research findings which indicated that novice nurses have a much higher-than-desirable error rate with patients (i.e., errors that cause patient harm) and, upon NCSBN’s investigation, the discovery that the overwhelming majority of these errors were caused by failures of clinical judgement.
Clinical judgement has been a foundation underlying nursing education for decades, based on the work of a number of nursing theorists. The theory of clinical judgement that most closely aligns to what NCSBN is basing their CJMM is the work by Christine A. Tanner.
The new version of the NCLEX-RN® is loosely being identified as the “Next-Generation NCLEX” or “NGN”, and will feature the following:
• 6 key skills in the CJMM: recognizing cues, analyzing cues, prioritizing hypotheses, generating solutions, taking actions, and evaluating outcomes.
• Approved item types as of June 2020: multiple response, extended drag and drop, cloze (drop-down), enhanced hotspot (highlighting), and matrix/grid. More question types may be added.
• All new item types are accompanied by mini-case studies with comprehensive patient information—some of it relevant to the question, and some of it not.
• Case information may present a single, unchanging moment in time (a “single episode” case study) or multiple moments in time as a patient’s condition changes (an “unfolding” case study).
• Single-episode case studies may be accompanied by 1-6 questions; unfolding case studies are accompanied by 6 questions.
For more information (and detail) regarding the NCLEX-RN® and changes coming to the exam, visit the NCSBNs website: https://www.ncsbn.org/11447.htm and https://ncsbn.org/Building _a_Method_for_Writing_Clinical_Judgment_It.pdf
For further NCLEX-RN® examination preparation resources, see Silvestri’s Canadian Comprehensive Review for the NCLEXRN Examination, Second Edition, ISBN 9780323709385. Prior to preparing for any nursing licensure examination, please refer to your provincial or territorial nursing regulatory body to determine which licensure examination is required in order for you to practice in your chosen jurisdiction.
WE WELCOME YOUR FEEDBACK
We always welcome comments from instructors and students who use this book so that we may continue to make improvements and be responsive to your needs in future editions. Please send any comments you may have for us to NHPInstructorPre mier@reedelsevier.com
Our part in this book would not have been possible without the original efforts of the American authors who conceptualized and wrote Pharmacology and the Nursing Process, which has shaped the content of Lilley’s Pharmacology for Canadian Health Care Practice. Linda Lane Lilley, RN, PhD; Shelly Rainforth Collins, PharmD; and Julie S. Snyder, MSN, RN, BC, are to be commended for their thorough and expert handling of a vast and complex subject matter and for creating an excellent foundation over which the Canadian content could be easily laid. We would like to express our gratitude to Beth Swart, the author of the inaugural Canadian editions of Pharmacology for Canadian Health Care Practice, 1ce–3ce. Over the years, she has written and revised an exemplar textbook used in nursing curricula across Canada. We thank her for her dedication and commitment to nursing education.
We dedicate Lilley’s Pharmacology for Canadian Health Care Practice to our students, both past and present, who inspire us with their curiosity for learning, passion for the nursing profession, and dedication to caring for the Canadian population. We could not have met the challenges of authoring this pharmacology textbook without the support and understanding from our families and colleagues.
We could not have accomplished this project without the assistance of Theresa Fitzgerald, who encouraged, altered deadlines to fit our busy schedules, reminded us of deadlines, and supported us throughout the huge task of co-editing this book. Roberta A. Spinosa-Millman, Content Strategist at Elsevier Canada, who provided this opportunity for both of us. Many individuals at Elsevier are responsible for this Canadian edition. Our thanks go to Laurie Gower, Content Director; Sherry Hinman, Copy Editor; Jerri Hurlbutt, Copy Editor; and Richard T. Barber, Senior Project Manager for handling all the details involved in the final production of the book.
Thanks are due to the Canadian reviewers who reviewed content of this book and gave their invaluable comments, expertise, and editing suggestions on the draft manuscript. As existing diseases and disorders and their treatments evolve, bringing with them new challenges and information in pharmacology, we will no doubt be looking forward to future editions of this textbook.
Dr. Kara Sealock, RN, EdD, MEd, BN, CNCC (C), CCNE Dr. Cydnee Seneviratne, RN, PhD, MN, BSc
Another random document with no related content on Scribd:
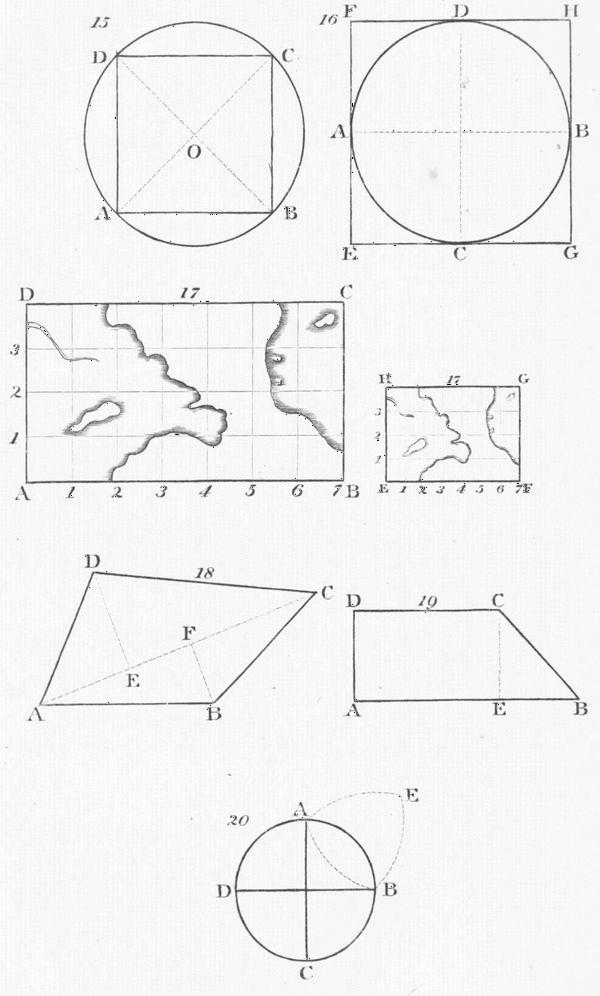
Tofindtheanglesatthecentre,andcircumferenceofaregular polygon.
Divide 360 by the number of the sides of the given polygon, and the quotient will be the angle at the centre; and this angle being subtracted from 180, the difference will be the angle, at the circumference, required.
Table,showingtheanglesatthecentre,andcircumference.
Names. No. of Angles Angles at sides. at centre. circumference.
Toinscribeanyregularpolygoninacircle.
From the centre C draw the radii C A, C B, making an angle equal to that at the centre of the proposed polygon, as contained in the preceding table. Then the distance A B will be one side of the polygon, which, being carried round the circumference the proper number of times, will complete the polygon required. Fig.13.
Fig. 15-20. Tocircumscribeacircleaboutatriangle.
Bisect any two of the given sides, A B, B C by the perpendiculars E F, D F. From the intersection F as a centre, and with the distance of any of the angles, as a radius, describe the circle required. Fig.14.
Tocircumscribeacircleaboutasquare.
Draw the two diagonals A C, B D intersecting each other in O. From O as a centre, and with O A, or O B, as a radius, describe the required circle. Fig.15.
Tocircumscribeasquareaboutacircle.
Draw the two diameters A B, C D perpendicular to each other, through the points A, C, B, D, draw the tangents E F, E G, G H, F H, and E G H F will be the square required. Fig.16.
Toreduceamap,orplan,fromonescaletoanother .
Divide the given figure A C by cross lines, forming as many squares as may be thought necessary. Draw a line E F, on which set off as many parts from the scale M, as A B contains parts of the scale N.
Draw E H, and F G perpendicular to E F, and each equal to the proportional parts contained in A D, or B C. Join H G, and divide the figure E G into the same number of squares as the original A C. Describe in every square what is contained in the corresponding square of the given figure; and E F G H will be the reduced plan required. The same operation will serve either to reduce, or enlarge any map, plan, drawing, or painting. Fig.17.
MENSURATION OF PLANES, AND SOLIDS.
Mensurationisofthreekinds, viz., lineal, superficial, and solid.
Linealmeasurehas reference to length only.
Superficialmeasure(orthesurface) includes length, and breadth.
Solidmeasure (or thecontent) comprehends length, breadth, and thickness.
MENSURATION OF PLANES.
Thearea of any plane figure is the superficial measure contained within its extremes, or bounds. This area is estimated by the number of small squares that may be contained in it, the side of these measuring squares being an inch, a foot, or any other fixed quantity, and hence the area is said to be so many square inches, square feet, &c. VideTable,Squaremeasure.Page275.
Tofindtheareaofaparallelogram,whetherasquare,rectangle,&c.
Multiply the length by the breadth, or perpendicular height, for the area required.
Example.—Required the area of a rectangle, whose length is 9 feet, and breadth 4 feet.
9 × 4 = 36 feet. The required area, or surface.
Tofindtheareaofatriangle,itsbase,andperpendicularheight beinggiven.
Multiply the base by the perpendicular height, and half the product will be the area.
Example.—Required the number of square yards contained in a triangle, whose base is 20 yards, and perpendicular height 14 yards.
20 × 14 2 = 140 square yards. Area required.
Tofindtheareaofatriangle,whosethreesidesaregiven.
From half the sum of the three sides, subtract each side severally; multiply the half sum, and the three remainders together, and the square root of the product will be the area required.
Example.—Required the area of a triangle, whose sides are 50, 40, and 30 feet.
50 + 40 + 30 2 = 60, half the sum of the three sides.
60 - 30 = 30 First difference.
60 - 40 = 20 Second difference.
60 - 50 = 10 Third difference.
30 × 20 × 10 × 60 = 360000.
Square root of 360000 = 600. Area required.
Twosidesofaright-angledtrianglebeinggiven,tofindthethird side.
1. When the two sides forming the right angle are given, to find the hypothenuse, or side opposite the right angle.
Take the square root of the sum of the two sides squared for the side required.
Example.—Required the length of the interior slope of a rampart, whose perpendicular height is 17 feet, and the base of the slope 20 feet.
17 × 17 = 289 20 × 20 = 400
The square root of 689 = 26·24. The length required.
2. When the hypothenuse, and one of the perpendicular sides are given.
From the square of the hypothenuse, subtract the square of the given side, and the square root of the remainder will be the side required.
Example.—The hypothenuse being 5 yards, and the base 4 yards, required the other side.
5 × 5 = 25 4 × 4 = 16
The square root of 9 = 3 yards. The side required.
Tofindtheareaofatrapezium,ABCD.
Draw the diagonal A C, upon which let fall from its opposite angles B, and D, the perpendiculars B F, D E. Find by measurement the diagonal A C, and the perpendiculars B F, D E, then multiply the sum of the perpendiculars by the diagonal, and half the product will be the area of the trapezium. Fig.18.
Example.—Required the area of the trapezium, whose diagonal A C is 100 feet, and perpendiculars B F 30 feet, and D E 40 feet.
(30 + 40) × 100 2 = 3500 square feet. Area required.
Or, divide the trapezium into two triangles by a diagonal, then find the areas of these triangles, and add them together.
Tofindtheareaofatrapezoid,ABCD.
Multiply the sum of the parallel sides A B, D C by the perpendicular distance E C, and half the product will be the area. Fig.19.
Example.—Required the area of the trapezoid A B C D, of which the parallel sides A B, D C are 120 feet, and 90 feet, and the perpendicular distance E C 40 feet.
(120 + 90) × 40 2 = 4200 square feet. Area required.
Tofindtheareaofanirregularfigure,orpolygon.
Draw diagonals dividing the figure into trapeziums, and triangles; then, having found the area of each, add them together, and the sum will be the area required.
Tofindtheareaofafigure,havingapartboundedbyacurve.
Draw a right line joining the extremities of the curve, then find the area of the trapezium. On the right line let fall as many perpendiculars as the several windings of the curve may require. Find their lengths, and divide their sum by the number of perpendiculars, and the quotient will be the mean breadth; which
being multiplied by the length of the right line, will give the area of the curved part. This area being added to that of the trapezium will give the area of the required figure.
Tomeasurelongirregularfigures.
Measure the breadth at both ends, and at several places atequal distances. Add together all these intermediate breadths, and half the two extremes, which sum multiply by the length, and divide by the number of parts for the area. If the perpendiculars, or breadths, be notatequaldistances, compute all the parts separately, as so many trapezoids, and add them all together for the whole area.
Example. The breadths of an irregular figure at five equi-distant places being 8, 2, 7, 9, 4, and the whole length 40, required the area.
8 + 4 = 12
6 + 2 + 7 + 9 = 24
12 ÷ 2 = 6
24 × 40 4 = 240. Area required.
Tofindthenumberofsquareacresinanyoftheprecedingfigures. [56]
Divide the superficial content in feet by 43560, and the quotient will be the number required.
Tobringsquarechainstoacres.
Of square chains strike off two decimal places to the right, and the rest of the figures will be acres.
Tobringsquarelinkstoacres.
Of square links cut off five of the figures on the right hand, for decimals, and the rest will be acres; then multiply these decimals by 4, for roods, cutting off five figures as before; and the decimals of
these again by 40, for perches, when five figures are again to be struck off.
Tofindtheareaofaregularpolygon.
Multiply the perimeter(or sum of the sides) of the polygon by the perpendicular drawn from its centre on one of its sides, and take half the product for the area.
Or, multiply the area of one of the triangles by the number of sides of the polygon, and the product will be the area of it.
Example.—Required, the area of a regular hexagon, whose side is 40 feet, and the perpendicular 34·64 feet.
40 × 6 = 240 the perimeter.
240 × 34·64 2 = 4156·8 square feet. Area required.
Tofindthediameter,andcircumferenceofanycircle,theonefrom theother .
Use either of the following proportions:
as 7 is to 22 } { so is the diameter or as 1 is to 3·1416 } { to the circumference.
as 22 is to 7 } { so is the circumference or, as 3·1416 is to 1 } { to the diameter.
or, instead of dividing the diameter by 3·1416, multiply it by ·3183, for the circumference.
Example 1.—Required, the circumference of a circle, whose diameter is 20 feet.
As 7 : 22 :: 20 : 62·857 feet. Circumference required.
Example 2.—Required, the diameter of a circle, whose circumference is 36 inches.
As 22 : 7 :: 36 : 11·45 inches. Diameter required.
Tofindthediameterofacircle,theareabeinggiven.
Divide the area by ·7854, and the square root of the quotient will be the diameter required.
Example.—Required, the diameter of a circle, whose area is 176·715 square feet.
176·715 ÷ ·7854 = 225.
Square root of 225 = 15 feet. Diameter required.
Tofindtheareaofacircle.
1. Multiply half the circumference by half the diameter, or multiply the whole circumference by the whole diameter, and take ¼ of the product.
2. Or, square the diameter, and multiply that square by ·7854 for the area.
3. Or, square the circumference, and multiply that square by 0·7958.
Example1.—Required the area of a circle, whose circumference is 55·548 inches, and its diameter 18 inches.
55·548 2 = 27·774 half circumference.
18 2 = 9 half diameter.
27·774 × 9 = 249·966, square inches. Area required.
Example 2.—Required the area of a circle whose diameter is 12 feet.
12 × 12 = 144, square of the diameter. ·7854 × 144 = 113·0976 square feet. Area required.
Example3.—Required the area of a circle, whose circumference is 22 feet.
22 × 22 = 484.
484 × ·07958 = 38·51672 square feet. Area required.
Tofindtheareaofacircularring, or space included between the circumferences of two circles, the one within the other.
1. Subtract the square of the less diameter from the square of the greater, and multiply their difference by ·7854.
2. Or, find the area of each circle separately, and subtract one from the other, for the area required.
3. Or, multiply the sum of the diameters by the difference of the same, and that product by ·7854 for the area.
Example.—Required the area of a ring, the diameters of whose bounding circles are 10, and 20.
ByRule3.
20 + 10 = 30, sum of diameters.
20 - 10 = 10, difference of diameters.
30 × 10 × ·7854 = 235·62. The area.
Tofindthelengthofanyarcofacircle.
1. As 360° is to the number of degrees in the arc, so is the circumference to the length of the arc.
2. Or, multiply the degrees in the given arc by the radius of the circle, and the product by ·01745 for the length of the arc.
Example.—Rule 2.—Required the length of an arc of 30°, the radius being 9 feet.
30 × 9 × ·01745 = 4·7115. Length of arc.
Tofindtheareaofthesectorofacircle.
Multiply the radius by the arc, and half the product will be the area.
Example.—Required the area of the sector, whose radius is 30 inches, and the length of the arc 36·6 inches.
36·6 × 30 2 = 549 square inches. Area required.
Tofindtheareaofthesegmentofacircle.
Find the area of the sector, by the preceding rule. Then find the area of the triangle formed by the chord of the segments, and the radii of the sector. Then, if the segment be less than a semicircle, subtract the area of the triangle from it; or, if the segment be greater than a semicircle, add the area of the triangle to it; for the area of the segment.
Example.—Required the area of a segment less than a semicircle, the radius being 20 inches, the chord 22·42 inches, the length of the arc 24·43 inches, and the perpendicular 16·56 inches.
24·43 × 20 2 = 244·3 square inches. Area of the sector.
22·42 × 16·56 2 = 185·6376 square inches. Area of the triangle.
244·3 - 185·6376 = 58·6624 square inches. Area required.
Tofindtheareaofasemicircle.
1. Multiply ¼ of the circumference by the radius, and the product will be the area.
2. Or, multiply the square of the diameter by ·7854, and half the product will be the area.
Example.—Rule 2.—Required the area of a semicircle, the diameter being 50 inches.
50 × 50 × ·7854 2 = 981·75 square inches. Area required.
Tofindtheareaofanellipsis,oroval.
Multiply the longest diameter, or axis, by the shortest, then multiply the product by ·7854 for the area.
Example.—Required the area of the ellipse, whose diameters are 25 inches, and 18 inches.
25 × 18 × ·7854 = 353·43 square inches. Area required.
Tofindtheareaofaparabola,oritssegment.
Multiply the base by the perpendicular height, and take two-thirds of the product for the area.
Example.—Required the area of a parabola, whose base is 20 feet, and height 12 feet.
20 × 12 = 240 ⅔ of 240 = 160 square feet. Area required.
MENSURATION OF SOLIDS.
Asolidis a body containing length, breadth, and thickness.
Solids are measured by cubes, whose sides are each an inch, a foot, a yard, &c., and the solidity, capacity, or content of any figure is computed by the number of such cubes as are contained in it.—Vide Cubicmeasure,page276.
Acubeis a solid contained by six equal square sides.
Apyramidis a solid whose sides are all triangles meeting together in a point, the base being any plane figure whatever. It is called a triangular pyramid when its base is a triangle; a square pyramid when its base is a square, &c.
Thesegmentofapyramid,cone,oranyothersolidis a part of D E F G cut off from the top by a plane D E F, parallel to the base A B C. —
VideFig.21,Plate2, HEIGHTS, DISTANCES, and PRACTICAL GEOMETRY.
A frustrum, or trunk, is a part A B C D E F, that remains at the bottom after the segment is cut off.
Aconeis a round pyramid, of which the base is a circle.
Theaxisofasolidis a line from the vertex (or point) to the centre of the base, or through the centres of the two ends. When the axis is perpendicular to the base, it is a right prism, pyramid, or cone; otherwise it is oblique.
A sphere is a solid contained under one convex surface, and is described by the revolution of a semicircle about its diameter, which remains fixed.
The centre of the sphere is such a point within the solid as is everywhere equally distant from the convex surface, or circumference of it.
Thediameter(or axis) ofasphere is a straight line, which passes through the centre, and is terminated by the convex surface.
Asegmentofasphere is a part cut off by a plane, the section of which is always a circle, called the baseofthesegment.
Asectorofasphere is that which is composed of a segment (less than an hemisphere) and of a cone.
Aprismis a solid, the sides of which are parallelograms, having its ends equal, and similar plane figures.
Prismsarenamedaccording to the number of angles in the base.
Acylinder is a solid, the two ends of which are circular; and it is described, or formed, by the revolution of a right-angled parallelogram about one of its sides, which remains fixed.
Tofindthesuperficiesofaprism,orcylinder .
Multiply the perimeter of one end of the prism by the length, or height of the solid, and the product will be the surface of all its sides. To which add also the area of the two ends of the prism, when required.
Or, compute the areas of all the sides, and ends separately, and add them all together.
Example.—Required the surface of a cube, whose sides are each 5 inches.
5 + 5 + 5 + 5 = 20, perimeter of one end.
20 × 5 = 100, surface of sides.
5 × 5 = 25, area of one end.
100 + 25 + 25 = 150 square inches. Surface of cube.
Tofindthesurfaceofapyramid,orcone.
Multiply the perimeter of the base by the slant height, or length of the side, and half the product will be the surface of the sides; to which add the area of the base when required.
Example.—Required the upright surface of a triangular pyramid, the slant height being 20 feet, and each side of the base 3 feet.
3 + 3 + 3 = 9, perimeter of base. 9 × 20 2 = 90 feet. Surface required.
Tofindthesurfaceofthefrustrumofapyramid,orcone.
Add together the perimeters of the two ends, multiply their sum by the slant height, and take half the product.
Example.—How many square feet are in the surface of the frustrum of a square pyramid, whose slant height is 10 feet, each side of the base 3 feet, and each side of the less end 2 feet.
3 + 3 + 3 + 3 = 12, perimeter of base.
2 + 2 + 2 + 2 = 8, perimeter of less end.
(12 + 8) × 10 2 = 100 feet. Surface required.
Tofindthesolidcontentofaprismorcylinder .
Find the area of the base, or end, and multiply it by the length of the prism, or cylinder. Fora cube, multiply its side twice by itself; and for a parallelopipedon, multiply the length, breadth, and depth together for the content.
Example.—Required the solid content of a cube, whose side is 24 inches.
24 × 24 × 24 = 13824 square inches. Content required.
Tofindthecontentofthesolidpartofahollowcylinder .
From the content of the whole cylinder considered as a solid, subtract the content of the hollow part, also considered as a solid, and the difference will be the solidity required.
Example.—Required the content of the solid part of the hollow cylinder whose exterior diameter is 12 inches, the interior diameter 8 inches, and height 20 inches.
12 × 12 × ·7854 = 113·0976, area of base of cylinder. 113·0976 × 20 = 2261·952, solidity of whole cylinder. 8 × 8 × ·7854 = 50·2656, area of base of hollow cylinder. 50·2656 × 20 = 1005·312, content of hollow part. 2261·952 - 1005·312 = 1256·64 cubic inches. Solidity required.
Tofindthesolidityofthefrustrumofacylinder .
Multiply the area of the base by half the greatest, and the least lengths, and the product will be the solidity.
Example.—Required the solidity of a frustrum, whose diameter is 24 inches, the greatest length 36 inches, and the least length 20 inches.
24 × 24 = 576. Square of the diameter.
576 × ·7854 = 452·3904. Area of the base.
452·3904 × (36 + 20) 2 = 12666·9312 Cubic inches. Solidity required.
Tofindthecontentofapyramid,orcone.
Find the area of the base, and multiply that area by the perpendicular height, and take ⅓ of the product.
Example.—Required the solidity of a square pyramid, each side of its base being 30, and its perpendicular height 25.
30 × 30 = 900, area of base.
900 × 25 3 = 7500, solidity required.
Tofindthesolidityofthefrustrumofacone,orpyramid.
Add into one sum the areas of the two ends, and the mean proportional between them: take ⅓ of that sum for the mean area, which multiply by the perpendicular height, or length of the frustrum.
Note.—Tofindameanproportional.
As one of the sides of the base is to the homologous, or corresponding side of the other end, so is the area of the base to the mean proportional required.
Example.—Required the number of solid feet in a piece of timber, whose bases are squares, each side of the greater end being 15 inches, and each side of the less end 6 inches; also the length of the perpendicular altitude 24 feet.
15 × 15 = 225, area of the base.
6 × 6 = 36, area of the top.
As 15: 6 :: 225: 90, mean proportional. 24 feet = 288 inches.
(225 + 36 + 90) × 288 3 = 33696 cubic inches = 19½ cubic feet.
Tofindthesurfaceofasphere,oranysegment.
Multiply the circumference of the sphere by its diameter, which will give the whole surface.
Or, square the diameter, and multiply by 3·1416.
Or, square the circumference, and multiply by ·3183; or divide by 3·1416.
Note. For the surface of thesegment, or frustrum, multiply the whole circumference of the sphere by the height of the part required.
Example.—Required the superficies of a globe whose diameter is 24 inches.
24 × 24 × 3·1416 = 1809·5616 square inches.
Tofindthesolidityofasphere,orglobe.
1. Multiply the surface by the diameter, and take ⅙ of the product.
Or, multiply the square of the diameter by the circumference, and take ⅙ of the product.
2. Cube the diameter, and multiply by ·5236.
3. Cube the circumference, and multiply by ·01688.
Example.—Required the content of a sphere, whose axis is 12.
12 × 12 × 12 × ·5236 = 904·7808. Content required.
Tofindthesolidityofanhemisphere.
Find the solidity of the sphere, and half the content will be that of the hemisphere.
Note 1.—Any sphere, or globe twice the diameter of another contains four times the superficies, or area of the other, and eight timesthe solid content. Hence the superficies of spheres are as the squares, and the solidity as the cubes of their diameters.
Note 2. The cube of the diameter of a sphere in inches, multiplied by ·00188, will give the number of imperialgallons it will contain.
Tofindthesolidcontentofasphericalsegment.
1. From three times the diameter of the sphere, take double the height of the segment; then multiply the remainder by the square of the height, and this product by ·5236.
2. Or, to three times the square of the radius of the segment’s base add the square of its height; then multiply the sum by the height, and the product by ·5236.
Example.—Required the content of a spherical segment 2 feet in height, cut from a sphere of 8 feet diameter.
(3 × 8) - (2 × 2) = 20
20 × 22 × ·5236 = 41·888 cubic feet. Content required.
Tofindthediameterofasphere,itssoliditybeinggiven.
Divide the solidity by ·5236, and take the cube root of the quotient.
Example. The solidity of a sphere being 113·0976 solid inches, what will be its diameter?
113·0976 ·5236 = 216, the cube root of which is 6 inches, the diameter required.
Tofindtheweightofanironshot,itsdiameterbeinggiven.
Take ⅛ of the cube of the diameter, and ⅛ of that eighth, and the sum of these two quotients will be the weight in pounds.
Or, as 64 is to 9 lb. so is the diameter cubed to its weight.
Example.—Required the weight of an iron shot whose diameter is 3·5 inches?
3·5 cubed = 42·875, cube of diameter. 42·875 8 = 5·359 5·359 8 = ·669 5·359 + ·669 = 6·028 pounds. Weight required.
Tofindtheweightofaleadenball,itsdiameterbeinggiven.
Take ⅓ of the cube of the diameter, and from it subtract ⅓ of this third, and the remainder will be the weight, nearly.
Or, take 3/14 of the cube of the diameter.
Example.—What is the weight of a leaden ball whose diameter is 3·3 inches?
3·3 cubed = 35·937, cube of diameter. 35·937 3 = 11·979 11·979 3 = 3·993 11·979 - 3·993 = 7·986 pounds. Weight required.
Tofindthediameterofanironshot,itsweightbeinggiven.
Multiply the cube root of the shot’s weight by 1·923 for the diameter.
Cube root. Diameter. 42 3·4760, &c. { } 6·684, &c. 32 3·1748 { Multiplied } 6·103 ” 24 2·8844 { by 1·923, } 5·545 ” 18 2·6207 { diameter } 5·038 ” 12 2·2894 { of a } 4·401 ”
9 2·0800 { 1 lb. } 3·999 ”
6 1·8171 { shot. } 3·494 ”
3 1·4422 { } 2·772 ”
Tofindthediameterofaleadenball,itsweightbeinggiven.
To 4 times the weight add half the weight, and 3/100 of half the weight; and the cube root of this sum will be the diameter in inches, nearly.
Example. What is the diameter of a leaden ball, whose weight is 8 pounds?
8 x 4 = 32 8 2 = 4 3 100 of 4 = ·12.
32 + 4 + ·12 = 36·12, of which the cube root is 3·3 inches, nearly.
Diameter required.
Tofindtheweightofanironshell,itsinteriorandexteriordiameter beinggiven.
Take 9 64 of the difference of the cubes of the external and internal diameters, for the weight of the shell in pounds.
Example.—What is the weight of a shell whose exterior diameter is 12·85 inches, and interior diameter 8·75 inches?
12·85 cubed = 2121·8241, 8·75 cubed = 669·9218. 2121·8241 - 669·9218 = 1451·9022. 9 64 of 1451·9022 = 204·1737 pounds. Weight required.
Tofindthequantityofpowderashellwillcontain.
Divide the cube of the interior diameter in inches by 57·3, and the quotient will be the weight in pounds.
Or, multiply the cube of the diameter by 11, and divide by 21 for the quantity in half ounces.
Example.—How much powder will fill a shell, whose internal diameter is 7 inches?
7 cubed = 343.
343 57·3 = 6 pounds nearly. Powder required.
Tofindthesideofacubicalboxtocontainagivenquantityof powder . [57]
Multiply the weight in pounds by 30, and the cube root of the product will be the side of the box in inches.
Example.—Required the side of a cubical box to hold 50 pounds of powder?
50 × 30 = 1500, the cube root of which is 11·44, which will be the side of the box in inches.
Tofindthequantityofpowdertofillthechamberofamortar,or howitzer.
Multiply the content of the chamber in inches by 55, and divide the product by 1728, and the quotient will be the quantity of powder in pounds.
Note.—The chamber of a mortar, or howitzer, is formed of a hollow frustrum of a right cone, and of a hollow hemisphere.
Example.—Required the quantity of powder to fill the chamber of a 13-inch mortar in which the diameter A B is 9·5 inches, the diameter C E 6·5 inches, and the length D G 21·5 inches. VideFig.22. Plate2.HEIGHTS AND DISTANCES, and PRACTICAL GEOMETRY.
The content of the chamber must be found by finding the content of the hollow frustrum of the cone, and that of the hemisphere (vide precedingrules): which in this example will be 999·9741875.
Then 999·9741875 × 55 1728 = 31 pounds, nearly.
Tofindthequantityofpowdertofillarectangularbox.
Divide the content (viz., length × breadth × depth) of the box in inches by 30 for the pounds of powder.
Example.—How much powder will fill a box, the length being 15 inches, the breadth 12, and the depth 10 inches.
15 × 12 × 10 30 = 1800 30 = 60 pounds. Number required.
Tofindthequantityofpowdertofillacylinder .
Multiply the square of the diameter by the length, then divide by 38·2 for the pounds of powder.
Example.—How much powder will the cylinder contain, whose diameter is 10 inches, and length 20 inches?
10 × 10 × 20 38·2 = 52⅓ pounds, nearly.
Tofindthesizeofashell,tocontainagivenweightofpowder .
Multiply the pounds of powder by 57·3, and the cube root of the product will be the diameter in inches.
Example.—Required the diameter of a shell to contain 6 lb. of powder?
6 × 57·3 = 343·8, the cube root of which is 7, the diameter required, in inches.
Tofindwhatlengthofacylinder(orboreofagun)willbefilledbya givenweightofpowder .
Multiply the weight in pounds by 38·2, and divide the product by the square of the diameter in inches, for the length.
Example. What length of a cylinder 8 inches in diameter will be filled with 20 lb. of powder?
20 × 38·2 8 × 8 = 11 15 16 inches.
Tofindthecontent,andweightofapieceofordnance.
Divide the length of the gun into as many sections as may be found necessary. Find the content of each (by preceding rules) and from their sum subtract the content of a cylinder, whose length is equal to that of the bore, and its diameter equal to that of the calibre of the piece; multiply the difference (if it be a brass gun) by 5·0833, (if an iron gun) by 4·2968, and the product will be the weight in ounces.
Note.—A cubic inch of gun metal weighs 5·0833 ounces. Ditto of castiron 4·2968 ounces.
Tofindthecontentofacask.
Multiply half the sum of the areas of the two interior circles, viz. at the head, and bung, by the interior length, for the content.
Or, to the area of the head add twice the area at the bung, multiply that sum by the length, and take one-third of the product.
Example.—Required the content of a cask, its greatest interior diameter being 24 inches, its least interior diameter 20 inches, and the interior length 30 inches.
24 × 24 × ·7854 = 452·3904, area of large circle.
20 × 20 × ·7854 = 314·1600, area of small circle. 452·3904 + 314·1600 2 = 383·2752, half sum.
Then 383·2752 × 30 = 11498·256, the content; which being divided by 277¼ (the number of cubic inches in a gallon) will give the number of gallons contained in the cask.
Thus 11498·256 277·25 = 41·4725, &c. Number of gallons required.
Note.-The content of any vessel in cubic feet, multiplied by 6·232 (or if in inches by ·003607) will give the number of imperialgallons itwillcontain.
EPITOME OF MENSURATION.
OF THE CIRCLE, CYLINDER, SPHERE, ETC.
1. The circle contains a greater area than any other plane figure, bounded by an equal perimeter, or outline.
2. The areas of circles are to each other as the squares of their diameters; any circle twice the diameter of another contains four times the area of the other.
3. The diameter of a circle being 1, its circumference equals 3·1416.
4. The diameter of a circle is equal to ·31831 of its circumference.
5. The square of the diameter of a circle being 1, its area equals ·7854.
6. The square root of the area of a circle, multiplied by 1·12837, equals its diameter.
7. The diameter of a circle, multiplied by ·8862, or the circumference multiplied by ·2821, equals the side of a square of equal area.
8. The sum of the squares of half the chord, and versed sine, divided by the versed sine, the quotient equals the diameter of the corresponding circle.
9. The chord of the whole arc of a circle taken from eight times the chord of half the arc, one-third of the remainder equals the length of the arc.
10. Or, the number of degrees contained in the arc of a circle, multiplied by the diameter of the circle, and by ·008727, the product equals the length of the arc in equal terms of unity.
11. The length of the arc of the sector of a circle multiplied by its radius, half the product is the area.
12. The area of the segment of a circle equals the area of the sector, minus the area of a triangle whose vertex is the centre; and base equals the chord of the segment.
13. The sum of the diameters of two concentric circles multiplied by their difference, and by ·7854, equals the area of the ring, or space contained between them.
14. The sum of the thickness, and internal diameter of a cylindric ring multiplied by the square of its thickness, and by 2·4674, equals its solidity.
15. The circumference of a cylinder multiplied by its length, or height, equals its convex surface.
16. The area of the end of a cylinder multiplied by its length, equals its solid content.
17. The area of the internal diameter of a cylinder multiplied by its depth, equals its cubical capacity.
18. The square of the diameter of a cylinder multiplied by its length, and divided by any other required length, the square root of the quotient equals the diameter of the other cylinder of equal solidity, or capacity.
19. The square of the diameter of a sphere multiplied by 3·1416 equals its convex surface.
20. The cube of the diameter of a sphere multiplied by ·5236, equals its solid content.
21. The height of any spherical segment, or zone, multiplied by the diameter of the sphere, of which it is a part, and by 3·1416, equals the area, or convex surface of the segment;
22. Or, the height of the segment multiplied by the circumference of the sphere of which it is a part, equals the area.
23. The solidity of any spherical segment is equal to three times the square of the radius of its base, plus the square of its height, and multiplied by its height, and by ·5236.
24. The solidity of a spherical zone equals the sum of the squares of the radii of its two ends, and one-third the square of its height, multiplied by the height, and by 1·5708.
25. The solidity of the middle zone of a sphere equals the sum of the square of either end, and two-thirds the square of the height, multiplied by the height, and by ·7854.
26. The capacity of a cylinder 1 foot in diameter, and 1 foot in length, equals 4·895 imperial gallons.
27. The capacity of a cylinder 1 inch in diameter, and 1 foot in length, equals ·034 of an imperial gallon.
28. The capacity of a cylinder 1 inch in diameter, and 1 inch in length, equals ·002832 of an imperial gallon.
29. The capacity of a sphere 1 foot in diameter, equals 3·263 imperial gallons.
30. The capacity of a sphere 1 inch in diameter, equals ·001888 of an imperial gallon.
31. Hence the capacity of any other cylinder in imperial gallons is obtained by multiplying the square of its diameter by its length; or the capacity of any other sphere by the cube of its diameter, and by the number of imperial gallons contained as above in the unity of its measurement.
OF THE SQUARE, RECTANGLE, CUBE, ETC.
1. The side of a square equals the square root of its area.
2. The area of a square equals the square of one of its sides.
3. The diagonal of a square equals the square root of twice the square of its side.
4. The side of a square is equal to the square root of half the square of its diagonal.
5. The side of a square, equal to the diagonal of a given square, contains double the area of the given square.
6. The area of a rectangle equals its length multiplied by its breadth.
7. The length of a rectangle equals the area divided by the breadth; or the breadth equals the area divided by the length.
8. The side, or end of a rectangle, equals the square root of the sum of the diagonal, and opposite side to that required, multiplied by their difference.
9. The diagonal in a rectangle equals the square root of the sum of the squares of the base, and perpendicular.
10. The solidity of a cube equals the area of one of its sides multiplied by the length of one of its edges.
11. The edge of a cube equals the cube root of its solidity.
12. The capacity of a 12-inch cube equals 6·232 gallons.
Surfaces, andsoliditiesoftheregularbodies, whenthelinearedge is1.
The tabular surface multiplied by the square of the linear edge, the product equals the surface required:
Or, the tabular solidity, multiplied by the cube of the linear edge, the product is the solidity required.
OF TRIANGLES, POLYGONS, ETC.
1. The complement of an angle is its defect from a right angle.
2. The supplement of an angle is its defect from two right angles.
3. The sine, tangent, and secant of an angle, are the cosine, cotangent and cosecant of the complement of that angle.
4. The hypothenuse of a right-angled triangle being made radii, its sides become the sines of the opposite angles, or the cosines of the adjacent angles.
5. The three angles of every triangle are equal to two right angles; hence the oblique angles of a right-angled triangle are each other’s complements.
6. The sum of the squares of the two given sides of a right-angled triangle is equal to the square of the hypothenuse.
7. The difference between the square of the hypothenuse, and given side of a right-angled triangle is equal to the square of the required side.
8. The area of a triangle equals half the product of the base multiplied by the perpendicular height;
9. Or, the area of a triangle equals half the product of the two sides, and the natural sine of the contained angle.
10. The side of any regular polygon multiplied by its apothem, or perpendicular, and by the number of its sides, half the product is the area.
Tableoftheareasofregularpolygonswhosesidesareunity.
Name of polygon.
No. of sides. Apothem, or perpendicular. Area, when side is one or unity. Interior angle. Central angle.
The tabular area of the corresponding polygon multiplied by the square of the side of the given polygon, equals the area of the given polygon.
OF ELLIPSES, CONES, FRUSTRUMS, ETC.
1. The square root of half the sum of the squares of the two diameters of an ellipse multiplied by 3·1416 equals its circumference.
2. The product of the two axes of an ellipse multiplied by ·7854 equals its area.
3. The curve surface of a cone is equal to half the product of the circumference of its base multiplied by its slant side, to which, if the area of the base be added, the sum is the whole surface.
4. The solidity of a cone equals one-third of the product of its base multiplied by its altitude, or height.
5. The squares of the diameters of the two ends of the frustrum of a cone added to the product of the two diameters, and that sum multiplied by its height, and by ·2618, equals its solidity.