Visit to download the full and correct content document: https://ebookmass.com/product/bayesian-statistics-for-beginners-a-step-by-step-appr oach-therese-m-donovan/
More products digital (pdf, epub, mobi) instant download maybe you interests ...
Elementary Statistics: A Step By Step Approach 10th Edition, (Ebook PDF)
https://ebookmass.com/product/elementary-statistics-a-step-bystep-approach-10th-edition-ebook-pdf/
Elementary Statistics: A Step By Step Approach, 11e ISE 11th/ISE Edition Allan Bluman
https://ebookmass.com/product/elementary-statistics-a-step-bystep-approach-11e-ise-11th-ise-edition-allan-bluman/
ISE Elementary Statistics: A Step By Step Approach - A Brief Version, 8e 8th Edition Allan G. Bluman
https://ebookmass.com/product/ise-elementary-statistics-a-stepby-step-approach-a-brief-version-8e-8th-edition-allan-g-bluman/
WordPress for Beginners 2019: A Visual Step by Step Guide to Mastering WordPress (Webmaster Series Book 2) (Ebook PDF)
https://ebookmass.com/product/wordpress-forbeginners-2019-a-visual-step-by-step-guide-to-masteringwordpress-webmaster-series-book-2-ebook-pdf/
Developing Helping Skills: A Step by Step Approach to Competency 3rd Edition, (Ebook PDF)
https://ebookmass.com/product/developing-helping-skills-a-stepby-step-approach-to-competency-3rd-edition-ebook-pdf/
Developing Helping Skills: A Step-By-Step Approach to Competency 3rd Edition Valerie Nash Chang
https://ebookmass.com/product/developing-helping-skills-a-stepby-step-approach-to-competency-3rd-edition-valerie-nash-chang/
Endovascular Interventions-A Step-by-Step Approach (Nov 6, 2023)_(1119467780)_(Wiley-Blackwell) Jose Wiley
https://ebookmass.com/product/endovascular-interventions-a-stepby-step-approach-nov-6-2023_1119467780_wiley-blackwell-josewiley/
Learn Data Mining Through Excel: A Step-by-Step Approach for Understanding Machine Learning Methods, 2nd Edition Hong Zhou
https://ebookmass.com/product/learn-data-mining-through-excel-astep-by-step-approach-for-understanding-machine-learningmethods-2nd-edition-hong-zhou/
Microsoft Project 2019 Step by Step (Step by Step (Microsoft)) Cindy Lewis & Carl Chatfield & Timothy Johnson [Lewis
https://ebookmass.com/product/microsoft-project-2019-step-bystep-step-by-step-microsoft-cindy-lewis-carl-chatfield-timothyjohnson-lewis/
BayesianStatistics forBeginners BayesianStatistics forBeginners THERESEM.DONOVAN RUTHM.MICKEY GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries ©RuthM.Mickey2019
Themoralrightsoftheauthorhavebeenasserted
FirstEditionpublishedin2019
Impression:1
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica BritishLibraryCataloguinginPublicationData
Dataavailable
LibraryofCongressControlNumber:2019934655
ISBN978–0–19–884129–6(hbk.)
ISBN978–0–19–884130–2(pbk.)
DOI:10.1093/oso/9780198841296.001.0001
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork.
Toourparents,ThomasandEarlineDonovanandRayandJeanMickey, forinspiringaloveoflearning.
Toourmentors,someofwhomwe’vemetonlybytheirwrittenwords, forteachinguswaysofknowing.
ToPeter,Evan,andAna foreverything.
Preface Greetings.ThisbookisourattemptatgainingmembershiptotheBayesianConspiracy. Youmayask, “WhatistheBayesianConspiracy?” TheanswerisprovidedbyEliezer Yudkowsky(http://yudkowsky.net/rational/bayes): “TheBayesianConspiracyisamulti national,interdisciplinary,andshadowygroupofscientiststhatcontrolspublication, grants,tenure,andtheillicittrafficingradstudents.Thebestwaytobeacceptedintothe BayesianConspiracyistojointheCampusCrusadeforBayesinhighschoolorcollege,and graduallyworkyourwayuptotheinnercircles.Itisrumoredthatattheupperlevelsofthe BayesianConspiracyexistninesilent figuresknownonlyastheBayesCouncil.”
Haha!Bayes’ Theorem,alsocalledBayes’ Rule,waspublishedposthumouslyin1763in thePhilosophicalTransactionsoftheRoyalSociety.InTheTheoryThatWouldNotDie, authorSharonBertschMcGrayneaptlydescribeshow “Bayes’ rulecrackedtheenigmacode, hunteddownRussiansubmarines,andemergedtriumphantfromtwocenturiesofcontroversy.” Inshort,Bayes’ Rulehasvastapplication,andthenumberofpapersandbooksthat employitisgrowingexponentially.
InspiredbytheknowledgethataBayesCouncilactuallyexists,webeganourjourneyby enrollingina5-day ‘introductory’ workshoponBayesianstatisticsafewyearsago.OnDay 1,wewereintroducedtoavarietyofBayesianmodels,and,onDay2,wesheepishlyhadto inquirewhatBayes’ TheoremwasandwhatithadtodowithMCMC.Inotherwords,the materialwaswayoverourheads.Withtailsbetweenourlegs,weslunkbackhomeand begantryingtosortoutthemanydifferentusesofBayes’ Theorem.
AswereadmoreandmoreaboutBayes’ Theorem,westartednotingourownquestionsas theyaroseandbegannarratingtheanswersastheybecamemoreclear.Theresultisthis strangebook,castasaseriesofquestionsandanswersbetweenreaderandauthor.Inthis prose,wemakeheavyuseofonlineresourcessuchasthe OxfordDictionaryofStatistics (UptonandCook,2014), WolframMathematics,andthe OnlineStatisticsEducation:An InteractiveMultimediaCourseforStudy (RiceUniversity,UniversityofHoustonClear Lake,andTuftsUniversity).Wealsoprovidefriendlylinkstoonlineencyclopediassuch as Wikipedia and EncyclopediaBritannica.Althoughtheseshouldnotbeconsidered definitive,originalworks,wehaveincludedthelinkstoprovidereaderswithareadily accessiblesourceofinformationandaregratefultothemanyauthorswhohavecontributedentries.
WearenotexpertsinBayesianstatisticsandmakenoclaimassuch.ThereseDonovanisa biologistfortheU.S.GeologicalSurveyVermontCooperativeFishandWildlifeResearch Unit,andRuthMickeyisastatisticianintheDepartmentofMathematicsandStatisticsat theUniversityofVermont.Wewereraisedonahealthydoseof “frequentist” andmaximumlikelihoodmethodsbuthavebegunonlyrecentlytoexploreBayesianmethods.We haveintentionallyavoidedcontroversialtopicsandcomparisonsbetweenBayesianand frequentistapproachesandencouragethereadertodigdeeper muchdeeper thanwe havehere.Fortunately,agreatnumberofexpertshavepavedtheway,andwereliedheavily onthefollowingbookswhilewritingourown:
• N.T.HobbsandM.B.Hooten.BayesianModels:AStatisticalPrimerforEcologists. PrincetonUniversityPress,2015.
• J.Kruschke.DoingBayesianDataAnalysis:ATutorialwithR,JAGS,andStan. Elsevier,2015.
• A.Gelman,J.B.Carlin,H.S.Stern,andD.B.Rubin.BayesianDataAnalysis.Chapman& Hall,2004.
• J.V.Stone.Bayes’ Rule:aTutorialIntroductiontoBayesianAnalysis.SebtelPress,2014.
• H.RaiffaandR.Schlaifer.AppliedStatisticalDecisionTheory.DivisionofResearch, GraduateSchoolofBusinessAdministration,HarvardUniversity,1961.
• P.GoodwinandG.Wright.DecisionAnalysisforManagementJudgment.JohnWiley& Sons,2014.
Althoughwereliedonthesesources,anymistakesofinterpretationareourown.
OurhopeisthatBayesianStatisticsforBeginnersisa “quickread” fortheuninitiatedand that,inoneweekorless,wecould findareaderhappilyensconcedinabookwrittenbyone oftheexperts.OurgoalinwritingthebookwastokeepBayes’ Theoremfrontandcenterin eachchapterforabeginningaudience.Asaresult,Bayes’ Theoremmakesanappearancein everychapter.Wefrequentlybringbackpastexamplesandexplainwhatwedid “back then,” allowingthereadertoslowlybroadentheirunderstandingandsortoutwhathas beenlearnedinordertorelateittonewmaterial.Forthemostpart,ourreviewerslikedthis approach.However,ifthisisannoyingtoyou,youcanskimovertherepeatedportions.
Ifthisbookisusefultoyou,itisdueinnosmallparttoateamofstellarreviewers.Weowe agreatdealofgratitudetoGeorgeAllez,CathleenBalantic,BarryHall,MevinHooten,Peter Jones,ClintMoore,BenStaton,SheilaWeaver,andRobinWhite.Theirenthusiasm, questions,andcommentshaveimprovedthenarrativeimmensely.Weofferaheartfelt thankyoutoGaryBishop,ReneeWestland,MelissaMurphy,KevinRoark,JohnBell,and StuartGemanforprovidingpicturesforthisbook.
ThereseDonovan RuthMickey October2018 Burlington,VT
SECTION1 BasicsofProbability
1IntroductiontoProbability
SECTION2 Bayes ’ TheoremandBayesianInference
3Bayes’ Theorem29
4BayesianInference37
5TheAuthorProblem:BayesianInferencewithTwoHypotheses48
6TheBirthdayProblem:BayesianInferencewithMultipleDiscreteHypotheses61
7ThePortraitProblem:BayesianInferencewithJointLikelihood73
SECTION3 ProbabilityFunctions
8ProbabilityMassFunctions
SECTION4 BayesianConjugates
10TheWhiteHouseProblem:TheBeta-BinomialConjugate
SECTION5 MarkovChainMonteCarlo
13TheSharkAttackProblemRevisited:MCMCwiththeMetropolisAlgorithm193
14MCMCDiagnosticApproaches212
15TheWhiteHouseProblemRevisited:MCMCwiththeMetropolis–Hastings Algorithm
16TheMapleSyrupProblemRevisited:MCMCwithGibbsSampling
SECTION6 Applications 17TheSurvivorProblem:SimpleLinearRegressionwithMCMC
Appendices SECTION1 BasicsofProbability Overview
Andsowebegin.This firstsectiondealswithbasicconceptsinprobabilitytheory,and consistsoftwochapters.
• InChapter1,theconceptofprobabilityisintroduced.Usinganexample,thechapter focusesonasinglecharacteristicandintroducesbasicvocabularyassociatedwith probability.
• Chapter2introducesadditionaltermsandconceptsusedinthestudyofprobability.The chapterfocusesontwocharacteristicsobservedatthesametime,andintroducesthe importantconceptsofjointprobability,marginalprobability,andconditional probability.
Aftercoveringthesebasics,yourBayesianjourneywillbegin.
CHAPTER1 IntroductiontoProbability Inthischapter,we’llintroducesomebasictermsusedinthestudyofprobability.Bytheend ofthischapter,youwillbeabletodefinethefollowing:
• Samplespace
• Outcome
• Discreteoutcome
• Event
• Probability
• Probabilitydistribution
• Uniformdistribution
• Trial
• Empiricaldistribution
• LawofLargeNumbers
Tobegin,let’sanswerafewquestions...
Whatisprobability? Answer: Thebestwaytointroduceprobabilityistodiscussanexample.Imagineyou’rea gambler,andyoucanwin$1,000,000ifasinglerollofadieturnsupfour.Yougetonlyone roll,andtheentryfeetoplaythisgameis$10,000.Ifyouwin,you’reamillionaire.Ifyou lose,you’reouttengrand.
Shouldyouplay? Answer: It’suptoyou!
Iftherollalwayscomesupafour,youshouldplay!Ifitnevercomesupfour,you’dbe foolishtoplay!Thus,it’shelpfultoknowsomethingaboutthedie.Isitfair?Thatis,iseach faceequallylikelytoturnup?Howlikelyareyoutorollafour?
Thistypeofquestionwasconsideredbypremiermathematicians GerolamoCardano (1501–1576), PierredeFermat (1601–1665), BlaisePascal (1623–1662),andothers.These brilliantmindscreatedabranchofmathematicsknownas probabilitytheory
Therollingofadieisanexampleofa randomprocess:thefacethatcomesupissubject tochance.Inprobability,ourgoalisto quantify arandomprocess,suchasrollingadie. Thatis,wewanttoassignanumbertoit.Ifwerolladie,thereare6possible outcomes (possibleresults),namely,one,two,three,four, five,orsix.The set ofallpossibleoutcomes iscalledthe samplespace.
BayesianStatisticsforBeginners:AStep-by-StepApproach.ThereseM.DonovanandRuthM.Mickey, OxfordUniversityPress(2019).©RuthM.Mickey2019. DOI:10.1093/oso/9780198841296.001.0001
Let’scallthenumberofpossibleoutcomes N,so N ¼ 6.Theseoutcomesare discrete, becauseeachresultcantakeononlyoneofthesevalues.Formally,theword “discrete” is definedas “individuallyseparateanddistinct.” Inaddition,inthisexample,thereisa finite numberofpossibleoutcomes,whichmeans “therearelimitsorbounds.” Inother words,thenumberofpossibleoutcomesisnotinfinite.
Ifwebelievethateachandeveryoutcomeisjustaslikelytoresultaseveryotheroutcome (i.e.,thedieisfair),thentheprobabilityofrollingafouris1/N or1/6.Wecanthensay, “In 6rollsofthedie,wewouldexpect1rolltoresultinafour,” andwritethatasPr(four) ¼ 1/6.
Here,thenotationPrmeans “Probability,” andwewillusethisnotationthroughout thisbook.
HowcanwegetagoodestimateofPr(four)forthisparticulardie? Answer: Youcollectsomedata.
Beforeyouhandoverthe$10,000entry,youaskthegamemasterifyoucouldrunan “experiment” androllthedieafewtimesbeforeyoumakethedecisiontoplay.Inthis experiment,whichconsistsoftossingadiemanytimes,yourgoalistogetaroughestimate oftheprobabilityofrollingafourcomparedtowhatyouexpect.Toyouramazement,the gamemastercomplies.
Youstartwithoneroll,whichrepresentsasingle “trial” ofanexperiment.Supposeyouroll athreeandgivethegamemasterasneer.Table1.1showsyourolled1three,and0fortherest.
Table1.1
Inthistable,thecolumncalled Frequency givesthenumberoftimeseachoutcomewas observed.Thecolumncalled Probability isthefrequencydividedbythesumofthe frequenciesoverallpossibleoutcomes,aproportion.Theprobabilityofaneventoffouris thefrequencyoftheobservednumberofoccurrencesoffour(whichis0)dividedbythe totalthrows(whichis1).Wecanwritethisas:
Thiscanbereadas, “Theprobabilityofafouristhenumberof “four” eventsdividedbythe numberoftotaltrials.” Here,theverticalbarsindicateanumberratherthananabsolute value.Thisisa frequentist notionofprobability,becauseweestimatePr(four)byasking “Howfrequentlydidweobservetheoutcomethatinterestsusoutofthetotal?”
Aprobabilitydistributionthatisbasedon rawdata iscalledan empiricalprobability distribution.OurempiricalprobabilitydistributionsofarlooksliketheoneinFigure1.1:
Figure1.1 Empiricalprobabilitydistributionfor dieoutcomes,given1roll.
Isonerollgoodenough? Answer: No.
Bynow,youshouldrealizethatonerollwillnevergiveusagoodestimateofPr(four). (Sometimes,though,that’sallwehave...wehaveonlyonePlanetEarth,forexample).
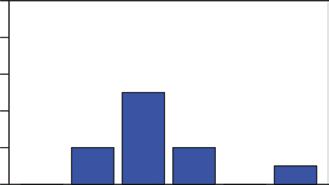
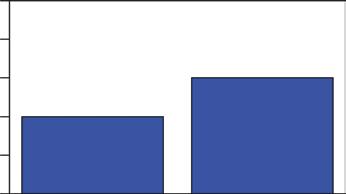
Next,yourollthedie9moretimes,andsummarizetheresultsofthe10totalrolls(i.e.,10 trialsor10experiments)inTable1.2.Thenumberoffoursis2,whichallowsustoestimate Pr(four)as2/10,or0.20(seeFigure1.2).
Outcome FourFiveSix
Figure1.2 Empiricalprobabilitydistributionfor dieoutcomes,given10rolls.
Table1.2
Whatcanyouconcludefromtheseresults?TheestimateofPr(four) ¼ 0.2seemsto indicatethatthediemaybeinyourfavor!(Remember,youexpectPr(four) ¼ 0.1667if thediewasfair).But$10,000isalotofmoney,andyoudecidethatyoushouldkeeptest rollinguntilthegamemastershouts “Enough!” Amazingly,youareabletosqueezein500 rolls,andyouobtaintheresultsshowninTable1.3.
Table1.3
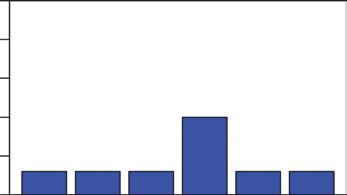
TheplotofthefrequencyresultsinFigure1.3iscalleda frequencyhistogram.Notice thatfrequency,notprobability,isonthey-axis.Weseethatafourwasrolled41times. Noticealsothatthesumofthefrequenciesis500.Thefrequencydistributionisanexample ofan empiricaldistribution:Itisconstructedfromrawdata.
Figure1.3 Frequencydistributionof500rolls.
WecannowestimatePr(four)as41/500 ¼ 0.082.Wecancalculatetheprobabilityestimates fortheotheroutcomesaswellandthenplotthemastheprobabilitydistributioninFigure1.4.
Figure1.4 Empiricalprobabilitydistributionfor 500rolls.
Accordingtothe LawofLargeNumbers inprobabilitytheory,theformula: probability ¼ jnumberofobservedoutcomesofinterestj jtotaltrialsj ð1 2Þ
yieldsanestimatethatiscloserandclosertothetrueprobabilityasthenumberoftrials increases.Inotherwords,yourestimateofPr(four)getscloserandclosertoorapproaches thetrueprobabilitywhenyouusemoretrials(rolls)inyourcalculations.
Whatwouldweexpectifthediewerefair? Table1.4liststhesixpossibleoutcomes,andtheprobabilityofeachevent(1/6 ¼ 0.167). Noticethatthesumoftheprobabilitiesacrosstheeventsis1.0.
Figure1.5showsexactlythesameinformationasTable1.4;bothareexamplesofa probabilitydistribution.Onthehorizontalaxis,welisteachofthepossibleoutcomes.On theverticalaxisistheprobability.Theheightofeachbarprovidestheprobabilityof observingeachoutcome.Sinceeachoutcomehasanequalchanceofbeingrolled,the heightsofthebarsareallthesameandshowas0.167,whichis1/N.Notethatthisisnotan empiricaldistribution,becausewedidnotgenerateitfromanexperiment.Rather,itwas basedontheassumptionthatalloutcomesareequallylikely.
Figure1.5 Probabilitydistributionforrollingafairdie.
Again,thisisanexampleofa discreteuniformprobabilitydistribution:discrete becausethereareadiscretenumberofseparateanddistinctoutcomes;uniformbecause eachandeveryeventhasthesameprobability.
Table1.4
Howwouldyouchangethetableandprobabilitydistributionifthe diewereloadedinfavorofafour?
Answer:Youranswerhere!
Therearemanywaystodothis.Supposetheprobabilityofrollingafouris0.4.Sinceall theprobabilitieshavetoaddupto1.0,thisleaves0.6todistributeamongtheremaining fiveoutcomes,or0.12foreach(assumingthese fiveareequallylikelytoturnup).Ifyouroll thisdie,it’snotasurethingthatyou’llendupwithafour,butgettinganoutcomeoffouris morelikelythan,say,gettingathree(seeTable1.5).
Theprobabilitieslistedinthetablesumto1.0justasbefore,asdotheheightsofthe correspondingbluebarsinFigure1.6.
Figure1.6 Probabilitydistributionforrollinga loadeddie.
Whatwouldtheprobabilitydistributionbeforthebet?
Answer: Thebetisthatifyourollafour,youwin$1,000,000,andifyou don’t rolla four,youlose$10,000.Itwouldbeusefultogroupour6possibleoutcomesintooneof two events.Asthe OxfordDictionaryofStatistics explains, “Aneventisaparticular collectionofoutcomes,andisasubsetofthesamplespace.” Probabilitiesareassigned toevents.
OurtwoeventsareE1 ¼ {four}andE2 ¼ {one,two,three, five,six}.Thebrackets{} indicatethesetofoutcomesthatbelongineachevent.The firsteventcontainsone
Table1.5
outcome,whilethesecondeventconsistsof fivepossibleoutcomes.Thus,inprobability theory,outcomescanbegroupedintoneweventsatwill.Westartedoutbyconsideringsix outcomes,andnowwehavecollapsedthoseintotwoevents.
Nowweassignaprobabilitytoeachevent.WeknowthatPr(four) ¼ 0.4.Whatisthe probabilityofNOTrollingafour?ThatistheprobabilityofrollingoneORtwoORthreeOR fiveORsix.Notethattheseevents cannotoccursimultaneously.Thus,wecanwrite Pr( four)astheSUMoftheprobabilitiesofeventsone,two,three, five,andsix(whichis 0.12 þ 0.12 þ 0.12 þ 0.12 þ 0.12 ¼ 0.6).Incidentally,the signmeans “complementof.” If Aisanevent, Aisitscomplement(i.e.,everythingbutA).ThisissometimeswrittenasAc. Theword OR isatipthatyou ADD theindividualprobabilitiestogethertogetyouranswer aslongastheeventsaremutuallyexclusive(i.e.,cannotoccuratthesametime).
Thisisanexampleofafundamentalruleinprobabilitytheory:iftwoormoreeventsare mutuallyexclusive,thentheprobabilityofanyoccurringisthesumoftheprobabilitiesof eachoccurring.Becausethedifferentoutcomesofeachroll(i.e.,rollingaone,two,three, five,orsix)aremutuallyexclusive,theprobabilityofgettinganyoutcomeotherthanfouris thesumoftheprobabilityofeachoneoccurring(seeTable1.6).
Notethattheprobabilitiesofthesetwopossibleeventssumto1.0.Becauseofthat,ifwe knowthatPr(four)is0.4,wecanquicklycomputethePr( four)as1 0.4 ¼ 0.6andsavea fewmentalcalculations.
TheprobabilitydistributionlooksliketheoneshowninFigure1.7:
Figure1.7 Probabilitydistributionforrollingafour ornot.
Remember:TheSUMoftheprobabilitiesacrossallthedifferentoutcomesMUSTEQUAL 1!Inthediscreteprobabilitydistributionsabove,thismeansthattheheightsofthebars summedacrossalldiscreteoutcomes(i.e.,allbars)totals1.
Table1.6
Doyoustillwanttoplay?Attheendofthebook,wewillintroducedecisiontrees,an analyticalframeworkthatemploysBayes’ Theoremtoaidindecision-making.Butthat chapterisalongwayaway.
DoBayesiansthinkofprobabilityaslong-runaverages?
Answer: We’reafewchaptersawayfromhittingonthisveryimportanttopic.You’llsee thatBayesiansthinkofprobabilityinawaythatallowsthetestingoftheoriesandhypotheses.Butyouhavetowalkbeforeyourun.Whatyouneednowistocontinuelearningthe basicvocabularyassociatedwithprobabilitytheory.
What’snext?
Answer: InChapter2,we’llexpandourdiscussionofprobability.Seeyouthere.
CHAPTER2 Joint,Marginal,andConditional Probability Nowthatyou ’ vehadashortintroductiontoprobability,it ’ stimetobuildonour probabilityvocabulary.Bytheendofthischapter,youwillunderstandthe followingterms:
• Venndiagram
• Marginalprobability
• Jointprobability
• Independentevents
• Dependentevents
• Conditionalprobability
Let’sstartwithafewquestions.
Whatisaneyeballevent? Agalathatcelebratesthesenseofvision?Nope.Theeyeballeventinthischapter referstowhetherapersonisright-eyeddominantorleft-eyeddominant.Youalready knowifyouareleft-orright-handed,butdidyouknowthatyouarealsoleft-orrighteyed?Here ’showtotell(http://www.wikihow.com/Determine-Your-Dominant-Eye;see Figure2.1):
Figure2.1 Determiningyourdominanteye.
1.Stretchyourarmsoutinfrontofyouandcreateaholewithyourhandsbyjoiningyour fingertipstomakeatriangularopening,asshown.
2.Findasmallobjectnearbyandalignyourhandswithitsothatyoucanseeitinthe triangularhole.Makesureyouarelookingstraightattheobjectthroughyourhands cockingyourheadtoeitherside,evenslightly,canaffectyourresults.Besuretokeep botheyesopen!
3.Slowlymoveyourhandstowardyourfacetodrawyourviewingwindowtowardyou.As youdoso,keepyourheadperfectlystill,butkeeptheobjectlinedupintheholebetween yourhands.Don’tlosesightofit.
4.Drawyourhandsinuntiltheytouchyourface yourhandsshouldendupinfrontof yourdominanteye.Forexample,ifyou findthatyourhandsendupsoyouarelooking throughwithyourrighteye,thateyeisdominant.
Theeyeballcharacteristichastwodiscreteoutcomes:lefty(forleft-eyeddominantpeople) orrighty(forright-eyeddominantpeople).Becausethereareonlytwooutcomes,wecan callthem events ifwewant.
Letussupposethatyouask100peopleiftheyare “ lefties ” or “ righties. ” Inthiscase, the100peoplerepresentour “universe ” ofinterest,whichwedesignatewiththeletter U .Thetotalnumberofelements(individuals)in U iswritten| U |.(Onceagain,the verticalbarsheresimplyindicatethat U isanumber;itdoesn ’ tmeantheabsolutevalue of U .)
Here,thereareonlytwopossibleevents: “lefty” and “righty.” Together,theymakeupa set ofpossibleoutcomes.Let A betheevent “left-eyedominant,” and A betheevent “right-eyedominant.” Here,thetildemeans “complementof,” andhereitcanbeinterpretedas “everythingbut A ” Noticethatthesetwoeventsare mutuallyexclusive:you cannotbebotha “lefty” anda “righty.” Theeventsarealso “exhaustive” becauseyoumust beeitheraleftyorrighty.
Suppose that70of100peoplearelefties.Thesepeopleareasubsetofthe largerpopulation.Thenumberofpeopleinevent A canbewritten| A |,andinthis example| A | ¼ 70.Notethat| A |mustbelessthanorequalto| A |,whichis100. Rememberthatweusetheverticalbarsheretohighlightthatwearetalkingabouta number.
Sincethereareonlytwopossibilitiesforeyedominancetype,thismeansthat100 70 ¼ 30 peoplearerighties.Thenumberofpeopleinevent A canbewritten| A |,andinthis example| A | ¼ 30.Notethat| A |mustbelessthanorequalto| U |. OuruniversecanbesummarizedasshowninTable2.1.
Table2.1
Frequency
A)|
Wecanillustratethisexampleinadiagrammaticform,asshowninFigure2.2.Here,our universeof100peopleiscapturedinsideabox.
Thisisa Venndiagram,whichshows A and A.Theuniverse U is100peopleandis representedbytheentirebox.Wethenallocatethose100individualsinto A and A.Theblue circlerepresents A;leftiesstandinsidethiscircle;rightiesstandoutsidethecircle,butinside thebox.Youcanseethat A consistsof70 elements,and A consistsof30elements.
WhyisitcalledaVenndiagram? Answer: Venndiagramsarenamedfor JohnVenn (seeFigure2.3),whowrotehisseminal articlein1880.
Lefty (A)
Righty (∼A) 30
Figure2.2
Figure2.3 JohnVenn.
Accordingtothe MacTutorHistoryofMathematicsArchive,Venn’ssondescribedhimas “ofsparebuild,hewasthroughouthislifea finewalkerandmountainclimber,akeen botanist,andanexcellenttalkerandlinguist.”
Whatistheprobabilitythatapersoninuniverse U isingroup A?
Answer: WewritethisasPr(A).Rememberthat Pr standsfor probability,soPr(A)means theprobabilitythatapersonisingroup A andthereforeisalefty.Wecandeterminethe probabilitythatapersonisingroup A as:
Probabilityisdeterminedasthenumberofpersonsingroup A outofthetotal.The probabilitythattherandomlyselectedpersonisingroup A is0.7.
Whataboutpeoplewhoarenotingroup A? Answer: Thereare30ofthem(100 70 ¼ 30),andtheyarerighties.
Withonlytwooutcomesfortheeyeballevent,ournotationfocusesontheprobability ofbeinginagivengroup(A ¼ lefties)andtheprobabilityof not beinginthegivengroup ( A ¼ righties).
I’msickofeyeballs.Canweconsideranothercharacteristic?
Answer: Yes,ofcourse.Let’sprobethesesame100peopleand findoutotherdetailsabout theiranatomy.Supposewearecuriousaboutthepresenceorabsenceof Morton’stoe
Peoplewith “Morton’stoe” havealargesecondmetatarsal,longerinfactthanthe first metatarsal(whichisalsoknownthebigtoeorhalluxtoe).Wikipediaarticlessuggestthat thisisanormalvariationoffootshapeinhumansandthatlessthan20%ofthehuman populationhavethiscondition.Nowweareconsideringasecondcharacteristicforour population,namelytoetype.
Let’slet B designatetheevent “Morton’stoe.” LetthenumberofpeoplewithMorton’s toebewrittenas| B |.Let B designatetheevent “commontoe.” Suppose15ofthe100 peoplehaveMorton’stoe.Thismeans| B | ¼ 15,and| B | ¼ 85.Thedataareshownin Table2.2,andtheVenndiagramisshowninFigure2.4.
Table2.2 Event Frequency
Morton’stoe(B)| B | ¼ 15
Commontoe( B)| B | ¼ 85 Universe(U)| U | ¼ 100
TheseeventscanberepresentedinaVenndiagram,whereaboxholdsouruniverseof 100people.
Notethesizeofthisredcircleissmallerthanthepreviousexamplebecausethenumberof individualswithMorton’stoeismuchsmaller.
Canwelookatbothcharacteristicssimultaneously?
Answer: Youbet.Withtwocharacteristics,eachwithtwooutcomes,wehavefourpossible combinations:
1.LeftyANDMorton’stoe,whichwewriteas A \ B.
2.LeftyANDcommontoe,whichwewriteas A \ B.
3.RightyANDMorton’stoe,whichwewriteas A \ B.
4.RightyANDcommontoe,whichwewriteas A \ B
Theupside-down \ isthemathematicalsymbolfor intersection.Here,youcanreaditas “BOTH” or “AND.”
Thenumberofindividualsin A \ B canbewritten j A \ B j,wherethebarsindicatea number(notabsolutevalue).Let’ssupposewerecordthefrequencyofindividualsineach ofthefourcombinations(seeTable2.3).
Let’sstudythistablecarefully.
Noticethatthistablehasfour “quadrants,” sotospeak.Ouractualvaluesarestoredinthe upperleftquadrant,shadeddarkblue.Theupperrightquadrant(shadedlightblue)sums thenumberofpeoplewithandwithoutMorton’stoe.Thelowerleftquadrant(shadedlight
Common toe (∼B) 85
Morton’s toe (B) 15
Figure2.4
Table2.3 Lefty(A)Righty( A)Sum
blue)sumsthenumberofpeoplethatareleftiesandrighties.Thelowerright(white) quadrantgivesthegrandtotal,or| U |.
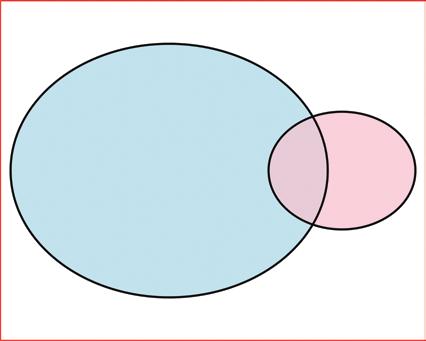
Nowlet’splottheresultsinthesameVenndiagram(seeFigure2.5).
TheupdatedVenndiagramshowsthebluecirclewith70lefties,theredcirclewith 15peoplewithMorton’stoe,andnooverlapbetweenthetwo.Thismeans j A \ B j¼ 0, j A j¼j A \ B j¼ 70,and j B j¼j A \ B j¼ 15.Bysubtraction,weknowthenumberof individualsthatarenotin A OR B j A \ B j is15becauseweneedtoaccountforall100 individualssomewhereinthediagram.
IsitpossibletohaveMorton’stoeANDbealefty?
Answer: Forouruniverse,no.IfyouareapersonwithMorton ’ stoe,youarestandingin theredcircleandcannotalsobestandinginthebluecircle.Sothesetwoevents (Morton ’ stoeandlefties)are mutuallyexclusive becausetheydonotoccuratthe sametime.
IsitpossibleNOTtohaveMorton’stoeifyouarealefty?
Answer: Youbet.All70leftiesdonothaveMorton’stoe.Thesetwoeventsarenonmutuallyexclusive.
Whatif fiveleftiesalsohaveMorton’stoe?
Answer: Inthiscase,weneedtoadjusttheVenndiagramtoshowthat fiveofthepeople thatareleftiesalsohaveMorton’stoe.Theseindividualsarerepresentedastheintersection betweenthetwoevents(seeFigure2.6).Notethatthetotalnumberofindividualsisstill 100;weneedtoaccountforeveryone!
Morton’s toe (B)
Righty
Figure2.5
We’llrunwiththisexamplefortherestofthechapter. ThisVenndiagramisprettyaccurate(exceptforthesizeoftheboxoverall).Thereare 70peoplein A,15peoplein B,and5peoplein A \ B.Thebluecirclecontains70elements intotal,and5ofthoseelementsalsooccurin B.Theredcirclecontains15elements(soisa lotsmallerthanthebluecircle),and5ofthesearealsoin A.So5/15(33%)oftheredcircle overlapswiththebluecircle,and5/70(7%)ofthebluecircleoverlapswiththeredcircle.
Ofthefourevents(A, A, B,and B),whicharenot mutuallyexclusive?
Answer:
• A and B arenotmutuallyexclusive(aleftycanhaveMorton’stoe).
• A and B arenotmutuallyexclusive(aleftycanhaveacommontoe).
• A and B arenotmutuallyexclusive(arightycanhaveMorton’stoe).
• A and B arenotmutuallyexclusive(arightycanhaveacommontoe).
InVenndiagrams,iftwoeventsoverlap,theyarenotmutuallyexclusive.
Areanyeventsmutuallyexclusive?
Answer: Ifwefocusoneachcircle, A and A aremutuallyexclusive(apersoncannotbea leftyandrighty). B and B aremutuallyexclusive(apersoncannothaveMorton’stoeanda commontoe).Apologiesforthetrickquestion!
Ifyouwereoneofthelucky100peopleincludedintheuniverse, wherewouldyoufallinthisdiagram?
Answer: Youranswerhere! It’shandytolookatthenumbersinatableformattoo.Table2.4showsthesamevaluesas Figure2.6.
Morton’s toe (B)
Righty
Figure2.6
Thisisanimportanttabletostudy.Onceagain,noticethattherearefourquadrantsor sectionsinthistable.Intheupperleftquadrant,the firsttwocolumnsrepresentthetwo possibleeventsforeyeballdominance:leftyandrighty.The firsttworowsrepresentthetwo possibleeventsfortoetype:Morton’stoeandcommontoe.
Theupperleftentryindicatesthat5peoplearemembersofboth A and B
• Lookfortheentrythatindicatesthat20peopleare A \ B,thatis, both not A andnot B.
• Lookfortheentrythatindicatesthat65peopleare A \ B.
• Lookfortheentrythatindicatesthat10peopleare A \ B
Thelowerleftandupperrightquadrantsofourtablearecalledthe margins ofthetable. Theyareshadedlightblue.Notethatthe total numberofindividualsin A (regardlessof B) is70,andthetotalnumberofindividualsin A is30.Thetotalnumberofindividualsin B (regardlessof A)is15andthetotalnumberofindividuals B is85.Anywayyousliceit,the grandtotalmustequal100(thelowerrightquadrant).
Whatdoesthishavetodowithprobability?
Answer: Well,ifyouareinterestedindeterminingtheprobabilitythatanindividual belongstoanyofthesefourgroups,youcoulduseyouruniverseof100individualstodo thecalculation.Doyourememberthe frequentist waytocalculateprobability?We learnedaboutthatinChapter1.
Ourtotal universe inthiscaseisthe100individuals.Togettheprobabilitythataperson selectedatrandomwouldbelongtoaparticularevent,wesimplydividetheentiretable abovebyourtotal,whichis100,andwegettheresultsshowninTable2.5.
We’vejustconvertedtherawnumberstoprobabilitiesbydividingthefrequencytableby thegrandtotal.
Table2.5
Table2.4
NotethatthisdiffersfromourdierollingexerciseinChapter1,whereyouwereunsure whattheprobabilitywasandhadtorepeatedlyrolladietoestimateit.BytheLawofLarge Numbers,themoretrialsyouhave,themoreyouzeroinontheactualprobability.Inthis case,however,wearegiventhenumberofpeopleineachcategory,sothecalculationis straightforward.These100peoplearetheonlypeopleofinterest.Theyrepresentour universeofinterest;wearenotusingthemtosamplealargergroup.Ifyoudidn’tknowthe make-upoftheuniverse,youcouldrandomlyselectonepersonoutoftheuniverseover andoveragaintogettheprobabilities,whereallpersonsareequallylikelytobeselected.
Let’ swalkthroughonecalculation.Supposewewanttoknowtheprobabilitythatan individualisaleftyANDhasMorton ’stoe.Thenumberofindividualsin A and B is written jA \ Bj andtheprobabilitythatanindividualisaleftywithMorton ’stoeis written:
Thisisofficiallycalledthe jointprobability andistheupperleftentryinourtable.The OxfordDictionaryofStatistics statesthatthe “jointprobabilityofasetofeventsisthe probabilitythatalloccursimultaneously.” Jointprobabilitiesarealsocalled conjoint probabilities.Incidentally,atablethatlistsjointprobabilitiessuchastheoneaboveis sometimesreferredtoasa conjointtable.
Whenyouheartheword joint,youshouldthinkoftheword AND andrealizethatyou areconsidering(andquantifying)morethanonecharacteristicofthepopulation.Inthis case,itindicatesthatsomeoneisin A AND B.Thisiswrittenas:
ðA \ BÞ or; equivalently;:::
Whatistheprobabilitythatapersonselectedatrandomisarighty andhasMorton’stoe?
Answer: Thisisequivalenttoasking,whatisthe jointprobability thatapersonis right-eyedominantANDhasMorton’stoe?Seeifyoucan findthisentryinTable2.5.The answeris0.1.
Inadditiontothejointprobabilities,thetablealsoprovidesthe marginal probabilities, whichlookattheprobabilityof A or A (regardlessof B)andtheprobabilityof B or B (regardlessof A).
Whatdoestheword “marginal” mean?
Answer: Theword marginal inthedictionaryisdefinedas “pertainingtothemargins;or situatedontheborderoredge.” Inourtable,themarginalprobabilitiesarejustthe probabilitiesforonecharacteristicofinterest(e.g., A and A)regardlessofothercharacteristicsthatmightbelistedinthetable.
Let’snowlabeleachcellinourconjointtablebyitsprobabilitytype(seeTable2.6).
Pr
PrðB \ AÞ ð2 5Þ