FLUIDDYNAMICS
DedicatedtoProf.P.Hall,Prof.F.T.SmithFRS,Prof.J.T.StuartFRS, andalsotoJosephandIsaac, andAndrei.
Preface
ThisisPart4ofabookseriesonfluiddynamicsthatiscomprisedofthe following fourparts:
Part1. ClassicalFluidDynamics
Part2. AsymptoticProblemsofFluidDynamics
Part3. BoundaryLayers
Part4. HydrodynamicStabilityTheory
Theseriesisdesignedtogiveacomprehensiveandcoherentdescriptionoffluiddynamics,startingwithchaptersonclassicaltheorysuitableforanintroductoryundergraduatelecturecourse,andthenprogressingthroughmoreadvancedmaterialuptothe levelofmodernresearchinthefield.Ourmainattentionisonhigh-Reynolds-number flows,bothincompressibleandcompressible.Correspondingly,the targetreadergroups areundergraduateandmastersstudentsreadingmathematics, aeronauticalengineering,orphysics,aswellasdoctoralstudentsandestablishedresearchersworkinginthe field.
InPart1,westartedwithadiscussionofthefundamentalconceptsoffluiddynamics,basedonthe continuumhypothesis.Wethenanalysedtheforcesactinginside afluid,anddeducedtheNavier–StokesequationsforincompressibleandcompressiblefluidsinCartesianandcurvilinearcoordinates.Theseweredeployedtostudythe propertiesofanumberofflowsthatarerepresentedbytheso-called exactsolutions oftheNavier–Stokesequations.Thiswasfollowedbyadetaileddiscussionofthetheoryofinviscidflowsforincompressibleandcompressiblefluids.Whendealingwith incompressibleinviscidflows,particularattentionwaspaidtotwo-dimensionalpotentialflows.Thesecanbedescribedintermsofthe complexpotential,allowingforthe fullpowerofthetheoryoffunctionsofacomplexvariabletobeemployed.Wedemonstratedhowthemethodofconformalmappingcanbeusedtostudyvariousflowsof interest,suchasflowspast Joukovskiiaerofoils andseparatedflows.Forthelatterthe Kirchhoffmodel wasadopted.ThefinalchapterofPart1wasdevotedtocompressible flowsofaperfectgas,includingsupersonicflows.Particularattentionwasgiventothe theoryofcharacteristics,whichwasused,forexample,toanalysethe Prandtl–Meyer flow overabodysurfacewithabendoracorner.Thepropertiesofshockwaveswere alsodiscussedindetailforsteadyandunsteadyflows.
InPart2weintroducedthereaderto asymptoticmethods.Alsotermed perturbation methods,theyarenowaninherentpartoffluiddynamics.Westartedwithadiscussion ofthemathematicalaspectsofasymptotictheory.Thiswasfollowedbyanexposition oftheresultsofapplicationofthetheorytovariousfluid-dynamicproblems.Thefirst ofthesewasthe thinaerofoiltheory forincompressibleandsubsonicflows,bothsteady andunsteady.Inparticular,itwasshownthatthistheoryallowedustoreducethe taskofcalculatingtheliftforcetotheevaluationofasimpleintegral. Wethenturned
Preface vii
ourattentiontosupersonicflows.Wefirstanalysedthelinearapproximationtothe governingEulerequations,whichledtoaremarkablysimplerelationshipbetweenthe slopeoftheaerofoilsurfaceandthepressure,knownasthe Ackeretformula.Wethen consideredthesecond-order Buzemannapproximation,andperformedtheanalysisof aratherslowprocessofattenuationoftheperturbationsinthefar-field.Part2also containedadetaileddiscussionofthepropertiesofinviscid transonic and hypersonic flows.WeconcludedPart2withanalysisofviscouslow-Reynolds-numberflows.Two classicalproblemsofthelow-Reynolds-numberflowtheorywereconsidered:theflow pastasphereandtheflowpastacircularcylinder.Inbothcasestheflowanalysis ledtoadifficulty,knownas Stokesparadox.Weshowedhowthisparadoxcouldbe resolvedusingtheformalismofmatchedasymptoticexpansions.
Part3wasdevotedtohigh-Reynolds-numberflows.Webeganwiththeanalysis oftheflowsthatcouldbedescribedintheframeworkofthe classicalboundary-layer theory putforwardbyPrandtlin1904.TothiscategorybelongtheBlasius boundary layeronaflatplateandtheFalkner–Skansolutionsfortheboundarylayeronawedge surface.WealsopresentedSchlichting’ssolutionforthelaminarjet andTollmien’s solutionfortheviscouswake.ThesewerefollowedbyanalysisofChapman’sshear layerthatwasperformedwiththehelpofPrandtl’stranspositiontheorem.Wealso consideredtheboundarylayeronthesurfaceofarapidlyrotating cylinderwiththe purposeoflinkingthecirculationaroundthecylinderwiththespeedofitsrotation.We concludedthediscussionofclassicalboundary-layertheorywithanalysisofcompressibleboundarylayers,includingtheinteractiveboundarylayersinhypersonicflows. Wethenturnedourattentiontoseparatedflows.Thesecouldnot bedescribedinthe frameworkofclassicalboundary-layertheory.Insteadtheconceptof viscous-inviscid interaction shouldbeused.Westartedwiththeso-called self-inducedseparation in supersonicflow.Thetheoryofself-inducedseparationwasdevelopedbyStewartson andWilliams(1969)andNeiland(1969),andledtotheformulationofthe triple-deck model.WethenpresentedSychev’s(1972)theoryoftheboundary-layerseparationin anincompressiblefluidflowpastacircularcylinder.Thiswasfollowedby adiscussion ofthetriple-deckflownearthetrailingedgeofaflatplatefirstinvestigatedbyStewartson(1969)andMessiter(1970).Thentheincipienceoftheseparationatcornerpoints ofthebodysurfacewasanalysedbasedontriple-decktheory.Part3concludeswith analysisoftheformationandburstingofshortseparationbubbles attheleadingedge ofathinaerofoil,forwhichpurposeaspecialversionoftriple-deck theory,referredto as marginalseparationtheory,wasdevelopedbyRuban(1981,1982)andStewartson etal. (1982).
Part4isdevotedto hydrodynamicstabilitytheory whichservestopredicttheonset of laminar-turbulenttransition influidflows.Westartwiththeclassicalresultsofthe theory.InChapter1weintroducetheconceptoflinearinstabilityoffluidflows,and formulatethe Orr–Sommerfeldequation describingthestabilitypropertiesof parallel and quasi-parallel flows.Inthelattercategoryaretwo-dimensionalboundarylayers wheretheOrr–Sommerfeldequationdescribestheinstabilityintheformof Tollmien–Schlichtingwaves.Wethenconsiderthestabilityof‘inviscidflows’governedbythe Rayleighequation.InadditiontodescribingthegeneralpropertiesoftheRayleigh equation,wepresentanumericalsolutionofthisequationforalaminarjet.Thisis
followedbyadiscussionoftheKelvin–Helmholtzinstabilityoftheshear layersthat form,forexample,whentheboundarylayerseparatesfromarigid bodysurface. WeconcludeChapter1withadiscussionoftwoothermodesofinstability,first, the Cross-Flowinstability thatisknowntodominatelaminar-turbulenttransitionon sweptwingsand,second,thecentrifugalinstabilityonaconcavesurface,takingthe formof Taylor–G¨ortlervortices.
InChapter2weconcentrateourattentiononparallelshearflows.ThelinearstabilityofsuchflowsisgovernedbytheOrr–Sommerfeldequation.Typically,computational solutionsofthisequation,whenplottedinthewavenumber–Reynoldsnumberplane, demonstratetheexistenceoftwodistinctbranchesalongwhichdisturbancesneither grownordecaybutremaininaso-calledneutralstate,withthesebranchesbounding aregionofinstability.InChapter2weemployasymptoticanalysis,andthemethodof matchedasymptoticexpansions,touncoverthenatureofthese modesinthevicinity ofthetwobranchesinthelimitoflargeReynoldsnumber.Theanalysis,inspiredby theworkofLin(1946),iscarriedoutspecificallyforboundary-layerflowsunderthe parallelflowassumption,andalsoforplanePoiseuilleflow.Forthelowerbranchwe recoverthe triple-deck flowmodeldiscussedindetailinPart3ofthisbookseries. Themodestructureinthevicinityoftheupperbranchisparticularly complicated, withviscouseffectsnotsimplyconfinedtonear-wallregions,butalsoplayingavital rolewithinaninternallayercentredaroundthelocationwherethedisturbancephase speedisequaltothebasicflowunderconsideration.Thislayerisknownasa critical layer anditspropertiesarestudiedinsomedetail,includingthechangesintheinternaldynamicsthatariseasthedisturbancesizeisincreased,usingideasdevelopedby BenneyandBergeron(1969),Haberman(1972),andSmithandBodonyi(1982b).
Wethenturnourattentiontomorerecentdevelopmentsinthefield.InChapter3 weintroducethereadertothe receptivitytheory thathasnowbecomeanintegralpart ofthetheoreticalpredictionsoflaminar-turbulenttransitioninaerodynamicflows.The theorystudiestheprocessofexcitationofinstabilitymodesintheboundarylayersby various‘externalperturbations’,suchasfree-streamturbulence,acousticnoise,and bodysurfaceroughness.Inthispresentation,weusethetriple-decktheorytodescribe thereceptivityphenomena.WestartwithTerent’ev’s(1981,1987)theoreticalmodelof earlierexperimentsofSchubauerandSkramstad(1948),whereTollmien–Schlichting wavesweregeneratedbyavibratingribbon.Wefirststudyharmonicoscillationsof theribbon,andcalculatetheamplitudeofthegeneratedTollmien–Schlichtingwave. Then,aninitial-valueproblemisconsideredwheretheribbonstartstooscillateat acertaintime,creatingawavepacketintheboundarylayer.Chapter3concludes withananalysisofthereceptivityoftheboundarylayertoacoustic perturbations. WhendescribingthisformofreceptivitywefollowthepapersbyRuban(1984)and Goldstein(1985).Theseauthorsdemonstratedthatwhenanacousticwaveinteracts withanisolatedroughnessonthebodysurface,aTollmien–Schlichtingwaveformsin theboundarylayerbehindtheroughness.Thetheoryallowsustopredicttheinitial amplitudeoftheTollmien–Schlichtingwave.
InChapter4wediscussthe weaklynonlinearstabilitytheory thatisaimedat predictinghowthegrowthoftheamplitudeoftheperturbationsaffectsthecritical Reynoldsnumber.Thegoverningequationofweaklynonlineartheorywasfirstfor-
mulatedbyLandau(1944)basedonphysicalarguments.Aformal derivationofthis equationwasgivenbyStuart(1960)andWatson(1960)withtheamplitudeofthe perturbationsassumedtobeasmallbutnon-zeroparameter.Sincethenthisequationisreferredtoasthe Landau–Stuartequation.Itappearsthatfluidflowscanbe subdividedintotwoclasses, subcriticallyunstable and supercriticallyunstable.Tothe firstcategorybelongs,forexample,planePoiseuilleflow.Forthisflow,anincreasein theamplitudeoftheperturbationleadstoadecreaseofthecriticalReynoldsnumber. Contrarytothat,theBlasiusboundarylayershowsasupercriticalbehaviourwhere thecriticalReynoldsnumberincreaseswiththeamplitudeoftheperturbations.We concludeChapter4withnumericalanalysisoffiniteamplitudeperturbationsthat leadstotheconceptofa neutralsurface
Finally,inChapter5weintroducethereadertotheconceptofaself-sustaining processwithinaviscousfluid.Thisisaseriesofinteractionsbywhichcertaindistinguishableflowstructures,whichwouldusuallydecayduetotheactionofviscosity, aremaintainedbyatransferofenergyvialong-scale/short-scale interplayfromother disturbancespresentintheflow.Inturn,thesedisturbancesarethemselvessupported bytheverystructuretheyhelptopreserve.Thistypeofprocess,whichisinherently nonlinearandtypicallythree-dimensionalinnature,isfoundtoberesponsiblefor thegenerationofso-calledexactcoherentstructuresinshearflows.Formoderateto largeReynoldsnumbers,theseequilibriumsolutionscorrespondtocertaincoherent statesvisitedbyturbulentflowsandhavebeenobservedexperimentally(e.g.seeHof etal.,2004).Wewillinvestigatethemathematicalnatureoftheseequilibriumstates atbothfiniteReynoldsnumber,wherecertainapproximationsneed tobemade,and atasymptoticallylargeReynoldsnumber,wherethetheorycanbegivenarigorous mathematicalfoundation.Weconcentrateinthemainonapplicationstochannelflow, whileindicatinghowtheanalysiscanbeappliedmorebroadly.
Thematerialpresentedinthisbookisbasedonlecturecoursesgivenbytheauthors atImperialCollegeLondon,theUniversityofManchester,andMoscowInstituteof PhysicsandTechnology.
1ClassicalHydrodynamicStabilityTheory 5
1.1LinearStabilityTheory5
1.1.1Globalstabilityanalysis9
1.2StabilityofParallelFlows14
1.2.1Poiseuilleflow14
1.2.2Analysisoftwo-dimensionalperturbations20 Exercises121
1.3StabilityofBoundaryLayers24
1.3.1Basicflow24
1.3.2Theparallelflowapproximation27
1.3.3Stabilityanalysis28
1.3.4Temporalandspatialinstabilities31 Exercises233
1.4InviscidStabilityTheory34
1.4.1PropertiesoftheRayleighequation34
1.4.2Inviscidinstabilityofalaminarjet40 Exercises343
1.5Kelvin–HelmholtzInstability46 Exercises452
1.6Cross-FlowVortices54
1.6.1Basicflow58
1.6.2Linearstabilityanalysis59 Exercises564
1.7CentrifugalInstability66
1.7.1Taylorvortices69
1.7.2G¨ortlervortices79 Exercises687
2High-Reynolds-NumberAnalysisofParallelandShearFlow Instabilities 89
2.1ProblemFormulation90
2.2AsymptoticAnalysisoftheOrr–SommerfeldEquationforBlasius Flow91
2.2.1Outerregion91
2.2.2Mainpartoftheboundarylayer92
2.3CriticalLayerandStokesLayerCoincident:LowerBranch99
2.3.1Theviscoussublayer99
2.3.2Canonicalformofthedispersionequation102
2.3.3Numericalsolutionofthedispersionequation105 Exercises7109
2.4CriticalLayerandStokesLayerDistinct:UpperBranch112
2.4.1Contributionofthecriticallayer114
2.4.2AnalysisoftheStokeslayer116
2.4.3Thedispersionrelationsfortheupperbranch117
2.5AsymptoticAnalysisoftheOrr–SommerfeldEquationforPlane PoiseuilleFlow120
2.5.1Derivationofthelowerbrancheigenrelation123
2.5.2Derivationoftheupperbrancheigenrelation125 Exercises8129
2.6CriticalLayerTheory132
2.6.1Linearcriticallayertheory135
2.6.2Nonlinearcriticallayertheory140 Exercises9146
3Boundary-LayerReceptivity 153
3.1Terent’ev’sProblem154
3.1.1Problemformulation156
3.1.2Boundarylayerbeforethevibratingribbon157
3.1.3Triple-deckregion158
3.1.4Viscous-inviscidinteractionproblem166
3.1.5Linearproblem167
3.1.6Receptivitycoefficient173 Exercises10176
3.2Initial-ValueProblem178
3.2.1Problemformulation179
3.2.2Numericalsolutionofthelinearproblem181
3.2.3Analysisofthewavepacket187
3.2.4Convectiveandabsoluteinstabilities195
3.2.5Centreofthewavepacket195 Exercises11196
3.3GenerationofTollmien–SchlichtingWavesbySound198
3.3.1Problemformulation199
3.3.2Unperturbedflow201
3.3.3Acousticnoise203
3.3.4Triple-deckregion210
3.3.5Viscous-inviscidinteractionproblem217
3.3.6Linearreceptivity219
3.3.7Receptivitycoefficient228 Exercises12234
3.4FurtherAdvancesinReceptivityTheory241
4WeaklyNonlinearStabilityTheory 243
4.1Landau’sConceptofLaminar-TurbulentTransition243
4.2Landau–StuartEquation244
4.2.1Problemformulation244
4.2.2Asymptoticprocedure247
4.2.3Linearperturbations248
4.2.4Quadraticapproximation249
4.2.5Cubicapproximation251
4.2.6PropertiesoftheLandau–Stuartequation253 Exercises13258
4.3Finite-AmplitudeNonlinearTravellingWaveSolutions262 Exercises14265
5CoherentStructuresandSelf-SustainingProcessesinShear Flows 268
5.1TheFundamentalBuildingBlocksofaSelf-SustainingProcess271
5.2TheSelf-SustainingProcess(SSP)atFiniteReynoldsNumber273
5.2.1Therollflow273
5.2.2Thestreamwisestreak276
5.2.3Thethree-dimensionaltravellingwave280
5.2.4Thenonlinearfeedbackontherolls283
5.2.5FullnumericalsolutionsforplaneCouetteflow286 Exercises15288
5.3Self-SustainingProcessesatHighReynoldsNumber:Vortex-Inviscid WaveInteraction292
5.3.1Thecoreflow293
5.3.2Asymptoticbehaviournearthecriticalcurve295
5.3.3Insidethecriticallayer298
5.3.4Thefullnonlinearinteraction303 Exercises16306
5.4Self-SustainingProcessesatHighReynoldsNumber:Vortex-Viscous WaveInteraction309
5.4.1Theunforcedroll/streakflow310
5.4.2Theviscouswalllayers311
5.4.3Wavefeedbackontheroll/streakcoreflow315
5.4.4Solutionforsmallamplitude:weaklynonlineartheory319
5.4.5Fullsolutionofthenonlinearinteractionequations324 Exercises17325
5.5MoreRecentDevelopments330
Introduction
Hydrodynamicstabilitytheoryisconcernedwiththeimportantquestionofhow(and why)alaminarflowundergoesatransitiontoaturbulentstate.Reynolds(1883) wasthefirsttoperformacarefulexperimentalinvestigationofthelaminar-turbulent transitionprocessintheHagen–Poiseuilleflowthroughacirculartube.Hisapparatus isshowninFigureI.1.Thetubewasplacedhorizontallyinsidealargeglasstankfilled withwater.Oneendofthetubewasconnectedthroughataptoasink;thetapwas usedtoregulatetheamountofwaterpassingthroughthetube.Theotherendofthe tubewasopentothesurroundingwater,allowingthewatertoenterthetubeoncethe tapwasopened.Inordertoreducethedisturbancesintheflowthroughthetube,the openendofthetubewasfittedwithatrumpetmouthpiece.Theflow visualization wasperformedwithhighlycolouredwateraddedtotheflowinfrontofthetrumpet. Itwassuppliedthroughathintubeconnectedtoareservoironthe topofthewater tank(seeFigureI.1).
Fig.I.1:Reynolds’apparatus(seeReynolds,1883).
(a)Laminarflow.
(b)Turbulentflow.
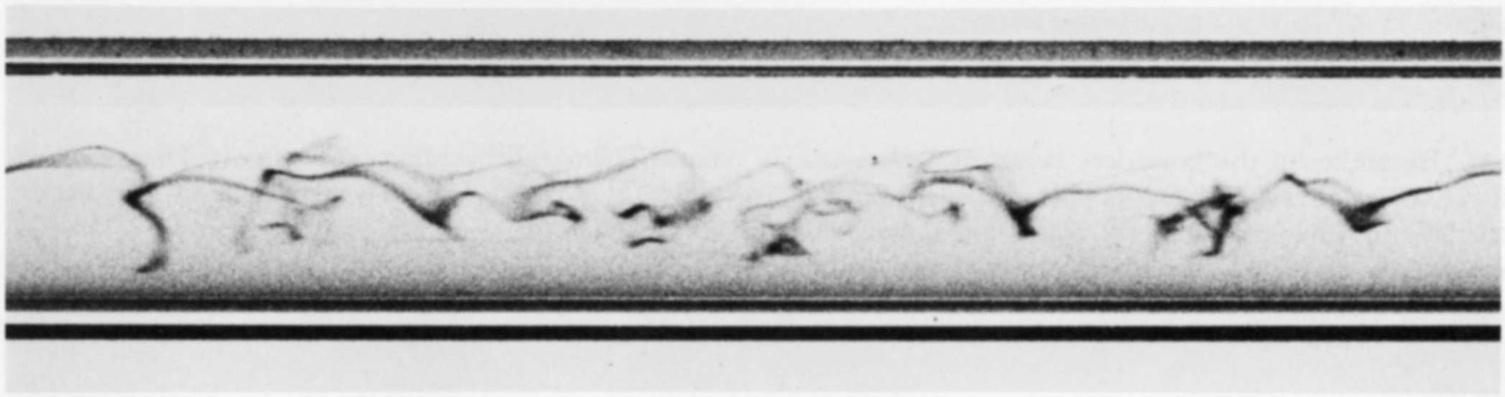
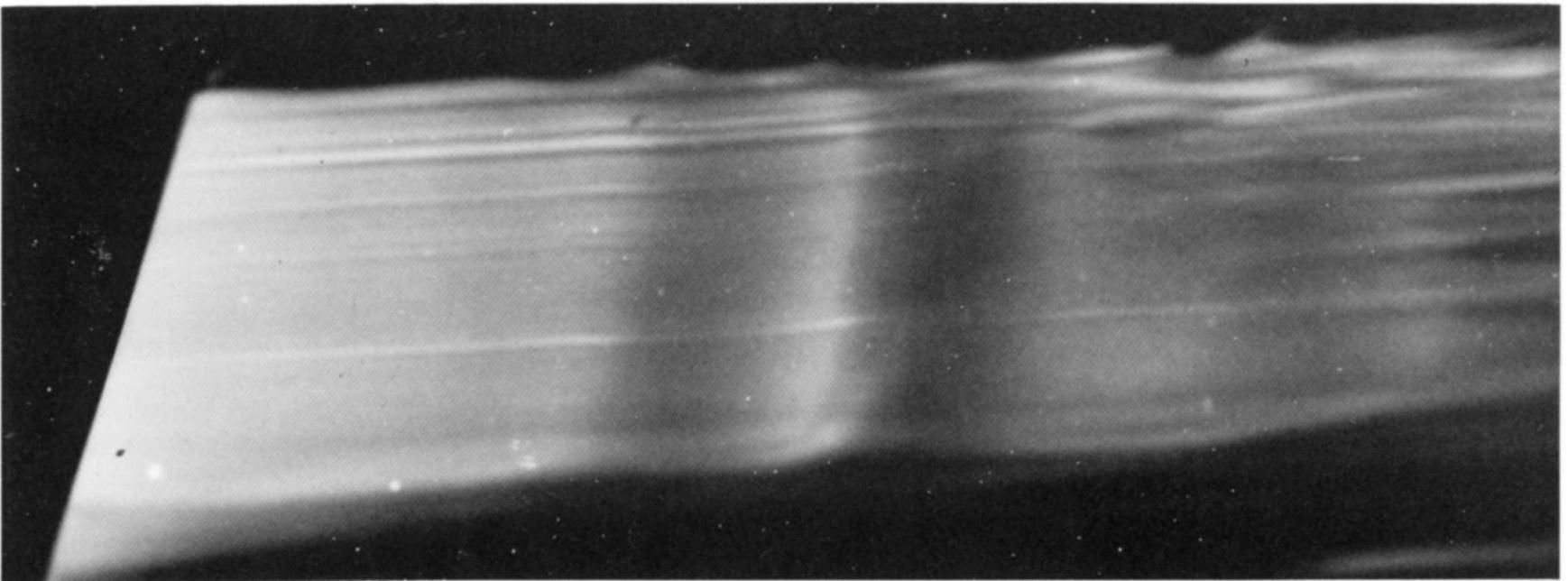
Fig.I.2:Laminar-turbulenttransitionintheHagen–Poiseuilleflowthroughacircular tube.ThesephotographsweretakenbyN.H.JohannesesandC. Loweusingthe originalReynolds’pipe.
AsaresultofhisobservationsReynolds(1883)arrivedatthefollowingconclusions:
1.Whenthefluidvelocitywassufficientlysmall,thecoloureddyestreakextended inaperfectlystraightlinethroughthetube;seeFigureI.2(a).This meansthat theflowwassteadywiththetrajectoriesofthefluidparticlesbeing straightlines paralleltothetubeaxis.
2.Asthevelocitywasincreasedinsmallsteps,theflowwouldsuddenlydevelop unsteadiness;seeFigureI.2(b).Reynolds(1883)reportedthat thishappenswhen thedimensionlessparameter
nowcalledtheReynoldsnumber,reachesthecriticalvalue Rec ≃ 13000.Here ˆ umax isthefluidvelocityalongthetubeaxis, a denotesthetuberadiusand ν the kinematicviscosityofwater.
Asthetransitionfromthe laminar flowregime(FigureI.2a)tothe turbulent one (FigureI.2b)takesplace,thefluidmotionbecomessignificantlymore complicated. Inadditiontotheprimaryflowparalleltothetubeaxis,thefluidparticlesarenow involvedinsecondarymotionsinplanesperpendiculartotheaxis;the secondaryflow isunsteadyandratherirregular.Thisleadstoamixingofthefluidand enhancesthe exchangeofmomentumbetweenthefluidparticles.Asaconsequence,insteadofthe parabolicvelocityprofile1
1SeeSection2.1.3inPart1ofthisbookseries.
(a)Laminarflow.
(b)Turbulentflow.
Fig.I.3:Velocitydistributionacrossthetubeforlaminarandturbulentflowregimes; in(b)thedashedlinereproducesthelaminarvelocityprofile.
characteristicofthelaminarflow(seeFigureI.3a),amoreuniformdistributionofthe velocityisobservedinthecoreofflownearthetubeaxis(seeFigure I.3b).Assuming thatthefluidfluxthroughthetuberemainsunchanged,thevelocitythenexhibitsa steeperrisefromzeronearthetubewall.Thisexplainswhytheresistanceofthetube totheflowappearstoincreaseintheturbulentflowregime.Itisknownthattheshear stressproducedbytheflowonthetubewallmaybecalculatedas2
Here µ isthedynamicviscositycoefficient,ˆ u istheaxialvelocitycomponent,andˆ r is theradialcoordinatemeasuredfromthetubeaxis;inthispresentationweuse‘hat’ todenotedimensionalvariables.Comparingthevelocitydistributionsinthelaminar andturbulentflows(seeFigureI.3)itiseasytoseethat τw is,indeed,largerinthe turbulentflow.
Ofcourse,Hagen–Poiseuilleflowisnottheonlyformoffluidmotionthatissubject tolaminar-turbulenttransition.FollowingReynolds’(1883)discovery,variousother flowswereinvestigated.Inparticular,thetransitionintheboundary-layerflowonaflat platewasfirstobservedbyBurgers(1924)andlaterstudiedinmoredetailbyDryden (1947)andKlebanoffandTidstrom(1959).Theyfoundthatneartheleadingedgethe flowisalwayslaminar,andmaybedescribedbytheBlasiussolution.3 However,ata
Fig.I.4:Tollmien–Schlichtingwavesintheboundarylayeronaflatplate.FlowvisualizationbyWerl´e(1980).
2Seethefifthequationin(1.8.65)onpage92inPart1ofthisbookseries.
3SeeSection1.1inPart3ofthisbookseries.
Fig.I.5:Laminar-turbulenttransitionintheboundarylayeronaflat plate.
certaindistanceˆ xc fromtheleadingedgetheunsteadinessstartstodevelopinthe flowintheformofso-called Tollmien–Schlichtingwaves thataresuperimposedon thesteadyBlasiusflow(FigureI.4).Typicallytheinitialamplitudeofthesewavesis toosmalltocausenoticeablechangesinthevelocityfield,buttheygrowdownstream, andthereexistsasecondcriticalpointˆ xt nearwhichlaminar-turbulenttransition takesplace.Asaresultofthetransitionthethicknessoftheboundarylayerincreases significantly,andthevelocityprofilesbecomes‘fuller’whichleadstoanincreasein theshearstressontheplatesurface;seeFigureI.5.
IfwenowdefinetheReynoldsnumberas
, where V∞ isthevelocityattheouteredgeoftheboundarylayer,thentransitionis typicallyobservedwhen Re reachesavalueof ≃ 5 105 .
ClassicalHydrodynamicStability Theory
1.1LinearStabilityTheory
ThetheoryofHydrodynamicStabilityisaimedatpredictingif,andwhen,thetransitionfromalaminartoaturbulentstateshouldbeexpectedforaparticularflow, andhowtheflowchangesthroughthetransitionregion.Tooutlinethemathematical approachusedinthestabilitytheory,weshallstartwithafairlygeneralflowpasta rigidbodyasdepictedinFigure1.1.WeuseaCartesiancoordinatesystem(ˆx, ˆ y, ˆ z) anddenotethecorrespondingcomponentsofthevelocityvector as(ˆu, ˆ v, ˆ w).Wefurtherdenotethetimeby ˆ t,thepressurebyˆ p,thefluiddensityby ρ andthekinematic viscosityby ν.Assumingtheflowincompressibleanddisregardingthebodyforce, we canwritetheNavier–Stokesequationsthatdescribethefluidmotionas1
Thesehavetobesolvedwiththeno-slipconditiononthebodysurface S
andthefollowingconditionsinthefree-streamflowfarfromthebody:
1Seeequations(1.7.6)onpage62inPart1ofthisbookseries. Hereweshalldenotethedimensional variablesby‘hat’.
Here(u∞,v∞,w∞)arethecomponentsofthefree-streamvelocityvector V∞,and p∞ denotesthefree-streampressure.
Letusnowexpressthegoverningequations(1.1.1)andboundaryconditions(1.1.2) indimensionlessform.Forthispurposeweintroducethecharacteristicscale L of thebody,anddenotethemodulusofthefree-streamvelocityvector V∞ by V∞ Usingthesequantities,thenon-dimensionalindependentanddependentvariablesare introducedthroughtheequations
Substitutionof(1.1.3)into(1.1.1)resultsin
where Re istheReynoldsnumber:
Theboundaryconditions(1.1.2)become
Fig.1.1:Flowlayout.
u → u∞/V∞, v → v∞/V∞, w → w∞/V∞, p → 0
as x 2 + y 2 + z 2 →∞. (1.1.5b)
Letusnowassumethatthebodyismotionless,andtheboundary-valueproblem (1.1.4),(1.1.5)admitsasteadysolution
u = U (x,y,z),v = V (x,y,z),w = W (x,y,z),p = P (x,y,z)(1.1.6)
forarangeofvaluesoftheReynoldsnumber Re.Weshallcall(1.1.6)the basicsolution Theexistenceofthissolutiondoesnot,however,guaranteethat thecorrespondingflow canbeactuallyobservedinnature.Forthistohappentheflowhastobestable,that is,ifwesuperimposeonthebasicstate(1.1.6)aperturbationofasmallamplitude ε, sothat
u = U (x,y,z)+ εu ′(t,x,y,z),v = V (x,y,z)+ εv ′(t,x,y,z), w = W (x,y,z)+ εw ′(t,x,y,z),p = P (x,y,z)+ εp ′(t,x,y,z), (1.1.7)
thentheperturbationhastodecayintimereturningthesolutionto itsbasicstate (1.1.6).
Substituting(1.1.7)intotheNavier–Stokesequations(1.1.4)andworkingwiththe O(ε)terms,yieldsthefollowingsetoflinearequationsfortheperturbationfunctions:
Thecorrespondingboundaryconditionsareobtainedbysubstituting(1.1.7)into (1.1.5a)and(1.1.5b).Wehave
Chapter1.ClassicalHydrodynamicStabilityTheory
Whatonewouldliketodonowistoconstructthesolutiontotheinitial-valueproblemwhere,givenaninitialdistributionoftheperturbationinspace,thesubsequent behaviourofthefunctions u′ , v′ , w′,and p′ ispredicted.Noticethatallthecoefficients inequations(1.1.8)areexpressedthroughthesolution(1.1.6)ofthesteadyproblem, andtherefore,donotdependontime t.Thismeansthattheinitial-valueproblem canbesolvedusingthemethodofLaplacetransforms.Recallthat ifweconsider,for example,thefunction u′(t,x,y,z),thenitsLaplacetransform˜ u(σ,x,y,z)iscalculated usingtheintegral
(σ,x,y,z)=
with σ beingacomplexparameter, σ = σr + iσi .Itisknownthatifthereexistsareal constant M> 0suchthat |u′| <Meλt forall t> 0,where λ isanotherrealconstant, thentheLaplacetransform(1.1.10)existsforall σ situatedinthecomplexplaneon theright-handsideoftheverticallinecrossingtherealaxisatthe point σr = λ;see Figure1.2. Forknown˜ u(σ,x,y,z)theoriginalfunction u′(t,x,y,z)mayberecoveredusing theBromwichintegral
wheretheintegrationisperformedinthecomplex σ-planealonganyverticalline σr = a situatedtotherightoftheline σr = λ.
Fig.1.2:Thecomplex σ-plane.
1.1.1Globalstabilityanalysis
Theformoftheinversionintegral(1.1.11)suggeststhatthesolutionofthelinearized equations(1.1.8)canrepresentedasasuperpositionofso-called normalmodes,that arewrittenas
Substitutionof(1.1.12)intoequations(1.1.8)yields
Onealsoneedstosubstitute(1.1.12)intotheboundaryconditions(1.1.9),whichleads to
Noticethattheboundary-valueproblem(1.1.13),(1.1.14)admitsatrivialsolution u ≡ 0, v ≡ 0, w ≡ 0, p ≡ 0.
Inorderforanon-trivialsolutiontoexist,theparameter σ shouldbechosenappropriately.Hence,theboundary-valueproblem(1.1.13),(1.1.14)isaneigen-valueproblem. Thesolutionofthisproblemisadifficultnumericaltaskreferredtoas the globalstabilityanalysis.Inthispresentationwewillillustratethisapproachusing,asanexample, theflowpastacircularcylinder.
Beforeturningtothecylinderproblemweshallmakethefollowingcomment. Supposethatasaresultofthecalculations,aspectrumofeigen-valuesof σ isfound. Thenonecanjudgeiftheflowconsideredisstableorunstablebythe positionof
Chapter1.ClassicalHydrodynamicStabilityTheory
theeigen-valuesinthecomplex σ-plane.Indeed,thetimedependenceofeachnormal mode(1.1.12)isgivenbytheexponential e σt = e(σr +iσi )t = e σr t cos(σit)+ i sin(σit) , whichshowsthattheflowperturbationsoscillatewiththefrequency σi andgrowor decaywiththeamplitude eσr t.Ifalltheeigen-valuesaresuchthat σr isnegative,then theflowisstablewithrespecttosmallperturbations.If,ontheotherhand,there existsatleastoneeigen-valuewithpositiverealpartof σ,thentheflowisunstable, namely,theperturbations u′ , v′ , w′,and p′ in(1.1.7)growwithtime,andtheflow willevolveawayfromtheinitiallaminarstate(U,V,W,P ).
Flowpastacircularcylinder
Letacircularcylinderofradius a beplacedinauniformflowofanincompressible viscousfluid;seeFigure1.3.Whendealingwiththisflowitisconvenienttousea Cartesiancoordinatesystemwithitsoriginatthecentreofthecylinder,the x-axis paralleltothefree-streamvelocityvector,the z-axisalongtheaxisofthecylinder,and the y-axisintheperpendiculardirection.Non-dimensionalvariablescanbeintroduced byonceagainusingthescalings(1.1.3)where L isreplacedbythecylinderradius a. Accordingly,theReynoldsnumberisnowdefinedas Re = V∞a/ν. Weshallassumethatthefree-streamvelocityvectorisperpendiculartothegeneratrixofthecylinder.Inthiscase,onecanexpecttheflowpastthecylindertobe two-dimensional;thatis,the‘spanwise’velocitycomponent w iszeroandnoneof thefluid-dynamicfunctionsdependon z,whichrenderstheNavier–Stokesequations (1.1.4)intheform
1.1.LinearStabilityTheory 11
Theseequationshavetobesolvedsubjecttothefree-streamconditions,
u =1,v =0,p =0at x 2 + y 2 = ∞, (1.1.16) andtheno-slipconditionsonthecylindersurface,
u = v =0if x 2 + y 2 =1 (1.1.17)
Theresultsofcalculationsofthesteadybasicflow
u = U (x,y),v = V (x,y),p = P (x,y) aredisplayedinFigure1.4intheformofstreamlineplots.Forsmallvaluesofthe Reynoldsnumber Re = V∞a/ν theflowremainsattachedtothecylindersurface asFigure1.4(a)plottedfor Re =2.5shows.However,anincreaseoftheReynolds numberleadstoflowseparationfromthecylindersurface.Asaresult,twoeddies formbehindthecylinder.TheseareclearlyseeninFigure1.4(b)plottedfor Re =5. Whentheeddiesfirstappear,theyoccupyasmallvicinityoftherearstagnationpoint.
Fig.1.4:SteadyflowpastacircularcylinderforReynoldsnumbers Re =2 5, 5, 10, and25.Thedashedlinesshowthestreamlinesintherecirculationeddies.
Chapter1.ClassicalHydrodynamicStabilityTheory
Then,astheReynoldsnumberincreases,theeddiesbecomeprogressivelylarger;see Figures1.4(c)and1.4(d).
Tostudythestabilityofthisflowweshallassumethattheperturbationsarealso two-dimensional,andthen,combining(1.1.12)and(1.1.7),wewillhave
Substitutionof(1.1.18)into(1.1.15)–(1.1.17)renderstheeigen-valueproblem(1.1.13), (1.1.14)intheform
TheresultsofthenumericalsolutionofthisproblemaredisplayedinFigure1.5 wheretheeigen-valuesof(1.1.19)areshowninthecomplex σ-plane.Ithasbeenfound thatthereexistsacriticalvalueoftheReynoldsnumber Rec ≈ 24 4.For Re<Rec
Fig.1.5:Thespectrumofthehundredleaststableeigen-valuesfor theflowpasta circularcylinderat Re = Rec.Arrowshighlighttheeigen-valueswhichcrossthe imaginaryaxis.
(a)Realpartof˜ u
(b)Imaginarypartof˜ u
Fig.1.6:Contourplotsoftherealandimaginarypartsofthestreamwisevelocity perturbationeigenfunction˜ u,attheonsetofinstability Re = Rec.Contourlevelsare inintervalsof0 1,andthepositiveandnegativelevelsareshownbysolidanddashed lines,respectively.Alsoweusethickersolidlinesforzerolevelsof ℜ{u} and ℑ{u} (notshown)theflowisstablewithalleigen-solutionslyingtotheleftoftheimaginary axis,where σr = ℜ{σ} < 0.Figure1.5‘capturesthemoment’whentheReynolds numberreachesitscriticalvalue Rec.Itdisplaysthespectrumofthehundredleast stableeigen-valuesatthecriticalReynoldsnumber.Noticethattheyoccurincomplex conjugatepairs.WhentheReynoldsnumberapproaches Rec,onepairapproachthe imaginaryaxis(thesesolutionsareshownbyarrowsinFigure1.5),andtheflow becomesunstable.Infact,at Re = Rec theflowperformsharmonicoscillationswith thefrequency σi = ℑ{σ} =0 3709.Thecorrespondingeigen-functionsarealsocomplex conjugatetooneanother.InFigure1.6weshowtherealandimaginarypartsofthe perturbedlongitudinalvelocitycomponent˜ u(x,y).Theperturbationfielddevelopsa ratherlongwakebehindthecylinder.Fortheattenuationcondition
u =˜ v =˜ p =0at x 2 + y 2 = ∞
tohold,thecomputationregionhadtobeextendedto x ≈ 300.InFigure1.6only apartofthewakeisshown.Itiseasilyseenthat˜ u(x,y)isanti-symmetricwith respecttothe x-axis.Theseresultsareinagreementwithlaboratoryobservations.It isknownfromexperimentthatwhentheReynoldsnumberreachesa criticalvalue, theflowbecomesoscillatory,withvorticesperiodicallysheddingfrom theupperand lowersidesofthecylinder.Thisvortexsystemisknownasthe K´arm´anvortexstreet. Theglobalstabilityanalysismaybeusedtoinvestigatethestabilitypropertiesof variousotherflows.Unfortunately,itisnotclearhowthemethodcanbeappliedto boundarylayers.AswecanseefromFigures(I.4)and(I.5),intheboundarylayerthe instabilitiesgrowwiththedownstreamcoordinate x,notwithtime t,whichmakesthe attenuationcondition(1.1.14b)inapplicable.Analternativeapproachisneeded(see Section1.3).
1.2StabilityofParallelFlows
Inordertoachievefurtherprogressinthetheoreticalanalysisofthestabilityequations (1.1.13),(1.1.14)weshallrestrictourattentiontoaspecialclassofflowsreferredto as parallelflows.WeshallstartwithplanePoiseuilleflowwhichbelongstothisclass.
1.2.1Poiseuilleflow
AdetaileddiscussionofthepropertiesofPoiseuilleflowwasgiveninSection2.1.2in Part1ofthisbookseries.Rememberthatthisistheflowofanincompressiblefluid throughachannelformedbytwoinfiniteplanesparalleltooneanother(Figure1.7). Thefluidmotionisdrivenbyalongitudinalpressuregradient.Tostudytheflow weshallusehereCartesiancoordinateswiththeˆ x-axisdrawnparalleltotheplates inthemiddleofthechannel,theˆ y-axisperpendiculartotheplates,andtheˆ z-axis perpendiculartotheplaneofthesketchinFigure1.7.Thedistancebetweentheplates is2h 2
Thefirststepinthestabilitytheoryistostudythebasicflow.Itisdescribedby thesteadyversionoftheNavier–Stokesequations(1.1.1):
Theseshouldbesolvedsubjecttotheno-slipconditiononthetwoplates:
Ifthechannelissufficientlylong,theninthemajorityoftheflow(excludingthe channelends)
Fig.1.7:Theproblemlayout.
2NoticethatinPart1,slightlydifferentnotationswereused.
1.2.StabilityofParallelFlows 15
Sincetheproblemconsideredisinvariantwithrespecttoanarbitraryshiftinthe ˆ z-direction,wecanalsoclaimthatthederivativeofanyfunctionwithrespecttoˆ z is zero,thatis
With(1.2.3)and(1.2.4)thecontinuityequation(1.2.1d)reducesto
which,beingintegratedwiththeboundaryconditionforˆ v in(1.2.2),yields
0(1.2.5) intheentireflowfield.
Using(1.2.3),(1.2.4),and(1.2.5)intheˆ x-momentumequation(1.2.1a),wefind that
Here µ = ρν isthedynamicviscositycoefficient.Sincetheflowconsideredisincompressible,wecanassume µ tobeconstantovertheentireflowfield.
Substitutionof(1.2.5)intotheˆ y-momentumequation(1.2.1b)yields
andweseethatinthebasicflowthepressuredoesnotvaryacross thechannel. Differentiating(1.2.6)withrespecttoˆ x wehave
which,inviewof(1.2.3),iszero.Consequently,thepressuregradientremainsconstant overtheentireflowfieldandmaybecalculatedas
where∆ˆ p isthepressuredifferencebetweenthechannelends,and L isthelengthof thechannel.
Integrating(1.2.6)withtheno-slipconditionsonthetwoplates
wefindthatthevelocityprofileisparabolic,
Themaximumvelocity
isachievedinthemiddleofthechannel(ˆ y =0).