ConstructingQuantumMechanics VolumeTwo
TheArch:1923–1927
AnthonyDuncanandMichelJanssen
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries
©AnthonyDuncanandMichelJanssen2023
Themoralrightsoftheauthorshavebeenasserted Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica BritishLibraryCataloguinginPublicationData Dataavailable
LibraryofCongressControlNumber:2023930769
ISBN978–0–19–888390–6
DOI:10.1093/oso/9780198883906.001.0001
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork.
DedicatedtothememoryofPhilipM.Stehle(1919–2013) andRogerH.Stuewer(1934–2022)
Preface
Thisisthesecondoftwovolumesonthegenesisofquantummechanicsinthefirst quarterofthetwentiethcentury.Forsomegeneralcommentsonourgoalsandapproach inthesevolumes,seetheprefaceofVolume1.AswedidforPartsIandIIinVolume1 (seeChapter1),webeginVolume2withanoverview,asnon-technicalaspossible,of thecontentsofPartsIIIandIV(seeChapter8).
AsinVolume1,wewrotemanysectionsofVolume2withtheideathattheyberead intandemwiththeoriginalpapersdiscussedinthem.Thepapersmostimportantfor thedevelopmentofbothmatrixandwavemechanics(coveredinPartIII)areavailableinEnglishtranslations.TheanthologyeditedbyB.L.vanderWaerden(1968) presentstranslationsofthepapersdocumentingthedevelopmentofmatrixmechanics(seeChapters10–12).Schrödinger(1982)convenientlycollectstranslationsofthe papersinwhichheintroducedwavemechanics(seeChapter14).Partialtranslationsof DeBroglie’s(1924)dissertationandfivekeypapersbySchrödingercanbefoundinan anthologyonwavemechanicseditedbyGünther(orGunter)Ludwig(1968).Werefer tothepapersincludedinvanderWaerden(1968)andSchrödinger(1982)byusingthe pagenumbersofthesevolumes.Unfortunately,severalofthepapersinwhichthetheory wasdevelopedfurtherin1926–1927(coveredinPartIV)havenotyetbeentranslated.
Ourdiscussionsoftheoriginalpapersservethreepurposes.First,theyshouldenable areaderwithabackgroundinphysicsandmathematicscomparabletothatofan advancedphysicsundergraduateorbeginninggraduatestudenttofollowthearguments andderivationsinthesepapers.1 Secondly,weexplainhowthesepapersarerelatedto otherpapersuponwhichtheybuildortowhichtheyrespond.Finally,weplacethese papersinthebroadercontextofthedebatesoverthedevelopingquantumtheory,in publishedpapers,atpublictalksandconferences,andinprivatecorrespondence.
Forthisthirdtaskwereliedheavilyoneditionsofcorrespondence(aswellaspapers andmanuscripts)ofseveralprominentprotagonistsinourstory.Especiallyimportant forVolume2wereNielsBohr’s CollectedWorks (Bohr 1972–2008,especiallyVols.4and 6), TheCollectedPapersofAlbertEinstein (Einstein 1987–2021,Vols.12–15),andthelate KarlvonMeyenn’seditionofthecorrespondenceofWolfgangPauli(inparticularVol. 1, Pauli 1979).ThemicrofilmsoftheArchiveforHistoryofQuantumPhysics(referred toasAHQPmicrofilm)areoursourceforunpublishedcorrespondence.Afindingaid preparedbyThomasS.Kuhn,JohnL.Heilbron,PaulForman,andLiniAllen(1967) givesthereelandframenumbersforalllettersincludedinthiscollection.
1 Tothisend,weaddedseveralmorewebresources(cf.theprefaceofVolume1):onBohr’satomictheory oftheearly1920s,onThomasprecession,onintensitiesofspectrallinesintheoldandthenewquantum theory,ontime-dependentperturbationtheoryintheThree-Man-PaperofBorn,Heisenberg,andJordan,on extremalprinciples,andon(Schrödinger’soriginalhandlingof)theradialSchrödingerequation.
Forthethirdtaskwealsomadeheavyuseofthemassivesix-volumehistoryof quantummechanicsbyJagdishMehraandHelmutRechenberg(1982a, 1982b, 1982c, 1982d, 1987, 2000–2001).WhileMehraandRechenbergofferlittlehelptothosetrying tounderstandthedetailedargumentsandderivations,theirworkremainsinvaluablein placingthoseargumentsandderivationsinabroaderbiographicalandinstitutionalcontext.Laterreminiscences,althoughtheyneedtobehandledwithcare,wereusefulaswell (see,e.g., FierzandWeisskopf 1960; Rozental 1967; Heisenberg 1971).Sowereseveral biographies(boththosewrittenforascholarlyandthosewrittenforageneralaudience), suchasDavidCassidy(1991, 2009)onWernerHeisenberg,MaxDresden(1987)on HansKramers,MichaelEckert(2013)onArnoldSommerfeld,GrahamFarmelo(2009) andHelgeKragh(1990)onPaulDirac,NancyGreenspan(2005)onMaxBorn,WalterMoore(1989)onErwinSchrödinger,AbrahamPais(1982a, 1991)onEinsteinand Bohr,and,morerecently,AnanyoBhattacharya(2022)onJohnvonNeumann.Wewere abletofindonWikipediathedatesandotherbiographicalinformationforallbutthe mostobscurecharacters.
Wehavealsotried,asmuchaswecould,toconsiderthesprawlingsecondary literatureonthegenesisofquantummechanics.EspeciallyimportantforVolume2 wereGuidoBacciagaluppiandAntonyValentini’s(2009)editionoftheproceedingsof1927Solvayconference(withadetailedhistoricalintroduction)and,asfor Volume1,OlivierDarrigol’s(1992) Fromc-Numberstoq-Numbers.Otherimportant secondarysourceswereaneditedvolume(BadinoandNavarro 2013),apairofdissertations(JordiTaltavull 2017; Jähnert 2016,sincepublishedasabook:Jähnert2019) andapairofpapers(JoasandLehner 2009; Blumetal. 2017)comingoutofthe quantumprojectinthecontextofwhichwestartedwritingourbook.Formoreinformationaboutthisproject,whichranfrom2006to2013andhaditsheadquarters attheMaxPlanckInstituteforHistoryofScienceinBerlin,seetheprefacetoVolume1andtheforewordbyAlexanderBlum,ChristophLehner,andJürgenRennto Eckert(2020).
Wealsomadeuseofourownearlierwork.Fordispersiontheoryanditsroleinthe run-uptoHeisenberg’s(1925c)“reinterpretation”(Umdeutung)paper(seeChapter 10),weusedDuncanandJanssen(2007).ForJordan’sderivationofEinstein’sfluctuationformulaintheThree-Man-Paper(Dreimännerarbeit)ofBorn,Heisenberg,and Jordan(1926)(seeSection12.3.5),weusedDuncanandJanssen(2008).Forourdiscussionof“Kuhnlosses”(seeSection15.2),weusedMidwinterandJanssen(2013).For theStarkeffectinwavemechanics(seeSection15.3.2),weusedDuncanandJanssen (2014, 2015).ForthestatisticaltransformationtheoryofJordan(1927b)andDirac (1927a)andvonNeumann’s(1927a, 1927b)Hilbertspaceformalism(seeChapters 16and17),weusedDuncanandJanssen(2013).Finally,forthearch-and-scaffold metaphor(seeChapter18),weusedJanssen(2019).Forpermissiontoreusethismaterial,wearegratefultoElsevier,publisherof StudiesinHistoryandPhilosophyofModern Physics (for DuncanandJanssen 2008, 2014);Springer,publisherof ArchiveforHistory ofExactSciences (for DuncanandJanssen 2007);theRoyalDanishAcademyofSciences andLetters(for DuncanandJanssen 2015);EditionOpenAccess(for Midwinterand Janssen 2013);andUniversityofMinnesotaPress(for Janssen 2019).
Inadditiontothosefriendsandcolleagueswealreadyacknowledgedintheprefaceof Volume1,wethankRudrajit(Rudi)Banerjee,AlexBlum,VictorBoantza,CindyCattell,PatrickCooper,PaulCrowell,MikeCuffaro,RafaelFernandez,MichaelJanas,Jim Kakalios,AlexKamenev,Karl-HenningRehren,andKurtSchönhammerforhelpful discussion.AsignificantpartofthisvolumewaswritteninBarcelona,whereweenjoyed thecompanyofanddiscussionswithEnricPérez.WethankOlivalFreireJr.forinviting ustocontributeabriefsynopsisofanimportantstrandinouraccountofthegenesisof quantumtheory(i.e.,theearlyhistoryofquantizationconditions)to TheOxfordHandbookoftheHistoryofQuantumInterpretations (seeDuncanandJanssen2022,in Freire 2022).OlivierDarrigolonceagaindeservesourspecialthanksforhisdetailedcomments ondraftsofseveralchaptersofthisvolume.WearegratefultoLaurentTaudinfordrawingthe“quantumcathedral”inFigure 18.1.Oneofus(MJ)thankstheAlexandervon HumboldtFoundationforaResearchGrantthatprovidedgenerousfinancialsupport forworkonthisbook.
WethanktheEmilioSegrèVisualArchivesoftheAmericanInstituteofPhysics (AIP),theBibliothèquenationaledeFrance,theSolvayInstitutes,Brussels,thePauli ArchiveatCERN,theNielsBohrArchiveinCopenhagen,theMITMuseum,theAmericanPhilosophicalSociety,andtheMathematischesForschungsinstitutOberwolfachfor permissiontouseimagesintheircollectionsfortheplatesinthisvolume.Wethank DominiqueBogaerts,UrteBrauckmann,JoeDiLullo,JenniferHinneburg,Samantha Holland,AllisonRein,RobSunderland,JensVigen,andArielWeinbergfortheirhelp inobtainingthesepermissions.
IthasonceagainbeenapleasuretoworkwithSonkeAdlung,oureditorat OxfordUniversityPress.WethankMicheleMariettaforhercarefulcopy-editingof themanuscriptandMarkAjinMilletforoverseeingtheproductionofthisvolume.
WededicatethisvolumetothememoryofPhilipM.Stehle(1919–2013)andRoger H.Stuewer(1934–2022).PhilStehleisresponsibleforoneofus(AD)developinga deeperappreciationforandaninterestincontributingtothehistoryofphysics.Phil Stehleisprobablybestknownasoneoftheauthorsofatextbookonclassicalmechanics thatisstillinprint(CorbenandStehle 1994,firstpublishedin1950)buthealsowrote anexcellenttextbookonquantummechanics(Stehle 1966).Heevenwroteabookon thesametopicasours: Order,Chaos,Order.TheTransitionfromClassicaltoQuantum Physics (Stehle 1994).RogerStuewer,inadditiontohismanyothercontributionstothe historyofphysics,createdthepositionofahistorianofphysicsembeddedintheSchool ofPhysicsandAstronomyattheUniversityofMinnesotacurrentlyheldbyoneofus. RogerStuewerisprobablybestknownforhisauthoritativepublicationsonthehistoryof nuclearphysics,synthesizedinhislastmonograph, TheAgeofInnocence:NuclearPhysics betweentheFirstandSecondWorldWars (Stuewer 2018).Thisisatopicbeyondthescope ofourbook.ButhealsowrotethedefinitiveaccountofthediscoveryoftheCompton effect(Stuewer 1975),aclassicinthehistoryofphysicsonwhichourtreatmentofthis topicisbased(seeSection10.4).Wewerealsoabletoconsultmanybooksinhisimpressiveandextensivelibrary,whichhedonatedtotheSchoolofPhysicsandAstronomyat theUniversityofMinnesota.Ourbookiswritteninthespiritandinfondmemoryof PhilStehleandRogerStuewer.
(exclusionprincipleandspin)
8.3Atomicstructure àla Bohr,X-rayspectra,andthediscoveryof theexclusionprinciple
8.3.1ImportantcluesfromX-rayspectroscopy
8.3.2Electronarrangementsandtheemergenceoftheexclusion principle
8.4.2DispersiontheoryandtheBohrmodel
8.4.3Finalstepstoacorrectquantumdispersionformula
8.4.4Ageneralizeddispersionformulaforinelasticlight scattering—theKramers–Heisenbergpaper
8.5Thegenesisofmatrixmechanics
Umdeutung
8.5.3Thenewmechanicsreceivesanalgebraicframing—Born andJordan’sTwo-Man-Paper
8.5.4Diracandtheformalconnectionbetweenclassical andquantummechanics
8.5.5TheThree-Man-Paper[Dreimännerarbeit]—completionof theformalismofmatrixmechanics
8.6Thegenesisofwavemechanics
8.6.1Themechanical-opticalroutetoquantummechanics
8.10VonNeumannputsquantummechanicsinHilbertspace
9.1.1Bohr’ssecondatomictheory
9.1.2CluesfromX-rayspectra
9.1.3Thefillingofelectronshellsandtheemergence oftheexclusionprinciple
9.2Thediscoveryofelectronspin
10.1Classicaltheoriesofdispersion
10.1.3Thetransmissionoflight:dispersionandabsorption
10.1.4TheFaradayeffect
10.1.5Theempiricalsituationuptoca.1920
10.2OpticaldispersionandtheBohratom
10.2.1TheSommerfeld–Debyetheory
10.2.2DispersiontheoryinBreslau:LadenburgandReiche
10.3Thecorrespondenceprincipleinradiationanddispersiontheory: VanVleckandKramers
10.3.1VanVleckandthecorrespondenceprincipleforemission andabsorptionoflight
10.3.2Dispersioninaclassicalgeneralmultiplyperiodicsystem
10.3.3TheKramersdispersionformula
10.4Intermezzo:theBKStheoryandtheComptoneffect
10.5TheKramers–HeisenbergpaperandtheThomas–Reiche–Kuhn sumrule:onthevergeof Umdeutung
11Heisenberg’s Umdeutung Paper
11.5Heisenberg’s Umdeutung paper:anewkinematics
11.6Heisenberg’s Umdeutung paper:anewmechanics
12TheConsolidationofMatrixMechanics:Born–Jordan,Dirac andtheThree-Man-Paper
12.1The“Two-Man-Paper”ofBornandJordan
12.2Thenewtheoryderiveddifferently:Dirac’sformulationof quantummechanics
12.3The“Three-Man-Paper”ofBorn,Heisenberg,andJordan
12.3.1Firstchapter:systemsofasingledegreeoffreedom
12.3.2Secondchapter:foundationsofthetheoryofsystems ofarbitrarilymanydegreesoffreedom
12.3.3Thirdchapter:connectionwiththetheoryofeigenvalues ofHermitianforms
12.3.4Thirdchapter(cont’d):continuousspectra
12.3.5Fourthchapter:physicalapplicationsofthetheory
13DeBroglie’sMatterWavesandEinstein’sQuantumTheoryof theIdealGas
13.1DeBroglieandtheintroductionofwave–particleduality
13.2Waveinterpretationofaparticleinuniformmotion
13.3Classicalextremalprinciplesinopticsandmechanics
13.4DeBroglie’smechanicsofwaves
13.5ThenewstatisticsofBoseandEinsteinandEinstein’squantum theoryoftheidealgas
14SchrödingerandWaveMechanics
14.1Schrödinger:earlyworkinquantumtheory
14.2Schrödingerandgastheory
14.3Thefirst(relativistic)waveequation
14.4Fourpapersonnon-relativisticwavemechanics
14.4.1Quantizationasaneigenvalueproblem.PartI
14.4.2Quantizationasaneigenvalueproblem.PartII
14.4.3Quantizationasaneigenvalueproblem.PartIII
14.4.4Quantizationasaneigenvalueproblem.PartIV
14.5The“equivalence”paper
14.6Receptionofwavemechanics
15SuccessesandFailuresoftheOldQuantumTheoryRevisited
15.1Finestructure1925–1927
15.2Intermezzo:Kuhnlossessufferedandrecovered
15.3Externalfieldproblems1925–1927
15.3.1TheanomalousZeemaneffect:matrix-mechanical treatment
15.3.2TheStarkeffect:wave-mechanicaltreatment
15.4Theproblemofhelium
15.4.1Heisenbergandtheheliumspectrum:degeneracy, resonance,andtheexchangeforce
15.4.2Perturbativeattacksonthemulti-electronproblem
15.4.3Theheliumgroundstate:perturbationtheorygivesway tovariationalmethods
PartIVTheFormalismofQuantumMechanicsandIts StatisticalInterpretation
16StatisticalInterpretationofMatrixandWaveMechanics
16.1Evolutionofprobabilityconceptsfromtheoldtothenewquantumtheory 559
16.2ThestatisticaltransformationtheoryofJordanandDirac 570
16.2.1Jordan’sandDirac’sversionsofthestatistical transformationtheory 571
16.2.2Jordan’s“Newfoundation(NeueBegründung)...”I
16.2.3Hilbert,vonNeumann,andNordheimonJordan’s“New foundation(NeueBegründung)...”I 599
16.2.4Jordan’s“Newfoundation(NeueBegründung)...”II 603
16.3Heisenberg’suncertaintyrelations 613
16.4DiscussionsofthenewquantumtheoryinComoandBrussels1927 627
17VonNeumann’sHilbertSpaceFormalism
17.2“Probability-theoreticconstruction...”
18.1Continuityanddiscontinuityinthequantumrevolution
18.2Continuityanddiscontinuityintwoearlyquantumtextbooks
18.3TheinadequacyofKuhn’smodelofascientificrevolution
18.4Evolutionofspeciesandevolutionoftheories
18.5Theroleofconstraintsinthequantumrevolution 682
18.6Limitationsofthearch-and-scaffoldmetaphor 683
18.7Substitutionandgeneralization
C.1Matrixalgebra
C.2Vectorspaces(finitedimensional)
C.3Inner-productspaces(finitedimensional)
C.4Ahistoricaldigression:integralequationsandquadraticforms 710
C.5Infinite-dimensionalspaces 714
C.5.1Topology:openandclosedsets,limits,continuous functions,compactsets 716
C.5.2ThefirstHilbertspace: l2 719
C.5.3Functionspaces: L2 726
C.5.4TheaxiomatizationofHilbertspace 732
C.5.5Anewnotation:Dirac’sbrasandkets
C.5.6OperatorsinHilbertspace:vonNeumann’sspectral theory
IntroductiontoVolume2
8.1 Overview
Thisisthesecondoftwovolumesonthegenesisofquantummechanicsinthefirst quarterofthetwentiethcentury.Itcoverstheperiod1923–1927andtrackshowwhatwe nowcalltheoldquantumtheorygavewaytomodernquantummechanics.AsinVolume 1(seeChapter1),1 webeginwithadetailedoverview,asnon-technicalaspossible,of thecontentsofVolume2(Chapter 8).Exceptforthisintroductorychapterandashort conclusion(Chapter18),thechaptersinthisvolume,liketheonesinVolume1,are dividedintotwoparts,PartIIIandPartIV.Mirroringtheappendixonthemathematics oftheoldquantumtheoryinVolume1(AppendixA),thisvolumehasanappendixon themathematicsforthenewquantumtheory(AppendixC).
InPartIII,consistingofsevenchapters(Chapters 9–15),wecoverthetransition fromtheoldtotwodistinctformsofthenewquantumtheory.InChapter 9,we startwithBohr’s(unsuccessful)attemptsintheearly1920stoaccountfortheperiodicityofthetableofelements,andtheintroductionoftwoingredients,thefirstof whichwasindispensableforthistask:Pauli’s(1925b)exclusionprincipleandUhlenbeck andGoudsmit’s(1925)electronspin(afterPaulihadtalkedKronigoutofpublishing theidea).Thenextfivechaptersaredevotedtotheemergenceofmatrixmechanics (Chapters 10–12)andwavemechanics(Chapters 13–14).InChapter 15,thefinal chapterofPartIII,werevisitthesuccessesandfailuresoftheoldquantumtheory (seeChapters6–7)andshowhowthenewtheorytookcareofthefailuresandputthe successesonamoresolidbasis.
MatrixmechanicsandwavemechanicsresultedfromdifferentstrandsinthedevelopmentscoveredinVolume1(cf. Darrigol 2009).Matrixmechanicsgrewoutofthe atomictheoryintroducedbyBohrinhispath-breaking1913trilogy(seeChapter4) andelaboratedbySommerfeldandothers,mostlyworkinginthethreemaincenters oftheoldquantumtheory,Copenhagen,Munich,andGöttingen(seeChapters5–7). Afterexaminingtherootsofmatrixmechanicsindispersiontheory(Chapter 10),we
1 Inallfurtherreferencesto(sections,equations,andfiguresin)PartsIandII,Chapters1–7,andAppendicesAandB,wewillnolongernoteexplicitlythatthesearereferencestomaterialinVolume1ofour book.
turntothe Umdeutung [reinterpretation]paperwithwhichHeisenberg(1925c)laidthe foundationsofmatrixmechanics(Chapter 11).Wethenexamineitselaborationinthe Two-Man-PaperofBornandJordan(1925b)andtheThree-Man-Paper[Dreimännerarbeit]ofBorn,Heisenberg,andJordan(1926),bothcomingoutofGöttingen,aswellas thepaperinwhichDirac(1925),workinginCambridge,introducedthecloselyrelated q-numbertheory(Chapter 12).
Wavemechanics,unlikematrixmechanics,grewoutofworkdonebythepioneersofquantumtheory before Bohr’s1913trilogy(seeChapters2and3).These pioneers—mostimportantlyPlanck,Einstein,andEhrenfest—werenotconcernedwith thestructureofindividualatoms,butratherwiththestatisticsoflargecollectionsof simplesystemsmodeledasharmonicoscillators.Insteadofspectroscopy,theystudied black-bodyradiationandthespecificheatofsolidsatlowtemperatures—twoareaswhere theequipartitiontheoremofthekinetictheoryofgasesofMaxwellandBoltzmannnotoriouslybrokedown.Theyearbeforethearrivalofmatrixmechanics,Indianphysicist SatyendraNathBose(1924)proposedanewderivationofthePlancklawforblack-body radiation,usinganewstatisticsforlightquanta,whichEinstein(1924, 1925a, 1925b) subsequentlytransferredtoatomsinhisquantumtheoryoftheidealgas.Einsteinfound thatthedensityfluctuationsinsuchagasaregivenbyaformulaliketheonehehadfound earlierforfluctuationsinblack-bodyradiation(1909a, 1909b),consistingofawaveand aparticleterm.ThissupportedasuggestionmadeinthedissertationbytheFrench physicistdeBroglie(1924)toextendthewave-particledualityEinsteinhadproposed forradiationtomatter.DrawingonthisworkbyDeBroglie,Bose,andEinstein(Chapter 13),andonthemucholderoptical-mechanicalanalogyduetoWilliamRowanHamilton(1834, 1835)(Section 13.3),Schrödinger(1926c, 1926d, 1926f, 1926h),working inZurichratherthaninoneofthecentersoftheoldquantumtheory,developedwave mechanicsinacelebratedfour-partarticle(Chapter 14).
InPartIV,consistingofjusttwochapters(Chapters16–17),wecoverthecompletionoftheformalismofquantummechanicsanditsprobabilisticinterpretation.Bythe middleof1926,threeauthors,independentlyofoneanother,hadalreadyestablished thatmatrixandwavemechanicsareintimatelyrelated(seeSection 14.5).Schrödinger (1926e)andEckart(1926)gavetheir“equivalenceproofs”inpublishedpapers,and Pauli(1979,Doc.131)gavehisinprivatecorrespondence.InDecember1926,Dirac (1927a)andJordan(1927b)published,againindependentlyofoneanother,whathas cometobeknownastheDirac–Jordan statisticaltransformationtheory (Section 16.2). Theirformalismunifiedallfourversionsofquantumtheorythathadmeanwhilebeen proposed:matrixmechanics,wavemechanics,Dirac’s q-numbertheory,andtheoperatorcalculusofBornandWiener(1926,seeSection 14.5).Astheterm“statistical” suggests,DiracandJordangeneralizedtheprobabilisticinterpretationofSchrödinger’s wavefunctionproposedbyBorn(1926a, 1926b)inpapersoncollisionprocesses,and byPauli(1979,Doc.143),truetoform,inprivatecorrespondence(Section16.1).As theterm“transformationtheory”suggests,canonicaltransformationsfamiliartoJordan andDiracfromthecelestialmechanicsusedintheoldquantumtheory(seeAppendix A)playedacentralroleintheDirac–Jordanformalism.Thesemathematicaltechniques, however,provedill-suitedtothetask.ThiswasclearlyrecognizedbytheyoungHungarianmathematicianJanosvonNeumann,whocametoworkwithHilbertinGöttingen
Quantumtheoryintheearly1920s:deficienciesanddiscoveries(exclusionprincipleandspin) 3 in1927.BuildingonrecentworkbyHilbertandothermathematiciansonwhatisnow knownasfunctionalanalysis(AppendixC),vonNeumann(1927a)introducedthemodernHilbertspaceformalisminapaperpresentedtotheGöttingenAcademyinMay 1927andusedittoformulatequantummechanicsinawaythatsteeredclearofsuch mathematicalmonstrositiesastheDiracdeltafunction,unavoidableinDiracandJordan’sapproach.PromptedinpartbyHeisenberg’s(1927b)uncertaintypaper(Section 16.3),vonNeumannpublishedtwomorepaperslaterthatyear(vonNeumann 1927b, 1927c).Inthesecondinstallmentofthis1927trilogy,drawingonvonMises’sideas aboutprobability(soontobepublishedinbookform:vonMises 1928),vonNeumann (1927b)reformulatedthestatisticalinterpretationofquantummechanicsintermsofhis Hilbertspaceformalism.ThispaperonlyappearedaftertheComoandSolvayconferencesofSeptemberandOctober1927,whichmarkthebeginningofthecontentious andongoingdebateovertheinterpretationofquantummechanics,atopicbeyondthe scopeofourbook.WethereforedecidedtocoverHeisenberg’s(1927b)uncertainty principleandBohr’s(1928b)complementarityprinciple(firstpresentedatComoand Solvay)inChapter 16,andtoendwithvonNeumann’sHilbert-spaceformalismin Chapter 17.
IntheshortconcludingChapter 18,weelaborateandreflectonthearch-and-scaffold metaphorweusedforthesubtitlesofVolumes1and2(Janssen 2019).Aswillbecome clearinthecourseofthisvolume,the“quantumrevolution”ofthemid-1920s,whilea majorturningpointinthehistoryofphysics,doesnotfollowthepatternofa“paradigm shift”familiarfromThomasS.Kuhn’s(1962)classic TheStructureofScientificRevolutions,inwhichtheoldparadigmcrumblesundertheweightofanaccumulationof anomaliesandanewparadigmiserectedonitsruins.Theoldquantumtheoryhadrun intoseriousdifficultiesbytheearly1920s,butthewayoutoftheresultingKuhniancrisis wasnot,asKuhn(1970,pp.256–257)himselfclearlyrecognized,totrashtheoldtheory andstartfromscratch.Amoreaptimage,ouranalysissuggests,isthatthenewquantum theorywasbuiltasanarchonthescaffoldprovidedbytheoldquantumtheoryand,in turn,theclassicalmechanicsandelectrodynamicsuponwhichitwasbuilt.Muchofthis scaffoldingwasdiscardedoncethearchcouldsupportitself,makingthediscontinuity initsconstructionlook,inhindsight,muchmorepronouncedthanitactuallywas.
8.2 Quantumtheoryintheearly1920s:deficiencies anddiscoveries(exclusionprincipleandspin)
Bythemiddleof1923,aswesawinChapter7,numerousseriousdeficiencieshadbeen exposedintheformalframeworkoftheoldquantumtheory,asdevelopedintheaftermathofSommerfeld’sgroundbreakingpapersof1916,inwhichtheBohr–Sommerfeld quantizationruleswereintroducedandappliedwithremarkablesuccesstoseveralcentralproblemsofatomicphysics.Thesedeficienciescanbroadlybedividedintotwo categories.First,therewereproblemsthatseemedatleastamenabletotheaccepted frameworkoftheoldquantumtheory—formulationofamechanicalproblemusingthe Hamilton–Jacobitechnique,giventhattheproblemallowedtreatmentintermsofamultiplyperiodicmotion,followedbyimpositionofthequantizationrulestotheassociated
actionvariables,butinwhichtheexecutionoftheformalismsimplyledtoanincorrectresult—oneincleardisagreementwiththeexperimentaldata.Thequintessential exampleofthistypewasthefailureoftheoldtheorytoobtainthecorrectbindingenergy ofthegroundstateofhelium,despitethediscoveryofaperfectly“reasonable”multiply periodiccoordinatedmotionforthetwoelectronsconsistentwithclassicalmechanics.
Thesecondsetoffailures—morenumerousthanthefirst—comprisedthoseproblems inatomicphysicsinwhichnosingleconsistenttreatmentbasedonmechanicalprinciples andtheBohr–Sommerfeldmethodologycouldbefoundforthephenomenainquestion. Theclusterofproblemsassociatedwiththeinterpretationofthecomplexstructureof opticalspectralmultiplets,andtheexplanationofthecomplicatedrulesthathadarisen fromthestudyofanomalousZeemanmultipletsbelongtothissecondcategory.Other problemsinthiscategorycropupinthetheoryofopticaldispersionandinthetheoryof theStarkeffect.Inallthesecases,therootoftheproblemwastheassociationofenergy levelswithdefiniteclassicalorbitsofcharged(butnon-magnetic)electronsinminiature solarsystems.
Theearly1920ssawanenormousincreaseintheinterestin,andattentionpaidto, twomoretopics,whichwereeventuallyfoundtoeludeconsistenttreatmentwiththe methodsoftheoldquantumtheory—theperiodicnatureofthechemicalandoptical propertiesoftheelements,presumablytobeexplainedbysomeshell-likearrangement oftheelectronsinlargeratoms,andtheappearanceofunexplained“superfluous”lines inX-rayspectra,withspectralsplittingswithaninexplicable(onoldquantumtheory grounds)dependenceontheatomicnumber Z.Thisclusterofproblemswouldturn outtobedeeplyconnectedwiththetwofinalmajordiscoveriesofthequantumtheory priortotheadventofmodernquantummechanics:theexclusionprincipleforatomic electronstatesproposedinDecember1924byWolfgangPauli,andtheexistenceofan intrinsicelectronspinangularmomentum,firstproposedbyRalphKroniginJanuary 1925,andindependentlyrediscoveredinNovemberofthesameyearbyGeorgeUhlenbeckandSamuelGoudsmit.Ignoranceofthesetwobasicfacts,quiteapartfromthe (inhindsight)deepkinematicalanddynamicaldefectsoftheoldtheorywhichwould becuredbymatrixandwavemechanics,explainsalargepartofthefailuretoarriveat aconsistenttreatmentofcomplexspectraortheanomalousZeemaneffectwithinthe frameworkoftheoldquantumtheory.Thediscoveryoftheexclusionprincipleinlate 1924,andshortlyafter,ofelectronspin,isourfocusinChapter9.Itisusefulhere,however,tobeginourbroadoverviewoftheconstructionofmodernquantummechanics bydescribingthedramaticprogressmadeinthesetwoareasintheyearsleadingupto theextraordinarydevelopmentsof1925.
8.3 Atomicstructure àla Bohr,X-rayspectra, andthediscoveryoftheexclusionprinciple
AswesawinChapter4,Bohr’searliesteffortsinattemptingtoinsertquantumprinciples intoanunderstandingofatomicstructure(posttheRutherfordnuclearatom)weresummarizedinthememorandumof1912thathesenttoRutherford.Here,wecanseehim
Atomicstructure àla Bohr,X-rayspectra,andthediscoveryoftheexclusionprinciple 5 wrestlingalreadywiththeproblemoftheconfigurationofelectronorbitsinanatom withmorethanoneelectron.Theserudimentaryconsiderationsweremuchamplified anddeepenedinthesecondpaperofhis1913trilogy,entitled“Systemscontainingonly asinglenucleus”(butingeneral,morethanoneelectron—seeSection4.5).Thebasic conclusionsatthisearlystageoftheoldquantumtheorywerenecessarilytentative,and indeed,onlytenablegiventherudimentaryquantitativeevidenceavailableatthetime concerningthedetailedenergeticsofthequantizedstatesofatoms.Forexample,even forthesimplestmulti-electronatom,helium,thetotalbindingenergyoftheatomwas onlyveryroughlyknown.Bohr’searliestattemptsinthisdirection,whichwemayterm here“Bohr’sfirstatomictheory”,canbesummarizedinthefollowingstatements,as regardstheconfigurationofelectronorbits:
1. Alltheelectronscirculateinasingleplanein(roughly)concentriccircularorbits. Thisis,ofcourse,analogoustothesolarsystem,inwhichthemajorplanetsorbit thesuninroughly(towithin6◦)thesame(“ecliptic”)plane.
2. Everyelectroninthegroundstateoftheatomhasaquantizedvalueof h/2π for itsorbitalangularmomentum.
3. Foragivennuclearcharge,thereisamaximumnumberofelectronsthatcan beaccommodatedineachoftheconcentricringscontainingelectrons.This numberwasdeterminedbyamechanicalstabilityconditionwithregardtosmall perturbationsoftheorbitperpendiculartothe“ecliptic”planeoftheatom.
Evenintheabsenceofdetailedquantitativeinformationonelectronbindingenergies, therewasclearevidencefromchemistryandopticalspectroscopyofa“periodic”characterinthepropertiesoftheelements,whichhadalreadybeencodifiedinMendeleev’s periodictable.Bohr’s(1913b)stabilityargumentswereanearly,but(asBohrhimself recognized)farfromsuccessful,attempttocometotermswiththisperiodicity.
Bytheearly1920s,itwasclearthatnoneofthesethreeprinciplescouldpossiblybe valid.Fornumerousreasons,including,butnotlimitedto,thediamagnetismoftherare gases,thecrystalstructureofvariouselements,opticaldispersionmeasurements,and (perhapsmostcritically)theextraordinarydualfeatureoftheheliumspectrum,which dividedintotwodisconnectedsetsoflinesseparatelyconnectingthetermsof“orthohelium”and“parahelium”,thepictureofelectronscirculatingincoplanarorbits,as originallyimaginedbyBohrin1913,hadbecomecompletelyuntenable.Thedefinitive abandonmentofthispictureinthecaseofheliumcamewiththeintroductionofthenoncoplanarBohr–Kemblemodelofthegroundstateofhelium(seeSection7.3),whichwas itselfanaturaldescendantoftheSommerfeld–Landémodelofhelium,developedinthe processofwrestlingwiththepeculiaritiesoftheheliumspectrum.
Remarksattheendofalongpaperentitled“Ontheseriesspectraoftheelements” (Bohr 1920),submittedto ZeitschriftfürPhysik intheFallof1920,offeraglimpseofthe methodologyBohrwastoadoptintheyears1920–1923inthestudyofatomicstructure. Mostofthispaperisdevotedtoadescriptionoftheunderstandingwhichhadbeen achievedoftheremarkableefficacyofRydberg-typeformulas(seeAppendixB)forthe
termsoftheopticalseriesoftheelements(especiallythealkalimetals,suchassodium) usingthemethodsoftheoldquantumtheory(seeSection7.1),aswellasarecapitulation oftheapplicationsofcorrespondence-principleideas,forexample,intheinterpretation ofspectraintheStarkeffect(seeSection6.3).Intheconcludingsection,Bohrapologizes forthelackofattentionspecificallytoquestionsofatomicstructure,andpointsforward totheneedforamoresophisticatedapproachtotheproblemoftheconfigurationof electronicorbits:
IntheforegoingIhaveintentionallynotdelvedmorecloselyintothequestionofthe structureofatomsandmolecules,althoughthissubjectisclearlyintimatelyconnectedwith thetheoryoftheoriginofspectrawhichwehaveconsidered...Ontheoccasionofthe firsttreatmentofthismatter[Bohr’strilogyof1913],theauthoralsoattemptedtosketch thefoundationsofatheoryforthestructureoftheatomsoftheelements[PartII]andfor thechemicalcombinationsofmolecules[PartIII]...Iwouldliketotaketheopportunityhere,however,tostatethatfromthestandpointofmorerecentdevelopmentsofthe quantumtheory...manyofthedetailedspecialassumptionsmadeinthe[earlier]theorymustbealtered,onthebasisofdisagreementofthetheorywithexperimentalresults whichhavebeenraisedonnumerousfronts.Inparticularitdoesnotseempossibleto justifytheorientingassumptionintroducedatthattime[1913],thatinthegroundstate electronsmoveingeometricallyparticularlysimpleorbits,suchas“electronrings.”Considerationsofthestabilityofatomsandmoleculeswithregardtoexternalinfluences,and onthepossibilityofconstructionoftheatombysuccessiveacquisitionofsingleelectrons, requireustoinsist,first,thattheelectronconfigurationstobeconsideredaremechanicallystable,andmoreoverpossessacertainstabilitywithregardtotherequirementsof theusualmechanics,andsecond,thattheconfigurationstobeusedaresoconstituted thattheymaybearrivedatbytransitionsfromotherstationarystatesoftheatom. These requirementsareingeneralnotfulfilledbysuchsimpleconfigurationsaselectronrings,and forceustolookaroundformorecomplicatedformofmotion (Bohr1920,pp.468–469,our emphasis).
Inthethreeyearsfollowingthiswork,Bohrdelvedmorecloselyintotheproblemof atomicstructure,specifically,indeterminingthemutualorientationoftheorbitsfollowedbyelectronsinmulti-electronicatoms,andrelatingtheproposedarrangementof atomicorbitstotheobservedchemicalpropertiesandopticalspectraoftheelements, withparticularattentiontotherecurringperiodicityofthesepropertieswithatomic numberembodiedintheperiodictable.Therewouldbetwoshort Nature papers(Bohr 1921a, 1921c)aswellasaseriesoflongerpapers,oftenelaboratedversionsoflectures Bohrpresentedatvariousvenues—andoftentoaudienceswhowerenotatomictheorists, andcouldnotthereforefollowthemoretechnicalaspectsofBohr’sprogram—suchas Bohr(1921d),agreatlyexpandedversionofalectureinCopenhageninOctober1921, andBohr(1922e),basedonhislegendaryWolfskehllecturesinGöttingeninJune1922, whichbecameknownasthe“Bohrfestival”(BohrFestspiele)(MehraandRechenberg 1982a,sec.III.4,pp.332–358).
Thegeneralnexusofideasproposedinthesepapershasbecomeknownas“Bohr’s secondatomictheory”(see Kragh 1979, 2012,Ch.7).Intheseworks,Bohrattempted todevelopandapplytheideasvisibleinembryoforminthequotegivenabove.First,an
Atomicstructure àla Bohr,X-rayspectra,andthediscoveryoftheexclusionprinciple 7
electricallyneutralmulti-electronicatomwithanatomicnucleusofcharge +Ze wouldbe builtupinstagesbyfirstputtingasingleelectronintothelowestenergyquantizedorbit availableforthebarenucleus,andthenasecondelectronwouldbeaddedinthelowest quantizedenergystatecompatiblewiththeexecutionofamultiplyperiodicmotion2 by bothelectrons.Athirdelectronwouldthenbeaddedinthesameway,allowedtosettle downintoanorbitwhichnecessarilyhadtopossessahighdegreeof“cooperation”with themotionsoftheprecedingtwoelectrons—andsoon,untilafullcomplementof Z electronshadbeenaddedtotheatom,renderingitelectricallyneutral.
ThemultiplyperiodiccharacterofthemotionateachstagewouldallowfortheapplicationoftheBohr–Sommerfeldquantizationprinciples,sothattheorbitofeachelectron couldbecharacterizedbyassigningthetwoquantumnumbersfamiliarfromtheold theory:theprincipalquantumnumber n,themaindeterminantoftheorbitalsizeand energy,andtheazimuthal(orbitalangularmomentum)quantumnumber k,sothatone couldspeakofanelectroninthestate nk (with k = 1,2,..., n).
Twoguidingprinciplesweresupposedtobeappliedintheexecutionofthis Aufbau (“build-up”)process:(a)thequantumnumbersofthepreviouslyaddedelectrons wouldnotbealteredbytheadditionofsubsequentelectrons,althoughofcoursethe detailedshapeandsizeoftheinnerorbitswouldbepresumedtochangeasnewelectronswereadded,inconformancewiththeclassicalequationsofmotion;and(b)the finalorbitreachedbythelatestelectronaddedmustcorrespondtoanallowedtransition asprescribedinthecorrespondenceprinciple.Here,oneshouldrecallthattheextended correspondenceprincipledevelopedbyBohrandKramersinthelateteenyearsassociatedtheprobabilityofaquantumtransitioninwhichelectromagneticradiationwas absorbed(oremitted)withtheFouriercomponentsofthemotionoftheabsorbing(or emitting)electron.Thisassociationwasquantitativelyexactinthelimitoflargequantumnumbers,butassumedtoholdroughlyforsmallquantumnumbers.Inparticular,a transitiondisallowedforsomesymmetryreason(givingzeroFouriercomponentsforthe correspondingemittedlightquantum)wasassumedtobedisallowedforall(andnotjust large)quantumnumbers,anextensionthatledtotheremarkablysuccessfulapplication ofthecorrespondenceprincipleinderivingselectionrulesforopticaltransitions.
TheguidingprinciplesBohrattemptedtoapplytohis“secondtheoryofatomicstructure”seemfairlystraightforwardinprinciple,butturnedouttobeextremelyslippery, andultimatelyuntenable,inpractice,asweexamineindetailinChapter9.Hisreferencestothecorrespondenceprincipleasdeterminingthechoiceoforbitsforeachnewly addedelectroninthe Aufbau procedurewereunsupportedbyexplicitcalculationsand forthemostpartexpressedinvagueandobscurelanguage.Atypicalexampleisthe thirdelectroninlithium,whichcannot(becauseoftheexclusionprinciple,aswenow know)occupy1s(n = 1, k = 1)orbitslikethefirsttwo,butwhich(accordingtoBohr) ispreventedfromjoiningthefirsttwoelectronsina1sstatebecausesuchastatecannot
2 Weremindthereaderthatamultiplyperiodicmotionof N electronsisoneinwhichthetimedependenceofeachofthe 3N CartesiancoordinatesofthesystemofelectronscanbewrittenasaFourierseries combinationinvolvingatmost 3N distinctfrequencies.
bereached(bythethirdelectron)fromhigherorbitsbyatransitioncompatiblewith correspondenceprincipleideas:
Suchatransitionprocess,ofwhichonemustassume(asamoredetailedexamination ofthepossibilitiesofmotionshows[thisisnevergiven])thatitwouldleadtoanatomic stateinwhichthethirdelectronwouldappearasaequivalentparticipantinthecollectivemotionofthethreeelectrons,wouldinfactbeofaquitedifferenttypeasthe transitionsbetweenstationarystatesconnectedwiththeemissionspectrumoflithium, andincontrasttothesewoulddisplaynocorrespondencetotheharmoniccomponents ofthemotionoftheatom(Bohr 1922b,p.35).
Sentencesofthissortaboundinthesequenceofarticlesandlecturesmentionedabove wheneverthephysico-chemicalpropertiesofanelementrequiredtheadditionofan electroninanew,less-boundorbittotheprecedingones.AppealstothecorrespondenceprinciplewerethereforeofcriticalimportanceinBohr’sattemptstounderstand theperiodicityofthesepropertiesintermsofashellstructure(moreprecisely,agroupingintosubclassesofsimilarorbits)oftheelectronssurroundinglargeratoms.Inasmuch asBohr’sfinal(pre-exclusionprinciple)specificationofelectronicshellstructures,in apaperco-authoredwithDirkCoster(BohrandCoster 1923,p.344),stillhasan incorrectassignmentofquantumnumbers(as,forexample,inthefilledthirdshellfor elementsfromcopperonward,containingsixeachof s, p,and d electrons,insteadof2, 6,and10,respectively),weknowthattheseargumentsmusthavebeenfaulty,evenif theyexistedinamoreexplicitmathematicalformthanisapparentfromthepublished work.InChapter9wediscussBohr’sargumentsinmoredetail,3 anddemonstratethat atomicsystemssubjecttothecorrespondenceprinciple,butlackingspinandexclusion properties,simplydonotbehaveasBohrasserted.
8.3.1 ImportantcluesfromX-rayspectroscopy
InourdiscussioninChapter7ofthevariousattemptstodealwiththeappearanceof “extra”lines—hence,extraquantumstates—inthestudyofthecomplexopticalspectrathatoccurredespeciallyinlargeratoms,wesawthatthenewlevelswereatfirst absorbedintothetheorybythepurelyphenomenologicalruseofintroducinganew quantumnumber,Sommerfeld’s“innerquantumnumber”.Adynamicalexplanation forthisnewdegreeoffreedomwouldeventually(inthefewyearsremainingtothe oldquantumtheory)cometobewidelyaccepted:namely,thatthesplittingofBohr–Sommerfeldlevelsassociatedwiththisnewquantumnumberwasduetothefreedom toalter(discretely)therelativeorientationoftheorbitalangularmomentumofanouter valenceelectron(thequantumstateofwhichwasunderconsideration)totheorientationofthecombinedangularmomentumoftheatomiccore(i.e.,alltheinnerelectrons). Afurtherintriguingphenomenologicalobservationwouldsoonprovetoplayacritical
3 Seealsothewebresource, Bohr’sSecondTheoryandAtomicAufbaubeforeSpinandtheExclusionPrinciple
Atomicstructure àla Bohr,X-rayspectra,andthediscoveryoftheexclusionprinciple 9 role—whenaweakmagneticfieldwasapplied,avalenceenergylevelwouldsplitintoa numberofcloselevelsequaltotwicetheinnerquantumnumber.
By1920,theincreasingaccuracyanddetailavailablefromX-raystudies—especially, thestudiesofX-rayabsorptionedgesbyGustavHertz(thenephewofHeinrichHertz) atthe PhysikalischesInstitut oftheUniversityofBerlin—hadshownquiteclearlythe existenceofasimilarsetof“extra”levelsintheatomicenergylevels(“terms”)associated withtheinnermost,andmosttightlybound,electronsoflargeratoms(allthewayup touranium,with Z = 92).The L levels,correspondingtoprincipalquantumnumber 2,werefoundtobeassociatedwithatripletofenergyvalues,whichwerelabeledby Sommerfeldasthe L1, L2,and L3 levels.
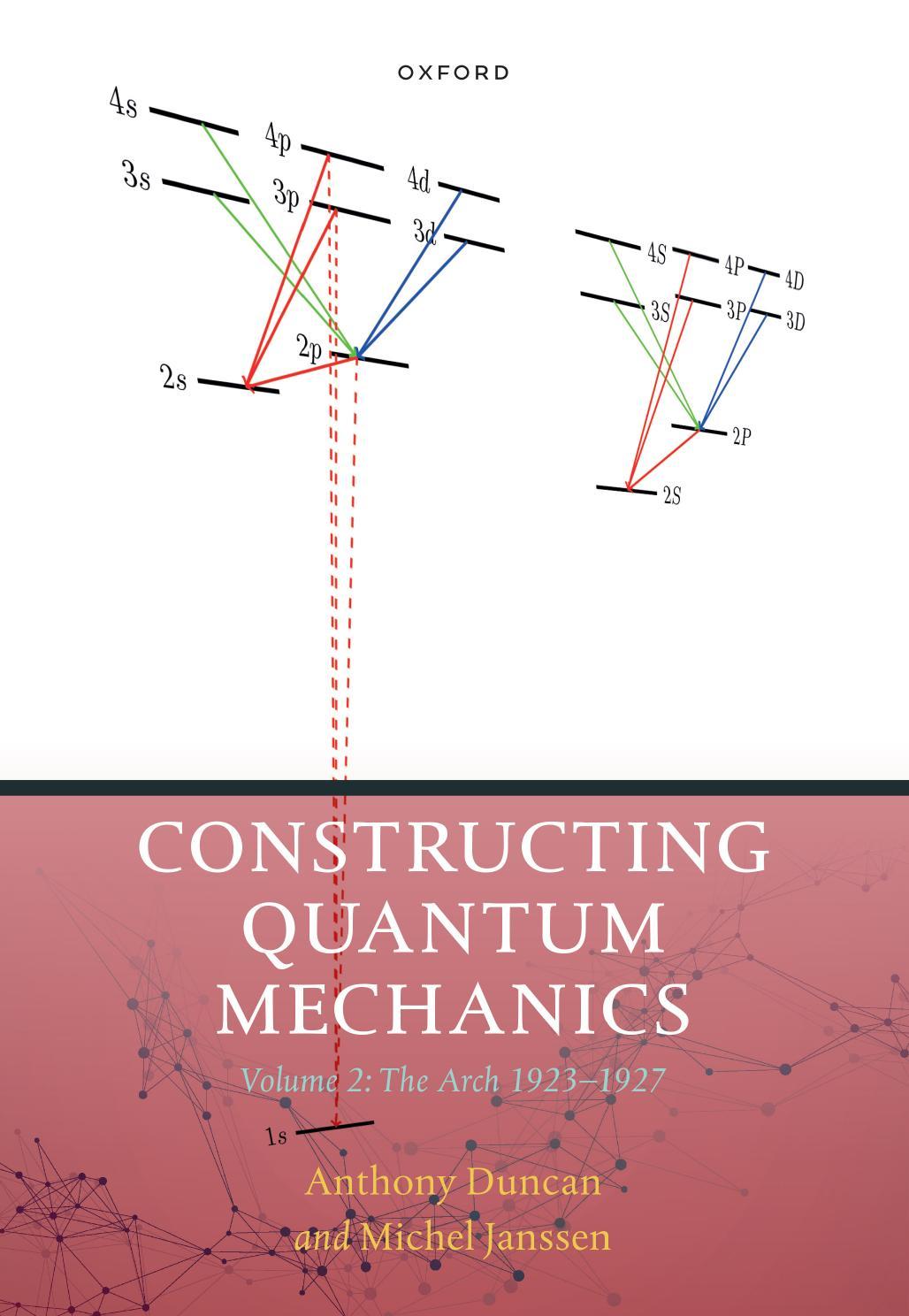
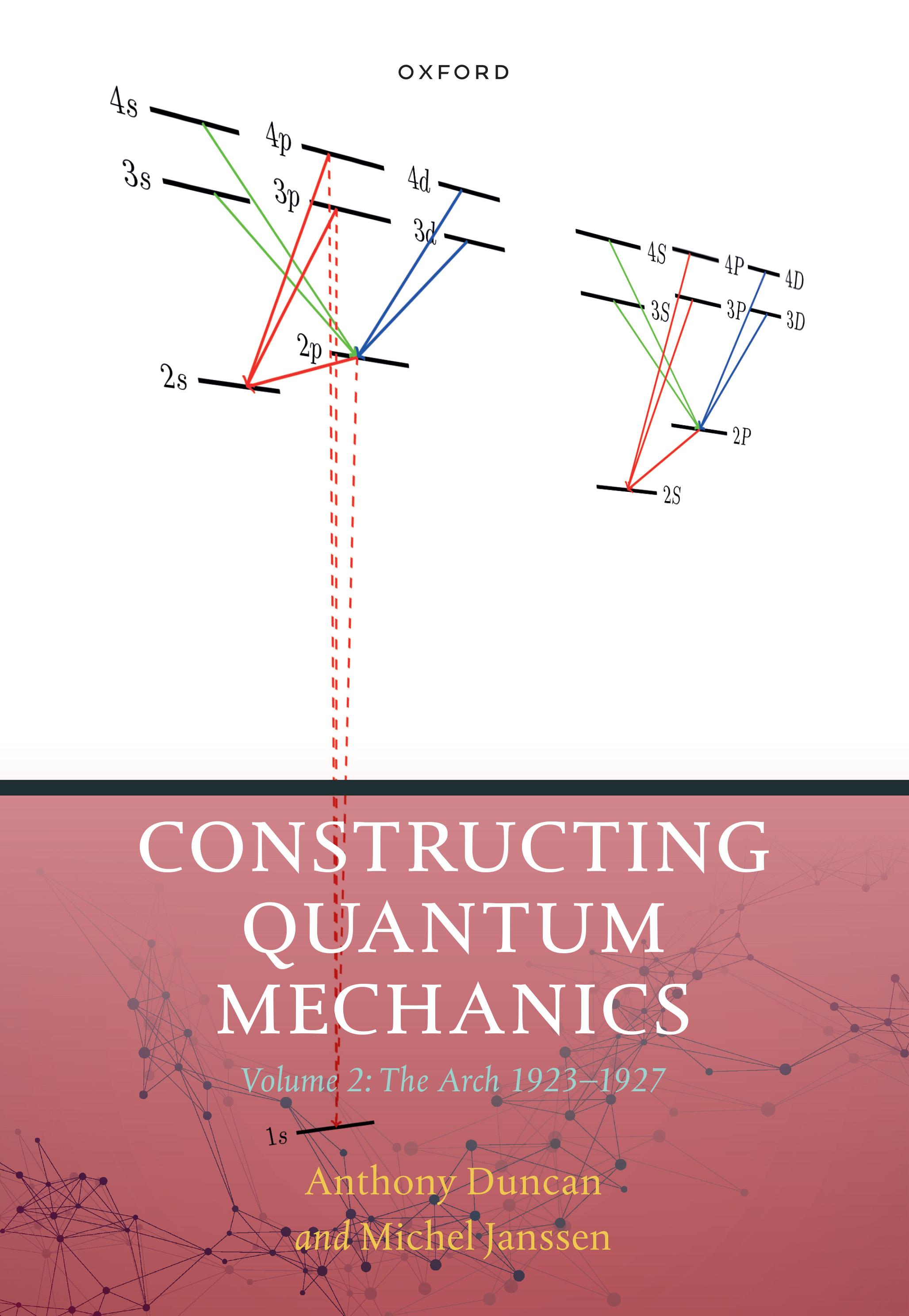
TheincreasingimportanceofX-raystudies,morespecifically,offocusingattention ontheinnermostelectrons,waspreciselythatsuchelectronsshouldmostcloselyapproximatethebehaviorofsingleelectronsinahydrogenicatom(nowoflargenuclearcharge) giventhedominanceofthenuclearelectrostaticfield,andtherelativeweaknessofthe influenceoftheothersingleelectrons(eachhavingamuchsmallerchargethanthe nucleus).Outerelectronswereassumedtosurroundtheinnerones(andnucleus)more orlesssymmetrically,andtherefore,byawell-knowntheoremofclassicalelectrostatics, exertno(orverylittle)netCoulombforceontheinnerones.Aninnerelectron(say, an L electronwithprincipalquantumnumber N = 2)wouldseealmostthefulleffect oftheatomicnucleusofcharge +Ze,andthesmallscreeningeffectoftheotherinner electronscouldbetakenintoaccountquiteaccuratelybyreplacing Z → Zeff = Z σ, wherethescreeningfactor σ wastypicallyoforderunity(comparedto Zsofinterestin theX-raystudiesbetween50and90).ThesquarerootoftheBohrbindingenergyfor electronsofagivenprincipalquantumnumber,whichwasthequantitytypicallyplotted astheverticalordinateinX-raytermdiagramspost-Moseley,4 wasthereforeroughly proportionalto Z formediumtolarge Z.
Sommerfeld’scalculationofrelativisticeffects,givingrisetothefamousfinestructure formula(seeEqs.(6.51)–(6.53)),showedthatthevaryingeccentricityoforbitsofdiffering n (orbitalangularmomentum)forafixedprincipalquantumnumber5 N would leadtodifferentrelativisticcorrectionstotheelectronbindingenergy—correctionsof orderofmagnitude (v/c)2 relativetotheleadingenergyterm,wherethetypicalvelocity v ofanelectroncirculatinginaBohrorbitaroundanucleusofcharge Ze satisfies v/c ≃ Zα (with α ≃ 1/137theSommerfeldfinestructureconstant).Thepresenceof suchrelativisticeffectswouldthereforenecessarilyinduceshiftsintheinnerelectron termenergiesoforder Z4 (comparedtotheleading Z2 Balmerterm),oradivergenceof order Z3 betweentheroughlylinearMoseleysquare-root-of-bindingenergyordinates fororbitsofdiffering n value(hence,orbitaleccentricities).
4 Moseley’sX-raydataweretypicallydisplayedwiththeatomicnumberontheverticalaxis(ordinate)and thesquarerootofthetermenergyonthehorizontalaxis(abscissa).Cf.Figure6.3.
5 Weapologizeherefortheconfusingevolutionofconflictingnotationsforelectronicquantumnumbers, with N, n (forprincipalandorbitalangularquantumnumbers)ofthelateteensgivingwaylaterto n, k (as inourdiscussionofBohr’s Aufbau),andsubsequently n, l.Wehavetriedtoholdtothenotationusedbythe authorsbeingdiscussedasmuchaspossible.
Letusfirstconsiderthesimplestcase,the“L”X-raytermscorrespondingtoinner electronswithprincipalquantumnumber N = 2,inatomsoflarge Z (> 50,say). PairsofX-raytermsdivergingforlarge Z fromeachotherasthecubeoftheatomic numberwereindeedwellestablishedbytheworkofGustavHertzinearly1920,and weredubbed“regulardoublets”bySommerfeld.Then,therewerethe“extra”terms, whichmaintainedamoreorlessconstant(i.e., Z-independent)difference(ratherthan increasingasthecubeofatomicnumber)inMoseleyordinatefromoneofSommerfeld’s “regular”terms!Infact,thissituationistheoneweshouldhaveanticipatedfromthe factthatelectronorbitsofdifferingangularmomentumwouldpenetratetheinnermost regionoftheatom(andbeexposedtothefullnuclearcharge)todifferingdegrees, andhence,wouldhavedifferentscreeningconstants.Twosuchtermswouldthenhave Moseleytermsexhibitingaconstantdifferenceinthe leading (i.e.,Balmer)energysquare root: (Z
(hence,independentof Z ).Thiswouldbe muchlargerthan,andshouldthereforealwaysdominate,theSommerfeldfine-structure shifts(withtheirextrafactorofthesquareof α).Theproblemwasthatonefound both the“regular”doublets,withasplittingthatlookedjustlikerelativisticfinestructure,and “irregular”doubletswithaconstantMoseleysplitting—whichwasperfectlyreasonable onthebasisoftheexpecteddifferenceinnuclearchargescreeningfororbitsofdifferent shape(seeFigure9.2),butseemedtolacktheexpectedrelativisticcorrectionsfororbits differinginangularmomentum.
Asmentionedearlier,animportantreasonfortheincreasinginterestinX-raystudies atthispointwasthehope(alreadyexpressedbySommerfeldinthefirsteditionof AtombauundSpektrallinien;cf.Volume1,p.277)thatthenuclearCoulombattractiononan innerelectronwouldsodominatetherelativelysmallinter-electronrepulsiveinteractions(whichcouldbeignoredfortheouterelectrons)thatthemotionoftheseelectrons wouldbeveryclosetothatexpectedonthebasisoftheBohr–Sommerfeldformalism.In particular,thepeculiarcomplexspectraeffectsinopticalspectra(i.e.,intheenergiesof theouterelectronorbits)presumedtoarisefromaninteractionofthevalenceelectron orbitwithamagneticfieldproducedbythe“core”(i.e.,thenucleusplusinnerelectrons) shouldnolongerberelevant,astheinnermostelectrons were thecore,andthescreening effectsexertedoneachothercouldapparentlybeaccountedforveryaccuratelysimply byasmallshiftintheeffectivenuclearcharge, Z → Zeff,asindicatedabove.
Nevertheless,thetripletof L (N = 2)terms,quintupletof M (N = 3)terms,etc., clearlyindicatedthatanadditionaldegreeoffreedomwasinplayfortheseinnerelectrons aswell,givingriseto“extra”stationary-stateenergylevels.Andthe Z-dependenceof theextrasplittings,aswehavejustseen,wasinexplicableintermsofsimplescreening plusrelativisticeffects.
8.3.2 Electronarrangementsandtheemergence oftheexclusionprinciple
Thesematterscametoaheadinaninfluentialpaperwritteninlate1922byBohrand Coster(1923)entitled“Röntgen[X-ray]spectraandtheperiodicsystemoftheelements.”CosterhadworkedonX-rayspectroscopyatLundUniversitywithManne
Atomicstructure àla Bohr,X-rayspectra,andthediscoveryoftheexclusionprinciple 11
Siegbahn’sgroupintheprecedingtwoyearsbeforecomingtovisittheNielsBohrInstituteinCopenhageninthesummerof1922.Infact,hisdissertation,completedunderthe directionofPaulEhrenfestattheUniversityofLeydenearlierthatyear,hadbeenpreciselyonthesubjectof“RöntgenspectraandtheatomictheoryofBohr”(Coster 1922). CosterhadathisfingertipsallthelatestresultsforX-raytermlevelsinawiderangeof elements,whichnowrepresentedagreatlyexpandedcornucopiaofphenomenological information,comparedtotherelativelysparseresultsofHertzjusttwoyearsearlier.Bohr andCosterundertookanextensivereviewofthedataandgaveadetaileddiscussionof thevariousscreeningeffectstobeexpectedinthemotionofaninnerelectron.This motion,whiledominatedbytheverystrongnuclearCoulombfield(wearethinkingof atomswithafairlylargeatomicnumberhere),wouldalsobeaffectedoccasionallybythe penetrationofanouterelectronwithaveryellipticalorbit(i.e.,lowangularmomentum) intotheinnerregion,andmorefrequentlybythepresenceoftheelectrostaticrepulsion oftheelectronsofthesameorsmallerprincipalquantumnumberastheelectronin question.BohrandCosterassertedthattheseeffectscouldbesubsumedintoscreening shifts(suchasthefactor σ shiftingthenuclearcharge Z discussedabove).Unfortunately,theappearanceofextra“anomalous”(intheBohr–Costerterminology)energy levelsleadingtotheapparentlyincompatiblesimultaneousappearanceof“screening” and“relativistic”doubletscouldnotbereconciledwiththefundamentaltenetofthe Aufbau program,whichassumedthattheadditiontoorsubtractionfromtheatomof asingleelectronwouldnotappreciablyaffecttheorbits(orenergies)oftheremaining energies.Instead,aswediscussinmoredetailinChapter9,onewasforcedtoassume thattheremovalofaninnerelectronresultedinanessential(wesentliche)changeof thebehavioroftheotherelectronsinthesameshell(or“group”,intheBohr–Coster language).Infact,theauthorsstate
Suchaconceptionisnecessitatedbythetheoryifitisassumedthatthecompletionofan electrongroupisessentiallydeterminedbytheinteractionofelectronswithinthevarious subgroups[oftheshell](BohrandCoster 1923,p.365).
Themysterious“interactionbetweensubshells”referredtoherecan(withhindsight!) beregardedasaforeshadowingoftheconstraintsthatwould,bytheendofthenextyear, berecognizedtoarisefromtheexclusionprinciple,wherethecompletionoftheelectron subshellswithinashell(ofgivenprincipalquantumnumber)isindeeddeterminedby thepreviousoccupancyofthesesubshells.Butintheabsenceofanyunderstandingof eithertheadditionalphysicalspindegreeoffreedomoftheelectronsorthecompletely non-classicalconstraintsimposedontheelectronstatesbyexclusion,BohrandCoster hadtoadmitthat“itisstillquiteunclearhowamoredetailedexecutionofthisidea couldprovideanexplanationfortheseparateappearanceofscreening-andrelativitydoublets”(p.365).
AfewmonthsafterthepublicationofBohrandCoster’spaper,amajorsteptoward theexclusionprincipleappearedinanarticleentitled“Thedistributionofelectrons amongatomiclevels,”submittedtothe PhilosophicalMagazine byEdmundStoner
(1924),agraduatestudentworkingwithRutherfordandFowlerattheCavendishLaboratoryinCambridge.IndiscussingStoner’scontribution,weshouldfirstnoteyet anothershiftinterminologyindescribingelectronicconfigurations.WhereBohrand Costerspeakofelectron“groups”and“sub-groups”,wefindinStonerthedesignation ofelectron“levels”(electronssharingagivenvalueoftheprincipalquantumnumber n), whicharesubdividedinto“sub-levels”characterizedbyagivenvalueoftheazimuthal (orbitalangularmomentum)quantumnumber k (=1,2,..., n).6
ForStonertheappearanceof“extra”termsinX-rayspectra,whichseemedverysimilartotheextratermswhichhadbeenknowninoptical“complex”spectrafordecades, wasmorethanacoincidence.ThenumberoftermsappearingintheX-raydata,just asintheopticalcase,suggestedthateachstationarystatewithanazimuthalnumber k = 2,3,...(thus,the p, d,...states)wasduplicated,withthetwostatesdistinguished bythenumerologicalartificeofanextra“inner”quantumnumber( j forStoner),which couldtakethetwovalues k 1and k.The s states,with k = 1,ontheotherhand, appearedsingly,withnoextra“twin.”Nowintheopticalcase,numerousstudiesofthe anomalousZeemaneffecthadshownthatinaweakmagneticfieldastationarystate withinnerquantumnumber j splitsintoexactly2j evenlyspacedenergylevels.Stoner suggestedthatthissplittingrevealedpreciselythenumberofdynamicallypossibledistinguishableelectronstates,notjustfortheouterlight-emittingvalenceelectronsrelevant totheopticalspectra,butalsofortheinnerelectronsoccupyingalreadyfilledlevels(or “groups”,or“shells”,...)inlargeratoms.7 Stonerrefusedtocommithimselftoany specificmodel-theoretic“explanation”fortheexistenceofthesestates,excepttoaccept thewidelyheldpropositionthatthesplitenergylevelsrevealedintheZeemaneffectcorrespondedtoaspace-quantizedvariationoftheorientationoftheorbits.Heconcludes thefifthchapterofhispaperwiththesummary
Inbrief,then,itissuggestedthat,correspondingroughlytothedefiniteindicationin theopticalcase,thenumberofpossiblestatesoftheatomisequalto 2j;so,fortheXraysub-levels, 2j givesthenumberofpossibleorbitsdifferinginorientationrelativeto theatomasawhole; andthatelectronscanenterasub-leveluntilalltheorbitsareoccupied (Stoner1924,p.726,ouremphasis).
Notethattheterm“sub-level”hereindicatesthespecificationofallthreequantumnumbers:principal(n),azimuthal(k),andinner( j ).Thisremarkisfollowedimmediately inthenextsectionofthepaperbytheassertionthatall2j electronstates(forgiven n and k)haveidenticalstatisticalweight,“forthereisthenoneelectronineachpossible equallyprobablestate”(p.726).AlthoughStonerdoesnotputitthisway,itisveryhard toseehowallofthisworksifonedoesnotalsograntthatmorethanoneelectronisin
6 Wearenowadopting,inplaceofSommerfeld’suseof n fortheazimuthalquantumnumber,thedenotation k,whichwasincreasinglyusedinthelastfewyearsoftheoldquantumtheory.Themodernnotation n for theprincipalquantumnumberalsobecomesmoreusualatthistime.Theextrainnerquantumnumberalso exhibitedaconfusingabundanceofdifferentnotations:forBohrandCosteritwas k2 (with k1 = k theusual azimuthalquantumnumber),whileStoner,followingLandé,uses j fortheinnerquantumnumber.
7 Itisimportanttorealizethattherelativelyverysmallsplittingsinducedbyapplicationofaweakmagnetic fieldwerenotatthisstageempiricallyaccessibleintheX-raydata.
Atomicstructure àla Bohr,X-rayspectra,andthediscoveryoftheexclusionprinciple 13 fact excluded fromoccupyingthesameorbit,atleastinthecaseofcompletedgroups. However,itmustbeadmittedthatthestatementofidenticalstatisticalweightforthe variouslevelsrevealedaftermagneticsplittingcannotbetakentoimplythateachsuch levelcanbeoccupiedatmostbyasingleelectron,onlythattheprobabilityofoccupancy onaverageisthesameforthelevels(intheweakfieldlimit).
AsimpleexampleofhowStoner’sconfigurationsdifferfromBohrandCoster’scan beseeninthesuggesteddistributionofelectronsintheinertgasargon(atomicnumber Z = 18).IntheBohrscheme(usingthe nk notation)thereweretwo11 (1s)states; four21 (2s)andfour22 (2p)states;andfour31 (3s)andfour32 (3p)states.Stoner’s assignmentsinsteadcorrespondexactlytothemoderndistributionofelectrons:two1s, two2s,six2p (dividedintoasub-shelloftwo j = 1andfour j = 2electrons),two3s, andsix3p electrons(againdividedintotwosub-shellsof j = 1,2).Inthefinalpartofhis paper,Stonergivessomeheuristicargumentstosupporthisnumericalassignmentsof electronorbits.Themostconvincingofthesecomefromconsiderationoftheintensity ofX-raylinesarisingfromtransitionsofelectronsoutofdifferentsub-levels,asinthe comparisonof L2 → K and L3 → K transitions,andfromtherelativeabsorptionof X-raysbyelectronsinvarioussub-levels,asintherelativeabsorptionof L1, L2,and L3 electrons.
Stoner’spaperwasreadwithgreatenthusiasmbyWolfgangPauli,whofullyapproved ofthestrategyoftryingtocombineinformationavailablefromX-rayspectroscopywith theinsightsobtainedfromthe(bynow)multi-decadestrugglewiththemysteriesofthe anomalousZeemaneffect.Theresultsofhisstudyoftheproblemwerepublishedina paperentitled“Ontheconnectionbetweentheclosingofelectrongroupsintheatom withthecomplexstructureofspectra,”submittedonJanuary16,1925(Pauli 1925b).
Afterabriefreviewofthedifficultiesencounteredbytheoldquantumtheoryin arrivingatasatisfying—thatis,dynamicallyconsistentmodel-theoretic—accountofthe anomalousZeemaneffectforweakmagneticfields,Pauliturnstothemostbasicproblem facedbythequantumtheoryinexplainingtheregularitiesoftheperiodictable:namely, theappearanceoftheperiodlengths2,8,18,32,...(moreconcisely,thenumbers2n2 for n = 1,2,3,4,...),whichsuggestthatthegroupofelectronswithprincipalquantum number n isunabletoaccommodatetheadditionofanyfurtherelectronsoncethere are,asinthecaseoftheraregases,already2n2 electronspresent.Paulifullyaccepts Stoner’sinterpretationofthiscounting,reproducingbothBohr’sandStoner’sproposed electrondistributionsfortheraregasesfromheliumupto“radiumemanation”(i.e., radon)(Pauli1925b,Tables1and2,respectively).
IncommonwithStoner,Paulialsoproposesthatcriticalinsightsintothefillingof atomicelectrongroupscouldbeobtainedfromthesplittingsobservedintheoptical Zeemaneffect,butinPauli’scase,theimportantcluesaretobefoundinthespecialcase oflargemagneticfields(Paschen–Backregime;cf.Section7.2.3),wherethestructure ofthesplittingsimplifies,astheinteractionbetweenthemagneticmomentduetothe orbitalangularmomentofavalenceelectronwiththatoftheputative“atomiccore” becomesnegligible,andthemagneticenergyshiftstakeontheformofasumoftwo terms,oneproportionaltothecomponentofthevalenceelectronangularmomentum inthedirection(say, z)ofthemagneticfield,andtheothertothe z-componentofthe