Mathematical Rigour and Informal Proof 1st Edition Fenner Stanley Tanswell Visit to download the full and correct content document: https://ebookmass.com/product/mathematical-rigour-and-informal-proof-1st-edition-fe nner-stanley-tanswell/
More products digital (pdf, epub, mobi) instant download maybe you interests ...
Syllogistic Logic and Mathematical Proof Prof Paolo. Mugnai Mancosu (Prof Massimo.)
https://ebookmass.com/product/syllogistic-logic-and-mathematicalproof-prof-paolo-mugnai-mancosu-prof-massimo/
Corruption and Norms: Why Informal Rules Matter 1st Edition Ina Kubbe
https://ebookmass.com/product/corruption-and-norms-why-informalrules-matter-1st-edition-ina-kubbe/
Big Chance Cowboy Teri Anne Stanley [Stanley
https://ebookmass.com/product/big-chance-cowboy-teri-annestanley-stanley/
Final Proof Rodrigues Ottolengui
https://ebookmass.com/product/final-proof-rodrigues-ottolengui-2/
https://ebookmass.com/product/final-proof-rodrigues-ottolengui/
Socioeconomic Protests in MENA and Latin America: Egypt and Tunisia in Interregional Comparison 1st ed. Edition Irene Weipert-Fenner
https://ebookmass.com/product/socioeconomic-protests-in-mena-andlatin-america-egypt-and-tunisia-in-interregional-comparison-1sted-edition-irene-weipert-fenner/
The Burden of Proof upon Metaphysical Methods 1st Edition Conny Rhode
https://ebookmass.com/product/the-burden-of-proof-uponmetaphysical-methods-1st-edition-conny-rhode/
An Introduction to Proof Theory: Normalization, CutElimination, and Consistency Proofs 1st Edition Paolo Mancosu
https://ebookmass.com/product/an-introduction-to-proof-theorynormalization-cut-elimination-and-consistency-proofs-1st-editionpaolo-mancosu/
Artificial Intelligence and Deep Learning in Pathology 1st Edition Stanley Cohen Md (Editor)
https://ebookmass.com/product/artificial-intelligence-and-deeplearning-in-pathology-1st-edition-stanley-cohen-md-editor/
The Philosophy of Mathematics Mathematical Rigour and Informal Proof Fenner Stanley Tanswell
ElementsinthePhilosophyofMathematics Ediitedby PenelopeRush
UniversityofTasmania
StewartShapiro
TheOhioStateUniversity
MATHEMATICALRIGOUR ANDINFORMALPROOF FennerStanleyTanswell TechnischeUniversitätBerlin
ShaftesburyRoad,CambridgeCB28EA,UnitedKingdom OneLibertyPlaza,20thFloor,NewYork,NY10006,USA 477WilliamstownRoad,PortMelbourne,VIC3207,Australia
314–321,3rdFloor,Plot3,SplendorForum,JasolaDistrictCentre, NewDelhi – 110025,India
103PenangRoad,#05–06/07,VisioncrestCommercial,Singapore238467
CambridgeUniversityPressispartofCambridgeUniversityPress&Assessment, adepartmentoftheUniversityofCambridge.
WesharetheUniversity’smissiontocontributetosocietythroughthepursuitof education,learningandresearchatthehighestinternationallevelsofexcellence.
www.cambridge.org Informationonthistitle: www.cambridge.org/9781009494380
DOI: 10.1017/9781009325110
©FennerStanleyTanswell2024
Thispublicationisincopyright.Subjecttostatutoryexceptionandtotheprovisions ofrelevantcollectivelicensingagreements,noreproductionofanypartmaytake placewithoutthewrittenpermissionofCambridgeUniversityPress&Assessment. Whencitingthiswork,pleaseincludeareferencetotheDOI 10.1017/9781009325110
Firstpublished2024
AcataloguerecordforthispublicationisavailablefromtheBritishLibrary.
ISBN978-1-009-49438-0Hardback
ISBN978-1-009-32510-3Paperback
ISSN2399-2883(online)
ISSN2514-3808(print)
CambridgeUniversityPress&Assessmenthasnoresponsibilityforthepersistence oraccuracyofURLsforexternalorthird-partyinternetwebsitesreferredtointhis publicationanddoesnotguaranteethatanycontentonsuchwebsitesis,orwill remain,accurateorappropriate.
ElementsinthePhilosophyofMathematics
DOI:10.1017/9781009325110 Firstpublishedonline:March2024
FennerStanleyTanswell TechnischeUniversitätBerlin
Authorforcorrespondence: FennerStanleyTanswell, fenner.tanswell@gmail.com
Abstract: ThisElementlooksatthecontemporarydebateonthenature ofmathematicalrigourandinformalproofsasfoundinmathematical practice.Thecentralargumentisforrigourpluralism:thatmultiple differentmodelsofinformalproofaregoodataccountingfordifferent featuresandfunctionsoftheconceptofrigour.Toillustratethis pluralism,theElementsurveyssomeofthemainoptionsinthe literature:the “standardview” thatrigourisjustformal,logicalrigour; themodelsofproofsasargumentsanddialogues;therecipemodelof proofsasguidingactionsandactivities;andtheideaofmathematical rigourasanintellectualvirtue.Thestrengthsandweaknessesofeach areassessed,therebyprovidinganaccessibleandempiricallyinformed introductiontothekeyissuesandideasfoundinthecurrentliterature.
Keywords: mathematicalrigour,informalproof,mathematicalpractice, formalisation,epistemologyofmathematics
©FennerStanleyTanswell2024
ISBNs:9781009494380(HB),9781009325103(PB),9781009325110(OC) ISSNs:2399-2883(online),2514-3808(print)
1Prologue:ThreeProofs? Beforewebeginwiththephilosophy,anElementaboutmathematicsshould startwithsomemathematics.
Proof1:SumsofOddIntegers Hereisaclassicproofby DeMorgan(1838),updatedintomodernnotation:1
Theorem: Thesumofthe first n oddpositiveintegers,startingfromone,is n2 :
Proof: LetPnðÞ bethestatement “Xn k ¼1 2k 1 ðÞ¼ n 2 ”
Since X1 k ¼1 2k 1 ðÞ¼1 ¼ 12 weseeP 1 ðÞ istrue.
AssumePnðÞ istrue.Then
1
1
HencePn þ 1 ðÞ istrue.
SinceP 1 ðÞ istrueandPn þ 1 ðÞ followsfromPnðÞ weconcludethatPnðÞ istrue forallnbytheprincipleofmathematicalinduction.
Thisproofisatypicalrigorousproof,thesortstudentsaregivenwhenthey first learnaboutmathematicalinduction.Intheirstudyofmathematicalrigour, SangwinandKinnear(2021) foundthisprooftoberatedbyfarthemost rigorouspresentationofthisresultamongstaselectionofdifferentproof methodsandstyles.Therearenoerrorsandnogaps.Thisproofaccordingly canbetakenasaparadigmexampleofinformalrigour.
Proof2:Malfatti’sMarbleProblem Incontrasttothepreviouscorrectandrigorousproof,letuslookatthehistoryof a failed proof:2 thatofMalfatti’smarbleproblem.3 Theproblemisabouthowtocut threecircular “pillars” outofatrianglewhileminimisingtheamountofmarble wasted.Mathematically:withinagiventriangle,to findthreenon-overlapping
1 TheexactversionI’musinghereisby Sangwin(2023)
2 Aterminologicalnoteontheword “proof”:onewayofusing “proof” isasasuccessterm, meaningthat “failedproof” isa nonsequitur,orhastobereadas “afailed attempt ataproof” . AcentralthemeofthisElementisthephilosophicalcomplexityofseparatingcorrect,valid,or rigorousproofsfromincorrect,invalid,orunrigorousones.Therefore,Iwilluse “proof” inthe weakersenseofsomethinglikea “purportedproof” ora “possiblecandidateforbeingaproof” , meaningsomethingcreatedtobeaproof,presentedaccordingtothenormsofproofpresentation, withoutobviousreasonsforjudgingtheminvalid,andsoon.
3 Thishistoricaldescriptionprimarilydrawson Andreattaetal.(2011) and Lombardi(2022a).
circleswiththegreatesttotalarea.ThisproblemwasnamedafterGianfrancesco Malfatti(1803),thoughithadalsoappearedearlierinJapanintheworkof ChokuyenNaonobuAjimaandwasstudiedforthespecialcaseofisosceles trianglesbyJacobBernoulli(see Andreattaetal.2011).
Inhisarticle, Malfatti(1803) assumesthatthesolutiontothemarbleproblem isgivenby findingwhatarecalledthe “Malfatticircles”:theuniquetrioof circlesinsideatrianglethataretangenttooneanotherandtouchtwosidesofthe triangleeach(Figure1).4
ForMalfatti,theproblemwasto findawaytoconstructthesecirclesfor agiventriangle.Thatis,hebelievedtheareamaximisationproblemwassolved viathecircleconstructionproblem.Malfattihimselfworkedonthelatter problemtogiveaninitialsolution,andanelegantstraightedge-and-compass solutionwasgivenby Steiner(1826).Foracentury,Malfatti’smarbleproblem wasconsideredsettled.
However,itwasshownby LobandRichmond(1930)thattheMalfatticircles donotalwaysmaximisethearea,becauseinanequilateraltrianglethe “greedy” arrangementhasaslightlylargerarea(see Figure2).Thegreedyarrangement involvesplacingthelargestpossiblecircle first,thenthelargestpossibleonein theremainingspace,thendoingsooncemore.
Figure2 Malfatticirclesandthe “greedy” arrangementforanequilateral triangle.
4 Imagespublicdomain,viaWikimediaCommons,createdbyuserPersonline.
Figure1 Malfatticircles.
Likewise, Eves(1965,pp.245–7)noticedthatforalongisoscelestriangleit isbettertostackthreecircles,asin Figure3,thantouseMalfatti’scircles.
Amazingly, ZalgallerandLos’ (1994) eventuallyshowedthattheMalfatti circles never havethemaximumarea,andMalfattiwassimplymistaken. ZalgallerandLos’ (1994) werethemselvesalsoattemptingtomakeworkby Los’ fouryearsearlierrigorous,workwhichtheysay “containedsignificant gaps” (p.3163).Eventhen,theirproofoftheoptimalityofthegreedyalgorithm isincomplete,asarguedby Lombardi(2022a).Theirsolutionisbasedon enumeratingthepossiblearrangementsofcirclesandthenexcludingallbut thegreedyarrangementfrombeingmaximal,butthelemmathatenumeratesthe possiblearrangementsisunproven.Furthermore,thetrickiestcasetoexcludeis tackledbynumericalcheckingonsamplepointsgiveninatable,ratherthanby amathematicalproof.Thenumbersbeingcheckedarealsoobtainedbysubtractingonedecreasingfunctionfromanother,butthenumericalchecking missesthefactthatthetotalwillnotnecessarilytherebybedecreasingtoo.5
Onlyrecentlyhas Lombardi(2022a) closedthesegapsandproducedafully rigorousproofofthemaximalsolution,whichisthegreedyarrangementandnotthe Malfatticircles.Thishistoryrevealsfourdifferentfailuresofrigour:(1)themistaken assumptionsmuggledinthatoneproblemhasthesamesolutiontoanother;(2) makinguseofunprovenlemmas;(3)usingnumericalmethodsthatarenotsufficient toestablishtheresult;and(4)simplemathematicalerrors,likethinkingadecreasing sequencesubtractedfromanotherisalwaysdecreasing.Therearethusmultiple seductivewaysthatmathematicscangowrong,evenforsuchaseeminglysimple problem.Nonetheless,thisstoryalsorevealssomeofthecomplexityofdeveloping rigorousmathematics,ultimatelyculminatinginasuccessfulproof.
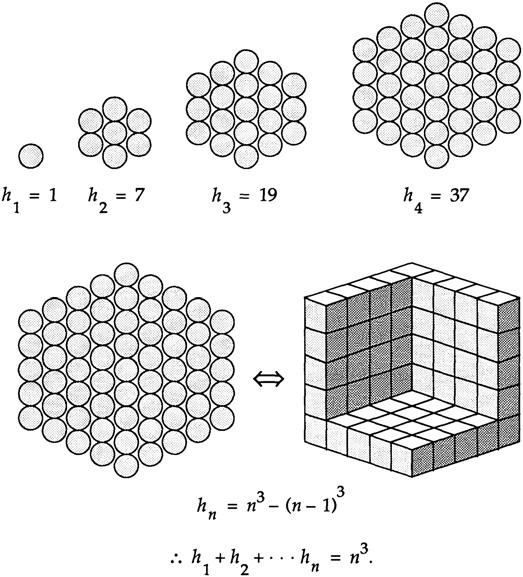
Proof3:HexNumbers Finally,letuslookatatrickycase.Thefollowingisoneofmyfavouriteproofs fromthe firstvolumeofthe ProofsWithoutWords series(Nelsen1993, 2000, 2015)andiscalled “SumsofHexNumbersareCubes” (Nelsen1993,p.109), withthereadershownthe firstfourhexnumbersatthetoptolearnwhatthey are,followedbytheproof(Figure4).
5 Lombardi(2022b) detailsvariousothergapsanderrors.
Figure3 Optimal “greedy” arrangementforalongisoscelestriangle.
Figure4 Nelsen’sproofthatsumsofhexnumbersarecubes. ProofWithout Words ©1993heldbytheAmericanMathematicalSociety.
Onemightcallthisa “proofbyGestaltshift”,wherethemainideainvolves ashifttoseeinghexnumbersinadifferentway,astheouterlayerofacube.While thisisinmyviewaproof – ifoneunderstandsitproperly,onecanseewhythe resultmustfollow – itwouldbehardtoarguethatthisisa rigorous proof.Firstof all,itneverevengivesanalgebraicdefinitionofwhathexnumbersare.Second,it implicitlycontainsaninductionproofbutdoesnotmakethekeyingredientsofan inductionexplicit.Third,theGestaltshiftismerelyillustratedfortheparticular caseofthe fifthhexnumber,sounderstandingtheinductivesteprequiresusto fill inthereasoningofwhyitholdsgenerally.Sufficientunderstandingandmathematicalinsightareenoughto fillinthesegaps,butthereisnodenyingthattheyare gaps,andthattheproofisgappyenoughnottoberigorousbyitself.
Thequestionsweface,then,are:whatisthedifferencebetweenthethree “proofs” wehaveseen?Andwhatismathematicalrigouranyway?
2Introduction InthisElementIwillsetouttherangeofanswersthatareavailablein contemporaryphilosophyofmathematicstothequestionsaboutrigourand informalproofs.Recentdecadeshaveseena practicalturn thatshiftsaway
fromtryingtoanswerphilosophicalquestionsaboutmathematicsintheabstract aloneandtowardsphilosophicalpositionsthatareinformedbythepracticesof mathematicians. 6 Theideaisthatmathematics,whilebeingabstractandlogical initssubjectmatter,isalsoadisciplineshapedbyhumaninterestsandvalues likeanyother,andthatanswerstoquestionsaboutmathematicalrigourarenot independentoftheactivitiesinvolvedindoingmathematics.
Theconceptofrigourcanapplytomanykindsofmathematicalpractices.The onethathasinterestedphilosophersthemost,andwhichIshallfocuson throughout,istheideaof rigorousproof.Arough firstpassisthatarigorous proofisadetailed,logicalproofthatisfreeoferrorsandgaps.Anotherimportant applicationis rigorousdefinition,adefinitionthatispreciseenoughtosettleforall caseswhetheritappliesornot.7 Thequestfor rigorousfoundations involves findingexplicitaxiomsandinferencerulestoencodeacceptableassumptionsand reasoningformathematics.8 Furthermore, rigorousareasofmathematics are thosewhereresultsandtechniquesarereliable,well-defined,andreproducible, withclear,agreed-uponinferentialpracticesandfoundations.9 Itisalsocommon tosee mathematicalrigourinphysics contrastingscrupulousandcarefulreasoningwithmoreconjectural,empirical,orexperimentalapproaches.10
Exploringthenotionofrigourinallofthesesenseswouldbetoomuchfor suchashortwork,somytaskwillbetosetoutthecontemporarydebateson mathematicalrigourandinformalproofs.Broadlyspeaking,informalproofsare thoseproofsaswritteninactualmathematicalpractice,suchasinjournals, textbooks,lectures,seminars,classrooms,onlineforums,emails,scribbledon napkins,andsoon.Thecentralquestionisthis:isthereasingleconceptof rigouracrossthesemanymathematicalcontexts,andwhatisit?
2.1ThePurposesofRigour Ithinkitisimportanttoconsiderthepurposeofhavingaconceptofrigourand whatitisbeingusedforinthemanycontextsinformalproofsmightshowup.In fact,theconceptofmathematicalrigourcanbeputtomanydifferentuses.This matchestheideathatproofsthemselvesdonothaveasinglepurpose.Catarina DutilhNovaes(2021,§11.4)surveyssomeofthemainusesofproofs,listing
6 Overviewsofthestateofthe fieldof ‘philosophyofmathematicalpractice(s)’ havebeengiven by VanBendegem(2014), Löwe(2016), Carter(2019),and HamamiandMorris(2020)
7 Formoreondefinitionsinmathematics,see Tappenden(2008), Cellucci(2018), Coumans (2021),and CoumansandConsoli(2023)
8 See,forexample, Maddy’s(2017, 2019)carefulworkonthemanypossiblepurposesofsettheoreticfoundations.
9 Foracasestudyofthisgoingawry,see DeToffoliandFontanari(2022, 2023)ontheItalian schoolofalgebraicgeometry.
10 SeethediscussionoftheJaffe–Quinndebatein Section5.3.
verification,certification,persuasion,explanation,innovation,andsystematisation.Likewise,wecanlistvariousfunctionsthattheconceptofrigourisoften saidtobeusedfor:
(1) Soundness. Arigorousproofprotectsusfromerrorsandcounterexamples. Historically,rigourwasadrivingforceinthemodernisationofmathematics.Concernsaboutinfiniteandinfinitesimalquantities,especiallyin analysis,reachedapeakinthenineteenthcenturywiththeappearanceof mathematical ‘monsters’ suchastheWeierstrassfunction,necessitatingthe “rigorisationofanalysis” and ε-δ definitions.
(2) Verification. Arigorousproofverifiesthatatheoremistrue.
(3) Certainty. Rigorousproofsarethosethatcanbeusedtoobtainmathematicalknowledge.Theycanprovideahighlevelofapriorijustification,and absolutecertaintyinthetruthofthetheorem.
(4) BodyofKnowledge.Rigorousproofsformabodyofknowledgethatother mathematicianscanaccessandbuildon.
(5) Social. “Rigorous” isusedasalabeltoidentifywhichpiecesofmathematicsbyothermathematiciansaregoodandworthspendingtimeon.
(6) Demarcation. Theuseofrigorousproofsistakentobeoneofthemain criteriathatseparatesmathematicsfromotherdisciplines.11
(7) Conviction.Arigorousproofshouldconvinceareasonablebuttough audienceofthetruthofthetheorem.
(8) PeerReview. Beingrigorousisoneofthestandardsforpublishable mathematics.Inassessingtheworkofothermathematiciansinpeerreview, primarilyforresearchjournals,rigourisoneofthemainpropertiesthe proofsneedtohave.
Thislistisfarfromexhaustivebutgivessomeofthemainpotentialpurposesof rigour.12 Obviously,someofthesepurposesalsolinktopurposesof proof,such astheideathatonlyarigorousproofcantrulyverifyatheorem.Ontheother hand,somepurposesofproofsmightbebetterachievedinalessrigorous fashion,forexample,aproofmightbemoreexplanatorybyproviding acompellingintuitiveideathanbyrigorouslygoingthroughallofthedetails. Thesepurposesaredebatabletovaryingdegrees,sotheycanguideourdiscussioninthe followingsection butcannotbeimmutableconstraintsonaccountsof rigour.Aswewillseeshortly,thepluralityofpurposesforrigourwillconnectto myproposalthatweneedtobe rigourpluralists.
11 Thisgoalisnotablydefendedby Auslander(2009).
12 Italsoremainstobeseenhowsuccessfulmathematicsisatmeetingthesefunctions.For example,theideathatmathematicalproofscanproducecertaintyisapopularonebuthas beenwidelychallenged(e.g. Kitcher1984; Ernest1998; DeToffoli2021a).
Onetrickyfeatureofmathematicalrigouristhatitisusedbothdescriptivelyand normatively.The descriptive useconcernswhenandwhycertainproofsare called “rigorous” inpractice.The normative useconcernsrigourasanidealfor mathematics,thatis,thatmathematicsoughttobedoneinawaytomeetthe standardsofrigour.Thesedifferentusesraisedifferentquestionsaboutrigour. Thedescriptiveuseofrigourposesanempiricalquestion:whichkindsof mathematicsareactuallydescribedas “rigorous”?Thenormativeuseofrigour promptstwofurtherquestions.The firstquestionisthe thoroughlynormative one:whatstandardsoridealsshouldmathematicsbeheldto?Thesecond questionisa hybriddescriptive–normative one:whatstandardsdomathematicians say or believe theyapply?Itispossiblefortheanswerstoallthree questionstocomeapartorcoincideinanycombination.Lifewouldbesimple ifthedescriptiveusefollowedthenormative;thattheproofsdescribedas rigorouswerejusttheonesthatmeettheidealstandards,whicharealsojust whatmathematicianssaytheyare.Alternatively,itcouldbethattheanswersall comeapart;thatthestandardsbeingappliedarenottheonesthatmathematicianssaytheyapply,whicharealsonotthestandardsthatoughttobeused.
Ofthethreequestions,onlythenormativeonelooksimmediatelyphilosophicaland,eventhen,mathematiciansmightprefertokeepitforthemselvesto sortout.So,whatroledoesphilosophyplayinuntanglingthesevarious purposesandquestionsaboutrigour?ThewayIseethephilosophers’ job hereisingivingaccountsofmathematicalrigourthatenlightenandinform. Theconceptofrigourismultifaceted,unwieldy,andmessy,soanaccountof rigourshouldtrytounifyandexplainitsmainfeatures.Thelistofpurposesin the previoussection isanexampleofthismessiness:someofthemarenormativeideals,someofthemaredescriptive,andotherscanbereadeitherway.
Intheexistingliterature,theimplicitapproachtogivinganaccountofrigour seemstobeto findsomethinglikethe “trueessence” ofmathematicalrigour. Thiswouldseemtosupposethatoneconceptisfulfillingall – oratleastthe mostimportant – functionsofrigour.Aproponentofthisapproachwouldalso likelysaythattheyaremostinterestedinthenormativequestionofwhatthe idealstandardsofmathematicsare.Forthemitwouldbebetter,butnotessential,ifthisweretotrackmathematicians’ practicesandwhattheysaythose standardsare.However,theymuststillbecommittedtoatleastapproximating thedescriptivefeaturesofmathematicalpracticebecauseatheorypredicting thatallproofsdescribedasrigorousarenotactuallyrigorouswouldnotbeof muchuseinsatisfyingthefunctionalrolesoftheconcept.Thisleadstotwo connectedchallengesforanaccountofrigourtomeet:
(1) Functionaladequacy:tosatisfysomeorallofthemainfunctionsofthe conceptofrigour.
(2) Descriptiveadequacy:tocoherewithorapproximatemathematicalpractices concerningrigour.
OnepurposeofthisElementistosurveytheexistingpositionsandtoarguethat noneofthemprovidesanaccountofrigourthatmeetstheseconditionswell enoughtobethe “trueessence” ofrigour.
2.3RigourPluralism ThroughoutthisElement,IintendtoadoptanovelpositionIshallcall rigour pluralism.Insteadofsearchingfora “trueessence” ofrigourandauniquecorrect account,Iwilltakethedifferentproposalsintheliteratureasdifferent modelsof rigour,inthesenseofscientificmodelling,andarguethatalloftheseconvey importantinsights.Onthisview,theexistingaccountsofmathematicalrigourare seenasdifferenttheoreticalmodelsthateachattempttocapturesomecombinationoffunctionsanddescriptiveandnormativeaspectsofrigour.Wewill investigatewhichfeaturesofmathematicalpracticeareincorporatedintoeach model,andwhichareabstractedoridealisedaway.Unlikethe “trueessence” approach,however,thesemodelswillnotbeassessedasultimatelyrightor wrong.Ibelievethatnosuchmodelissufficientforallthepurposesofthe conceptofrigour,norareanyofthemodelswithoutmerit.Therigourpluralist approachwillbetoassessthestrengthsandweaknessesofdifferentmodels, evaluatingwhichaspectsofrigourtheycapturewell,andwhichtheydonot.
Aproponentofthe “ trueessence ” approachmighttrytoobjectthatthe modellingapproachislessplausiblebecauseitsrigourisultimatelyabout logic,andthat arigorousproofisalogicalproof.WhileIagreewiththis slogan,Idonotbelievetheappealtologicisde finitivehere.Morebasicthan logicality,rigorousproofisaboutonewayofdoing good mathematics.Onthe modellingapproach,wecansaythatformallogiccanprovide models ofgood mathematicsandthemathematicalreasoningfoundinproofs.Themovetosee thisasalsoinvolvingscientifi cmodelling fi tsdirectlyintothe “ logicas modelling” viewputforwardby Cook(2000 , 2010 ), Shapiro(2014),and Kurji(2021) 13 Furthermore,itcanbeseenasexemplifyingtheapproachof conceptualmodellingproposedby LöweandMüller(2011).
13 Thephilosophyoflogichasobviousimporttoquestionsaboutthephilosophyofmathematics here,buthasbeensurprisinglyunderutilisedindebatesaboutrigour.Forexample,thewider debatesonlogicalpluralism(see Beall&Restall2005; Cook2010; Shapiro2014; Russell2019) andlogicalnihilism(see Franks2015; Cotnoir2018; Russell2018; Kurji2021)alsoshowusthat logicality isnotasettledmatter.
Wewillreturntotheideaofrigourpluralismacrossthecomingsectionsto weighhowthevariousmodelsofrigourandproofsucceedandfailatcapturingthe featuresweareinterestedin.Furthermore,theselectionofmodelsisalsomeantto illustratethepluralistpositionbyshowingthateachofthemmodelssomeaspects ofrigourandinformalproofswell,butthatnoaccountmodelsallofthefeatures well.AfulldefenceofpluralismwouldtakeupmoreroomthanIhavehere,but Ihopethatconsideringthemeritsofaselectionofmodelswillillustratethevalue ofrigourpluralismasaviableandpromisingpositionforthesedebates.
2.4TheHistoryofRigour MyfocusinthisElementwillbeonsettingoutthecontemporaryresearchon mathematicalrigourandinformalproofs,soIwillnotbediggingintothehistory ofthedevelopmentofmathematicalrigour.Suchashorttreatmentwouldnotdoit justice.Nonetheless,thehistoryofmathematicsisveryimportantand,likeany otherconcept,Iholdthattheconceptofrigourcannotbefullyunderstoodwithout referencetothehistoricalandsocialcontextfromwhichitemerged.For aphilosophicalworkthatengagesmoreexplicitlywiththehistoricaldevelopment ofrigour,see Burgess(2015,chs.1&2).Foramorerecentpartofthepictureof proofandrigour,see Mackenzie(2004).Alotofexcellentresearchinthehistory ofmathematicsisdirectlyengagedwithquestionsaboutthehistoryofmathematicalrigourandhowconceptionsofithavechangedovertime(e.g., Barany 2011, 2013; Haffner2021; Cantù&Luciano2021; DeToffoli&Fontanari2022).
2.5Outline Inthefollowingsections,Iwilloutlineandevaluateaselectionofmodelsof rigourandinformalproofs,groupedintofourbroadfamilies.The first,in Section3,isthemostprominentandorthodox,sometimescalledthe “standard view”:that rigourisformality.In Section4,wewilllookatmodelsofinformal proofsandrigourthatanalyseproofsasargumentsanddialogues. Section5 will focusonthe recipemodelofproofs,whereproofsareakintorecipesfor mathematicalactivities.Finally,in Section6,Iwillconsidertheideaof rigour asanintellectualvirtue ofthemathematician.
WiththiswideselectionofmodelsofrigourandinformalproofIhopeto illustratetheideaofrigourpluralism.Thesemodelsareatdifferentstagesof development,withsomelong-establishedandothersmorerecent,butIbelieveall ofthemareviablemodelsofmathematicalrigour.Myclaimisthattryingtosettle whichamongsttheseistheultimatecorrectaccountofrigourandproofis fruitless.Instead,eachoffersadifferentwayofmodellingimportantfeaturesof themessyconceptofrigourthattanglestogethernormsoflogicandmathematical
reasoning,realpracticesofmathematiciansandtheircommunities,andacomplex historyofdevelopment.TheprojectofthisElementistoconsiderthestrengths andweaknessofeachfamilyofmodels,andtorevealhowbetweenthemtheylet usseethediversefeaturesofmathematicalrigour.
3TheStandardView:RigourasFormality 3.1Introduction Our firstmodelofmathematicalrigourisoftenreferredtoasthe ‘standardview’ becauseitisseenasthedefaultpositioninmoderndiscussionsofmathematical rigour.14 Thestandardviewis,roughly,thatrigourinmathematicsshould simplyandstraightforwardlybeunderstoodas formal rigour.Thesenseof formalityinquestionisthatofformallogic,sothatarigorousproofmustbe alogicalderivationinsomesystemofformallogic.15 Thestandardview emergedalongsidemodernlogic,pioneeredbyprominentmathematicallogicianslike Frege(1884), Hilbert(1899),and WhiteheadandRussell(1910),as partofaquestto findthelogicalfoundationsofmathematics(see Ferreirós 2008).Thesefoundationsrequiredawaytoguaranteethateverystepinaproof isinaccordancewiththeexactrulesoflogic.Beforelong,thishadsolidified intothedominantviewamongmathematiciansandphilosophers,exemplified mostprominentlybytheBourbakigroup(see Hamami2019; Barany2020).In turn,thislegacyhasbeeninheritedbythecontemporaryproponentsofformal, computer-checkablemathematics,suchas Hales(2008), Gonthier(2008), Wiedijk(2008),and Avigad(2021).
Theobviousmotivationforthisviewisthatformalderivationsareby definitiongap-freeandhavepreciseandexplicitlystatedstandardsofcorrectness.So,itissafetosaythatallformalderivationsarerigorous.Itisextremely temptingtoclaimthatformalityisalsothe only waytoberigorous.Ifaproof hasgapsorreliesoninferentialmovesthatarenotexplicitlystated,thenthiscan introduceassumptionsthatarenotjustifiedorreasoningthatcouldleadto flawedconclusions.AnexampleofthiswasseeninthestoryofMalfatti’s marbleprobleminthePrologue,wherebothincorrectassumptionsandunrigorousmethodsledtounrigorousproofs. Detlefsen(2009)summarisedthe motivationforthestandardviewsuccinctly:
14 In Tanswell(2015) and Azzouni(2020)thisclassofviewshasalsobeencalled “derivationist” Aswillbecomeclear,Iactuallythinkthatcallingitthe “standardview” inthesingularis misleadingbecauseitisreallyafamilyofoverlappingviewswithimportantdifferences, somethingalsopointedoutby BurgessandDeToffoli(2022)
15 Infact,whatcountsasformalityisnotsostraightforward. DutilhNovaes(2011) identifiesmany differentwaysthatlogiccanbesaidtobeformal.
Thereasoningbehindthisviewisstraightforward:(i)properproofsare proofsthateitherareorcanreadilybemaderigorous;(ii)proofsthatareor canreadilybemaderigorousareformalizable;therefore(iii)allproperproofs areformalizable(Detlefsen2009,p.17).
Inthissection,wewillstartin Section3.2 withasimplisticversionofthisview, whichinvolvesaprocessof fillinginthegapsofinformalproofs,notingthatthis doesnotstanduptoscrutiny.Next,in Section3.3,Iwilloutlinevariousdesiderata foramoredefensibleversionoftheview.Withtheseinhand, Sections3.4, 3.5, and 3.6 willlookatarangeofmoresophisticatedversionsofthestandardview, specificallyonesinvolvingroutinetranslations, inprinciple formalisability,and derivation-indication. Section3.7 willthengivealonglistofcriticismsofthe standardview.Finally,in Section3.8 Iwillmakethecasethatthestandardviewis notacorrectaccountofmathematicalrigourbyitself,butthatitisapowerful familyof models ofinformalproofandmathematicalrigour.
3.2FillingintheGaps Whiletheideathatrigourreducestoformalitycanbeusefulasanormative ideal,thestandardviewneedstooffermoreinordertosuccessfullydescribe howpeoplejudgerigour.Mostproofsproducedbymathematiciansarenot formal,anditwouldbeanoddresultforsomethingcalledthe “standardview” topredictthatalmostnomathematicsiseverrigorous.Thestandardviewmust thereforeincludeanothercomponentthatexplainshowinformalproofscan nonethelessberigorousinsomesense.Thiscanbeapproachedinmanydifferentways,butthecommonthreadbetweenthemistheideathatinformalproofs canberigorousbycorrespondingtoformalproofs,eveniftheythemselves aren’tformalproofs.Inthisway,formalitycanstillbethegoldstandardfor rigour,butinformalproofscanmeetthisstandardindirectly.
Whatthecorrespondenceshouldamounttoinordertoidentifyrigorous informalproofsvariesfordifferentproposals.Thesimplestversionofthis ideaisthatinformalproofs abbreviate theirformalcounterparts,meaningthat simple,straightforwardstepsareleftoutfrominformalproofs,butcouldbe restoredbyaprocessof fillinginthegaps.Especiallyforsimpleproofs,thisidea isveryappealingbecauseitexplainswhylinkinginformalproofstoformalones stillmaintainsrigour.Thereasonisthatthemainstepsareallstillpresent,and the “missingsteps” areactuallyjusttheeasylogicalmovesthataretooobvious toneedstating.Theinformalproofisrigorousdespitethegapsbecauseany mathematiciancouldeasilysupplythestepsthathavebeenleftout.
However,theabbreviationapproachglossesovermanyoftheimportant details.Forexample,thestepsthat are givenininformalproofsarealsotypically
12 PhilosophyofMathematics notinaformallanguage,sotheywouldalsoneedtobeseenasabbreviationsof formulas,whichleadstothequestionofhowexactlytheyshouldbetranslated. Informalproofsalsodon’t flagwhichformalsystemisbeingusedinthe first place,andtherearemany,manyoptions.Translatinginformalsentencesinto formalonesisnotasstraightforwardasthe “fillinginthegaps” ideawouldmake itsound,ascanbeattestedbyanyonewhohaseverattemptedit.Furthermore,the abbreviationapproachwouldalsobelessclearformoreadvancedmathematics, wherethemissingstepsmaybelessobvious.Therefore,therearefurther complexitiesthatthestandardviewneedstoaddress.
3.3AimsfortheStandardView Beforewegetdeeperintopossiblewaysof fillingoutthestandardview,let’s discusswhatitshouldbeaimingtoachieve.InsomeofmypreviousworkIhave givenvariousdesideratathatthestandardviewmightaimtomeet(Tanswell 2015,sect.2).Letusbrieflysurveythese.
Tobegin,themainideabehindthestandardviewistoexplainrigorous informalproofs:
(Rigour) Togiveanaccountofhowinformalproofsare(orcanbesaidtobe) rigorousthroughtheirconnectiontoformalproofs.
Furthermore,theaccountshouldbeofpracticaluse,inthatitwouldideally provideinsightintowhichproofsdonotliveuptothecriteriaitestablishes:
(Correctness) Todistinguishcorrectinformalproofsfromincorrectones, thatis,thecorrespondenceshouldonlylinktheinformalproofsthatare correcttothejustifyingformalproofs.
Rigourandcorrectnessarecloselyconnected.Arigorousproofwillalsobe acorrectone,andsospecifyingcriteriaforwhenaproofisrigorouswillalso specifyaclassofcorrectproofs.Conversely,onemightthinkthattherearecorrect proofsthatarenotrigorous,suchasbyskippingtoomanydetailswhilegettingthe overallideasright,asinthesumofhexnumbersproofthatwesawinthe Prologue.Thisclassofproofswillhavegapsbutnoterrors,ascorrectproofs cannotcontainerrors.16 Onecould,alternatively,arguethatthisclassdoesn’t, strictlyspeaking,existatall,thatallproofsworthyofthenamemustberigorous. Inthatcase,therewouldbeonlytwocategories:correct,rigorousproofs,and
16 Eventhismightbetoostrongforactualpractice.Injointworkwith JoshuaHabgood-Coote (2023),weconsidertheenormousproofofthe ClassificationofFiniteSimpleGroups.Inthis case,themathematiciansseeminglyaccepttheproofdespitebelievingitwillinevitablycontain someerrorsduetoitssize,becausetheyareconvincedthattheseerrorswillbeso-calledlocal errorsthatcouldbe fixedwithouttoomucheffort,andwhichdonotaffectthecorrectnessofthe theoremoverall.
failedproofs.Thiswouldamounttorejectingtheproposedproofofthesumof hexnumbers.(Maybeonecoulddemoteittosomeintermediatething,like a “proofsketch” or “proofidea”.)Ideally,then,ifthestandardviewisappealing toformalproofstoidentifygapsanderrors,itshouldprovideguidanceonhowto separatecorrectandrigorousproofsfromthosewhicharenot.
Toarticulatethestandardviewproperlyrequiresonetoaddressthedetailsof howaspecificinformalproofwilllinktoaformalproofthatexplainsitsrigour. Thatis:
(Content) Toshowhowthecontentofaninformalproofdeterminesthe structureoftheformalproof(s)itcorrespondsto.
Wewillseeinthefollowingsectionsthatdifferentversionsofthestandardview takequitesubstantiallydifferentapproachestothistask.
Aparticulardifficultythatneedstobeaddressedbythestandardview concernsinformaltechniques:
(Techniques) Toprovideanexplanationofapparently inherently informal techniques.
Themostobviousofthesewouldbetosetoutwhatistobesaidaboutdiagramsin proofs.Therearemultipleoptionsforthis,rangingfromdenyingthatdiagrams canplayanessentialroleinproofsatall,toexplainingwhichdiagramsare amenabletoformalisationandhow(see Brown1999,ch.3; DeToffoli2023).
Finally,sincethestandardviewisalsoattemptingtogiveadescriptive accountofhowmathematiciansjudgerigourinpractice,anotheraimthey haveistoaccountforthemechanismbywhichmathematicians agree onthe rigourandcorrectnessofinformalproofs:
(Agreement) Toexplainhow,inpractice,mathematiciansmanagetoconverge andagreeontherigourandcorrectnessofinformalproofs.
Itiscommonlytakenasoneofthevirtuesofthestandardviewthatitwouldhelp toexplainagreementamongmathematicians.Forexample,Azzounisays, “[M] athematicianshaveawayofagreeingaboutproofthatisvirtuallyunique (agreementofanysortamonghumansisalwaysasurprise,andalwayshasto beexplainedsomehow),andtheexplanationofthissurelyisthatsomesortof recognitionofmechanicalproceduresisinvolved.” (2004,p.103).
However,recentempiricalworkhasshownthatmathematiciansdosometimes disagreeonwhatcountsasavalidproof(Weber2008; Inglis&Alcock2012; Weber&Czocher2019)andwhatcountsasagaporerrorinaproof(Inglisetal. 2013; Daviesetal.2021).Thisdoesnotmeanthereisnoagreementtoexplain; onenotable findingfromthesearticlesistheimportanceofthecontextofthe
proofforevaluatingitsvalidity.Thedisagreementwasalsoelicitedbyasking aboutdifficultcaseslikediagrammaticproofsandcomputerproofs.So,by keepingthecontext fixedandchoosinglessborderlinecases,theremightstill behigheragreementamongmathematiciansthanresearchersinother fields.One mightalsopositthatthereissomethinglikelong-termconvergenceonagreement, sothateveniftherecanbedisagreementaboutvalidityaboutsomesteportypeof proof,overthelongtermmathematicianswillconvergeonagreement.Ofcourse, thesearealsoempiricalclaimsthatcanandshouldbetested.
In Section2.1,Igavesomeofthepurposesofhavingaconceptofrigourat all,butitisnoteworthythatthiswasnotthesameastheambitionsofthe standardview.Thestandardviewseemstobeinterestedprimarilyinasubsetof thebroaderusesoftheconcept,mostobviously Soundness and Verification, though Agreement linkstothesocialsideofmathematics.Ingeneral,the explanationforthisisthatthestandardviewleansmoretowardsthenormative questionofhowmathematicaltheoremsoughttobefullyjustifiedratherthan thedescriptiveclaimofmathematicaljustificationinpractice.
Bysettingouttheseaimsforthestandardview,wecanjudgeindividual componentsofthevariousproposalsagainsttheiraims.Forexample,thesimple “fillinginthegaps” abbreviationmodelwealreadysawhasproposalstoanswer Rigour, Correctness,and Agreement.However,wefoundthestoryfor Content tobelackinginimportantdetails,andtheanswerto Techniques wouldlikelyneedtorejectanything,likediagrams,thatcannotundergothe “fillinginthegaps” processeasily.
Withanumberofpossibleaimsforthestandardview,andaselectionof optionsforwhatitmightmeanforinformalproofstocorrespondtoformalones, itnowbecomesclearthatthereisnotreallyonestandardview,butinstead afamilyofstandardviews whichshareacommitmenttothegeneralideathat formalproofsexplainwhichinformalproofsarerigorous.In Sections3.4, 3.5, and 3.6,Iwillsurveythreeofthemostprominentproposedoptionsinmore detail,andlikewiseevaluatethemagainsttheaimsIhavejustconsidered.
3.4Hamami’sRoutineTranslations Letusbeginwiththeversionofthestandardviewsetoutby Hamami(2019) HamamiclaimsthatheisgivinganexpositionofthestandardviewasunderstoodbymostmathematiciansandfollowingtheideasofSaunders MacLane (1986) andthecollective Bourbaki(1968) group. 17 Forexample,hequotes themasalreadydefendingsomeversionofthestandardview:
17 ForadiscussionofthesocialdynamicsoftheBourbakigroup,see Barany(2020).
AMathematicalproofisrigorouswhenitis(orcouldbe)writtenoutinthe fi rstorderpredicatelanguage L 2 ðÞ asasequenceofinferencesfromthe axiomsZFC,eachinferencemadeaccordingtooneofthestatedrules. To besure,practicallynooneactuallybotherstowriteoutsuchformalproofs.In practice,aproofisasketch,insufficientdetailtomakepossiblearoutine translationofthissketchintoaformalproof.(MacLane1986,p.377)
Inpractice,themathematicianwhowishestosatisfyhimselfofthe perfectcorrectnessor “ rigour ” ofaprooforatheory iscontentto bringtheexpositiontoapointwherehisexperienceandmathematical fl airtellhimthattranslationintoformallanguagewouldbenomore thananexerciseofpatience(thoughdoubtlessaverytediousone). (Bourbaki1968,p.8)
Hamamidescribeshowthestandardviewwillhaveanormativeand adescriptivecomponent:thenormativecomponentwillgivetheidealof howaproofoughttoberigorous,while thedescriptivecomponentwillpick outhowjudgementsofrigourareactuallymadeinpractice.Hearguesthatthe conditionthataninformalproofshouldbe “ routinelytranslatable” into aformalproofprovidesausefulmiddlegroundbetweenthesenormative anddescriptiveparts.Theideaisthatr outinetranslatabilityisaweakenough conditionthatproofscanmeetitinpractice,butnonethelessmaintainsthe strongconnectiontotheidealofformalderivations.Hisproposalisthat advocatesofthestandardviewhaveanimplicitconceptionofthemechanism forjudgingrigour,withreasonsforthinkingtheywillsucceedinidentifying whenaproofconformstothenormativestandard.The “ conformitythesis ” is Hamami ’sclaimthateveryproofthatis “descriptively ” rigorousinpractice alsosatisfi esthenormativeidealofformalrigour.Inotherwords:thepractice ofrigourconformstotheidealviaanimplicitlyunderstoodmechanismof formalisability.
Hamami’sprimarycontributionistogivespecificationsofwhatthedescriptiveandnormativeaccountsofrigourareforhisversionofthestandardview,18 andhowtheyconformtooneanother.Letustaketheseinturn.
Forthedescriptiveaccount,thegeneralideathatHamamiproposesisthat informalproofsinvolvesequencesof “higher-level” inferencepatterns.These kindsofinferencesareacquiredasonelearnsmathematics.Onebeginswith basicknowledgeofmathematicalstatementsandsimple,obviousinferential moves,thenproceedstocumulativelygainknowledgebyprovingmorethings, andrecognisingmorecomplicatedhigher-levelinferencesasacceptableby
18 Hamamiclaimstobemerelyexplicatingthestandardviewasitiscommonlyheldbymathematiciansand fillingoutthedetailsimplicitintheworksofBourbakiandMacLane.Idon’tthinkthis givescredittothesubstantialadditionalideashebringstothisdebate.
verifyingthattheymerelyabbreviatesomelonger-establishedpatternof inferences.19
Forthenormativeaccount,Hamamiattemptstosetoutwhata “routine translation” is,andtogiveapreciseinsightintohowitwillproceed.Hisview isthattheroutinetranslationisbestunderstoodascomposedofthreestages.The firststagetakesaninformalproofand fillsindetailssothattheinferencesuse higher-levelinferencerules.Thesecondstageunpacksthosehigher-levelinferencerules,fullybreakingthemdownintothemorebasicinferencesthatthey abbreviate.Thethirdstagetakesthesequenceofbasicinferencesandformalises itintosomeformalsystem.Importantly,Hamamiclaimsthatthisprocedureis routineinthesensethatitisalgorithmic,mechanical,andautomatic.
Finally,theargumentfortheconformitythesisusesthecentralroleofhigherlevelinferencesinboththedescriptiveandnormativeparts:Hamami’sideais thatadescriptivelyrigorousproofwillbemadeupofhigher-levelinferential moves,forwhichtheroutinetranslationwillsucceed,therebyreachingthe normativeideal.
Intermsoftheaimsoftheaccount,Hamami ’sversionofthestandardview isclearlymoresophisticatedthantheoriginal “ fi llinginthegaps ” account. Whileheisstilladdressing Rigour and Correctness ,thedetaileddescriptionoftheroutinetranslationhegivesisalsoaddressing Content . Furthermore,theideathatmathemati ciansimplicitlyrecognisethemechanismbywhichrigourisjudgedisintendedtoaddress Agreement ,becausethe mechanismis,presumably,sharedbymathematicianswhoareabletomake therelevantjudgements.Thequestionof Techniques islessstraightforward becauseitisnotobviousthatHamami ’saccountwillapplyandhedoesnot explainhowtodealwithcasessuchasdiagrammaticproofs.Thedescriptive accountcouldpotentiallybethesame:thatonebuildsupatoolboxof acceptablediagrammaticinferences cumulatively.However,onequick objectionisthatthisassumesthattheacceptableinferencesalwayscome fromthiskindofprocess,anddonotrelyonpreviouslyuntestedinferences thattakeadvantageofvisualelementsofthediagram,ratherthanbeing madeupofsmallerinferences.
3.5 InPrinciple Formalisability Anotherversionofthestandardviewistothinkthatrigorousinformalproofs arethosethatwouldbeformalisable inprinciple.Thatis,ratherthanthinking
19 Thisdescriptiveaccountissimilartothatgivenby Tatton-Brown(2023) whoalsothinksthat mathematicallearningiscumulativeandtherebyallowsustorecognisemoresubstantial mathematicalinferencesasrigorous,whilestillhavingthoseinferencesultimately “deductively grounded” informalcorrectness.
thereisaroutinetranslationfromarigorousinformalprooftoaformalderivation,theyinsteadrelyonthetheoreticalpossibilityofsuchatranslation. Prominentproponentsofthiskindofapproachinclude Steiner(1975) and Burgess(2015)
StartingwithBurgess,hebuildsontwogeneralideasaboutrigorous proof.The fi rstisthat: “ Aproofiswhatconvincesareasonableperson; arigorousproofiswhatconvinces[even]anunreasonableperson ” ( Burgess 2015 ,p.91). 20 Thesecondideaisthatrigorousinformalproofsarenotabout givinganabbreviatedversionofaformalproof,butinsteadareprimarily aboutconvincingothermathematiciansthatsuchaproofexists.Burgess referstothisprinciplefromHymanBass,whosays:
Thenotionofmathematicalproofisaprecisetheoreticalconstruct,butitis quiteformal,rulebound,andponderous.Mathematicianstypicallydonot producesuchformalproofs,butratherconvinceexpertcolleaguesessentially thatsuchaproofexists,thepresumptionbeingthattheconvictioncarriesthe beliefthatunderduressandwithsufficienttimesuchaproofcouldbe suppliedbytheproponent.(Bass2003,p.770)
Burgesssummarisesthisinsloganform: “ Aproofiswhatconvincesmathematiciansthataformalproofexists ” ( Burgess2015 ,p.91).However,this isnotadequatebyitselfbecauseitisrelevant how theconvictioncomes about.Beingconvincedcanhappeninnumerousways,suchasthrough experttestimonyorbrainwashing.Evenanunreasonablepersonmightbe convincedforthewrongreasons – giventheirunreasonableness,wemight expectthisevenmore – andcertainlyexperttestimonycanconvincepeople oftheexistenceofformalproofs.WhatBurgessisafteristhattheconvincingisn ’tofthisdefectivesort;thattheconvincinghappens intherightway. Hetentativelysuggeststhattherightwayforthisconvictiontocomeabout isbecausethestepssuppliedshow enough oftheformalproof: “ Whatrigor requiresisthateachnewresultshouldbeobtainedfromearlierresultsby presentingenoughdeductivestepstop roduceconvictionthatafullbreakdownintoobviousdeductivestepswouldinprinciplebepossible ” ( Burgess 2015 ,p.97).
InhisreviewofBurgess ’sbook, Pettigrew(2016) respondsthatitisn ’t aboutsupplyingenoughsteps,butaboutsupplyingtherightsteps.He observesthatanadvancedmathematicianmightonlyneedtoseeasingle trivialstepofaverydif fi cultprooftoconvincethemselvesthataformal proofexists,invirtueoftheirabilitytocomeupwithproofs,butthatcannot
20 BurgessascribesthisideatoMarkKac.I’venotmanagedtotraceadirectquotation,otherthanin hisobituaryby Thompson(1986).
betherelevantsenseofthe “ rightway ” tobringaboutconviction,because onlysupplyingatrivialstepdoesnotmakeforarigorousproof.Pettigrew proposesthatwhatismissingfromBurgess ’saccountisadistinction between ingenious and routinesteps .Aproofshoulddisplayallofthe ingeniousstepsandtherebyconvinceitsaudienceoftheexistenceof aformalproof: “ Arigorousproofisonethatconvincesitsaudiencethat thereexistsaformallyrigorousproofbyprovidingthosestepsinthe formallyrigorousproofthatitisnotsimplyroutinetoprovide ” ( Pettigrew 2016 ,pp.132 – 3).Theideaisthattheroutinestepsarethosethatonecan reasonablyexpectanothermathematiciantocomeupwithforthemselves, whileingeniousstepsmustbegiven.Therefore,toconvinceothermathematiciansoftheexistenceofaformalproof,oneneedstosupplythose ingenioussteps,butmaytaketheroutinestepsforgranted.
Asimilarlineofthoughtispresentin Steiner ’s(1975) accountofmathematicalknowledge.Hethinksthatonecangainmathematicalknowledgefrom aproofonlyifthatproofisinprincipleformalisable.To filloutwhat “in principle” meanshedeploysthethoughtexperimentofbeingabletoproduce aformalproofwiththeassistanceofahypotheticallogicianhelper.Most mathematiciansdon’tknowenoughformallogictoproduceformalproofs,so itcannotbeexpectedthattheythemselvescanproduceformalequivalentsof theirproofs.Steinersolvesthisbyimaginingwhatwouldhappeniftheywere pairedwithalogicianwhocouldproduceformalproofs.Thelogicianwouldbe abletohandlethelogicitselfandthedetailsoftheroutinesteps,whilethe mathematicianmustsupplytheingeniousandcreativepartsofthemathematical reasoning.If,inthehypothetical,thetwoofthemcouldproduceaformal derivationtogether,thentheinformalproofwouldbesufficienttoestablish themathematician’sknowledgeallalong.
The inprinciple formalisabilityapproachisclearwithregardto Rigour butunderspeci fi edwithrespectto Correctness .Afterall,itisnotobvious thatsupplyingenough(orenoughingenious)stepsofaproofissuf fi cientto guaranteeitsformalisability,norisitclearthatthehypotheticallogician canreallyunderpinanaccountofcorrectproofs.The inprinciple account seemstobypassthedemandof Content altogetherbecauseitdoesnotwant tospecifyatallwhataninformalproof ’scorrespondingformalproofis,let alonehowthetwoarelinked.For Techniques ,thisaccountrejectsany prooftechniquesthatare inherently informal,sincetheycouldn ’tbeformalisedeveninprinciple.For Agreement ,astoryisneededofhow mathematiciansconvergeonwhichproofsareformalisable inprinciple , thoughthesuggestionsofBurgessandPettigrewprovideanoutlineofhow thiscouldgo.
Oneofthemostinfluentialproposalsformakinginformalrigourdependenton formalproofscomesfromtheearlierworkofJody Azzouni(2004) onhis derivation-indicator view.21 Wehaveseenthe routinetranslations viewtryto specifyhowformalproofscorrespondtoagiveninformalproof,andthe in principleformalisability viewthatinformalproofsonlyneedtobeformalisable inprinciple.Incontrast,thederivation-indicatorviewisthatinformalproofsdo indicate correspondingderivations,butwithoutthemathematiciansneedingto knowhowthatcorrespondenceworks.Theseindicatedderivationsexplain thingslike Rigour, Correctness,andespecially Agreement,butdonotneed tobeknowntothemathematicians,norarethey fixedtoaparticularformalism.
Theoverallideaisthatformalderivationsareimplicitininformalproofs,in awaythatsecuresmathematicalrigourbecausethosederivationsaremechanicallycheckable,whichindirectlysecurestheinformalproofstoo.
Itakeaproofto indicate an ‘underlying’ derivation Since(a)derivationsare (inprinciple)mechanicallycheckable,andsince(b)thealgorithmicsystems thatcodifywhichrulesmaybeappliedtoproducederivationsinagivensystem are(implicitlyor,oftennowadays,explicitly)recognizedbymathematicians,it followsthatifproofsreallyaredevicesmathematiciansusetoconvinceone anotherofoneoranothermechanically-checkablederivation,thissufficesto explainwhymathematiciansaresogoodatagreeingwithoneanotheron whethersomeproofconvincinglyestablishesatheorem.(Azzouni2004,p.84)
Mathematicianscanagreeonrigorousandcorrectproofsbecausetheyare implicitlysensitivetowhichinformalproofsindicateformallyvalid,mechanicallyrecognisablecounterparts.Nonetheless,thisdoesn’trequirethemto actuallyknowwhatthoseindicatedderivationsare,whichexplainshowmathematicscouldfunctioninthiswaydespitethelonghistoryofmathematics beforetheinventionofformalproofsanddespitethemanymathematicianswho arenotabletoproduceformalproofs.
Theproposalthattheformalderivationsareimplicitandnotnecessarily knownbythemathematiciansthemselvesworksinpartbecausethederivations Azzounihasinmindarenot fixedtoasingleformalsystem.Instead,theycanbe foundacrossawholefamilyofalgorithmicsystems(withsometechnical caveatsthatwedonotneedtoexplorehere).Mathematiciansarenotboundto someparticularformalism,soneitherarethederivationsthatunderlieproofs.
21 Inmorerecentwork, Azzouni(2020)hasmovedawayfromthederivation-indicatorview towardsthe algorithmicdevice viewofinformalproofs.Whilethishassomefamilialrelationshiptothederivation-indicatorview,italsohassomesubstantialdifferencesthatmeanit explicitlynolongerfallsunderthelabelofthe “standardview” .
Furthermore,newtechniquescanleadtoneedingtheresourcesofdifferent formalsystems,andAzzouniseesmathematiciansas flexibleandfreetomove tonewformalsystemsthatcanaccommodatetheirneeds: “Onthederivationindicatorviewofmathematicalpractice,themathematicianisseeninsteadas gracefullysprintingupanddownalgorithmicsystems,manyofwhichheorshe inventsforthe firsttime” (Azzouni2004,p.103).
Thismeansthatinformalproofsthatmakeuseofmoremeta-levelreasoning arehappeninginahigher-levelsystemthatcanhandlethem.Azzouni’sexample isusinga “proofbysymmetry”,wherejustoneofseveralcasesisprovenin detailandtherestarearguedtofollowsymmetrically.Healsotakesthistoallow the flexibilityfortheretobealgorithmicsystemsthatareindicatedbydiagrammaticreasoning,allowingforananswerto Techniques.
Inotherpapers, Azzouni(2005, 2009)developsanovelaccountof “inference packages”,whichare “psychologically-bundledwaysofphenomenologically exploringtheeffectofseveralassumptionsatoncewithoutexplicitrecognition ofwhatthoseassumptionsare” (Azzouni2005,p.9).Theseworklikecognitive blackboxeswhichallowustocarryoutmathematicalmanipulationswithout havingtobeabletointrospectivelyknowtheunderlyingformaljustification,or eventorecognisewhichassumptionsarebeingmanipulated.Thatmathematiciansoftenuseinferencepackagestothinkaboutmathematicsaddstothe accountbyexplaininghow Techniques canseemsoinherentlyinformaland compellingwhilestillindicatingunderlyingderivations.Furthermore,it fills outhowindicatedderivationsmightsecure Agreement amongmathematicians despitethemnotknowingtheexactderivationsthemselves.
Overall,Azzouni’sderivation-indicatorviewdoeswellataccountingfor Rigour and Correctness,usingtheindicatedfamilyofderivations.For Agreement, mathematiciansaremeanttoagreeabout validitybecausetheirjudgementsare trackingtheimplicit,indicatedderivation.Meanwhile,bynotneedingmathematicianstobeawareofwhichderivationisindicated,theaccountcanaddress apparentlyinherentlyinformal Techniques andnotrelyonthemathematicians knowingsubstantialformallogic,whichisuncommonevennowandwasimpossiblepriortotherelativelyrecentdevelopmentofmodernlogic.Onethingthatis leftsomewhatunderspecifiedis Content:theindicatedderivationsaremeantto providetheultimatesourceofjustificationfortheinformalproofs,butitisnotclear howtheydosoorwhatthe “indication” relationamountsto.
3.7CriticismsoftheStandardView Sofar,wehavebeenassessingthemeritsofthevariousversionsofthestandard viewbythecriteriafrom Section3.3.However,thishastakenforgrantedthat
theviewsbroadlysucceedinthe firstplace.Thisisfarfromclear.Oneofthe majorcontributionsofthepracticalturninthephilosophyofmathematicshas beentochallengethestandardviewwithawideselectionofcriticisms.Inthis section,Iwillsurveysomeofthemostprominentonesandaddsomemoreof myown.Wewon’thavespacetogointomuchdepth,butthereadercanfollow thereferencesforfurtherdiscussion.
3.7.1NoFormalSystem The fi rstobjectiontothestandardviewistheabsenceofaspeci fi cformal systemunderdiscussion.Differentsy stemswillhavedifferentthingsthey canproveanddifferentwaysofprovingthem,sowhatsystemunderliesthe rigourofinformalproofsisfarfromani dlequestion.Iftheinferencesfound inaninformalproofarewarrantedbyoneformalsystembutnotbyanother, whatisthestatusofthatinformalproof?Thisquestionappliesatseveral levels.First,onemightaskwhatunderlyinglogicisbeingused.Thedefault assumptionwouldbeclassicallogic,thoughtheconstructivistsandproponentsofotheralternativelogicswouldr ejectthis.Evenwithinclassicallogic, onemustsettleonusing fi rst-orderlogic,somehigher-orderlogic,orsomethinginbetween.Onemustdecideabouttheacceptabilityofin fi nitary proofs. 22 Atthetechnicallevel,thesechoiceswillmatterastowhatcanbe formalisedandhow.Beyondthelogic,onemustsettleonwhichaxiomsare used.Again,thedefaultwouldprobablybethoseofZFCsettheory,which itselfcanbesupplementedwithall kindsofextraaxioms,butthereare alternativeproposalsforfoundationsofmathematicstoo,suchasthrough categorytheoryorhomotopy-typetheory.Again,thesewouldaffectwhat couldbeformalised.
Multipleformalisationprojectsareunderwaytousecomputer-checkingin mathematics,suchasinLean,Coq,theHOLfamilyincludingIsabelle,and Mizar.Theseallhavedifferentimplementationsofhowproofsarewrittenand howthingsareformalised.Ifthesuccessesoftheseformalisationprojectsare tobeusedtosupportthestandardviewbyvindicatingthepossibilityof formalisingmathematics,itseemsthatwemustacceptthatthesesystems arecapableofjustifyingrigorousproofs.However,thesesystemsareall idiosyncratictosomeextent,andtheproductofvariouscontingentprogrammingchoices,soitisunlikelythatthe yarereallyexplainingtherigourof mathematicalproofs.
22 Forexample, Rav(1999) and Azzouni(2004) disagreeonthismatter. Weir(2016) arguesthat allowingproofstobeinfinitaryisnecessaryforthestandardview.
Theproponentsofthestandardviewwouldpointoutthatthekeyfeatureof thesevarioussystemsisthattheyshouldcontainenoughstandard,everyday mathematics.Themanysystemsallprovelargelythesamethings,using mostlythesametools.AsAzzounimakesexplicitforhisderivationindicatorview,thedetailsoftheexactsystemarenotimportantsolongasit capturestherightinferences.Itcouldalsobethatanysystemis finesolongas itsatisfi essomelistofcriteria,thoughIknowofnosuchlist.Nonetheless,we haveseenthatthedetailsareimportantifthestandardviewistoexplain mathematicalrigour.
3.7.2IncompletenessandInconsistency OnelimitationonformalsystemscomesfromGödel ’stwoincompleteness theorems.The fi rstshowsthatanyconsistentformalsystemthatissuf fi cient toproveacertainamountofmathematicswillfailtobecomplete,meaning thattherewillbestatementsthatitcannotproveordisprove.Thesecond thenprovesthat,ifsuchaformalsystemisconsistent,thenthestatement thatthesystemisconsistentwillnotbeprovablewithinthesystem.Gödel ’s proofsinvolveusingacodingtoconstructaGödelsentence GF (relativeto aformalsystem F ),whichisprovablyequivalenttotheformulaexpressing that GF isunprovableinthesystem F .Thesentence GF willnotbeprovable in F ,onpainofcontradiction,butwillthereforebetrueofthesystem F . Priest(1987,ch.2),whowantstoarguefordialetheism – theviewthatthere aretruecontradictions – and,insupportofthis,thatmathematicsisinherently inconsistent,usesthestandardviewasamainpremiseofhisargument.Theidea isthatifonetakesthestandardviewseriously,thenrigorousinformalproof procedurescanbeformalised,andhencecanbeusedtogenerateaninconsistencyusingGödel’stheorems:
Forlet T be(theformalisationof)ournaïveproofprocedures.Then,since T satisfiestheconditionsofGödel’stheorem,if T isconsistentthereisasentence ’ whichisnotprovablein T ,butwhichwecanestablishastruebyanaïve proof,andhenceisprovablein T .Theonlywayoutoftheproblem,otherthan toacceptthecontradiction,andthusdialetheismanyway,istoacceptthe inconsistencyofnaïveproof.Soweareforcedtoadmitthatournaïveproof proceduresareinconsistent.Butournaïveproofproceduresjustarethose methodsofdeductiveargumentbywhichthingsareestablishedastrue.It followsthatsomecontradictionsaretrue;thatis,dialetheismiscorrect. (Priest1987,p.44)
Inmyownwork(Tanswell2016a),Ihavearguedthattheplacewherethis argumentbreaksisinadoptingthestandardviewinthe fi rstplace.
Aproponentofthestandardviewisthereforechallengedtoofferadifferent solution,ortoacceptPriest ’sconclusionthatmathematicsisinconsistent.
3.7.3UnformalisableproofsandFaithfulness Amajorstrategyforattackingthestandardviewhasbeentopresentproofs thatwouldappeartobeunformalisable.Ifthereexistsarigorousproofthat isunformalisable,thiswouldbeaco unterexampletothestandardview. Likelycandidateswouldbediagrammaticproofsorproofsthatrelyessentiallyondiagrams. 23 However,whilethesemaybehardtocapturein language-basedformalsystems,th ereareformalsystemsforcertain kindsofdiagramstoo,suchas Mumma ’s(2010) formalsystemfor Euclid ’sElementsand Shin ’s(1994) systems Venn-I and Venn-II .This suggeststhatrigorousdiagramscouldbeamenabletotreatmentby aformalsystemfordiagrams.Nonetheless, DeToffoli(2023) showsthat therearerigorousdiagrammaticproofsthatcannotbefaithfullytranslated intoformalcounterparts.
Likewise,recalltheproofby “Gestaltshift ” .Itmaynotbepossibleto capturefaithfullyreasoningthatreliesonsuchaswitchofperspective.24 However,theword “ faithfully” isimportanthere,becausewiththeresources offormallogicagreatmanythingsareformalisableinsomebroadsense,but intryingtounderwritearigorousinformalproofwewanttheformalisationto befaithfultothereasoningpatternoftheoriginal.25 Faithfulnesswillmean somethinglikepreservingthemainideas,structure,andmethodsoftheproof. Tothecriticofthestandardview,itmay beobviousthatatranslationshouldbe faithfulinordertosecurerigour,butfortheproponentthisrequirementcould beseenasunfairlyrestrictingthetoolsoflogicbysettinganebulousextra requirementontranslation.After all,whojudgesthefaithfulnessof atranslation,andbywhatstandards?26
23 Azzouni(2020)arguesagainstthestandardviewalongtheselines,witharecentreplyby Weisgerber(2022).
24 Thespecificversionwesawwasgivenasanexampleofanunrigorousbutcorrectproof,sothis suggeststhatthisexamplecouldberejected.However,thereisnoobviousreasonwhythere couldnotbearigorousproofbyGestaltshift.Eventheonewesawcouldbemademoreexplicit whilestillrelyingontheGestaltshiftasitsmainstrategy,anditisthismovethatseemstobe difficulttoformalisefaithfully.In SangwinandTanswell(2023) wealsolookattheprocessof translatingbackandforthbetweenalgebraicanddiagrammaticproofs.
25 Thesignificanceoffaithfulnessoftranslationsintheliteraturemightbetracedto Lakatos(1976) Forexample: “Alpha:Areyousurethatyourtranslationof`polyhedron’ intovectortheorywas a true translation?” (Lakatos1976,p.121).Iwilldiscussthisbookin Section3
26 Thisproblemisalsoconsideredby DeToffoli(2023) whorightlypointsoutthatidentity conditionsforproofsarehardtopindownandarecontext-dependent.
24 PhilosophyofMathematics 3.7.4KnowledgeandExplanatoryRedundancy
Amainlineofattackfrommathematicalpracticeonthestandardviewhasbeen epistemic,arguingthatformalproofsarenotneededtoexplainhowinformal rigorousproofsprovidemathematicalknowledge.Thatis:formalproofsare explanatorilyredundantintheepistemologyofmathematics.27
Rav(1999) listsvariousareasofmathematicsthatareacceptedasrigorous andproceedwithoutaxiomatisationorformalisationasanintermediary.28
Therefore,asadescriptiveaccountofhowrigoursecuresmathematicalknowledgeinpractice,itdoesnotsucceed.Thethreemoreadvancedversionsofthe standardviewwouldreplythattheirmodelsarenecessarytoexplainrigouras anormativeidealforproof,andthattheactualpracticesaretryingtomeetthis idealinvariousways.Nonetheless,otherliteraturechallengesthesesolutions.
Forexample,replyingtothe routinetranslations view, Weber(2023) givestwo examplesfromcomputabilitytheorywhereproofsaretakentoberigorousby themathematicalcommunity,butarenotverifiablebymathematiciansinthe wayHamamihassetout,norarethetechniquesdevelopedinthecumulative waythathedescribes.
Similarly, AntonuttiMarfori(2010) arguesthatthelackofformalisationsin mathematicalpractice,eitherinpresentingproofsorresolvingcontroversies aboutproofs,meansthatanepistemicaccountbasedonformalisationwould makemathematicalknowledgemysterious.Eitherthisleavesmathematical practice “lazyandunsuccessful” (AntonuttiMarfori2010,p.267)oritallows informalproofstotrackmathematicaltruthwithoutthepractitionersknowing how,whichmakesforanunconvincingaccountofmathematicalknowledge.
Pelc(2009) alsoarguesthatformalproofsmightbetoolongtoplayarole inmathematicalknowledge.Inpractice,formalisationsarelongerthantheir informalcounterparts.Pelcarguesthatforcomplicatedproofs,suchas Wiles ’sproofofFermat ’sLastTheorem,itisnotknownwhetherthe formalisationissolongthatitwouldeverbeveri fi able,evenifallthe resourcesintheuniversewerededicatedtothetask. 29 Therefore,formal
27 Besidesthoselistedinthetext, Buldtetal.(2008) usethisargumentasalaunchpadfor demandinganewepistemologyofmathematicsthatdoesnotrelyonthestandardview. GoetheandFriend(2010) alsogiveaversionofthisargument.
28 Thelistof “unaxiomatised” theories Rav(1999,p.16–18)givesnowlooksratherquaintbecausein theinterveningyearsalotmoreformalmathematicshasbeendone,andmanyofthelistedareashave beenformalisedandverifiedinsystemslikeLeanandMizar.Thisdoesn’tundermineRav’spoint, though,whichisthatthemathematicalpracticeswereperfectly fineandrigorouswithoutthose formalisations.
29 FreekWiedijkhasalisttrackingtheformalisationeffortsof100 “top” theoremsinvarious formalsystems,inanexercisetofollowdevelopmentsinformalmathematics(www.cs.ru.nl/ ~freek/100/).Funnilyenough,theonlytheoremthathasnotyetbeenformalisedinanyofthe mainsystemsisFermat’sLastTheorem.Thefactthattheother99haven’tseenthehumongous