TimeRegained Symmetry andEvolutionin
ClassicalMechanics
Volume1
SeanGryb
UniversityofGroningen
KarimP.Y.Thébault
UniversityofBristol
GreatClarendon Street,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries ©SeanGrybandKarimP.Y.Thébault2024
Themoralrightsoftheauthorshavebeenasserted Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica BritishLibraryCataloguinginPublicationData
Dataavailable
LibraryofCongressControlNumber:2023946171
ISBN9780198822066
DOI:10.1093/oso/9780198822066.001.0001
Printedandboundby
CPIGroup(UK)Ltd,Croydon,CR04YY
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork.
Preface
Thisbookisthefirstvolumeofatwo-partproject, TimeRegained,articulatinga newapproachtotheanalysisoftimeinmodernphysicaltheory.OurparticularconcerniswiththeProblemofTimeasitoccursintheorieswhichfeaturedynamical lawsthatareinvariantundertimereparameterizationsymmetries.Theclassofsuch theoriesincludesbothsimplemechanicaltheoriesandthegeneraltheoryofrelativity andprospectivetheoriesofquantumgravity.Ourgoalistoprovideasolutiontothe problemoftimesuchthatdeterminatetime-orderingstructurecanbereconciledwith reparameterizationsymmetry.Thepresentvolumeisfocusedonanalyticalformulationsofclassicalmechanicaltheory.Thisrestrictedcontextwillallowustodevelop anewframeworkfortheanalysisofsymmetryandstructureinphysicaltheoryand provideafullygeneralandexplicitresolutionoftheclassicalmechanicalproblemof time.Inthesecondvolume,theframeworkwillbeextendedtothecontextofclassical andquantumgravitationaltheoriestowardsbothformalresolutionofthegravitational problemoftimeingeneraltermsandanexplicitsolutionrealizedinthecontextof simplecosmologicalmodels.Thiscosmologicalsolutionwillbefoundtohaveattractive novelconsequencesincludingunitarityandsingularityresolution.
Inthemostgeneralsenseourprojectisoneconcernedwiththe naturalphilosophy oftime.Assuch,weintendourworkasacontributiontobothphysicsandphilosophy. Oursisnot,however,aprojectregardingthe interpretation ofphysicaltheoryorthe metaphysics oftime.Rather,ourprincipalgoalistomotivateandarticulateanovel proposalforthe development ofphysicaltheory.Themainfocusofthepresentvolume istheproblemoftimeasitoccursinclassicalmechanicaltheoriesandourproposal isdesignedspecificallyasaresponsetotheprobleminthatcontext.Firstandforemost,therefore,thisbookisintendedasacontributiontomathematicalphysics.In ordertoformulateandimplementoursolutiontotheclassicalmechanicalproblemof timenewworkonthegeometricfoundationsofmechanicaltheorieswillberequired. Inparticular,wewillprovideaformalismforthecomprehensiveandrigorousanalysisofreparameterizationsymmetriesthatsupersedesthatprovidedbythestandard approachduetoDirac.
Ourformalanalysiswillbebuiltuponthesustainedanalysisofatangledknot ofhistoricalandphilosophicalproblemsrelatingtotimeandsymmetry.Mostsignificantly,wewillconsiderphilosophicalargumentsregardingtime,asfoundinthework ofNewton,Leibniz,andMach,andphilosophicalargumentsregardingsymmetry,as foundintheworkofvariouscontemporaryauthorsinphilosophyandfoundationsof physics.Inthisrespect,thisbookisalsoaresearchmonographinthephilosophyof physicswhichengageswithcoreissuesinthehistoryofnaturalphilosophy.Wedo nottakethemathematicalphysics,philosophical,andhistoricalaspectstobedisconnected.Rather,wewilladoptthemethodologicaloutlookofwhatmightbecalled
vi Preface
a‘three-field’approachtothefoundationsofphysics:aninterdisciplinaryapproach simultaneouslyapplyingmethodsandinsightsfrommathematicalphysics,thehistory ofnaturalphilosophy,andthephilosophyofphysics.
Ourultimategoalisnot,however,merelytoprovideaunifiedphysical,philosophical,andhistoricalanalysisoftheproblemoftimetakeninisolation.Rather,wefind theproblemoftimetobebothadomainofenquiryinitsownrightanda‘resource’, providingtoolsthatcanbeproductivelyappliedtootherdomains,cf.Rickles(2020).
Ontheonehand,wewillviewtheproblemoftimeasaphysical,philosophical,and historicalsubjectinitsownright,withattendantproblems,questionsandformalchallenges.Butontheother,wewillviewtheproblemasanarenafordevelopingnew concepts,tools,andtechniques,whichfindapplicationsinotherdomains.Whenseen fromthisperspective,theproblemoftimegainsconsiderablevalueasatopicofstudy sinceitbringsintoreliefkeyissuesinthestudyoftimeinclassicalmechanicaltheories.
Acknowledgements
SupportandFunding. Thegenesisofthisprojectcanbetracedtoaaprecisespatiotemporalcoincidenceinthetermsofthefirstdiscussionofitstopicinthefirst meetingofitsauthorsataconferenceinBrisbanein2011,anditsdevelopmenthas beenspreadacrossspaceandtimeencompassingAustralia,Canada,theChannelIslands,theNetherlands,Germany,theUnitedKingdom,andRomania.Thedebtswe havejointlyaccruedincompletingthisbookaredifficulttoexhaustivelyexpress.Of particularnoteareearlydiscussionsregardingtheproblemoftimewhichoneorboth authorsprofiteddeeplyfromwithJulianBarbour,OliverPooley,andHansWestman.PartsofthebookhavegreatlyprofitedfromfurtherinteractionswithEdward Anderson,RicArthur,AlexBlum,MartinBojowald,HarveyBrown,JeremyButterfield,AdamCaulton,DavidCobb,ErikCuriel,Ana-MariaCret , u,KarenCrowther, RadinDardashti,RichardDawid,PeteEvans,SamFletcher,SimoneFriedrich,SteffenGielen,HenriqueGomes,JonathanHalliwell,StephanHartmann,PhilippH¨ohn, NickHuggett,LucyJames,TimKoslowski,JamesLadyman,HuwPrice,JamesRead, DeanRickles,BryanRoberts,DonaldSalisbury,SimonSaunders,StevenSavitt,Lee Smolin,TonyShort,DaveSloan,KurtSundermeyer,TzuChienTho,JimWeatherall, andChrisW¨uthrich.WeareparticularlyappreciativetoRicArthurandErikCuriel fordetailedcommentsondraftchaptersofthemanuscript.Materialdevelopedtowards thisbookhasalsoreceivedfeedbackfromawidevarietyofaudiencesinpresentations andfromvariousanonymousreviewersofresearcharticles.KTisgratefultoUniversity ofBristolstudentsonthecourses Space,TimeandMatter and AdvancedPhilosophy ofPhysics forfeedbackonmaterialthathasusedinthepresentbook.
InitialworkonthisprojectwassupportedbythePerimeterInstituteforTheoretical Physics,theCentreforTime(UniversityofSydney),RadboudUniversity,UtrechtUniversity,andtheMunichCenterforMathematicalPhilosophy(Ludwig-MaximiliansUniversit¨atM¨unchen).WearegratefultoHuwPriceandStephanHartmannforfacilitatingthisearlyinstitutionalsupportaswellastotheAlexandervonHumboldt FoundationandtheNetherlandsOrganisationforScientificResearch(NWO)(Project No.620.01.784)forfinancialsupport.KTisparticularlygratefultocolleagues,students,andacademicvisitorsattheBristolDepartmentofPhilosophy.Thisworkcould nothavebeencompletedwithouttherichscholarlyandcollegialatmospherethatBristolhasprovidedoverthelasteightyears.Significantworktowardsthisprojectwas completedbyKTduringaUniversityResearchFellowshipin2018/19,supportedby theUniversityofBristol.ThanksisalsoduetoOxfordUniversityPress,andinparticularSonkeAdlungandGiuliaLipparini,forpatienceandsupportnotwithstanding thesomewhatglacialprogressofthisproject.
AfinalandmostsignificantnoteofthanksisduetoAnaandNienkefortheir constantsupportandencouragement.
PreviouslyPublishedMaterial Thevastmajorityofthematerialpresentedhereis new.Thatsaid,variouselementsbuildindifferentwaysonexistingpublishedworksof theauthors.Whenwearedrawingexplicitlyonpublishedmaterial,thisisindicatedbelow.Therearetwosubstantialtranchesofmaterialthatarereproducedfromprevious work.First,weareparticularlygratefultoElsevierforpermissiontorepublishpartsof
viii Acknowledgements
thearticle‘OnMachonTime’whichwaspublishedin StudiesinHistoryandPhilosophyofSciencePartA,89,84–102whichisincludedinChapter4.Second,Chapter12 featuresmaterialfromthepresubmission,preprintversionofthearticle‘Schr¨odinger EvolutionfortheUniverse:Reparameterization’,philsci-archive.pitt.edu/11299/.Finally,atamoreminorlevel,wearegratefultoOxfordUniversityPressforpermission torepublishseveralparagraphsfromthearticle‘TimeRemains’, BritishJournalfor thePhilosophyofScience,67(3),663–705,whicharereproducedinChapter14.
1Introduction 1
1.1TheObjectsofOurEnquiry1
1.2SymmetryandEvolution4
1.3TransformingStructures10 1.4TimeRegained17
1.5DirectedTimeOrderingandTime’sArrow22
PARTINATURALPHILOSOPHYOFTIME
2OnNewtonOnTime 27
2.1OnNewton’sMethodologyintheScholium27
2.2TheTripartiteNatureofNewtonianTime30
5StructureandPossibility
x Contents
6.4IsolatedSubstructuresandNarrowSymmetries100
6.5NomicStructureofNewtonianMechanics103 6.6ChapterSummary109
7IrregularNomicStructure 110
7.1IrregularLagrangians110
7.2ConstrainedHamiltonianMechanics112
7.3Dirac’sTheorem116
7.4Noether’sSecondTheorem119
7.5ChapterSummary121
8DiagnosingDynamicalRedundancy 122
8.1VariationalSymmetriesofHistories122
8.2Noether’sSecondTheoremRevised125
8.3InitialValueConstraints131
8.4DynamicalRedundancy136
8.5NomicStructureofBarbour–BertottiTheory140 8.6ChapterSummary150
9TheNewFramework 151
9.1TheAIRClassification151 9.2TheNomic-AIRAnalysis156
9.3GlobalandLocalStructures160
9.4ChapterSummary161
PARTIIITHEPROBLEMOFTIMEINCLASSICALMECHANICS
10SpatiotemporalStructureandTheoryRe-Articulation 165 10.1StructuresandHeuristics165 10.2SpatiotemporalStructureinNewtonianMechanics170 10.3SpatiotemporalStructureinBarbour–BertottiTheory175 10.4ChapterSummary177
11LocalTemporalSymmetry 178
11.1TimeReparameterizationInvariance178 11.2DynamicalRedundancyandEvolution181 11.3TemporalLeibnizShifts185 11.4ChapterSummary186
12ReparameterizationInvariantDynamics 187
12.1JacobiActionsasGeodesicPrinciplesonConfigurationSpace187 12.2TotalEnergyasaConstantofMotion189 12.3GeneralizedHamilton–JacobiFormalism192 12.4IntegralsofMotionandCompleteObservables195 12.5ChapterSummary200
13TemporalStructureRegained 201
13.1DifferentiatingDynamicalRedundancyandEvolution201 13.2ADynamicalViewofHamiltonianConstraints204
Introduction
1.1TheObjectsofOurEnquiry
Atoncepossessingaunityofnatureandaninfinitevariegationofform.Singularly constitutiveofhumanexperienceandthesubjectofinexhaustiblydiverseartistic, philosophical,andscientificdiscourses.Suffusedthrougheverythingandyetnothing in-and-ofitself.Timeisproblematic.Weknowpreciselywhatitis,untilwebeginto discussit.Itisthiscombinationofunityandmultiplicity,familiaritiesandintangibility, thatshouldperhapsbedesignatedthemasterproblemoftime,ofwhichallothersare mereshadows.Yet,therecanbenosubstantiveprogressinanyphilosophicalenquiry intothenatureoftimewithoutfirstsettingafirmdelimitationofitsremit.Whatwill wemeanbytheproblemoftime?Whatapproachwillwetaketowardsitsinvestigation? Whatwouldconstituteasolution?
Letusstartbyprovidingabriefcommentonourmethodologicaloutlook,echoingtheremarksofthePreface.Theprimaryrestrictionwewillmakeinwhatfollows istheassumptionofacontemporaryscientificperspectiveinwhichouroutlookon boththeproblemanditssolutionwillbeanchoredinmethodsofmoderntheoretical physics.Ourmethodologywillbeaninherentlyinterdisciplinaryone,drawing,inaddition,upontoolsfromanalyticphilosophy,thephilosophyofphysics,andthehistory ofnaturalphilosophy.Theoverridingapproachwewilladopt,however,willbethat ofmathematicalphysics.Ourgoalwillbetopreciselyformulateandsolveaspecific probleminthearticulationofclassicalmechanicaltheory,understoodfromamodern geometricperspective.Indoingthiswewillberequiredtoconstructnewformalapproachestothegeometricanalysisofsymmetryandevolutioninmechanicaltheory. Thereisnoscopeforapurelyinterpretativesolutiontotheproblemoftimeinclassical mechanics.Anapproachfoundeduponthemethodologicaloutlookofmathematical physicsisthusunavoidable.
Wecanfurtherconstrainthescopeofourinvestigationsbydelimitingtwodimensionsofanalysis.Thefirstdimensionistheaspectsoftimeor,asweshallmore preciselyframethem,the temporalstructures thatwewillconsider.Ourenquiryisa foundationaloneinthesensethatthetargetofourformalexcavationsshallbethe bare substratum oftimeasrepresentedinmechanicaltheory.Wewillfocusoursustained attentionupontheprovisionofamaximallyprecisephysico-mathematicalcharacterizationofthebasicstructuralcharacteristicsoftime.Thelimitationinthescopeofour enquirytobasictemporalstructureallowsustocentreouranalysisuponthetemporal structureofmechanicaltheoriesinwhichthefunctionoftimeandtemporalityisat itsmostminimalintermsofproviding undirectedtimeorderings and durations.The firstwewillcall chronordinalstructure,thesecond chronometricstructure.Athird
keytemporalstructurerelatestotherepresentationof empiricalfeatures oftimeor temporality.Thiswewillcall chronobservable structure.Amajorpreoccupationin whatfollowsshallbetheexplicationandanalysisofchronordinal,chronometricand chronobservabletemporalstructuresasfoundwithinclassicalmechanicaltheories.
Theseconddimensionofanalysisthatwillactasaframeforourinvestigationsis theidentificationoftheproblemitself.Thatis,ourendeavourswillbefocusedupon aspecificchainofinterrelatedissuesintheanalysisofparticularaspectsoftimein classicalmechanicaltheorywhichcantogetherbeidentifiedas the problemoftime. Inordertobetterunderstandtheproblemasitoccursinmodernphysicaltheoryit willserveusparticularlywelltoconsidertwo precursorproblems,eachofwhichcan beidentifiedinhistoricaldebatesregardingthenatureoftime.Inordertopresent theseproblemswemustfirstmaketwocrucialfurtherterminologicalspecifications, eachofwhichwillbeexplicatedinmoredetailshortly.First,temporalstructurethat isunchangedundervariationbetweensymmetryrelateddynamicalmodelsinatheory is invariant structure.Second,temporalstructurethatischangedundervariation betweendynamicallyrelatedmodelsinatheoryis dynamicallyrelative structure. The chronordinalproblem isthentofix determinatechronordinalstructure asboth invariantanddynamicallyrelative.The chronometricproblem istofix determinate chronometricstructure thatis invariantanddynamicallyrelative. Eachoftheseproblemscomesfromadesiretorepresenttemporalstructureas invariantanddynamicallyrelative,inthesensewewilldefinebelow,combinedwitha requirementfortwokeytypesofsuchstructure,chronometricstructureandchronordinalstructure,tobedeterminate.Therequirementfordeterminatechronordinalstructurewillbeunderstoodasa pragmaticnecessity,whiletherequirementfordeterminate chronometricstructurewillbeunderstoodasan empiricalnecessity.Thusineachcase, thesearemorethaninterpretativeproblems;rathertheyarephysico-mathematical problems,relatingtothetemporalstructureswhicharerequiredtobemathematically well-definedinordertoprovideanadequatemechanicalrepresentationofdynamical motions.
Anovelachievementinwhatfollowswillbetheidentificationoftheprecursorproblemsattwocrucialjunctureswithinhistoricaldiscussionsofthenaturalphilosophy oftime.Theprecursorproblemswewillidentifyarefoundwithintheearlymodern debatesregardingthe‘absolute’and‘relative’statusoftimeinmechanicaltheory,in particular,withintheclassicabsolutevsrelativetimedialectic,asexpressedinthe correspondencebetweenLeibnizandClarkeintheearly1700s.Stillinthehistorical naturalphilosophicalcontext,wewillalsofindtheseproblemsperspicuouslyexpressed intheworkofErnstMachtowardstheendofthe1800s.OurdiscussionoftheMachian viewoftimewilltakeplacenotonlyintheparticularcontextofadialecticwiththe originalNewtoniantreatmentbutalsoincomparisonwithworkbyMach’scontemporariesonthereframingofNewtonianabsolutetimeintermsofinertialclocks.Ineach case,wewillargue,theinformalproblemisattheheartofkeydebates,disputes,and ambiguities.Newton,Leibniz,andMachallgrappledwiththeprecursorproblemsof time,andvaluablelessonscanbelearnedfromtheirstruggles.Itwillproveofinvaluableprofittoourconstructiveprojecttodeepenourunderstandthefoundationsof theprogenitorproblemsoftimeasfoundinthewritingsofthesethreethinkers.
DiscussionoftheprecursorproblemsinthecontextofthehistoryofnaturalphilosophyoftimeandtheviewsofNewton,Leibniz,andMachwillbethefocusofPartI ofthismonograph.Thiswillleadintoamoreformalandgeneralanalysisofsymmetry andstructureinphysicaltheorythatwillbedevelopedinPartII,themainideasof whichwillbesummarizedshortly.Theformalizedmodernproblemoftimeisfocusof PartIII.Itwillbeworthwhiletogiveabriefoverviewofhowweproposetoformulate andsolvethisproblemnow.
Thisproblemoftimeoccurswithinallmechanicaltheoriesinwhichthelawsare invariantunderlocaltimerelabelling.Such reparameterizationinvarianttheories are thecontextinwhichthemodernclassicalmechanicalproblemoftimecanbeformally statedandinwhichoursolutionshallbearticulated.Theproblemcanbestatedas follows: theproblemoftimeinclassicalmechanicsisthatthesymmetryproperties ofreparameterization-invarianttheorieswithregardtochronometricandchronobservablestructureenforceindeterminacywithregardtosuchstructureunderthestandard approachtogaugesymmetry.
Oursolutionwillbefirsttodemonstratethatthestandardapproachtogauge symmetryisinadequatetothetreatmentofreparameterizationinvarianttheoriesand secondtoformulateageneralandfullyadequatealternativebaseduponamoreperspicuousanalysisoftemporalsymmetryandstructure.Ourapproachissuchthat reparameterizationinvarianceisdemonstratedtobefullycompatiblewithdeterminatechronordinalstructure.Assuch,thenovelapproachtosymmetryandevolution inclassicalmechanicsthatwewillestablishinthismonographwillprovidearesolution oftheproblemoftimeinclassicalmechanics.Wewillprovideaformalanalysisofthe symmetryandstructureofreparameterizationinvarianttheoriesthatallowsfordeterminateandwell-behavedchronometric,chronobservable,andchronordinaltemporal structures.
Thisworkwillprovideaformalbasistorejectalternativeviewsontheproblemof timeinclassicalmechanics.Mostsignificantly,wewilldemonstratetheformalinadequacyofapproachesbaseduponsupposedequivalencebetweendynamicsandgauge symmetry,whichisoftentakentoleadtowardstheoutrightdenialoftemporalevolution.Thisviewisoftenonlyimplicitlyexpressedintheclassicalmechanicalcontext butisastraightforwardimplicationofthestandardinterpretationofHamiltonian constraintswhenappliedtoreparameterizationinvarianttheories.Theessenceofthis viewhasbeenmostvividlyexpressedintermsofthesloganthat‘motionistheunfoldingofagaugetransformation’(HenneauxandTeitelboim,1992,p.103).That suchparadoxicalstatementscanbefoundwithintextbooktreatmentsofcontemporaryphysicaltheoryiswithoutdoubtremarkable.Onemightplausiblyclassifysuch anunderstandingasthepseudo-problemoftime.Onemajorgoalofourprojectwill betodemonstratethatthepseudo-problemispreciselythat.Supposedequivalence betweenmotionandgaugesymmetryrestsuponaformalconflation.Inparticular, wewillimplementanewformalanalysisthatallowsonetoexplicitlydifferentiatethe generatorsofevolutionand‘gauge’symmetryinreparameterizationinvarianttheories. Fundamentaltimelessnessthusrestsuponamistake.Motionisnottheunfoldingofa gaugetransformation.Withthecorrectmathematicaltoolsonecanclearlydistinguish
thefundamentallydistinctrolesofsymmetryandevolutioninreparameterizationinvarianttheoriesofclassicalmechanics.
Onamoreconstructivenote,weshouldmentionasecondalternativeapproachto theproblemoftimethatworkstowardsadeflationratherthanasolution.Theessence ofthisviewisideathatafunctionallyadequatemechanicscanberecoveredbasedupon arelativizedandunderdeterminedchronordinalstructure.Underthisview,chronordinalstructurecanbebuiltinternallytoamechanicalsystembyreferencetoparticular degreesoffreedomthatplaytheroleofinternalclocks.Thisviewhasbeenadvocated consistentlyinthecontextofreparameterizationinvariantclassicalmechanicaltheoriesbyRovelli.1 Formally,thisapproachwillbeshowntobeacomplementary,yetin acertainspecificsensemorelimited,thanourownanalysis.
1.2SymmetryandEvolution
Ouranalysisofsymmetryandevolutioninclassicalmechanicsisdesignedtobeof independentvalueoutsidetheanalysisofreparameterizationinvarianttheoriesand theproblemoftime.Weconstructanewframeworkfortheanalysisofsymmetry andstructureinmechanicaltheorywhichallowsfortheanalysisofthefullsetof transformationpropertiesofanystructurethatcanbedefinedonthemodelspace ofatheory.Thisframeworkallowsforafine-grainedandunambiguousidentification of‘gaugesymmetries’intermsoftheexistence,ornot,ofinitialvalueconstrains. Moreover,ourframeworkwillalsoallowfortheidentificationofcoreheuristicsfor theoryextensionandre-articulation.Thecoreaspectsofourframeworkcanbeoutlined informallyasfollows.FullformaldefinitionsandproofswillbeprovidedinPartII.
1.2.1ThreeLevelsofTheoreticalStructure
Aphysicaltheorycanbeanalysedintermsofthreelevelsofstructure,eachwith differentformsandfunctions.Atthemostbasiclevel, constitutivestructure isthe mostbasicstructureofatheory.Thisisthestructurethatonemustassumeinorder tobuildthespaceofkinematicallypossiblemodels.Thatis,thespacewhichrepresents thebasic‘pre-nomic’setofpossibilitiesadmittedbythetheory.Eachofthesemodels canbethoughtofassomethinglikeabareuniverse,strippedoflawsanddynamics.The constitutivestructuresarethoserequiredtoformulatethespace, K,of kinematically possiblemodels (KPM)ofthetheory.Forthemostpartwewillassumethatthe constitutivestructuresconsistof:i)amanifoldstructureusedtocharacterizephysical events,andrepresentedbyadifferentialmanifold;ii)geometricstructures,usedto characterizerelationsofordering,distanceandorientationbetweentheevents;and iii)matterstructures,usedtocharacterizethenon-geometricmaterialcontent.
Modelswithdifferenttokensofthesametypeofconstitutivematterandgeometric structurearetypicallyconstitutivelydistinctKPMsofthesametheorydespitethefact thattheysharethesameconstitutivestructure.Thus,forexample,two-andthreebodyparticlemodelscanbeunderstoodashavingthedistincttokensofacommon Newtonianconstitutivestructure.
1 SeeinparticularRovelli(2002,2004,2007).
Thetoken-typedistinctionwillallowustodistinguishbetweenthefollowingtwo cases.FirstwehavestructurecommonbetweenallKPMswhichsharethesame type ofstructure.Suchstructureisconstitutivelyfixed.Constantsofnaturecantypically beunderstoodasanexampleofconstitutivelyfixedstructuresofatheory.Second wehavestructurethatiscommonbetweenallKPMswhichsharethesame token of structurebutwhichvariesbetweenatleasttwodistincttokensofthesametypeof constitutivestructure.Constantsofmotioncantypicallybeunderstoodasanexample ofconstitutivelyfixedstructuresofatheory.Thisdistinctionallowsfordifferentiation betweenthemodalstatusoftwodifferenttypesofstructure.Thatis,structurethat isthesameinallKPMsofthesamemodeltype,andstructurethatcanvarybetween kinematicallypossiblemodelsthatinstantiatedifferenttokensofthattype.
WithregardtoKPMs,ourframeworktakesaformsimilartothatofwhatweshall callthe StandardFormalism usedtocharacterizethemodelspaceofaphysicaltheory. ThestandardformalismisarticulatedintermsofaspecificationofthespaceofKPMs togetherwithasetofsolution-independent‘fixed’(or‘non-dynamical’)fieldscommon toallKPMs,andasetof‘non-fixed’(or‘dynamical’)fieldsnotcommonbetweenall KPMs.Constitutivelyfixedinoursensethuscoincideswithfixedwithinthestandard formalism.WewilldiscussthisrelationshipatlengthinChapter5andreturnbriefly totheconceptoffixedstructureshortly.
Nomicstructureorlaw-likestructureisthestructurethatrepresentsthelawsof aparticulartheory.Inourframeworknomicstructurewillhavetwoimportantand distinctfunctions.Thefirstfunctionofnomicstructureistopickoutapartitionin thespaceofKPMs:thatis,totelluswhichmodelsaredynamicallypossibleand whicharenotdynamicallypossible.Wecanformalizethispartitioningfunctionin termsofanomicstructurethatpartitionsthespaceofKPMsintothepropersubspaceofdynamicallypossiblemodels,orDPMs, D ⊂ K.Thesecondfunctionofnomic structureistoprovideuswithanequivalencerelationbetweenDPMs.Theequivalence relationfunctionprovidesamethodologyfordeterminingwhichDPMsaredynamically distinctandwhicharedynamicallyidentical.Therelevantnotionofdistinctnessand identityishereanomiconeratherthananonticone;thatis,adistinctionbasedupon adifferencethatthelawspickoutbetweentwomodelsandnotadistinctionthatis necessarilyequivalenttoastrongmetaphysicalnotionofdistinctnessandidentity.
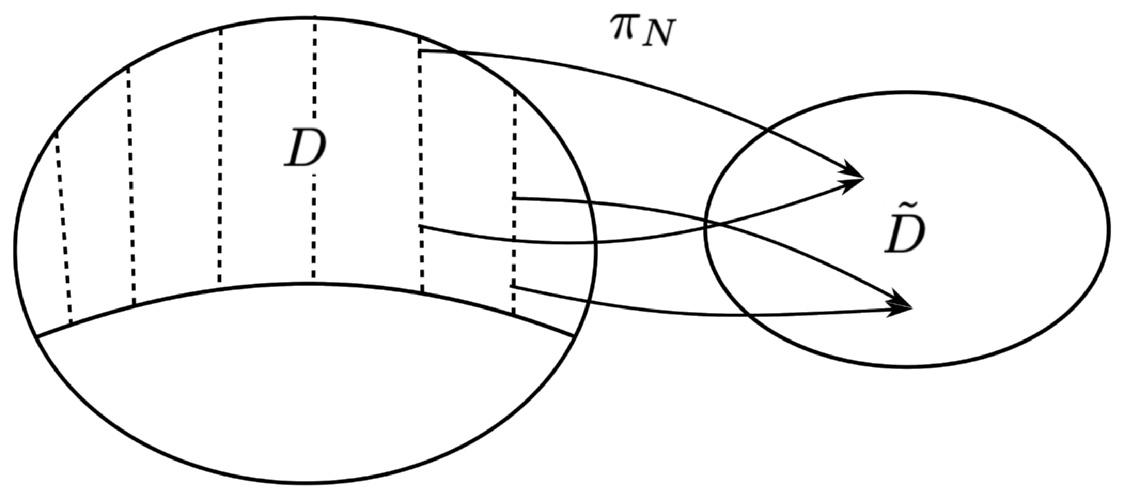
Wecanexplicitlyformalizetheequivalencerelationfunctionofnomicstructurein termsofa ProjectionMap, πN .Thisissomenomicstructurethatservesto‘projectout’ distinctionsbetweenmodelsaccordingtosomedynamicalequivalenceprinciple.We candesignatethespaceofequivalenceclasses D of D thespaceofDistinctDynamically PossibleModels(DDPMs);thisallowsustoconsidertheprojectionfromthespace ofDPMstothespaceofDDPMs: πN : D → ˜ D.Theroleofthenomicstructure canbegivenaschematicrepresentationasperFig.1.1wherewehaveintroducedthe terminologyofa‘fibre’fortheequivalenceclassofDPMs.
1.2.2SymmetryandEquivalence
Theterminologywehaveintroducedthusfaralreadyaffordsusresourcestodemarcate anumberofconceptsofsymmetryandequivalence.Inparticular,wearenowina
namicallypossiblemodels.Thedottedlinesare‘fibres’thatrepresentdynamically equivalentmodelswhichtheprojectionmap, πN ,mapsintosinglepointsinthespace ofdistinctdynamicallypossiblemodels, ˜ D positiontodisambiguatetheideaofasymmetryasatransformationwhich‘maps solutionsintosolutions’viaathreefolddistinction.
Firstwecandistinguish non-symmetrymaps.ThesearemapsbetweenDPMsof atheorythatareconstitutivelydistinctatthetokenlevel;thatis,mapsbetween differenttokensofthesameconstitutivestructure.Thesemapstakesolutionsinto solutionsbutarenotsymmetriesinanyrelevantsensesincetheydonotpreserve constitutivestructureatthetokenlevel.Simpleexamplesincludemappingbetween two-bodyandthree-bodysolutionsinNewtonianmechanicsandmappingbetween SchwarzschildanddeSittersolutionsingeneralrelativity.
Second,wecandistinguish broadsymmetrymaps.Thesearemapswhichtransform betweenDPMsthatareconstitutivelyequivalentatthetokenlevel.Broadsymmetry mapstransformbetweenDPMswiththesametokenoftheconstitutivestructure;for example,mapsthattransformbetweenthedifferentinitialconditionsofathree-body Newtoniangravitationalsystem.
Third,wecandistinguish narrowsymmetrymaps.Anarrowsymmetryisasub-set ofthebroadsymmetrieswhichcorrespondtomapsbetweenDPMswhichareconstitutivelyequivalentanddynamicallyequivalent.Theintuitiveandvaguelyexpressedidea of‘symmetrytransformation’canbeprecisifiedasourconceptofnarrowsymmetry.
FollowingBelot(2013),itisworthmentioningatthisstageofouranalysisthat thestandardapproachestothedynamicalformalisationofsymmetriesintermsof variationalsymmetries,divergencesymmetries,orHamiltoniansymmetrieswillnot ontheirownfurnishareliablenotionofnarrowsymmetry.Thisisbecause,aswill bediscussedinmoredetaillater,therearealwayscaseswheresuchformalisationsof dynamicalsymmetriesleadusto:i)designateasequivalentDPMswhichwewantto thinkofasdynamicallydistinct;andii)designatedistinctDPMswhichwewantto thinkofasdynamicallyequivalent.Ourmethodologywillbetoapproachtheresolutionofsuchproblematicambiguitiesinstages.Thefirststageistheformulationofa deliberatelytooweakpreliminarystancetowardstheclassificationofnarrowsymmetriesbuiltuponanappropriaterefinementofoneofthestandardformalsymmetry
Fig. 1.1: Schematic representation of the nomic structure. D is the partition of dy-
definitions.Thesecondstagewillthenbetomodifythenomicstructuresuchthatthe furtherphysicallywell-motivatednarrowsymmetriescanbestipulated.
Wecanspecifyourweaknotionofnarrowsymmetryviaasufficientbutnotnecessaryconditionasfollows: preliminarystanceonnarrowsymmetries:allbroadsymmetrieswhicharevariationalsymmetries(i.e.transformationsthatleavethevariational probleminvariant)ofthefullsystemunderstudyarenarrowsymmetries. Hereweare usingtheword‘stance’followingapartialinspirationfromvanFraasen’sepistemic voluntarisminthecontextofphysicalreasoningregardingsymmetries,laws,andtheoreticalmodels.Inparticular,wetaketheretobesignificantroomfor‘operationofthe will’whenitcomestoourchoiceofnarrowsymmetryprinciples(vanFraassen,1989; vanFraassen,2008;Okruhlik,2014).Further,thestanceisbydesignapreliminary one,opentorevisionandmodificationbutconstitutingasolidworkinghypothesis thatcanbeusedasafirststepintheanalysisofthenarrowsymmetriesofaphysical theory.
Thepreliminarystanceallowsustoclassifyasnarrowsymmetriesthemostbasic andnaturalexamplesofmapsbetweendynamicallyequivalentmodels.Forexample, time-independentrigidEuclideantransformationsofasetofgravitatingNewtonian pointparticlesarevariationalsymmetriesandthuswewillrecovertheexpectation thatre-embeddingthesamesetofNewtoniangravitationalmotionsinauniformly spatiallyshiftedspacewillleadtoadynamicallyequivalentmodelofthetheory.
Theobviouscomplicationforeventhissimplecasearetime-dependenttransformationssuchasGalileanboosts.Thesearenotvariationalsymmetriesofasetof gravitatingNewtonianpointparticlesandthus,underthepreliminarystance,models relatedbysuchtransformationsaretakentobedynamicallydistinct.However,the physicalproblemathandmayindicatethattherelevanttransformations should be narrowsymmetries.Thisiswherethesecondstagecomesin.Onourapproach,such transformationsmaybepromotedtonarrowsymmetriesbyamodificationofthevariationalprinciple.Thenarrowsymmetriesofatheorycanbeadaptedtotheparticular contextinwhichthetheoryisbeingapplied,butatthecostofexplicitlychangingthe variationalprincipleusedtodefinethesolutionsofthetheory.Explicitconsideration ofthiscasewillbeprovidedin §6.5and §8.5.
1.2.3IrregularNomicStructure
Thephysicalsignificanceoftheambiguitiesinthedynamicaldefinitionofnarrowsymmetryshouldnotbeoverstated.Theprimaryroleofdynamicalequivalenceprinciples, andthusthedefinitionofnarrowsymmetries,withinmechanicaltheoryisinthespecificationofthedynamicalevolutionofagivensystemintermsofwell-posedequations ofmotion.Fromtheperspectiveofthevariationalproblem,themostfundamentalsubdivisionisbetweenthosetheoriesinwhichthenomicstructure enforces aprojection asarequirementforwell-posednessandthosetheoriesinwhichthenomicstructure whichallowsforindependentwell-posedequationsofmotionforallmodelswhichare DPMs.
InthecontextofLagrangianactionprinciplesthisisadistinctionwhichis(almost)entirelybetweenwhatareusuallycalled‘regular’Lagrangiansand‘irregular’ Lagrangians.Withthisinmindwecanintroducethedistinctionbetweenregularand
irregularnomicstructure. RegularNomicStructure isnomicstructurethatenforcesa partitionbutnotaprojection.ForatheorywithregularnomicstructureitisinprinciplepossibletotreatallDPMsasprimefaciedynamicallydistinct.However,thereare typicallygoodphysicalreasonstoapplyaprojectionbasedonpreliminarystance.It is,however,inprinciplepossibletotreatallDPMsasprimefaciedynamicallydistinct, notwithstandingthepreliminarystance.
Bycontrast, IrregularNomicStructure isnomicstructurethatenforcesapartition andaprojection.Foratheorywithirregularnomicstructureitismandatoryto classifyatleastsomeDPMsasdynamicallyequivalentinordertoconstructawellposedinitialvalueproblem.ItisinprinciplethenpossibletotreatallDPMswhichare independentlywell-posedasdynamicallydistinct.However,againtherearetypically goodphysicalreasonstoapplyaprojectionbasedonthepreliminarystance.
Thecrucialphysicalideaisthatintheorieswithregularnomicstructure,alldegreesoffreedomhaveindependentlywell-posedequationsofmotionassociatedwith them.Foratheorywithregularnomicstructure,thereisanimportantsenseinwhich thereis formally noredundancyorunderdeterminedequations.Theclassoftheories withirregularnomicstructureisimportantlydifferent.Inparticular,withafewimportantexceptions,thesetheoriesaresuchthatthereexistdegreesoffreedomwhich donothaveindependentlywell-posedequationsofmotionassociatedwiththem.In suchcircumstances,wetypicallyencounteraperniciousformof dynamicalredundancy whereinthereexisttransformationsofthedynamicalvariablesthatleadtoanunderdeterminationintheequationsofmotion.Suchredundancy must beinterpreted asnarrowsymmetrysinceotherwisetheinitialvalueproblemwillnotbewell-posed. Thestandardterminologyforsuchtransformationsis‘gaugetransformations’andthe underdetermineddynamicalvariablesarestandardlyunderstoodas‘gauge’degreesof freedom.
Theinterconnectedproblemsofunderdetermination,gaugesymmetries,andredundancyhavebeenthesubjectofalargeamountofdiscussioninbothphysicsand thephilosophyofphysics,bothingeneraltermsandinthespecificcanonicalcontext thatisthefocusofthisbook.2 Noneoftheextantaccountsarefullysatisfactory,however.Furthermore,asalreadynoted,wetaketheproblemoffindingsuchanaccount tobethekeychallengetothecorrectdiagnosisandresolutionoftheproblemoftime inclassicalmechanics.
Thestandardtreatmentoftherelationshipbetweensymmetryandredundancy derivesfromtheDiracanalysisofconstrainedHamiltoniansystems.3 Inparticular, thekeydiagnostictoolcomesfromaprescriptionduetoDiracfortheidentification of‘gaugetransformations’andtheassociatedredundancyinsystemswithirregular nomicstructure.Thisapproachisbuiltupontheidentificationof canonicalconstraints asgeneratorsofgaugetransformations.Inbrief,theideaisthatcertainconstraint functionsthatoccurinthederivationofthecanonicalmomentaaretakentogether
2 Extensivereferencetothephysicsliteraturewillbeprovidedinwhatfollows.Keycontributions fromphilosophersare(BelotandEarman,2001;Belot,2003;Earman,2003;Rickles,2004;Rickles, 2007;Pitts,2013;PooleyandWallace,2022).Ourownanalysisprovidedbelowisbaseduponan extensionofthatprovidedin(GrybandTh´ebault,2014;GrybandTh´ebault,2016a).
3 ThetextbooktreatmentsareprovidedinDirac(1964),SudarshanandMukunda(1974),Sundermeyer(1982),GitmanandTyutin(1990),andHenneauxandTeitelboim(1992).
withrelevantconsistencyconditionstoformanalgebrathatexpressesthefailureof thecanonicalsystemtobeindependentlywell-posed.Thesolutionisthentotreat asdynamicallydistinctonlythosesolutionsthatareindependentoftheconstraint algebraintermsofthedirectionsoftheassociatedflowsonphasespace.Conversely, accordingtotheDiracprescription,phasespacepointsthatliealongtheorbitofa constraintshouldbetakentorepresentphysicallyidenticalstatesofaffairs.Thusthe transformationbetweensuchpoints,asgeneratedbytheconstraint,ismeregauge. TherearehowevervariousgeneralconsiderationsthatcallintoquestiontheDirac prescription.Thefirstisthattheprescription,bothinoursketchandinthedetailed presentationbothbyDiracandbysomelaterauthors,elidesthesignificantdifference betweentransformationsofinstantaneousstatesandtransformationsofdynamical histories.Clearly,onewouldliketobeabletomovebackandforthbetweenthe symmetriesdefinedatthelevelofhistoriesandthedynamicalredundancywhich existsattheleveloftheinitialvalueproblem.However,considerablecareisneeded insettingupsuchcorrespondences,andonitsowntheDiracapproachprovestoo coarse-toothedfortherelevantpurpose.Onegoalofourapproachistoprovidea geometricframeworkthatallowsforthedisambiguationoftheconnectionsbetween constraints,redundancy,and‘gauge’symmetriesatboththelevelofhistoriesandthe levelofinstantaneousstates.
ThesecondmorefundamentalissuewiththeDiracprescriptionisitsimplicationfor theorieswhichareinvariantundertimereparameterizations.Ageneralfeatureofsuch theoriesisthattheHamiltonianfunctionisitselfnecessarilyaconstraint.Thisthen meansthattheDiracprescriptionimpliesthattheHamiltonianfunctionisagenerator ofgaugetransformations.However,weofcourseapplytheHamiltonianfunctionalsoin theroleofthegeneratorofdynamicalmotions.Wethenarriveatourparadox:motion istheunfoldingofagaugetransformation!Herethelinesofinterpretationbecome rathercriss-crossed.Dirachimselfinfactneverendorsedsuchaparadoxicalconclusion. Moreover,theargumentthathehimselfprovidedfortheprescriptionclearlydoesnot supporttheconclusioneither.WhatisoftencalledDirac’stheoremwillbeexplicitly reconstructedin §7.3.FollowingonfromthediscussionofBarbourandFoster(2008), itshallbemadeexplicitinourrenditionofthetheoremthattheresultthatisproved byDiracislimitedinscopebytheassumptionthatconstrainedHamiltoniantheory inquestioncontainsanexternaltimevariable.Dirac’stheoremthussimplydoesnot applytoreparameterizationinvarianttheories.
AtthispointitmightbehopedthattheambiguitiesinthissituationcanberesolvedbyappealtoNoether’ssecondtheorem.Thisisbecausethesecondtheorem establishesaconnectionbetweeninvarianceofanactionunderinfinitesimaltransformationsofaninfinitecontinuousgroupparameterizedbyarbitraryfunctionsandthe existenceofgeneralized‘gauge’identitieswhichholdirrespectiveofthesatisfaction oftheEuler–Lagrangeequations.Sincereparameterizationinvarianceispreciselyan invarianceoftheactionunderaninfinitesimaltransformationofaninfinitecontinuous groupparameterizedbyarbitraryfunctions,oneisthusguaranteedtheexistenceofa gaugeidentityinthiscasealso.Onemightexpect,then,thattherelevantgaugeidentitiesallowonetoidentifydynamicalredundancywithintheinitialvalueproblemand thusremovetheambiguityintheDiracprescriptionforthecaseofreparameterization
invarianttheories.
Thesituationisnot,however,sostraightforward.Infact,newworkwillberequiredtoestablishingeneraltermstheconnectionbetweenirregularnomicstructure, Noether’ssecondtheorem,andtheexistenceof initialvalueconstraints.Itisthelatter whichareindicativeofthespecificspeciesofunderdeterminationproblemassociated withdynamicalredundancyandwhicharerequiredfortheisolationofgaugedegrees offreedom.Themajorformalachievementofthismonographistheestablishmentof afirst-ordergeometricformalismthatprovidesgeneralcriteriaforisolatingdynamical redundancy.ThesecriteriageneralizeandsupersedethoseprovidedbyeitherNoether’s secondtheoremortheDiracapproach.Theyarealsoimportantinidentifyingthecrucialambiguityregardingthepreliminarystanceinthecontextofthedistinctionbetweenvariationalsymmetries-over-historiesandvariationalsymmetries-at-an-instant. Asweshallsee,reparameterizationsshouldbeunderstoodasvariationalsymmetriesover-historiesandthusinthatsensearenarrowsymmetries.However,reparameterizationsarenotvariationalsymmetries-at-an-instantandthereforearenotnarrow symmetriesinthatsense.
Ourprojectistoprovidenewandmorefundamentaldiagnostictoolsforinterpretinggaugetheories.Thischallengeshallbetakenupintwostages.ThefirstinChapter 8willbetosetoutourfirst-orderformalismforthecaseoftheorieswithafixed timeparameterization.Theproblemofextendingouranalysistoreparameterization invarianttheorieswillbethesubjectofanextendedanalysisinPartIII.Crucialto interpretingtheimplicationsofthisnewformalismwillbethenewframeworkforthe analysisofsymmetryandstructurethatwewillsummarizebelow.
1.3TransformingStructures
1.3.1AbsoluteandRelativeStructures
Distinctconceptsof‘absolute’and‘relative’areoftenconflatedindiscussionsofthe statusofspaceandtimeinphysicaltheory.Itwillproveessentialtoourdiscussionto differentiate three basiccontrastsinthecontextofourdiscussionsofspatiotemporal structuresinphysicaltheory.HerewearetakinginspirationfromFriedman(1983, II.3).Theseare:i)absolutevsrelationalspatiotemporalstructure,whichisanontologicaldistinctionrelatingtodependencyrelations;ii)absolutevsrelativespatiotemporalstructure,whichisaformaldistinctionrelatingtonon-dynamicaltransformation properties;andiii)absolutevsdynamicalspatiotemporalstructure,whichisaphysical distinctionrelatingtodynamicaltransformationproperties.Forclarity,wewillmakea terminologicalrefinementarenamethetrioofdistinctionsas substantival vs. relational (ontologicaldistinction), invariant vs. surplus (formaldistinction),and dynamically absolute vs dynamicallyrelative (physicaldistinction).Withthisterminologyinhand letusthenconsidereachcontrastinalittlemoredetail.4
4 Thereisavastliteraturethatdiscussesindifferentwaysandusingdifferentterminologieseach ofthesedistinctions.OuraccountismostcloselyrelatedtothatofFriedman(1983,II.3).Further generaldiscussionscanbefoundinSklar1974;Earman1989;Rickles2007;Maudlin2012;Pooley2013; Dasgupta2015.Theliteraturespecificallydealingwithabsoluteandrelativespacetimestructurein thecontextofanalyticalmechanicswillbeintroducedinthecontextofourspecificdetaileddiscussions inPartsIIandIII.
Thefirstcontrastbetweenabsoluteandrelationalrestuponadistinctionwith regardtothe‘onticdependency’betweenmaterialandspatiotemporalentities.FollowingPooley(2013,p.522),asubstantivalistaboutspatiotemporalstructurewill maintainthatacompletecatalogueofthefundamentalobjectsintheuniverselists, inadditiontotheelementaryconstituentsofmaterialentities,thebasicpartsofthe relevantspatiotemporalstructure.Relationalistsmaintainthatspatiotemporalstructuredoesnotenjoyabasic,non-derivativeexistence.Accordingtotherelationalist, claimsapparentlyaboutspatiotemporalstructureareultimatelytobeunderstoodas claimsaboutmaterialentitiesandthepossiblepatternsofspatiotemporalrelations thattheycaninstantiate.
Thecontrastbetweenrelationalismandsubstantivalismcanbeconnectedtodifferentaccountsofhowonecountsdistinctontologicalpossibilities.Thisisonthebasis oftherelationalistadmittingfeweronticpossibilitiesthanthesubstantivalistprecisely becausetherelationalist,butnotthesubstantivalist,deniesthattwostatesofaffairs thatareidenticalintheirrelationalspatiotemporalstructurecanbeontologicallydistinct.Adirectequationoftheviewswithstrategiesforpossibilitycountingrestupon anoversimplificationhowever,sincesomeprominentsubstantivalviewsthatcount possibilitiesinthesamewayasrelationalists.5 Asweshallexplaininmoredetail shortly,wewillseekto‘bracket’theontologicaldistinctionbetweenrelationalismand substantivalisminourdiscussionswheneverpossible.Thattheconnectionbetween possibilitycountingandontologyprovestobesounderdeterminedisarguablyavindicationofsuchastrategy.Inanycase,thesignificanceforourcurrentdiscussionis thatanyontologicaldistinctionbetweenrelationalismandsubstantivalism doesnot haveacorrelateinthetransformationbehaviourofspatiotemporalstructuresunder mapsbetweenDPMsascharacterizedintheframeworkintroducedin §1.2.
Thesecondcontrastcanbecharacterizedpreciselyinourframeworkviathebehaviourofaspatiotemporalstructureundernarrowsymmetriestransformations.As notedabove,forclarity,wewillrefertothe‘absolute’spatiotemporalstructuresthat donotchangeundernarrowsymmetrytransformationsas invariant structuresand the‘relative’spatiotemporalstructuresthatdochangeinawell-behavedmanneras surplus structures.Thisclassificationwill,ofcourse,onlybedefinedinthecontext ofadefinitionofnarrowsymmetriesforaparticulartheory.Itwillthusinheritall thecomplexitiesandqualificationsinthedefinitionofnarrowsymmetriesasperour earlierdiscussions.
Theimportantpointisthatforanygivenspecificationofnomicstructureinterms ofapartitionandprojection,onehasathandanentirelyunambiguousdefinitionof themapsthattransformbetweenDPMswhichareidenticalaccordingtotherelevant nomicstandardofequivalence.Thesetransformationswithinanequivalenceclassare graphicallyrepresentedasmovingalongthe‘fibres’givenbytheverticaldottedlines inFig.1.1.Invariantspatiotemporalstructureisthenstructurewithtransformations thatareentirelytrivialasonemovesalongthefibre.Surplusspatiotemporalstructure
5 Applicationofthisgeneralstrategyforsubstantivalismwithreducedpossibilitycountingcanbe foundforinstanceinMaudlin1988;Butterfield1989;Brighouse1994.SeealsoRickles(2007)and Pooley(2013).
bycontrastisstructurethathasnon-trivial,butwell-definedtransformationproperties asonemovesalongthefibre.
Finally,wecanconsiderthethirdcontrastthatrelatestothetransformationbehaviourofaspatiotemporalstructureunder‘dynamicaltransformations’,definedas thebroadsymmetrieswhicharenotnarrowsymmetries.Wewillrefertospatiotemporalstructuresthatdonotchangeunderdynamicaltransformationsas dynamically absolute andtemporalstructuresthatdochangeinawell-behavedmanneras dynamicallyrelative 6 Itisimportantnoteherethatbyourdefinitionthedynamical transformationsaremapswhichtransformsbetweenDPMsthatareconstitutively equivalentatthetokenlevelandyetdynamicallydistinct.Thisisthecomplementof thenarrowsymmetrieswithinthesetofbroadsymmetries.
Inparalleltothesecond‘formal’distinction,inthecaseofthisthird‘physical’ distinction,itisimportantthatforanygivenspecificationofnomicstructureinterms ofapartitionandprojection,onehasathandanentirelyunambiguousdefinitionof themapsthattransformbetweenDPMswhicharedistinctaccordingtotherelevant nomicstandardofdistinctness.Thesetransformationsbetweenequivalenceclassesare graphicallyrepresentedasmovingbetweenthe‘fibres’givenbytheverticaldotted linesinFig.1.1.Dynamicallyabsolutespatiotemporalstructureisthenstructurethat issuchthatitstransformationsareentirelytrivialbetweenthefibres.Dynamically relativespatiotemporalstructurebycontrastisstructurethathasnon-trivial,butwelldefined,transformationpropertiesasonemovesbetweenthefibres.Movingbetween thefibresinspaceofDPMs D isofcourseequivalenttomovingbetweenpointsin thespaceofDistinctDPMs D,givenbytheprojection πN : D → D.Thusbyour definitionsdynamicallyabsolutestructuredoesnotchangebetweenanypointin ˜ D but dynamicallyrelativestructuredisplayedwell-definedandnon-trivialtransformation propertiesundertransformationsin D.
Asabriefaside,itisworthnotingthatdynamicaltransformationsdonotconstitute thefullsetoftransformationsbetweendistinctDPMs.Thisisbecausewearealso excludingfromourdefinitionofdynamicaltransformationsmapsbetweenDPMsof atheorywhichareconstitutivelydistinct;thatis,mapsbetweendifferenttokensof thesameconstitutivestructure.Thesemapstakesolutionsintosolutionsbutare notsymmetriessincetheydonotpreserveconstitutivestructureatthetokenlevel. Returningtoourfavouriteexamples,considermappingbetweentwo-bodyandthreebodysolutionsinNewtonianmechanicsormappingbetweenSchwarzschildandde Sitteringeneralrelativity.Whilsttheinvarianceornotofspatiotemporalstructure inthecontextofsuchconstitutivelydistinctmodelsisofgreatphilosophicaland physicalsignificance,especiallyinthecontextoftheproblemofprovidingasubstantive definitionofbackgroundindependence,theformalstructureoftransformationsinthis widercontextisnotamenabletotheanalysiswewillprovideandwillthusbetreated asadistinctcasefromdynamicaltransformationswhenrequired.
Torecap,wehaveintroducedthreebinarycontrasts:anontologicalcontrastbetweensubstantivalandrelational;aformaldistinctionbetweeninvariantandsurplus;
6 Dynamicallyabsolutestructuresinoursenseareanalogues,insomeways,toso-calledAbsolute Objects.SeePooley(2017, §7)andCuriel(2019).
AbsoluteRelative
Ontological Substantival Relational Formal Invariant Surplus Physical DynamicallyAbsolute DynamicallyRelative
Table1.1 Tableillustratingthreebinarycontrastsregardingsensesinwhichaspatiotemporalstructuremaybeabsoluteorrelative.Undertheassumptionofindependencethreebinary choicesyieldseightpossibilities.
andaphysicaldistinctionbetweendynamicallyabsoluteanddynamicallyrelative.For easeofreferenceandunderstandingwehavesetoutthesedistinctionsinTable1.1.
1.3.2BracketingOntology
Inprincipleitispossibleforagivenspatiotemporalstructuretobeunderstoodas realizedanyoftheeightpossibilitiesgivenbyarbitrarycombinationsofthethree binarydistinctions.Forexample,inprinciple,onemightholdthatagivenstructure issubstantival,surplus,anddynamicallyrelativeorrelational,invariant,anddynamicallyabsolute.Withinthecontextofourpositiveprojectwewillmakethesignificantmethodologicalchoicetotreatthethreedistinctions,substantivalvsrelational, invariantvssurplus,anddynamicallyabsolutevsdynamicallyrelativeasmutually independentandtofocusouranalysisonthesecondandthirdtotheexclusionofthe firstwhichwillbe‘bracketed’inwhatfollows.
Thisisnottosaythatwedonotrecognizethatadeepconceptualallianceexistsbetween,forexample,relationalismanddynamicalrelativity.Suchconnections willbeconsideredatlengthinourdiscussionoftheviewsofNewtonandLeibniz inPartI.Moreover,ingeneralterms,itisplausiblythecasethatatleastsomekey argumentsareatleastinpartoverlapping.Forexample,epistemologicalarguments infavourofrelationalandinvariantstructure.However,inourviewtherelationalist/substantivalistontologicaldisputecaninfactbelargelydetachedfromwhatwe taketothe physicallysignificant issuesregardingthe formalrepresentation ofspatiotemporalstructureinphysicaltheory.Theseissues,inourview,arealwaysissues regardingtheinvariant/surplusanddynamicallyabsolute/relativedistinctions.Inline withourprogrammaticaimofresolvingtheproblemoftimeinclassicalmechanics, ratherthaninterveningindebatesregardingthemetaphysicsoftime,wewillseek to‘bracket’theontologicaldisputeandfocusourenergiesonthesecondandthird physico-mathematicaldisputes.
Onespecificmeansthatwewillusetoachievethisbracketingistoleaveopenthe representationalrelationshipbetweendistinctDPMsandtheontologytheystandin forintheworld;thatis,wewillrefrainfromassumingan interpretation thatfixes eitheramodel-worldrepresentationrelationorstandardofrepresentationalequivalencebetweenmodels.Itisonlygivenachoiceofaparticularinterpretativeattitude towardsrepresentationthatournotionofdynamicallydistinctmodelscanbetakento fixarelevantnotionof ontological distinctmodels.Inparticular,sofarasthedebate betweenrelationalistsandsubstantivalistsreducestothecorrectonticpossibility,this debateistransformedintoachoiceofattitudetowardsrepresentationthatwerefrain
frommaking.Theimportantpoint,fromourperspective,isthatitisperfectlypossibleforallpartiestoadisputeregardingontologyandrepresentationtoagreeonthe appropriatecriterionofdynamicalequivalencewhilstdisagreeingwithregardtothe furtherinterpretationalmovethatfixesanotionofontologicalequivalence.
1.3.3IncompleteandInhomogenousTransformations
Afurtherimportantpointrelatestohowwewillimplementtheinvariant/surplus anddynamicallyabsolute/relativedistinctions.Itwillinfactproveofgreatutilityto understandtheseastripartiteratherthanbipartitedistinctionsbyallowingforthecase inwhichthestructureinquestiondonotvaryinawellbehavedwayundertherelevant transformation.Thatis,aswellashavingstructuresthatdonotchange(i.e.are invariant/dynamicallyabsolute)anddochange(i.e.aresurplus/dynamicallyrelative) undertherelevanttransformations,wewillconsiderstructuresthatare‘incomplete’ andthusare‘broken’bytherelevanttransformation.
Asalreadynoted,foranygivenspecificationofnomicstructureintermsofapartitionandprojection,onecanconsiderthemapsthattransformbetweenDPMswhich aredistinctaccordingtotherelevantnomicstandardofdistinctnessandthosemaps thattransformbetweenDPMswhichareequivalentaccordingtotherelevantnomic standardofequivalence.RecallingFig.1.1oncemore,thefirstsetoftransformations movebetweenthefibresandthesecondsetmovealongthefibres.Wecandistinguish dynamicallyincomplete asstructurethathasill-definedtransformationpropertiesinducedbythetransformationsbetweendynamicallydistinctmodels,correspondingto movementbetweenthefibres(orequivalentlybetweendifferentpointsin ˜ D). Kinematicallyincompletestructure whichisstructurethathasill-definedtransformation propertiesinducedbythetransformationsbetweendynamicallyequivalentmodels, correspondingtomovementalongthefibres.
Oncewebrackettheontologicaldistinctionbutaddthetwopossibilitiesforincompletestructureweareleftwith twotrinary distinctions.Wecanthinkofthese sixcombinationsaspickingout invariant structurethatdoesnotvaryundernarrowsymmetriestransformations, surplus structurethatiscovariantundernarrow symmetries, dynamicallyabsolute structurethatdoesnotvaryinawelldefinedway underdynamicaltransformations, dynamicallyrelative structurethatdoesvaryunder dynamicaltransformations,andthen kinematicallyincomplete and dynamicallyincomplete structuresthathaveill-definedtransformationpropertiesundertherelevant transformations.
Wecannowconsidercombinationsofthesecombinations:structurethatisboth invariantdynamicallyandrelativeorbothsurplusanddynamicallyabsolute.Since wehavetwotrinarydistinctionstherearesixpossibilities.Foreasyofreferenceand understandingwehavesetoutthesedistinctionsinTable1.2.Mostsignificantlywithin thesixpossiblechoicesisthecombinationthatwewilllabel fixedstructure.Thisis structurewhichisbothinvariantanddynamicallyabsolute.Suchstructureisidentical forallDPMs.Recallingourdefinitionsabove,clearlyallstructurethatisthesamefor allKPMs,andthusconstitutivelyfixedorcontingentlyfixed,willbethesameforall DPMs,andthusfixedstructure.Theconverseneednotholdofcourse,sincestructure
AbsoluteRelativeIncomplete
Formal Invariant Surplus KinematicallyIncomplete Physical DynamicallyAbsolute DynamicallyRelative DynamicallyIncomplete
Table1.2 Tableillustratingtwotrinarycontrastsregardingthetransformationpropertiesof spatiotemporalstructure.Undertheassumptionofindependencetwotrinarychoicesequates tosixpossibilities.
thatisthesameforallDPMsneednotbethesameforallKPMsateitherthetoken ortypelevel.
Afinalfeatureofourframeworkisthemeansbywhichwedifferentiatetransformationsthatare‘local’fromthosethatare‘global’.Localityinthissensewillbedefined intermsofthe homogeneity ofthetransformationsonthespaceofDPMs.Inparticular, global transformationsarethosethatacthomogeneouslyacrossalldynamical modelsand local transformationsacthomogeneouslywithrespecttoparticularevents. Thisisanessentiallyformaldistinctionandwewilltakesometimeinthediscussionof §9.3insettinguptherelevantmathematicalmachinerycarefully.Wewillgiveabrief informalsketchheresincetheglobalvslocaldistinctionisofconsiderableimportance totheproblemoftimeinclassicalmechanics.
Thecoreideaisasfollows.Recallthatallmodels,bothkinematicallypossible anddynamicallypossible,arebuiltoutofthreelevelsofconstitutivestructures:a manifoldstructureusedtocharacterizephysicalevents;geometricstructures,usedto characterizerelationsbetweentheevents;andmatterstructures,usedtocharacterize thenon-geometricmaterialcontent.Consideraparticulartransformationbetweentwo DPMs, φ : D → D.Thistransformationactsontheconstitutivestructuresofthetwo models,respectivelytransformingthemanifold,matter,andgeometricstructures.In thiscontextwecanconsiderthe point-wiseaction of φ onthemanifoldstructure;that is,howthetransformation φ actsonagivenpoint p intheeventspace.
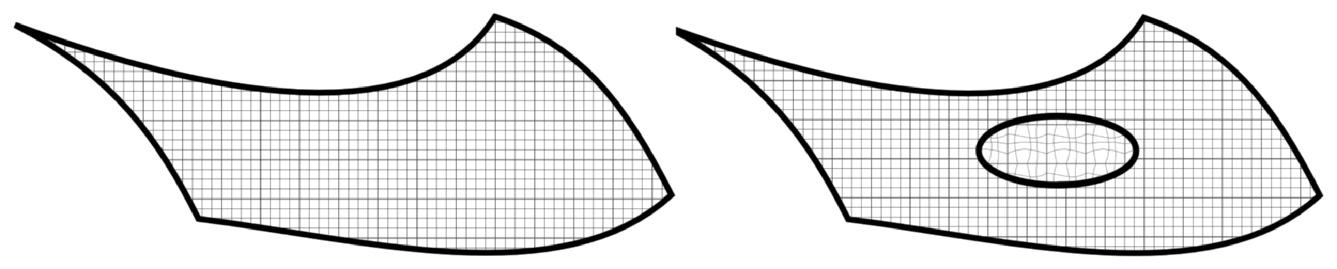
Letusthenconsidersomecoordinationofthemanifoldstructureintermsofa timelikefoliation wherewehaveaseriesofspatialsliceslabelledbyatimeparameter, t; see §9.3forthecoordinate-freeversionoftheseideas.Ifatransformationis spatially homogenous itisunchangedaswevarybetweenspatiallyseparatedpointsonthesame spatialslice.Suchatransformationwillthereforebesuchthatthepartialderivative withrespecttoourcoordinatesadaptedtothespatialslicesarezero.Wethushave that ∂iφ =0forspatiallyhomogenoustransformations.Suchtransformationsare spatiallyglobal.Conversely,ifatransformationis spatiallyinhomogenous itchanges aswevarybetweenatleastsomespatiallyseparatedpointsonthesamespatialslice. Suchatransformationwillthereforebesuchthatthepartialderivativewithrespect toourcoordinatesadaptedtothespatialslicesarenotalwayszero.Wethushave that ∂iφ =0forspatiallyinhomogeneoustransformations.Suchtransformationsare spatiallylocal.SeeFig.1.2foragraphicalrepresentationofaspatiallyinhomogenous transformation
Similarly,ifatransformationis temporallyhomogenous itisunchangedaswevary betweentemporallyseparatedpointsinthemanifoldstructure.Suchatransformation
Fig. 1.2: Representation of a spatially inhomogenous transformation of the event space. Left-hand picture is the event space before the transformation. Right-hand picture is the event space after being acted on by the transformation. The transformation acts only on the spatial region inside the ‘hole’ represented by the oval shape. Inhomogenous transformations formalize the idea of a local transformation.
willthereforebesuchthatthepartialderivativewithrespecttoourtimeparameter iszero.Wethushavethat ∂tφ =0fortemporallyhomogenoustransformations.Such transformationsaretemporallyglobal.Contrarily,ifatransformationis temporally inhomogeneous itchangesaswevarybetweenatleastsometemporallyseparated pointsinthemanifoldstructure.Suchatransformationwillthereforebesuchthatthe partialderivativewithrespecttoourtimeparameterisnotalwayszero.Wethushave that ∂tφ =0fortemporallyinhomogeneoustransformations.Suchtransformationsare temporallylocal.Ingeneral,wewillworkwithadefinitionsuchthatatransformation φ isglobalifandonlyifitisbothspatiallyandtemporallyglobalandatransformation φ islocalifitiseitherspatiallyortemporallylocal.
1.3.4StructureandHeuristics
Itisworthsayingafewwordsaboutthemotivationforconsideringincompletestructures.Whylookatspatiotemporalstructureswithinaphysicaltheorythatare‘broken’ bysomeelementsofthesymmetryordynamicaltransformations?Itisherethatthe widercontextofourprojectbecomesapparent.Thisis not abookabouttheinterpretiveanalysisofspatiotemporalstructureinwell-establishedphysicaltheories.Rather, asnotedinthePreface,thisisa‘three-field’foundationalinvestigation,wherephilosophicalapproachesareintegratedwiththoseofhistoryofscienceandtheoretical physics.Ultimately,oneofourprincipalaimsistoapplyphilosophicalandhistoricalmethodstowardsthedevelopmentofnovelapproachestooutstandingproblems oftheoryconstruction.Incompletestructuresareimportantbecausetheyprovidekey heuristicsforidentifyingnovelroutestowardsmodifyingandextendingtheories.Once more,herewearedrawinginspirationfromFriedman(2001).Inparticular,wetake identificationandmodificationofincompletestructurestobepartofa regulativemetaframeworkfortheoryconstruction (p.66).Wewillreturntothisconnectionin §10.1.
Ingeneralterms,ourgoalindevelopingthenewframeworkhasbeentoconstruct generalheuristicsfortheoryextensionandre-articulation.Perhapsthemostnovel ofthesewillbepreciselythe completionheuristic drawnfromtheanalysisofincompletestructures.Furtherheuristics,whicharemorefamiliar,canbeidentifiedand systematicallycategorizedwithintheframework.Ofparticularimportancearethe eliminationofsurplusstructureviaa reductionheuristic,theconversionofinvariant tosurplusstructurebya surplusingheuristic whichreliesuponexpansionofthenar-
TimeRegained 17
rowsymmetriesofatheory,andtheconversionofadynamicallyabsolutestructureto adynamicallyrelativestructureviaa relativizationheuristic ofwhichbestmatching isaspecificform.Articulatingthebasisfortheseheuristics,andalsotheattendant drawbacks,willbethecentralconcernin §10.1.
Thefinalheuristicthatweshallconsiderisdrawnfromtheconversionofastructure withglobalpropertiestoastructurewithlocalproperties;thatis,modificationofthe theoryandstructuresuchthatthetransformationsonthespaceofDPMsthatthe structureiswellbehavedunderareconvertedfromhomogenoustoinhomogeneous. Thisisthe localizationheuristic thatwillprovidethefinaltoolthatwillprovecrucial toouranalysisoftheproblemoftime.
1.4TimeRegained
1.4.1TheHierarchyofStructures
Abasicpresuppositionofourapproachisthattemporalandspatiotemporalstructures aredefinedwithinthe dynamical modelsofaphysicaltheory.Definingthingsinthis mannermightseemtoindicatethatweassumenomicstructuretobemorebasicthan temporal.Andthismightappearproblematicsinceplausibly some temporalstructure isnecessarytoformulatenomicstructure.However,onourviewoneshouldnotthink oftherebeingageneralhierarchybetweenthenomicandtemporalstructure.Rather, wetaketherelationshipbetweennomicandtemporalstructureasamattertobe investigatedaposteriori.7
Afurtherimmediateconcernregardingourclassificationofstructuresiswhether thegeometricstructurethatisneededtoplaytheconstitutiveroleindefiningthe KPMsofthetheorywillalsofunctionasatleastpartoftherelevanttemporalstructure.Thiswillalsooftenbethecase.However,whatissignificantforourpurposesis thattheconstitutiveandtemporalrolesofgeometricstructuresaredistinct.Inthe constitutiverole,geometricobjectsareprovidingstructuretoapurelykinematical representationoftheuniverse.Assuch,thereisnonecessaryconnectionbetweenthe relevantgeometricstructureandtherepresentationoftimewithinphysicallypossible universes.Incontrast,inthetemporalrole,thegeometricstructuresare,byassumption,representingtemporalfeaturesofphysicallypossibleuniverses.Aswithmuch else,thesesubtletieswillbecomeclearonceexamplesareconsideredindetail.
1.4.2TheStructureofTime
Theprimary,andmostfundamental,motivationbehindouranalysisistoprovidea suitablypreciseformalandconceptualrepresentationofthedifferentconceptsoftime inaphysicaltheory.Thisconceptualrefinementwillbeachievedbyintroducingformal representationsoftemporalstructureswhichcorrespondtocore‘propertiesoftime’. Forthemostpart,thesetemporalstructureswillbeintroducedonacase-by-case
7 Aratherdifferentwayofapproachingtherelationshipbetweennomicandtemporalstructureis thatespousedbyCallender(2017).Onthisview,timeisdistinguishedbyits‘simplifying’functional rolewithlaws,understoodaspartialdifferentialequationswithawellposedCauchyproblem.For criticaldiscussionofCallender’sviewseeBaronandEvans(2018),andJames(2022).Theseinteresting debatesaretangentialtothequestionsatissuehere.