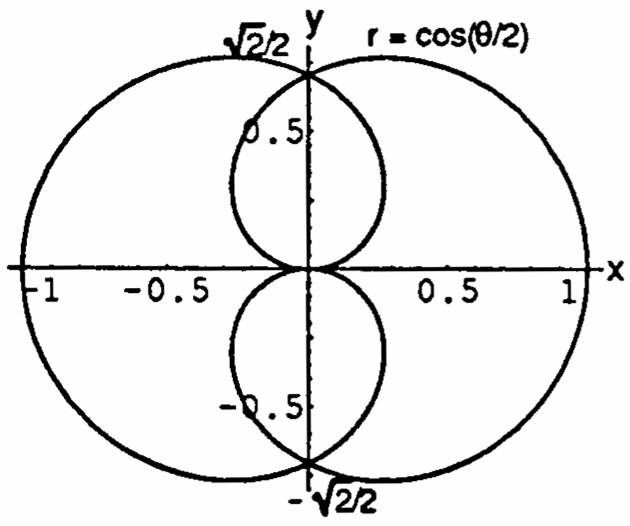
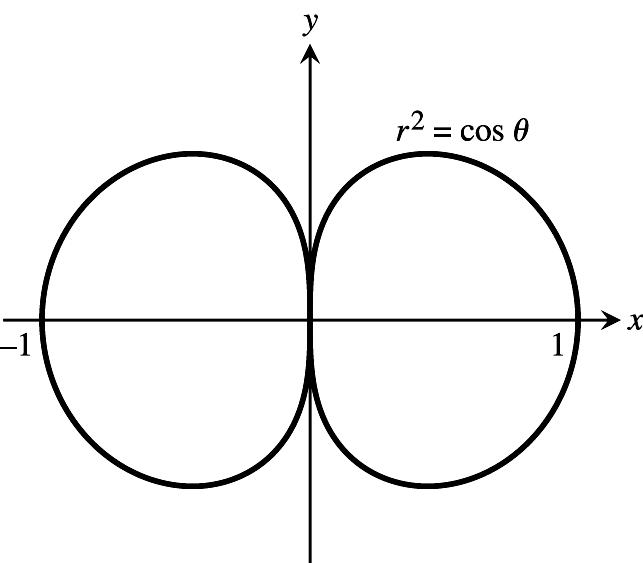
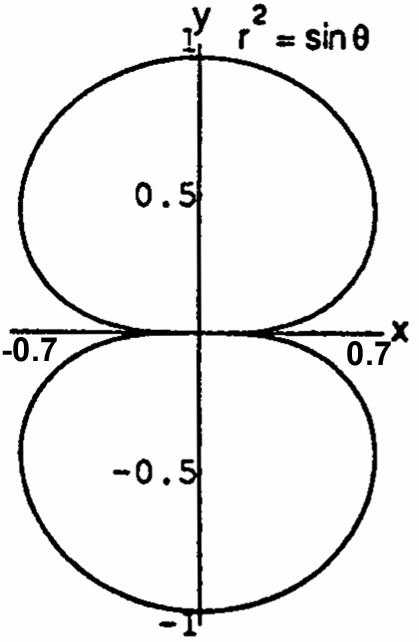
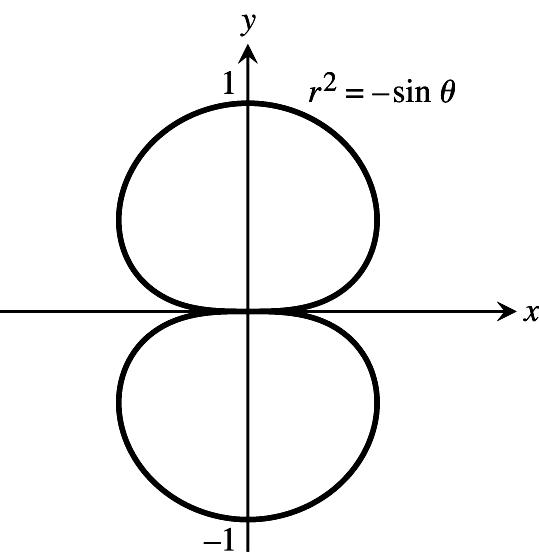
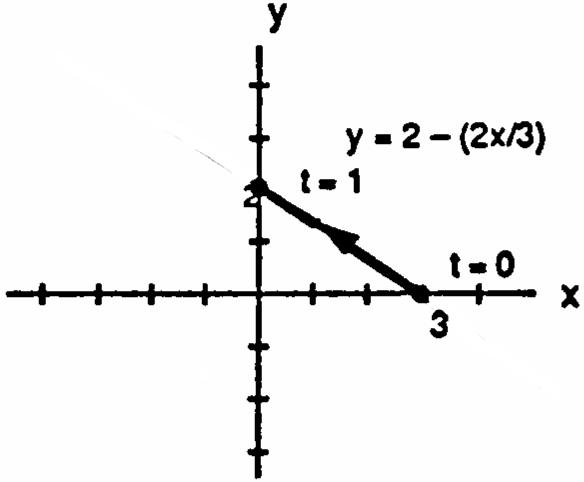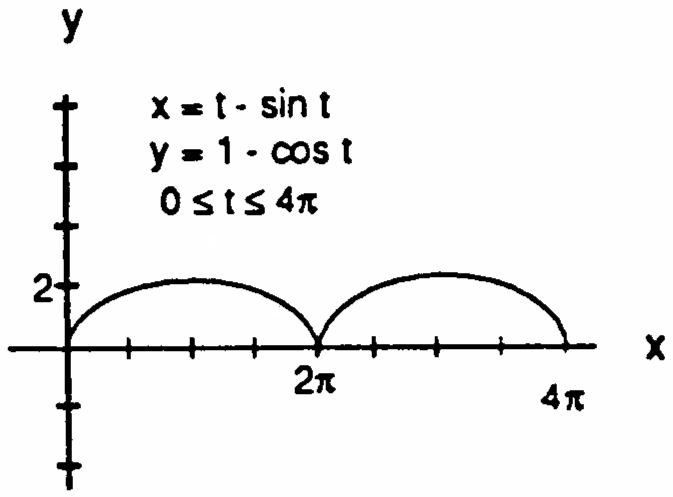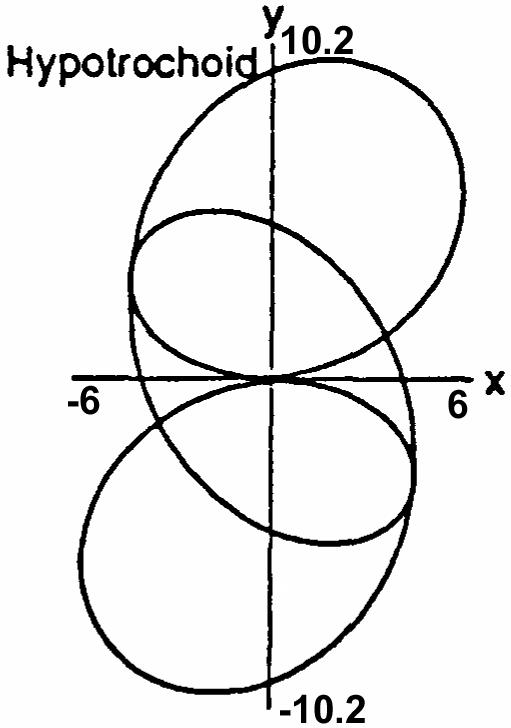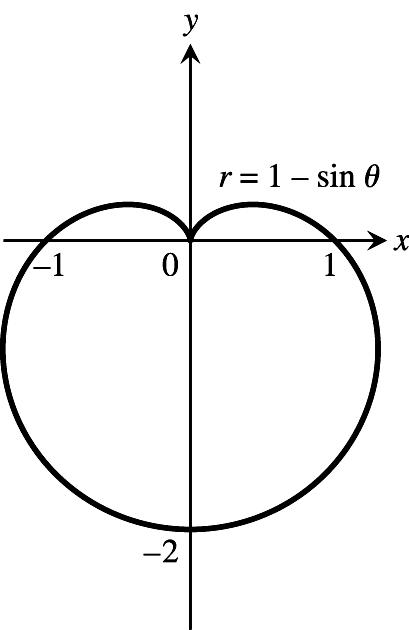Instructor' solutions manual, multivariable for Thomas' calculus & Thomas' calculus early transcendental a, 12/E 12th Edition Weir-Hass
Visit to download the full and correct content document: https://ebookmass.com/product/instructor-solutions-manual-multivariable-for-thomascalculus-thomas-calculus-early-transcendental-a-12-e-12th-edition-weir-hass/
More products digital (pdf, epub, mobi) instant download maybe you interests ...
Thomas' Calculus: Early Transcendentals. Fifteenth Edition Joel Hass
https://ebookmass.com/product/thomas-calculus-earlytranscendentals-fifteenth-edition-joel-hass/
Thomas' Calculus in SI Units 14th Edition Hass
https://ebookmass.com/product/thomas-calculus-in-si-units-14thedition-hass/
Complete Solutions Manual for Calculus of a Single Variable, Early Transcendental Functions 7th Edition
Ron Larson
https://ebookmass.com/product/complete-solutions-manual-forcalculus-of-a-single-variable-early-transcendental-functions-7thedition-ron-larson/
Student Solutions Manual, Chapters 10-17 for Stewart’s Multivariable Calculus, 8th (James Stewart Calculus) 8th
https://ebookmass.com/product/student-solutions-manualchapters-10-17-for-stewarts-multivariable-calculus-8th-jamesstewart-calculus-8th/
Thomas’ Calculus: Early Transcendentals 14th Edition, (Ebook PDF)
https://ebookmass.com/product/thomas-calculus-earlytranscendentals-14th-edition-ebook-pdf/
Calculus: Early Transcendental Functions 4th Edition, (Ebook PDF)
https://ebookmass.com/product/calculus-early-transcendentalfunctions-4th-edition-ebook-pdf/
Student Solutions Manual, Chapters 10-16 for Stewart/Clegg/Watson's Multivariable Calculus (9th edition) James Stewart
https://ebookmass.com/product/student-solutions-manualchapters-10-16-for-stewart-clegg-watsons-multivariablecalculus-9th-edition-james-stewart/
Calculus Early transcendental functions 7e 2019 Rob Larson
https://ebookmass.com/product/calculus-early-transcendentalfunctions-7e-2019-rob-larson/
Thomas' Calculus for the JEE 13th Edition George B. Thomas Jr
https://ebookmass.com/product/thomas-calculus-for-the-jee-13thedition-george-b-thomas-jr/
INSTRUCTOR’S SOLUTIONS MANUAL MULTIVARIABLE WILLIAM ARDIS Collin County Community College
T HOMAS ’ C ALCULUS TWELFTH EDITION BASED ON THE ORIGINAL WORK BY
George B. Thomas, Jr.
Massachusetts Institute of Technology
AS REVISED BY
Maurice D. Weir
Naval Postgraduate School
Joel Hass
University of California, Davis
The author and publisher of this book have used their best efforts in preparing this book. These efforts include the development, research, and testing of the theories and programs to determine their effectiveness. The author and publisher make no warranty of any kind, expressed or implied, with regard to these programs or the documentation contained in this book. The author and publisher shall not be liable in any event for incidental or consequential damages in connection with, or arising out of, the furnishing, performance, or use of these programs.
Reproduced by Addison-Wesley from electronic files supplied by the author.
Copyright © 2010, 2005, 2001 Pearson Education, Inc.
Publishing as Pearson Addison-Wesley, 75 Arlington Street, Boston, MA 02116.
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Printed in the United States of America.
ISBN-13: 978-0-321-60072-1
ISBN-10: 0-321-60072-X
1 2 3 4 5 6 BB 14 13 12 11 10
PREFACE TO THE INSTRUCTOR ThisInstructor'sSolutionsManualcontainsthesolutionstoeveryexerciseinthe12thEditionofTHOMAS'CALCULUS byMauriceWeirandJoelHass,includingtheComputerAlgebraSystem(CAS)exercises.ThecorrespondingStudent's SolutionsManualomitsthesolutionstotheeven-numberedexercisesaswellasthesolutionstotheCASexercises(because theCAScommandtemplateswouldgivethemallaway).
InadditiontoincludingthesolutionstoallofthenewexercisesinthiseditionofThomas,wehavecarefullyrevisedor rewritteneverysolutionwhichappearedinprevioussolutionsmanualstoensurethateachsolution conformsexactlytothemethods,proceduresandstepspresentedinthetext ì ismathematicallycorrect ì includesallofthestepsnecessarysoatypicalcalculusstudentcanfollowthelogicalargumentandalgebra ì includesagraphorfigurewhenevercalledforbytheexercise,orifneededtohelpwiththeexplanation ì isformattedinanappropriatestyletoaidinitsunderstanding ì
EveryCASexerciseissolvedinboththeMAPLEandcomputeralgebrasystems.Atemplateshowing
MATHEMATICA anexampleoftheCAScommandsneededtoexecutethesolutionisprovidedforeachexercisetype.Similarexerciseswithin thetextgroupingrequireachangeonlyintheinputfunctionorothernumericalinputparametersassociatedwiththeproblem (suchastheintervalendpointsorthenumberofiterations).
FormoreinformationaboutotherresourcesavailablewithThomas'Calculus,visithttp://pearsonhighered.com.
TABLE OF CONTENTS 10 Infinite Sequences and Series 569 10.1Sequences569
10.2InfiniteSeries577
10.3TheIntegralTest583
10.4ComparisonTests590
10.5TheRatioandRootTests597
10.6AlternatingSeries,AbsoluteandConditionalConvergence602
10.7PowerSeries608
10.8TaylorandMaclaurinSeries617
10.9ConvergenceofTaylorSeries621
10.10TheBinomialSeriesandApplicationsofTaylorSeries627 PracticeExercises634
AdditionalandAdvancedExercises642
11 Parametric Equations and Polar Coordinates 647 11.1ParametrizationsofPlaneCurves647
11.2CalculuswithParametricCurves654
11.3PolarCoordinates662
11.4GraphinginPolarCoordinates667
11.5AreasandLengthsinPolarCoordinates674
11.6ConicSections679
11.7ConicsinPolarCoordinates689 PracticeExercises699
AdditionalandAdvancedExercises709
12 Vectors and the Geometry of Space 715 12.1Three-DimensionalCoordinateSystems715
12.2Vectors718
12.3TheDotProduct723
12.4TheCrossProduct728
12.5LinesandPlanesinSpace734
12.6CylindersandQuadricSurfaces741 PracticeExercises746
AdditionalExercises754
13 Vector-Valued Functions and Motion in Space 759 13.1CurvesinSpaceandTheirTangents759
13.2IntegralsofVectorFunctions;ProjectileMotion764
13.3ArcLengthinSpace770
13.4CurvatureandNormalVectorsofaCurve773
13.5TangentialandNormalComponentsofAcceleration778
13.6VelocityandAccelerationinPolarCoordinates784 PracticeExercises785
AdditionalExercises791
14 Partial Derivatives 795 14.1FunctionsofSeveralVariables795
14.2LimitsandContinuityinHigherDimensions804
14.3PartialDerivatives810
14.4TheChainRule816
14.5DirectionalDerivativesandGradientVectors824
14.6TangentPlanesandDifferentials829
14.7ExtremeValuesandSaddlePoints836
14.8LagrangeMultipliers849
14.9Taylor'sFormulaforTwoVariables857
14.10PartialDerivativeswithConstrainedVariables859
PracticeExercises862
AdditionalExercises876
15 Multiple Integrals 881 15.1DoubleandIteratedIntegralsoverRectangles881
15.2DoubleIntegralsoverGeneralRegions882
15.3AreabyDoubleIntegration896
15.4DoubleIntegralsinPolarForm900
15.5TripleIntegralsinRectangularCoordinates904
15.6MomentsandCentersofMass909
15.7TripleIntegralsinCylindricalandSphericalCoordinates914
15.8SubstitutionsinMultipleIntegrals922
PracticeExercises927
AdditionalExercises933
16 Integration in Vector Fields 939 16.1LineIntegrals939
16.2VectorFieldsandLineIntegrals;Work,Circulation,andFlux944
16.3PathIndependence,PotentialFunctions,andConservativeFields952
16.4Green'sTheoreminthePlane957
16.5SurfacesandArea963
16.6SurfaceIntegrals972
16.7Stokes'sTheorem980
16.8TheDivergenceTheoremandaUnifiedTheory984
PracticeExercises989
AdditionalExercises997
CHAPTER 11 PARAMETRIC EQUATIONS AND POLAR COORDINATES 11.1 PARAMETRIZATIONS OF PLANE CURVES
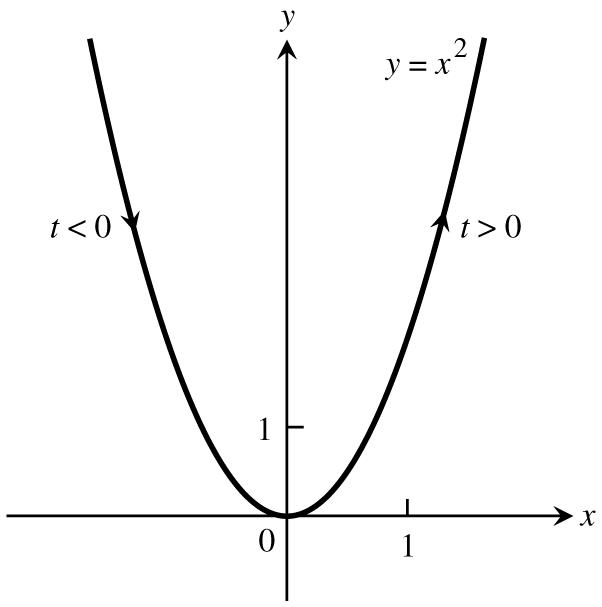
1.x3t,y9t,tyx2.xt,yt,t0xy œœ _ _Êœœ œ Êœ ## È È oryx,x0 œŸ #
3.x2t5,y4t7,t4.x33t,y2t,0t1t œ œ _ _œ œŸŸÊœ y # x52t2(x5)4tx332x63y Ê œÊ œÊœ Êœ ˆ‰ y # y2(x5)7y2x3y2x,xÊœ Êœ Êœ !ŸŸ$ 2 3
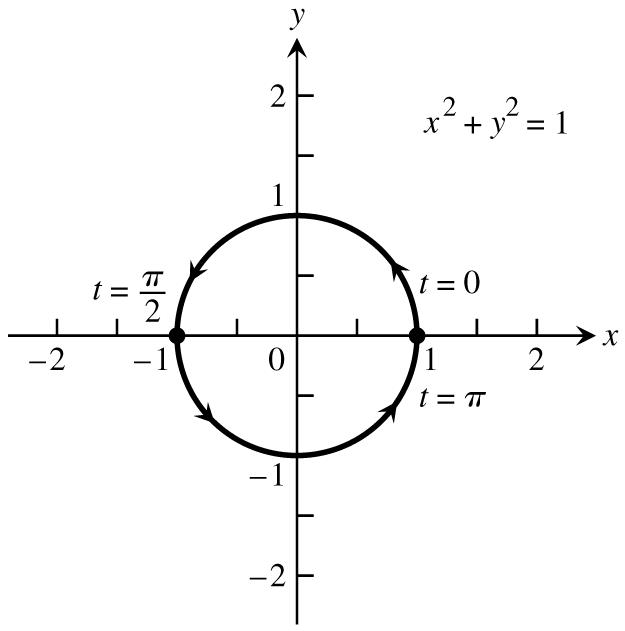
5.xcos2t,ysin2t,0t6.xcos(t),ysin(t),0t œœŸŸœ œ ŸŸ 1111 cos2tsin2t1xy1cos(t)sin(t)1 Ê œÊ œÊ œ ######11 xy1,y Ê œ ! ##
648Chapter11ParametricEquationsandPolarCoordinates
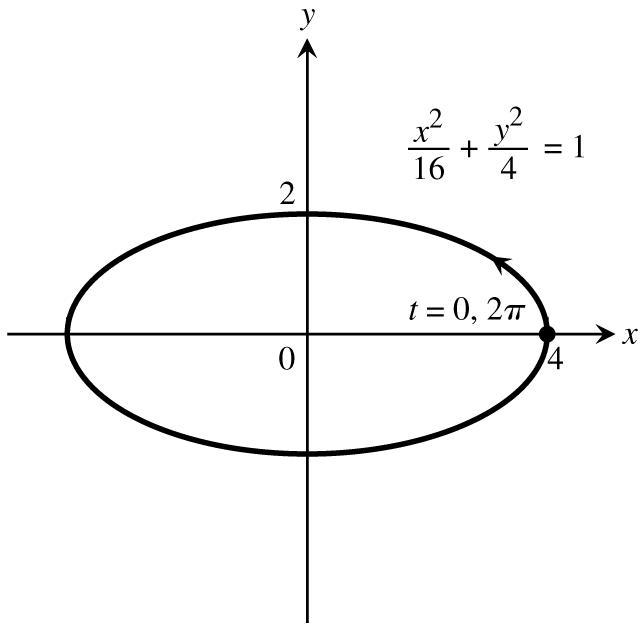
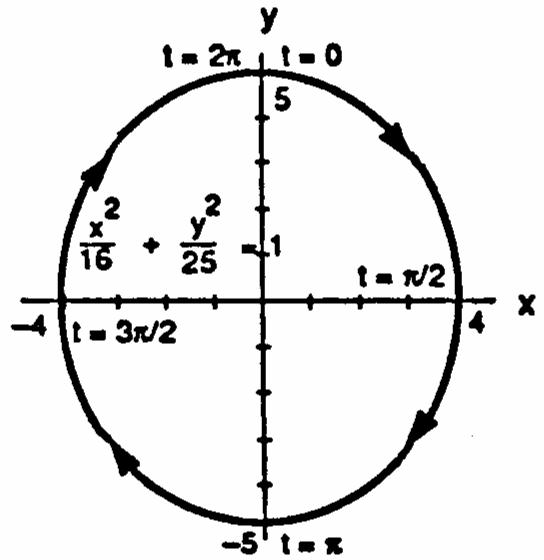
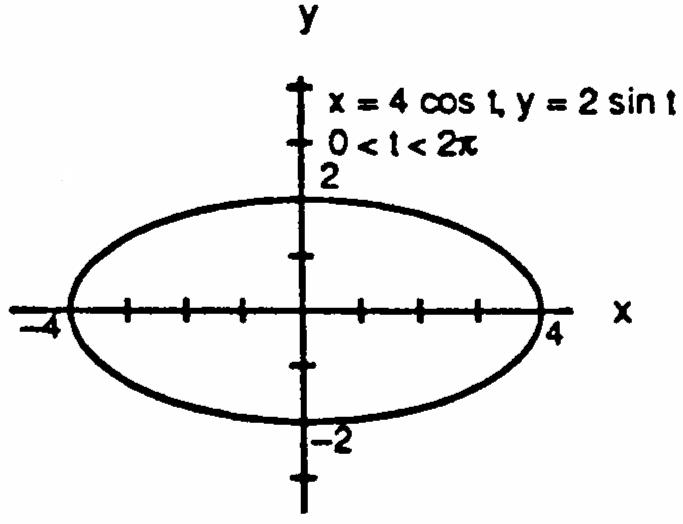
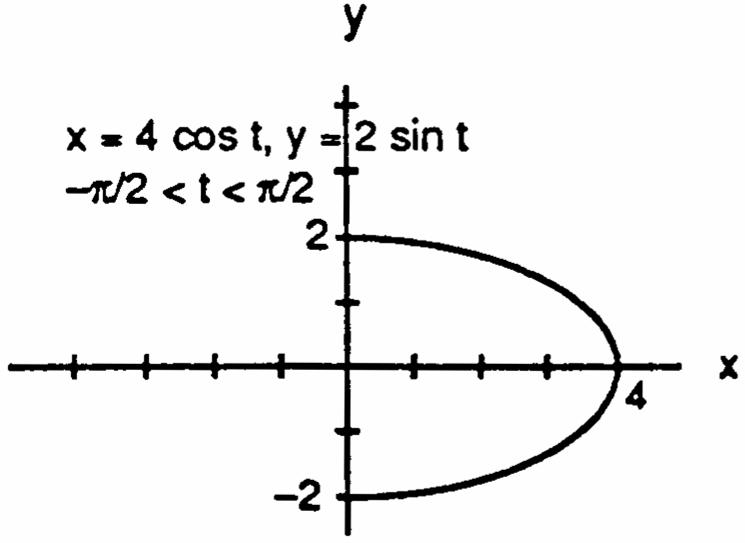
7.x4cost,y2sint,0t28.x4sint,y5cost,0t2 œœŸŸœœŸŸ 11 1111 Ê œÊ œÊ œÊ œ 16cost4sintx16sint25costx 1641641625165 yy ###### # # #
9.xsint,ycos2t,t10.x1sint,ycost2,0t œœ ŸŸœ œ ŸŸ 11 22 1 ycos2t12sinty12xsintcost1x1y21Êœœ Êœ Ê œÊ œ ##### 2 abab
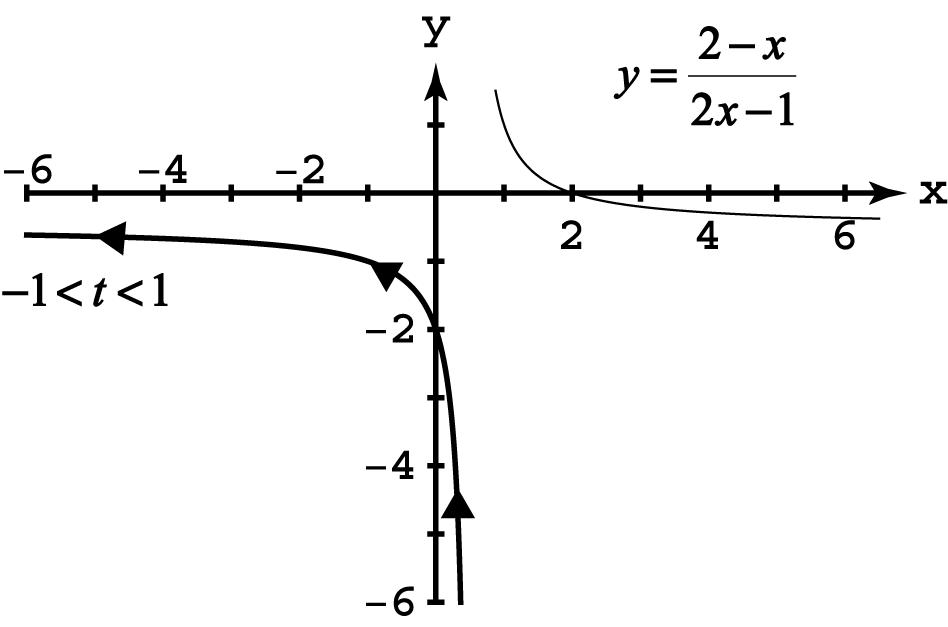
11.xt,yt2t,t12.x,y,1t1 œœ _ _œœ 264tt2 t1t1 yt2tyx2xtyÊœ Êœ ʜʜ abab2232 32x2x x12x1
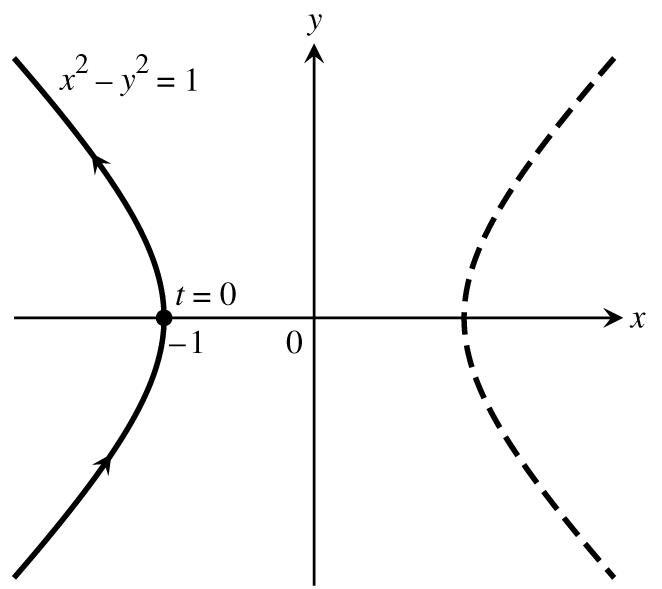
13.xt,y1t,1t014.xt1,yt,t0 œœ ŸŸœ œ È È È # y1xytxy1,y0Êœ ʜʜ È È ## #
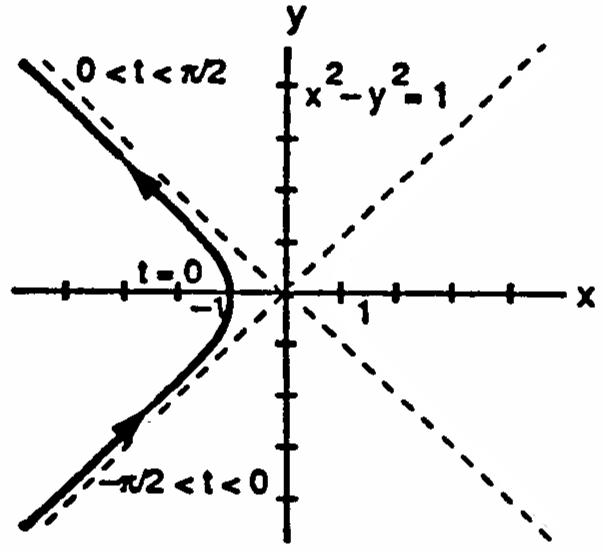
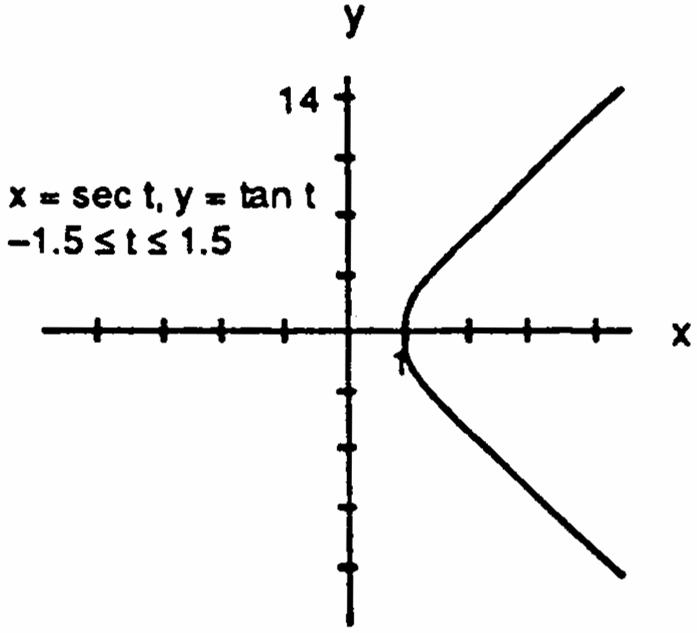
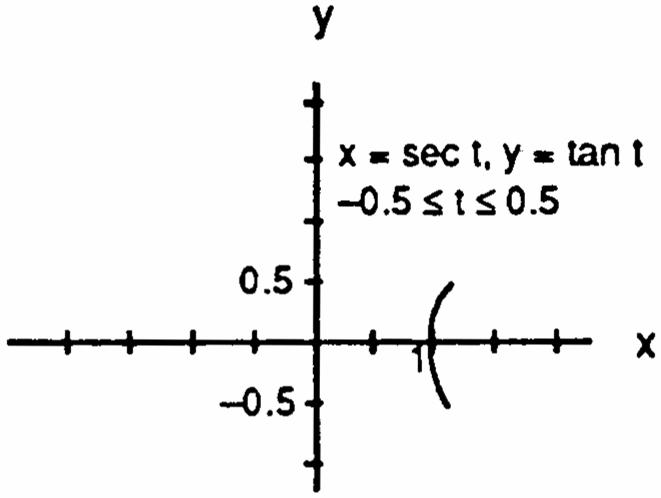
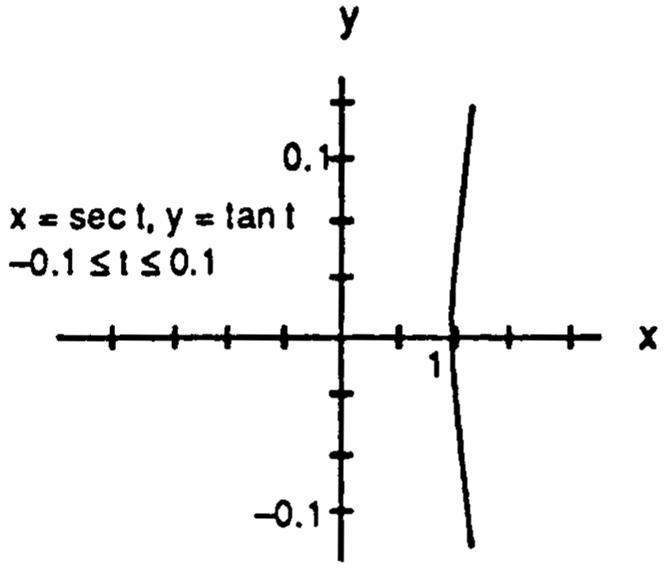
15.xsect1,ytant,t16.xsect,ytant,t œ œ œ œ # #### 1111 sect1tantxysecttant1xy1 Ê œÊœÊ œÊ œ #######
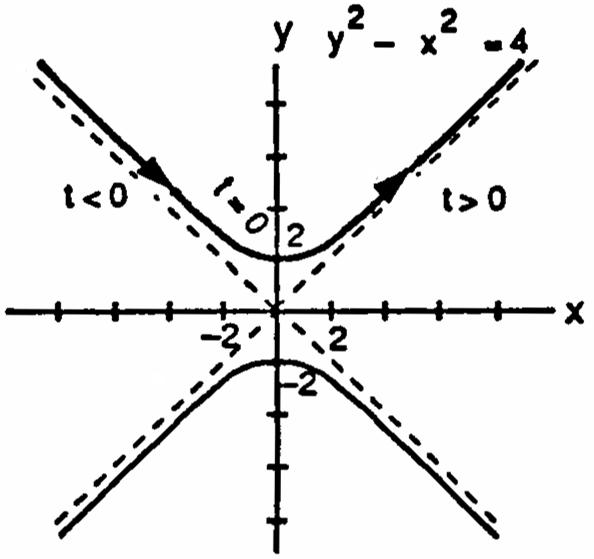
17.xcosht,ysinht,118.x2sinht,y2cosht,t œ œ _ _œœ _ _ coshtsinht1xy14cosht4sinht4yx4 Ê
19.(a)xacost,yasint,0t220.(a)xasint,ybcost,t œœ ŸŸœœŸŸ 1 11 ## 5 (b)xacost,yasint,0t2(b)xacost,ybsint,0t2 œœŸŸœœŸŸ 11 (c)xacost,yasint,0t4(c)xasint,ybcost,t œœ ŸŸœœŸŸ 1 11 ## 9 (d)xacost,yasint,0t4(d)xacost,ybsint,0t4 œœŸŸœœŸŸ 11
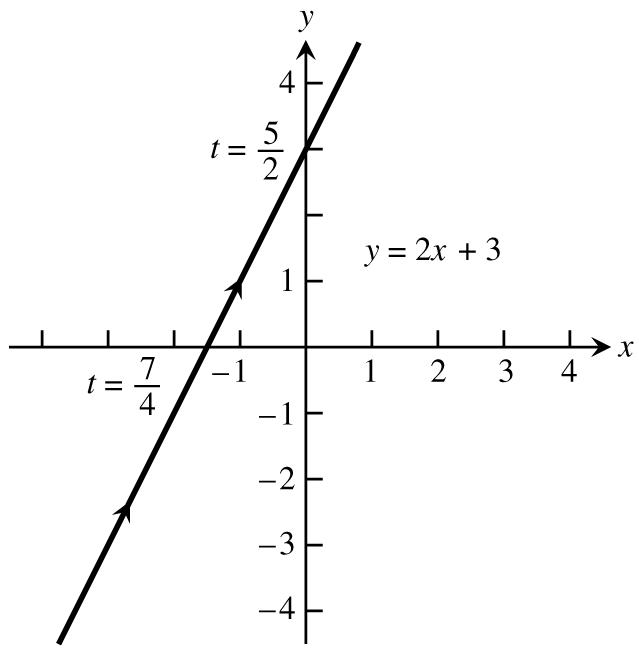
21.Usingwecreatetheparametricequationsxatandybt,representingalinewhichgoes ab "ß $œ " œ $ throughatt.Wedetermineaandbsothatthelinegoesthroughwhent. abab "ß $œ!%ß"œ" Sinceaa.Sincebb.Therefore,onepossibleparameterizationisxt, %œ " Êœ&"œ $ Êœ%œ " & yt,0t. œ $ %ŸŸ"
22.Usingwecreatetheparametricequationsxatandybt,representingalinewhichgoesthrough ab"ß$œ " œ$ att.Wedetermineaandbsothatthelinegoesthroughwhent.Sinceaa.abab "ß$œ!$ß #œ"$œ " Êœ% Sincebb.Therefore,onepossibleparameterizationisxt,yt,0t. #œ$ Êœ &œ " %œ$ &ŸŸ"
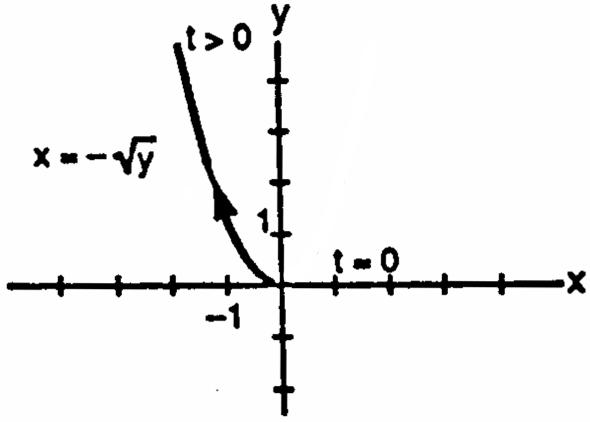
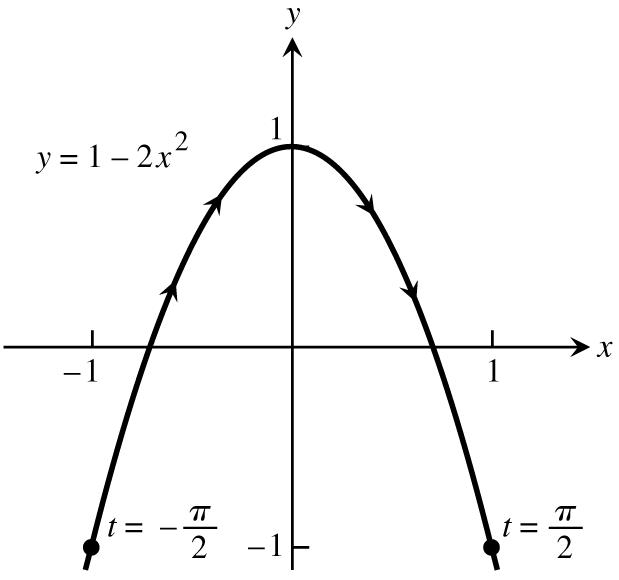
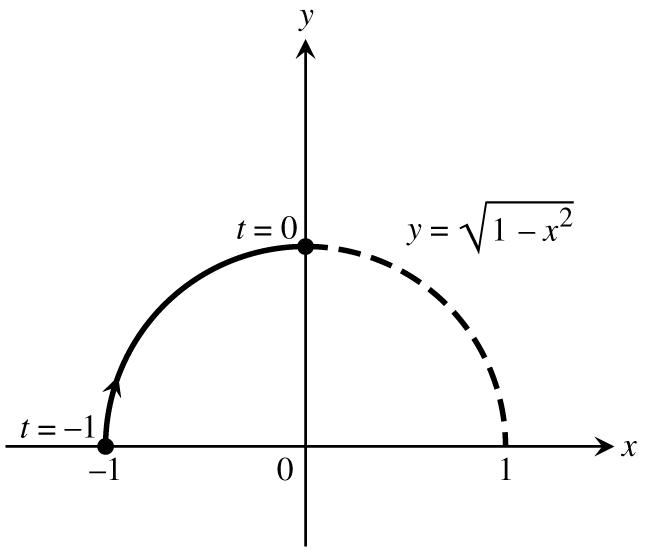
23.Thelowerhalfoftheparabolaisgivenbyxyfory.Substitutingtfory,weobtainonepossible œ "Ÿ! # parameterizationxt,yt,t0 œ "œŸÞ #
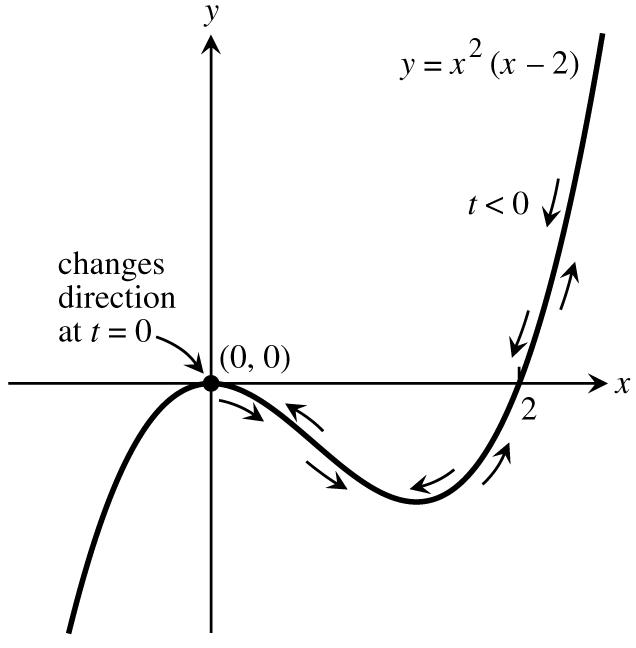
24.Thevertexoftheparabolaisat,sothelefthalfoftheparabolaisgivenbyyxxforx.Substituting ab "ß "œ #Ÿ " # tforx,weobtainonepossibleparametrization:xt,ytt,t. œœ #Ÿ " #
25.Forsimplicity,weassumethatxandyarelinearfunctionsoftandthatthepointx,ystartsatfortandpasses abab#ß$œ! throughatt.Thenxft,wherefandf. abababab "ß "œ"œ!œ#"œ " Sinceslope,xfttt.Also,ygt,wheregandg. œœœ $œœ $ #œ# $œ!œ$"œ " ? ? x t " # " ! abababab Sinceslope4.ygttt. œœœ œœ % $œ$ % ? ? y t 3 " " ! ab Onepossibleparameterizationis:xt,yt,t. œ# $œ$ % !
Copyright © 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
26.Forsimplicity,weassumethatxandyarelinearfunctionsoftandthatthepointx,ystartsatfortand abab"ß#œ! passesthroughatt.Thenxft,wherefandf. abababab !ß!œ"œ!œ ""œ!
Sinceslope,xfttt.Also,ygt,wheregandg. œœœ"œœ" "œ " œ!œ#"œ! ? ? x t !" " ! ab ababababab Sinceslope.ygttt. œœœ #œœ # #œ# # ? ? y t !# " ! ab Onepossibleparameterizationis:xt,yt,t. œ " œ# # !
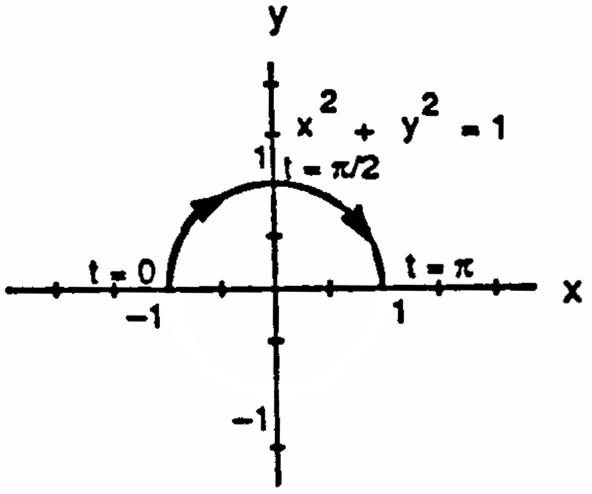
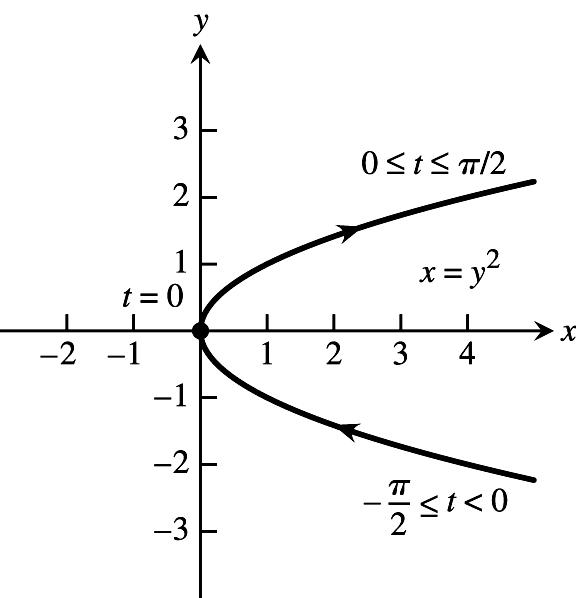
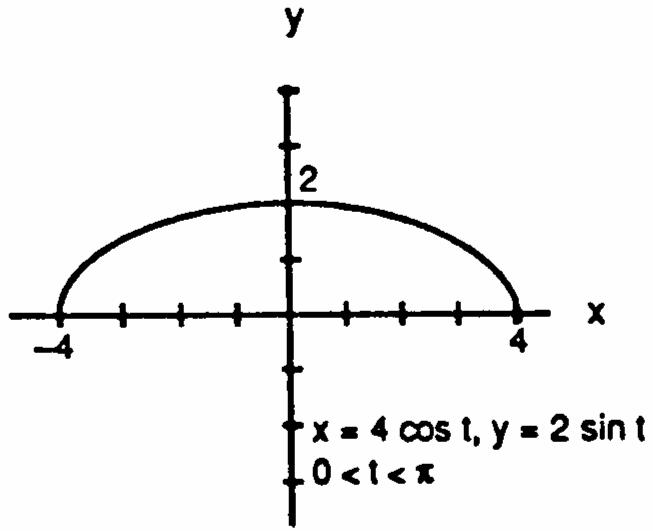
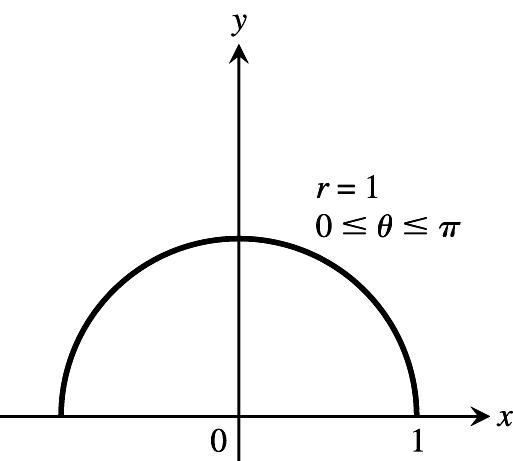
27.Sinceweonlywantthetophalfofacircle,y0,soletx2cost,y2sint,0t4 œœllŸŸ 1
28.Sincewewantxtostaybetween3and3,letx3sint,theny3sint9sint,thusx3sint,y9sint, œœœœœ ab2 ## 0t Ÿ _
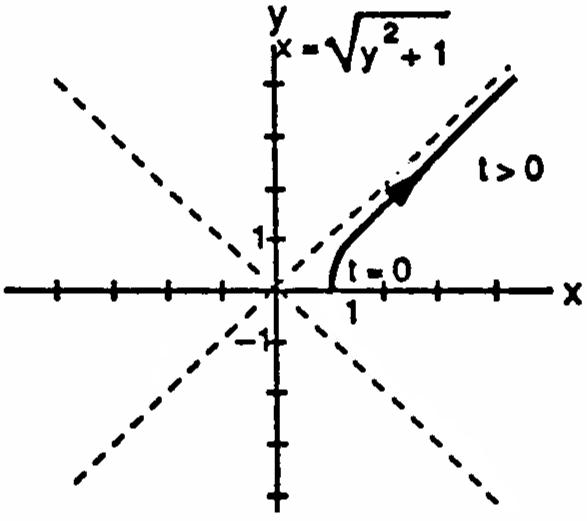
29.xya2x2y0;letttxyt.Substitutionyields ###œÊ œÊœ œÊ œÊœ dydydy dxdxydxy xx ytyayandx,t ####œÊœœ _ _ aat 1t1t
30.Intermsof,parametricequationsforthecirclearexacos,yasin,02.Since,thearc ))))1) œœŸ œ s a lengthparametrizationsare:xacos,yasin,and020s2aistheintervalfors. œœŸ ÊŸŸ sss aaa 11
31.Dropaverticallinefromthepointx,ytothex-axis,thenisanangleinarighttriangle,andfromtrigonometrywe ab ) knowthattanyxtan.Theequationofthelinethrough0,2and4,0isgivenbyyx2.Thus )) œÊœœ y x2 1 abab xtanx2xandywhere0. )) œ ÊœœŸ144tan 22tan12tan12 )) )1
32.Dropaverticallinefromthepointx,ytothex-axis,thenisanangleinarighttriangle,andfromtrigonometrywe ab ) knowthattanyxtan.Sinceyxyxxtanxxcotycotwhere ))))) œÊœœÊœÊœÊœÊœ y x 22 2 È ab 0. Ÿ ) 1 2
33.Theequationofthecircleisgivenbyx2y1.Dropaverticallinefromthepointx,yonthecircletothe abab œ 22 x-axis,thenisanangleinarighttriangle.Sothatwecanstartat1,0androtateinaclockwisedirection,let ) ab x2cos,ysin,02. œ œŸŸ )))1
34.Dropaverticallinefromthepointx,ytothex-axis,thenisanangleinarighttriangle,whoseheightisyandwhos ab ) e baseisx2.Bytrigonometrywehavetanyx2tan.Theequationofthecircleisgivenby œÊœ )) y x2 ab xy1xx2tan1xsec4xtan4tan10.Solvingforxweobtain 2222222 2 œÊ œÊ œ ab ab ))))
x2sincoscos3sin œœœ „ „„4tan4tan4sec4tan1 2sec2sec 4tan213tan222 2222 2 22 22 )))) )) )) Éabab È )))) È 22coscos4cos3andy22coscos4cos32tan œ „ œ „ 2222 )))))))
2sincossin4cos3.Sinceweonlyneedtogofrom1,0to0,1,letœ„)))) È abab 2 x22coscos4cos3,y2sincossin4cos3,0tan. œ œ ŸŸ 21 221 2 )))))))) ÈÈ ˆ‰
Toobtaintheupperlimitfor,notethatx0andy1,usingyx2tan12tantan. )))) œœœ ʜʜ ab ˆ‰11 2
35.ExtendtheverticallinethroughAtothex-axisandletCbethepointofintersection.ThenOCAQx œœ andtantx2cott;sintOA;and(AB)(OA)(AQ)ABx œœÊœœœÊœœÊœ 222222 OCxtantOAsintsint ## ˆ‰ ABAB.Nexty2ABsinty2sint ʜʜœ Êœ œ ˆ‰ˆ‰ˆ‰ 222sint2sint sinttanttanttant # # # 222cost2sint.Thereforeletx2cottandy2sint,0t. œ œœœ 2sint tant # # ### 1
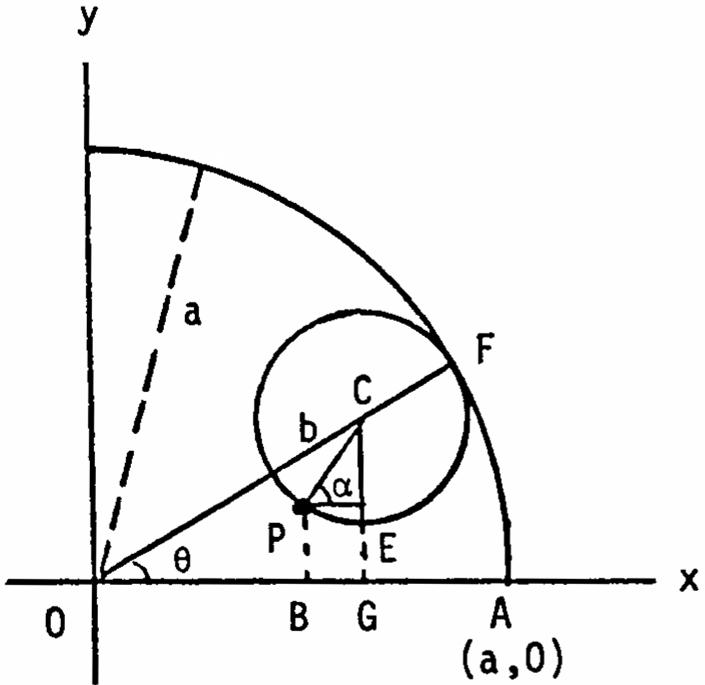
36.ArcPFArcAFsinceeachisthedistancerolledand œ ArcFCPArcPFb(FCP); PFArcAF ba œnÊœnœ )
ArcAFaab(FCP)FCP; ʜʜnÊnœ ))) a b
OCG;OCGOCPPCEnœ nœn n 1 # )
OCP.NowOCPFCPœn nœ n ˆ‰ 1 # !1
.ThusOCG œ nœ Ê 1)1)!) aa bb 11 ## œ Êœ œ 1)!!1))1) aaab bbb 1 # ˆ‰
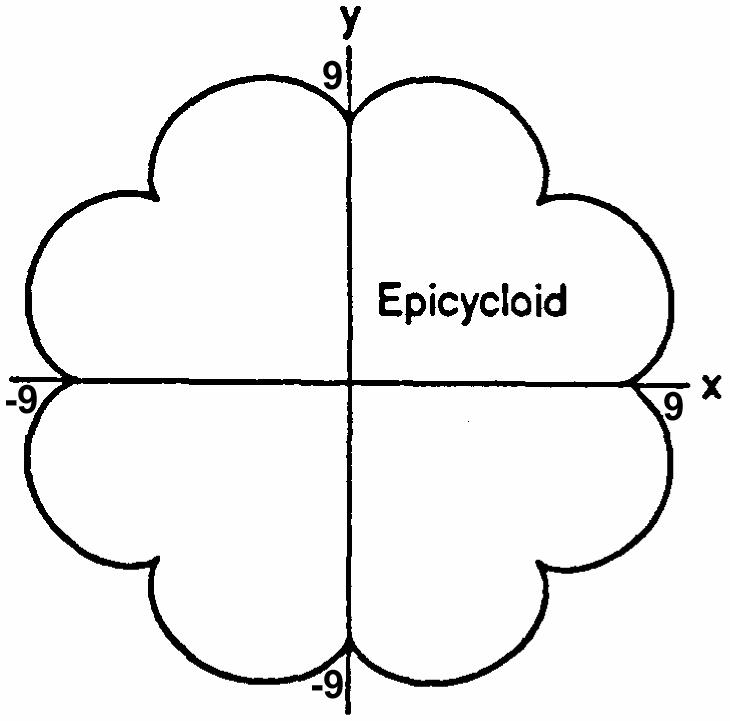
ThenxOGBGOGPE(ab)cosbcos(ab)cosbcos œ œ œ œ )!)1) ˆ‰ ab b (ab)cosbcos.AlsoyEGCGCE(ab)sinbsin œ œœ œ )))! ˆ‰ ab b (ab)sinbsin(ab)sinbsin.Therefore œ œ )1))) ˆ‰ˆ‰ abab bb x(ab)cosbcosandy(ab)sinbsin. œ œ )))) ˆ‰ˆ‰ abab bb
Ifb,thenxacoscos œœaaa 444 a ˆ‰ Š‹)) ˆ‰ ˆ‰ a 4 a 4 coscos3cos(coscos2sinsin2) œ œ 3aa3aa 4444))))))) cos(cos)cossin(sin)(2sincos) œ 3aa 44))))))) ab ab ## coscoscossinsincos œ 3aaa2a 4444)))))) $## coscos(cos)1cosacos; œ œ 3aa3a 444))))) $#$ ab
yasinsinsinsin3sin(sincos2cossin2) œ œ œ ˆ‰ Š‹ aa3aa3aa 444444 a ))))))))) ˆ‰ ˆ‰ a 4 a 4 sin(sin)cossin(cos)(2sincos) œ 3aa 44))))))) ab ab ## sinsincossincossin œ 3aaa2a 4444)))))) #$# sinsincossin œ 3a3aa 444)))) #$ sin(sin)1sinsinasin. œ œ 3a3aa 444))))) ab#$$
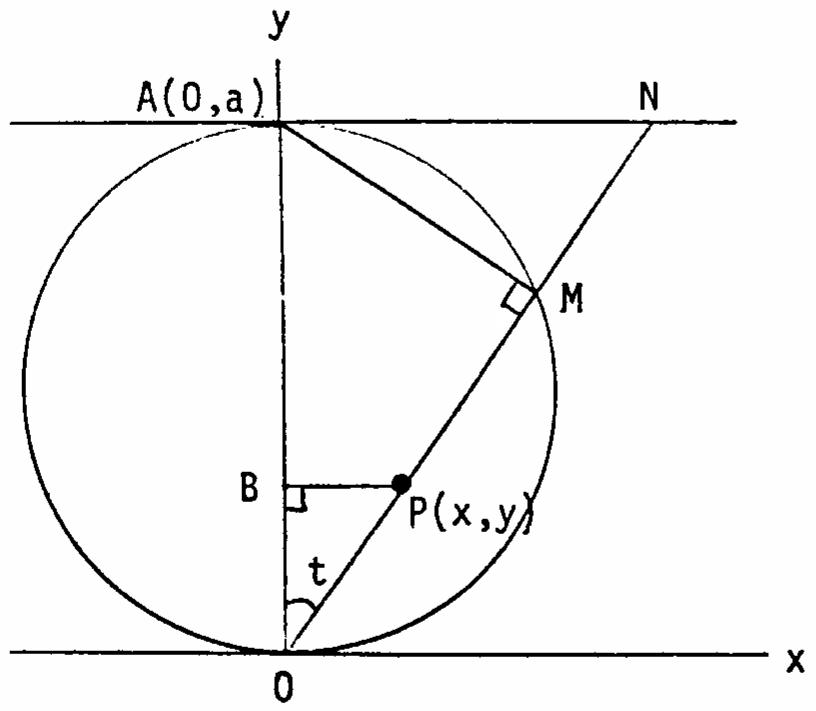
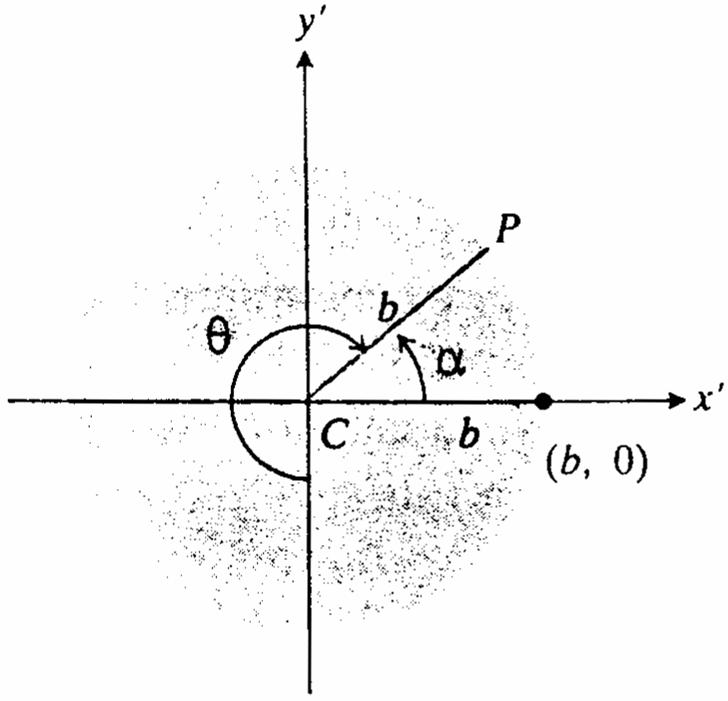
37.DrawlineAMinthefigureandnotethatAMOisaright n anglesinceitisaninscribedanglewhichspansthediameter ofacircle.ThenANMNAM.Now,OAa, ### œ œ tant,andsint.NextMNOPANAM aa œœœ OPANAMatantasintÊœ œ ####### OPatantasintÊœ È #### (asint)sect1.IntriangleBPO, œ œ È # asint cost # xOPsintasinttantand œœœ asint cost $ # yOPcostasintxasinttantandyasint. œœÊœœ###
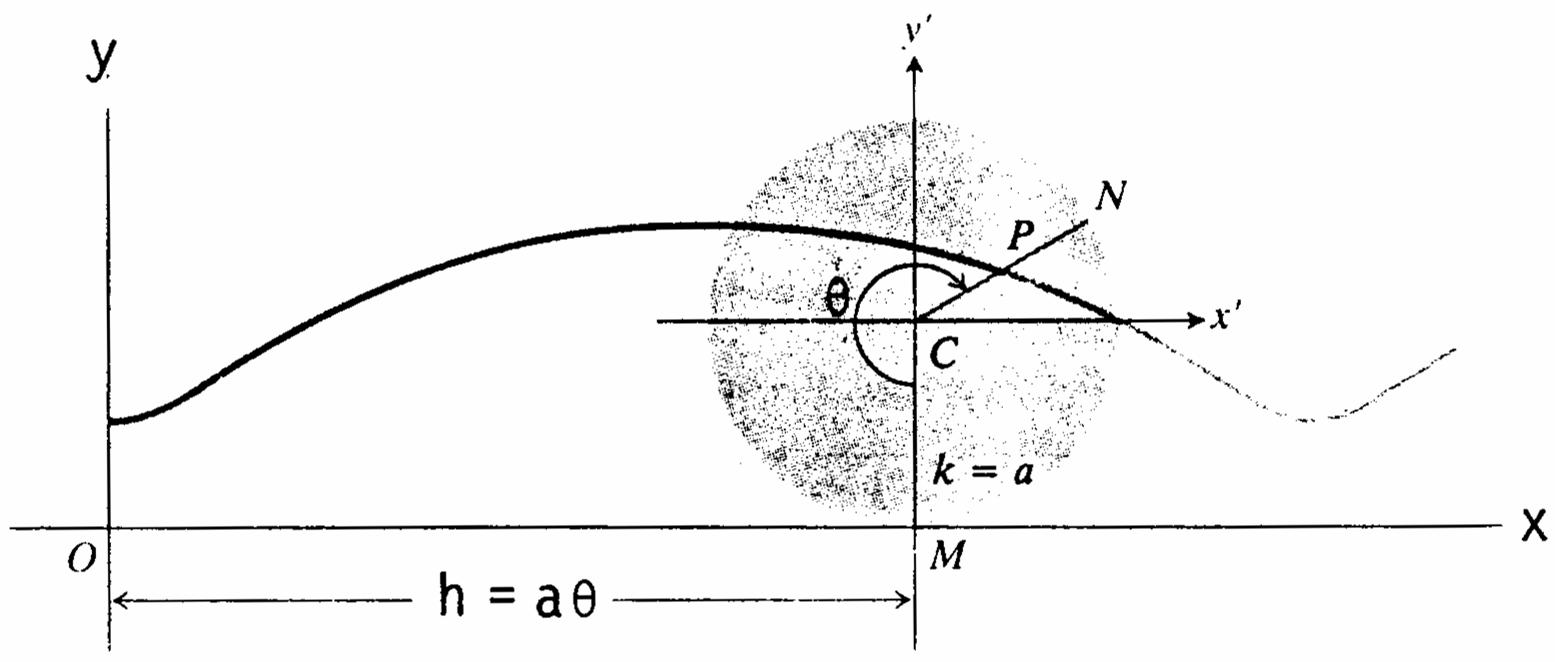
38.Letthex-axisbethelinethewheelrollsalongwiththey-axisthroughalowpointofthetrochoid (seetheaccompanyingfigure).
Letdenotetheanglethroughwhichthewheelturns.Thenhaandka.Nextintroducexy-axes ))œœ ww paralleltothexy-axesandhavingtheiroriginatthecenterCofthewheel.Thenxbcosand w œ ! ybsin,where.Itfollowsthatxbcosbsinandybsin www ### œœ œ œ œ !!)))) 333 111
bcosxhxabsinandykyabcosareparametricequationsofthetrochoid. œ Êœ œ œ œ )))) ww
39.D(x2)yD(x2)y(t2)tDt4t œ Êœ œ Êœ É ˆ‰ˆ‰ˆ‰ #""" ### ########% 17 4
4t40t1.Thesecondderivativeisalwayspositivefort0t1givesalocal Êœ œÊœÁÊœ dD dt ab # $ minimumforD(andhenceD)whichisanabsoluteminimumsinceitistheonlyextremumtheclosest # Ê pointontheparabolais(11). ß
40.D2cost(sint0)D2costsint œ Êœ Ê Éˆ‰ˆ‰ 33 44dt dD ##### ab # 22cost(2sint)2sintcost(2sint)3cost02sint0or3cost0 œ œ œÊ œ œ ˆ‰ˆ‰333 4 ## t0,ort,.Now6cost3cost6sintsothat(0)3relative Êœœœ œ Ê 1 11 33dtdt 5dDdD ## ## # # abab ## maximum,()9relativemaximum,relativeminimum,and dDdD dtdt32 9 #### # # abab 1 œ ÊœÊ ˆ‰ 1 dDrelativeminimum.Thereforebothtandtgivepointsontheellipseclosestto dt333 595 ## # ab ˆ‰111 œÊœœ # thepoint1and1arethedesiredpoints. ˆ‰ Š‹Š‹ 3 4 33ß!ÊßßÈÈ ##
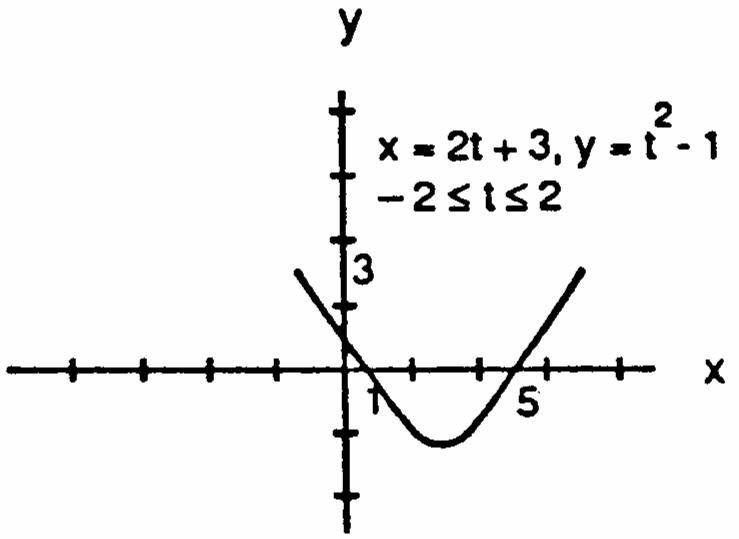
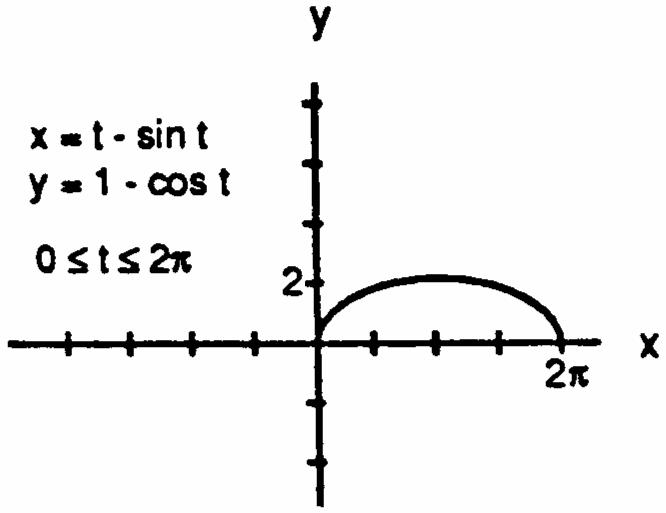
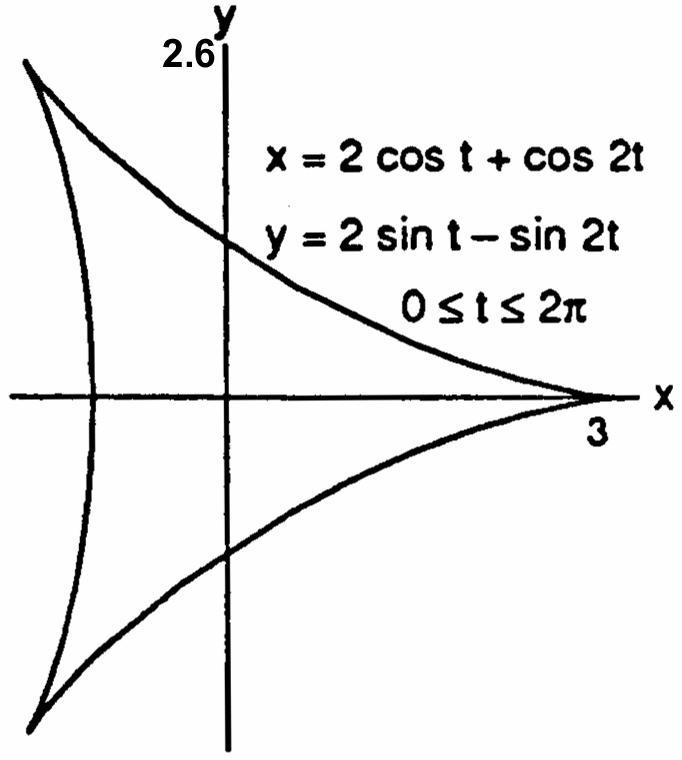
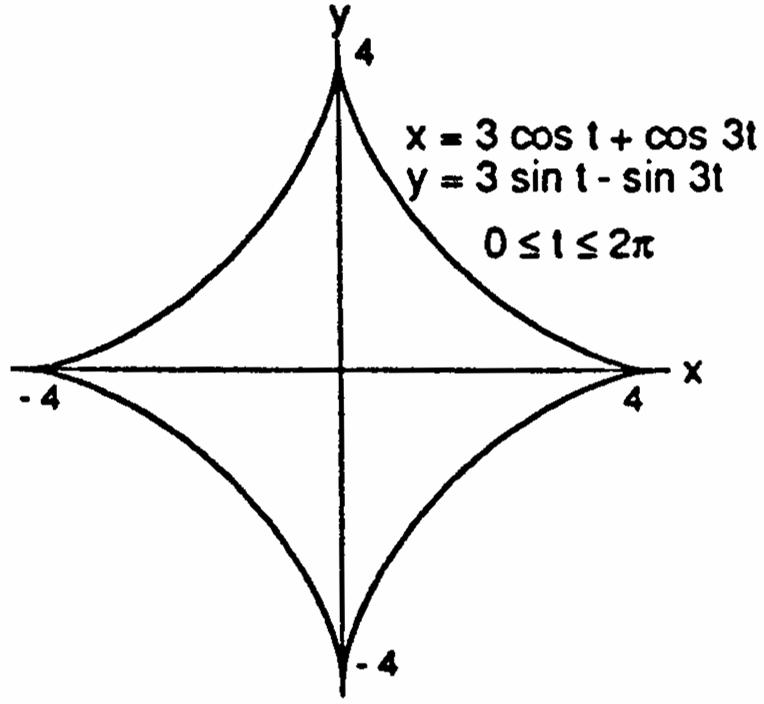
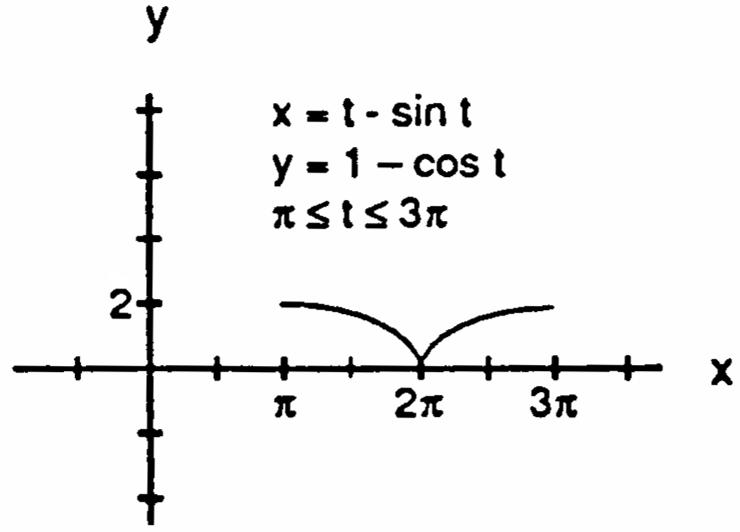
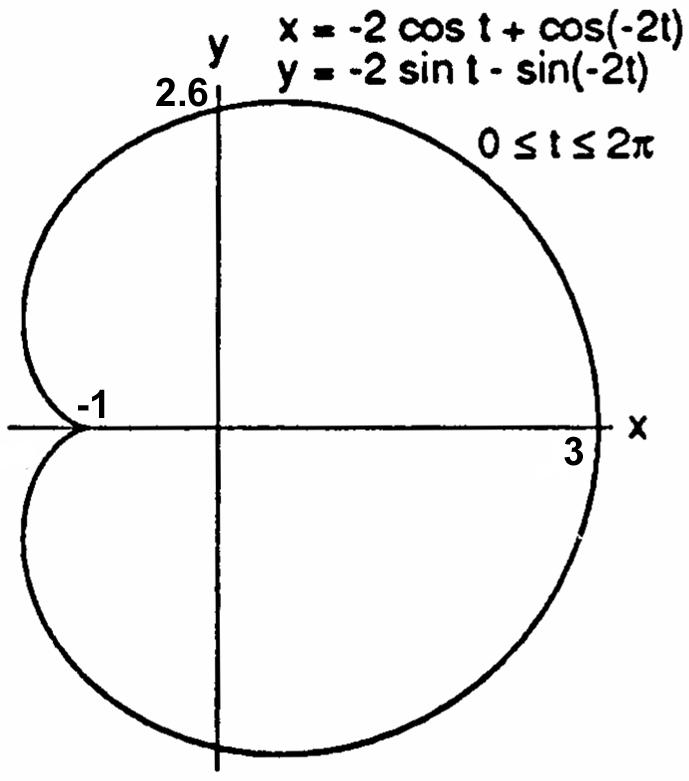
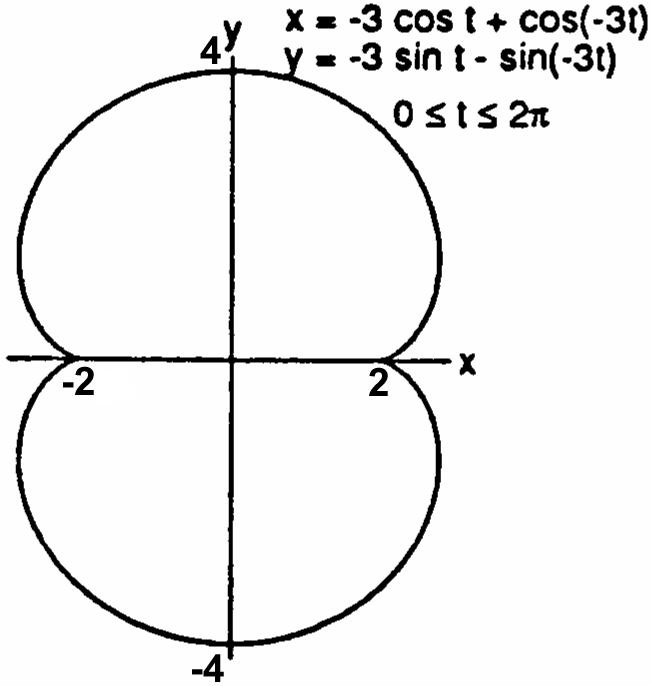
41.(a)(b)(c)
42.(a)(b)(c)
47.(a)(b)(c)
48.(a)(b) (c)(d)
11.2 CALCULUS WITH PARAMETRIC CURVES
1.tx2cos2,y2sin2;2sint,2costcott œÊœœœœœ œÊœœœ 111 444dtdtdxdx/dt2sint dx2cost dydydy/dt ÈÈ cot1;tangentlineisy21x2oryx22;csct Êœ œ œ œ œ ¹Š‹ÈÈÈ dydy dx4dt tœ 1 4 1 w # 2 Êœœœ Êœdydy/dtdy dxdx/dt2sint2sintdx csct #w# #$# # " ¹ È t 1 4
2.txsin2sin,ycos2cos;2cos2t, œ Êœ œ œ œ œ œœ"""" ## 66363dt 3dxˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰ˆ‰ 1111 11 È 2sin2ttan2ttan2tan3;dydydy dtdx2cos2tdx63 2sin2t œ Êœœ Êœ œ œ 1111 " 11 1 11 ¹ ˆ‰ˆ‰ ˆ‰ È tœ 1 6 tangentlineisy3xory3x2;2sec2t œ œ œ Êœ " ## # ÈÈ ’“ Š‹ È 3dydy dtdx2cos2t 2sec2t w# # # 11 11 11 8 œ Êœ " cos2tdx dy $# # 1 ¹ tœ 1 6 Copyright © 2010 Pearson Education,
Section11.2CalculusWithParametricCurves655
3.tx4sin22,y2cos2;4cost,2sint œÊœœœœœœ Êœœ 111 444dtdtdxdx/dt4cost dx2sint dydydy/dt ÈÈ
tanttan;tangentlineisy2x22oryx22; œ Êœ œ œ œ """"" ##### ¹Š‹ÈÈÈ dy dx4 tœ 1 4 1
sect dydydy/dtdy2 dtdxdx/dt4cost8costdx4
sect w#w# #$# " # # œ Êœœœ Êœ "" # # ¹ tœ 1 4 È
4.txcos,y3cos;sint,3sint3 œÊœœ œœ œ œ Êœœ 222dx 333dtdtdxsint 33sint dydy 111 " ##ÈÈÈ ÈÈ
3;tangentlineisy3xory3x;00 Êœ œ œœÊœœ¹Š‹ÈÈÈ ˆ‰‘ dydydy dxdtdxsint 30 t23 1 È ## " w# # 0 Êœ ¹ dy dx # # t23 1
5.tx,y;1,1;tangentlineis œÊœœœœÊœœÊœœ 11dx1 44dtdtdxdx/dtdx dydydy/dtdy t2t """ ### ÈÈ É ¹ tœ 1 4 " 4 y1xoryx;tt2 œ œ œ Êœœ Êœ """"" # $Î#$Î# † ˆ‰ ¹ 44dt4dxdx/dt4dx dydydy/dtdy w#w# ## tœ 1 4
6.txsec11,ytan1;2secttant,sect œ Êœ œœ œ œœ 111 444dtdt dxdy ### ˆ‰ˆ‰ cottcot;tangentlineisÊœœœÊœ œ dydy dx2secttant2tantdx4 sect # # """" ### ¹ ˆ‰ tœ 1 4 1 y(1)(x1)oryx;csctcott œ œ œ Êœœ """"" #### #$dydy dtdx2secttant4 csct w# ## " # # Êœ ¹ dy dx4 # # tœ 1 4 "
7.txsec,ytan;secttant,sect œÊœœœœœœÊœ 111 666dtdtdxdx/dt 2dx 33 dydydy/dt ÈÈ "# csctcsc2;tangentlineisy2xory2x3;œœÊœœ œ œ sect2 secttantdx6 dy 33 # ¹Š‹ È tœ 1 6 1 " ÈÈ
csctcottcott33dydydy/dtdy dtdxdx/dtsecttantdx
csctcott w#w# ## œ Êœœœ Êœ $ ¹ È tœ 1 6
8.t3x312,y3(3)3;(t1),(3t) œÊœ œ œœœ œÊœ È È dx3 dtdtdx dydy(3t) (t1) " ## "Î#"Î# ˆ‰ ˆ‰ 3 # "Î# " # "Î# 2;tangentlineisy32[x(2)]ory2x1; œ œœœ œ œ 3t1331 3t dy dx3(3) ÈÈ ÈÈ ¹ t3 œ dydy dt3tdx 3t(t1)3t1(3t)33 2t3tt1t3t w # ## "Î# "Î# # œœÊœœ È ‘ ‘ È ÈÈ È Š‹ Š‹ 333 2t3tt1 1 2t1 È È È
Êœ ¹ dy dx3 # # t3 œ "
9.t1x5,y1;4t,4tt(1)1;tangentlineis œ ÊœœœœÊœœœÊœ œ dx4t dtdtdxdx/dt4tdx dydydy/dtdy$## $ ¹ t1 œ y11(x5)oryx4;2t œ œ œÊœœœÊœ dydydy/dtdy dtdxdx/dt4tdx 2t w#w# ## "" ## ¹ t1 œ
10.t1x1,y2;,t1;tangentlineis œÊœœ œ œÊœœ Êœ dx dttdttdxdx dydydy"" # " " # ˆ‰ Š‹ t t ¹ t1 œ y(2)1(x1)oryx1;1t1 œ œ œ ÊœœÊœdydydy dtdxdx 1 w## ## " # # Š‹ t ¹ t1 œ
11.txsin,y1cos1;1cost,sint œÊœ œ œ œ œœ œÊœ 11111 33333dtdtdxdx/dt 3dxdydydy/dt È ### "" 3;tangentlineisy3x œÊœœœ œ sint 1costdx3 dysin 1cos 3 ## " ¹Š‹ ÈÈ t 1 3 ˆ‰ ˆ‰ Š‹ ˆ‰ È 1 1 3 3 3 È # " # 1
y3x2;Êœ œœÊœœ È 1 È ˆ‰ 3 3dt(1cost)1costdxdx/dt1cost
dy(1cost)(cost)(sint)(sint)dydy/dt 1 w #w ## 1 1cost 4 œÊœ 1 (1cost)dx dy ## # ¹ tœ 1 3
12.txcos0,y1sin2;sint,costcott œÊœœœ œœ œÊœœ 111 222dtdtdxsint dxcost dydy cot0;tangentlineisy2;csctcsct1 Êœ œœœÊœœ Êœ ¹ ¹ dydydydy dxdtdxsintdx csct tt œ œ 1 1 22 1 # #$ w## ## #
13.t2x,y2;,9; œÊœœœœœœÊœÊœœ 112dx11 21321dtdtdxdxt1t1t121 dydydyt121 abababab abab 2222 22 ¹ t2 tangentlineisy9x1;108 œ œ ʜʜœdydydy dtdxdx 4t14t1421 t1t121 w## ## ababab ababab 333 33 ¹ t2 œ
14.t0x0e1,y1e0;1e,e; œÊœ œœ œœ œ ʜʜœ 00ttdxee1 dtdtdx1edx1e2 dydydyt0 t0 ¹ t0 œ tangentlineisyx; œ œÊœÊœœ 11eee1 22dtdxdx8 dydydy 1e1e1e w## ## tt0 tt 233 0 abab ab ¹ t0 œ
15.x2t93x4t03x4t; 322dxdxdx4t dtdtdt3x œÊ œÊœ Êœ # 2 2y3t46y6t0;thus;t2 $## œÊ œÊœœœœœœœdydydydy/dtt(3x) dtdt6yydxdx/dty(4t)4y 6tt3x #### # Š‹ Š‹ t y 4t 3x2 22 x2(2)9x89x1x1;t22y3(2)4 Ê œÊ œÊœÊœœÊ œ 333#$# 2y16y8y2;therefore ʜʜʜœœ $$" # ¹ dy dx16 3 4 3 t2 œ ab ab 2 #
16.x5t5tt;y(t1)ty(t1)t œ Êœ œ œÊ œ É ÈÈÈ ˆ‰ˆ‰ dx dtdt 4t5t dy """" ### "Î#"Î#"Î# ÈÈ É t1y;thus Ê œ Êœœœœœ† ab dydydy dtdtt1dx ttt2t yyt " ## "# ÈÈÈ ab È " ## " # " ÈÈÈ È ÈÈ É ttt2t yt 4t5t dy dt dx dt " # # " " yt tt 4t5t È È ab ÈÈ É ;t4x543;t4y34yœœÊœ œœÊ†œÊœ #" #& " ˆ‰ÈÈ É ytt t É ÈÈ È 2 3 therefore, ¹ dy dx9 103 t4 œœ 2244 4 Š‹abÈÈ É " & " 2 3 È
17.x2xtt3x2t113x2t1;yt12ty4 œ Ê œ Ê œ Êœ œ $Î##"Î#"Î#dxdxdxdx2t1 dtdtdtdt13x ˆ‰ È È "Î# t1y(t1)2y2ty0t12y0 Ê œÊ œ dydydyydy dtdtdtydt 2t1 t ÈȈ‰ˆ‰ÈÈ Š‹ "" ## "Î#"Î# ÈÈ t12y;thus Ê œ Êœœ Š‹ È È t ydtdt dyydy 2t1ÈÈ Š‹ È Š‹ È È È È È y 2t1 t y È È 2y t1 yy4yt1 2y(t1)2tt1 dydy/dt;t0x2x0x12x0x0;t0 dxdx/dtœœœÊ œÊ œÊœœ Œ Š‹ "Î# yy4yt1 2y(t1)2tt1 2t1 13x È È È È $Î#"Î#ˆ‰ y012(0)y4y4;therefore6 Ê œÊœœœ È È ¹ dy dxt0 œ Œ Œ "Î# 444(4)01 24(01)2(0)01 2(0)1 13(0) È È È È
18.xsint2xtsintxcost21(sint2)1xcost; œÊ œÊ œ Êœ dxdxdxdx1xcost dtdtdtdtsint2 tsint2tysinttcost2;thus;txsin2x œÊ œœœÊ œ dydy dtdx sinttcost2 ˆ‰ 1xcost sint2 111 x;therefore4 Êœœœœ 11111 1 # ¹ dy dx2 sincos248 tœ1 –— 1cos sin2 # Š‹ 1 1 1
Copyright © 2010 Pearson Education, Inc. Publishing
19.xtt,y2t2xt3t1,6t22t23t12t6t2t2 œ œ Êœ œ Êœ œ 3322222 dxdx dtdtdtdt dydy ab 1 ʜʜœ dydy dx3t1dx 2t2212 31122 ¹ t1 ab ab
20.tlnxt,yte11xt1xt1,tee; œ œÊœ Ê œ Êœ œ ab ˆ‰ ttt 1dxdxdx xtdtdtdtdt dy ;t00lnx0x1ÊœœÊœ ʜʜœdydy dxxt1dx1012 tee1 tt0ee00 ab ¹ t0 œ ab
21.Aydxa1costa1costdta1costdta12costcostdt œœ œ œ '''' 0000 2222 222 2 1111 abababab a12costdta2costcos2tdtat2sintsin2t œ œ œ 222 22 1cos2t3131 22224 2 '' 00
11
a30003a œ œ 22 ab11
22.Axdyttedtuttdu12tdt;dvedtve œœ œ Êœ œ Êœ '' 00 11 2t2tt abababab”• ette12tdtu12tdu2dt;dvedtve œ œ Êœ œÊœ t2ttt 11 ababº”• 0 0' ette12t2edtette12t2e œ œ t2ttt2tt 111 1 ababababº”º•”•º 000 0' e0e12ee0e12e13e1 œ œ œ abab abababab 11100013 e
23.A2ydx2bsintasintdt2absintdt2abdtab1cos2tdt œœ œœœ ''''' 11 111 00 000 21cos2t 2 ababab abtsin2tab0ab œ œ !œ ’“ ab ab 1 20 1 11
24.(a)xt,yt,0t1Aydxt2tdt2tdtt0 œœŸŸÊœœœœœ œ 26678 111 111 444 0 1 ''' 000 ab ’“
(b)xt,yt,0t1Aydxt3tdt3tdtt0 œœŸŸÊœœœœœ œ 39921112 111 111 444 0 1 ''' 000 ab ’“
ʈ‰ Š‹ Éabab È ####
25.sintand1costsint1cost22cost dxdx dtdtdtdt dydy œ œ Ê œ œ
Length22costdt2(1cost)dt2dtÊœ œ œ ''' 000 1costsint 1cost1cost 111 È ÈÈ Éˆ‰ É # 2dt(sincesint0on[0]);[u1costdusintdt;t0u0, œ ßœ ÊœœÊœ È '0 sint 1cost 1 È 1 tu2]2udu22u4 œÊœÄœœ 1 ÈÈ ‘ '0 2 "Î#"Î# # !
26.3tand3t3t(3t)9t9t3tt1sincet0on03 dxdx dtdtdtdt dydyœœÊ œ œ œ ß #####%## # ʈ‰ Š‹Š‹ Éab È È ’“ È
Length3tt1dt;ut1du3tdt;t0u1,t3u4Êœ œ ÊœœÊœœÊœ '0 3 È È ’“ È ## # 3 uduu(81)7Äœœ œ '1 4 3 # "Î#$Î# % " ‘
27.tand(2t1)t2t1t1t1t1since0t4 dxdx dtdtdtdt dydyœœ Ê œ œ œ œ ŸŸ "Î##### ʈ‰ Š‹ È ababkk É
Lengtht1dtt8412Êœ œ œ œ '0 4 t 2 abab ’“ # % ! Copyright © 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
28.2t3and1t2t31tt4t4t2t2 dxdx dtdtdtdt dydy œ œ Ê œ œ œ œ abababkk ʈ‰ Š‹ É È "Î##### since0t3Length(t2)dt2t ŸŸÊœ œ œ '0 3 t21 2 3 ’“ # !#
29.8tcostand8tsint8tcost8tsint64tcost64tsint dxdx dtdtdtdt dydyœœÊ œ œ ʈ‰ Š‹ Éabab È ######## 8t8tsince0tLength8tdt4t œœŸŸÊœœœ kkcd 1 1 1 # Î## Î# ! '0 2 1
30.secttantsectcostsectcostandsint dxdx dtsecttantdtdtdt dydy œ œ œ Ê ˆ‰ˆ‰ ab Ê Š‹ "### sectcostsintsect1tanttanttantsince0t œ œ œœœŸŸÉababkk ÈÈ #### 1 3 Lengthtantdtdtlncostlnln1ln2 Êœœœ œ œ '' 00 33 sint cost 11 1 ÎÎÎ$ ! " # cd kk
31.sintandcostsintcost1Area2yds dxdx dtdtdtdt dydy œ œÊ œ œÊœ ʈ‰ Š‹ Éabab #### ' 1 22sint1dt22tcost2[4101]8 œ œ œ œ '0 21 1 11111 ababcdabab # ! #
32.tandtttArea2xds dxdxt1 dtdtdtdtt dydyœœÊ œ œÊœ "Î#"Î###" ʈ‰ Š‹ È É # ' 1 2tdttt1dt;ut1du2tdt;t0u1,œœ œ ÊœœÊœ '' 00 33 ÈÈ 1 ˆ‰É È c 2t4 3t3 $Î## "# # 1 t3u4uduu ’“ È È ‘ œÊœÄœœ '1 4 2428 399 111 $Î# % "
Note:2tdtisanimproperintegralbutlimftexistsandisequalto0,where '0 3 È 1 ˆ‰É ab 2t1 3t $Î# # t Ä!
ft2t.Thusthediscontinuityisremovable:defineFtftfort0andF00 abababab ˆ‰É œœ œ 1 2t 3t $Î#" #
Ftdt.Êœ '0 3 È ab 28 9 1
33.1andt21t2t22t3Area2xds dxdx dtdtdtdt dydyœœ Ê œ œ Êœ ÈÈÈ ÊÊ ˆ‰ Š‹Š‹ É' ##### 1 2t2t22t3dt;ut22t3du2t22dt;t2u1, œ œ Êœ œ Êœ ' È È 2 2 1 Š‹’Š‹ ÈÈÈÈÈ É ## t2u9uduu271 ’“ È È ‘ ab œÊœÄœœ œ '1 9 2252 33311 $Î# * " 11
34.FromExercise30,tantArea2yds2costtantdt2sintdt ʈ‰ Š‹ dx dtdt dy 00 33 ##ÎÎ œÊœœœ''' 111 11
2cost2(1) œ œ œ 111 cd ‘ 1 Î$ ! " #
35.2and1215Area2yds2t15dt dxdx dtdtdtdt dydy1œœÊ œ œÊœœ ʈ‰ Š‹ È ÈÈ ab #### ''11 0
25t35.Check:slantheightis5Areais12535. œ œÊ œ 1111 ÈÈÈÈÈ ’“ ab t 2 # " !
36.handrhrArea2yds2rthrdt dxdx dtdtdtdt dydy1œœÊ œ Êœœ
2rhrtdt2rhrrhr.Check:slantheightishrAreais
1 È ##
37.Letthedensitybe1.Thenxcosttsinttcost,andysinttcosttsint $ œœ Êœœ Êœ dx dtdt dy dm1dsdt(tcost)(tsint)tdttdtsince0t.Thecurve'smassisÊœœ œ œœŸŸ † ʈ‰ Š‹ È kk dx dtdt dy #### # 1
Mdmtdt.AlsoMydmsinttcosttdttsintdttcostdt œœœœœ œ µ '''''' 0000 2222 8 1111 1 ÎÎÎÎ# # x ab
sinttcosttsint2sint2tcost3,whereweintegratedbyparts.Therefore, œ
œœœ
costtsinttcost2cost2tsint3,againintegratingbyparts.Hence œ œ cdcd 1 1 1 Î# ! #Î# !# 3 x.Thereforexy2. œœœ ßœ ß M M y31224122424 ˆ‰
38.Letthedensitybe1.Thenxecostecostesint,andyesintesintecost $ œœÊœ œÊœ tttttt dx dtdt dy dm1dsdtecostesintesintecostdt2edt2edt.Êœœ œ œœ ʈ‰ Š‹ Éabab È È dx dtdt dytttt2tt ####
Thecurve'smassisMdm2edt2e2.AlsoMydmesint2edt œœœ œœ µ '''' 00 tt 11 ÈÈÈÈabŠ‹ t x 1
2esintdt2(2sintcost)2y.œœ œ Êœœœ '0 eee 555M5e1 M2 2e2 1 1 ÈÈÈ’“Š‹ 2t2t22 e2 55 ! "" 11 1 1 1 x ÈŠ‹ ÈÈ ab "
NextMxdmecost2edt2ecostdt22costsint2 y 2t œœœœ œ µ ''' 00 tte2e2 555 11 1 ababŠ‹’“Š‹ ÈÈÈÈ2t2 ! 1 x.Thereforexy.Êœœœ ßœ ß M M5e15e15e1 2 2e2 y2e22e2e1 ÈŠ‹ ÈÈ ababab 2e2 2 55222 1 1 111 111 ab Š‹
39.Letthedensitybe1.Thenxcostsint,andytsint1cost $ œœÊœ œ Êœ dx dtdt dy dm1dsdtsint1costdt22costdt.Thecurve'smassÊœœ œ œ ʈ‰ Š‹ Éabab È dx dtdt dy #### isMdm22costdt21costdt22cosdt2cosdt œœ œ œœ ''''' 0000 tt 1111 ÈÈÈÈ É ˆ‰¸¸ ˆ‰ # ## 2cosdtsince0t022sin4.AlsoMydm œŸŸÊŸŸœœœ µ '' 0 ttt 2 1 1 1 ˆ‰ˆ‰ ˆ‰‘ ###! 1 x tsint2cosdt2tcosdt2sintcosdt œ œ ''' 000 ttt 111 abˆ‰ˆ‰ˆ‰ ### 24cos2tsin2costcost4y. œ œ Êœœœ ‘ ˆ‰ˆ‰ˆ‰ˆ‰‘ tt3164 233M43 M4 ###!! "" 1 1 1 11 x ˆ‰ 16 3
NextMxdmcost2cosdtcostcosdt2sin2 y œœœœ œ µ ''' 00 ttt2 233 sint 11 1 abˆ‰ˆ‰ˆ‰’“ ##! ˆ‰ 3 # x.Thereforexy.œÊœœœßœß 44 3M4333 My ˆ‰ 4 3 "" ab ˆ‰ 1
40.Letthedensitybe1.Thenxt3t,andy3tdm1ds $ œœÊœœÊœÊœ $# # dx3t dtdt dy #
ʈ‰ Š‹ ÉabkkÈÈ È dx dtdt dy ###### # isMdm3tt1dtt17.AlsoMydm3tt1dt œœ œ œœœ µ '''' 00 33 x È È ÈÈ’“Š‹ ab ## #$Î# !# È 3 3t# tt1dt17.4(bycomputer)y2.49.NextMxdm œ œœÊœœ¸œ µ 98717.4 5M7 M # $# '' 0 3 y È È x
dt3t(3t)dt3tt1dt3tt1dtsince0t3.Thecurve'smass œ œ œ œ ŸŸ
t3tt1dt3tt1dt16.4849(bycomputer)x2.35.œ† œ ¸Êœœ¸ '' 00 33 ÈÈ $%##Èab È M M7 y16.4849
Therefore,xy2.352.49. abab ߸ß
41.(a)2sin2tand2cos2t2sin2t2cos2t2 dxdx dtdtdtdt dydy œ œÊ œ œ
Length2dt2t Êœœœ '0 2 1 1 ÎÎ# ! cd 1
(b)costandsintcostsint dxdx dtdtdtdt dydyœœ Ê œ œ 111111111 ʈ‰ Š‹ Éabab ####
Lengthdtt Êœœœ ' Î Î"Î# "Î# 12 12 111 cd
42.(a)xgyhastheparametrizationxgyandyyforcydgyand1;then œœœŸŸÊœœ ababab dx dydy dy w
Lengthdy1dy1[gy]dy œ œ œ ''' ccc ddd dy dydydy dxdxÊÊ Š‹Š‹Š‹ È ab ### w#
(b)xy,0yyL1ydy1ydy1y œŸŸÊœÊœ œ œ† 32124dx339429 3dy224934 00 43431232 0 43 ÎÎÎÎ
41 œ œ 8856 272727 3232ababÎÎ (c)xy,0y1yL1ydy1dydy œŸŸÊœÊœ œ œ 3dx1 2dy 2313
43.x12sincos,y12sinsin2cossin12sin,2cossincos12sin œ œ Êœ œ abababab ))))))))))) dx dd 2dy )) Êœœœ dy dx2cossin12sin2cos2sinsin2cos2sin 2cossincos12sin4cossincos2sin2cos )))) )))))))) ))))) ab ab 222
(a)x12sin0cos01,y12sin0sin00; œ œœ œœœœ abababab abab º dy dx2cos20sin0202 0 2sin20cos0011 ) œ abab ab abab ab
(b)x12sincos0,y12sinsin3;0 œ œœ œœœœ ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰ˆ‰ º 1111 )1 #### œ dy dx21 /2 2sin2cos 2cos2sin 00 ˆ‰ˆ‰ ˆ‰ ˆ‰ˆ‰ ˆ‰ 11 11 ## ##
(c)x12sincos,y12sinsin; œ œœ œœ
œ 44 33 44 33 11 11 433 œœœ È È È 3 1 231 32 1 2 3 2 È
ˆ‰ˆ‰ º 4444 332332dx 3133dy 4/3 2sin2cos 2cos2sin 1111 )1 ÈÈ ˆ‰ˆ‰
44.xt,y1cost,0t21,sintsintcostcost.The œœ ŸŸÊœœÊœœÊœÊœœ 1 dxsintdcost dtdtdx1dtdxdx1 dydydydy Š‹ 2 2 maximumandminimumslopewilloccuratpointsthatmaximize/minimize,inotherwords,pointswhere0 dydy dxdx 2 2 œ cost0tort 232 ʜʜœÊœ
11 22dx 3dy 2 2 11
(a)themaximumslopeissin1,whichoccursatx,y1cos1 dy dx222 t2º ˆ‰ˆ‰ œÎ 1
(a)theminimumslopeissin1,whichoccursatx,y1cos1 dy dx222 t32 333 º
45.costand2cos2t;then00 dx2cos2t dtdtdxdx/dtcostcostdxcost dydydy/dtdy22cost122cost1 œœÊœœœœÊœ abab ## 2cost10costt,,,.Inthe1stquadrant:txsinand Ê œÊœ„ÊœœÊœœ#" # È È 2444444 3572 111111 ysin211isthepointwherethetangentlineishorizontal.Attheorigin:x0andy0 œœÊßœœ ˆ‰ Š‹ 1 4 2 È #
sint0t0ortandsin2t0t0,,,;thust0andtgivethetangentlinesat ʜʜœœÊœœœ 111 11 ## 3 theorigin.Tangentsatorigin:2y2xand2y2x
¹¹ dydy dxdx t0t œÊœœ Êœ 1
46.2cos2tand3cos3tdx3cos3t dtdtdxdx/dt2cos2t22cost1
dydydy/dt3(cos2tcostsin2tsint)œœÊœœœ ab # œœœ 32cost1(cost)2sintcostsint 22cost122cost122cost (3cost)2cost12sint(3cost)4cost3 cd ab ababab abab # ### ### 1;then dy003cost0or4cost30:3cost0t,and dx22cost1 (3cost)4cost33œÊœÊœ œœÊœ ab ab # # ## # 11 4cost30costt,,,.Inthe1stquadrant:txsin2 # ## œÊœ„ÊœœÊœœ È È 33 666666 5711 111111ˆ‰ andysin311isthepointwherethegraphhasahorizontaltangent.Attheorigin:x0 œœÊßœ ˆ‰ Š‹ 1 6 3 È # andy0sin2t0andsin3t0t0,,,andt0,,,,,t0andtgive œÊœœÊœœÊœœ 111111 ##111 3245 3333 thetangentlinesattheorigin.Tangentsattheorigin:yx,and ¹¹ dydy dx2cos0dx 3cos033 t0t œœÊœ## 1 yx œœ Êœ 3cos(3) 2cos(2) 33 1 1 ##
47.(a)xatsint,ya1cost,0t2a1cost,asintLength œ œ ŸŸÊœ œÊ ababab 1 dx dtdt dy a1costasintdta2acostacostasintdt œ œ '' 00 22 11 Éabab ab È ######## a21costdta22sindt2asindt4acos œ œœœÈÈ È É ˆ‰ˆ‰ˆ‰ ’“ ''' 000 222 2ttt 2220 2 111 1 4acos4acos08a œ œ 1 ab (b)a1xtsint,y1cost,0t21cost,sintSurfacearea œÊœ œ ŸŸÊœ œÊœ 1 dx dtdt dy 21cost1costsintdt21cost12costcostsintdt œ œ '' 00 22 11 11 abababab É È #### 21cost22costdt221costdt221cos2dt œ œ œ † 111 ''' 000 22232t 2 32 111 abab È ÈÈ
ÎÎ 222sindt8sindt œœ È ˆ‰ˆ‰ ˆ‰ 11 '' 00 22 23 tt 22 32 11 Î
ududtdt2du;t0u0,t2u ’“ œÊœÊœœÊœœÊœ t1 22 11 16sinudu16sinusinudu161cosusinudu16sinudu16cosusinudu œœœ œ 11111 ''''' 00000 3222 11111 ab 16cosucosu1616 œ œ œ ’“
11116161664 3333 3 0 1111 1
48.xtsint,y1cost,0t2;Volumeydx1cost1costdt œ œ ŸŸœœ111 '' 00 222211 abab
13cost3costcostdt13cost3costcostdt œ œ 11 '' 00 22 232 1cos2t 2 11 ab
3costcos2t1sintcostdt4costcos2tsintcostdt œ œ 11 '' 00 22 5353 2222 22 11 ˆ‰ˆ‰ ab t4sintsin2tsint500005 œ œ œ 1111 ’“ ab 531 243 32 0 21
47-50.ExampleCAScommands: :Maple with(plots); with(student); x:=t->t^3/3; y:=t->t^2/2; a:=0; b:=1; N:=[2,4,8]; forninNdo
tt:=[seq(a+i*(b-a)/n,i=0..n)];
pts:=[seq([x(t),y(t)],t=tt)];
L:=simplify(add(student[distance](pts[i+1],pts[i]),i=1..n));#(b) T:=sprintf("#47(a)(Section11.2)\nn=%3dL=%8.5f\n",n,L); P[n]:=plot([[x(t),y(t),t=a..b],pts],title=T):#(a) enddo:
display([seq(P[n],n=N)],insequence=true);
ds:=t->sqrt(simplify(D(x)(t)^2+D(y)(t)^2)):#(c) L:=Int(ds(t),t=a..b): L=evalf(L);
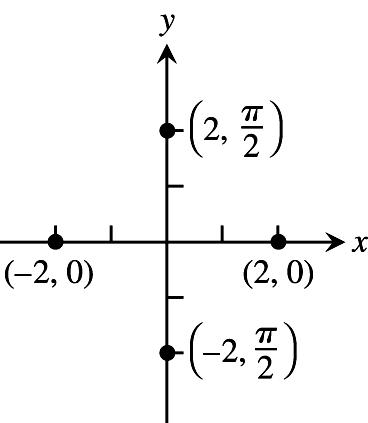
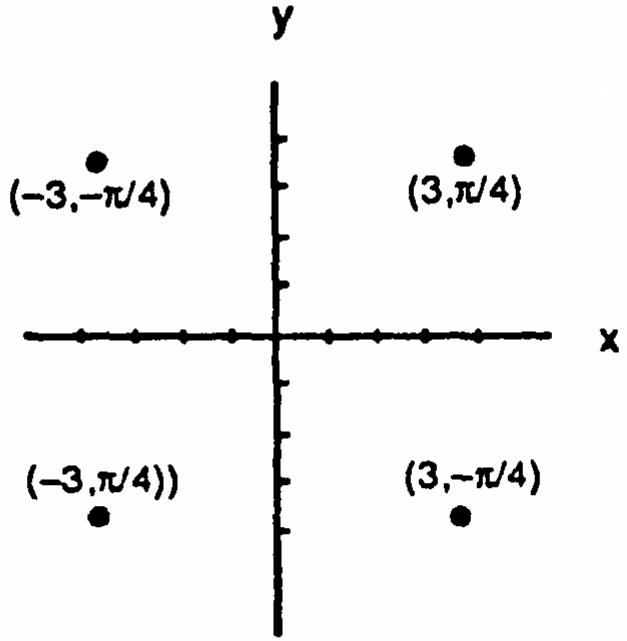
11.3 POLAR COORDINATES 1.a,e;b,g;c,h;d,f2.a,f;b,h;c,g;d,e
3.(a)22nand2(2n1),naninteger ˆ‰ˆ‰ ß ß 11 ##11 (b)(2n)and((2n1)),naninteger #ß #ß 11 (c)22nand2(2n1),naninteger ˆ‰ˆ‰ ß ß 33 11 ##11 (d)((2n1))and(2n),naninteger #ß #ß 11
4.(a)32nand32n,naninteger ˆ‰ˆ‰ ß ß 11 44 5 11
(b)32nand32n,naninteger ˆ‰ˆ‰ ß ß 11 44 5 11
(c)32nand32n,naninteger ˆ‰ˆ‰ ß ß 11 44 3 11
(d)32nand32n,naninteger ˆ‰ˆ‰ ß ß 11 44 3 11
5.(a)xrcos3cos03,yrsin3sin00Cartesiancoordinatesare(0) œœœœœœÊ$ß ))
(b)xrcos3cos03,yrsin3sin00Cartesiancoordinatesare(0) œœ œ œœ œÊ $ß ))
(c)xrcos2cos1,yrsin2sin3Cartesiancoordinatesare13 œœœ œœœÊ ß ))22 33 11
(d)xrcos2cos1,yrsin2sin3Cartesiancoordinatesare13 œœœœœœÊß ))77 33 11 ÈÈŠ‹
(e)xrcos3cos3,yrsin3sin0Cartesiancoordinatesare(30) œœ œœœ œÊß )1)1
(f)xrcos2cos1,yrsin2sin3Cartesiancoordinatesare13 œœœœœœÊß ))11 33
(g)xrcos3cos23,yrsin3sin20Cartesiancoordinatesare(30) œœ œ œœ œÊ ß )1)1
(h)xrcos2cos1,yrsin2sin3Cartesiancoordinatesare13 œœ œ œœ œÊ ß ))ˆ‰ˆ‰ ÈÈŠ‹ 11 33
6.(a)x2cos1,y2sin1Cartesiancoordinatesare(11) œœœœÊß ÈÈ11 44
(b)x1cos01,y1sin00Cartesiancoordinatesare(10) œœœœÊß
(c)x0cos0,y0sin0Cartesiancoordinatesare(0) œœœœÊ!ß 11 ##
(d)x2cos1,y2sin1Cartesiancoordinatesare(11) œ œ œ œ Ê ß ÈȈ‰ˆ‰ 11 44
(e)x3cos,y3sinCartesiancoordinatesare œ œœ œ Êß 5533 626 333311 È È ###Š‹
(f)x5costan3,y5sintan4Cartesiancoordinatesare(4) œœœœÊ$ß ˆ‰ˆ‰ "" 44 33
Copyright © 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
Section11.3PolarCoordinates663
(g)x1cos71,y1sin70Cartesiancoordinatesare(10) œ œœ œÊß 11
(h)x23cos3,y23sin3Cartesiancoordinatesare33 œœ œœÊ ß ÈÈÈÈŠ‹ 22 33 11
7.(a)1,1r112,sinandcosPolarcoordinatesare2, ab È ÈÈŠ‹ Êœ œœœÊœÊ2211 2244))) ÈÈ 11
(b)3,0r303,sin0andcos1Polarcoordinatesare3, ababab É Êœ œœœ ÊœÊ 22 )))11
(c)3,1r312,sinandcosPolarcoordinatesare2, Š‹ÊŠ‹ ÈÈ ab ˆ‰ Êœ œœ œÊœÊ 2211111 2266 3 ))) È 11
(d)3,4r345,sinandcosarctanPolarcoordinatesare abab É ˆ‰ Êœ œœœ Êœ Ê 22434 553)))1
5,arctan ˆ‰ ˆ‰ 1 4 3
8.(a)2,2r2222,sinandcosPolarcoordinatesare ababab É È Êœ œœ œ Êœ Ê 22113 224))) ÈÈ 1
22, Š‹ È 3 4 1
(b)0,3r033,sin1andcos0Polarcoordinatesare3, ab È ˆ‰ Êœ œœœÊœÊ 22 22 ))) 11
(c)3,1r312,sinandcosPolarcoordinatesare2, Š‹ÊŠ‹ ÈÈ
Êœ œœœ ÊœÊ 2 2155 2266 3 ))) È 11
(d)5,12r51213,sinandcosarctanPolarcoordinatesare abab É ˆ‰ Êœ œœ œÊœ Ê 2212512 13125))) 13,arctan ˆ‰ ˆ‰ 12 5
9.(a)3,3r3332,sinandcosPolarcoordinatesare ab È È Êœ œ œ œ ÊœÊ22115 224))) ÈÈ 1 32, Š‹ È 5 4 1
(b)1,0r101,sin0andcos10Polarcoordinatesare1,0 ababab É Êœ œ œœÊœÊ 22 )))
(c)1,3r132,sinandcosPolarcoordinatesare Š‹ÊŠ‹ ÈÈ ab Êœ œ œ œÊœÊ 223 223 15))) È 1 2, ˆ‰ 5 3 1
(d)4,3r435,sinandcosarctanPolarcoordinatesare abab É ˆ‰ Êœ œ œœ Êœ Ê 22343 554)))1 5,arctan ˆ‰ ˆ‰ 1 4 3
10.(a)2,0r202,sin0andcos10Polarcoordinatesare2,0 ababab É Êœ œ œœÊœÊ 22 )))
(b)1,0r101,sin0andcos1orPolarcoordinatesare1,or ab ab È Êœ œ œœ Êœœ Ê 22 )))1)11 1, ab 1
(c)0,3r033,sin1andcos0Polarcoordinatesare3, abab É ˆ‰ Êœ œ œœÊœÊ 22 22 ))) 11
(d),r1,sinandcosorPolarcoordinates Š‹ÊŠ‹ ˆ‰ ÈÈÈ 333 22222266 11175 22 Êœ œ œ œ Êœœ Ê ))))11 are1,or1,ˆ‰ˆ‰ 75 66 11
27.rcos2x2,verticallinethrough(0)28.rsin1y1,horizontallinethrough(01) )) œÊœ#ßœ Êœ ß
29.rsin0y0,thex-axis30.rcos0x0,they-axis )) œÊœœÊœ
31.r4cscrrsin4y4,ahorizontallinethrough(04) œÊœÊœÊœß )) 4 sin )
32.r3secrrcos3x3,averticallinethrough(30) œ ʜʜ Êœ ß )) 3 cos )
33.rcosrsin1xy1,linewithslopem1andinterceptb1 )) œÊ œœ œ
34.rsinrcosyx,linewithslopem1andinterceptb0 ))œÊœœœ
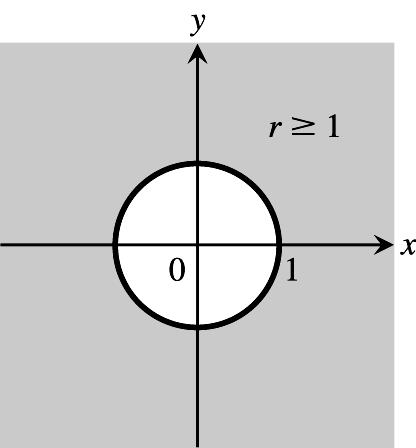
35.r1xy1,circlewithcenterC(0)andradius1 ### œÊ œœ!ß
36.r4rsinxy4yxy4y44x(y2)4,circlewithcenterC(02)andradius2 ####### œÊ œÊ œÊ œœß )
37.rrsin2rcos5y2x5,linewithslopem2andinterceptb5 œÊ œÊ œœœ 5 sin2cos)) ))
38.rsin222rsincos2(rsin)(rcos)1xy1,hyperbolawithfocalaxisyx ##))))) œÊœÊœÊœœ
39.rcotcscrsincosrsinrcosyx,parabolawithvertex(00) œœÊœÊœÊœß )))))) ˆ‰ˆ‰ cos sinsin ) )) "#### whichopenstotheright
40.r4tansecr4rcos4sinrcos4rsinx4y,parabolawith œÊœÊœÊœÊœ )))))) ˆ‰ sin cos ) ) # #### vertex(0)whichopensupward œ!ß
41.r(csc)ersineye,graphofthenaturalexponentialfunction œÊœÊœ ))rcosrcosx ))
42.rsinlnrlncosln(rcos)ylnx,graphofthenaturallogarithmfunction ))) œ œÊœ
43.r2rcossin1xy2xy1x2xyy1(xy)1xy1,twoparallel ####### œÊ œÊ œÊ œÊ œ„ )) straightlinesofslope1andy-interceptsb1 œ„
44.cossinrcosrsinxyxyxy,twoperpendicular ######## )))) œÊœÊœÊœÊ„œ kkkk linesthroughtheoriginwithslopes1and1,respectively.
45.r4rcosxy4xx4xy0x4x4y4(x2)y4,acirclewith ######### œ Ê œ Ê œÊ œÊ œ ) centerC(20)andradius2 ß
666Chapter11ParametricEquationsandPolarCoordinates
46.r6rsinxy6yxy6y0xy6y99x(y3)9,acirclewith ######### œ Ê œ Ê œÊ œÊ œ ) centerC(03)andradius3 ß
47.r8sinr8rsinxy8yxy8y0xy8y1616x(y4)16,a œÊœÊ œÊ œÊ œÊ œ ))######### circlewithcenterC(04)andradius4 ß
48.r3cosr3rcosxy3xxy3x0x3xy œÊœÊ œÊ œÊ œ ))#######99 44 xy,acirclewithcenterCandradius Ê œß! ˆ‰ˆ‰3933 4 ### ##
49.r2cos2sinr2rcos2rsinxy2x2yx2xy2y0 œ Êœ Ê œ Ê œ ))))##### (x1)(y1)2,acirclewithcenterC(11)andradius2 Ê œß ## È
50.r2cossinr2rcosrsinxy2xyx2xyy0 œ Êœ Ê œ Ê œ ))))##### (x1)y,acirclewithcenterC1andradius Ê œß #"" ### # ˆ‰ˆ‰ 5 4 5 È
51.rsin2rsincoscossin2rsinrcos2yx2 ˆ‰ˆ‰ ))))) œÊ œÊ œÊ œ 111 666 33 ÈÈ #### "" 3yx4,linewithslopemandinterceptb Ê œœ œ È " ÈÈ 33 4
52.rsin5rsincoscossin5rcosrsin5xy5 ˆ‰ˆ‰ 222 333 33 111 œÊ œÊ œÊ œ )))))ÈÈ #### "" 3xy10,linewithslopem3andinterceptb10 Ê œœ œ ÈÈ
53.x7rcos754.y1rsin1 œÊœœÊœ ))
55.xyrcosrsin56.xy3rcosrsin3 œÊœÊœ œÊ œ ))))) 1 4
57.xy4r4r2orr2 ###œÊœÊœœ
58.xy1rcosrsin1rcossin1rcos21 ########## œÊ œÊ œÊœ))))) ab
59.14x9y364rcos9rsin36 x 94 y # # œÊ œÊ œ ######))
60.xy2(rcos)(rsin)2rcossin22rcossin4rsin24 œÊœÊœÊœÊœ ))))))) ###
61.y4xrsin4rcosrsin4cos #### œÊœÊœ))))
62.xxyy1xyxy1rrsincos1r(1sincos)1 ####### œÊ œÊ œÊ œ ))))
63.x(y2)4xy4y44xy4yr4rsinr4sin ####### œÊ œÊ œÊœÊœ))
64.(x5)y25x10x25y25xy10xr10rcosr10cos œÊ œÊ œÊœÊœ####### ))
65.(x3)(y1)4x6x9y2y14xy6x2y6r6rcos2rsin6 œÊ œÊ œ Êœ####### ))
66.(x2)(y5)16x4x4y10y2516xy4x10y13 œÊ œÊ œ ###### r4rcos10rsin13Êœ # ))
67.()whereisanyangle !ß ))
68.(a)xarcosarrasec œÊœÊœÊœ)) a cos ) (b)ybrsinbrrbcsc œÊœÊœÊœ)) b sin )
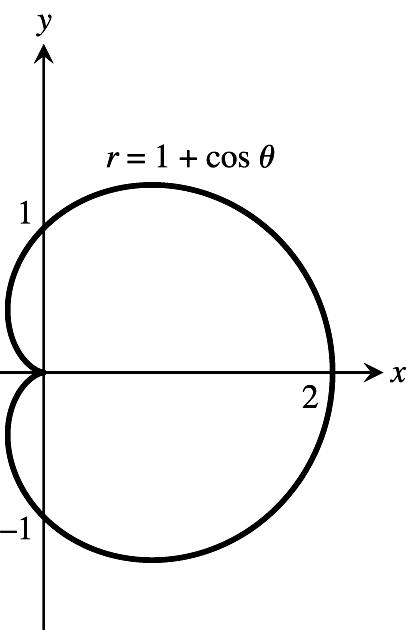
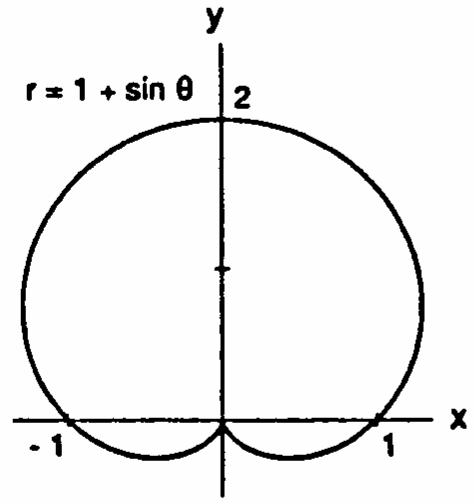
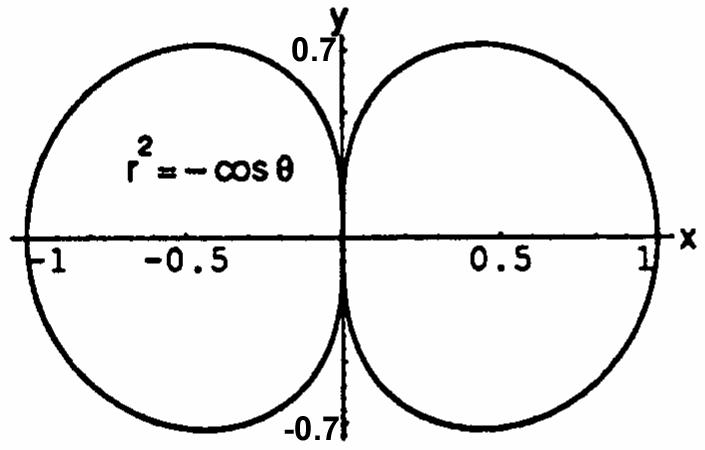
11.4 GRAPHING IN POLAR COORDINATES 1.1cos()1cosrsymmetricaboutthe œ œÊ )) x-axis;1cos()rand1cos() Á )1)
1cosrnotsymmetricaboutthey-axis; œ ÁÊ ) thereforenotsymmetricabouttheorigin
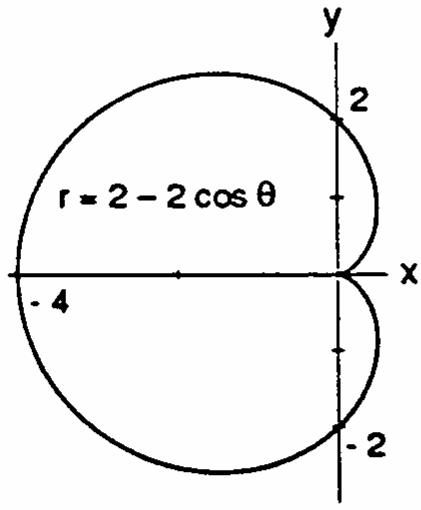
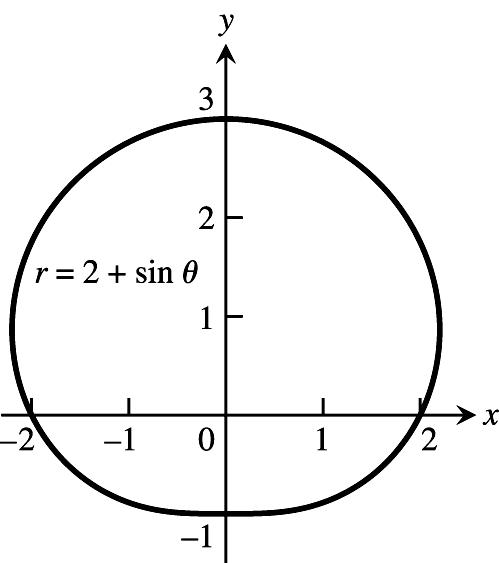
2.22cos()22cosrsymmetricaboutthe œ œÊ )) x-axis;2cos()rand22cos() # Á )1)
22cosrnotsymmetricaboutthey-axis; œ ÁÊ ) thereforenotsymmetricabouttheorigin
3.1sin()1sinrand1sin() œ Á ))1)
1sinrnotsymmetricaboutthex-axis; œ Á Ê )
1sin()1sinrsymmetricabout œ œÊ 1)) they-axis;thereforenotsymmetricabouttheorigin
4.1sin()1sinrand1sin() œ Á ))1)
1sinrnotsymmetricaboutthex-axis; œ Á Ê )
1sin()1sinrsymmetricaboutthe œ œÊ 1)) y-axis;thereforenotsymmetricabouttheorigin
668Chapter11ParametricEquatinsandPolarCoordinates
5.2sin()2sinrand2sin() œ Á ))1)
2sinrnotsymmetricaboutthex-axis; œ Á Ê )
2sin()2sinrsymmetricaboutthe œ œÊ 1)) y-axis;thereforenotsymmetricabouttheorigin
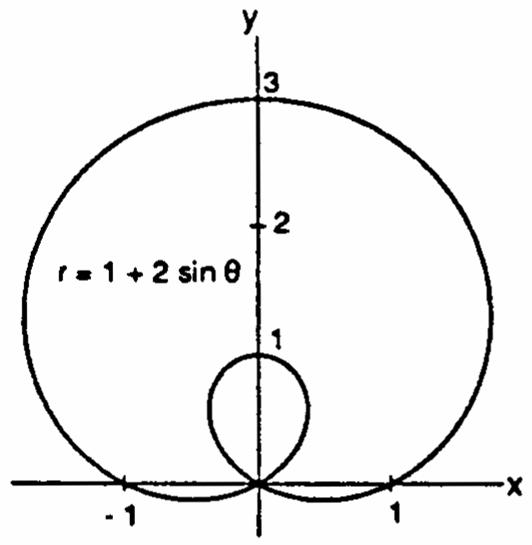
6.12sin()12sinrand12sin() œ Á ))1)
12sinrnotsymmetricaboutthex-axis; œ Á Ê ) 12sin()12sinrsymmetricaboutthe œ œÊ 1)) y-axis;thereforenotsymmetricabouttheorigin
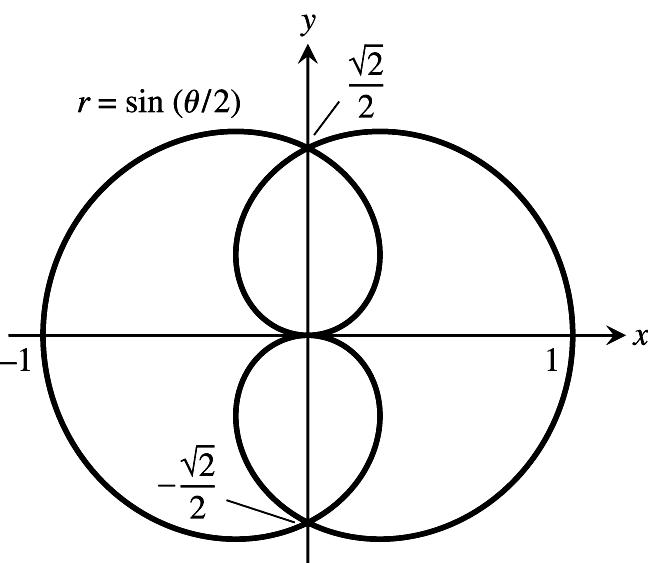
7.sinsinrsymmetricaboutthey-axis; ˆ‰ˆ‰ œ œ Ê )) ## sinsin,sothegraphsymmetricaboutthe ˆ‰ˆ‰ 2 2 1)) # œ is x-axis,andhencetheorigin.
8.coscosrsymmetricaboutthex-axis; ˆ‰ˆ‰œœÊ)) ## coscos,sothegraphsymmetricaboutthe ˆ‰ˆ‰ 2 2 1)) # œ is y-axis,andhencetheorigin.
9.cos()cosr(r)and(r)areonthe œœÊß ß )))) # graphwhen(r)isonthegraphsymmetricaboutthe ßÊ ) x-axisandthey-axis;thereforesymmetricabouttheorigin
10.sin()sinr(r)and(r)areon 1))1)1) œœÊß ß # thegraphwhen(r)isonthegraphsymmetricabout ßÊ ) they-axisandthex-axis;thereforesymmetricaboutthe origin
11.sin()sinr(r)and(r) œ œÊß ß 1))1)1) # areonthegraphwhen(r)isonthegraphsymmetric ßÊ ) aboutthey-axisandthex-axis;thereforesymmetricabout theorigin
12.cos()cosr(r)and(r)areon œ œÊß ß )))) # thegraphwhen(r)isonthegraphsymmetricabout ßÊ ) thex-axisandthey-axis;thereforesymmetricaboutthe origin
13.Sincerareonthegraphwhen(r)isonthegraph ab „ß ß ))
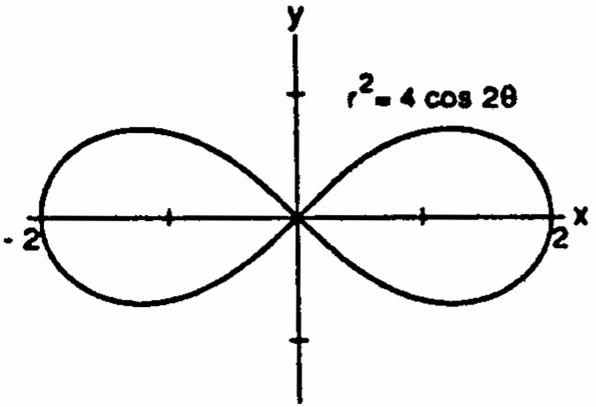
r4cos2()r4cos2,thegraphisˆ‰ ab„œ Êœ # # )) symmetricaboutthex-axisandthey-axisthegraphis Ê symmetricabouttheorigin
14.Since(r)onthegraph(r)isonthegraph ßÊ ß ))
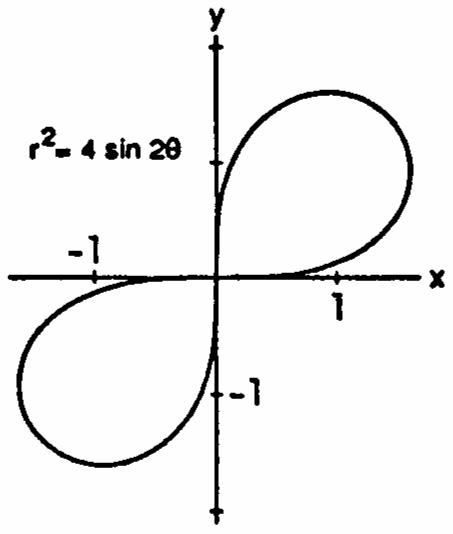
r4sin2r4sin2,thegraphisˆ‰ ab„œÊœ # # )) symmetricabouttheorigin.But4sin2()4sin2 œ )) rand4sin2()4sin(22)4sin(2) Á œ œ # 1)1))
4sin2rthegraphisnotsymmetricabout œ ÁÊ ) # thex-axis;thereforethegraphisnotsymmetricabout they-axis
15.Since(r)onthegraph(r)isonthegraph ßÊ ß ))
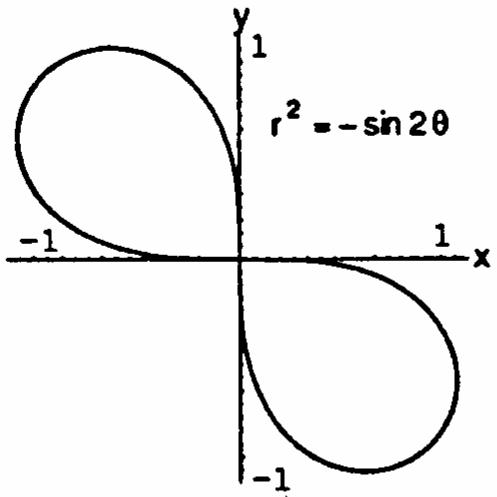
rsin2rsin2,thegraphisˆ‰ ab„œ Êœ # # )) symmetricabouttheorigin.Butsin2()(sin2) œ )) sin2randsin2()sin(22) )1)1) Á œ #
sin(2)(sin2)sin2rthegraph œ œ œÁÊ))) # isnotsymmetricaboutthex-axis;thereforethegraphis notsymmetricaboutthey-axis