Chapter 2
The Particle in a Box
2.1 (a) Theauxiliaryequationis260 ss + −= and[1124]/22 s = −±+= and–3.So
23 12 xx ycece =+
(b) Setting x =0and y =0,weget12 0 cc = + (Eq.1).Differentiationof y gives 23 12 23. xx ycece ′ =− Setting x =0and1, y ′ = wehave12 123cc = (Eq.2).Subtracting twiceEq.1fromEq.2,weget2 15c = and20.2. c = Equation1thengives10.2. c =
2.2 For0, ypyqy ′′′++= theauxiliaryequationis212 0()(),spsqssss ++==−− where1 s and2 s aretheroots.ComparisonwithEq.(2.8)showsthat12si = + and22, si =− so theauxiliaryequationis20(2)(2)45. sisiss =−−−+=−+ Therefore4 p =− and 5. q = Thedifferentialequationis450. yyy ′′′ +=
2.3 (a) Thequadraticformulagivesthesolutionsoftheauxiliaryequation20 spsq++= [Eq.(2.7)]as2(4)/2.sppq =−±− Tohaveequalrootsoftheauxiliaryequation requiresthat240 pq−= .Setting2/4 qp = inthedifferentialequation(2.6),wehave
2 (/4)0ypypy ′′′++= (Eq.1).Theauxiliary-equationsolutionis/2. sp =− Thuswe mustshowthat/2 2 px yxe = isthesecondsolution.Differentiationgives /2/2 2/2 pxpxyepxe ′ =− and/22/22/4. pxpxypepxe ′′ =−+ SubstitutioninEq.(1)gives theleftsideofEq.(1)as/22/2/22/22/2 /4/2/4pxpxpxpxpx pepxepepxepxe −++−+ , whichequalszeroandcompletestheproof. (b) Theauxiliaryequation2221(1)0sss+=−= hasroots s =1and s =1.Frompart (a),thesolutionis12xx ycecxe =+
2.4 IncomparingEqs.(1.8)and(2.2), y in(2.2)isreplacedby x,and x in(2.2)isreplacedby t. Therefore x anditsderivativesin(1.8)mustoccurtothefirstpowertohavealinear differentialequation. (a) Linear; (b) linear; (c) nonlinear; (d) nonlinear; (e) linear.
2.5 (a) F; (b) F; (c) T; (d) F(onlysolutionsthatmeetcertainconditionssuchasbeing continuousareallowedasstationary-statewavefunctions); (e) T.
2.6 (a) Maximumat x = l/2.Minimumat x =0and x = l,wheretheendsoftheboxareat x = 0and l.
(b) Maximumat l/4and3l/4.Minimumat0, l/2,and l.
(c) Minimumat0, l/3,2l/3,and l.Maximumat l/6, l/2,5l/6.
2.7 (a) /42/42/4 000 ||(2/)sin(/)(2/)[/2(/4)sin(2/)]| lll dxlnxldxlxlnnxl ψπππ ∫=∫=− = 1/4(1/2)sin(/2), nn π π where(A.2)intheAppendixwasused.
(b) The(1/2) nπ factorintheprobabilitymakestheprobabilitysmalleras n increases, andthemaximumprobabilitywilloccurforthesmallestvalueof n forwhichthesine factorisnegative.Thisvalueis n =3.
(c) 0.25.
(d) Thecorrespondenceprinciple,sinceinclassicalmechanicstheprobabilityisuniform throughoutthebox.
2.8 (a) Theprobabilityis222||(2/)sin(/)(1/Å)sin(0.600/2)(0.001Å) dxlxldx ψππ==⋅⋅ =6.55×10–4.Thenumberoftimestheelectronisfoundinthisintervalisabout 106(6.55×10–4)=655.
(b) Theprobabilityratioforthetwointervalsis 22 sin[(1.00/2.00)]sin[(0.700/2.00)] ππ =1.260andabout1.260(126)=159 measurementswillbeinthespecifiedinterval.
2.9 (a) Thenumberofinteriornodesisonelessthan n.
(b) 22(2/)sin(4/) lxl ψ π = and2()/(4/)(4/)sin(4/)cos(4/). ddxllxlxl ψπππ =
At x = l/2,2()/(4/)(4/)sin(2)cos(2)0. ddxll ψπππ ==
2.10 (a) 2222upperlower(21)/8 EEhml−=−=
3(6.626×10–34Js)2/8(9.109×10–31kg)(1.0×10–10m)2=1.81×10–17J. (b) ||/ Ehhc ν λ Δ== and/|| hcE λ = Δ= (6.626×10–34Js)(2.998 × 108m/s)/(1.81×10–17J)=1.10×10–8m=110Å. (c) Ultraviolet.
2.11 222 /8 Enhml = and1/2(8)/ nmElh = .Wehave2/2 Em = v =½(0.001kg)(0.01m/s)2 = 5×10–8J,so n =[8(0.001kg)(5×10–8J)]1/2(0.01m)/(6.626×10–34Js)=3×1026 .
2.12 upperlower EEhν −== (52–22)22 /8 hml and1/2 (21/8)lhmν = = [21(6.626×10–34Js)/8(9.1×10–31kg)(6.0×1014 s –1)]1/2=1.78×10–9m=1.78nm.
2.13 2222 upperlower(1)/8, EEhnhml ν −==− so 222 18/8/ nmlhmlch νλ ===
8(9.109×10–31kg)(2.00×10–10m)2(2.998×108m/s)/[(8.79×10–9m)(6.626×10–34Js)] =15.So216 n = and n =4
2.14 2222 ()/8, ba hnnhml ν =− so ν isproportionalto22 bann For n =1to2,22 bann is3and for n =2to3,22 bann is5.Henceforthe2to3transition, ν =(5/3)(6.0×1012 s –1)= 10×1012 s –1 .
2.15 2222 ()/8, ba hnnhml ν =− so 2228/ ba nnmlh ν ==
8(9.109×10–31kg)(0.300×10–9m)2(5.05×1015 s –1)/(6.626×10–34Js)=5.00. Thesquaresofthefirstfewpositiveintegersare1,4,9,16,25,…,andtheonlytwo integerswhosesquaresdifferby5are2and3. n =5 n (=5 l/2)ψ (2 l/2)1/2
2.16 1122222 upperlower ()(/8)()(/8), u hEEhhmlnnhmlk ν =−=−= where k isaninteger.
For1 u nn−= and1,2,3,, n = … wegetthefollowing k values: 222222 213;325;437;9,11,13,15,etc. kkkk =−==−==−==
For3 u nn−= and1,2,3,, n = weget 2222 4115;5221;kk=−==−= 22 6327;33,39,etc.kk=−==
For5 u nn−= and1,2,3,, n = … weget35,45,55,etc. k = Thesmallest k thatcorrespondstotwodifferenttransitionsis15 k = forthe1to4 transitionandthe7to8transition.
2.17 Eachdoublebondconsistsofonesigmaandonepibond,sothetwodoublebondshave4 pielectrons.Withtwopielectronsineachparticle-in-a-boxlevel,the4pielectrons occupythelowesttwolevels, n =1and n =2.Thehighest-occupiedtolowest-vacant transitionisfrom n =2to n =3,so2222 ||/(32)/8 Ehhchml νλ Δ===− and 2311028 34 88(9.10910kg)(7.010m)(2.99810m/s) 55(6.62610Js) mlc h λ ××× == × = 3.2107m × = 320nm
2.18 Outsidethebox,0. ψ = Insidethebox, ψ isgivenby(2.15)as
11/211/2 cos[(2)]sin[(2)]. amExbmEx ψ =+
Continuityrequiresthat ψ =0at/2 xl = andat/2, xl = theleftandrightendsofthebox.Using(2.14),wethushave
11/211/2 0cos[(2)/2]sin[(2)/2] amElbmEl =− [Eq.(1)] 11/211/2 0cos[(2)/2]sin[(2)/2] amElbmEl =+ [Eq.(2)].
AddingEqs.(1)and(2)anddividingby2,weget11/20cos[(2)/2], amEl = so
either a =0or11/2cos[(2)/2]0 mEl = [Eq.(3)].
SubtractingEq.(1)from(2)anddividingby2,weget11/20sin[(2)/2], bmEl = so either b =0or11/2sin[(2)/2]0 mEl = [Eq.(4)].
If a =0,then b cannotbe0(becausethiswouldmake ψ =0),soif a =0,then 11/2 sin[(2)/2]0 mEl = [Eq.(5)]and11/2sin[(2)]. bmEx ψ = TosatisfyEq.(5),we musthave11/2[(2)/2], mElkπ = where k isaninteger.Thewavefunctionsandenergies when a =0are sin[2/] bkxl ψ π = and222 (2)/8 Ekhml = ,where k =1,2,3,….[Eq.(6)]
(ForreasonsdiscussedinChapter2, k =0isnotallowedandnegativevaluesof k donot giveadifferent ψ.)
If b =0,then a cannotbe0(becausethiswouldmake ψ =0),soif b =0,then 11/2 cos[(2)/2]0 mEl = [Eq.(7)]and11/2cos[(2)]. amEx ψ = TosatisfyEq.(7),we musthave11/2[(2)/2](21)/2, mElj π =+ where j isaninteger.Thewavefunctionsand energieswhen b =0are cos[(21)/] ajxl ψ π =+ and222 (21)/8 Ejhml =+ ,where j =0,1,2,3,…[Eq.(8)] (AsdiscussedinChapter2,negativevaluesof j donotgiveadifferent ψ.)
InEq.(8),2j +1takesonthevalues1,3,5,…;inEq.(6),2k takesonthevalues 2,4,6,….Therefore222/8,Enhml = where n =1,2,3,…,aswefoundwiththeoriginat theleftendofthebox.Also,thewavefunctionsinEqs.(6)and(8)arethesameaswith theoriginattheleftend,ascanbeverifiedbysketchingafewofthem.
2.19 UsingsquarebracketstodenotethedimensionsofaquantityandM,L,Ttodenotethe dimensionsmass,length,andtime,wehave[E]=ML2 T –2=[h]a[
L
= (ML2 T –2)aTaM b Lc =M a+b L2a+cT –a .Inordertohavethesamedimensionsoneachsideof theequation,thepowersofM,L,andTmustmatch.So1= a + b,2=2a + c,–2=–a Weget a =2, b =1– a =–1,and c =2–2a =–2.
2.20 FromEqs.(1.20)and(2.30),
1/21/2 /(2)/(2)/ 12 () iEtimEximEx ececeΨ=+ .
2.21 (a) Let21/21/2 0 (2/)() rmVE ≡− and21/21/2 (2/) smE ≡ .ThenI rx Ce ψ = and IIcossin. AsxBsx ψ =+ WehaveI rx Cre ψ ′ = andIIsincos. sAsxsBsx ψ ′ = −+ The conditionIII(0)(0) ψ ψ ′′ = gives CrsB = ,so 1/21/2 0 //()/ BCrsArsAVEE ===− ,since C = A,asnotedafewlinesbeforeEq.(2.33).
(b) III Gerx ψ = andIII. rGerx ψ ′ =− From(a),IIsin(/)cos. sAsxsArssx ψ ′ = −+ The relationsIIIII()() ll ψ ψ ′′′ = andIIIII()() ll ψ ψ = givesincossAslrAslrGerl −+=− and cos(/)sin. AslArsslGerl += Dividingthefirstequationbythesecond,weget 1 sincos cossin sslrsl r slrssl −+ =− + and222cos()sin. rsslsrsl =− Substitutionfor r and s gives 221/21/221/2 00 2(2/)()cos[(2)/](2/)(2)sin[(2)/] mVEEmElmEVmEl −=− ,whichis (2.33).
2.22 (a) As0, V →∞ 2E ontheleftsideof(2.33)canbeneglectedcomparedwith V0,and E2 ontherightsidecanbeneglectedtogive1/21/200tan[(2)/]2()/ mElVEV = −= 1/2 0 2(/). EV Therightsideofthisequationgoesto0as0, V →∞ so 1/2 tan[(2)/]0. mEl = Thisequationissatisfiedwhen1/2(2)/, mElnπ = where n isan
integer.Solvingfor E,weget2228.Enhml = (Zeroandnegativevaluesof n are excludedforthereasonsdiscussedinSec.2.2.)
(b) ψIand ψIIIaregivenbytheequationspreceding(2.32).In ψI,x isnegative,andin ψIII, x ispositive.As0, V →∞ ψIand ψIIIgoto0.Tohave ψ becontinuous, ψ in(2.32)must bezeroat x =0andat x = l,andweget(2.23)asthewavefunctioninsidethebox.
2.23 V0=(15.0eV)(1.602×10–19J/eV)=2.40×10–18J.1/2 0 (2)/ bmVl = = [2(9.109×10–31kg)(2.40×10–18J)]1/22π(2.00×10–10m)/(6.626×10–34Js)=3.97and b/π =1.26.Then N –1<1.26 ≤ N,so N =2.
2.24 With b =3.97,useofaspreadsheettocalculatetheleftsideof(2.35)forincrementsof 0.005in ε showsthatitchangessignbetweenthe ε values0.265and0.270andbetween 0.900and0.905.Linearinterpolationgives ε ≡ E/V0=0.268and0.903,and E = 0.268(15.0eV)=4.02eVand13.5eV.
2.25
2.26 (a) Thedefinition(2.34)showsthat b >0;hence b/π >0.Ifthenumber N ofboundstates were0,thenwewouldhavetheimpossibleresultthat b/π ≤ 0.Hence N cannotbe0and thereisalwaysatleastoneboundstate. (b) TheSchrödingerequationis2(2/)(). mEV ψ ψ
Since V isdiscontinuousat x =0,theSchrödingerequationshowsthat ψ ′′ mustbediscontinuousat x =0.
2.27 /0EV ε == (3.00eV)/(20.0eV)=0.150.Equation(2.35)becomes 0.700tan(0.387)0.7140, b −−= sotan(0.387)1.02. b = Fromthedefinition(2.34), b cannotbenegative,so0.3870.7952.35 b π = −+= and b =6.07.(Additionofintegral multiplesof π to2.35gives0.387b valuesthatalsosatisfyEq.(2.35),buttheselarger b valuescorrespondtowellswithlarger l valuesandlargervaluesof N,thenumberof boundlevels;seeEq.(2.36).Inthesewiderwells,the3.00eVlevelisnotthelowest level.)Equation(2.34)gives1/2 0 (2)lbmV = = 34 31191/2 6.07(6.62610Js) 2[2(9.10910kg)(20.0eV)(1.60210J/eV)] π × ×× =2.65×10–10m=0.265nm.
2.28 Equation(2.36)gives2π <1/2 0 (2)/ mVl ≤ 3π, so 1/2 0 2(2)lmV π > = (6.626×10–34Js)/[2(9.109×10–31kg)(2.00×10–18J)]1/2=3.47×10–10m=3.47 Ǻ. Also,(3/2) l π π ≤ (3.47 Ǻ)=5.20 Ǻ.
2.29 (a) FromEq.(2.36),anincreasein V0increases b/π,whichincreasesthenumber N of boundstates.
(b) Anincreasein l increases b/π,whichincreasesthenumber N ofboundstates.
2.30 (a) FromIII(0)(0) ψ ψ = ,IIIII()() ll ψ ψ = ,and0, E = weget C = b (Eq.1)and 21/21/2(2/)0 albGemVl += (Eq.2).TheconditionsIII(0)(0) ψ ψ ′ ′ = andIIIII()() ll ψ ψ ′′ = give 21/21/2(2/)0 CmVa = (Eq.3)and
21/21/221/21/2(2/)0(2/)0 amVGemVl =− (Eq.4).
(b) If C >0,thenEqs.1and3give b >0and a >0.Equation4thengives G <0andEq. 2gives G >0,whichisacontradiction.If C <0,thenEqs.1and3give b <0and a <0. Equation4thengives G >0andEq.2gives G <0,whichisacontradiction.Hence C =0. (c) With C =0,Eqs.1and3give b =0and a =0.HenceII0. ψ =
2.31 Althoughessentiallynomoleculeshaveenoughkineticenergytoovercomethe electrostatic-repulsionbarrieraccordingtoclassicalmechanics,quantummechanics allowsnucleitotunnelthroughthebarrier,andthereisasignificantprobabilityfornuclei tocomecloseenoughtoundergofusion.
2.32 (a) F; (b) F; (c) T(Fig.2.3shows ψ ′ isdiscontinuousattheendsofthebox.); (d) F; (e) T; (f) F(SeeFig.2.4.); (g) T; (h) F; (i) T.
Operators
3.1 (a) ˆ22(/)cos(1)2sin(1);gAfddxxxx ==+=−+
(b) ˆˆ 5sin5sin; Afxx ==
(c) ˆ2sin;Afx = (d) ln exp(ln); x xex ==
(e) 222 (/)ln3(/)3[1(3)]1/; ddxxddxxx ==−
(f) 2233 (/3/)(4)2436; ddxxddxxxx +=+
(g) 22 (/)[sin()]2cos(). yxyxyxy∂∂=
3.2 (a) Operator; (b) function; (c) function; (d) operator; (e) operator; (f) function.
3.3 ˆ232(/). Axxddx =⋅+
3.4 ˆ22 1,(/),(/). ddxddx
3.5 (a) Somepossibilitiesare(4/x) × and d/dx.
(b) (x/2) ×,(1/4)()2
(c) (1/x 2) ×,(4x)–1 d/dx,(1/12) d2/dx2
3.6 Toprovethattwooperatorsareequal,wemustshowthattheygivethesameresultwhen theyoperateonanarbitraryfunction.Inthiscase,wemustshowthat ˆˆ ()ABf + equals
(). BAf + Usingthedefinition(3.2)ofadditionofoperators,wehave ˆˆˆˆ ()ABfAfBf +=+ and
(), BAfBfAfAfBf +=+=+ whichcompletestheproof.
3.7 Wehave ˆˆ ˆ ()ABfCf += forallfunctions f,so
ACB =−
AfBfCf += and ˆˆˆ AfCfBf =− Hence
3.8 (a) 222343 (/)(/)520; ddxxxddxxx == (b) 222323 (/)(6)6; xddxxxxx == (c) 22222 (/)[()](/)(2)24; ddxxfxddxxfxffxfxf ′ =+=++′′′
(d) 2222 (/).xddxfxf ′′ =
3.9 ˆ33 ˆ (/) ABfxddxfxf ′ == ,so ˆ3 ˆ /. ABxddx = Also323 ˆˆ (/)()3, BAfddxxfxfxf ′ ==+ so ˆˆ233/ BAxxddx =⋅+
3.10 ˆˆˆˆˆˆ
[()]()()[()], ABCfABCfABCf == where(3.3)wasusedtwice;firstwith ˆ A and ˆ B in (3.3)replacedby ˆˆ AB and ˆ C ,respectively,andthenwith f in(3.3)replacedwiththe function ˆ . Cf Also,
[()][()][()] ABCfABCfABCf == ,whichequals ˆˆ ˆ [()]ABCf .
3.11 (a) 2
()()()()()()() ABfABABfABAfBfAAfBfBAfBf +=++=++=+++ (Eq.1),wherethedefinitionsoftheproductandthesumofoperatorswereused.Ifwe interchange ˆ A and ˆ B inthisresult,weget2 ˆˆ ()BAf + = ˆˆˆˆˆˆ ()(). BBfAfABfAf +++ Since ˆˆ ˆˆ , AfBfBfAf +=+ weseethat22 ˆˆ
()(). ABfBAf +=+ (b) If ˆ A and ˆ B arelinear,Eq.1becomes2 ˆˆ ()ABf + = 22 ˆˆˆˆˆˆ AfABfBAfBf +++ .If ˆˆ ˆˆ ,ABBA = then222 ˆˆˆˆˆˆ ()2 ABfAfABfBf +=++
3.12
ˆˆˆˆˆ [,]() ABfABBAfABfBAf =−=− and ˆˆˆˆˆ
[,]() BAfBAABfBAfABf = −=−=
[,]. ABf
3.13 (a) [sin,/]()(sin)(/)()(/)[(sin)()] zddzfzzddzfzddzzfz =−= (sin)(cos)(sin) zfzfzf ′′ (cos), zf = so[sin,/]cos zddzz = . (b) 222222222 [/,](/)[()]()(/) ddxaxbxcfddxaxbxcfaxbxcddxf ++=++−++ 22 (/)[(2)()]() ddxaxbfaxbxcfaxbxcf ′ ′′ =++++−++ 22 22(2)()()2(42) afaxbfaxbxcfaxbxcfafaxbf =+++++−++=++′′′′′′ , so 222 [/,]2(42)(/). ddxaxbxcaaxbddx ++=++ (c) 222222 [/,/](/)(/)(/)(/)0 ddxddxfddxddxfddxddxffff ′′′′′′ =−=−=⋅ so 22 [/,/]0. ddxddx =
3.14 (a) Linear; (b) nonlinear; (c) linear; (d) nonlinear; (e) linear.
3.15 ()()(1)(1) 110 [()/()/()/()]()() nnnn nn AxddxAxddxAxddxAxyxgx ++++=
3.16 Given: ˆˆˆˆˆˆˆˆˆˆ (),(),(),()(). AfgAfAgAcfcAfBfgBfBgBcfcBf +=+=+=+=
Prove:
ˆˆˆˆˆ (),(). ABfgABfABgABcfcABf +=+=
Useofthegivenequationsgives
ˆˆˆˆˆ ()()()() ABfgABfBgABfABg + =+=+= ˆˆˆˆ , ABfABg + since ˆ Bf and ˆ Bg arefunctions;also,
ˆˆˆˆ ()()(). ABcfAcBfcABfcABf ===
3.17 Wehave
()()(defn.ofsumofops.and)
()()(linearityof)
ˆ (defn.ofop.prod.)
ˆ ()(defn.ofsumofops.and) ABCfABfCfBC ABfACfA ABfACf ABACfABAC +=+ =+ =+ =+ Hence
ˆˆ (). ABCABAC +=+
3.18 (a) Usingfirst(3.9)andthen(3.10),wehave ˆˆˆˆˆ ()()(). AbfcgAbfAcgbAfcAg +=+=+ (b) Setting b =1and c =1in(3.94),weget(3.9).Setting c =0in(3.94),weget(3.10).
3.19 (a) Complexconjugation,since()*** fgfg + =+ but()****. cfcfcf = ≠ (b) ()–1(d/dx)()–1,since()–1(d/dx)()–1cf =()–1(d/dx)c –1f –1 = ()–112[()] cff ′ = 2/ cff ′ and c()–1(d/dx)()–1f = c()–1(d/dx)f –1 = 12 ()() cff ′ = 2/ cff ′ ,but ()–1(d/dx)()–1( f + g)=()–1(d/dx)( f + g)–1=–()–1[( f + g)–2() fg′′ + ]= –( f + g)21 () fg′′ + ≠ ()–1(d/dx)()–1f +()–1(d/dx)()–1 g = 22// ffgg ′′ .
3.20 (a) Thisisalwaystruesinceitisthedefinitionofthesumofoperators.
(b) Onlytrueif ˆ A islinear.
(c) Notgenerallytrue;forexample,itisfalsefordifferentiationandintegration.Itistrue if ˆ A ismultiplicationbyafunction.
(d) Notgenerallytrue.Onlytrueiftheoperatorscommute.
(e) Notgenerallytrue.
(f) Notgenerallytrue.
(g) True,since. fggf =
(h) True,since ˆ Bg isafunction.
3.21 (a) ˆˆˆ [()()]()()()(). hhh TfxgxfxhgxhTfxTgx +=+++=+ Also, ˆˆ [()]()(). hh TcfxcfxhcTfx =+= So ˆ hT islinear.
(b) 2222 111 ˆˆˆ (32)(2)3(1)221. TTTxxxxx −+=+−++=−+
3.22 ˆ ˆˆ23 ()(1/2!/3!)()()()()/2!()/3!. D efxDDDfxfxfxfxfx ′′′′′′ =++++=++++ 1 ˆ ()(1).Tfxfx=+ TheTaylorseries(4.85)inProb.4.1with x changedto z gives 2 ()()()()/1!()()/2!. fzfafazafaza ′′′ =+−+−+ Letting, hza ≡ theTaylorseries becomes2()()()/1!()/2!. fahfafahfah ′′′ +=+++ Changing a to x andletting 1, h = weget(1)()()/1!()/2!, fxfxfxfx ′ ′′ +=+++ whichshowsthat ˆ 1 ˆ . D efTf =
3.23 (a) 22 (/) xxddxee = andtheeigenvalueis1.
(b) 222 (/)2 ddxx = and2 x isnotaneigenfunctionof22 / ddx .
(c) 22 (/)sin(/)cossin ddxxddxxx ==− andtheeigenvalueis–1.
(d) 22 (/)3cos3cos ddxxx =− andtheeigenvalueis–1.
(e) 22 (/)(sincos)(sincos) ddxxxxx +=−+ sotheeigenvalueis–1.
3.24 (a) 222223232323 (//)()4913. xxyxyxyxy yeeeeeeee∂∂+∂∂=+= Theeigenvalueis13. (b) 22223333 (//)()66. xyxyxyxy∂∂+∂∂=+ Notaneigenfunction.
(c)
2222 (//)(sin2cos4)4sin2cos416sin2cos420sin2cos4. xyxyxyxyxy ∂∂+∂∂=−−=− Theeigenvalueis20.
(d) 2222 (//)(sin2cos3)4sin29cos3. xyxyxy ∂∂+∂∂+=−− Notaneigenfunction,
3.25 222 (/2)(/)()() mddxgxkgx−= and2()(2/)()0.gxmkgx ′′ + = Thisisalinear homogenousdifferentialequationwithconstantcoefficients.Theauxiliaryequationis 22(2/)0smk+= and1/2(2)/.simk =± Thegeneralsolutionis 1/21/2 (2)/(2)/ 12. imkximkx gcece =+ Iftheeigenvalue k wereanegativenumber,then1/2 k wouldbeapureimaginarynumber;thatis,1/2, kib = where b isrealandpositive.This wouldmake1/2 ik arealnegativenumberandthefirstexponentialin g wouldgoto ∞ as x →−∞ andthesecondexponentialwouldgoto ∞ as. x →∞ Likewise,if k werean imaginarynumber(, ikabire θ =+= where a and b arerealand b isnonzero),then1/2 k wouldhavetheform, cid + and1/2 ik wouldhavetheform, dic + where c and d are real.Thiswouldmaketheexponentialsgotoinfinityas x goestoplusorminusinfinity. Hencetokeep g finiteas, x →±∞ theeigenvalue k mustberealandnonnegative,andthe allowedeigenvaluesareallnonnegativenumbers.
Copyright©2014PearsonEducation,Inc.
3.26 (). dxffdxkf ∫∫== Differentiationofbothsidesofthisequationgives (/). ddxfdxfkf ′ == ∫ So1 / dfdxkf = and1(1/). fdfkdx = Integrationgives ln1fkxc =+ and//, fcxkxk eeAe== where A isaconstantand k istheeigenvalue.To preventtheeigenfunctionsfrombecominginfiniteas, x →±∞ k mustbeapure imaginarynumber.(Strictlyspeaking,/Axk e isaneigenfunctionof dx ∫ onlyifweomit thearbitraryconstantofintegration.)
3.27 22/2/ dfdxdfdxkf += and20. ffkf ′′′ + −= Theauxiliaryequationis220 ssk+−= and1/2 1(1).sk =−±+ So 1/21/2 [1(1)][1(1)] , kxkxfAeBe =+−++−−+ where A and B arearbitrary constants.Topreventtheeigenfunctionsfrombecominginfiniteas, x →±∞ thefactors multiplying x mustbepureimaginarynumbers:1/21(1), kci±+= where c isanarbitrary realnumber.So1/2(1)1kci±+=+ and2 1(1) kci + =+= 122 icc + and2 2.kicc =−
3.28 (a) ˆ333333 (/)(/)/ y piyiy =∂∂=∂∂ ; (b) ˆˆˆˆ(/)/(/)/; xyxpypxiyyix −=∂∂−∂∂ (c) 22 [(/)/](,)(/)(/) xiyfxyxyxfy ∂∂=−∂∂∂∂= 2222 (/). xfy−∂∂ Hence22222 ˆˆ ()(/). xypxy =−∂∂
3.29 (/)(/)idgdxkg = and/(/). dggikdx = Integrationgivesln(/)gikxC = + and // , ikxCikxgeeAe == where C and A areconstants.If k wereimaginary(, kabi =+ where a and b arerealand b isnonzero),then, ikiab = andthe/ bx e factorin g makes g gotoinfinityas x goestominusinfinityif b ispositiveoras x goestoinfinityif b is negative.Hence b mustbezeroand, ka = where a isarealnumber.
3.30 (a)
ˆˆ [,](/)[/(/)](/)[/(/)()] x xpfixxxxfixfxxxf =∂∂−∂∂=∂∂−∂∂= (/)[//](/), ixfxfxfxif ∂∂−−∂∂=− so ˆˆ [,](/). xxpi = (b) ˆˆ22222222222 [,](/)[/(/)][/(/)()] x xpfixxxxfxfxxxf =∂∂−∂∂=−∂∂−∂∂= 222222 [//2/]2/. xfxxfxfxfx −∂∂−∂∂−∂∂=∂∂ Hence22 ˆˆ [,]2/. xxpx = ∂∂
(c) ˆˆ [,](/)[/(/)](/)[/(/)]0 y xpfixyyxfixfyxfy =∂∂−∂∂=∂∂−∂∂= ,so ˆˆ [,]0 y xp = (d) ˆ ˆ [,(,,)]()0. xVxyzfxVVxf=−=
(e) Let2/2. Am ≡− Then ˆ ˆ [,]xHf = { } 222222222222 [(///)][(///)] xAxyzVAxyzVxf ∂∂+∂∂+∂∂+−∂∂+∂∂+∂∂+=
222222222222 [////2///] Axfxxfyxfzxfxfxxfyxfz ∂∂+∂∂+∂∂−∂∂−∂∂−∂∂−∂∂+ 2 2/(/)/, xAVfAVxfAfxmfx −=−∂∂=∂∂ so ˆˆ2 [,](/)/. xHmx = ∂∂
(f) ˆˆˆ2 ˆ [,] xxyzpf = 2222222222 [/(/)()][//2/] xyzfxxxyzfxyzfxxyzfxyzfx −∂∂−∂∂=−∂∂−∂∂−∂∂= 2 2/, yzfx ∂∂ so ˆˆˆ22 ˆ [,]2/. xxyzpyzx =∂∂
3.31 22222222 222222 12111222 ˆ 22 T mmxyzxyz ⎛⎞⎛⎞ ∂∂∂∂∂∂ =−++−++⎜⎟⎜⎟
3.32 ˆ22222 (/2)(), Hmcxyz =−∇+++ where2222222 ///. xyz ∇ =∂∂+∂∂+∂∂
3.33 (a) 22 0|(,)|xtdx ∫Ψ ; (b) 22 0|(,,,)|xyztdxdydz
; (c) 22 0111222111222 |(,,,,,,)|xyzxyztdxdydzdxdydz
3.34 (a) 2|| dx ψ isaprobabilityandprobabilitieshavenounits.Since dx hasSIunitsofm, theSIunitsof ψ arem –1/2 .
(b) Tomake2 || dxdydz ψ dimensionless,theSIunitsof ψ arem –3/2 .
(c) Tomake2111 || nnndxdydzdxdydz ψ dimensionless,theSIunitsof ψ arem –3n/2 .
3.35 Letthe x, y,and z directionscorrespondtotheorderusedintheproblemtostatetheedge lengths.Thegroundstatehas xyznnn quantumnumbersof111.Thefirstexcitedstate hasonequantumnumberequalto2.Thequantum-mechanicalenergydecreasesasthe lengthofasideoftheboxincreases.Henceinthefirstexcitedstate,thequantum-number value2isforthedirectionofthelongestedge,the z direction.Then 22222222 222222 112111 88 hh h mmabcabc ν
3.36 (a) UseofEqs.(3.74)and(A.2)gives3.00nm2.00nm0.40nm2 2.00nm1.50nm0|| dxdydz ψ = ∫∫∫ 0.40nm2 0(2/)sin(/)axadx π ∫ 2.00nm2 1.50nm(2/)sin(/)bybdy π ∫ 3.00nm2 2.00nm(2/)sin(/)czcdz π ∫ =
Copyright©2014PearsonEducation,Inc.
0.40nm2.00nm3.00nm 01.50nm2.00nm sin(2/)sin(2/)sin(2/) 222 xxayybzzc abc πππ πππ
⎢⎥⎢⎥⎢⎥ ⎣⎦⎣⎦⎣⎦ = 0.40sin(20.40/1.00)2.001.50sin(22.00/2.00)sin(21.50/2.00) 1.0022.002 πππ ππ
3.002.00sin(23.00/5.00)sin(22.00/5.00)
(0.3065)(0.09085)(0.3871)=0.0108.
(b) The y and z rangesoftheregionincludethefullrangeof y and z,andthe y and z factorsin ψ arenormalized.Hencethe y and z integralseachequal1.The x integralisthe sameasinpart(a),sotheprobabilityis0.3065.
(c) Thesameas(b),namely,0.3065.
3.37 ˆ/. x pix =−∂∂ (a) (sin)/cos, kxxkkx∂∂= so ψ isnotaneigenfunctionofˆ. x p
(b) 222222 (3.73)(3.73)(3.73) ˆ(/)(1)(/) xx pxna ψψπψ =−∂∂=−− ,where(3.73) ψ isgivenby Eq.(3.73).Theeigenvalueis222/4, x hna whichisthevalueobservedif2 x p ismeasured.
(c) 222222 (3.73)(3.73)(3.73) ˆ(/)(1)(/) zz pznc ψψπψ =−∂∂=−− andtheobservedvalueis 222/4. z hnc
(d) (3.73)(3.73)(3.73) ˆ(const.) xx ψ =≠ψψ , so ψ isnotaneigenfunctionofˆ x
3.38 Since2, y n = theplane/2 yb = isanodalplanewithinthebox;thisplaneisparallelto the xz planeandbisectsthebox.With3, zn = thefunctionsin(3/) zc π iszeroonthenodal planes/3 zc = and2/3; zc = theseplanesareparalleltothe xy plane.
3.39 (a) 2|| ψ isamaximumwhere|| ψ isamaximum.Wehave()()(). fxgyhz ψ = For 1, xn = 1/2 ()(2/)sin(/) fxaxa π = isamaximumat/2. xa = Also,() gy isamaximum at/2 yb = and() hz isamaximumat/2. zc = Therefore ψ isamaximumatthepoint (/2,/2,/2), abc whichisthecenterofthebox.
(b) 1/2 ()(2/)sin(2/) fxaxa π = isamaximumat/4 xa = andat3/4. xa = ()gy isa maximumat/2 yb = and() hz isamaximumat/2. zc = Therefore ψ isamaximumat thepoints(/4,/2,/2) abc and(3/4,/2,/2), abc
3.40 Whenintegratingoveronevariable,wetreattheothertwovariablesasconstant;hence ()()()()()()()()() FxGyHzdxdydzFxGyHzdxdydzGyHzFxdxdydz ∫∫∫∫∫∫∫∫∫==⎡⎤⎡⎤ ⎣⎦⎣⎦
Copyright©2014PearsonEducation,Inc.
()()()()()() FxdxGyHzdydzFxdxHzGydydz ⎡⎤⎡⎤⎡⎤ ===
()()() FxdxGydyHzdz ∫∫∫ .
3.41 Iftheratiooftwoedgelengthsisexactlyaninteger,wehavedegeneracy.Forexample,if b = ka,where k isaninteger,then22222222 //(/)/ xyxy nanbnnka +=+ .The(,,) xyz nnn states(1,2,) zkn and(2,,) z kn havethesameenergy.
3.42 With V =0,wehave
.Assume (,,)()()(). xyzFxGyHz ψ = SubstitutionintotheSchrödingerequationfollowedby divisionby FGH,gives
Then,since F isafunctionof x only, x E isindependentof y and z.ButEq.1shows x E is equaltotherightsideofEq.1,whichisindependentof x,so x E isindependentof x Hence x E isaconstantand222(/2)(/). x mdFdxEF−= Thisisthesameastheonedimensionalfree-particleSchrödingerequation(2.29),so F(x)and x E aregivenby(2.30) and(2.31).Bysymmetry, G and H aregivenby(2.30)with x replacedby y andby z, respectively.
3.43 Foralinearcombinationofeigenfunctionsof ˆ H tobeaneigenfunctionof ˆ H ,the eigenfunctionsmusthavethesameeigenvalue.Inthiscase,theymusthavethesame valueof222. xyz nnn ++ Thefunctions(a)and(c)areeigenfunctionsof ˆ H and(b)isnot.
3.44 Inadditiontothe11statesshowninthetableafterEq.(3.75),thefollowing6stateshave 22 (8/)15:Emah <
xyznnn 123132213231312321 22 (8/)Emah 141414141414
These6statesandthe11listedinthetextbookgiveatotalof17states.These17states have6differentvaluesof22(8/)Emah ,andthereare6energylevels.
3.45 (a) FromthetableafterEq.(3.75),thereisonlyonestatewiththisvalue,sothedegreeof degeneracyis1,meaningthislevelisnondegenerate. (b) FromthetableintheProb.3.44solution,thedegreeofdegeneracyis6.
Copyright©2014PearsonEducation,Inc.
(c) Thefollowing xyznnn valueshave22(8/)Emah =27;115,151,511,333.Thedegree ofdegeneracyis4.
3.46 (a) Thesearelinearlyindependentsincenoneofthemcanbewrittenasalinear combinationoftheothers.
(b) Since221 8 313()(8), xx−=− thesearenotlinearlyindependent.
(c) Linearlyindependent.
(d) Linearlyindependent.
(e) Sincecossin, ix exix =+ thesearelinearlydependent.
(f) Since221sincos, xx=+ thesearelinearlydependent.
(g) Linearlyindependent.
3.47 SeethebeginningofSec.3.6fortheproof.
3.48 (a) 222 000|()||()||()| cba xxfxgyhzdxdydz 〈〉=∫∫∫= 222 000|()||()||()|,abc xfxdxgydyhzdz ∫∫∫ where f, g,and h aregivenprecedingEq. (3.72).Since g and h arenormalized,22 00|()|(2/)sin(/)aa xxxfxdxaxnxadx π 〈〉=∫=∫ = 22 22 0 2 sin(2/)cos(2/) 442 8 a xx xx xaxaa nxanxa ann ππ π π
,whereEq.(A.3)wasused.
3.49
(b) Bysymmetry,/2 yb〈〉= and/2. zc 〈 〉=
(c) ThederivationofEq.(3.92)forthegroundstateappliestoanystate,and0. x p 〈〉= (d) Since g and h arenormalized, 22222 00|()|(2/)sin(/)aa xxxfxdxaxnxadx π 〈〉=∫=∫= 3232 3322 0 2 64sin(2/)cos(2/) 84 a xx xxx xaxaax nxanxa annn ππ π ππ
⎛⎞ −−−= ⎢⎥ ⎜⎟
22 322 2 x aa n π , whereEq.(A.4)wasused.Wehave222/4.xax 〈 〉=≠〈〉 Also, 222 000|()||()||()| cba xyxyfxgyhzdxdydz〈〉=∫∫∫ = 222 000|()||()||()|abc xfxdxygydyhzdz ∫∫∫ =. xy 〈 〉〈〉
. AB 〈〉+〈〉 Also
3.50 (a) Notacceptable,sinceitisnotquadraticallyintegrable.Thisisobviousfromagraphor from22(1/2)|.axaxedxae ∞−−∞ −∞−∞ ∫=−=∞
(b) Thisisacceptable,sinceitissingle-valued,continuous,andquadraticallyintegrable whenmultipliedbyanormalizationconstant.SeeEqs.(4.49)and(A.9).
(c) Thisisacceptable,sinceitissingle-valued,continuous,andquadraticallyintegrable whenmultipliedbyanormalizationconstant.SeeEqs.(4.49)and(A.10)with n =1.
(d) Acceptableforthesamereasonsasin(b).
(e) Notacceptablesinceitisnotcontinuousat x =0.
3.51 Given:11 ˆ / itH∂Ψ∂=Ψ and22 ˆ / itH∂Ψ∂=Ψ .Provethat 11221122
()/()icctHcc ∂Ψ+Ψ∂=Ψ+Ψ .Wehave1122()/ icct ∂ Ψ+Ψ∂= 1122 [()/()/] ictct ∂Ψ∂+∂Ψ∂= 1122 // citcit ∂Ψ∂+∂Ψ∂= 1122 ˆˆ cHcH Ψ +Ψ= 1122 ˆ ()HccΨ+Ψ ,since ˆ H islinear.
3.52 (a) AninefficientC++programis
#include <iostream> using namespace std; int main() { int m, i, j, k, nx, ny, nz, L[400], N[400], R[400], S[400]; i=0; for (nx=1; nx<8; nx=nx+1) { for (ny=1; ny<8; ny=ny+1) { for (nz=1; nz<8; nz=nz+1) { m=nx*nx+ny*ny+nz*nz; if (m>60) continue; i=i+1; L[i]=m; N[i]=nx; R[i]=ny; S[i]=nz; } } } for (k=3; k<61; k=k+1) { for (j=1; j<=i; j=j+1) { if (L[j]==k) cout<<N[j]<< " "<<R[j]<< " "<<S[j]<< " "<<L[j]<<endl; } } return 0;
Afreeintegrateddevelopmentenvironment(IDE)todebugandrunC++programsis Code::Blocks,availableatwww.codeblocks.org.ForaWindowscomputer,downloading thefilewithmingw-setup.exeaspartofthenamewillincludetheMinGW(GCC)compiler forC++.FreeuserguidesandmanualsforCode::Blockscanbefoundbysearchingthe Internet.
Alternatively,youcanruntheprogramatideone.com.
(b) Onefinds12states.
3.53 (a) T. (b) F.SeetheparagraphprecedingtheexampleattheendofSec.3.3.
(c) F.Thisisonlytrueif f1and f2havethesameeigenvalue.
(d) F. (e) F.Thisisonlytrueifthetwosolutionshavethesameenergyeigenvalue.
(f) F.Thisisonlytrueforstationarystates.
(g) F. (h) F.(5)(const.)(5). xxx ≠
(i) T.///
(j) T. (k) T. (l) F.
(m) T.22 ˆˆˆˆˆ ()(), AfAAfAafaAfaf ==== provided ˆ A islinear.Notethatthe definitionofeigenfunctionandeigenvalueinSec.3.2specifiedthat ˆ A islinear.
(n) F. (o) F.
The Harmonic Oscillator
4.1 Taking(/)ddxm of(4.84)gives()0()(1)(2)(1)() mnm nn fxcnnnnmxa ∞ = =−−−+− ∑
Thefactors n,(1),... n makethetermswith0, n = 1, n = …,1 nm = vanish,so ()()(1)(2)(1)() mnm nmn fxcnnnnmxa ∞ = =−−−+− ∑ (Eq.1).(Ifthisistooabstract foryou,writetheexpansionas2 ()012 k k fxccxcxcx = +++++ anddothe differentiation.)With xa = inEq.1,the() nm xa factormakesalltermsequaltozero exceptthetermwith, nm = whichisaconstant.Equation(1)with xa = gives ()()(1)(2)(1)! m fmm acmmmmmcm =−−−+= and()()/! m m cfam = .
4.2 (a) (iv) ()sin,()cos,()sin,()cos,()sin, fxxfxxfxxfxxfxx ′′′′′′ ===−=−= …; a =0and(iv)(0)sin00,(0)cos01,(0)0,(0)1,(0)0, fffff ′′′′′′ = =====−= ….The Taylorseriesis35 sin0/1!0/3!0/5! xxxx =++−+++= 21 0(1)/(21)! kk kxk ∞ + = −+ ∑ . (b) 24242 0 cos1/1!3/3!5/5!1/2!/4!(1)/(2)! kk xkxxxxxk ∞ = =−+−=−+−=− ∑ .
4.3 (a) Weuse(4.85)with0. a = Wehave()fx xe = and()(). fnx xe = ()0(0)1. n fe== So23 0 1/1!/2!/3!/! xn n exxxxn ∞ = =++++= ∑ . (b) 2345 1()/1!()/2!()/3!()/4!()/5! i eiiiii θ θθθθθ =++++++= 2435 1/2!/4!(/1!/3!/5!) i θθθθθ −+−+−+− cossin. i θ θ = +
4.4 From(4.22)and(4.28),/2cos(2) dxdtAtb πνπν = + and22222cos(2). TmAtb πνπν = + From(4.22)and(4.27),22222sin(2). VmAtb πνπν =+ Then222 2,TVmA πν += since 22 sincos1. θθ+=
4.5 (a) Let 0 n ynncx ∞ = = ∑ .Then1 0 n ynnncx ∞ = ′ = ∑ and2 0(1) n ynnnncx ∞ = ′′ =− ∑ .Since thefirsttwotermsinthe y ′′ sumarezero,wehave2 2(1). n nn ynncx ∞ = ′′ =− ∑ Let 2. jn≡− Then22 00 (2)(1)(2)(1)jn jnjn yjjcxnncx ∞∞ ==++ ′′ =++=++ ∑∑ .Substitution inthedifferentialequationgives
2 0000 (2)(1)(1)230 nnnn nnnn nnnn nncxnncxncxcx ∞∞∞∞ + ==== ∑∑∑∑++−−−+= . Wehave2 02 [(2)(1)(3)]0. n nnn nncnncx ∞ + = +++−−= ∑ Settingthecoefficientof n x equaltozero,wehave22(3)/[(2)(1)].nn cnncnn + =+−++ (b) Therecursionrelationof(a)with0 n = gives203/2cc = andwith2 n = gives 42200 3/12/4(3/2)/43/8. ccccc ===−=− With1 n = and3 n = intherecursion relation,weget31/6 cc =− and53119/209(/6)/203/40.cccc = =−=−
4.6 (a) Odd; (b) even;(c) odd; (d) neither; (e) even; (f) odd; (g) neither;(h) even.
4.7 Given:()(),()(),()(),()(). fxfxgxgxhxhxkxkx −=−=−=−−=− Let()()(). pxfxgx ≡ Wehave()()()()()(), pxfxgxfxgxpx =−−== sotheproduct oftwoevenfunctionsisanevenfunction.Let()()(). qxhxkx ≡ Then ()()()()[()]()()(), qxhxkxhxkxhxkxqx −=−−=−−== sotheproductoftwoodd functionsisanevenfunction.Let()()(). rxfxhx = Then ()()()()[()]()()() rxfxhxfxhxfxhxrx −≡−−=−=−=− .
4.8 (a) Given:()(). fxfx =− Differentiationofthisequationgives ()()/()[()/](), fxdfxdxfxdxdxfx ′′′ =−=−−=−− so f ′ isanoddfunction.
(b) Differentiationof()() fxfx =−− gives()(1)()(). fxfxfx ′ ′′ = −−−=−
(c) Differentiationof()() fxfx =− gives()(), fxfx ′ ′ = asin(a).Putting0 x = in thisequation,weget(0)(0), ff′′ =− so2(0)0 f ′ = and(0)0 f ′ = .
4.9
22 ˆ21/2/222/2 *(/2)(/)(/)xx TTdmeddxedx αα ψψταπ ∞ −∞ 〈〉==−∫ ∫ =
22 21/2/222/2 (/2)(/)()xx mexedx αα απαα ∞ −∞ −∫− = 21/2222 0 (/2)(/)2() x mxedx α απαα ∞ −∫−= 21/221/23/21/2 (/)(/)[(1/4)(/)(1/2)(/)] m απαπααπα −−= 2/4 m α = 2(2/)/4/4, mmh πνν = where(A.9)and(A.10)wereused. 22 ˆ1/2/2222/2 *(/)(2)xax VVdemxedx α ψψταππν ∞ −∞ 〈〉=== ∫∫
1/22222 0 (/)2(2) ax mxedx αππν ∞ = ∫
3/21/221/23/222 4(1/4)(/)/ mm π ανπαπνα = = 221/(2)/4. mmhT πνπνν==〈〉
4.10 From(4.54), 22 222221/23/2 1 11014 1||2||2||/ xx cxedxcxedxc αα π α ∞∞ −∞ === ∫∫ ,where (4.49)and(A.10)with n =1wereused.Weget1/23/41/4 1 ||2 c απ = .From(4.56),
4-2
Copyright©2014PearsonEducation,Inc.
211/21/23/221/25/2 0 2||[2(/)4(1/4)/4(3/8)/] c πααπααπα =−+= 21/2 0 2||(/) c πα where(A.9)and(A.10)wereused.Hence1/21/4 0 ||2(/). c απ =
4.11 From(4.47), 2 3/2 313(). ax cxcxe ψ =+ From(4.46),311[2(13)/6]2/3.ccc α α = −=− So 2 3/2 31[(2/3)] x cxxe α ψ α =− .Wehave 224262 10 1||2[(4/3)(4/9)] x cxxxedx α αα ∞ =−+= ∫
221/23/231/25/2241/27/2 1 2||[(1/2)/(4/3)(3/2)/(4/9)(15/2)/] c πααπααπα −+= 21/23/2 1 ||/3 c πα and1/23/41/4 1 ||3. c απ = Then 2 1/23/41/43/2 33[(2/3)]. x xxe α ψ =−απα
4.12 From(4.47), 224 4024(). x eccxcx α ψ =++ From(4.46)with4, = v
200 2(4)/24 ccc α α =−=− and 422 2(24)/(34)/3ccc α =−⋅=−α 0 (4)/3 c α α = 2 0 4/3. c α = Then 2224 40(144/3). x cexx α ψ =−+αα
4.13 Atthemaximaintheprobabilitydensity2 || ψ ,wehave2||/0. x ψ ∂ ∂= From(4.54), 222223 11 0(/)()(22), xx cxxecxxe αα α =∂∂=− so 32 0(1). xxxx =−=−αα Thesolutions are0 x = and1/2. x =±α FromFig.4.4b,0 x = isaminimuminprobabilitydensity,so themaximaareat1/2. x =±α
4.14 Thewavefunctionisanoddfunctionwithfivenodes,oneofwhichisattheorigin.
Alternatively,onecouldtake1timesthe ψ functiongraphedabove.
Copyright©2014PearsonEducation,Inc. 2222242224 000 1||(144)2||(144)xx cxxedxcxxedx αα αααα ∞∞ −∞ =−+=−+ ∫∫
4-3
4.15 ˆ2 *||. xxdxdx ψψτψ ∞ −∞ 〈〉==∫ ∫ v Thewavefunction ψv iseitherevenorodd,so2 || ψv isanevenfunction.Hence2 || x ψv isanoddfunctionand2||0.xdx ψ ∞ −∞ ∫ = v Theresult 0 x 〈〉= isobviousfromthegraphsof2 || ψ thatcorrespondtoFig.4.4.
4.16 (a) T. (b) T. (c) F(since ψ canbemultipliedby–1andremainavalidwave function). (d) T. (e) T.
4.17 Similarities:Thenumberofnodesbetweentheboundarypointsiszerofortheground stateandincreasesbyoneforeachincreaseinthequantumnumber.Thequantum numbersareintegers.Thereisazero-pointenergy.Theshapesofcorrespondingwave functionsaresimilar.Iftheoriginisplacedatthecenterofthebox,thewavefunctions alternatebetweenbeingevenoroddasthequantumnumberincreases.Theenergylevels arenondegenerate.Thereareaninfinitenumberofbound-stateenergylevels
Differences:Theenergylevelsareequallyspacedfortheharmonicoscillator(ho)but unequallyspacedfortheparticleinabox(pib).Fortheho,thereissomeprobabilityfor theparticletobefoundintheclassicallyforbiddenregion,butthisprobabilityiszerofor thepib.
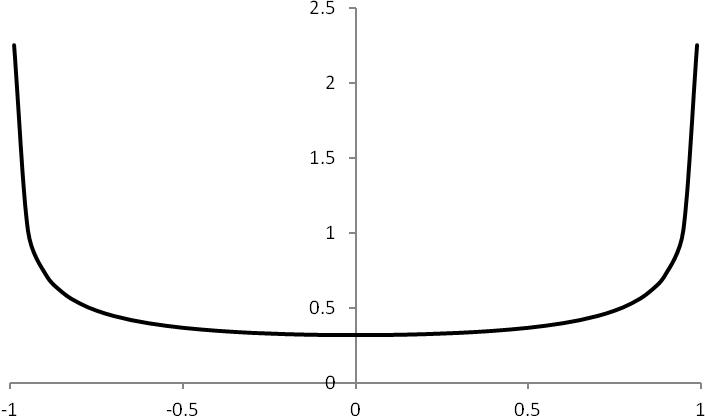
4.18 (a) 11 (2)[sin(/)] txAb πν =− and1121/2 /(2)[1(/)] dtdxAxA πν =− ,so 121/2 (2)[1(/)]. dtAxAdx πν =− Theperiodis1/ν ,sotheprobabilitythattheparticleis foundbetween x and xdx + is121/2 2()[1(/)]. dtAxAdxνπ=− (b) At, xA =± theclassicalprobabilitydensityisinfinite. (c) x/A
Forhighvaluesofthequantumnumber v ,theouterpeaksin2 ψ aremuchhigherthan theinnerpeaks,andthehighestprobabilitydensityisneartheclassicalturningpointsof themotion,asistruefortheclassicalprobabilitydensitygraphedabove.Thisisinaccord withthecorrespondenceprinciple.
4.19 For0, x ≥ theHamiltonianoperatoristhesameasthatoftheharmonicoscillator.Hence thesolutionsoftheSchrödingerequationfor0 x ≥ arethefunctions(4.42),wherethe coefficientsobeytherecursionrelation(4.39).Tomake ψ quadraticallyintegrable, ψ mustgotozeroas x →∞ Thisboundaryconditionthenrestrictsthesolutionstothe harmonic-oscillatorfunctions(4.47).Since V isinfinitefor0 x < , ψ mustbezerofor 0 x < (asfortheparticleinabox).Theconditionthat ψ becontinuousthenrequiresthat 0 ψ = at0 x = .Theevenharmonic-oscillatorfunctionsin(4.47)arenotzeroatthe origin,sotheseareeliminated.Hencethewell-behavedsolutionsaretheharmonic oscillatorwavefunctionswith1,3,5,..., = v and1 2 () Ehν =+ v with1,3,5,.... = v If wedefine(1)/2 n ≡− v ,then3 2 (2) Enhν =+ ,with0,1,2,.... n =
4.20 (a) Thetime-independentSchrödingerequation(3.47)is 2222222222 111 222 (/2)(///)(). xyz mxyzkxkykzE ψ ψψψψ −∂∂+∂∂+∂∂+++= TheHamiltonianoperatoristhesumoftermsthateachinvolveonlyonecoordinate,so wetryaseparationofvariables,taking()()(). fxgyhz ψ = Substitutionofthis ψ intothe Schrödingerequationfollowedbydivisionby fgh gives 2222
222111 222222 2() xyz dfdgdh ghfhfgkxkykzfghEfgh mdxdydz
2222 222111 222222 111 2 xyz dfdgdhkxkykzEmfghdxdydz
(Eq.1) 22222 222111 222222 111 22 xxyz dfdgdh EkxEkykz mfmgh dxdydz
Since f isafunctionof x only,thedefinedquantity x E isindependentof y and z.Since x E equalstherightsideofthelastequationand x doesnotappearonthisside, x E is independentof x.Therefore x E isaconstant.Multiplicationofthe x E definitionby f gives2222 1 (/2)(/)2 xx mdfdxkxfEf−+= ,whichisthesameastheone-dimensional harmonic-oscillator(ho)Schrödingerequation(4.32)[seealso(4.26)]with ψ replaced by f, k replacedby, x k and E replacedby x E .Hence f ( x)istheone-dimensionalhowave function(4.47)with v replacedby x v ,and x E isgivenby(4.45)and(4.23)as 11/2 2 (),(1/2)(/).xxxxx Ehkm =+=ννπ v Since x, y,and z occursymmetrically, g(y)and h(z)arehofunctionswith y and z asthevariable.Equations1and2give,
4-5
Copyright©2014PearsonEducation,Inc.
111 222 ()()(), xyzxxyyzz EEEEhhh ν =++=+++++νν vvv where 0,1,2,,0,1,2,0,1,2,xyz === vvv
(b) Whenthe k’sareequal,wehave xyzν ννν = =≡ and3 2 (). xyz Ehν =+++ vvv The lowestenergylevelis000andisnondegenerate,wherethenumbersgivethevaluesof thequantumnumbers,,. xyz vvv Thenext-lowestlevelisthreefolddegenerate, consistingofthestates100,010,and001.Thenextlevelissixfolddegenerateandhas thestates200,020,200,110,101,011.Thenextlevelistenfolddegenerateandhasthe states300,030,003,111,210,201,012,021,102,120.
4.21 (a) 022 0(1)1. zzHee=−= 2222 1(1)(/)(2)2. zzzz Heddzeezez =−=−−= 22222 2(24)42, zzz Heezez =−+=− 222233 3(488)812. zzzz Hezezezezz =−+−=−
(b) For n =0,0zHz = and11 2 Hz = For n =1,2 12 zHz = and22 1 0221212. HHzz +=+−= For n =2,3242 zHzz =− and33 1 13 2 244642. HHzzzzz +=+−=−
(c) For0, = v (4.86)is
2 1/4/2 0(/), x e α ψ απ = asin(4.53).For1, = v (4.86)is
22 1/21/4/21/21/23/41/4/21(21!)(/)(2)2xx exxe αα ψ =⋅=απααπ ,asin(4.55).Finally, 22 21/21/4/21/221/21/42/2 2(22!)(/)[4()2]2(/)(21) xx exxe αα ψ απααπα =⋅−=− asin (4.57).
4.22 Forverylarge||, x thefirstterminparenthesesin(4.32)canbeneglectedcomparedwith thesecondterm,and(4.32)becomes220. x ψ αψ ′′ = With 2/2 x e α ψ = ,wehave 2222 22/222/222/2/2 . xxxx xexexee αααα ψ αψαααα ′′ −=−+−=− Forverylarge||, x 2/2 x e α α isextremelyclosetozero,so 2/2 x e α ψ = isanapproximatesolutionforvery large||. x
4.23 (a) Let1/2 r xx α ≡ .ThenEq.(4.40)becomes
2 246 /26 24 023 000 /1 r xr rrcxcxcx ce ccc ψ α αα
Let2// r EmEEh α ν ≡= .ThenEq.(4.39)becomes 2/(212)/[(1)(2)] nnrn ccnEnnf α + =+−++≡ ,where n f wasdefinedasshown.We have66244242 020420 23 020420 00 ,,, cc ccccccffffff cccccc cc αααααα αα ===== .Hence
4-6
Copyright©2014PearsonEducation,Inc.
Wehave2 22(4412)/[(221)(222)(432)/(42) fnrrnEnnnEnn =−+−−+−+=−−− .
AC++programis
#include <iostream>
#include <cmath> using namespace std; int main () { int n; double er, xr, fac, sum, term, psi; label2: cout << "Enter Er (enter 1000 to quit)"; cin >> er; if (er > 999) { return 0; } for (xr=0; xr<=6; xr=xr+0.5) { fac=exp(-xr*xr/2); sum=1; term=1; for (n=1; n<=9500; n=n+1) { term=term*(4*n-3-2*er)*xr*xr/(4*n*n-2*n); if (fabs(fac*term) < 1e-15) { goto label1; } sum=sum+term; } cout << "Did not converge"; return 0; label1: psi=fac*sum; cout << " xr = " << xr << " Psi = " << psi << " n = " << n << endl; } goto label2; }