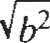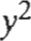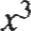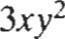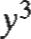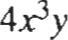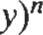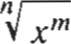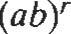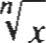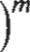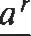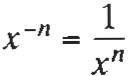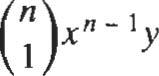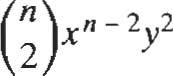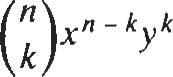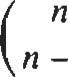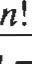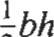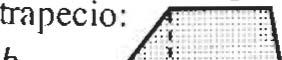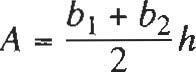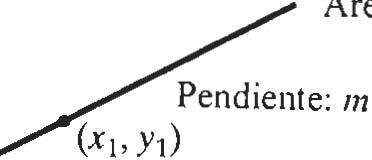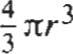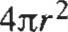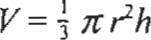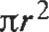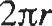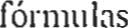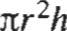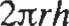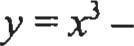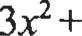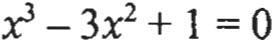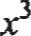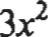Visit to download the full and correct content document: https://ebookmass.com/product/calculo-diferencial-e-integral-4th-edition-c-h-edwards/
More products digital (pdf, epub, mobi) instant download maybe you interests ...
Matematicas II: Calculo Integral Tenth Edition, Ap Edition. Edition Bruce Edwards
https://ebookmass.com/product/matematicas-ii-calculo-integraltenth-edition-ap-edition-edition-bruce-edwards/
Understandable Statistics 12th Edition Brase C.H.
https://ebookmass.com/product/understandable-statistics-12thedition-brase-c-h/
Matemáticas 1 Cálculo Diferencial Ron Larson
https://ebookmass.com/product/matematicas-1-calculo-diferencialron-larson/
Travel Medicine 4th Edition Phyllis E. Kozarsky
https://ebookmass.com/product/travel-medicine-4th-editionphyllis-e-kozarsky/
Proceso integral de la actividad comercial Mcgrawhill
https://ebookmass.com/product/proceso-integral-de-la-actividadcomercial-mcgrawhill/
Endosonography E-Book. 4th ed. Edition Paul Fockens https://ebookmass.com/product/endosonography-e-book-4th-ededition-paul-fockens/
Rich’s Vascular Trauma 4th Edition Todd E. Rasmussen
https://ebookmass.com/product/richs-vascular-trauma-4th-editiontodd-e-rasmussen/
Captivated by the Lyon (The Lyon's Den) C.H. Admirand
https://ebookmass.com/product/captivated-by-the-lyon-the-lyonsden-c-h-admirand/
Deep Waters Martin Edwards
https://ebookmass.com/product/deep-waters-martin-edwards/
CUARTAEDICÔN ALCULO DIFERENCIAL EINTEGRAL ÁLGEBRA Fórmula cuadrática
Las soluciones de la ecuación cuadrática
ax 2 + bx + e = O están dadas por -b + - 4ac x= 2a
Notacion factorial
Para cada entero positivo n, n! = n(n - l)(n - 2) .. , 3·2·1; por definición, O! = l.
Radicales
Fórmula binomial
(x + y)2 = x 2 + 2xy + y2
(x + y)3 = x3 + 3x 2y + 3xy2 + y3
(x + y)4 = x 4 + 4x3y + 6x 2y 2 + 4 xy 3 + y4
Exponentes
(ab)' = a'b' (a')S = a rs
n.¡;;;, =( V; r = x m /n
GEOMETRÍA
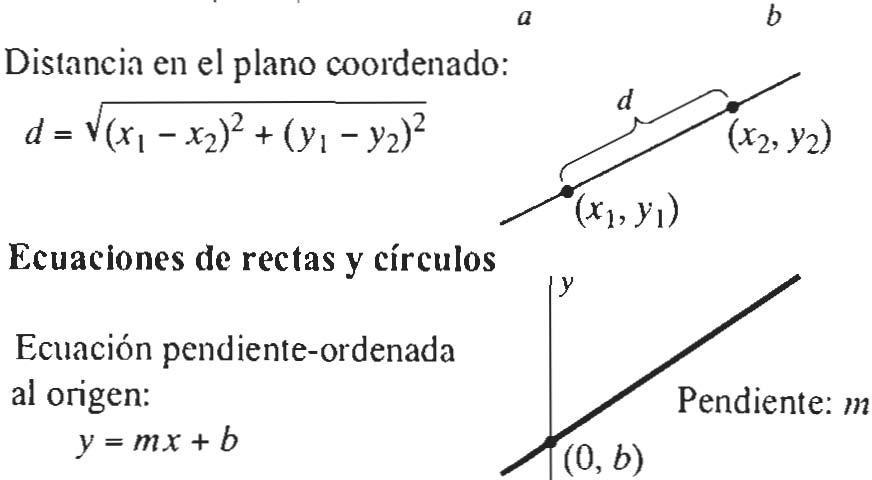
Fórmulas para la distancIa
Distancia en la recta munérica real:
d = la - b l
Ecuación pend iente-ordenada al origen : y = mx + b
Ecuación punto-pendiente: y - YI = m(x - xl)
Circulo con centro (h,k) y radio r:
En general, (x+ yt =x n + + G)x n - 2/
+.oo + G)x n - kyk +oo. + (n: ¡)x yn1 + yn,
donde el coeficiente binomial (n) es el entero I( )1' m m. n m.
Factorlzaclón
Si n es llil entero positivo, entonces x n yn = (x y)(x n - 1 + x n - 2y + xn - 3y 2 + oo. + xn - k - 1yk + , + xyn - 2 + yn - 1).
Si n es llil entero positivo impar, entonces x n + yn = (x + y)(x n - I_ x n - 2y + xn - 3y 2 , ±xn-k-1yk:¡:oo. xy n-2+ y n-I), = ar - s aS
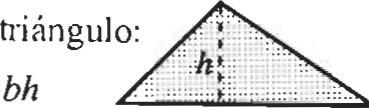
Area del A=b l ;b 2h b, Área del A = l-bh .• ' ..•... 2 b
Vohunen de la esfera:
TRIGONOMETRíA:
sen 2 A + cos 2A = 1 (la identidad jimdalllental) tan 2A + 1 = sec 2A
V = }rrr 3
Área de la superficie:
A = 4rrr 2
Área de la superficie lateral: A = 2rrrh b2
Área del círculo :
Área de la superficie lateral:
A = rrr r 2 + h 2
A = rrr 2
Circunferencia: e = 2rrr ¡:·, uu(:!u )1h b
Volumen del cilindro:
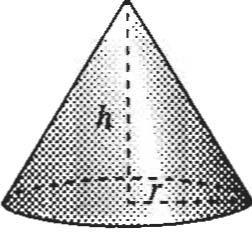
(x-h)2+(y-k?=r 2 x Volumen del cono: V=.jJr?h
cos 2A = cos 2 A - sen 2 A = 1-2 sen 2 A = 2 cos 2 A - 1
sen 2A = 2 sen A cos A
Vé;¡se los apéndices p;¡ra más fór111ubs de referencia.
V = rrr 2 h
cosCA + B) = cos A cos B - sen A sen B
cosCA - B) = cos A cos B + sen A sen B
sen(A + B) = sen A cos B + cos A sen B
sen(A - B) = sen A cos B - cos A sen B
cos 2A = 1 + cos 2A 2
sen2A = 1 - cos 2A 2
LossiguientesproyectosusanvariastecnologIasysonlabaseparaelestudioindividualoparalastareasenlaboratorio.
1 2 3 4 5 6 7 8 9
1.1
1.3
1.4
2.1
2.2
2.4
3.1
3.5
3.6
3.9
4.4
4.5
4.6
5.4
5.8
5.9
6.2
Solucióndeecuacionespormediodelmétododetabulación(pág.13)
Solucióndeecuacionespormediodelmétododeaproximacionessucesivas(pág.31)
Másacercadelasolucióndeecuacionesmedianteaproximaciones(pág.42)
Aproximacióngráficadependientesdecurvas(pág.59)
Estudionuméricodeloslimites(pág.70)
Aplicacionesdelasecuacionescübicasycuárticas(pág.91)
Estudiograficodelcrecimientodepoblaciones(pág.106)
Extremosmedianteaproximaciónaloscerosdederivadas(pág.139)
SolucióngráficadeproblemasdeaplicacióndemáximosymInimos(pág.154)
ImplantaciónencalculadoralcomputadoradelmétododeNewton(pág.183)
Solucióngráficadeproblemasdecajasnoestándar(pág.218)
Gráficasysolucionesdeecuacionespolinomiales(pág.226)
Básquedadepuntoscriticosypuntosdeinflexiónengráficasexóticas(pág.241)
CálculonuméricodesumasdeRiemann(pág.287)
Cálculoautomáticodeareas(pág.322)
BásquedadeIn2yjrmedianteintegraciónnumérica(pág.335)
Aproximaciónnuméricadevokimenesderevolución(pág.359)
6.3 IntegralesdevolumenyjoyerIadediseñadopersonalizado(pág.367)
6.4 AproximaciónnuméricadeIalongituddearco(pág.375)
7.1
Aproximacióndelnñmeroemedianteelcálculodependientes(pág.407)
7.2 Aproximacióndelnuimeroemedianteintegraciónnuménca(pág.417)
7.3 Aproximacióndelniimeroemediantecuadradossucesivos(pág.424)
7.4 Paseográficopordondenadiehapaseado(pág.430)
8.3 EstudiográficodelosIImitesdeformasindeterminadas(pág.463)
8.5 MatemáticasdelarcodeSanLuis(pag.477)
9.2 4Cuándosonequivalentesdosrespuestas(integrales)?(pág.484)
9.5 CrecimientoacotadodepoblacionesyIaecuaciónIogIstica(pág.507)
9.8 Aproximaciónnuméricadeintegralesimpropias(pág.527)
Cálculo Diferencial eIntegral Qilculo Diferencial eIntegral CuartaEdición C.H.EDWARDS,Jr.
TheUniversityofGeorgia,Athens
DAVIDE.PENNEY TheUniversityofGeorgia,Athens
Traducción:
OSCARALFREDOPALMASVELASCO FacultaddeCiencias,UNAM
Revisióntécnica: VICTORHUGOIBARRAMERCADO LicenciadoenFIsicayMatemáticas ESFM,IPN EscueladeActuarla,UniversidadAnáhuac Pearson
EDIClON EN Acquisiúons Editor: George Lobell
Edilor in ChieF. Tim Bozik
Developmenr Editor: Karen Kadin
Produclion Editor: Edward Thomas
Markeling Manager: Melissa Acuña
SupplemenlS EdiIOr: Mary Hornby
Producl Manager: T rudy Pisciolli
Design Direclor: F10rence Dara Silverman
Texr Designer: Andrew ZUlis
Page LaYOUI: Andrew Zutis, Karen Noferi
Cover Designer: Patricia McGowan
Cover PhOIO: Michael Portland
PhOIO EdiIOr: Lorinda Morris-Nanrz
PhOlO Research : Mira Schachne
Edilorial Assislance : Joanne Wendelken
Texl Composilion: Inreraclive Composiúon Corporalion
Art Sludio: Necwork Graphiés
Copy EdiIOr: !Jnda Thompson
EDWARDS: cALCULO DIFERENCIAL E INTEGRAL. 4a. Ed
Traducido del inglés de la obra : CALCULUS WITH ANALYI1C GEOMETRY (Brief edition) , FOURTH EDITION
A11 righlS reserved. AUlhorized lranslaúon from English language edition published by Prenrice-Hall. Inc.
Todos los derechos reservados. Traducción autorizada de la edición en inglés publicada por Prenrice-Hall, Inc.
A11 righlS reserved No parl of rhis book may be reproduced or lransmilled in any form or any means. eleclronic or mechanical, including pholocopying. recording or by any informalion slorage and relrieval syslem, wimoul permission in wriling from me publisher
Prohibida la reproducción 10lal o parcial de esla obra, por cualquier medio o mélodo sin autorización por escrilo del edilor.
Derechos reservados © 1997 respeclo a la primera edición en español publicada por
Calle 4 N' 25-2' piso Frace Ind. Alce Blanco. Naucalpan de Juárez. Edo de México. C.P 53370
ISBN 970-17-0056-2
Miembro de la Cámara Nacional de la Indusrria Editorial. Reg Núm. 1524
Original English Language Edilion Published by Prenrice-Hall, Inc.
A Simon & Schusler Company.
Copyrighl © MCM.'XCrv
A11 rights reserved
ISBN 0-13-457912-7
IMPRESO EN M8crCO / PRINTED IN MEXICO
Contenido Sobre los autores
Prefacio
CAPÍTULO 1 Funciones y gráficas
1.1 Funciones y números reales 2 PROYECTOS 13
1.2 El plano coordenado y las líneas rectas 14
1.3 Gráficas de ecuaciones y funciones 23 PROYECTOS 31
1.4 Un breve catálogo de funciones 33 PROYECTOS 42
1.5 Una vista preliminar: ¿Qué es el cálculo? 42
REPASO: DEFINICIONES, CONCEPTOS, RESULTADOS 46
CAPÍTULO 2 Preludio al cálculo
2.1 Rectas tangentes y la derivada: Un primer vistazo 50 PROYECTO 59
2.2 El concepto de límite 59 PROYECTO 70
2.3 Más acerca de los límites 71
2.4 El concepto de continuidad 81 PROYECTOS 91
REPASO: DEFINICIONES, CONCEPTOS, RESULTADO 92
xili
I(x)
3.1Laderivadaylasrazonesdecambio95 PROYECTO 106
3.2Reglasbásicasdederivación107
3.3Laregladelacadena118
3.4Derivadasdefuncionesalgebraicas125
3.5Máximosyminimosdefuncionesenintervaloscerrados131 PROYECTO 139
3.6ProblemasdeaplicacióndemáximosymInimos140 PROYECTOS154
3.7Derivadasdelasfuncionestrigonométricas155
3.8DerivaciónimplIcitayrazonesrelacionadas164
3.9AproximacionessucesivasyelmétododeNewton173 PROYECTOS 183
REPASO:FORMuLAs,CONCEPTOS,DEFII'ilCIONES185
(0,1) Máximolocal, interseccióncon eLejey /(2.5) " Minimolocal / I=I:asjntotavertical x
CAPITULO4Aplicacionesadicionalesdeladerivada 190
4.1Introduccjón191
4.2Incrementos,diferencialesyaproximaciónlineal191
4.3Funcionescrecientesydecrecientesyelteoremadelvalormedio198
4.4Elcriteriodelaprimeraderivada209 PROYECTO 218
4.5Graficaciónsencilladecurvas219 PROYECTOS226
4.6Derivadasdeordensuperioryconcavidad227 PROYECTOS241
4.7TrazodecurvasyasIntotas242
REPASO:DEFINICIONES,CONCEPTOS,RESULTADOS250
5.1Introducción255
5.2Antiderivadasoprimitivasyproblemasconcondicionesiniciales255
5.3Cálculodeareaselementales268
5.4SumasdeRiemannylaintegral279 PROYECTOS287
5.5Evaluacióndeintegrales289
5.6Valorespromedioyelteoremafundamentaldelcãlculo296
5.7Integraciónporsustitución306
5.8AreasderegiOnesplanas313 PROYECTOS322
5.9Integraciónnumérica323 PROYECTOS335
REPASO:DEFINICIoNEs,CONCEPTOS,RESULTADOS336
CAPITULO6ApilcacionesdeIaintegral
6.1Construccióndeformulasintegrales341
6.2Volñmenesporelmétododeseccionestransversales348 PROYECTO 359
6.3VolOmenesporelmétododecapascilIndricas360 PROYECTO 367
6.4LongituddearcoyareadesuperficiesderevoluciOn367 PROYECTO 375
6.5Ecuacionesdiferencialesseparables376
6.6Fuerzaytrabajo383
REPASO:DEFrN1CIONES,CONCEPTOS,RESULTADOS393
CAPITIJLO7FuncionesexponencialesylogarItmicas 397
7.1Exponenciales,logaritmosyfuncionesinversas398 PROYECTO 407
7.2Ellogaritmonatural408 PROYECTO 417
7.3LafunciOnexponencial418 PROYECTO 424
7.4FuncionesexponencialesylogarItmicasgenerales425 PROYECTO 430
7.5Crecimientoydecaimientonaturales431
*7.6Ecuacionesdiferencialeslinealesdeprimerordenyaplicaciones439
REPASO:DEFrN1CI0NEs,CONCEPTOS,RESULTADOS445
CAPITULO8MásacercadelcálculodeLasfuncionestrascendentes 448
8.1IntroducciOn449
8.2Funcionestrigonométricasinversas449
8.3Formasindeterminadasyregladel'Hôpital458 PROYECTO 463
8.4Formasindeterminadasadicionales464
8.5FuncioneshiperbólicasyfuncioneshiperbOlicasinversas468 PROYECTO 477
REPASO:DEFINICIONESYF6RMuLps478
9.1Introducción481
9.2Tablasdeintegralesysustitucionessimples481
PROYECTO 484
9.3Integralestrigonométricas 485
9.4Integraciónporpartes492
9.5Funcionesracionalesyfraccionesparciales499
PROYECTO 507
9.6Sustitucióntrigonométrica508
9.7Integralesquecontienenpolinomioscuadráticos514
9.8Integralesimpropias519
PROYECTO 527
RESUMEN528
Apéndices
A RepasodetrigonometriaA-i
B DemostracionesdelaspropiedadesdellImiteA-7
C LacompletituddelsistemadenuimerosrealesA-12
D DemostracionesdelaregladeIacadenaA-17
E ExistenciadelaintegralA-18
F AproximacionesysumasdeRiemannA-24
G Reglade1'HôpitalyteoremadelvalormediodeCauchyA-28
H DemostracióndelaformuladeTaylorA-30
I UnidadesdemedidayfactoresdeconversionA-31
J FOrmulasdealgebra,geometrIaytrigonometrIaA-32
K ElalfabetogriegoA-34
Sobrelosautores C.HenryEdwards,UniversityofGeorgia,recibiósuPh.D.delaUniversityof Tennesseeen1960.DespuésimpartióclasesenlaUniversityofWisconsinpor tresañosyunafloenelInstitutforAdvancedStudies(Princeton),comoAlfredP. SloanResearchFellow.ElprofesorEdwardsacabadecumplirsuaño35enla enseflanza(incluyendolaenseñanzadelcálculocasitodoslosaños)yharecibido premiosdeenseñanzadenumerosasuniversidades.Sucarrerahaidodela investigaciónydireccióndetesisentopologlaehistoriadelasmatemáticasalas matemáticasaplicadas,alascomputadorasylatecnologIaenmatemáticas(su puntodeatenciónenlosilltimosaños).Ademásdesustextosdecálculo,cálculo avanzado,algebralinealyecuacionesdiferenciales,esbienconocidoporlos maestrosdecálculocomoelautordeTheHistoricalDevelopmentoftheCalculus (Springer-Verlag,1979).HatrabajadocomoinvestigadorprincipalentresproyectosrecientesapoyadosporlaNSF:(1)UnproyectoparaintroducirtecnologIa entodoelcurriculumdematemáticasendossistemasdeescuelaspñblicasdel norestedeGeorgia(incluyendoMapleparaestudiantesdelosprimeroscursosde algebra);(2)unprogramapilotoCalculuswithMathematicaenlaUniversityof Georgia;y(3)unproyectodelaboratoriodecomputaciónbasadoenMATLAB paraestudiantesdeültimosnivelesdeanálisisnuméricoymatemáticasaplicadas.
DavidE.Penney,UniversityofGeorgia,terminósuPh.D.enTulaneUniversity en1965,alavezqueimpartlaclasesenlaUniversityofNewOrleans.AnteriormentehablatrabajadoenbiofisicaexperimentalenTulaneUniversityyenel Veteran'sAdministrationHospitaldeNuevaOrleans.Enrealidad,comenzóa impartirclasesdecálculoen1957ydesdeentonceshaimpartidodichocursocada periodo.SeunioaldepartamentodematemáticasenGeorgiaen1966ydesde entoncesharecibidopremiosdeenseñanzaenvariasuniversidades.Elesautorde variosartIculosdeinvestigacionenteorladenimerosytopologlayesautoro coautordelibrosdealgebralineal,ecuacionescliferencialesycálculo.
Características de la cuarta edición
Prefacio El papel y la práctica de las matemáticas a nivel global y mundial está sufriendo una revolución, con la influencia principal de la tecnología de cómputo . Las calculadoras y los sistemas de cómputo proporcionan a estudiantes y maestros la fuerza matemática que ninguna generación anterior podría haber imaginado Incluso leemos en los periódicos eventos impresionantes, como el reciente anuncio de la demostración del último teorema de Fermat. En términos de las matemáticas, ¡seguramente ésta es la época más excitante en toda la historia! Así, al preparar esta nueva edición de CALCULO diferencial e integral, deseamos llevar a los estudiantes que lo utilicen algo de esta excitación.
También notamos que el curso de cálculo es la puerta principal para las carreras técnicas y profesionales para un número cada vez mayor de estudiantes en un rango cada vez mayor de curricula. Adonde volteemos (en las empresas, el gobierno, la ciencia y la tecnología), casi todo aspecto del trabajo profesional está relacionado con las matemáticas. Por tanto, hemos repensado el objetivo de proporcionar a los estudiantes de cálculo la base sólida para su trabajo posterior que deben obtener de su texto de cálculo.
Por primera vez desde que la versión original de este libro se publicó en 1982 , esta cuarta edición ha sido revisada desde el principio hasta el fin. Los análisis y explicaciones han sido reescritos en un lenguaje que los estudiantes verán más vivo y accesible. Los temas que rara vez se tocan han sido recortados, para adecuarlos a un curso de cálculo más accesible. Hemos agregado notas históricas y biográficas para mostrar a los estudiantes el lado humano del cálculo , así como proyectos con calculadoras gráficas y laboratorios de cómputo (con opciones para Derive. Maple y Mathematica) para las secciones fundamentales del texto De hecho, en esta edición se percibe un espíritu y un enfoque nuevos que reflejan el interés prevaleciente en las calculadoras gráficas y los sistemas de cómputo. En forma consistente con el énfasis gráfico del movimiento actual de reforma del cálculo , hemos casi duplicado el número de figuras en el texto, donde gran parte del nuevo material gráfico es generado por computadora. Muchas de estas figuras adicionales sirven para ilustrar un enfoque de más deliberación y exploración a la solución de problemas Nuestra propia experiencia en la enseñanza sugiere que el uso de la tecnología contemporánea puede hacer que el cálculo sea más concreto y accesible a los estudiantes .
Al preparar esta edición, hemos aprovechado de los numerosos y valiosos comentarios y sugerencias de los usuarios de las primeras tres ediciones . Esta revisión ha sido tan completa que las modificaciones son demasiadas como para enumerarse aquí. Sin embargo, los párrafos siguientes resumen las modificaciones de mayor interés.
xüi
Problemasadicionales
Elnimerodeproblemashacrecidopocoapocodesde laprimeraediciónyahorasumancasi6000.Enlaterceraycuartaedicioneshemos insertadomuchosejerciciosdeprácticaadicionalesalprincipiodelosconjuntos deproblemas,paragarantizarquelosestudiantesobtenganlaconfian.zayhabilidaddecómputosuficienteantesdepasaralosproblemasmásconceptualesque constituyenelobjetivorealdelcálculo.Enestaediciónhemosagregadotambién problemasbasadosengráficosqueenfaticenIacomprensiónconceptualyacostumbrenalosestudiantesautilizarlascalculadorasgráficas.
NuevosejemplosydetallesdecômputoEnmuchasdelasseccionesdeesta edición,hemosinsertadounprimerejemplomássencillooreemplazadoejemplos yaexistentesporotroscuyocómputoesmássencillo.Además,insertadounalInea odosmásdedetallesdecómputoenmuchosdelosejemplosresueltosparafacilitar suseguimientoalestudiante.Realizamosestoscambiosdemodoqueloscómputos noseanunabarreracontralacomprensiónconceptual.
Materialproyecto Hemosinsertadoproyectoscomplementarios(untotalde48) entodoellibro.CadaproyectoutilizaalgiinaspectodelatecnologIaactualde cómputoparailustrarlasideasprincipalesdelasecciónqueloprecede,ycada unocontieneporlogeneralproblemasadicionalescuyasoluciónpretendeusar unacalculadoragráficaounacomputadora.Lasfigurasylosdatosilustraneluso decalculadorasgráficasysistemasdecómputocomoDerive,MapleyMathematica.Estematerialproyectoesadecuadoparasuusoenunlaboratoriodecomputadorasocalculadorasconducidoenrelaciónconuncursoestándardecálculo,tal vezconunareunionalasemana.Tambiénsepuedeutilizarcomobaseparalas tareasconcalculadorasgráficasocomputadorasquelosestudiantesdebenrealizar fueradeclaseoparasuestudioindividual.
GráficosporcoinputadoraAhoraquelascalculadorasgráficasylascomputadorashanllegadoparaquedarse,esposibleyrecomendableelcrecienteénfasis enlavisualizacióngrafica,juntoconeltrabajonuméricoysimbólico.Cercade 250figurasnuevasgeneradasconMATLABilustraneltipodefigurasquelos estudiantespuedenproducirporsimismosconlascalculadorasgraficas.Muchas deéstasseincluyenconmaterialnuevoparaproblemasgráficos.Incluimoscerca de100gráficosacolorgeneradosconMathematicapararesaltartodaslas seccionesrelacionadasconelmaterialtridimensional.
MaterialhistóricoybiograficoHemosinsertadomaterialhistóricoybiográfico alpnncipiodecadacapItuloparadaralosestudiantesunaideadeldesarrollode nuestramateriaporsereshumanosreales,vivos.Ambosautoressebasanenla historiadelasmismasycreenquepuedeinfluirdemanerafavorableenla enseñanzadelasmatemáticas.Porestarazón,tambiénapareceneneltextovarios comentarioshistóricos.
CapItulosintroductoriosHemosinsertadoloscapItulos1y2parauniniciomás claroyrapidodelcálculo.ElcapItulo1secentraenlasfuncionesylasgraficas. Incluyeahoraunasecciónquecatalogalasfuncioneselementalesdelcálculoy proporcionaunabaseparaunénfasistempranoenlasfuncionestrascendentes.El capItulo1concluyeahoraconunaseccióndedicadaalapregunta"LQueesel cálculo?"ElcapItulo2,delImites,comienzaconunasecciónrelativaalasrectas tangentesparamotivarlaintroducciónoficialdeloslImitesenIasección2.2.En
contrasteconlaterceraedición,estaedicióntratalosilmitestrigonométricosen todoelcapItulo2,paraapoyarunaintroducciOnmásricaymásvisualdelconcepto deilmite.
CapItulosdederivaciônLasecuenciadelostemasenloscapItulos3y4varIa unpococonrespectodelordentradicional.Intentamosdarconfianzaalestudiante presentandolostemasenordencrecientededificultad.LaregladeIacadena apareceunpocotemprano(enlasección3.3)ytratamoslastécnicasbásicasde derivacióndefuncionesalgebraicasantesdeanalizarlosmáximosymInimosen lassecciones3.5y3.6.Laaparicióndelasfuncionesinversassedifiereahorahasta elcapItulo7.Lasección3.7trataahoradelasderivadasdelasseisfunciones trigonométricas.LaderivaciónimplIcitaylasrazonesrelacionadasconéstase combinanenunasolasección(Sección3.8).Elteoremadelvalormedioysus aplicacionessedifierenhastaelcapItulo4.Lassecciones4.4acercadelcriterio delaprimeraderivaday4.6acercadelasderivadasdeordensuperioryla concavidadsehansimplificadoyadecuadoalflujodeltexto.Sehaagregadogran cantidaddematerialgráficoenlasseccionesdetrazodecurvasconlasque concluyeelcapItulo4.
CapItulosdeinfegraciónSehaninsertadonuevosejemplosmássencillosenlos capItulos5y6.Lasprimitivas(anteriormentealfinaldelcapItulo4)abrenahora elcapItulo5.Lasección5.4(sumasdeRiemann)sehasimplificadoengran medida,eliminandolassumassuperioreseinferiores,enfatizadoenvezdeellas lassumasconpuntosmediosoconextremos.Muchosmaestrospiensanahoraque lasprimerasaplicacionesdelaintegralnodebenconfinarsealestándardecálculo deareasyvoliimenes;lasección6.5esunasecciónopcionalquepresentalas ecuacionesdiferencialesseparables.Paraeliminarlaredundancia,elmaterialde centroidesyelteoremadePappussepasaalcapItulo15(Integralesmultiples), dondesepuedeestudiarenuncontextomásnatural.
OpcionestempranasparalasfuncionestrascendentesSedisponededos versiones"tempranasdefuncionestrascendentes":unaqueincluyeelcálculo devariasvariablesyunaquesolotrataelcálculodeunavariable.Enlaversion "regular",laflexibleorganizacióndelcapItulo7comienzaconel"enfoquedel bachillerato"delasfuncionesexponenciales,seguidodelaideadeunlogaritmocomolapotenciaalaquedebemoselevarlabaseaparaobtenerelnümero x.Sobreestabase,13secciOn7.1haceunrepasosencillodelasleyesdelos exponentesydeloslogaritmoseinvestigademanerainformalladerivación delasfuncionesexponencialylogarItmica.Estasecciónacercadelcálculo diferencialelementaldelasexponencialesyloslogaritmossepuedeestudiar encualquiermomento,despuésdelasección3.3(regladelacadena).Siesto sehace,entoncessepuedeestudiarlasección7.2(basadaenladefinicióndel logaritmocomounaintegral)encualquiermomento,despuésdedefinirla integralenelcapItulo5(juntocongranpartedelrestodelcapItulo7,como deseeelmaestro).Deestaforma,eltextosepuedeadecuarauncursomás sencilloqueincluyademaneratempranalasfuncionesexponencialesenel cálculodiferencialybdemaneratempranalasfuncioneslogarItmicasenelcálculointegral.
Lasdemásfuncionestrascendentes(funcionestrigonométricasinversase hiperbOlicas)seestudianahoraenelcapItulo8.EstecapItuloreciénreorganizado incluyeahoralasformasindeterminadasylaregladel'Hôpital(mástempranoque enlaterceraediciOn).
Mantenimientodela fuerzatradicional
TécnicasdeintegraciônmodernizadasElcapItulo9estáorganizadoparaadecuarsealosmaestrosquepiensanquelosmétodosdeintegraciónformalnecesitan ahoraunmenorénfasis,envistadelastéçnicasmodernasparalaintegración numéricaysimbólica.Esdesuponerquetodosdeseentratarlasprimerascuatro seccionesdelcapItulo(hastalaintegraciónporpartesenlasección9.4).Elmétodo defraccionesparcialesapareceenlasección9.5ylassustitucionestrigonométricas ylasintegralesconpolinomioscuadráticosaparecendespués,enlassecciones9.6 y9.7.Lasintegralesimpropiasaparecenahoraenlasección9.8ylassustituciones deracionalizaciónmásparticulareshansidodesplazadasalosproblemasdel capItulo9.EstereordenamientodelcapItulo9lohacemásconvenientepara detenersecuandoelmaestrolodesee.
EcuacionesdiferencialesMuchosmaestrosdecálculopiensanahoraquelas ecuacionesdiferencialesdebenestudiarsedelaformamástempranayfrecuente posible.Lasecuacionesdiferencialesmássencillas,delaformay'=f(x),aparecen enunasubsecciónalfinaldelasección5.2.Lasección6.5ilustralasaplicaciones delaintegralalasolucióndeecuacionesdiferencialesseparables.Lasección9.5 incluyeaplicacionesdelmétododefraccionesparcialesaproblemasdepoblación yalaecuaciónlogistica.Deestaforma,hemosdistribuidoalgodelespIrituyel sabordelasecuacionesdiferencialeseneltexto,demodoqueparecIaclaro eliminareliltimocapItulodenuestraterceraediciOn,dedicadoexclusivamentea lasecuacionesdiferenciales.Sinembargo,losqueasIlodeseenpuedencomunicarseconPrenticeHallparasolicitarlasseccionesadecuadasparaelusocomplementariodeEdwardsyPenney,Ecuacionesdferencialeselementalesyproblemas concondicionesenlafrontera,terceraedición.
AunquesehanagregadomuchascaracterIsticasnuevas,siguenpresentescinco objetivosrelacionadosentresi:concretez,legibiidad,motivación,aplicabilidadyprecision.
ConcretezLafuerzadelcálculoesimpresionanteporsusrespuestasprecisasa preguntasyproblemasreales.Enelnecesanodesarrolloconceptualdelcálculo, mantenemossiemprelapreguntacentral:j,Cómocalcularlorealmente?Enfatizamosdemaneraparticularlosejemplos,aplicacionesyproblemasconcretosque sirvenpararesaltareldesarrollodelateorlaydemostrarlaadmirableversatilidad delcálculoenelestudiodeimportantescuestionescientIficas.
Legibilidad Lasdificultadesenelaprendizajedelasmatemáticassecomplican confrecuenciaporlasdificultadesenellenguaje.Nuestroestilodeescrituraparte delacreenciadequelaexposiciónliana,intuitivayprecisa,hacemásaccesibles lasmatemáticas(yportantomásfácilesdeaprender)sinpérdidaderigor.Enesta ediciónhemosintentadohacerquenuestrolenguajeseaclaroyatractivoparalos estudiantes,demodoqueellospuedanyquieranleerlo,permitiendoentoncesa losmaestrosconcentrareltiempodelaclaseenlosaspectosmenosrutinariosde laenseñanzadelcálculo.
MotivaciónNuestraexposiciónsecentraenlosejemplosdelempleodel cálculopararesolverproblemasrealesdeinterésparalaspersonasreales.Al seleccionartalesproblemasparalosejemplosyejercicios,hemosutilizadoel puntodevistadequeelinterésestimulanteyelestudioeficazmotivantevande
lamano.IntentamosaclararalosestudiantesIaformaenqueelconocimiento obtenidoconcadaconceptootécnicavaldráelesfuerzo.Enlosanálisisteóricos, enparticular,intentamosproporcionarunaimagenintuitivadelobjetivoantes deperseguirlo.
AplicacionesLasdiversasaplicacionesdelcálculosonloqueatraeamuchos estudianteshacialamateria,ylasaplicacionesrealistasproporcionanuna valiosamotivaciónyrefuerzoparatodosellos.Nuestrolibroesbienconocido porelampliorangodeaplicacionesincluidas,peronoesnecesarionirecomendablequecadacursoabarquetodaslasaplicacionesenelmismo.Cadasección osubsecciónquesepuedaomitirsinpérdidadecontinuidadsemarcaconun asterisco.Estoproporcionaflexibilidadparaqueunmaestrodeterminesu propioénfasis.
PrecisionNuestrotratamientodelcálculoescompleto(aunqueesperamosque seamenosqueenciclopédico).Másquesusantecesores,estaediciónfuesujetaa unprocesoamplioderevisionparaayudaragarantizarsuprecisiOn.Porejemplo, esencialmentetodaslasrespuestasaproblemasenlasecciOnderespuestasa!final deestaediciónhasidoverificadaconMathematica.Conrespectoalaseleccióny secuenciadelostemasmatemáticos,nuestroenfoqueestradicional.Sinembargo, unexamencercanodeltratamientodelostemasestándarpuededelatarnuestra propiaparticipaciónenelmovimientoactualporrevitalizarlaenseñanzadel cálculo.ContinuamosenfavordeunenfoqueintuitivoqueenfaticelacomprensiOn conceptualyelcuidadoenlaformulacióndelasdefinicionesyconceptosfundamentalesdelcálculo.Algunasdelasdemostracionesquesepuedenomitira criteriodelmaestroaparecena!finaldelassecciones,mientrasqueotrassedifieren alosapéndices.Deestaforma,damosampliomargenparalavariaciónenla büsquedadelequilibrioadecuadoentreelrigorylaintuición.
TodoslosautoresexperimentadosconocenelvalordelarevisioncrIticadurante lapreparaciOnyrevisiondeunmanuscrito.Ennuestrotrabajoconvariasediciones deestelibro,noshemosbeneficiadoengranmedidaconelconsejodelos siguientesrevisores,excepcionalmentehábiles:
LeonE.Arnold,DelawareCountyCommunityCollege
H.L.Bentley,UniversityofToledo
MichaelL.Berry,WestVirginiaWesleyanCollege
WilliamBlair,NorthernIllinoisUniversity
GeorgeCain,GeorgiaInstituteofTechnology
WilClarke,AtlanticUnionCollege
PeterColwell,IowaStateUniversity
WilliamB.Francis,MichiganTechnologicalUniversity
DianneH.Haber,WestfieldStateCollege
JohnC.Higgins,BrighamYoungUniversity
W.CaryHuffrnan,LoyolaUniversityofChicago
CalvinJongsma,DordtCollege
MorrisKalka,TulaneUniversity
LouiseE.Knouse,LeTourneauCollege
CatherineLilly,WestfieldStateCollege
JoyceLongman,VillanovaUniversity
E.D.McCune,StephenF.AustinStateUniversity
ArthurL.Moser,IllinoisCentralCollege
BarbaraMoses,BowlingGreenUniversity
BarbaraL.Osofsky,RutgersUniversityatNewBrunswick
JohnPetro,WesternMichiganUniversity
JamesP.Qualey,Jr.,UniversityofColorado
ThomasRoe,SouthDakotaStateUniversity
LawrenceRunyan,ShorelineCommunityCollege
WilliamL.Siegmann,RensselaerPolytechnicInstitute
JohnSpellman,SouthwestTexasStateUniversity
VirginiaTaylor,UniversityofLowell
SamuelA.Truitt,Jr.,MiddleTennesseeStateUniversity
RobertUrbanski,MiddlesexCountyCollege
RobertWhiting,VillanovaUniversity
CathleenM.Zucco,LeMoyneCollege
Muchasdelasmejorasrealizadasaestaobradebenacreditarseanuestros colegasylosusuariosdelasprimerastresedicionesenEstadosUnidos,Canada yotrospalses.Estamosagradecidosconaquellosquenoshanescrito,particularmentelosestudiantes,yesperamosquecontinüenhaciéndolo.Agradecemosa BettyMillerdeWestVirginiaUniversitysudiligenteresolucióndelosproblemas yaTernBittner,quienjuntoconsuequipoenLaurelTutoring(SanCarlos, California)verificaronlaprecisiondetodasoluciónalosejemplosylosejercicios impares.Tambiénpensamosquelacalidaddellibroterminadoesuntestimonio adecuadodelacapacidad,diligenciaytalentodeunequipoexcepcionalen PrenticeHall.DamoslasgraciasparticularmenteaGeorgeLobellyPriscilla McGeehon,editoresdematemáticas;KarenKarlin,editordedesarrollo,Ed Thomas,editordeproducción;yAndyZutis,diseñador.Porültimo,nopodemos agradecerlosuficienteaAliceFitzgeraldEdwardsyCarolWilsonPenneysu apoyo,ánimoypacienciacontinuos.
Cálculo Diferencial eIntegral 1 Funciones y gráficas o Es posible que el erudito francés del siglo XVII RenéDescartes sea más recordado hoy en día como filósofo que como matemático. Pero muchos de nosotros estamos fami1iarizados con el "plano cartesiano", en donde la posición de un punto P queda determinada por sus coordenadas (x, y).
o Durante su época de estudiante, con frecuencia Descartes tenía permiso de levantarse tarde, debido a su supuesta salud quebrantada. Él afirmaba que pensaba más claramente acerca de la filosofia, la ciencia y las matemáticas cuando estaba cómodamente acostado en las frías mañanas. Después de graduarse en derecho (lo que estudió aparentemente con poco entusiasmo), Descartes viajó con varios ejércitos por algunos años, pero más como un caballero que como un militar profesional.
o Después de establecerse por fin (en Holanda), Descartes publicó en 1637 su famoso tratado filosófico Discurso del método (Del buen razonamiento y la búsqueda de la verdad en las ciencias) Uno de los tres apéndices de su obra establecía su nuevo enfoque "analítico" de la geo-
metría. Su principal idea (establecida casi en forma simultánea por su coterráneo Pierre de Fermat) fue la correspondencia entre una ecuación y su gráfica, que era por 10 general una curva en el plano. La ecuación se podía utilizar paraestudiar la curva, o viceversa
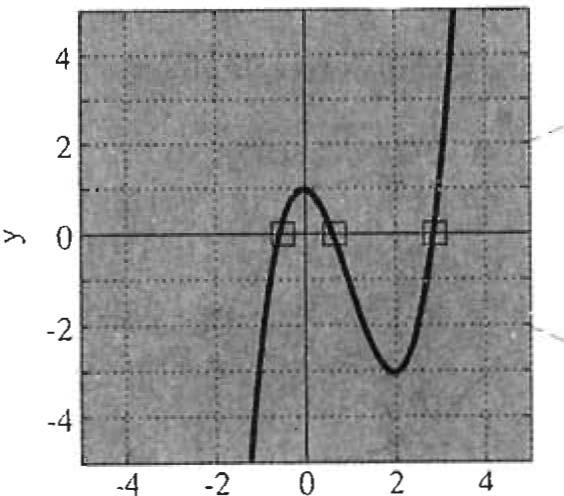
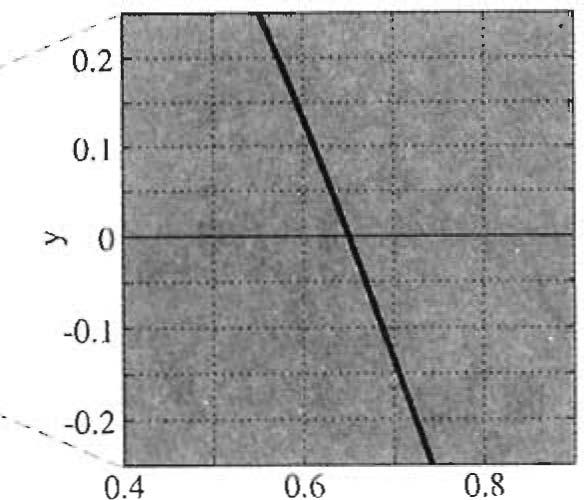
o Supongamos que queremos resolver la ecuaciónf(x) = O. Sus soluciones son los puntos de intersección de la gráfica y = f(x) con el eje x, de modo que una imagen precisa de la curva muestra el número y posiciones aproximadas de las soluciones de la ecuación. Por ejemplo, la gráfica de y=.0- 3r+ 1
tiene tres intersecciones con el ejex, 10 que muestra que la ecuación
tiene tres soluciones reales (una entre-1 yO,otraentreOy 1,yunamás entre 2 y 3) Una calculadora gráfica moderna o un programa de graficación para computadora pueden aproximar estas soluciones de manera más precisa, amplificando las regiones donde se localizan. Por ejemplo, la región central agrandada muestra que la solucióncorrespondiente es x "" 0.65.
La gráfica de y = - 3x2 + 1
/ FuncionesynUmeros reales
Elcálculoesunodeloslogrossupremosdelintelectohumano.Estadisciplina matemáticasurgeprincipalmentedelosestudiosrealizadosenelsigloXVIIpor IsaacNewton(1642-1727)yGottfriedWilhelmLeibniz(1646-1716).Sinembargo,algunasdesusideasdatandelaépocadeArquImedes(287-212a.C.)ytuvieron suorigenenculturastandiversascomoladeGrecia,Egipto,Babilonia,India, ChinayJapón.MuchosdelosdescubrimientoscientIficosquehanformado nuestracivilizacióndurantelosültimostressigloshubieransidoimposiblessinel usodelcálculo.
Elprincipalobjetivodelcálculoeselanálisisdeproblemasdecambioy movimiento.Estosproblemassonfundamentales,puesvivimosenunmundode cambiosconstantes,plenodecuerposenmovimientoyconfenómenosdeflujoy reflujo.Enconsecuencia,elcálculosiguesiendoantemadegrantrascendencia; enlaactualidad,estecuerpodetécnicasdecómputocontinuasirviendocomoel lenguajecuantitativoprincipaldelacienciaylatecnologIa.
Granpartedelcálculoimplicaelempleodelosnümerosrealesodevariables paradescribirlascantidadescambiantesyelusodeflincionespamdescribirlas relacionesentrelasdiversasvariables.Enestaseccióninicialharemosenprimer lugaranrepasodelanotaciónyterminologIadelosnómerosrealesydespués analizaremoslasfuncionesconmásdetalle.
NUMEROSREALES Losnümerosrealessonfamiliaresallector.Sonlosnimerosqueseusanenforma comünenIamayorpartedelasmediciones.Lamasa,lavelocidad,latemperatura yIacargadeancuerposemidenmediantenümerosreales.Estossepueden representarpordesarrollosdecimalesfinitosoinfinitos;dehecho,todonümero realtieneundesarrollodecimalinfinito,puesundesarrollofinitopuedeseguircon unainfinidaddeceros:
=0.375=0.375000000.
Cualquierdecimalperiódico,como
=0.31818181818.
representaunniimeroracional,dadocomoelcocientededosenteros.RecIprocamente,todonümeroracionalserepresentamedianteundesarrollodecimal periódico,comolosquesemuestranaqul.Eldesarrollodecimaldeannñmero irracional(annümeroquenoesracional),como
1.414213562. orr=3.141592653589793
esinfinitoynoperiOdico.
Lainterpretacióngeométricadelosnümerosrealescomopuntosenlarecta real(orectanuméricareal)Rtambiéndebeserlefamiliar.Cadanimeroreales representadoprecisamenteporanpuntodeR,ycadapuntodeRrepresenta
3 precisamenteannümeroreal.Porconvención,losnümerospositivosestnaIa I derechadeceroylosniimerosnegativosalaizquierda,comoenIafigura1.1.1.
2 1 0 1 2 Lassiguientespropiedadesdelasdesigualdadesdenümerosrealesson
fundamentalesyseusanconfrecuencia:
1-31=3 141=4
I I I J -3 0 4
Figura1.1.2Elvalorabsoluto deunniirnerorealessimplemente sudistanciaa!cero(Ejemplo1)
b-alola-bi I- I a b
Figura1.1.3Ladistanciaentreayb
Sia<byb<c,entoncesa<c. Sia<b,entoricesa+c<b+c. (1)
Sia<byc>0,entoncesac<bc. Sia<byc<0,entoncesac>bc.
Lasiltimasdosproposicionessignificanqueunadesigualdadsepreservacuando susmiembrossemultipiicanporunnñmeroposilivo,peroseinviertecuandose multiplicanporunnimeronegativo.
VALORABSOLUTO Ladistancia(nonegativa)enIarectarealentreceroyelnümerorealaeselvalor absolutodea,queseescribeIaI.Enformaequivalente, Ia sia0; al -asia<0. (2)
Lanotacióna0significaqueaesmayorquecerooigualacero.Laecuación (2)implicaquea10paratodornimerorealayquea1=0siysólosia=0.
EJEMPLO1Comolomuestralafigura1.1.2, 141=4y =3
Adernás,lo=0yHh-2I=2-V,dondeestouiltimoescierto,pues2> Asi,'f-2<0yentonces
Laspropiedadessiguientesdelosvaloresabsolutosseusanconfrecuencia: al=al=\/a20, abI=ab HaIalalj (3) al<bsiysólosi-b<a<b.
Ladistanciaentrelosniimerosrealesaybsedefinecomoa-b(o b-aI;noexistediferencia).Estadistanciaessimplementelalongituddel segmentoderectadeIarectarealRconextremosayb(figura1.1.3).
Laspropiedadesdelasdesigualdadesydelosvaloresabsolutosenlas ecuaciones(1)a(3)implicancisiguienteeimportanteteorema.
Desiguaidaddcitriángulo
Sección1.1/Funcionesynitmerosreales
Paratodoslosnümerosrealesayb, a+bIal+Ibl. (4) 3
0a+b a=IalIaI+lbI
Figura1.1.4Ladesigualdaddel triángulocona>0,b<0y bI<lal (1,3)
Den:ostraciOnHayqueconsiderarvarioscasos,segünsilosrnimerosaybson positivosonegativosycuáldeellostengaelmayorvalorabsoluto.Siambos sonpositivos,entoncestambiénloesa+b;portanto, a+b=a+b=a+b. (5)
Sia>Oyb<0,conb<aLentonces 0<a+b<a, demodoque a+b=a+b<a=Ia<a+bI, (6) comosemuestraenIafigura1.1.4.Losdemáscasossonsimilares.Enparticular, vemosqueladesigualdaddeltriánguloesenrealidadunaigualdad(comoenla ecuación(5))amenosqueaybtengansignosdistintos,encuyocasoesuna desigualdadestricta[comoenIaecuación(6)].0
INTERVALOS SupongarnosqueSesunconjunto(colección)deni'imerosreales.Escomtin descrihirSmedianteIanotacón
S={x:condición}, dondeIa"condición"esverdaderaparatodoslosnümerosxenSyfalsaparatodos losnt'imerosxquenoestànenS.Losconjuntosmásimportantesdenimerosreales encálculosonlosintervalos.Sia<b,entonceselintervaloabierto(a,b)se definecomoelconjunto
(a,b)={xa<x<b}
denürnerosreales,yelintervalocerrado[a,b]es
[a,b]={x:a<x b}.
AsI,unintervalocerradocontieneasusextremos,mientrasqueanintervaloabierto no.Tambiénusaremoslosintervalossemiabiertos
[a,b)={x:ax<b}y(a,b]={x:a<x b}.
(Co,2)
Figura1.1.5Algunosejemplos deintervalosdenümerosreales
AsI,elintervaloabierto(1,3)ese]conjuntodeaquellosnümerosrealesxtalesque I<x<3,elintervalocerrado[-1,2]eselconjuntodenmerosrealesxtales que1x2yelintervalosemiabierto(-1,2)eselconjantodenñmerosrealesx talesque1x2.EnIafigura1.1.5mostramosalgunosejemplosdetales intervalos,asicomoalgunosintervalosnoacotados,quetienenformastalescomo [a,cc)={x:xa}, (cc,a]={x:x (a,cc)=:x>a}y (cca)={x:x<a}.
ElsImbolo00quedenotainfinito,essimplementeunaconvencióndenotacióny norepresentaaunnmeroreal;IarectarealRnotiene"extremoseninfinito".El usodeestesImboloesmotivadoporIadescripciOnbreveynatural(J?oc)y(oo,2) paralosconjuntos
detodoslosni'imerosrealesxtalesquexiryx<2,respectivamente.
Capirulo1IFuncionesygráficas {x:xir}y{x:x<2}
Figura1.1.6CIrculo:áreaA=irr2, circunferenciaC=2,rr
Figura1.1.7Esfera:volumen V=4/3,r?,areadeIasuperficie S=4,r?
FUNCIONES LadaveparaelanálisismatemáticodeunasituacióngeométricaocientIficaes porlogeneralelreconocimientodelasrelacionesentrelasvariablesquedescriben lasituación.Talrelaciónpuedeserunaformulaqueexpreseaunavariableen funcióndeotra.Porejemplo,elareaAdeuncIrculoderadiorestádada porA=lrr2(figura1.1.6).ElvolumenVyareadelasuperficieSdeunaesferade radiorestándadospor
V=irr3yS=4r2, respectivamente(figura1.1.7).Despuésdetsegundos(s)queuncuerposedeja caerdesdeelreposo,éstehacaldounadistancia
S=gt2
piesytieneunavelocidaddev=gipies/seg(fils),dondeg32pies/seg2esIa aceleracióndebidaalagravedad.ElvolumenVenlitros(L)de3gramos(g)de bióxidodecarbono(CO2)a27°CestádadoentérminosdesupresiOnpenatmósferas (atm)porV=I.68/p.Estossonejemplosdefuncionesrealesdevariablereal.
Definiciónde'función UnafunciónrealfdefinidaenunconjuntoDdenámerosrealesesuna reglaqueasignaacadanümeroxenDexactamenteunnuimeroreal, denotadoconf(x).
ElconjuntoDdetodoslosnümerosrealesparalosquef(x)estádefinidaes eldominioodominiodedefinicióndelafunciOnjElnümerof(x),queselee"f dex",eselvalordefenelnámero(opunto)x.Elconjuntodelosvaloresy=f(x) eselrangodefEsdecir,elrangodefeselconjunto
{y:y=f(x)pamalgiinxenD
Enestasecciónnosocuparemosmásdeldominiodeimafunciónquedesurango. Confrecuencia,unafunciónquedadescritamedianteunaformulaqueespecificalaformadecalcularelmimerof(x)entérminosdelnümerox.ElsImbolo f()sepuedeconsiderarcomounaoperaciOnarealizarsiemprequeseinserte nñmerooexpresióndentrodelosparéntesis.
EJEMIPLO2Laformula f(x)=x2+x-3 (7)
esIaregladeunafunciónfcuyodominioestodaIarectarealR.Algunosvalores defsonf(-2)=],f(0)=3yf(3)=9.AlgunosvaloresmásdeIafuncionfson f(4)=(4)2+4-3=17, f(c)=c2+c3, f(2+h)=(2+h)2+(2+h)-3 =(4+4h+h2)+(2+h)-3=3+5h+h2y f(t2)=(-t)2+(-t2)3= -3.
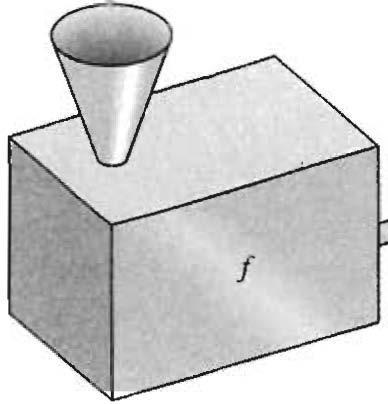
Una"rnáquina función"
CuandodescribimoslafuncionfconIaformulayf(x),liamamosaxla variableindependienteyaylavariabledependientepuescivalordeydepende (mediantef)delaeleccióndex.Cuandoxcambia,ovarla,tambiénlohacey.La formaenqueyvarIaconxquedadeterminadaporIaregladelafunciónfPor ejemplo,sifeslafunciOndelaecuaciOn(7),entoncesy=1cuandox=2, y=3cuandox=0yy=9cuandox=3.
TalvezseaOtilvisualizarIadependenciadelvalory=f(x)conrespectodex pensandounafuncióncomounaespeciedemáquinaqueaceptacomoentradaun nOmeroxyqueproduceentoncescomosalidacinñmerof(x),desplegándoioo imprimiéndoio(figura1.1.8).
UnamáquinadeestetipoesIacaiculadoracomándebolsillo,conunatecla paralaraIzcuadrada.CuandoseusacomodatounnOmerononegativoxyse oprimeestatecia,lacaiculadoradespliega(unaaproximaciOnde)cinimero ObservequecidominiodeestafunciónraIzcuadradaf(x)=xesciconjunto detodoslosnümerosrealesnonegativos,puestoqueningmnOmeronegativo tieneunaraIzcuadradareal.Surangoestambiénciconjuntodetodoslosnámeros realesnonegativos,puescisImboloIisiempredenotalaraIzcuadradano negativadex.Lacaiculadorailustrasuconocimientodeldominio,despiegando unareacciOnadversasipedimosquccalculelaraIzcuadradadeunnOmero negativo(amenosqueseaunadelascalculadorasmássofisticadas,comolaTI-85 oIaHP-48S,quepuedentrabajarconnOmeroscompiejos).
NotodafuncióntieneunaregladadaporunainicafOrmulasencilla,como f(x)= Porejemplo,siescribimos
entonceshemosdefinidounafunciónperfectamenteválida,condominioR. Algunosdesusvaloressonf(-3)=3,f(0)=0yf(2)=4.LafimciOndelejemplo 3sedefineinicialmentepormcdiodeunadcscripciónverbalenvezdeutilizar formulas.
EJEMPLO3 ParacadanOmerorealx,conf(x)sedenotacimáximoenteroque esmenoroiguaiquex.Forejemplo,f(2.5)=2,f(0)=0,f(-3.5)=4yf(r)=3. Sinesunentero,entoncesf(x)=nparatodonOmcrorealxenciintervalo semiabierto[n,n+1).EstafunciOnfsellamalafunciOnmáximoenteroysc denotaconfrecuenciacomo (8)
AsI,[2.5]]=2,([0]]=0,l[-3.5]]=4y[[ir]]=3.Observequeaunquel[x]Iestadefinida paratodorealx,cirangodelafunciónmáximoenterosOloconstadclconjuntode losenteros.
tCuáidebcrIasercidomjniodeunafunciOnsiéstenohasidoespecificado? EstacsunasituaciOricomOnyocurrecuandodamosunafuncionfescribiendo solamentesufórmulay=f(x).Sinoseespecificaundominio,seconvienequeci dominioDesciconjuntodetodoslosnOmerosrealesxparalosquelaexpresión f(x)produceunnámeroreal.Forejemplo,cidominiodef(x)=lIxesciconjunto detodoslosnümerosrealesdistintosdecero(pues1/xestádefinidoprecisamente cuandox0).
Figura1.1.8
Figura1.1.9Lacajadel
ejemplo5
EJEMPLO4
DetermineeldominiodeIafuncióngconIaformula g(x)= 1 'I2x+4
SolucibnParaqueIaraIzcuadrada'Ti±4estédefinida,esnecesarioque -2x+40.Estoesválidosi2x4yportantocuaridox ParaqueelrecIproco 1/i2x+4estédefinido,tambiénnecesitamosquef2x+4 yasIquex2. Enestostérminos,eldominiodegeselintervaloD=(-2,oo).
FUNCIONESVAPLICACIONES ElestudiodeunproblemadeaplicaciOnsebasaconfrecuenciaenladefinición deimafunciOnquecaptureIaesenciadeunasituacióngeométricaofisica.Los ejemplos5y6ilustranesteproceso.
EJEMPLO5
Unacajarectangularconbasecuadradatienevolumen125. ExpreseelareatotaldesusuperficieAcomounafuncióndeIalongituddeuna aristaxdesubase.
SoluciónE]primerpasoeshacerundibujoyetiquetarlasdimensionesadecuadas.Lafigura1.1.9muestraunacajarectangularconbasecuadradaconlongitud dearistaxenlabaseyalturay.TenemosqueelvolumendeIacajaes
V=x2y=125. (9) Tantolatapacomoelfondodelacajatienenareax2ycadaunodesuscuatrolados verticalestieneareaxy,porloqueelareatotaldesusuperficiees
A=2x2+4xy. (10) PeroéstaesunaformulaparaAentérminosdelasdosvariablesxyy,antesque unafuncióndelasolavariablex.ParaeliminaryyobtenerentoncesAsolamente entérminosdex,despejamosyenlaecuación(9)pamobtenery=125/x2ydespués sustituiresteresultadoenIaecuación(10),obteniendo
A=2x2+4x
AsI,elareadeIasuperficie,dadacomounafunciOndelalongitudxdeunaarista es
500
A(x)=2x2+,0<x<co. (11) x
Esnecesarioespecificareldominio,pueslosvaloresnegativosdextienensentido enlafórmuladeIaecuación(11)peronopertenecenaldominiodelafuncionA. Estosedebeaquetodox>0determinaunadeestascajas,eldominiosicontiene atodoslosnñmerospositivos.
COMENTARLOEnelejemplo5,nuestroobjetivoeraexpresarlavariabledependienteAcomofunciondelavariableindependientex.Enunprincipio,lasituación geometricanosproporcionaba
1.LafórniuladeIaecuaciOn(10)queexpresaAentérminosdexylavariable adicionaly,y