Hirsch
Visit to download the full and correct content document: https://ebookmass.com/product/introduction-to-biostatistical-applications-in-health-res earch-with-microsoft-office-excel-and-r-2nd-edition-robert-p-hirsch/
More products digital (pdf, epub, mobi) instant download maybe you interests ...
Microsoft Excel Formulas and Functions (Office 2021 and Microsoft 365) Paul Mcfedries
https://ebookmass.com/product/microsoft-excel-formulas-andfunctions-office-2021-and-microsoft-365-paul-mcfedries/
Financial Analysis with Microsoft Excel 8th Edition Timothy R. Mayes
https://ebookmass.com/product/financial-analysis-with-microsoftexcel-8th-edition-timothy-r-mayes/
New Perspectives Microsoft Office 365 & Excel 2016: Intermediate 1st Edition
https://ebookmass.com/product/new-perspectives-microsoftoffice-365-excel-2016-intermediate-1st-edition/
An Introduction to Statistical Learning with Applications in R eBook
https://ebookmass.com/product/an-introduction-to-statisticallearning-with-applications-in-r-ebook/
GO! with Microsoft Excel 2016 Comprehensive (GO! for Office 2016 Series) 1st Edition – Ebook PDF Version
https://ebookmass.com/product/go-with-microsoftexcel-2016-comprehensive-go-for-office-2016-series-1st-editionebook-pdf-version/
Essentials of Modern Business Statistics with Microsoft Excel 8th Edition David R. Anderson
https://ebookmass.com/product/essentials-of-modern-businessstatistics-with-microsoft-excel-8th-edition-david-r-anderson/
eTextbook 978-1305880412 New Perspectives Microsoft Office 365 & Excel 2016: Intermediate
https://ebookmass.com/product/etextbook-978-1305880412-newperspectives-microsoft-office-365-excel-2016-intermediate/
Microsoft ® Excel ® Workbook 2nd Edition Paul Mcfedries
https://ebookmass.com/product/microsoft-excel-workbook-2ndedition-paul-mcfedries/
Introduction to Research and Medical Literature for Health Professionals
https://ebookmass.com/product/introduction-to-research-andmedical-literature-for-health-professionals/
INTRODUCTIONTO BIOSTATISTICALAPPLICATIONS
INHEALTHRESEARCHWITH MICROSOFTOFFICEEXCEL® ANDR
INTRODUCTIONTO BIOSTATISTICAL APPLICATIONSIN HEALTHRESEARCH WITHMICROSOFT OFFICEEXCEL® ANDR
SecondEdition
ROBERTP.HIRSCH
FoundationfortheAdvancedEducationintheSciences Bethesda,MD,USA
Thissecondeditionfirstpublished2021 ©2021JohnWiley&Sons,Inc.
EditionHistory
JohnWileyandSons,Inc.(1e,2016)
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedinaretrievalsystem,or transmitted,inanyformorbyanymeans,electronic,mechanical,photocopying,recordingor otherwise,exceptaspermittedbylaw.Adviceonhowtoobtainpermissiontoreusematerialfromthis titleisavailableathttp://www.wiley.com/go/permissions.
TherightofRobertP.Hirschtobeidentifiedastheauthorofthisworkhasbeenassertedinaccordance withlaw.
RegisteredOffice
JohnWiley&Sons,Inc.,111RiverStreet,Hoboken,NJ07030,USA
EditorialOffice 111RiverStreet,Hoboken,NJ07030,USA
Fordetailsofourglobaleditorialoffices,customerservices,andmoreinformationaboutWiley productsvisitusatwww.wiley.com.
Wileyalsopublishesitsbooksinavarietyofelectronicformatsandbyprint-on-demand.Somecontent thatappearsinstandardprintversionsofthisbookmaynotbeavailableinotherformats.
LimitofLiability/DisclaimerofWarranty
Whilethepublisherandauthorshaveusedtheirbesteffortsinpreparingthiswork,theymakeno representationsorwarrantieswithrespecttotheaccuracyorcompletenessofthecontentsofthiswork andspecificallydisclaimallwarranties,includingwithoutlimitationanyimpliedwarrantiesof merchantabilityorfitnessforaparticularpurpose.Nowarrantymaybecreatedorextendedbysales representatives,writtensalesmaterialsorpromotionalstatementsforthiswork.Thefactthatan organization,website,orproductisreferredtointhisworkasacitationand/orpotentialsourceof furtherinformationdoesnotmeanthatthepublisherandauthorsendorsetheinformationorservices theorganization,website,orproductmayprovideorrecommendationsitmaymake.Thisworkissold withtheunderstandingthatthepublisherisnotengagedinrenderingprofessionalservices.Theadvice andstrategiescontainedhereinmaynotbesuitableforyoursituation.Youshouldconsultwitha specialistwhereappropriate.Further,readersshouldbeawarethatwebsiteslistedinthisworkmay havechangedordisappearedbetweenwhenthisworkwaswrittenandwhenitisread.Neitherthe publishernorauthorsshallbeliableforanylossofprofitoranyothercommercialdamages,including butnotlimitedtospecial,incidental,consequential,orotherdamages.
LibraryofCongressCataloging-in-PublicationDataAppliedfor:
ISBN978-1-119-72259-5
Coverimage:©(insetfigure)CourtesyofRobertP.Hirsch,(background)©iconeer/GettyImages CoverdesignbyWiley
Setin10/12pt,TimesLTStdbySPiGlobal,Chennai,India. 10987654321
PARTONEBASICCONCEPTS1
1THINKINGABOUTCHANCE3
1.1PropertiesofProbability / 4
1.2CombinationsofEvent / 8
1.2.1Intersections / 8
1.2.2Unions / 13
1.3Bayes’Theorem / 16
ChapterSummary / 19
Exercises / 20
2DESCRIBINGDISTRIBUTIONS25
2.1TypesofData / 26
2.2DescribingDistributionsGraphically / 27
2.2.1GraphingDiscreteData / 27
2.2.2GraphingContinuousData / 30
2.3DescribingDistributionsMathematically / 36
2.3.1ParameterofLocation / 37
2.3.2ParameterofDispersion / 41
2.4TakingChanceintoAccount / 48
2.4.1StandardNormalDistribution / 49
ChapterSummary / 59
Exercises / 62
3EXAMININGSAMPLES65
3.1NatureofSamples / 66
3.2Estimation / 67
3.2.1PointEstimates / 67
3.2.2TheSamplingDistribution / 73
3.2.3IntervalEstimates / 78
3.3HypothesisTesting / 82
3.3.1RelationshipBetweenIntervalEstimationand HypothesisTesting / 89
ChapterSummary / 91
Exercises / 93
4UNIVARIABLEANALYSISOFACONTINUOUS DEPENDENTVARIABLE101
4.1Student’s t-Distribution / 103
4.2IntervalEstimation / 106
4.3HypothesisTesting / 109
ChapterSummary / 113
Exercises / 114
5UNIVARIABLEANALYSISOFANORDINALDEPENDENT VARIABLE119
5.1NonparametricMethods / 120
5.2Estimation / 123
5.3WilcoxonSigned-RankTest / 124
5.4StatisticalPowerofNonparametricTests / 128
ChapterSummary / 128
Exercises / 129
6UNIVARIABLEANALYSISOFANOMINALDEPENDENT VARIABLE133
6.1DistributionofNominalData / 134
6.2PointEstimates / 135
6.2.1Probabilities / 136
6.2.2Rates / 138
6.3SamplingDistributions / 142
6.3.1BinomialDistribution / 143
6.3.2PoissonDistribution / 146
6.4IntervalEstimation / 149
6.5HypothesisTesting / 151
ChapterSummary / 155
Exercises / 156
PARTTHREEBIVARIABLEANALYSES161
7BIVARIABLEANALYSISOFACONTINUOUSDEPENDENT VARIABLE163
7.1ContinuousIndependentVariable / 163
7.1.1RegressionAnalysis / 165
7.1.2CorrelationAnalysis / 189
7.2OrdinalIndependentVariable / 207
7.3NominalIndependentVariable / 207
7.3.1EstimatingtheDifferencebetweentheGroups / 208
7.3.2TakingChanceintoAccount / 209
ChapterSummary / 218
Exercises / 221
8BIVARIABLEANALYSISOFANORDINALDEPENDENT VARIABLE227
8.1OrdinalIndependentVariable / 228
8.2NominalIndependentVariable / 236
ChapterSummary / 241
Exercises / 243
9BIVARIABLEANALYSISOFANOMINALDEPENDENT VARIABLE245
9.1ContinuousIndependentVariable / 246
9.1.1Estimation / 247
9.1.2HypothesisTesting / 255
9.2NominalIndependentVariable / 258
9.2.1DependentVariableNotAffectedbyTime:Unpaired Design / 259
9.2.2HypothesisTesting / 266
9.2.3DependentVariableNotAffectedbyTime:Paired Design / 277
9.2.4DependentVariableAffectedbyTime / 283
ChapterSummary / 286
Exercises / 288
10.1ContinuousIndependentVariables / 296
10.1.1MultipleRegressionAnalysis / 297
10.1.2MultipleCorrelationAnalysis / 317
10.2NominalIndependentVariables / 319
10.2.1AnalysisofVariance / 320
10.2.2PosteriorTesting / 331
10.3BothContinuousandNominalIndependentVariables / 340
10.3.1Indicator(Dummy)Variables / 341
10.3.2InteractionVariables / 343
10.3.3GeneralLinearModel / 348
ChapterSummary / 355 Exercises / 358
11.1NonparametricAnova / 369
11.2PosteriorTesting / 375
ChapterSummary / 380
Exercises / 381
12MULTIVARIABLEANALYSISOFANOMINALDEPENDENT
12.1Continuousand/orNominalIndependentVariables / 387
12.1.1MaximumLikelihoodEstimation / 387
12.1.2LogisticRegressionAnalysis / 389
12.1.3CoxRegressionAnalysis / 399
12.2NominalIndependentVariables / 401
12.2.1StratifiedAnalysis / 402
12.2.2RelationshipBetweenStratifiedAnalysisandLogistic Regression / 410
12.2.3LifeTableAnalysis / 414
ChapterSummary / 424
Exercises / 427
13TESTINGASSUMPTIONS433
13.1ContinuousDependentVariables / 436
13.1.1AssumingAGaussianDistribution / 437
13.1.2TransformingDependentVariables / 477
13.1.3AssumingEqualVariances / 485
13.1.4AssumingAdditiveRelationships / 494
13.1.5DealingWithOutliers / 506
13.2NominalDependentVariables / 507
13.2.1AssumingaGaussianDistribution / 507
13.2.2AssumingEqualVariances / 510
13.2.3AssumingAdditiveRelationships / 511
13.3IndependentVariables / 511
ChapterSummary / 513
Exercises / 516
THINKINGABOUTCHANCE
1.1PropertiesofProbability4
1.2CombinationsofEvent8
1.2.1Intersections8 1.2.2Unions13
1.3Bayes’Theorem16 ChapterSummary19 Exercises20
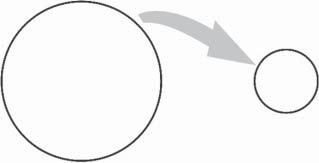
Intheintroductiontothisfirstpartofthetext,welearnedthatchanceisusedtoselect samplesfromthepopulationthatare,inthelongrun,representativeofthepopulationfromwhichtheycame(Figure1.1).Beforewecanappreciatehowchance influencesthecompositionofthosesamples,however,weneedtounderstandsome thingsaboutchanceitself.Inthischapter,wewilllookatthebasicpropertiesof chanceandseehowthechancesofindividualeventscanbecombinedtoaddress healthissues.
IntroductiontoBiostatisticalApplicationsinHealthResearchwithMicrosoftOfficeExcel® andR, SecondEdition.RobertP.Hirsch. ©2021JohnWiley&Sons,Inc.Published2021byJohnWiley&Sons,Inc. Companionwebsite: www.wiley.com/go/hirsch/healthresearch2e
Figure1.1 Chancedetermineswhichdatavaluesinthepopulationendupinthesample.
1.1PROPERTIESOFPROBABILITY
Tobeginwith,weshouldpointoutthattherearetwotermsthatcanbeusedinterchangeably: chance and probability.Ineverydaylanguage,probability(orchance) tellsushowmanytimessomethinghappensrelativetothenumberoftimesitcould happen.Forexample,wemightthinkoftheprobabilitythatapatientpresenting withasorethroathasstreptococcalpharyngitis.Ifwecanexpect1patienttoactuallyhavestreptococcalpharyngitisoutofevery10patientsseenwithasorethroat, thentheprobabilityofhavingstreptococcalpharyngitisis0.10.Orequivalently, thereisa10%chancethatapersonselectedatrandomfromamongpersonswith sorethroatswouldhavestrepthroat.
Instatisticalterminology,thenumberoftimessomethinghappensiscalledits frequency andthat“something”iscalledan event.Theopportunitiesforaneventto occurarecalled observations. 1 Whenusingtheconceptofprobability,weneedto understandthattherearetwopossibleresultsforeachobservation:eithertheevent occursortheeventdoesnotoccur.Inthepreviousexample,theeventwasstreptococcalpharyngitisandthepatientsseenwithasorethroatweretheobservations.
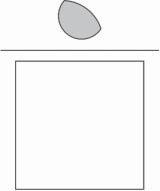
Everydaylanguageisoftencumbersomewhendiscussingissuesinstatistics. Analternativeapproachistoexamineeventsandobservationsgraphically.Wedo thisbyconstructinga Venndiagram.InaVenndiagram,weusearectangleto symbolizealloftheobservationsandacircletosymbolizethoseobservationsin whichtheeventoccurs.Figure1.2isaVenndiagramwecouldusetothinkabout theprobabilitythatapatientwithasorethroathasstreptococcalpharyngitis.
TherearesomeaspectsofobservationsandeventsthatareevidentinaVenn diagram.Forinstance,wecanseethattheentirerectangleoutsideofthecirclecorrespondstoobservationsinwhichtheeventdoesnotoccur.Whenaneventdoesnot occur,wesaythatthe complement oftheeventoccurs.Inthiscase,theeventis havingstrepthroatanditscomplementisnothavingstrepthroat.
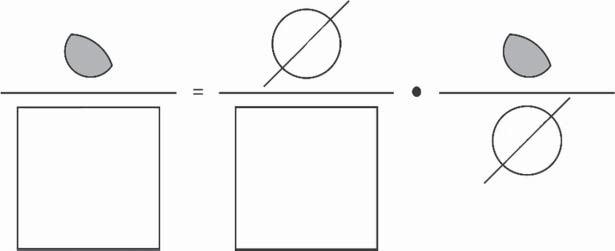
ThewayaVenndiagramtellsusaboutthemagnitudeoftheprobabilityisbythe areaofthecirclerepresentingtheeventrelativetotheareaoftheentirerectangle.A waywecancomparetheseareasisbycreatinga Vennequation.AVennequation
1 Statisticiansalsorefertotheopportunityforaneventtooccurasa trial.Sincetheterm trial refers toaclinicalexperimentinhealthresearch,wewillexclusivelyusetheterm observation torefertothe opportunityforaneventtooccur.
Figure1.2 AnexampleofaVenndiagram.Therectangulararearepresentsallobservations. Thecirculararearepresentstheobservationsinwhichtheeventoccurs.Theareawithinthe rectanglebutoutsideofthecirclerepresentsthoseobservationsinwhichtheeventdidnot occur.
Figure1.3 AVennequationillustratingtheprobabilityapatientwithsorethroathasstreptococcalpharyngitis.
usesthepartsofaVenndiagraminamathematicalequationthatshowshowthe probabilityofaneventiscalculated.Fortheprobabilitythatapatientwithsore throathasstreptococcalpharyngitis,theVennequationwouldlooklikeFigure1.3. AVennequationhelpsusseeanotherpropertyofprobabilitiesthatprobabilitieshaveadistinctrangeofpossiblevalues.Sinceaneventcannotexistwithoutan observation,thecirclecanonlybeasbigastherectangle.Inotherwords,thenumeratormustbeasubsetofthedenominator.Theresultofthispropertyistomakethe largestpossiblevalueforaprobabilityequalto1(or100%).Thevalueof1occurs wheneveryobservationinthedenominatorisalsoaneventinthenumerator.When
Probability of strep throat =
All patients with sore throat
Patients with strep throat
theprobabilityofanobservationbeinganeventhasavalueof1,itis certain that theeventwilloccur.
Thenumeratorofaprobabilitycontainsthenumberofevents.Thelargestvalue possibleisequaltothenumberofobservations.Thesmallestvaluepossibleis0.If thenumeratorofaprobabilityisequalto0,thisimpliesthatnoneoftheobservations areeventsand,therefore,theprobabilityisequalto0aswell.Aprobabilityof0 indicatesthatitis impossible foraneventtooccur.Aprobabilitycanbenosmaller than0andnolargerthan1.2
Whenwewanttocalculateaprobability,itiseasiertousesomemathematicalshorthand.Tosymbolizeaprobability,weusealowercase p followedbyaset ofparentheses.Withinthoseparentheses,weidentifytheeventaddressedbythe probability.Then,theequationlookslikethis:
p(event)= numberofevents numberofobservations (1.1)
Next,letustakealookatanexamplethatillustratescalculationofaprobability anditsinterpretation.
◼ EXAMPLE1.1
Supposewedidthroatculturesfor100patientswhocomplainedofasorethroat and10ofthosecultureswerepositiveforstreptococcus.Whatistheprobabilitya personpickedatrandomwouldhaveapositivestrepculture?
Inthisquestion,apositivestreptestistheeventandsomeonewithsorethroat isanobservation.Tocalculatetheprobabilityofapersonhavingapositivestrep culture,wecanuseEquation(1.1).
p(event)= numberofevents numberofobservations = 10
Thus,thereisaprobabilityof0.1(ora10%chance)thatapersonselectedfromthe groupofpatientswithasorethroatwouldbepositiveforstreptococcus. ◼
Apartoftheshorthandweusetoshowhowprobabilitiesarecalculatedconcerns thecomplementofanevent(i.e.,anobservationinwhichtheeventdoesnotoccur). Ratherthaninsertingthedescriptionofthecomplementoftheeventwithinthe parentheses,wemoreoftenputabaroverthedescriptionoftheevent.So,p(event) standsfortheprobabilityofthecomplementoftheeventoccurring(i.e.,theprobabilityoftheevent not occurring).Forthecomplementofhavingstrepthroat,we coulduse p(strep).Therearetwopropertiesofacollectionofeventsthatanevent anditscomplementalwaysdemonstrate.Thefirstis mutualexclusion.Acollection ofeventsissaidtobemutuallyexclusiveifitisimpossiblefortwoormoreevents
2 Thisrangeofpossiblevaluesbetween0and1meansthataprobabilityisalsoaproportion.
tooccurinasingleobservation.Inthiscase,itiscertainlyimpossibleforaperson bothtohavestrepthroatandtonothavestrepthroat.
Thesecondpropertyofaneventanditscomplementisthattheyare collectively exhaustive.Acollectionofeventsissaidtobecollectivelyexhaustiveifevery observationiscertaintoconsistofatleastoneoftheevents.Here,thisimplies thateverypersonwithasorethroateitherhasordoesnothavestrepthroat.Clearly, thisistrue.
Foreventsthatarebothmutuallyexclusiveandcollectivelyexhaustive(likean eventanditscomplement),thereisaspecialrelationshipamongtheevents:the sumoftheirprobabilitiesisequalto1.Inmathematicallanguage,therelationship betweentheprobabilityofaneventoccurringandtheprobabilityofthecomplement oftheeventoccurringisshowninEquation(1.2):
Alittlebitofalgebrashowsusthatwecancalculatetheprobabilityofthecomplementofaneventbysubtractingtheprobabilityoftheeventfrom1.Thisisshown inEquation(1.3):
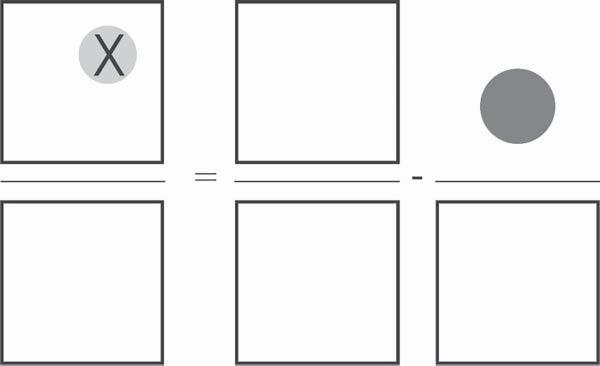
ThisrelationshipcanalsobedescribedingraphiclanguageasintheVennequation inFigure1.4.
Sofar,wehaveseenhowwecanthinkaboutprobabilitiesusingeverydaylanguage,graphiclanguage,andmathematicallanguage.Eachoneofthesewaysof examiningstatisticalissueshasitsownadvantages.Thesortofthingswehave
Figure1.4 AVennequationillustratingtherelationshipbetweentheprobabilityofthe complementoftheevent(e.g.,nothavingstrepthroat)andtheprobabilityoftheevent(e.g., havingstrepthroat).
learnedaboutprobabilityincludesthefactthatprobabilitieshaveadiscreterangeof possiblevaluesrangingfrom0(indicatingthattheeventcannotoccur)to1(indicatingthattheeventalwaysoccurs).Also,wehaveexaminedtherelationshipbetween aneventanditscomplement.Thisrelationshiphastwoimportantpropertiesof acollectionofevents.Thesepropertiesaremutuallyexclusiveandcollectively exhaustive.Acollectionofeventsismutuallyexclusiveifonlyoneoftheevents canoccurinasingleobservation.Tobecollectivelyexhaustive,thecollectionof eventsneedstoencompasseverypossibilitysothatatleastoneoftheeventsoccurs ineveryobservation.Next,wewilltakealookatotherkindsofcollectionsofevents.
1.2COMBINATIONSOFEVENT
Therearetwowayswemightbeinterestedinhowtwoormoreeventsrelatetoeach other.Onewayisthattheeventsoccurtogetherinthesameobservation.Wecall thisthe intersection ofevents.Anotherwayisthatatleastoneeventoccursinan observation.Wecallthisthe union ofevents.
1.2.1Intersections
Inhealthresearchandpractice,weareofteninterestedinsituationsinwhichmore thanoneeventoccursinasingleobservation.Forinstance,wemightbeinterested intherelationshipbetweenahigh-fatdietanddevelopmentofatherosclerosis.The sortsofpeopleinwhomwewouldbemostinterestedarethosewhohavebothof thoseevents,sincetheyaretheonesforwhomahigh-fatdietcouldhavecontributed totheriskofdisease.
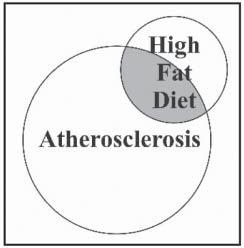
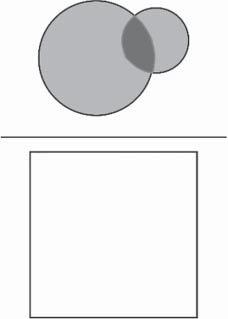
Instatisticalterminology,werefertotheoccurrenceoftwoormoreevents inasingleobservationastheintersectionoftheevents.Figure1.5illustratesthe
Figure1.5 Venndiagramillustratingtherelationshipbetweenahigh-fatdietanddevelopmentofatherosclerosis.Theareainwhichthecirclesoverlaprepresentsthosepersonswho havebothahigh-fatdietandatherosclerosis.
probabilitiesofahigh-fatdietandatherosclerosisandtheintersectionofthose twoevents.Theirintersectioniswherethetwocirclesoverlap.Thesearethe observationsinwhichapersonhasbothahigh-fatdietandatherosclerosis.
Theprobabilityofanobservationincludingbothevents(i.e.,theintersection ofthoseevents)considersthesizeoftheoverlaprelativetoalltheobservations. Figure1.6showsaVennequationrepresentingtheprobabilityoftheintersectionof high-fatdietandatherosclerosis.
Ifwewanttocalculatetheprobabilityofanintersectionofevents,weusewhat iscalledthe multiplicationrule.Toseehowthemultiplicationruleworks,letus beginwithaVennequation(Figure1.7).
TotheleftoftheequalssignintheVennequationinFigure1.7istheprobability oftheintersectionofhavingahigh-fatdietanddevelopingatherosclerosisasshown inFigure1.6.Inthenumeratorofthatprobabilityarethepersonswhohadboth events.Inthedenominatorareallpersonsregardlessofdietordisease.Immediately totherightoftheequalssignistheprobabilitythatsomeonehasahigh-fatdiet.In thenumeratorofthatprobabilityarethepersonswithahigh-fatdietandinthe denominatorare,asbefore,allpersonsregardlessofdietordisease.
p (fat and atherosclerosis) =
persons
Figure1.6 Vennequationfortheprobabilitythatapersonhasbothahigh-fatdiet(fat)and hasatherosclerosis.Inthenumeratoristheareaofoverlap(intersection)ofthetwocircles intheVenndiagram(Figure1.5).Thedenominatorrepresentseveryonewhetherornotthey haveahigh-fatdietoratherosclerosis(i.e.,theentirerectangle).
persons
persons
Figure1.7 Vennequationofthemultiplicationruleusedtocalculatetheintersectionof high-fatdietandatherosclerosis.
Thesecondfractiontotherightoftheequalssignalsoisaprobability,3 butit looksdifferentfromanyprobabilitywehaveencounteredsofar.Specifically,itdoes notincludealltheobservations(representedbytherectangleinaVenndiagram)in itsdenominator.Rather,itincludesonlythosepersonswithahigh-fatdietinits denominator.Thisisanexampleofaveryimportantkindofprobability,calleda conditionalprobability. Aconditionalprobabilitytellsustheprobabilityofan eventoccurringgiventhatanothereventhasoccurred.Inthiscase,theconditional probabilitytellsustheprobabilityofapersonhavingatherosclerosisgiventhatthe personhasahigh-fatdiet.
Inmathematicalnotation,aconditionalprobabilityalsolooksdifferentfrom otherprobabilitieswehaveencountered.Equation(1.4)illustratesthemathematical notationfortheVennequationinFigure1.7.
where
p(A and B) = probabilitythatanobservationwillincludebothevent A andevent B (i.e.,theprobabilityoftheintersectionof A and B)4
p(A) = probabilitythatanobservationincludesevent A (i.e.,theunconditional probabilityofevent A)
p(B ∣ A) = probabilitythatanobservationwillincludeevent B giventhatit includesevent A (i.e.,aconditionalprobabilityofevent B)
Or,intermsofahigh-fatdietandatherosclerosis,
Fromastatisticalpointofview,itdoesnotmatterwhicheventisaddressedbythe conditionalprobability.5 Thus,theprobabilityoftheintersectionofhigh-fatdiet andatherosclerosiscouldalsobecalculatedas
3 Recallthat,tobeaprobability,afraction’snumeratormustbeasubsetofitsdenominator.Thisisthe casehere,becausethosepersonswithbothahigh-cholesteroldietandatherosclerosis(thenumerator) areallincludedinthecirclerepresentingpersonswithatherosclerosis(thedenominator).
4 Insetnotation,thisis p(A ∩ B).
5 Thewaytheprobabilityoftheintersectioniscalculateddependsonlyonwhichprobabilitiesare obtainedaspartofaparticularhealthresearchstudy.Ifourinformationabouttherelationshipbetween thehigh-fatdietandatherosclerosiscomesfromacohortstudy(astudyinwhichtheprobabilityofdiseaseiscomparedbetweenexposedandunexposedpersons),forexample,theconditionalprobabilitywe wouldmeasureistheprobabilityofthediseasegivenexposurestatus.Inacase–controlstudy(astudyin whichtheoddsofbeingexposediscomparedbetweenpersonswhohaveanddonothavethedisease), however,theconditionalprobabilitywemeasureistheprobabilityoftheexposuregiventhedisease status.
InEquations(1.5)and(1.6),wecanseethataverticallineisusedtoseparatethe twoeventsintheparenthesesofaconditionalprobability.Theeventtotheleftofthe verticallineiscalledthe conditionalevent.Itistheconditionaleventthattheprobabilityaddresses.InEquation(1.5),theconditionaleventishavingatherosclerosis,so thisconditionalprobabilitytellsusaboutthechancethatsomeonehasatherosclerosis.Theeventtotherightoftheverticallineiscalledthe conditioningevent. Theconditioningeventdefinesthecircumstanceinwhichweareinterestedinthe probabilityoftheconditionalevent.Here,havingahigh-fatdietistheconditioning event.Thus,Equation(1.5)tellsusthatweareinterestedintheprobabilityofhaving atherosclerosisgiven(i.e.,underthecondition)thatsomeonehasahigh-fatdiet. Thereasonthatconditionalprobabilitiesaresoimportantinhealthresearchis thefactthattheytellusaboutanimportantaspectoftherelationshipbetween events.Namely,conditionalprobabilitiescanbeusedtoseeiftheoccurrenceofone eventchangestheprobabilityoftheoccurrenceofanotherevent.If,forexample, weareinterestedinwhetherthereisthissortofrelationshipbetweenahigh-fat dietandhavingatherosclerosis,wecouldcomparetheconditionalprobabilityin Equation(1.5)withtheprobabilitythatsomeonehasatherosclerosisgiventhatthey donothaveahigh-fatdiet(p(atherosclerosis ∣ fat)).Ifthosetwoconditionalprobabilitieshavethesamevalue,thenwecanconcludethatahigh-fatdietdoesnot influencethechanceofhavingatherosclerosis.Inthatcase,thethreeprobabilities inEquation(1.7)areallequaltothesamevalue.
Or,inmoregeneralterms,
p(B ∣ A)= probabilitythatanobservationwillincludeevent B giventhatitdoes notincludeevent A (i.e.,anotherconditionalprobabilityofevent B)
Instatisticalterminology,wesaytwoeventsare statisticallyindependent when theprobabilityofoneoftheeventsisnotaffectedbyoccurrenceoftheotherevent.6 Inbiologicterms,eventsthatarestatisticallyindependentcannothaveacausalrelationship(oranyothertypeofrelationship).
6 Theterm“statisticallyindependent”asstatisticiansuseitcanbeconfusingwhenweconsidertheeverydaymeaningof“independence.”Ifweweretosay,forexample,thattwopersonsareindependent,we arelikelytoinferthatthereisnoconnectionbetweenthem.Thisisnotwhatthestatisticianisimplying.Rather,thestatisticianissayingthatyoudonotneedtoconsiderwhetherornotoneeventhas occurredwhenaddressingtheprobabilityofanotherevent.Whenastatisticianimpliesthatthereisno overlapbetweenevents,thestatisticiansaysthattheyare“mutuallyexclusive”ratherthan“statistically independent.”
Todetermineifeventsarestatisticallyindependent,weneedtocompareonlytwo ofthethreeprobabilitiesinEquation(1.8).Ifthosetwoprobabilitiesareequaltothe samevalue,thenallthreeprobabilitiesarethesameandtheconditionalandconditioningeventsarestatisticallyindependent.Wewilltakealookatanexampleofthis relationshipshortly,butfirstletusseehowconditionalprobabilitiesarecalculated.
Tocalculateaconditionalprobability,weuseEquation(1.4)algebraicallyrearrangedasinEquation(1.9).
Or,intermsofahigh-fatdietandhavingatherosclerosis,
ThisprocessofidentifyingstatisticalindependenceisillustratedinExample1.2.
◼ EXAMPLE1.2
Supposethat,inaparticularvalleyoftheMojaveDesert,thereare2,500residents. Ofthose2,500residents,625workforACMEBorax,Inc.,acompanythatrecovers chemicalsfromthebrineunderasaltflatthatcoversmostofthevalleyfloor.Ofthe 2,500residentsofthevalley,500havebeendiagnosedwithleukemia.Ofthe500 diagnosedwithleukemia,125arepersonswhoworkforACMEBorax,Inc.Given thatinformation,isworkingforACMEstatisticallyindependentofbeingdiagnosed withleukemia?
First,letusconsidertherelationshipbetweenworkingforACMEandhaving leukemia.Wearetoldthat625personsworkforACMEand,ofthose,125have leukemia.Fromthatinformation,wecancalculatetheprobabilityofhaving leukemiaundertheconditionthatapersonworksforACMEusingEquation(1.9): p(leukemia ∣ ACME)= p(leukemiaandACME) p(ACME) = 125∕2,500 625∕2,500 = 0.2
TodetermineifworkingforACMEandhavingleukemiaarestatisticallyindependentevents,weneedtocomparethatconditionalprobabilitywitheithertheprobabilityofhavingleukemiagiventhatapersondoesnotworkforACMEorwiththe overall(i.e.,unconditional)probabilityofhavingleukemia.Thelatterprobabilityis
p(leukemia)= numberwithleukemiainvalley numberinvalley = 500 2,500 = 0.2
Sincethesetwoprobabilitiesareequaltothesamevalue,wecanconcludethatworkingforACMEandhavingleukemiaarestatisticallyindependentevents.Inother words,workingforACMEdoesnotchangetheprobabilityofhavingleukemia. ◼
Sofar,wehaveseenthatwecanusethemultiplicationruletocalculatetheprobabilityoftwoeventsoccurringinasingleobservation(i.e.,theintersectionofthose events).Tocalculatetheprobabilityoftheintersectionofmorethantwoevents, wesimplyincludeeachadditionaleventinthemultiplicationofconditionalprobabilities.Foreachadditionalevent,weincludetheconditionalprobabilityofthe eventwiththeconditioningeventsbeingalloftheeventslistedpreviouslyinthe equation.Forexample,wecancalculatetheintersectionofthreeeventsasshown inEquation(1.11).
where
p(C ∣ A and B) = probabilitythatanobservationwillincludeevent C givenit includesevents A and B (i.e.,aconditionalprobabilityofevent C)
Iftheeventsarestatisticallyindependent,wecanuseasimplifiedversionofthe multiplicationrule.Thissimplificationistomultiplytheunconditionalprobabilities oftheevents.Equation(1.12)showsthesimplifiedversionfortheintersectionof threeeventsexaminedinEquation(1.11).
Thereasonwecanusethissimplifiedversionofthemultiplicationruleisthat,by definition,theconditionalandunconditionalprobabilitiesarethesameforstatisticallyindependentevents(asshowninEquation(1.8)).Ifthethreeeventsarenot statisticallyindependent,however,weneedtouseEquation(1.11)tocalculatethe intersectionofevents.
1.2.2Unions
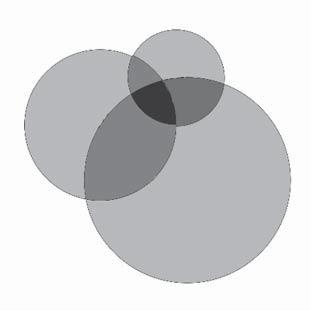
Whenourinterestisintheprobabilityofany(i.e.,1ormore)ofacollectionofevents occurringinthesameobservation,wesayweareinterestedintheunionofthose events.Suppose,forexample,weareconsideringtworiskfactorsforatherosclerosis:high-fatdietandsmoking.Inthatcase,wemightbeinterestedincalculatingthe probabilityapersonhasatleastoneoftheseriskfactors(i.e.,eitherhigh-fatdietor smokingorbothhigh-fatdietandsmoking).Toillustratethis,letusaddsmoking totheVenndiagraminFigure1.5.ThentheVenndiagramofallthreeeventswill looksomethingliketheoneinFigure1.8.
Theunionofthetworiskfactorsissatisfiedifapersoneitherhasahigh-fatdiet orsmokes(orboth).Thus,thenumeratoroftheprobabilityoftheunionofthose twoeventsincludesthepartoftheVenndiagramcoveredbyeithercircle.
Atherosclerosis
Figure1.8 Venndiagramshowingtherelationshipbetweenhigh-fatdiet,smoking,and atherosclerosis.
p (fat and/or smoke) =
All persons
Figure1.9 Vennequationshowingtheprobabilityoftheunionofsmokingand/orhigh-fat diet
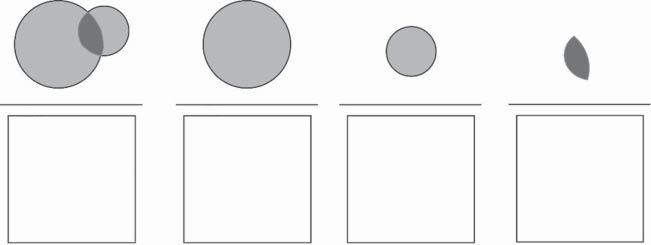
Figure1.9showstheVennequationfortheunionofsmokingandhigh-fatdiet. Tocalculatetheprobabilityoftheunionoftwoevents,weusethe additionrule. Asthenameimplies,intheadditionruletheprobabilitiesofeachoftheeventsare addedtogether.
Sinceaddingtheprobabilitiestogetherincludestheintersectionofthoseevents twice,theprobabilityoftheintersectionoftheeventsmustbesubtractedfromthe sum.Thiscalculationfortheunionofsmokingandahigh-fatdietisillustratedby theVennequationinFigure1.10.
persons
personsAll personsAll persons
Figure1.10 Vennequationshowingcalculationoftheunionofsmokingandahigh-fatdiet usingtheadditionrule.
Inmathematicalterms,thecalculationoftheunionoftwoeventsisperformed asshowninEquation(1.13).
where
p(A and/or B) = probabilityanobservationwillincludeevent A and/orevent B (i.e.,theprobabilityoftheunionofevents A and B)7
Now,letustakealookatanexampleaddressingtheunionoftwoevents.
◼ EXAMPLE1.3
Supposeweareplanningaclinicaltrialofanewlivevaccine.Inthisstudy,wewant toexcludepersonswhoareeitherpregnantorimmunocompromised.Supposewe estimatethatthepopulationfromwhichweareplanningtotakeoursampleincludes 20%ofthetotalnumberofpersonswhoarepregnantand10%ofthetotalnumberof personswhoareimmunocompromised.Ifbeingpregnantandbeingimmunocompromisedarestatisticallyindependentevents,whatproportionofoursamplewill beexcludedduetoeitherofthesecharacteristics?
Tocalculatetheprobabilityoftheunionoftwoevents,weuseEquation(1.13). Forthisapplication,Equation(1.13)lookslikethefollowing: p(pregand∕orcomp)= p(preg)+ p(comp)− p(pregandcomp)
Weknowtheprobabilitythatapersonselectedatrandomfromthepopulationwill bepregnant(p(preg) = 0.2)andtheprobabilitythatapersonselectedatrandomfrom
7 Insetnotation,thisis p(A ∪ B).
thepopulationwillbeimmunocompromised(p(comp) = 0.1).Wearenotgiventhe probabilityoftheintersectionofthesetwoevents(i.e.,theprobabilityaperson willbebothpregnantandimmunocompromised).Wearetold,however,thatthese twoeventsarestatisticallyindependent.Thistellsusthatwecanusethesimplified versionofthemultiplicationruleillustratedforthreestatisticallyindependentevents inEquation(1.12).Forthetwostatisticallyindependenteventsofbeingpregnant andbeingimmunocompromised,theirintersectioncanbecalculatedasfollows:
Nowthatwehavetheprobabilityoftheintersectionofthetwoevents,weareready tocalculatetheirunion.
Thus,wecanexpectthat28%ofthepersonsweselectfromthepopulationwillbe excludedfromthestudybecausetheyareeitherpregnantorimmunocompromised (orboth).
Aswiththemultiplicationruleweusedtocalculatetheprobabilityoftheintersectionofevents,theadditionruleforcalculationoftheprobabilityoftheunion ofeventshasasimplifiedversionthatcanbeusedunderaspecialcondition.For theadditionrule,theconditionisthattheeventsaremutuallyexclusive.Ifso,the probabilityoftheunionofeventscanbecalculatedbysimplyaddingtogetherthe probabilitiesoftheevents.Theintersectionsoftheeventsdonotneedtobesubtractedfromthatsumbecause,bydefinition,theprobabilityoftheintersectionof twomutuallyexclusiveeventsisequalto0.
1.3BAYES’THEOREM
Earlier,welearnedtherearetwotypesofeventsinaconditionalprobability:the conditionalevent(s)andtheconditioningevent(s).Wealsolearnedthatthesetypes ofeventshaveverydifferentrolesinaconditionalprobability.Theconditionalevent istheeventforwhichtheprobabilityiscalculated(i.e.,conditionalprobabilitiestell usthechanceoftheconditionaleventoccurring).Allofthecharacteristicsofunconditionalprobabilities(thosediscussedatthebeginningofthischapter)applytothe conditionalevent.Forinstance,theprobabilityofthecomplementoftheconditional eventisfoundbysubtractingtheconditionalprobabilityfrom1(seeEquation(1.3)). Equation(1.14)showsthatrelationshipforconditionalprobabilities: