Dedication
To our parents
Preface
There is no longer a need to argue about the importance of solar energy and the necessity of furthering the photovoltaic (PV) industry. These issues have been addressed by many sources in the media and publications. Excellent books have been published covering the basics of photovoltaics including both the underlying classical physics and material implementations.
Taking advantage of the above issues sufficiently presented, this book will concentrate on several subjects left beyond the scope of the exiting photovoltaic texts. These subjects are all related to thin film photovoltaics (such as CdTe, CIGS, or a-Si:H based) whose properties and operations turn out to be quite different from that of the classical PV presented mostly by the crystalline Si structures. The obvious differences lie in the device thinness (microns instead of millimeters) and its morphology (polycrystalline or amorphous instead of crystalline).
The thinness effect may be so significant that the photogenerated charge carriers reach the electrodes without much recombination even in the imperfect non-crystalline material, which deemphasizes the classical concept of recombination limited PV performance. On the other hand, the transversal resistance not self-averaging across thin disordered structures leaves a possibility of significant lateral nonuniformities, some of which can be quite detrimental. In addition, the non-crystalline morphology leads to continuous energy spectra of localized states instead of discrete levels in crystals, which results in new transport mechanisms (hopping) and recombination features. Finally, an important part of thin film PV possess piezo-electric properties, which leads to the concept of piezo-PV unknown in the classical PV science.
Taken together, the latter subjects form the physics of thin film PV as a distinctive field of its own. This book will for the first time provide a consistent presentation of that field. In other words, this book will not describe the material of classical PV science, which has been masterfully described in other PV books, but will instead introduce material that has never been presented in PV books before.
To better explain our book title, we would like to emphasize the term of physics as defining the filed that is not necessarily related to the object’s materials, chemistry or engineering. The physics was always related to phenomena per se, regardless of the material specificity. Think, for example, of the Newton’s second law where the material structure does not matter, think about the fact that the Planck’s constant and Boltzmann’s constant do not depend on which material they describe, and how, in the physics of disordered systems, it does not matter what is the chemical composition of a system, etc. Similarly, in the photovoltaic science, the basics (built-in field, junction, and so on) remain material unspecific. Along these lines, our book concentrates on the aspects that are not sensitive to the material structure or composition. That is not to denigrate the known great contributions to photovoltaics from the materials sciences and chemistry, which appear dominant from any query of recent publications, but rather to preface our book limitations.
In our experience, the concept of a distinctive field of thin film PV physics may not appear obvious to everybody: quite a few in the community believe that thin film PV must be understood in the framework of classical PV science developed earlier and proven for thick crystalline systems. Such a resistance appears rather paradoxical given that thin film PV is made of materials that seem unacceptable from the classical PV perspective, and yet they often outperform classical PV. Our book solves that paradox by switching to a new physics paradigm.
The book is naturally broken into six parts, each containing several interrelated sections.
Part I, consisting of just section I, gives a general introduction to PV including the concepts of junctions, material requirements, and distinctive features of thin film PV.
Part II, encompassing sections II to V, concentrates on one-dimensional concepts relevant to thin film PV. It presents a densely populated zoo of various diodes, some quite different from p-n junctions, including the ones that play a significant role in thin film PV operations. It then extends that diode consideration on one-dimensional analysis of solar cells, including some important case studies.
Part III, made up of sections VI to XIII, takes the consideration beyond one-dimensional physics considering lateral effects, such as shunting, random micro-diodes, weak diodes, etc., addressing both the related theory and observations.
Part IV, including sections XIV to XVIII, concentrates on electronic processes in disordered materials of thin film PV which addresses morphology, fluctuations, transport properties, recombination in the quasi-continuous
Preface xiii spectrum of localized states, operations of nonocrystalline junctions, and, finally, piezo photovoltaics.
Part V, formed by sections XIX to XXIV, presents the subject of electro-thermal instabilities in thin film PV starting from the exactly solved two-diode model and current hogging to spontaneously formed hot spots conducive of performance degradation.
Part VI includes sections XXV to XXVIII and discusses a sensitive issue of device degradation for thin film PV, including both solar cells and PV modules. It then discusses the problematic of accelerated life testing and risk analyses.
Finally, our book has an Appendix that comprise three parts of methodical value” the validity of in-series representation of complex band diagrams, the nature of saturation current in diode models, and accurate estimates for the electron potential fluctuations.
We are grateful to many people who have helped us to learn the subjects presented in this book. Our exposure to PV science and industry started with First Solar LLC (Perrysburg, OH) before the year 2000, at which time its research and production groups combined many enthusiastic contributors including H. McMaster, G. Dorer, G. Nelson, R. C. Powell, D. Rose, U. Jayamaha, E. Bykov, T. Maxon, R. Harju, T. Colman, L. McFaul, N. Reiter, T. Kahle, G. Khouri, G. Rich, M. Steel, and many others, to all of whom we are grateful for their intelligent friendly support. We would like as well to acknowledge our interactions with the PV group of the University of Toledo including A.D. Compaan, X. Deng, A. Vijh, D. Giolando, A. Vasko, Y. Roussillon, V. Parikh, L. Attigalle (Cooray), M. Mitra, M. Nardone, X. Li, V. Plotnikov, K. Wieland, and J. Drayton. Finally, we would like to express our gratitude to the members of CdTe PV National Team at NREL, starting with their remarkable managers K. Zweibel, B. von Roedern, H. Ulllal, and brilliant contributors B. McCandless, D. Albin, V. Kaydanov, T. Ohno, J. Sites, T. Sampath, A. Fahrenbruch, and so many others.
This book is intended for three readership categories. One is that of graduate and advanced undergraduate students with some understanding of the general physics and familiarity with the basic concepts of condensed matter. We hope that our book will bring to them a flavor of live physics in an informal manner as used by practicing researchers. It may help to open their eyes to a more general fact that the science of physics often evolves in its own ways quite different from those implied by the standard curriculum textbooks, and, for some, to become an evidence that physics can be relevant for PV.
Our next category of readers belongs to those in academic teaching and research revolving around semiconductors, device physics, and thin film structures. For that category, we aim to provide a fresh look at a number
Preface
of subjects so established that they appear “carved in stone” for ages as dictated by the classical photovoltaic science developed during the times when thin film technology PV did not exist. Our book will invite that category of readers to pay more attention to the issues of variability and statistics apparent to those working for industry rather than for academia. Finally, we hope that some of our book topics and approaches can become a part of university curricula for PV/device physics or related disciplines.
We identify our third category of readers as the industrial R&D professionals of all levels. Their business responsibilities and hectic environment do not often leave much time to follow the published research and appreciate new concepts. We believe that our book will help the curious readers of that category to broaden their horizons and open new approaches towards technology goals. On top of that, adopting some concepts of our book could create beneficial synergy between physics and solar technology.
Victor Karpov
Diana
Shvydka
Sylvania, Ohio, USA
February 2021
General and Thin Film PV
I. Introduction to Thin Film PV
A number of brilliant texts are readily available describing the general photovoltaic (PV) principles and their classical implementations [1–6], as well as various specifics of thin film PV [7–11], and we are not going to duplicate them in any form. This section will briefly overview main book concepts especially addressing the underlying physics of PV functionality different between the crystalline and thin film devices. Such a synthetic view will help to inter-relate various sides of the physics of thin film PV as a subject of its own.
A. The Origin of PV. Junctions
We recall that PV effect in general is presented by the light generated voltage. The PV voltage when the system absorbed light creates electric asymmetry in the form of spatially separated opposite electric charges, electrons and holes, which can be extracted and utilized in the form of electric current. For the charge separation to occur, there must be a built-in electric field as illustrated in Fig. 1 presenting a basic design of PV devices made of two semiconductor layers. The built-in field originates from the junction formed by those layers. Historically, such junctions were between p- and n-types of semiconductor layers; hence, the name of p-n junctions traditionally associated with PV devices. However, p-n junctions are neither necessary nor sufficient elements of systems with built-in fields as discussed below. For example, semiconductor/metal junctions in Fig. 1 will generate their own built-in fields that can be either beneficial or detrimental to PV device functionality.
In general, the built-in electric fields always emerge with junctions of any two chemically different materials. The underlying physics is that one of the materials will be energetically more favorable for the electrons than the other. To minimize the system energy, the electrons will therefore
Victor Karpov and Diana Shvydka. Physics of Thin-Film Photovoltaics, (1–12) © 2022 Scrivener Publishing LLC
Fig. 1 Conceptual design of a solar cell. Front and back contacts are metallic, and the former one is transparent to light (shown in waving lines). The presented built-in electric field E is caused by the dark positive and negative charges shown as + and –. R is a load resistor. For specificity, the diagram presents a two semiconductor layer design, such as p- and n- materials with the field E in their junction proximity. However, sufficient electric fields can exist as well in the proximities of semiconductor-metal junctions.
move there leaving the one with unbalanced positive charge; hence, the built-in field between the spatially separated opposite charges of electrons and holes, qualitatively similar to that of electric capacitor. The number of electrons moving across the junction is determined by the balance between the above mentioned energy gain and the energy loss due to the necessity of overcoming the Coulomb attraction to the positive charges left behind. The built-in electric fields of that nature are omnipresent and are not limited to photovoltaics, or p-n junctions, or other artificial structures.
Another reading of the latter statement is that photovoltaics do not necessarily have to be related to or understood in terms of p-n junctions. In reality, any (not only p-n) junctions of different materials produce built-in electric fields. Some of them, but not all, create photovoltaic effect.
For example, a junction of two metals produces the built-in field underlying the phenomenon of thermoelectricity, but not suitable for PV because the light does not penetrate in a metal deep enough and because that field is screened (by metal electrons) beyond a nanometer thin region, insufficient for light absorption. However the built-in fields of metal/semiconductor (rather than metal/metal) junctions can make good diodes and PV devices.
As another example, we point at a charge acquired by a solid particle immersed in a liquid. Curiously, that example explains how wines and many other liquid products consist of charged micro particles suspended in a somewhat ionized water. We will return to that example later in the book describing the so called “red wine effect” in PV.
Note that junction fields require electronic exchange between two materials while their direct physical contact is not necessary. As an illustration,
chemically different metal electrodes of a capacitor will spontaneously acquire opposite charges proportional to the difference in their work functions. That process often called the ‘dielectric absorption’ takes time sufficient for the inter-plate electron transfer. Along the same lines, two different metals separated by a dielectric or semiconductor layer will exchange electrons forming the built-in electric field throughout that layer as described more in detail next (Sec. II).
B. Fundamental Material Requirements
A well known feature of all PV devices is that at least some of their constituting materials must have a not-too-wide forbidden gap, say G ~ 1–2 eV. The origin of that criterion is that larger band gaps exceeding the energies of most of sun spectra photons would not allow efficient light absorption necessary to produce enough electrons and holes. However, there is also the opposite requirement of those gaps being not too small, so that efficiently absorbing narrow band semiconductors are not good for PV either. As a result, semiconductors with substantial but not-too-wide forbidden gaps G ~ 1–2 eV, such as Si, Ge, CdTe, CIGS and some others are most suitable for PV.
The not-too-narrow gap limitation is less intuitive and may be worth explaining here. It is dictated by PV functionality as a power source. The power is a product of electric current and voltage, P = IV where both I and V components must be not too small. I is proportional to the light induced charge generation rate favoring significant absorption coefficients in the sun spectral region of ħω ~ 0.5–2 eV. Forbidden gaps G ~ 1–2 eV of many semiconductors fall in that region. To the contrary, the typical dielectric gaps G ≳ 4 eV are too wide for sufficient absorption (for example, window glass that is practically transparent and does not absorb light).
The requirement that undermines the suitability of narrow gap semiconductors (despite their strong absorption coefficients) is related to the voltage component: V ≤ G/q, where q is the electron charge. To explain the latter inequality we note that V can be related to the difference in Fermi energies in two metal electrodes as illustrated in Fig. 2. We recall that the Fermi (quasi-Fermi) energy describes the energy change due to removing one particle from the system. Therefore, ∆EF ≡ EF1 – EF2 gives the energy change due to transferring one electron between the two metals, and so does qV. On the other hand, the metal Fermi energies must not overlap with the semiconductor conduction or valence bands because such an overlap would mean that the semiconductor has in reality metal conductivity (no gap between the Fermi level and forbidden gap edges). As illustrated
Fig. 2 Band diagram of a metal/semiconductor/metal structure where EF1 and EF2 represent quasi-Fermi levels determined by voltage drop V across the semiconductor.
in Fig. 2, G presents the upper limit of the difference between the electron and hole Fermi levels allowing their steady state spatial separation. Increasing V beyond G/q would shift the Fermi levels beyond the forbidden gap turning the semiconductor into metal thus shorting the built in field and the circuit.
Another wording of the same is that electrons and holes recombine very efficiently when the two Fermi levels are close thus suppressing their spatial separation and the built-in field. Assuming point defect mediated recombination, it can be shown more quantitatively [12] that the electron-hole recombination rate strongly accelerates with decrease of the gap G. As a result, there exists a range of gaps optimizing PV performance, G ≲ 2 eV. It should be remembered however, that the latter optimum gap prediction was derived under certain assumptions about the nature of (defect facilitated) recombination, lack of traps, insignificant leakage due to shunts, and others clearly outlined in the original work [12].
C. Charge Transport. Definition of Thin Film PV
We now consider charge carriers transport in the junction region where the built in field is significant; that region is often called the space charge region, simply because the field and charge density are E = 4πρ (where E and ρ are correspondingly the field and charge density, and we use the Gaussian system of units). The built-in field extends through a limited thickness lE determined by the condition that the change of electron energy through lE equals the difference in Fermi levels ∆EF of the materials involved. In the order of magnitude, the latter condition yields ε qnlE /~ ∆ EF 22 where n is the charge concentration (cm–3) and ε is the dielectric permittivity (for simplicity, we neglect possible differences in n and ε between the junction components). Using the ballpark values, ∆EF ~ 1 eV, ε ~ 10,
n ~ 10 16 cm –3 yields lE ~ 1 μm. This estimate is consistent with the published data for various junctions.
In the built-in field region, the charge carrier transport is dominated by drift with velocity v = μF where μ is the mobility and F = qE = qV/lE is the electric force. The diffusion with coefficient D = μkT (according to the Einstein formula where k is the Boltzmann constant and T is the temperature) is insignificant contributing to the transport time a relatively small fraction of kT/qV ≪ 1 assuming the typical V ~ 1 V and kT ~ 0.025 eV (room temperature).
The drift transport approximation is sufficient if the light absorption is limited to the space charge region, which applies to many thin-film structures. That approximation is well justified when the light absorption length is short enough, labs ≲ lE, limiting charge carrier generation to the built-in field region, which takes place in CdTe, CIGS, and a variety of other thin-film PV materials. However, some crystalline structures, such as Si and Ge, possess the non-direct band structures with absorption lengths in the hundred of microns range. In such materials, charge carriers generation extends way beyond the built-in region, and the transport is dominated by diffusion rather than drift. We recall that the characteristic diffusion distance and time are related as LDt D where D is the diffusion coefficient.
The above discussed drift and diffusion times,
τE = l/v = l2/(μqV) and τD = l2/D, (1)
describe how long it take for a charge carrier to travel distance l to the device terminals. These times must be short enough to avoid significant electron-hole recombination. If the characteristic recombination time is τ r, we must require that the relevant transport time to device terminals, τ e or τ d be shorter than τ r. The corresponding criteria are discussed in Sec. XVI below. Here, it suffices to note that τr is extremely sensitive to material parameters and device structure, which brings in multiple elements of materials science and PV technology. In particular, recombination processes are strongly facilitated by structural defects (imperfections, impurities, surface states) that depend on details of material composition; interfacial recombination can play a significant role for some junctions, etc.
At a qualitative level, we discriminate between thick and thin PV structures. Typical of crystalline PV, the former are such that the electrons and holes diffuse long distances to the device terminals and τd can be longer than τr, i.e. interaction with defects becomes inevitable during their long trips. To the contrary, the characteristic drift time τe is much
shorter than τ r in thin PV where recombination becomes almost immaterial. As a result, defects and imperfections determine thick PV efficiency quite significantly. That observation undisputable for thick PV, can become confusing when uncritically extended over thin film PV where it is not warranted. Furthermore, a century-long successful history of crystalline (Si, in the first place) PV made the concept of defect facilitated recombination literary a commandment dominating all PV understanding across the discipline. That paradigm has triggered various defect characterization studies in thin film structures, and, while no correlations between defects and thin film PV performances was established, that activity continues.
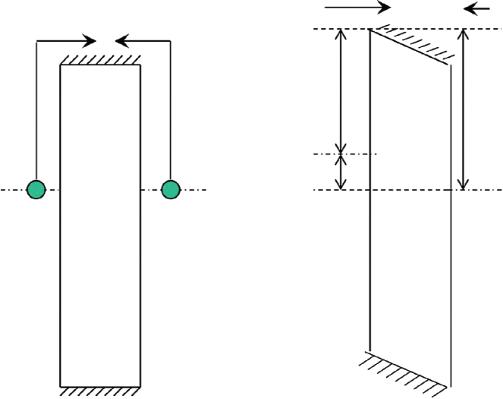
Of course, the difference between ‘thick’ and ‘thin’ devices is related to the fact that the former have thickness l ≫ lE where lE is the linear dimension of the built-in field region, as presented in Fig. 3. To the contrary, l ≲ lE or l is just slightly greater than lE for ‘thin’ devices. In the absence of field, charge carriers have to travel by diffusion. Taking into account the Einstein relation between the mobility and diffusion coefficient, the ratio of ‘thick’ over ‘thin’ device transport times is estimated as
where V is the voltage across the device, q is the electron charge. Given the typical |Ve| ~ 1 eV, kT ~ 0.025 eV (room temperature), l on the order of hundreds of micron and lE in microns, the ratio in Eq. (2) can be as large as 105–106. The latter inequality is consistent with the typical experimental
Fig. 3 Diffusion of the photogenerated electrons and holes to the electrodes in a ‘thick’ device. White circles represent defect recombination centers. The figure is aimed to show that interactions with such centers may be likely when charge carriers exercise long-time diffusion movements.
data: the diffusion times τd,thick ~ 10–100 μs (in crystalline Si PV) and td ~ 1–10 ns in thin film PV. With those numerical values, using the typical recombination times τ r in the range of micro- to milliseconds (as evaluated for various semiconductors [3, 13–17]), one should expect τ r ≫ τd for thin film PV.
Based on the latter estimate, thin film PV can operate in the opposite limit τ ≪ τ r where the role of defect related recombination is on average insignificant. Unfortunately, they have other vulnerabilities related to lateral nonuniformity of their parameters. From a very general point of view, such nonuniformity originates from the lack of transversal self-averaging across too thin structures, which allows significant fluctuations between different spots. Due to device thinness, some sparse spots represent parasitic conductive paths (ohmic or non-ohmic) between opposite electrodes. These paths work as recombination highways degrading PV efficiency. We emphasize that such a nonuniform recombination is qualitatively different from that by point defects in thick PV and call for different mitigating strategies.
Furthermore, having reached the electrodes their respected terminals, electrons and holes undergo fast lateral transport inside the contact metals taking them to the above mentioned recombination channels, through which they disappear. We will see in what follows that the recombination times τ rc of such channels (presented in Fig. 4) form an exponentially broad spectrum decaying towards shorter values. The channels with characteristic recombination times of the order of charge carrier travel times τ dominate because the channels with τ rc ≫ τ are inefficient, while those with τ rc ≪ τ are too rare. This feature is more quantitatively explained in Sec. XVI following Fig. 104 and subsequent chapters. At this point, we conclude that thin film PV can operate through multidimensional processes where electric currents across and along films are strongly coupled. From the practical perspective, surface treatments that can block the recombination channels appear to be a strategy improving thin film efficiency. That approach has been successful as established on purely empirical grounds before it was theoretically substantiated.
D. Distinctive Features of Thin Film PV
Another distinctive feature of thin film PV is that their forming layers are noncrystalline, but rather polycrystalline (CdTe and CIGS types of PV) or amorphous (a-Si:H based PV). That type of ’imperfect’ morphology is
Fig. 4 In thin film devices, drift rather than diffusion can determine the kinetics of photogenerated carriers. They readily arrive at the corresponding electrodes avoiding interactions with recombination centers. Having reached the electrodes they can move to the entrances of rare but highly efficient recombination channels shorting between the electrodes and playing the role of recombination highways.
inevitable with inexpensive fast deposition techniques not giving enough time for satisfactory crystallization. The polycrystalline films consist of tightly packed individual grains, each having more or less perfect crystalline order inside. They are formed during deposition and subsequent treatments where random atomic configurations are ordered within local regions dictating grain sizes. In the course of such crystallization, material pushes away all ’foreign’ atoms and structural units towards grain boundaries (GB). (Similar to apples in a freezer where water crystallization breaks and pushes away organic tissues.) As a result, GB material is chemically different from that of interior. These chemical differences entail built-in electric fields that will spatially separate electrons and holes between the grain interior and GB (see Fig. 5) creating local electric field and potential variations. One other general consequence of independently forming grains is that having grown enough they compete for space and exert pressure on each other upon physical contact. The resulted compressive stress can translate into electric potential when the material structure is piezoactive, such as with CdS, ZnO and some others, as explained more in detail next (Sec. XVIII).
As illustrated in Fig. 5, spatial separation of charge carriers at GB can significantly decrease the probability of their recombination compared to crystalline materials where electrons and holes are distributed uniformly. That creates a possibility for polycrystalline thin film PV to potentially outperform their crystalline counterparts. On the other hand, high concentration of impurities and defects in the grain boundary interfaces enhances the recombination processes, which can make grain boundaries detrimental and polycrystalline material PV devices perform worse
Fig. 5 Role of grain boundaries in noncrystalline thin film PV. Left: Sketch of the electron hole pair creation by a photon of energy exceeding the forbidden gap G. E c and E v are conduction and valence band edges, EF is the Fermi energy. Short horizontal lines represent defect states located at the grain boundary. Note that the positive (attractive to electrons) GB charge is assumed arbitrarily. For the case of negative GB charge, the potential well (barrier) for electrons (holes) will turn into a barrier (well). Right: the GB barrier requires charge carrier activation [with probability proportional to exp(–VB/kT)] which suppresses recombination (presented by vertical arrows).
than crystalline PV. The latter feature was evidenced in some polycrystalline Si structures. Furthermore, it will be shown below (Sec. XVI) that the very nature of recombination processes in non-crystalline materials can be significantly different from that dominating crystalline PV and affecting both the GB and main junction processes. Overall, the role of grain boundaries remains debatable and material/recipe specific with experiments exhibiting either beneficial or detrimental GB effects. It is possible that some of GBs in thin films form, with certain probability, much more effective recombination channels than others. Those channels can play the role of recombination highways depicted in Fig. 4.
A physically nontrivial and practically important property of thin film PV (further discussed in Sec. V) is that, under certain conditions, they exhibit thermal runaway instabilities favored by low heat transfer parameters as well as low sheet resistances along with significant currents and voltages. These instabilities result in local (~ 1 mm) spots of elevated temperature that can degrade PV performance and trigger nonuniform structure damage. We will discuss later their underlying physics and factors that can be tweaked to mitigate the latter detrimental effects by proper device engineering.
A more specific structure of the two major brands, CdTe and CIGS based thin film PV is presented in Fig. 6. It is understood that in reality the glass is facing up in CdTe cells. The CdTe and CIGS layers are absorbers responsible for the light conversion into photogenerated electrons and holes. The question of their doping has been debatable for decades, with
Fig. 6 A cross-sectional view of a superstrate (glass sheet up) CdTe based and substrate (glass sheet down) CIGS based thin film solar cell (not to scale). The CdTe cell front contact is formed by the transparent conductive oxide (TCO). The typical layer thicknesses are 2-4 µm for CdTe and CIGS, 0.1-0.2 µm for CdS, 0.5 µm for TCO and buffer layer, 0.1-0.2 µm for back metal (Mo for CIGS), 1-3 mm for glass. The drawing does not show the polycrystalline structure of CdTe, CIGS, and CdS layers. Red arrows represent incident sunlight.
extreme views ranging from that these materials cannot be effectively doped to that of beneficial or detrimental role of certain impurities. Many of such mutually exclusive points have found experimental confirmations with particular device recipes.
Furthermore, the role of CdS layer often found with CdTe and CIGS remained mysterious long after it was empirically found to be extremely important and practically irreplaceable in spite of its lack of contribution to photocurrent. We shall see in what follows (Sec. XVIII) that its piezoelectric properties may be a key leading to piezo-photovoltaic coupling beneficial for PV operations.
Finally, the back contact layer renders yet another set of puzzles. While the Mo back contact is typical of CIGS PV, there are several successful recipes of back contact in CdTe based PV. It was found indeed that the back contact has profoundly strong effect on device operations in spite of the fact that it is not photoactive (light does not penetrate there). The so-called back barrier due to the junction field between the semiconductor and back metal turns out to be a culprit. More in detail, the physics of back contact functionality will be discussed in Sec. VB. The front contact layer, such as TCO in CdTe based PV or ZnO in CIGS, has its nontrivial properties as well, as also discussed in the subsequent chapters.
Last but not the least is the issue of thin film PV degradation. Light, elevated temperatures, and humidity can all play a detrimental role in
degradation processes. Some PV companies went under being unable to solve these problems. It often happened that the most efficient PV devices exhibited the highest degradation rates calling upon tradeoffs between efficiency and stability. It should be understood that PV degradation is inevitable with any PV in full compliance with the general Le ChatelierBrown principle stating that when a settled system is disturbed, it will adjust to diminish the change that has been made to it, or, roughly stated, any change in status quo prompts an opposing reaction in the responding system [18]. With respect to PV, that principle predicts that PV structures will evolve in such a way as to decrease the light induced electric currents; hence, degradation. While all PVs degrade, the thin film ones are especially vulnerable due to their thinness allowing formation of conductive transverse channels (shunts). In addition, thin film structures accumulate extremely high electrostatic energy density (similar to narrow gap (~ 1 µm) electric capacitors) capable of discharging with huge power dissipation transforming material structure towards electric shorts that minimize the electric energy. A more in detail discussion of these issues will be given in Sec. XXVII B.
References
1. M. A. Green, Solar Cells: Operating Principles, Technology and System Applications, Prentice Hall, Englewood Cliffs, N.J., 1982.
2. A. L. Fahrenbruch, R. H. Bube, Fundamentals of Solar Cells, Academic Press (1983).
3. J. L. Gray, The physics of Solar Cells, in Handbook of Photovoltaic Science and Engineering, p. 61, Edited by A. Lique and S. Heggedus, Wiley (2002).
4. J. Nelson, The Physics of Solar Cells, Imperial College Press (2003).
5. P. Wurfel, Physics of Solar Cells, Wiley (2005).
6. T. Dittrich, Material Aspects of Solar Cells, Imperial College Press (2015).
7. T. J. Coutts, J. S. Ward, D. L. Young, K. A. Emery, T. A. Gessert, and R. Noufi, Critical Issues in the Design of Polycrystalline, Thin-film Tandem Solar Cells, Prog. Photovolt: Res. Appl. 11, 359 (2003).
8. Thin Film Solar Cells Fabrication, Characterization, and Applications, Edited by J. Poortmans and V. Arkhipov, Wiley (2007).
9. S. R. Kodigala, Cu(In1xGaxSe2 Based Thin Film Solar Cells Elsevier, Amsterdam New York, (2010).
10. R. Scheer and H.-W. Schock, Chalcogenide Photovoltaics, Wiley (2011).
11. Advanced Characterization Techniques for Thin Film Solar Cells, Edited by D. Abou-Ras, T. Kirchartz, and U. Rau, Wiley (2011).
12. W. Shockley and H. J. Queisser, Detailed Balance Limit of Efficiency of p-n Junction Solar Cells, J. Appl. Phys., 32, 510 (1961).
13. A. G. Milns, Deep impurities in semiconductors, Wiley Interscience (1973).
14. D. K. Schroder, Carrier Lifetimes in Silicon, IEEE Trans. Electron Devices, 44, 160 (1997).
15. S. Parola, et al, Study of photoluminescence decay by time-correlated single photon counting for the determination of the minority-carrier lifetime in silicon, 4th International Conference on Silicon Photovoltaics, SiliconPV 2014, Energy Procedia 55, 121 (2014).
16. S. Khatavkar et al, Measurement of Relaxation Time of Excess Carriers in Siand CIGS Solar Cells by Modulated Electroluminescence, Technique, Phys. Stat. Solidi. A, 215, 1700267 (2018).
17. V. N. Abakumov, V. I. Perel, I. N. Yassievich, Nonradiative Recombination in Semiconductors (Modern Problems in Condensed Matter Sciences), NorthHolland (1991).
18. Wikipedia paper https://en.wikipedia.org/wiki/Le_Chatelier%27s_principle