Photoionization and photo-induced processes in mass spectrometry: fundamentals and applications ralf by Education Libraries

Photoionization and Photo-Induced Processes in Mass Spectrometry: Fundamentals and Applications Ralf Zimmermann

Visit to download the full and correct content document: https://ebookmass.com/product/photoionization-and-photo-induced-processes-in-mas s-spectrometry-fundamentals-and-applications-ralf-zimmermann/

More products digital (pdf, epub, mobi) instant download maybe you interests ...

Fundamentals and Applications of Fourier Transform Mass Spectrometry 1st Edition Philippe Schmitt-Kopplin

https://ebookmass.com/product/fundamentals-and-applications-offourier-transform-mass-spectrometry-1st-edition-philippe-schmittkopplin/

Ambient Ionization Mass Spectrometry in Life Sciences: Principles and Applications Kei Zaitsu (Editor)

https://ebookmass.com/product/ambient-ionization-massspectrometry-in-life-sciences-principles-and-applications-keizaitsu-editor/

Heat and mass transfer : fundamentals and applications 6th Edition Yunus A Çengel

https://ebookmass.com/product/heat-and-mass-transferfundamentals-and-applications-6th-edition-yunus-a-cengel/

Applications in High Resolution Mass Spectrometry: Food Safety and Pesticide Residue Analysis 1st Edition Romero-Gonz Lez

https://ebookmass.com/product/applications-in-high-resolutionmass-spectrometry-food-safety-and-pesticide-residue-analysis-1stedition-romero-gonz-lez/

Heat And Mass Transfer: Fundamentals And Applications

5th Edition – Ebook PDF Version

https://ebookmass.com/product/heat-and-mass-transferfundamentals-and-applications-5th-edition-ebook-pdf-version/

Nanofluids for Heat and Mass Transfer Fundamentals, Sustainable Manufacturing and Applications Bharat Bhanvase

https://ebookmass.com/product/nanofluids-for-heat-and-masstransfer-fundamentals-sustainable-manufacturing-and-applicationsbharat-bhanvase/

High-Throughput Mass Spectrometry in Drug Discovery 1. Edition Chang Liu

https://ebookmass.com/product/high-throughput-mass-spectrometryin-drug-discovery-1-edition-chang-liu/

Energy Sources. Fundamentals of Chemical Conversion Processes and Applications 1st Edition Balasubramanian Viswanathan

https://ebookmass.com/product/energy-sources-fundamentals-ofchemical-conversion-processes-and-applications-1st-editionbalasubramanian-viswanathan/

Introduction to Spatial Mapping of Biomolecules by Imaging Mass Spectrometry Bindesh Shrestha

https://ebookmass.com/product/introduction-to-spatial-mapping-ofbiomolecules-by-imaging-mass-spectrometry-bindesh-shrestha/

PhotoionizationandPhoto-InducedProcessesinMassSpectrometry

PhotoionizationandPhoto-Induced ProcessesinMassSpectrometry

FundamentalsandApplications

Editedby

RalfZimmermann LukeHanley

Editors

RalfZimmermann

HelmholtzZentrumMünchen InstitutfürÖkologischeChemie IngolstädterLandstr.1 85764Oberschleißheim Germany

LukeHanley UniversityofIllinois DepartmentofChemistry UnitedStates

CoverImages: CourtesyofJonathan Aldrich,TheUniversityofIllinoisat Chicago

Allbookspublishedby Wiley-VCH arecarefullyproduced.Nevertheless, authors,editors,andpublisherdonot warranttheinformationcontainedin thesebooks,includingthisbook,to befreeoferrors.Readersareadvised tokeepinmindthatstatements,data, illustrations,proceduraldetailsorother itemsmayinadvertentlybeinaccurate.

LibraryofCongressCardNo.: appliedfor

BritishLibraryCataloguing-in-Publication Data

Acataloguerecordforthisbookis availablefromtheBritishLibrary.

Bibliographicinformationpublishedby theDeutscheNationalbibliothek TheDeutscheNationalbibliotheklists thispublicationintheDeutsche Nationalbibliograﬁe;detailed bibliographicdataareavailableonthe Internetat <http://dnb.d-nb.de>.

Allrightsreserved(includingthoseof translationintootherlanguages).No partofthisbookmaybereproducedin anyform–byphotoprinting, microﬁlm,oranyothermeans–nor transmittedortranslatedintoa machinelanguagewithoutwritten permissionfromthepublishers. Registerednames,trademarks,etc.used inthisbook,evenwhennotspeciﬁcally markedassuch,arenottobe consideredunprotectedbylaw.

PrintISBN: 978-3-527-33510-7

ePDFISBN: 978-3-527-68223-2

ePubISBN: 978-3-527-68222-5

oBookISBN: 978-3-527-68220-1

CoverDesign: Wiley Typesetting SPiGlobal,Chennai,India PrintingandBinding

Printedonacid-freepaper 10987654321

Preface xi

1FundamentalsandMechanismsofVacuumPhotoionization 1 JohannesPassig,RalfZimmermann,andThomasFennel

1.1Preface 1

1.2Light 2

1.3Photoabsorption 5

1.3.1TransitionsinFirstOrderPerturbationTheory 5

1.3.2PerturbationTheory 6

1.3.3Absorption 7

1.3.4DipoleApproximation 9

1.3.5SelectionRules 11

1.3.6ElectronicLineWidthandLifetime 11

1.3.7ElectronicTransitionsofMolecules 13

1.3.8Single-photonIonization(SPI) 15 References 20

2FundamentalsandMechanismsofResonance-Enhanced MultiphotonIonization(REMPI)inVacuumanditsApplication inMolecularSpectroscopy 23 UlrichBoeslandRalfZimmermann

2.1IntroductoryRemarks 23

2.2BeginningsofREMPI 25

2.3PrincipleofREMPI:RateEquationsandQuantiﬁcationofDetection Eﬃciency 29

2.3.1RateEquations 29

2.3.2QuantiﬁcationoftheREMPIDetectionEﬃciency 31

2.3.3SpecialSituationsandProblemsinREMPIProcessesand Countermeasures 33

2.3.3.1Situation(A):Tooenergeticionizationthreshold 34

2.3.3.2Situation(B):Tooenergeticintermediatestate 35

2.3.3.3Situation(C):ToosmallFC-factors 36

2.3.3.4Situation(D):Toofastrelaxationofintermediatestate 37 2.4REMPIandDissociation 40

2.5ApplicationofREMPIforOpticalSpectroscopy 45

2.5.1EﬀusiveGasBeamMoleculesatRoomorElevatedTemperature: REMPISpectrawithMediumOpticalSelectivity 45

2.5.2SupersonicGasBeamsforColdMolecules:REMPISpectrawithHigh OpticalSelectivityforDiscriminationofStructuralIsomersand SpectroscopicStudiesontheTransitionState 48

2.5.2.1REMPISpectroscopyofJet-CooledBiphenylene 50

2.5.2.2REMPISpectroscopyofJet-CooledDibenzo-p-dioxinandIts Derivativesaswellasof[2,2]-Paracyclophane 61

2.5.3SupersonicGasBeamsforColdMolecules:REMPISpectrawithHigh OpticalSelectivityforDiscriminationofIsotopomers 67

2.5.4ChiralMolecules:DiscriminationofEnantiomersbyEnantioselective REMPISpectroscopy 69

2.5.5AdvancedPhotoelectronSpectroscopyBasedonREMPI:ThePES, TPES,ZEKE,MATI,Anion-PES,andAnion-ZEKEApproaches 72 References 79

3AnalyticalApplicationofSingle-PhotonIonizationMass Spectrometry(SPI-MS) 89

ThorstenStreibel,HendrykCzech,andRalfZimmermann

3.1VUVLightSources 89

3.2Lamp-BasedVUVLightSources 90

3.3Laser-BasedVUVLightSources 92

3.4MassSpectrometrywithLamporLaser-BasedVUVLight Sources 94

3.5On-lineAnalysisofComplexMixturesbySingle-PhotonIonization (SPI)MassSpectrometry 95

3.6SPI-MSinHyphenatedApplications 107

3.7AmbientMonitoring 117

3.8CommercialSolutions 118 References 119

4AnalyticalApplicationofResonance-EnhancedMultiphoton IonizationMassSpectrometry(REMPI-MS) 125

ThorstenStreibel,UlrichBoesl,andRalfZimmermann

4.1InvestigationofModelFlames 129

4.2ApplicationstoInternalCombustionEngines 130

4.3MonitoringCombustionProcessEmissionsinanIndustrial Environment 135

4.4FurtherApplicationsofREMPIMassSpectrometry 138

4.5REMPI-MSinHyphenatedAnalyticalSystems 142

4.6CommercialREMPI-MSSolutionsandApplications 150 References 152

5ProbingChemistryatVacuumUltravioletSynchrotronLight Sources 159

KevinR.WilsonandFeiQi

5.1Introduction 159

5.2CombustionChemistry 162

5.2.1PyrolysisinFlowReactor 163

5.2.2Jet-StirredReactorOxidation 166

5.2.3PremixedFlames 167

5.2.3.1Low-PressureLaminarPremixedFlame 167

5.2.3.2AtmosphericPressureLaminarPremixedFlame 171

5.2.4CoﬂowDiﬀusionFlame 173

5.2.5Biomass/CoalPyrolysis 174

5.3Isomer-ResolvedStudiesofElementaryChemicalReactions 176

5.3.1MultiplexedChemicalKineticsPhotoionizationMass Spectrometer 177

5.3.2ShockTubeKinetics 179

5.3.3PyrolysisReactors 180

5.3.3.1BimolecularKinetics 181

5.3.3.2UnimolecularKinetics 181

5.3.4Low-TemperatureElementaryReactionsinaPulsedLaval Nozzle 182

5.4Summary 186

5.4.1AtmosphericAerosolChemistry 188

5.4.1.1AerosolMassSpectrometry 189

5.4.1.2GasChromatographyandSVUVPhotoionizationMass Spectrometry 195

5.4.2FutureOutlook 202 Acknowledgments 203 References 203

6ResonanceIonizationMassSpectrometry(RIMS): FundamentalsandApplicationsIncludingSecondaryNeutral MassSpectrometry 215 MichaelSavinaandRetoTrappitsch

6.1Introduction 215

6.2ResonanceIonizationFundamentals 217

6.2.1LaserSpectroscopy 217

6.2.2SelectionRules 220

6.2.3Odd–EvenEﬀect 222

6.3ReductiontoPractice 224

6.3.1LaserSelection 224

6.3.2MassSpectrometerSelection 225

6.3.3LaserOverlap 229

6.4Applications 230

6.4.1UsefulYieldandAbundanceSensitivity 231

6.4.2StardustGrains 234

6.4.3MultielementAnalysis 236

6.4.4ElectronicProcessesDuringVaporization 238

6.5Resources 240 References 241

7UltrashortPulsePhotoionizationforFemtosecondLaserMass Spectrometry 245

CorneliusL.Pieterse,JasonM.Gross,andLukeHanley

7.1Introduction 245

7.2MechanismsofUltrashortPulsePhotoionization 246

7.3StudiesofAminoAcids,Dipeptides,andC60 LeadingtoAdvancedSFI Models 249

7.4VolumetricIntensityDependenceandMultiplyChargedIons 251

7.5DirectandGasChromatography-CoupledAnalysisofExplosives 253

7.6GasChromatography-CoupledAnalysisofPolyaromatic Hydrocarbons,Pesticides,andFragrances 255

7.7LaserSecondaryNeutralMassSpectrometry 256

7.8Conclusions 259 Acknowledgments 260 DisclosureStatement 260 References 261

8PhotoionizationatElevatedorAtmosphericPressure: ApplicationsofAPPIandLPPI 267 TiinaJ.KauppilaandJackSyage

8.1Introduction 267

8.2AtmosphericPressurePhotoionization 267

8.2.1AtmosphericPressurePhotoionizationIonSource 267

8.2.2GeneralPrinciplesofAtmosphericPressurePhotoionization 268

8.2.2.1IonizationMechanisminPositiveIonAPPI 268

8.2.2.2EﬀectoftheDopant 270

8.2.2.3IonizationMechanisminNegativeIonAPPI 271

8.2.3APPIinLiquidChromatographyMassSpectrometry 272

8.2.4APPIinGasChromatographyMassSpectrometry 274

8.2.5APPIAsanInterfaceforCapillaryElectrophoresisMass Spectrometry 277

8.2.6APPIinMultimodeIonSources 278

8.2.7AmbientMassSpectrometryUtilizingPhotoionization 278

8.3Low-PressurePhotoionization(LPPI) 279

8.4ApplicationsofAPPIandLPPI 281

8.4.1Drugs,Pharmaceuticals,andMetabolites 281

8.4.2Steroids 288

8.4.3OtherEndogenicCompounds 288

8.4.4PlantResearch 289

8.4.5EnvironmentalMonitoring 289

8.4.6OilAnalysis 291

8.4.7FoodAnalysis 291

8.5Conclusions 292 Acknowledgments 292 References 292

9FundamentalsofLaserDesorptionIonization 305 FabrizioDonnarumma,KermitK.Murray,andLukeHanley

9.1Introduction 305

9.2ExperimentalandComputationalParametersandObservables 306

9.3GeneralMechanisticConsiderations 307

9.4Laser-InducedThermalorAcousticDesorptionofNeutralsfrom MetalSurfaces 307

9.5MolecularResonantlyEnhancedDesorption:UV-MALDIand IR-LA 309

9.5.1MALDIwithUVLasers 310

9.5.2NanosecondtoPicosecondIRLaserAblation 313

9.6NanophotonicDesorption 314

9.7FemtosecondLaserAblation 315

9.8InternalEnergyTransferredbyLDIandSupersonicCooling 317

9.9Conclusions 318 Acknowledgments 319 DisclosureStatement 319 References 319

10ApplicationsofLaserDesorptionIonizationandLaser Desorption/AblationwithPostionization 327 YeniP.Yung,FabrizioDonnarumma,KermitK.Murray,andLukeHanley

10.1NatureofSamplesandInformationtobeGainedfromLaser DesorptionandLaserAblationMassSpectrometry 327

10.2LaserAblationandLaserDesorptionIonizationMSforElemental Analysis 328

10.3NonimagingMALDI-MSforMolecularAnalysis 329

10.3.1QualitativeandQuantitativePerformanceforDiﬀerentTypesof Analytes 329

10.3.2Peptides,Proteins,Lipids,andSugars 330

10.3.3DNAandRNA 330

10.3.4Polymers 331

10.4MALDI-MSImagingforMolecularAnalyses 332

10.5ExampleofStandardMALDI-MSvs.ImagingMode: Pseudomonas aeruginosa333

10.6MALDIAlternatives:MatrixFree,Ambient,NanostructureInduced, andHighEnergy 335

10.7MolecularLD/LA-MSBeyondNanosecondUVLasers 336

10.8Laser,Electrospray,andOtherPostionizationofPlumesFormedby LD/LA 337

x Contents

10.8.1LDPI-MS:LaserDesorptionPostionizationofNeutralsin Vacuum 337

10.8.2PostionizationCoupledtoLD/LAatElevatedPressures 340

10.9LaserAblationSamplingforSolidorLiquidCollection 341

10.9.1LaserAblationSamplingwithOnlineMSAnalysis 342

10.9.2LaserAblationSamplingwithOﬀ-lineAnalysis 343

10.10Conclusions 344

Acknowledgments 345

DisclosureStatement 345 References 345

11LaserIonizationinSingle-ParticleMassSpectrometry 359 JohannesPassigandRalfZimmermann

11.1RelevanceofAtmosphericAerosolsforClimateandHealth–The Single-particlePerspective 359

11.2AnalysisofIndividualParticlesbyLaserIonizationMS–Historical DevelopmentandBasicPrinciple 362

11.3IonizationinSingle-ParticleMassSpectrometry:Laser Desorption/Ionization(LDI) 365

11.3.1Single-ParticleLDI–ThePhysicalFramework 366

11.3.2LaserLightSourcesforLDI 371

11.3.3ChemicalQuantiﬁcationApproachesforLDI 372

11.4IonizationinSPMS:LaserPhotoionizationofPreviouslyDesorbed Species 373

11.5InstrumentalRealizations 381

11.5.1MassAnalyzers 381

11.5.2AerosolInlet 383

11.5.3ParticleSizing 384

11.6DataEvaluation 386

11.7Applications 387

11.7.1AmbientAerosolsinUrbanandDenselyPopulatedAreas 387

11.7.2AmbientAerosolsinRuralandMarineEnvironments 388

11.7.3Aircraft-BasedStudies 389

11.7.4InSituCharacterizationofCloudandIceCondensationNuclei 389

11.7.5FocusonOrganicCompounds 390

11.7.6Bioaerosols 392

11.7.7CombustionAerosols 392

11.8CommercialLaserIonizationSingle-ParticleMassSpectrometry Systems 393 References 394

Index 413

Preface

Thegoalofthisbookistoexplainthefundamentalsofphotoionization(PI)and theassociatedapplicationsofPIthatareplayinganincreasinglyimportantrole inmassspectrometry(MS).Thetargetaudienceofthisbookincludespracticingscientists,includingPhDandMScstudents,whoseprimaryinterestisinthe applicationofPItoelementalormolecularanalysisbymassspectrometry.An overlysimplisticanalysisprovidesseveralmotivationsfortheuseofPIinmass spectrometry:

1.Enhanceionyieldsforspeciﬁcimportantcompoundsofsubstanceclasses whereotherionizationstrategieshaveproveninsuﬃcient,

2.Selectivelyionizeindividualmolecularstructuresorclassesofmoleculesfrom mixtures,

3.Formionsfromneutralswithreducedorcontrolleddegreeoffragmentation, and

4.Inducedesorptionorablationofsolidsforsampling.

Photoionizationcomesindiﬀerentversionsandtechnologicalrealizations, makingitsomewhatmorecomplicatedandthuslesspopularthanstandard ionizationmethodsinmassspectrometrysuchaselectrosprayionizationand electronionization.Nevertheless,onegoalofthisbookistodemonstratehow theseandothermotivationsdrivetheuseofPIinMS-basedanalyses.Theeditors andauthorshopethatthereaderswillusethisworkasaseriesofbuildingblocks forfutureadvancesinthispromisingarea.

Actually,PIwascentraltotheearlydevelopmentofmassspectrometryand singlephotonionization(SPI)remainsperhapsthebestmethodforintroducing awell-definedamountofinternalenergyintoamolecularion.Earlyworkin SPIusedvacuumultraviolet(VUV)gasdischargelamps.However,theadvent oflasersandtheassociatednonlinearopticalmethodsmademultiphoton ionization(MPI)possible,dramaticallyexpandingPIasafundamentalstrategy toprobemolecularstructure.Thecontinuingimprovementoflasertechnology hasalsocreatedongoingopportunitiesforMS-basedapplicationsofPI.For example,MPIviatheexcimerlaser-pumpeddyelaserwasdeployedinmany earlyfundamentalstudies,butwascostly,difficulttouse,andrelativelyunreliable.However,thedevelopmentofsmallerandrugged,field-deployablelaser sources,suchascompactexcimerlasers,solid-statelasersasNd:YAGlaserswith integratedharmonicgeneration,andtunablesolid-statelaserssuchassealed,

Nd:YAG-pumpedopticalparametricoscillators(OPOs)orTi:sapphirecavities renderedMPIsuﬃcientlyrobustformorewidespreadMSapplications. Thisinterplaybetweenfundamentalmethodsandinstrumentalconsiderations hasdriventhedevelopmentofanalyticalapplicationsofPI,soattentionispaid heretobothconsiderations.Photodissociationisonlydiscussedherewhenit occursinconjunctionwithPI,suchasviatheformationoffragmentionsfrom neutralprecursorsduringMPIorSPI.Thus,theburgeoninguseofphotodissociationoftheprecursorormolecularionstoformfragmentionsforstructural elucidationoftheformerisnotdiscussedhere.Thefundamentalsandmechanismsoflowpressure,gas-phasemolecularPIformassspectrometryiscovered inChapters1,2,5,and7,whilemolecularatmosphericpressurePIisatopicin Chapter8.Applicationsandexperimentalmethodsoflow-pressure,gas-phase photoionizationmassspectrometry(PIMS)arepresentedinChapters3,4,and7. ElementalanalysisbyPIiscoveredexclusivelyinChapter5.Processesandapplicationsthatincludealaserdesorption(LD)ordirectlaserdesorption/ionization (LDI)ofanalytesfromthecondensedphasearecoveredinChapters9and10, whileChapter11focusesonthedirectanalysisofindividualaerosolparticles usingLDI,LD,andPI.

Inthefollowing,thecontentofthebookisbrieﬂyhighlightedchapterwise.

Theﬁrstchapterentitled FUNDAMENTALSandMECHANISMSofVACUUM PHOTOIONIZATION ,isservingasanintroductiontomechanisticissuescommontoPIofmolecules,atoms,andclustersundervacuum.Itprovidesafundamentaldescriptionoflightandtheinteractionoflightandmatterintheformof photoabsorptiononaquantummechanicallevel.Thisincludesanexcursionin perturbationtheoryandthedipoleapproximationandleadstoanelucidationof thephotonabsorptionselectionrules.Finally,theSPIprocess,asanabsorption inacontinuum,nonboundstate,isdiscussedandthemostimportantparameters forSPI,theSPIcrosssectionsandionizationenergies,arededucted.

FundamentalaspectsofMPIofmoleculesintheabsenceofgas-phasecollisionsarecoveredinthefollowingchapter,entitled FUNDAMENTALSand MECHANISMSofRESONANCE-ENHANCEDMULTIPHOTONIONIZATION(REMPI)inVACUUMandAPPLICATIONofREMPIforMOLECULAR SPECTROSCOPY(Chapter2).Here,thetheoreticalconsiderationofphotoionizationprocessesisextendedtoMPIprocessesofmolecularspeciesand MPI-basedspectroscopy,whilemultiphotonionizationofatomsiscovered inChapter6.DifferentMPIandREMPIprocessesarepresentedandarate equationapproachisusedtodeducttheinfluenceofmolecularphysicalpropertiesonionizationefficiency.SpecialREMPIschemesarediscussed,whichcan bypassunfavorablephotophysicalproperties.Inthefollowing,MPI-induced fragmentationanddissociationprocessesarediscussed.Theapplicationof REMPIformolecularspectroscopywithandwithoutsupersonicjetcoolingis demonstratedinanexemplarymannerviaadetaileddiscussionoftheREMPI wavelengthspectrumofsupersonicjet-cooledbiphenyleneandsomeother interestingaromaticmolecules.REMPIwavelengthspectroscopy,inparticular withsupersonicjetcooling,revealstheselectivityoftheREMPIprocessthat connectshigh-resolutionultraviolet(UV)spectroscopytomassspectrometry. Theselectiveionizationofisomericandisobariccompounds,however,canbe

Preface xiii extendedtothediﬀerentiationofisotopomersand–byusingaspecialREMPI techniquewithcircularpolarizedlaserlight–evenofenantiomers.Finally,in thischapter,REMPI-basedphotoelectronspectroscopic(PS)techniquessuchas zerokineticenergyphotoelectronspectroscopic(ZEKE-PS)areintroduced.The explanationofthefundamentalaspectsofSPIandREMPIleadstotheanalytical applicationofthesetwoPIapproaches.

InthebeginningofChapter3,whichisentitled“ANALYTICALAPPLICATIONSofSINGLE-PHOTONIONIZATIONMASSSPECTROMETRY ,”abrief introductionintocommonVUV–lightsources,isgiven.Thesecanbedistinguishedasincoherentlightsources(“lamp”-basedtechnologies)orcoherent lightsources(lasers).Also,abriefintroductiontothegenerationofsynchrotron lightintheVUVrangeiselaborated(forapplicationsofsynchrotron-based SPI,seeChapter5).ThegeneralsetupofSPImassspectrometrysystemswith laser-andlamp-basedsourcesisintroduced.DependingontheusedVUV wavelengths,SPIcanbeaverysoftionizationmethod,enablingthedetection ofthemolecularmassfingerprintofcomplexmixtures.ThisrendersSPI-MS toanidealapproachfordirectrealtimemonitoringofcomplexgasandvapor mixtures.Differentapplicationsforonlinemonitoringofcombustionandpyrolysisprocessesareintroduced,includingonlinemonitoringofgasphasesfrom industrialprocesses,suchasthecoffee-roastingand/orthebiomasspyrolysis process.Hyphenatedinstrumentalanalyticalconcepts,e.g.gaschromatography (GC)orthermalanalysis(TA)coupledtoSPImassspectrometry,arepresented andtypicalresultsareshown.

Chapter4, “ANALYTICALAPPLICATIONofRESONANCE-ENHANCED MULTIPHOTONIONIZATIONMASSSPECTROMETRY(REMPI-MS), ” gives, inasimilarwayasChapter3forSPI,anoverviewofanalyticalapplicationsof REMPImassspectrometry.Thepreferentialdetectionofaromaticanalytesby theREMPIprocesswithcommonlaserisemphasizedinChapter3.Anoverview ontypicalfixed-frequencylaserlines(excimerlasersorfrequency-multiplied, solid-statelasers)isprovidedalongwithtypicalwavelengthrangesoftunable lasersystems.Inthefollowing,severalexemplaryanalyticalconceptsand applicationsusingtunableandfixed-frequencylasersarepresented.Thetunable lasersourcescanbeusedtofocusonspecificanalytes,whichworkparticularly wellwithsupersonicjetexpansioninletsystems.Formanyapplications,however,fixed-frequencywavelengthlaserandeffusive,heatedgasinletscanbe appliedforausefulandoftenverysensitive“overview”MS-profilingofmany aromaticcompounds.Exemplaryprocessmonitoringapplicationscomprise detectionofcombustionby-productsinfluegasesofincinerationplantsor flavorandroastdegree,indicatingcompoundsincoffee-roastingoff-gas. Hyphenatedinstrumentsconnectinggaschromatographyorathermo-optical carbonanalyzer(foraerosolloadedfilters)toREMPI-MSdevicesarediscussed. AdirectinletofliquidsamplesintoREMPImassspectrometryispossiblevia amembraneinletoradirectliquidintroductionintotheionsource.Notethat SPIandREMPIprocessescanbeperformedinthesameMSsystem.Finally, REMPIunderatmosphericconditionsisdiscussed(atmosphericpressurelaser ionization–APLI;seealsoChapter8forSPI-basedatmosphericpressure-based ionization).

TheapplicationofsynchrotronVUVlightforSPI-MS-basedinvestigationof combustionandpyrolysisprocessesislaidoutinChapter5, “PROBINGCHEMISTRYATVACUUMULTRAVIOLETSYNCHROTRONLIGHTSOURCES.” Bydirectmolecularbeamsamplingfromflamesaswellasfromoxidationor pyrolysisreactors,moleculesfromthereactionzonecanbedirectlyintroduced inthemassspectrometerwithoutwallcontact.Thisenablestheanalysisofstable moleculesandintermediatesfromthereactionzones.Theflowreactorsand modelflameapparatusisoftencompactenoughtobebroughttosynchrotron lightsourcefacilitiesandcanbeusedforkineticinvestigations.Unlikeclassical VUVsources,thesynchrotronlightfromappropriatebeamlines(i.e.equipped withVUVmonochromators)exhibitawidetunability,highenergyresolution, andarelativelyhighphotonflux.Theidentificationofindividualcompounds fromisobaricmixturecomponentsispossiblebyphotoionizationefficiency (PIE)spectroscopy,i.e.therecordingoftheionyieldasafunctionoftheVUV wavelength.Chapter5alsopresents,anoverviewondifferentsynchrotron-based PIMSapparatusandanalyticalresultsforseveralreactorsandapplications.

REMPIofatomsiscommonlyreferredtoas“resonanceionizationmass spectrometry(RIMS).TheRIMStechnologyandapplicationsaredescribed intheChapter6, RESONANCEIONIZATIONMASSSPECTROMETRY (RIMS):FUNDAMENTALSANDAPPLICATIONSINCLUDINGSECONDARY NEUTRALMASSSPECTROMETRY .Unlikeinmolecules,atomictransitions areverynarrowandthusveryhighionizationeﬃcienciescanbeachieved.Laser spectroscopicprinciples,atomicselectionrules,andtheprinciplesetupofRIMS instrumentsarediscussed.Inmanycases,twoormoretunablelasersarerequired forhigh-resolutionRIMS.Thishigheﬀort,however,inmanycasesallowseven anisotope-selectiveionizationandthesuppressionofnearlyallinterferences. Applicationsarefocusingontheanalysesofultratracesofradioactiveelements intheenvironment(e.g.plutoniumfallout)orthecharacterizationofvery precioussamplessuchasstardustgrains.

MPIisoftenperformedwithnanosecondlaserpulses,butshorteningthe pulsesintothesubpicosecondregimecanfundamentallychangetheionization process,asdiscussedinChapter7,“ULTRASHORTPULSEPHOTOIONIZATIONforFEMTOSECONDLASERMASSSPECTROMETRY ”.Themechanisms ofultrashortpulseionization,inparticularnonresonantmultiphotonionization (NRMPI)andstrongﬁeldionization(SFI),areelucidated.Oneadvantageof ultrashortpulseionizationistoovercomeproblemsinREMPIionizationcaused bytheshortlifetimeofintermediatedstates(seealsoChapter2).Thus,for example,molecularionsofexplosives,suchastrinitrotoluene(TNT),which exhibitanunstableS1 stateduetofastpredissociation(NO-cleavagefromnitro groups),canbeobtainedbyafs-laserionizationprocess.Inadditiontogas-phase ionization,ultrashortpulseionizationisalsobeneﬁcialforpostionizationof neutralstoenhanceionsignalinsecondaryionmassspectrometry(SIMS)or laserdesorption(LD)-basedmassspectrometry.

Massspectrometryofsamplesatambientpressurehasbecomeamajorapplication,whichisservedbyatmosphericpressurephotoionization(APPI)usingVUV forinductionoftheionizationprocess.Chapter8,“PHOTOIONIZATIONat ELEVATEDorATMOSPHERICPRESSURE:APPLICATIONofAPPIandLPPI ,”

Preface xv isdevotedtosuchionizationmechanismsatelevatedpressuresandtheir experimentalimplementation.Furthermore,somecharacteristicapplicationsof APPIareshown.ThehigherpressuresduringAPPIallowabundantgas-phase ion-moleculeandmolecule-moleculecollisionsthatﬁnallyleadtoenergyand/or chargetransferintheAPPIprocess.Therefore,veryhighsensitivitiescanbe observedinAPPI.However,althoughsuchsecondarychemicalionization processesoftenaredominatingtheionizationprocess,APPIiscommonlyseen asaphotoionizationtechnology,althoughtheterm“photoinducedchemical ionization”maybetterdescribetheAPPIprocessinmanycases.Inadditionto SPI,theREMPIprocesscanalsobeusedtoinitiateionizationunderatmospheric conditions(atmosphericpressurelaserionization,APLI,seeChapter4).

LaserirradiationofcondensedphasemattercanalsoleadtoPIaswellas otherenergytransfereventsthatinturnleadtodesorptionand/orablation thatiswidelyusedforsampling.Althoughthisbookisfocusingonphotoionizationprocessesinvacuumorinthegasphase,laserdesorption-based processesandapplicationsinmassspectrometryarenotbeexcluded.Chapter9, “FUNDAMENTALSofLASERDESORPTION/IONIZATION ,”introducesthe mechanismsoflaserdesorption/ionization(LDI)andmatrix-assistedlaser desorption/ionization(MALDI),whileChapter10,“APPLICATIONSOFLASER DESORPTIONIONIZATIONANDLASERDESORPTION/ABLATIONWITH POSTIONIZATION ,”introducesthecorrespondingapplications.TheMALDI approachforionizationofbiopolymers(e.g.proteinsorlipids),polymers,and otherlargermoleculesisbroadlyapplied,andnumerousreviewsandbook chaptersandwholebookshavealreadycoveredthistopic.However,forcompleteness,theknowledgeontheMALDIprocessissummarizedinChapter9, althoughmorefocusisputonlesscommonstrategiessuchasfs-laserablation. InthelaserdesorptionapplicationsdiscussedinChapter10,inadditiontothe moleculardetectionalso,MALDIimagingapplicationsareconsideredanda focusisputontheapproachesusingpostionizationoflaserdesorbedneutrals.

Finally,Chapter11,“LASERIONIZATIONinSINGLE-PARTICLEMASS SPECTROMETRY ,”elaboratesonanonlinelasermassspectrometricsingle (aerosol)-particlemeasurementtechnique,whichisbasedeitherontheLDIoron alaserdesorption–laserpostionizationapproach.Afteranintroductiontothe historicaldevelopmentofsingle-particlelaserionizationMSsystems,theLDI processisdiscussedincontextoftheparticleanalysisbackground.Thisincludes theionizationmechanism,lasersources,andquantiﬁcationaspects.Afterthe discussionofapproachesbasedonthelaserpostionizationofmoleculesdesorbedfromindividualparticles,instrumentalrealizationsandapplicationsare presentedanddiscussed.

Finally,wehopethatthereaderswillenjoyandlearnfromourexpositionof photoionizationfundamentalsaswellastheversatilityofthephotoionization massspectrometrymethodologyforcuttingedgeapplications.

LukeHanley RalfZimmermann

UniversityofIllinois,Chicago,USA UniversityofRostock,Germany

FundamentalsandMechanismsofVacuumPhotoionization

JohannesPassig 1,2 ,RalfZimmermann 1,2 ,andThomasFennel 3

1 UniversitätRostock,InstitutfürChemie,AnalyticalChemistryandJointMassSpectrometryCentre(JMSC), Dr.-Lorenz-Weg2,D-18059Rostock,Germany

2 HelmholtzZentrumMünchen,GermanResearchCenterforEnvironmentalHealthGmbH,ResearchUnit ComprehensiveMolecularAnalytics(CMA)andJointMassSpectrometryCentre,GmunderStr.37,D-81379 München,Germany

3 InstituteofPhysics,UniversityofRostock,Albert-Einstein-Straße23,D-18059Rostock,Germany

1.1Preface

Withinthepastdecades,theprogressoflaser-basedlightsourceshaveopened variousnewresearchdirectionsintheareaoflight-matterinteractions.The ionizationoffreemoleculeswiththepurposeoftheirdetectionandmass-based identificationmayappearasaneasytaskinthiscontext.However,experience hasshownthatalreadythesimplestapproach,thefragment-freeionizationwith singlephotonsofsufficientenergy,remainstechnicallychallenging.Beyond practicalissuesandapplications,advancedphotoionizationtechniquesare animportantfieldofstudyinspectroscopyandfundamentalresearch.Asan example,resonance-enhancedmultiphotonionization(REMPI,seechapters 2and4ofthisbook)bridgesthegapbetweenmassspectrometry(MS)and molecularspectroscopy,offeringtwo-dimensionalselectivitybothinmassand instructure.Ingeneral,theabsorptionofasinglephotonbyamoleculecan leadtoitsionizationifthephotonenergy E = h�� = ℏ�� isequaltoorlargerthan theionizationpotential IP ,where h = 2��ℏ isthePlanckconstant, �� = c∕�� isthe photonfrequency; �� isitswavelength,and c isthespeedoflight.Itisworthto havealookonthetypicalenergy-andtimescalesthatconstitutetheframework ofphotoionizationprocessesasillustratedinFigure1.1.Electronmotionand electronictransitionsaremuchfasterthanatomicmotiononmolecularscales. Thisisthebasisforimportantapproximationsinatomandmolecularphysics andspectroscopy.Currenttabletoplasersystemsareavailablefrominfrared (IR)toultraviolet(UV),withultrashortpulsesthatallowtoanalyzemolecular processesontheirphysicalornaturaltimescale.Laserintensitiesfor(multi-) photoionizationMSspantherangefromtheonsetofREMPI(≈ 106 W∕cm2 )to thestrongfieldregime(> 1014 W∕cm2 )andbeyondforcomplexlasersources. Tuningthephotonenergyremainsrathercomplicatedbothforlamp-and laser-basedsources.However,thelatterimplicatesfurtherparametersasphase

Microscopic processes

Figure1.1 Typicalenergy-andtimescalesofprocessesrelatedtophotoionization.

orchirp,whicharelinkedtothecoherenceoflaserpulsesandarelikelyto increasetheselectivityinfutureapplications.

WhendealingwithphotoionizationMS,naturalquestionsabouttheunderlyingmechanismsofphotoabsorptionandphotoionizationariseatsomepoint. Abriefstandardanswermightbeasfollows:Assumetwoeigenstatesofamolecularsystemwithdifferentelectronicchargedistributions.Uponexcitationfrom thelowertotheupperstateandassumingasingleactiveelectron,thesystem correspondstoaquantumsuperpositionofthosetwostatesandtheelectronic chargeoscillateswithanamplitudethatreflectsthetransitiondipolemoment. Now,assumealightfieldactingonit.Thus,theelectron“feels”anoscillating electricfieldfromthelight.Ifthefrequencies,direction(polarization),andshape ofchargedistributionassociatedwithatransition,matchthelightfieldandthe moleculecoupleandtheelectronwillberesonantlydrivenintotheexcitedstate whilethelightwaveisdamped.Iftheexcitedstateisacontinuumstate,theelectronisejected.

Thisdescriptionprovidesabasic,phenomenologicalunderstanding,and somereadersconsidernowtoskipthefollowingpageswithcomplicated formulas.However,itisaproblematicsimpliﬁcation,mixingdiﬀerentconcepts andprinciples.Thefollowingsectionwillprovideanintroductorysurveyon photoabsorption,beingthephysicalbasicsofphotoionization.Thescopeisnot totreatthefullcomplexityofopticsandspectroscopybuttogiveanoutlineof somefundamentalprinciplesbeingusefulforitsconceptualunderstanding.

1.2Light

Thephysicsofclassicallightpropagation,optics,andelectromagnetismisbased ontheMaxwellequations,asetofpartialdifferentialequationsthatdescribethe behavioroftheelectricfield E(r, t ) andthemagneticfield B(r, t ) withrespectto charges

1.2Light 3

Thedivergence �� ⋅ F = �� Fx �� x + �� Fy �� y + �� Fz �� z ofavectorfield F producesascalarfield, givingthequantityof F’ssource(outwardflux)ateachpoint.Anexpandingvectorfield(e.g.heatedair)yieldspositivedivergencevalues,whereasacontracting one(e.g.cooledair)yieldsnegativevalues.Thecurl �� × F yieldsavectorfieldthat describestheinfinitesimalrotationof F ateachpoint,e.g.thecirculationdensity ofaflow.

Fundamentalpropertiesoflightcanbederivedfromthissetofequations.Later, wewillhavetoconstructaHamiltoniantodescribephotoabsorption.Because itrepresentsthesystemtotalenergyinquantummechanics,itwillbenatural tousepotentialsratherthanﬁelds.Inelectrostatics,theﬁeldisrelatedtothe electrostaticpotentialthrough

E(r)=−��Φ(r) (1.5)

However,foraﬁeldthatvariesintimeandinspace,theelectrodynamicpotential mustbeexpressedintermsofboththetime-dependentscalarpotential ��(r, t ) andthevectorpotential A(r, t ).AccordingtoEq.(1.5),theﬁelds E(r, t ) and B(r, t ) canbeexpressedas

(r, t )=−��(r, t )− �� t A(r, t

ThisdeﬁnitionautomaticallyfulﬁllsEqs.(1.2)and(1.3).Furthermore,it allowsatransformationofthepotentialsintoCoulombgauge,where A is divergence-free(�� ⋅ A = 0),whereasthephysicalobservables E(r, t ) and B(r, t ) remainunchanged(notshownhere).InCoulombgauge,thescalarpotentialis identicalwiththeCoulombpotential,yielding �� =−��∕��0 forEq.(1.1).Furthermore,ifchargesandcurrentsareabsent,onlyEq.(1.4)determines A (andthus E and B)inthefollowingformofawaveequation:

Solutionsarelinearlypolarizedplanewaves

withamplitude Ã,polarizationvector ��,imaginaryunit i,wavevector k ,angularfrequency ��,andphaseoﬀset �� .Severalprimarypropertiesoflightcannow bederived,suchasthedispersionrelation �� = ck wheninsertingthesolution intoEq.(1.8)ortheorthogonalityofwaveandpolarizationvectors k ⋅ �� = 0that directlyresultsfromthegaugecondition �� A = 0.Theelectricandmagnetic ﬁeldsfollowasplanewaves,mutuallyorthogonalalsowiththepropagationdirectionduetothevectorproduct k × �� E(r, t )= E �� sin(k ⋅ r ��t + �� ) (1.10) B(r, t )= ̃ E �� (k × ��) sin(k r ��t + �� ) (1.11)

Figure1.2 Illustrationofalinearly polarizedlightwaveasasolutionof Eq.(1.8)withmutuallyorthogonalelectric ﬁeld E,magneticﬁeld B,andpropagation aswellasenergytransportindirectionof thePoyntingvector S.Polarizationvector �� Eq.(1.16).

with ̃ E =−��Ã.Akeyparameterformanyapplicationsisthelightintensity, respectivelythephotondensity.Theyfollowfromthe(instantaneous)energy densityoftheelectromagneticﬁeld

Therapidoscillationscanbeaveragedas ⟨sin2 ⟩ = 1∕2,yieldingthemeanenergy thatcanalternativelybeexpressedintermsofthephotondensity n

EnergytransportbylightpropagationischaracterizedusingthePoyntingvector

Theabsolutevalueofitstime-average |⟨S⟩| isthecommonlyusedlightintensity (unitW∕m2 )

Notethattheintensity I isproportionaltothesquareoftheﬁeld(amplitude)

̃ E 2 .Thephotonﬂux �� (unitphotons∕(m2 s))canbeexpressedintermsofthe intensityandphotonenergyorviathephotondensity nph andthespeedof light c. �� = I ℏ�� = nph c

Next,thegeneralcrosssection �� isacoeﬃcientofproportionalitybetweenthe rate W ofaninducedtransitionandthephotonﬂux

withunitmegabarn (1Mb = 10 18 cm2 ).

1.3Photoabsorption

Inclassicalphysics,lightabsorptionisinterpretedasdampingofaperiodic electricfieldbydipolesoscillatingwithoppositephaseatthesamefrequency. Thisbasicpictureprovidesadescriptiveexplanationofopticalpropertiesand somefundamentalinteractions.However,adescriptionofthephotoionization ofatomsandmoleculesisonlypossibleinaquantummechanicalcontext. Uponlightabsorption,asystemundergoesatransitionfromaninitialstateto afinalstateofhigherenergywithenergydifference ℏ��.Becausethecharge distributionsofthestatesdiffer,theircoherentsuperpositionresultsinan oscillatingdipolethatcancoupletothelightfieldunderappropriateconditions.

1.3.1TransitionsinFirstOrderPerturbationTheory

Someessentialprinciplesneededforthequantummechanicaldescriptionarethe representationof(electronic)statesbywavefunctions Ψ(r, t ) andphysicalobservablesbytheircorrespondingoperators.

Inquantummechanics,thestate |�� ⟩ ofasystemcanbedescribedbyacomplex wavefunction �� (r, t ) incoordinatespacerepresentation.Aphysicalobservableis representedbyalinearoperator Ô actingonthestateproducinganewvector Ô|�� ⟩ = |�� ∗ ⟩.If |�� ⟩ isaneigenstateofanobservable,theequation Ô|�� ⟩

|�� ⟩ yieldstheassociatedeigenvalues a,correspondingtothevalueoftheobservable inthateigenstate.Eigenvalues a canbecontinuous(e.g.forthepositionoperator ̂ r)ordiscreteasfortheangularmomentumoperatorandthusbeexpressedby quantumnumbers.

Thetimeevolutionofaphysicalsystemisdescribedbysolutionsofthe time-dependentSchrödingerequation(TDSE)initsgeneralform

where i istheimaginaryunit, ℏ isthePlanckconstant,and ̂ H istheHamiltonian operatorrepresentingthesystem’stotalenergy.

Ananalyticalsolutionisonlypossibleforverysimplesystems,suchasthehydrogenatom.Alreadythepresenceofanexternalfieldorasecondelectronrenders closedandanalyticalsolutionsimpossible.Typically,severalapproximationsallow forthetreatmentofamolecularsystemwithminimumdeficiency,dependingon theframeworkofthescientificproblem.Commonapproachesforatom-lightinteractionsapplythesingleactiveelectronapproximation(SAE)thattreatsasingle interactingelectroninaneffectivepotential(e.g.Hartree-Fock)resemblingboth theatomiccoreandthe(mean)electron-electroninteractions.

1FundamentalsandMechanismsofVacuumPhotoionization

Ingeneral,photoionizationcanbeunderstoodasoneofseveralpossible secondaryprocessesuponphotoabsorption.Fortheweakfieldregime1 ,which appliesevenbeyondtypicalREMPIintensitiesofabout107 W∕cm2 ,the descriptionofphotoabsorptionisconvenientviaperturbationtheory.Itsbasic conceptisthepartitionoftheHamiltonian ̂ H intothecalculableHamiltonian ̂ H0 ofasimplifiedandknownsystem(whichmaybeartificial)andanadditionalHamiltonian ̂ H ′ representingtheweakdisturbancetothesystemthatis quantifiedusingapproximatemethods.

1.3.2PerturbationTheory

Forourbasicconsiderationsofphotoabsorptionviaelectronicstates,wedescribe anatombyasingleelectronofcharge q = e andmass me = m inaCoulomb potential VC =−Ze2 ∕4��0 r ,whichrepresentsastationarynucleus.Thevector potentialremainsclassical.ConsideringthatinCoulombgauge,thescalarpotentialequals VC (seeSection1.2),theHamiltonianoftheelectronsplitsintoa stationarypartoftheundisturbedatom ̂ H0 andatime-dependentpart ̂ Hint (t ) fortheinteractionwiththelightﬁeld. ̂ Hint (t ) canbederivedfromtheclassical Hamiltonianforachargedparticleinaradiationﬁeld(notshownhere)

̂ H =− ℏ2 2m ��2 + Vc

Fortheﬁrstterm ̂ H0 ,theanalogytothecorrespondingclassicaltotalenergy Ekin + V = p2 2m + V isclearlyvisible,ifthenotationofthemomentumoperator ̂ p =−iℏ �� x isconsidered.

Formoderateﬁeldstrengths(I ≪ 1015 W∕cm2 ),thelasttermissmallcomparedtothecrossterm,whichsimpliﬁestheinteractionHamiltonian Hint to

Accordingtoperturbationtheory,thewavefunction Ψ(r, t ) canbeexpressed asalinearcombinationofunperturbatedeigenstates Ψ(r) ofthestationary Schrödingerequation(time-independentHamiltonian) H0 Ψj (r)= Ej Ψj (r) with thetime-dependentcoeﬃcients cj (t )

Ψ(r, t )= ∑ j cj (t )Ψj (r)e iEj t ∕ℏ (1.21)

1Theterm“weakdisturbance”indicatesanimportantlimitationforlaser-basedphotoionization: Theexternallaserﬁeld,treatedasperturbation,hastobesmallagainsttheinneratomicforces. Thus,laserintensitiesexceeding1012 W∕cm2 andmolecularinteractionsinducedtherebyareoften referredtoas“nonperturbative”(BaumertandGerber1997),whiletypicalintensitiesfor single-photonionization(SPI)andREMPIapplicationsarebelow108 W∕cm2

InsertingintheTDSE(Eq.(1.18))yields ∑ j (iℏ d dt cj (t )+ Ej )e iEj t ∕ℏ |Ψj ⟩ = ∑ k (Ek + Hint (t ))ck (t )e iEk t

The“ket”vector |Ψ⟩ representsthestatethatisassociatedwiththewavefunction Ψ(r , t ).Withthecorresponding“bra”vector ⟨Ψ|,thatcorrespondstothecomplex conjugatedwavefunction Ψ∗ (r , t ) incoordinatespace,andwiththeinnerproduct ⟨Ψ|Ψ⟩ = ∫ Ψ∗ Ψdr andtheoperator H actingon |Ψ⟩,wecanexpresstheexpectationvalueoftheobservable(hereenergy)representedbyoperator H inthestate |Ψ⟩ by ⟨Ψ|H |Ψ⟩

Consideringtheorthogonalityoftheeigenstates,theresultisasetofcoupled equationsforthetimeevolutionofcoeﬃcients cj (t ) withthetransitionfrequency ��jk =(Ej Ek )∕ℏ: d dt cj (t )= 1 iℏ ∑ k ⟨Ψj |Hint (t )|

H jk

Assumingatwo-levelsystemwithinitialstate |Ψa ⟩ andtheinteraction Hamiltonian(1.20),thecoeﬃcient cb (t ) forthestate |Ψb ⟩ canbeexpressedin thefollowingform.

cb (t )= 1 iℏ ∫ t 0 H ba int (t ′ )ei��ba t ′ dt ′ =− e m ∫ t 0 ⟨

Applyingthevectorpotential A fortheelectromagneticﬁeldrepresentingthe classicdescriptionoflight(Section1.2)

yieldsthetime-dependentamplitudeofstate |Ψb ⟩ inﬁrst-orderperturbation theory

cb (t )=− e 2m Ã[ei�� ⟨Ψb |eikr ��

Theﬁrstintegraldescribestheabsorptionofaphoton.Becausethecomplex e-functionisperiodicwithmeanvaluezerofor ��ba ≠ ��,itcontributesonlyfor ��ba = �� ⇒ Eb = Ea + ℏ�� whilethesecondintegralcorrespondstothephoton emissionif ��ba =−�� ⇒ Eb = Ea ℏ��.

1.3.3Absorption

Thematrixelementassociatedwiththeperturbation Mba (��)= ⟨Ψb |eikr �� ⋅ ��|Ψa ⟩ inEq.(1.26)connectstheinitialstatewiththeﬁnalstateandthusdetermines thesysteminteractionstrengthwiththelight.Beforeitsfurtherevaluation,we

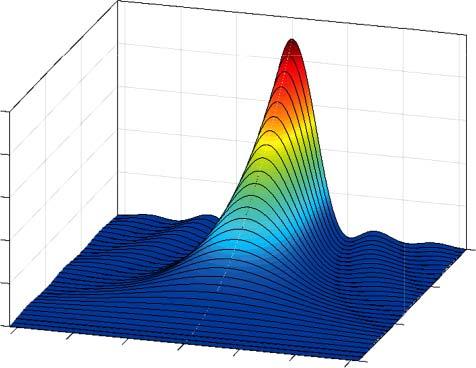
Figure1.3 Behaviorofthefunction F (��, t ) (Eq.(1.28))thatdeterminesthetimeevolutionof thetransitionwhentheﬁeldandthesystemareinresonance.Ifthelightfrequency �� equals thetransitionfrequency ��ba ofthestates |Ψa ⟩ and |Ψb ⟩,thefunctionpeaksincreasinglyand transformsintothe �� -functioninthelong-timelimit.

derivecorrespondingtransitionratesandcrosssections.Duringabsorption,the occupationprobability cb (t ) ofthestate |Ψb ⟩ increaseswithtime,whichcanbe expressedthroughintegrationoftheﬁrstterminEq.(1.26)

andthefrequencyoﬀset �� = �� ba .AsillustratedinFigure1.3,thetransition probabilityincreasessharplywithtimeaccordingtofunction(1.28)whenthe externalﬁeldandthesystemarein resonance,hence �� = ��ba .

Equations(1.27)and(1.28)describetheevolutionoftheoccupationprobabilityof state |Ψb ⟩ withtimeandthuscharacterizetheratewithwhichtransitionsappears. Duringexcitation,thestates |Ψa ⟩ and |Ψb ⟩ formacoherentsuperpositionandthe associateddipoleoscillateswiththetransitionfrequency.

Fortimescaleslongerthanacycle (t ≫ 2�� ∕|��ba |),Eq.(1.28)changestoadelta function F (t ,̃��) ⇒ �� t �� (�� ba ) (note: �� ( ̃ ��) → ∞ for ̃ �� → 0).Furthermore,we expresstheamplitude Ã ofthevectorpotentialbythelightintensity I (compare Eq.(1.15)).

andﬁndthefrequency-dependentabsorptionrate

Sofar,weassumedperfectlymonochromaticlightcorrespondingtoaninﬁnite planewave.However,theintensityofrealisticlighthascomponentscoveringat leastanarrowbandoverafrequencyrange I (��)= dI ∕d ��;thus,thetotalabsorptionratehastobeintegratedovertheentirespectrum

Inthelong-timelimit,onlythevalueat ��ba contributesto Wba bynatureofthe deltafunction

Toexpresstheassociatedcrosssection,weuseEq.(1.17)

whichyieldstheabsorptioncrosssectionforthespectralintensityassociated withtheconsideredtransition.Notethattheunitofthecrosssectionistherefore areatimesfrequency.

Ofnote,theintegration(1.31)assumesasumofincoherentspectralcomponents. Thetreatmentofabsorptionfromcoherentandultrashortlaserpulseshastoconsidertheexplicitpulsewaveform.

Moleculestypicallyhavenumerousstatesinasmallenergyintervalthatcontributestotheabsorption.Hence,thetransitionprobabilityintothisbandisthe sumofalltransitionprobabilitiesmatchingthefrequencyoftheincidentlight. Thenumberofstatesinanenergyrangebetween Eb and Eb + dE canbeexpressed as ��(Eb )dE ,where ��(Eb ) iscalledthedensityofstates.Assumingthatthematrix elementsfortransitionsintosuchabandofstatesarecomparable,Fermi’sgolden rulecanbederivedviaspectralintegrationofthetransitionrates(notshown).

Thus,tocalculatethetransitionrateintoaband,multiplythesquareofthematrix elementbythedensityofstatesoftheinvolvedbands.

1.3.4DipoleApproximation

Sofar,thematrixelementsaredependentonthewavelengthanddirectionofthe lightwave(photon)viathe eikr term.Forinteractionswithvisible,(V)UV,andIR (butnotX-ray)radiation,thewavelengthismuchlargerthantheatomiclength scale;hence,thesystem“feels”anoscillatingdipoleﬁeld.Asaconsequence,the wavevectordependenceofthevectorpotentialcanbeneglected,accordingto

1FundamentalsandMechanismsofVacuumPhotoionization

eikr ≈ 1for �� → ∞; k → 0.Inthisso-called dipoleapproximation,thevector potential A(r, t ) → A(t ) describingthelightfieldbecomesspatiallyhomogenous and,asaconsequence,themagneticfield B = �� × A vanishes.Descriptively,the electronvelocity ve islowenoughtoneglectboththemagneticLorentzforce e(ve × B) andtherelativisticeffectsthatariseiftheelectronisdrivenatveryhigh intensities(> 1016 W∕cm2 ),predominantlyforlongwavelengths.Thematrix elements M D ba cannowexpressedbythedipolematrixelementintheso-called lengthformviathetransitiondipolemoment Dba =−erba containingspatial coordinates ( ̂ x, ̂ y, ̂ z) ofthepositionoperator r

Thus,thematrixelementoftheinteractionHamiltonian,representingthe expectationvalueofitsenergyspectrum,isnowrelatedtothemuchmore descriptivedipolematrixelement Dba ,whichrepresentsthechargedistribution withinthewavefunction.

Thedipolematrixelement Dba (andalso Mba )determinestheinteractionstrength betweenlightandtheatomormolecule.Itsscalarpartdescribesthechangeof chargedistributionduringtransitionfrom |Ψa ⟩ to |Ψb ⟩ thatdeterminesthetransitionprobability.Thevectorpartdemandsprojectionofthelightﬁeldontothe dipolemoment,i.e.itdeﬁnestherequiredlightpolarization.

Thecorrespondingabsorptionratecanbederivedto

Ifthedipolematrixelementiszero,thetransitionisso-called dipole-forbidden. However,suchtransitionsareoftenobservedbecausetheymaybeallowedas (weaker)magneticdipoleorelectricquadrupoletransitions.Commonlyusedin spectroscopytodescribetheabsorptionstrengthisthedimensionless oscillator strengthfij ofatransitionbetweenstates i and j

Oscillatorstrengthvaluesarebetween0and1.Typicalvaluesareshownin Table1.2.

Aninterestingapplicationoftransitionratesisrelatedtothefamous Einstein coefficients.Therefore,theBoltzmanndistributionisappliedtothelevelpopulationofanensembleofatomsinequilibriumandthePlanckdistributiontothe photonfield.AninterestingfindinginthecontextofVUVsourcesisthatspontaneousemissionincreasesrelativetostimulatedemissionasthecubeoflight frequency.Hence,populationinversion,whichisabasisoflasersources,isdifficult togenerateandmaintaininhighlyexcitedsystems.Insteadofcooperatingina stimulatedemissionprocess,theexcitedpopulationsrandomlylooseenergyvia spontaneousemission.

1.3.5SelectionRules

Tocalculateabsorptionrates,thecorrespondingmatrixelementshaveto beevaluatedbyspatialintegrationoverthecorrespondingwavefunctions ⟨Ψb |r|Ψa ⟩ = ∫ Ψb r Ψa d r inEq.(1.36).Iftheintegralvanishes,atransition doesnotoccur(withtheexceptionofhigherordertransitions),whichiscalled dipole-forbidden.Inparticular,thisisthecaseifthefunction Ψb r Ψa isantisymmetric,andthus,itsintegraloverspaceyieldszero.Thiscanoftenbedetermined byanalysisofthewavefunctionsymmetrywithoutexplicitcalculationofthe integral.Forexample,dipoletransitions(e.g. |s⟩ → |s⟩)arenotallowedforthe hydrogenatom.Thesymmetrybehaviorisreﬂectedbytheparityselectionrule (ref.thirdcolumninTable1.1).Usingquantumnumberstotermthestates, furtherselectionrulesfordipoletransitionscanbederivedbyevaluationof zeroandnonzeromatrixelements,as Δl =±1and Δm = 0, ±1,where l isthe angularmomentumquantumnumberand m isthemagneticquantumnumber inaone-electronsystem.Descriptively,theserulesreﬂectconservationof angularmomentumbecausethespinoftheabsorbedphotoncontributestothe system’sangularmomentum L.The z-componentof L isassociatedwiththe electrons’magneticmoment,whichcouplestothephotonspin,thusyielding Δm = 0inthecaseoflinearpolarizationand Δm =±1forcircularlypolarized light.Formultielectronsystems,thetotalangularandorbitalmomentumas wellasthetotalspinisevaluated,andcouplingschemesofangularmomentumsourcesareconsidered.Inrealisticsystems,especiallymolecules,several dipole-forbiddentransitionscanneverthelessbeobserved.Forexample,the dipole-forbiddentransitionsmaybeallowedasmultipoletransitions.Typically, theratedropsdownbythreeordersofmagnitudefromonemultipoletothenext, seeTable1.2.

1.3.6ElectronicLineWidthandLifetime

Sofar,weassumedthatthestateshavesharpeigenenergiesandcanbedescribed viatime-dependentwavefunctionsoftheform �� e iEt ∕ℏ (ref.Figure1.4a,d). Supposeastatethatisexponentiallydecayinginamplitudeasthesystem changestoanotherstate(Figure1.4b).Thedecayingfunctioncorresponds

Table1.1 DipoleselectionrulesforelectronictransitionsinaHydrogen-likeatom. J = L + S is thetotalangularmomentum, L isthetotalorbitalmomentumquantumnumber, S isthetotal spinquantumnumber, MJ isthetotalmagneticquantumnumber,and �� istheparity.

RigorousLScoupling

a)Rigorousforone-electronsystems.

b)SmallatomswithlowLS-coupling.

c)Heavieratomswithtransitionsbetweenseveralmultipletstates.

Intermediate coupling

iEt/ħ]

re[e–iEt/ħ–t/2τ]

Figure1.4 Schematicwavefunctions(top)andtheirspectra(bottom).(a,d)Stationarystate. (b,e)DecayingstateandresultingLorentzianlineproﬁle.(c,f)Collision-inducedphase distortionanditsresultingspectrum(fastFouriertransformed).

toasuperpositionofoscillationswhosefrequenciescanbeFourieranalyzed accordingto

where �� isthetimeconstantofthedecay.Therefore,thedecayingdipoleoscillationisassociatedwithaﬁniteenergyrange.Thewidthathalfheightofthe Lorentzianfunction g (E ′ ) is ℏ∕�� andcalled naturallinewidth (Figure1.4e).Consideringthatthestatetowhichthetransitionappearsmayalsohaveaﬁnitelifetime ��b ,thelinewidthisgivenby

Hence,theshorterthestatelifetime,thelesspreciseitsenergyandvice versa.ThisconceptisparticularlyimportantforREMPI(seeChapter2),where ionizationratesdependontheenergymatchbetweenthephotonandpossible intermediatestatesaswellasthephotondensity.Itfurthergivesrisetothe conceptofvirtualstatesofuncertainenergy,whichmaybeemployedathigh photondensities.

Measuredlinewidthsaretypicallymuchlarger,whichcanbeattributedto theotheroriginsofbroadening.First,collisionswithotheratomsmaylead to(radiativeornonradiative)transitionsandrandomizethephaseofemitted radiation(ref.Fig.1.4c,f).Bothreducestheeﬀectivelifetimeofthestateand leadstothe(pressure-dependent) collisionbroadening oftheLorentzianline proﬁle.Secondary,therelativemotionofatomsresultsinfrequencyshift.Thus, theso-called Dopplerbroadening increaseswithtemperatureanddecreases

1.3Photoabsorption 13 withatomicmassandproducesaGaussianproﬁle,whichconvolveswiththe Lorentzianproﬁle.

1.3.7ElectronicTransitionsofMolecules

Sofar,wetreatedlightabsorptionusingasimplemodelsystemundergoing electronictransitions.However,realelectronicspectraofmoleculesarehighly complex.Thiscannotbecomprehendedbysingle-electrontransitionsinastatic potentialmodelasthenucleicmotioniscompletelyneglected.Indeed,anyelectronictransitionchangesarealsystem’schargedistributioninducingvibration ofthenuclei,which,inturn,changestherotationalstate.Moreover,fullunderstandingofthemoleculeresponseimpliesconsiderationofallpossiblesources ofangularmomentumandtheircouplingscheme.Notethatforphotoionization, REMPIcrosssectionsareaconsequenceoftheactualelectronicstructure.In directSPI,theoutgoingstatesarecontinuumstates,beinglessrestricted.

Correspondingtoatoms,selectionrulesarisefromtheconservationof totalangularmomentumandthetotalparitychangesindipoletransitions, referTable1.2.Initialestimatesoncrosssectionscanbederivedfromtypical oscillatorstrengthvaluesandrespectivetransitionprobabilities,assummarized inTable1.2andindicatedbyexemplaryabsorptionspectrumofbenzene (Figure1.5).

Severalschemesallowfor(atleastqualitative)indicationsonthemolecules’ electronicspectraandtransitionprobabilities.Hund’srulesdescribehowthefour sourcesofangularmomentum(electronorbitalangularmomenta L,rotationof nuclearframework O,andspinofelectrons S andnucleus I),arecoupled(ina diatomicmolecule).Anyelectronictransitionchangesthechargedistribution. Thenucleireadjusttotheseforcescausingvibration.Consequently,electronic transitionsinmoleculesareaccompaniedwithvibrationaltransitions,givingrise totheterm vibronic transitionsthathavemanylinesintheabsorptionspectra. Ofnote,nuclearrearrangementismuchslowerthanelectronictransitions,see alsoFigure1.1.ThisisthebasisfortheFranck–Condonprinciplethatmakes statementsonthemostprobablevibronic(electronic + inducedvibrational)transitions,seeFigure1.6.Electronicexcitationisvirtuallyinstantaneousbeforethe nucleicanreadjusttothedistance rB andmustthereforebedrawnasa“vertical” transition(bluearrow).Fromthenumerousvibrationalstatesoftheupperelectroniclevel,theonewiththegreatestoverlapwiththeoriginalstatevibrational wavefunctionisoccupied.

Table1.2 Typicaloscillatorstrengthsfortransitionsaccordingtotheselectionrules

Symmetry-/ electric dipole-forbidden singlet

dissociation

Rydbergseries

Figure1.5 Absorptionspectrumofbenzene,illustratingthedipoletransitionprobabilities accordingtoselectionrules.Source:ModiﬁedfromBarrow(1962).

Figure1.6 Electronictransitionsare fasterthannuclearmotion.The nucleirearrangeafterelectronic excitation(verticalbluearrow)to thenewdistance rB .Transition probabilityishighestbetweenthe vibrationstatesofthegreatest waveformoverlap,determiningthe possibleﬁnalstates(Franck-Condon principle).Forexampleson Franck-Condoncontrolledvibronic spectrum,seetheanalysisofthe biphenyleneREMPIspectrumand othermoleculesinchapter2.

Vibronictransitionsinturninducerotationaltransitionscontributingmany moreabsorptionlines,accordingtotheselectionrules.Comparabletoiceskaters, whoextendtheirarmsduringapirouettetoslowdowntheirspin,thevibration aﬀectsmolecularrotation.

Complexityfurtherincreasesforpolyatomicmolecules.Forsmallmolecules, applicationoftheselectionrulesmustconsidertheirwholesymmetry,

1.3Photoabsorption 15 astheelectronicexcitationaffectsthecompletestructure.Detailedelectronic structuresarecalculatedwithmethodsofcomputationalchemistrythatarebased onseveralapproximations,e.g.Hartree-Fock(abinitio),Post-Hartree-Fock (considerselectroncorrelations),ordensityfunctionaltheory.Inmanyapplications,aparticulargroupofatomsinthemoleculeisconsideredbecausethey showacharacteristicabsorptionfeature.Thesesubgroups,called chromophores, mayoccurindifferentmoleculescontributingabsorptionbandsofthesame wavelength.Basicconsiderationsonamolecule’sabsorptionbehaviorcanoften bereducedtothepresenceofsuchchromophoresandperturbationsfromother groupsinthemolecule.Aprominentexampleisthe B-bandofbenzeneand derivativesoriginatingfrom �� → �� ∗ transitions.Althoughthis benzenoid band isforbiddenbysymmetryforpureelectronicstates,itisallowedwithrespectto theoverallsymmetryofvibronicstates.Incontextofanalyticalapplications,it contributestheintermediateREMPIstatesgivingthearomaticringstructures highREMPIcrosssectionsfore.g.,thefourthharmonicoftheNd:YAGlaser (266nm).Comprehensivecollectionsofphotoabsorptionspectralinformation canbefoundintheliterature,e.g.Berkowitz(2002).Havingregardtothe scopeonphotoionizationforanalyticalmassspectrometry,manystructuraland spectroscopicdetailscanbeomittedhere,andinthefollowing,wecanfocus onspecificaspectsthathavepracticalimplicationstomassspectrometry.In chapter2theapplicationofREMPIinmolecularspectroscopyusingtunable lasersisdiscussedwiththehelpofphotoabsorptionandionizationspectraof suitedinterestingmolecularsystems.

1.3.8Single-photonIonization(SPI)

Sofar,electronictransitionsbetweenboundstatesweretreated.Theirprobabilitiesatgivenphotonenergiesandradiationintensitiesareformallydetermined by(dipole-)transitionmatrixelementsormorepracticallybyabsorptioncross sections(ref.Eqs.(1.33,1.34))(Berkowitz2002).Correspondingabsorptionspectraareoftencharacterizedusingoscillatorstrengthvalues(Eq.(1.38)).Ifanelectronisreleasedbytheabsorptionprocess,theﬁnalstatehasafreeelectron, allowingcontinuousvaluesforitsenergy Ekin andmomentum pe (continuum state).Consequently,SPIislessconstrainedtostructuralandelectronicproperties,anditscrosssectionsshowarathernarrowdistribution,enablingtouseSPI forauniversalionizationofmolecules(thresholdselectivity Eh�� ≥ IE ),seealso Chapter3forSPI-MSapplications.SPIandpossiblesubsequentfragmentation ofamolecule AB inthegroundvibronicstatecanbeformallywrittenas

withthequotationmarkindicatingtheexcitedstate.Again,thetimescaleofthe electronejectionprocess(Eq.(1.41))ismuchshortercomparedtotherelaxation describedbyEq.(1.42).Consequently,theelectronenergy Ekin canbemeasured toprobetheenergy EB oftheexcitedstateofthemolecularion [AB+ ]′ viaphotoelectronspectroscopy(PES)accordingto Ekin = h�� EB .Detailedionization andfragmentationstudiesarefacilitatedbycombiningMSwithPES,ideallyin