Optimizations and programming: linear, non-linear, dynamic, stochastic and applications with matlab

Matlab Abdelkhalak El Hami

Visit to download the full and correct content document: https://ebookmass.com/product/optimizations-and-programming-linear-non-linear-dyn amic-stochastic-and-applications-with-matlab-abdelkhalak-el-hami/

More products digital (pdf, epub, mobi) instant download maybe you interests ...

Reliability of High-Power Mechatronic Systems 2: Aerospace and Automotive Applications Issues,Testing and Analysis

Abdelkhalak El Hami (Editor)

https://ebookmass.com/product/reliability-of-high-powermechatronic-systems-2-aerospace-and-automotive-applicationsissuestesting-and-analysis-abdelkhalak-el-hami-editor/

Linear Algebra and Its Applications, Global Edition Lay

https://ebookmass.com/product/linear-algebra-and-itsapplications-global-edition-lay/

Reliability Of High Power Mechatronics Systems 1

Abdelkhalak El Hami (Editor)

https://ebookmass.com/product/reliability-of-high-powermechatronics-systems-1-abdelkhalak-el-hami-editor/

Linear Algebra with Applications, Global Edition 9th Edition, (Ebook PDF)

https://ebookmass.com/product/linear-algebra-with-applicationsglobal-edition-9th-edition-ebook-pdf/

Linear Algebra and Its Applications 5th Edition, (Ebook PDF)

https://ebookmass.com/product/linear-algebra-and-itsapplications-5th-edition-ebook-pdf/

Linear Algebra and Its Applications 4th Edition, (Ebook PDF)

https://ebookmass.com/product/linear-algebra-and-itsapplications-4th-edition-ebook-pdf/

Embedded Mechatronic Systems, Volume 2: Analysis of Failures, Modeling, Simulation and Optimization 2nd Edition

Abdelkhalak El Hami

https://ebookmass.com/product/embedded-mechatronic-systemsvolume-2-analysis-of-failures-modeling-simulation-andoptimization-2nd-edition-abdelkhalak-el-hami/

Embedded Mechatronic Systems, Volume 1: Analysis of Failures, Predictive Reliability 2nd Edition

Abdelkhalak El Hami

https://ebookmass.com/product/embedded-mechatronic-systemsvolume-1-analysis-of-failures-predictive-reliability-2nd-editionabdelkhalak-el-hami/

Dynamic System Modelling and Analysis with MATLAB and Python 1st Edition Jongrae Kim

https://ebookmass.com/product/dynamic-system-modelling-andanalysis-with-matlab-and-python-1st-edition-jongrae-kim/

Optimizations and Programming

Linear, Nonlinear, Dynamic, Stochastic and Applications with Matlab

Abdelkhalak El Hami

Bouchaib Radi

First published 2021 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc.

Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address:

ISTE Ltd

27-37 St George’s Road

John Wiley & Sons, Inc.

111 River Street London SW19 4EU Hoboken, NJ 07030

UK USA

www.iste.co.uk

www.wiley.com

© ISTE Ltd 2021

The rights of Abdelkhalak El Hami and Bouchaib Radi to be identified as the authors of this work have been asserted by them in accordance with the Copyright, Designs and Patents Act 1988.

Library of Congress Control Number: 2020948478

British Library Cataloguing-in-Publication Data

A CIP record for this book is available from the British Library

ISBN 978-1-84821-953-3

Chapter1.LinearProgramming ........................3

1.1.Introduction.................................3

1.2.Definitions..................................3

1.3.Geometryofthelinearprogram......................5

1.3.1.Polyhedra.................................5

1.3.2.Extremepointsandvertices......................6

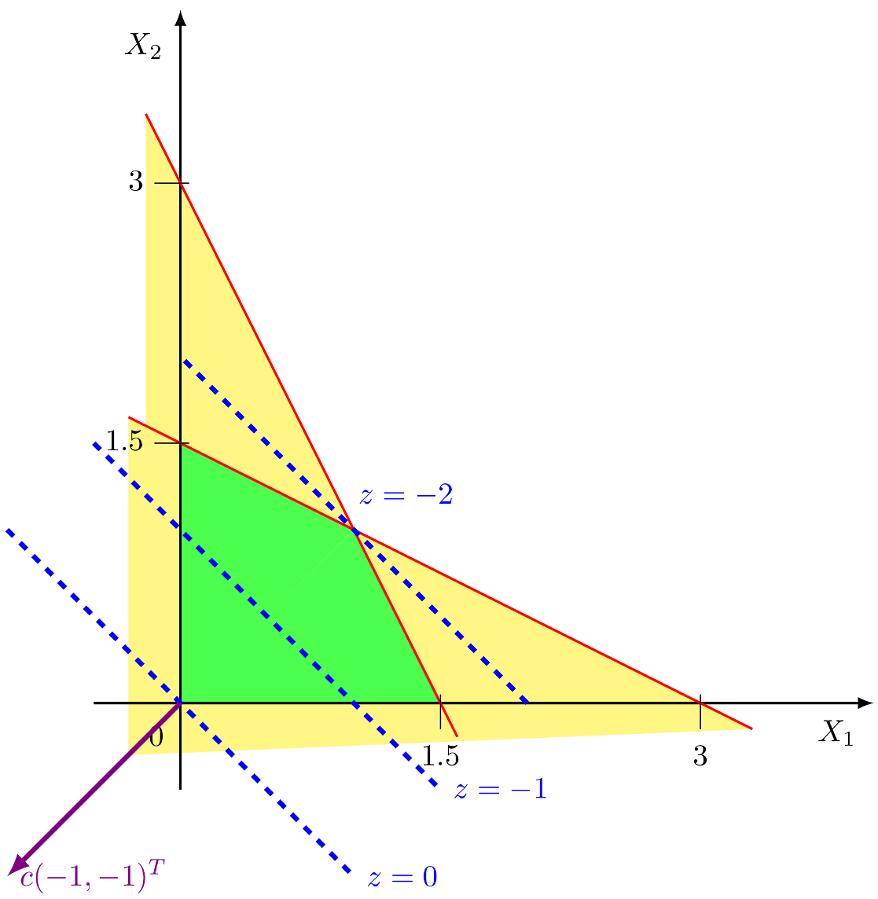
1.4.Graphicalsolvingofalinearprogram...................6

1.5.Simplexalgorithm..............................9

1.5.1.Basicsolutionsandbasicfeasiblesolutions..............9

1.5.2.Simplextableau.............................10

1.5.3.Changeoffeasiblebasis........................11

1.5.4.Existenceanduniquenessofanoptimalsolution...........14

1.6.Initializationofthesimplexalgorithm...................15

1.6.1.Big M method..............................15

1.6.2.AuxiliaryprogramorPhaseI......................17

1.6.3.Degeneracyandcycling.........................20

1.6.4.Geometricstructureofrealizablesolutions..............21

1.7.Interior-pointalgorithm...........................22

1.8.Duality....................................23

1.8.1.Dualitytheorem.............................25 1.9.Relaxation..................................27

1.9.1.Lagrangianrelaxation..........................27

1.10.Postoptimalanalysis............................29

1.10.1.Effectofmodifying

1.10.2.Effectofmodifying

1.11.Applicationtoaninventoryproblem...................34

1.11.1.Optimalsolution............................34

1.11.2.Sensitivitytovariationinstock....................35

1.11.3.Dualproblemofthecompetitor...................36 1.12.UsingMatlab................................36

Chapter2.IntegerProgramming

2.1.Introduction.................................41

2.2.Solvingmethods...............................41

2.2.1.Branch-and-boundmethod.......................42

2.2.2.Thebranch-and-cutmethod......................44

2.3.Binaryprogramming............................49

2.3.1.Knapsackproblem............................49

2.3.2.Investmentproblem...........................50

2.4.Decompositionprinciple..........................57

2.4.1.Bendersdecomposition.........................58 2.5.UsingMatlab.................................62

Chapter3.DynamicProgramming

3.1.Introduction.................................65

3.3.1.Bellman’sequationandtheprincipleofoptimality.........68

3.3.2.Approachofthemethod........................70

3.3.3.AfewexamplesofDP.........................70

3.3.4.SolvinganLP..............................73

3.3.5.Shortestpathproblem..........................74

3.3.6.Knapsackproblem............................79

3.3.7.Stockmanagementproblem......................81

3.4.ContinuousDP................................83

3.4.1.Hamilton–Jacobiequation.......................84

3.4.2.Applicationtoaconsumption-savingsmodel.............84

3.5.StochasticDP................................85

3.5.1.Decision-chanceprocess........................85

3.5.2.Solvingmethod.............................86

3.5.3.Applicationtoacontractproblem...................86

3.5.4.Optimalbinarysearchtree.......................87

3.6.UsingMatlab.................................91

Chapter4.StochasticProgramming

4.1.Introduction.................................93

4.2.Presentationoftheproblem.........................94

4.3.Optimalfeedbackinanopenloop.....................94

4.4.Stochasticlinearprogramming.......................95

4.4.1.Modelswithprobabilitythresholdsontheconstraints........96

4.5.Stochasticlinearprogramswithrecourse.................96

4.5.1.L-shapedmethod............................97

4.5.2.MulticutL-shapedmethod.......................99

4.5.3.Interiorlinearizationmethod......................100

4.6.Nonlinearstochasticprogramming.....................100

4.6.1.Approachestotwo-stepproblemswithrecourse...........100

4.6.2.Regularizeddecompositionmethod..................101

4.6.3.MethodsbasedontheLagrangian...................101

4.6.4.Frank–Wolfemethodforproblemswithsimplerecourse......103

4.6.5.Approximationbysamplingaverage:MonteCarlomethod.....105

4.6.6.Stochasticgradientmethod.......................106

4.7.Stochasticdynamicprogramming.....................107

4.7.1.Markovdecisionprocess........................108

4.7.2.Scenariotree...............................109

4.8.Applicationtothereliabilityofmechanicalsystems...........111

4.8.1.Positionandmodelingofthereliabilityproblem...........113

4.9.UsingMatlab.................................121

5.1.Introduction.................................129

5.2.SymmetricTSP...............................131

5.2.1.Historicaloverview...........................132

5.2.2.Solvingmethods.............................134

5.3.Asymmetrictravelingsalesmanproblem.................140

5.3.1.VariantsoftheATSP..........................140

5.3.2.Mathematicalformulations.......................142

5.3.3.MethodsforsolvingtheATSP.....................144

5.4.Vehicleroutingproblem...........................148

5.4.1.Definition.................................148

5.4.2.Fieldsofapplication...........................149

5.4.3.ParametersoftheVRP.........................150

5.4.4.VariantsoftheVRP...........................151

5.4.5.MathematicalformulationoftheVRP.................153

5.4.6.Algorithmiccomplexity.........................155

5.5.Selectiveroutingproblem..........................156

5.5.1.ProblemssimilartotheVRP......................157

5.5.2.Mathematicalformulation.......................157

5.6.UsingMatlab.................................158

Chapter6.UnconstrainedNonlinearProgramming

6.1.Introduction.................................

6.2.Mathematicalformulation.........................

6.2.1.Existenceanduniquenessresults....................

6.3.Optimalityconditions............................

6.4.Quadraticproblems.............................

6.4.1.Gradientmethodwithoptimalstepsize................

6.4.2.Conjugategradientmethod.......................

6.5.Newton’salgorithm.............................

6.6.Methodsofdescentandlinearsearch...................

6.6.1.Presentationofmethodsofdescent..................

6.6.2.Methodofgreatestslope........................

6.6.3.Acceptablestepsize...........................

6.6.4.Linearsearch...............................

6.6.5.Newton’smethodwithlinearsearch..................

6.7.Quasi-Newtonmethods...........................

6.7.1.DFPandBFGSmethods........................

6.8.Relaxationmethod..............................

6.9.Gradientmethod...............................

6.10.Leastsquaresproblem...........................

6.10.1.Gauss–Newtonmethod........................

6.10.2.Levenberg–Marquardtalgorithm...................

6.12.Applicationtoanidentificationproblem.................

6.13.1.The fminsearch

6.13.2.The fminunc

Chapter7.ConstrainedNonlinearOptimization

7.1.Introduction.................................

7.2.Mathematicalformulation.........................

7.3.Lagrangemultipliers............................

7.4.Optimizationwithinequalityconstraints.................

7.4.1.First-orderconditionsofoptimality..................

7.4.2.Presentationofsaddlepoints......................

7.4.3.Saddlepointandoptimization.....................

7.4.4.Convexcase...............................

7.5.Constrainedminimizationalgorithms...................

7.5.1.Relaxationmethod............................

7.5.2.Projectionmethod............................202

7.5.3.Exteriorpenaltymethod........................204

7.5.4.Uzawa’salgorithm............................205

7.6.Newtonalgorithms:SQPmethod.....................206

7.6.1.Equalityconstraints...........................207

7.6.2.Inequalityconstraints..........................209

7.7.Applicationtostructureoptimization...................210

7.8.UsingMatlab.................................217

7.8.1.The fmincon

7.8.2.The fminbnd

7.8.3.Penaltymethod.............................221

Appendix2.Remindersaboutfunctionsfrom

Appendix3.OptimizationToolbox

Optimizationisthedomainofmathematicsthatstudieshowtominimize(or maximize)acertainobjective,forexample,aneconomicparameterorsometypeof energy.Thisisbothanancienttopic,withtheearliestoptimizationproblemsgoing backtoEuclid,andarelativelynewtopic,withtherecentdevelopmentofnumerical methodssuchaslinearprogramming,whichonlytrulybegantoflourishinthe secondhalfofthe20thcentury.Asanillustration,imaginetheproblemofsearching forapaththatjoinstwopointsonamapintheshortesttime.Someparametersofthe problemmightbeuncertain;forexample,wemightencounteratrafficjamonthe road.Optimizationseekstofindthebestcompromisebetweenthevariouspossible risks.

Inthepresenceofuncertainty,theoptimizer(ordecider)willoftentakeadvantage ofinformationaboutthesystemthatbecomesavailabledynamically,i.e.gradually overtime.Forexample,wewillgraduallydiscoverwhichroadsaremostsusceptible totrafficjamsovertime,aswetrythemout.Thedifficultyofanoptimizationproblem iscloselylinkedtotheamountofinformationneededtomakeanoptimaldecision. Aproblemissaidtobelargeifthisquantityofinformationistoobigforclassical solvingtechniquestobeappliedbybruteforce.

Thisbookisdividedintotwoparts:programming(Part1)andoptimization (Part2).Intheprogrammingpart,wepresentacollectionoftoolsforoperations research,includinglinearprogramming,integerprogramming,binaryprogramming, dynamicprogrammingandstochasticprogramming.Operationsresearchfirstarose intheUnitedKingdomduringtheSecondWorldWar,whenscientificmethodswere usedtostudyvariousaspectsofmilitaryoperations.Sincethen,ithasbecomeakey elementofdecision-makingprocessesinvariouscommercial,industrialand governmentalcontexts,offeringasystematicwaytoapprehendtheeverincreasing complexityofthemanagementproblemsfacedbyboththeprivateandpublicsectors.

FollowingitssuccessinmilitarymattersduringtheSecondWorldWar, operationsresearchwasappliedtooperationalproblemsintheindustryandprivate sectorformanyyears.Inthelastdecadeorso,itsapplicationshavebeenextendedto otherdomains,suchaseconomics,finance,marketingandcorporateplanning.More recently,operationsresearchhasbeenusedtomanagehealthcareandeducation systems,solveenvironmentalproblemsandinotherareasofpublicinterest.Its principalusersaremanufacturing,distributionandretailcompaniesinthemining, energy,transportationandconstructionsectors,aswellasservicecompaniessuchas banks,andvariousgovernmentbodies.Noteworthyexamplesofrecentapplications ofoperationsresearchincludelogisticalstudies,railwaysafety,packagingdesign, strategicworkforceplanning,aerialtransportation,forestryoperations,nuclearfuel optimization,productionplanning,andsoon.

Theoptimizationpartofthisbookisdividedintothreechapters:combinatorial optimization,nonlinearoptimizationwithoutconstraintsandnonlinearoptimization withconstraints.Itisentirelydedicatedtonumericaloptimizationalgorithms,their theoreticalfoundationsandconvergenceproperties,theirimplementationand application,andotherpracticalaspects.Theobjectiveistofamiliarizereaderswith thesenumericalalgorithmsinordertounderstandhowtheybehaveinpractice,how toproperlytakeadvantageof Matlab asatool,howtodesignandadequately implementsuchalgorithmsandhowtocorrectlydiagnoseanydifficultiesthatmight arise.

Eachchapterstartswithafewremindersofkeyresults,butreadersshouldnot hesitatetoconsultthereferenceslistedattheendofthebook.Thisbookisorganized accordingtoastrictlylinearapproach.Asageneralrule,theconceptsareillustrated withexamples.Eachchapterendswithanexamplein Matlab.

Acknowledgments

Wewouldliketothankeveryonewhocontributed,directlyorindirectly,tothe writingofthisbookandespecially,theengineeringandPhDstudentsofINSARouen whomwehavehadthepleasureofsupervisingoverthepastfewyears.

PART 1 Programmation

1.1.Introduction

Linearprogrammingcanbedefinedasamathematicaltechniqueforsolving managementproblems.Forexample,supposethatamanagerfacedwithvarious optionswishestodeterminetheoptimalwaytousetheresourcesofacompanyto achieveaspecificobjective,suchasmaximizingtheutilityorminimizingthecost. Thecompany’sproblemscanusuallybemodeledasalinearprogram(LP)consisting ofacertainnumberofresources[HIL90].Forinstance,thelabor,rawmaterials andcapitalareallresourcesavailableinlimitedquantitiesthatmustbedistributed optimallyovervariousmanufacturingprocesses.Theapproachtosolvingthistypeof problemisdividedintotwokeysteps:

–modeltheproblemwithlinearequationsorinequalitiesthatallowustoproperly identifyandstructuretheconstraintssatisfiedbythevariablesofthemodel.The contributionofeachvariabletothecompany’soverarchingobjectivemustalsobe definedasafunctionthatwillbeoptimized;

–findthemathematicaloptimumusingspecificlinearprogrammingtechniques. Wewillstudythreemethodsforsolvingthevarioustypesoflinearprogramming problems.Thefirstisbasedongraphicalsolvingandisthereforelimitedtotwoor threevariables.Thesecondmethodismorealgebraic;itmotivatesthethirdmethod presentedinthischapter,whichisknownasthesimplexmethod(oralgorithm).

1.2.Definitions

D EFINITION 1.1.– AnLPisincanonicalformifitisexpressedasfollows:

A

∈Mp,n (R),b ∈ Rp , and x ∈ Rn Wewrite x =(x1 ,...,xn )T ≥ 0 if x1 ,...,xn ≥ 0

AnLPisinstandardformifitisexpressedasfollows:

max cT x s.t. Ax = b x ≥ 0

Everylinearproblemcanbeexpressedincanonicalform: min cT x = max cT x.

T HEOREM 1.1.–EveryLPinstandardformcanbeexpressedincanonicalformand viceversa.

Terminology

–Thefunction cT x isthe objectivefunction, costfunction or lossfunction.

–Thecomponentsofthevector x arecalled decisionvariables.

–Ifthevector x satisfiesallconstraints,then x isan admissiblesolution.

–Thesetofalladmissiblesolutionsisthe admissibleset or admissibleregion.

–Anadmissiblesolution x∗ thatmaximizesthelossfunction(i.e. cT x∗ ≥ cT x for everyadmissible x)iscalledan optimaladmissiblesolution or optimalsolution.

E XAMPLE 1.1.–Afactorymanufacturestwoproducts P1 and P2 whileconsuming certainresources:equipment,laborandrawmaterials.Theneedsarelistedinthe followingtable.Eachresourceisavailableinlimitedquantities. P1 P2 Availability Equipment 3 9 81 Labor 4 5 55 Rawmaterials 2 1 20

Thetwoproducts P1 and P2 yieldeffectiveprofitsof6dhsand4dhsperunit. Thegoalistodeterminewhich(possiblynon-integer)quantitiesoftheproducts P1 and P2 thefactoryshouldproducetomaximizethetotalprofitfromsellingthesetwo products,subjecttotheavailabilityoftheresources.

Let x1 and x2 bethequantitiesoftheproducts P1 and P2 ,respectively.

TheLPmaybeexpressedasfollows:maximize z (x1 ,x2 )=6x1 +4x2 subjectto:

–availabilityofresources:

3x1 +9x2 ≤ 81

4x1 +5x2 ≤ 55

2x1 + x2 ≤ 20

–positivityofvariables: x1 ,x2 ≥ 0

1.3.Geometryofthelinearprogram

1.3.1. Polyhedra

D EFINITION 1.2.– Apolyhedronisasetthatcanbedescribedas

P = {x ∈ Rn | Ax ≤ b}, where A isan m × n matrixand b isavectorin Rm Notethattheadmissiblesetof anLPisapolyhedron.

D EFINITION 1.3.– Apolyhedron P issaidtobeboundedifthereexistsaconstant c suchthat x ≤ c forevery x ∈ P.

Figure1.1. Boundedpolyhedron(left)andunboundedpolyhedron (right).Foracolorversionofthisfigure,see www.iste.co.uk/radi/optimizations.zip

D EFINITION 1.4.– Let a beanon-zerovectorof Rn ,andlet b beascalar.

–Theset {x ∈ Rn |aT x = b} issaidtobeahyperplane.

–Theset {x ∈ Rn |aT x ≥ b} issaidtobeahalf-space.

Notethatahyperplaneistheboundaryofthecorrespondinghalf-spaceandthe vector a isperpendiculartothehyperplanethatitdefines[TEG12].

1.3.2. Extremepointsandvertices

Let P beapolyhedronand x∗ ∈ P. Thepoint x∗ isanextremepointifandonlyif x∗ isavertexand x∗ isabasicadmissiblesolution.

D EFINITION 1.5.– Let P beapolyhedron.Avector x ∈ P isanextremepointof P if itcannotbeexpressedasaconvexcombinationoftwootherpointsof P.

D EFINITION 1.6.– Let P beapolyhedron.Avector x ∈ P isavertexof P ifthere exists c suchthat

c T x<cT y forevery y in P notequalto x.

T HEOREM 1.2.–Inlinearprogramming,iftheadmissibledomainisneitheremptynor thewholeof Rn ,itisaconvexpolytopewithfinitelymanyverticesthatcaneitherbe boundedorunbounded.Ifanextremepointexists,itisattainedatoneofthevertices ofthepolytope.Apointintheinteriorofthedomainisneveranextremepointif f =0.Ifthepolytopeisbounded, f attainsbothaminimumandamaximumonit.

Thistheoremgivesusagraphicalsolvingmethod.

1.4.Graphicalsolvingofalinearprogram

Thegraphicalmethodworksbyplottinglinesandsearchingforasolutionas follows:

–identifytheadmissibledomain;

–identifythecontours;

–contoursperpendiculartothevector c,andthereforemutuallyparallel;

–eachvalueof z isassociatedwithacontour;

–thevalueof z increasesinthedirectionof c

E XAMPLE 1.2.–Consider,again,theexamplefromearlier.Itsmathematicalmodelis definedbythefollowinglinearprogram:

max (x1 ,x2 )∈R2 6x1 +4x2 s.t. 3x1 +9x2 ≤ 81 4x1 +5x2 ≤ 55

2x1 + x2 ≤ 20 x1 ,x2 ≥ 0

Theintersectionofthehalf-planesdeterminedbythelinescorrespondingtoeach constraintrepresentsthesetofsolutionsthatsatisfytheconstraints(shadedarea).The directionofthecostfunctionisgivenby

z (x1 ,x2 )=6x1 +10x2 = constant

Thisgivesustheoptimalsolution x = 15 2 , 5 byslidingthelinewiththis directionupwards,whilekeepingitparallel,untilitsintersectionwiththey-axisis maximal.Graphicalsolutionsareofcourseonlyapplicablewithprogramsof,at most,threevariables(seeFigure1.2).

Figure1.2. Graphicalsolution.Foracolorversionofthis figure,seewww.iste.co.uk/radi/optimizations.zip

E XAMPLE 1.3.–Considerthelinearprogram:

min z = x1 x2

s.t. x1 +2x2 ≤ 3 2x1 + x2 ≤ 3 x1 ,x2 ≥ 0

ThegraphicalsolutionisshowninFigure1.3.Wehave z ∗ = 2,with x∗ 1 =1 and x∗ 2 =1

Figure1.3. Graphicalsolutionwithisoprofitlines.Foracolorversionof thisfigure,seewww.iste.co.uk/radi/optimizations.zip

1.5.Simplexalgorithm

Ifalinearprogrammingprobleminstandardformhasanoptimalsolution,thena basicadmissiblesolutionthatisoptimalexists.Thesimplexalgorithmisan algorithmforsolvinglinearoptimizationproblems.IntroducedbyGeorgeDantzigin 1947,itwasprobablytheearliestalgorithmforminimizingfunctionsonsetsdefined byinequalities.Thealgorithmmovesfromonebasicadmissiblesolutiontothenext whilereducingthecost.

Theideaofthemethodisasfollows:

–Let x0 beabasicadmissiblesolution.

–For k =0,..., findanadjacentbasicadmissiblesolution xk +1 suchthat cT xk +1 <cT xk

–Untilnoadjacentbasicadmissiblesolutionimprovestheobjective.

Thisgivesalocalminimum,whichisinfactaglobalminimuminlinear programming.

1.5.1. Basicsolutionsandbasicfeasiblesolutions

Considerasystemof m linearequations Ax = b with n variables (m ≤ n)

D EFINITION 1.7.– Abasicsolutionofthesystemofequations Ax = b isobtainedby setting n m variablestozeroandsolvingthesystemfortheremaining p variables. Thesolutionofthesystemof p equationsin m unknownsisassumedtobeunique.The n p variablessettozeroaresaidtobenon-basicvariables,andthe p remaining variablesaresaidtobebasicvariables.AnLPadmits,atmost, C m n basicsolutions.If thebasicsolutionalsosatisfiesthenon-negativityconstraints,itissaidtobeabasic feasiblesolution.

D EFINITION 1.8.– Abasicsolutionissaidtobedegenerateifatleastonebasic variableiszero.Thistypeofsolutionisobtainedwhenthenumberoflinespassing throughanextremepointisgreaterthanthenumberofdecisionvariables.Abasic feasiblesolutionwhose m basicvariablesarepositiveissaidtobeanon-degenerate basicfeasiblesolution.

R EMARK .–Eachbasicfeasiblesolutioncorrespondstoanextremepoint.However, therecanbemorethanonebasicfeasiblesolutionforthesameextremepoint.This occurswhenthebasicfeasiblesolutionisdegenerate.

R EMARK .–Thenumberofbasicsolutionsquicklybecomesverylarge,evenin modestlysizedmodels.Forexample,amodelinstandardformwith 12 constraints and 25 variablescanhaveupto C 12 25 =5200300 basicsolutions.

1.5.2. Simplextableau

Supposethatwewishtosolve

max z (x1 ,x2 ,x3 ,x4 )=4x1 +3x2

s.t. 3x1 +4x2 + x3 =12 7x1 +2x2 + x4 =14,xi ≥ 0(i =1,..., 4)

Let c =(4, 3, 0, 0)T ,b =(12, 14)T , (A,I2 )= 3410 7201 .Itiseasytoseethat

x =(x1 ,x2 ,x3 ,x4 )T =(0, 0, 12, 14)T satisfiestheconstraints.Thus, x isabasic feasiblesolutionwithbasis J = {3, 4} (thethirdandfourthcomponentsof x),whose basicvariablesare x3 =12 and x4 =14.

Notethat x isnotoptimal: z (x)= cT x =0. Theoptimizationprocedure constructsasequenceoftables,calledsimplextableaus.Thefirsttableausummarizes thedata c,b,A andthebasicvariables.Thelastrowisequalto cT . x1 x2 x3 x4 3410 x J 1 = x3 =12 7201 x J 2 = x4 =14

-4-300 z (x)=0

Table1.1. Firstsimplextableau

Generalcase

Considertheproblem (P ) ⎧ ⎪

⎪ ⎩ max z (x)= cT x s.t. Ax = b, x ≥ 0

where x ∈ Rn + ,c ∈ Rn ,b ∈ Rm , and A isan m × n matrix.Wemayassumewithout lossofgeneralitythatrank A = m<n.

D EFINITION 1.9.– Let A =(a1 ,a2 ,...,an ) (where aj isthe j thcolumnof A),and, for J ⊂{1, 2,...,n}, let AJ = {aj ,j ∈ J }. – J ⊂{1, 2,...,n} isabasisof(P)if |J | = m andifrank AJ =rank (aj ,j ∈ J )= m;

–let x =(x1 ,...,xn )T ∈ Rn + .Then xj isabasicvariable(respectively, non-basicvariable)if j ∈ J (respectively, j/ ∈ J ).Wewrite xJ =(xj ,j ∈ J );

–basicfeasiblesolution: x =(x1 ,...,xn )T ∈ Rn + suchthat xj =0 for j/ ∈ J andsuchthat Ax = AJ xJ = b.

R EMARK .–Theadvantageofpassingfromthecanonicalformtothestandardform isthatweimmediatelyobtainabasicfeasiblesolutionthatcanbeusedasastarting pointforthesimplexalgorithm.Thebasicvariablesaretheslackvariables.

1.5.3. Changeoffeasiblebasis

Let x beabasicfeasiblesolutionof(P).Then

z (x)= c T x = c J x J where c J =(cj ,j ∈ J ).

Ourgoalistofindanotherfeasiblebasis J andabasicfeasiblesolution x such that z (¯ x) >z (x) (meaningthat x isbetterthan x).Thesimplexmethodproceedsby replacingoneofthebasicvariables xr withanon-basicvariable xk . Wesaythat

–thevariable xr entersthebasis J : xr → xr =0;

–thevariable xk leavesthebasis J : xk =0 → xk > 0.

Thus, J =(J −{r }) ∪{k }.Weneedrulestochoose r and k. Theserulesareas follows:

–Choose r suchthat xJ

–Choose k suchthat z

E XAMPLE 1.4.–Returningtothepreviousexample: J = {3, 4},c3 = c4 =0, andso zj =0 for j =1, 2, 3, 4 Thus, zj cj = cj ,j =1, 2, 3, 4 Hence, k =1

Tochoose r, xJ r ar 1 =min x

Thus, r =2,x4 leavesthebasis,and x1 entersthebasis.Thenewbasisis J = {3, 1} Wehave

Hence, x =(2, 0, 6, 0)T and z (¯ x)=

Passing from J = {3, 4} to J = {3, 1} increasesthevalueof z to8,butthisvalueisnotyet maximal.

Calculatingthenewtableau

Wenowapplythetransformation x → x thatincreasedthevalueof z. Sincethe value z (¯ x) (>z (x))isnotnecessarilymaximalingeneral,wemayneedtorepeatthe stepsforchoosing r and k severaltimesuntilwefindabasicfeasiblesolutionthatis alsoamaximumof z

Todothis,weneedasecondtableauwhere xJ isreplacedby xJ ,interpretedin thesamewayasthefirst.Thesamelineartransformationthatallowedustopassfrom x to x isappliedtothecolumnsof A.

Thematrix A =(aij ,i =1,...,m,j =1,...,n) isreplacedby A =(¯ aij ,i = 1,...,m,j =1,...,n) asfollows:

Thisgives

where bi , i =1,...,m, arethenewbasicvariables xJ i

Thelastrowofthenewtableauiscomputedinthesameway:

E XAMPLE 1.5.–Ifweapplytheaboveproceduretoourexample,weobtainTable1.2.

x1 x2 x3 x4

022/71-3/7 x J 1 = x3 =6

12/701/7 x J 2 = x1 =2

0-13/704/7 z (¯ x)=8

Table1.2. Secondsimplextableau(J = {3, 1})

Aswesawabove,thevalueof z increasesfrom 0 to 8,buttherearestillnegative valuesinthelastrowofthetableau,soweneedtoperformanotherchangeofbasisby applyingtheformulas[1.4]and[1.3]aftersubstituting J .Thisgives:

k =2, min xJ i ai2 ; i =1, 2 =min 2 2/7 , 6 22/7 =min 7, 21 11 = 21 11 ,

r =1,x3 leavesthebasis. ˜ J = {2, 1} isthenewbasis.

ThecomputationwiththisnewbasisispresentedinTable1.3. x1 x2 x3 x4

017/22-3/22 x J 1 = x2 =21/11

10-1/112/11 x J 2 = x1 =16/11

0013/227/22 z (˜ x)=127/11

Table1.3. Thirdsimplextableau(J = {2, 1})

Thevalueof z nowincreasesfrom 8 to 127 11 .Thisvalueismaximalbecauseevery valueinthefinalrowisnon-negative.Theoptimalsolutionistherefore ˜ x =(˜ x1 , x2 )= ( 16 11 , 21 11 ). Thissolutionisuniquebecausenofurtherchangeofbasisispossible.

E XAMPLE 1.6.–Considerthelinearproblem:

min z = 800x1 300x2

s.t. 2x1 + x2 ≤ 400 x1 ≤ 150 x2 ≤ 200 x1 ,x2 ≥ 0 [1.8]

Letusintroduceslackvariables x3 ,x4 and x5 : min z = 800x1 300x2 s.t. 2x1 + x2 + x3

Thisgivesthefollowinginitialtableauwiththebasis (x3 ,x4 ,x5 ):

Thenewbasisis (x3 ,x1 ,x5 ) givenas:

Thenextbasisis (x2 ,x1 ,x5 ) givenas:

Sincethereducedcostsareallpositive,thistableauisoptimal.Theoptimal solutionis x1 =150 and x2 =100, givinganoptimalvalueof z = 1, 500, 000 for theobjectivefunction.

1.5.4. Existenceanduniquenessofanoptimalsolution

Afterwritingoutthefirstsimplextableauandadding zj = cj tothelastrow, therearethreepossiblecases:

1) zj cj ≥ 0 for j =1,...,n. Thebasicfeasiblesolution x isalreadyoptimal. Thisoptimalsolutionmayormaynotbeunique;

2)thereexists j ∈{1,...,n} suchthat zj cj < 0 and aij ≤ 0 forevery i ∈ J. In thiscase,thedomainofrealizablesolutionsisunboundedandtheproblemisill-posed, since max z (x)=+∞;

3)theusualcase:thereexists j ∈{1,...,n} suchthat zj cj < 0,andthere exists i ∈ J suchthat aij > 0 Thechangeinbasisdescribedearlierisnowpossible andshouldbeperformed,possiblyseveraltimes,untilcase(1)isreached.

Couldthesimplexalgorithmeverfailtoterminateifcase(3)leadstoaloop?The answerisyes,andexampleshavebeensuccessfullyconstructed.However,theyare veryrareinpractice.

Letusthereforestatetwoimportanttheoremsaboutthesimplexmethod.

T HEOREM 1.3.–Let x ∈ Rn + beabasicrealizablesolutionof(P )withrespectto abasis J (|J | = m = rank (A)).Let zj =

J ci aij . If zj cj ≥ 0 forevery j =1,...,n, then x isanoptimalbasicrealizablesolution.

T HEOREM 1.4.–Let x ∈ Rn + beabasicrealizablesolutionof(P )withrespectto abasis J (|J | = m = rank (A)).Let zj = i∈J ci aij .Supposethat aij ≤ 0 for every i ∈ J andforevery j ∈{1,...,n} suchthat zj cj < 0 Thentheset {z (x),x isarealizablesolution} isunbounded.

R EMARK .–Foracomprehensivediscussionoftheefficiencyofthesimplexmethod, referto[CHV83].

1.6.Initializationofthesimplexalgorithm

Thissectionpresentstwotechniquesforfindingabasicrealizablesolutionto initializethesimplexalgorithm:thefirstistheBigMmethod,andthesecondisthe PhaseImethod.

1.6.1. Big M method

SupposethatwewishtosolvetheLP (P )

max z (x)= cT x s.t. Ax = b, x ≥ 0

where A isan m × n matrix,rank A = m<n.

Byaddingslackvariables(withpositiveornegativesigns),wecanalwaysreduce theLPtotheform(P)describedabove,with b ∈ Rm + .Ifthereisnoobviousbasic realizablesolutiontoinitializethesimplexalgorithm,weproceedbyaddingartificial variables yi ≥ 0 totheconstraints:

Ax = b isreplacedby Ax + y = b,y =(y1 ,y2 ,...,ym )T ∈ Rm + .

Thenewconstraintsarenotequivalenttotheinitialconstraints.The yi > 0 are penalizedbyreplacingtheobjectivefunction z (x) with z = c T x M m i=1 yi , where M issomeverylargepositivevalue.Wewillchoose yi = bi , i =1,...,m,as abasicfeasiblesolutiontoserveastheinitialsolution.

Sincethe yi significantlyreducethevalueof z , theywilldisappearfromthebasis overthecourseofthesimplexalgorithm.Astheyarenon-basicvariables,theirvalue willbeequaltozero,andtheLPthatisultimatelysolvedisthesameastheprogram (P).

E XAMPLE 1.7.–ConsidertheLP

max z (x)= x1 +2x2 2x3

s.t. x1 + x2 x3 =3 x1 +3x2 = 4 x1 ,x2 ,x3 ≥ 0

Thenewprogramisgivenas

max z (x,y )=( 1+2M )x1 +(2 2M )x2 +( 2 M )x3

s.t. x1 + x2 x3 + y1 =3 x1 +3x2 + y2 = 4

x1 ,x2 ,x3 ,y1 ,y2 ≥ 0