WileySeriesinMicrowaveandOpticalEngineering
KaiChang,Editor TexasA&MUniversity Acompletelistofthetitlesinthisseriesappearsattheendofthisvolume.
InverseSyntheticApertureRadarImaging withMATLABAlgorithms
WithAdvancedSAR/ISARImagingConcepts, Algorithms,andMATLABCodes
SecondEdition
CanerÖzdemir,Phd
MersinUniversity
Mersin,Turkey
Thissecondeditionfirstpublished2021
©2021JohnWiley&Sons,Inc.
EditionHistory
JohnWiley&Sons,Inc.(1e,2012)
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedinaretrievalsystem,or transmitted,inanyformorbyanymeans,electronic,mechanical,photocopying,recordingorotherwise, exceptaspermittedbylaw.Adviceonhowtoobtainpermissiontoreusematerialfromthistitleis availableathttp://www.wiley.com/go/permissions.
TherightofCanerÖzdemirtobeidentifiedastheauthorofthisworkhasbeenassertedinaccordance withlaw.
RegisteredOffice
JohnWiley&Sons,Inc.,111RiverStreet,Hoboken,NJ07030,USA
EditorialOffice
111RiverStreet,Hoboken,NJ07030,USA
Fordetailsofourglobaleditorialoffices,customerservices,andmoreinformationaboutWiley productsvisitusatwww.wiley.com.
Wileyalsopublishesitsbooksinavarietyofelectronicformatsandbyprint-on-demand.Some contentthatappearsinstandardprintversionsofthisbookmaynotbeavailableinotherformats.
LimitofLiability/DisclaimerofWarranty
MATLAB® isatrademarkofTheMathWorks,Inc.andisusedwithpermission.TheMathWorks doesnotwarranttheaccuracyofthetextorexercisesinthisbook.Thiswork’suseordiscussionof MATLAB® softwareorrelatedproductsdoesnotconstituteendorsementorsponsorshipbyThe MathWorksofaparticularpedagogicalapproachorparticularuseoftheMATLAB® software.While thepublisherandauthorshaveusedtheirbesteffortsinpreparingthiswork,theymakeno representationsorwarrantieswithrespecttotheaccuracyorcompletenessofthecontentsofthiswork andspecificallydisclaimallwarranties,includingwithoutlimitationanyimpliedwarrantiesof merchantabilityorfitnessforaparticularpurpose.Nowarrantymaybecreatedorextendedbysales representatives,writtensalesmaterialsorpromotionalstatementsforthiswork.Thefactthatan organization,website,orproductisreferredtointhisworkasacitationand/orpotentialsourceof furtherinformationdoesnotmeanthatthepublisherandauthorsendorsetheinformationorservices theorganization,website,orproductmayprovideorrecommendationsitmaymake.Thisworkis soldwiththeunderstandingthatthepublisherisnotengagedinrenderingprofessionalservices.The adviceandstrategiescontainedhereinmaynotbesuitableforyoursituation.Youshouldconsult withaspecialistwhereappropriate.Further,readersshouldbeawarethatwebsiteslistedinthiswork mayhavechangedordisappearedbetweenwhenthisworkwaswrittenandwhenitisread.Neither thepublishernorauthorsshallbeliableforanylossofprofitoranyothercommercialdamages, includingbutnotlimitedtospecial,incidental,consequential,orotherdamages.
LibraryofCongressCataloging-in-PublicationData
Names:Özdemir,Caner,author.
Title:InversesyntheticapertureradarimagingwithMATLABalgorithms: withadvancedsar/isarimagingconcepts,algorithms,andmatlabcodes/ CanerOzdemir,PhDMersinUniversity,Mersin,Turkey.
Description:2ndedition.|Hoboken,NJ,USA:Wiley,2021.|Series:Wiley seriesinmicrowaveandopticalengineering|Includesbibliographical referencesandindex.
Identifiers:LCCN2020031216(print)|LCCN2020031217(ebook)|ISBN 9781119521334(cloth)|ISBN9781119521365(adobepdf)|ISBN 9781119521389(epub)
Subjects:LCSH:MATLAB.|Syntheticapertureradar.|MATLAB.
Classification:LCCTK6592.S95O932020(print)|LCCTK6592.S95(ebook) |DDC621.3848/5–dc23
LCrecordavailableathttps://lccn.loc.gov/2020031216
LCebookrecordavailableathttps://lccn.loc.gov/2020031217
CoverdesignbyWiley
Coverimage:CourtesyofCanerÖzdemir,(background)©Maxiphoto/GettyImages Setin9.5/12.5ptSTIXTwoTextbySPiGlobal,Pondicherry,India 10987654321
To: MywifeBetül, Mythreedaughters, Mybrother, Myfather, andthememoryofmybelovedmother
Contents
PrefacetotheSecondEdition xvi
Acknowledgments xix
Acronyms xx
1BasicsofFourierAnalysis 1
1.1ForwardandInverseFourierTransform 1
1.1.1BriefHistoryofFT 1
1.1.2ForwardFTOperation 2
1.1.3IFT 3
1.2FTRulesandPairs 3
1.2.1Linearity 3
1.2.2TimeShifting 3
1.2.3FrequencyShifting 4
1.2.4Scaling 4
1.2.5Duality 4
1.2.6TimeReversal 4
1.2.7Conjugation 4
1.2.8Multiplication 4
1.2.9Convolution 5
1.2.10Modulation 5
1.2.11DerivationandIntegration 5
1.2.12Parseval’sRelationship 5
1.3Time-FrequencyRepresentationofaSignal 5
1.3.1SignalintheTimeDomain 6
1.3.2SignalintheFrequencyDomain 6
1.3.3SignalintheJointTime-Frequency(JTF)Plane 7
1.4ConvolutionandMultiplicationUsingFT 11
1.5Filtering/Windowing 12
1.6DataSampling 14
1.7DFTandFFT 16
1.7.1DFT 16
1.7.2FFT 17
1.7.3BandwidthandResolutions 17
1.8Aliasing 19
1.9ImportanceofFTinRadarImaging 19
1.10EffectofAliasinginRadarImaging 23
1.11MatlabCodes 26
References 33
2RadarFundamentals 35
2.1ElectromagneticScattering 35
2.2ScatteringfromPECs 38
2.3RadarCrossSection 39
2.3.1DefinitionofRCS 40
2.3.2RCSofSimple-ShapedObjects 43
2.3.3RCSofComplex-ShapedObjects 44
2.4RadarRangeEquation 44
2.4.1BistaticCase 46
2.4.2MonostaticCase 49
2.5RangeofRadarDetection 50
2.5.1Signal-to-NoiseRatio 51
2.6RadarWaveforms 53
2.6.1ContinuousWave 53
2.6.2Frequency-ModulatedContinuousWave 56
2.6.3Stepped-FrequencyContinuousWave 59
2.6.4ShortPulse 61
2.6.5Chirp(LFM)Pulse 62
2.7PulsedRadar 69
2.7.1PulseRepetitionFrequency 69
2.7.2MaximumRangeandRangeAmbiguity 69
2.7.3DopplerFrequency 70
2.8MatlabCodes 74
References 82
3SyntheticApertureRadar 85
3.1SARModes 86
3.2SARSystemDesign 87
3.3ResolutionsinSAR 88
3.4SARImageFormation 91
3.5RangeCompression 92
3.5.1MatchedFilter 92
3.5.1.1ComputingMatchedFilterOutputviaFourierProcessing 95
3.5.1.2ExampleforMatchedFiltering 96
3.5.2AmbiguityFunction 99
3.5.2.1RelationtoMatchedFilter 100
3.5.2.2IdealAmbiguityFunction 101
3.5.2.3Rectangular-PulseAmbiguityFunction 102
3.5.2.4LFM-PulseAmbiguityFunction 102
3.5.3PulseCompression 105
3.5.3.1DetailedProcessingofPulseCompression 105
3.5.3.2Bandwidth,Resolution,andCompressionIssuesforLFMSignal 109
3.5.3.3PulseCompressionExample 110
3.6AzimuthCompression 110
3.6.1ProcessinginAzimuth 110
3.6.2AzimuthResolution 116
3.6.3RelationtoISAR 117
3.7SARImaging 118
3.8SARFocusingAlgorithms 118
3.8.1RDA 119
3.8.1.1RangeCompressioninRDA 120
3.8.1.2AzimuthFourierTransform 126
3.8.1.3RangeCellMigrationCorrection 128
3.8.1.4AzimuthCompression 129
3.8.1.5SimulatedSARImagingExample 130
3.8.1.6DrawbacksofRDA 133
3.8.2ChirpScalingAlgorithm 133
3.8.3The ω-kA 133
3.8.4Back-ProjectionAlgorithm 134
3.9ExampleofaRealSARImagery 135
3.10ProblemsinSARImaging 136
3.10.1RangeMigrationandRangeWalk 136
3.10.2MotionErrors 137
3.10.3SpeckleNoise 140
x Contents
3.11AdvancedTopicsinSAR 140
3.11.1SARInterferometry 140
3.11.2SARPolarimetry 142
3.12MatlabCodes 143 References 158
4InverseSyntheticApertureRadarImagingandItsBasicConcepts 162
4.1SARversusISAR 162
4.2TheRelationofScatteredFieldtotheImageFunctioninISAR 166
4.3One-Dimensional(1D)RangeProfile 167
4.41DCross-RangeProfile 172
4.5Two-Dimensional(2D)ISARImageFormation(SmallBandwidth,Small Angle) 176
4.5.1ResolutionsinISAR 180
4.5.1.1RangeResolution 181
4.5.1.2Cross-RangeResolution: 181
4.5.2RangeandCross-RangeExtends 181
4.5.3ImagingMultibouncesinISAR 182
4.5.4SampleDesignProcedureforISAR 185
4.5.4.1ISARDesignExample#1: “AircraftTarget” 189
4.5.4.2ISARDesignExample#2: “MilitaryTankTarget” 193
4.62DISARImageFormation(WideBandwidth,LargeAngles) 197
4.6.1DirectIntegration 198
4.6.2PolarReformatting 201
4.73DISARImageFormation 205
4.7.1RangeandCross-Rangeresolutions 209
4.7.2ADesignExamplefor3DISAR 210
4.8MatlabCodes 217 References 243
5ImagingIssuesinInverseSyntheticApertureRadar 246
5.1Fourier-RelatedIssues 246
5.1.1DFTRevisited 246
5.1.2PositiveandNegativeFrequenciesinDFT 250
5.2ImageAliasing 252
5.3PolarReformattingRevisited 255
5.3.1NearestNeighborInterpolation 255
5.3.2BilinearInterpolation 258
5.4ZeroPadding 260
5.5PointSpreadFunction 264
5.6Windowing 269
5.6.1CommonWindowingFunctions 269
5.6.1.1RectangularWindow 269
5.6.1.2TriangularWindow 269
5.6.1.3HanningWindow 272
5.6.1.4HammingWindow 272
5.6.1.5KaiserWindow 272
5.6.1.6BlackmanWindow 276
5.6.1.7ChebyshevWindow 277
5.6.2ISARImageSmoothingviaWindowing 277
5.7MatlabCodes 280 References 304
6Range-DopplerInverseSyntheticApertureRadarProcessing 306
6.1ScenariosforISAR 306
6.1.1ImagingAerialTargetsviaGround-BasedRadar 307
6.1.2ImagingGround/SeaTargetsviaAerialRadar 309
6.2ISARWaveformsforRange-DopplerProcessing 312
6.2.1ChirpPulseTrain 312
6.2.2SteppedFrequencyPulseTrain 314
6.3DopplerShift’sRelationtoCross-Range 316
6.3.1DopplerFrequencyShiftResolution 317
6.3.2ResolvingDopplerShiftandCross-Range 318
6.4FormingtheRange-DopplerImage 319
6.5ISARReceiver 320
6.5.1ISARReceiverforChirpPulseRadar 320
6.5.2ISARReceiverforSFCWRadar 321
6.6QuadratureDetection 323
6.6.1I-ChannelProcessing 324
6.6.2Q-ChannelProcessing 324
6.7RangeAlignment 326
6.8DefiningtheRange-DopplerISARImagingParameters 327
6.8.1ImageFrameDimension(ImageExtends) 327
6.8.2RangeandCross-RangeResolution 328
6.8.3FrequencyBandwidthandtheCenterFrequency 328
6.8.4DopplerFrequencyBandwidth 328
6.8.5PulseRepetitionFrequency 329
6.8.6CoherentIntegration(Dwell)Time 329
6.8.7PulseWidth 330
6.9ExampleofChirpPulse-BasedRange-DopplerISARImaging 331
6.10ExampleofSFCW-BasedRange-DopplerISARImaging 336
6.11MatlabCodes 339 References 347
7ScatteringCenterRepresentationofInverseSyntheticAperture Radar 349
7.1Scattering/RadiationCenterModel 350
7.2ExtractionofScatteringCenters 352
7.2.1ImageDomainFormulation 352
7.2.1.1ExtractionintheImageDomain:The “CLEAN” Algorithm 352
7.2.1.2ReconstructionintheImageDomain 355
7.2.2FourierDomainFormulation 362
7.2.2.1ExtractionintheFourierDomain 362
7.2.2.2ReconstructionintheFourierDomain 364
7.3MatlabCodes 368 References 382
8MotionCompensationforInverseSyntheticApertureRadar 385
8.1DopplerEffectDuetoTargetMotion 386
8.2StandardMOCOMPProcedures 388
8.2.1TranslationalMOCOMP 389
8.2.1.1RangeTracking 389
8.2.1.2DopplerTracking 390
8.2.2RotationalMOCOMP 390
8.3PopularISARMOCOMPTechniques 392
8.3.1Cross-CorrelationMethod 392
8.3.1.1ExamplefortheCross-CorrelationMethod 394
8.3.2MinimumEntropyMethod 398
8.3.2.1DefinitionofEntropyinISARImages 398
8.3.2.2ExamplefortheMinimumEntropyMethod 399
8.3.3JTF-BasedMOCOMP 402
8.3.3.1ReceivedSignalfromaMovingTarget 403
8.3.3.2AnAlgorithmforJTF-BasedRotationalMOCOMP 404
8.3.3.3ExampleforJTF-BasedRotationalMOCOMP 406
8.3.4AlgorithmforJTF-BasedTranslationalandRotationalMOCOMP 408
8.3.4.1ANumericalExample 410
8.4MatlabCodes 415 References 436
9BistaticISARImaging 440
9.1WhyBi-ISARImaging? 440
9.2GeometryforBi-IsarImagingandtheAlgorithm 444
9.2.1Bi-ISARImagingAlgorithmforaPointScatterer 444
9.2.2BistaticISARImagingAlgorithmforaTarget 448
9.3ResolutionsinBistaticISAR 449
9.3.1RangeResolution 449
9.3.2Cross-RangeResolution 450
9.3.3RangeandCross-RangeExtends 451
9.4DesignProcedureforBi-ISARImaging 452
9.5Bi-IsarImagingExamples 455
9.5.1Bi-ISARDesignExample#1 455
9.5.2Bi-ISARDesignExample#2 457
9.6Mu-ISARImaging 465
9.6.1ChallengesinMu-ISARImaging 467
9.6.2Mu-ISARImagingExample 468
9.7MatlabCodes 472 References 483
10PolarimetricISARImaging 484
10.1PolarizationofanElectromagneticWave 484
10.1.1PolarizationType 485
10.1.2PolarizationSensitivity 486
10.1.3PolarizationinRadarSystems 487
10.2PolarizationScatteringMatrix 488
10.2.1RelationtoRCS 490
10.2.2PolarizationCharacteristicsoftheScatteredWave 491
10.2.3PolarimetricDecompositionsofEMWaveScattering 493
10.2.4ThePauliDecomposition 494
10.2.4.1DescriptionofPauliDecomposition 494
10.2.4.2InterpretationofPauliDecomposition 495
10.2.4.3PolarimetricImageRepresentationUsingPauliDecomposition 496
10.3WhyPolarimetricISARImaging? 497
10.4ISARImagingwithFullPolarization 497
10.4.1ISARDatainLPBasis 497
10.4.2ISARDatainCPBasis 498
10.5PolarimetricISARImages 499
10.5.1Pol-ISARImageofaBenchmarkTarget 499
10.5.1.1The “SLICY” Target 499
10.5.1.2FullyPolarimetricEMSimulationofSLICY 499
10.5.1.3LPPol-ISARImagesofSLICY 500
10.5.1.4CPPol-ISARImagesofSLICY 502
10.5.1.5PauliDecompositionImageofSLICY 503
10.5.2Pol-ISARImageofaComplexTarget 507
10.5.2.1The “MilitaryTank” Target 507
10.5.2.2FullyPolarimetricEMSimulationof “Tank” Target 508
10.5.2.3LPPol-ISARImagesof “Tank” Target 508
10.5.2.4CPPol-ISARImagesof “Tank” Target 510
10.5.2.5PauliDecompositionImageof “Tank” Target 512
10.6FeatureExtractionfromPolarimetricImages 515
10.7MatlabCodes 515
References 529
11Near-FieldISARImaging 533
11.1DefinitionsofFarandNear-FieldRegions 534
11.1.1TheFar-FieldRegion 534
11.1.1.1TheFar-FieldDefinitionBasedonTarget’sCross-RangeExtend 534
11.1.1.2TheFar-FieldDefinitionBasedonTarget’sRangeExtend 535
11.1.2TheNear-FieldRegion 537
11.2Near-FieldSignalModelfortheBack-ScatteredField 537
11.3Near-FieldISARImagingAlgorithms 540
11.3.1 “FocusingOperator” Algorithm 540
11.3.2Back-ProjectionAlgorithm 541
11.3.2.1FourierSliceTheorem 542
11.3.2.2BPAFormulation(3DCase) 543
11.3.2.3BPAFormulation(2DCase) 544
11.4DataSamplingCriteriaandtheResolutions 546
11.5Near-FieldISARImagingExamples 547
11.5.1PointScatterersintheNear-Field:ComparisonofFar-andNear-Field ImagingAlgorithms 547
11.5.2Near-FieldISARImagingofaLargeObject 552
11.5.3Near-FieldISARImagingofaSmallObject 555
11.6MatlabCodes 560
References 569
12SomeImagingApplicationsBasedonSAR/ISAR 571
12.1ImagingSubsurfaceObjects:GPR-SAR 572
12.1.1TheGPRProblem 572
12.1.2B-ScanGPRinComparisontoStrip-MapSAR 577
12.1.3FocusedGPRImagesUsingSAR 577
12.1.3.1GPRFocusingwith ω-kAlgorithm(ω-kA) 579
12.1.3.2GPRFocusingwithBPA 582
12.1.3.3OtherPopularGPRFocusingTechniques 589
12.2Thru-the-WallImagingRadarUsingSAR 590
12.2.1ChallengesinTWIR 591
12.2.2TechniquestoImproveCross-RangeResolutioninTWIR 591
12.2.3TheUseofSARinTWIR 592
12.2.4ExampleofSAR-BasedTWIR 594
12.3ImagingAntenna-PlatformScattering:ASAR 596
12.3.1TheASARImagingAlgorithm 597
12.3.2NumericalExampleforASARImagery 603
12.4ImagingPlatformCouplingBetweenAntennas:ACSAR 605
12.4.1TheACSARImagingAlgorithm 606
12.4.2NumericalExampleforACSAR 609
12.4.3ApplyingACSARConcepttotheGPRProblem 611 References 615
Appendix 619 Index 628
PrefacetotheSecondEdition
Inthefirsteditionofthebook,Itriedtocovermostoftheaspectsofinversesyntheticapertureradar(ISAR)imagingstartingfromFourieranalysistosome advancedISARconceptssuchasrange-DopplerISARprocessingandISARmotion compensationtechniques.Themaingoalwastopresentaconceptualdescription ofISARimageryandtheexplanationofbasicISARresearchtopics.Althoughthe primaryaudiencewouldbegraduatestudentsandotherinterestedresearchersin thefieldsofelectricalengineeringandphysics,Ihopedthatcolleaguesworkingin radarresearchanddevelopmentorinarelatedindustrymightalsobenefitfrom thebook.
Ithasbeenmorethaneightyearssincethepublicationofthefirstedition.Since then,IhavebeenreallygratefulthatIhavereceivedpositiveresponsesfromthe researchersandcolleaguesthatareinterestedand/orinvolvedinradarimaging, andespeciallyISARimaging.Undoubtedly,ISARhasbeengainingmoreattention amongresearchers,scholars,andengineersasemergingnewdevelopmentsin ISARresearchhavebeenreportedbyvariouscolleaguesdaybyday.
Inthissecondeditionofthebook,Ihavetriedtoincludetherecentprogress madeinISARimagingresearchandalsogiveinsightstomoreadvancedconcepts. Therefore,inthiseditionofthebook,Ihavemadethefollowingalterationsand additions:
• Allthechaptersinthefirsteditionhavebeenrevisedincludingallthetexts, equations,andfigureswithsomeadditions.Typosinthefirsteditionhavealso beencorrected.
• Chapter3thatisdevotedtotheissuesofsyntheticapertureradar(SAR)hasbeen extendedtoincludetheSARfocusing/processingalgorithmssuchasrangeDoppleralgorithm(RDA),back-projectionalgorithm(BPA)andfrequencywavenumberalgorithm(ω-kA).TheMatlabcodesforthesealgorithmsare beingprovidedwiththeassociatednumericalexamples.Briefexplanationsof
otherSARfocusing/processingalgorithmsincludingchirpscalingalgorithm (CSA)andphaseshiftalgorithm(PSA)havealsobeenmentioned.
• InChapters4,5,7,and12wherewehandlevariousaspectsofISARimaging technology,newscatteredfieldrawdat aandthecorrespondingISARimages thataremorevisuallyattractivearep resentedtogetherwiththeassociated Matlabcodesthatcanbeusedtogeneratetheseimages.
• Atotalofthreenewchaptershavebeenwrittentocoverthetopicsthatwerenot consideredinthefirsteditionandalsotoincludemoredetailedsubjectsofISAR imagingtobeabletoreflecttherecentresearchstudies.Thesearelistedbelow:
– The “BistaticISAR(Bi-ISAR)Imaging” conceptiscoveredinChapter9.While theISARimagingalgorithmspresentedinpreviouschaptersarebasedon monostaticusageofISARimaging,weintroducetheformulationofISAR imagingforthebistaticusagesbypresentingkeyaspectssuchasresolutions inrange/cross-rangedirectionsandusagelimitations.Also,extensionofBiISARtomultistaticISAR(Mu-ISAR)imagingisderivedwiththeassociated Matlabexamples.AgeneralassessmentofBi-ISARandMu-ISARimaging toconventionalmonostaticISARimagingisbeingmadethroughoutthechapterbycomparingtheoutcomesofquantitativemetricsandgivingtheconcludingstatementsabouttheiradvantagesanddisadvantagesbasedonthese measurableevaluations.
– InChapter10,wehaveaddedanewandexcitingresearchtopicofISARcalled “PolarimetricISARImaging.” AsthetraditionalISARimagingalgorithmsare basedonlyonasinglepolarizationofthebackscatteredelectricfield,wedemonstrateinthischapterthatveryexcitingfeaturesofthetargetcanbe extractedwiththeuseofotherpossiblepolarizationsforthereflectedwave. PolarizationdecompositiontechniquesarebeingintroducedandPauli decompositionschemeistakenasthetooltobeappliedtothedifferentpolarizationISARimagesinthisbook.TheformulationandtheusageofPauli decompositiontechniquearepresentedtogetherwithitsMatlabcodes.Variousrealisticsimulationexamplesbasedonlinearpolarization,circularpolarization,andalsoPaulidecompositionaregiventogetherwithobtained polarimetricISARimages.Ithasbeendemonstratedthroughtheexamples thatpolarizedISARimagesdefinitelyincreasetherecognitionandclassificationoftargetsbyprovidingincreasednumberofextractedtargetfeatures.
– Thankstotherecentdevelopmentinthemicrowavecircuittechnologyand antennadesign,ISARimagingalgorithmshavebeenstartedtobeusedinthe near-fieldregion.Therefore,Ihaveaddedanewpartentitled “Near-field ISARimaging ” asChapter11.Thenear-fieldISARimagingalgorithmsare beingintroduced.Twoofthemcalled “Focusingoperator” andthebackprojectionbasedfocusingalgorithmsaregivenbypresentingtheirtheoretical formulationandalgorithmstepstogetherwithcorrespondingMatlabcodes.
Also,numericalandmeasuredexamplesbasedonrealscenariosarebeing shared.
• InChapter12inwhichsomeexamplesbasedonSAR/ISARimagingtechnologiesareprovided,IhavepreviouslyintroducedalgorithmscalledantennaSAR (ASAR)andantennacouplingSAR(ACSAR)astheuniqueradarimagingalgorithmstoimageantennamountedonaplatform-to-radarreceiverinteraction overthetargetandtoimageplatformcouplingovertheantennasmounted onatarget,respectively.Inthiseditionofthebook,Ihaveaddedsomenew applicationssuchas ground-penetratingradar (GPR)and through-the-wallimagingradar (TWIR)thatalsomakeuseofSAR/ISARimagingalgorithms.MeasuredexamplesofGPRandTWIRradarimagesareprovidedtodemonstratehow SAR/ISARimagingalgorithmscanbeeffectivelyusedinsomepopularradar imagingapplications.
Ihopethat,withtheneweditionofthebook “InverseSyntheticApertureRadar ImagingwithMATLABAlgorithms,” thereaderwouldbenefitmoreintermsof abovementionednewISARimagingtopicsandalsofromtheMatlabcodesprovidedattheendofchapters.
AllMATLABfilesmaybeaccessedonthefollowingFTPsite:ftp://ftp.wiley. com/public/sci_tech_med/inverse_synthetic.
CanerÖzdemir
Mersin,October2020
Acknowledgments
Iwouldliketoaddressspecialthankstothepeoplebelowfortheirhelpandsupportduringthepreparationofthisbook.First,Iamthankfultomywife,Betüland mythreechildrenfortheirpatienceandcontinuoussupportwhilewritingthis book.IamverygratefultoDr.HaoLing,EmeritusProfessorinEngineeringof theUniversityofTexasatAustinforbeingavaluablesourceofknowledge,ideas, andalsoinspirationthroughoutmyacademiccarreer.Hehasbeenagreatadvisor sinceImethim,andhisguidanceonscientificresearchispricelesstome.
Iwouldliketoexpressmysincerethankstomyformergraduatestudents;Dr. ŞevketDemirci,Dr.EnesYiğit,Dr.BetülYılmaz,Dr.DenizÜstün,ÖzkanKırık, andDr.HakanIşıkerwhohavehelpedcarryingoutsomeoftheresearchpresented inthisbook.IwouldalsoliketothankmygraduatestudentRasheedKhankanfor hishelpinpreparingreferences.
Lastbutnotleast,IwouldliketoconveymyspecialthankstoDr.KaiChangfor invitingmetowritethefirstandthensecondeditionofthebook.Withouthiskind offer,thisbookprojectwouldnothavebeenpossible.
CanerÖzdemir
Acronyms
1DOne-dimensional
2DTwo-dimensional
3DThree-dimensional
ACSARAntennacouplingsyntheticapertureradar
ADCAnalog-to-digitalconverter
ANNArtificialneuralnetwork
ASARAntennasyntheticapertureradar
ATCAutomatictargetclassification
ATRAutomatictargetrecognition
Bi-ISARBistaticinversesyntheticapertureradar
BPABack-projectionalgorithm
CADComputeraideddesign
CDFCumulativedensityfunction
CFARConstantfalsealarmrate
COContrastoptimization
Co-polCo-polarization
CPCircularpolarization
Cross-polCross-polarization
CSAChirpscalingalgorithm
CWContinuouswave
DCRDihedralcornerreflectors
DFTDiscreteFouriertransform
DTVDigitaltelevision
EFIEElectricfieldintegralequation
EMElectromagnetic
ESMExplodingsourcemodel
FMFrequencymodulated
FMCWFrequencymodulatedcontinuouswave
FTFouriertransform
GOGeometricoptics
GPRGround-penetratingradar
GPSGlobalpositioningsystem
GWNGaussianwhitenoise
HHorizontal
HHHorizontal–horizontal
HSAHyperbolicsummationalgorithm
HVHorizontal–vertical
IInphase
IDFTInversediscreteFouriertransform
IFTInverseFouriertransform
IMUInertialmeasurementunit
InSARInterferometricSAR
ISARInversesyntheticapertureradar
JTFJointtime-frequency
KBKbytes
KMAKirchhoffmigrationalgorithm
LLeft
LFMLinearfrequencymodulated
LFMCWLinearfrequencymodulatedcontinuouswave
LHCPLeft-handcircularpolarized
LHEPLeft-handellipticallypolarized
LLLeft–left
LOSLineofsight
LPLinearpolarization
LRLeft–right
MBMbytes
MDAMap-driftautofocus
MFIEMagneticfieldintegralequation
MIMOMultiple-inputmultiple-output
MOCOMPMotioncompensation
Mu-ISARMulti-staticinversesyntheticapertureradar
PECPerfectelectricconductor
PGAPhasegradientautofocus
P-ISARPassiveinversesyntheticapertureradar
POPhysicaloptics
PolSARPolarimetricsyntheticapertureradar
PPPProminentpointprocessing
PRFPulserepetitionfrequency
PRIPulserepetitioninterval
PSDPowerspectraldensity
PSFPointspreadfunction
PSLRPeak-to-sideloberatio
PSMAPhase-shiftmigrationalgorithm
PSRPoint-spread-response
QQuadrature
QDQuadraduredetection
RRight
RCMRangecellmigration
RCMCRangecellmigrationcorrection
RCSRadarcrosssection
RDARange-doppleralgorithm
RFRadiofrequency
RGBRedgreenblue
RHCPRight-handcircularpolarized
RHEPRight-handellipticallypolarized
RLRight–Left
RLOSRadarlineofsight
RRRight–right
RxReceiver
[S]Polarizationscatteringmatrix
SACShiftandcorrelate
SARSyntheticapertureradar
SBRShootingandbouncingray
SFCWSteppedfrequencycontinuouswave sincSinuscardinalis
SNRSignal-to-noiseratio
SPUSignalprocessingunit
STFTShort-timeFouriertransform
TCRTrihedralcornerreflector
TFDSTime-frequencydistributionseries
TWIRThrough-the-wallimagingradar
TWRThrough-the-wallradar
TxTransmitter
VVertical
VHVertical–horizontal
VNAVectornetworkanalyzer
VVVertical–vertical
ω-kAFrequency-wavenumberalgorithm
xxii Acronyms
BasicsofFourierAnalysis
1.1ForwardandInverseFourierTransform
Fouriertransform(FT)isacommonandusefulmathematicaltoolthatisutilized ininnumerousapplicationsinscienceandtechnology.FTisquitepracticalespeciallyforcharacterizingnonlinearfunctionsinnonlinearsystems,analyzingrandomsignals,andsolvinglinearproblems.FTisalsoaveryimportanttoolinradar imagingapplicationsasweshallinvestigateintheforthcomingchaptersofthis book.BeforestartingtodealwiththeFTandinverseFouriertransform(IFT),a briefhistoryofthisusefullinearoperator,anditsfoundersarepresented.
1.1.1BriefHistoryofFT
JeanBaptisteJosephFourier,agreatmathematician,wasbornin1768,Auxerre, France.Hisspecialinterestinheatconductionledhimtodescribeamathematical seriesofsineandcosinetermsthatcouldbeusedtoanalyzepropagationanddiffusionofheatinsolidbodies.In1807,hetriedtosharehisinnovativeideaswith researchersbypreparinganessayentitledas OnthePropagationofHeatinSolid Bodies.TheworkwasexaminedbyLagrange,Laplace,Monge,andLacroix. Lagrange’soppositionscausedtherejectionofFourier’spaper.Thisunfortunate decisioncostcolleaguestowaitfor15moreyearstomeethisremarkablecontributionstomathematics,physics,andespeciallyonsignalanalysis.Finally,his ideaswerepublishedthruthebook TheAnalyticTheoryofHeat in1822 (Fourier1955).
DiscreteFouriertransform(DFT)wasdevelopedasaneffectivetoolincalculatingthistransformation.However,computingFTwiththistoolinthenineteenth centurywastakingalongtime.In1903,C.Rungehasstudiedontheminimization
InverseSyntheticApertureRadarImagingwithMATLABAlgorithms:WithAdvancedSAR/ISAR ImagingConcepts,Algorithms,andMATLABCodes,SecondEdition.CanerÖzdemir. ©2021JohnWiley&Sons,Inc.Published2021byJohnWiley&Sons,Inc.
2 1BasicsofFourierAnalysis
ofthecomputationaltimeofthetransformationoperation(Runge1903).In1942, DanielsonandLanczoshadutilizedthesymmetrypropertiesofFTtoreducethe numberofoperationsinDFT(DanielsonandLanczos1942).Beforetheadventof digitalcomputingtechnologies,JamesW.CooleyandJohnW.Tukeydevelopeda fastmethodtoreducethecomputationtimeofDFToperation.In1965,they publishedtheirtechniquethatlateronhasbecomefamousasthefastFourier transform(FFT)(CooleyandTukey1965).
1.1.2ForwardFTOperation
TheFTcanbesimplydefinedasacertainlinearoperatorthatmapsfunctionsor signalsdefinedinonedomaintootherfunctionsorsignalsinanotherdomain.The commonuseofFTinelectricalengineeringistotransformsignalsfromtime domaintofrequencydomainorvice-versa.Moreprecisely,forwardFTdecomposesasignalintoacontinuousspectrumofitsfrequencycomponentssuchthat thetimesignalistransformedtoafrequencydomainsignal.Inradarapplications, thesetwoopposingdomainsareusuallyrepresentedas “spatial-frequency(or wave-number)” and “range(distance).” SuchuseofFTwillbeoftenexamined andappliedthroughoutthisbook.
TheforwardFTofacontinuoussignal g(t)where ∞ < t < ∞ isdescribedas
where representstheforwardFToperationthatisdefinedfromtimedomainto frequencydomain.
ToappreciatethemeaningofFT,themultiplyingfunctionexp( j2π ft)and operators(multiplicationandintegration)ontherightofsideofEq.1.1should beexaminedcarefully:Thetermexp j2π f i t isacomplexphasorrepresentation forasinusoidalfunctionwiththesinglefrequencyof “fi. ” Thissignaloscillates withthesinglefrequencyof “fi” anddoesnotcontainanyotherfrequencycomponent.Multiplyingthesignalininterest, g(t)withexp j2π f i t providesthesimilaritybetweeneachsignal,thatis,howmuchof g(t)hasthefrequencycontentof “fi. ” Integratingthismultiplicationoveralltimeinstantsfrom ∞ to ∞ willsum the “fi” contentsof g(t)overalltimeinstantstogive G(fi)thatistheamplitudeof thesignalattheparticularfrequencyof “fi. ” Repeatingthisprocessforallthefrequenciesfrom ∞ to ∞ willprovidethefrequencyspectrumofthesignalrepresentedas G(f).Therefore,thetransformedsignalrepresentsthecontinuous spectrumoffrequencycomponents;i.e.representationofthesignalin “frequency domain.”
1.2FTRulesandPairs 3
1.1.3IFT
ThistransformationistheinverseoperationoftheFT.IFT,therefore,synthesizes afrequency-domainsignalfromitsspectrumoffrequencycomponentstoits timedomainform.TheIFTofacontinuoussignal G(f)where ∞ < f < ∞ is describedas
wheretheIFToperationfromfrequencydomaintotimedomainisrepresentedby 1 .
1.2FTRulesandPairs
TherearemanyusefulFourierrulesandpairsthatcanbeveryhelpfulwhenapplyingtheFTorIFTtodifferentreal-worldapplications.Wewillbrieflyrevisitthem toremindthepropertiesoftheFTtothereader.ProvidedthatFTandIFTare definedasinEqs.1.1and1.2,respectively,FTpairisdenotedas
andthecorrespondingalternativepairisgivenby
Basedonthesenotations,thepropertiesofFTarelistedbrieflybelow.
1.2.1Linearity
If G(f)and H(f)aretheFTsofthetimesignals g(t)and h(t),respectively,thefollowingequationisvalidforthescalars a and b.
Therefore,theFTisalinearoperator.
1.2.2TimeShifting
Ifthesignalisshiftedintimewithavalueof to,thenthecorrespondingfrequency signalwillhavetheformof
1.2.3FrequencyShifting
Ifthetimesignalismultipliedbyaphasetermofexp j2π f o t ,thentheFTofthis timesignalisshiftedinfrequencyby fo asgivenbelow
1.2.4Scaling
Ifthetimesignalisscaledbyaconstant a,thenthespectrumisalsoscaledwiththe followingrule
1.2.5Duality
Ifthespectrumsignal G(f)istakenasatimesignal G(t),then,thecorresponding frequencydomainsignalwillbethetimereversalequivalentoftheoriginaltime domainsignal, g(t)as
1.2.6TimeReversal
Ifthetimeisreversedforthetime-domainsignal,thenthefrequencyisalso reversedinthefrequencydomainsignal.
1.2.7Conjugation
Iftheconjugateofthetime-domainsignalistaken,thenthefrequency-domain signalconjugatedandfrequency-reversed.
1.2.8Multiplication
Ifthetime-domainsignals, g(t)and h(t)aremultipliedintime,thentheirspectrum signals G(f)and H(f)areconvolvedinfrequency.
1.3Time-FrequencyRepresentationofaSignal 5
1.2.9Convolution
Ifthetime-domainsignals, g(t)and h(t)areconvolvedintime,thentheirspectrum signals G(f)and H(f)aremultipliedinthefrequencydomain.
1.2.10Modulation
Ifthetime-domainsignalismodulatedwithsinusoidalfunctions,thenthefrequency-domainsignalisshiftedbytheamountofthefrequencyatthatparticular sinusoidalfunction.
1.2.11DerivationandIntegration
Ifthederivativeorintegrationofatime-domainsignalistaken,thenthecorrespondingfrequency-domainsignalisgivenasbelow.
1.2.12Parseval’sRelationship
AusefulpropertythatwasclaimedbyParsevalisthatsincetheFT(orIFT)operationmapsasignalinonedomaintoanotherdomain,theirenergiesshouldbe exactlythesameasgivenbythefollowingrelationship.
1.3Time-FrequencyRepresentationofaSignal
WhiletheFTconceptcanbesuccessfullyutilizedforthestationarysignals,there aremanyreal-worldsignalswhosefrequencycontentsvaryovertime.Tobeableto displaythesefrequencyvariationsovertime;therefore,jointtime–frequency(JTF) transforms/representationsarebeingused.
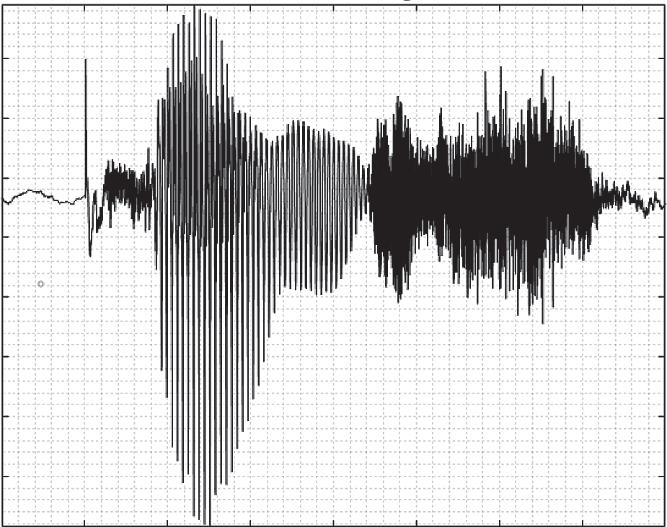
Figure1.1 Thetime-domainsignalof “prince” spokenbyalady. 6 1BasicsofFourierAnalysis
1.3.1SignalintheTimeDomain
Theterm “timedomain” isusedwhiledescribingfunctionsorphysicalsignals withrespecttotimeeithercontinuousordiscrete.Thetime-domainsignalsare usuallymorecomprehensiblethanthefrequency-domainsignalssincemostof thereal-worldsignalsarerecordedanddisplayedversustime.Commonequipmentistoanalyzetime-domainsignalsisthe oscilloscope.InFigure1.1,atimedomainsoundsignalisshown.Thissignalisobtainedbyrecordingofanutterance oftheword “prince” byalady.Bylookingattheoccurrenceinstantsinthe x-axis andthesignalmagnitudeinthe y-axis,onecananalyzethestressoftheletters insidetheword “prince.”
1.3.2SignalintheFrequencyDomain
Theterm “frequencydomain” isusedwhiledescribingfunctionsorphysicalsignalswithrespecttofrequencyeithercontinuousordiscrete.Frequency-domain representationhasbeenproventobeveryusefulininnumerousengineeringapplicationswhilecharacterizing,interpreting,andidentifyingsignals.Solvingdifferentialequations,analyzingcircuits,signalanalysisincommunicationsystemsare fewamongmanyotherswherefrequency-domainrepresentationismuchmore
domain signal