Geometric and Topological
Mesh Feature Extraction for 3D Shape Analysis Hetroy-Wheeler Visit to download the full and correct content document: https://ebookmass.com/product/geometric-and-topological-mesh-feature-extraction-fo r-3d-shape-analysis-hetroy-wheeler/
More products digital (pdf, epub, mobi) instant download maybe you interests ...
Feature extraction and image processing for computer vision Fourth Edition Aguado
https://ebookmass.com/product/feature-extraction-and-imageprocessing-for-computer-vision-fourth-edition-aguado/
Mesh Adaptation for Computational Fluid Dynamics 1: Continuous Riemannian Metrics and Feature-based Adaptation Alain Dervieux
https://ebookmass.com/product/mesh-adaptation-for-computationalfluid-dynamics-1-continuous-riemannian-metrics-and-feature-basedadaptation-alain-dervieux/
Extraction Techniques for Environmental Analysis John R. Dean
https://ebookmass.com/product/extraction-techniques-forenvironmental-analysis-john-r-dean/
Fruit Juices: Extraction, Composition, Quality and Analysis Gaurav Rajauria
https://ebookmass.com/product/fruit-juices-extractioncomposition-quality-and-analysis-gaurav-rajauria/
Riemannian geometric statistics in medical image analysis Pennec X (Ed.)
https://ebookmass.com/product/riemannian-geometric-statistics-inmedical-image-analysis-pennec-x-ed/
I Kissed
Shara Wheeler Casey Mcquiston https://ebookmass.com/product/i-kissed-shara-wheeler-caseymcquiston/
Geometric Dimensioning and Tolerancing for Mechanical Design 2/E 2nd Edition
https://ebookmass.com/product/geometric-dimensioning-andtolerancing-for-mechanical-design-2-e-2nd-edition/
Geometric Dimensioning and Tolerancing for Mechanical Design, 3E Gene R. Cogorno
https://ebookmass.com/product/geometric-dimensioning-andtolerancing-for-mechanical-design-3e-gene-r-cogorno/
Geometric Modeling of Fractal Forms for CAD Christian Gentil
https://ebookmass.com/product/geometric-modeling-of-fractalforms-for-cad-christian-gentil/
Geometric and Topological Mesh Feature Extraction for 3D Shape Analysis Jean-Luc Mari
Franck Hétroy-Wheeler
Gérard Subsol
First published 2019 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc.
Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address:
ISTE Ltd
John Wiley & Sons, Inc.
27-37 St George’s Road 111 River Street London SW19 4EU Hoboken, NJ 07030
UK USA
www.iste.co.uk
www.wiley.com
© ISTE Ltd 2019
The rights of Jean-Luc Mari, Franck Hétroy-Wheeler and Gérard Subsol to be identified as the authors of this work have been asserted by them in accordance with the Copyright, Designs and Patents Act 1988.
Library of Congress Control Number: 2019946683
British Library Cataloguing-in-Publication Data
A CIP record for this book is available from the British Library
ISBN 978-1-78630-041-6
1.3.7.Tensorofcurvature:Taubin’sformula
1.3.8.Tensorofcurvaturebasedonthenormalcycle theory
1.3.9.Integralestimators
1.3.10.Processingunstructured3Dpointclouds
1.3.11.Discussionofthemethods
1.4.Featurelineextraction
1.5.1.Meshsegmentation
1.5.2.Shapedescriptionbasedongraphs
2.1.Mathematicalbackground
2.2.1.Connectedcomponentsandgenus
2.2.2.Homologygroups
2.3.Combininggeometricandtopologicalfeatures
2.3.1.Persistenthomology
2.3.2.ReebgraphandMorse–Smalecomplex
2.3.3.Homologygenerators
3.1.Introduction
3.2.Medicine:linesofcurvatureforpolypdetectioninvirtual colonoscopy
3.3.Paleo-anthropology:crest/ridgelinesforshapeanalysisof humanfossils
3.4.Geology:extractionoffracturelinesonvirtualoutcrops
3.5.Planetaryscience:detectionoffeaturelinesfortheextraction ofimpactcratersonasteroidsandrockyplanets
3.6.Botany:persistenthomologytorecoverthebranching structureofplants
Preface Three-dimensionalsurfacemeshes,composedofcollectionsofplanar polygons,arethemostcommondiscreterepresentationofthesurfaceofa virtualshape.These3Dsurfacemeshesneedtobeinspectedinorderto understandorevaluatetheiroverallstructureorsomedetails.Thiscanbe donebyextractingrelevantgeometricortopologicalfeatures.Suchshape characteristicscansimplifythewaytheobjectislookedat,canhelp recognitionandcandescribeandcategorizeitaccordingtospecificcriteria.
Shapecharacteristicscanbedefinedinmanyways.Thisbooktakesthe pointofviewofdiscretemathematics,whichaimstoproposediscrete counterpartstoconceptsmathematicallydefinedincontinuousterms.More specifically,inthisbook,wereviewhowstandardgeometricandtopological notionsofsurfacescanbedefinedandcomputedfora3Dsurfacemesh,as wellastheiruseforshapeanalysis.Inparticular,recentmethodsare describedtoextractfeaturelineshavingameaningrelatedtoeithergeometry ortopology.Differentialestimatorssuchasdiscreteprincipalcurvaturesare detailedastheyplayacriticalroleinthecomputationofsalientstructures.An emphasisisthenplacedontopologysincetheglobalstructureandthe connectivityoffeaturesplayanimportantroleintheunderstandingofa shape.Severalapplicationsarefinallydeveloped,showingthateachofthem needsspecificadjustmentstogenericapproaches.Theseapplicationsare relatedtomedicine,geology,botanyandothersciences.
Focusingonshapefeatures,thetopicofthisbookisnarrowerbutmore detailedthanothershapeanalysisbooks,whichdonot,oronlybriefly,refer tofeaturedefinitionandcomputation.Itisintendednotonlyforstudents,
xGeometricandTopologicalMeshFeatureExtractionfor3DShapeAnalysis
researchersandengineersincomputerscienceandshapeanalysis,butalso numericalgeologists,anthropologists,biologistsandotherscientistslooking forpracticalsolutionstotheirshapeanalysis,understandingorrecognition problems.Wehopethatourbookwillbeausefulreviewofexistingworkfor allofthem.
Finally,wewouldliketothankMarcDanielforgivingustheopportunity towritethisbookandAldoGonzalez-Lorenzoforhisreadingofchapter2and forhisconstructiveremarks.
FranckH ÉTROY-W HEELER GérardS UBSOL August2019
Jean-LucM ARI
Introduction I.1.Context:3Dshapeanalysis Shapes,whetherfromthenaturalworldormanufactured,aremoreand moreoftendigitizedforvisualizationormeasurementpurposes,among others.Thisprocessgenerallyresultsin3Dsurfacemeshes,whichare composedofcollectionsofplanarpolygons.Suchmeshesnowadaysarethe mostcommondiscreterepresentationofthesurfaceofavirtualshape.These meshesareautomatically,orsometimesinteractively,examined,inorderto understand,evaluateormatchtheiroverallstructureorsomedetails.This processiscalled 3Dshapeanalysis andcanbedonebyextractingrelevant geometricortopological features.Suchshapecharacteristicscansimplifythe waytheobjectislookedat,canhelprecognitionandcandescribeand categorizeitaccordingtospecificcriteria.Inthisbook,wewillreview variousmathematicaldefinitionsofmeshfeaturesandsomealgorithmsto computethem.Wewillthengiveafewapplicationexampleswherethese featuresareusedtogloballyorlocallyanalyzea3Dshape.
Itisimportanttonotethatthisbookis not about3Dshapeanalysis,but onlyaboutfeaturedefinitionandcomputation.3Dshapeanalysishasawider spectrumthanfeaturedetection.Amongconceptsthatwillnotbetackledin thisbookareglobalshapedescriptor/signaturedefinitionandspectralshape analysis.Theinterestedreadercanreferto[BIA14]or[LÉV10]tolearnmore aboutthesenotions.
Beforegoingintodetailsaboutsurfacefeaturesfromamathematicaland computationalpointofview,anddetailingsomeapplicationsinChapters1–3,
westartbygivingsomegeneraldefinitionsaboutmeshes,whichwillbeuseful inthefollowingchapters.Fortheinterestedreader,wealsoquicklygoover howfeaturesaredefinedandcalculatedinotherfields.
I.2.Backgroundonmeshes Inmany(butnotall)contextswhereasamplingofasurfaceisavailable, thissurfaceisapproximatedbyamesh.Asurface mesh isformallydefined asatripletofsets M =(V,E,F ),where V isthesetof vertices,whichare pointsinthe3DEuclideanspace R3 samplingthesurfaceatstake; E isthe setof edges,whicharesegmentswhoseendpointsareverticesof V : E ⊂ V × V ;and F isthesetof faces,whicharepolygonswhoseverticesandedges areverticesandedgesof V and E respectively.Avolumemeshisdefinedas aquadrupletofsets (V,E,F,T ).Theadditionalset T isasetofpolyhedra whosevertices,edgesandfacesarepartof V , E and F respectively.Sincein thisbookwewillfocusonthesurfaceofashape,wewillnotconsidersuch volumemeshesandwewillrestrictourselvestosurfacemeshes.Inpractice, severalpropertiesareoftenrequired.Thepolygonalfacesmustbeplanar.It isoftenconvenienttolimitoneselftotriangularfacessincesuchfacesare necessarilyplanar,butsometimesitisusefultoallow quadrangular faces,i.e. faceswithfouredges.Formostapplications,facesmustbeconvex.Hereagain, restrictingtheworktotrianglesisawaytoensureconvexity.
Ameshapproximatesthesurfaceofanobjectwithafinitenumberof geometricprimitives(points,segmentsandpolygons).The geometry ofthe meshisthusasimplificationofthegeometryoftheunderlyingshapeandis givenbythe3Dcoordinatesofitsverticesandbythegeometricinformation carriedbytheedgesandthefaces.Forexample,thenormalvectorstothe facesarelocalestimatesofthenormalvectortothesurface.Thisgeometryis decorrelatedtothe topology ofthemesh,whichencodestheneighboring informationbetweenprimitives.Twomeshescansharethesametopologybut notthesamegeometryorviceversa(seeFigureI.1).Notethatwhatwecall heretopologyisnotcloselyrelatedtothetopologyofthesurface,aswillbe studiedinChapter2.
Thetopologyofameshisdefinedwiththefollowingnotions,whichcome fromtheterminologyusedforgraphsincomputerscience. Incidence:two primitives(vertices,edges,faces)areincidenttoeachotherifoneisaborder
oftheother.Avertexandanedgeareincidenttoeachotherifthevertex isanendpointofthisedge.Avertexandafaceareincidenttoeachother ifthevertexisavertexoftheface.Finally,anedgeandafaceareincident toeachotheriftheedgeisanedgeoftheface. Adjacency:twoprimitives (vertices,edges,faces)ofdimension n areadjacenttoeachotheriftheyshare thesamedimensionandareincidenttothesameprimitiveofdimension n 1 or n +1.Twoverticesareadjacentiftheyareendpointsofthesameedge. Twoedgesareadjacentiftheyshareacommonendpointoracommonface. Twofacesareadjacentiftheyshareacommonedge.Notethatingraphtheory, twoedgesthatshareacommonendpointaresaidtobeincident.Weusethe termadjacenthereforthesakeofsimplicity. Neighborhood :thetopological kneighborhoodofavertex v onameshisgivenbythesetofverticeswhichcan bereachedfrom v usingatmost k adjacencyrelationships.Forexample,the 1-neighborhoodof v isthesetofverticeswhichshareanedgewith v ,andthe 2-neighborhoodof v alsoincludesthesetofverticeswhichshareanedgewith avertexofthe1-neighborhoodof v .Finally,wecallthe degree or valency of avertex v thenumberof1-neighborsof v .Equivalently,thisisthenumberof edgesincidentto v .
FigureI.1. Threemeshesthatshareeitherthesametopology butnotthesamegeometry(leftandmiddle)orthesame geometrybutnotthesametopology(middleandright)
Sincethemeshrepresentstheboundaryofavolumetricobject,itisusually requiredthatthesurface“lookslike”adisklocally,andthatthereisno pinchpointforexample,orthreefacessharinganedge.Thisisformalized throughthenotionof manifoldness,whichwewillstudyinChapter2.Roughly speaking,asurfaceissaidtobeamanifoldiftheneighborhoodofeachpoint canbesmoothlydeformedtoadisk,withoutshearingorgluing.Alternatively, asurfaceisamanifoldwithboundaryiftheneighborhoodofeachpointcanbe smoothlydeformedtoadiskorahalf-disk.Forexample,aneggisamanifold (itisequivalenttoaspherefromatopologicalpointofview,althoughitis notgeometricallyasphere),andaneggonwhichthetophasbeenremoved
xivGeometricandTopologicalMeshFeatureExtractionfor3DShapeAnalysis
isamanifoldwithboundary.Moregeneralthanamanifoldisthenotionof simplicialcomplex.Asimplicialcomplexisamesh M withthefollowingtwo properties:
1)everyedgeofafaceof F isin E ,andeveryvertexofanedgeof E is in V ;
2)theintersectionofanytwoprimitivesof M iseitheremptyoraprimitive of M .Forexample,theintersectionoftwodifferentfacesiseitheremptyora vertexoranedgeofthemesh.Itcannotbeasegmentorapointinsidethese faces.
Notethat,forexample,isolatedverticesorfacesonlyconnectedbyavertex andnotanedgeareallowedinasimplicialcomplexwhiletheyarenotina manifoldmesh.
Meshesarewidelyusedbecauseofseveralgoodproperties.First,theyare relativelyeasyandfasttocreatefromasetofpoints.Second,theirstorage costislow,sinceonlythe3Dcoordinatesoftheverticesandsometopological information(e.g.theverticesdefiningeachface)needtobestored.Third, theyareadaptable,canhandleevencomplicatedgeometriesandcanbeused invariousscenarios.Finally,theyareofteneasytoprocesssincethe neighborhoodinformationisexplicitlygivenbytheprimitives.However,they faceafewdrawbacks:theresultingsurfaceisnotsmoothandtheymaybe difficulttoeditsincethisusuallyrequiresthecomputationofanextended neighborhoodforeachvertex.
I.3.Definitionofafeature
AccordingtotheEnglishOxfordDictionaries[OXF17],afeatureis “adistinctiveattributeoraspectofsomething”.Thisraisestwomainquestions relatedtotheobjectunderstudy:
– distinctive:whatisinvolvedintheprocessofdistinguishing?
– attribute:howisanattributedefined?
Differentdefinitionsoffeatureshavebeenproposedfor3Dshapes,which differontheiranswerstothesetwoquestions.Forthesakeofcompleteness,
wereviewhereafewofthembeforeintroducingthecoreofourtopic,which willbedevelopedinthefollowingchapters.
I.3.1. Surfacefeaturefromatopographicpointofview Intopography,expertshavedefinedalimitednumberofEarth(oranother planet)surfacefeatures.Thesefeaturesareoftwokinds:pointsorlines.The mainonesare:
–a hill correspondstoapointwherethegroundslopesdowninall directions.Inotherwords,itisalocalheightmaximum;
–a depression isalocalheightminimum;
–a saddle isalowpointbetweentwohills.Thegroundslopesupintwo oppositedirections,butslopesdowninthetwoother,orthogonaldirections;
–a ridge isalinewhereateachpointthegroundslopesupinonedirection anddowninthethreeotherones;
–a valley isalinewhereateachpointthegroundslopesupinthree directionsanddowninthelastdirection.
Thesetermscanactuallybemathematicallydefinedandarenotrestricted toplanets,aswewillseeinChapter1.Otherfeaturesincludedraws,spurs, cliffs,cutsandfills[DEP11].Themainadvantageofthesedefinitionsisthat anynon-expertisabletodistinguishafeatureonaterrain,assoonasheor sheisabletocheckinwhichdirectionsthegroundslopesupordown.The maindrawbackisthattheysomehowdependonthechoiceofthescale:the groundcanbeslightlyslopingdownforafewmetersinadirectionbutoverall slopingupinthesamedirectionforalongerdistance.Hence,morerobustand general-purposedefinitionshavebeenproposedinotherfields.
I.3.2. Surfacefeaturefromaperceptualpointofview Invisualperception,afeatureisusuallydefinedasasalientpointorregion ona3Dshape,i.e.apointorregionthatcaneasilybedistinguishedfrom itssurroundingsbythehumaneye.Multiplemathematicaldefinitionshave beenproposed,whichusuallyrelatefeaturestosurfacegeometricpropertiesat multiplescales.
Incomputergraphics,seminalworkincludestheintroductionofthe conceptof meshsaliency byLee,VarshneyandJacobs[LEE05],which extendsto3Dmeshesthedefinitionproposedby[ITT98]for2Dimages. Earlierworksmostlyprojecteda3Dsurfaceintoa2Dimagetodetermineits visualfeatures.Lee etal.definemeshsaliencyforagivenvertexasa combinationofsalienciesatdifferentscales.Thesesalienciesarethemselves computedasdifferencesbetweenGaussian-weightedaveragesofthemean curvatureofneighboringverticescomputedatafineandacoarsescale.A featureisthendefinedasaregiononthemeshwithhigh,orlocally maximum,saliencyvalues.Notethatthisoriginalmeshsaliencydefinitionis purelygeometry-based,butotherinformationsuchascolorcanbe incorporated.
Almostatthesametime,GalandCohen-Orproposedanotherpurely geometricapproach,inwhichthesurfaceisfirstapproximatedbyquadric patches[GAL06].Adescriptoristhendefinedforeachpatch,asthecenterof massofthepatchtogetherwiththehighestGaussiancurvatureacrossthe patch.Asalientgeometricfeatureisfinallydefinedasaclusterofdescriptors withlocallyhighcurvatureandahighvarianceofcurvatures.Leifman etal. defined regionsofinterest ona3Dmeshaccordingtothreeproperties:vertex distinctness,shapeextremitiesandpatchassociation[LEI16].Adistinct vertexisdefinedasavertexwhosespinimagedescriptor[JOH99]isfarfrom others,usingdiffusiondistanceatthreedifferentscales.Contrarytothese purelylocalapproaches,Song etal.consideredglobalgeometricpropertiesof theshape[SON14].Specifically,thespectrumoftheLaplacianmatrixofthe meshisusedthroughamultiscaleapproachtofindthemostobvious saliencies.
FollowingLee etal.,someauthorshavetakeninspirationfromvisual perceptiontheoriestodefinesalientfeaturesona3Dsurface.Basedonthe conceptof visualmasking,Lavouédefinedaperceptualmeasureofnoiseona meshcalled roughness,whichiscomputedateveryvertexasanasymmetric differencebetweenthemaximumcurvatureonthemeshandonasmoothed versionofit[LAV09].Detectedroughverticesaredistinctfromsharpedge features.Wu etal.linearlycombinealocalproperty,thevisualcontrastanda globalone, rarity,todefinesaliency[WU13].Thelocalcontrastiscomputed bysegmentingthemeshintoalmostplanarpatchesandcomputingdistances betweenthemeansofmultiscaledescriptorsofallverticesinneighboring patches.Theglobalrarityvalueofavertexissimplythesumofthedistances
betweenthedescriptorofthisvertexandthedescriptorsofallothervertices inthemesh.Nader etal.proposedabottom-upapproachbasedonuser experimentstoestimatethevisualcontrastonaflat-shaded[NAD16a]or smooth-shaded[NAD16b]3Dmesh.Similarlyto[LAV09],theirworkis basedontheconceptofvisualmasking,aswellasotherssuchas contrast sensitivity and visualregularity.
Sinceafeatureshould,bydefinition,bedistinctive,Shilaneand Funkhouserintroducedtheideaofdefiningafeatureonanobjectwithrespect tosimilarobjects[SHI07].Intheirapproach,aregionissaidtobedistinctive ifitsshapeisconsistentwithregionsonobjectsofthesameclassbutdifferent fromobjectsinotherclasses.Theshapeofaregionisdescribedthrougha multiscale HarmonicShapeDescriptor [KAZ03],whichdecomposesa sphericalregionintoconcentricshellsofvaryingradii.Goingfurther,Chen etal.studiedthepointsselectedon3Dsurfacesbymorethan1,000 non-trainedusers[CHE12].Thequestionaskedtotheuserswastoselect pointsthattheotherpeoplewerelikelytoselect.Theyfoundoutthatthemost obviousfeaturepointscanberetrievedatminimumcurvaturelocalextrema. Locationsforlessobviousfeaturepointsincludesymmetryaxesandcenters oflargeconvexparts.Lau etal.extendedtheconceptofmeshsaliencyto detecttheregionsonthesurfaceofa3Dobjectwhicharethemostlikelyto begrasped,pressedortouchedbyahumanuser[LAU16].Theseregionsare learnedfrommanuallylabeledsalientregionsusingdeepneuralnetworks.
I.3.3. Surfacefeaturefromamachinevisionpointofview Automaticallycomputingdistinctivefeaturesinanimageisoneofthe maingoalsofcomputervision.Inthiscontext,features,alsocalled keypoints, areusuallydefinedaspixels,orconnectedsetsofpixels,withspecific appearanceorgeometricproperties(motioncanalsobetakenintoaccountin thecaseofvideos).Forexample,afeaturecanbelocatedataplaceofasharp changeincolorortexture,orattheedgeortheendpointofanobject.Features shouldrepresentinacompactmannertherelevantinformationwithrespectto aspecificgoal,suchasdescribingtheobjectsintheimage.Theyshouldalso bestableintheimageundersomegeometrictransformations,suchasrotation orscaling.Featuredefinitionusuallycomprisestwostages: detection and description.Featuredetectionaimstocomputetherelevantkeypointsfora givenapplication,whilefeaturedescriptionexpressesthespecificproperties
oftheimageatthesepoints.Toeachkeypointisassociatedaneighborhood sizecalled scale.Thisscaleiscomputedinthedetectionstageandisthen usedinthedescriptionstage.Notethatinearlydetectionmethodsthescaleis auser-definedparameterandisthesameforallkeypoints.Suchmethodsare called fixedscale methods.Mostrecentworkspropose adaptivescale methods,whichautomaticallycomputethescaleofeachkeypoint.
Thisframeworkhasbeenextendedbeyond2D,inparticulartomesh surfaces,bymanydifferentapproaches.Ourgoalhereisnottosurveyor comparethem,andwereferthereadertorecentreviewssuchas [BRO12,TOM13,GUO14]forthesepurposes.Weonlydescribeheretwo keypointdetectionmethodsfor3Dmeshesthathavebeeninspiredbyimage detectors.Otherpopularfeaturedetectorsfor2DimagessuchasSIFT [LOW04]andSURF[BAY08]havealsobeenadaptedto3D,butonlyfor rangeimages(i.e.imagesinwhicheachpixelisassociatedwithadepth value,whichcanbeseenaspointclouds)intheformercase[LO09]andby voxelizingthemeshinthelatterone[KNO10].
In2011,SipiranandBustosproposedtoextendtheHarriscornerdetection method[HAR88]for2Dimagesto3Dmeshes[SIP11].TheHarrismethod ispopularbecauseofitsrobustnesswithrotations,scaling,noiseandchanges inillumination.Thismethodconsidersaneighborhood W = {(xk ,yk )} aroundeachpixel (x,y ) andshifts W byaprescribedamount (Δx, Δy ). Then,foreachpixel,itcomputesthesumofsquareddifferencesinintensity (theimageisconvertedintoagrayscaleimage)betweenbothneighborhoods. Thisboilsdowntothecomputationofa2by2matrix E (x,y ) involvingthe partialderivativesoftheintensityin x and y ,evaluatedinthepixelsof W . Eachpixelisthenassignedthevalue R(x,y )= detE (x,y ) κtr (E (x,y ))2 , with κ beingaconstant.Cornersarethendetectedasthelocalmaximaof R(x,y ).Themaindifficultyin3Dliesinthecomputationofthe neighborhood.SipiranandBustosproposetoconsiderthe k -ring neighborhood Nk (v ) ofthevertex v tobeanalyzed.Thecentroidof Nk (v ) is calculated,thentheverticesinthisneighborhoodarerotatedsothatthe normalofthebestfittingplanegoingthroughthecentroidalignswiththe z -axis.Then,aparaboloid f (x,y ) fittingthetransformedneighborhoodis computed,andthepartialderivativesof f in x and y areusedtocomputethe matrix E (v ).
Similarly,Zaharescu etal.proposedanadaptedversionofthedifference ofGaussians(DoG)frameworkformeshes,whichiscalledMeshDOG
[ZAH12].Originally,thisframeworkconvolvestheintensityvaluesofthe pixelsintheimagewithGaussiankernelsofincreasinglylargevariance, leadingtoincreasinglyblurredversionsoftheimage[MAR80]. Thesubtractionoftwosuccessiveresultsoftheconvolutionenhancesthe highfrequenciesintheimageandallowsthedetectionofedges,i.e. connectedsetsofpixelswithasharpintensitychange.Alternatively,a scale-spacerepresentation oftheimagecanbebuilt.Thisisdonebyfirst convolvingtheimagewithaGaussiankernelofauser-definedvariance,then iterativelyconvolvingtheresultwiththesameGaussiankernel.The MeshDOGdetectorproposedbyZaharescu etal.buildssuchascale-space representation,usinggeodesicdistancesbetweenavertexanditsneighborsto definetheGaussiankernel.Featureverticesarethenselectedamongthe maximainthisscale-space.Notethatthemethodhasbeendesigned independentlyofthescalarfunctiondefinedoverthemesh.Inotherwords, thevalueusedforeachvertexisnotnecessarilyrestrictedtothelocal geometryandcaninclude,forexample,colorinformation.
I.3.4. Surfacefeaturesfromamathematicalpointofview Wehaveseenintheprevioussectionsthatdefiningdistinctiveattributes,to becalledfeatures,onameshedsurfacecanbedoneindifferentways. Featurescanbedefinedbyexpertsoftheapplicationdomain,withtheaimof distinguishingrelevantlocationsonthesurface.Thisis,forexample,thecase intopography(sectionI.3.1).Invisualperception(sectionI.3.2),featuresare salientpointsforthehumaneye.Theircomputationoftenusespropertiesof thehumanvisualsystem.Finally,inthemachinevisionapproach (sectionI.3.3),featuresaredefinedwithrespecttocapturedgeometricor appearanceinformation,sothattheypossessusefulpropertiessuchas invariancewithrespecttosometransformations.Theprocesstodetectthemis usuallyfullyautomatic.
Intheremainderofthisbook,wereviewsurfacefeaturesasdefinedintwo areasofmathematics,namely geometry (Chapter1)and topology (Chapter2). Whythesetwo?Geometrygivestoolstoexpresstheshapeofthesurface locally,whiletopologyexploresit globally.Moreover,geometrytakes distances onthesurfaceintoaccount,whiletopologyseeksforinvariantson thesurfacewhenitiscontinuouslydeformed.Bothcanbecombinedand algorithmshavebeendevelopedtocomputetopologicalfeatureswithspecific
geometricproperties,orgeometricobjectsthatcapturesometopologyofthe surface(seesection2.3).
Computingmathematicalfeaturesondiscrete,point-sampledsurfaces suchasmeshesleadstoseveralproblems,sincethesefeaturesareinitially definedinthecontinuoussetting.Thefirstofthemisthedefinitionofdiscrete counterpartsforsuch“continuous”features.Thiscanbetrivial(e.g.the numberofconnectedcomponentsandthegenus,section2.1.1)butisoften challenging(e.g.curvature,section1.3).Thesecondoneisthecomputation itself,whichcanbepronetoinaccuracies(e.g.curvatureagain)orbe time-consuming(e.g.homologygroups,section2.2).
ThesechallengesarediscussedinbothChapters1and2,wherewefirst recallhowfeaturesaredefinedinthecontinuouscase,beforereviewingthe definitionsandfeaturecomputationalgorithmsinthediscretecase.Chapter3 thendetailssomeapplicationfields,suchasmedicine,geologyorbotany,for whichcomputingpreviouslydefinedsurfacefeaturescanbeuseful.
GeometricFeaturesbasedonCurvatures 1.1.Introduction
In1983,theauthorsof[HAR83]proposedtouse differentialgeometry (i.e.themathematicalanalysisofthegeometryof3Dcurvesandsurfaces)to describetheshapeofadiscretesurface(intheircase,definedasanelevation image).Forthispurpose,theyintroducedthe topographicprimalsketch, whichiscomposedoffeaturepoints(aspeaks,pitsorsaddles),featurelines (asridgesorravines)andfeaturesurfacepatches(whichmaybeflat). Twoyearslater,theauthorsof[BRA85]describedanotherdifferential geometry-basedframeworktoanalyzetheshapeof3Dsurfacesandthey applieditonseveralrealexamples.Theyalsousedfeaturelines(ascurvature lines)andplanarsurfacepatches.Duringthesameperiod,inhisdissertation [BES88a],Beslproposedtocomputethedifferentialparametersofasurface inordertocreatea HK-signmap thatallowsthesegmentionofasurfaceinto homogeneousregionswheresomebasicgeometricprimitivescanbefitted.
Sincethen,extensiveresearchhasbeendoneontheextractionandthe applicationofgeometricfeaturesbasedondifferentialgeometry.In section1.2,weproposeanoverviewinanutshell(butwiththemathematical formulas)ofthedifferentialgeometryofsurfaces.Insection1.3,wepresent themainmethodsthatallowustoefficientlycomputethedifferential parametersonadiscrete3Dmesh.Insections1.4and1.5,wefocus respectivelyonlineandsurfacefeatures.
2GeometricandTopologicalMeshFeatureExtractionfor3DShapeAnalysis
1.2.Somemathematicalremindersofthedifferentialgeometryof surfaces
Thefollowingremindersareessentiallybasedonthebook[HOS92].More detailscanbefoundinmanymathematicsbookssuchas[WEA55],[CAR76], [SPI99],[TOP05]or[PAT10].
1.2.1. Fundamentalformsandnormalcurvature Let Σ beasurfaceofclass C k with k ≥ 3,whichisparameterizedby (u,v ). Σ isthendefinedbythesetofpoints P(u,v )= {x(u,v ),y (u,v ),z (u,v )}.
Aninfinitesimaldisplacementaroundthepoint P willbemodeledasthe vector dP,whichwillbeinthetangentplanedefinedbytheframe (P, ∂ P ∂u , ∂ P ∂v ):
Thenormofthisdisplacementcanbecomputedas:
Ifwedefinetheterms E , F and G as:
weget:
Thisexpressioniscalledthe firstfundamentalform ofthesurface.Its coefficients E , F and G enableustocalculate dP thatdefinesthelengthsof localcurvesonthesurfacearound P.Theyarealsousedtodefinetheareaof localregions.
Letusnowdefine n asthenormalvectorat P,i.e.thevectorgoingthrough P andorthogonaltothetangentplane.Foranyunitvector t inthetangent
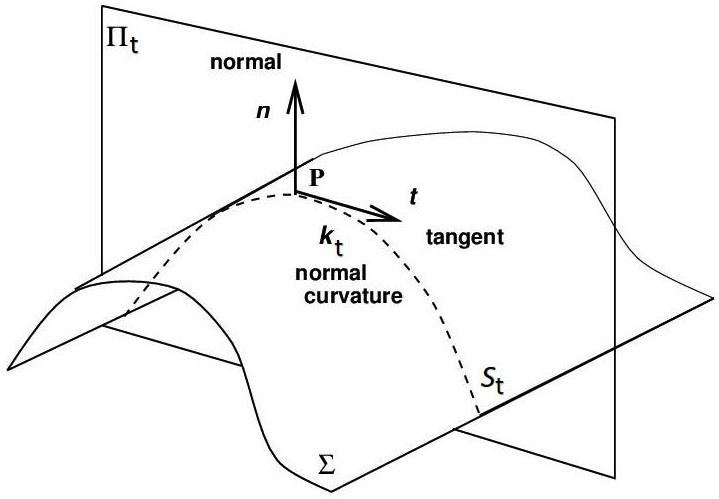
plane,wecandefinetheplane Πt thatgoesthrough P andcontains n and t. Πt iscalleda normalplane to Σ andcuts Σ alongtheplanecurve St ,whichis calledthe normalsection alongthedirection t (seeFigure1.1).
Figure1.1. Atapoint P,thenormalplane Πt isdefinedbythe normalvector n andthetangentvector t Πt cuts Σ alongaplane curve St .Thecurvatureof St in P iscalledthe normalcurvature kt at P ofthesurface Σ alongthedirection t
Byconstruction, t and n are,respectively,thetangentandthenormal vectorof St at P.Thecurvatureoftheplanecurve St at P isaninteresting parametertocharacterizethelocalshapeof Σ around P alongthedirection t. Thiscurvature,denoted kt ,isgivenbythefirstFrenet–Serretformulathat relatesthetangentandthenormalvectorsofaplanarcurve:
t ds = kt n [1.2] where s isthearclength(alsocalledthecurvilinearabscissa)along St thatis definedby ds = |dP|.
Thisimplies:
4GeometricandTopologicalMeshFeatureExtractionfor3DShapeAnalysis
Wecandeveloptherightexpressionwithrespecttotheparameters (u,v ) byusingthechainrule:
Adotproductwith n eliminatesthetwofirsttermsbecause
belongtothetangentplanewhichisorthogonalto n.Wethenget:
and
Theparameters L, M and N arecalledthecoefficientsofthe second fundamentalform ofthesurface.
As ds2 =(dP)2 ,wecanrewriteequation[1.5]byusingequation[1.1]as:
kt iscalledthe normalcurvature of Σ atpoint P alongthedirection t.
Notethatanotherconventionexists,wherethesignofthecurvatureis inverted(i.e. dt/ds = kt n).Thischangesthesigninmostofthe mathematicalexpressionsgiveninthischapter,asexplainedinTable3.2of [PAT10].
1.2.2. Principalcurvaturesandshapeindex
Now,ifweset γ = dv/du,definedforalldirectionsexceptalongthe u isoparametriclines,wecandefineanytangentvector t withrespectto γ using equation[1.4]: t = du ds ∂
Letusnowparameterizethenormalcurvature kt by γ andwriteitas k (γ ). As dv = γdu,equation[1.6]becomes:
k (γ )= L +2Mγ + Nγ 2 E +2Fγ + Gγ 2
Letusstudytheextremalvalueswhenthecuttingplane Πt rotatesaround theaxisdefinedby(P, n). k (γ ) isthenaperiodicfunctionastheplane Πt is invariantafterahalf-turn.Moreover,as k isacontinuousfunctionof γ ,there areamaximumandaminimumwhicharedefinedby:
dk (γ ) dγ =0
Ifwedifferentiateequation[1.8]withrespectto γ andifweapplytheabove extremumcondition,weget:
Andifwesubstitutethisresultinequation[1.8]:
Wecannowwrite γ asafunctionof k (γ ) inthefirstequationandeliminate γ inthesecondone,whichleadsto:
6GeometricandTopologicalMeshFeatureExtractionfor3DShapeAnalysis
Weobtainaquadraticequationin k (γ ).Inthegeneralcase,thetworoots correspondtothetwoextrema(onemaximumandoneminimum)ofthe normalcurvaturewhicharecalledthe principalcurvatures andaredenoted k1 and k2 .
Thearithmeticmeanofthetwoprincipalcurvatures km = 1 2 (k1 + k2 ) is calledthe meancurvature.
Theproductofthetwoprincipalcurvatures kg = k1 .k2 iscalledthe Gaussiancurvature.Inparticular,theGaussiancurvatureallowsustodefine thelocalshapeofthesurfaceas:
– kg > 0:thetwoprincipalcurvatureshavethesamesign.Itimpliesthat allthenormalcurvaturesareofthesamesignregardlessofthedirection.This meansthatthesurfaceiseitherlocallyconvexorlocallyconcave;
– kg < 0:thetwoprincipalcurvatureshaveanoppositesign.Thenormal curvaturechangesitssignandvanishesalongadirection.Thismeansthat locallythesurfacegoesthroughitstangentplane.
Inthecasewherethereisauniqueroot,itmeansthat k1 = k2 andthat thenormalcurvaturehasaconstantvalueregardlessofthedirection.Thisis possibleonlyifthesurfaceislocallyplaneorsphericalaroundthepoint P. Suchapointisthencalledan umbilic.
Inordertocharacterizetheshapeofasurfacewithauniqueparameter,the shapeindex wasproposedin[KOE92]:
s takesitsvaluesin [ 1, 1].Positive(respectivelynegative)valuescorrespond toconvex(resp.concave)partsandtheextremalvalues 1 or 1 characterize umbilics.
1.2.3. Principaldirectionsandlinesofcurvature
Wecall principaldirections thedirectionsofthetangentvectorsalong whichthenormalcurvatureisextremal.Inthegeneralcase,wehavetwo
distinctprincipaldirectionscorrespondingtotheprincipalcurvatures k1 and k2 whicharedefinedbythetwotangentvectors t1 and t2 .Notethatwetalk ofdirectionssothesenseofthetangentvectorsmustnotbetakeninto account.Thus,theprincipaldirectionassociatedwith k1 canbedefinedby either t1 or t1 .If P isanumbilic,weconsiderthatallthedirectionsare principal.
Exceptinthislastcase,wecancalculatethedotproductbetweenthetwo principaldirections.Forthis,weusetheexpressionofthetangentvectorgiven inequation[1.7]:
Bydevelopingandusing E , F and G,weget:
Now,wearegoingtodefineaquadraticequationwhosesolutionsarethe valuescorrespondingto γ1 and γ2 .Forthis,wewrite k (γ ) asafunctionof γ byusingequation[1.9]andeliminateitinequation[1.10].Weobtain:
Thisallowsustocomputethesumandtheproductoftherootsofthis equationas:
γ1 + γ2 = NE GL MG NF γ1 γ2 = FL ME MG NF
Ifweusethesetwoexpressionsinequation[1.13],weget:
t1 · t2 =0
Thisprovesthattheprincipaldirectionsare orthogonal (exceptwhenthe pointisanumbilic).
8GeometricandTopologicalMeshFeatureExtractionfor3DShapeAnalysis
Wecanalsodrawonthesurface Σ thecurveswhicharetangent,ateach point,tothedirectionofoneoftheprincipalcurvatures t1 or t2 .Thesecurves arecalled linesofcurvature.Duetothepropertiesoftheprincipalcurvatures, wecanconcludethattwolinesofcurvaturepassthrougheachnon-umbilic pointandthattheyareorthogonal.
AswecanseeontheexampleoftheellipsoidinFigure1.2,thelinesof curvatureformanetworkoforthogonalcurvesalloverthesurfaceexceptat umbilics.Notethatforthislastparticularcase,thelocalpatternoflinesof curvaturehasbeenintensivelystudiedin[SOT08].
Figure1.2. Networkoflinesofcurvaturesonanellipsoid:somelinesof curvaturearevisualizedinblueandpink,thetwovisibleumbilics(the twoothersareontheopposite)arelocalizedasreddots 1.Foracolor versionofthisfigure,seewww.iste.co.uk/mari/analysis.zip
Atanypoint P ofthesurface Σ,wehaveanorthogonalityrelationship betweenthesurfacenormal n andanytangentvector t: n · t =0.
Now,ifwemoveonthesurfacealong t byadistance ds,wecanthenwrite:
1http://commons.wikimedia.org/wiki/File%3AEllipso-KL-NP.svgbyAg2gaeh[CCBYSA4.0]