ChargeandEnergyTransferDynamicsin MolecularSystems
FourthEdition
VolkhardMayandOliverKühn
Authors
Dr.VolkhardMay Humboldt-UniversitätzuBerlin InstitutfürPhysik,Newtonstraße15 12489Berlin Germany
Prof.Dr.OliverKühn UniversitätRostock InstitutfürPhysik Albert-Einstein-Str.23-24 18059Rostock Germany
CoverImage: FigurecourtesyofOliver Kühn
Allbookspublishedby WILEY-VCH arecarefully produced.Nevertheless,authors,editors,and publisherdonotwarranttheinformation containedinthesebooks,includingthisbook, tobefreeoferrors.Readersareadvisedtokeep inmindthatstatements,data,illustrations, proceduraldetailsorotheritemsmay inadvertentlybeinaccurate.
LibraryofCongressCardNo.: appliedfor
BritishLibraryCataloguing-in-PublicationData Acataloguerecordforthisbookisavailable fromtheBritishLibrary.
Bibliographicinformationpublishedby theDeutscheNationalbibliothek TheDeutscheNationalbibliotheklists thispublicationintheDeutsche Nationalbibliografie;detailedbibliographic dataareavailableontheInternetat <http://dnb.d-nb.de>.
©2023WILEY-VCHGmbH,Boschstr.12, 69469Weinheim,Germany
Allrightsreserved(includingthoseof translationintootherlanguages).Nopartof thisbookmaybereproducedinanyform–by photoprinting,microfilm,oranyother means–nortransmittedortranslatedintoa machinelanguagewithoutwrittenpermission fromthepublishers.Registerednames, trademarks,etc.usedinthisbook,evenwhen notspecificallymarkedassuch,arenottobe consideredunprotectedbylaw.
PrintISBN: 978-3-527-33978-5
ePDFISBN: 978-3-527-69626-0
ePubISBN: 978-3-527-69628-4
oBookISBN: 978-3-527-69627-7
Typesetting Straive,Chennai,India
Contents
PrefacetotheFourthEdition xiii
PrefacetotheThirdEdition xv
PrefacetotheSecondEdition xvii
PrefacetotheFirstEdition xix
1Introduction 1
2ElectronicandVibrationalMolecularStates 7
2.1Introduction 7
2.2MolecularSchrödingerEquation 9
2.3Born–OppenheimerSeparation 11
2.3.1Born–OppenheimerApproximation 13
2.4ElectronicStructureMethods 15
2.4.1TheHartree–FockEquations 17
2.4.2DensityFunctionalTheory 19
2.5PotentialEnergySurfaces 21
2.5.1HarmonicApproximationandNormalModeAnalysis 24
2.5.2OperatorRepresentationoftheNormalModeHamiltonian 27
2.5.3ConstructionofSystem–BathModels 31
2.6AdiabaticversusDiabaticRepresentationoftheMolecular Hamiltonian 36
2.6.1AdiabaticPicture 36
2.6.2DiabaticPicture 37
2.6.3Two-StateCase 40
2.7Condensed-phaseApproaches 42
2.7.1DielectricContinuumModel 43
2.7.1.1MediumElectrostatics 43
2.7.1.2ReactionFieldModel 47
2.7.2ExplicitQuantum-classicalSolventModel 49
2.8Supplement 51
2.8.1Franck–CondonFactors 51
2.8.2TheTwo-levelSystem 52
2.8.3TheLinearMolecularChainandtheMolecularRing 55 References 57 FurtherReading 57
3DynamicsofIsolatedandOpenQuantumSystems 59
3.1Introduction 60
3.2Time-dependentSchrödingerEquation 66
3.2.1WavePackets 66
3.2.2TheInteractionRepresentation 69
3.2.3MultidimensionalWavePacketDynamics 71
3.3TheGoldenRuleofQuantumMechanics 75
3.3.1TransitionfromaSingleStateintoaContinuum 75
3.3.2TransitionRateforaThermalEnsemble 78
3.3.3Green’sFunctionApproach 81
3.4TheNonequilibriumStatisticalOperatorandtheDensityMatrix 84
3.4.1TheDensityOperator 84
3.4.2TheDensityMatrix 86
3.4.3EquationofMotionfortheDensityOperator 88
3.4.4WignerRepresentationoftheDensityOperator 90
3.4.5DynamicsofCoupledMultilevelSystemsinaHeatBath 93
3.5TheReducedDensityOperatorandtheReducedDensityMatrix 96
3.5.1TheReducedDensityOperator 96
3.5.2EquationofMotionfortheReducedDensityOperator 97
3.5.3Mean-fieldApproximation 98
3.5.4TheInteractionRepresentationoftheReducedDensityOperator 99
3.5.5TheNakajima–ZwanzigEquation 101
3.5.6Second-orderEquationofMotionfortheReducedDensity Operator 105
3.6QuantumMasterEquation 107
3.6.1MarkovApproximation 109
3.7TheReservoirCorrelationFunction 112
3.7.1GeneralPropertiesof Cu�� (t) 112
3.7.2HarmonicOscillatorReservoir 114
3.7.3TheSpectralDensity 116
3.7.4LinearResponseTheoryfortheReservoir 120
3.7.5ClassicalDescriptionof Cu�� (t) 122
3.8ReducedDensityMatrixinEnergyRepresentation 123
3.8.1TheQuantumMasterEquationinEnergyRepresentation 123
3.8.2MultilevelRedfieldEquations 126
3.8.2.1PopulationTransfer: a = b, c = d127
3.8.2.2CoherenceDephasing: a ≠ b, a = c, b = d129
3.8.2.3RemainingElementsof Rab,cd 129
3.8.3TheSecularApproximation 130
3.8.4StateExpansionoftheSystem–ReservoirCoupling 131
3.8.4.1SomeEstimates 132
3.9CoordinateandWignerRepresentationoftheReducedDensity Matrix 133
3.10ThePathIntegralRepresentationoftheDensityMatrix 135
3.11HierarchyEquationsofMotionApproach 140
3.12CoherenttoDissipativeDynamicsofaTwo-levelSystem 143
3.12.1CoherentDynamics 143
3.12.2DissipativeDynamicsUsingEigenstates 144
3.12.3DissipativeDynamicsUsingZeroth-orderStates 147
3.13Trajectory-basedMethods 149
3.13.1TheMean-fieldApproach 149
3.13.2TheSurfaceHoppingMethod 152
3.14GeneralizedRateEquations:TheLiouvilleSpaceApproach 155
3.14.1ProjectionOperatorTechnique 156
3.14.2GeneralizedRateEquations 157
3.14.3RateEquations 159
3.14.4TheMemoryKernels 159
3.14.5Second-orderRateExpressions 161
3.14.6Fourth-orderRateExpressions 164
3.14.6.1Three-levelSystemwithSequentialCoupling 165
3.15Supplement 168
3.15.1ThermofieldDynamics 168
3.15.2StochasticSchrödingerEquation 172
References 175
FurtherReading 176
4InteractionofMolecularSystemswithRadiationFields 177
4.1Introduction 178
4.2AbsorptionofLight 182
4.2.1LinearAbsorptionCoefficient 182
4.2.2Dipole–DipoleCorrelationFunction 184
4.3NonlinearOpticalResponse 186
4.3.1NonlinearPolarization 186
4.3.2NonlinearResponseFunctions 189
4.3.3EigenstateExpansionoftheResponseFunctions 191
4.3.4CumulantExpansionoftheResponseFunctions 194
4.3.5RotatingWaveApproximation 197
4.3.6Pump–ProbeSpectroscopy 198
4.3.7Two-dimensionalSpectroscopy 202
4.4FieldQuantizationandSpontaneousEmissionofLight 206 References 208
FurtherReading 209
5VibrationalDynamics:EnergyRedistribution,Relaxation,and Dephasing 211
5.1Introduction 211
5.2IntramolecularVibrationalEnergyRedistribution 215
5.2.1Zeroth-orderBasisandStateMixing 215
5.2.2GoldenRuleandBeyond 219
5.3IntermolecularVibrationalEnergyRelaxation 223
5.3.1TheSystem–ReservoirHamiltonian 223
5.3.2InstantaneousNormalModes 226
5.3.3GeneralizedLangevinEquation 228
5.3.4ClassicalForce–ForceCorrelationFunctions 231
5.3.5DissipativeDynamicsofaHarmonicOscillator 234
5.4PolyatomicMoleculesinSolution 237
5.4.1System–ReservoirHamiltonian 237
5.4.2HigherOrderMultiquantumRelaxation 238
5.5Quantum–ClassicalApproachestoRelaxationandDephasing 243 References 247 FurtherReading 247
6IntramolecularElectronicTransitions 249
6.1Introduction 249
6.1.1OpticalTransitions 250
6.1.2InternalConversionProcesses 255
6.2TheOpticalAbsorptionCoefficient 255
6.2.1GoldenRuleFormulation 255
6.2.2TheDensityofStates 258
6.2.3AbsorptionCoefficientforHarmonicPotentialEnergySurfaces 260
6.2.4AbsorptionLineshapeandSpectralDensity 263
6.2.5CumulantExpansionoftheAbsorptionCoefficient 264
6.2.6AbsorptionCoefficientforModelSpectralDensities 266
6.3AbsorptionCoefficientandDipole–DipoleCorrelationFunction 269
6.3.1AbsorptionCoefficientandWavePacketPropagation 269
6.3.2AbsorptionCoefficientandReducedDensityOperatorPropagation 273
6.3.3MixedQuantum–ClassicalComputationoftheAbsorption Coefficient 275
6.4TheEmissionSpectrum 280
6.5OpticalPreparationofanExcitedElectronicState 281
6.5.1WaveFunctionFormulation 281
6.5.1.1CaseofShortPulseDuration 284
6.5.1.2CaseofLongPulseDuration 284
6.5.2DensityMatrixFormulation 284
6.6InternalConversionDynamics 286
6.6.1TheInternalConversionRate 287
6.6.2UltrafastInternalConversion 288
6.7Supplement 290
6.7.1AbsorptionCoefficientforDisplacedHarmonicOscillators 290 References 294 FurtherReading 294
7ElectronTransfer 295
7.1ClassificationofElectronTransferReactions 295
7.2TheoreticalModelsforElectronTransferSystems 305
7.2.1TheElectronTransferHamiltonian 305
7.2.2TheElectron–VibrationalHamiltonianofaDonor–Acceptor Complex 310
7.2.2.1TheSpin-BosonModel 312
7.2.2.2TwoIndependentSetsofVibrationalCoordinates 313
7.2.3Electron–VibrationalStateRepresentationoftheHamiltonian 314
7.3RegimesofElectronTransfer 315
7.3.1Landau–ZenerTheoryofElectronTransfer 319
7.4NonadiabaticElectronTransferinaDonor–AcceptorComplex 323
7.4.1High-temperatureCase 323
7.4.2High-temperatureCase:TwoIndependentSetsofVibrational Coordinates 327
7.4.3Low-temperatureCase:NuclearTunneling 330
7.4.4TheMixedQuantum–ClassicalCase 333
7.4.5DescriptionoftheMixedQuantum–ClassicalCasebyaSpectral Density 335
7.5Bridge-MediatedElectronTransfer 336
7.5.1TheSuperexchangeMechanism 338
7.5.2ElectronTransferThroughArbitraryLargeBridges 340
7.5.2.1CaseofSmallIntrabridgeTransferIntegrals 340
7.5.2.2CaseofLargeIntrabridgeTransferIntegrals 341
7.6NonequilibriumQuantumStatisticalDescriptionofElectron Transfer 343
7.6.1UnifiedDescriptionofElectronTransferinaDonor–Bridge–Acceptor System 344
7.6.2TransitiontotheAdiabaticElectronTransfer 347
7.7HeterogeneousElectronTransfer 347
7.7.1NonadiabaticChargeInjectionintotheSolidStateDescribedina Single-ElectronModel 348
7.7.1.1Low-temperatureCase 351
7.7.1.2High-temperatureCase 352
7.7.1.3HET-inducedLifetime 352
7.7.2UltrafastPhotoinducedHETfromaMoleculeintoaSemiconductor. ACaseStudy 354
7.7.3NonadiabaticElectronTransferfromtheSolidStateintothe Molecule 355
7.8ChargeTransmissionThroughSingleMolecules 356
7.8.1InelasticChargeTransmission 359
7.8.1.1AnExample 360
7.8.2ElasticChargeTransmission 361
7.8.2.1AnExample 364
7.8.2.2InclusionofVibrationalLevels 365
7.9PhotoinducedUltrafastElectronTransfer 367
7.9.1QuantumMasterEquationforElectronTransferReactions 372
7.9.2RateExpressions 377
7.10Supplement 378
7.10.1Landau–ZenerTransitionAmplitude 378
7.10.2TheMultimodeMarcusFormula 379
Contents
7.10.3Second-orderElectronTransferRate 380
7.10.4Fourth-orderDonor–AcceptorTransitionRate 382
7.10.5RateofElasticChargeTransmissionThroughaSingleMolecule 385 References 387 FurtherReading 388
8ProtonTransfer 389
8.1Introduction 389
8.2ProtonTransferHamiltonian 395
8.2.1HydrogenBonds 395
8.2.2ReactionSurfaceHamiltonianforIntramolecularProtonTransfer 399
8.2.3TunnelingSplittings 400
8.2.4TheProtonTransferHamiltonianintheCondensedPhase 404
8.2.4.1AdiabaticRepresentation 405
8.2.4.2DiabaticRepresentation 406
8.3AdiabaticProtonTransfer 407
8.4NonadiabaticProtonTransfer 410
8.5TheIntermediateRegime:FromQuantumtoQuantum–Classical HybridMethods 412
8.5.1MultidimensionalWavePacketDynamics 413
8.5.2SurfaceHopping 415
8.6Proton-coupledElectronTransfer 417 References 419 FurtherReading 419
9ExcitationEnergyTransfer 421
9.1Introduction 421
9.2TheAggregateHamiltonian 427
9.2.1TheIntermolecularCoulombInteraction 430
9.2.1.1Dipole–DipoleCoupling 432
9.2.2TheTwo-levelModel 433
9.2.2.1ClassificationoftheCoulombInteractions 433
9.2.3SingleandDoubleExcitationsoftheAggregate 436
9.2.3.1TheGroundStateMatrixElement 438
9.2.3.2TheSingleExcitedStateMatrixElements 438
9.2.3.3TheDoubleExcitedStateMatrixElements 439
9.2.3.4Off-DiagonalMatrixElementsandCouplingtotheRadiationField 440
9.2.3.5NeglectofIntermolecularElectrostaticCoupling 441
9.2.4IntroductionofDelocalizedExcitonStates 441
9.2.4.1TheMolecularHeterodimer 443
9.2.4.2TheFiniteMolecularChainandtheMolecularRing 443
9.3Exciton–VibrationalInteraction 444
9.3.1ExclusiveCouplingtoIntramolecularVibrations 445
9.3.2CouplingtoAggregateNormalModeVibrations 448
9.3.3DifferentiatingBetweenIntramolecularandReservoirNormalMode Vibrations 449
9.3.4Exciton–VibrationalHamiltonianandExcitonicPotentialEnergy Surfaces 449
9.4RegimesofExcitationEnergyTransfer 450
9.4.1QuantumStatisticalApproachestoExcitationEnergyTransfer 452
9.5TransferDynamicsintheCaseofWeakExcitonicCoupling:Förster Theory 453
9.5.1TheTransferRate 454
9.5.2TheFörsterRate 456
9.5.3NonequilibriumQuantumStatisticalDescriptionofFörster Transfer 458
9.5.3.1CaseofCommonVibrationalCoordinates 462
9.5.3.2CaseofVibrationalModulationoftheExcitonicCoupling 464
9.6TransferDynamicsintheCaseofStrongExcitonicCoupling 465
9.6.1RateEquationsforExcitonDynamics 465
9.6.2DensityMatrixEquationsforExcitonDynamics 466
9.6.3SiteRepresentation 468
9.6.4ExcitationEnergyTransferAmongDifferentAggregates 471
9.6.5ExcitonTransferintheCaseofStrongExciton–Vibrational Coupling 472
9.6.6NonperturbativeandNon-MarkovianExcitonDynamics 475
9.7OpticalPropertiesofAggregates 477
9.7.1CaseofNoExciton–VibrationalCoupling 479
9.7.1.1StaticDisorder 481
9.7.2InclusionofExciton–VibrationalCoupling 484
9.7.2.1The n-ParticleExpansion 484
9.7.2.2WeakExciton–VibrationalCoupling 487
9.7.2.3StrongExciton–VibrationalCoupling 488
9.8ExcitationEnergyTransferIncludingCharge-transferStates 490
9.8.1ExcitationEnergyTransferViaTwo-electronExchange 490
9.8.2Charge-transferExcitonsandChargeSeparation 493
9.9Exciton–ExcitonAnnihilation 496
9.9.1Three-levelDescriptionoftheMoleculesintheAggregate 498
9.9.2TheRateofExciton–ExcitonAnnihilation 499 9.10Supplement 500
9.10.1SecondQuantizationNotationoftheAggregateHamiltonian 500
9.10.2Photon-mediatedLong-rangeExcitationEnergyTransfer 501
9.10.2.1PreparatoryConsiderationsfortheRateComputation 503
9.10.2.2PhotonCorrelationFunctions 505
9.10.2.3TheRateofPhoton-mediatedExcitationEnergyTransfer 506
9.10.2.4SomeEstimates 508
9.10.3Fourth-orderRateofTwo-electron-transfer-assistedEET 509 References 513 FurtherReading 514
Index 515
PrefacetotheFirstEdition
Theinvestigationofthestationaryanddynamicalpropertiesofmolecularsystems hasalonghistoryextendingoverthewholecentury.Consideringthepastdecade only,oneobservestwotendencies:First,itbecamepossibletostudymoleculeson theirnaturalscales,thatis,withaspatialresolutionofsomeÅngström(10 10 m) andonatimescaledowntosomefemtoseconds(10 15 s).Andsecond,oneis abletodetectandmanipulatethepropertiesofsinglemolecules.Thisprogress comesalongwithasteadilygrowingnumberoftheoreticalandexperimentalefforts crossingthetraditionalborderlinesbetweenchemistry,biology,andphysics.In particular,thestudyofmoleculartransferprocessesinvolvingthemotionofelectrons,protons,smallmolecules,andintramolecularexcitationenergyresultedin adeeperunderstandingofsuchdiversephenomenaasthephotoinduceddynamics inlargemoleculesshowingvibrationalenergyredistributionorconformational changes,thecatalysisatsurfaces,andthemicroscopicmechanismsofchargeand energytransferinbiologicalsystems.Thelatterareofconsiderableimportance forunravelingthefunctionalityofproteinsandallrelatedprocessessuchasthe primarystepsofphotosynthesis,theenzymaticactivity,andthedetailsoftherepair mechanismsinDNAstrands,tomentionjustafewexamples.Inamoregeneral context,molecularelectronics,thatis,thestorageandprocessingofinformation inmolecularstructuresonananometerlengthscale,hasalsotriggeredenormous efforts.Finally,withtheincreasingsophisticationoflasersources,firststepstoward thecontrolofchemicalreactiondynamicshavebeentaken.
Theever-growingprecisionoftheexperimentsrequiresonthetheoreticalsideto havemicroscopicmodelsforsimulatingthemeasureddata.Forexample,theinterpretationofopticalspectroscopiesinatimeregionofsometenthsoffemtoseconds demandsforanappropriatesimulationofthemoleculardynamicsfortheconsidered system.Or,understandingthecharacteristicsofthecurrentflowingthroughasingle moleculeinthecontextofscanningtunnelingmicroscopyneedsdetailedknowledge oftheelectroniclevelstructureofthemoleculeaswellastheroleofitsvibrational degreesoffreedom.Thesefewexamplesalreadydemonstratethatadvancedtheoreticalconceptsandnumericalsimulationtechniquesarerequired,whicharethecombinationofmethodsknownfromgeneralquantummechanics,quantumchemistry, molecularreactiondynamics,solid-statetheory,nonlinearoptics,andnonequilibriumstatisticalphysics.
Suchabroadapproachisusuallybeyondthetheoreticaleducationofchemistsand biologists.Ontheotherhand,quantumchemistryandchemicalreactiondynamics arequiteoftennotonthecurriculumofphysicsstudents.Webelievethatthisdiscrepancyquitenaturallydoesnotfacilitatecommunicationbetweenscientistshavingdifferentbackgrounds.Therefore,itisoneofthemainintentionsofthepresent booktoprovideacommonlanguageforbridgingthisgap.
Thebookstartswithanintroductionandgeneraloverviewofdifferentconcepts inChapter1.Theessentialsoftheoreticalchemicalphysicsarethencoveredin Chapter2.Forchemistrystudentsthiswillbemostlyarepetitionofquantum chemistryandinparticularthetheoryofelectronicandvibrationalspectra.Itisby nomeansacompleteintroductionintothissubjectbutintendedtoprovidesome backgroundmainlyforphysicsstudents.Theprerequisitesfromtheoreticalphysics forthedescriptionofdynamicalphenomenainmolecularsystemsarepresented inChapter3.Here,wegiveadetaileddiscussionofsomegeneralaspectsofthe dynamicsinopenandclosedquantumsystems,focusingontransferprocessesin thecondensedphase.
Thecombinationofqualitativearguments,simplerateequations,andthepowerfulformalismofthereducedstatisticaloperatorconstitutesthebackboneofthe secondpartofthebook.WestartinChapter4withadiscussionofintramolecular transferofvibrationalenergythattakesplaceinagivenadiabaticelectronicstate. Here,wecoverthelimitsofisolatedlargepolyatomicmolecules,smallmolecules inamatrixenvironment,uptopolyatomicsinsolution.InChapter5,wethenturn toprocessesthatinvolveatransitionbetweendifferentelectronicstates.Special emphasisisputonthediscussionofopticalabsorption,whichisconsideredtobe areferenceexampleformoreinvolvedelectron-vibrationaltransferphenomena suchasinternalconversion,whichisalsopresentedinthischapter.Chapter6 thenoutlinesthetheoreticalframeofelectron-transferreactions,focusingmainly onintramolecularprocesses.Here,wedevelopthewell-knownMarcustheoryof electrontransfer,describenucleartunnelingandsuperexchangeelectrontransfer,anddiscusstheinfluenceofpolarsolvents.InChapter7,itwillbeshown that,eventhoughprotontransferhasmanyuniqueaspects,itcanbedescribed byadaptingvariousconceptsfromelectron-transfertheory.Theintermolecular excitationenergytransferinmolecularaggregatesisconsideredinChapter8.In particular,themotionofFrenkelexcitonscoupledtovibrationalmodesofthe aggregatewillbediscussed.Inthelimitofordinaryrateequations,thisleadsusto thewell-knownFörsterexpressionforthetransferrateintermsofemissionand absorptioncharacteristicsofthedonorandacceptormolecules,respectively.
Bypresentingavarietyoftheoreticalmodelsthatexistfordifferenttypesof transferprocessesonacommonformalbackground,wehopethattheunderlying fundamentalconceptsarebecomingvisible.Thisinsightmaypreparethereader totakeuponeofthemanychallengingproblemsprovidedbythisfascinating fieldofresearch.Somepersonalreflectionsonthecurrentandpossiblefuture developmentsaregiveninChapter9.
Theideaforwritingthisbookemergedfromlecturesgivenbytheauthorsat theHumboldtUniversityBerlin,theFreeUniversityBerlin,andattheJohannes
PrefacetotheFirstEdition xxi GutenbergUniversityMainzduringthepastdecade.Thesecourseshavebeen addressedtotheoreticallyandexperimentallyorientedundergraduateandgraduate studentsofMolecularPhysics,TheoreticalChemistry,PhysicalChemistry,and Biophysics,beinginterestedinthefastdevelopingfieldoftransferphenomena. Thebookisself-containedandincludesdetailedderivationsofthemostimportantresults.However,thereaderisexpectedtobefamiliarwithbasicquantum mechanics.Mostofthechapterscontainasupplementarypartwheremoreinvolved derivationsaswellasspecialtopicsarepresented.Attheendofthemaintext,we alsogivesomecommentsonselectedliterature,whichshouldcomplementthe studyofthisbook.
Ofcourse,thisbookwouldnothavebeenpossiblewithoutthehelp,thecritical comments,andthefruitfuldiscussionswithmanystudentsandcolleagues.Inthis respect,itisapleasureforustothankI.Barvik,N.P.Ernsting,W.Gans,L.González, O.Linden,H.Naundorf,J.Manz,S.Mukamel,A.E.Orel,T.Pullerits,R.Scheller, andD.Schirrmeister.Wearealsogratefulforcontinuousfinancialsupportthat hasbeenprovidedbytheDeutscheForschungsgemeinschaft,inparticularthrough theSonderforschungsbereich450“AnalysisandControlofUltrafastPhotoinduced Reactions.”
VolkhardMayandOliverKühn Berlin,September1999
Introduction
Theunderstandingoftransferphenomenain molecularsystems callsforaunified theoreticaltreatmentthatshouldhaveitsfoundationinamicroscopicdefinition oftheconstituentpartsandtheirinteractions.Therearethreeimportantquestions thatneedtobeansweredinthisregard. First,whatistheappropriatetheoretical descriptionofthemolecularsystem? Second,whatistheformofthedynamical equationsthatdescribethetransferprocess?And third,howcanthecomputed resultsberelatedtoexperimentalobservations?
Inwhatfollowstheterm“molecularsystem”willcoversinglemoleculesand simplemolecularaggregatesaswellaslargerarrangementsofmoleculessuchas supramolecularcomplexes.Inparticular,moleculesembeddedindifferenttypesof environmentswillbeofinterest.Here,thescoperangesfrommoleculesinsolution tobiologicalmacromoleculessuchasmembrane-boundproteincomplexes.The commonlinkbetweenthesemolecularsystemsisthattheyshow transferprocesses. By“transferprocess,”weunderstandtheflowofvibrationalenergyandthe dynamicsofelectrons,protons,andelectronicexcitationenergy.
Fromageneralpointofview,quantummechanicsgivestheframeworkforallphenomenaoccurringinmolecularsystems.Giventhebroadscopeoftransferprocesses tobediscussed,itisclearthatanexactquantummechanicaltreatmentisimpossibleifwegobeyondthelevelofsimplemodelsystems.Therefore,itisaparticular challengefortheorytodevelopversatilemodelsthatprovideanswerstotheinitially raisedthreequestions.
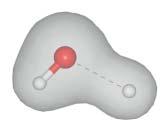
Chapter2addressesthefirstquestiondiscussingthestepsthatleadusfrom theformallyexacttosomeapproximatemolecularHamiltonoperator.Givena moleculeingasphase(vacuum)asshowninFigure1.1a,the Born–Oppenheimer separation ofnuclearandelectronicmotionscanbeperformed.Here,themolecular wavefunctionissplitupintoanelectronicandanuclearpart,aprocedurethatis justifiedbythelargemassdifferencebetweenbothtypesofparticles.Thisresults inaSchrödingerequationfortheelectronicwavefunctionalone,forgivenfixed positionsofthenuclei.Calculatingtheelectronicenergyspectrumfordifferent positionsofthenuclei,oneobtains potentialenergysurfaces thatgovernthemotion ofthenuclei.Thesepotentialenergysurfacesareattheheartofourunderstanding ofstationarymolecularspectraandmoleculardynamics.Ifnuclearandelectronic
ChargeandEnergyTransferDynamicsinMolecularSystems, FourthEdition.VolkhardMayandOliverKühn. ©2023WILEY-VCHGmbH.Published2023byWILEY-VCHGmbH.
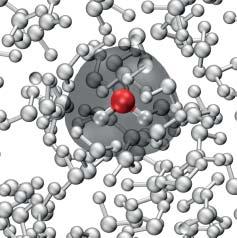
Figure1.1 Theproblemoftheinteractionbetweenelectronsandnucleiistransformedto sometractablelevelbyemployingtheBorn–Oppenheimerseparationoftheirmotions. (a)Three-atomicmolecule(H2 O)withtheelectrondensityshownfortheequilibrium distance(left)aswellasforastretchedbond(right).Theelectrondensityadjusts instantaneouslytotheconfigurationofthenuclei.Asaresult,apotentialenergycurveis formeddeterminingthedynamicsofthebonddistancecoordinate.(b)Ifthemoleculeis takenfromthegasintothecondensedphase,itsstationaryanddynamicpropertieshaveto takeintoaccounttheinteractionwiththesurroundingmolecules.Thismaygiverise,for instance,toachangeinequilibriumgeometryandelectrondensity(figurecourtesyof AshourAhmed).
motionareadiabaticallyseparable,thatisifthecouplingbetweendifferentelectronicstatesisnegligible,onecancarryouttheBorn–Oppenheimerapproximation. Undercertainconditions,however,theso-callednonadiabatictransitionsbetween differentelectronicstatesasaconsequenceofthenuclearmotionstakeplace.
IfwemovefromthegastothecondensedphaseasshowninFigure1.1b,theeffect ofthemolecule–environmentinteractionhastobetakenintoaccount.Thesimplest waytodothisistoaddanadditionalexternalpotentialtothemolecularHamiltonian.Often,theenvironmentcanbedescribedasamacroscopicdielectric,andits influencecanbejudgedfromitsdielectricproperties.
Havingdiscussedthestationarymolecularproperties,weturninChapter3to thesecondquestionrelatedto moleculardynamics.Here,thereaderwillbecome familiarwiththeconceptsrangingfromincoherenttocoherenttransferevents.The connectionbetweentheselimitsisprovidedbytherelevanttimescales;ofparticularimportanceistherelationbetweenintramolecularrelaxationandintermolecular transfertimes.Inviewofexperimentaladvancesinultrafastspectroscopy,ourtreatmentreflectsthehistoricalevolutionofknowledgeaboutmoleculardynamicsfrom simpletransferratestoquantummechanicalwavepacketdynamics.
Animportantingredientforthetheoreticalmodelingistheconceptofan open molecularsystemS interactingwithits environment (reservoir) R bycollision processesorviaothermeansofenergyexchange.Aschematicillustrationofthis
Figure1.2 Thetotalsystemconsistingofarelevantsystem(S )interactingwithareservoir (R)iscompletelydescribedbythequantum-statisticaloperator ̂ W .Bymeansofareduction procedure,onecanfocusontherelevantsystemusingthereducedstatisticaloperator ̂ �� Effectsofthe S –R interactionarestillaccountedfor.Inaddition,thesystemmaybe influencedbyexternalfields(wigglyline).
situationisgiveninFigure1.2.The relevant system S mayrepresentanytypeof molecule,butitmayalsocompriseselectedso-calledactivedegreesoffreedomofa particularmolecule.
Themostgeneraldescriptionofthetotalsystem, S plus R,isgivenbythe quantum-statisticaloperator ̂ W ,asindicatedintheleft-handpartofFigure1.2.This operatorisbasedontheconceptofa mixed quantumstateformedby S anditsmacroscopicenvironment.However,theoperator ̂ W containsmuchmoreinformation thanwilleverbeneeded,forinstance,tosimulateaparticularexperiment.Indeed,it istherelevantsystem S whosepropertiesweareinterestedin.Makinguseofareductionprocedure,weobtaina reducedstatisticaloperator ̂ �� thatcontainstheinformationonthedynamicsof S onlybutincludingtheinfluenceoftheenvironment R (right-handpartofFigure1.2).Whenderivingequationsofmotionforthereduced statisticaloperator,theso-calledquantummasterequations,anumberofapproximationshavetobeinvoked.Mostfundamentalinthisrespectwillbetheassumption ofaweakinteractionbetweenthesystem S andthereservoir R,whichinpractice requiresaproperseparationintorelevantandenvironmentalcoordinatesforthe molecularsystemathand.Undercertainconditions,however,anumericalexact descriptionofthedynamicsoftherelevantsystembecomespossible.Ifthereisno interactionatall,thequantummasterequationisequivalenttothetime-dependent Schrödingerequation.Thisistheregimeof coherent dynamics.Iftheinteraction isnotnegligible,however,thesystemdynamicsgraduallychangeswithincreasing couplingstrengthfroma partiallycoherent onetoan incoherent one.Theincoherent motionofaquantumsystemiscommonlydescribedusingordinaryrateequations thatarebasedonthe GoldenRule rateexpressionofquantummechanics.
Theconceptofthestatisticaloperatorprovidesa quantum-statistical descriptionof S and R.However,inmanysituationsitissufficienttodescribe R bymeansofclassicalmechanics.Then, S canbecharacterizedbyawavefunction Ψ,andthedynamics oftheenvironmentaldegreesoffreedomisgovernedbyNewton’sequations.Often, thedynamicsissplitupinsuchawaythattheclassicalparticlesmoveinthemean fieldofthequantumparticle.ThissituationisvisualizedinFigure1.3.
Theoverwhelmingamountofdataontransferprocessesinmolecularsystems isobtainedbyspectroscopictechniquesworkingintheinfrared,thevisibleto
Figure1.3 Mixedquantum–classical descriptionofcondensedphasedynamics. Theclassicalparticlesmoveinthemean fieldgeneratedbythequantumparticle describedbythewavefunction Ψ.
ultraviolet,and,morerecently,alsointheX-rayregion.Wewilldiscussthethird questionrelatedtoexperimentalobservationmostlyinthecontextofspectroscopy, withfocusontheinfraredtoultravioletdomain.Asameansofpreparation, Chapter4givesabriefaccountonthegeneraltheoreticalconceptsoftheinteraction ofmolecularsystemswiththeelectromagneticradiationfield.Further,aformulationoflinearandnonlinearspectroscopyintermsofcorrelationfunctionswillbe introduced.
ThegeneralconceptspresentedinChapters2–4arethenappliedtodescribedifferenttransferphenomena.Inprinciple,transferprocessescanbeclassifiedaccording tothetypeoftransferredparticle.Inaddition,onecandistinguishbetweenintra-and intermolecularparticletransfer.Thecommonframeisprovidedbythemolecular SchrödingerequationtogetherwiththeBorn–Oppenheimerseparationofelectronic andnuclearmotionsasmentionedabove.
Thecouplednucleardynamicsinpolyatomicmoleculesthatmightbeimmersed insomecondensedphaseenvironmentistreatedinChapter5.Weshowhowaninitiallypreparedvibrationalstatedecayswhileitsexcitationenergyisdistributedover allpossibleenvironmentalmodes,asillustratedintheleft-handpartofFigure1.4. Forsmallpolyatomicmolecules,theenergyflowoutoftheinitialstateiscalled intramolecularvibrationalenergyredistribution.Forcondensedphasesituations,the dissipationofenergyintotheenvironmentiscalled vibrationalenergyrelaxation.In bothcases,thetransferredobjectsarethequantaofvibrationalenergy.
Thepreparationoftheinitialstatecanbeduetoanopticaltransitionbetween twoelectronicstatesasaconsequenceoftheinteractionbetweenthemolecularsystemandanexternalelectromagneticfield(cf.Figure1.4).InChapter6,wediscuss theprocessesofphotonabsorptionandemissionsketchedinFigure1.4.Itwillbe shownthatthecoupledelectron-vibrationaldynamicsresponsiblefortheabsorptionlineshapecanbedescribedbyacombineddensityofstatesthatistheFourier transformofsomecorrelationfunction.Thistheoreticalresultwillturnouttobe quitegeneral.Inparticular,weshowthatdifferenttypesoftransferprocessescanbe accommodatedinsuchaframework.Forexample,the internalconversion dynamics ofnonadiabaticallycoupledelectronicstates(right-handpartofFigure1.4)can,in theincoherentlimit,bedescribedbyacombineddensityofstates.
Theexternalfieldinteraction,ontheotherhand,providesthemeansforpreparingnonequilibriuminitialstatesthatcanactasadonorinaphotoinduced
Figure1.4 Schemeofmolecularpotentialenergysurfacesincludingthelevelsofthe quantizedmotionofsomereactioncoordinate.Afteropticalpreparationofanelectronically andvibrationallyexcitedinitialstate(absorption),differenttransferprocessescanoccur.If theelectronicstateisnotchanged,butthereisacouplingtosomemanifoldofvibrational states,intramolecularvibrationalenergyredistribution(IVR)orvibrationalenergy relaxation(VER)canbeobserved.Ifthereissomecouplingtoanotherelectronicstate, intramolecularinternalconversion(IC),orelectrontransfer(ET)takesplace.Atthesame time,onehasVERasindicatedbythewigglylines.Inaddition,thesystemmayreturntothe groundstatebyemittingaphoton.
electron-transferreaction,whichisdiscussedinChapter7.Theconcerted electron-vibrationaldynamicsaccompanyingelectron-transferreactionscanoften bemodeledintheso-calledcurve-crossingpictureoftwocoupledpotentialenergy surfacesrepresentingtwoelectronicstatesalonga reactioncoordinate (right-hand partofFigure1.4).Generalizationsofthispicturetolargermolecularsystemsand tothecasewherethemoleculeisincontactwithmetalelectrodesandavoltageis appliedwillalsobediscussed.
Incontrast,theprotonorhydrogenatomtransferinvestigatedinChapter8usually doesnotinvolveelectronictransitions.InFigure1.5,wehavesketchedatypicalsituationforintramolecularprotontransferthatisrealizedasanisomerizationreaction intheadiabaticelectronicgroundstate.Sincetheprotonhasarathersmallmass, tunnelingprocessesmayplayanimportantroleforprotontransfer.Thesmallmass ratiobetweentheprotonandtheotherheavyatomsprovidesthebackgroundfor
Figure1.5 Hydrogenbonding,which governstheprotontransfer(PT)dynamics, oftenleadstoadoubleminimumpotential alongareactioncoordinate.Theinteraction betweentheprotonandsomeenvironment maycausevibrationalrelaxation(wiggly lines).
Figure1.6 Excitationenergytransfer(EET),whichoccursafteropticalpreparationofan electronicallyandvibrationallyexcitedinitialstate(donor,left).TheCoulombinteractionis responsiblefordeexcitationofthedonorandexcitationoftheacceptor(right).Thenuclear dynamicsmaybesubjecttorelaxationprocesses(wigglylines).Often,twoindependent nuclear(reaction)coordinatesareusedforthedonorandtheacceptormolecules.
theintroductionofasecondBorn–Oppenheimerseparation.Thiswillenableusto adaptmostoftheconceptsofelectron-transfertheorytothecaseofprotontransfer.
InChapter9,wediscussexcitationenergytransferortheso-calledexcitontransfer inmolecularaggregatesasanotherexampleofcoupledelectron-vibrationalmotion. InFigure1.6,themechanismofexcitationenergytransferinthelimitoflocalized excitationsisshown.Thedonor(left)isinitiallyexcited,forexample,byanexternal field.AsaconsequenceoftheCoulombinteraction,excitationenergyistransferred betweentheexcitedmoleculeandsomeacceptormolecule(right).Often,donorsand acceptorsretaintheirchemicalidentityuponaggregationand,therefore,areusually describedbydifferentsetsofnuclear(reaction)coordinates.Intheincoherentlimit, therateoftheprocesscanbeexpressedintermsofanoverlapintegralbetweendonor emissionandacceptorabsorptionspectra.IftheCoulombinteractionbetweendifferentmoleculesbecomeslargeenough,thenexcitationenergytransferhastobe discussedbyintroducingquantummechanicalsuperpositionstatesofallexcited molecules,theso-calledFrenkelexcitons.Theirintroductiongivesanewviewon excitationenergytransferviathemotionofspatiallydelocalizedstates.Arigorous nonequilibriumquantum-statisticalmodelcandescribeboththeincoherentandthe coherentlimits.