PartitionofUnityMethods
StéphaneP.A.Bordas
UniversityofLuxembourg,Luxembourg,UK
AlexanderMenk
RobertBoschGmbH,Germany
SundararajanNatarajan
Indian InstituteofTechnologyMadras,India
Thiseditionfirstpublished2024
© 2024JohnWiley&SonsLtd
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedinaretrievalsystem,ortransmitted,inanyformorbyanymeans, electronic,mechanical,photocopying,recordingorotherwise,exceptaspermittedbylaw.Adviceonhowtoobtainpermissiontoreuse materialfromthistitleisavailableat http://www.wiley.com/go/permissions
Therightofeditornamestobeidentifiedastheauthorsoftheeditorialmaterialinthisworkhasbeenassertedinaccordancewithlaw.
RegisteredOffices
JohnWiley&Sons,Inc.,111RiverStreet,Hoboken,NJ07030,USA
JohnWiley&SonsLtd,TheAtrium,SouthernGate,Chichester,WestSussex,PO198SQ,UK
Fordetailsofourglobaleditorialoffices,customerservices,andmoreinformationaboutWileyproductsvisitusat www.wiley.com
Wileyalsopublishesitsbooksinavarietyofelectronicformatsandbyprint-on-demand.Somecontentthatappearsinstandardprintversions ofthisbookmaynotbeavailableinotherformats.
Trademarks: WileyandtheWileylogoaretrademarksorregisteredtrademarksofJohnWiley&Sons,Inc.and/oritsaffiliatesintheUnited Statesandothercountriesandmaynotbeusedwithoutwrittenpermission.Allothertrademarksarethepropertyoftheirrespectiveowners. JohnWiley&Sons,Inc.isnotassociatedwithanyproductorvendormentionedinthisbook.
LimitofLiability/DisclaimerofWarranty
Whilethepublisherandauthorshaveusedtheirbesteffortsinpreparingthiswork,theymakenorepresentationsorwarrantieswithrespectto theaccuracyorcompletenessofthecontentsofthisworkandspecificallydisclaimallwarranties,includingwithoutlimitationanyimplied warrantiesofmerchantabilityorfitnessforaparticularpurpose.Nowarrantymaybecreatedorextendedbysalesrepresentatives,writtensales materialsorpromotionalstatementsforthiswork.Thisworkissoldwiththeunderstandingthatthepublisherisnotengagedinrendering professionalservices.Theadviceandstrategiescontainedhereinmaynotbesuitableforyoursituation.Youshouldconsultwithaspecialist whereappropriate.Thefactthatanorganization,website,orproductisreferredtointhisworkasacitationand/orpotentialsourceoffurther informationdoesnotmeanthatthepublisherandauthorsendorsetheinformationorservicestheorganization,website,orproductmay provideorrecommendationsitmaymake.Further,readersshouldbeawarethatwebsiteslistedinthisworkmayhavechangedordisappeared betweenwhenthisworkwaswrittenandwhenitisread.Neitherthepublishernorauthorsshallbeliableforanylossofprofitoranyother commercialdamages,includingbutnotlimitedtospecial,incidental,consequential,orotherdamages.
AcataloguerecordforthisbookisavailablefromtheLibraryofCongress
HardbackISBN:9780470667088;ePubISBN:9781118535882;ePDFISBN:9781118535899
CoverDesign:Wiley
CoverImage:CourtesyofAuthors
Setin9.5/12.5ptSTIXTwoTextbyIntegraSoftwareServicesPvt.Ltd,Pondicherry,India
Contents
ListofContributors xi
Preface xiii
Acknowledgments xv
1Introduction 1
1.1TheFiniteElementMethod 2
1.2SuitabilityoftheFiniteElementMethod 9
1.3SomeLimitationsoftheFEM 11
1.4TheIdeaofEnrichment 16
1.5Conclusions 19 References 21
2AStep-by-StepIntroductiontoEnrichment 23
2.1HistoryofEnrichmentforSingularitiesandLocalizedGradients 25
2.1.1Enrichmentbythe“MethodofSupplementarySingularFunctions” 25
2.1.2FiniteElementwithaSingularity 31
2.1.3PartitionofUnityEnrichment 33
2.1.4MeshOverlayMethods 35
2.1.5EnrichmentforStrongDiscontinuities 36
2.2WeakDiscontinuitiesforOne-dimensionalProblems 38
2.2.1ConventionalFiniteElementSolution 41
2.2.2eXtendedFiniteElementSolution 44
2.2.3eXtendedFiniteElementSolutionwithNodalSubtraction/Shifting 54
2.2.4Solution 55
2.3StrongDiscontinuitiesforOne-dimensionalProblem 58
2.4Conclusions 61 References 61
3PartitionofUnityRevisited 67
3.1Completeness,Consistency,andReproducingConditions 67
3.2PartitionofUnity 68
3.3Enrichment 69
3.3.1DescriptionofGeometryofEnrichmentFeatures 71
3.3.2ChoiceofEnrichmentFunctions 75
3.3.3Impositionofboundaryconditions 80
3.3.4NumericalIntegrationoftheWeakForm 86
3.4NumericalExamples 86
3.4.1One-DimensionalMultipleInterface 86
3.4.2Two-DimensionalCircularInhomogeneity 89
3.4.3InfinitePlatewithaCenterCrackUnderTension 91
3.5Conclusions 95 References 96
4AdvancedTopics 99
4.1SizeoftheEnrichmentZone 99
4.2NumericalIntegration 100
4.2.1PolarIntegration 100
4.2.2EquivalentPolynomialIntegration 101
4.2.3ConformalMapping 102
4.2.4StrainSmoothinginXFEM 104
4.3BlendingElementsandCorrections 108
4.3.1BlendingBetweenDifferentPartitionsofUnity 108
4.3.2InterpolationErrorinBlendingElements 109
4.3.3AddressingBlendingPhenomena 113
4.4PreconditioningTechniques 116
4.4.1TheFirstPreconditionerProposedfortheXFEM 117
4.4.2AdomainDecompositionPreconditionerfortheXFEM 117 References 123
5Applications 125
5.1LinearElasticFractureinTwoDimensionswithXFEM 125
5.1.1InclinedCrackinTension 126
5.1.2ExampleofaCrackInclusionInteractionProblem 126
5.1.3EffectoftheDistanceBetweentheCrackandtheInclusion 127
5.2NumericalEnrichmentforAnisotropicLinearElasticFractureMechanics 130
5.3CreepandCrackGrowthinPolycrystals 133
5.4FatigueCrackGrowthSimulations 138
5.5RectangularPlatewithanInclinedCrackSubjectedtoThermo-MechanicalLoading 140 References 142
6Recovery-BasedErrorEstimationandBoundinginXFEM 145
6.1Introduction 145
6.2ErrorEstimationintheEnergyNorm.TheZZErrorEstimator 147
6.2.1TheSPRTechnique 148
6.2.2TheMLSApproach 149
6.3Recovery-basedErrorEstimationinXFEM 151
6.3.1TheSPR-CXTechnique 151
6.3.2TheXMLSTechnique 161
6.3.3TheMLS-CXTechnique 163
6.3.4OntheRolesofEnhancedRecoveryandAdmissibility 169
6.4RecoveryTechniquesinErrorBounding.PracticalErrorBounds. 174
6.5ErrorEstimationinQuantitiesofInterest 179
6.5.1Recovery-basedEstimatesfortheErrorinQuantitiesofInterest 179
6.5.2TheStressIntensityFactorasQoI:ErrorEstimation 181 References 187
7 ��-FEM:AnEfficientSimulationToolUsingSimpleMeshesforProblemsinStructure MechanicsandHeatTransfer 191
7.1Introduction 191
7.2LinearElasticity 194
7.2.1DirichletConditions 195
7.2.2MixedBoundaryConditions 199
7.3LinearElasticitywithMultipleMaterials 204
7.4LinearElasticitywithCracks 208
7.5HeatEquation 212
7.6ConclusionsandPerspectives 214 References 215
8eXtendedBoundaryElementMethod(XBEM)forFractureMechanicsandWaveProblems 217
8.1Introduction 217
8.2ConventionalBEMFormulation 218
8.2.1Elasticity 219
8.2.2HelmholtzWaveProblems 222
8.3ShortcomingsoftheConventionalFormulations 226
8.4PartitionofUnityBEMFormulation 228
8.5XBEMforAccurateFractureAnalysis 228
8.5.1WilliamsExpansions 228
8.5.2LocalXBEMEnrichmentatCrackTips 229
8.5.3Results 231
8.5.4AuxiliaryEquationsandDirectEvaluationofStressIntensityFactors 232
8.5.5FractureinAnisotropicMaterials 234
8.5.6Conclusions 235
8.6XBEMforShortWaveSimulation 235
8.6.1BackgroundtotheDevelopmentofPlaneWaveEnrichment 235
8.6.2PlaneWaveEnrichment 236
8.6.3EvaluationofBoundaryIntegrals 238
8.6.4CollocationStrategyandSolution 238
8.6.5Results 239
8.6.6ChoiceofBasisFunctions 240
8.6.7ScatteringfromSharpCorners 242
8.7ConditioninganditsControl 243
8.8Conclusions 245 References 245
9CombinedExtendedFiniteElementandLevelSetMethod(XFE-LSM)for FreeBoundaryProblems 249
9.1Motivation 249
9.2TheLevelSetMethod 250
9.2.1TheLevelSetRepresentationoftheEmbeddedInterface 250
9.2.2TheBasicLevelSetEvolutionEquation 251
9.2.3VelocityExtension 252
9.2.4LevelSetFunctionUpdate 254
9.2.5CouplingtheLevelSetMethodwiththeXFEM 255
9.3BiofilmEvolution 256
9.3.1Biofilms 257
9.3.2BiofilmModeling 257
9.3.3Two-DimensionalModel 258
9.3.4SolutionStrategy 260
9.3.5VariationalForm 261
9.3.6EnrichmentFunctions 262
9.3.7InterfaceConditions 263
9.3.8InterfaceSpeedFunction 264
9.3.9AccuracyandConvergence 265
9.3.10NumericalResults 266
9.4Conclusion 269 Acknowledgment 269 References 269
10XFEMfor3DFractureSimulation 273
10.1Introduction 273
10.2GoverningEquations 274
10.3XFEMEnrichmentApproximation 275
10.4VectorLevelSet 280
10.5ComputationofStressIntensityFactor 282
10.5.1BrittleMaterial 282
10.5.2DuctileMaterial 286
10.6NumericalSimulations 288
10.6.1ComputationofFractureParameters 288
10.6.2FatigueCrackGrowthinCompactTensionSpecimen 297
10.7Summary 300 References 300
11XFEMModelingofCrackedElastic-PlasticSolids 303
11.1Introduction 303
11.2ConventionalvonMisesPlasticity 303
11.2.1ConstitutiveModel 303
11.2.2AsymptoticCrackTipFields 305
11.2.3XFEMEnrichment 307
11.2.4NumericalImplementation 308
11.2.5RepresentativeResults 309
11.3StrainGradientPlasticity 312
11.3.1ConstitutiveModel 313
11.3.2AsymptoticCrackTipFields 314
11.3.3XFEMEnrichment 316
11.3.4NumericalImplementation 317
11.3.5RepresentativeResults 319
11.4Conclusions 323 References 324
12AnIntroductiontoMultiscaleanalysiswithXFEM 329
12.1Introduction 329
12.1.1TypesofMultiscaleAnalysis 329
12.2MolecularStatics 330
12.2.1AtomisticPotentials 332
12.2.2Asimple1DHarmonicPotentialExample 333
12.2.3TheLennard-JonesPotential 335
12.2.4TheEmbeddedAtomMethod 335
12.3HierarchicalMultiscaleModelsofElasticBehavior–TheCauchy-BornRule 336
12.4CurrentMultiscaleAnalysis–TheBridgingDomainMethod 338
12.5TheeXtendedBridgingDomainMethod 340
12.5.1SimulationofaCrackUsingXFEM 342
References 344
Index 345
ListofContributors
StéphaneCotin UniversitedeStrasburg,Strasburg France
RavindraDuddu SchoolofEngineering,VanderbiltUniversity Nashville,USA
MichelDuprez UniversitedeStrasburg,Strasburg France
OctavioAndrésGonzález-Estrada EscueladeIngenieríaMecánicaColombia
JuanJoséRódenasGarcía UniversidadPolitecnicaDeValencia Valencia,Spain
RobertGracie UniversityofWaterloo,Ontario,Canada
VanessaLleras IMAG,UnivMontpellier,CNRS,Montpellier,France
AlexeiLozinski LaboratoiredeMathématiques,Universitéde Franche-Comté,BesançonCedex,France
EmilioMartínez-Pañeda ImpericalCollege,London,UK
IndraVirSingh IndianInstituteofTechnologyRoorkee Uttarakhand,India
JonTrevelyan DurhamUniversity,Durham,UK
KillianVuillemot LaboratoiredeMathématiques,Universitéde Franche-Comté,BesançonCedex,France
Preface
Thisbookhasbeenamovingtargetforthepast13years(2009–2022).Wearedelightedtoseeitsfirstedition published.Wetellthestoryofextensionstothefiniteelementmethodwhicharenowgloballyaccepted,andimplementedinindustrialsimulationsoftware.Thebookreliesontheexpertiseoftheauthorsandborrowsadditional know-howandexperiencefromchapterscontributedfromleadingexpertsinrelatedmethods.Thismakesthis bookthemostcompleteaccountofenrichmentmethods,bothinfiniteelementsandboundaryelementmethods. Wealsodiscussthecriticallyimportanttopicoferrorestimationandadaptivityaswellaspracticalapplications.
Thisbookhasalongandcomplexhistory,typicalofacademicresearch.Theideaforthebookwasbornaround 2007,whenAlexanderMenk,thenfundedbyBoschGmbH,wasaPhDstudentwithStéphaneBordasinGlasgow. Theoriginalideawastofocusontheextendedfiniteelementmethod,butbecamealotmoreambitiousasthe authorsinvestigatedotherdiscretizationmethods,industrializedtheirwork,andcollaboratedwithotherresearch groups.
Westartbyanintroductionontheoriginofenrichedmethods,startingwithglobalenrichmentoffiniteelement methodsorspecializedenrichments(e.g.forfracturemechanics),introducedinthe1970s.Weexplainhowlocal enrichmentmethodstookprecedence,withtheintroductionofpartitionofunitymethodsinthe1990s.Wegive detailson apriori errorestimates(Cea’slemma),toexplainhowenrichmentpalliateslimitationsofpolynomial approximationsofnon-smoothsolutions.
Bystartingwiththenotionofpartitionofunity,wemotivatehowarbitraryfunctionscanbeexactlyreproduced bytheapproximationspacebymultiplyingthisfunctionwithapartitionofunity.Wecomparethisapproachto othermethods,putforwardwithinthecontextofmeshfreemethods,suchasintrinsicenrichmentofmovingleast squares.
Enrichmenttechniquesrequirespecialtreatmentstosupportthegeneralityoftheenrichmentfunctionsused, whicharenotnecessarilycontinuous,norevenpolynomial.Wethereforediscussandcomparedifferentoptions fornumericalintegration,indetail.Thelocalityofenrichmentimpliestheexistenceofinterfacesbetweenenriched andnon-enrichedregions,withinthedomainwhichcanleadtodecreasedoptimalityinconvergencerates,inaccuracies,andspuriousoscillationsinthesolutionclosetotheinterface.Wedescribepossibilitiestoovercomethese difficulties.
Aftertacklingtheseadvancedtopics,wediscussawidevarietyofapplicationsofenrichmentschemes,including fracturemechanics,treatmentofheterogeneities,andboundarylayers.
Inordertotacklespecialtopics,weaskedexpertsinfreeboundaryproblems, aposteriori errorestimation, nonlinearmaterialmodeling,fracturesimulations,andmultiscalemethodstoprovidethereaderwithup-to-date informationonsuchimportantareasrelatedtopartitionofunityenrichment.Thebookhasachapteronanexcitingtopicrelatedtotheenrichedboundaryelementmethodforfractureandwavepropagation.Thebookendswith achapteronanexcitingtopicrelatedtomultiscalemodelingoffracture.
ThisbookisdedicatedtoourteachersandProfessors.StéphaneBordasthinksinparticularaboutMonsieur Martin(mathteacheratage10and11),MadameJanuel(mathteacheratage16),andMadameGoubet(math teacherinpreparatoryclasses),aswellasMonsieurCarsique(mathteacherinpreparatoryclasses).But,aswhen oneteaches,twolearn,thisbookisalsodedicatedtoourstudents,inparticularourPhDstudents,andtoourteamat large,whoallcontributedstronglytooureducationthroughtheirownwork,research,questionings,philosophical orotherwise.WealsothankourmentorsProfessorTedBelytschko,NenadBićanić,BhushanKarihaloo,Brian Moran,andChrisPearce.
Acknowledgments
Writingthisbookonthepartitionofunitymethodshasbeenanultramarathon,andasalong-distancerunner, Irealizethepoweroftakingsmallsteps.Iwouldliketoexpressmyheartfeltgratitudetotheindividualsand organizationswhohavesupportedmethroughoutthis15-yearjourney.
Firstandforemost,Iextendmyappreciationtomymentorsandeducatorswhoignitedmypassionforexcellence andinstilledinmetheimportanceofunderstandingtheintricatedetailsofanyfield.IamgratefultoMonsieur Martin,MadameJanuel,andMadameGoubetfortheirguidanceduringmyformativeyearsatLycéeSaintLouis inParis.Theyshowedmethebeautythatliesinmasteryandtheendlessquestforknowledge.BrianMoran,my PhDadvisor,playedapivotalrolebybelievinginmeandintroducingmetothefieldofcomputationalmechanics, particularlysolidmechanics.Hisunwaveringsupportandguidanceshapedmycareer.
ThelateTedBelytschkoremainsacherishedrolemodelwhoseleadershipandinfluencecontinuetoinspireme.I fondlyremembertheFridaygroupmeetingsatNorthwesternUniversity.BhushanKarihaloo’strustinmyabilities andhisdecisiontoentrustmewiththeleadershipoftheInstituteofMechanicsandAdvancedMaterialsinCardiff wereinstrumentalinmyprofessionalgrowth.Withouthissupport,ourachievementswouldhavebeendelayed significantly.Thankyouforhelpingmediscovermyinnerpotential.Iextendmygratitudetothehundredsofcoauthorsonourresearchpaperswhohaveenrichedmyunderstandingofdiverseresearchareas.Specialthanksgo tomyPhDstudentswhoplacedtheirtrustinmeandmyresearchgroup.Theyshowedmethat“whenoneteaches, twolearn.”Inparticular,IthankNguyenVinhPhu,myfirstMaster’sStudent,withwhomIjustco-signedabook onthematerialpointmethod.
IthankSundararajanNatarajanwhohasconsistentlyshowedmealternatewaysintolifeandwithwhomIhad longwalks,busrides,anddiscussionsinGlasgow,Cardiff,andChennai.IalsothankAlexMenk,withwhom SundararajanandIco-signthisbook.Alexwasalwaysanexampleofpragmatismmixedwithmathematicalrigor. Myheartfeltthanksgotothefundingorganizations,includingtheEU,EPSRC,andFNR(Luxembourg),for providingover€25millioninfundingforourresearch.Iamgratefultotheuniversitiesthattrustedme,including theUniversityofGlasgow,EPFL,CardiffUniversity,andespeciallytheUniversityofLuxembourg,whichallowed metoflourishattheheartofEurope.
Iwouldliketoexpressmydeepappreciationtomychildren,Iphigénie,Augustin,Anatole,andOscarBordas, whohavebeenconstantsourcesofinspiration.Eachofyouhasauniquequalitythatremindsmeofthebeauty andeleganceinmathematics,science,andknowledge.Iphigénie,yourgrowthmindset,yourgrit,competitiveness, andhumilityinthefaceofcomplexityinspiremedaily.Augustin,yourcamaraderie,simplicity,andcommitment toauthenticityandbeautyremindmeofwhattrulymatters.Anatole,yourgoodhumor,linguisticprowess,your drivetothrive,andyourunwaveringpositivesupporthavebeenmypillars.Oscar,yourperpetualoptimism,love formathematics,chess,andlogicalongwithyourinfectiouspositivitybrighteneveryinstantofmyday.Iamalso gratefultotheirmother,LaurelleDemaurex,forhersupportduringtheearlyyearsofmyresearchgroupandto
Acknowledgments
helpmebringoutthebestofmyselfbychallengingmeinwaysIdidnotanticipateIwouldbechallenged.Ialso thankherfather,Marc-OlivierDemaurex,forshowingmetheimportanceofreadingbetweenthelines.Ialso thankBeverlyJohnstonfordailyremindersofthepoweroflogicandsoundreasoningoversophism.
Finally,Ithankmyparents(PierreBordasandChristianeRenault)andgrandparents(RaymondRenault,Lucette Dusservaix,SuzanneLebobe,andAndréBordas)fortheirunwaveringsupportandforintroducingmetotheworld ofhardwork,mathematics,andscience.TheywerethebestpacersIcouldhavehopedforintheraceoflife.Iwill neverforgettheadvicegivenbymygrandfatherRaymond,hisgenerosity,harmony,strength,andpositivitywhich continuetolivewithinusandwithinmysonOscar,whobearshisname.Asaconclusion,Ileaveyouwitha profoundSufistorythathasresonatedwithmethroughoutmyjourney:“Youseeinpeoplewhatyouyourselfare. Peoplearethesameeverywhere.Therealproblemisaboutyou.Rememberthis.”
Inourpursuitofknowledgeandexcellence,weoftenlookoutwardforanswersandinspiration.However,this storyremindsusthattrueunderstandingbeginswithinourselves.Itisourownperspective,attitudes,andactions thatshapeourperceptionoftheworldandthepeopleinit.
Aswereflectontheacknowledgmentsandthejourneychronicledinthisbook,maywerememberthatour interactionswithothers,ourmentors,students,colleagues,andlovedones,areareflectionofourowninner world.Bycontinuallystrivingtoimproveourselvesandfosteringasenseofhumility,empathy,andgratitude,we canbetternavigatethecomplexitiesoflifeandcontributetothebettermentoftheworldaroundus.
Thankyoutoeveryonewhohasbeenapartofthisremarkablejourney.Yoursupport,trust,andsharedexperienceshaveenrichedmylifeandthisbookinimmeasurableways.Withheartfeltgratitudeandacommitmentto ongoinggrowth,wewouldliketohonorIvoBabuška,whopioneeredthepartitionofunitymethods.Hisclarity andsagacityhavedeeplyinspiredmeandmotivatedmetocompletethiswork.
IwouldliketothankmywifeKathrinLydiaMenkandmychildrenJuliusandMagdalenaforcontinuously supportingmewithmyworkandforallthegoodtimeswehadsofar.Ialsowouldliketothankmyparentsand mybrotherforhelpingmebecomethepersonIamtoday.LastbutnotleastIwouldliketothankStéphaneP.A. BordasforgivingmetheopportunitytobecomeactiveinacademicresearchandSundararajanNatarajanforall thefruitfuldiscussionswehadduringourtimeinGlasgow.
IwouldliketothankmyparentsGeethaNatarajanandNatarajan,mywifeRamyaChandrasekaran,andson Vaibhavforcontinuouslysupportingmewithmyworkandstandingbymeonnumerousoccasions.Iadmire Vaibhav’sabundantsourceofenergy,constantthirsttolearnanddonewthings,andespeciallytheattitude ofcarryingouttaskswithoutthefearoffailureandpursuingthemuntilsuccessisattained.Iamthankfulfor mysisterParvathi’sabundantloveandaffection.MythanksextendtoBhagirath,Nirmal,Mahalakshmi,and ChandrasekaranandShanthaChandrasekaranfortheirsupport,trust,andencouragement.Specialthanksto Youngphilosophers,Pranav,AyushandShubha.IwouldliketothankStéphaneP.A.Bordasforsupportingme throughdifferentphasesasastudent,post-doctoralresearcherandnowasanacademicresearcherandAlexander MenkforallthegoodtimeswehadduringourtimeinGlasgow.Finally,Iwouldliketothanktheomnipresent forgivingmethestrengthtoswimthroughdifferenthurdles.
SundararajanNatarajan
StéphaneP.A.Bordas
AlexanderMenk
Acknowledgments
WewouldliketothankourfriendsProfessorsStéphaneCotin,RavindraDuddu,MichelDuprez,OctavioAndrés González-Estrada,JuanJoséRódenasGarcía,RobertGracie,VanessaLleras,AlexeiLozinski,EmilioMartinezPañeda,IndraVirSingh,JonTrevelyan,andKillianVuillemotforsharingtheirexpertisebycontributing specializedtopicsonthepartitionofunitymethods.Wewouldliketothankourfriends/studentsChintanJansari, AbirElbeji,DulceCanha,SaurabhDeshpande,QiaolingMin,AravindKadhambariyil,ZhaoxiangShen,Meryem AbbadAndaloussi,GeremyLoachamínSuntaxi,VincentdeWit,ParisPapavasileiou,SofiaFarina,andEhsan Mikaeiliforextensiveproofreadingandforthenumeroussuggestionsandcorrections.
Introduction
StéphaneP.A.Bordas1,AlexanderMenk2,andSundararajanNatarajan3
1 UniversityofLuxembourg,Luxembourg,UK
2 RobertBoschGmbH,Germany
3 IndianInstituteofTechnologyMadras,India
Physicalsystemsareoftenmodeledusingpartialdifferentialequations(PDEs).Theexactsolutionorclosedformor analyticalsolutionstothesePDEsisonlyavailableinspecialcasesforspecificgeometries.Numericalmethodscan beusedtoapproximatetheexactsolutioninmoregeneralsettings.Theresultofanumericalsimulationisrarely exact.Nonetheless,computer-basednumericalsimulationhasrevolutionalizedindustrialproductdevelopment throughoutengineeringdisciplines.Whencomparingexperimentsandsimulationwiththeaimofimprovinga simulationproceduretogivemoreaccurateresults,itisnecessarytounderstandthedifferentsourcesoferror.
Figure 1.1 showsanoverviewoferrorsthatoccuratdifferentstagesofmodelingandnumericalsimulationfora givennumericalmethod.
Oneofthesenumericalmethodsiscalledthe“finiteelementmethod”(FEM).Itismostcommonlyusedin structuralmechanics,althoughthefieldofapplicationismuchbroader.ThehistoricoriginsoftheFEMcannotbe uniquelydetermined.Mathematiciansandengineersseemedtodevelopsimilarmethodssimultaneouslywhich laidthefoundationsforwhatisnowpopularlyknownastheFEM.Inthemathematicalcommunity,thedevelopmentscanbesummarizedasfollows.In1851,SchellbachobtainedanapproximatesolutiontoPlateausproblem byusingpiecewiselinearfunctionsonasurface.Variationalprinciplestosolvepartialdifferentialequationswere usedbyRitzin1909.BasedontheRitzmethod,Courantproposedatriangulationofatwo-dimensional(2D)
Figure1.1 Sourcesoferrorinsimulation.
structuretosolvetheplanetorsionproblem.ThefirstbookprovidingasolidmathematicalbasisfortheFEM isattributedtoBabuškaandAziz(BabuškaandAziz,1972).Intheengineeringcommunity,thedevelopments ofFEMaremotivatedbyphysicalanalogiestodescribecontinuousproblemsinadiscretefashion.Hrenikoff (Hrennikoff,1941)combinedtrussesandbeamstomodelplaneelasticityproblems.Turner,Clough,Martin,and Toppintroducedplaneelementsin1956.Theterm“ finiteelement”wascoinedbyCloughin1960.Thefirstbook abouttheFEMwrittenfromanengineeringperspectiveisattributedtoZienkiewicz(Zienkiewicz,1971)in1971. Wewillassumeacertainfamiliarityofthereaderwiththismethodthroughoutthebook,butwewanttoprovide ashortintroductiontotheFEMatthispoint,inordertointroducethemainnotations.
1.1 TheFiniteElementMethod
Assume Ω tobeadomainof R��,��∈{1,2,3}.Letustakealookatthefollowingboundaryvalueproblem:
where ��∶ R�� → R isanunknownscalarfieldand ��∶ R�� → R.
Equation(1.1a)isknownasPoisson’sequationwhen �� ≠ 0 andasLaplaceequationwhen �� ≡ 0.Theopen domain Ω couldbearegionin R��,boundedbya (��−1) dimensionalsurface ��Ω whoseoutwardnormalis ��. Wearelookingforascalarfunction �� thatfulfillsPoisson’sequationeverywherein Ω.Onthedomainboundary ��Ω,thefunctionshouldbezero(c.f.Equation(1.1b)).Inphysics,thisequationcanbeusedtomodelavarietyof phenomena,forexample,anelasto-staticrodunderatorsionalload,Newtoniangravity,electrostatics,diffusion, themotionofinviscidfluid,Schrödinger’sequationinQuantummechanics,themotionofbiologicalorganisms inasolutionandcanalsobeusedinsurfacereconstruction.
Here,letusassumethatthescalarfunction �� couldforinstancebeatemperaturedistribution, ��,thathas cometoanequilibrium.Then �� describestheheatsupplyinsidethedomain.Itiseasytointerprettheequation physicallyundertheseassumptions.Theheatfluxisproportionalto ∇��,thegradientof ��.Becausethesystem isinequilibrium,thesumoftheheatflowinginandoutofaninfinitesimalsubregionshouldbethesameasthe heatsuppliedbytheheatsourcesinsidethatregion.Inotherwords,thedivergenceoftheheatflux∇(∇��)should beequalto �� atanypoint,whichisequivalentto −∆�� =��.Assumingaconstanttemperaturedistributionat thedomainboundarycouldbereasonableifamaterialwithahighthermalconductivityisattachedtotheregion ofinterest.Tosimplifythings,wepostulateinEquation(1.1b)thatthisconstanttemperatureiszero.Pleasenote thatoncethisproblemissolved,onecanaddanarbitraryconstantto �� andEquation(1.1a)isstillfulfilled.Ifthe problemisposedthisway,thenanysolution �� mustbedifferentiabletwicein Ω.Thisisastrongerconditionon thechoiceof �� andmoreoverinmanysituationsthesolutionisnotdifferentiabletwice,althoughtheunderlying physicsisthesame.
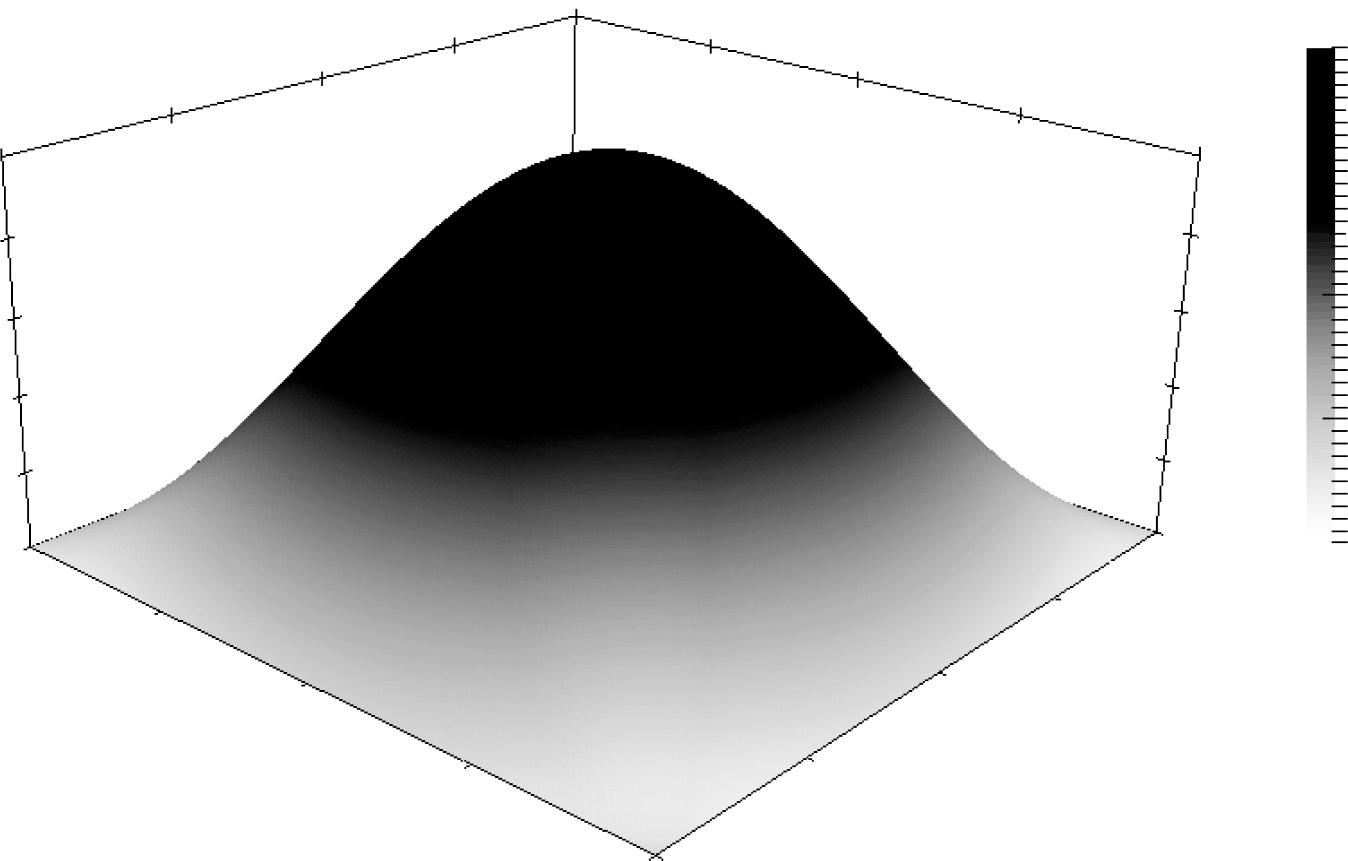
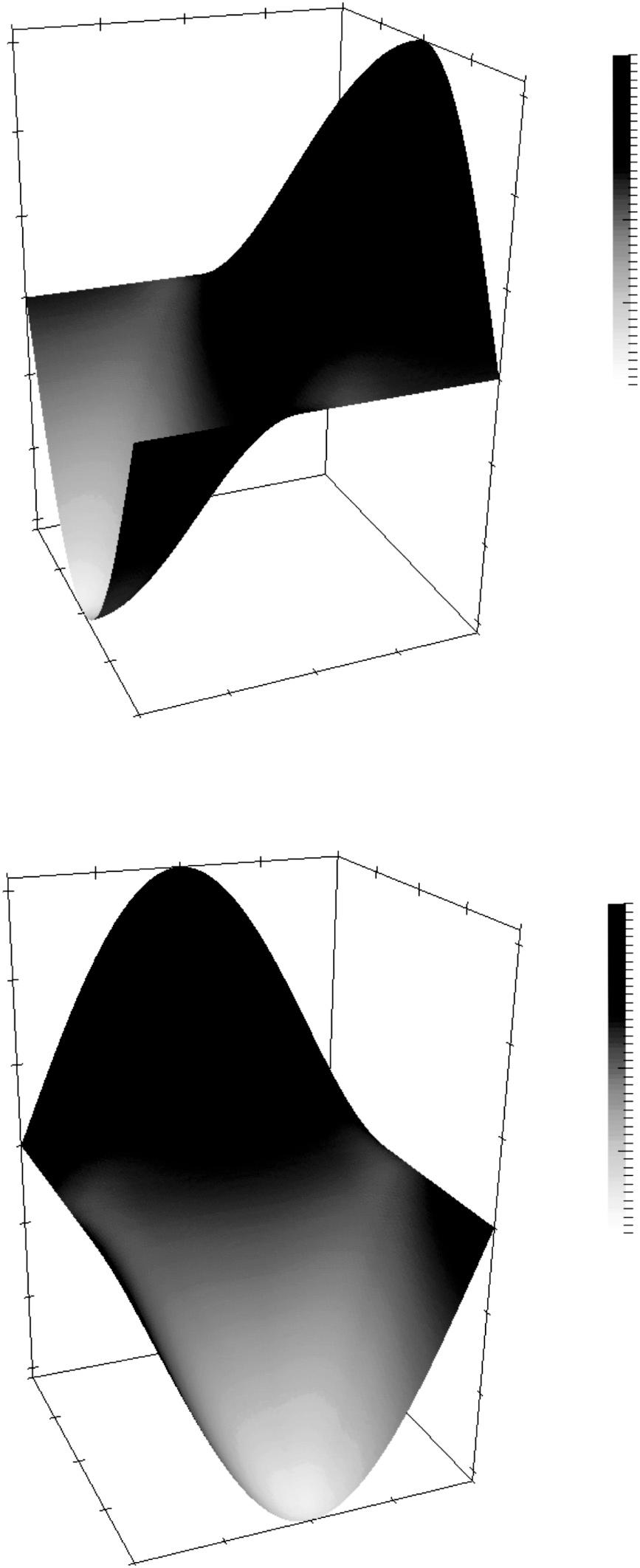
Letusconsideranexample.Assumethatthetemperaturedoesnotvaryinthe ��-direction.Inthatcase,the problemcanbeposedina2Dsetting.Letthedomainbetheopenunitsquare Ω=[0,1]2.Ascalarfunction definedontheunitsquareisshowninFigure 1.2.Thefunctionispiecewiseconstant.Wetakethisfunctiontobe theheatsupply ��.Adiscontinuousheatsupplyisarealisticassumptioninseveralsituations.Onecouldimagine anelectriccurrentflowingthroughametal.Thentheheatisgeneratedateverypointinsidethemetal,butnot outside.Assumingthattheheatgenerationatsomepointisproportionaltotheelectricalcurrent,afunction �� containingjumpsreallyisphysicallymeaningful.Experimentally,onewouldmeasureatemperaturedistribution similartotheoneshowninFigure1.3.The��-componentofthegradientofthistemperaturedistributionisshown inFigure1.4.Itiseasilyobservedthatthegradientisnotdifferentiableatcertainpoints.Therefore,thetemperature distributioninFigure 1.3 isnotasolutionofEquation(1.1a),althoughitisthecorrectsolutionfromaphysical pointofview.

Apiecewiseconstantfunctionontheunitsquareasanexamplefor f.
Thismotivatesthesearchforanotherproblemdescription.Equation(1.1a)willsubsequentlybereferredtoas theclassicalformulationoftheproblemandasolutioniscalledaclassicalsolution.Toobtainanewformulation, wemultiplyequationEquation(1.1a)byascalarfunctionvdefinedonthedomainΩandintegrateoverthewhole domaintoget:
Figure1.2
Figure1.3 Temperaturedistribution.
Thefunctionvisnotcompletelyarbitrary,butfornowitsufficestoassumecertainnicepropertiessuchthatwecan performthenecessaryintegrationsanddifferentiationsinthefollowingdiscussion.Applyingpartialintegration totheleft-handsideofEquation(1.2),weobtain:
ItisobviousthatEquation(1.3)isfulfilledforanyfunction v if �� isaclassicalsolution.Letusassumethatthere isafunctionspace V whichcontainsallthefunctionsthatarephysicallyreasonable.Bythatwemeanespecially thattheclassicalsolutionisin V ifitexistsandthatallthefunctionsin V vanishattheboundary1.Oncesucha spaceisknown,theproblemcouldbestatedinthefollowingabstractform,knownastheweakform:
Weakform: Find T ∈ V,suchthatforall v ∈ V a(T, v)=(v, f) (1.4)
where a(T, v)=∫Ω(∇v)∇T dΩ and (v, f)=∫Ω vf dΩ arethesymmetricbilinearandlinearforms,respectively.
⨀ Example1. Findtheweakformforthefollowingstrongformandidentifythelinearandbilinearform:
�� d2u(x) dx2 ��u(x)+ f(x)= 0, 0 < x < 1 where ��,�� areconstantsindependentof x andsubjecttothefollowingDirichletboundaryconditions: u(0)= 1, u(1)=−2
⨀ Example2. Repeattheaboveexample,subjectedtothefollowingDirichletandNeumannboundary conditions: u(0)= 0, du dx (1)=−2.
UsingtheweakformgivesthefunctioninFigure 1.3 achanceofbeingasolutiontotheproblembecausea solutionofEquation(1.1a)needsonlyonetimecontinuouslydifferentiable.Itremainstobecheckedunderwhich circumstancesasolutionexists,andifthisisauniquesolution.Therefore,theterm“physicallymeaningful,”used wheninitiallydescribing V,needstobedefinedmoreprecisely.Todothis,weneedtoaddresstheintegrationand thedifferentiationinEquation(1.3).Tomotivatewhytheclassicalintegrationanddifferentiationoperationsare notusefulforourpurposewetakeafirststeptowardthenumericalsolutionoftheproblem.Thefunctionspace V willgenerallyhaveinfinitelymanydimensions.Tocomputeanapproximationtotheexactsolutiononecould trytosolvetheweakformulationinafinitedimensionalsubspaceof V,whichwewilldenoteby Vℎ ⊂ V.The solutionassociatedwiththisrestrictedformulationisdenotedby ��ℎ.Withoutfurtheranalysis,itisnotclearhow ��ℎ isrelatedtothesolutionofEquation(1.3).Butonecanshowthat��ℎ minimizestheerrorover Vℎ inaparticular normcalledthe“energynorm.”Theproblemthenbecomes:
1Theinterestedreaderisreferredto,e.g.BrennerandScott(2002)forconceptsoffunctionalanalysisrelevanttofiniteelementanalysis
Find��ℎ ∈ Vℎ suchthatforall vℎ ∈ Vℎ ∶ ��(��ℎ,vℎ)=(vℎ,��) (1.5)
Thereexistsabasis ��1,...,���� for Vℎ,thatis,wecanwritetheelementsof Vℎ as:
Then,certainly ��ℎ ∈ Vℎ canalsobewritteninthisform:
ℎ =∑ �� �������� (1.7)
Todeterminetheunknowncoefficients a =(��1,...,����) of ��ℎ,weinsertEquation(1.7)inEquation(1.5)and postulatethatEquation(1.5)holdsforallbasisfunctions:
∫Ω(∇��1)��∇(∑ �� ��������)dΩ=∫Ω v1��dΩ
Ω
Becauseofthelinearityoftheintegrationoperation,theseequationsareequivalenttopostulatingthat Equation(1.5)holdsforallvℎ ∈ Vℎ.Duetothelinearityofthegradientoperatorandtheintegrationoperation,we canrewriteEquation(1.8)as:
Therefore,todeterminetheunknowncoefficientsonehastosolvealinearsystemofequations:
Differentchoicesfor Vℎ arepossible.Onecouldchoose Vℎ tobethesetofallglobalpolynomialsdefinedon Ω up toacertainorder.Inthatcase,allpointsin Ω arerelatedtoeachother,andhencemostoftheentriesof �� will benon-zero.Itisdisadvantageousiftheequationsystemsbecomelarge,becausememorystoragegrowswiththe squareofthesystemsize�� andsolvinglargesystemsofequationsusingdirectsolveriscomputationallyexpensive (��(��3)).
Inpractice,largeequationsystemsaresolvedusingiterativesolvers.Iterativesolversmultiplyavectorwith �� ateachiteration.Thismultiplicationtakesalargeamountoftimeif �� isfullypopulated.Itismucheasiertodeal withsparseequationsystems,inwhichmostoftheentriesarezero.Thezeroentriesdonothavetobestoredand canbeneglectedwhenevaluatingthematrix-vectorproduct.Nowthequestiononewouldtrytoansweris:
Canwefindfunctionspaces Vℎ thatresultinsparseequationsystems?
AssumethatΩiscoveredbyatriangularmeshsuchastheoneshowninFigure1.5.Thetriangleswillbecalled elements andtheintersectionsoftheelementedgesarecalled nodes.Wecouldchoose Vℎ tobethespaceofall
Figure1.5 Meshexample.
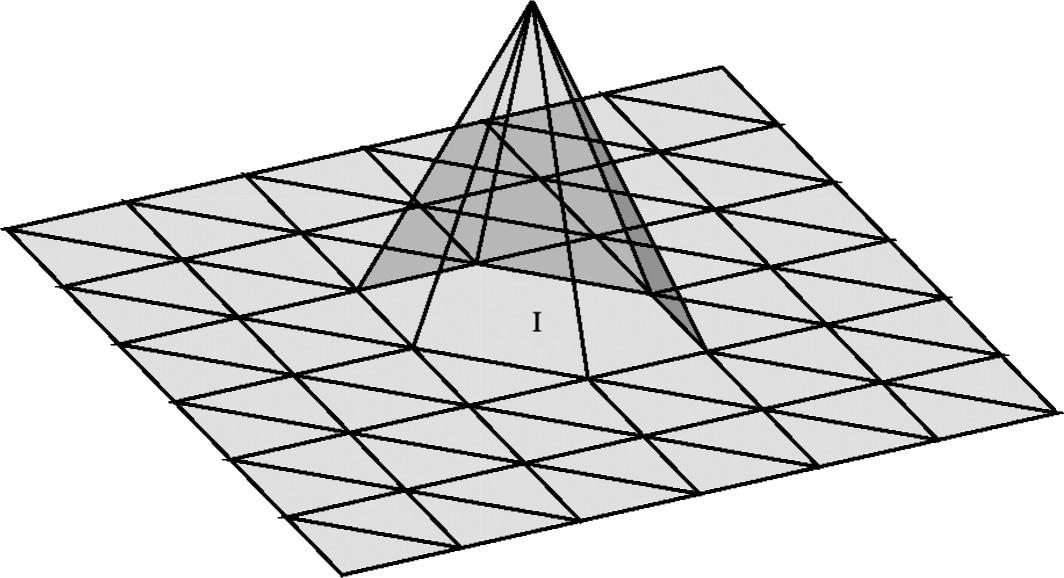
Figure1.6 Atypicalbasisfunctionwithitsnodalsupport.
functionsthatarecontinuousin Ω,linearinsideeachelement,andvanishattheboundary.Abasisfunction ���� ∈ Vℎ isdefinedasfollows:
● ���� is1atthe ��th interiornode,i.e., ����(����)=1;
● ���� is0atallothernodes; ��, ∀��,����(����)=0;
● foreachelementthefunctionvaluescanbeobtainedbyalinearinterpolationbetweenthefunctionvaluesabove.
Together,ifchosenasdescribedabove,thebasisfunctions v�� formabasisforthespace Vℎ.Figure 1.6 showsthe basisfunctionforanode �� insideadomaincoveredbyatriangularmesh.Onecouldalsocoverthedomainwith elementswithmorethan three sides.Thishasledtothe“polygonalfiniteelementmethods.”Theshapefunctions overarbitraryelementsarecollectivelyknownas“barycentriccoordinates.”
Itisinterestingtonotethatthereisnouniquewaytorepresenttheshapefunctionsoverpolytopes.Any setoffunctionsthatsatisfytheaforementionedpropertiesisacandidatureforbasisfunctions.
Withachoiceofsuchbasisfunctions,wewouldhaveproblemsevaluatingtheelementsofmatrix ��,since thefunctions vℎ arenotdifferentiableattheelementboundaries.Wecouldneglectthisandevaluatetheintegrationandthedifferentiationonlyforpointsinsidetheelements.Theresultingmatrixwouldthenbesparse.Since thebasisfunctionsarezeroinmostelements,thesameistruefortheirgradient.Therefore,mostofthematrix entriesinEquation(1.9)arealsozero.Fromacomputationalpointofviewthisisexactlywhatisdoneinthe FEM.Pleasenotethatduetothelinearityofthebasisfunctionsinsideeachelement,theevaluationofthematrix entriescanbedoneinafewcomputationalsteps.Sincethegradientofthebasisfunctionsisconstantinsideeach element,theintegralscanbecomputedbyevaluatingthefunctiononlyatthemidpoint(Gaussquadratureof orderone).
WenowreturntothediscussionaboutthedifferentiationandtheintegrationoftermsinEquation(1.9). Weneedmodifiedoperationswhich,insomeway,neglectsubsetsof Ω withmeasurezero,suchaslinesand points.Withthoseoperationswewillbeabletoformulatetheprobleminarigorousmannersuchthatthebasis functionswejustdiscussedarepartofspace Vℎ.Forintegration,thiscanbeachievedbyusingtheLebesgue integral.
LebesgueIntegral:
TheLebesgueintegralhasthesamevalueforfunctionsthatdifferonlyonapointsetofmeasurezero. TheLebesgueintegralcanalsobeusedwithfunctionsthatareundefinedonsuchsetsandstilldeliver meaningfulvalues.Wewilldenotethespaceofallinfinitelydifferentiablefunctionsthatvanishonthe boundaryof Ω by C∞ 0 (Ω).Then,theweakderivative dv dx ofascalarfunction v(x, y) isfoundifitfulfillsforall
Thederivative dw dx isdefinedintheclassicalsense.Similarly,otherpartialderivativesofhigherordercanbe defined.Theweakderivative,ifitexists,isunique.Iftheclassicalderivativeofafunctionexists,theweak derivativeisthesame(neglectingsubsetsofmeasurezero).
Withourpiecewisepolynomialapproximationfunctions,theweakderivativeisnotdefinedattheelement boundaries,whileinsidetheelementsitcoincideswiththeclassicalderivative.Together,theLebesgueintegral andtheweakderivativemakeitpossibletoevaluateEquation(1.9)forourapproximationfunctions.Moreover, wecannowdefinethespace Vℎ.Thisspacewillbedenotedby ��1 0(Ω) andafunction v isanelementofthis spaceif:
● ∫Ω v2 dΩ canbeevaluatedintheLebesguesenseandissmallerthaninfinity;
● theweakderivativeof v exists;
● ∫Ω(��v ����)2 dΩ and ∫Ω(��v ����)2 dΩ canbeevaluatedintheLebesguesenseandaresmallerthaninfinity;
● v vanishesalongtheboundary.
Thespaceofsquare-integrablefunctionsisourstartingpoint.Postulatingthattheweakpartialderivatives existandthattheyaresquare-integrableisnecessary,otherwiseoneisnotabletoevaluatetheweakform. Postulatingthatthefunctionsvanishattheboundaryisnecessarytomakesurethattheessentialboundary conditionsarefulfilled.
Wemotivatedthedefinitionof��1 0(Ω)fromaphysicalandfromacomputationalpointofview.Butthedefinition hasmuchmorefundamentalconsequencesfromamathematicalpointofview.Onecandefineaninnerproduct, suchthatthisspacebecomesaHilbertspace.Hilbertspacesareinnerproductspacesinwhichgeometricaloperationslikeprojectionscanbegeneralized.ThismakesageometricinterpretationoftheFEM-procedurepossible. Theexactsolutionisavectorinthisspace.InthisHilbertspace,theexistenceandtheuniquenessoftheexact solutioncanbeproven.Butmoreadvancedtoolsfromfunctionalanalysisareneededforthis.Space Vℎ formsa hyperplane,andthenumericalsolutionistheprojectionoftheexactsolutionontothatplane.Therefore,insome sensethenumericalsolutionisthebestapproximationonecanget.Toincreasetheaccuracyofthenumerical solution,onemay,forexample,increasethedimensionofthehyperplanewhichwilldecreasetheerror.Inthe FEM,thisisdonebyrefiningthemesh.However,since ��1 0(Ω) isinfinitedimensionalnoteverymeshrefinement strategyresultsinconvergence.
⨀ Example3. Usingtriangularelements,writeaprogramforanFEM-solverforthePoissonproblem onarectangularsquareandaright-handsidegivenbythefunctioninFigure 1.2.Checkhowthesolution behavesfordifferentelementsizes.
⨀ Example4. Matlabs minres()-functionisaniterativesolver.Measurethetimeittakestosolve theFEM-equationsfromExercise1.1directly.Comparethiswiththetime minres() needstosolvethe equationsystem.Howdothecomputationtimeschangeifasparsematrixispassedto minres()?How doesthisdifferencebehaveifthemeshisrefined?
1.2 SuitabilityoftheFiniteElementMethod
Inthissection,wediscusstheconvergenceoftheFEM.Attheendofthissection,youshouldbeable:
● toassesswhattheconvergencerateoftheFEMdependson;
● toestimatetheerror;
● tocommentonhowitcanpossiblybeimproved.
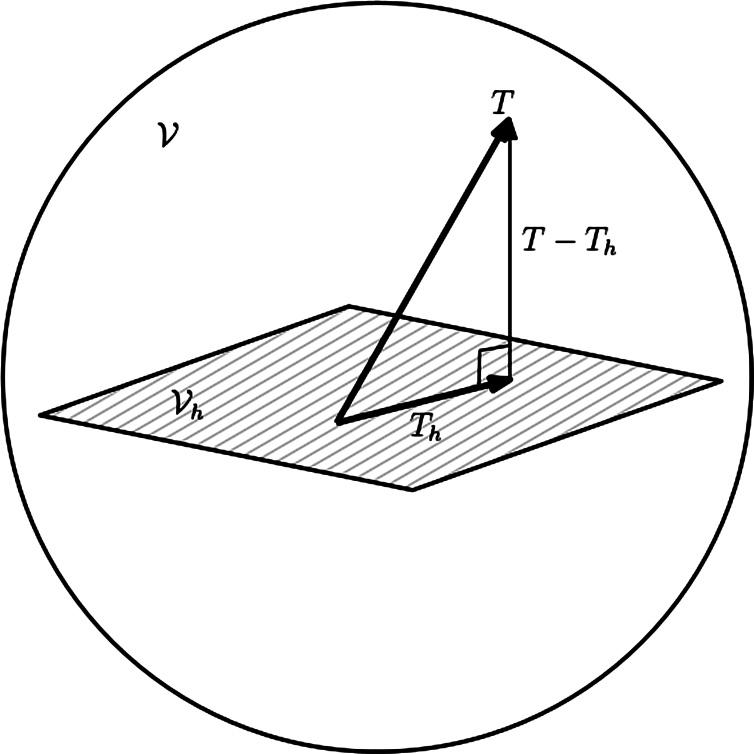
Todothis,wereferbacktotheweakforminthefinitedimensionalspace(Equation(1.5)).Weareinterestedin therelationof ��ℎ totheexactsolution ��.Definingtheerrorduetothefiniteelementapproximation �� = �� ��ℎ.Thismeansthatforallfunctions vℎ in V0 ℎ, ��(��,vℎ)=0,or,equivalently,thattheapproximatesolution ��ℎ istheorthogonalprojectionoftheexactsolution �� on Vℎ.ThisisdepictedgeometricallyinFigure 1.7,wherein, onecanthinkof �� = �� ��ℎ asavectorialidentity.Thespacewheretheexactsolution, ��,livesisrepresented artificiallyasa3Dspace(inrealityitisaspaceofinfinitedimensions).Thefiniteelementsubspaceisaplane (dimension2).Theerror, ��,isamemberof V,andthefiniteelementsolutionamemberof Vℎ.Consideringthe righttriangleinthefigure,itcanbeimmediatelyseenthatthelengthof �� (squared)equalsthelengthof ��ℎ (squared)plusthelengthof��,squared,i.e.,��(��,��)=��(��ℎ,��ℎ)+��(��,��)2.Thisisanimportantproperty,ifweadd afunction,whichisnotinthespanof Vℎ tothebasisof Vℎ andthusincreaseitsdimension,theerrorwillalways decrease.
2ThisidentityissimilartothePythagoreantheoreminEuclideanspaces.
Figure1.7 Theorthogonal(withrespecttobilinearform a(, )) projectionoftheexactsolution u onthefiniteelementspace Vh ⊂ V isthefiniteelementsolution uh.Inthisfigure,youcanthinkof e = u uh asavectorialidentity.Inthisfigure,thespacewherethe exactsolution, u,livesisrepresentedartificiallyasa three-dimensionalspace(inrealityitisaspaceofinfinite dimensions).Thefiniteelementsubspaceisaplane(dimension2). Theerror, e,isamemberof V,andthefiniteelementsolutiona memberof Vh.Consideringtherighttriangleinthefigure,itcanbe immediatelyseenthatthelengthof u (squared)equalsthelengthof uh (squared)plusthelengthof e,squared,i.e., a(u, u)= a(uh, uh) +a(e, e).ThisidentityissimilartothePythagoreantheoremin Euclideanspaces.Interpretationoftheerror e = u uh asa projection.
GalerkinOrthogonality a(e, vh)= 0 istheGalerkinorthogonalityrelationfortheerror.FromtheGalerkin orthogonality,followsthattheGalerkinapproximationisthe“bestapproximant”withrespecttotheassociatedbilinearform a(⋅ , ⋅).Thisbestapproximationpropertymeansthatthefiniteelementsolutionisaleast squarefitoftheexactsolutioninthesenseofthebilinearform a(⋅ , ⋅).
ThesuccessoftheFEMisprobablyduetoitsrichmathematicalanalysisanditselegantframework.Thisfacilitatesaccurate apriori and aposteriori estimatesofthediscretizationerror.Here,webrieflyoutlinethe apriori errorestimates.Assumethat ‖ ‖ isanormonthefunctionspace Vℎ.Andfurthermoreassumethattheproblem hasauniquesolution(i.e.,appropriateessentialboundaryconditionsareprescribed).Then,let ��∈{⋯} bethe orderofthenorminwhichtheerrorismeasured, ℎ ameasureoftheelementsize3 , �� isthepolynomialorder (chosenas1intheexampleabove), �� theregularityoftheexactsolution ��,Cea’sLemmastatesthattheerrorof thefiniteelementapproximationinnorm ‖⋅‖ satisfiesthefollowinginequality:
Inotherwords,uptoaconstant �� whichisindependentofthemeshsize,thesolution ��ℎ isthebestpossible solutioninthechosenfunctionspace.Ifnostatementcanbemadeaboutthecontinuityoftheexactsolution, meshrefinementguaranteesatleastalinearconvergence,providedthefollowingistrue:
Theaboveconditioncanberewrittenas:
or,equivalently,
ThismeansthatthatinorderfortheFEMtoconvergeoptimallyinnorm ‖⋅‖��,wemustboth:
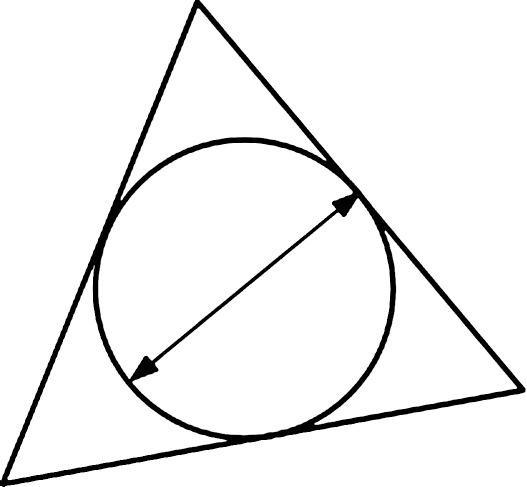
3TypicallythelargestelementinthemeshinFigure 1.8
Figure1.8 Themeshsize, h,isthediameterofthesmallestcircleenclosingthe largestelementinthemesh.
● selectthepolynomialorder �� largerthan (��−1).
● makesurethattheexactsolution �� ismoreregularthantheorderofthenorm ‖⋅‖��
Iftheorderofthecontinuityoftheexactsolutionishigh,increasingthepolynomialorder �� mightbeabetter strategythanrefiningthemesh.However,iftheregularityofthesolutionislow,thereisnouseincreasingthe polynomialorder��,becauseif�� issmall,then(�� ��)willremainthedeterminingterminmin(��+1−��,�� ��). ThisisfurtherdiscussedindetailinSection1.3.
Apriori estimationdiscussedabovedoesnotaccountfor:
● numericalintegrationerrortocomputethebilinearandlinearform;
● interpolatingDirichletboundaryconditions;
● approximatingtheboundary ��Ω bypiecewisepolynomialfunctions.