Organogermanium compounds. theory, experiment, and applications vladimir ya. lee all chapter instant by Education Libraries

Organogermanium Compounds

Theory, Experiment, and Applications

Edited by Vladimir Ya. Lee

Volume 1

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by law. Advice on how to obtain permission to reuse material from this title is available at http://www.wiley.com/go/permissions.

The right of Vladimir Ya. Lee to be identified as the author of editorial material in this work has been asserted in accordance with law.

Registered Office

John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, USA

For details of our global editorial offices, customer services, and more information about Wiley products visit us at www.wiley.com.

Wiley also publishes its books in a variety of electronic formats and by print-on-demand. Some content that appears in standard print versions of this book may not be available in other formats.

Trademarks: Wiley and the Wiley logo are trademarks or registered trademarks of John Wiley & Sons, Inc. and/or its affiliates in the United States and other countries and may not be used without written permission. All other trademarks are the property of their respective owners. John Wiley & Sons, Inc. is not associated with any product or vendor mentioned in this book.

Limit of Liability/Disclaimer of Warranty

In view of ongoing research, equipment modifications, changes in governmental regulations, and the constant flow of information relating to the use of experimental reagents, equipment, and devices, the reader is urged to review and evaluate the information provided in the package insert or instructions for each chemical, piece of equipment, reagent, or device for, among other things, any changes in the instructions or indication of usage and for added warnings and precautions. While the publisher and authors have used their best efforts in preparing this work, they make no representations or warranties with respect to the accuracy or completeness of the contents of this work and specifically disclaim all warranties, including without limitation any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives, written sales materials or promotional statements for this work. The fact that an organization, website, or product is referred to in this work as a citation and/or potential source of further information does not mean that the publisher and authors endorse the information or services the organization, website, or product may provide or recommendations it may make. This work is sold with the understanding that the publisher is not engaged in rendering professional services. The advice and strategies contained herein may not be suitable for your situation. You should consult with a specialist where appropriate. Further, readers should be aware that websites listed in this work may have changed or disappeared between when this work was written and when it is read. Neither the publisher nor authors shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.

A catalogue record for this book is available from the Library of Congress

Hardback ISBN: 9781119613435; Set ISBN: 9781394177561 (Volume 1); ePub ISBN: 9781119613527; ePDF ISBN: 9781119613473; oBook ISBN: 9781119613466

Cover Images: © ALFRED PASIEKA/Getty Images; © Intothelight Photography/Shutterstock Cover design by Wiley

Set in 9.5/12.5pt STIXTwoText by Integra Software Services Pvt. Ltd, Pondicherry, India

Preface ix List of Contributors xiii

1 Computational and Theoretical Aspects of Structure and Bonding in Doubly Bonded Organogermanium Compounds 1

Miriam Karni and Yitzhak Apeloig

2 Organogermanium Compounds of the Main Group Elements 103

Kirill V. Zaitsev

3 Transition Metal Complexes of Germanium 195

Kohtaro Osakada

4 Germanium Cages and Clusters 225

Tanja Kunz and Andreas Schnepf

5 Arylgermanium Hydrides, ArnGeH4-n (n = 1–3) - Synthesis, Characterization, Reactivity 277

Ana Torvisco and Frank Uhlig

6 Germylium Ions and Germylium Ion-like Species 299

Thomas Müller

7 Germanium-Containing Radicals 339

Alexander Hinz and Frank Breher 8 Germanium-Centered Anions 361

Christoph Marschner 9 Germylenes 387

Norio Nakata

10 Multiple Bonds to Germanium 435

Vladimir Ya. Lee

Preface vii

List of Contributors xi

11 Germaaromatic Compounds 477

Yoshiyuki Mizuhata and Norihiro Tokitoh

12 Germanium-centered Ion Radicals 507

Mikhail P. Egorov, Viatcheslav V. Jouikov, Elena N. Nikolaevskaya, and Mikhail A. Syroeshkin

13 Donor-acceptor Stabilization of Species with Low-coordinate Germanium 561

Sakya S. Sen and Herbert W. Roesky

14 Synthesis of the Penta- and Hexacoordinate Germanium(IV) Complexes 597

Naokazu Kano

15 Dynamic Stereochemistry of Penta- and Hexacoordinate Germanium(IV) Complexes 629

Vadim V. Negrebetsky and Alexander A. Korlyukov

16 X-ray Crystallography of Organogermanium Compounds 667

Catherine Hemmert and Heinz Gornitzka

17 Organogermanium Photochemistry 745

William J. Leigh

18 Oligo- and Polygermanes 787

Charles S. Weinert

19 Bioorganic and Medicinal Organogermanium Chemistry 839

Takashi Nakamura, Yasuhiro Shimada, and Katsuyuki Sato

Index 867

Preface ix

List of Contributors xiii

1 Computational and Theoretical Aspects of Structure and Bonding in Doubly Bonded Organogermanium Compounds 1

Miriam Karni and Yitzhak Apeloig

2 Organogermanium Compounds of the Main Group Elements 103

Kirill V. Zaitsev

3 Transition Metal Complexes of Germanium 195

Kohtaro Osakada

4 Germanium Cages and Clusters 225

Tanja Kunz and Andreas Schnepf

5 Arylgermanium Hydrides, ArnGeH4-n (n = 1–3) - Synthesis, Characterization, Reactivity 277

Ana Torvisco and Frank Uhlig

6 Germylium Ions and Germylium Ion-like Species 299

Thomas Müller

7 Germanium-Containing Radicals 339

Alexander Hinz and Frank Breher

8 Germanium-Centered Anions 361

Christoph Marschner

9 Germylenes 387

Norio Nakata

10 Multiple Bonds to Germanium 435

Vladimir Ya. Lee

Preface

Germanium is one of the few chemical elements in the Periodic Table, for which the theoretical prediction of its very existence has preceded its actual experimental discovery. This prediction was made by the Russian chemist Dmitri Mendeleev based on the general trends of valence and atomic weights within his Periodic Table of the chemical elements (1869) [D. Mendelejeff “Ueber die Beziehungen der Eigenschaften zu den Atomgewichten der Elemente”, Z. Chem 1869, 12, 405–406]. In an updated version of this Periodic Table (1871-1872) [D. Mendelejeff “Die Periodische Gesetzmässigkeit der Chemischen Elemente”, Ann. Chem. Pharm 1872, Suppl. 8, 133–229; D. Mendelejeff “Zur Frage über das System der Elemente”, Ber. Dtsch. Chem. Ges. 1871, 4, 348–352], Mendeleev proposed that there was a missing element in the carbon family with the atomic weight 72 that should be placed in the fourth row, just below silicon and just above tin within the carbon group. He named this non-existing (at that time) element as “eka-silicium”. Following this seminal Mendeleev prediction, German chemist Clemens Winkler finally succeeded in 1886 in the isolation of “eka-silicium” from the mineral argyrodite (Ag8GeS6) and named this new element as germanium (Ge) [C. Winkler “Germanium, Ge, Ein Neues, Nichtmetallisches Element”, Ber. Dtsch. Chem. Ges. 1886, 19, 210–211; C. Winkler “Mittheilungen über das Germanium”, J. Prakt. Chem. 1886, 34, 177–229]. Winkler also pioneered the preparation of the first organic derivative of germanium, namely, tetraethylgermane Et4Ge, in 1887 [C. Winkler “Mittheilungen über das Germanium”, J. Prakt. Chem. 1887, 36, 177–209]. Since then and up the present date, the chemistry of organogermanium compounds (that is, compounds featuring Ge–C bonds) has experienced an explosive growth, especially after the recognition of the key role of metallic germanium in semiconductor electronics in the midtwentieth century, followed by the extensive use of germanium and its organic derivatives in optical fibers, polymerization catalysts, microchip manufacturing, and biomedical applications. Given the undoubted importance of organogermanium compounds, it comes as no surprise that the field of organogermanium chemistry is continuously growing, thus requiring regular reviewing and updates on its latest advances. Among the most important previously published books on organogermanium chemistry, one should first of all mention excellent monograph by Satgé and coworkers [J. Satgé, M. Lesbre, P. Mazerolles, “The Organic Compounds of Germanium, Wiley, 1971] and two comprehensive volumes of the Patai’s series of books [(a) The Chemistry of Organic Germanium, Tin, and Lead Compounds (Eds. S. Patai, Z. Rappoport), Wiley, 1995; (b) The Chemistry of Organic Germanium, Tin, and Lead Compounds, Volume 2 (Ed. Z. Rappoport), Volume 2, Parts 1–2, Wiley, 2002]. Patai’s latest book was published 20 years ago, and since then, critical progress has been made in organogermanium chemistry with the majority of milestone developments achieved since 2000. That is why we have attempted in this book to survey, analyze and summarize the current state of affairs in the field of organogermanium chemistry, focusing on the latest (published mostly after 2000) groundbreaking advances with comprehensive and up-to-date literature coverage up to the end of 2021.

Our “Organogermanium Compounds” book is organized into the three major parts, Theory, Experiment, and Applications, made up of a total of 19 chapters, each written by leading experts in their respective fields comprehensively covering the relevant literature, first published within the last two decades.

1) The first part, Theory (one chapter) includes a contribution “Computational Aspects of Structure and Bonding in Doubly Bonded Organogermanium Compounds” from Miri Karni and Yitzhak Apeloig (Technion – Israel Institute of Technology, Haifa, Israel). In their chapter, the authors present state-of-the-art computational approaches to the flourishing field of doubly bonded organogermanium compounds and thoroughly discuss their structural and bonding aspects depending on the nature of the double bond and its substituents.

2) The second part, Experiment (16 chapters), deals with the most fundamental experimental advances that were achieved in synthetic and physico-chemical studies, and is accordingly divided into two sections, Synthesis of Organogermanium Compounds and Physico-Chemical Studies of Organogermanium Compounds. The first section, Synthesis of Organogermanium Compounds, is further subdivided into three subsections (in accord with the coordination number of the central germanium): 1) Organogermanium Compounds of Tetracoordinate Germanium, 2) Organogermanium Compounds of Low-Coordinate Germanium, 3) Organogermanium Compounds of Hypercoordinate Germanium

In the first subsection, Organogermanium Compounds of Tetracoordinate Germanium, there are four contributions. Kirill V. Zaitsev (Moscow State University, Moscow, Russia) in his chapter “Organogermanium Compounds of the Main Group Elements” provides a detailed overview of synthetic and structural aspects of organogermanium compounds containing Ge–E bonds (where E is an element of groups 13–17). The following chapter “Transition Metal Complexes of Germanium” by Kohtaro Osakada (Tokyo Institute of Technology, Tokyo, Japan) comprehensively covers chemistry of transition metal complexes featuring metal–germanium single bonds. In their chapter “Germanium Cages and Clusters”, Tanja Kunz and Andreas Schnepf (University of Tübingen, Tübingen, Germany) discuss syntheses, structural characterization, and reactivity of germanium clusters of the polyhedral-, metalloid-, and Zintl-type. In the final chapter of this subsection, “Arylgermanium Hydrides RnGeH4–n (n = 1–3) – Synthesis, Characterization, Reactivity”, Ana Torvisco and Frank Uhlig (Graz University of Technology, Graz, Austria) describe a variety of aryl-substituted organogermanium hydrides focusing on their synthesis, structural aspects (including 73Ge NMR properties), and selected applications.

The most abundant second subsection (eight chapters), Organogermanium Compounds of Low-Coordinate Germanium, focuses on the emerging field concerned with the stable germanium analogues of pivotal organic reactive intermediates, such as germanium-centered cations, free radicals, anions, ion-radicals, germylenes, multiply-bonded organogermanium compounds, germaaromatics, and donor-acceptor complexes of low-coordinate germanium. In the first chapter in this subsection, “Germylium Ions and Germylium Ion-Like Species”, Thomas Müller (University of Oldenburg, Oldenburg, Germany) summarizes the chemistry of germylium ions [R3Ge]+ and ion-like species [R3Ge(Do)]+ (Do = electron donor) with particular emphasis on their synthesis, characterization, and specific reactivity. The chapter “Germanium-Containing Radicals” by Alexander Hinz and Frank Breher (Karlsruhe Institute of Technology, Karlsruhe, Germany) discusses general methods for generation and isolation of Ge-centered radicals (including those with redox-non-innocent ligands), polyradicals, as well as their reactivity and synthetic applications. The following chapter “Germanium-Centered Anions”, written by Christoph Marschner (Graz University of Technology, Graz, Austria), focuses on the general methods for the preparation and synthetic utilization of a variety of germyl anions, as well as germyl dianions, and compounds with a negative charge on the sp2 Ge atom. Recent advances in the field of the stable germylenes (including N-heterocyclic germylenes) and their transition metal complexes, with focus on their preparation, characterization and specific reactivity, are presented in the chapter “Germylenes” by Norio Nakata (Saitama University, Saitama, Japan). The story of the low-coordinate organogermanium compounds is further continued by Vladimir Ya. Lee (University of Tsukuba, Tsukuba, Japan) in his chapter “Multiple Bonds to Germanium,” which summarizes the latest developments in the field of doubly and triply bonded organogermanium derivatives containing both homonuclear and heteronuclear multiple bonds. Another challenging topic of contemporary organogermanium chemistry, namely, germaaromatic compounds (both neutral and charged) including non-classical aromatic systems, is overviewed by Yoshiyuki Mizuhata and Norihiro Tokitoh (Kyoto University, Kyoto, Japan) in their chapter “Germaaromatic Compounds”. The following chapter “Germanium-Centered Ion Radicals”, written by Mikhail P. Egorov, Viatcheslav V. Jouikov, Elena N. Nikolaevskaya, and Mikhail A. Syroeshkin (Institute of Organic Chemistry, Moscow, Russia and University of Rennes, Rennes, France), covers recent progress in the field of anion-radicals and cation-radicals discussing general methods for their generation and identification, both experimental and computational. The Organogermanium Compounds of Low-Coordinate Germanium subsection is completed by a contribution “Donor-Acceptor Stabilization of Species with Low-Coordinate Germanium” by Sakuya S. Sen and Herbert W. Roesky (National Chemical Laboratory, Pune, India and University of Göttingen, Göttingen, Germany), which highlights the progress in the field of compounds with low-coordinate germanium stabilized by donor-acceptor interactions. The Synthesis of Organogermanium Compounds section ends with the subsection Organogermanium Compounds of Hypercoordinate Germanium containing two contributions. In the first one, “Synthesis of the Penta- and Hexacoordinate Germanium(IV) Complexes”, Naokazu Kano (Gakushuin University, Tokyo, Japan) classifies the title compounds bearing bi-, tri-, and tetradentate ligands (as well as carbene ligands), and discusses their synthesis and reactivity. The second contribution “Dynamic Stereochemistry of Penta- and Hexacoordinate Germanium(IV) Complexes”, written by Vadim V. Negrebetsky and Alexander A. Korlyukov (Russian National Research Medical University, Moscow, Russia and Institute of Organoelement Compounds, Moscow, Russia), summarizes and analyzes the data on stereochemical processes involving organic complexes of hypercoordinate germanium.

The Experiment part is completed by the Physico-Chemical Studies of Organogermanium Compounds section which comprises two contributions each dealing with state-of-the-art instrumental techniques for assessing the structures of organogermanium compounds. In the first one, “X-Ray Crystallography of Organogermanium Compounds”, Catherine Hemmert and Heinz Gornitzka (University of Toulouse, Toulouse, France) comprehensively overview the vast literature on the structurally characterized organogermanium compounds discussing their particular X-ray crystallographic features. The following chapter “Organogermanium Photochemistry”, by William J. Leigh (McMaster University, Hamilton, Canada) deals with developments in the photochemistry of organogermanium compounds, particularly emphasizing systems involving low-coordinate organogermanium compounds as either photoproducts or photoreactants.

3) The last, third, part of the book, Applications (two chapters), reports on the synthetic approaches towards materials based on organogermanium compounds and their practical use. In the first contribution, “Oligo- and Polygermanes”, Charles S. Weinert (Oklahoma State University, Stillwater, USA) reviewed and updated the recent advances in the field of the oligo- and polygermanes, discussing general synthetic methods for their preparation and also their peculiar physical properties (luminescence, electrochemistry). In the very final chapter of the Applications part (and the whole book) “Bioorganic and Medicinal Organogermanium Chemistry”, Takashi Nakamura, Yasuhiro Shimada, and Katsuyuki Sato (Asai Germanium Research Institute, Hakodate, Japan) give an account on the production and use of bioactive organogermanium compounds (such as Ge-132) in medicinal chemistry.

As an editor of the volume, I highly appreciate the works of all above-mentioned authors whose excellent contributions will hopefully turn this book into a guide to contemporary organogermanium chemistry and a useful reference source, to further inspire those already working in the field and to attract newcomers to join the fascinating world of organogermanium compounds. Although the book is primarily and foremost addressed to specialists in the field of organogermanium and organometallic chemistry, it could also be of interest to both Main Group and transition metal chemistry experts, as well as to computational and material science chemists, and to the rest of the chemical community, including undergraduate, graduate, and post-graduate students of the advanced levels.

Vladimir Ya. Lee (Editor) University of Tsukuba, Tsukuba, Japan April 2022

List of Contributors

Yitzhak Apeloig

Schulich Faculty of Chemistry

Technion-Israel Institute of Technology Haifa, Israel

Frank Breher

Institute of Inorganic Chemistry Karlsruhe Institute of Technology (KIT) Karlsruhe, Germany

Mikhail P. Egorov

N. D. Zelinsky Institute of Organic Chemistry Moscow, Russia

Heinz Gornitzka

Laboratoire de Chimie de Coordination du CNRS

Université Toulouse Toulouse, France

Catherine Hemmert

Laboratoire de Chimie de Coordination du CNRS

Université Toulouse Toulouse, France

Alexander Hinz

Institute of Inorganic Chemistry

Karlsruhe Institute of Technology (KIT) Karlsruhe, Germany

Viatcheslav V. Jouikov

N. D. Zelinsky Institute of Organic Chemistry Moscow, Russia

Naokazu Kano

Department of Chemistry

Gakushuin University Tokyo, Japan

Miriam Karni

Schulich Faculty of Chemistry

Technion-Israel Institute of Technology Haifa, Israel

Tanja Kunz Institut für Anorganische Chemie Universität Tübingen Tübingen, Germany

Alexander A. Korlyukov Pirogov Russian National Research Medical University Moscow, Russia

Vladimir Ya. Lee Department of Chemistry University of Tsukuba Tsukuba, Japan

William J. Leigh Department of Chemistry & Chemical Biology McMaster University Hamilton, Ontario, Canada

Christoph Marschner Institut für Anorganische Chemie Technische Universität Graz Graz, Austria

Yoshiyuki Mizuhata Institute for Chemical Research Kyoto University Kyoto, Japan

Thomas Müller

Institute of Chemistry

Carl von Ossietzky University Oldenburg Oldenburg, Germany

Takashi Nakamura

Asai Germanium Research Institute Co., Ltd. Hokkaido, Japan

Norio Nakata Department of Chemistry

Saitama University Saitama, Japan

Vadim V. Negrebetsky Pirogov Russian National Research Medical University Moscow, Russia

Elena N. Nikolaevskaya

N. D. Zelinsky Institute of Organic Chemistry Moscow, Russia

Kohtaro Osakada Chemical Resources Laboratory Tokyo Institute of Technology Yokohama, Japan

Herbert W. Roesky Institute of Inorganic Chemistry

Georg-August-University Göttingen Göttingen, Germany

Katsuyuki Sato

Asai Germanium Research Institute Co., Ltd. Hokkaido, Japan

Andreas Schnepf Institut für Anorganische Chemie Universität Tübingen Tübingen, Germany

Sakya S. Sen

Institute of Inorganic Chemistry

Georg-August-University Göttingen Göttingen, Germany

Yasuhiro Shimada

Asai Germanium Research Institute Co., Ltd. Hokkaido, Japan

Mikhail A. Syroeshkina

N. D. Zelinsky Institute of Organic Chemistry

Moscow, Russia

Norihiro Tokitoh Institute for Chemical Research

Kyoto University

Kyoto, Japan

Ana Torvisco Institute for Inorganic Chemistry

Graz University of Technology

Graz, Austria

Frank Uhlig Institute for Inorganic Chemistry

Graz University of Technology

Graz, Austria

Charles S. Weinert Department of Chemistry

Oklahoma State University Stillwater, Oklahoma

Kirill V. Zaitsev Department of Chemistry

Moscow State University Moscow, Russia

Computational and Theoretical Aspects of Structure and Bonding in Doubly Bonded Organogermanium Compounds

Miriam Karni and Yitzhak Apeloig

Schulich Faculty of Chemistry, Technion - Israel Institute of Technology, Haifa, Israel

In memory of Professor Robert (Bob) West, a pioneer in main group chemistry and group 14 compounds in particular, and a unique human being.

List of Abbreviations

1-Ad 1- adamantyl

AIM atoms in molecules

Ar aryl

B3LYP Becke, 3-parameter, Lee–Yang–Parr functional

Bbt 2,6-[CH(SiMe3)2]2-4-[C(SiMe3)3]-C6H2

BDE bond dissociation energy

CCSD(T) coupled cluster, singles, doubles (triples)

CDA charge delocalization analysis

CGMT Carter-Goddard-Malrieu-Trinquier model

CV cyclic voltammetry

Dip (or Dipp) 2,6-iPr2-C6H3

DMAP 4-Dimethylaminopyridine

Dmp 2,6-dimethylphenyl

DSSE divalent state stabilization energy

EDA energy decomposition analysis

Eind 1,1,3,3,5,5,7,7-octaethyl-s-hydrindacen-4-yl

EMind 1,1,7,7-tetraethyl-3,3,5,5-tetramethyl-s-hydrindacen-4-yl

EPR electron paramagnetic resonance

Etind Et Et Et Et

HOMO highest occupied molecular orbital

LDA/NL local density approximation with non-local corrections

LDF London Dispersion Forces

LUMO lowest unoccupied molecular orbital

Mes 2,4,6-Me3-C6H2

Mes* 2,4,6-tBu3-C6H2

NBO natural bond orbital

NHC N-Heterocyclic carbene

NICS nucleus independent chemical shift

NMR nuclear magnetic resonance

NPA natural population analysis

NRT natural resonance theory

PES potential energy surface

Organogermanium Compounds: Theory, Experiment, and Applications, Volume 1, First Edition. Edited by Vladimir Ya. Lee.

RRKM Rice-Ramsberger-Kassel-Marcus theory

SDD Sttutgart-Dresden Double zeta Electron Core Potential (ECP)

SOJT second-order Jahn Teller

Tbb

2,6-[CH(SiMe3)2]2-4-tBu-C6H2

Tip 2,4,6-triisopropylphenyl

VB valence bond

WBI Wiberg bond index

Xylyl (CH3)2C6H3

1.1 Introduction

Unsaturated hydrocarbons having C=C double bonds; heteroelement- substituted doubly bonded carbon compounds, e.g., ketones; alkynes with C≡C triple bonds; hydrocarbons with an extended number of double bonds, such as dienes and allenes; all are of fundamental importance to chemistry and the chemistry of life. In contrast stable heavier group 14 analogues, with Si, Ge, Sn and Pb atoms, were believed to be nonexistent until several decades ago (see below the historical overview). The last four decades have witnessed an enormous progress in the synthesis and in the theoretical understanding of the properties of these groups of compounds. The experimental progress was accompanied, and in many cases even preceded, by theoretical and computational studies. These advances were enabled by two important developments: (a) the substantial advances in quantum mechanical computational methodology [1–10] that now enables reliable, accurate and efficient calculations of the properties of relatively large molecules possessing heavy elements. These developments make quantum chemical calculations a reliable tool for the quantitative analysis of chemical phenomena and a reliable guide to experiment; and (b) the dramatic developments in computer technology that have accelerated calculations dramatically [11, 12].

The synthesis, molecular structure determination, physical and chemical properties, and the development of bonding models of multiply bonded compounds of heavier group 14 elements, Si, Ge, Sn and Pb, have been reviewed extensively in the past three decades [13–26]. The numerous experimental and theoretical studies carried out in this field have revealed fundamental differences in the structures, physical properties and chemical behavior between carbon multiply bonded compounds and analogous group 14 heavier congener compounds. The heavier group 14 compounds were considered “unusual”. In contrast, Kutzelnigg suggested that the heavier main group element compounds have “regular” behavior, while carbon compounds are the exception [27]. This revolutionary view is now widely accepted by main group researchers (not only for group 14 elements). The trends in the physical properties of group 14 elements, E, are largely responsible for the unprecedented structures and chemical behavior of the heavier group 14 compounds compared to those of the analogous carbon compounds. Selected properties of group 14 elements are given in Table 1.1. A comparison of the important physical properties of group 14 elements was also provided by Basch and Hoz [28]. The effects of the trends in the properties of the E atoms shown in Table 1.1, on the structure and nature of bonding of group 14 multiply bonded compounds, are discussed in section 1.4.1.

The unusual structures and bonding motifs of multiply bonded heavier group 14 molecules attracted the attention of many theoreticians, who studied their molecular structures, nature of bonding, kinetic and thermodynamic stability, potential energy surfaces for a variety of their reactions, etc. Many of these theoretical studies were carried out before stable compounds of these classes were synthesized, and were therefore truly predictive, and in some cases directed experiment. Two comprehensive reviews on the theoretical studies of the chemistry of organic Si, Ge, Sn and Pb compounds were published: one by Apeloig, Karni and Schleyer in 2001 [44] and one in 2002 by Frenking and coworkers [45].

In this chapter we review the theoretical studies of doubly bonded organogermanium compounds, mainly those published in the years 2000–2020 but occasionally we added important studies published in 2021. We have highlighted the insights that these theoretical studies provide on molecular structures, nature of bonding, stability vs. isomeric forms, and the physical properties, of these intriguing compounds. We do not include in this review their reactions and reaction mechanisms. Where available, we relate and compare the computational results to reported experimental studies. In our view, it is important to examine organogermanium compounds in comparison to their closest neighbors in the Periodic Table, Si and Sn. Thus, when available, we discuss comparisons with analogous organosilicon compounds (the element most similar to germanium) and other group 14 elements, mainly Sn. For pre-year 2000 theoretical studies, the readers are referred to the above-mentioned reviews [44, 45] and to specific papers cited in this chapter.

Table 1.1 Selected physical properties of group 14 elements.

Pauling

Allen

Hybridization of E in EH4e

Hybridization of E in H2E=EH2 (C2h) f

a Metallic distance;

b Difference of orbital radii between the valence p and s orbitals;

c For the transition: ns2np2(3P) → ns1np2(4P);

d For the transition: ns2np2(3P) → ns2np1(2P);

e Calculated using NBO analysis;

f Calculated using NBO analysis at B3LYP/6-31++G(d,p).

The theoretical literature of organogermanium compounds is vast. When we collected the literature for this review, we were amazed how vast is this field, and because of space limitations we had to limit the scope of this review, which even so includes more than 540 references! In this chapter, we concentrate on doubly bonded organogermanium compounds, which in their bonding and other fundamental properties are significantly different from analogous carbon compounds. We discuss homonuclear and heteronuclear organogermanium compounds, R2Ge=ER2, E=C, Si, Ge, and extended doubly bonded organogermanium compounds such as germadienes, germaallenes, and germaaromatic derivatives, i.e., germabenezene analogues. For lack of space, we do not discuss doubly bonded compounds between group 14 elements and groups 13, 15 and 16 elements or triply bonded compounds.

For completeness, we present a brief historic overview of the field, since the isolation of the first stable doubly bonded heavier group 14 element compounds in 1976.

1.2 Computational Methods

For the benefit of readers unfamiliar with the theoretical methods and terms, we bring a brief overview of the theoretical methods that are currently frequently used in theoretical calculations of organogermanium compounds. Details of the specific computational methods or of the basis sets mentioned in this review can be found in the cited papers.

The rapid development of computational packages for electronic structure calculations in the last three decades has been recently reviewed [10] (for a comprehensive list of available software packages see Ref. [46]). These computational software packages apply state-of-the-art theoretical methods for electronic

modelling of molecules in the gas phase,

solution, and the solid-state. Currently, these software packages apply mainly two theoretical approaches, ab initio wavefunction based molecular orbital (MO) methods [1–5], and electron density based Density Functional Theory (DFT) methods [6–8]. These software packages enable highly reliable calculations of molecular structures, potential energy surfaces, electron density and population analysis, vibrational frequencies, UV-Vis, NMR, EPR, IR and Raman spectroscopic properties, electronic circular dichroism (ECD), excitation energies, and other properties [1–9, 47].

Below we briefly summarize the theoretical approaches most commonly used for the calculation of the above-mentioned molecular properties. A detailed description of the field is given in the monographs cited above. Specific definitions and description of the computational methods used in the studies reviewed in this chapter are provided in the cited papers and references therein.

1.2.1 Ab initio Methods

Ab initio MO methods are based on Hartree-Fock (HF) self-consistent field (SCF) calculations, in which the total multielectron wave function Ψ is composed from single electron spin orbital wave functions ϕl (MO) via a single anti-symmetrized determinant (the Slater determinant). The single electron wave functions are expressed by a sum of basis functions (basis sets). A very large choice of basis sets exists; they differ in size and in their adaptation for a specific calculated property [48, 49]. In addition to choosing the appropriate computational method, a correct choice of a basis set determines the computational accuracy and efficiency. However, even with the largest basis set and reaching the HF limit, the HF method recovers only 95–99% of the total energy. The missing fraction is relatively small in absolute terms, but most chemistry happens in this small remaining fraction. The missing fraction is corrected by including electron correlation energy.

The most frequently used methods for including electron correlation are by perturbation theory, i.e., Møller-Plesset [50] in the nth order, (MPn) [51], configuration interaction (CI) [52], and coupled-cluster (CC) [53] methods [1–5, 46]. Today, coupled-cluster methods provide the most accurate results among the practical ab initio electronic structure theories and often serve as a benchmark for evaluating, in the absence of experimental results, the reliability of new computational methods, e.g., density functionals. Ab initio methods can be improved systematically by increasing the size of the basis sets and the amount of correlation energy that is included. It is assumed that with a complete basis set and full CI the exact solution to the Schrödinger equation can be obtained. However, the major drawback of these methods is the large computer resources required, and they are therefore applicable only to moderately-sized molecules.

1.2.2 Density Functional Theory ( DFT) Methods

DFT methods [6–8], which include electron correlation indirectly, have become the most popular electronic structure methods in computational chemistry over the last 30 years. Recent advances in the development of density functionals (DF) allow one to reliably describe numerous properties of large systems at an affordable computational expense. A major difficuly in developping reliable DFs is that in contrast to the rigor of ab intio methods, DFT methods do not allow systematic improvement of the theoretical method. The strategy for improving DFs is by adding new ingredients and parametrizing them by fitting to a set of properties, e.g., atomization energy, thermochemistry, barrier heights, etc. For example, addition of a small percentage of exact HF exchange (i.e., hybrid DFs) improves significantly the performance of local DFs as shown in Figure 1.1. For example, the performance of the PBE (Perdew–Burke-Ernzerhof) functional is improved by a factor of two in PBE0, which mixes the PBE exchange energy with 25% exact Hartree–Fock exchange energy [8, 54]. Figure 1.2 shows the importance of including London dispersion corrections (D2 [55] and D3(BJ) [56]) that capture noncovalent interactions more effectively. Based on an assessment of 200 DFs tested on 84 data sets including thermodynamic data, isomerization energies, barrier heights, etc., it was concluded that addition of dispersion corrections should be applied with caution [8]. Recommendations for effective use of DFs that are suited for specific applications are given in Refs. [8] and [57], and the reader is advised to consult these references before applying a specific method to his own research or when evaluating the research of others. As can be seen in Figures 1.1 and 1.2, calculated errors can be very large, e.g., with BLYP, B3LYP, and BP86.

The common notations of the theoretical methods used in the literature are the following: each computational level (ab initio and DFT) is defined by the type of method and the basis sets which are used. By convention, the computational level is designated as follows: [method 1/basis set 1]//[method 2/basis set 2]. Method 2 and basis set 2 are those used for geometry optimizations while method 1 and basis set 1 are those used for obtaining the final energy or other properties that are calculated.

Figure 1.1 Stacked root-mean-square deviations (RMSD, in kcal/mol) for a set of six popular local/hybrid pairs (e.g., BLYP/B3LYP, BP86/B3P86, etc.) derived from 155 isomerization energies (ID), 206 barrier heights (BH), and 91 noncovalent (NCD) interactions. Reproduced with permission from Ref. [8]. Copyright (2017) Taylor and Francis, Ltd.

Figure 1.2 Stacked root-mean-square deviations (RMSD, in kcal/mol) for a set of four DFs and their dispersion corrected (D2 and D3(BJ)) counterparts. Based on 1744 non-covalent dimer interactions (NCED) and on 755 isomerization energies (IE). Reproduced with permission from Ref. [8]. Copyright (2017) Taylor and Francis, Ltd.

1.2.3 Methods for Analysis of Electronic Structure

Important information and deeper insight into the chemical and physical properties of the studied molecules can be gained by analyzing their wave function, the electron distribution, hybridization at various atoms, the nature of the chemical bond, etc. Several analysis methods are mentioned throughout this chapter. The most popular is the Natural Bond Orbital method (NBO) [58–63] that calculates the Natural Population Analysis charges (NPA). The NPA charges are believed to be more accurate [64, 65] than the Mulliken atomic charges [66, 67], which are still often used. Several other methods for calculating atomic charges are available and a comparison of their accuracy for specific purposes was discussed, e.g., in References [64] and [65]. NBO analysis, based on localized orbitals, provides a Lewis structure of the molecule, bond orders, hybridization at the various atoms, and suggests possible resonance structures that contribute to the molecular electronic structure and their relative weights (NRT)[68], thus providing important information for analyzing the structures and bonding of the studied molecules. Other frequently used computational procedures are: (a) Atoms in Molecules (AIM), developed by Bader [69], which is based on a topological analysis of the electron density in atomic basins, and calculates also atomic AIM charges; and (b) Energy Decomposition Analysis and Natural Orbitals for Chemical Valence (EDA-NOCV), which proved to be a powerful tool for bonding analysis. For a detailed description of the above-mentioned methods and their performance, the reader is referred to the recent review by Frenking, Schwerdtfeger, and coworkers [70].

1.2.4

How Important are Relativistic Effects for Ge?

As the nuclei become heavier the strong attraction of the electrons by the heavier nuclear charge causes the electrons to move faster and behave relativistically [71, 72], i.e., their relative mass increases and the effective Bohr average radius for

Figure 1.3 (a) Stabilization of the ns valence orbital due to relativistic effect. Reprinted from Ref. [73] by permission of Gordon and Breach science publishers, 1999; (b) The contraction of the E–H bond length of EH4 (E=C, Si, Ge, Sn and Pb) calculated using FockDirac (rectangle) and Fock-Dirac-Breit (*) relativistic approaches relative to non-relativistic calculations. Reprinted with permission from Ref. [74]. Copyright (1992) Springer Verlag.

the inner-electrons contracts. It was found that the relativistic contraction of the 1s orbital of Ge, Sn, and Pb, is 3, 8, and 20%, respectively [71]. Due to the orthogonality of the higher ns orbitals to the 1s orbital, the relativistic effect on higher ns orbitals is similar [71].

As shown in Figure 1.3a, the relativistic effect stabilizes the ns orbitals of Ge–Pb atoms. However, the effect for Ge is relatively small [73]. The relativistic contraction of the E–H bond in EH4 is 0.01% for CH4, 0.05% for SiH4, 0.37% for GeH4 1.16% for SnH4, and 3.9% for PbH4, leading to nearly identical E–H bond lengths in SnH4 (1.734 Å) and PbH4 (1.737 Å). These data show relatively small relativistic effects for Ge, and consequently most calculations of Ge compounds do not include relativistic effects.

1.3 Historical Overview

Until the early 1970s, compounds with heavier group 14 elements, E, having double and triple bonds, were unknown (i.e., homonuclear or heteronuclear compounds possessing E=E’ double bonds and E≡E’ triple bonds (E, E’=Si, Ge, Sn, and Pb; E’=group 13–16 elements). Many experimental failures [75–78] to synthesize such compounds and some theoretical studies [79, 80] led to formulation of the classical “double bond rule” stating that “elements having a principal quantum number greater than 2 should not be able to form (p–p) π bonds with themselves or with other elements” [81]. Therefore, this group of compounds were believed not to exist. However, the pursuit for such compounds continued, leading in the late 1970s to early 1980s to detection of transient intermediates having E=E’ bonds of heavier group 14 elements [22, 75–78, 82, 83]. The first important breakthrough occurred in 1976, interestingly in germanium and tin chemistry, with the synthesis, isolation, and characterization of alkyl substituted digermene and distannene, [(Me3Si)2CH]2E=E[CH(SiMe3)2]2, (E=Ge (1) and E=Sn, (2)) by Lappert and coworkers [84–87]. The X-ray structure of digermene 1 shows a Ge–Ge bond length of 2.347 Å [86, 87], significantly shorter than the single Ge–Ge bond length of 2.463 Å in (GePh2)6 [87]. The Ge atoms in 1 are pyramidal featuring a trans-bent structure with sum of angles around Ge, Σ∠(Ge) = 348.5°, and a trans-bent angle of 32°. The X-ray structure of 2 [84, 85] revealed a Sn–Sn bond distance of 2.764 Å, similar to typical Sn–Sn single bond distances of 2.78–2.82 Å [44, 87], and pyramidal Sn atoms, Σ∠(Sn) = 342°, and a trans-bent angle of 41.6°. The twist angle around the

double bond in both 1 and 2 is 0°. Based on these geometries, the authors suggested that 1 and 2 result from a double donor-acceptor interaction of two singlet 1A1 ER2 monomers, in which the filled lone-pair orbital on one E(II) atom donates electrons into the vacant p orbital of the second E(II) monomer (Scheme 1.1, for E=Sn). However, 1 and 2 were stable only in the solid state, while in solution they dissociate to their corresponding monomers [87]. (tBu2MeS i)2Sn=Sn(SiMetBu2)2 synthesized in 2004 by Sekiguchi et al. [88] was the first, of only few isolated distannenes, that are stable also in solution [15, 89].

Lone-pair donation Sn

Scheme 1.1 Mode of interactions of two stannylenes producing a trans-bent distannene.

In 1981, in two milestone papers, Brook and West and their coworkers reported independently the syntheses, isolation, and characterization, including by X-ray crystallography, of the first stable silene, (Me3Si)2Si=C(OSiMe3)1-Ad (3) [90–92] and disilene, Mes2Si=SiMes2 (4), [93–96], respectively. Silene 3 has a planar skeleton with a Si=C bond length of 1.764 Å, (r(Si-C) = 1.869 Å in H3CSiH3 [97]). In disilene 4, r(Si=Si) = 2.143 Å (r(Si-Si) = 2.327 Å in H3SiSiH3 [97]), and the Si centers are slightly pyramidal with Σ∠(Si) = 358° and a trans-bent angle of 12°.

Since these pioneering landmark achievements, this field has witnessed an enormous progress. The key point to success is the use of large bulky substituents that protect the highly reactive E=E’ double bonds from further reactions. Stable compounds with a variety of E=E and E=E’ bonds (E, E’=Si, Ge, Sn, Pb; E’=group 13–16 elements), as well as compounds having an extended number of conjugated double bonds, i.e., heavier allenes and butadiene analogues, and heavier benzene analogues, were synthesized, isolated, and characterized and their chemistry has been reviewed extensively [16, 18, 24, 98–100].

Heavy alkyne analogues RE≡ER (E=Si, Ge, Sn) have also been isolated, but they are much less abundant than heavy doubly bonded compounds [17, 18, 24]. Unlike the linear alkynes, all known heavy alkynes have a highly trans-bent geometry [17, 18, 24]. The first digermyne ArGe≡GeAr (5) and distannyne ArSn≡SnAr (6) [Ar = 2,6-(2,6-iPr2-C6H3)2C6H3], were reported by Power and coworkers in 2002 [101]. Several digermynes and distannynes with other substituents on the aryl groups were reported by these authors in 2010 [102]. In 2006, Tokitoh et al. reported the synthesis of BbtGe≡GeBbt (7) (Bbt = 2,6-[CH(SiMe3)2]-4-[C(SiMe3)3]-C6H2) [103]. The synthesis and characterization by X-ray crystallography of the first stable disilyne RSi≡SiR, R=[SiiPr{CH(SiMe3)2}2] (8) was reported by Sekiguchi’s group in 2004 [104, 105]. Wiberg reported earlier the detection of a relatively stable disilyne, RSi≡SiR, R=SiMe(Sit-Bu3)2 (9), but its crystal structure could not be obtained [106]. A second known stable disilyne with R = Bbt (10) was reported in 2008 by Tokitoh’s group [107, 108]. In 1999, Schwarz and Apeloig reported the identification of two silynes HC≡SiX (X=F, Cl) in neutralization–reionization mass-spectrometric experiments, and demonstrated their microsecond existence under high-vacuum conditions [109]. More recently, Kato and Baceiredo reported a base stabilized silyne that was stable up to −30°C. Its X-ray structure revealed a short Si–C bond length of 1.667 Å, indicating the possible existence of a Si–C triple bond [110, 111]. Germa- [112] and stanna [113]-acetylenes were identified only as intermediates in a low-temperature matrix or by their trapping reactions [113]. To date, efforts to synthesize isolable E≡C (E=Si, Ge, Sn) triply bonded molecules were not successful.

It should be emphasized that all known stable multiply bonded heavier alkene and alkyne analogues are substituted with very bulky substituents that stabilize them kinetically, preventing their dimerization and significantly slowing their other reactions. Theoretical studies in the last decade pointed to the importance of attractive noncovalent London Dispersion Forces (LDF) [114] between the bulky substituents, in stabilizing these weakly bonded multiply bonded molecules against dissociation to their tetrylene monomers [115–118].

In Table 1.2 we provide a list of characterized doubly bonded germanium compounds and some of their important geometric parameters (both homo- and heteronuclear) that were synthesized since 2010 and not covered in the reviews of Power [18] and Lee [24]. Table 1.2 also includes, where available, the results of theoretical calculations of these compounds’ structures.

Table 1.2 Doubly bonded organogermanium compounds, R 2 Ge=E’R’ 2 , reported in 2010–2020. Compound

[119,120]

[124] 2018

[125] 2016

(Ge 2 )

R 2 Ge=GeRSiMe 2 Ph R = Tip = 2,4,6i Pr 3 C 6 H 2 –

R 2 Ge=GeRSiMe 3 R = Tip = 2,4,6i Pr 3 C 6 H 2 –

R 2 Ge 2 =Ge 1 RLi 2dme R = Tip = 2,4,6i Pr 3 C 6 H 2 , dme = 1,2-dimethoxyethane 2.284

K 2 2+ [(boryl)Ge=Ge(boryl)] 2–Boryl = (HCDippN) 2 B, Dipp = 2,6i Pr 2 C 6 H 3 h 2.392

Compound Ge=E’ (Å) Σ ∠ (Ge); Σ ∠ (E’) (°)

476 (Ge=Ge) and 386 (C=O) i [123] 2019

[127] 2019

R 2 Ge 2 =Ge 1 R(C(R’) = O) R = Tip = 2,4,6i Pr 3 C 6 H 2; R’ = (a) t Bu, (b) 2-methylbutan-2-yl and (c) 1-adamantyl –

22 ( E )-(L)HGe=GeH(L) L = N(Si i Pr 3 )R R = 2,6-[CHPh 2 ]-4i PrC 6 H 2 2.486

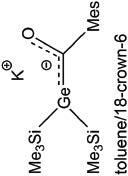
460 [126] 2013 23 ( E )-(L)HGe=GeH(L) N B N Dip Dip N SiMe 3 Dip=Diisopropylphenyl L= toluene/18-crown-6

[128] 2018 25 ArBrGe=GeBrAr a) Ar = Bbt = 2,6-[CH(SiMe 3 ) 2 ] 2 -4[C(SiMe 3 ) 3 ]-C 6 H 2 b) Ar = Tbb = 4t Bu-2,6-[CH(SiMe 3 ) 2 ] 2 -C 6 H 2

494 [131] 2015 (Continued)

24 ( E )-(Eind)XGe=GeX(Eind) X= (a) Br and (b) Cl j Et Et Et Et Et Et Et Et Eind

Ge Ge B b t B b t Bbt = 2,6-[CH(SiMe 3 ) 2 ]-4-[C(SiMe 3 ) 3 ]C 6 H 2 r(Ge=Ge) = 2.413 r(C-C) = 1.532 ∠ C(Bbt)-Ge-Ge- C(Bbt) = 133.6 39.5 b

Table 1.2 (Continued)

413 [119] 2010

[141] 2021

Compound Ge=E’ (Å)

ii) Ge=Si bonds 36 ( t BuMe 2 Si) 2 Ge=Si(SiMe 2 t Bu) 2 2.221 0.6 b

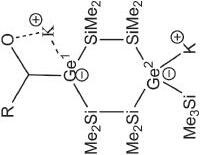
C Si Ge Si K 18-crown-6 Tip Tip Tip N Xyl • r(Ge=Si) = 2.246 r(Ge-K) = 3.407

iii) Ge=E’ (E’=group 13, 15 and 16 elements)

[143] 2016

[142] 2020 39 N Ge 1 Ge 2 N Di pp Di pp P 1 P 2 N N Di pp Dipp Dipp=2,6i Pr C 6 H 3 r(Ge 1 -P 1 ) = 2.266, r(Ge 1 -P 2 ) = 2.272 –

38 Ge B Ph 2 P X X= Cl, Br Ar * =2,6-Tip 2 -C 6 H 3 (Tip=2,4,6-iPr 3 C 6 H 2 ) 1.886 X=Cl: 359.6 (Ge), 360.0 (B)

q , 450 r [144] 2018 41 Eind 2 Ge=O

297 (IR (Ge=O) 916 cm −1 ) [145,146] 2012

40 ( t Bu 2 MeSi) 2 Ge=As-Mes* Mes* = 2,4,6t Bu 3 -C 6 H 2 2.273

Table 1.2 (Continued)

c) Extended doubly bonded compounds

B b t Ge Si GeBbt Bbt = 2,6-[CH(SiMe 3 ) 2 ]-4-[C(SiMe 3 ) 3 ]C 6 H 2 2.268, 2.290 t, u –

[152] 2015

[151] 2017 d) Germabenzenes 50 Ge Ge T bb T bb Tbb = 4t Bu-2,6-[CH(SiM e 3 ) 2 ] 2 -C 6 H 2

[153] 2019

r(Ge-C 1 ) = 1.890 v r(Ge-C 3 ) = 1.866 v

a A preliminary X-ray diffraction –poor refinement; b trans -bent angle; c At B3LYP/6–31G(d); d HOMO-LUMO gap in eV;

e Trans -bent angle = 23.7°; f Trans -bent angle = 21.3°;

g Unavailable data; X-ray crystal structure could not be obtained. Characterized as digermenes by their NMR spectra;

h For previously synthesized digermene dianions, see Ref. [46] cited in Ref. [125] [Pu, L. et al. J. Am. Chem. Soc ., 1998 , 120 , 12682–12683]. For a review, see: Wang, Y. and Robinson, G. H. Chem. Commun ., 2009 , 5201–5213; i For R’ = 1-adamantyl; j For earlier papers on dihalodigermenes, see references [5] and [6] cited in Ref. [128]; k Best described as a germanium/carbon ylide, with the negative charge located at the germanium atom;

l Indicates the presence of an active lone pair at the germanium atom, and excludes the possibility of a Ge–C (of the three-membered carbocycle) π bonding;

m The three-membered ring is oriented almost perpendicular to the germole ring; n r(K-Ge) = 3.946 Å, r(K-O) = 2.782 Å, r(C-O) = 1.241 Å; o r(K-Ge) = 3.855 Å, r(K-O) = 2.730 Å, r(C-O) = 1.236 Å; p r(K-Ge) = 3.613 Å, r(K-O) = 2.740 Å, r(C-O) = 1.231 Å; q HOMO [π(As = Ge)] –LUMO [π*(As = Ge)]; r HOMO-1 [n(As), lone pair] –LUMO [π*(As = Ge)];

s For R = Me; t Best described as R 2 Ge: → Si(0) ← :GeR 2 ;

u ∠ GeSiGe = 80.1°; v For compound 51a

1.4 Doubly Bonded Compounds

The structures of RR’E=ERR’ (E=Si, Ge, Sn, Pb) compounds were studied and analyzed extensively by both theory and experiment over the last four decades. These studies were reviewed in many comprehensive reviews [15, 16, 18, 24, 25, 44, 45, 70, 154, 155]. The main structural and bonding aspects of these compounds, which were previously reviewed, are briefly summarized below. New insights gained more recently regarding the nature of bonding in these doubly bonded compounds have been added.

The most surprising structural feature of the heavier group 14 alkene analogues, R2E=ER2, which attracted great attention, is probably their nonplanar structures (Table 1.1) [15, 16, 18, 24, 25, 44, 45, 154, 155], in sharp contrast to the planar structure of alkenes R2C=CR2. This contrast indicates that simplistic analogy between carbon and its heavier analogues is wrong, and that the heavier group 14 elements have entirely different bonding characteristics. This unexpected experimental observation was predicted by theory before many of these compounds were synthesized [156, 157], and in many cases after their synthesis, the experimental bending angles were nicely reproduced by theory [44, 45, 70, 158, 159]. The successful computational predictions in this field that preceded experiments were among the early victories of computational chemistry, which in the 1970s and 1980s still met considerable scepticism by experimentalists.

1.4.1 Bonding Models

As mentioned above, for many decades the heavier group 14 elements were believed to be reluctant to form π bonds (classical “double bond rule” [79, 80]). After the first multiply bonded compounds were isolated, new questions of great theoretical relevance arose. Why, in contrast to carbon, do its heavier analogues form compounds with very different geometries than the analogous carbon compounds? For example, why are doubly bonded compounds non-planar and have trans-bent structures? Why are triply bonded compounds bent and not linear? What is the nature of these distorted π bonds? Are they “real” double bonds? These questions raised a burst of theoretical research accompanied by vibrant debate in the last four decades [18, 25, 44, 45, 70, 160–164]. Below we review the different views of theory on these intriguing fundamental questions.

Figure 1.4 Calculated ns and np orbital radii of maximal electron density of group 14 elements [27, 37, 115]. Reproduced with permission from reference [115]. Copyright (2020) American Chemical Society.

A major fundamental difference between elements of the first (C to F) and higher rows of the Periodic Table is their most probable valence orbital radii. For carbon, the most probable radius of the 2s orbital is relatively expanded due to Pauli repulsion from the 1s electrons, while the 2p orbital that is not shielded by an inner p shell is relatively contracted. This results in very similar radii of the 2s and 2p orbitals. Moving down group 14, the atomic np orbitals are much more expanded as a consequence of intraatomic Pauli repulsion from orthogonal inner shell (n-1)p orbitals. Consequently, the radii of the ns and np orbitals (n > 2) diverge significantly [27]. Δr = rp–rs exhibits a zigzag increase from Si to Pb, caused by d-block contraction (Ge) and relativistic effects (Sn, Pb) (Table 1.1 and Figure 1.4). The similar radii of the s and p valence orbitals of carbon (and other first row elements) facilitates hybridization. In contrast, for the heavier main group elements, hybridization is much less favorable due to the dissimilar radii of their valence ns and np orbitals. Kutzelnigg introduced the term “hybridization defects” for this phenomena [27]. The increasing “hybridization defects” down group 14 have a crucial effect on the structures and bonding of heavier group 14 compounds [70, 165]. The increase in the trans-bending angle, and in the planarization energy of the trans-bent H2E=EH2 (C2h) (Table 1.3) moving down group 14, are manifestations of increasing “hybridization defects” [27, 42, 115]. Similarly, the much higher inversion barriers of e.g., PH3 (35.1 (calculated) [166]) vs. NH3 (5.8−6.0 kcal/ mol [166–168] (calculated)) and SiH3- (26 kcal/mol (MP2/6-31+G(d)) [169] vs. CH3- (2.5 kcal/mol (CCSD(T)/ aug-cc-PVQZ) [169]), was also rationalized by the smaller tendency for hybridization of the ns and np orbitals in the heavier elements [115, 166]. The decrease in the

Organogermanium compounds. theory, experiment, and applications vladimir ya. lee all chapter instant

The

Pincer

Coal Bed Methane: Theory and Applications Pramod Thakur