Introduction to Modeling and Simulation Mark W. Spong
Visit to download the full and correct content document: https://ebookmass.com/product/introduction-to-modeling-and-simulation-mark-w-spon g/

More products digital (pdf, epub, mobi) instant download maybe you interests ...

Fuel Cell Modeling and Simulation: From Microscale to Macroscale Gholam Reza Molaeimanesh
https://ebookmass.com/product/fuel-cell-modeling-and-simulationfrom-microscale-to-macroscale-gholam-reza-molaeimanesh/

An Introduction to Multiphase, Multicomponent Reservoir Simulation Matthew Balhoff
https://ebookmass.com/product/an-introduction-to-multiphasemulticomponent-reservoir-simulation-matthew-balhoff/

Modeling and Simulation of Dynamic Systems 1st Edition Robert L. Woods
https://ebookmass.com/product/modeling-and-simulation-of-dynamicsystems-1st-edition-robert-l-woods/

Process Control: Modeling, Design, and Simulation 2nd Edition B. Wayne Bequette
https://ebookmass.com/product/process-control-modeling-designand-simulation-2nd-edition-b-wayne-bequette/

Petroleum Reservoir Modeling and Simulation. Geology, Geostatistics, and Performance Reduction Sanjay Srinivasan
https://ebookmass.com/product/petroleum-reservoir-modeling-andsimulation-geology-geostatistics-and-performance-reductionsanjay-srinivasan/

Power Electronics Step-by-Step: Design, Modeling, Simulation, and Control Weidong Xiao
https://ebookmass.com/product/power-electronics-step-by-stepdesign-modeling-simulation-and-control-weidong-xiao/

An
Introduction to System
Modeling
and Control 1st Edition John Chiasson
https://ebookmass.com/product/an-introduction-to-system-modelingand-control-1st-edition-john-chiasson/

Statistical Mechanics: Theory and Molecular Simulation 2nd Edition Mark E. Tuckerman
https://ebookmass.com/product/statistical-mechanics-theory-andmolecular-simulation-2nd-edition-mark-e-tuckerman/

New Horizons in Modeling and Simulation for Social Epidemiology and Public Health Daniel Kim
https://ebookmass.com/product/new-horizons-in-modeling-andsimulation-for-social-epidemiology-and-public-health-daniel-kim/

Table of Contents
1. Cover
2. Title Page
3. Copyright
4. Dedication
5. Preface
1. Organization of the Text
2. A Note to the Instructor
3. Acknowledgements
6. About the Companion Website
7. 1 Introduction
1. 1.1 Introduction
2. 1.2 Model Classification
3. 1.3 Simulation Languages
4. 1.4 Outline of the Text
5. Problems
6. Linear Algebra Background
7. Real Analysis Background
8. Probability Background
9. Matlab
8. 2 Second‐Order Systems
1. 2.1 Introduction
2. 2.2 State‐Space Representation
3. 2.3 Trajectories and Phase Portraits
4. 2.4 The Direction Field
5. 2.5 Equilibria
6. 2.6 Linear Systems
7. 2.7 Linearization of Nonlinear Systems
8. 2.8 Periodic Trajectories and Limit Cycles
9. 2.9 Coupled Second‐Order Systems
10. Problems
9. 3 System Fundamentals
1. 3.1 Introduction
2. 3.2 Existence and Uniqueness of Solution
3. 3.3 The Matrix Exponential
4. 3.4 The Jordan Canonical Form
5. 3.5 Linearization
6. 3.6 The Hartman–Grobman Theorem
7. 3.7 Singular Perturbations
8. Problems
10. 4 Compartmental Models
1. 4.1 Introduction
2. 4.2 Exponential Growth and Decay
3. 4.3 The Logistic Equation
4. 4.4 Models of Epidemics
5. 4.5 Predator–Prey System
6. Problems
11. 5 Stability
1. 5.1 Introduction
2. 5.2 Lyapunov Stability
3. 5.3 Basin of Attraction
4. 5.4 The Invariance Principle
5. 5.5 Linear Systems and Linearization
6. Problems
12. 6 Discrete‐Time Systems
1. 6.1 Introduction
2. 6.2 Stability of Discrete‐Time Systems
3. 6.3 Stability of Discrete‐Time Linear Systems
4. 6.4 Moving‐Average Filter
5. 6.5 Cobweb Diagrams
6. Problems
13. 7 Numerical Methods
1. 7.1 Introduction
2. 7.2 Numerical Differentiation
3. 7.3 Numerical Integration
4. 7.4 Numerical Solution of ODEs
5. 7.5 Stiff Systems
6. 7.6 Event Detection
7. 7.7 Simulink
8. 7.8 Summary
9. Problems
14. 8 Optimization
1. 8.1 Introduction
2. 8.2 Unconstrained Optimization
3. 8.3 Case Study: Numerical Inverse Kinematics
4. 8.4 Constrained Optimization
5. 8.5 Convex Optimization
6. Problems
15. 9 System Identification
1. 9.1 Introduction
2. 9.2 Least Squares
3. 9.3 Regression
4. 9.4 Recursive Least Squares
5. 9.5 Logistic Regression
6. 9.6 Neural Networks
7. Problems
16. 10 Stochastic Systems
1. 10.1 Markov Chains
2. 10.2 Monte Carlo Methods
3. Problems
17. 11 Feedback Systems
1. 11.1 Introduction
2. 11.2 Transfer Functions
3. 11.3 Feedback Control
4. 11.4 State‐Space Models
5. 11.5 Optimal Control
6. 11.6 Control of Nonlinear Systems
7. Problems
18. 12 Partial Differential Equation Models
1. 12.1 Introduction
2. 12.2 The Wave Equation
3. 12.3 The Heat Equation
4. 12.4 Laplace's Equation
5. 12.5 Numerical Solution of PDEs
6. Problems
19. 13 Complex Networks
1. 13.1 Introduction
2. 13.2 Graph Theory: Basic Concepts
3. 13.3 Matlab Graph Functions
4. 13.4 Network Metrics
5. 13.5 Random Graphs
6. 13.6 Synchronization in Networks
7. Problems
20. Appendix A: Linear Algebra
1. A.1 Vectors
2. A.2 Matrices
3. A.3 Eigenvalues and Eigenvectors
21. Appendix B: Real Analysis
1. B.1 Set Theory
2. B.2 Vector Fields
3. B.3 Jacobian
4. B.4 Scalar Functions
5. B.5 Taylor's Theorem
6. B.6 Extreme‐Value Theorem
22. Appendix C: Probability
1. C.1 Discrete Probability
2. C.2 Conditional Probability
3. C.3 Random Variables
4. C.4 Continuous Probability
23. Appendix D: Proofs of Selected Results
1. D.1 Proof of Theorem 2.2
2. D.2 Proof of Theorem 5.1
3. D.3 Proof of Theorem 5.5
4. D.4 Proof of Theorem 13.3
5. D.5 Proof of Corollary 13.2
6. D.6 Proof of Proposition 13.2
7. D.7 Proof of Proposition 13.3
24. Appendix E: Matlab Command Reference
25. References
26. Index
27. End User License Agreement
List of Tables
1. Chapter 2
1. Table 2.1 Summary of isolated fixed points for nonzero eigenvalues. The cas...
2. Chapter 8
1. Table 8.1 Income versus occupancy rate. The income increases to a maximum a...
3. Chapter 10
1. Table 10.1 Pseudo‐random sequences of numbers between and , with differe...
4. Chapter 13
1. Table 13.1 Three different centrality measures for the graph in Figure 13...
2. Table 13.2 Clustering coefficients for the graph in Figure 13.32.
List of Illustrations
1. Chapter 1
1. Figure 1.1 A general characterization of a system as an object or process th...

2. Figure 1.2 An electric circuit with input voltage and output voltage . Th...

3. Figure 1.3 A mass–spring–damper system with input force and output positio...
4. Figure 1.4 A DC motor with input voltage and output speed . Both electric...
5. Figure 1.5 An economic system with multiple inputs and outputs. The choice o...
6. Figure 1.6 A manufacturing plant transforms input raw materials into output ...
7. Figure 1.7 A machine learning (ML) system takes input data and produces outp...
8. Figure 1.8 A feedback system is one where the output affects future inputs....
9. Figure 1.9 Warehouse robots for order retrieval are an example of factory au...
10. Figure 1.10 Oil and chemical refineries are large‐scale, complex systems tha...
11. Figure 1.11 The electric power grid consists of an interconnected network of...
12. Figure 1.12 A wind farm is a collection of wind turbines connected to the po...
13. Figure 1.13 Supply chains and logistics systems are responsible for moving m...
14. Figure 1.14 Systems of autonomous vehicles are already changing the trucking...
15. Figure 1.15 Surgical robots are examples of human/machine/computer interface...
2. Chapter 2
1. Figure 2.1 A mass–spring–damper system (left) and an circuit (right). Both...
2. Figure 2.2 Mass–spring system that undergoes harmonic motion.
3. Figure 2.3 Oscillation of a leaky bucket. As the mass of the water in the bu...
4. Figure 2.4 A solution trajectory in . The vector field is tangent to the ...
5. Figure 2.5 A single trajectory for the harmonic oscillator. The two state va...
6. Figure 2.6 Multiple trajectories in time (left, center) and a portion of the...
7. Figure 2.7 A simple pendulum with length rotating in a vertical plane unde...
8. Figure 2.8 The load transported by an overhead crane is modeled as a hanging...
9. Figure 2.9 Inverted pendulum model for bipedal locomotion. The stance leg be...
10. Figure 2.10 A rocket ascending vertically is modeled as an inverted pendulum...
11. Figure 2.11 The Segway Human Transporter. The controller for the Segway trie...
12. Figure 2.12 Solution trajectories and a portion of the phase portrait for th...
13. Figure 2.13 Direction field for the harmonic oscillator, which shows qualita...
14. Figure 2.14 Direction field and a portion of the phase portrait for the simp...
15. Figure 2.15 The simple pendulum has infinitely many isolated equilibrium poi...
16. Figure 2.16 Unique equilibrium states of the simple pendulum by identifying
17. Figure 2.17 Phase portraits in modal coordinates for a stable node (left); u...
18. Figure 2.18 Phase portraits of the stable node in modal coordinates (left) a...
19. Figure 2.19 Phase portraits of the saddle node in modal coordinates (left) a...
20. Figure 2.20 Jordan node phase portraits in modal coordinates (left) and in t...
21. Figure 2.21 Stable focus (sink) left; unstable focus (source) right
22. Figure 2.22 Phase portrait of the nonlinear system (2.18).
23. Figure 2.23 Phase portraits of the linear approximations of the nonlinear sy...
24. Figure 2.24 Phase portrait of the damped simple pendulum. Oscillatory soluti...
25. Figure 2.25 Direction field and phase portrait of the Van der Pol oscillator...
26. Figure 2.26 Illustrating a Hopf bifurcation in the Van der Pol system as the...
27. Figure 2.27 Phase portrait of the FitzHugh–Nagumo system with parameters ,
28. Figure 2.28 Direction field and a portion of the phase portrait of the Bruss...
29. Figure 2.29 Illustrating the Poincaré–Bendixson theorem. The annular region ...
30. Figure 2.30 Phase portrait for the system (2.28).
31. Figure 2.31 Two pendula coupled by a linear spring with stiffness .
32. Figure 2.32 Response of the coupled pendula. With the given initial conditio...
33. Figure 2.33 Double Pendulum
3. Chapter 3
1. Figure 3.1 Trajectories for the system exhibiting finite escape. The amoun...
2. Figure 3.2 Illustrating the Hartman–Grobman theorem.
3. Figure 3.3 Solution trajectory of the system (3.5) in . The trajectory rapi...
4. Figure 3.4 Schematic of a permanent‐magnet DC motor connected to a load.
5. Figure 3.5 Full‐order and reduced‐order responses for . The other state var... 4. Chapter 4
1. Figure 4.1 Example of a compartmental model. The arrows represent flows or t...
2. Figure 4.2 Example of a multi‐compartmental model.
3. Figure 4.3 One‐compartment model.
4. Figure 4.4 Two‐compartment drug distribution model.
5. Figure 4.5 Drug concentrations in the blood and tissue with a constant input...
6. Figure 4.6 Drug concentrations in the blood and tissue with initial concentr...
7. Figure 4.7 Solution of the logistic equation.
8. Figure 4.8 SI epidemic model consisting of two compartments, susceptible ( )...
9. Figure 4.9 Response of the SI model with .
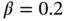
10. Figure 4.10 The SIS epidemic model. Infected individuals recover at a certai...
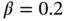
11. Figure 4.11 Response of the SIS model with , , and . The basic reproducti...

12. Figure 4.12 The SIR epidemic model.
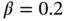
13. Figure 4.13 Response of the SIR model with and .
14. Figure 4.14 Flattening the curve with three different values for , namely,
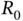
15. Figure 4.15 The SEIR compartmental model. In this model individuals transfer...
16. Figure 4.16 SIR model with vital dynamics. The birth and death rates are bot...
17. Figure 4.17 Phase portrait of the predator–prey system in the first quadrant...
18. Figure 4.18 A two‐predator, two‐prey model. Predator feeds on both prey sp...
19. Figure 4.19 Response of the two‐predator, two‐prey system with , , , , 5. Chapter 5





1. Figure 5.1 The intuitive notion of stable and unstable equilibria. The equil...
2. Figure 5.2 Illustrating the – definition of stability. Solutions starting ...
3. Figure 5.3 The intuitive idea of Lyapunov stability. The condition means t...
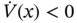
4. Figure 5.4 Phase portrait for the system (5.2)–(5.3), showing that the origi...
5. Figure 5.5 Level sets for Lyapunov function candidate in Equation (5.4).
6. Figure 5.6 Illustrating the basin of attraction and an estimate using the le...
7. Figure 5.7 Pendulum with friction example. The trajectories point toward the...
8. Figure 5.8 Phase portrait for the system. For any initial conditions, the va...
6. Chapter 6
1. Figure 6.1 Response of the system (6.6) for different values of the coeffici...
2. Figure 6.2 Response of the system (6.6) with (right) and with (left).
3. Figure 6.3 stairs(y) (left), bars(y) (middle), stem(y) (right) for a sequenc...


4. Figure 6.4 Plot of (top) and (bottom) for the discrete‐time nonlinear sy...
5. Figure 6.5 Seven‐day moving‐average filter for a set of stock price data plo...
6. Figure 6.6 Moving‐average filter response to noisy input data.
7. Figure 6.7 Cobweb diagram for Equation (6.12) with iterations. A decreasin...
8. Figure 6.8 Cobweb diagrams for different slopes of the supply and demand cur...
9. Figure 6.9 Equilibrium points of the discrete logistic equation at and ....

10. Figure 6.10 Cobweb diagram for . In this case the only equilibrium is at th...
11. Figure 6.11 Cobweb diagram for . In this case, the solutions converge to th...
12. Figure 6.12 Stable equilibrium for (left) and unstable equilibrium for (...
13. Figure 6.13 Chaotic solution for .
7. Chapter 7
1. Figure 7.1 Illustrating the forward, backward, and middle difference approxi...
2. Figure 7.2 Numerical computation of the derivative of using the Matlab com...
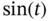
3. Figure 7.3 Illustrating the left‐endpoint, right‐endpoint and midpoint integ...
4. Figure 7.4 Illustrating trapezoidal integration. The area under a representa...

5. Figure 7.5 Illustrating Simpson's rule. The function is approximated by a ...

6. Figure 7.6 Euler's method for with , , and step sizes ( ) and ( ). T...
7. Figure 7.7 Response of the simple pendulum model using Euler's method with a...
8. Figure 7.8 Euler's method ( ) and the Euler predictor–corrector method ( ) f...
9. Figure 7.9 Comparison of Euler's method ( ) with a fourth‐order Runge–Kutta ...
10. Figure 7.10 Solution of the stiff system using ode45 . The expanded view on t...
11. Figure 7.11 Solution of the stiff system using ode23s . As an implicit method...
12. Figure 7.12 Solution of the DAE system using ode15s . ode15s should be used w...
13. Figure 7.13 Response of the DAE model of the SI‐epidemic system.
14. Figure 7.14 Response of the falling object. The simulation terminates when

15. Figure 7.15 The bouncing ball starting at initial height with coefficient ...

16. Figure 7.16 Simulink blocks from the Simulink library.
17. Figure 7.17 Realization of the second‐order system using two integrator bl...

18. Figure 7.18 Step response of the system (7.21) starting with initial conditi...
19. Figure 7.19 Simulink integrator block.
20. Figure 7.20 A practical differentiator built from an integrator. With input
21. Figure 7.21 The practical differentiator with input produces a signal that...

22. Figure 7.22 Simulink block diagram representation of the nonlinear system (7...
23. Figure 7.23 Simulink block diagram representation of the Van der Pol equatio...
8. Chapter 8
1. Figure 8.1 is a strict local minimizer; is a strict local maximizer; i...
2. Figure 8.2 The search directions in gradient descent are orthogonal to level...

3. Figure 8.3 If the condition number of is , the level sets are concentric ...

4. Figure 8.4 If the condition number of is large, the convergence of the met...
5. Figure 8.5 Newton's method for finding a root of .

6. Figure 8.6 A selective compliant articulated robot arm. SCARA robots are use...
7. Figure 8.7 Schematic representation of a two‐link robot. and are the joi...

8. Figure 8.8 Inverse kinematics solution using Newton's method. Desired end‐ef...

9. Figure 8.9 Inverse kinematics solution using gradient descent. Desired end‐e...

10. Figure 8.10 Level sets of the objective function with and the graph of t...

11. Figure 8.11 Feasible region for the linear programming problem.
12. Figure 8.12 Illustrating the notion of a convex function. The convexity cond...
13. Figure 8.13 The set on the left is convex. The set on the right is nonco...
14. Figure 8.14 Illustrating Proposition 8.4. The condition (8.19) means that th... 9. Chapter 9

1. Figure 9.1 The range of is an ‐dimensional subspace of . If is not i...
2. Figure 9.2 Estimate of the resistance from measurements. The horizontal ...
3. Figure 9.3 Linear regression example. The straight line is estimated from th...
4. Figure 9.4 Linear and quadratic polynomial fitting. The choice of which mode...
5. Figure 9.5 The logit function (left) and the inverse logit function (right)....
6. Figure 9.6 Best‐fit logistic curve for the given credit score data.
7. Figure 9.7 A brain neuron
8. Figure 9.8 An artificial neuron model
9. Figure 9.9 Examples of activation functions
10. Figure 9.10 A one‐layer neural network
11. Figure 9.11 The decision boundary separating the two data sets.
12. Figure 9.12 Results of training the perceptron on the data set
10. Chapter 10
1. Figure 10.1 Transition diagram for a Markov chain. The numbered circles repr...
2. Figure 10.2 Transition diagram for Example 10.1. Each month a fraction of cu...
3. Figure 10.3 Computing the transition probabilities for months and .
4. Figure 10.4 The Markov mouse.
5. Figure 10.5 Transition diagram for the Markov mouse. The probabilities are c...
6. Figure 10.6 Transition diagram for the Markov mouse assuming that the mouse ...
7. Figure 10.7 Two compartments containing a number of gas molecules.
8. Figure 10.8 Transition diagram for the Ehrenfest model.
9. Figure 10.9 Number of gas molecules in compartment over time. The number f...
10. Figure 10.10 An example of an absorbing Markov chain. Once the state reaches...
11. Figure 10.11 An example of isomorphic Markov chains.
12. Figure 10.12 Transition diagram for Example 10.8.
13. Figure 10.13 Transition diagram for the tennis example. The data are fictiti...
14. Figure 10.14 Counting the fraction of points inside the quarter circle gives...
15. Figure 10.15 Monte Carlo simulation to predict stock prices. Fifty random si...
16. Figure 10.16 Monte Carlo simulation of the SIR model showing the estimated n...
11. Chapter 11
1. Figure 11.1 A closed‐loop feedback system where the output affects future in...
2. Figure 11.2 Open‐loop system (left) and closed‐loop system (right).
3. Figure 11.3 Examples of feedback systems: the outrigger canoe, flyball gover...
4. Figure 11.4 A transfer function representation of a linear system as a ratio...
5. Figure 11.5 Dominant second‐order pole location. Second‐order systems are an...
6. Figure 11.6 Underdamped, critically damped, and overdamped second‐order step...
7. Figure 11.7 A second‐order system step response showing overshoot, rise time...
8. Figure 11.8 Step response of the third‐order system with DC gain equal to ....
9. Figure 11.9 Block diagram showing the basic components of a control system....

10. Figure 11.10 First‐order system with compensator .

11. Figure 11.11 Satellite attitude control. The satellite is equipped with thru...
12. Figure 11.12 Simulink model of the satellite control. The sensor block integ...
13. Figure 11.13 Position, velocity, and control input torque for the satellite....
14. Figure 11.14 Simulink model of a PI speed control system.

15. Figure 11.15 Responses of the PI control gains, , , . The disturbance inp...


16. Figure 11.16 Controller canonical form. The variables are the outputs, , ...
17. Figure 11.17 Observer canonical form
18. Figure 11.18 Inertias coupled by a torsional spring.
19. Figure 11.19 Step response of the closed‐loop system.
20. Figure 11.20 Simulink system for the observer
21. Figure 11.21 Estimation errors for the observer. The initial conditions were...
22. Figure 11.22 Simulink model of the observer/state feedback control system.
23. Figure 11.23 Output response of the observer/state feedback control system....
24. Figure 11.24 Pendulum response.
25. Figure 11.25 The reaction‐wheel pendulum.
26. Figure 11.26 Simulink model of adaptive control using the MIT rule.
27. Figure 11.27 Response of the adaptive control system. The trajectory initi...

12. Chapter 12
1. Figure 12.1 Coupled mass–spring system.
2. Figure 12.2 Snapshots of the vibrating spring with initial shape . The solu...

3. Figure 12.3 The square wave function is a piecewise‐continuous, odd function...
4. Figure 12.4 Fourier series approximation of the square wave function with ,...
5. Figure 12.5 Fourier series approximation of the delta function for , respec...
6. Figure 12.6 Series solution of the wave equation. Note that the response is ...
7. Figure 12.7 Insulate rod with heat flowing in one dimension along the rod.

8. Figure 12.8 The temperature is a thin bar with both ends held at zero temp...
9. Figure 12.9 Rectangular region with values of specified on the boundary.

10. Figure 12.10 Slab of width . The left‐hand side is held at temperature an...
11. Figure 12.11 Grid of mesh points discretizing time in increments of and sp...
12. Figure 12.12 Points used in the finite‐difference approximation.
13. Figure 12.13 Temperature distribution generated by the Matlab simulation usi...
13. Chapter 13
1. Figure 13.1 A Network of interconnected agents. Depending on the application...
2. Figure 13.2 An undirected graph of order and size . We say that is a
3. Figure 13.3 A nonsimple graph (left) containing loops and a multigraph (righ...
4. Figure 13.4 Example of a weighted, directed graph. The edge weights may repr...
5. Figure 13.5 A ‐regular graph. Each vertex in the graph has degree .
6. Figure 13.6 The first five complete graphs .

7. Figure 13.7 The two graphs above are not isomorphic despite the fact that th...
8. Figure 13.8 The graph on the right is connected. It is possible to reach eve...
9. Figure 13.9 Example of a subgraph. The graph on the right is a subgraph of t...
10. Figure 13.10 An example of a graph containing two connected components
11. Figure 13.11 The graph on the left is strongly connected. The graph on the r...
12. Figure 13.12 A graph with cut vertices and a bridge.
13. Figure 13.13 A tree contains no cycles (i.e., no closed paths). This also me...
14. Figure 13.14 Graph and spanning tree (bold edges).
15. Figure 13.15 Example of a bipartite graph. The sets partitioning the graph a...
16. Figure 13.16 A tree (left) redrawn as a bipartite graph (right).
17. Figure 13.17 The above two graphs are isomorphic and so both are planar. The...
18. Figure 13.18 Utility connections to three houses. The bipartite graph repres...
19. Figure 13.19 Example of a planar graph with regions, vertices, and edg...

20. Figure 13.20 A graph example with its associated Laplacian matrix.
21. Figure 13.21 With four edges, the oriented incidence matrix will have four c...
22. Figure 13.22 A simple undirected graph created by the Matlab graph function....
23. Figure 13.23 A weighted directed network created by Matlab digraph function....
24. Figure 13.24 A railway network. The degree distribution of this network is a...
25. Figure 13.25 An airline network showing several hub airports. Most other air...
26. Figure 13.26 Magnitude versus frequency of earthquakes plotted on a log‐log ...
27. Figure 13.27 Income of the top 100 (left) and the top 10 (right). Despite th...
28. Figure 13.28 The length of a path is the number of ‘hops’ between nodes. The...
29. Figure 13.29 A low‐degree node may be important if it is adjacent to high de...

30. Figure 13.30 A graph with different values of degree centrality, betweenne...
31. Figure 13.31 The neighbors of are . The subgraph formed by these nodes ha...
32. Figure 13.32 Graph clustering example for Example 13.19.
33. Figure 13.33 A triangle and a triple
34. Figure 13.34 A graph with three distinct cliques.
35. Figure 13.35 ER random graphs showing the emergence of a giant component. Bo...
36. Figure 13.36 Fraction of nodes outside the giant component as a function of ...

37. Figure 13.37 network. With probability , the graph is regular with each n...



38. Figure 13.38 networks with (top) (bottom). To access Matlab code to co...
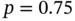
39. Figure 13.39 Average shortest path length and clustering coefficient versus ...
40. Figure 13.40 Network grown with preferential attachment with and edges a...
41. Figure 13.41 Flocking of birds (left), swarming of insects (middle) and scho...
42. Figure 13.42 Four agents interconnected in a ring.
43. Figure 13.43 Response of the four‐agent network showing that the states sync...
14. Appendix B
1. Figure B.1 A connected set. Every pair of points and in can be connect...
2. Figure B.2 A simply connected set is one with no holes. The set shown is not...
3. Figure B.3 Level sets of a function in .
15. Appendix C

1. Figure C.1 The binomial distribution with an .

2. Figure C.2 The Poisson distribution with mean .
3. Figure C.3 A normal or Gaussian distribution and cumulative distribution fun...
4. Figure C.4 The exponential distribution and cumulative distribution function...
5. Figure C.5 A power‐law distribution for .