QuantumMechanics
MathematicalStructure and PhysicalStructure PartII
JohnR.Boccio EmeritusProfessorofPhysics SwarthmoreCollege
Copyright © 2020byProfessorJohnBoccio Donotreproduceordistributecopiesofthisbookwithoutpermission.
May6,2022
Contents
9 Time-DependentPerturbationTheory683
9.1Theory................................... 683
9.1.1Whatisthephysicalmeaningofthisresult?........ 689
9.2AtomicRadiationandSelectionRules................ 702
9.2.1TheElectricDipoleApproximation............. 703
9.2.2InducedEmissionandAbsorption.............. 705
9.3ARealPhysicalProcess-Ionization................. 708
9.3.1EvaluationoftheMatrixElement.............. 710
9.4AdiabaticandSuddenApproximations................ 712
9.5Problems.................................. 720
9.5.1SquareWellPerturbedbyanElectricField......... 720
9.5.23-DimensionalOscillatorinanelectricfield......... 720
9.5.3Hydrogenindecayingpotential................ 721
9.5.42spinsinatime-dependentpotential............ 721
9.5.5AVariationalCalculationoftheDeuteronGroundState Energy............................... 721
9.5.6SuddenChange-Don’tSneeze................ 722
9.5.7AnotherSuddenChange-Cuttingthespring....... 722
9.5.8Anotherperturbedoscillator................. 722
9.5.9NuclearDecay.......................... 722
9.5.10TimeEvolutionOperator................... 723
9.5.11Two-LevelSystem........................ 723
9.5.12InstantaneousForce....................... 723
9.5.13Hydrogenbeambetweenparallelplates........... 723
9.5.14ParticleinaDeltaFunctionandanElectricField..... 724
9.5.15Nastytime-dependentpotential[complexintegrationneeded]725
9.5.16NaturalLifetimeofHydrogen................. 725
9.5.17Oscillatorinelectricfield.................... 726
9.5.18SpinDependentTransitions.................. 726
9.5.19TheDrivenHarmonicOscillator............... 727
9.5.20ANovelOne-DimensionalWell................ 728
9.5.21TheSuddenApproximation.................. 728
9.5.22TheRabiFormula........................ 729
9.5.23RabiFrequenciesinCavityQED............... 729
10 QuantumMeasurement 731
10.1BasicQuantumMechanicsReviewed................. 731
10.1.1Whereisthe“collapse”postulate?.............. 734
10.2TheMeasurementProcess....................... 735
10.2.1TheDensityOperator..................... 736
10.2.2ACrucialExampleoftheNeedfortheDensityOperator 739
10.3Theso-calledGambler’sRuinproblem-apossiblewaytogetto theirreversiblerecording........................ 746
10.3.1MathematicalProblemofthePoints............. 746
10.4Anothershortdigression-anotherwaytogettotheirreversible recording-Decoherence......................... 750
10.5Lookcloselyat“which-path”experiments.............. 751
10.6ResolvingParadoxesandUnderstandingMeasurement...... 757
10.6.1TheapparentparadoxofSchrödinger’scat........ 757
10.6.2DensityOperatortotheRescue................ 758
10.7SomeRepetitionandMoreIntricateDetails............. 763
10.7.1Rememberthestandarddiscussionfromearlier:...... 763
10.7.2TheLocalStateSolution(duetoJauch)oftheProblemof DefiniteOutcomes........................ 765
10.7.3Nowforevenmoredetailsandnewinterpretations.... 768
10.7.4Anevenmoredramaticexperiment-Experimentalnonlocalityandentanglement................... 772
10.8TheEnvironmentasMonitor...................... 785
10.8.1TheProblemofIrreversibility................. 787
10.8.2HowEnvironmentalDecoherenceCollapsesSuperpositions 789
10.8.3DecoherenceandtheMeasurementProblem........ 793
10.9LastThoughts.............................. 817
11 TheEPRArgumentandBellInequality 821
11.1HiddenvariablesandBell’sInequalities-1stTry.......... 821
11.1.1TheElectronSpin........................ 821
11.1.2CorrelationsBetweentheTwoSpins............. 822
11.1.3ASimpleHiddenVariableModel............... 825
11.2Bell’sTheoremandExperimentalResults.............. 827
11.3TheEPR(Einstein-Podolsky-Rosen)Argument-QuickOverview. 829
11.3.1TheBellInequalityagain................... 831
11.4EPRandBell-TheDetails...................... 834
11.4.1Single-PhotonInterference................... 834
11.4.2BasicFormalism......................... 849
11.5InseparablePhotons(theEPRParadox)includingsomehistory. 852
11.5.1ThePhilosophicalStakesintheDebate........... 852
11.5.2FromComotoBrussels(1927-30).............. 853
11.5.3FromBrusselstotheEPRParadox(1930-35)....... 854
11.5.4ElementaryIntroductiontotheEPRParadox....... 855
11.5.5TheEPRParadox(1935-52)................. 857
11.5.6TheBCHSHInequality(1964)................ 858
11.5.7BCHSHInequality(Bell’sinequalityinrealworld)..... 861
11.5.8TheBeginningsoftheExperimentatOrsay(1976).... 864
11.6ThePrincipleofNon-Separability................... 872
11.7AnExampleandaSolution-Bell’sTheoremwithPhotons... 874
11.8Non-Locality,EPRandBell-alasttime.............. 878
11.8.1TheBellInequalities...................... 882
11.9BayesianProbabilityinQM...................... 884
11.9.1UsingBayesianIdeasinAnalysisofExperiments..... 884
11.9.2SimpleExample......................... 886
11.9.3SimpleIdeas........................... 886
11.9.4MoreabouttheGreenberger-Horne-Zeilinger(GHZ)State 895
11.10Problems.................................. 896
11.10.1BellInequalitywithStern-Gerlach.............. 896
11.10.2Bell’sTheoremwithPhotons................. 898
11.10.3Bell’sTheoremwithNeutrons................. 899
11.10.4Greenberger-Horne-ZeilingerState.............. 899
12 IdenticalParticles901
12.1Theoreticalideas............................. 901
12.2BosonswithSpin=0.......................... 906
12.3Spin=1/2Fermions........................... 908
12.4TheN-ElectronAtom.......................... 914
12.5TheHeliumAtom............................ 920
12.6MultielectronAtoms........................... 928
12.6.1Screening............................. 930
12.6.2ShellStructure.......................... 931
12.7AngularMomentumCoupling..................... 935
12.7.1LSCoupling........................... 936
12.7.2Hund’sRules........................... 943
12.7.3JJ-Coupling........................... 944
12.8SphericalHarmonicsAdditionTheorem............... 948
12.8.1OrbitalAngularMomentum.................. 948
12.8.2TheAdditionTheorem..................... 951
12.9Problems.................................. 953
12.9.1TwoBosonsinaWell...................... 953
12.9.2TwoFermionsinaWell.................... 954
12.9.3Twospin 1/2 particles..................... 954
12.9.4HydrogenAtomCalculations................. 955
12.9.5Hund’srule............................ 956
12.9.6Russell-SaundersCouplinginMultielectronAtoms.... 956
12.9.7Magneticmomentsofprotonandneutron......... 957
12.9.8Particlesina3-Dharmonicpotential............ 958
12.9.92interactingparticles...................... 958
12.9.10LSversusJJcoupling...................... 959
12.9.11Inaharmonicpotential.................... 959
12.9.122particlesinteractingviadeltafunction.......... 959
12.9.132particlesinasquarewell................... 960
12.9.142particlesinteractingviaaharmonicpotential...... 960
12.9.15TheStructureofhelium.................... 960
13 SomeExamplesofQuantumSystems963
13.1CoherentandSqueezedStates..................... 963
13.2Electroninacircularwire....................... 968
13.3Spin-OrbitCouplinginComplexAtoms............... 972
13.4ZeemanEffectinComplexAtoms................... 975
13.4.1Method#1:PlausibilityDerivation............. 976
13.4.2Method#2:FullFormalDerivation............. 976
13.5NeutronInterferometry......................... 977
13.5.1NeutronInterferences...................... 979
13.5.2TheGravitationalEffect.................... 980
13.6ThePenningTrap............................ 982
13.6.1MotionofanElectroninaPenningTrap.......... 982
13.6.2TheTransverseMotion..................... 984
13.6.3MeasurementofElectronAnomalousMagneticMoment. 985
13.7Schrodinger’sCat............................ 986
13.7.1Schrodinger’sCat-amoredetailedpresentation..... 987
13.7.2ConstructionofaSchrodinger-CatState.......... 996
13.7.3QuantumSuperpositionVersusStatisticalMixture.... 997
13.7.4TheFragilityofaQuantumSuperposition......... 1000
13.8TheQuantumEraser.......................... 1002
13.8.1MagneticResonance...................... 1003
13.8.2RamseyFringes......................... 1005
13.8.3DetectionoftheNeutronSpinState............. 1009
13.8.4TheActualQuantumEraser................. 1011
14 SolidStatePhysics
1015
14.1CrystalStructureandSymmetry................... 1015
14.1.1SymmetryoftheCrystalSystem............... 1016
14.2BlochTheorem,theReciprocalLatticeandBrillouinZones... 1029
14.2.1TranslationOperatorsinConfigurationSpace....... 1029
14.2.2DerivationofBloch’sTheorem................ 1031
14.3Free-ElectronandWeak-BindingApproximations;1-Dimension. 1045
14.3.1TheFree-ElectronApproximation.............. 1046
14.4IntroductiontotheWeak-BindingApproximation......... 1054
14.5TheKronig-PenneyModel....................... 1065
14.5.1ExactAnalysis.......................... 1065
14.6Free-ElectronandWeak-BindingApproximations;2-Dimensions. 1072
14.6.1TheFree-ElectronApproximation.............. 1073
CONTENTS v
14.7Born-Oppenheimerdescriptionoftwoatomsinacombinedoscillatorandlatticetrap.......................... 1096
14.7.1Introduction........................... 1096
14.7.2LatticeHamiltonian....................... 1097
14.7.3Relative-andCenter-of-MassQuasi-Momenta....... 1099
14.7.4Born-OppenheimerSeparation................ 1102
14.7.5ExactandBorn-OppenheimerApproximateSolutions.. 1107
14.7.6Conclusions............................ 1115
14.8Spontaneoussymmetrybreakinginquantummechanics..... 1115
14.8.1Introduction........................... 1116
14.8.2TheHarmonicCrystal..................... 1116
14.8.3TheThinSpectrum....................... 1117
14.8.4Subtleties............................. 1120
14.8.5Discussion............................ 1121
14.9Problems.................................. 1121
14.9.1PiecewiseConstantPotentialEnergy
OneAtomperPrimitiveCell................. 1121
14.9.2PiecewiseConstantPotentialEnergy
TwoAtomsperPrimitiveCell................. 1122
14.9.3Free-ElectronEnergyBandsforaCrystalwithaPrimitive RectangularBravaisLattice.................. 1123
14.9.4Weak-BindingEnergyBandsforaCrystalwithaHexagonalBravaisLattice....................... 1123
14.9.5AWeak-BindingCalculation#1............... 1124
14.9.6Weak-BindingCalculationswithDelta-FunctionPotential Energies.............................. 1125
14.9.7Isthespectrumoftheharmoniccrystalexamplereally thin?1126
14.9.8Arethelimitsreallynoncommutativeintheharmonic crystalexample?......................... 1126
14.9.9TheBogoliubovtransformationintheharmoniccrystal example.............................. 1127
15 RelativisticWaveEquations
ElectromagneticRadiationinMatter 1129
15.1Spin0particles:Klein-GordonEquation............... 1129
15.1.1Howtofindcorrectformofrelativisticwaveequation?.. 1130
15.1.2NegativeEnergyStatesandAntiparticles.......... 1134
15.2PhysicsoftheKlein-GordonEquation................ 1137
15.3FreeParticlesasWavePackets..................... 1143
15.4BoundStateProblems.......................... 1147
15.4.1NonrelativisticLimit...................... 1150
15.5RelativisticSpin1/2Particles-TheDiracEquation........ 1151
15.5.1LorentzTransformationofSpin................ 1151
15.6TheDiracEquation........................... 1160
15.6.1NonrelativisticLimit...................... 1161
15.6.2CurrentsandContinuityEquations............. 1163
15.6.3FreeParticleSolutions..................... 1165
15.6.4MoreAboutCurrents...................... 1169
15.6.5Non-relativisticLimit...................... 1171
15.6.6TheDiracHydrogenAtom................... 1174
15.7ElectromagneticRadiationandMatter................ 1193
15.7.1InteractingwiththeClassicalRadiationField....... 1193
15.7.2RelationtoGaugeInvariance................. 1195
15.7.3Interactions............................ 1196
15.7.4InducedAbsorptionandEmission.............. 1197
15.7.5QuantizedRadiationFieldandSpontaneousEmission.. 1199
15.8Problems.................................. 1204
15.8.1DiracSpinors........................... 1204
15.8.2LorentzTransformations.................... 1205
15.8.3DiracEquationin 1 + 1 Dimensions............. 1205
15.8.4TraceIdentities......................... 1205
15.8.5Right-andLeft-HandedDiracParticles........... 1206
15.8.6GyromagneticRatiofortheElectron............ 1206
15.8.7Dirac → Schrodinger...................... 1207
15.8.8PositiveandNegativeEnergySolutions........... 1207
15.8.9HelicityOperator........................ 1207
15.8.10Non-RelativisiticLimit..................... 1207
15.8.11GyromagneticRatio....................... 1207
15.8.12Propertiesof γ5 ......................... 1208
15.8.13LorentzandParityProperties................. 1208
15.8.14ACommutator.......................... 1208
15.8.15SolutionsoftheKlein-Gordonequation........... 1208
15.8.16MatrixRepresentationofDiracMatrices.......... 1208
15.8.17WeylRepresentation...................... 1209
15.8.18TotalAngularMomentum................... 1209
15.8.19DiracFreeParticle....................... 1210
Chapter9
Time-DependentPerturbationTheory
9.1 Theory
Time-independentorstationary-stateperturbationtheory,aswedevelopedearlier,allowsustofindapproximationsfortheenergyeigenvaluesandeigenvectors incomplexphysicalsystemsthatarenotsolvableinclosedformandwherewe couldwrite ˆ H intwopartsas
Fortheseperturbationmethodstowork, ˆ V mustbe weak and time-independent
Wenowturnourattentiontothecase
where ˆ Vt is weak and time-dependent.
Examplesmightbethedecaysofanatomicsystembyphotonemissionorthe ionizationofanatombyshininglightonit.
Weassumethatatsometime t0 thesystemhasevolvedintothestate ∣ψ(0)) t ⟩, i.e.,thestate ∣ψ(0 t ⟩ satisfiesthetimeevolutionequation
Itisasolutionofthetime-dependentSchrodingerequationwithnoperturbing interactionsbefore t0 where
Attime t0 we turnon theinteractionpotential(orperturbation)sothat
Thenewstateofthesystemthensatisfies
withthe boundarycondition(initialvalue)
Aswesaid,weassumethatthefulltime-dependentSchrodingerequationcannot besolvedinclosedformandsowelookforapproximatesolutions.
Welet ˆ Vt beasmallperturbation,i.e.,weassumethereisanaturalsmall parameterin ˆ Vt (aswesawintime-independentperturbationtheory)andwe makeanexpansionofthesolutioninpowersof ˆ Vt orthissmallparameter.
Sincetheeffectof ˆ H0 willbemuchgreaterthantheeffectof ˆ Vt,mostofthetime dependencecomesfrom ˆ H0.Ifwecouldneglect ˆ Vt,thensince ˆ H0 isindependent oftime,wewouldhavethesimpletimedependence
Letusassumethatthisisstillapproximatelytrueandremovethisknowntime dependencefromthesolution.Thisshouldremovethemajorportionofthe totaltimedependencefromtheproblem.Wedothisbyassumingasolutionof theform
andthendeterminingandsolvingtheequationforthenewstatevector
(t)⟩
Substitutingthisassumptioninouroriginalequation,theequationfor ∣ψ(t)⟩ is thengivenby
Thesubstitutionhasremoved H0 fromtheequationandchangedthetimedependenceoftheperturbingpotential.Weareintheso-called interactionpicture orrepresentation where both thestatevectorsandtheoperatorsdependontime aswediscussedearlier.
Wedevelopa formalsolution byintegratingthisequationofmotionforthe statevectortoget
sothattheformalsolutionisgivenby
Thisisan integralequation for ∣ψ(t)⟩.Wesolveitasapowerseriesin ˆ Vt bythe methodofiteration
The 0th orderapproximationisfoundbyneglectingtheperturbingpotential. Weget
The 1st orderapproximationisobtainedbyinsertingthe 0th orderapproximationintothefullequation.Weget
The 2nd orderapproximationisobtainedbyinsertingthe 1st orderapproximationintothefullequation.Weget
Noticethatinallsubsequentiterationstheoperators ˆ V (t′), ˆ V (t′′), ,etc,always occurinorderofincreasingtimefromrighttoleft.
Wecanwritethegeneralresultas
where
Thecomplete,formalsolutiontotheproblemisthengivenby
sothat
thetotaltimedevelopmentoperator(9.20)
Beforedevelopingthedetailedtechniquesoftime-dependentperturbationtheory,letusspendsometimewiththeoperator ˆ U (t,t0) anddiscusssomeofits properties.
Wefirstintroducetheideaofa time-orderedproduct ofoperatorsasfollows. Thesymbol
meanstheproductoftheoperatorswheretheoperatorsarewrittenfromright toleftinorderofincreasingtimes,i.e.,
Now,wehaveusingthetime-orderedproductdefinition
andingeneral
becausethereare n! possibleorderingsofthe n termsinvolved.Thislastform isidenticaltotheexpressionfor ˆ U (t,t0) andthuswehave
Thelastexpressionisjusta convenientshorthandfortheinfinitesum.Inorder toverifythatthisisinfactasolutionof
wemustprovethat
Substituting,wehave
Inthedifferentiationwedonothavetoworryaboutthenon-commutationofthe operatorsinsidethetime-orderedproductsincethe orderisalreadyspecified
Since t iscertainlythelatesttimeinthetime-orderedproductandtherefore
alltheotheroperatorswillbeontherightof ˆ V (t) wecanpullitoutsidethe time-orderedproductandwrite
asrequired.
The mostimportantquestion (reallytheonlyquestion)thatisusuallyaskedin quantummechanicsisthefollowing:
Supposethatthesystemisinitiallyinaneigenstate ∣n⟩ of ˆ H0,i.e., ˆ H
⟩ = n
n⟩.Whatistheprobability thatthesystemwillbeobserved,aftertheperturbation hashadtimetoact,inadifferent(andthusorthogonal) eigenstateof ˆ H0,say ∣m⟩?
Alternatively,thequestionissometimesposedthisway:
Whatistheprobabilitythattheinteractioncausesthe systemtomakea transition fromthestate ∣n⟩ tothe state ∣m⟩?
Theprobabilityamplitudeforobservingthesysteminthestate
m⟩ attime t isgivenby
where
istheinitialstate.
Setting t0 = 0 forsimplicityandusingthe 1st orderapproximationfor ˆ U (t, 0) andalsousing
weget
Theprobabilityofthetransitionisthen
Thesimplestexampleiswhen Vt isnotafunctionof t,or Vt = V .Wethenhave
Ifwedefine ∆ = m n,thenwehave
forthetransitionprobability.
9.1.1 Whatisthephysicalmeaningofthisresult?
Wemustbe verycareful whenweusethewords theperturbationcausesatransition betweeneigenstatesof ˆ H0
Whatthismeansphysicallyisthatthesystemhasabsorbedfromtheperturbing field(oremittedtoit)theenergydifference ∆ = m n andthereforethesystem haschangeditsenergy.
Doesthestatementalsomeanthatthestatevectorhaschangedfromaninitial value ∣ψ(0)⟩ = ∣n⟩ toafinalvalue ∣ψ(t)⟩ = ∣m⟩?
Wecangetabetterfeelingforthecorrectanswertothisquestionbyderiving theresultinadifferentmanner.
Wehave
and
Asinourdevelopmentoftime-independentperturbationtheory,welet
where g isasmallparameter.
Thesetofeigenvectors {∣n⟩} isacompletesetandthereforewecanuseitasa basisforthespaceand,inparticular,wecanwrite
Thereasonforpullingoutthephasefactorswillbeclearshortly.
Itisclearthatif g = 0,thenthisisthecorrectgeneralsolutionwith
Thephasefactorswepulledoutrepresentthetimedependencedueto ˆ H0 and thisis,byassumption,themajortimedependenceinthesystem.
If g issmallweexpectthetimedependenceof an(t),whichisduetotheperturbationtobeweakorthat dan(t) dt issmall(9.42)
Itisinthissensethatwecanproposetouseperturbationtheoryonthesystem.
Usingtheeigenbasisexpansionwehave
Applyingthelinearfunctional ⟨m∣ fromtheleftandusingtheorthonormality relation
(9.44)
weget
where
Thisisanexactequation.Itimpliesthatthetimedependenceof an(t) isdue entirelyto ˆ Vt (becauseweexplicitlyextractedoutthedependencedueto ˆ H0). Thisistheinteractionpicturethatwehadearlier.
ExactlySolvable2-StateExample
Considera2-statesystemwith
Intheinteractionpicture,asderivedabove,wehave
or
Wecanwritetheseequationsas
Wecanfindanexactsolution.Withinitialconditions
weget
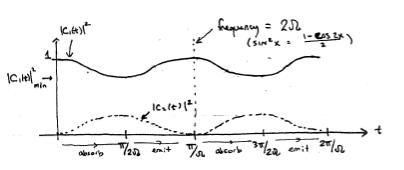
AgraphofthesefunctionsisshowninFigure9.1below.
Figure9.1:ExactSolution
Astraightforwardcalculationgives
Atresonance, ω = ω21,wehave
asshowninFigure9.2below.
Figure9.2:AtResonance
Theamplitudeasafunctionof ω isshowninFigure9.3below.
Figure9.3:Amplitudeversus ω
where ∆ = fullwidthathalfmaximum = 4δ/h.Theamplitudeispeakedat resonanceandthewidthisproportionalto δ (thestrengthoftheperturbation).
Thisperiodicallyforced 2 statesystemisabasicproblem-itdemonstratesthe fundamentalfeaturesofabsorptionandemission.
Wenowreturntothefull,generalequationsandlookforaperturbationsolution. Nowweassume(powerseries)
Substitutingandarrangingthetermsinapowerseriesin g wehave
(0) n
orlookingateachorderseparatelywehave
0th order da(0) n dt = 0 1st order ih da(1)
(r + 1)st order ih da(r+1) m dt
Notethatthecoefficients a(0) n followfromtheinitialcondition
Thesolutionproceedsasfollows: initialcondition → a(0) n a(0) n → a(1) n usingthe 1st orderequation
a(r) n → a(r+1) n usingthe (r + 1)st orderequation
Nowconsiderthefollowingexample.Weassumethat
(9.60) where
andduringthetimeinterval 0 ≤ t ≤ T aperturbation Vt isappliedtothesystem andthe an(t) changewithtime.
Finally,for t ≥ T theperturbationisturnedoffand an(t) = an(T ).
Theprobabilitythat,asaresultoftheperturbation,theenergyofthesystem becomes r,isgivenby
andas
Nowto 1st orderwehave
If ∣ψ(0)⟩ = ∣i⟩,then
Thisgives
Integratingwehave
and
whichisidenticaltoourearlierresultas
Nowletreturntoourquestion.Hasthestatechangedalso?
Intheexamplewefoundthattheperturbationproducesafinalstate ∣ψt⟩ for t ≥ T whichto 1st orderis
Thisisacoherent(definiterelativephases)superpositionofeigenvectorsof ˆ H0 Thisis NOT astationarystate.Interferenceeffectsbetweenthetermsinthe sumaredetectable.Theydonot,however,affect
∣ar(T )∣2 = probabilitythattheenergychangesto εr (9.70)
Thus,theperturbationdoesnotcausea jump fromonestationarystate ∣i⟩ of ˆ H0 toanother ∣r⟩,butinsteaditproducesanon-stationarystate.
Theconventionallanguageofquantummechanicsproducesthisambiguitybetweenthetwostatements
theenergyis r and thestateis ∣r⟩
Forthestate
itiscorrecttosay
theprobabilityoftheenergybeing r is
or
Prob(E = r
Thestate,however,is ∣ψt⟩ and NOT
Anexample
Supposeweperturbanoscillatorwithadecayingelectricfieldoftheform
To 1st order,startingwiththeinitialstate ∣n⟩ withenergy
wehave
where
Welet n = 0 (thegroundstate)forthisexample.Wethenhave
Using
weget(letting t → ∞)
andfinally,
Wenowreturntotheearliergeneralresult(9.36)wederivedfortheprobability, namely,
InFigure9.4belowweplotthisfunction.
Figure9.4:Probability(0,n)versusDelta
Theheightofthecentralpeakisproportionalto t2 andthelocationofthefirst zeroisat
= 2πh
sothatthewidthofthepeakdecreasesas 1/t.
Theformulaimpliesthatforveryshorttimes
As t → ∞,however,theprobabilityislargestforthosestateswhoseenergylies underthesharpbumpnear ∆ = 0 orthosestateswithwhoseenergyliesunder thepeakaround 0.Nowtheenergy n ≈ 0 liesunderthesharpbumpwhen
Theareaunderthebumpisproportionalto t andtherestoftheareaoscillates intimearoundzero.Thislatterfeaturemeansthatif n ≠ 0,thetransition probabilityoscillatesintimewitharepetitiontimeof
Thecase,wherewearelookingforatransitiontoasinglestate,is,thus,only validinperturbationtheoryforverysmalltime t.Otherwisetheconditionthat the
willnotbetrueandperturbationtheorybreaksdown.Wealsonotethatthe probabilitycannotgrowlargerthanoneorthat,afterawhile,thehigher-order effectsoftheperturbationwhichwehaveneglectedsofarmustbecomeimportantandpreventtheprobabilityfromexceedingone.
Theconditionthattellsuswhetheratransitionprobabilitytoastatewith anenergyappreciablydifferentthantheoriginalenergyisthesamecondition intime-independentperturbationtheorythattellswhetherthestatevector changesappreciablyfromtheunperturbedstate,namely
Physically,amoreinterestingcaseoccurswhenthestate ∣n⟩ isoneofacontinuumofenergystates,oritliesinagroupofverycloselyspacedlevels.
Inthiscaseweaskadifferentexperimentalquestion,namely,
Whatistheprobabilitythatthesystemmakes atransitiontoasmallgroupofstatesnear
n⟩ (orhasenergynear n)?
Sincetheareaunderthebumpnear ∆ = 0 or n ≈ 0 isproportionalto t,we expectthatthetransitionprobabilitytoasmallgroupofstatesnear 0 will growlinearlywith t andthus
0→n(t) t = transitionrate = Γ = constantas t → ∞ (9.88)
Quantitiesthatwemeasurearerelatedtothetransitionrateandthisresult saysthatthesemeasurementswillmakesense.
Letusnowcarryoutthisderivationindetail.
Tocalculatethistransitionratewemustsum P0→n overthegroupof final states. Weassumethat ∣⟨b
ˆ Vt
∣0⟩∣2 isrelativelyconstantoverthesmallgroupofstates near ∣n⟩ (hasaweakenergydependence).
Wethenhave
⎥ ⎦ 2 (9.89) where
n ingroup
ρ(εn) = numberofstatesperunitenergy
ρ(εn)dεn = numberofstatesintheinterval dεn
Nowinthelimit t → ∞
i.e.,ingeneral,forasequenceoffunctions
wehavethat
Therefore,
Usingthisresult,wehave
andthus
whichiscalled Fermi’sGoldenRule
Wenowconsideraperturbationthatdependsexplicitlyontime.Inparticular, supposewehaveaharmonicperturbationoftheform
and ∣ψ(t0)⟩ = ∣0⟩,wherewelet t
.The
factorisnecessarytomake themathematicaloperationsvalidinthelimit.Itisequivalentforsmall η to turningtheperturbationonslowly.Intheendwewilllet η → 0
Wehave
Thus,theprobabilityoftheenergybeing n atthetime t is
Thefirsttermcomesfromthe e iωt partof ˆ Vt (positivefrequency)andthe secondtermcomesfromthe eiωt partof ˆ Vt (negativefrequency).Thelastterm represents interferenceeffects
Since
wehave
The sin ωt and cos ωt termsarisefromtheinterferenceterm.Inthelimit η → 0 andassumingthat ∣n⟩ isinthecontinuumpartofspectrum,wehave
1. thefirsttwotermsarenotequaltozeroonlyif εn ε0 = ±hω
2. the sin ωt and cos ωt termsaveragetozeroifweassumethat Γ0→n is dP0→n(t)/dt averagedoverafewcyclesof ˆ Vt whichgivestheresult
Thepositiveandnegativefrequencypartsactindependentlyandtheinterference averagestozero.
Thus,the e iωt partproduceda ∆E > 0 process(absorption),whilethe eiωt partproduceda ∆E < 0 process(emission).
Toenhanceourunderstandingoftime-dependentperturbationtheory,welook atavariationofthisharmonicperturbation.Supposewehaveaharmonic perturbationoftheform
whichisonlyappliedforafinitetimeinterval 0 ≤ t ≤ T .Ifwestartwithenergy i inthestate ∣i⟩,thenatanytime t ≥ T
a(1) f (t) = 1st orderamplitudeforthestate ∣ψ(t)⟩ tohaveenergy εf (beinstate ∣f ⟩ ?) f ≠ i
isgivenby
(1) f (T ) = 1
(9.105) and ∣a(1) f (T )∣2 = probabilitythatthefinalenergywillbe f (9.106)
Asanexampleweconsiderspinresonance(wesolvedthisproblemexactlyearlier).
Weconsideraspin = 1/2 particleinastaticmagneticfield B0 (inthe z direction). ThissaysthattheunperturbedHamiltonianis
Thisoperatorhastheeigenvectorsandeigenvalues
Wenowperturbthesystemwithanothermagneticfield B1,whichisrotating inthe x y planewithangularvelocity ω.Thisimpliesthat
Wechoosetheinitialstatetobe
(spinupinthez-direction)(9.111)
Thefirstorderperturbationtheoryapproximationforthisresultis
andwehaveused
Whenisthefirstorderperturbationtheoryresultvalid?
Ifwecomparetheexactresultwithperturbationtheorybyexpandingtheexact resultinapowerseries,wefindthatthetworesultsagreeexactlyif
whichcorresponds B1 ≪ B0 (aslongas ω0 + ω ≠ 0).When ω0 + ω = 0 wehavea phenomenoncalledresonance.Theexactsolutiongives
andperturbationtheorygives
Thus,theresultsagreeonlyif ∣ω1T ∣ ≪ 1 oriftheperturbationonlyactsfora shorttime.
9.2 AtomicRadiationandSelectionRules
Wenowapplytime-independentperturbationtheorytotheabsorptionand emissionelectromagneticradiationbymatter.
TheHamiltonianforanelectroninanatominteractingwithandelectromagnetic fieldis
where q = e, U = thepotentialenergyfunctionthatbindstheelectronsinthe atom,and ⃗ A and ϕ arethevectorandscalarpotentialsassociatedwiththe electromagneticfield.
Thesepotentialsimplytheelectricandmagneticfields
Notethatif ⃗ A = 0,the ⃗ B = 0 and
Werewrite H as
where
ˆ H0 = ⃗ p2 op
e + U = Hamiltonianfortheatomwithnoelectromagneticfield (9.123) and
istheperturbationduetothepresenceoftheelectromagneticfield,i.e.,the term ˆ V tellsushowtheatominteractswiththeelectromagneticfield.
9.2.1 TheElectricDipoleApproximation
Thetypicalwavelengthofvisibleelectromagneticradiationis ≈ 5000 andthe typicaldimensionofanatomis ≈ afew.Thisimpliesthattheelectromagnetic fieldsareapproximatelyconstantoverthevolumeoftheatom.
InGaussianunits ∣E
B∣,buttheforcedueto B ≈ (v/c)× theforcedueto E
Thus,magneticeffectsarenegligibleinmostatomscomparedtoelectriceffects. Wethereforeassume
1. ⃗ E ≈ constantoverthevolumeoftheatom
2. ⃗ B canbeneglected
Thisistheso-calledelectricdipoleapproximation.
Inthisapproximation,wehave ⃗ A = 0 andaswesaidabove(11.121), ⃗ B = 0 and
Thislastintegralisindependentofpathsince
⃗ E = 1 c ∂B ∂t = 0 (9.126)
Sinceweareassumingthat ⃗ E ≈ constantoverthevolumeoftheatom,weget