Ying Dai
Visit to download the full and correct content document: https://ebookmass.com/product/calculations-and-simulations-of-low-dimensional-mate rials-tailoring-properties-for-applications-1st-edition-ying-dai/
More products digital (pdf, epub, mobi) instant download maybe you interests ...
Ferroic materials for smart systems from fundamentals to device applications Dai
https://ebookmass.com/product/ferroic-materials-for-smartsystems-from-fundamentals-to-device-applications-dai/
Low-Dimensional Halide Perovskites: Structure, Synthesis, and Applications Yiqiang Zhan
https://ebookmass.com/product/low-dimensional-halide-perovskitesstructure-synthesis-and-applications-yiqiang-zhan/
Optical properties of materials and their applications
Second Edition Singh
https://ebookmass.com/product/optical-properties-of-materialsand-their-applications-second-edition-singh/
Working Guide to Pump and Pumping Stations: Calculations Simulations 1st Edition
https://ebookmass.com/product/working-guide-to-pump-and-pumpingstations-calculations-simulations-1st-edition/
Two-Dimensional Materials for Nonlinear Optics: Fundamentals, Preparation Methods, and Applications
Qiang Wang
https://ebookmass.com/product/two-dimensional-materials-fornonlinear-optics-fundamentals-preparation-methods-andapplications-qiang-wang/
Two-Dimensional-Materials-Based Membranes: Preparation, Characterization, and Applications Gongping Liu
https://ebookmass.com/product/two-dimensional-materials-basedmembranes-preparation-characterization-and-applications-gongpingliu/
(eTextbook PDF) for Medical Dosage Calculations: A Dimensional Analysis Approach 11th Edition
https://ebookmass.com/product/etextbook-pdf-for-medical-dosagecalculations-a-dimensional-analysis-approach-11th-edition/
Electrical Properties of Materials 10th Edition Solymar
https://ebookmass.com/product/electrical-properties-ofmaterials-10th-edition-solymar/
Defects in Two-Dimensional Materials Rafik Addou
https://ebookmass.com/product/defects-in-two-dimensionalmaterials-rafik-addou/
CalculationsandSimulationsof
Low-DimensionalMaterials
CalculationsandSimulationsof
Low-DimensionalMaterials
TailoringPropertiesforApplications
YingDai
WeiWei
YandongMa ChengwangNiu
Authors
Prof.YingDai ShandongUniversity SchoolofPhysics Shandananlu27 250100Jinan China
Prof.WeiWei ShandongUniversity SchoolofPhysics Shandananlu27 250100Jinan China
Prof.YandongMa ShandongUniversity SchoolofPhysics Shandananlu27 250100Jinan China
Prof.ChengwangNiu ShandongUniversity SchoolofPhysics Shandananlu27 250100Jinan China
CoverImage: ©YuichiroChino/Getty Images
Allbookspublishedby WILEY-VCH arecarefully produced.Nevertheless,authors,editors,and publisherdonotwarranttheinformation containedinthesebooks,includingthisbook, tobefreeoferrors.Readersareadvisedtokeep inmindthatstatements,data,illustrations, proceduraldetails,orotheritemsmay inadvertentlybeinaccurate.
LibraryofCongressCardNo.: appliedfor BritishLibraryCataloguing-in-PublicationData Acataloguerecordforthisbookisavailable fromtheBritishLibrary.
Bibliographicinformationpublishedby theDeutscheNationalbibliothek TheDeutscheNationalbibliotheklists thispublicationintheDeutsche Nationalbibliografie;detailedbibliographic dataareavailableontheInternetat <http://dnb.d-nb.de>
©2023WILEY-VCHGmbH,Boschstraße12, 69469Weinheim,Germany
Allrightsreserved(includingthoseof translationintootherlanguages).Nopartof thisbookmaybereproducedinanyform–by photoprinting,microfilm,oranyother means–nortransmittedortranslatedintoa machinelanguagewithoutwrittenpermission fromthepublishers.Registerednames, trademarks,etc.usedinthisbook,evenwhen notspecificallymarkedassuch,arenottobe consideredunprotectedbylaw.
PrintISBN: 978-3-527-34909-8
ePDFISBN: 978-3-527-83211-8
ePubISBN: 978-3-527-83212-5
oBookISBN: 978-3-527-83213-2
Typesetting Straive,Chennai,India
Contents
Preface ix
1AnIntroductiontoDensityFunctionalTheory(DFT)and Derivatives 1
1.1TheProblemofaN-electronSystem 1
1.2TheThomas–FermiTheoryforElectronDensity 3
1.3TheFirstHohenberg–KohnTheorem 3
1.4TheSecondHohenberg–KohnTheorem 5
1.5TheKohn–ShamEquations 5
1.6TheLocalDensityApproximation(LDA) 7
1.7TheGeneralizedGradientApproximation(GGA) 8
1.8TheLDA+UMethod 8
1.9TheHeyd–Scuseria–ErnzerhofDensityFunctional 9
1.9.1IntroductiontoTight-BindingApproximation 9
1.9.2MatrixElementsofTight-BindingHamiltonian 10
1.9.3MatrixElementswiththeHelpofWannierFunction 10
1.9.4ExampleforaGrapheneModel 10
1.10Introductionto k • p PerturbationTheory 11
1.10.1SolutionforNon-degenerateBands 11
1.10.2SolutionforDegenerateBands 12
1.10.3ExplicitHamiltonianof k • p PerturbationTheory 12 References 13
2NewPhysicalEffectsBasedonBandStructure 17
2.1ValleyPhysics 17
2.1.1SpontaneousValleyPolarization 22
2.1.2ValleyPolarizationbyForeignAtomDoping 31
2.1.3ValleyPolarizationinvanderWaalsHeterostructures 37
2.2RashbaEffects 43 References 55
3FerromagneticOrderinTwo-andOne-Dimensional Materials 65
3.1IntrinsicFerromagneticOrderin2DMaterials 66
3.2IntrinsicFerromagneticOrderin1DMolecularNanowires 73 References 75
4Two-DimensionalTopologicalStates 81
4.1TopologicalInsulators 82
4.1.1Graphene 82
4.1.2HgTe/CdTeQuantumWells 83
4.1.3 Z 2 InvariantandSpinChernNumber 84
4.1.4LargeGapQuantumSpinHallInsulators 86
4.2TopologicalCrystallineInsulators 91
4.2.1SnTeThinFilms 91
4.2.2IV–VIMonolayers 93
4.2.3TopologicalPhaseTransitionBetween2DTCIandTI 94
4.2.4DualTopologicalInsulator 96
4.2.5TCIin2DFerromagnets 100
4.3QuantumAnomalousHallEffect 103
4.4AntiferromagneticTopologicalInsulators 107
4.5MixedTopologicalSemimetals 113 References 118
5CalculationofExcited-StateProperties 123
5.1Green’sFunctionMany-BodyPerturbationTheory 123
5.2ExcitonicEffectsandBandGapRenormalizationinTwo-Dimensional Materials 130
5.3Electron–PhononEffectsontheExcited-stateProperties 133
5.4NonlinearOpticalResponse 136
5.5OpticalPropertiesofvanderWaalsHeterostructuresof Two-DimensionalMaterials 137 References 139
6ChargeCarrierDynamicsfromSimulations 145
6.1Time-DependentDensityFunctionalTheoryandNonadiabatic MolecularDynamics 145
6.2ApplicationsofTDDFTandNAMDinTwo-DimensionalMaterials 148 References 155
7SimulationsforPhotocatalyticMaterials 159
7.1PhotocatalysisandPhotocatalyticReactions 159
7.2PhotoresponsivityandPhotocurrentfromSimulations 164
7.3SimulationforLocalizedSurfacePlasmonResonance 174 References 182
8SimulationsforElectrochemicalReactions 195
8.1Single-atomCatalysts 195
8.2StabilityofCatalyst 197
8.3ElectrochemicalReactions 199
8.3.1HydrogenEvolutionReaction(HER) 199
8.3.2OxygenEvolutionReaction(OER) 203
8.3.3OxygenReductionReaction(ORR) 204
8.3.4NitrogenReductionReaction(NRR) 204
8.3.5ElectrocatalyticActivityEvaluatedfromtheFirst-principles Calculations 209
8.3.6SimulationsforNitrogenReductionReaction 220 References 232
Index 239
Preface
Inmodernsociety,theoreticalcalculationandsimulationareadvancingthedevelopmentofphysics,chemistry,andmaterialsscience,etc.,alongwiththegreatsuccesses incomputertechnology.Afterthesuccessfulexfoliationofgraphenefromgraphite bySirAndreGeimandKonstantinNovoselov,thenvarioustwo-dimensionalmaterialsarepredicted,synthesized,transferred,andcharacterized,andwearewitnessing thecomingoftheearoftwo-dimensionalmaterials.Incomparisontothecorrespondingbulkcounterparts,materialsinlowdimensionexhibitunprecedented novelchemicalandphysicalproperties.Meanwhile,manynovelphenomenaaswell aspromisingpotentialdevicesareproposedbasedonlow-dimensionalmaterials.
Amongtheseintriguingphysicsintwo-dimensionallattices,forexample,the valleyphysics,excitoniceffects,andRashbaeffectattractspecialinterestfromthe standpointsofbothfundamentalandappliedlevel.Thus,thereisanimpressing progressintheresearchontheseexcitingtopics.Forthemagneticproperty,itwas extensivelystudiedinconventionalbulksystems,asithadlongbeenconsidered tosurviveinlow-dimensionalsystemsduetothethermalfluctuationsaccording totheMermin–Wagnertheorem.Inrecentyears,withthediscoveryoflong-range magneticorderintwo-dimensionallattice,magneticmaterialsintwodimensions spurredextensiveattention.Currently,therearemanyworksdevotedtoinvestigate themagneticpropertiesintwo-dimensionalmaterials.Also,thepastdecadeshave witnessedtheevolutionoftopologicalphasesandtopologicalmaterialswhich reshapeourunderstandingofphysicsandmaterials.First-principlescalculations basedonthedensityfunctionaltheoryprovideeffectivedescriptionsoftopological phasesandplayimportantrolesinpredictingrealistictopologicalmaterials,from insulatorstosemimetals,andfromnonmagneticsystemstomagneticones.In fieldsofphotochemistryandphotoelectrochemistry,thetheoreticalcalculations andsimulationsaresopowerfulindesigning,screening,andcharacterizingthe photocatalystsandelectrocatalystsofhighstability,selectivity,andactivity.Indeed, calculationandsimulationareguiding,leading,andmovingforwardthesefields.
Thebookisdividedintoeightchapters.InChapter1,densityfunctionaltheory anditsderivatives(e.g.,thetight-bindingmethod)arebrieflyintroduced,and inChapter2,therecentdevelopmentofvalleyphysicsandRashbaeffectin two-dimensionalmaterialsfromthefirst-principlesarereviewed.InChapter3, calculationsandsimulationresultsforlow-dimensionalferromagneticmaterials
x Preface arediscussed.Chapter4providesagentleintroductionoftopologicalphases andtopologicalmaterialsespeciallyintwodimensions.Theconceptsofdifferent topologicalstatesarediscussedusingfirst-principlesbandstructuresandtopologicalinvariants.InChapter5,ingredientsinthemany-bodyGreen’sfunction perturbationtheoryforcalculatingtheexcited-statepropertiesoflow-dimensional materialsaresummarized,andinChapter6,time-dependentdensityfunctional theoryandnonadiabaticmoleculardynamicsareintroducedforthosewhoare studyingphotoexcitedchargecarrierdynamics.Processofhowtocalculateand simulatephotocatalyticreactionispresentedinChapter7,andelectrochemical reactionsfromcalculationsandsimulationsarereviewedinChapter8.
Thisbookwouldnothavebeenpossiblewithouthelpfrommanypeople.
Jinan,China Summer,2022
YingDai WeiWei YandongMa ChengwangNiu
AnIntroductiontoDensityFunctionalTheory(DFT)and Derivatives
1.1TheProblemofaN-electronSystem
Thedensityfunctionaltheory(DFT)isfirstresultedfromtheworkbyHohenberg andKohn[1],whereinthecomplicatedindividualelectronorbitalsaresubstituted bytheelectrondensity.Namely,theDFTisentirelyexpressedintermsofthefunctionalofelectrondensity,ratherthanthemany-electronwavefunctions.Inthiscase, DFTsignificantlyreducesthecalculationsofthegroundstatepropertiesofmaterials.ThatiswhyDFTisusefulforcalculatingelectronicstructures,especiallywith manyelectrons.AsthefoundationofDFT,twotheoremsareproposedbyHohenberg andKohn[1].Thefirsttheorempresentsthatthegroundstateenergyisafunctional ofelectrondensity.Thesecondtheoremshowsthatthegroundstateenergycanbe achievedbyminimizingsystemenergyonthebasisofelectrondensity.
Itshouldbenotedthat,althoughHohenbergandKohnpointouttherearerelationsbetweenpropertiesandelectrondensityfunctional,theydonotpresentthe exactrelationship.Butfortunately,soonaftertheworkofHohenbergandKohn, KohnandShamsimplifiedthemany-electronproblemsintoamodelofindividual electronsinaneffectivepotential[2].Suchapotentialcontainstheexternalpotentialandexchange-correlationinteractions.Forexchange-correlationpotential,itis achallengetodescribeitrigorously.
Thesimplestapproximationfortreatingtheexchange-correlationinteractionis thelocaldensityapproximation(LDA)[3],whereintheexchangeandcorrelation energiesareobtainedbytheuniformelectrongasmodelandfittingtotheuniform electrongas,respectively.LDAcanprovidearealisticdescriptionoftheatomicstructure,elastic,andvibrationalpropertiesforawiderangeofsystems.Yet,becauseLDA treatstheenergyofthetruedensityusingtheenergyofalocalconstantdensity,it cannotdescribethesituationswherethedensityfeaturesrapidchangessuchasin molecules[4,5].Toaddressthisproblem,thegeneralizedgradientapproximation (GGA)isproposed[6–8],whichdependsonboththelocaldensityandthespatial variationofthedensity.Andinprinciple,GGAisassimpletouseasLDA.Currently, inthevastmajorityofDFTcalculationsforsolids,thesetwoapproximationsare adopted.
CalculationsandSimulationsofLow-DimensionalMaterials:TailoringPropertiesforApplications, FirstEdition.YingDai,WeiWei,YandongMa,andChengwangNiu. ©2023WILEY-VCHGmbH.Published2023byWILEY-VCHGmbH.
1AnIntroductiontoDensityFunctionalTheory(DFT)andDerivatives
ByconsideringtheBorn–Oppenheimerandnon-relativisticapproximations,the effectiveHamiltonianofaN-electronsysteminthepositionrepresentationcanbe givenby,
Thefirsttermiskineticenergyoperator.Thesecondtermisanexternalpotential operator.Insystemsofinteresttous,theexternalpotentialissimplytheCoulomb interactionofelectronswithatomicnuclei:
wherethe r i isthecoordinateofelectron i andthechargeonthenucleusat R�� is Z ��
ThethirdtermofEq.(1.1)istheelectron-electronoperator.Theelectronicstatecan beobtainedbytheSchrödingerequation:
Here, Ψ(r 1 , r 2 , r N )isawavefunctionintermsofspace-spincoordinates.Apparently, thewavefunctionisantisymmetricunderexchangingthecoordinates.UnderDirac notation,theEq.(1.1)canbeexpressedinrepresentation-independentformalism:
Inprinciple,thegroundstateenergy E0 oftheN-electronsystemcanbefound basedonthevariationaltheorem,whichisobtainedbytheminimization:
Here,thesearchisoverallantisymmetricwavefunctions Ψ.Inthisregard,betterapproximationsfor Ψ canreadilyresultinthegroundstateenergy E0 ofthe N-electronsystem,butthecomputationalcostwouldbeveryhigh.Therefore,the directsolutionisnotfeasible.Toaddressthisissue,DFTisdeveloped,whichisbased onareformulationofthevariationaltheoremintermsofelectrondensity.
Weknowthat|Ψ|2 =Ψ* Ψ representstheprobabilitydensityofmeasuringthefirst electronat r 1 ,thesecondelectronat r 2 , … andthe N thelectronat r N .Byintegrating |Ψ|2 overthefirst N 1electrons,theprobabilitydensityofthe N thelectronat r N is determined.ThentheprobabilityelectrondensitythatdefinesanyoftheNelectrons attheposition r isgivenby:
Andtheelectrondensityisnormalizedtotheelectronnumber:
Theenergyofthesystemisexpressedas:
Here,
1.3TheFirstHohenberg–KohnTheorem 3
1.2TheThomas–FermiTheoryforElectronDensity
BeforediscussingtheHohenberg–Kohntheorems,wefirstintroducetheThomas–Fermitheory.TheThomas–Fermitheoryisimportantasitgivestherelationbetween externalpotentialandthedensitydistributionforinteractingelectronsmovinginan externalpotential:
and �� isthe r independentchemicalpotential.ThesecondtermisEq.(1.12)isthe classicalelectrostaticpotentialraisedbythedensity ��(r ).BasedontheThomas–Fermitheory,HohenbergandKohnbuilduptheconnectionbetweenelectrondensityandtheSchrödingerequation.Andinthefollowing,wewillintroducethetwo Hohenberg–Kohntheorems,whichlieattheheartofDFT.
1.3TheFirstHohenberg–KohnTheorem
Byreplacingtheexternalpotential vne (r )withanarbitraryexternallocalpotential v(r ),thecorrespondinggroundstatewavefunction Ψ canbefoundbysolving theSchrödingerequation.Basedontheobtainedwavefunction,thegroundstate density ��(r )canbecomputed.Andobviously,twodifferentlocalpotentialswould givetwodifferentwavefunctionsandthustwodifferentelectrondensities.This givesthemap:
BasedontheThomas–Fermitheory,HohenbergandKohndemonstratedthatthe precedingmappingcanbeinverted,namely, thegroundstateelectrondensity ��(r ) of aboundsystemofinteractingelectronsinsomeexternalpotentialv(r)determinesthe potentialuniquely:
ThisisknownasthefirstHohenberg–Kohntheorem.
1AnIntroductiontoDensityFunctionalTheory(DFT)andDerivatives
Todemonstratethistheorem,weconsidertwodifferentlocalpotentials v1 (r )and v2 (r ),whichdifferbymorethantheconstant.Thesetwopotentialsyieldtwodifferentgroundstatewavefunctions Ψ and Ψ′ ,respectively.Andapparently,thesetwo groundstatewavefunctionsaredifferent.Assume v1 (r )and v2 (r )correspondtothe samegroundstatewavefunction,then
BysubtractingEq.(1.17)fromEq.(1.16),wecanobtain:
whichcanbeexpressedinpositionrepresentation,
Thissuggeststhat
thusincontradictionwiththeassumptionthat v
)and
(
)differbymorethan aconstant.Accordingly,twodifferentlocalpotentialsthatdifferbymorethanthe constantcannotsharethesamegroundstatewavefunction,whichdemonstratethe map:
Then,wedemonstratethemap:
Let Ψ and Ψ′ bethegroundstatewavefunctionscorrespondingto v1 (r )and v2 (r ), respectively.Assumingthat Ψ and Ψ′ exhibitthesamegroundstateelectrondensity ��(r ),thenthevariationaltheoremgivesthegroundstateenergyas:
BysubtractingEq.(1.23)fromEq.(1.24),wecanobtain:
Thismakesnosense.Thisfinallyleadstotheconclusionthattherecannotexisttwo localpotentialsdifferingbymorethananadditiveconstantthathasthesameground statedensity.
1.4TheSecondHohenberg–KohnTheorem
AccordingtothefirstHohenberg–Kohntheorem,thegroundstatedensity ��(r )determinesthelocalpotential v(r ),andinturndeterminestheHamiltonian.Therefore, foragivengroundstatedensity ��0 (r )thatisgeneratedbyalocalpotential,itispossibletocomputethecorrespondinggroundstatewavefunction Ψ0 .Thatistosay, Ψ0 isalsoauniquefunctionalof ��0 (r ):
AccordingtoEq.(1.26),thegroundstateenergy E0 isalsoafunctionalof ��0 (r ):
HohenbergandKohndefinetheuniversaldensityfunctional:
Here, Ψ[��]isanygroundstatewavefunctioncorrespondingtothegroundstatedensity ��(r ).BycombiningEq.(1.10),thetotalenergyfunctionalcanbedefinedas:
FromtheRitzprinciple,wehave:
ThisisknownasthesecondHohenberg–Kohntheorem.
1.5TheKohn–ShamEquations
Forasystemwithnoninteractingelectrons,theeffectiveHamiltonianncanbe givenby:
ThecorrespondingSchrödingerequationis:
Thenthedensityisgivenby:
Here,thesingleparticleorbital �� i (r )isconstructedbasedontheeffectivepotential vs (r ).
Thetotalenergycanbeexpressedas:
1AnIntroductiontoDensityFunctionalTheory(DFT)andDerivatives
Thefirsttermisthekineticenergyofthenoninteractingelectrons,whichisgivenby:
Thesecondtermistheeffectivepotential,whichisgivenby:
Accordingly,thetotalenergycanbegivenby:
BycombiningEqs.(1.36)and(1.37),thekineticenergycanbeexpressedas:
UsingthemethodofLagrangemultipliers,wecanobtainthefollowingequation:
SolutionofEq.(1.39)yieldsthedensity ��s (r ).
Theclassicalelectrostaticinteractionenergyisgivenby:
And
Thenthefollowingequationisobtained:
Thethirdtermisexchangeandcorrelationenergyfunctional:
Theexchange-correlationpotentialisdefinedas:
UsingthemethodofLagrangemultipliers,wecanobtainthefollowingequation:
AndsolutiontoEq.(1.45)is ��(r ).
Therefore,giventherelation:
Wehave:
WethenarriveattheKohn–Shamequation:
1.6TheLocalDensityApproximation(LDA) 7
Solvingthisequationgivestheorbitalandthenthedensityoftheoriginalinteracting system.
Theexchangeandcorrelationfunctionalcanbewrittenas:
Here, ��xc (r ′ ; ��)istheexchange-correlationenergydensity.Andtheexchangepotentialisdefinedas:
Thenthetotalenergycanbegivenby:
Fromprecedingequation,wecanseethat,exceptfortheexchange-correlationfunctional,alltheaforementionedexpressionsareexact.Inpractice,wehavetouse approximationsforexchange-correlationpotential,astheexactformisunknown.
1.6TheLocalDensityApproximation(LDA)
LDAisoneofthemostwidelyusedandsimplestapproximationsfor Exc .InLDA, theexchange-correlationfunctionalisapproximatedas:
Here, ��unif xc [��(r )] istheexchange-correlationenergyperelectroninhomogeneous electrongasatdensity ��.LDAworkswellforhomogeneouselectrongas,andthusis validforsystemswhereelectrondensitydoesnotchangerapidly.
Theexchange-correlationenergydensitycanbebrokendownintotwoparts:
Thefirsttermistheexchangeterm,whichisgivenby:
WhileforthesecondtermofEq.(1.53),itisthecorrelationdensity,whichdoes nothaveananalyticformula.However,thecorrelationenergiescanbeobtained numericallyfromquantumMonteCarlo(QMC)calculationsbyCeperleyand Alder[9].
1AnIntroductiontoDensityFunctionalTheory(DFT)andDerivatives
Andforspin-polarizedsystems,thespin-upandspin-downdensitiesaretakenas twoindependentdensitiesintheexchange-correlationenergy.Andinthiscase,the Eq.(1.52)canbeexpressedas:
Forcalculatingtheelectronicstructure,LDAapproachisestimatedtobesuccessful. However,forsomesystems,itdoesnotwork.Asaresult,manyeffortsaredevoted toimproveit.Oneofthemistoincludethegradientofthedensityintheexchange correlationfunctional,aswewillshownext.
1.7TheGeneralizedGradientApproximation(GGA)
Tointroducethegradientofthedensityintheexchangecorrelationfunctional,the gradientexpansionapproximation(GEA)isfirstproposed.Startingfromtheuniformelectrongas,aslowlyvaryingexternalpotential v(r )isintroduced.Andthen theexchange-correlationenergyisexpandedintermsofthegradientsofthedensity:
Here, Cxc (��)isthesumoftheexchangeandcorrelationcoefficientsofthegradient expansion.Asthereduceddensitygradientissmall,GEAapproachshouldbesuperiortoLDAapproach.However,becausethereduceddensitygradientcanbelarge insomeregionofspaceforrealsystems,GEAisshowntobeworsethanLDA. ToovercometheshortcomingsofGEA,theGGAisdeveloped.InGGA,the exchange-correlationfunctionalisapproximatedas:
Here, f issomefunction.ManyGGAfunctionalshavebeenproposed,includingB88 [10],Lee-Yang-Parr(LYP)[11],PW91[12],andPerdew–Burke–Ernzerhof(PBE)[13] exchange-correlationfunctionals.
1.8TheLDA+UMethod
WhileLDAandGGAareestimatedtobeabletodealwiththemanysystemsandphenomena,theydonotworkwellforthesystemswithrare-earthandlate-transition metalelements.Thisisbecausetheeffectivesingle-particlemethodsareapplicableforhighlydelocalizedbandstatesbutnotforstronglylocalizedstates.Forthe dandfelectronsofrare-earthandlate-transitionmetalelements,theyessentially retaintheiratomiccharacterinsolids.Asaconsequence,standardDFTfunctionalssuchasLDA,localspindensityapproximation(LSDA),andGGAitinerantd statesandmetallicgroundstateformanytransitionmetaloxides,forwhichsemiconductingbehaviorisdemonstratedexperimentally.Forimprovingtheseissues, LDA+Umethodisdeveloped[14–16].Here,ifnotspecifiedelsewhere, +Uindicates aHubbard,andLDAindicatesthestandardDFTfunctionals,i.e.LDA,LSDA,and
1.9TheHeyd–Scuseria–ErnzerhofDensityFunctional 9 GGA.TheideaofLDA+Umethodisonthebasisthatthestronglycorrelatedelectronicstates(i.e.dandfsates)aretreatedbytheHubbardmodel,andtherestof thevalenceelectronsaredescribedbythestandardDFTfunctionals.Therefore,the totalenergywithinLDA+Umethodcanbegivenby:
Here,thefirsttermisthestandardDFTtotalenergyfunctionalbeingcorrected, thesecondtermrepresentstheHubbardHamiltoniantomodelcorrelatedstates, andthethirdisthedouble-countingterm.TheLDA+Umethodcanwelldescribe theelectronicpropertiesoftheMottinsulatorsandincreasethebandgapsinthe Kohn–Shamspectrum.
1.9TheHeyd–Scuseria–ErnzerhofDensityFunctional
InstandardDFT,theFockexchangeenergyiscomputedbasedonalocalenergy densityanditsderivatives.However,theexactformfortheFockexchangeenergy isknownasnonlocalfromtheHartree–Focktheory.Toimprovetheaccuracy, thePBEexchangeenergyshouldbemixedwithafractionoftheexactnonlocalFockexchangeenergy,givingrisetothehybridfunctionals,suchasthe Heyd–Scuseria–Ernzerhof(HSE)functional[17].TheHSEexchange-correlation energyisgivenby:
Here, EHF x and EPBE x ,respectively,representtheexactFockexchangeenergyandthe PBEexchangeenergy. EPBE c isthePBEcorrelationenergy. �� istherange-separation parameter. �� isthemixingparameter.FromEq.(1.59),itcanbeseenthattheHSE functionalissplitintoshort-andlong-rangeterms.Inthiscase,itcanimprovethe accuracy,whileavoidingthecomputationalcost.
1.9.1IntroductiontoTight-BindingApproximation
Considerinasingleatomtherearemultipleatomicorbitals ��m (r)withmbeingthe orbitalindices.Here, ��m (r)mustbeeigenfunctionsoftheHamiltonianofthatsingle atom H atom .Whenweplaceitinacrystalwithplentyofatoms,thewavefunction ofdifferentatomsoverlapeachothertoformadifferentwavefunction.Duetothat ��m (r)isnotarealeigenfunctionforaHamiltonianofcrystalandweneedtofind outwhatthetrueeigenfunctionsare.Iftheoverlapofoneatomonanotherissmall enough,wecanstillassumethatelectronsaretightlyboundtothecorresponding atoms,whichisexactlythereasonwhywecallitastight-bindingapproximation.The approximateHamiltonianis H (r) = H atom (r) +ΔU (r),whoseBlochwavefunction canbetakenasacombinationofalltheisolatedorbitals:[18,19]
��m (r)= ∑ Rn bm (Rn )��m (r Rn ),
where Rn denotesalllatticepointsand bm (Rn )isjustacoefficientnumberfororbital m.Inthepresenceoftranslationsymmetry,coefficientnumberscanbereplacedby
1AnIntroductiontoDensityFunctionalTheory(DFT)andDerivatives aBlochform,whichgives:
1.9.2MatrixElementsofTight-BindingHamiltonian
TogetHamiltonianinthemomentumspace,weshalldoabasistransformationsuch as:[20]
When Ri isequalto Rj ,wewillfindtheonsiteenergyrepresentedfortheatomic energyshiftduetotheoverlapofotheratoms,whichcanbegivenas:
If Ri isnotequalto Rj ,hoppingenergybetweendifferentlatticesitescanbedefined as:
1.9.3MatrixElementswiththeHelpofWannierFunction
Usually,Blochwavefunctionsarenotorthogonal,whichmayresultinsomeproblems.ToresolvethatweshoulddefinetheorthogonalWannierfunctionas:
(r Ri )= 1
Byusingabra-ketnotation,theHamiltonianintherealspacetakestheformof:[21]
where �� i and tij denotetheonsiteenergyandhoppingenergy,respectively.Toget theenergyofHamiltonian,weshalldoabasistransformationintothemomentum space,whichisimplementedbyaFouriertransform:
1.9.4ExampleforaGrapheneModel
Byusinggraphenelattice[22]asanexample,wegiveadetaileddescriptionabout howtousetight-bindingmethod.Here,weconsidertwoatomswithsorbitalina singleunitcellofunitlatticeconstant,whoselatticevectorcanbewrittenas: a1 = 1 2 (3, √3) , a2 = 1 2 (3, √3) .
Eachatomisconnectedwiththreenearest-neighboratomswithadistanceof: ��1 = 1 2 (1, √3) ,��2 = 1 2 (1, √3) ,��3 =(−1, 0)
1.10Introductionto k • p PerturbationTheory 11
Inthemomentumspace,weconsidertheonsiteenergyfortwosorbitalsis �� 1 .The nearest-neighborhoppingstrengthis t,whichleavesaHamiltonianmatrixasfollows:
Wecangettheenergydispersionwithanimplementationofdiagonalization, whichresultsin:
1.10Introductionto k p PerturbationTheory
Asingleelectroninaperiodicpotential V (r)obeysaSchrödingerequation,andsuch aformcanbewrittenas[23,24]:
[ p2 2m + V (r)] ��(k,r) = E��(k,r) ,
wheretheeigenvaluesandeigenfunctionscanbewrittenas En (k)and �� n (k, r) = eik • r un (k, r).TheperiodicpartthatiscalledasaBlochfunctionsatisfiessuchan equationas:
H0 (k)un (k, r)= En (k)un (k, r), wheretheHamiltonianlocatedatmomentumpointof k0 canbegivenas: H0 (k0 )= p2 2m + ℏ m k0 ⋅ p + ℏ2 k2 0 2m + V (r).Iftheeigenvaluesandeigenfunctionsareassumedtobe solvedforpointas k0 ,wecangetthesolutionsofnearbypointssuchas k = k0 + �� k throughthefollowingequation:
[H0 (k0 )+ ℏ m �� k ⋅ p] un (k, r)= [En (k0 )+ ℏ2 2m (k2 0 k2 )] un (k, r).
Then,theperturbationHamiltoniangainsaformof H ′ (k)= ℏ m �� k p.Withthehelp ofperturbationtheory,wecansolvetheenergyofnearbypointsundertwodifferent situations,whichisillustratedinthefollowingchapter.
1.10.1SolutionforNon-degenerateBands
Ifthebandsarenotdegeneratefor k0 ,theperturbatedeigenvaluesofthepoints k = k0 + �� k canbegivenby[25,26]: En (k)= En (k0 )+ 2 2m (k2 0 k2 ) + ℏ m �� k⟨unk0 (r )∣ p ∣ unk0 (r )⟩ + ℏ2 m2 ∑ n′ ≠n ⟨unk0 (r )∣ p ∣ un′ k0 (r )⟩⟨un′ k0 (r )∣ p ∣ unk0 (r )⟩�� k2 En (k0 )− En′ (k0 ) ,
1AnIntroductiontoDensityFunctionalTheory(DFT)andDerivatives
wherethefirsttermandsecondtermofright-handsidearezeroorderapproximation,andthethirdtermandfourthtermserveasthefirstandsecondorderapproximation.Here,wegiveanexplicitexampletodescribehowtogetaHamiltonian basedonthefollowingequation.Weassumetheeigenvaluesandeigenfunctionsof k0 = 0areknownbyfirst-principlescalculationsorexperiment.Consideracubic latticewithapointgroupof Oh andtwobands|u1k (r)⟩ and|u2k (r)⟩ thattransform as Γ+ 1 and Γ1 representation,andthesymmetryrepresentationof H ′ isthevector representationas Γ15 .
Forthefirstorderapproximation,thedirectproduct Γ+ 1 ⊗ Γ15 ⊗ Γ+ 1 =Γ15 changes therepresentation Γ+ 1 into Γ15 ,resultinginavanishingmatrix.Whileforthesecond orderapproximation,thedirectproduct Γ15 ⊗ Γ+ 1 =Γ15 limitsthe |un′ k0 (r)⟩ tothe Γ15 representation,whichisjustthebandrepresentationofantibondingpbands. Therearethreebasis x , y,and z for Γ15 representation;onlythreetermscanexistas acrosstermof ⟨Γ+ 1 |px |x ⟩, ⟨Γ+ 1 |py |y⟩,and ⟨Γ+ 1 |pz |z⟩ accordingtotheselectionrules. Finally,wecangetthetotaleigenvaluesas:
(
u1k0 (r)|px |x ⟩|2 E1 (0)− En′ (0)
1.10.2SolutionforDegenerateBands
Ifthebandsaredegeneratefor k0 ,theeigenfunctionmustbealinearcombination ofdegeneratedbands.Here,weassumeband i isdegeneratewithband j,andthe firstorderperturbationequationcanbewrittenas:[27] | | | | | ⟨i|H0 + H ′ |i⟩ �� ⟨i|H0 + H ′ | j⟩ ⟨ j|H0 +
Thefourtermsonleft-handsidecanchangetheformsas ⟨i|H0 + H ′ |i⟩
|
⟩ = (
/
)
• ⟨j|p|i⟩.Thesolutionyields: ��( ⃗ �� )= E0 i + E0 j 2 ± 1 2 √(E0 i E0 j )2 + 4ℏ2 m2 k ⋅ p↔ ij ⋅ k, where p↔ ij isathirdordertensor.Foracubiclattice,suchatensorhasaformof: p↔ ij = ⎛ ⎜ ⎜ ⎜ ⎝ p2 ij 00 0 p2 ij 0 00 p2 ij ⎞ ⎟ ⎟ ⎟ ⎠
1.10.3ExplicitHamiltonianof k p PerturbationTheory
Generally,any4 × 4Hamiltoniancanbeexpandedwith16Diracmatricesas: H = �� (k)I + ∑ i di (k)Γi + ∑ ij dij (k)Γij ,
where I istheidentifymatrices,andthefiveDirac Γi matricescanbedefinedas Γ1 = �� 1 ⊗��
]/2i with �� i and �� i aretwosetsofPaulimatrices.
First,weshouldwritethesymmetrymatrixinthebasiswechoose.TakenBi2 Se3 asanexample,[28,29]wechoosefourstatesas:
and
.Accordingtothetransformation formula,foursymmetrymatricesD(R)canbeconstructedas:
1.Time-reversalsymmetry: T = i�� y K ⊗ 1.
2.Threefoldrotationsymmetryalong z axis: R3 = ei(��3 ⊗1
3.Twofoldrotationsymmetryalong x axis: R2 = i�� 1 ⊗�� 3 .
4.Inversionsymmetry: P = 1 ⊗�� 3 .
Second,weapplythesymmetrymatricesinto16Diracmatricestogettherepresentationofmatrices,whichisimplementedby D(R)Γi D(R) 1 .Inthepresenceof time-reversalsymmetry,weonlyneedtotakeintoconsiderationoneidentitymatrix andfiveDirac Γi matrices.
Third,wecombinedtheDiracmatriceswithcorrespondingpolynomialsofthe momentum k whosharegettheHamiltonian.Itcanbewrittenas:
References
1 Hohenberg,P.andKohn,W.(1964).Inhomogeneouselectrongas. Phys.Rev. 136: B864–B871.
2 Kohn,W.andSham,L.J.(1965).Self-consistentequationsincludingexchange andcorrelationeffects. Phys.Rev. 140:A1133–A1138.
3 Jones,R.O.andGunnarsson,O.(1989).Thedensityfunctionalformalism,its applicationsandprospects. Rev.Mod.Phys. 61:689–746.
4 Grossman,J.C.,Mitas,L.,andRaghavachari,K.(1995).Structureandstabilityofmolecularcarbon:importanceofelectroncorrelation. Phys.Rev.Lett. 75: 3870–3873.
5 Zupan,A.,Blaha,P.,Schwarz,K.,andPerdew,J.P.(1998).Pressure-induced phasetransitionsinsolidSi,SiO2,andFe:Performanceoflocal-spin-density andgeneralized-gradient-approximationdensityfunctionals. Phys.Rev.B 58: 11266–11272.
6 Perdew,J.P.,Burke,K.,andErnzerhof,M.(1996).Generalizedgradientapproximationmadesimple. Phys.Rev.Lett. 77:3865–3868.
7 Perdew,J.P.,Burke,K.,andWang,Y.(1996).Generalizedgradientapproximation fortheexchange-correlationholeofamany-electronsystem. Phys.Rev.B 54: 16533–16539.
1AnIntroductiontoDensityFunctionalTheory(DFT)andDerivatives
8 Becke,A.D.(1997).Density-functionalthermochemistry.V.Systematicoptimizationofexchange-correlationfunctionals. J.Chem.Phys. 102:8554–8560.
9 Ceperley,D.M.andAlder,B.J.(1980).Groundstateoftheelectrongasbya stochasticmethod. Phys.Rev.Lett. 45:566–569.
10 Becke,A.D.(1988).Density-functionalexchange-energyapproximationwith correctasymptoticbehavior. Phys.Rev.A 38:3098–3100.
11 Lee,C.,Yang,W.,andParr,R.G.(1988).DevelopmentoftheColle-Salvetti correlation-energyformulaintoafunctionaloftheelectrondensity. Phys.Rev.B 37:785–789.
12 Colle,R.andSalvetti,O.(1975).Approximatecalculationofthecorrelation energyfortheclosedshells. Theor.Chim.Acta 37:329–334.
13 Miehlich,B.,Savin,A.,Stoll,H.,andPreuss,H.(1989).Resultsobtainedwiththe correlationenergydensityfunctionalsofbeckeandLee,YangandParr. Chem. Phys.Lett. 157:200–206.
14 Anisimov,V.I.andGunnarsson,O.(1991).Density-functionalcalculationof effectiveCoulombinteractionsinmetals. Phys.Rev.B 43:7570–7574.
15 Anisimov,V.I.,Zaanen,J.,andAndersen,O.K.(1991).BandtheoryandMott insulators:HubbardUinsteadofStonerI. Phys.Rev.B 44:943–954.
16 Anisimov,V.I.,Solovyev,I.V.,Korotin,M.A.etal.(1993).Density-functionaltheoryandNiOphotoemissionspectra. Phys.Rev.B 48:16929–16934.
17 Heyd,J.,Scuseria,G.E.,andErnzerhof,M.(2003).Hybridfunctionalsbasedona screenedCoulombpotential. J.Chem.Phys. 118:8207–8215.
18 Papaconstantopoulos,D.-A.(1986). HandbookoftheBandStructureofElemental Solids.Springer.
19 Madelung,O.(2012). IntroductiontoSolid-StateTheory,vol.2.SpringerScience &BusinessMedia.
20 Wieder,B.-J.,Bradlyn,B.,Wang,Z.-J.etal.(2018).Wallpaperfermionsandthe nonsymmorphicDiracinsulator. Science 361:246.
21 Liu,G.-B.,Shan,W.-Y.,Yao,Y.etal.(2013).Three-bandtight-bindingmodel formonolayersofgroup-VIBtransitionmetaldichalcogenides. Phys.Rev.B 88: 085433.
22 Kane,C.-L.andMele,E.-J.(2005).Quantumspinhalleffectingraphene. Phys. Rev.Lett. 95:226801.
23 Luttinger,J.-M.(1955).Quantumtheoryofcyclotronresonanceinsemiconductors:generaltheory. Phys.Rev. 102:1030.
24 Pikus,G.-E.(1962).Anewmethodofcalculatingtheenergyspectrumofcarriers insemiconductors.I.Neglectingspin-orbitinteraction. Sov.Phys.JETP 14:898.
25 Bir,G.-L.andPikus,G.-E.(1975). SymmetryandStrain-InducedEffectsin Semiconductors.NewYork:Wiley.
26 Ivchenko,E.-L.andPikus,G.-E.(1995). SuperlatticesandOtherHeterostructures. Berlin:Springer.
27 Voon,L.-C.-L.-Y.andWillatzen,M.(2009). ThekpMethod:ElectronicProperties ofSemiconductors.(SpringerScience&BusinessMedia.
28 Liu,C.-X.,Qi,X.-L.,Zhang,H.-J.etal.(2010).ModelHamiltonianfortopological insulators. Phys.Rev.B 82:045122.
29 Zhang,W.,Yu,R.,Zhang,H.-J.etal.(2010).First-principlesstudiesofthe three-dimensionalstrongtopologicalinsulatorsBi2 Te3 ,Bi2 Se3 andSb2 Te3 . NewJ. Phys. 12:065013.
NewPhysicalEffectsBasedonBandStructure
2.1ValleyPhysics
Valleyreferstothelocalminimumintheconductionbandorthelocalmaximum inthevalencebandinthemomentumspace.Giventhesystemswithtwoormore valleys,ifthevalleyscanbepolarizedanddetected,thevalleycanformanewdegree offreedomofcarriersinadditiontochargeandspin.Analogytochargeforelectronicsandspinforspintronics,thepossibilityofutilizingvalleydegreeoffreedomas informationcarriergivesrisetotheconceptofvalleytronics[1–3].Theideaofusing valleydegreeoffreedomdatesbacktothestudiesinthelate1970s,whichinvestigatedthevalleybehaviorandinter-valleycouplinginsiliconinversionlayers[4–6]. Moreover,bytuningtheintravalleyexchangeandcorrelation,theelectronswould preferentiallyoccupythevalleys,therebygeneratingthevalleypolarization.Subsequentlyaftertheworksonsiliconinversionlayer,severalothersystemsliketheAlAs quantumwell,siliconheterostructures,bismuth,anddiamondarealsoshowntofeaturethevalleyfeature[7–11].Despitetheseextensiveefforts,therelacksanintrinsic physicalpropertythatcorrelatedwiththevalleyoccupancy.Thisisinsharpcontrastwiththecaseofspin,wherethemagneticmoment,thespinopticalselection rule,andthespin-orbitcoupling(SOC)canbeemployedastheintrinsicproperties associatingwiththespin.Therefore,theutilizationofthevalleyindexisseverely limitedascomparedwiththespintronics,andtheintrinsicpropertyassociatedwith thevalleyoccupancyisunderexploration.
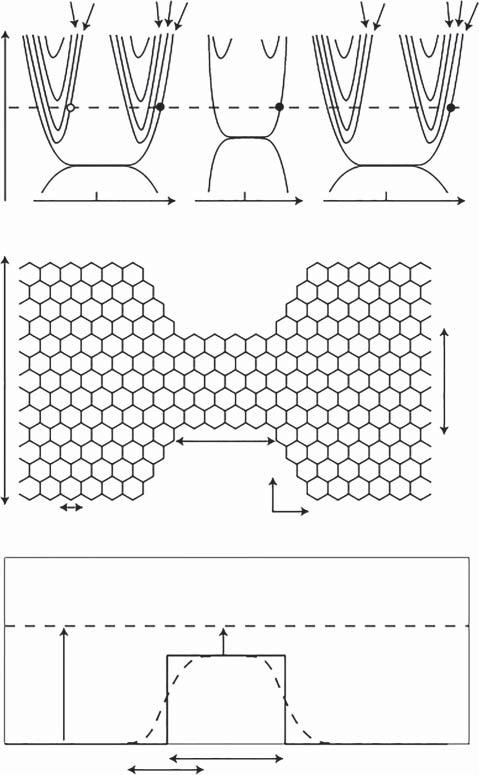
Therecentriseof2Dmaterials[12–14]providesanunprecedentedopportunityto addresstheaforementionedissues.Thefirst2Dsystemharboringthevalleyphysics isproposedingraphene(Figure2.1)[1].Ingraphenewithbrokeninversionsymmetry,thebandedgesofthebandstructurelieatthe +K and K pointsofthe2D Brillouinzone,formingtwodegeneratebynonequivalentvalleys.Importantly,the carriersinthe +K and K valleysaresubjectedtooppositeBerrycurvaturesand orbitalmagneticmoment.Thesetwoquantitiescanbeusedtodistinguishthevalleys.TheBerrycurvaturecanbehavelikeeffectivemagneticfields,whichwould resultinananomalousvelocityperpendiculartoanelectricfield.ThisisaHall effect,whichisreferredtoasthevalleyHalleffect[15].Whilefortheorbitalmagneticmoment,itresultsfromself-rotating,soanenergyshiftcanbeexpectedunder
CalculationsandSimulationsofLow-DimensionalMaterials:TailoringPropertiesforApplications, FirstEdition.YingDai,WeiWei,YandongMa,andChengwangNiu. ©2023WILEY-VCHGmbH.Published2023byWILEY-VCHGmbH.
Figure2.1 Schematicdiagramofthevalleyfilterbasedongraphene.Toppanel: Dispersionrelationinthewideandnarrowregions.Anelectroninthefirstvalley(modes n = 0,1,2, …)istransmitted(filledcircle),whereasanelectroninthesecondvalley(modes n =−1, 2, )isreflected(opencircle).Middlepanel:Honeycomblatticeofcarbonatoms inastripcontainingaconstrictionwithzigzagedges.Bottompanel:Variationofthe electrostaticpotentialalongthestripforthetwocasesofanabruptandsmoothpotential barrier(solidanddashedlines).Thepolarityofthevalleyfilterswitcheswhenthepotential height, U 0 ,intheconstrictioncrossestheFermienergy, E F .Source:Rycerzetal.[1]/with permissionofSpringerNature.
themagneticfield.Itshouldbenotedthat,undertheinversionsymmetry,the +K and K valleyscanbetransformedintoeachother,makingitnotpossiblefordistinguishingthevalleys.Therefore,breakingtheinversionsymmetryisanecessary conditionforutilizingBerrycurvatureandorbitalmagneticmomenttodistinguish thevalleyoccupancy.Currently,severalapproachesareproposedtobreaktheinversionsymmetryofgraphene,includingthecreationofedgemodes[16]anddefect lines[17].However,theseapproachesarechallenginginexperiments,limitingtheir practicalapplications.
Afterdiscoveringthevalleybehaviorsingraphene,themonolayergroup-VItransitionmetaldichalcogenides(TMDs),i.e.MoS2 ,WS2 ,MoSe2 ,andWSe2 ,areidentified asthemostpromisingplatformtostudythenovelvalley-contrastingphysics[18–21]. InmonolayerTMDs,theMatomiclayerissandwichedbetweentwoXatomiclayers,whichbreakstheinversionsymmetrynaturally(Figure2.2a).Moreover,there aretwodegeneratebutnonequivalentvalleyslocatingatthe +K and K points,generatingtwovalleys.Therefore,underanin-planeelectricfield,thecarriersin +K and K valleyswouldbeaccumulatedattheoppositeedgesofthesample,which isrelatedtotheoppositeBerrycurvaturesatthetwovalleys(Figure2.2c).More importantly,asthevalleysaredominatedbythedorbitalsoftheMatoms,thevalleysexperienceavalleyspinsplittingduetothestrongSOCstrengthwithinM-d orbitals[22].Andduetothein-planecharacterofthedorbitalsforthevalleysinthe valencebands,theyhaveaverylargevalleyspinsplitting.Whileforthevalleysin theconductionbands,becauseoftheout-of-planecharacter,thevalleyspinsplitting (a)
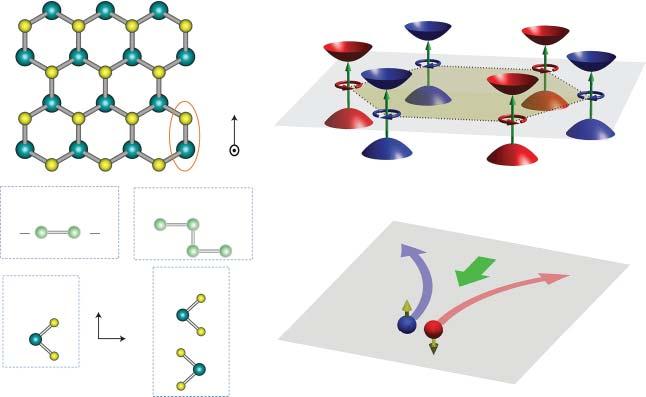
Figure2.2 CrystalstructureandvalleyphysicsinmonolayerTMDs.(a)2Dhexagonal lattice.(b)Valleycontrastingopticalselectionrulesina2Dhexagonallatticewithbroken inversionsymmetry.Theinterbandtransitioninvalley K ( K )couplesto �� + (�� )circularly polarizedlightonly(circulararrows).(c)DiagramofthevalleyHalleffectinmonolayer TMDs.Arrowssuggestthepseudo-vectorquantities,i.e.Berrycurvatureororbitalmagnetic moment,ofthecarriers.Source:Xuetal.[18]/withpermissionofSpringerNature.
(b)
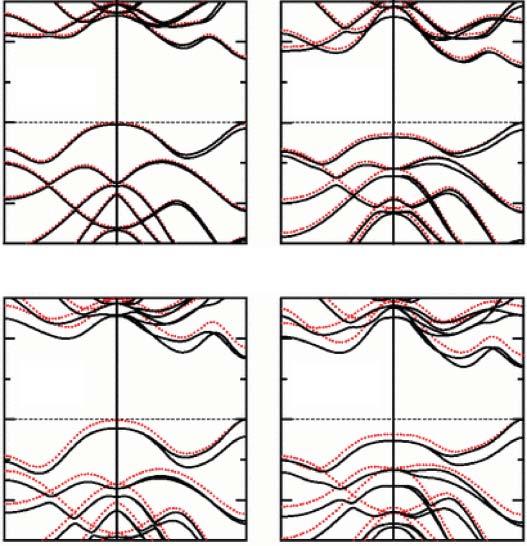
Figure2.3 ElectronicbandstructurescalculatedfortheMX2 monolayersystemswith (solidline)andwithout(dottedline)inclusionofthespin-orbitinteraction.Source:Zhu etal.[22]/withpermissionofAmericanPhysicalSociety.
israthersmall(Figure2.3).Undersuchsplitting,wecanmanipulatethecarrierwith onespininonevalley.Thisindicatesnovelspinandvalleyphysicsthatareabsentin graphene.Consideringthesemerits,monolayerTMDsareconsideredasoneofthe mostpromising2Dvalleytronicmaterials.
BesidesgrapheneandmonolayerTMDs,manyother2Dmaterialspresentingthe valley-contrastingphysicsareproposed.Forexample,usingfirst-principlescalculations,wereportedthatmonolayerH-Tl2 Oisacompelling2Dvalleytronicmaterial withspin-valleycoupling[23].SoonaftertheworkonmonolayerH-Tl2 O,wediscoveredanotherclassof2DvalleytronicmaterialsinmonolayerMN2 X2 (M = Mo, W;X = F,H),whichareshowntobedynamicallyandthermallystable.Monolayer MN2 X2 isanindirectgapsemiconductorwiththevalencebandmaximumlocating atthe +K and K points,formingtwodegeneratebutnonequivalentvalleysinthe valenceband[24].
Recently,Luetal.proposedthathexagonalmonolayerMoSi2 N4 andMoSi2 As4 exhibitapairofvalleysatthe +K and K points[25].Thecircularlypolarized photonscanbeadoptedtodistinguishthe +K and K valleys.Arisingfromthe valley-contrastingBerrycurvature,theintriguingvalleyHallandspinHalleffects
canberealized.Inadditiontothetraditionaltwolevelvalleys,thevalleysin monolayerMoSi2 As4 areshowntobemultiplefolded.Thissuggestsanadditional intrinsicdegreeoffreedomformonolayerMoSi2 N4 andMoSi2 As4 .Moreover, monolayerMoSi2 N4 andMoSi2 As4 haveseveraladvantagesovermonolayerTMDs. Forexample,whilemonolayerTMDssufferfromthelimitedsizeofgrowth[26]and lowelectron/holemobility[27],whichrestrictsthemforfurtherquantum-transport applications,monolayerMoSi2 N4 andMoSi2 As4 weresuccessfullysynthesizedwith largesizeupto15mm × 15mm[28]andispredictedtobewithalargeelectron/hole mobilityoffourtosixtimeslargerthanthatofmonolayerMoS2 [29].Therefore, monolayerMoSi2 N4 andMoSi2 As4 arebelievedtobepromisingcandidatesforthe potentialofvalleystobeappliedinmultipleinformationprocessing.
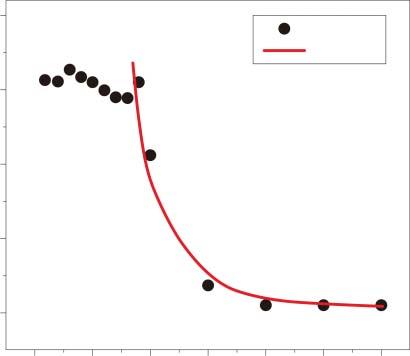
Afterdiscoveringthesepromisingvalleytronicmaterials,thenextstepistoexplore howtousethesematerialsforapplicationsinvalleytronicdevices.Tomakeavalleytronicdevice,thecrucialstepistoliftthedegeneracybetweenthe +K and K valleys,therebyproducingthevalleypolarization[15].In2Dvalleytronicmaterials,the valley-contrastingorbitalmagneticmomentisaccompaniedbyavalley-contrasting opticalselectionrule.Indetail,theinterbandtransitionsinthevicinityofthe +K and K valleyscorrelatewiththeright-andleft-handedcircularlypolarized,see Figure2.2b[18].Tothisend,themethodofopticalpumpingisproposedtoachieve thevalleypolarizationinmonolayerTMDs.Cuietal.foundthatthephotoluminescenceinmonolayerMoS2 hasthesamehelicityasthecircularlypolarizedcomponentoftheexcitationlaser[30].Thisisastrongsignatureofthevalleypolarization inducedbyopticalpumping.Belowtemperature90K,ahighphotoluminescence circularpolarizationisobtained,anditdecayswithtemperature,seeFigure2.4. Toconfirmthatthepolarizedphotoluminescenceisrelatedtothevalleyinsteadof spin,theHanleeffectisinvestigated.TheyshowedthatthepersistentphotoluminescencepolarizationisobservedinmonolayerMoS2 whentraversingthemagnetic field.Thisconfirmsthatthepolarizedphotoluminescenceisattributedtothevalley
Figure2.4 Thevariation ofdegreeofcircular polarizationPwith temperature.Forfittingthe relationship,assumingan inter-valleyscattering proportionaltothephonon populationisassumed. Source:Zengetal. [30]/withpermissionof SpringerNature.
2NewPhysicalEffectsBasedonBandStructure
polarizationasatransversemagneticfieldcausesthespintoprecess.Furthermore, forbilayerMoS2 withinversionsymmetry,thephotoluminescenceisfoundtobe unpolarizedbyapplyingthesameexcitationcondition,whichagainconfirmsthe opticallypumpedvalleypolarizationinmonolayerMoS2 .Similartothiswork,Mak etal.alsoidentifiedtheviabilityofopticalcontrolofvalleysandthevalleytronicsin monolayerMoS2 [20].Besidesthesetwoexperimentalworks,therearealsomany otherexperimentalbreakthroughsinopticalpumpedvalleypolarization.Formore detail,pleaseseethereviewofRef.[18].
Althoughvalleypolarizationissuccessfullyachievedthroughopticalpumping, itissubjectedtothequiteshortlifetimeofcarriers.Consideringthispoint,opticalpumpingisunabletorobustlytunethevalley,makingitnotapplicablefor developingpracticalinformationdevices.Analternativeapproachforrealizing thevalleypolarizationistobreaktime-reversalsymmetry.Thatisbecausethe time-reversalsymmetryrequiresthespinsatthe +K and K valleytobeenergeticallydegenerate,butopposite,formingthevalley-spinlockingrelationship.By breakingthetime-reversalsymmetry,thevalleydegeneracywouldbelifted.Infact, liftingthevalleydegeneracyinmonolayerTMDshasbeenachievedbyapplying anexternalmagneticfieldinsomeexperimentalworks[31,32].However,this approachisshowntoberathermodest.Forinstance,thevalleypolarizationis estimatedtobe0.1–0.2meVT 1 [31,32].Thisissuitableforthedevelopmentof valleytronicdeviceswherethelargevalleypolarizationisrequired,analogousto largespinpolarizationforspintronics.Recently,theresearcheffortsforbreaking thetime-reversalsymmetryinthisfieldhavebeendevotedtointroducingforeigner atomdopingandproximity-inducedmagneticinteraction,andmanybreakthroughs havebeenmade.Inaddition,withtherecentdiscoveryof2Dmagneticmaterials, theintrinsicvalleypolarizationisalsoidentified,whichattractsmoreandmore attention.Inthefollowing,wewilldiscusstherecenttheoreticaldevelopmentson thespontaneousvalleypolarization,valleypolarizationinducedbyforeignatom doping,andvalleypolarizationinvanderWaalsheterostructures.
2.1.1SpontaneousValleyPolarization
Spontaneousvalleypolarizationwasfirstproposedin2013[33].Usingthe tight-bindingmodel,Fengetal.proposedthetheoryofspinandvalleyphysics ofanantiferromagnetichoneycomblattice.Intheantiferromagnetichoneycomb lattice,thereisanemergentelectronicdegreeoffreedomofcarriers,whichis characterizedbytheproductofspinandvalleyindices(s•�� ).Thisgivesriseto the s•�� -dependentopticalselectionrule.Whenthespin-valleycouplingisweak, namelythevalleydegeneracyisconsideredtobekept,thesystemwouldexhibit an s•�� -selectivecirculardichroism(CD).Illuminatedbytheleft-polarizedlight,the spin-upelectronsatthe +K valleyandspin-downelectronatthe K valleywould beexcitedtotheconductionband.Andbyillustratingtheright-polarizedlight,the spin-downelectronsatthe +K valleyandspin-upelectronatthe K valleywould beexcitedtotheconductionband.Forthecasewithstrongspin-valleycoupling,the valleydegeneracyislifted,andthusthegapsatthe +K and K pointsaredifferent.
Inthisregard,bytuningthefrequencyofthepolarizedlight,onespinfromone valleycanbeexcited.Besidestheopticalselectionrule,theBerrycurvatureisalso s•�� -dependent.Chargecarrierwithopposite s•�� indiceswouldexhibitopposite transversalanomalousvelocities.Afterestablishingthetheoryofspinandvalley physicsinanantiferromagnetichoneycomblattice,Fengetal.suggestedoneactual materialofmonolayermanganesechalcogenophosphates,MnPX3 ,X = S,Se[33]. Bycalculatingtheirbandstructure,theyshowedthatthegapsat +K and K differ by43meV,indicatingthespontaneousvalleypolarizationandthe s•�� -dependent physics.
Afterdiscoveringthespontaneousvalleypolarizationintheantiferromagnetic honeycomblattice,thespontaneousvalleypolarizationintheferromagneticlattice isalsoproposed.Usingthetwo-bandk⋅pmodel,Duanetal.alsoproposedthatthe coexistenceofSOCandintrinsicexchangeinteractioncanresultinthatthevalley polarizationoccursspontaneously[34].Theyfurtherpredictedonesuchrealmaterialofmonolayer2H-VSe2
SimilartotheanomalousHalleffect,Duanetal.definedthevalleyHalleffectin ferromagneticmaterialasanomalousvalleyHalleffect[34].Notethatthecharge Hallcurrentiseasiertobedetectedexperimentally,andtheanomalousvalleyHall effectwouldprovideapromisingwaytorealizethevalley-basedinformationstorage. OnthebasisoftheanomalousvalleyHalleffect,Duanetal.proposedthepossible electricallyreadingandmagneticallywritingmemorydevices[34].Thissignificantly advancesthepracticalapplicationsofvalleytronics.
Basedontheprecedingtwoworks[33,34],thespontaneousvalleypolarizationis wellestablished.However,formonolayerMnPX3 ,theyshowthe s �� -selective,rather thanthe �� -selective,CD,andBerrycurvature.Andvalleyisnotanindependent degreeoffreedomofcarriersanymore.Whileformonolayer2H-VSe2 ,thismonolayerphaseisnotstableinexperiments.Therefore,thecandidatematerialswith spontaneousvalleypolarizationarestillunderexploration.Inthefollowing,wewill discussthesystemsthatarerecentlyidentifiedwithspontaneousvalleypolarization.
Usingfirst-principlescalculations,Luetal.investigatedthevalleyphysicsin monolayerVAgP2 Se6 [35].TheyfoundthatmonolayerVAgP2 Se6 canbeeasily exfoliatedfromitsbulkcounterpart.MonolayerVAgP2 Se6 isintrinsicallyspin polarized.MonolayerVAgP2 Se6 isaferromagneticsemiconductor.Theeasymagnetizationaxisisalongtheout-of-plane,withamagnetocrystallineenergyof1.5meV perunitcell,enablingthepossiblestableferromagnetism.Thespin-polarized bandstructureofmonolayerVAgP2 Se6 withoutSOCshowsthattheup-spinand down-spinchannelsaresplitsignificantly,andthebandsneartheFermilevelare dominatedbytheup-spinstatesandarecharacterizedbythetwomassiveDirac coneswithabandgap.Thisformstwodegeneratevalleys.UponconsideringSOC, thegapat +K valleydecreasesto29meVandincreasesto44meVatthe K valley, thusliftingthevalleydegeneracy.Basedontheseresults,Luetal.designedavalley pseudospinfieldeffecttransistor.Anddifferentfromtheconventionaltransistors, suchtransistorcouldcarryinformationofnotonlytheelectronsbutalsothevalley pseudospins,whichopensanapproachtoanavenueforrealizingthelow-power andhigh-performancevalleytronicdevicesinthefuture.