Nuclear Electronics with Quantum Cryogenic Detectors Vladimir Polushkin
Visit to download the full and correct content document: https://ebookmass.com/product/nuclear-electronics-with-quantum-cryogenic-detectors -vladimir-polushkin/
More products digital (pdf, epub, mobi) instant download maybe you interests ...
Quantum Computing by Practice: Python Programming in the Cloud with Qiskit and IBM-Q Vladimir Silva
https://ebookmass.com/product/quantum-computing-by-practicepython-programming-in-the-cloud-with-qiskit-and-ibm-q-vladimirsilva/
Hacking Electronics: Learning Electronics with Arduino and Raspberry Pi, 2nd Edition Simon Monk
https://ebookmass.com/product/hacking-electronics-learningelectronics-with-arduino-and-raspberry-pi-2nd-edition-simon-monk/
Quantum Bullsh*t: How to Ruin Your Life with Advice from Quantum Physics Chris Ferrie
https://ebookmass.com/product/quantum-bullsht-how-to-ruin-yourlife-with-advice-from-quantum-physics-chris-ferrie/
Introduction to Quantum Field Theory with Applications to Quantum Gravity 1st Edition Iosif L. Buchbinder
https://ebookmass.com/product/introduction-to-quantum-fieldtheory-with-applications-to-quantum-gravity-1st-edition-iosif-lbuchbinder/
Nuclear Physics 1: Nuclear Deexcitations, Spontaneous Nuclear Reactions Ibrahima
Sakho
https://ebookmass.com/product/nuclear-physics-1-nucleardeexcitations-spontaneous-nuclear-reactions-ibrahima-sakho/
Cryogenic Valves for Liquefied Natural Gas Plants Karan Sotoodeh
https://ebookmass.com/product/cryogenic-valves-for-liquefiednatural-gas-plants-karan-sotoodeh/
Quantum Communication, Quantum Networks, and Quantum Sensing Ivan Djordjevic
https://ebookmass.com/product/quantum-communication-quantumnetworks-and-quantum-sensing-ivan-djordjevic/
The Wretched Atom: America's Global Gamble with Peaceful Nuclear Technology Hamblin
https://ebookmass.com/product/the-wretched-atom-americas-globalgamble-with-peaceful-nuclear-technology-hamblin/
YO ESTOY CONTIGO J. Vladimir Polanco
https://ebookmass.com/product/yo-estoy-contigo-j-vladimirpolanco/
NuclearElectronicswithQuantumCryogenicDetectors
NuclearElectronicswithQuantumCryogenicDetectors
SecondEdition
VladimirPolushkin BusinessandTechnologicalConsultant,MA,PhD,MBA
Thissecondeditionfirstpublished2022
©2022JohnWiley&SonsLtd
EditionHistory
JohnWiley&SonsLtd(1e,2004)
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedinaretrievalsystem,ortransmitted,inanyformorbyanymeans, electronic,mechanical,photocopying,recordingorotherwise,exceptaspermittedbylaw.Adviceonhowtoobtainpermissiontoreusematerial fromthistitleisavailableathttp://www.wiley.com/go/permissions.
TherightofVladimirPolushkintobeidentifiedastheauthorofthisworkhasbeenassertedinaccordancewithlaw.
RegisteredOffice
JohnWiley&Sons,Inc.,111RiverStreet,Hoboken,NJ07030,USA
JohnWiley&SonsLtd,TheAtrium,SouthernGate,Chichester,WestSussex,PO198SQ,UK
EditorialOffice
TheAtrium,SouthernGate,Chichester,WestSussex,PO198SQ,UK
Fordetailsofourglobaleditorialoffices,customerservices,andmoreinformationaboutWileyproductsvisitusatwww.wiley.com.
Wileyalsopublishesitsbooksinavarietyofelectronicformatsandbyprint-on-demand.Somecontentthatappearsinstandardprintversions ofthisbookmaynotbeavailableinotherformats.
LimitofLiability/DisclaimerofWarranty
Inviewofongoingresearch,equipmentmodifications,changesingovernmentalregulations,andtheconstantflowofinformationrelatingtothe useofexperimentalreagents,equipment,anddevices,thereaderisurgedtoreviewandevaluatetheinformationprovidedinthepackageinsertor instructionsforeachchemical,pieceofequipment,reagent,ordevicefor,amongotherthings,anychangesintheinstructionsorindicationofusage andforaddedwarningsandprecautions.Whilethepublisherandauthorshaveusedtheirbesteffortsinpreparingthiswork,theymakeno representationsorwarrantieswithrespecttotheaccuracyorcompletenessofthecontentsofthisworkandspecificallydisclaimallwarranties, includingwithoutlimitationanyimpliedwarrantiesofmerchantabilityorfitnessforaparticularpurpose.Nowarrantymaybecreatedorextended bysalesrepresentatives,writtensalesmaterialsorpromotionalstatementsforthiswork.Thefactthatanorganization,website,orproductis referredtointhisworkasacitationand/orpotentialsourceoffurtherinformationdoesnotmeanthatthepublisherandauthorsendorsethe informationorservicestheorganization,website,orproductmayprovideorrecommendationsitmaymake.Thisworkissoldwiththe understandingthatthepublisherisnotengagedinrenderingprofessionalservices.Theadviceandstrategiescontainedhereinmaynotbesuitable foryoursituation.Youshouldconsultwithaspecialistwhereappropriate.Further,readersshouldbeawarethatwebsiteslistedinthisworkmay havechangedordisappearedbetweenwhenthisworkwaswrittenandwhenitisread.Neitherthepublishernorauthorsshallbeliableforanyloss ofprofitoranyothercommercialdamages,includingbutnotlimitedtospecial,incidental,consequential,orotherdamages.
LibraryofCongressCataloging-in-PublicationDatahasbeenappliedfor
ISBN9781119834687(Hardback);9781119834694(AdobePDF);9781119834717(e-Pub)
CoverDesign:Wiley
CoverImage:©AlexanderRaths/Shutterstock
Setin9.5/12.5ptSTIXTwoTextbyStraive,Pondicherry,India
Contents
PrefacetotheSecondEdition xi
PrefacetotheFirstEdition xv
1InteractionoftheNuclearRadiationwithDetectorAbsorbers 1
Introduction 1
1.1 The IntrinsicQuantumEfficiencyofRadiationDetectors 3
1.2DetectionofChargedParticles 4
1.2.1Light-ChargedParticles 5
1.2.2TheContinuous “Braking” Radiation(Bremsstrahlung) 9
1.2.3BackscatteringofChargedParticles 9
1.2.4Heavy-ChargedParticles 10
1.3PrimaryInteractionsofX-and γ-RayPhotonswithSolid-StateAbsorbers 12
1.3.1PhotoelectricEffect 12
1.3.2ComptonScattering 13
1.3.3ThePairProduction 14
1.3.4AttenuationofPhotonRadiationinSolid-StateDetectorAbsorbers 15
1.4DetectionofNeutronswithSolid-StateRadiationSensors 16
1.4.1 10B(n,α)7LiNuclearReaction 17
1.4.2 6Li(n,α)3Η NuclearReaction 18
1.5HeatGenerationinAthermalQuasiparticleAbsorbers 20
References 20
2RadiationDetectorswithSuperconductingAbsorbers 23 Introduction 23
2.1 Selected TopicsoftheSuperconductivityTheory 25
2.1.1TheElectron –PhononInteractionandCooperPairingMechanisms 25
2.1.2TheBehaviorofSuperconductorsintheMagneticField 27
2.1.3TheTunnelJosephsonJunction 28
2.1.4TheSuperconductingTransmissionLine:TheKineticInductance 30
2.2SuperconductingAbsorbers:TheDown-ConversionofParticleEnergyandIntrinsicEnergyResolution 35
2.2.1TheEnergyDown-ConversionProcessinSuperconductingAbsorbers 35
2.2.2TheIntrinsicEnergyResolutionofQuasiparticleDetectorswithSuperconductingAbsorbers 37
2.3TransportintheNonequilibriumSuperconductors:IncompleteChargeCollectionMechanisms 38
2.3.1TheRecombinationTimeofQuasiparticlesinSuperconductorAbsorbers 39
2.3.2TheRothwarf–Taylor(R–T)PhenomenologicalFramework 40
2.3.3TheDiffusionofQuasiparticlesinThin-FilmSuperconductingAbsorbers:IncompleteChargeCollection 41
2.3.4NoiseEquivalentPower(NEP)ofSuperconductingAbsorbers 43
2.4QuasiparticleRadiationDetectorswithSuperconductingTunnelJunction(STJ)Readout 45
2.4.1TheBandgapEngineeringandFabricationofSTJDetectors 45
2.4.2TheGiaeverI–VCurveoftheSTJs 46
2.4.3TheTunnelingMechanismsinSTJs 49
2.4.4PileupandCountRateCapabilityoftheSTJDetectors 50
2.5QuasiparticleRadiationDetectorswithMicrowaveKineticInductanceSensors(MKID) 54
2.5.1TheOperatingPrincipleofMicrowaveKineticInductanceSensors 54
2.5.2TheDROIDX-rayDetectorwithMicrowaveKineticInductanceSensorReadout 62
2.6IntegrationofSTJDetectorswithMicrowaveSQUIDMultiplexedReadout 66
2.6.1BandwidthConsiderations 67 References 68
3RadiationDetectorswithNormalMetalAbsorbers 73
Introduction 73
3.1 Spectrometer sBasedonTransition-EdgeSensor(TES)Microcalorimeters 73
3.1.1FundamentalsofTESDesign 73
3.1.2TheElectrothermalFeedbackinTESMicrocalorimeters 78
3.2TESMicrocalorimeterswithMicrowaveSQUIDReadout(μMUX):ImagingCameras 83
3.2.1TheQuantumEfficiency 84
3.2.2TheEnergyResolution 85
3.2.3TheThroughput 85
3.2.4TheBandwidthPertheCoreTESChannel 86
3.3HotElectronMicrocalorimeterwiththeNISTunnelJunctionThermometer 88 References 92
4RadiationDetectorswithSemiconductorAbsorbers 95
Introduction 95
4.1 SemiconductorTransport 96
4.1.1ValenceBondandEnergyBandModels 96
4.1.2CarrierScatteringMechanismsandMobilityinSemiconductorBulkMaterials 104
4.1.3CarrierGenerationandRecombination(G–R)Processes 108
4.1.4EffectsoftheG–RTransportonthePerformanceofRadiationDetectors 117
4.1.5Tunneling-AssistedTransportinSemiconductorMaterials 118
4.1.6TunnelingTransportAcrosstheThinDielectricBarrier 122
4.1.7TheSemiconductor–VacuumInterface:SurfaceTransport 125
4.2MacroscopicModelingofSemiconductorDevices 129
4.2.1MicroscopicTransportModelsBasedontheSchrödingerEquation 131
4.2.2TheSemiclassicalTransportModels 132
4.2.3TheInitialandBoundaryConditionsinDeviceModeling:TheRamo–ShockleyTheorem 139
4.3FrontWindowsinSemiconductorRadiationDetectors 141
4.3.1EntranceWindowBasedonSchottkyBarrierJunction 142
4.3.2FrontWindowBasedonMetal–Insulator–Semiconductor(MIS)Junction 150
4.3.3Thep–nJunction-BasedFrontWindowinRadiationDetectors 156
4.4FabricationofSiliconDriftDetectors(SDD) 164
4.4.1TheEpitaxiallyGrownUltra-shallowp+nJunctionEntranceWindows 165
4.4.2ThePureBoronTechnologyforUltra-shallowEntranceWindows 166
4.5SemiconductorDriftDetectors 167
4.5.1SemiconductorDetectors:OperationPrincipleandPerformanceSpecifications 167
4.5.2TheIntrinsicEnergyResolutionofSemiconductorDetectors 170
4.5.3TimeResponseofSDDs 173
4.6TheQuantumCalorimetricElectron–HoleDetectorwithSemiconductorAbsorber 174
4.6.1ThePhononSystemDynamicsinSemiconductorMaterials 175
4.6.2TheDesignandPerformanceoftheQuantumElectron–HoleDetector 176 References 178
5Front-EndReadoutElectronicCircuitsforQuantumCryogenicDetectors 183
Introduction 183
5.1 JFET TransconductancePreamplifiers 184
5.1.1PrinciplesofJFETTransconductanceAmplifiers 185
5.1.2SettlingTimeofPreamplifiers 187
5.2DynamicsandNoiseofJFETAmplifiers 189
5.2.1StaticandDynamicParametersofJFETs 191
5.2.2NoiseCharacteristicsofJFETs 193
5.2.3PentaFET:HighPrecisionResetMechanism 195
5.2.4TheJFETCascodeStage 196
5.2.5TheSourceFollower-BasedCharge-SensitivePreamplifier 197
5.2.6TheDifferentialStageBasedonMatchedJFETs 198
5.3TheLowNoiseAmplifiersBasedonHighElectronMobilityTransistor(HEMT) 200
5.4ThedcSQUIDCurrentAmplifiers 204
5.4.1ThedcSQUIDasaSuperconductingParametricAmplifier 204
5.4.2ThedcSQUIDwithanIntermediaryInputTransformer 207
5.4.3TheCoupledEnergyResolutionofaDoubleTransformerdcSQUID 209
5.4.4ThedcSQUIDReadoutElectronics 212
5.4.5TheSQUIDwiththeDigitalBodeFLLController 216
5.4.6ThedcSQUIDAmplifierintheSmall-SignalLimit(Noise) 219
5.4.7SQUIDCurrentAmplifierintheLargeSignalLimit(Dynamics) 223
5.4.8SQUIDCurrentAmplifierintheLargeSignalLimit(Noise) 226
5.5ThedcSQUIDCurrentAmplifieratUltralowTemperature(ULT) 228
5.5.1ADouble-StageAmplifierwithaSingleFrontULTSQUID 228
5.5.2ADouble-StageAmplifierwiththeFrontULTSQUIDArray 233
5.6MicrowaveSQUIDParametricAmplifiers 234
5.6.1OperationPrincipleofMicrowaveSQUIDswithExternalPumping(MSQUIDs) 234
5.6.2TheNonlinearitiesintheMSQUIDReadout 236
5.6.3TheFluxRampModulationMethodology 237
5.6.4PerformanceofMSQUIDCurrentAmplifier 238
5.7DesignMethodologyofAnalogCircuitries 242
5.7.1TheLaplaceTransform:TransferFunctionsofElectronicNetworks 242
5.7.2DesignofAnalogPulse-ShapingFilterCells 246
5.7.3DesignofLow-PassFilters 253
5.7.4GraphicalMethodsofAnalysisandSynthesisintheFrequencyDomain 259
5.7.5TheDescribingFunctionofNonlinearElementsintheFrequencyDomain 271
5.7.6SystemswithSynchronousMultipliers 274 References 280
6TheEnergyResolutionofRadiationSpectrometers 285
Introduction 285
6.1 Signal-to-NoiseRatio,EquivalentNoiseChargeofRadiationSpectrometers:GeneralDefinitions 287
6.2EnergyResolutionofQuasiparticleDetectors(STJs,SDDs) 290
6.2.1TheTunnelJunctionCoupledtoaJFETTransconductanceAmplifier 290
6.2.2EnergyResolutionofSTJSensorsReadoutwithSQUIDCurrentPreamps 296
6.3OptimalFiltrationinRadiationSpectrometers 300
6.4EnergyResolutionofTESMicrocalorimeters 302
6.5MatrixReadoutMultiplexingofSTJDetectors 306
6.5.1MatrixReadoutofSTJSensorswithJFETTransconductanceAmplifiers 306
6.5.2MatrixReadoutwithSQUIDCurrentAmplifiers 307
6.6Time-DivisionMultiplexor(TDM) 309
6.7FrequencyDivisionMultiplexingwithMicrowaveSQUIDs(μMUX) 311
6.8CodeDivisionMultiplexing(CDM):Spread-SpectrumModulation(SSM) 314 References 317
7SignalProcessinginRadiationSpectrometers 321
Introduction 321
7.1 Signal ConditioningUnits 322
7.1.1OverviewoftheDigitalPulseProcessingArchitectures 322
7.1.2AC-CoupledDigitalSpectrometers 325
7.1.3DigitalPulseProcessingwiththeMovingWindowDeconvolution 328
7.1.4DC-CoupledDigitalPulseProcessors 329
7.1.5DC-CoupledDigitalPulseProcessorswithaSlidingWindowSignalConditioner 330
7.2Analog-to-DigitalConversion 332
7.2.1Analog-to-DigitalConverters:BasicInformation 332
7.2.2TheQuantizationNoiseModelofADC 332
7.2.3NonlinearitiesofADC 335
7.2.4ApertureTimeofADCs 337
7.2.5ApertureUncertaintyofADCs 338
7.2.6ReductionoftheDifferentialNonlinearitywiththeSlidingScaleMethod 339
7.3DigitalFiltration 340
7.3.1 Z-TransformMethodology 340
7.3.2DesignofDigitalFilterswith Z-transform 347
7.3.3TheStabilityofDigitalFilters 351
7.3.4TrapezoidalPulse-ShapingDigitalFilter 352
7.3.5MovingAveragePulseProcessing 354
7.4ThroughputofDigitalSpectrometers 355
7.4.1PulseRecognitionChannel:PileupDetection 355
7.4.2TimingResolutionofDigitalSpectrometers 357
7.4.3ThePileupDecodinginDigitalPulseProcessors 359
7.4.4DigitalRise(Fall)TimeDiscrimination 360
7.5SelectedTopicsoftheHardwareDesign 363
7.5.1NoiseReductioninSystemswithSwitchingPowerSupplies 364
7.5.2PCBLayout 366
7.5.3Layout,Decoupling,andGroundingofADCs 368
7.5.4GroundingAspectsoftheSystemDesign 369 References 371
8UltralowTemperature(ULT)CryogenicArrangements 373 Introduction 373
8.1 Cooling TechnologiesforSub-1KTemperature 374
8.1.1The 3HeRefrigerator 375
8.1.2TheAdiabaticDemagnetizationRefrigerator(ADR) 376
8.1.3TemperatureControlinADRs 381
8.2MagneticShieldingatLowTemperature 384
8.2.1The μ-MetalShields 384
8.2.2TheSuperconductingShielding 386
8.2.3SolenoidInsideaCylindricalSuperconductingShield 387
8.3ThermalLoadonULTCoolingStages 388
8.3.1ThermalConductionThroughSolids 389
8.3.2ThermalConductionThroughtheGas 390
8.3.3ThermalRadiation 391
8.4CryogenicPackagingfortheFocalPlaneArray(FPA)Unit 391
8.4.1DesignoftheFPAUnitImplementingtheTDMTechnique 392
8.4.2TheCollimationoftheFPAUnit 395
8.4.3SolidAngleoftheNuclearRadiationSpectrometer 396
8.4.4FocusingPolycapillaryX-rayOptics 397
8.4.5WiringatmKTemperatures 400
8.5CryogenicDesignforDetectorswithMicrowaveFrequency-divisionMultiplexing 401
8.6TheCollectionEfficiencyofRadiationSpectrometers 404
References 407
9ApplicationsofRadiationSpectrometersBasedonQuantumCryogenicDetectors 409
Introduction 409
9.1 Nanoanal yticalChemistrywiththeSEMElectronProbe 411
9.1.1TheSEM-BasedEnergy-DispersiveSpectroscopy(EDS) 411
9.1.2TheDualArrayTES-BasedEDS 416
9.1.3ComplementaryTechniquesintheElectronProbeNanoanalysis:TheAugerSpectroscopy 417
9.1.4ComplementaryTechniquesintheElectronProbeNanoanalysis:TheWavelengthDispersiveSpectrometers 418
9.2Energy-DispersiveMALDI–TOFMassSpectrometryforBiochemicalAnalysis 420
References 425
Index 427
NuclearElectronicsasascientificfieldmakesavitalcontributiontooureverydaylife.Eventhenon-technicalgeneralpublic wouldrecognizemanyapplicationsofthedisciplineandtheirsignificanceforoursociety,e.g.systemsthatsustainoperation andsafetyofnuclearreactorsinpowerstations,shipengines,orsubmarines,NuclearMagneticResonanceImaging(MRI) machines,ComputedControlledTomographyScannersinmedicine,largetelescopesinAstrophysics.Lessknown,but equallycriticallyimportantnuclearanalyticalinstrumentsensurethefoodsafetyonsupermarketshelves,securityof ourairports,forensicinvestigationsofresiduesincriminalistics,monitoringpetrolquality,andmanyotherimplementations.Thetechnologicaladvanceinnanotechnology,lifescience,biochemistry,ecology,medicine,semiconductors,remote sensinghasbecomemoreandmoredependentontheinformationwhichcomesuniquelyfromthenuclearradiationsensors.Theinformationtheyproducecaneitherbeachemicalcompositionofvarioussamples,oracrystalstructure,ora surfacemorphology,orrecognitionandcharacterizationofindividuallayersinamultilayerformation,oramassdistributioninmolecularspecimens,orDNAstructure.Thepossibilities,alreadyveryimpressive,stillexpandrapidly,practicallyon thedailybasis.Besides,inalmostallalreadyknownapplications,thereisanever-pressingdemandformoredetailedanalysiscombinedwithimprovedproductivitytoscanincreasingvolumesofsamplesperunittime.Tomeetthisdemand, NuclearElectronicsspecialistsconductcontinuousresearchintonewmoreadvanceddetectiontechniquesandperfect thosethatalreadyexisttodeliverthebestpossibleresolution,throughput,detectionefficiency,performancestability, anddatareproducibility.
NuclearElectronicsevolvedfromthestartasadistinctscientificfieldalongsidethelarge-scalenuclearphysicsprojects primarilybecausethemainstreamelectronicindustrydidnotaddressspecificrequirementsandregulations.Examples include,forinstance,theexceptionalpurityrequirementfordetectormaterials,moredemandingelectroniccomponent performancespecifications,reliability,theoperationinextremeenvironments,speciallytailoreddesigntoolsand manufactureprocesses,etc.Thedetachmentofthedisciplinehasbeenfromthestartandremainstothistime.Nosingle general-purposefoundrywillacceptdesignsinvolvingthemanufactureofasystem-on-chipthat, e.g.combinestheultrashallowblockingjunctiondriftdetectorsandassociatedreadout/processingelectronicsonthehighpuritysemiconductor wafer.Thistypeofworkrequiresspecializedequipmentandappropriatelytrainedpersonnel.Therefore,itisadvisablefor engineersandscientistsenteringthefieldtoacquireinterdisciplinaryskillsinadditiontothoseattributednormallytomainstreamelectronics.Theseskillsarenecessaryfornegotiationswithfoundrystaff,sub-contractors,applicationspecialists. Themostcriticaltechnologiesarenormallybeingdevelopedin-house.Fig.p1givesasummaryofcompetenciesassociated withtheRadiationMeasurementInstrumentation,aspecificbranchofNuclearElectronics,whichwillbedealtwithinthis manuscript.
Thecryogenicsolid-statedetectorsusedforhighprecisionradiationmeasurementscanbeclassifiedintotwogroups:
1)Ultra-LowTemperature(ULT)Detectorsoperatinginasub-1Krange(Chapters2,3);
2)Semiconductor-basedDriftChambersorCCDs(ChargeCoupledDevices)moderatelycooledbelowroomtemperature, normallyabovealiquidnitrogen77K(Chapter4).
Thesub-1Ksuperconductingdetectorstendtoservethemostchallengingapplicationsintermsoftherequiredenergy resolution,whereaslessprecisesemiconductorcounterpartsareoftenreferredtoasthe “workinghorse” oftheSpectroscopicIndustries.Manypublicationsperceivethesetechnologiesascompetitive.Inreality,theyco-existcomplementarily. Thestate-of-artSiliconDriftDetectors(SDDs)withanareaupto200mm2,energyresolutionof125eV(MnKα),andcount
ratecapabilityabove106 countspersecond(cps)[1,2]arenaturalcandidatesforthewide-anglecameras.Thesecameras collectbroaddatafromlargeareasof,forinstance,skyorspecimens,whereasthenarrow-anglecamerasbuiltonthebaseof ULTdetectorsextendthecapabilitiesofSDDsbyzoomingintopointsofparticularinterest.Thebestsuperconductingdetectorshaveasmallerfocalplanecoveragebutdemonstratedanenergyresolutiondownto(2to5)eVatMnKα forafewhundredcpsperpixel[3].Fig.p2illustratesthecomplementarityofthesetwosensingtechnologies(reproducedfrom[8]with permissionofSpringerNature,license5125391328507).ItshowsacombinedX-rayenergyspectrumdiagrammeasuredona coppersamplewitha2MeVprotonexcitationbeamwithSDDandTES-basedspectrometers.Thearrangementforthis ParticleInducedX-rayEmission(PIXE)experimentisdescribedinthemanuscript(seeFig.8.4.1andrelatertext).ThebenefitfromusingtheintegratedSDD/TESinstrumentintermsofimprovementintheresolvingpowerandspeedisevident. Wecontinuouslygetnewconfirmationstoitfromthelatestcomparativestudies,e.g.theXANES(nearedgestructure)analysisofdilutesamplesandtraceelementsdescribedin[9].
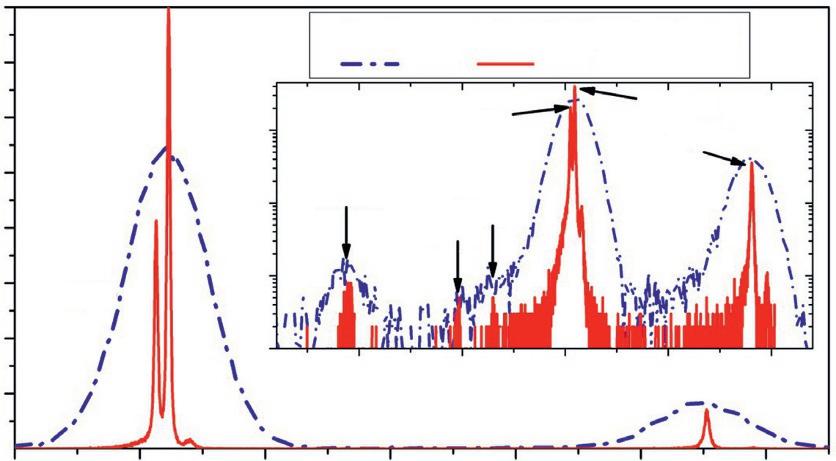
Figurep2 ThecombinedCu-sampleX-rayspectraexitedwith2MeVprotonbeamandmeasuredwithTESandSDDdetectors.Inset showsthesamedatainlogarithmicscaletorevealdetailsintheresolvingpower(reproducedfrom[8]withpermissionofSpringerNature, license5125391328507).
Figurep1
Duetothecompatibilityofsemiconductorandsuperconductortechnologies,itfeltreasonabletoaddanewChapter4on SDDsinthissecondedition.Thisshouldgiveamorebalancedoverviewoftheentirefield.Besides,modernsemiconductor devicesundoubtedlybelongtotheclassofquantumcryogenicdevicesbydefinitionforatleasttworeasons:
1)insemiconductortechnologywithcontinuouslyreducingfeaturesandsharpinterfaces,thequantummodelshierarchy (orimportanceofquantumcorrectionstosemi-classicalmodels)isincreasing[4],
2)Siliconisreadilyavailableinthehighlypurifiedcrystallineformwitharesistivityupto50kΩ m.Suchhighresistivity togetherwithmodernprocessingtechniquesreducingthedensityofunsaturatedchargestatesattheSi-SiO2 interface downtojust5x108 cm-2,450 μmthickSDDsdemonstrategoodperformancealreadyatfewtensdegreesbelow0 C. However,extendingtheenergyrangeofmeasurednuclearradiationwiththemaximizedquantumefficiencywillrequire thickerSiwafersormaterialswithahigheratomicnumberZ.ThequantumefficiencyscalesapproximatelyasZ5 GermaniumwithZ=28enablessubstantialimprovementoversilicon(Z=14)andhasexcellentprospectsasamaterial ofchoiceforfurtheradvancingthedriftchamberperformancespecifications.Ithasasmallerenergygapof0.66eV(as oppositeto1.12eVforSi)whichobviouslywillimprovetheenergyresolvingpower.Gemaywellbecomethematerialof choiceforthenextstageofthelarge-scaledevelopmentinsemiconductordetectors.Similartosilicon,theCzochralski techniqueforhighpuritycrystallineGegrowthhasalreadybeendeveloped[5],thebasicprocessingtechniquesand foundryservicesalsoexist.GeDriftDetectorswillrequirecoolingtolowertemperaturesdowntoatleast90K.However, SEMcompatiblesingle-stage/lowvibrationpulsetubecoolers,usedwiththebulkLithiumCompensatedSi,caneasilybe recycledforthisapplications.
NuclearElectronics,asascientificdiscipline,isnotlimitedtojustdesigningandperformanceverificationofprimary sensors.Italsoinvolvesothersystemizationtopicssuchasequivalentcircuitsmodellingthesignalformationandnoise sources,lownoisereadoutpreamplifiers,multiplexingthelargeformatsensorarrays,theoptimumfiltrationmaximizing thesignal-to-noiseratio,signalprocessing/recognitioninanalogueanddigitalforms,timemeasurementandtriggering, dataacquisition,etc,aslistedinFig.p1.ThesetopicswillbepresentedinthesubsequentChapters5to7.
Chapter8isdedicatedtothesystematizationissuesofthenuclearradiationspectrometerswithemphasisontheultra-low temperaturedesign.Itwillincludetopicslikecoolingtechniques,magneticshielding,front-endassemblypackaging,collimation,windowing,thedefinitionofthesolidangle,X-rayoptics,andspecificsofmicrowaveconnectivityoftheULT/ roomtemperatureinterface.
UptonowthefundamentalresearchinparticlephysicsandastrophysicshasdrivenprogressinRadiationDetection. Presently,however,weobserveadefiniteshiftofinteresttowardsindustrialapplications(nano-materialscience, biochemistry,medicalimaging,environmentalcontrol,security,etc.).Amongalltypesoflow-temperaturesuperconducting detectors,theSuperconductingTunnelJunctions(STJs)andtheTransitionEdgeSensor(TES)quantumcalorimetersare theclosestcandidatesforcommercialization.Systemsontheirbasehavealreadydemonstratedasub10eVenergyresolutionFWHM(thefullwidthatthehalfmaximum)for5.9keVX-raydetectionandupto5to10kcpscountingspeed.The speedcanbefurtherimprovedbyconfiguringtheminamultiplexedarchitecture.Theprogressinthedevicemultiplexabilitywasthemostremarkableovertheperiodbetweenthetwoeditions.Themicrowavefrequencymultiplexingofsinglejunctionquantuminterferometers(μMUX)enableshundredsofdetectorstobebundledtoasinglecoaxialcablewitha bandwidthof4to6GHzprovidedbymodernlownoiseHEMTpreamps.Theresultsofthenewtechnologydemonstrations weresoimpressivethatitisnowbeingconsideredforbuildingaspacetelescopewithahundredofthousands(yes100,000!) pixelarray.
Theoverallperformanceofdetectorarraysisgettingbetterasthetechnologybecomesmoremature[3].Thecryo-spectrometershavealreadygonethroughrigorousapplicationtests.W.Doriese etal reportedabouttwelveTESbaseddetector systemsinstalledinlargeX-raylaserfacilitiesforthesynchrotron-basedabsorption/emissionspectroscopyandenergyresolvedscattering;accelerator-basedspectroscopyofhadronicatomsandparticle-induced-emissionspectroscopy;laboratory-basedtime-resolvedabsorptionandemissionspectroscopywithatabletop,broadbandsource;andlaboratory-based metrologyofX-ray-emissionlines[3].M.Frank, etal,R.Wenzel etal havepublishedresultsontheSTJperformanceas iondetectorsintheenergydispersiveMatrix-assistedlaserdesorption/ionizationTime-Of-Flightmassspectrometry (Maldi-TOF)in[6]and[7],respectively.Anearly100%efficiencyresponsetothedetectionoflargemassparticleshasbeen verifiedupto1.5MDa.Thesecondgenerationofinstrumentswillbeupgradedwithlarge-formatarraysofcryogenicdetectorsimplementingawide(4-6GHz)bandwidthmicrowavefrequency-divisionmultiplexors.Thesesystemsshoulddeliver unprecedentedlyhigh-qualityspectraenablingnewapplicationareasfortheMALDI-TOF,inparticular,thecritically importantfieldslikeviralandbacterialresearchwherethesesystemscangenerateanalyticalresultswithmuch-improved productivity.
Laboratorytestsconfirmedthecapabilityofsuperconductingdetectorsinstalledinallmentionedfacilitiestomaintain theirhigh-performancepotentialanddeliverexceptionalqualityinformation,whichcannotbeobtainedwithanyother techniques.Chapter9willbededicatedtothediscussionofLow-TemperatureEnergyDispersiveandMaldi-TOFSpectrometersaswellasoutlinesomeotherpotentiallyveryinterestingapplications.
Anotherissueusuallyperceivedasproblematicisthatthesuperconductingtechnologyneedsliquidcryogenstoprovide thesub1Ktemperatureenvironment.Thecryogenicpartisassociatedwiththehighermaintenancecost,thenecessityfor trainedcryogenicpersonnel,boilingliquidandevaporatinggasinterferingwithtechnologicalprocesses.The “dry” pulsetubecoolers,nowcommerciallyavailable,solvedtheproblembyeliminatingcryogenliquidsatallorbycondensingandrecirculatingitonsite.Thecryogenicsisfullycomputer-controlled.Fromtheuser’sperspective,theULTinstrumentsare indistinguishablefromtheirroomtemperaturecounterparts.Thisencouragestheindustriestograduallyacceptnewsuperconductingdetectortechnologyandbenefitfromitsextendedcapabilities.
Toconcludethepreface,onecanpredictwithoptimismthatanewgenerationofexceptionallytalentedscientists,engineers,andpost-graduatestudentswillbejoiningthischallenging,butexcitingscientificfieldeitherassystemdevelopersor application/maintenancespecialists.Themajorgoalofthisbookistobringallaspirantsuptospeedinthesubjectasquickly andpainlesslyaspossible.Particulareffortwasundertakentomaketheoverviewpossiblycompleteandself-containedso thatitcouldserveasasingleinformationsourceonallimportantfundamentalissuesofNuclearElectronicswithCryogenic QuantumDetectors.Certainly,itwasnotfeasibleinpracticetoaccommodatealldevelopmentsinthefieldorgointoagreat depthofeachparticulardevelopmentinonebook.Whereasthededicatedconferencereviewmanuscriptssummariseoften thelatesttrendsintheprimarysensors,thesystemintegrationissuesareusuallyscatteredinmultiplepapersorhavenot beenaddressedproperlyatall.Anefforthasbeenmadetobalanceit.Allpublicallyavailablemajormaterialsonthe topicwereanalyzed,systemized,andexistinggapswerefilledusingmypersonaltechnicalexperienceorthrough communicationswithcolleagues.Iwouldliketothankallofthemheartily.
References
1 G.Lutz.SilicondriftandpixeldevicesforX-rayimagingandspectroscopy. JournalofSynchrotronRadiation 13, 99(2006).
2 E.Kenik.EvaluatingtheperformanceofacommercialSiliconDriftDetectorforX-raymicroanalysis. MicroscopyToday May,40(2011).
3 W.Doriese,P.Abbamonte,B.Alpert,etal.ApracticalsuperconductingmicrocalorimeterX-rayspectrometerforbeamlineand laboratoryscience. ReviewofScientificInstruments 88, 053108(2017).
4 A.Juengel. TransportEquationsforSemiconductors.Springer,2009.
5 G.Wang,H.Mei,D.Mei,Y.Guan,G.Yang.Highpuritycrystalgrowth. JournalofPhysics 606, 012012(2015).
6 M.Frank,S.Labov,GWestmacott,H.Benner.Energy-sensitivecryogenicdetectorsforhigh-massbiomoleculemass spectrometry. MassSpectrometryReviews 18,155(1999).
7 R.Wenzel,U.Matter,L.Schultheis,R.Zenobi.AnalysisofmegadaltonionusingcryodetectionMALDItime-of-flightmass spectrometry. Anal.Chem. 77,4329(2005).
8 M.Palosaari,K.Kinnunen,J.Julin,et.al.TESforparticleinducedX-rayemissionmeasurements. J.LowTemp.Phys. 176, 285(2014).
9 S.Yamada,Y.Ichinoe,H.Tatsuno,et.al.BroadbandhighenergyresolutionhardX-rayspectroscopyusingTESatSpring-8. Rev. Sci.Instrum. 92,013103(2021).
Thenuclearelectronicsisoftenassociatedprimarilywiththefundamentalresearchconductedinnuclearlaboratoriesand astrophysics.Yetmanywouldbequitesurprisedtofindoutanextentitdirectlyaffectsoureverydaylife.Thefoodsafety,the securityatairports,medicalexaminations,dopingtests,forensicinvestigationsandsoonareallprovidedwiththenuclear analyticalinstrumentation.Thetechnologicaladvanceinthelifescience,biology,ecology,medicine,semiconductors, remotesensingandmanyothersrelayheavilyupontheinformationwhichcomesuniquelyand,whatisparticularlyimportant,non-destructivelyfromnuclearsensors.Thisinformationcanbeeitherachemicalcompositionofamaterialdealt with,oracrystaloratomicstructure,orthethicknessofindividuallayersinamultilayerformationofacomplexshape, orthemassofmolecules,oraDNAstructure.Thenumberofpossibleapplicationsiswideandexpandingrapidlyalmoston adailybasis.Besides,evenintraditionalareasoftheresearchanddevelopmentspecialistsneedtoobservesmallerfeatures, alesserpercentageofcontaminations,etc.,but,atthesametime,scanninglargerareasorvolumes.Therefore,thenuclear electronicsasadisciplinemustcontinuouslyevolveinitssearchfornewdetectionmethodsormoreelaborateprocessing techniquesinordertodelivermuchneededsystemswithabetterresolution,accuracy,reproducibilityandthespeedof operation.
Abigstepintheradicaladvanceofthenuclearanalyticalinstrumentationwillundoubtedlybethecommercialisationof cryogenicparticleandradiationdetectors.LeadingrepresentativesofthesedevicesaretheSuperconductingTunnelJunction(STJ)andquantumcalorimeters.Bothtypeshavealreadydemonstratedasub10eVenergyresolutionFWHM(thefull widthatthehalfmaximum)at5.9keV(MnKα)asoppositeto125eVachievedwiththebestsemiconductordetectors.Initial laboratoryexperimentshaveproventhenewclassofdetectorstobeveryaccurate,stable,adequatelyfastandwellsuitedfor thehigh-densitymultipixelintegration.Theonlydisadvantageassociatedwiththesuperconductingtechnologywasaneed inliquidcryogensastheonlymeanstoensurethesub1Ktemperatureenvironmentrequiredfortheiroperation.Besides theinconvenienceandthemaintenancecost,thepresenceofacryogenoritsevaporatedgascouldinterfereadverselywith someoftechnologicalprocesseswhichinstrumentsweresupposedjusttomonitor.Arecentcommercialintroductionof “dry” pulse-tubecoolers,however,hasaddressedtheproblemand,infact,changedprioritiesinthehighprecisionnuclear measurements.Onecanseethattheindustrystarteddivertingapartofthedevelopmentbudgetintoadvancingthesenew technologies.Despitetheextracostassociatedwithcryogenics,anaddedvaluesuchasamorethanoneorderofmagnitude increaseinresolvingcapabilitiesfullyjustifiesit.
Tosummarisethisbriefpreface,itiseasytopredictthatanincreasingnumberofscientists,engineersandpost-graduate studentsisexpectedtobeinvolvedinthenuclearmeasurementsbasedoncryogenicdetectorswhomaywishtoupdateor refreshtheirskillsonthesubject.Whereastheinformationonsensorsandthephysicsbehindthemisscatteredinthousands ofpapers,somesystemintegrationissueshavenotbeenaddressedsofaratall.Theprimegoalofthisbookistosystematise thepublishedmaterialonthesubjectofinterestandpossiblyfillinexistinggaps.Wewillavoidreprintingcomplexexpressionsofthemicroscopicsuperconductivityortheinformationtheory.Forthoseinterestedingainingadeeperbackground intheseandsomeotherrelevantissues,appropriatereferenceswillbegiventhroughoutthebook.
ThebookisprimarilybasedonresearchwhichwasdoneincollaborationwithmycolleaguesattheJointInstitutefor NuclearResearch(Dubna),Physikalisch-TechnischeBundesanstalt(Berlin)andThinFilmGroupofOxfordInstruments (Cambridge)aswellasaresultofmultiplediscussionsofthematterwithmyfriendsandcolleaguesfromotherinstitutions worldwide.Iwouldliketoexpressmygratitudetoallofthemhopingthebookwillbeusefulintheirfurtherresearch.
InteractionoftheNuclearRadiationwithDetectorAbsorbers
Introduction
Radiationsensorsareintendedforthequalitativedetectionofvariouselementarynuclearparticlesand,inmanyapplications,measuretheirquantitativecharacteristicparameters,suchasflux,energydistribution,positioncoordinates,timing information,etc.Thedetectionstartsfromamomentwhenanincomingparticleinteractswiththesensor’sactivevolume. Insomepublicationsontheradiationmeasurements,theauthorsproceeddirectlytothedown-conversionprocesstransformingdepositednuclearparticleenergy Ep intoeitheracorrespondingnumberofquasiparticles Nqp in nonthermal devicesoratemperaturerise ΔT in thermalcalorimeters inproportionto Ep.Ifthatwastrue,detectorsexposedtothemonochromaticbeamwouldbeproducingasinglepeakoutputontheenergyspectrumcenteredat Ep.Inpractice,however,we normallyobservespectraenrichedbyexcitationsofsecondarycharacteristicradiations,backgroundevents,escapeordoublepeaks,tales,etc.Thisenrichmentisfurthersuperimposedbytheincompletechargecollectionduetovarioustransport lossmechanismsandsensor/readoutnoise.Veryoften,wehavetoapplyquitecomplexmathematicalmodelssolving inverseproblemstorestoreenergyandtiminginformationofincomingnuclearparticles.Todothatefficiently,itisuseful todividethedetectionprocessintofourphases:
1)Theprimarynuclearreactionofaparticlewiththeabsorbermatter,whichwillbethetopicofthepresentchapter.
2)Theenergydown-conversionprocessgeneratingaresponseinproportiontotheenergydepositedintheactivevolume.
3)Thedrift/diffusionofgeneratedinformativecarrierstowardthesensorcollectionelectrodes.
4)Themeasurementprocessofasignalgeneratedbyaradiationabsorberwithoneofthesensortypes,e.g.thetunnel junction,transitionedgethermometer,kineticinductance,semiconductorbarrier,etc.
Thedown-conversionandtransportinsuperconducting,semiconducting,andnormalmetalabsorberswillbediscussed inthecorrespondingsectionsofChapters2,3,and4.
Thequantumcryogenicsensorspresentedinthismanuscriptarecapabletorespondtopracticallyalltypesofknown radiations:chargedparticles,opticalphotonsfrominfraredtoX-raysand γ-rays,andunchargedparticles,e.g.neutrons andweaklyinteractingmassiveparticles(WIMPs).Amongthesetypes,onlyelectronsarecapabletoinitiateandparticipate directly intheenergydown-conversionprocessthroughtheinelasticelectron –electronandelectron–phononinteractions. Detectiontechniquesofotherparticlesinvolve indirect energycascades.Intheindirectcascades,theprimaryinteractions liberatenormallyenergeticatomicelectrons(δ-ray),whichfurtheractaslightchargeparticlescreatingontheirpathameasurableamountofquasiparticlesinachainofsecondaryprocesses:ionization(semiconductors),ortheCooperelectron pair-breaking(superconductors),orhot-electroncarriergeneration(normalmetalabsorbers).
Therearetwobasicenergyexchangereactionmechanismsbetweentheprimarynuclearparticlesandtargetatoms:the absorption andthe inelasticscattering.Theinelasticscatteringeventstakeplacewhenincomingparticlessharetheirkinetic energywithatomicandfreeelectronsbyelectromagneticinteractions.
Figure1.1.1illustratesschematicallytheabsorptionprocess,inwhichanincidentparticledisappearscompletelycaptured bythetargetmatter.Theseinteractionsaremoretypicalforthephotonbeams,althoughchargedparticlescanequallybe absorbedinnuclearreactionstogenerateothertypesofsecondaryradiation.Aphotonenteringthesensitivepartofdetectorsnormallyencountersandtransferselectromagneticallyallitsenergy Eph toanatomicphotoelectron.Dependingona
2 1InteractionoftheNuclearRadiationwithDetectorAbsorbers
Incident particle Target atom
Recoiling target
The pre-interaction state
The post-interaction state
valueof Eph,theexcitedphotoelectroncan(i)raisetoahigherboundstateandgeneratesecondaryphotonsduringthe relaxationprocess,(ii)leaveatomcompletely(theionization)andinitiate/participateintheenergyconversion,and (iii)stayintheoriginalboundstate,butgeneratephononparticlesthat,inthecaseofsuperconductors,contributeto theCooperpair-breakingprocessorgenerateinformativeheatinnormalmetalcalorimetricabsorbers.Thephenomenon isoftenreferredtoas thephotoelectriceffect.WewillreturntoitinSection1.3.1.
Aswementionedearlier,someofchargedparticlesandneutronsintheincidentbeamscomeveryclosetotargetnuclei thatmayresultinthenuclearparticlereactions.Onecandistinguishbetweentwotypesofnuclearreactions:(i)interaction ofincomingparticleswithnucleonsand(ii)penetrationofincomingparticlesintothetargetnuclei(theradiativecapture). Bothnuclearreactionsleavetherecoilnucleiinanexcitedstate,whichsubsequentlyrelaxesbyemittingnewparticlesor/ andtransmutationintodifferentnuclearspecies.Thesecondarynuclearreactionproducts,i.e.photonsandchargedcarriers,canbemeasuredbyradiationdetectors.Forthat,theyarebuiltas “sandwiches” includingnuclearreactionlayerson topoforinthemiddleofthesensingdeviceabsorber.Providedthatthenatureofnuclearreactionsinvolvedisknown, measurementdatafromthesecondarysensorcanbeusedtorestoreinformationabouttheprimaryparticlesofinterest. WewillgivemoredetailsonthatinSection1.3whenwetalkaboutdetectingneutronsandinChapter4whenwediscuss WIMPhybridsemiconductor – transitionedgesensor(TES)detectors.
Thescatteringinteractionsarecharacterizedbythefractionalenergyand/ormomentumexchangebetweenparticlesand recoilingtargets.Intheseinteractions,particlesthemselvesexistasindependentobjectsbeforeandaftercollisions.Sometimes,theabsorptionprocessofaparticleby,e.g.nucleus,whichisfollowedbysubsequentexpelofthesameparticleor anothersimilarparticle,isalsoreferredtoasscattering.
Figure1.1.2demonstratestwotypesofscatteringinteractions.In theelasticscattering (Figure1.1.2a),thetotalkinetic energyofaparticleandaparticipatingtargetdoesnotchangebeforeandaftercollisions.Thecollisions,inwhichthekinetic energyischanneleddowntotheexcitationoftargetatoms,arereferredtoas theinelasticscattering (Figure1.1.2b).Inboth cases,thestrongCoulombforcesoftargetatomsdiverttheinitialtrajectoryofcollidedparticlesbyasuccessionofangles, whicharecalled thescatteringangles
Withthesebasicdefinitions,wecannowdiscussselectedaspectsofprimarynuclearreactionsinmoredetail.Thegeneric scopeofthistopicissimplyenormous.Therearemultiplenuclearphysicsmanuscriptsdedicatedtoit.Alotofusefulquantitativeinformationcanbefound,forinstance,inthebooksandscientificpapersontheparticleprobeanalyticalchemistry. ThemoderncomputationpowerhasbroughttheMonteCarlosimulationroutinetoeverylaboratory.Thepassageof radiationthroughmattercannowbemodeledbydedicatedparticlephysicssoftwaretoolkits,likeGEANT4[1].Modern softwareisveryadvancedintermsofcomputationaccuracyandinputinterface.Itshouldtakecareofthemajorityof possiblenuclearreactionsandinteractionmechanisms.Still,theresearchersandengineersmusthaveadetailedunderstandingofmodelsemployedtogivetherightinterpretationstothesimulationresultsandmakesuresimulateddatadoes notunder-/overshoottheexpectedballparkvaluesduetothecodeinstability.
Section1.1willdefinetheintrinsicquantumefficiency(IQE)oftheradiationdetectors.Thefollowingtextwillbestructuredaroundselectedaspectsofparticleinteractionwithsolid-stateabsorberstocharacterizedetectorsintermsofthecollectionefficiency,requiredgeometry,transportmechanisms,etc.Itisessentialforthequantitativemeasurementswith radiationdetectorstoeithercontainthefullenergydepositedbyanincomingbeamoratleastawell-knownpartofit tobeabletodeliveraccurateresults.Section1.2willdealwithchargedparticles.Wewilldifferentiatebetweenthelight andheavyparticlesanddefinetheirpenetrationdepthdependingontheirenergies.Section1.3willfocusonthephoton measurements.ThedetectionofneutronsandWIMPswillbethesubjectsofSections1.4and1.5,respectively.
Figure1.1.1 Schematicrepresentationofthenuclearparticleabsorptionprocess.
Recoiling target
Target atom
Incident particle
The pre-interaction state
Incident particle
Scattering angle
Elastic scattering Scattered particle
The post-interaction state
The pre-interaction state
Scattering angle
The post-interaction state
Figure1.1.2 Twotypesofscatteringinteractionsbetweentheincomingparticleandthetargetatom.(a)Thekineticenergyofthe particleintheelasticscatteringdoesnotchangebeforeandaftercollisions.(b)Intheinelasticscattering,thekineticenergyispartially channeledtowardtheexcitationorionizationoftheatom.
1.1TheIntrinsicQuantumEfficiencyofRadiationDetectors
TheIQEcanbedefinedingeneraltermsasthepercentageofincidentnuclearparticlesthattheabsorberconvertsinto informativechargecarrierssampledbysensingdevice[2].Forthefirstphaseofthedetectionprocess,asoutlinedin theIntroductionearlier,thequantumefficiency(QE)isquantifiedby theintensityattenuationfunction and theincomplete chargecollection.Theattenuationfunctionisdefinedas α
where I0 and I(tabs)representintensitiesoftheincidentradiationbeamandradiationpassedthroughtheabsorberwithout interaction,respectively,and tabs denotesthethicknessoftheabsorber.Bytheintensityofradiation,wemeanthenumberof nuclearparticlespassingthroughaunitareaperunittime(thebeamcurrent).TheIQEdependsonthetypeofradiation, energydistributioninthebeam,absorbermaterial,anditsgeometricaldimensions.
Providedthateachparticleinthebeamcurrenttransfersitsenergyinasinglecollisionandthendisappears(theabsorptionprocess),theintensityattenuationfunctiontakesthefollowingform:
where μabs istheabsorptioncoefficientreciprocaltothelinearattenuationfactor λabs.Both μabs and λabs aretabulatedforthe majorityofmaterialsutilizedinradiationdetectors(see,forinstance[3]).
Themajorityofincomingchargedparticlestendtorelaxthroughmultiplescatteringeventsbeforetheydisappearfrom thebeam.Therefore,appropriatecorrectionfactorsmustbeintroducedinEq.(1.1.2)totakeintoaccountthedifferencein behavior.Wewilldiscussthesecorrectionsinthefollowingsections.
Passivation layer
Sensitive volume
Quasiparticle clouds
Figure1.1.3 Thelowenergytailoriginatedfromthesplittingofthequasiparticleenergydown-conversionspheresbetweenthe passivation/insulationlayerandthesensitivevolumeoftheabsorber.Thedown-conversionprocesseslocatedwhollyinthepassivation andthesensitivevolumecontributetothezeroandmainpeaks,correspondingly.
Theincompletechargecollectiontakesplaceinallthreephasesofthedetectionprocess.Onemechanism,relevanttothe primarynuclearreaction(thephase1underconsideration),relatestothesplittingofelectroncloudsformedbytheenergy down-conversionchannels.Thecloudsgetdividedbetweenthesensitivepartoftheabsorberandthesurfacepassivationor thegateinsulationlayer.Figure1.1.3illustratesthismechanism.Theinteractionsphereslocatedwhollyinthesensitive volumeoftheabsorbercontributetothedesirablemainpeakoftheenergyspectrum.Sincetheinsulationmaterialshave largeenergygaps,thepassivationlayernormallygeneratessignificantlyfewernonthermalquasiparticlesthantheabsorber material.Therefore,dividedinteractionspherescontainapartialamountofchargecarriers.Theycontributetothelow energytailthatneedstobeminimized.Thespheressituatedentirelyinthepassivationlayertendtoformnear-zeropeaks. Concerningphotons,theirdensityabsorbedbythepassivationlayer Nabs canbeevaluatedusing(1.1.2)as N abs = N ph 1 exp μpl t pl
where Nph isthephotondensityintheoriginalbeamand μpl and tpl denotetheabsorptioncoefficientandthicknessofthe passivationlayer.Again,Eq.(1.1.3)shouldbeadaptedforthechargedparticlebeams.
1.2DetectionofChargedParticles
Asmentionedintheintroduction,theinelasticcollisionofachargedparticlewithavalenceelectroninthetargetatom resultsineitherthedirectionizationorexcitationoftheatom.Theexcitationmayelevateboundelectronstohigherenergy shellsinthevalenceband,whereastheionizationremovesatleastoneofthemfromtheatomcompletelycreatingafree electron–holepair.Inotherwords,directionizationtakesplaceifachargedparticletransferstothevalenceelectronenergy thatexceedstheionizationpotentialoftheatomintheaffectedcovalentbond(inthecaseofthecovalentsemiconductors). Theactualenergytransferismediatedbyelectromagneticfieldssurroundingtheinteractingatoms.Duetothelongrangeof theelectromagneticforces(mainlytheelectricCoulombforcethatdecaysas1/r2,with r beingthedistancebetweenparticles),theionizinginteractionsmayoccurevenwhentheincidentparticledoesnotpassthetargetatomincloseproximity. Thekineticenergyoffreedelectronsisestimatedas
E el = E t Δ 1 2 1 where Et istheenergytransferredtoavalenceelectronasaresultoftheinelasticcollisionand Δ isthebinding(orgap) energy. Eel canbesufficientforthefreedrecoilelectronstoinitiatesubsequentchainsofexcitationandionizationevents. Secondaryelectronsareessentiallylight-chargedparticlesthemselveswithsimilarphysicsbehindtheirrelaxationprocess.
1.2DetectionofChargedParticles
Light particles
particles Super-heavy ions
Heavy nuclei
Biomolecules
microorganisms
-Particles
Chargedparticleswithenergiesbelowtheatomionizationpotentialcanstillproduceameasurableamountofinformative quasiparticlesthroughthephonongeneratingmechanisminthesuperconducting(athermal)andnormalmetalabsorbers attachedtolow-temperaturedetectors(thermalhotelectrons).
Conditionally,allchargedparticlescanbedividedintothreegroups[4].Thefirstgroupcompriseslightparticles,e.g. electrons, β -particles,andpositrons.Thesecondgroupincludesheavy-chargedparticles,suchasprotons, α-particles,heavy ions,mesons.Super-heavyionizedbiomolecularparticlesandmicroorganismsconstitutetheirseparategroup.Figure1.2.1 summarizestheclassificationinadiagramform.Inthefigure,wedistinguishtheelectronfromthe β -particletoemphasize itsdualnature.Theterm “β -particle” referstoanelectronspecificallyreleasedfromnuclei.
1.2.1Light-ChargedParticles
Theinelasticcollisionsoflight-chargedparticleswithabsorbermediaproduceaseriesofcharacteristicradiations.Theseare asfollows:
– Thesecondaryelectrons;
– TheAugerelectrons;
– Thediffractedelectrons;
– Thebackscatteredelectrons;
– ThecharacteristicX-rays;
– Thebremsstrahlung(brakingradiation);
– Others.
Figure1.2.2givesaschematicillustrationoftheprimaryandsecondaryvolumesinwhichincomingchargednuclear particlesinteractwitharadiationdetectionabsorber.Thedrawingalsodefinessub-volumeswherespecificnuclearreactionsgenerateeachofthepreviouslylistedcharacteristicproducts.Callingtheradiations’“characteristic” meansthatthey containimportantinformationaboutthephysicalpropertiesandchemicalcompositionofthetargetmaterial.Theyare fundamentalformultiplenuclearanalyticalmethodologiesandtoolsusedwidelyinelectronmicroscopy,chemicalanalysis, crystallography,medicine,radiometry,etc.Themajorityoftheseanalyticalinstrumentsutilizethesemiconductorand superconductorradiationsensors,whichwewilldiscussinthefollowingchaptersofthismanuscript,duetotheirsuperior performancespecifications. Charged
Figure1.2.1 Theclassificationofchargednuclearparticles.
Characteristic X-rays
Bremsstrahlung Primary interaction volume
Auger electrons
Secondary electrons
Backscattered electrons
Figure1.2.2 Aschematicvisualizationofprimaryandsecondaryvolumeswheretheinteractionofincomingchargednuclearparticles withradiationdetectionabsorbertakesplace.
Sincethecryogenicdetectorsdemonstratesensitivitytoalltypesofradiations,thelight-chargedparticlesbombardingthe detectionmediumofsensorsexcitesimilarcharacteristicproductsintheabsorber’ssensitivevolumeitself,asshownin Figure1.2.2.Theseexcitationsborrowenergyfrommaininformativepeaks,giverisetoadditional(unwanted)peaks, absorptionminimums,lowenergytails,backgrounds,andothertracesintheradiationspectrometeroutputontheacquired energyspectrumdiagram.Therefore,agoodunderstandingofallnuclearreactionsinaparticularabsorber’smaterialof choiceisabsolutelyimportantforachievinghighaccuracyintheradiationmeasurements.Modelingthedetectorresponse canassistinselectingtherightabsorbertype,optimizationoftheoveralldetectordesign,anddevelopingtheappropriate mathematicalmodelstointroducecorrectionstotheacquiredrawdata.
Attheverybeginningoftheenergydown-conversioncascade,theincidentchargedparticlestendtolosetheirenergy(ifit isaboveafewkeV)mainlythroughthelong-rangecollisionswithtargetatomsandcontinuousradiation(bremsstrahlung). Then,thequasiparticlegenerationprocessproceedsthroughmultiplechainsoftheenergypartitionsbetweenelectron–electronshort-rangeandelectron–phononlonger-rangeinteractions.Attheendoftherelaxationprocess,theathermal detectorabsorbershouldcontainquasiparticleswithaninformativedensity Nqp thatcorrelateswiththeenergydeposited byincidentevents.Variousenergylossmechanisms,includingallthecharacteristicradiationproductsplustheenergy storedinthephononsystemattheendofthedown-conversion,influencethemajordetectorperformancespecifications, e.g. εqp and F.Here, εqp istheaverageenergyrequiredtogenerateasingleinformativequasiparticle(oftenreferredtoasthe ionizationpotentialinsemiconductordetectors),and F denotestheFanofactor. εqp and F definethestatisticalintrinsic energyresolution(seeChapter2).Someofthecharacteristicradiations,especiallybremsstrahlung,contributesignificantly tothebackgroundnoise,furtherlimitingtheresolvingpowerofdetectors.
1.2.1.1AttenuationFunctionforChargedNuclearParticles
Now,wewillgiveanestimatefortheIQEofabsorbersintendedtocapturethechargedparticlesandtransformtheirenergy intoinformativequasiparticlescollectedbythecharge-sensitivepreampeitherdirectlyorthroughtheattachedsensing devices,e.g.superconductingtunneljunctions.Aswementionedbefore,chargedparticlesundergomultipleelasticand inelasticcollisions,inwhichtheycorrespondinglyloseonlyfractionsoftheirenergiesremaininginthebeamforsometime (seeFigure1.2.3).Thepenetrationdepthforeachparticlevaries,but,statistically,thereexistsanaveragepropagationdistanceovertheensemble,whichisusuallyreferredtoas therange, R.Attheendofthestraight-linelength, R,particlesare assumedtobestatisticallyrelaxedtothethermalequilibrium.Intermsofthequasiparticleresponsetotheincoming
Interaction volume
Figure1.2.3 Penetrationofparticlesintotheinteractionmediumofasolid-stateradiationdetector.
chargedparticleitself,aspecificallydefined ionizationrange canbeofinterest.Theionizationrangecharacterizesparticle trajectoriesfromapointwithaninitialenergy Ep toapoint wheretheparticlerelaxestoathresholdenergylevelof ~3/2Δ sothatonefinalscatteringfromthevalenceelectron removesitfromthebeam.Theattenuationfunctioncanthen beapproximatedeitherbytheshiftedexponent,i.e. I = I 0 at0< x < R
ortheGaussianfunction(see,forinstance[5]).Inthelatter case, R representsthemeanvalueofthedistributionatthehalf maximum,asshowninFigure1.2.4.Astatisticaldistribution of R isoftenreferredtoas therangestruggling. Forsimplifiedballparkevaluations,onecanuseasemiempiricalformulaforthemeanrangegivenby[4]:
The beam current
Figure1.2.4 Radiationintensityasafunctionofthecharged particlepenetrationdepth. R representsthemeanpenetration rangeoftheradiation. 1.2DetectionofChargedParticles
R (mean range) I(0) I(0)/2 x
Inthisequation, Emin istheminimumenergyatwhichtheBethe–Blochtheoreticalmodelingisvalid.Forincomingcharged particleswithenergiesaboveafewkeV,theBethe–Blochformulaforthelinearenergytransferasafunctionofthepenetrationdepth, x,isgivenby[5]
with Na beingtheAvogadronumber, A and ρ aretheatomicmassanddensityofthedetectionmedium, Z istheatomic number, re =2.817×10 13 cmistheclassicalelectronradius, me =9.108×10 31 kgistherestmassofanelectron, c isthe
velocityoflight, β = v c , ek = E k me c2 denotethedimensionlessreducedvelocityandthekineticenergyoftheincident
particle,respectively, Ip isthemeanexcitationpotential,and δ, C representthedensityandshellcorrectionfactors.Sincethe massesofinteractingobjectsintheinelasticscatteringarealmostthesame(nottrueforrelativisticparticles),themaximum energytransferpercollisioncannotexceedhalfofthekineticenergyoftheincidentchargedparticle.Thus,thefunction F(ek)takesthefollowingforms:
a)Forelectronsand β -particles,
b)Forpositrons,
Forthosewhopreferevensimplersolutions,anempiricalexpressionhasbeenderivedforacaseof E>Emin [6,7]:
Equation(1.2.7)providesadequateaccuracyforthedetectorefficiencyevaluationinanenergyrangeof10–1000keV. Forlight-chargedparticleswithenergies10eV< Ep <10keV,thetotalnumberofcollisionsperparticleisinsufficientto justifytheusageoftheBethe–Blochstatisticalformalism.TheenergylossinsolidscanbeestimatedusingtheLindhard dielectricresponseofamediumtoapassingparticletransferringitskineticenergy ℏω andchangingitsmomentumby ℏk onitsway[8,9].Themeanrangeforcontinuousenergylossfrom Ep ~10keVto10eVisgivenby[10]:
where S(E)istheenergylossperunitpathlengthorstoppingpoweroftheabsorbermaterial.Calculated R(Ep)and S(E)for 58elementalmaterialsincludingthosethatarenormallyusedinradiationdetectorsarepublishedinTanumaetal.[11,12].
Figure1.2.5givesanexampleofthemeanrangeasafunctionofchargedparticleenergy R(Ep)inarangefrom50eVto5keV calculatedusingdatafromTanumaetal.[11].
Anaveragenucleusdiameterisonlya10 5 fractionofthe atomsize.Theremainingvolumeisoccupiedbytheorbital electrons(electrongas).Thisimpliesthattheprobability forachargedparticletointeractwithanucleusinthe close-rangecollision(nuclearreaction)ismuchsmaller comparedwiththeprobabilityofinteractionwithvalence electrons.Forsilicon,scatteringsfromthevalenceelectronsrepresentthemajorlossmechanismattheelectron energiesfrom10eVto10keV.Below10eV,ionizationcollisionratedropsexponentiallyreachingavalueof5×1010 s 1 at2eV.Furtherrelaxationisdominatedbythefastinelasticelectron–phononinteractions.
Itisimportanttoreemphasizeagainthatthesecomputationsarenormallyperformedwithdedicateddesign/simulationtools.Givingtheseequations,wearenottryingto advocateperformingcalculationsintheold-fashioned style.Weratherhighlightthepointthatallsimulationtools employspecificmodelsthathavetheirlimitations.Engineerscanonlyrelyonthemifallissuescomplicatingthe analysisandtheapplicabilityofbuilt-inmodelsforachievingcorrectresultsarewellunderstood.
Figure1.2.5 Aplotofthemeanrangeasafunctionofcharged particleenergy R(Ep)inarangefrom50eVto5keVcalculatedusing datafromTanumaetal.[11].
1.2.2TheContinuous “Braking” Radiation (Bremsstrahlung)
Thelong-rangeCoulombforcesofnucleiexertastronginfluence onchargedparticletracks.Evenelasticscatteringeventsaffect detectorquantumefficiency.Theydivertparticlesfromtheir originaldirectioncausingbremsstrahlungorbackscatteringof particlesfromthedetectorabsorber.Theinteractionvolumealso emanatesAugerelectronscreatedasaresultoftheinelasticcollisionsneartheentrancewindowregion(Figure1.2.2).
1.2DetectionofChargedParticles
Bremsstrahlung
Kramer’s law
Photon energy
Duane–hunt limit
Emax
Thechargedparticlesdecelerateprimarilythroughthedeflectionbythenucleus’ sstrongelectricfield(althoughthescreeningeffectfromvalenceelectronsalsoplaysitspartinthe process).Adeflectedparticlelosessomeofitskineticenergy thatisemittedasabreakingphoton,i.e. hv = Ep( before ) Ep( after ).Here, hv istheenergyofthephotonand Ep( before )and Ep(after )denotetheparticlekineticenergybefore andafterthedeflection.
Freeelectronsandpositronsdonothavediscreteallowedenergylevels.Therefore,the “braking” radiationhasacontinuousenergyspectrumextendingfromnear-zerotothemaximumenergyofincomingchargedparticlesminusthebinding energy Δ oftheabsorbermaterial.Sincetheemitteddecelerationphotonsgenerateanincreasingnumberoffreecarriers withprogressivelysmallerenergies,theircontinuumdistributionfunctionhasashapeasshowninFigure1.2.6.Thecurve wasderivedfromtheKramer’sequationfortheintensityinphotonspersecondperunitenergyintervalperincidentelectron[13]:
where E isanenergyofinterest.
Thepartitionofthetotalstoppingpowerofthematerial dE dx Σ between dE dx col duetoinelasticcollisionsand dE dx brem dueto bremsstrahlungvarieswithenergy.Inthelowenergyrange,particlestendtorelaxmostlyviainelasticscatteringfromatom electrons,i.e. dE dx Σ dE dx coll.Atveryhighenergies,theenergylossisdominatedbybremsstrahlung,i.e. dE dx Σ dE dx brem Contributionsfrombothmechanismsmustbetakenintoaccountforchargeparticlesacceleratedtointermediaryenergies. Thereisacrossoverenergy Ec atwhichthesecontributionsbecomeequal, dE dx coll = dE dx brem.Fortheinteractionofelectrons withsemiconductors,acrossoverpoint Ec ~fewtensofMeV.
Counts per channel
Si Kα
Characteristic X-ray
Bremsstrahlung
Duane–hunt limit
Emax
1.2.3BackscatteringofChargedParticles
Thedeflectionofchargedparticlesfromtheiroriginaldirections bytheCoulombforcesofnucleiwithstrongfieldgradients hasotherimplicationsonthedetectionprocessbesides
Figure1.2.6 Thedistributionfunctionofcontinuum photonscausedbybremsstrahlung. 246810 1214161820
Bremsstrahlungmanifestsitselfasabackgroundcontinuumontheenergyspectrumhistogram.Anexampleofsucha diagramexperimentallyobtainedfromthepurebulksiliconisshowninFigure1.2.7.TheX-rayattenuationatlow energiesseeminglyopposestheKramer ’ sfunction.Inreality, thisresultsfromphotonabsorptionbymatter.Thesephotons existbutsimplydonotreachthedetectormeasuringtheX-ray irradiation.Todemonstratetheintensityofthebrakingradiation,Figure1.2.7alsoincludesastrongSi K α characteristicpeak. Onecanseethatapartofthepeakissmeared.Thebackground continuummaymaskcompletelysomeofthelower-intensity signalsgeneratedbythemeasuredradiation.Italsocomplicates theseparationofcloselyspacedpeaksontheenergyspectrum. Bothproblemsbecomeparticularlyseriousinthelow-energy region.
Photon energy (keV)
Figure1.2.7 Bremsstrahlungmanifestsitselfas backgroundcontinuumontheenergyspectrumhistogram. LowenergyattenuationasoppositetotheKramer’sfunction isduetothephotonabsorptionbymatter.
Particle escape
By deflection (a) (b) By backscattering
Figure1.2.8 (a)Alarge-anglescatteringeventneartheedgedivertsan incomingparticleoutofthedetectionvolumebeforeitsrelaxationhasbeen completed.(b)Thebackscatteringeffectwhenthetotaldeflectionangle becomeslargerthan π /2,sothattheparticleisejectedbackfromthe detectorfrontsurface.
bremsstrahlung.Multipleelasticinteractionsshapepropagationpathsintomeander-likeformsthatincreasetheinteraction volumeandcanmoveittowardsurfaceswithalargedensityoftrappingstates.Alarge-anglescatteringeventneartheedge candivertanincomingparticleoutofthedetectionvolumebeforeitsrelaxationhasbeencompleted(orevenstarted).
Figure1.2.8aillustratesthiscase.Asuccessionofseveralelasticcollisionsmayleadto thebackscatteringeffect.Ithappens whenthetotaldeflectionanglebecomeslargerthan π /2sothattheparticleisejectedbackfromtheentrancewindowofthe detector.ThebackscatteringeffectisillustratedinFigure1.2.8b.Freeelectronsproducedbytheionizationprocesscanalso escapefromthedetectorasthesecondaryandAugerelectrons.Tobeabletoleavethedetectionvolume,theirenergiesneed tobelargerthanthesurfaceworkfunction, Fw,ofthesurfacematerial(ormaterialsiftheentrancewindowcontainsseveral layers).Byconvention,onlyelectronswithenergiesbelow50eVemittedfromadepthlessthan1nmarereferredtoas secondary.Theyaredistinguishedfromothers,moreenergeticelectronsthatcancomeoutfromadepthupto50nm.
Thebackscatteringprocessisnormallyquantifiedby thebackscatteringcoefficient,whichrepresentsthefractionofthe totalnumberofincidentparticlesthatthedetectoremitsbackfromthefrontsurfaceto,i.e.
Thecoefficientdependsontheatomicnumberofthemedium.Forallelementalmaterialsusedasradiationabsorbers, ηbs increasesastheparticleenergiesbecomelower.Highenergyparticlestendtopenetratedeeplyintothemedium(R >50nm) whereevenscatteredathighanglestheycanbereabsorbedefficientlybythelattice.
Thebackscatteringofparticlesoutofthedetectionvolumebeforetheyhaverelaxedtobelow Δ leadsto thechargecollectiondeficit.Itaffectsthelowenergyquantumefficiencyofdetectors.Inaddition,theincompletechargecollectionmarks itspresencethroughtheshiftandbroadeningofmajorinformativepeaksontheenergyhistogram.Italsoaddsspurious peaksandvoidstothebremsstrahlungcontinuum.
1.2.4Heavy-ChargedParticles
Theclassofheavy-chargedparticlesincorporatesallelementaryparticleswithmassesexceedingtheelectronmass,i.e.protons, α-particles,muons,pions,lightnuclei,etc.Theprinciplebehindtheirinteractionphysicswithsolid-stateabsorbersis similartothatofelectronsandpositronsthatweanalyzedinSection1.2.1.Thus,inadditiontowhatwasdiscussed,weonly needtointroducesomequantitativecorrectionsintoequationsdescribingtheenergychannelingprocess.
Theinitialvelocityofaheavy-chargedparticleisapproximately M me timeslowerthanthevelocityoftheelectronwiththe sameenergy(M isthemassofaheavyparticleunderconsideration).Thisreductioninthevelocityextendstheinteraction timebetweenparticlesandatoms,whichleadstoincreasedenergylosspercollision.Thevalenceelectronsofinteracting targetatomshaveenoughtimetoacquireenergyclosetoamaximumvaluethatisevaluatedas[14]
where s = me M , η = βγ , γ = 1 1 β 2 .Moreefficientinelasticscatteringshavetwopositiveconsequencesfordetector designers:(i)therangeofheavy-chargedparticlesbecomesshorterand(ii)betterdefinedatthesametime(reducedthe rangestruggling).
Providedthat β >0.1,theBethe–Blochequationforthelinearenergytransferhasthefollowingmodifiedform[4]:
where z isthechargeofanincidentparticleinunitsofelementaryelectroncharge, e0
Statistically,equallychargedparticlesexperienceanaverageCoulombdecelerationforcefromnuclei, F b .Thisforceis responsibleforthebrakingradiation dE dx brem .Thedeceleration, d ,isinverselyproportionaltothesquareoftheparticle mass, M,i.e. d F b M 2 .Thismeansthattherelativecontributionof dE dx brem tothetotalstoppingpowerreducesinproportionto 1 M 2 aswell.Inotherwords,theinelasticscatteringfromvalenceelectronsisthemajorenergylossmechanismfor heavy-chargedparticlesinasolid-statemediumintheenergyrangeuptoafewGeV:
Intuitively,thepathofaheavyparticleinthemattershouldbelessperturbedbylarge-angledeflectionscomparedwith thatofelectronsorpositrons.Indeed,collisions,inwhichparticlescanlose 4 me M fractionoftheirenergyasamaximum, cannotincuranysubstantialscatteringangle.TheaveragescatteringanglebytheCoulombforcesfromnucleialsohasa downwardtrendinproportiontothesquareoftheparticlemassmultipliedbythescreeningeffectfromsurrounding electrons.
Aquasi-straighttrack,thereducedmeanfreepath(reciprocaltothenumberofcollisionsperunitlength
in totalduringtheparticlepassage),andabetter-definedenergylossratepercollisionenabletherangetobepredictedwitha verygoodaccuracyusingsimpleanalyticalexpressions.PlotsinFigure1.2.9presentrangesof α-particlesandprotonsin comparisonwiththeelectronrangesforSi(a)andGe(b)absorbers.Similarplotsfortheseparticlesindetector-sensitive volumesmadeofothermaterialscanbeevaluatedfollowingtheempiricalBragg–Kleemanrule[15]:
where Rdet, ρdet,and Adet denotetherange,density,andatomicweightofadetectormediumofinterestand RSi, ρSi,and ASi aretherespectivevaluesforSi.Inthecaseofcompoundmaterial, Adet denotesaneffectiveatomicweight,whichis definedas
where η1 and η2 aretheatomicfractionsofchemicalelementsinthecompoundwithatomicweights
Somelow-energyparticleschargedpositively(includingthosethatlosttheirenergyincollisions)canattractfreeelectrons fromthemediumforsomeperiodoftimeand,thereby,usingtheirscreeningeffectpropagatemuchdeeperintheabsorber asaquasi-neutralparticle.Thismayresultinthechargecollectiondeficitifparticlesleavetheinteractionvolumebeforethe thermalizationprocessiscompleted.Thephenomenonisparticularlypronouncedinthenormalmetalandsuperconductingabsorbers.Insemiconductordetectors,interactionvolumesaredepletedoffreecarriers.Therefore,positivechargeparticlescanonlyattractelectronsunboundedasaresultoftheirinelasticscatteringevents.Thismeansthatthephenomenon isinfluencedbytheenergyofincomingparticlesandthebeamintensity.
1.3PrimaryInteractionsofX-and γ-RayPhotonswithSolid-StateAbsorbers
Thedualnatureofmatterbecomesparticularlyevidentwhenwedealwiththelight.Infrared,visiblelight,ultraviolet,X-rays, and γ-raysdemonstratewavelikephenomenasuchasinterference,diffraction,andpolarization.Atthesametime,wetreat themasphotonparticles(i.e.packetsofelectromagneticwaves),toexplainthefollowingquantummechanicaleffects:
1)Thephotoelectriceffect; 2)TheComptonscattering; 3)Thepairproduction.
Theseeffectsrepresentthemajorinteractionmechanismsbetweenphotonsandabsorbermaterials.Theyalsoconstitutethe basefortheX-and γ-raydetectionmethodologies.Sincephotonshavenocharge,thelistedabovethreeeffectsinitiateindirectionizationenergycascadesbytheejectionofenergeticprimaryphotoelectrons.Afterthat,theprimaryphotoelectrons startparticipatingintheenergydown-conversionprocesssimilartotheprocessinitiatedbythelight-chargedparticlesdiscussedinSection1.2.Inthisrespect,thereisnoneedtorepeattheanalysisofthecompleteinteractionroutine.Wewillfocus primarilyontheprimarynuclearreactionmechanisms.
1.3.1PhotoelectricEffect
Thephotoelectriceffecttakesplaceattheabsorptioncollisionsbetweenincomingphotonsandtargetatoms.Atthefirst collision,photonstendtotransferalltheirenergies Ex andmomentums Mph tothetargetatomsanddisappearfromthe beam.Theabsorbedphotonenergyisthenforwardedtooneoftheboundelectrons,whereasthenucleuscaptivatesthe recoilmomentum,asshowninFigure1.3.1a.Providedthatthecondition Ex > Ej holds,theatomejectsaphotoelectron withkineticenergygivenby E e = E x E j 1 3 1 where Ej isthebindingenergyofthe jthshell.
Figure1.3.1bshowsthecaseof Ex >> Ek whentheoutgoingelectronleavestheinnerKshelloftheatoms.Thisenergetic photoelectroninitiatesasubsequentionization(orthepairbreakinginacaseofsuperconductingabsorber)energycascades. TheremainingtwodiagramsofFigure1.3.1c,dillustratethede-excitationprocessintheatominwhichtheelectronstructurerearrangesitselftooccupythelowestenergystatesavailable.ThetransitionsfromLshelltoKshellandfromMshellto LshellarefollowedbyemissionofcharacteristicX-rayswiththefollowingenergies:
ThecharacteristicX-raysmayparticipateintheirownphotoelectricinteractionsfollowedbycorrespondingdownconversionprocesses.ThismeansthataradiationdetectorexposedtoamonochromaticX-and γ-raybeamproducesan energyspectrumenrichedbymultiplepeaksfromcharacteristicX-rayemissions.Theoverallenergyofthesepeakstogether withotherartifactsdiscussedinSection1.2isborrowedfromthemaininformativepeakatthephotonenergy Ex.Toimprove measurementaccuracytheborrowedenergydeficitneedstobereturnedbacktothe Ex linebyapplyingappropriatecorrectionfactorsderived,e.g.,fromtheMonteCarlomodeling.
Thechainofpossiblephotoelectriceventslastsuntilenergiesofremainingphotonsandenergeticquasiparticlesbecome insufficienttofreeinnershellvalenceelectrons.Ifthephotoelectriceffectistheonlyprimaryinteractionmechanism
1.3PrimaryInteractionsofX-and γ -RayPhotonswithSolid-StateAbsorbers
Characteristic
Characteristic
Figure1.3.1 TheshelldiagramsillustratingX-rayphotoninteractionwiththetargetatomthroughthephotoelectriceffect.(a)The photontransferringallitsenergytothek-shellelectron;(b)theelectronwithkineticenergy Ex Ek vacatesthek-shelloftheatom;(cand d)theelectronstructurerearrangementwiththecharacteristicX-raysemissions.
betweenphotonsandthemedium,thecombinedenergyof photoelectronsapproachesveryclosetotheenergyofincomingparticles,i.e.
e Σ ≈ E x 1 3 4
Equation(1.3.4)representsthenecessaryconditionthatdefines theaccuracyofsolid-stateradiationdetectorswithregardto X-and γ-raymeasurements[16].AgenericexampleofacorrectedphotoelectricspectrumispresentedinFigure1.3.2. Moreinformationonmathematicalmodelingofthephoton interactionwithmattercanbefoundinliteraturediscussing theX-rayprobeanalysistechniquesanddescriptionofthe specializedsimulationsoftware,e.g.GEANT4.
1.3.2ComptonScattering
ThephotoelectriceffectismorecommonforrelativelylowenergyX-rays.InthemiddleoftheX-and γ-rayenergyrange, someoftheincomingphotonsrelaxviainelasticscatterings fromouterlooselycoupledatomicelectrons.ThephenomenonisnamedafterArthurH.Comptonwhowasthefirst toobserveandexplainitin1923[17].Figure1.3.3illustrates theessenceoftheComptonscatteringmechanism. Letusassumethatanelectronwithamass me restsjust beforetheinteractionevent.Then,anincidentphotonwith energy Eγ andmomentum kγ collideswiththeelectron.This resultsintheelectronrecoilingwithanenergy Ee and momentum ke andthephotonscatteredintoanewstatewith
Counts
Figure1.3.2 Anenergyspectrumrepresentingthecorrected primaryphotoelectriceffect.
Figure1.3.3 AschematicrepresentationoftheCompton scattering.
energy Ep andmomentum kp.Theconservationlawofthe energyandmomentumgivenby
suggestthatthephotonisscatteredwithareducedenergy Ep < Eγ orincreasedwavelength λp > λγ (accordingtothe Planckrelation: E = h c λ,with h beingthePlanckconstant and c isthelightvelocity).Comptondiscoveredthatthe wavelengthshiftcorrespondsto
where λc = h me c istheComptonwavelength.
Combiningallthreeequations(1.3.5)–(1.3.7),thekinetic energyoftherecoilelectrontakesthefollowingform:
Counts
Thescatteringangle θ canbeofanyvaluefrom0to π .Therefore,asolid-statedetectorexposedtomiddlerangeX-and
-rays willyieldanenergyspectrumthatshouldlooklikeacontinuumextendingfromthezerolinetotheComptonedge. Figure1.3.4givesanillustrationoftheenergyspectrumincludingtheComptoncontinuum.TheComptonedgecorresponds tothemaximumenergyimpartedfromthebackscatteredincomingphotontotherecoilelectron(θ = π ),whichisgivenby
UnlesstheComptonscatteringisinformative(i.e.usedasadetectionmethodcharacterizingpropertiesofincomingparticles),ittendstodegradethedetectorperformance.Thecontinuumcanmasklow-intensitypeaksintherangewhereitis pronouncedandhaveasignificantimpactontheintensitiesandpositionsofphotoelectricpeaksborrowingenergyfrom down-conversionchannelsthatotherwisewouldcontributetotheintensityofphotoelectriclinesinthehistogram.Onthe positiveside,theComptonscatteringmechanismiswellunderstoodandquantifiedtoveryhighaccuracy.Modernquantum microscopicmodelsarecapabletodeliverasetofhighprecisionspectrumcorrectionfactorstoreduceitsinfluenceonthe finalmeasurementresultifnecessary.
ItisworthmentioningthatingeneraltheComptoneffectmaymanifestitselfinamoresophisticatedformcomparedwith theclassicalrepresentationbyEq.(1.3.7).Dependingonthematerial,thespectrumcontinuumcantakevariousshapesand containmultiplepeaksoriginatingfromassociatedsubtleeffects.Wewillnotgodeeplyintothistopic.Numerousdedicated papersandmanuscriptsdiscussitingreatdetail.Forexample,interestedreaderscanfindagoodoverviewofthesubject in[18,19].
Thedesignandsimulationtoolsshouldalsoincorporatemoreinclusivequantummechanicalmodelscomparedto Eq.(1.3.7).Foragoodaccuracyoftheanalysis,itwouldbeusefultotakeintoconsiderationmorerealisticinitialconditions, forinstance,thefactthattheatomelectronsarenotrestingbeforeandduringtheinteractionevents.Incomingphotons interactratherwiththeplasmaelectroncloudaroundthetargetatoms(quasiparticles)ratherthanwithstandaloneelectrons.Thismeansthatexcitedquasiparticlescanalsotransfertheirkineticenergytothelow-energyphotonsandboosttheir energylevels.Inthiscase,therightsideofEq.(1.3.7)takestheoppositesignimplyingthatthewavelengthoftheoutgoing photonbecomesshorter.Thisphenomenonisalsoknownas theinverseComptonscattering.Forinstance,infraredphotons incollisionswithrelativisticelectronscanbeboostedwellbackintotheX-rayregion.TheinverseComptonscatteringalso influencesthedetectorperformance.Someoftheinteractionelectronswith E > Eg restoreionization(pairbreaking)capabilityoflowenergyphotons,whichotherwisewould “quietly” relaxthroughthephononsystem.Theseboostedphotonsadd countstothebackgroundcontinuuminawaysimilartobremsstrahlung.
1.3.3ThePairProduction
Thepairproductionreferstothetransformationofphotonsintotheelectron–positronpairsintheCoulombfieldofnuclei. ThetransformationisillustratedinFigure1.3.5.
Photoelectric
Figure1.3.4 TheComptoncontinuumontheenergyspectrum diagram.
1.3PrimaryInteractionsofX-and
Theminimumenergyrequiredforthiseffecttotakeplaceisderived fromthemassandenergyconservationlaw,i.e.
where mn isthemassofthetargetnucleus,2mec 2 isthecombinedrest mass–energyoftheelectron–positronpair.Inpractice, mn me,which enablesthecondition(1.3.10)toberewritteninasimplifiedformas
Theexcessenergy Eγ 2mec 2 isdividedequallybetweenthefreedelectronandpositron.Withthisenergy,bothparticles,iftheystayinsidethe detectorabsorbervolume,continueparticipatingintherelaxationprocesssimilartolight-chargedparticlesasdiscussedinSection1.2.
Thelifetimeofthepositronisquiteshort.Within1nsitisusuallycapturedbyelectronclouds.Twoanti-particlesannihilatewiththeemission oftwo mec 2 photonsinoppositedirections.TheprocessoftheannihilationandreconversionintophotonsisillustratedinFigure1.3.6a,b, respectively.Theannihilationphotonseitherrelaxintheinteraction withmediumelectronsbytheComptonandphotoelectricprocesses orescapefromthedetectionvolumealtogether.Aspectralresponse exampleoftheradiationdetectorexposedtohigh-energy γ-rayphotons ispresentedinFigure1.3.7.Itcontainsthreephotoelectricpeaks.The singleescapeanddoubleescapepeakscorrespondtocaseswhenone andbothrespectiveannihilationphotonsdepositedalltheirenergies inthedetectionvolumethroughthephotoelectricnuclearreaction.
1.3.4AttenuationofPhotonRadiationinSolid-State DetectorAbsorbers
Letusconsideracasewhentheparallelbeamofmonoenergeticphotons penetratesadetectorabsorberofathickness, x,asshowninFigure1.3.8. Afractionofincomingphotonsinteractswiththemedium,sothatthe intensityofthetransmittedbeam, I,issmallerthantheintensityof theincidentbeam, I0.Iftheenergyabsorptionoccursbyeitherthephotoelectriceffectorthepairproduction,photonstransferalltheirenergy anddisappearfromthebeamontheirfirstinteraction.Inthiscase, Eq.(1.1.2)describesthetransmissionadequately.Itcanberewritten intermsofbeamintensitiesasfollows:
where
Figure1.3.5 Thepairproductionprocess.An incomingphotonistransformedintotheelectron–positronpairintheCoulombfieldofthenucleus. (a) (b)
Figure1.3.6 Theprocessofelectron–positron annihilation(a)andreconversionintophotons(b).
isthetotallinearattenuationcoefficient.Bydefinition,thetotallinearattenuationcoefficientcombinestheindividualattenuationcoefficientsforphotoelectric,pairproductionprocesses,andtheComptonscattering,i.e.
Indoingso,however,oneneedstorememberthattheComptonscatteringdoesnotremoveaphotonfromthebeamina singlecollision.Similartochargedparticles,photonsrelaxingviatheComptonmechanismalonewouldhavetobecharacterizedbytherangefunctionsimilartothechargedparticletreatment.
Theinteractionofparticleswithmatterisoftentabulatedintermsoftheindividualortotalcrosssections.Thecross sectionisdefinedastheinteractionprobabilitypertargetatom.Itsrelationtothelinearattenuationcoefficientisgivenby
where
Σ = σ ph + σ pp + σ C, σ ph, σ pp,and σ C representindividualcrosssectionsofthephotoelectric,pairproduction, andComptonprocesses,respectively.
1.4DetectionofNeutronswithSolidStateRadiationSensors
Theneutronisafundamentalparticlewithamassof1 amu,whichequalsapproximatelytotherestmassof 1839electrons.Theparticleiselectricallyneutraland, therefore,notcapabletodirectlyionizeatomsvialongrangeCoulombforces.Instead,penetratingthematter,it undergoesshort-rangeinteractionswithatomicnuclei (nuclearreactions).Fornon-relativisticneutrons,onecan distinguishthreemajortypesofnuclearreactions.These areasfollows:
1)Theabsorptionofneutronsbynuclei; 2)Theelasticscatteringsfromnuclei; 3)Theinelasticscatterings.
Inthescatteringcollisions,theneutronimpartsonlya fractionofitsenergyand,thus,mayinteractwithmultiple targetnucleionitstrack.Thenucleusconvertstheexcitationenergyreceivedfromtheneutronintosomeformof radiativeemission,e.g.X-ray, γ-rayphotons,chargedparticle.Ifthethicknessoftheabsorberpermits,thereaction chainlastsuntiltheparticleeitherhasbeencapturedbya nucleusordisintegratesintoaproton, β -particle,andneutrinoattheendofitslifetime.
Thetotalcrosssection(ortheprobabilityforparticlesto interactwiththedetectorsensitivevolume)includesall crosssectionsresponsibleforeachnuclearreactionmechanism,i.e.[4]
Figure1.3.7 Atypicalspectralresponseofradiationdetectors exposedtohighenergyphotonsinitiatingthepairproduction events.Thehistogramcontainsthreephotoelectricpeaks.The singleescapeanddoubleescapepeakscorrespondtocaseswhen oneandbothannihilationphotonsescapefromthedetection volumewithoutinteractions,respectively.
Interaction volume x
Figure1.3.8 Theinteractionofaphotonradiationbeamwiththe solid-stateabsorber. I0 and I representtheincomingandtransmitted beamcurrents.
Itdependsstronglyonthekineticenergy, Ek (orvelocity, v)ofneutronsinthebeam.Forinstance,theabsorptionprobability increasesinproportiontothetimedurationitspendsinthecloseproximity(~10 15 m)withnuclei,i.e.
Thistypeofnuclearreactionislikelytobedominatingfor slow neutronswith Ek <1eV,while fast neutronswith Ek >100keVtendtotransfertheirenergypredominantlyviascatteringmechanismsuntiltheybecome moderated toan energy Ek <1eV.
Figure1.4.1presentsamorecompleteclassificationofpossiblenuclearreactiontypesbetweenneutronsandnuclei.The fourmechanismsaddedtotheabsorptionandelastic/inelasticscatteringsmakesignificantcontributionsforhighenergy (relativistic)particles.Wewillnotbediscussingtheminthismanuscript.Interestedreaderscanfinddetailedinformationin specializedliterature,e.g.[20].