Distributed Acoustic Sensing Yingping Li Visit to download the full and correct content document: https://ebookmass.com/product/distributed-acoustic-sensing-in-geophysics-methodsand-applications-yingping-li/
More products digital (pdf, epub, mobi) instant download maybe you interests ...
Techniques and methods in urban remote sensing Weng
https://ebookmass.com/product/techniques-and-methods-in-urbanremote-sensing-weng/
Tactile Sensing, Skill Learning, and Robotic Dexterous Manipulation Qiang Li
https://ebookmass.com/product/tactile-sensing-skill-learning-androbotic-dexterous-manipulation-qiang-li/
System Reliability Assessment and Optimization : Methods and Applications 1st Edition Yan-Fu Li & Enrico Zio
https://ebookmass.com/product/system-reliability-assessment-andoptimization-methods-and-applications-1st-edition-yan-fu-lienrico-zio/
Gas Injection Methods Zhaomin Li
https://ebookmass.com/product/gas-injection-methods-zhaomin-li/
Systems programming: designing and developing distributed applications Anthony
https://ebookmass.com/product/systems-programming-designing-anddeveloping-distributed-applications-anthony/
Emerging 2D Materials and Devices for the Internet of Things: Information, Sensing and Energy Applications (Micro and Nano Technologies) 1st Edition Li Tao (Editor)
https://ebookmass.com/product/emerging-2d-materials-and-devicesfor-the-internet-of-things-information-sensing-and-energyapplications-micro-and-nano-technologies-1st-edition-li-taoeditor/
Hyperspectral Remote Sensing: Theory and Applications Prem Chandra Pandey
https://ebookmass.com/product/hyperspectral-remote-sensingtheory-and-applications-prem-chandra-pandey/
Atmospheric Remote Sensing: Principles and Applications Abhay Kumar Singh
https://ebookmass.com/product/atmospheric-remote-sensingprinciples-and-applications-abhay-kumar-singh/
Basic Principles of Induction Logging. Electromagnetic Methods in Borehole Geophysics 1st Edition Edition Alexander Kaufman And Gregory Itskovich (Auth.)
https://ebookmass.com/product/basic-principles-of-inductionlogging-electromagnetic-methods-in-borehole-geophysics-1stedition-edition-alexander-kaufman-and-gregory-itskovich-auth/
GeophysicalMonographSeries 212TheEarlyEarth:AccretionandDifferentiation JamesBadroand MichaelWalter(Eds.)
213GlobalVegetationDynamics:ConceptsandApplicationsinthe MC1Model DominiqueBacheletandDavidTurner(Eds.)
214ExtremeEvents:Observations,ModelingandEconomics Mario Chavez,MichaelGhil,andJaimeUrrutia-Fucugauchi(Eds.)
215AuroralDynamicsandSpaceWeather YongliangZhangand LarryPaxton(Eds.)
216Low-FrequencyWavesinSpacePlasmas AndreasKeiling,DongHunLee,andValeryNakariakov(Eds.)
217DeepEarth:PhysicsandChemistryoftheLowerMantleand Core HidenoriTerasakiandRebeccaA.Fischer(Eds.)
218IntegratedImagingoftheEarth:TheoryandApplications Max Moorkamp,PeterG.Lelievre,NiklasLinde,andAmirKhan(Eds.)
219PlateBoundariesandNaturalHazards JoaoDuarteandWouter Schellart(Eds.)
220IonosphericSpaceWeather:LongitudeandHemispheric DependencesandLowerAtmosphereForcing TimothyFullerRowell,EndawokeYizengaw,PatriciaH.Doherty,andSunanda Basu(Eds.)
221TerrestrialWaterCycleandClimateChangeNaturaland Human-InducedImpacts QiuhongTangandTaikanOki(Eds.)
222Magnetosphere-IonosphereCouplingintheSolarSystem CharlesR.Chappell,RobertW.Schunk,PeterM.Banks,JamesL. Burch,andRichardM.Thorne(Eds.)
223NaturalHazardUncertaintyAssessment:Modelingand DecisionSupport KarinRiley,PeterWebley,andMatthew Thompson(Eds.)
224HydrodynamicsofTime-PeriodicGroundwaterFlow:Diffusion WavesinPorousMedia JoeS.DepnerandToddC Rasmussen(Auth.)
225ActiveGlobalSeismology IbrahimCemenandYucel Yilmaz(Eds.)
226ClimateExtremes SimonWang(Ed.)
227FaultZoneDynamicProcesses MarionThomas(Ed.)
228FloodDamageSurveyandAssessment:NewInsightsfrom ResearchandPractice DanielaMolinari,SciraMenoni,and FrancescoBallio(Eds.)
229Water-Energy-FoodNexus – PrinciplesandPractices P.Abdul Salam,SangamShrestha,VishnuPrasadPandey,andAnil KAnal(Eds.)
230Dawn–DuskAsymmetriesinPlanetaryPlasmaEnvironments SteinHaaland,AndreiRounov,andColinForsyth(Eds.)
231BioenergyandLandUseChange ZhangcaiQin,UmakantMishra, andAstleyHastings(Eds.)
232MicrostructuralGeochronology:PlanetaryRecordsDownto AtomScale DesmondMoser,FernandoCorfu,JamesDarling, StevenReddy,andKimberlyTait(Eds.)
233GlobalFloodHazard:ApplicationsinModeling,Mappingand Forecasting GuySchumann,PaulD.Bates,GiuseppeT. Aronica, andHeikoApel(Eds.)
234Pre-EarthquakeProcesses:AMultidisciplinaryApproachto EarthquakePredictionStudies DimitarOuzounov,Sergey Pulinets,KatsumiHattori,andPatrickTaylor(Eds.)
235ElectricCurrentsinGeospaceandBeyond AndreasKeiling, OctavMarghitu,andMichaelWheatland(Eds.)
236QuantifyingUncertaintyinSubsurfaceSystems CelineScheidt, LewisLi,andJefCaers(Eds.)
237PetroleumEngineering MoshoodSanni(Ed.)
238GeologicalCarbonStorage:SubsurfaceSealsandCaprock Integrity StephanieVialle,JonathanAjo-Franklin,andJ.William Carey(Eds.)
239LithosphericDiscontinuities HuaiyuYuanandBarbara Romanowicz(Eds.)
240ChemostratigraphyAcrossMajorChronologicalEras AlcidesN. Sial,ClaudioGaucher,MuthuvairavasamyRamkumar,and ValderezPintoFerreira(Eds.)
241MathematicalGeoenergy:Discovery,Depletion,andRenewal PaulPukite,DennisCoyne,andDanielChallou(Eds.)
242OreDeposits:Origin,Exploration,andExploitation Sophie Decree andLaurenceRobb (Eds.)
243 KuroshioCurrent:Physical,BiogeochemicalandEcosystem Dynamics TakeyoshiNagai,HiroakiSaito,KojiSuzuki,and MotomitsuTakahashi(Eds.)
244GeomagneticallyInducedCurrentsfromtheSuntothePower Grid JenniferL.Gannon,AndreiSwidinsky,andZhonghua Xu(Eds.)
245Shale:SubsurfaceScienceandEngineering ThomasDewers, JasonHeath,andMarceloSánchez(Eds.)
246SubmarineLandslides:SubaqueousMassTransportDeposits FromOutcropstoSeismicProfiles KeiOgata,AndreaFesta,and GianAndreaPini(Eds.)
247Iceland:Tectonics,Volcanics,andGlacialFeatures TamieJ Jovanelly
248DaysideMagnetosphereInteractions QiugangZong, PhilippeEscoubet,DavidSibeck,GuanLe,and HuiZhang(Eds.)
249CarboninEarth’sInterior CraigE.Manning,Jung-FuLin,and WendyL.Mao(Eds.)
250NitrogenOverload:EnvironmentalDegradation,Ramifications, andEconomicCosts BrianG.Katz
251BiogeochemicalCycles:EcologicalDriversandEnvironmental Impact KaterinaDontsova,ZsuzsannaBalogh-Brunstad,and GaëlLeRoux(Eds.)
252SeismoelectricExploration:Theory,Experiments,and Applications NielsGrobbe,AndréRevil,ZhenyaZhu,andEvert Slob(Eds.)
253ElNiñoSouthernOscillationinaChangingClimate MichaelJ. McPhaden,AgusSantoso,andWenjuCai(Eds.)
254DynamicMagmaEvolution FrancescoVetere(Ed.)
255LargeIgneousProvinces:ADriverofGlobalEnvironmentaland BioticChanges Richard.E.Ernst,AlexanderJ.Dickson,and AndreyBekker(Eds.)
256CoastalEcosystemsinTransition:AComparativeAnalysisofthe NorthernAdriaticandChesapeakeBay ThomasC.Malone, AlenkaMalej,andJadranFaganeli(Eds.)
257Hydrogeology,ChemicalWeathering,andSoilFormation Allen Hunt,MarkusEgli,andBorisFaybishenko(Eds.)
258SolarPhysicsandSolarWind NourE.RaouafiandAngelos Vourlidas(Eds.)
259MagnetospheresintheSolarSystem RomainMaggiolo, NicolasAndré,HiroshiHasegawa,andDaniel T.Welling(Eds.)
260IonosphereDynamicsandApplications ChaosongHuangand GangLu(Eds.)
261UpperAtmosphereDynamicsandEnergetics WenbinWangand YongliangZhang(Eds.)
262SpaceWeatherEffectsandApplications AntheaJ.Coster,PhilipJ. Erickson,andLouisJ.Lanzerotti(Eds.)
263MantleConvectionandSurfaceExpressions HaukeMarquardt, MaximBallmer,SanneCottaar,andJasperKonter(Eds.)
264CrustalMagmaticSystemEvolution:Anatomy,Architecture,and Physico-ChemicalProcesses MatteoMasotta,ChristophBeier, andSilvioMollo(Eds.)
265GlobalDroughtandFlood:Observation,Modeling,and Prediction HuanWu,DennisP.Lettenmaier,QiuhongTang,and PhilipJWard(Eds.)
266MagmaRedoxGeochemistry RobertoMorettiandDanielR. Neuville(Eds.)
267WetlandCarbonandEnvironmentalManagement KenW. Krauss,ZhiliangZhu,andCamilleL.Stagg(Eds.)
268DistributedAcousticSensinginGeophysics:Methodsand Applications YingpingLi,MartinKarrenbach,andJonathanB. Ajo-Franklin(Eds.)
DistributedAcousticSensingin Geophysics MethodsandApplications YingpingLi MartinKarrenbach
JonathanB.Ajo-Franklin Editors
Thisworkisaco-publicationoftheAmericanGeophysicalUnionandJohnWiley&Sons,Inc.
Thiseditionfirstpublished2022
©2022AmericanGeophysicalUnion
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedinaretrievalsystem,ortransmittedinanyformorbyany means,electronic,mechanical,photocopying,recording,orotherwise,exceptaspermittedbylaw.Adviceonhowtoobtain permissiontoreusematerialfromthistitleisavailableathttp://www.wiley.com/go/permissions.
TherightsofYingpingLi,MartinKarrenbach,andJonathanB.Ajo-Franklintobeidentifiedastheeditorsofthisworkhavebeen assertedinaccordancewithlaw.
PublishedundertheaegisoftheAGUPublicationsCommittee
MatthewGiampoala,VicePresident,Publications CarolFrost,Chair,PublicationsCommittee
FordetailsabouttheAmericanGeophysicalUnionvisitusatwww.agu.org.
RegisteredOffice
JohnWiley&Sons,Inc.,111RiverStreet,Hoboken,NJ07030,USA
EditorialOffice 111RiverStreet,Hoboken,NJ07030,USA
Fordetailsofourglobaleditorialoffices,customerservices,andmoreinformationaboutWileyproducts,visitusatwww.wiley.com. Wileyalsopublishesitsbooksinavarietyofelectronicformatsandbyprintondemand.Somecontentthatappearsinstandardprint versionsofthisbookmaynotbeavailableinotherformats.
LimitofLiability/DisclaimerofWarranty
Whilethepublisherandauthorshaveusedtheirbesteffortsinpreparingthiswork,theymakenorepresentationsorwarrantieswith respecttotheaccuracyorcompletenessofthecontentsofthisworkandspecificallydisclaimallwarranties,includingwithout limitationanyimpliedwarrantiesofmerchantabilityorfitnessforaparticularpurpose.Nowarrantymaybecreatedorextendedby salesrepresentatives,writtensalesmaterials,orpromotionalstatementsforthiswork.Thefactthatanorganization,website,or productisreferredtointhisworkasacitationand/orpotentialsourceoffurtherinformationdoesnotmeanthatthepublisherand authorsendorsetheinformationorservicestheorganization,website,orproductmayprovideorrecommendationsitmaymake. Thisworkissoldwiththeunderstandingthatthepublisherisnotengagedinrenderingprofessionalservices.Theadviceand strategiescontainedhereinmaynotbesuitableforyoursituation.Youshouldconsultwithaspecialistwhereappropriate.Further, readersshouldbeawarethatwebsiteslistedinthisworkmayhavechangedordisappearedbetweenwhenthisworkwaswrittenand whenitisread.Neitherthepublishernortheauthorsshallbeliableforanylossofprofitoranyothercommercialdamages,including, butnotlimitedto,special,incidental,consequential,orotherdamages.
LibraryofCongressCataloging-in-PublicationData
Names:Li,Yingping,editor.|Karrenbach,Martin,editor.|Ajo-Franklin, Jonathan,editor.
Title:Distributedacousticsensingingeophysics:methodsand applications/YingpingLi,MartinKarrenbach,JonathanAjo-Franklin, editor.
Description:Firstedition.|Hoboken,NJ:Wiley-AmericanGeophysical Union,[2021]|Series:Geophysicalmonographseries|Includes bibliographicalreferences.
Identifiers:LCCN2021015330(print)|LCCN2021015331(ebook)|ISBN 9781119521792(cloth)|ISBN9781119521822(adobepdf)|ISBN 9781119521778(epub)
Subjects:LCSH:Geophysics–Methodology.|Opticalfiberdetectors.| Imagingsystemsingeophysics.|Microseisms.|Tomography.
Classification:LCCQC808.5.D572021(print)|LCCQC808.5(ebook)|DDC 681/.25–dc23
LCrecordavailableathttps://lccn.loc.gov/2021015330
LCebookrecordavailableathttps://lccn.loc.gov/2021015331
CoverDesign:Wiley
CoverImage:©JonathanAjo-Franklin
Setin10/12ptTimesNewRomanbyStraive,Pondicherry,India
10987654321
CONTENTS ListofContributors .................................................................................................................................................vii
ListofReviewers ....................................................................................................................................................xiii
Preface ....................................................................................................................................................................xv
PartIDistributedAcousticSensing(DAS)Concept,Principle,andMeasurements
1HighDefinitionSeismicandMicroseismicDataAcquisitionUsingDistributedandEngineered FiberOpticAcousticSensors ...........................................................................................................................3 SergeyShatalin,TomParker,andMahmoudFarhadiroushan
2ImportantAspectsofAcquiringDistributedAcousticSensing(DAS)DataforGeoscientists .......................33 MarkE.Willis,AndreasEllmauthaler,XiangWu,andMichelJ.LeBlanc
3DistributedMicrostructuredOpticalFiber(DMOF)BasedUltrahighSensitiveDistributedAcoustic Sensing(DAS)forBoreholeSeismicSurveys .................................................................................................45 QizhenSun,ZhijunYan,HaoLi,CunzhengFan,FanAi,WeiZhang,XiaoleiLi,DemingLiu, FeiLi,andGangYu
4DistributedAcousticSensingSystemBasedonPhase-GeneratedCarrierDemodulationAlgorithm ............57 TuanweiXu,ShengwenFeng,FangLi,LilongMa,andKaihengYang
PartIIDistributedAcousticSensing(DAS)ApplicationsinOilandGas,Geothermal, andMiningIndustries
5FieldTrialofDistributedAcousticSensinginanActiveRoom-and-PillarMine ...........................................67 XiangfangZeng,HerbertF.Wang,NealLord,DanteFratta,andThomasColeman
6OntheSurmountableLimitationsofDistributedAcousticSensing(DAS)VerticalSeismic Profiling(VSP) – DepthCalibration,Directionality,andNoise:LearningsFromFieldTrials .......................81 AlbenaMateeva,YutingDuan,DenisKiyashchenko,andJorgeLopez
7DenoisingAnalysisandProcessingMethodsofDistributedAcousticSensing(DAS)Vertical SeismicProfiling(VSP)Data ...........................................................................................................................93 Yuan-ZhongChen,Guang-MinHu,Jun-JunWu,GangYu,Yan-PengLi,Jian-HuaHuang, Shi-ZeWang,andFeiLi
8High-ResolutionShallowStructureatBradyHotSpringsUsingAmbientNoiseTomography(ANT) onaTrenchedDistributedAcousticSensing(DAS)Array ...........................................................................101 XiangfangZeng,CliffordH.Thurber,HerbertF.Wang,DanteFratta,andKurtL.Feigl
PartIIIDistributedAcousticSensing(DAS)ApplicationsinMonitoringofDeformations, Earthquakes,andMicroseismsbyFracturing
9IntroductiontoInterferometryofFiber-OpticStrainMeasurements ..........................................................113 EileenR.Martin,NathanielJ.Lindsey,JonathanB.Ajo-Franklin,andBiondoL.Biondi
10UsingTelecommunicationFiberInfrastructureforEarthquakeMonitoringandNear-Surface Characterization ...........................................................................................................................................131
BiondoL.Biondi,SiyuanYuan,EileenR.Martin,FantineHuot,andRobertG.Clapp
11ProductionDistributedTemperatureSensingversusStimulationDistributedAcousticSensing fortheMarcellusShale .................................................................................................................................149 PayamKavousiGhahfarokhi,TimothyRobertCarr,CodyWilson,andKeithanMartin
12CoalescenceMicroseismicMappingforDistributedAcousticSensing(DAS)andGeophone HybridArray:AModel-BasedFeasibilityStudy ...........................................................................................161 TakasheiMizuno,JoelLeCalvez,andDanielRaymer
PartIVDistributedAcousticSensing(DAS)ApplicationsinEnvironmental andShallowGeophysics
13ContinuousDownholeSeismicMonitoringUsingSurfaceOrbitalVibratorsandDistributed AcousticSensingattheCO2CRCOtwayProject:FieldTrialforOptimumConfiguration .........................177 JuliaCorrea,RomanPevzner,BarryM.Freifeld,MichelleRobertson,ThomasM.Daley, ToddWood,KonstantinTertyshnikov,SinemYavuz,andStanislavGlubokovskikh
14IntroductiontoDistributedAcousticSensing(DAS)ApplicationsforCharacterizationof Near-SurfaceProcesses ................................................................................................................................191
WhitneyTrainor-GuittonandThomasColeman
15SurfaceWaveImagingUsingDistributedAcousticSensingDeployedonDarkFiber:Moving BeyondHigh-FrequencyNoise .....................................................................................................................197
VerónicaRodríguezTribaldos,JonathanB.Ajo-Franklin,ShanDou,NathanielJ.Lindsey, CraigUlrich,MichelleRobertson,BarryM.Freifeld,ThomasDaley,InderMonga,andChrisTracy
16UsingDistributedAcousticSensing(DAS)forMultichannelAnalysisofSurfaceWaves(MASW) .............213 ChelseaE.Lancelle,JonathanA.Baldwin,NealLord,DanteFratta,AthenaChalari,and HerbertF.Wang
17ALiteratureReview:DistributedAcousticSensing(DAS)GeophysicalApplicationsOverthe Past20Years ................................................................................................................................................229
YingpingLi,MartinKarrenbach,andJonathanB.Ajo-Franklin
LISTOFCONTRIBUTORS FanAi
SchoolofOpticalandElectronicInformation NationalEngineeringLaboratoryforNextGeneration InternetAccessSystem HuazhongUniversityofScienceandTechnology Wuhan,China
JonathanB.Ajo-Franklin DepartmentofEarth,EnvironmentalandPlanetary Sciences RiceUniversity Houston,Texas,USA and EnergyGeosciencesDivision LawrenceBerkeleyNationalLaboratory Berkeley,California,USA
JonathanA.Baldwin U.S.ArmyCorpsofEngineers Washington,DistrictofColumbia,USA
BiondoL.Biondi DepartmentofGeophysics StanfordUniversity Stanford,California,USA and InstituteforComputationalandMathematical Engineering Stanford,California,USA
JoelLeCalvez Schlumberger Houston,Texas,USA
TimothyRobertCarr DepartmentofGeologyandGeography WestVirginiaUniversity Morgantown,WestVirginia,USA
AthenaChalari SilixaLtd. Elstree,UK
Yuan-ZhongChen SchoolofInformationandCommunicationEngineering UniversityofElectronicScienceandTechnology ofChina Chengdu,China and BGPInc. ChinaNationalPetroleumCorporation Zhuozhou,China
RobertG.Clapp DepartmentofGeophysics
StanfordUniversity Stanford,California,USA
ThomasColeman SilixaLLC., Missoula,Montana,USA
JuliaCorrea EnergyGeosciencesDivision LawrenceBerkeleyNationalLaboratory Berkeley,California,USA and CentreforExplorationGeophysics CurtinUniversity Perth,Australia and CO2CRCLimited Melbourne,Australia
ThomasM.Daley EnergyGeosciencesDivision LawrenceBerkeleyNationalLaboratory Berkeley,California,USA
ShanDou VisierInc. Vancouver,BritishColumbia,Canada
YutingDuan ShellTechnologyCenter Houston,Texas,USA
AndreasEllmauthaler Halliburton Houston,Texas,USA
CunzhengFan SchoolofOpticalandElectronicInformation NationalEngineeringLaboratoryforNextGeneration InternetAccessSystem HuazhongUniversityofScienceandTechnology Wuhan,China
MahmoudFarhadiroushan SilixaLtd. Elstree,UK
KurtL.Feigl DepartmentofGeoscience UniversityofWisconsin–Madison Madison,Wisconsin,USA
ShengwenFeng KeyLaboratoriesofTransducerTechnology InstituteofSemiconductors ChineseAcademyofSciences Beijing,China and CollegeofMaterialsScienceandOpto-Electronic Technology UniversityofChineseAcademyofSciences Beijing,China
DanteFratta DepartmentofCivilandEnvironmentalEngineering UniversityofWisconsin–Madison Madison,Wisconsin,USA
BarryM.Freifeld ClassVISolutionsInc. Oakland,California,USA
StanislavGlubokovskikh CentreforExplorationGeophysics CurtinUniversity Perth,Australia and CO2CRCLimited Melbourne,Australia
Guang-MinHu SchoolofInformationandCommunicationEngineering UniversityofElectronicScienceandTechnology ofChina Chengdu,China
Jian-HuaHuang BGPInc. ChinaNationalPetroleumCorporation Zhuozhou,China
FantineHuot DepartmentofGeophysics StanfordUniversity Stanford,California,USA
PayamKavousiGhahfarokhi DepartmentofGeologyandGeography WestVirginiaUniversity Morgantown,WestVirginia,USA
MartinKarrenbach OptaSenseInc.(ALUNACompany) Brea,California,USA
DenisKiyashchenko ShellTechnologyCenter Houston,Texas,USA
ChelseaE.Lancelle DepartmentofCivilandEnvironmentalEngineering UniversityofWisconsin–Platteville Platteville,Wisconsin,USA
MichelJ.LeBlanc Halliburton Houston,Texas,USA
FangLi KeyLaboratoriesofTransducerTechnology InstituteofSemiconductors ChineseAcademyofSciences Beijing,China and CollegeofMaterialsScienceandOpto-Electronic Technology UniversityofChineseAcademyofSciences Beijing,China
FeiLi BGPInc. ChinaNationalPetroleumCorporation Zhuozhou,China
HaoLi SchoolofOpticalandElectronicInformation NationalEngineeringLaboratoryforNextGeneration InternetAccessSystem HuazhongUniversityofScienceandTechnology Wuhan,China
XiaoleiLi OVLINKInc. Wuhan,China
Yan-PengLi BGPInc. ChinaNationalPetroleumCorporation Zhuozhou,China
YingpingLi BlueSkyDas(formerlyShell) Houston,Texas,USA
NathanielJ.Lindsey FiberSense Sydney,Australia
DemingLiu SchoolofOpticalandElectronicInformation NationalEngineeringLaboratoryforNextGeneration InternetAccessSystem HuazhongUniversityofScienceandTechnology Wuhan,China
JorgeLopez ShellBrasilPetróleoLtda. RiodeJaneiro,Brazil
NealLord DepartmentofGeoscience UniversityofWisconsin–Madison Madison,Wisconsin,USA
LilongMa KeyLaboratoriesofTransducerTechnology InstituteofSemiconductors ChineseAcademyofSciences Beijing,China and CollegeofMaterialsScienceandOpto-Electronic Technology UniversityofChineseAcademyofSciences Beijing,China
EileenR.Martin DepartmentofMathematics VirginiaPolytechnicInstituteandStateUniversity Blacksburg,Virginia,USA
KeithanMartin DepartmentofGeologyandGeography WestVirginiaUniversity Morgantown,WestVirginia,USA
AlbenaMateeva ShellTechnologyCenter Houston,Texas,USA
TakashiMizuno Schlumberger Houston,Texas,USA
InderMonga EnergySciencesNetwork LawrenceBerkeleyNationalLaboratory Berkeley,California,USA
TomParker SilixaLtd. Elstree,UK
RomanPevzner CentreforExplorationGeophysics CurtinUniversity Perth,Australia and CO2CRCLimited Melbourne,Australia
DanielRaymer Schlumberger Houston,Texas,USA
MichelleRobertson EnergyGeosciencesDivision LawrenceBerkeleyNationalLaboratory Berkeley,California,USA
VerónicaRodríguezTribaldos EnergyGeosciencesDivision LawrenceBerkeleyNationalLaboratory Berkeley,California,USA
SergeyShatalin SilixaLtd. Elstree,UK
QizhenSun SchoolofOpticalandElectronicInformation NationalEngineeringLaboratoryforNextGeneration InternetAccessSystem HuazhongUniversityofScienceandTechnology Wuhan,China
KonstantinTertyshnikov CentreforExplorationGeophysics CurtinUniversity Perth,Australia and
CO2CRCLimited Melbourne,Australia
CliffordH.Thurber DepartmentofGeoscience UniversityofWisconsin–Madison Madison,Wisconsin,USA
ChrisTracy EnergySciencesNetwork LawrenceBerkeleyNationalLaboratory Berkeley,California,USA
WhitneyTrainor-Guitton DepartmentofGeophysics ColoradoSchoolofMines Golden,Colorado,USA and
WTeamGeosolutions TwinFalls,Idaho,USA
CraigUlrich EnergyGeosciencesDivision LawrenceBerkeleyNationalLaboratory Berkeley,California,USA
HerbertF.Wang DepartmentofGeoscience UniversityofWisconsin–Madison Madison,Wisconsin,USA
Shi-ZeWang BGPInc.
ChinaNationalPetroleumCorporation Zhuozhou,China
MarkE.Willis Halliburton Houston,Texas,USA
CodyWilson DepartmentofGeologyandGeography WestVirginiaUniversity Morgantown,WestVirginia,USA
ToddWood EnergyGeosciencesDivision LawrenceBerkeleyNationalLaboratory Berkeley,California,USA
Jun-JunWu BGPInc. ChinaNationalPetroleumCorporation Zhuozhou,China
XiangWu HalliburtonFarEastPte.Ltd. Singapore
TuanweiXu KeyLaboratoriesofTransducerTechnology InstituteofSemiconductors ChineseAcademyofSciences Beijing,China and CollegeofMaterialsScienceandOpto-Electronic Technology UniversityofChineseAcademyofSciences Beijing,China
ZhijunYan SchoolofOpticalandElectronicInformation NationalEngineeringLaboratoryforNextGeneration InternetAccessSystem HuazhongUniversityofScienceandTechnology Wuhan,China
KaihengYang
KeyLaboratoriesofTransducerTechnology InstituteofSemiconductors ChineseAcademyofSciences Beijing,China and CollegeofMaterialsScienceandOpto-Electronic Technology UniversityofChineseAcademyofSciences Beijing,China
SinemYavuz CentreforExplorationGeophysics CurtinUniversity Perth,Australia and CO2CRCLimited Melbourne,Australia
GangYu BGPInc. ChinaNationalPetroleumCorporation Zhuozhou,China and SchoolofInformationandCommunicationEngineering UniversityofElectronicScienceandTechnology ofChina Chengdu,China
SiyuanYuan DepartmentofGeophysics StanfordUniversity Stanford,California,USA
XiangfangZeng StateKeyLaboratoryofGeodesyandEarth’s Dynamics InnovationAcademyforPrecision MeasurementScienceandTechnology ChineseAcademyofSciences Wuhan,China and DepartmentofGeoscience UniversityofWisconsin–Madison Madison,Wisconsin,USA
WeiZhang SchoolofOpticalandElectronicInformation NationalEngineeringLaboratoryforNextGeneration InternetAccessSystem HuazhongUniversityofScienceandTechnology Wuhan,China
LISTOFREVIEWERS RezaBarati
MattBecker
GaryBinder
BiondoL.Biondi
StefanBuske
DongjieCheng
FengCheng
SteveCole
JuliaCorrea
ThomasM.Daley
TimothyDean
YutingDuan
MahmoudFarhadiroushan
BarryM.Freifeld
AndrewGreenwood
AlirezaHaghighat
GeJin
JohnMichaelKendall
HunterKnox
IvanLimChenNing
NathanielJ.Lindsey
MinLou
LinquingLuo
StefanLüth
EileenR.Martin
RobertMellors
KhalidMiah
DouglasMiller
TakashiMizuno
GerritOlivier
RomanPevzner
MichelleRobertson
VerónicaRodríguezTribaldos
BillRoggenthen
BaishaliRoy
AliSayed
AlirezaShahkarami
RobertStewart
AlekseiTitov
WhitneyTrainor-Guitton
MilovanUrosevic
GuchangWang
HerbertF.Wang
ErikWestman
EthanWilliams
MarkE.Willis
XiangfangZeng
GeZhan
ZhongwenZhan
HaijiangZhang
RanZhou
DingZhu
TieyuanZhu
PREFACE Distributedacousticsensing(DAS)systemsareoptoelectronicinstrumentsthatmeasureacousticinteractions (distributedstrainorstrainrate)alongthelengthofa fiber-opticsensingcable.DASobservationsystemscan recordsoundandvibrationsignalsalongseveraltensof kilometersofsensingopticalfiberwithfinespatial resolution(1–10m)andoverawidefrequencyrange (frommillihertztotensofkilohertz).DASprovidesa largesensingapertureforacquiringhigh-resolution acousticdatainbothtimeandspacedomains.TheadvantagesofDAStechnologyhaveenableditsrapidadoption acrossarangeofapplications,includinggeophysics geohydrology,environmentalmonitoring,geotechnical andcivilengineering(railroad,tunnel,andbridgemonitoring),hazardmitigationandprevention,andsafety andsecurityfields.
ThismonographfocusesonvariousDASapplications ingeophysics.TheuseofDASintheoil,gas,geothermal, andminingindustriesforhigh-resolutionboreholeand surfaceseismicimaging,andmicroseismicmonitoring forhydraulicfractureshasacceleratedwithimprovements inthesensitivityofDASinstruments,advancesinrealtimebigdataprocessing,andflexibleandeconomic deploymentoffiber-opticsensingcables.Thereisalso growinginterestinusingDASforcriticalgeophysical infrastructureapplications,suchasearthquakeand near-surfacepassiveseismicanalysis,includingthedevelopmentoftailoredornovelnumericaltechniques.This bookaimstoengageboththescientificandindustrial communitiestosharetheirknowledgeandexperiences ofusingDASfornovelgeophysicalapplications.
Theoriginofthisbookwasthe2017American GeophysicalUnion(AGU)FallMeeting,whenscientists andengineersfrombothindustryandacademiagathered inNewOrleanstopresenttheirfantasticresearchoutcomes onDASinstrumentationsandapplicationsingeophysics andseismology.AsDAStechnologieshavecontinuedto advance,moreandmoresuccessfulgeophysicalDAS applicationshavebeenreportedandpublishedindifferent geophysicalandseismologicaljournals,abstracts,andproceedingsoftechnicalconferences,suchastheAGU,the SocietyofExplorationGeophysicists(SEG),theEuropean AssociationofGeoscientistsandEngineers(EAGE),the SocietyofPetroleumEngineers(SPE),andtheSeismologicalSocietyofAmerica(SSA).However,fewDASbooks areavailableonDASprinciples,instrumentation,andgeophysicalapplications.ManyattendeesattheDASsessions atthe2017AGUFallMeetingexpressedthattherewasa
needforabookonDASgeophysicalapplications.Wehad interestingdiscussionswithmanyscientistsandengineers workingonthefrontierofDASgeophysicalapplications aboutthepotentialforabook.Wespeciallyrecognize BiondoL.Biondi,ThomasM.Daley,WilliamEllsworth, MahmoudFarhadiroushan,BarryM.Freifeld,Albena Mateeva,RobertMellors,CliffordH.Thurber,Herbert Wang,andMarkE.Willis,aswellasmanyothersfortheir encouragement.
Duringthe2017AGUFallMeetinginNewOrleans, wefortunatelygotanopportunitytomeetwiththe AGUBooksEditor,Dr.Bose,whowasalreadyaware ofthisrapidlygrowingscientificfield.Wediscusseda potentialbookonDASgeophysicalapplications,and shewasverysupportiveandinvitedustosubmitabook proposalforanAGUmonograph.Withnosurprise,this DASbookproposalreceivedverypositivecommentsand constructivesuggestionsfromallreviewers.Several reviewersalsoaskedforanopportunitytosubmittheir owncontributionstothismonograph.Wearegrateful tothoseanonymousreviewersofthebookproposalfor theirpositivecommentsandconstructivesuggestionsthat ledthisbooktobeinitiated.
Thismonographisorganizedintofourparts.PartI startswithprinciplesofDASmeasurementsandinstruments.DASinterrogationunitstransmitapulseoflaser lightintothefiber.Asthispulseoflighttravelsdown thefiber,interactionswithinthefiberresultinlightreflectionsknownasbackscatter(Rayleighscattering).Backscattersaredeterminedbytinystraineventswithinthe fiber,whichinturnarecausedbylocalizedacoustic energy.Thisbackscatteredlighttravelsbackupthefiber towardtheinterrogationunitwhereitissampled.PartII introducesvariousDASapplicationsintheoilandgas, geothermal,andminingindustries.PartIIIlooksat DASapplicationsinseismicmonitoring.DASmicroseismicmonitoringofhydraulicfracturingisanindustry applicationbutwithpassiveseismicsources.ThemicroseismicDASmethodhasbeenshowntohavesufficient sensitivitytorecordverysmallmagnitudemicroearthquakeswithDASdeployedinboreholes.Microseismic DASsystemscanbenaturallyextendedtomonitoringlargerearthquakeactivity,andslowdeformationofEarth’ s structurewithlarge-scalefiber-opticnetworks.PartIV discussesDASenvironmentalandshallowgeophysical applicationssuchasgeologicalcarbondioxidesequestration.Thefinalchapterpresentsareviewoffiberoptical sensingapplicationsingeophysicsincludinghistorical
developmentsandrecentadvances.Thelistofover900literaturereferencesofDASandrelatedtechnologieswill benefitreaders,especiallynewcomerswhohavejust steppedintothisfast-growingfield.
WewouldliketothanktheAGUBooksEditorial Boardforsupportingthismonograph.Withoutthe effortsfromcontributingauthorsitwouldnothave beenpossibletoaccomplishthisproject.Wewould alsoliketothankthemanyvolunteerreviewerswho spenttremendousamountsoftimeandefforttoensure thateachchapterisofthehighestquality.WeappreciateJonathanB.Ajo-Franklin,BiondoL.Biondi, MahmoudFarhadiroushan,AlbenaMateeva,and SiyuanYuanforprovidingtheirpicturesascandidates forthebookcoverdesign.Thanksarealsoextendedto theAGUBookseditorialteamatWiley,especiallyDr. RituparnaBose,LaylaHarden,NoelMcGlinchey, VaishaliRajasekar,SangaprabhaMohan,Bobby Kilshaw,NithyaSechin,andEmilyBae,fortheir organization,management,andcoverdesign.
ThismonographwillbethefirstcomprehensivehandbookforanyoneinterestedinlearningDASprinciples andapplications.Wehopethatthebookwillhaveawide spectrumofreaders – suchasgeophysicists,seismologists, geologists,andgeoscientists;environmentalscientists;and graduateandundergraduatestudentsingeophysicsand geoscience – withacommoninterestinDASgeophysical applications.Thisbookalsoprovidesacommonplatform tothescientificandindustrycommunitiestosharestate-ofthe-artDAStechnology.
YingpingLi BlueSkyDas(formerlyShell),USA
MartinKarrenbach OptaSenseInc.(ALUNACompany),USA
JonathanB.Ajo-Franklin RiceUniversityandLawrenceBerkeley NationalLaboratory,USA
Concept,Principle,and Measurements HighDefinitionSeismicandMicroseismicDataAcquisitionUsing DistributedandEngineeredFiberOpticAcousticSensors
SergeyShatalin,TomParker,andMahmoudFarhadiroushan
ABSTRACT Thedistributedacousticsensor(DAS)offersanewversatiletoolforgeophysicalapplications.Thesystemallows seismicsignalstoberecordedalongtensofkilometersofopticalfiberandoverawidefrequencyrange.Inthis chapterweintroducetheconceptofDASandderiveanexpressionforthesystemresponsebymodelingthe superpositionofthecoherentbackscatterfieldsalongthefiber.Expressionsarederivedforconvertingtheoptical phasetostrainrateandequivalentparticlemotion.WediscussDASsignalprocessinganddenoisingmethodsto dealwiththerandomnatureoftheRayleighscattersignalandtofurtherimprovedynamicrangeandsensitivity. NextweconsiderDASparameterssuchasspatialresolution,gaugelengthanddirectionalityincomparisonwith geophones.WepresentsomefieldtrialresultsthatdemonstratethebenefitsoftheDASforverticalseismic profilingandmicroseismicdetection.FinallywediscussthefundamentalsensitivitylimitofDAS.Weconsider howthescatteringpropertiesofconventionalfibercanbeengineeredtodeliverastep-changeDASperformance, beyondthatofconventionalgeophonesandseismometers.Theoreticalfindingsareillustratedbythefielddata examples,includinglow-frequencystrainmonitoringandmicroseismicdetection.
1.1.DISTRIBUTEDACOUSTICSENSOR(DAS) PRINCIPLESANDMEASUREMENTS Inthischapter,weconsidertheprinciplesandperformanceofdistributedandprecisionengineeredfiberoptic acousticsensorsforgeophysicalapplications(Hartog etal.,2013;Parkeretal.,2014).Inparticular,system paramete rs such asspatialresolution,dynamicrange,sensitivity,anddirectionalityareexaminedforseismicand microseismicmeasurements.
Inthisfirstsection,weconsiderthemeasurement principle ofDAS,whichusesnaturallyoccurring
SilixaLtd.Elstree,UK
randomscattercentersalongthefiber.Weusetheterm acoustics inabroadphysicalsensehere,likeany propagationofmechanical disturbances(Lewis, 1985 ).WereviewdifferentDASsystems,including direct-intensi ty-detection a ndphase-detectionschemes, wherewederiveamathematicalrelationshipfor opticalphaserecovery.Ouraimistoexplainthenature ofthedistributedacousticsignalanddescribethe naturallimitationsforDASmeasurements.SuchinformationisneededtooptimizeDASrecordingparametersforgeophysicalapplications.Examplesof DASparameteroptimizatio nforseismicapplications canbefoundinSection1.2.Wealsopresentsome examplesofactiveandpassiveseismicfielddatain Sections1.2and1.3.
DistributedAcousticSensinginGeophysics:MethodsandApplications,GeophysicalMonograph268,FirstEdition. EditedbyYingpingLi,MartinKarrenbach,andJonathanB.Ajo-Franklin. ©2022AmericanGeophysicalUnion.Published2022byJohnWiley&Sons,Inc. DOI:10.1002/9781119521808.ch01
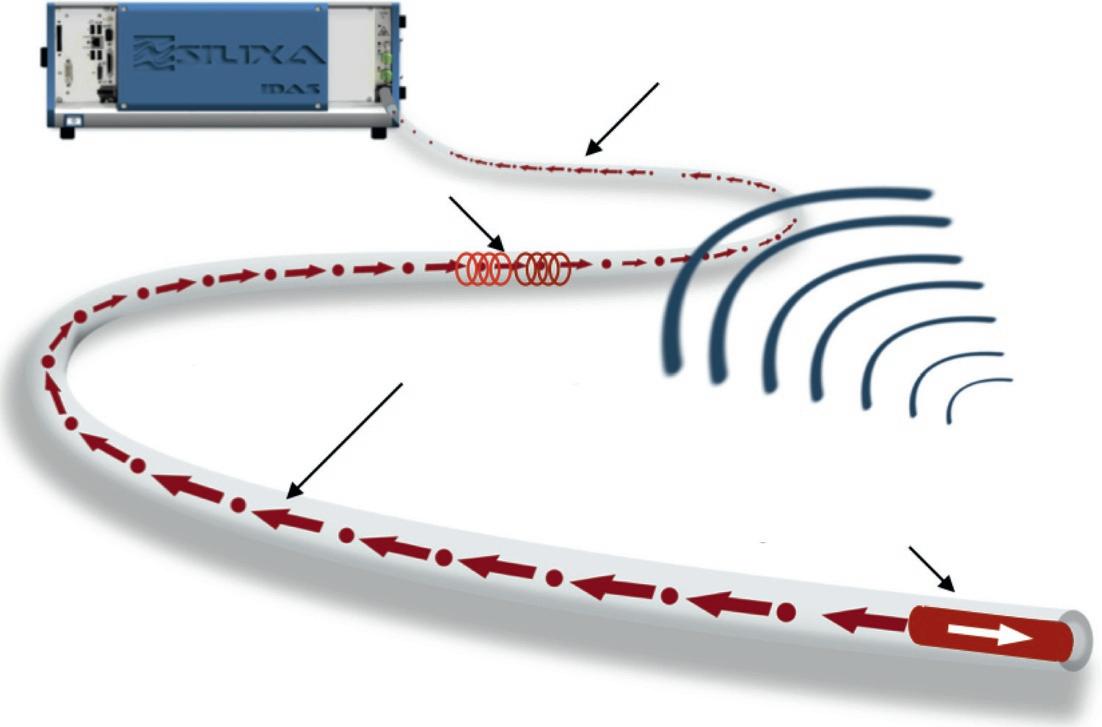
1.1.1.DASConcept Theprincipleofdistributedsensingisbasedon optical timedomainreflectometry (OTDR),asindicatedin Figure1.1.Whenalaserpulsetravelsdownanoptical fiber,atinyportionofthelightisnaturallyscattered throughRayleigh,Raman(Dakin&Culshaw,1989), andBrillouin(Parkeretal.,1998)interactionsandreturns totheoptoelectronicsensorunit.Themeasurementlocationcanbedeterminedfromthetimetakenforthelaser pulsetotraveldownthesensingfiber,andthebackscatter lighttoreturntotheoptoelectronicsensorunit.
Figure1.1 showsthebasicprincipleofDAS,wherethe sensingfiberisexcitedwithacoherentlaserpulseandthe Rayleighbackscatteredinterferencealongthefiberis detectedanddigitized.Anacousticwaveelongatesthe fiberandsochangestheopticalphaseshiftbetweenbackscattercomponentsfromtheleadingandtrailingpartsof theopticalpulse.Asaresultofinterference,theintensity ofthereturninglightchangesfrompulsetopulse.Itisalso possibletodeterminetheopticalphasetorecoveracoustic phasesotherearetwoclassesofDAS,basedonthedetectionof:(i)opticalintensityand(ii)opticalphase.Withthe intensityDAStechnique,alsoreferredtoas coherentopticaltimedomainreflectometry (COTDR),aperturbation alongthefiberisdetectedbymeasuringthechangesin thebackscatterintensityfrompulsetopulse,asindicated inFigure1.2.COTDRhasbeenusedforthedetectionof temperaturechanges(Rathodetal.,1994;Shatalinetal., 1991)andacousticvibration(Juškaitisetal.,1992;Posey
etal.,2000),alongmulti-kilometerfibercables(Juarez etal.,2005;Shatalinetal.,1998).
TheprincipleoftheCOTDRsystemcanbeunderstood byanalyzingtheradiationgeneratedbylocalizedscatter centers(Taylor&Lee,1993).Here,thecoherentscattered lightcanberepresentedastheresultoftworeflections withrandomamplitudeandphase.Whenthefiberis strained,thebackscatterintensityvariesinaccordance withthestrainrate(Figure1.2),butwithanunpredictable amplitudeandphase,whichchangesalongthefiber (Shatalinetal.,1998).Asaresult,thesignalcannotbe effectivelyaccumulatedformultipleseismicpulses:the fiberresponsetostrainishighlynonlinear,andtherefore thechangesinamplitudeandphasecannotbedirectly matchedtotheoriginalstrainaffectingthefiber.Thenext sectiondiscusseswaysofaddressingthis.Therefore, COTDRsystemsarenotthatusefulforseismic applications.
WiththephaseDAStechnique,themethodforoptical phaseanalysisisakeyfeatureofsystemdesign.Alltechniquesrelyonphasemodulationbetweenthebeginning andendofapulse,whichcanbeconsideredasadouble pulse.Suchmodulationcanbeperformedbeforeorafter lightpropagationoveropticalfiber,asindicatedin Figure1.3.Wehavelimitedourdiscussiontoschemas thathavebeenpatentedandimplementedinpractice. Inonescheme,whichissimilartothatusedformultiplexedinterferometersensors(Dakin,1990),twolaser pulseswithdifferentfrequenciesmaybesentdownthe fiber(Figure1.3a).Inthiscase,theacousticphaseshift
Light pulse propagating through the fiber
Acoustic field
Optical fiber
Optical phase shift between beginning and end of pulse
Backscattered light returning to DAS
Distributed Acoustic Sensor (DAS)
Figure1.1 Operationprincipleofdistributedacousticsensing.
Figure1.2 COTDR.
Two pulses with shifted frequencies and embedded delay
Interferometer with 3x3 coupler and embedded delay
Reference
Crickmore & Hill, 2010
Farhadiroushan et al., 2010
Hartog & Kader 2012
Farhadiroushan et al., 2010
Handerek, 2016
Crickmore & Ku, 2017
willbetransferredtoafrequencydifferenceandcanbe measuredinthephotocurrentradiofrequencydomain.
Othersolutions,suchasthatshowninFigure1.3b,containanembeddeddelaylinethatdefinesthespatialresolution.Wewillfocusouranalysisonthisclassofsystems. Anotherconfigurationusesopticalheterodyne,asshown inFigure1.3c,wherethebackscattersignaliscontinuouslymixedwithaslightlyfrequencyshiftedlocaloscillatorlaser.Inthiscase,theelongationalongthefiberis measuredbycomputingthedifferenceoftheaccumulated opticalphasebetweentwosectionsoffiber,andthemeasurementiscarriedoutatdifferentialfrequency f1 f2 Althoughthistechniqueoffersaflexiblespatialresolution,itrequiresalasersourcewithextremelyhighcoherencetoachievereasonablesignal-to-noiseratio(SNR) performanceoverseveraltensofkilometersoffiber. Thedetailsoftheheterodyneconceptarethoroughlycoveredelsewhere(Hartog,2017).Anothermethodinvolves sendingmultiplepulsesofdifferentfrequencies,eitherin seriesorfrompulsetopulse,andthencomputingthe phaseofthebackscattersignal,asindicatedin Figure1.3d.Thephasecalculationinthiscaseissimilar tofirstcase(Figure1.3a).
1.1.2.DASInterferometricOpticalResponse ThetheoreticalconceptofDASisbasedontheassumptionthattheRayleighcentershavenomicroscopic motion,buttheyare “frozen” insideglassduringmanufacture.Inthiscase,thepositionsofthecentersdepend onthemacroscopicmotionoffiberandcancoincidewith thegroundspeedaroundaburiedfiber(v).Therearetwo timescalesofrelevancetoDAS:(1)asopticalpulsetravels withspeed c,significantlyfasterthangroundmotion,this dictatesthespatialresolution;(2)seismicmotionis responsibleforinterferencechangespulsetopulse,which canbeusedtorecovertheseismicsignal.Allparameters forbothfastandslowmotionsaresummarizedinthe tableofvariablesattheendofthechapter.
Letuscalculatehowtheintensityofbackscatteredlight changeswhenasectionoffiberismovingwithspeed v(z) underaseismicwave(Figure1.4).TheRayleighcenters willmovewiththefiber,sothefrequencyofthebackscatteredlightwillexperienceaDopplershift Ω(z)proportionaltoitsspeed,likeforBrillouinscattering(Hartog, 2017).TheaimofDAScanbeconsideredasthemeasurementofDopplershiftforRayleighscatteringderived fromthedetectedphotocurrent.Thephaseshiftcanbe measuredbetweentwoseparatepointsinspace,andthen theresultantDopplershiftcanberecoveredwithspatial integration,aswillbeshownlaterinthetext.Thefirststep istoanalyzechangesinintensitybetweendifferentoptical pulsestoderivethefiberspeedinformation,whichwillbe equaltothegroundspeedinaseismicwave.
Consideracoherentopticalpulse e(t )thatislaunched intoasingle-modeopticalfiber.Thebackscatteredoptical field E(t )attime t forlightreemergingfromthelaunch endcanbeexpressedasasuperimpositionofdelayedpartialfieldsbackscatteredwithareflectioncoefficient r0(z) alongthefiberaxis z (Shatalinetal.,1998).Thisamplitudecoefficientrepresentscouplingbetweentheforward andbackwardmodes.Foraspeedoflightinthefiber c ≈ 2108m/c,andwavepropagationconstant β ,we canusegroupandphasedelays2z/c and2 z 0 β x dx , respectively.So,theemergingfieldwilldependoninterferometeropticaldelay,orgaugelength, L0 as:
Foraregularfiber,thephaseshiftterminEquation1.1 canbeseparatedintoaconstantpartandapartchanging with “slow” time t,representingpulse-to-pulseparameter
Figure1.4 DASopticalsetup.Distanceisproportionaltoflytime.
variationwithDopplershiftfrequency Ω(z),whichisproportionaltoscatteringparticlevelocity v(z)andwavelengthfrequency ω
shift ΔΩ(z)= Ω(z) Ω(z L0)canberepresentedviavariationofintensity I(z, t)= E(z, t)E(z, t)∗ .Theexpressionin bracesinEquation1.6representsatwo-beaminterference,sotheintensitywillvaryharmonicallydepending onthephase.Asweareinterestedintheintensitychange, onlytheinterferencetermneedsbetakenintoconsideration,whichcanbereshapedusingtheintensityderivative:
Herethestraincoefficient Kε relatesthephysicaland opticallengthoffiber, neff isfibereffectiverefractive index,and λ isthelaserwavelength.Equations1.2–1.3 representawell-knowndualism,whenachangeininterferencecanbeconsiderednotonlyasaresultofachange inphase,butalsoasabeatingofafrequencyduetoa Dopplershift.TheconceptfindsapplicationinDoppler lidars,whereRayleighscatteringlightcontainswind speedinformation,sotheheightdistributionofthespeed canbedetectedusingOTDR(Garnier&Chanin,1992). TheDASconceptionissomewhatdifferent:wedonot measuretheabsolutevelocityofRayleighscatterers, butthedifferenceinsuchvelocityalongthegaugelength. AnotherdifferenceisthatRayleighcentersarefrozenina glassoffiberatameltingpointofabout800 .Theirmovementfollowsthemovementofthefiber,andhencevery lowDopplerfrequencies(downtomHz)canbemeasured. Forsimplicityoffurthercalculations,thereflective coefficient r0(z)canberedefinedastheeffectivereflective coefficient r(z):
Then,toextracttheDopplershiftfromtheintensity equation,weneedtocontrolthephaseshift ψ 0 between delayedopticalfieldsintheinterferometer.SoEquation1.1 canberearrangedusingEquations1.2–1.4to:
Thenusingconvolutionproperties
(
)/∂ t,wecanfindintensityvariationviaphaseshift Φ ofbackscatteredlightwherethereisargumentofbackscatteringcomplexfunction:
Heretheconvolutionsymbol isusedtosimplifythe expression,andtheOTDRscale z =2ct forthe “fast” time t isused.Theconvolutioncommuteswith translations(Goodman,2005),meaningthatEquation1.5 canbeconvertedusing a(z1 z2) b(z1)= a(z1) b(z1 z2) to:
TheCOTDRsignalcanbededucedfromEquation1.8 ifweset L0 =0 and ψ 0 =0.Evensuchasimplesetup candeliverinformationontheDopplershiftand hencethegroundspeed v(z)throughtheintensityvariation ∂ I/∂ t Δv inaccordancewithEquations1.3,1.8. Unfortunately,theproportionalityfactorcontainsan oscillationterm,sowecannotdistinguishpositivespeed fromnegative.
Letusconsiderfirstthesimplecaseofshortpulse e(z)= δ(z)when δ istheDiracdeltafunction.ThenconvolutioncanberemovedfromEquation1.5 because δ(z) a(z)= a(z),andthedistancevariationofDoppler
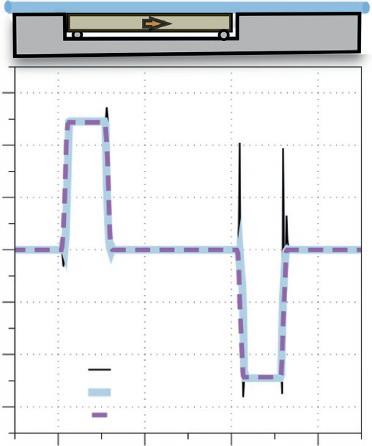
TheresultofcomputermodelingofaCOTDRresponse onadifferentialRickerwaveletforgroundspeed(Hartog, 2017)ispresentedinFigure1.5.Therightsideshows1D seismicwavemovinginthezdirection(inm)withareflectionfromaninterfacewithapositivereflectioncoefficient.Belowtheimageisatimeseriesofapparent velocity,whenunitsarenormalizedtotheexpectedopticalphaseshiftinradiansbetweenpointsseparatedby gaugelength10m.Theleftsideofthefigurecorresponds totherelativepulse-to-pulsevariationoftheCOTDRsignalcalculatedinaccordancewithEquations1.8–1.9.The signofresponsechangesrandomlyinaccordancewithan opticalpulsewidthof50nsor5m.Asaresult,thesignal cannotbeeffectivelyaccumulatedformultipleseismic pulselosityesbecauseofthetemperaturedriftbetween seismicshots.Temperaturedriftchangesthephaseconstantofthefiber β 0 and,inaccordancewithEquation1.4, theeffectivereflectioncoefficient r(z)alsochanges.Asa resultofsuchdrift,everyseismicshotwillhaveaunique, random,alternating,speckle-likesignaturethatcancels theaveragingsum.Fortunately,thisproblemcanbeovercomebyopticalphaserecovery,when,aftersimilaraveraging,averagevaluesappear.Thus,theactualDAS outputwillbeacombinationoffiberspeedinformation andtheunaveragedportionoftherandomCOTDR signal.
Figure1.5 COTDRresponse(Equation1.6)shownintheleftpanelofthesimulatedsignalofagroundvelocity waveletshownintherightpanel.Thesignals’ cross-sectionalongthewhitelineisshowninthebottompanels inradians. Source:BasedonCorreaetal.(2017).
1.1.3.DASOpticalPhaseRecovery
TherandomnessoftheCOTDRsignalcanbereduced throughpropercontroloftheexternalinterferometer phaseshift ψ 0,whichcanbeachievedinmanyways. AllthesemethodsarebasedonthefactthatCOTDR intensityisrandomindistancebutwillvaryharmonically dependingonthephase,asfollowsfromEquation1.1 (see Figure1.6).So,phasecontrolcanrevealphaseinformationregardlessoftherandomnatureofthesignal.
Wewillstartourphaseanalysiswithasimple,although notverypractical,approach,wherethephaseshift ψ 0 is lockedontoafringesin(ψ 0 + Φ) ≡ 1.Suchanapproach wasusedearliertoanalyzethespatialresolutioninphase microscopy(Reaetal.,1996).ThenEquations1.8and1.9 canbeaveragedoveranensembleofdeltacorrelated backscatteringcoefficients
)as:
Thesamedatacanbeextracteddirectlyfromphaseinformation,asisclearfromEquation1.11.
Sofar,wehaveanalyzedtheshortpulsecase,wherethe pulsewidthissignificantlysmallerthantheexternalinterferometerdelay.Inreality,suchpulsescannotdeliversignificantopticalpower,whichisnecessaryforprecise measurements.Fortunately,Equations1.10–1.11canbe generalizedforanonzerolengthopticalpulse e(z)directly fromEquation1.5inthesamewaythatanopticalincoherentimagewasobtainedinGoodman(2005)usingcorrelationaveraging (a r1)(a r2) = a 2 r1r2 .This expressionisvalidforanuncorrelatedfield,generatedby randomreflectionpoints r1(z1)r2(z2) = δ(z1 z2).This calculationconfirmsthatEquation1.11remainsthe same,asitrepresentsaveragingoverdifferentharmonic signals,butEquation1.10willbereshapedto:
Equation1.10 demonstratesthatthesignofDoppler shiftcanbemeasuredbyDASwithproperphasecontrol.
Equation1.11 givesusthepossibilitytointroducea dimensionlesssignalasaphasechangeoverarepetition orsamplingfrequency FS period A(z)= FS ∂Φ/∂ t,and sotheDASoutput A(z)canberepresentedforpulsewidth τ (z)= e(z)2 fromEquations1.3,1.10,and1.11as:
Z
InEquation1.14,theelongationcorresponding to ΔΦ =1 rad is A0 =115nm,calculatedfor λ =1550, neff =1.468and Kε =0.73,whichhasbeenmeasured forconventionalfiber(Kregeretal.,2006).TheDASsignalisaconvolutionofpulseshape(asistypicalfor OTDR-typedistributedsensors)withameasuredfield, whichisthespatialdifferenceinfiberelongationspeed ofpointsseparatedbyagaugelength.
Phasemeasurementscanbemadeinamorepractical waythanlockingtheinterferometerontoafringebyusing intensitytrace Ij(z, t) j =1,2,..P from P multipleinterferometerswithdifferentphaseshifts.Suchdatacanbecollectedconsequentiallyin P opticalpulses,butitreduces sensorbandwidthby P times.Alternatively,theinformationcanbecollectedforonepulseusingamulti-output opticalcomponent,suchasa3×3coupler.Inthegeneral case,thephaseshift Φ(z, t)canberepresented(Todd, 2011)viathearctangentfunctionATANoftheratioof imaginaryIm Z torealpartRe Z oflinearcombinations ofintensities:
3I 1 3I 3 andRe Z = I1 2I2 + I3.AnadditionalmodificationofEquation1.15 includingphase unwrappingwillbediscussedinthenextsection.Itis interestingtomentionthataheterodyneapproach (Hartogetal.,2013)canalsousequadraturemeasurementssimilartoEquation1.15,butinthatcasephase diversityisrealizedintheOTDRtime/distancescale, whichcanaffectspatialresolution.Also,wecanmention thattheinterferometerapproachdoesnotneedahighly coherentlaser,astheopticallengthsofinterferingrays arenearlycompensated(Poseyetal.,2000).
ThetheoreticalexpressionforDASresolution (Equation1.13)wasobtainedfromanalysisofaninterferometerlockedontoafringe,anditisnecessarytotesthow thisisapplicabletopracticalphasemeasurementalgorithms.Also,Equation1.13containsaveragingoverastatisticalensemble,anditisimportanttounderstandwhatit meansinarealapplication.Toanswerthequestions,we havecomparedtheoreticalvalueswithasimulationbased ona3×3couplersetupfor100differentrandomRayleigh scatteringpatternsforawidevarietyofparametersand foundgoodcomparisonafteraveraging.Toillustratethis analysis,threeopticalpulsewidthsettingswereusedfor interferometerdelay(gaugelength)of L0 =10m anda groundvelocityzoneof40m(Figure1.7a–c).
where V isthevisibilitygivenbytheratioofpeak-to-peak intensityvariationtoaverageintensityoftheinterference signal.Inparticular,forasymmetrical3×3coupler,
Alltraces(Figure1.7a–c)correspondtostrainmeasurementsratherthantogroundvelocityprofilemeasurements.Ifthepulsewidthissmall, τ =10ns,then averagingisnotimportant,andthecorrespondence betweendifferentphaserecoveryalgorithmsareclear (Figure1.7a).Forareasonablepulsewidth, τ =50ns,only averagedsimulationresultscorrespondtotheory (Figure1.7b).Ifpulsewidth τ =100ns becomesequalto L0 =10m intheOTDRscale,thenaveragingiscritical, butafterit100timesaveragingcorrespondenceisgood (Figure1.7c).Itisimportanttomentionthatthissimulationdidnotincludephotodetectornoise,andnoise-like performanceinFigure1.7ccanbeexplainedbythe
Im
=
Figure1.6 Intensitychangesareirregularalongdistancebutharmonicalongphaseshiftaxis.
COTDRsignal,whichwillbeoverlaidontheDASsignal withnonzeropulsewidth.Thisisanaturallimitfor increasingSNRbyextendingpulsewidth;wehaveacompromisebetweenSNRandsignalqualityataround L0 =2τ .Finally,wecanexpectthatthetheoreticalexpression(Equation1.13)canbeusedforspatialresolution analysisfordifferentphaserecoveryalgorithmsaftera properaveraging.
1.1.4.DASDynamicRangeAlgorithms Anacousticalgorithm(Equation1.15)transformsthe DASintensitysignalintoaphaseshiftproportionalto fiberelongationvalue;aquestionthenishowlargecan thisphaseshiftbe?AnalgorithmbasedonsuchambiguousfunctionasATAN(x)cangivearesultonlyinsidea limitedregion.Theclassicapproachtorecoverlarge phasechangesisunwrapping:stitchingtogethertwoconsecutivepoints t and t + Δt fromdifferentbranchesofsignal(Itoh,1982):
Equation1.18givesanideaofthis.Ifthephaseisa smoothfunction,wecandifferentiateintime Φ(t)before unwrapping.Then,thefirstdifferentiallineartermis removed,andconditionbecomesmorerelaxed:
So,thesecondordertrackingalgorithmcanbe obtainedbydifferentiatingthesignalbeforeunwrapping:
Thisunwrapping,orphasetracking,conceptworks onlyifthephasedifferenceisinsidetwoquadrants:
Equation1.17 makesitpossibletomeasuresignificant fiberelongation,muchlongerthanthewavelength.Ifthe samplingrate FS =1/Δt ishigherthantheacousticfrequency F,alargeracousticamplitudecanbeintegrated A0FS/2F ≈ 68μ overtimefor F =50Hz and FS =50kHz Moreover,eventhisvaluehasimproved,and
Equation1.20 hasananaloginclassicaloptics,where, insteadofthewavefrontphasegradient,thewrappedcurvatureofthewavefrontcanbeunwrappedtoincreasethe dynamicrange(Servinetal.,2017).Acomparisonofthese algorithmsispresentedinFigure1.8usingmodelingfora harmonicsignalwithalinearlyincreasingamplitude.Itis visiblethatbothalgorithmscanrecoverasignificant phaserange,butthesecondordertrackingalgorithm candeliverinexcessofa10timeslargerdynamicrange.
Theoretically,evenhigherorderalgorithmscanbe designedbyrepeatingthisprocessusinghigherorderderivatives,buttheyarenoisierasmorepointsareinvolvedin thecalculation ascanbeseenbycomparingEquations1.18 and1.19.Fromapracticalpointofview,the proposed1D(intime)unwrappingalgorithmsareerrorfreeandsimpleenoughtobeimplementedinrealtime. Potentially,noiseimmunitycanbeimprovedbytransition to2D(intimeanddistance)unwrapping,similartothat usedinasyntheticapertureradarsystem(Ghiglia&Pritt, 1998).Thissolutioncanextractasmuchinformation aboutthephaseaspossible,butitisdifficulttoimplement withoutpost-processing.
Figure1.7 ComparisonofDAStheoreticalresponse(Equation1.13)withsimulationfora3×3coupler.
ComparisonoffirstandsecondordertrackingalgorithmsforDAS.
1.1.5.DASSignalProcessingandDenoising
Inallphase-detectionschemes,thechangeinoptical phasebetweenthelightscatteredintwofibersegments isdetermined,meaningwearemeasuringthedeterministicphasechangebetweentworandomsignals.Therandomnessoftheamplitudeofthescatteredradiation imposescertainlimitationsontheaccuracyofthesensor, throughtheintroductionofphaseflickernoise.The sourceofflickernoiseisanambiguity:whenthefiberis stretched,thescatteringcoefficientvaries,andcan becomezero.Inthiscase,thedifferentialphasedetector generatesanoiseburstregardlessofwhichopticalsetup isused.Theamplitudeofsuchnoiseincreaseswith decreasingfrequency(asisexpectedforflickernoise) whenthephasedifferenceisintegratedintothedisplacementsignal.
Fromaquantumpointofview,weneed,forsuccessive phasemeasurements,anumberofinterferingphoton pairsscatteredfrompointsseparatedbythegaugelength distance.Insome “bad” points,therearenosuchpairs,as onepointofscatteringisfaded.Anaturalwaytohandle thisproblemistoreject “bad” unpairedphotonsbycontrollingthevisibilityoftheinterferencepattern.Asa result,theshotnoisecanincreaseslightlyastheprice forthedramaticreductionofflickernoise.Therejection offadingpointscanbepracticallyimplementedbyassigningaweightingfactortoeachmeasurementresultand performingaweightedaveraging.
Thisaveragingcanbedoneoverwavelengthifamultiwavelengthsourceisused.Alternatively,wecanslightlysacrificespatialresolutionandsolvetheproblembydenoising
usingweightedspatialaveraging(Farhadiroushanetal., 2010).ThemaximumSNRisrealizedwhentheweighting factorofeachchannelischosentobeinverselyproportional tothemeansquarenoiseinthatchannel(Brennan,1959), meaningthesquaredinterferencevisibility, V2,canbeused fortheweightingfactoras:
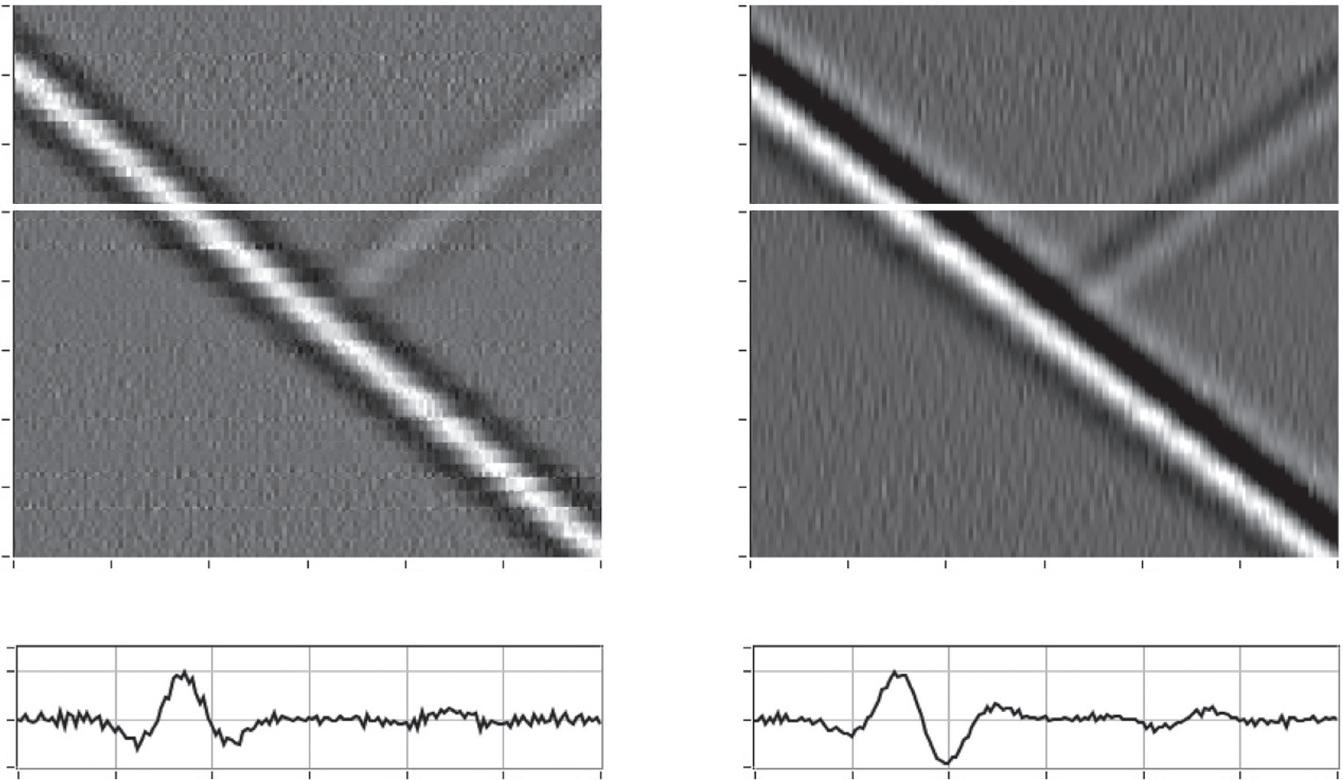
Theaveragingfunction p(z)=5m shouldoptimallybe chosentobecompatiblewiththepulsewidth τ (z)=50ns, whichshouldbearoundhalftheinterferometerlength L0 =10m.Withthiswidthoftheaveragingfunction,it hasnosignificanteffectonthespatialresolutionofthe DAS.Modelingwithandwithoutweightedaveragingis presentedinFigure1.9,whichdemonstratesthatsignificantnoisereductioncanbeachieved.Itshouldbenoted thatthisnoisereductionisparticularlymarkedincomparisonwiththecoherentOTDRresponse,bycontrasting withFigure1.5.Nevertheless,weightedaveragingsuppressesratherthancompletelyremovestheeffectof flickernoise,andsomechannelsstilldemonstrateexcessivenoise(inadditiontoshotnoise).Hence,theresponse overalldepthsatagiventimeforFigure1.9willcontain spikesforfadedchannels.
AsisexploredinSection1.3,theproblemofflicker noisecanbeovercomebyintroducingengineeredbright scatterzonesalongthefiberwithconstantspatialseparationanduniformamplitude.Suchscatterzonesalso reflectmorephotons,andsoimprovetheshotnoisedetectionlimitation.Inaddition,theuseofsuchengineered
Az ≈ Az V 2 z pz V 2 z pz (1.21)
Figure1.8
Figure1.9 Theleft-handpanelshowsmodelingofrawDASacousticdata(Equation1.12);theright-handpanel showsthesameshotwithweightedaveragingdenoising(Equation1.13)applied.Thesignals’ cross-section alongthewhitelineisshowninthebottompanelsinradians.Themodeled sourceisshownintherightpanel ofFigure1.5.
fiberallowstheuseofphase-detectionalgorithmswith improvedsensitivityandextendeddynamicrange.
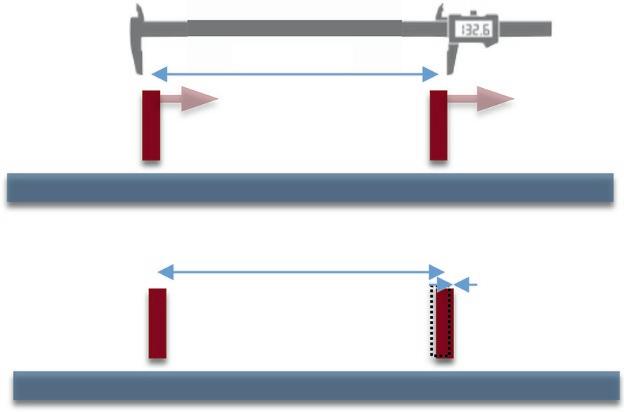
1.1.6.TimeIntegrationofDASSignal ADASinterrogatormeasures,inaccordancewith Equation1.13,thespeeddifferencebetweentwosections offiberthatareseparatedbyinterferometerlength L0 (referredtoalsoasthe gaugelength),aspresentedin Figure1.10.Inpulse-to-pulseconsideration,theDAS responseislinearlyproportionaltothefiberelongation averagedoverthegaugelengthinthenanometerscale, orstrainrateinthenanostrainpersecondscale.Theconsiderationcanalsobeextendedtomultiplepulsesbytime integrationoftheDASsignal.So,iffiberrestsinitially andgrounddisplacementequalstozero u(z, t1)=0,then:
Figure1.10 Illustrationoftwotime-consecutivemeasurements whenDASoutputisproportionaltofiberelongationbetween twoprobepulses.
seismographthatcanmeasurechangesindistance betweentwopointsontheground(Benioff,1935).
meaningatimeintegratedDASsignalcanbeconsidered asanoutputofahugecaliperthatismeasuringfiberelongationbetweentwopointswithsub-nanometerprecision. Thismeasuringprincipleisdifferentfromthatofageophonebutissimilartoanelectromagneticlinearstrain
1.2.DASSYSTEMPARAMETERSAND COMPARISONWITHGEOPHONES Inthissection,weconsiderhowDASparameters(such asspatialresolution),gaugelength,frequencyresponse,
andSNRenableDAStobecomeaneffectivetoolforseismicmeasurements.Fielddataarealsopresented,with DASoutputcomparedtogeophonedata.
1.2.1.DASOptimizationforSeismicApplications Distributedfibersensorsmeasurephysicalparameters ofanexternalenvironmentcontinuouslythroughtheintegrationpropertiesoflighttravelingalongalengthyopticalpath.Thisisquitedifferentfrompointsensors,suchas geophones,whichmakeaninertialmeasurementof groundspeedatfixedpositions(SEAFOM,2018).The DASrecordsalocalstrainrate,whichcanbeconverted intoparticlevelocitytoallowdirectcomparisonwithgeophonedata.FollowingJoussetetal.(2018),wecan approximatelyrepresentDASsignal A(z, t)viaground displacement u(z, t),where FS istheDASsamplingfrequencyand L0 isthegaugelength.
isrepresented(Equation1.5)asaconvolutionofapoint spreadfunctionwith v(z).
Spatiallyintegratedsignal(Equation1.27)wasmodeledfor10mgaugelengthand50nspulsewidth,asshown inFigure1.5(rightpanel).Theresultsofmodeling (Equation1.25)arepresentedinFigure1.11(leftpanel), andtheresultisconvertedtogeophone-styledata (Equation1.26)intherightpanel.Fromapracticalpoint ofview,lowtemporalfrequencies,outoftherangeof interest,canbefilteredout,andalsospatialantialiasing filteringcanbeused.Itisworthmentioningthattheright panelofFigure1.11demonstratestherealchangein polarityofthereflectedseismicpulse.Also,spatialintegration(Equation1.26)actsasstatisticalaveraging, whicheliminatestherandomnessofthe “staircasing” in Figure1.5leftpanel.
If FS ∞, L0 0,thentheDASsignalcanbepresentedinadoubledifferentialform:
Themostvaluablegeophysicalinformationisdelivered bysoundwaveswithfrequenciesbelow FMAX =150Hz,as higherfrequenciesareattenuatedbytheground.Fora speedofsoundC =3000m/s,thiscorrespondstoanacousticwavelength C/FMAX =20m,soNyquist’slimitdictates that LG ≤ C/2FMAX =10m isthemaximumspacingof conventionalsensors.Formally,thelinearsplineapproximation G(z)ofconventionalantennavelocity v(z)output canberepresentedusingexpressionsfrom(Unser, 1999),as:
Thesesimplifiedexpressions(Equations1.23–1.24)give usaqualitativesenseoftheDASalgorithmoutput.Fora subsequentquantitativeanalysis,weshallneedthe detailedexpressionthatwasobtainedintheprevioussection.Namely,foranonzerointerferometergaugelength L0 andopticalpulsewidth τ ,averagedoverrandomscatteringDASoutput, A(z)canberepresentedbyEquation1.15inexpandedform:
Az = 1 A0 F S τ z δ z δ z L0 vz (1.25) where FS issamplingfrequencyand A0 =115nm isascale constant(Equation1.14).So,thevelocityfieldcanbe recoveredbyspatialintegrationstartingfromamotionlesspointas:
= z 0 Au du = Az θ z (1.26)
ThenDASsignal(Equation1.25)canbetransformed usingshiftinvariant a(z1) b(z1 + z2)= a(z1 + z2) b(z1)to:
= 1
where θ (z)istheHeavisidestepfunction,whosevalueis zeroforanegativeargument.Asexpected,theDASsignal
ThespatialspectralresponseofDASinacousticangularwavenumber Kz canberepresentedbyFouriertransform ℑ(Kz)followingGoodman(2005):
G K z =sinc K z LG 2 comb K z LG 2π ℑ K z (1.29)
Suchspectralresponsescanbenormalizedforaconstantsignal ℑ(K)=1(seeblacklineinFigure1.12). Thecombfunctionin(Equation1.29)isresponsiblefor therepeatingofthespatialspectrumwithashiftof2π / Λ,asisshownbythedottedline.Topreventaliasing, thesignalspectrumshouldbeinsideNyquist’slimit, whichisshownbythegrayverticalline.
Letuscomparetheconventionalvelocitysensorwith theDASspectrum,calculatedfromthespatialresolution expression(Equation1.25),byFouriertransformas:
A K z =sinc K z τ 2 sin K z L0 2 ℑ K z (1.30)
TwocasesarepresentedinFigure1.12:whentheopticalpulselengthisalmostequaltotheinterferometer gaugelength τ = L0,andwhenitishalftheinterferometer gaugelength τ = L0/2(seedashedandsolidbluelines, respectively).Theabsolutevalueispresentedinthefigure toaidcomparisonbetweencurves.Inthesecondcase,we
ℑ
ℑ
Figure1.11 AcousticmeasurementsusingDAS:Theleftpanelrepresentsstrainratemeasurementandtheright paneldisplaysgroundspeedmeasurement,thetransformtowhichcomprisesfilteringandintegration.The signals’ cross-sectionalongthewhitelineisshowninthebottompanelsinradians.Themodeledsourceis shownintherightpanelofFigure1.5.
wavenumber, K/2π, 1/m
DAS τ=5m Lo=10m
DAS τ=10m Lo=10m
Sensors array 10m
Sensors array aliasing
Figure1.12 ComparisonofDASspectralresponsewiththatfroma10msensorantennaarray.
haveagain,whichishighlightedbythebluefilling.This gaincanbeexplainedbysignalsmearingovera longpulse.
ItseemsfromFigure1.12 thatDASlowfrequencysensitivityissignificantlylowerthanthatofageophone.
Practically,however,thisisnotthecase,asthegeophone noiserisesatlowfrequencies,andthiscanbecharacterizedbysomehigh-pass(HP)filtersthatlimittherange tofrequenciesaround10Hz(seedottedlinein Figure1.13).However,DAShasthepotentialtoincrease
Acoustic
LowspatialfrequencygaininDASbyusinglonginterferometer.
thespectralresponseatlowfrequenciesbyincreasing interferometerlength forexample,from L0 =10m to L0 =30m (seeFigure1.13).So,potentially,theDAS responsecanbesynthesizedfromtwomeasurements:with ashortinterferometergaugelengthtodeliverhighspatial frequencybandwidth,andalongonetodeliverlowfrequency.Astheresult,full-frequencycoveragecanbeas goodasfromageophoneantenna,orpossiblyevenbetter, aswillbeshowninalaterSNRcomparison.Anadditionaladvantageovergeophonesisthelargedynamic rangeofDASatlowfrequencies,whichwillbediscussed later.
1.2.2.DASDirectionalityinSeismicMeasurements Intheprevioussection,weanalyzedthecorrespondence betweenDASandgeophonesintheone-dimensionalcase andfoundthat “geophone-style” velocitydatacanbe extractedfromDASsignalsbyspatialintegration.However,in3Danalysis,weshouldconsiderthatDASisnota velocitysensorbutadifferentialstrainsensor.Thisisa fundamentaldifference:DAScanmeasureacomponent of3Dtensor(strain)butnot3Dvector(velocity).
DirectionalityoftheDASresponsedependsonthefiber opticcableconfigurationandthecabledesign,asthe deviceitselfissensitiveonlytofiberelongation.Wewill startourconsiderationwherethefiberisplacedlinearly insideacable,withnoslippagebetweenfiberandcable, norbetweenthecableandtheground.Inthiscase,fiber displacementwillfollowgrounddisplacement,andsensitivitywilldependontherelativepositionoffiberandseismicsource.Asimilarmechanicalprinciplewasusedfor theelectromagneticlinearstrainseismographtomeasure variationsinthedistancebetweentwopointsofthe ground(Benioff,1935).DASdirectionalresponsewith
respecttoincidentangle Γ canbefoundbytransformation ofthestraintensorcomponentswithrotationusinggeometricalconsideration.Foralongitudinal(P)apparent wave,itwillbecos2Γ,andfortransversal(S)wavesin Γ cos Γ,similartoBenioff(1935)(seeFigure1.14). DetailedanalysisanddiagramsforRayleighandLove wavescanbefoundinMartinetal.(2018).
Inverticalseismicprofiling(VSP),intheverticalpartof thewell,bothcableandseismicwavesareinthesame directionfornear-offsets,sotheDASismoresensitive toP-waves,inwhichtheacousticdisplacementvector coincideswiththefiberdirection.Inotherapplications, suchasfracking,themicroseismicsourceisusuallyona sideofthecable,soshearwavescanbeeffectively detected.
Cableorientationisresponsiblenotonlyforacoustic amplitudebutalsoforacousticspatialresolution,even forthesameacousticwavelength.Thecableactsasan acousticantennawherethesignalvariesrapidlyinspace iftheP-waveandcabledirectioncoincide,butthesignal remainsthesameoverdistanceiftheacousticwavefront isparalleltothecable.Totakethiseffectintoconsideration,weneedtoexpandtheexpressionforacousticwavelength Kz alongthecableforEquations1.29–1.30as:
Foraharmonicwave,directionalitywilldirectlyaffect notonlythespatialresolutionbutalsothetemporalfrequency.AfterFouriertransferinthetimedomain,Equation1.30,intheabsenceofaliasing,canbepresentedas:
Acoustic wavenumber, K/2π, 1/m
Figure1.13