A scuola con Pitti 3 | Guida per l'insegnante

Camillo Bortolato

GUIDA

al percorso Classe terza

Camillo Bortolato

GUIDA

RISORSE DIGITALI

Guida per l’insegnante

Dalle risorse online puoi scaricare la Guida anche in formato PDF. La Guida in formato PDF verrà aggiornata con nuovi suggerimenti stimolati dall’uso in classe.

Per desktop, LIM e tablet

Libro digitale

Sfoglia il volume in versione digitale, in classe sulla LIM o a casa, e accedi direttamente alle risorse integrative.

Video di approfondimento

Inquadrando i QR code, o direttamente dal libro digitale, puoi accedere a risorse video che supportano la pratica didattica.

Come accedere alle risorse digitali

Esegui le sottrazioni

per eseguire la sottrazione. Guarda il video per scoprire la sottrazione dal basso.

– Collegati a risorseonline.erickson.it/mab – Se è la prima volta che accedi, seleziona Registrati; se invece hai già un account, clicca su Accedi ed effettua il login. – Una volta effettuato l’accesso, inserisci il codice di attivazione che trovi nei volumi del kit «A scuola con Pitti 3». Se sei già registrato, clicca su Riscatta un altro codice.

GUIDA

al percorso

Classe terza

Premessa

Italiano – Il mio libro di lettura

Italiano – Il mio quaderno di scrittura

Matematica

Storia

Geografia

Scienze

«A scuola con Pitti»… perché questo titolo?

Perché Pitti è l’immagine della tenerezza e della voglia di crescere.

È un uccellino piccolo ma forte, come ogni bambino che va a scuola.

NOTA

Questa Guida contiene indicazioni generali sul Metodo Analogico e suggerimenti disciplina per disciplina per utilizzare in classe A scuola con Pitti 3. È inclusa nelle risorse digitali in formato PDF stampabile.

A scuola con Pitti può essere adottato come libro di testo — attraverso l’adozione alternativa ai libri di testo ministeriali —, in coerenza con il piano dell’offerta formativa, con l’ordinamento scolastico e con il limite di spesa stabilito per ciascuna classe di corso.

A scuola con Pitti 3 è composto da quattro volumi: Il mio libro di lettura, Il mio quaderno di scrittura, Il mio libro di matematica e Il mio libro di storia, scienze e geografia, che contengono il codice per accedere alle Risorse digitali.

È possibile inoltre acquistare il kit in accoppiata con gli Strumenti del 1000 per rendere il percorso di matematica maggiormente veloce e intuitivo.

Per maggiori dettagli e informazioni, consulta il sito Erickson www.erickson.it, il sito di Camillo Bortolato www.camillobortolato.it, o scrivi a metodoanalogico@erickson.it.

PREMESSA

In un panorama di crescenti difficoltà, si può pensare di vivere nella propria classe un’oasi di serenità e soddisfazioni con i propri alunni?

È la sfida di questo materiale, alternativo ai libri di testo classici, giunto al terzo anno.

A scuola con Pitti 3 è un invito a volare indirizzato prima di tutto all’insegnante. Più in alto va, più i bambini lo seguono con le loro piccole ali, come sono abituati a fare fin dalla nascita.

Dopo l’ebrezza del volo verrà il tempo anche per scendere a esplorare il terreno, con la sicurezza però di non perdersi mai.

Questo andirivieni costante dalla sintesi all’analisi e viceversa è il processo imponderabile per la conoscenza che vale per tutti, grandi e piccini.

Lo sguardo panoramico

L’intuizione a cui il Metodo Analogico fa riferimento insistentemente è questo sguardo panoramico che ci fornisce la comprensione in anteprima.

Nella didattica «parcellizzata» questa comprensione si ottiene alla fine del percorso quando, guardando indietro, il cammino fatto al buio prende luce.

«AHH! Adesso capisco tutto.

Adesso comprendo la bellezza della lettura…

Adesso che ho finito comprendo cos’è l’analisi grammaticale e la distinguo bene da quella logica!

Adesso percepisco bene la differenza tra il calcolo mentale e il calcolo scritto nella sua prescrittività.

Adesso comprendo la storia che ho studiato in anni e anni».

Troppe volte la gradualità scolastica corrisponde a tenere i contenuti nascosti ai bambini.

Allora succede che si affannano a carpire le intenzioni dell’insegnante, perché sanno che lui vede tutto il percorso.

Spoilerare

La nostra proposta, invece, è che l’insegnante scelga fin da subito di condividere e presentare il percorso completo ai suoi alunni. Così, non appena apre bocca, sanno già le risposte.

La scelta dell’insegnante di «spoilerare» gli argomenti che si andranno ad affrontare è il principio di umanità, di condivisione, quasi di complicità, che può portare il sereno nella propria classe.

La privacy dell’apprendimento

Con questa ottica ribaltata nei confronti del sapere da trasmettere, i bambini emergono con tutta la loro energia e presenza.

Il focus della comprensione si sposta su di loro. Ciascuno si fa carico di trovare una strada propria , come ha già fatto fin da piccolo imparando la lingua, i giochi e a relazionarsi con gli altri.

È una espansione travolgente in cui l’unica variabile che li può mettere in crisi è quella del tempo. Specialmente i bambini in difficoltà non sopportano la dilatazione del tempo che per loro è infinita. Rischiano di perdere la speranza di essere come gli altri, cioè uccellini nati per volare.

ITALIANO – Il mio libro di lettura

Premessa

Leggere per conoscere il mondo degli altri e scrivere per raccontare il proprio, usando parole ed espressioni adeguate: questi sono gli obiettivi sostanziali del programma di italiano di classe terza, da perseguire con la giusta determinazione.

Perciò ecco questo libro di lettura che presenta le storie scritte dagli altri, ed ecco questo quadernetto che fornisce esempi e spunti su come raccontare le proprie.

Con quale metodologia?

Con la stessa con cui si impara a guidare sulla strada aggiustando continuamente il volante per evitare ostacoli. E, se nascerà la passione, dopo un po’ ci si troverà ad essere autori quasi senza accorgersene.

Anche quest’anno il libro di lettura è alternativo al pot-pourri antologico di molti testi scolastici convenzionali, che costringono l’alunno a cambiare contesto, scena e personaggi a ogni pagina, con inevitabili problemi di comprensione e conseguenti domande tese ad accertare quanto i piccoli lettori abbiano capito.

È composto da una storia principale e da altri quindici racconti, proposti solo per il piacere di leggere e narrare.

La volpe misteriosa

La storia della volpe riprende la vicenda di Pitti e della gatta Luna, protagonisti dei libri di lettura per le classi prima e seconda. L’ambientazione è la stessa, ma Anna e Giulio, i due fratelli che vivono nella casa della betulla, sono cresciuti e vogliono uscire dai confini del giardino, desiderosi di scoprire il mondo. Vogliono essere attenti, concreti, informati e la loro curiosità scientifica si risveglia davanti a una foglia o a un mucchietto di terra.

Alla fine, troveranno questa attività più appagante del mondo immaginario delle favole.

Per questa ragione la vicenda che li vede protagonisti nel racconto viene sviluppata su un piano di verosimiglianza. Ciascun bambino può immedesimarsi, tanto che il racconto termina con un’esortazione al lettore a diventare lui stesso autore di una storia.

In che modo? Raccontando, ad esempio la storia di un altro animale. Oppure facendo parlare un altro personaggio della stessa storia. I bambini fanno esperienza di queste tipologie narrative ogni giorno davanti alla televisione.

E si può raccontare da soli o in gruppo, sempre accompagnati dall’insegnante, giungendo a scrivere poi elaborati profondi sviluppati su più pagine, anche divisi in capitoli per non far morire subito la narrazione. Nel costruire la storia si discute, si sceglie la vicenda migliore, come fanno gli sceneggiatori di un film.

La comprensione

Non ci sono domande finali di comprensione perché essa accompagna naturalmente il percorso di lettura.

I disegni non invadenti, messi nel punto giusto del testo, sono come fotogrammi della scena che si va registrando nella mente. Tutta la comprensione avviene trasformando il linguaggio scritto in «film».

Nelle consegne operative alla fine di ogni capitolo troviamo che ricorre sempre il compito di prendere delle matite colorate per evidenziare espressioni e descrizioni interessanti, come se fossero pietre preziose. Alla fine, il libro sarà un tesoro di queste pepite che diventano strumenti per costruire narrazioni proprie, come fanno gli scrittori.

La prosecuzione della storia

Finita la storia, la lettura condivisa può proseguire con il libro «La volpe si racconta» dove la vicenda viene raccontata dalla volpe stessa con tutte le sue emozioni di cucciola e poi di mamma.1

Confrontando queste due versioni i bambini potranno scoprire che la stessa realtà può essere vissuta e raccontata in modo diverso.

1 C. Bortolato (2022), La volpe si racconta, Trento, Erickson.

Altre storie

La seconda parte del volume presenta quindici storie tratte prevalentemente dalla tradizione popolare; sono nate per essere raccontate a voce.

La consegna operativa è di conseguenza quella di ritradurle in racconto orale, ravvivando la loro funzione originale.

L’indicazione, quindi, è di raccontarle oralmente in classe ma, data la difficoltà di ascoltare tutti, possono essere avviate attività di gruppo in cui i bambini si ascoltano a vicenda.

Ciascun bambino si preparerà a casa per proprio conto, in autonomia.

Il fatto di raccontare a voce sviluppa molteplici abilità, compresa quella del riassumere, che utilizza forme linguistiche evolute.

Inoltre, la fiaba popolare, rifacendosi a drammi ancestrali, ha da sempre uno scopo terapeutico. Aiuta il bambino a esorcizzare i mostri della paura e dell’abbandono, dando alla fine una soluzione di speranza. Tratte dai drammi del passato, le storie stemperano le angosce che i bambini continuano a vivere ancora oggi.

Filastrocche e canzoni

Dopo i racconti segue un corredo di 13 filastrocche e 5 canzoni per godere della loro musicalità.

I testi sono tutti in rima perché il ritmo li rende divertenti e più facili per essere recitati.

L’invito è quello di cimentarsi nella loro memorizzazione controllando in autonomia i progressi.

I testi delle canzoni, caratterizzati anche loro a livello linguistico dalla presenza della rima, sono pensati per creare un momento di leggerezza e di condivisione in classe.

Dopo averli letti insieme si può trovare la versione musicata in internet.

ITALIANO – Il mio quaderno di scrittura

Il quaderno si suddivide in cinque sezioni:

• scrivere bene

• comporre

• descrivere

• avvio alla poesia

• grammatica.

Scrivere bene

L’attività dei primi giorni riprende l’esercizio sulla grafia, che è importante come il vestito che uno indossa. Trasmette qualcosa al di là dei contenuti. La grafia può essere elegante, sobria e ordinata, oppure sciatta e trasandata.

Il messaggio che intendono passare queste prime pagine è che si può amare la propria scrittura e la si può migliorare ogni giorno purché lo si faccia con la necessaria cura e lentezza.

Se la lettura è veloce, la scrittura necessita di sofisticate angolature e di millimetrici avanzamenti.

Meglio quindi dedicarvi ogni tanto qualche momento ricordando anche che il corsivo personale è sempre in evoluzione verso la semplificazione.

Comporre

Si consiglia di usare un quaderno a righe da tre millimetri perché la scrittura piccola risulta meno faticosa e più veloce.

In quest’ottica anche lo stampato maiuscolo diventa oggetto di sperimentazione perché, come nelle pubblicità seguite dai bambini, il font è parte del messaggio.

Non è una proposta formale di lavoro, ma un suggerimento per i momenti di pausa o di attesa, come le cornicette.

Lo scopo di questa sezione è trasformare il quaderno personale da ricettario di schede ortografiche a contenitore di racconti che parlano della propria vita quotidiana.

Che cosa raccontare?

Il quaderno presenta un’ampia gamma di testi che fungono da modello fornendo spunti su cosa e come raccontare. Prima si legge per accendere i ricordi. Subito dopo si inizia a scrivere per non spegnere il fuoco emotivo.

Ciascuno lavora in silenzio direttamente sul quaderno personale o in brutta copia, a discrezione dell’insegnante.

L’insegnante aiuta, suggerisce, incentiva.

Il messaggio da trasmettere è che, per elaborare un bel testo, bisogna soffermarsi sulle cose più piccole, quelle che gli altri non vedono.

Descrivere

Basta prendere la lente d’ingrandimento per vedere le piccole cose, così anche ciò che potrebbe apparire una banalità diventa un’eclatante sorpresa che fa sorridere chi legge.

Gli scrittori sono coloro che puntano sulle sensazioni interne, che si vedono ancora meno.

Vengono suggeriti due tipi di racconto, due strade che si possono riconoscere già dalle parole iniziali. Si può partire, ad esempio, dalla parola «Ricordo» e proseguire ricostruendo il racconto al passato. Oppure si inizia il testo con la parola «Adesso» per descrivere la situazione presente, come un nastro che si srotola in quel momento. Si segue il flusso dei pensieri mano a mano che insorgono.

Fermare il tempo e rallentare i pensieri raccontando ciò che si vive diventa un’esperienza di incontro con se stessi.

Il tempo della narrazione si ferma quando si decide di descrivere qualcosa.

In questo caso sono particolarmente utili le «strisce», da dove attingere espressioni e sinonimi interessanti.

Anche in questa sezione vengono proposti testi modello che sembrano scritti da coetanei e offrono numerosi spunti per le descrizioni personali.

Avvio alla poesia

Un esempio sono i testi che usano la strategia della personificazione dove gli oggetti vengono descritti dando loro caratteristiche umane.

Si passa poi al testo poetico, inteso come gioco linguistico. Il passaggio allo stile poetico avviene gradualmente quando le parole si diradano e le brevi frasi si giustappongono andando a capo ogni volta.

Si sfalda il costrutto logico ed emerge quello associativo.

Le parole, diventando rare, assumono valore.

Le metafore prevalgono sulle similitudini che sono più lunghe e convenzionali.

Gli scarti semantici hanno una funzione rivitalizzante.

Ciascuno può essere poeta.

Per le poesie con intenti lirici, contemplativi o didascalici ci sarà tempo più avanti. Ora è il momento di giocare con le rime, le filastrocche, le associazioni di idee e le ninne nanne senza senso.

Grammatica

La quinta sezione del quaderno è dedicata in primo luogo a rinforzare la correttezza ortografica e ad ampliare il lessico, per poi proseguire nella conoscenza dell’analisi grammaticale.

Per la correttezza ortografica e sintattica vengono proposti dei testi appositamente sconnessi e scorretti, perché ai bambini piace mettersi nei panni dell’insegnante e cercare gli errori nel quaderno degli altri. Da indagati diventano indagatori. Da ricercati diventano ricercatori.

L’utilizzo di questi brani permette di prendere in esame anche la coordinazione del periodo che sfugge alle consuete schede ortografiche.

Sarà preferibilmente un’attività di rielaborazione da svolgere insieme prima di essere assegnata come lavoro individuale, perché non deve avere il sapore della verifica.

Si passa quindi all’analisi grammaticale che va anticipata dalla relativa striscia generale (3A), a cui va fatto subito riferimento. In questa striscia vengono presentate le nove parti del discorso per mantenere la visione d’insieme, requisito portante del Metodo analogico.

Nelle pagine che seguono vengono presentati i barattoli, uno per uno, soffermandosi particolarmente su quello del nome. Per ciascun nome da analizzare è come se si svitasse il coperchio del vasetto e si scendesse approfondendo in ordine la classificazione.

I bambini vanno avvertiti che non sempre si arriva fino in fondo al barattolo.

Per alcune parti del discorso l’approfondimento è rimandato ad anni successivi, per cui è opportuno attenersi agli esercizi del quadernetto o della striscia.

Tutto deve rimanere leggero.

Gli strumenti

Nell’ultima parte si affrontano i verbi soffermandosi sugli ausiliari essere e avere che sono fondamentali.

Per la presentazione dei modi e dei tempi viene utilizzata l’immagine di un armadio, che ben si adatta all’idea dell’organizzazione degli spazi. Questo permette di dare a ogni voce verbale un posto definito permettendone un’immediata individuazione.

Il magazzino di parole corrette in aletta, le strisce nelle ultime pagine e l’armadio dei verbi nell’aletta finale completano la proposta del Quaderno.

Questi strumenti sono lo sguardo panoramico che permette di avere tutto davanti fin dall’inizio, sono il punto da cui partire e a cui arrivare. Convalidano l’idea di camminare sulla strada giusta, fungendo da punto di informazione e conferma anziché da barriera di controllo.

In questo senso rappresentano:

• il riassunto dato in anticipo;

• il punto costante di rinforzo;

• la carta geografica a cui ricorrere nel momento del dubbio.

Magazzino delle parole corrette

Gli elenchi di parole corrette presenti in aletta sono pensati per il dettato confermativo che ha l’obiettivo

di consolidare la forma corretta delle parole difficili prevenendo l’errore. Ciascun elenco condensa il lavoro solitamente diluito in molte schede didattiche.

Si procede con le seguenti modalità:

• si legge coralmente un elenco di parole;

• i bambini lo rileggono individualmente;

• l’insegnante detta le stesse parole nello stesso ordine;

• i bambini scrivono e, al bisogno, consultano l’elenco in aletta;

• alla fine, si ritorna al magazzino per l’autocorrezione finale.

Risulta utile anche il dettato confermativo a coppie di bambini, che si alternano nel ruolo di chi detta e di chi scrive.

Comporre al volo (Strisce 1-2)

Ogni striscia del comporre che si trova alla fine del quaderno va considerata come un tesoro che raccoglie parole ed espressioni preziose. Non sarà necessario impararle a memoria, basterà leggerle più volte per poterle ricordarle spontaneamente durante la scrittura personale.

Si procede così:

• assemblare secondo le indicazioni le 2 strisce, ritagliando le pagine finali;

• leggere individualmente o coralmente un lato di ciascuna striscia;

• soffermarsi sulle varie espressioni per commentarle insieme;

• ripetere a distanza di tempo la lettura corale e individuale;

• tenere le strisce a disposizione sul banco in fase di produzione personale.

Si raccomanda sempre di curare comunque il piacere e la spontaneità durante la composizione libera, evitando forzature nel ricorso alle strisce.

Grammatica al volo (Striscia 3)

Segue la striscia dell’analisi grammaticale da assemblare e utilizzare con questa modalità:

• evitare spiegazioni non richieste preservando la sorpresa del gioco;

• per cominciare, l’insegnante dice una parola tra quelle contenute nella striscia e i bambini la cercano dicendo il nome del barattolo a cui appartiene;

• proseguire il gioco con parole non contenute nella striscia;

• su richiesta dei bambini dare spiegazioni emozionali in chiave di analogia. Ad esempio: l’articolo è una presina per prendere il nome; l’aggettivo accompagna il nome; l’avverbio è come un aggettivo del verbo; ecc. È

possibile spiegare che i pronomi sono gli aggettivi che rimangono «orfani» del nome;

• tenere conto che lo studio della striscia viene prima degli approfondimenti sulle pagine del Quaderno di scrittura.

Gli armadi dei verbi

Nell’aletta finale si trovano gli armadi dei verbi ausiliari essere, avere e un verbo della prima coniugazione (cantare).

Si consiglia di procedere in questo modo:

• far conoscenza degli armadi esaminando le simmetrie e le differenze;

• cominciare con il gioco della ricerca, in cui l’insegnante nomina una singola voce verbale e i bambini la trovano nell’armadio pronunciando il nome del cassetto;

• lasciare che i bambini proseguano a coppie questo gioco;

• concentrarsi sui verbi essere, avere e sulle figure gancio, che per associazione aiutano a ricordare le iniziali delle voci verbali;

• rovesciare il gioco: l’insegnante dice il nome dell’armadio, del cassetto e della persona (ad esempio, «armadio avere, cassetto futuro semplice, terza persona plurale») e la classe risponde con la voce verbale corrispondente («avranno»).

Per un approccio interattivo allargato a tutte le coniugazioni e ai modi del verbo, si consiglia la web app

Analisi e grammaticale e logica utilizzabile sul PC, tablet e sui monitor interattivi di classe/LIM. 2

2 C. Bortolato (2024), Analisi grammaticale e logica, Trento, Erickson.

MATEMATICA

… e se alla fine del percorso qualche alunno avrà la sensazione di non aver imparato niente di più di quel che già sapeva, tranne nuove parole, allora vuol dire che avrà capito tutto della matematica…

Premessa

Il percorso di matematica si svolge tenendo fede ad alcuni principi del Metodo Analogico che invitano l’insegnante a:

• limitarsi a fare l’essenziale a scuola;

• focalizzarsi su un obiettivo per volta;

• evitare una didattica parcellizzata in favore di un apprendimento panoramico, che favorisce gli slanci intuitivi dei bambini;

• procedere attraverso il provare, l’agire, il fare, lo sperimentare.

Il tutto nella consapevolezza che le energie sono limitate e che non si deve abusare dell’attenzione di chi ascolta.

L’itinerario si articola nella consueta distinzione funzionale di obiettivi, lasciando l’insegnante libero di procedere secondo l’ordine che preferisce.

Il calcolo mentale

Al termine di ogni esercitazione l’autocorrezione conferisce leggerezza e velocità a tutto il lavoro.

Anzitutto viene affrontato il calcolo mentale che nella sua libertà e autonomia è un’esperienza tutta interna, veicolata dalle immagini e che si svolge indipendentemente dalla presenza delle cifre, come al tempo degli antichi Romani quando i nostri simboli numerici non esistevano.

Deduciamo questo fatto dall’osservazione in classe di quei bambini che trovano tutto facile e immediato perché evidentemente conoscono la via giusta e non si sono fatti distrarre dalla presenza frastornante delle cifre. Quando, ad esempio, pensano alla quantità «mille», vedono unicamente l’immagine corrispondente che si sono creati. Non si lasciano irretire dalle disquisizioni circa la presenza degli zeri nella scrittura dei numeri, cioè all’uno seguito dai tre zeri («1000»): per loro sarebbe lo stesso se ci fosse scritto «M» come nella numerazione romana. Per questo tutto riesce loro facile.

Quando pensano a «diecimila» viene loro spontaneo riferirsi, come proponiamo loro, a dieci case, ciascuna con dieci finestre, ciascuna con dieci ripiani di palline: niente di speciale o eccezionale.

In questa fase trattano con disinvoltura i numeri scritti come fossero delle etichette.

Il cambio e lo zero

La preoccupazione per il significato dello zero non passa per la loro mente che è invece occupata a trovare le soluzioni del calcolo tramite composizione o ritaglio di immagini.

Alla luce di questa constatazione, la didattica qui proposta rappresenta, per la gioia di alunni, insegnanti e genitori, una «liberazione» dall’assillo dello zero e del cambio, con tutto il bagaglio di spiegazioni verbali ed esercitazioni a base di h, da, u.

Viene meno l’inganno di dover rappresentare il cambio facendo uso di palline sull’abaco, poiché è un meccanismo della scrittura che segue regole interne. Non ha a che fare con la semantica delle quantità che, essendo indipendente dalla scrittura, è universale e non cambia mai.

Addentrarci nell’argomento del cambio con i bambini equivarrebbe a rallentare la pellicola di un film. Il «1000» corrisponderebbe a «un cambio di un cambio di un cambio», cambi su cambi intersecati tra loro come tanti fotogrammi di una pellicola.

Tanto più che sono ancora i nomi latini dei numeri — cioè il codice verbale — a guidarci nelle operazioni di calcolo mentale. Prima la semantica e poi il linguaggio.

Non ci deve passare per la testa l’idea che la decina, prima di ogni suo compimento, provochi una trasmutazione. Il cambio è solo un fenomeno relativo alla scrittura, quasi fosse un codice a barre.

Il Metodo analogico, in definitiva, è nient’altro che la scelta rilassante di evitare disquisizioni che, in fase iniziale, appesantiscono e confondono inutilmente il percorso.

Agendo in questo modo, si guadagnerà tempo e, forse, più avanti sorgerà la curiosità di indagare la meraviglia di questa scrittura così facile da leggere, da scrivere e da usare, ma difficile da capire.

Euro, numeri decimali e frazioni

Sciolti questi nodi, l’alunno è pronto ad affrontare in serenità il campo dei linguaggi, cioè i numeri decimali e le frazioni decimali partendo dagli euro, che spesso fanno già parte delle sue conoscenze.

Nel testo vengono presentati questi apprendimenti «contestualmente» e contemporaneamente perché nella sintesi si ha la cognizione delle parti.

Frazioni decimali e numeri decimali sono in questo modo percepiti come linguaggi o scritture che fanno riferimento alla stessa immagine, che è ancora quella del centinaio.

Cambia il modo di scrivere: sopra e sotto nel caso delle frazioni, destra e sinistra nel caso dei decimali. La virgola è l’equivalente della congiunzione «e». Niente di così particolare: si fanno sempre le stesse cose. Anche in questo caso, coerentemente con il Metodo analogico, il percorso è quello della salita alla cima della montagna

dove incontriamo prima le immagini, poi il linguaggio verbale che fa da ponte e, infine, il linguaggio scritto.

Invertendo il percorso ci troviamo con simboli scritti che equivalgono a gusci vuoti.

Si può ora passare allo studio delle frazioni associate anche al concetto di percentuale. Tutto ha il sapore di cose già note perché, prima di essere linguaggi della matematica, le frazioni sono metafore semplificanti, prese dalla vita quotidiana.

Frazioni

Dire che il 100% dei bambini è presente in classe non significa dire che i bambini sono 100. Dire che la batteria del cellulare è al 10% vuol dire che si sta scaricando. Dire che 3/4 dei bambini ama la pizza significa dire che sono la grande maggioranza. Tutto è immediato.

Alle frazioni viene dedicata una serie di proposte per comprendere in modo intuitivo i vari aspetti: le parti di un intero, le parti di una quantità, il confronto tra frazioni, il calcolo di quantità frazionarie.

In particolare, le frazioni complementari si avvalgono dell’immagine del puzzle per recuperare il significato di completamento.

Le definizioni di frazioni (proprie, improprie, apparenti), care alla disciplina, arriveranno dopo, come parole che non incrinano la forza delle immagini già incontrate.

La sostituzione del segno uguale con le bilance serve a dire che la vera matematica, a volte, si presenta come un gioco.

I problemi

Dopo aver rafforzato il calcolo mentale, invece di passare al calcolo scritto che comporterebbe mesi di lavoro, se non anni, è il momento di affrontare i problemi in un capitolo loro dedicato.

Che cosa sono i problemi aritmetici scolastici? Sono spesso esercitazioni in cui la difficoltà non sta tanto nella risoluzione, quanto nella comprensione delle consegne, come se il linguaggio fosse «inespressivo». Per questo motivo viene scelto di presentare prima i problemi con le immagini, spostando alla fine quelli con solo il testo.

Nella vita i bambini risolvono situazioni ben più difficili, ma a scuola tutto è artificiosità e linguaggio.

I bambini bravi sono addestrati a capire che tutto in matematica è sempre un gioco di parole e partecipano alla finzione considerando ogni problema al pari di una piccola indisposizione fisica da superare.

Sanno che gli strumenti a disposizione della disciplina sono sempre quattro, ed equivalgono alle operazioni della mente dell’aggiungere (addizione), togliere (sottrazione), aggiungere tante volte (moltiplicazione), togliere tante volte (divisione). Quest’ultima va bene sia nei casi in cui bisogna dividere in varie parti (ripartizione), sia in parti prefissate (contenenza).

Problemi proporzionali intuitivi

Il pensiero proporzionale fa parte dei meccanismi cognitivi di ogni persona compresi i bambini. Per questo motivo, viene dedicata la sezione finale dei problemi a questo tipo di risoluzione, affrontata in modo intuitivo cioè senza dar regole.

A pagina 64, di fronte ai problemi rappresentati in tabella, il piacere dei bambini è di scoprire che i «rapporti» nascosti a sinistra valgono anche a destra.

Ciascuno, con in mano la calcolatrice, si sente libero di sperimentare soluzioni vantaggiose che non implichino necessariamente la ricerca del prezzo unitario.

Nei problemi a pagina 68, quando non è immediato trovare questi rapporti semplificanti, viene suggerito il procedimento a incrocio che anticipa la risoluzione in riga che si presenta alla scuola secondaria:

3 : 6,40 = 5 : x

Prima moltiplicando e poi dividendo basterà un attimo per scoprire questa modalità risolutiva che si faceva in origine nella matematica del commercio di 500 anni fa.3

Uno strumento per espandere questo galvanizzante campo di intuitività con gli alunni è il Disfaproblemi con le proporzioni. 4

3 Si veda: Q.A. Bortolato (2021), Larte de labbacho. Il primo libro di aritmetica stampato al mondo, Trento, Erickson.

4 Si veda: C. Bortolato (2021), Disfaproblemi con le proporzioni, Trento, Erickson.

La

calcolatrice

Ciò che conta nella risoluzione dei problemi è saper individuare di volta in volta l’operazione giusta da usare.

Per questo si consiglia vivamente l’uso della calcolatrice, consapevoli che l’abilità risolutiva del calcolo appartiene a un altro percorso di apprendimento routinario che anche una macchina sa fare.

La vera intelligenza è scegliere il tasto giusto.

La possibilità data a tutti i bambini di usare la calcolatrice, oltre a ridurre l’ansia e la fatica legate al calcolo, trasforma la comprensione in un gioco di tasti dove il tasto + permette di «incollare», il tasto — di «togliere», il tasto × di «incollare tante volte» dati uguali, il tasto : di «tagliare» in tante parti uguali. Proprio come quando si è alle prese con la spesa al supermercato.

Per questo molte situazioni sono pensate come acquisti e valutazione di prezzi come fanno «i grandi».

In questo modo, risolvere problemi diventa galvanizzante e si prova e si riprova come gli adulti, facendo anche tantissime operazioni.

Alla fine si stima se la soluzione può essere valida e si controlla con l’autocorrezione.

Ai bambini viene lasciata la libertà di pensare a soluzioni intuitive che li portino gradualmente a sviluppare un’attitudine a «indovinare il procedimento» autocorreggendosi.

Cambia del tutto l’approccio ai problemi. La sofferenza diventa gioia.

Le equivalenze

Anche le equivalenze non devono costituire un problema.

Con le tabelle proposte, la comprensione dura pochi minuti, il tempo di orientarsi. Muovendo una mascherina trasparente dove prima è stata disegnata una virgola, è possibile cogliere che la marca e la virgola sono collegate e si spostano con un gesto equivalente a quello di spostare un bicchiere da un punto all’altro del tavolo, per poi constatare che il valore è inalterato: cambia solo il modo di leggere le stesse quantità. Ora le leggo come dm, ora come hm…

È un dono offerto da questo tipo di scrittura, che è organizzata proprio secondo ordini di grandezze h, da, u… Perché non approfittarne?

Importante è far rilevare agli alunni come la virgola sulla mascherina appartenga alla marca che sta a sinistra.

La modalità di spiegare le equivalenze nei termini di «moltiplicare andando a destra e di dividere andando a sinistra» si presta a capovolgimenti infiniti. Le cose simmetriche si ribaltano facilmente.

È meglio affidarsi a una simulazione senza parole.

Nelle tabelle proposte nelle pagine di esercitazione basta scrivere i numeri negli appositi spazi e muovere la

tesserina trasparente. Tutto diventa immediato. Quando la sequenza delle diverse marche verrà memorizzata questo strumento potrà essere spontaneamente abbandonato per servirsi della visualizzazione mentale che è ancora più veloce.

Il calcolo in colonna

Si passa quindi al calcolo in colonna dove lo zero e il cambio svolgono una funzione imprescindibile, nel senso che senza di loro non sarebbe possibile il calcolo scritto. Quest’ultimo, nella sua funzionalità, può essere accostato alla calcolatrice di oggi.

3 6 3 ×

2 1 5 = 1 8 1 5

3 6 37 2 6 - -

Tuttavia, per il momento, quello che più conta è che l’alunno si interessi esclusivamente all’aspetto utile di questi meccanismi.

Lo scopo per cui è valsa l’introduzione di questa scrittura così «strana» era infatti quello di alleggerire l’umanità dal peso del calcolo a mente. Fare meno fatica...

Se nel calcolo mentale l’alunno doveva «isolarsi» per consultare le immagini del suo schermo mentale, assorbendo giga di memoria, nel calcolo scritto può tenere gli occhi aperti perché i calcoli sono risolvibili, per via procedurale, un pezzo alla volta.

Nel caso delle moltiplicazioni e divisioni la condizione è quella di sapere a memoria i prodotti pitagorici. Tale sforzo, come impegno mentale, equivale a conoscere i nomi dei giocatori di dieci squadre di calcio, con la dif-

ferenza che costoro hanno un volto mentre i prodotti pitagorici hanno bisogno di essere riempiti di emozionalità per essere ricordati.

Tabelline

Infine, lo strumento Tabelline da ritagliare e assemblare presente in chiusura del testo, è pensato per affrontare «fin da subito» moltiplicazioni e divisioni in tranquillità .

In questo modo si ottiene un doppio risultato. La mente degli alunni può concentrarsi con successo sugli aspetti procedurali insiti nelle operazioni e, contemporaneamente, può avviarsi in loro un apprendimento delle tabelline «soft», cioè rilassato, quasi inavvertito.

Un effetto straordinario di proficuità determinato dall’aver scisso l’obiettivo della memorizzazione da quello dell’acquisizione delle procedure.

Nelle divisioni lo strumento funziona in questo modo: contando il numero di caselle si ottiene il quoziente e contando i puntini che avanzano si scopre il resto.

Dopo l’acquisizione immediata delle procedure rimane la fatica di continuare anche da soli il compito di studiare le tabelline servendosi dello strumento.

Un compito, una consegna, in cui ogni bambino deve essere responsabilizzato nel modo giusto. Ad esempio, con parole simili a queste:

«Caro bambino, dandoti questo strumento non ti esonero dall’impegno di imparare le tabelline, che è pura fatica. Ma ti do il tempo che ci vuole, anche in classe.

Dovrai ripetertele a mente tante volte utilizzando lo strumento. E, soprattutto, prima c’è bisogno che tu decida di fare un po’ di posto per loro nel tuo mondo di giochi. C’è bisogno che tu riservi loro un po’ di energia per conservarle nella mente anche quando corri in cortile o a casa quando guardi la televisione. È una forma di accettazione. Anche dimenticare è spesso una scelta: dipende da dove scegli di dirigere il tuo interesse, la tua attenzione e il tuo cuore. Se vivi le tabelline come un compito difficile, gravoso e forzato, la tua mente cercherà di estrometterle per liberarti dal pensiero della scuola. Però, se affronti la loro memorizzazione con serietà ma senza ansia, allora diventeranno parte di te».

Capiterà di trovare bambini per cui è utile non insistere sullo «svezzamento» dallo strumento, a causa di pregressi fallimenti. Per loro vale tanto più il principio di apprendere in uno stato vigile di rilassamento. Il troppo impegno gioca contro, annebbia lo schermo come quando in auto c’è umidità.

Geometria

Nelle discipline scolastiche le parole sono strumenti importantissimi, ma parlando di geometria è meglio assicurarsi prima di tutto che i bambini sappiano usare

i suoi strumenti concreti, che sono la riga, il compasso, il goniometro, ecc.

La riga ci fa comprendere il sistema di misurazione decimale senza bisogno di averlo studiato. Poi si può passare a usare il goniometro per divertirsi a disegnare mandala e poligoni. Così facendo, ciascun alunno e ciascuna alunna possono sviluppare l’intuizione di angolo senza neppure accorgersene. Lo stesso avviene con il compasso. Leggendo le consegne si imparano i vari termini del linguaggio geometrico in situazioni che li rendono significativi.

Le cornicette, da replicare fino a occupare l’intera pagina del quaderno, sono un suggerimento utile per vari motivi:

• sono un momento gratificante;

• sono una performance di attenzione in cui, se sbagli un punto, devi disfare tutto come nel lavoro a maglia;

• sono un modo di «liberare» la mente occupandola in un’attività piacevole;

• sono un momento in cui si può stare soli.

Dal punto di vista didattico:

• sono una palestra di rapporti spaziali in cui ti trovi in ogni momento a scegliere da che parte andare: l’orientamento è una metafora della comprensione;

• sono un’occasione per giocare con l’emozionalità dei colori;

• sono un’esperienza di bellezza attraverso le simmetrie, specchio dell’equilibrio interno;

• inoltre, e non da ultimo, rappresentano una soluzione per l’insegnante che si trova a fronteggiare le richieste dei bambini che finiscono il problema troppo presto rispetto agli altri e lo assillano con la domanda: «E ora cosa facciamo?».

Infine, sono l’occasione per un po’ di silenzio e pausa per tutti.5

La busta degli strumenti del 1000

Per maggior chiarezza e approfondimento è possibile integrare il percorso di matematica con «Gli strumenti del 1000». Si tratta di una busta con otto strumenti che riguardano: calcolo mentale, frazioni, percentuali, equivalenze, tabelline. Usare il pennarello cancellabile per lavorare sugli strumenti, provando, cancellando, correggendo, rifacendo, ecc. permette di raggiungere la comprensione in modo operativo e di consolidare gli apprendimenti. Così come accade nella vita extrascolastica, l’imparare attraverso strumenti (manipolando immagini oppure utilizzando rappresentazioni) accorcia i tempi e diventa una misura di eccellenza per tutti.

5 Per avere altre proposte simili vedi: C. Bortolato (2010), Concentrazione e serenità con le cornicette e i mandala. Proposte grafiche per armonizzare i tempi di lavoro nella scuola primaria, Trento, Erickson.

INDICAZIONI OPERATIVE

Calcolo mentale

Una finestra vale cento, mezza vale cinquanta, una riga vale dieci, un pezzettino vale uno.

Nel riconoscimento istantaneo delle quantità conta la disposizione delle finestre in uno spazio fisso, non solo il loro valore simbolico come nel materiale multibase. È importante svolgere in breve tempo queste pagine.

p. 4 Svolgere a voce collettivamente l’esercizio prima di passare alla compilazione. L’attenzione va focalizzata sui nomi dei numeri (codice verbale) e solo alla fine sui numeri (codice scritto). La presenza di spazi preimpostati per i risultati diminuisce la possibilità di errori sintattici.

p. 5 Il linguaggio verbale fa da guida: ogni numero è una composizione additiva di parole prima di essere steso in cifre. Nell’ultimo esercizio, scegliere l’ordine di lettura delle immagini più comodo.

p. 6 Spiegare alla lavagna come muoversi tra le varie case, cioè da sinistra a destra, dall’alto al basso.

p. 7 Proporre operazioni che presuppongono una limitata scomposizione mentale.

p. 8 Il secondo e il terzo esercizio della pagina servono per sviluppare nuove strategie sganciandosi dalla semantica.

p. 9 Spiegare agli alunni che il calcolo nel «grande» avviene come nel «piccolo» facendo riferimento alle nostre dieci dita. I numeri grandi non fanno paura. Il gioco è sempre lo stesso…

p. 10 Soffermarsi sulle immagini per procedere intuitivamente nelle divisioni. Si consiglia di eseguire gli esercizi più volte a voce anche in giorni diversi prima di scrivere.

p. 11 Confrontare gli esercizi consecutivi per intuire i nuovi risultati. Si consiglia di favorire la memorizzazione dei prodotti fondamentali

p. 12 Suggerire di scrivere i risultati parziali accanto a ogni riga o dove si ritiene più conveniente (colonna o gruppo). È importante far scoprire simmetrie tra gruppi. Consentire l’uso della calcolatrice.

p. 13 Avvisare che si tratta di un lavoro di strategie lungo e complesso, che richiede lo studio delle configurazioni in verticale e in orizzontale. L’esercizio aiuta a sperimentare che a volte l’uso della calcolatrice rappresenta un aiuto, altre invece rallenta il calcolo.

p. 14 Presentare questa proposta come una sfida e lasciare liberi i bambini di scegliere le strategie e gli strumenti che preferiscono. È possibile utilizzare la proprietà associativa della moltiplicazione che fa risparmiare operazioni.

p. 15 Avvertire gli alunni che la risoluzione comporta molto tempo. Dopo l’esecuzione confrontare i percorsi scelti per trovare le soluzioni più convenienti.

Euro, numeri decimali, frazioni

È importante una presentazione sintetica dei vari argomenti. Frazioni decimali e numeri decimali si riferiscono a un’immagine che i bambini hanno già studiato. Si raccomanda quindi all’insegnante di procedere con coraggio e fiducia poiché gran parte dei bambini sa già usare i decimali attraverso gli euro. La comprensione si gioca tutta in alcuni minuti di attenzione.

p. 16 Tutto è presentato insieme. Gli euro sono un riferimento della vita quotidiana e i decimali hanno le stesse immagini del centinaio. La virgola viene accolta come un nuovo linguaggio, con «accettazione». Lasciare la gioia della scoperta, posticipando le spiegazioni.

p. 17 Far notare che lo stesso linguaggio si può rappresentare con scritture diverse, decimali destra/sinistra, frazioni sopra/sotto. Le immagini sono le stesse. Evitare di dare spiegazioni non richieste e lasciare spazio alle intuizioni dei bambini.

p. 18 Prima di compilare la pagina, studiare insieme alla lavagna il procedimento e le varie strategie di calcolo.

p. 19 È utile la strategia di aggiungere lo zero ai centesimi per favorire un confronto tra le cifre dopo la virgola.

p. 20 Subentrano le frazioni non decimali più complesse delle precedenti. Tutta l’attenzione è sulle immagini che, essendo confrontabili, sono il riferimento costante per non perdersi. Rimane inalterata la rappresentazione dell’intero per consentire il confronto su base percettiva e intuitiva. Nell’esercizio 3 suggerire di osservare i disegni del primo esercizio.

p. 21 Nell’esercizio 6 avvisare che ci sono puntini sovrabbondanti.

p. 22 Far comprendere come le frazioni con la scelta di scrittura sopra/sotto siano una trasposizione del linguaggio verbale comune. Focalizzare l’attenzione sulle immagini comparate facendo esercizi di confronto a voce.

p. 23 Riflettere sull’immagine della bilancia che vuole indicare l’equivalenza. A volte è utile tornare allo schema di pagina 22 (esercizio 1). Riprodurlo nel quaderno aiuterà a confrontarsi con le misure reali cogliendone l’equiestensione.

p. 24 Suggerire di mettere a confronto numeratore e denominatore senza bisogno di ricorrere alla visualizzazione semantica.

p. 25 Far notare che il linguaggio verbale guida alla comprensione della scrittura matematica e va analizzato bene.

p. 26 Spiegare che bisogna sempre risalire al valore di una parte dividendo per il denominatore. Le frecce aiutano a capire da dove si parte.

p. 27 Le tesserine del puzzle sono un’immagine gancio, cioè un rimando associativo familiare per spiegare il termine «complementari».

Problemi

I problemi presenti nel libro fungono da modello. Affrontare insieme alla lavagna, alla LIM o sul libro varie pagine insieme per esaminare la tipologia delle situazioni, rimandando a un momento successivo il computo esecutivo.

Suggerire, quindi, di scrivere le operazioni sotto in riga permettendo l’uso della calcolatrice quando i calcoli sono troppo complessi per il calcolo mentale.

Puntare sulla capacità di scegliere le operazioni con la consapevolezza che la capacità di eseguirle in colonna appartiene a un altro percorso di apprendimento. Implementare, se si vuole, i problemi con altre situazioni complesse che scaturiscono dalla vita di tutti i giorni.

p. 28 Soffermarsi sulle immagini che suggeriscono il significato delle operazioni e consigliare di pensare a questi oggetti e al loro significato nel momento della scelta delle operazioni. La calcolatrice permetterà di concentrarsi sulla scelta di queste operazioni.

p. 29 Esaminare insieme varie soluzioni con l’addizione e la moltiplicazione. L’obiettivo è confrontare le procedure possibili e scegliere le migliori, cioè le più funzionali.

p. 30 Il termine «suddividere» rimanda all’operazione della divisione sia di ripartizione che di contenenza. Permettere l’uso della calcolatrice.

pp. 31-32 Qui l’obiettivo è trovare le strategie più comode usando le operazioni convenienti come in un gioco.

p. 33 Scegliere tra addizione e moltiplicazione, preferendo la moltiplicazione quando è possibile. Concedere l’uso della calcolatrice.

p. 34 Per ogni problema mettere a fuoco le diverse strategie del calcolo mentale e del calcolo scritto. Far osservare che qui risulta più veloce calcolare a mente che con la calcolatrice.

p. 35 «Entrare nell’immagine» simulando le operazioni del nascondere, togliere, dividere. Poi pensare alle operazioni scritte. Far osservare che nell’esercizio 24 con la calcolatrice è possibile procedere consecutivamente con le operazioni diversamente dal calcolo in colonna.

p. 36 Lasciare spazio alle strategie della mente (nascondere, aggiungere) e, successivamente, rappresentare il procedimento con le operazioni della matematica. Far osservare che nella sottrazione la calcolatrice assimila varie sottrazioni consecutive.

p. 37 Studiare l’immagine per cercare «simmetrie». Poi scegliere la divisione opportuna. Far osservare che ci sono varie strategie più o meno veloci.

p. 38 Simulare mentalmente più operazioni osservando la figura.

p. 39 Studiare insieme le strategie risolutive a partire dalle immagini prima di pensare alle operazioni aritmetiche. Permettere l’uso della calcolatrice.

p. 40 Viene qui introdotta una terminologia nuova: «resto» e «debito». Spiegare bene i termini.

p. 41 Aumenta la complessità delle situazioni: le quantità sono da immaginare.

p. 42 Viene ora introdotta la divisione di contenenza che complica la situazione portando a tre le opzioni, come si vede nell’etichetta. Far osservare gli indizi linguistici evidenziati nel testo dei problemi.

p. 43 Spiegare ai bambini che dividendo € per € si ottengono merendine, pacchetti, ecc. Queste scoperte generano stupore e alimentano la motivazione.

Equivalenze

Per iniziare, eseguire le equivalenze indicate sugli strumenti muovendo il cursore, quindi passare a quelle del libro. L’esecuzione di questi esercizi deve essere libera da altre spiegazioni che non siano quelle di spostare la virgola da una parte o dall’altra.

La comprensione è solo una questione di orientamento. Altre connotazioni riguardanti l’argomento delle misure vanno trattate a sé.

pp. 44-45 Accogliere le conoscenze della classe in merito agli strumenti presenti nella pagina o di altri di cui hanno esperienza. Approfondire l’utilità di tutti gli strumenti usandoli possibilmente in classe. L’esercizio in fondo è da fare a casa con l’aiuto di un adulto.

p. 45 Presentare insieme le diverse unità di misura osservando sia le immagini sia la costruzione dei termini. La tabella del peso/massa è priva dei multipli del chilogrammo a favore della comprensione.

p. 46 È utile chiedere agli studenti di osservare le tabelle vuote a confronto e far ripetere i nomi delle diverse marche. Spiegare che l’immagine della bilancia sta ad indicare che con le equivalenze cambiano la scrittura e i nomi ma non il «peso», cioè il valore. Da questo deriva la parola «equivalenza». Si consiglia di ricavare la mascherina da una copertina di quaderno trasparente, preferibilmente gialla.

p. 47 Condurre delle esperienze concrete per familiarizzare con le misure. Per la misurazione dell’aula, se possibile, è consigliabile usare il metro laser per stupire i bambini.

p. 48 Riportare a matita le cifre nella tabella e utilizzare la mascherina mobile con la virgola, il risultato sarà immediato.

p. 49 Invitare a visualizzare le sequenze delle marche, anche ripetendole insieme a voce, se qualcuno ha difficoltà farle scrivere a matita sopra alle stringhe.

p. 50 La mascherina evidenzia la virgola insieme alla marca che identifica la quantità. Il procedimento deve essere svolto senza troppa riflessione per evitare disorientamento.

p. 51 Eseguire equivalenze è un compito di orientamento e visualizzazione. Nel QR code della pagina è possibile vedere un video esplicativo. Nell’esercizio 8 l’alunno deve ricostruire mentalmente la successione delle marche.

p. 52 Dopo aver cancellato nella tabella le cifre dell’esercizio precedente, inserire a matita le cifre del successivo e utilizzare la mascherina mobile con la virgola, così il risultato sarà immediato. Nell’esercizio 10 far rilevare come la marca contrassegni sempre l’ultima cifra del numero prima della virgola.

p. 53 È utile evitare giustificazioni e spiegazioni preservando la leggerezza di questi automatismi. La comprensione semantica relativa alle misure deve essere sviluppata a parte.

p. 54 Portare l’attenzione sulle marche presenti all’interno del problema. Le immagini aiutano a comprendere a quale dimensione si riferiscono le misure.

p. 55 Indicare agli alunni l’importanza di considerare per prima la marca della domanda.

p. 56 Avvertire gli alunni che la chiave di comprensione dei problemi è la ricerca nel testo del prezzo unitario, motivo per cui è importante cercarlo sempre. Far notare che le marche sono discordanti.

p. 57 Avvertire gli alunni di dare precedenza alla marca contenuta nella domanda.

p. 58 In questi problemi viene privilegiata una strategia intuitiva di risoluzione. Fare attenzione al linguaggio verbale più che ai numeri.

p. 59 La decodifica del testo dipende da una comprensione sintagmatica in cui hanno valore anche gli articoli. Portare l’attenzione degli alunni sulle parole. Spiegare che si tratta solo di un uso di termini commerciali.

p. 60 Avvertire che si tratta di esercizi per familiarizzare con un linguaggio specifico come decilitri, decalitri, ecc. Attenzione al testo. Rintracciare come primo obiettivo il prezzo unitario.

p. 61 Spiegare che la tabella aiuta a organizzare i dati e guida al risultato: se manca un dato in basso si divide; se manca un dato in alto si moltiplica. Chiarire che la marca €/l indica il prezzo al litro.

p. 62 Spiegare agli alunni che ogni frazione prevede due operazioni. Puntare l’attenzione sull’immagine del rettangolo che rappresenta la frazione considerata in modo che la comprensione avvenga prima sul piano semantico e poi su quello routinario. Far scrivere il risultato finale in rosso.

p. 63 Far osservare che scoprire l’unità frazionaria, cioè un quadratino, è fondamentale.

p. 64 Con queste tabelle si potenzia un approccio intuitivo alla risoluzione proporzionale dei problemi. La prima riga rappresenta il prezzo unitario. Si consiglia l’uso della calcolatrice per i calcoli meno intuitivi.

p. 65 È utile assicurarsi che la consegna sia stata ben compresa, chiarendo ciò che viene rappresentato nella tabella. Far osservare che scoprire il prezzo unitario è fondamentale. Si consiglia l’uso del libro digitale alla LIM che agevola la condivisione delle pagine in classe.

p. 66 Invitare i bambini a confrontare i dati a destra o sinistra per risolvere intuitivamente i problemi. Si consiglia l’uso del libro digitale alla LIM. Permettere l’uso della calcolatrice.

p. 67 Non appare il prezzo unitario. Studiare bene le strategie che permettono di intuire il rapporto confrontando tra loro le quantità. Si può arrivare alla soluzione con procedimenti diversi.

pp. 68-69 Si tratta di un approccio che anticipa le risoluzioni proporzionali che si studiano alla secondaria di primo grado. La disposizione in colonne dei dati piuttosto che in riga aiuta nella scelta delle operazioni. Presentare questa risoluzione solo come un gioco, senza dare spiegazioni di significato sulle operazioni da usare. Le frecce aiutano a seguire il percorso: prima si moltiplica e poi si divide il prodotto ottenuto per l’altro dato presente nell’incrocio. Consentire l’uso della calcolatrice.

pp. 70-71 Lo schema a colonne aiuta a decodificare i dati e prepara alla risoluzione, che può avvenire tramite il sistema a incrocio o risalendo al valore unitario. Non ci sono più le immagini ma basta concentrarsi sui dati.

Calcolo in colonna – addizioni e sottrazioni

Questo argomento è presentato alla fine, ma può essere anche anticipato durante l’anno, dato che qui l’impegno richiesto è solo procedurale.

Il calcolo in colonna è anch’esso calcolo mentale scomposto colonna per colonna. Per ogni colonna dell’addizione gli alunni devono esercitarsi a scegliere l’ordine dei vari addendi di composizione più facile.

Nella sottrazione è possibile, anzi auspicabile, svolgere l’algoritmo partendo dal basso, cioè dal sottraendo, e salendo al minuendo (per riempimento), come avviene in molti Paesi europei e come si era soliti fare nelle procedure più antiche (si veda: Q.A. Bortolato, Larte de labbacho. Il primo libro di aritmetica stampato al mondo, Trento, Erickson, 2021). In tal caso, semplificando tutto il procedimento, non si parla di «prestito» ma di «riporto» da aggiungere alla cifra del sottraendo successivo. Prima di procedere nella spiegazione assicurarsi tuttavia di conoscere bene la procedura e che sia condivisa dai genitori per non disorientare l’alunno con spiegazioni contraddittorie.

Nei casi di maggiori difficoltà nell’effettuare il calcolo colonna per colonna si può ricorrere alla Linea del 20 o alla Linea del 100 (presentate, rispettivamente, in A scuola con Pitti 1 e A scuola con Pitti 2 e in altri volumi del Metodo Analogico dedicati alla matematica). Si consiglia di studiare alla lavagna le difficoltà di ogni esercizio prima di assegnarlo. Gli alunni vanno preparati.

p. 72 Le operazioni sono già in colonna per evitare errori e rendere più veloce il lavoro.

p. 73 Focalizzare, attraverso esempi alla lavagna, l’ordine degli addendi più conveniente, colonna per colonna: l’addizione lo permette. Si tratta sempre di strategie di calcolo mentale.

p. 74 Evitare sovraccarichi di spiegazioni e mantenere un training verbale di supporto sintetico. È possibile utilizzare una procedura «per riempimento» che parte dal basso, come spiegato. In questo caso il «riporto» va aggiunto alla cifra del sottraendo.

p. 75 Nella procedura, colonna per colonna, considerare di operare come se si trattasse sempre con unità. Infatti, sono unità di ordine superiore.

p. 76 Evitare spiegazioni. Sollecitare una risoluzione senza interruzioni a ogni operazione.

p. 77 Quando ci sono più zeri accostati, semplificare il procedimento eseguendo immediatamente i cambiamenti necessari e riducendo il training verbale. «Oltrepassare» gli zeri e andare subito a reperire il prestito.

Calcolo scritto – moltiplicazioni

È utile dedicare tempo allo studio delle varie difficoltà previste negli esercizi da svolgere prima di passare alla compilazione scritta.

Per gli alunni è il momento più intenso che richiede determinazione e impegno.

È possibile anche procedere all’esecuzione dell’esercizio con lo strumento Tabelline (p. 106) per restare concentrati sulla procedura.

È auspicabile, comunque, dedicare spesso qualche minuto al ripasso delle tabelline e procedere appena possibile anche senza questo strumento.

p. 78 Lo strumento consente di dedicare tutta l’attenzione alle procedure che riguardano soprattutto la disposizione delle cifre. È un compito di orientamento spaziale.

p. 79 È fondamentale utilizzare le dita per memorizzare il riporto, così la mente può dedicarsi alla rievocazione dei prodotti numerici.

p. 80 Per la complessità delle operazioni è indispensabile una presenza completa della mente, che deve contemporaneamente consultare la memoria e fare attenzione ai procedimenti. La compostezza del corpo facilita la concentrazione.

p. 81 Consultando lo strumento si consolida l’apprendimento delle tabelline, grazie alle immagini gancio e al vissuto privo di ansia.

Calcolo scritto – divisioni

Lo strumento Tabelline è molto efficace nella fase di apprendimento dell’algoritmo della divisione. A pagina 83 c’è un QR code che ne spiega l’uso. Successivamente è utile diminuirne l’utilizzo e limitarsi a usarlo con gli alunni che incontrano maggiori difficoltà. Far precedere lo svolgimento dell’esercizio da un momento di studio della tabelline è un’indicazione metodologica molto proficua. Si tratta sempre di intensificare lo sforzo ottimizzando la concentrazione e la determinazione.

p. 82 Le caselle e i puntini sullo strumento sono delle metafore per indicare il significato diverso dei numeri coinvolti nell’algoritmo. Usare un training verbale semplice e costante.

p. 83 Aiutare a scoprire il «resto limite» per ciascuna tabellina. Il QR code nella pagina permette la visione di un video esplicativo.

pp. 84-85 La divisione viene scomposta. Prima di ciascun esercizio è utile esaminare e studiare la tabellina sullo strumento evidenziando il «resto limite».

Esercitazioni

Non usare questi esercizi come controllo ma, prevenendo le difficoltà, fare in modo che l’esecuzione avvenga nella modalità di «un apprendimento senza errori».

pp. 86-87 È bene che gli esercizi presentati in queste pagine siano eseguiti senza l’uso dello strumento Tabelline.

pp. 88-89 Per chi è ancora incerto è utile dedicare un momento di rievocazione della tabellina per poi procedere all’esecuzione senza strumento.

p. 90 Si consiglia di analizzare con gli alunni le varie strategie senza eccedere in spiegazioni e di svolgere questi esercizi molte volte oralmente prima di passare alla loro compilazione per iscritto.

Geometria

Per eseguire i vari disegni usare il quaderno a quadretti scegliendo se disporre la pagina orizzontalmente o verticalmente, a seconda delle dimensioni.

Creare un’atmosfera adeguata di ascolto e compostezza poiché questi esercizi hanno anche un valore formativo per la persona. Il procedimento va esemplificato alla lavagna tutto in una volta servendosi di strumenti adeguati come una riga e un compasso da lavagna.

Evitare di dare indicazioni passo per passo agli alunni che potrebbero sentirsi troppo agevolati e quindi esonerati dall’impegno della comprensione. È importante che sviluppino una memoria di molte sequenze.

Attraverso la comprensione delle consegne l’alunno viene introdotto al linguaggio della geometria. È sempre utile far precedere il lavoro sul quaderno da una esemplificazione alla lavagna. Si raccomanda agli alunni di munirsi di un goniometro a 360° e di un compasso di qualità, possibilmente con il dispositivo a vite per fissare l’ampiezza dell’apertura.

La felicità e lo stupore dei bambini saranno grandi.

p. 92 Utilizzare il quaderno a quadretti in orizzontale o in verticale a seconda della figura in modo da avere più spazio e comodità. Insegnare a puntare la matita e poi avvicinare la riga. Curare l’ordine nell’esecuzione e poi lasciare libertà agli alunni nel trovare varianti e nel colorare a piacere.

p. 93 Il goniometro viene qui usato solo come strumento per l’esecuzione delle forme al posto del compasso. Negli esercizi 5 e 6 curare l’intreccio. Si tratta di difficili esercizi di orientamento. Per l’uso corretto del goniometro è possibile utilizzare il QR code presente nella pagina o utilizzare il libro digitale alla LIM.

p. 94 Spiegare il procedimento per cui, ad esempio, per ottenere un decagono basta dividere 360 per 10, ecc. Attraverso questi disegni gli alunni acquisiscono contestualmente il linguaggio della geometria.

pp. 95-96 Per spiegare l’esecuzione è utile che l’insegnante illustri la procedura alla classe con un compasso da lavagna. È importante per gli alunni dotarsi di un compasso di buona qualità.

p. 97 Far stare i due triangoli affiancati sulla stessa pagina in orizzontale. La seconda figura ha il lato di base che non coincide con le linee dei quadretti del quaderno.

p. 98 Ogni esercizio ha un solo disegno. Spiegare il linguaggio contestualmente all’esecuzione.

p. 99 Guidare a disporre il goniometro in modo che il segmento coincida con il punto 0. Far notare che la lunghezza dei segmenti è irrilevante.

p. 100 Aiutare a riorientare il goniometro ruotandolo in modo che lo zero si trovi a destra.

pp. 101-102 Considerare il perimetro semplicemente come il contorno delle figure lasciando scegliere all’alunno la procedura più spontanea, senza formalizzare troppo la situazione geometrica.

p. 104 Utilizzare simultaneamente compasso e goniometro per il disegno.

Appendice: Tabelline

p. 106 È utile assemblare lo strumento quando si devono affrontare le moltiplicazioni e le divisioni in colonna, ma è possibile farlo anche prima per il ripasso individuale delle numerazioni. Non occorre spiegare i simboli agli alunni. È meglio mantenere un’elasticità totale poiché l’apprendimento associativo risponde solo alle emozioni.

STORIA

La novità qualificante di questo approccio alla disciplina è di distinguere gli obiettivi tra la narrazione dei fatti e la questione storiografica delle fonti e poi di perseguirli separatamente.

Nella prima parte infatti, viene affrontata la preistoria proprio come una narrazione, con il pathos emotivo che genera nei bambini.

Nella seconda viene riaffrontato il percorso dal punto di vista delle fonti, attraverso una immaginaria visita a un museo della preistoria.

Prima le emozioni e poi le riflessioni, come si fa sempre nella vita. Prima il fascino terribile di quel mondo popolato da mostri e da paure che risiedono nell’inconscio dei bambini e poi l’esame «freddo» dei reperti.

La prima sensazione dei bambini entrando nel museo sarà di delusione nel vedere che di tutta quella narrazione fantastica non rimangono altro che frammenti di sassi, pietre, ossa.

Ed ecco che si fa spazio un’altra forma di stupore.

«Come avranno fatto gli studiosi a ricostruire tutte le vicende drammatiche osservando questi residui silenziosi?».

La scelta di scindere i due aspetti risponde a un bisogno di chiarezza, funzionale nel momento dell’apprendimento.

Poi, però, non ci saranno cartelle separate nella mente dei bambini perché ognuno è predisposto a questa fusione di dati che si realizza in ogni pausa del respiro.

È l’interdisciplinarietà che non può che svilupparsi internamente.

Fra tutti gli obiettivi, quello più importante resta creare la passione per questa materia di studio.

La narrazione

Il libro si apre con un incipit narrativo che sa di fiabesco:

«Tutto cominciò miliardi e miliardi di anni fa…».

E procede poi con scene di lotta per la sopravvivenza alla fame e alle bestie feroci che «prendono» ed emozionano il bambino.

La narrazione si sviluppa come in un film, appesa alle immagini e ai testi sottostanti che integrano il visivo e si susseguono sempre con lo stesso ritmo dispositivo nella pagina.

La ritualità rende più facile la comprensione perché tutto è prevedibile, anche nella lunghezza dei testi.

Ne sortisce un racconto tale da poter essere letto tutto d’un fiato in autonomia come si fa con un libro non

Prima degli uomini

scolastico, per poi essere riletto con più riflessione con l’insegnante, attraverso un lavoro di scavo progressivo per far emergere quelle connessioni causali o consequenziali che rappresentano il filo della vera comprensione.

Primi uomini

La narrazione comincia dalla nascita dell’Universo spiegata con l’immagine del Big Bang, che rappresenta una delle ipotesi avanzata dagli scienziati. Altri scienziati, più che di una esplosione, parlano di una espansione ordinata di un primordiale atomo generativo.

Si passa poi a considerare la nascita della vita, sia vegetale che animale, in chiave evoluzionistica e con un evidente aggancio alle scienze.

Si arriva così alla comparsa dell’uomo, anzi dei primi ominidi che, piccoli di statura, cercavano di sopravvivere unicamente con la fuga e si sfamavano con la raccolta di frutti, radici, ecc.

Si succedono poi le varie popolazioni, ciascuna con le sue caratteristiche, fino ad arrivare all’Homo sapiens che possiamo definire come il nostro «vero» progenitore.

La mappa riassuntiva

Il nome delle varie specie di ominidi (Australopiteco, Homo habilis, Homo hergaster, ecc.) compare alla fine di ogni capitolo/sezione, cioè in second’ordine, per privi-

legiare la forza del racconto. E non ci sono volutamente date o altri elementi che risulterebbero poco significativi per i bambini.

In questo momento ognuno vive come se le vicende facessero parte della sua vita.

Come portare l’acqua, come accendere il fuoco, come trovare il cibo, ecc. stimolano la curiosità di ogni bambino, che si sente immerso in un «gioco della sopravvivenza».

La mappa finale consente in due pagine di riassumere il percorso.

Ed è qui che l’insegnante può dare finalmente alcune date metabolizzabili per i bambini.

Nella pagina di sinistra, c’è il Paleolitico che sembra una passeggiata ma è lungo due milioni di anni.

Visita al museo

A destra c’è il Neolitico, cioè la vita nei villaggi che possiamo collocare a 10.000 anni fa .

Sempre a destra si vede la fine del Neolitico, risalente a circa 5000 anni fa , nel momento in cui la scrittura aprì allo sviluppo delle prime civiltà.

È lo schema generale alla portata della comprensione dei bambini il cui raggiungimento può stabilire un successo nell’apprendimento.

Dopo la fantasia ci si tuffa nella realtà del museo.

Tutti gli aspetti che riguardano il lavoro dell’archeologo e del paleontologo sono affrontati in questa sezione del testo, dedicata alle fonti del sapere, dove lo spirito storiografico la fa da protagonista.

Ed è proprio qui che l’insegnante ha modo di approfondire la differenza tra i reperti e i documenti scritti.

I bambini, girando per le stanze come fossero in gita, si rendono conto che tutta la ricostruzione storica poggia su cocci di vasi, anfore, ossi, ecc. cioè su reperti a cui la gente comune non darebbe alcun valore.

Poi soffermandosi a leggere sull’etichetta di un coccio la parola «Paleolitico», ogni bambino ripenserà alla pagina sinistra della mappa e si congratulerà con se stesso: si sentirà esperto. Neandertal, Homo erectus, Homo sapiens, ecc. non sono parole vuote ma immagini già incontrate.

Andare al museo diventa così una conferma che dà emozione perché si ritrovano cose conosciute.

Così come fanno paleontologi e archeologi che, chissà, magari hanno sviluppato la loro passione sui banchi di scuola.

GEOGRAFIA

Orientarsi, viaggiare, vivere gli ambienti e infine il lavoro dell’uomo.

Sono i temi in cui si articola questo programma di geografia di classe terza che ha l’obiettivo di proporre contenuti pregnanti per corrispondere alle attese dei bambini.

Il principio guida è che tanto più questi contenuti sono ricchi e interessanti, quanto più stimoleranno la sete di nuovo dei nostri alunnni e delle nostre alunne.

Orientarsi

L’orientamento è il problema dei problemi, sia quando si tratta di esplorare luoghi geografici, sia quando si tratta di esplorare nuovi campi del sapere, di organizzare le conoscenze che si raccolgono e le questioni che emergono.

Un modo di procedere speculare tra dentro e fuori, tanto che, quando non comprendiamo qualcosa, invece di dire «non capisco» ricorriamo a metafore come «mi sono perso, ho smarrito la strada».

Breadcrump

Da questo punto di vista, la gran parte dei siti internet va incontro a questo bisogno costante di orientamento

presentando, solitamente in alto nella pagina di navigazione, una stringa chiamata breadcrumb, che letteralmente significa «briciole di pane». In questo modo, viene mostrata la posizione della pagina attuale all’interno del sito, il percorso fatto per arrivarci. È una citazione tratta dalla popolare fiaba di Pollicino che lasciava una scia di briciole di pane lungo il suo cammino per poterlo ripercorrere all’indietro.

Una strategia anti-smarrimento che richiama anche la vicenda del «filo di Arianna», che Teseo srotolava nel labirinto di Cnosso per riuscire a tornare indietro dopo aver ucciso il Minotauro.

La stessa soluzione, del resto, viene applicata negli ospedali quando il personale ci indica di seguire una fascia colorata sul pavimento per evitare di fornirci lunghe e complicate spiegazioni verbali.

Un tema, quello dell’orientamento, che i bambini hanno appena incontrato in storia quando i primitivi percorrevano le foreste, la savana e i deserti, sempre con il terrore di perdersi.

Nel testo, le prime immagini sono un invito per l’insegnante ad approcciare questo argomento in modo evocativo, come fosse una fiaba, facendo leva su una esperienza che ognuno vive di continuo. Può accadere di vivere questo smarrimento anche in tutte le materie, quando il contenuto da posizionale e circoscritto si fa vaporoso e astratto, come nuvole in cielo, e ogni riferimento diventa nullo.

Carte geografiche

Il principio fondante del Metodo analogico è dare un posto fisso alle cose perché tutto quello che si muove è perso per la conoscenza .

Le carte geografiche sono il linguaggio analogico che non descrive a parole ma comunica con le forme e i colori. È il ricorso alle immagini che talvolta rende persino superflue le legende perché ognuno può recuperare il loro significato in autonomia.

Quando usiamo una mappa digitale, il dito che si muove sulla cartina è il mouse che si muove sullo schermo.

Il navigatore consente di avere sottomano migliaia di cartine senza la necessità di troppe spiegazioni preventive. Muovendo le dita si aggiunge poi l’operazione di zumare, che è come appropriarsi dell’occhio di un falco che si alza e si abbassa a piacere.

L’idea di passare le ore di geografia a conoscere il mondo usando questo strumento può diventare ora una realtà.

«Oggi, cari bambini e bambine, vi guido con Google Earth a esplorare tutta l’Africa partendo dalle coste del Mediterraneo per poi attraversare il deserto del Sahara ed entrare nelle savane dove vivono i leoni.

Poi sorvoleremo anche tutto l’oceano popolato di balene fino al Polo Sud, così contagio anche voi con la mia passione per i viaggi».

Ma un’attività ancor più formativa — che dipende dall’insegnante poiché nessun libro scolastico di geografia può offrirla — è quella di fornire ai bambini una cartina tradizionale cartacea del proprio territorio e poi una cartina della provincia. Perché? Per guardarla all’infinito come fosse uno schermo fisso, grande come il banco per esplorarla con gli occhi e con le dita e assimilare il più possibile nomi di paesi, di fiumi, di località, strade e autostrade.

«Poi faremo un gioco per vedere chi sa più nomi di paesi confinanti con il nostro».

Un’attività benefica di nozionismo intelligente.

Un piacere enciclopedico ma circostanziato, che è quello che gli adulti maturano negli anni e che qui è perseguito come un «extra» divertente.

Un altro studio a cui dedicarsi sarà quello di scoprire come funziona il navigatore e come ricava i dati «spiando» e incrociando la rilevazione dei nostri movimenti dal cielo tramite i satelliti.

Tutto un altro mondo fantastico per educare al piacere di crescere in maniera consapevole.

Viaggiare

Dopo aver imparato a orientarsi, l’attenzione nel testo è dedicata a viaggiare scegliendo il mezzo di trasporto più adatto.

«Perché il treno, perché l’aereo, perché l’auto?

Quale mezzo è più indicato per le persone? E per le merci?

Le autostrade sono più o meno sicure delle strade urbane?».

Seguendo il testo, l’obiettivo è quello di stimolare la discussione a ogni immagine perché le risposte non sono sempre univoche.

«E come sono fatti questi mezzi di trasporto?

Costa di più un viaggio in treno o in aereo?

Quali sono le strade della tua città o paese?

Quale origine ha il nome della via in cui abiti?».

Tutti temi in cui si agganciano Scienze e Tecnologia e anche Storia, senza che per questo ci sia bisogno di perseguire dei collegamenti in modo mirato. Questi, infatti, scaturiranno come una conseguenza e dalla curiosità autentica dei bambini e delle bambine, alimentata da argomenti interessanti e coinvolgenti.

Gli ambienti

Il tema classico degli ambienti, già introdotto in classe seconda, viene ora approfondito soprattutto attraverso foto della realtà che, rispetto ai disegni, sono più difficili da leggere utilizzando la lente dell’osservazione guidata dai criteri geografici.

Vivere la montagna

Vivere la collina

L’intento è di superare la banalità del vedere senza osservare.

Ogni tipologia d’ambiente è introdotta da una tavola a tutta pagina per conoscere la terminologia e abituare all’osservazione. Perciò il gioco sarà quello di rintracciare nell’immagine almeno 30 dettagli.

Nelle pagine successive ogni rappresentazione diventerà uno spunto per fare emergere le correlazioni tra ambiente fisico e antropologico, sociale ed economico.

Quali sono i vantaggi e gli svantaggi di vivere in montagna?

È la domanda ricorrente a ogni inizio di capitolo, a cui i bambini sono invitati a rispondere usando le parole giuste che si trovano nei testi sottostanti.

Il testo verbale si presta ad acquisire il lessico specifico della disciplina: aspetto fisico, clima, risorse, flora e fauna, paesaggio, turismo invernale ed estivo, ecc.

Nella cartina introduttiva dell’Italia si vedono le colline senza che vengano specificati tutti i loro nomi.

Viene poi posta l’attenzione sul rapporto tra agricoltura e industria, accostando le immagini del vigneto a quelle della cantina, dell’uliveto a quelle del frantoio, le immagini del noccioleto all’industria dolciaria.

Vivere la pianura

Vivere il fiume

Vivere il mare

Nelle pianure si fa più forte la correlazione tra agricoltura, industria e commercio. Anche in questo caso si lascia molto spazio a quelle dell’intuizione e il testo verbale rimane semplificato al massimo.

Le immagini sono «pretesti», sono lo spunto, per discorsi importanti.

Affrontando il fiume in termini generali, si ha l’impressione che sia sia dotato di vita, perché nasce e poi muore. Può viaggiare in tranquillità o fare grossi danni.

Le casse di espansione sono un paradosso che colpisce l’immaginario dei bambini: sono degli allagamenti voluti per salvare da altri allagamenti che si vogliono invece evitare.

Anche il mare ha la sua vita burrascosa o tranquilla.

Può essere generatore di bellezza e salute o portatore di guai.

Può rappresentare una via preferenziale per i trasporti e i viaggi ma anche un ostacolo agli spostamenti.

Il lavoro

Il quarto capitolo, dedicato alle professioni, comporta un salto linguistico notevole con l’introduzione di espressioni specifiche del «gergo» geografico, come: settore primario, secondario, terziario, professioni, artigianato, industrie tessili, alimentari, meccaniche, e poi ancora lavoratori, disoccupati, anziani.

L’esame di ciascun testo va seguito parola per parola dall’insegnante, non spiegando, ma attendendo le domande dei bambini che saranno felici di cimentarsi in un linguaggio che appartiene al mondo degli adulti.

SCIENZE

Il mondo degli animali, delle piante e infine alcune nozioni riguardanti la materia che ci circonda: è il programma curricolare di scienze che ha l’obiettivo di stupire i bambini e insegnanti per l’importanza dei contenuti affrontati e la leggerezza di come sono presentati.

Studiare scienze è scoprire che dietro alla complessità c’è qualcosa di semplice a cui anche un bambino può arrivare.

E la sintesi finale per i bambini è questa:

«Possiamo pensare che, in qualche modo, animali e piante sono come noi, che per sopperire alla nostra fragilità abbiamo bisogno di trovare strategie intelligenti.

Però le piante hanno una particolarità unica rispetto agli animali perché si nutrono senza «rubare» il cibo a nessuno visto che lo ricavano dal «cielo». E poi dobbiamo proprio ringraziarle perché si nutrono di una sostanza come l’anidride carbonica che a noi proprio non serve, mentre rilasciano nell’atmosfera il prezioso ossigeno».

Sono i pensieri di un bambino che personifica ed estende al mondo le sue considerazioni intrise di un’ingenuità che molto spesso fa rima con genialità.

Perché il paradosso fa parte del suo pensiero che coniuga il piccolo e il grande rompendo i confini tra una disciplina e l’altra.

I bambini applicano d’istinto quell’interdisciplinarietà che non può essere veicolata completamente dai libri di testo perché troppo difficile da esprimere a parole. Sono come gli uccellini che vanno su e giù per vedere le cose da vicino e da lontano. Ed è la forma di pensiero migliore che ci sia.

Gli animali

Viene presentata per prima l’esperienza della classificazione degli animali che, indipendentemente dal suo valore e dal fatto di non essere completa, è un’esperienza di ordine imprescindibile in questo periodo in cui tutto affastellandosi diventa memoria volatile e temporanea.

Nella pagina 122 di presentazione si vedono tutti gli animali classificati in modo simmetrico: a sinistra gli invertebrati divisi in cinque gruppi e a destra i vertebrati suddivisi in altrettanti gruppi.

È il riassunto in anteprima di quello che verrà spiegato dopo e in cui viene privilegiata la simmetria rispetto all’esaustività dei contenuti, come consuetudine del Metodo analogico.

Sarà anche la pagina sintesi a cui ritornare alla fine del percorso quando, per dare una prova di comprensio -

Gli invertebrati

ne, l’insegnante potrà chiedere agli alunni di riscriverla a mente.

Mancano, per una scelta di semplificazione, riferimenti agli altri regni (come quello dei funghi) e ad altri esseri viventi come alghe, batteri, ecc.

I cinque gruppi di invertebrati scelti si succedono pagina per pagina ognuno con il sottotitolo che, come un occhiello del giornale, sintetizza il contenuto: una frase che, agendo da spoiler, trasforma la lettura successiva in validazione cioè in rinforzo.

Nella narrazione è tutto un crescendo di scoperte in un intreccio linguistico tra registro evocativo e informazioni di carattere scientifico.

Gli anellidi, come ad esempio i lombrichi, sono indifesi ma straordinari per la loro resistenza. La tenia che vive nell’intestino può essere lunga 10 metri e perde pezzi di coda.

I molluschi sono capaci di proteggersi in una conchiglia che il nemico non riesce ad aprire. Il calamaro gigante è lungo più di un peschereccio ma, per fortuna!, sta in fondo al mare.

I crostacei hanno una corazza snodabile come quella dei samurai.

Gli aracnidi, come il ragno, sono senza corazze ma catturano prede che sono più armate di loro. La tarantola golia lancia peli velenosi come frecce.

Gli insetti sono i più numerosi e sanno vivere in città organizzate dove ciascuno ha la sua mansione.

Ogni testo è pensato per suscitare stupore soprattutto per la capacità inaspettata di questi piccoli animali di sopravvivere. Non c’è altro impegno dell’insegnante che condividere questo stupore con i suoi alunni.

I vertebrati

Tutto ha il sapore di una narrazione anche quando si passa a considerare i vertebrati. Anzi, si incrementa mettendo in evidenza le giuste relazioni di causaeffetto.

I vertebrati si chiamano così perché hanno un sistema nervoso talmente sviluppato da prolungarsi dentro a una catena di ossa appositamente bucate: le vertebre.

I pesci «sono fortunati» perché non sentono il loro peso. Sono però confinati a vivere nell’acqua e si perdono tutto il mondo che resta fuori, tranne il pesce volante che fa dei voli, anche se brevi, fuori dall’acqua.

Gli anfibi, incuriositi dal mondo circostante, si sono avventurati nel terreno trasformando le pinne in zampe.

I rettili come i coccodrilli, per andare sempre più lontano dall’acqua, si sono provvisti di una pelle fatta di squame perché il sole non li secchi.

Vengono poi gli uccelli che per conquistare il mondo hanno trasformato il primo paio di zampe in ali precedendo il sogno degli uomini.

Per ultimi, i mammiferi che hanno bisogno di allevare per molto tempo i loro piccoli nel proprio ventre e poi di nutrirli in un lungo svezzamento prima che diventino adulti, proprio come succede a noi.

Si passa quindi ad approfondire alcuni argomenti che riguardano tutti questi animali:

• la meraviglia di come nasce la vita scoprendo che tutto parte da un uovo fecondato;

• lo stupore di scoprire come la vita degli uni dipende dalla vita degli altri, attraverso la metafora della catena;

• l’iperbole di scoprire che i lombrichi così piccoli e repellenti in verità sono indispensabili per la vita di tutti.

Le piante

Affrontando lo studio delle piante ci si accorge che sono degli esseri non meno «intelligenti» degli animali e che, osservandole con attenzione, nascono molte curiosità:

«Come fanno a resistere al freddo, al caldo, all’aggressione degli animali, alle intemperie, agli incendi?

Come sono fatte nel dettaglio le piante che, da un certo punto di vista, ricordano in parte il funzionamento del nostro corpo?

Che cosa mangiano?».

Viene suggerito come esperienza pratica in classe l’esempio di una patata che germina in un vasetto d’acqua.

Cosa succede in una foglia?

La tavola di pagina 151 rappresenta un tentativo di spiegazione e sintesi della fotosintesi clorofilliana , un argomento che spesso corre il rischio di essere affrontato affastellando una serie di spiegazioni vaghe e poco significative.

In chiave di ingenuità si vedono le molecole di anidride carbonica, composte da due palline di ossigeno e una di carbonio (come si capirà meglio a pagina 155), entrare negli stomi della foglia e combinarsi poi con l’acqua che sale dalle radici. Si vedono anche la clorofilla e la luce solare che giocano un ruolo fondamentale nel processo.

A destra c’è il condotto per l’ossigeno in uscita e a sinistra quello che trasporta il risultato della fotosintesi: gli atomi di anidride carbonica, che, unendosi all’acqua, si trasformano in zuccheri (carboidrati) che scenderanno a nutrire la pianta.

Un altro paradosso per i bambini è scoprire che lo zucchero, che per noi è bianco, «è fatto» di carbonio. Anche il nostro corpo «è fatto» di carbonio!

Lo schema di questa foglia e poi l’immagine personificata della molecola di anidride carbonica sono una riprova che gli argomenti più complessi possono diventare accessibili passando attraverso l’immaginazione. Sono rappresentazioni semplificate che possono apparire ingenue ma, come succede con il Metodo analogico in ogni materia, sono veicolo preferenziale per la comprensione.

Nello schema di pagina 154 viene messo in rilievo il ciclo del carbonio che dall’aria passa alle piante e al corpo di tutti gli esseri viventi per poi ritornare nell’aria.

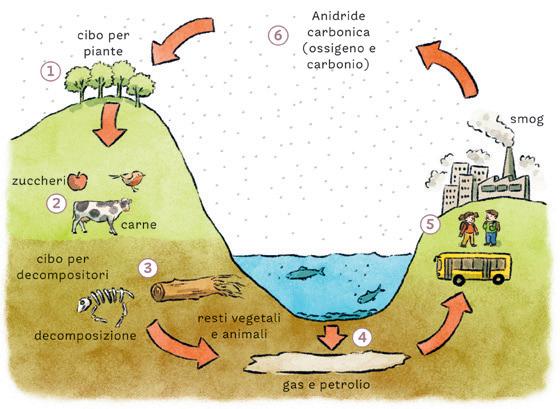
La vita continua e possiamo osservare in classe un ciclo analogo, coltivando una piantina di geranio che si

La materia

nutre dell’anidride carbonica del nostro respiro, liberando a sua volta l’ossigeno per noi. Un’esperienza di reciproco accudimento!

A pagina 162, troviamo la conclusione del percorso, che presenta in modo metaforico le somiglianze tra animali e piante: possiamo dire che tutti, in qualche modo, nasciamo da un embrione avvolto dal nutrimento preparato da una «madre».

Anche noi abbiamo avuto una storia simile nella pancia della mamma: l’amore, la cura e la generosità accompagnano ogni aspetto della vita.

L’ultima parte è dedicata alla materia di cui è formata ogni cosa che vediamo e non vediamo.

Zumando sulle molecole si scopre un mondo infinitamente piccolo che assomiglia al mondo infinitamente grande. Ritorna il discorso dell’analogia tra il piccolo e il grande.

Tutto ciò che è invisibile all’occhio umano, come le molecole e gli atomi, è rappresentato attraverso palline che si comportano tra loro come bambini che si tengono stretti per mano, oppure si lasciano andare liberi come le molecole dei gas.

A pagina 166 si vede l’acqua che fa un viaggio, come il carbonio, dal cielo alla terra e dalla terra al cielo.

Pur nella sua apparente inoffensività è capace di sciogliere la roccia, sgretolare le montagne, tagliare il ferro, ecc.

Anche l’aria che è invisibile possiede una forza inimmaginabile che risiede proprio nel suo cedere momentaneamente sotto la compressione.

Le caratteristiche diverse dell’acqua e dell’aria sono state sfruttate nel mondo del lavoro e possono essere anche occasione di osservazione in classe.

Le immagini suggeriscono alcuni esempi come la pentola a pressione che ha due valvole (di sicurezza e di sfogo), i flaconi spray, gli pneumatici o una comune pompa da bicicletta.

Oggetti questi che portati in classe possono offrire opportunità di studio in grado di incentivare l’interesse verso questo tipo di investimenti cognitivi.

Attività finali

Il gioco del cercaparole, a differenza delle consuete verifiche, induce nei bambini il gusto di cercare nel testo la soluzione come se si trattasse di una caccia al tesoro. Risparmia, quindi, l’ansia delle domande e genera ulteriore apprendimento.

Un’altra attività a cura dell’insegnante può essere quella di preparare dei quiz con decine di domande a risposta breve, proprio come se fosse un quiz televisivo a cui l’alunno dovrà prepararsi in autonomia per poi rispondere in classe. È un modo di studiare rassicurante che i bambini apprezzano molto. Anche questa attività consolida e stimola moltissimo l’apprendimento.

Un’attività finale importante dal punto di vista della valutazione dell’insegnante è quella che riguarda la capacità espositiva orale.

Non ci sono domande e risposte, ma ciascun alunno, preferibilmente davanti a un leggio, spiega con le sue parole l’argomento studiato seguendo le immagini.

Il suggerimento è quello di prepararsi nascondendo con una striscia di carta i testi che sono sotto alle immagini per provare a ripeterli in autonomia.

Oltre a queste attività finali, a piè di pagina di ogni argomento vengono suggeriti degli approfondimenti per stimolare ricerche personali e di classe.

Supervisione editoriale

Giuseppe Degara

Progettazione / Editing

Tommaso Martino

Lucia Dorigatti

Collaborazione

Mariarosa Fornasier

Laura Bordignon

Direzione artistica

Enrico Bortolato

Giordano Pacenza

Progetto grafico

CHIALAB

Enrico Bortolato

Illustrazioni

Michela Nava

Lorenzo Sangiò

Chiara Ficarelli

Illustrazioni di copertina

Enrico Bortolato

Impaginazione

Mirko Pau

Camillo Bortolato

Insegnante e pedagogista, autore di strumenti e materiali sul Metodo Analogico pubblicati con Erickson.

www.camillobortolato.it www.erickson.it

A scuola con Pitti è una proposta completa per svolgere il percorso curricolare di classe terza in modo diretto e veloce, all’altezza delle aspettative dei bambini e delle bambine.

Proprio per questo, persegue il principio del fare di meno per imparare di più, rinnovando ogni materia all’insegna dell’essenzialità che si traduce in maggior efficacia.

Una scelta di cambiamento che nasce da decenni di esperienza nelle classi con il Metodo Analogico.

Il mio libro di LETTURA

Il mio quaderno di SCRITTURA

Il mio libro di MATEMATICA

Un «vero» libro di narrativa, al posto di tanti brani frammentati, che racconta le avventure di una volpe misteriosa e dei bambini che si mettono sulle sue tracce. Seguono storie tratte dalla tradizione, filastrocche e canzoni, per appassionare gli alunni al piacere della lettura.

Permette di perfezionare il corsivo e l’ortografia con esercizi confermativi che prevengono l’errore. Inoltre, sviluppa il testo personale grazie a una serie di modelli e, mediante la striscia dell’analisi grammaticale e l’armadio dei verbi, approfondisce al volo questi argomenti.

Attraverso strumenti e rappresentazioni che veicolano le competenze, il volume consolida il calcolo mentale, per passare poi alla complessità dei problemi (centesimi, frazioni e misure) e alla fine affrontare senza timore moltiplicazioni e divisioni. Il tutto con il sorriso e senza paura di sbagliare.

Il mio libro di STORIA GEOGRAFIA e SCIENZE

Il libro propone le discipline in modo sintetico e chiaro, privilegiando, per presentare le informazioni, un approccio narrativo e ponendosi l’obiettivo principale di affascinare alunni e alunne con contenuti pregnanti.

LIBRO e RISORSE DIGITALI

I volumi e la Guida sono disponibili anche in formato digitale, con materiali e risorse aggiuntive.