Axel - carnet des savoirs 3e année by Les Éditions CEC

Mathématique, 3e année du primaire Carnet de savoirs

A× e l

Isabelle Lajeunesse

Marie-Andrée Latendresse

Stéphanie Marier

Annie Tremblay

Conforme à la PDA

Direction de l’édition

Geneviève Bruneau

Direction de la production

Manon Boulais

Direction de la coordination

Rodolphe Courcy

Charge de projet

Marie-Soleil Boivin

Marie Sylvie Legault

Julie Provost

Révision linguistique

Julie Provost

Correction d’épreuves

Jacinthe Caron

Conception graphique et réalisation technique

Chantale Richard-Nolin

Illustrations

Alexandre Roger

Illustrations techniques

Michel Rouleau

La Loi sur le droit d’auteur interdit la reproduction d’œuvres sans l’autorisation des titulaires des droits. Or, la photocopie non autorisée – le photocopillage – a pris une ampleur telle que l’édition d’œuvres nouvelles est mise en péril. Nous rappelons donc que toute reproduction, partielle ou totale, du présent ouvrage est interdite sans l’autorisation écrite de l’Éditeur.

Axel, Mathématique, 3e année

Carnet de savoirs

9001, boul. Louis-H.-La Fontaine

Anjou (Québec) H1J 2C5

Dépôt légal : 2023

Bibliothèque et Archives nationales du Québec

Bibliothèque et Archives Canada

ISBN 978-2-7662-0754-1 (Carnet de savoirs)

ISBN 978-2-7662-0859-3 (Cahiers A et B, Carnet de savoirs)

ISBN 978-2-7662-0868-5 (Version maZoneCEC, accès élève

1 an, livraison électronique)

Imprimé au Canada

Sources iconographiques

Shutterstock

3 : Calculatrice © siridhata. 4 : Billes © Kellis ; Bonbons © Reamolko. 7 : Augmentation de volume © Mark stock. 8, 35 : Cartes © filiz buber. 12 : Crayon rouge © Anton Starikov. 12, 26 : Règle © NiRain. 15 : Blocs emboîtable © PhoebeChang. 16 : Pastilles de gouache © NsdPower.

17 : Crayons © Iryna Stegniy ; Pinceau © Sergey Zhukov. 18 : Tache © Sofia Shimanovskaia.

20 : Brocolis © Magicleaf ; Assiette © yingthun. 21 : Gaufre © Tetsuo Buseteru ; Bleuets © Ekaterina Shabalina ; Tarte © Alfmaler ; Biscuits © Tartila. 22 : Avocat © Angela Ksen ; Orange © CRStocker. 22, 36 : Fraise © uiliaaa. 22, 36, 41 : Carotte © Vasilisa Kryuchkova. 23 : Fourmis © PainterMaster ; Coccinelles © iMacron ; Feuille © azure1. 24 : Loupe © Ardiyana ; Boîte à fleurs et arrosoir © Nadiyka U ; Étiquette © moore_moore. 26 : Lit, tapis © pichayasri ; Corbeille © yura borson. 29 : Eau bouillante © MarySan ; Robinet © mera haval ; Glaçons © SpicyTruffel ; Thermomètre © DigitalArtHurkova ; Tasse © Nadejda Emelyanova ; Sucette glacée

© mollicart ; Pichet © Vector Tradition. 34, 39 : Ballon chien © ebe_dsgn ; Chien © ViJul. 34, 39 : Balance © Paitoon Pornsuksomboon. 34, 42 : Ballon © Anastasiia_Kulyk ; Mongolfière © Maria Averburg. 35 : Dés © Other-4.

iStockphoto 29 : Thermomètre © Talaj.

1 2 3 4 5 27 26 25 24 23

A× e l

Quelques conseils pour utiliser ton carnet de savoirs.

Tu dois faire une fiche Pour la maison ou une Activité supplémentaire ?

Tu trouveras toutes les notions expliquées dans la première section de ton carnet.

Tu ne comprends pas un mot de vocabulaire en mathématiques ?

Rends-toi à la page 36, tu trouveras tout le vocabulaire mathématique du 2e cycle !

Un symbole étrange te donne des maux de tête ?

Consulte la légende des symboles à la page 43.

Tu as oublié combien font 9 × 8 ou 56 ÷ 7 ?

Consulte les tables de multiplication et de division à la page 45.

9001, boul. Louis-H.-La Fontaine, Anjou (Québec) Canada H1J 2C5 Téléphone : 514-351-6010 • Télécopieur : 514-351-3534

Cahier A Notion 1 ............................................ 3 Notion 2 ............................................ 4 Notion 3 ............................................ 5 Notion 4 ............................................ 6 Notion 5 7 Notion 6 ............................................ 8 Notion 7 ............................................ 9 Notion 8 .......................................... 10 Notion 9 .......................................... 11 Notion 10 .......................................... 12 Notion 11 .......................................... 13 Notion 12 .......................................... 14 Notion 13 15 Notion 14 .......................................... 16 Notion 15 .......................................... 17 Notion 16 .......................................... 18 Cahier B Notion 17 .......................................... 19 Notion 18 20 Notion 19 .......................................... 21 Notion 20 .......................................... 22 Notion 21 23 Notion 22 .......................................... 24 Notion 23 .......................................... 25 Notion 24 .......................................... 26 Notion 25 .......................................... 27 Notion 26 .......................................... 28 Notion 27 29 Notion 28 .......................................... 30 Notion 29 .......................................... 31 Notion 30 32 Notion 31 .......................................... 33 Notion 32 .......................................... 34 Notion 33 .......................................... 35 Vocabulaire du 2e cycle 36 Symboles du 2e cycle 43 Tables d’addition et de soustraction 44 Tables de multiplication et de division 45

Table des matieres

La représentation des nombres naturels

• Les nombres naturels servent, par exemple, à compter des objets ou des êtres vivants.

• On peut écrire tous les nombres à l’aide des 10 chiffres.

Chiffres

213

132 Nombres

• Représenter un nombre, c’est l’écrire ou l’illustrer avec un dessin ou du matériel.

Exemple

Voici 4 représentations du nombre 1 328.

Si j’ai bien … compris

Mille-trois-cent-vingt-huit

Représente le nombre 2 437 de 2 façons.

À l’aide d’un abaque

À l’aide de jetons dans un tableau de numération

UM C D U UM C D U

1 Notion 1 Cahier A, p. 2

0 -

- 3 - 4 - 5 - 6 - 7 -

8 - 9

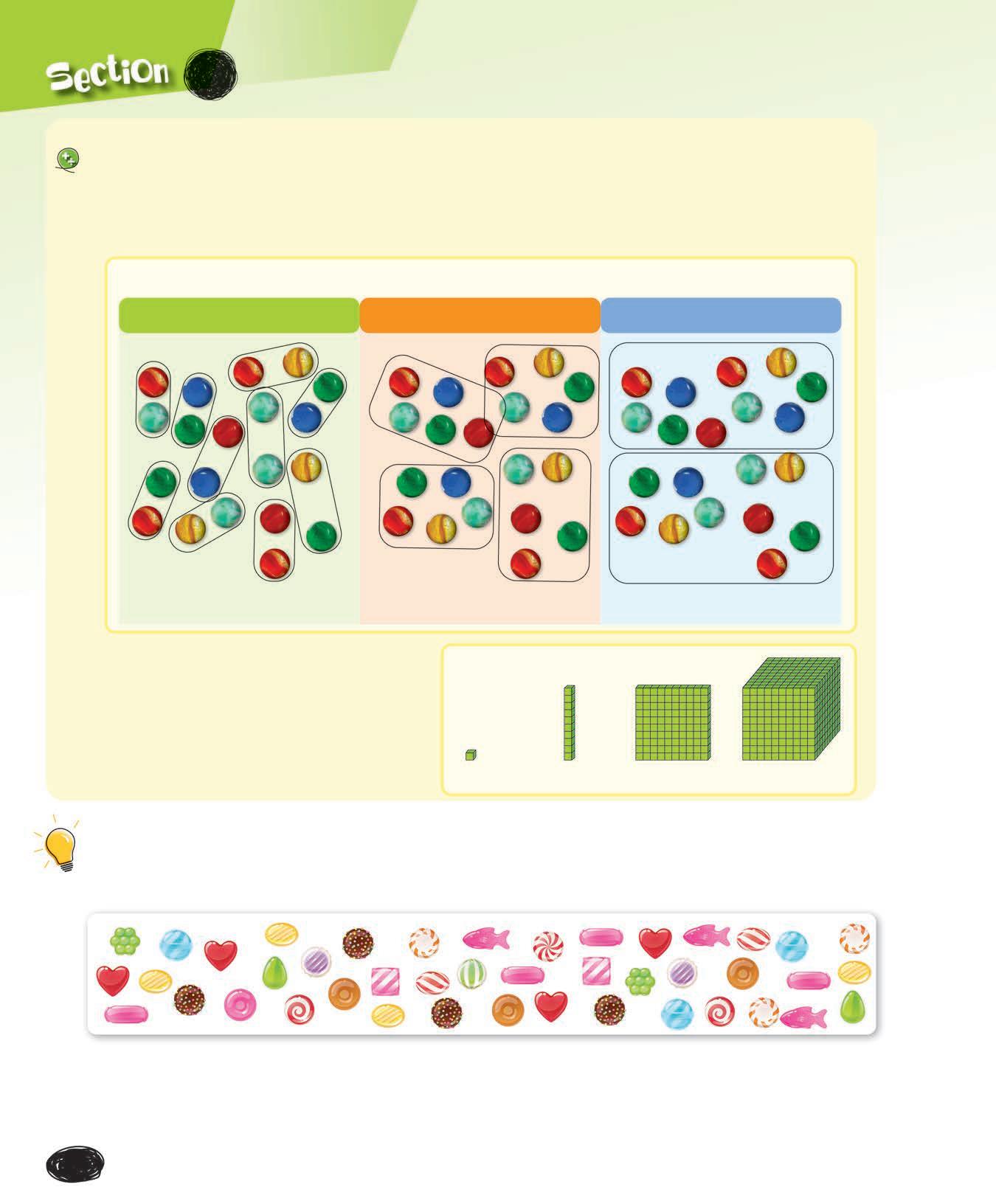
Le dénombrement et les groupements

• Dénombrer, c’est compter.

• Pour compter un grand nombre d’objets, on peut faire des groupements.

Pour compter 20 billes, on peut faire différents groupements. Des groupements de 2 Des groupements de 5 Des groupements de 10

• En mathématiques, on utilise souvent des groupements de 10 pour compter. C’est ce qu’on appelle la base 10

Si j’ai bien … compris

Observe ces bonbons. Fais des groupements de 5 ou de 10 pour les compter rapidement.

J’ai fait des groupes de bonbons. Il reste bonbons. Je peux compter par bonds de et compter le reste des bonbons par 1. En tout, il y a bonbons.

Cahier A, p. 8

1 Notion

La valeur de position

• La position de chaque chiffre dans un nombre a une valeur précise.

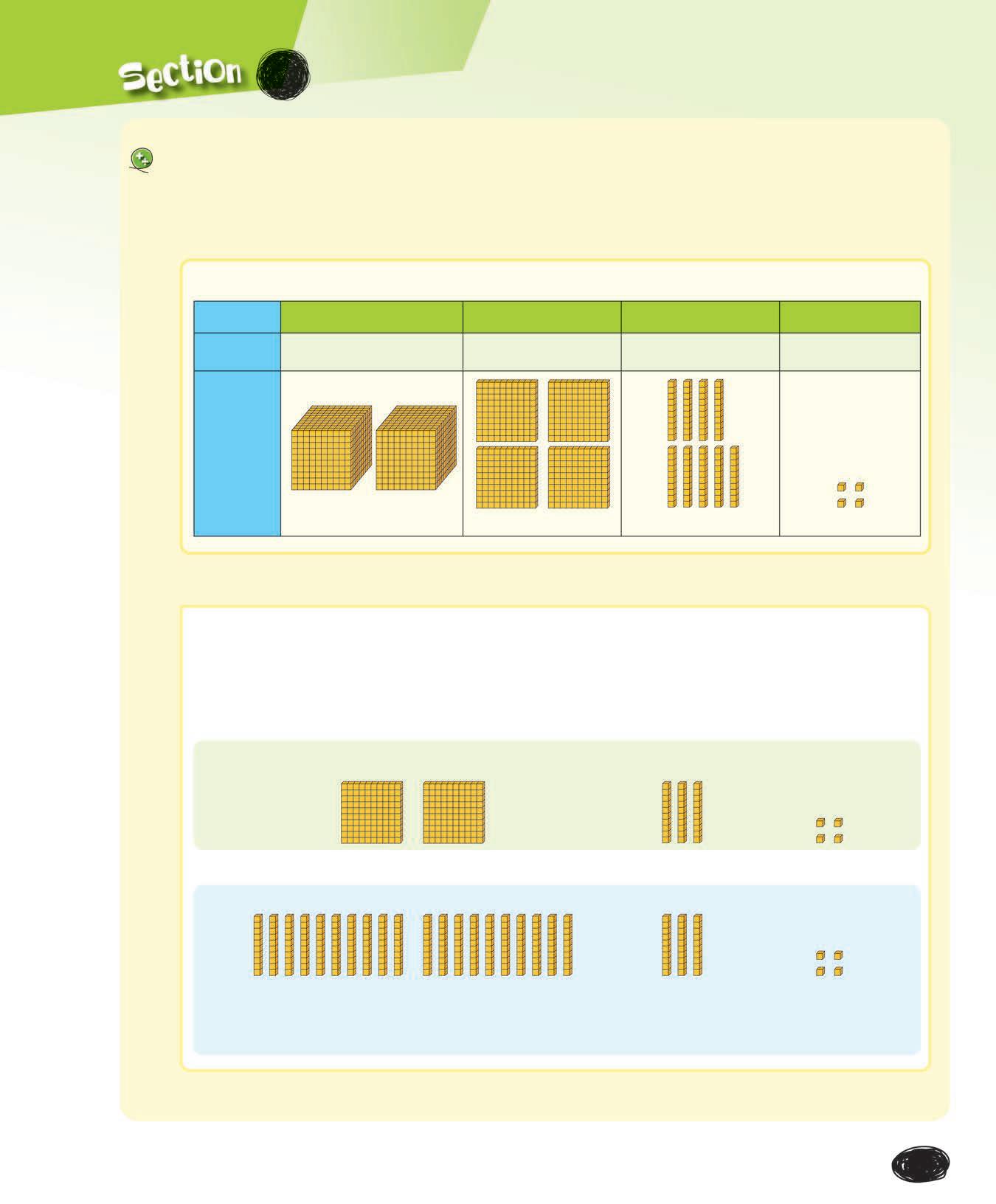
• Plus un chiffre est placé à gauche dans un nombre, plus sa valeur est grande.

Dans le nombre 2 4 9 4, le premier chiffre 4 n’a pas la même valeur que le deuxième.

Exemple

Dans le nombre 2 3 4, le 3 occupe la position des dizaines

On peut dire que 234 contient :

On peut aussi dire que 234 contient :

Cahier A, p. 13

1 Notion

Position Unités de mille Centaines Dizaines Unités Nombre 2 4 9 4 Valeur 2 000 400 90 4

Les droites et les angles

• Une droite est une ligne qu’on peut tracer avec une règle.

• Un angle est formé par 2 droites qui se croisent.

Angle

• Voici 3 types d’angles.

Angle droit

Angle aigu

L’angle aigu est plus petit que l’angle droit.

• Voici 2 types de droites.

Droites perpendiculaires ( )

2 droites perpendiculaires se croisent en formant des angles droits.

Angle obtus

L’angle obtus est plus grand que l’angle droit.

Droites parallèles ( )

Même distance

2 droites parallèles ne se croisent jamais. Il y a toujours la même distance entre elles.

Notion 4

A, p. 72 10

Cahier

Les polygones

• Un polygone est une figure plane formée par une ligne brisée et fermée.

• Chaque côté d’un polygone est un segment de droite. Un segment est une partie de droite limitée par 2 points.

Ces figures sont des polygones.

Elles sont toutes formées par des lignes brisées et fermées.

Ces figures ne sont pas des polygones.

Elles sont formées de lignes courbes.

Elles sont formées par des lignes brisées non fermées.

2 façons de classer les polygones

Nombre de côtés ou d’angles

3 côtés et 3 angles Triangles

4 côtés et 4 angles

Quadrilatères

Forme

Polygones convexes

Polygones non convexes

Trapèze

Parallélogramme Carré

Aucune partie ne rentre vers l’intérieur.

Au moins une partie rentre vers l’intérieur.

Notion 4

Cahier A, p. 78 11

Cahier A, p. 84

Les termes manquants

• Un terme manquant est un nombre inconnu dans une équation. Une équation est une égalité où un des termes est manquant.

• Lorsqu’on trouve le terme manquant, on rétablit l’égalité.

Terme manquant Terme manquant

Terme manquant

Pour rétablir l’équilibre, il faut ajouter 2 blocs au côté gauche.

ou ? + 1 = 3 1 + 2 = 3 5 –48 48

= = = = 14

Pour rétablir l’équilibre, il faut enlever 3 blocs du côté gauche.

Trouver le terme manquant

= 32 ?

5 – ? = 2 ? 16 ? 16

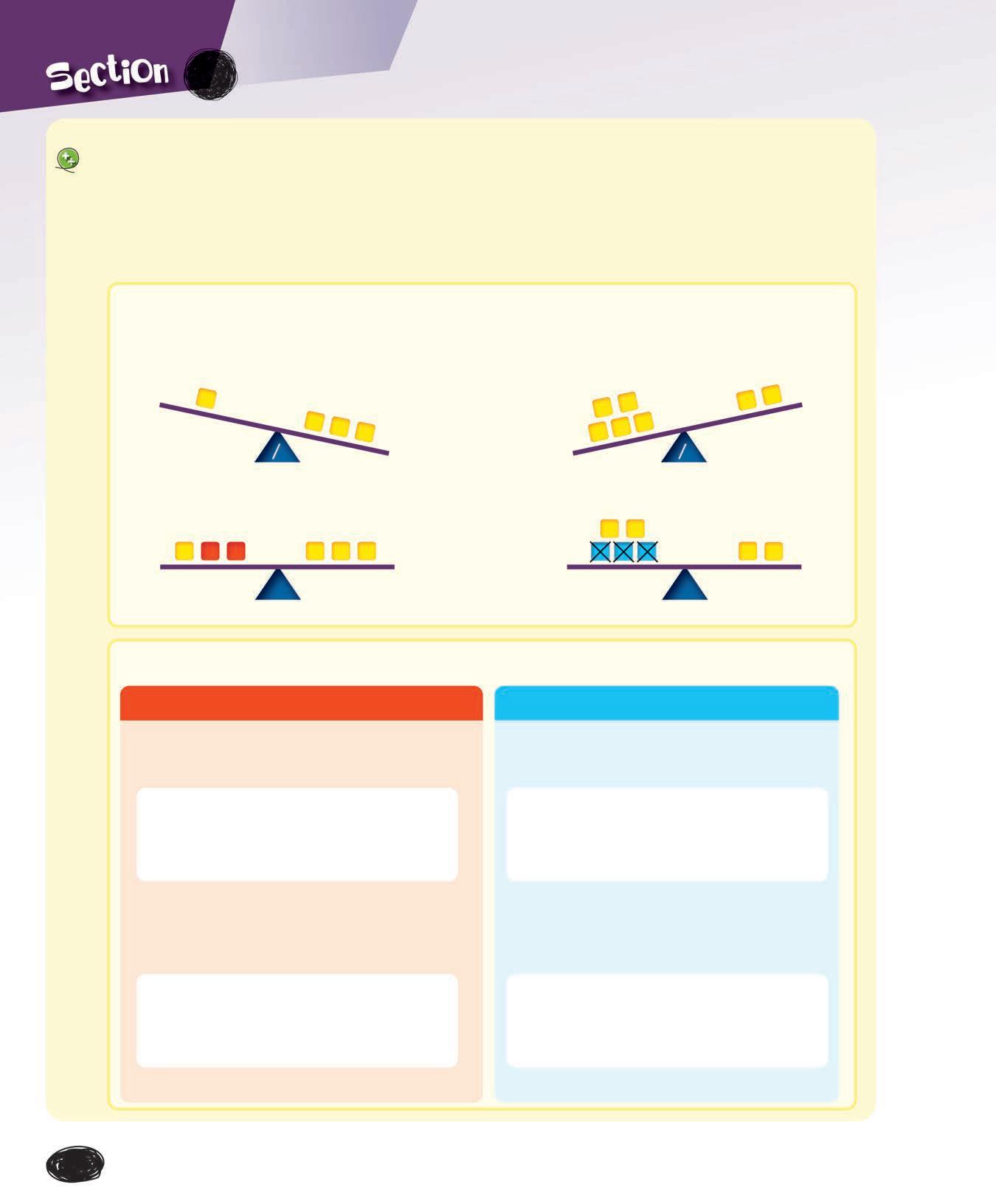
On fait une soustraction. Si le 2e terme est manquant, on fait une soustraction.

1 + ? = 3 48 – 32 = 16 48 – 32 = 16 48 – 16 = 32 16 + 32 = 48

Dans ? 32

Notion 4

Dans une addition

Si le 1er terme est manquant, on fait une addition une soustraction 32 + ? = 48 48 – ? = 32 ? + 16 = 48 ? – 16 = 32

Les suites de nombres

• Une suite de nombres est une liste de nombres placés dans un ordre qui respecte une régularité.

• Chaque nombre qui compose une suite est un terme.

est le lien qui permet de passer d’un terme à l’autre.

Mes strategies

• Pour trouver la régularité d’une suite, tu peux représenter les premiers termes à l’aide d’un dessin ou de matériel.

• Pour ajouter des termes à cette suite, tu répètes la régularité trouvée.

Si j’ai bien … compris

Complète les suites en respectant la régularité.

a) 40 36 32 + 10 + 10 + 10

b) 12 22 32

10 + 10

Notion 4

– 4 – 4 – 4 – 4 – 4

Cahier A, p. 90 13 1 3 5 7 9 11 + 2 + 2 + 2 + 2 + 2

régularité

La régularité peut être composée de plusieurs opérations régularité : + 5 régularité : – 3 60 65 70 75 80 85 + 5 + 5 + 5 + 5 + 5 90 87 84 81 78 – 3 – 3 – 3 – 3 régularité : – 10, + 3 60 50 53 43 46 36 39 29 32 – 10 – 10 + 3 – 10 + 3 + 3 + 3 – 10 15 © 2023, Les Éditions CEC inc. • Reproduction interdite Notion 13 • Section 4

Vocabulaire du

2e cycle

Aire

Mesure de la surface située à l’intérieur du contour d’une figure plane.

Unité de mesure :

Arête

Segment qui relie 2 faces d’un solide.

Arête

Angle

Aire = 6 carrés-unités

Figure formée par 2 droites qui se croisent.

Angle aigu

Angle plus petit qu’un angle droit.

Au moins Au minimum. Au plus Au maximum.

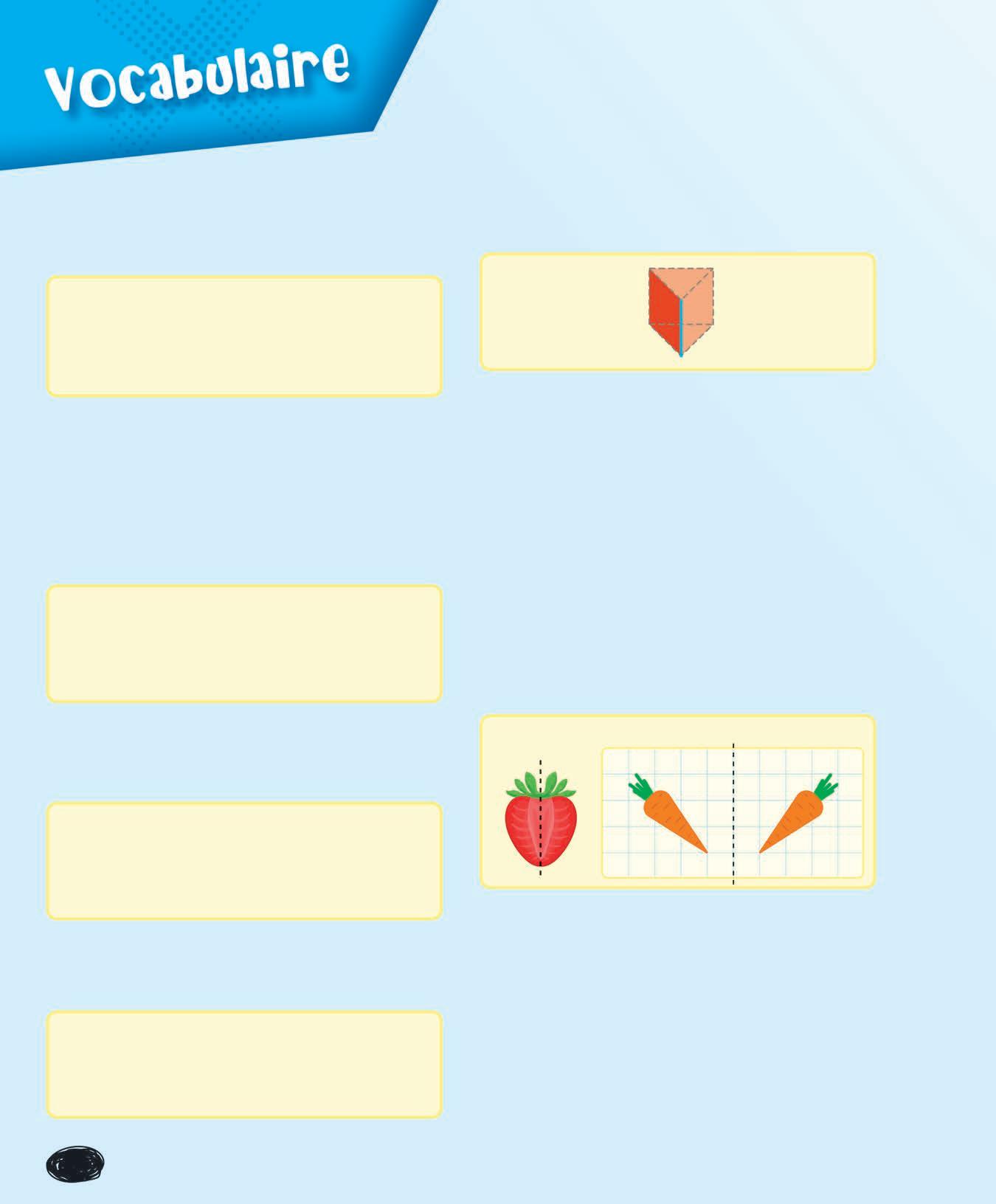
Axe de réflexion

Angle aigu

Ligne formée par le pli d’une figure qui la partage en 2 parties identiques, ou droite qui permet d’obtenir une image inversée de la figure de départ.

Axe de réflexion L’axe de réflexion agit comme un miroir.

Angle droit

Angle formé par 2 droites perpendiculaires.

Angle droit

Angle obtus

Angle plus grand qu’un angle droit.

Base dix

Système de groupements de 10 que l’on utilise en mathématiques. Tous les nombres sont formés à partir des 10 chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Angle obtus

Image Figure de départ

CEC inc. • Reproduction

Vocabulaire du 2e cycle

Éditions

interdite

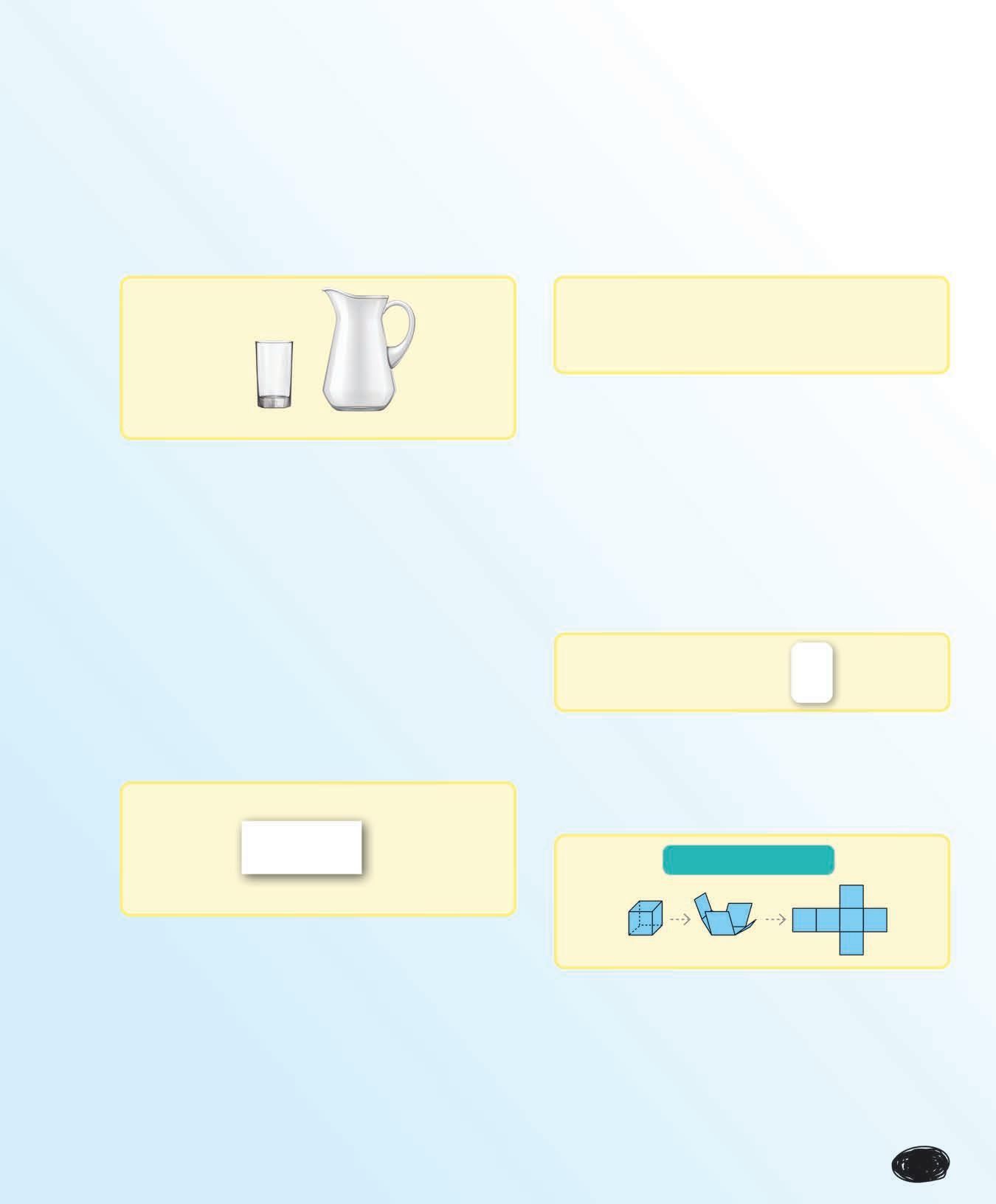
Capacité

Volume de matière que peut contenir un récipient.

Dallage

Répétition de figures qui recouvrent entièrement une surface, sans se superposer.

Motif de base

Plus petite capacité Plus grande capacité

Centième

Partie d’une unité divisée en 100 parties égales. Peut s’écrire 0,01 ou 1 100.

Chance

Possibilité qu’un résultat ou qu’un événement se produise.

Couple

Paire de nombres qui indique la position d’un point dans un plan cartésien.

Dénombrement

Action de compter tous les éléments d’un ensemble.

Dénominateur

Nombre total de parties équivalentes dans un tout. Dans une fraction, le dénominateur est le nombre situé sous le trait.

Le dénominateur

2 5

Développement d’un solide

Figure qui montre toutes les faces d’un solide, comme si on le dépliait.

Cycle

Période durant laquelle des phénomènes se répètent dans le même ordre de façon continue.

• Un cycle annuel est un cycle d’une année.

• Un cycle hebdomadaire est un cycle d’une semaine.

• Un cycle quotidien est un cycle d’une journée.

Diagramme à ligne brisée

Diagramme qui représente des données à l’aide de points reliés par des lignes.

Parenthèse Parenthèse Virgule Position

Position

du point ( 6 , 7 )

horizontale du point

verticale

Tables d’addition et de soustraction

Tables d’addition

Tables de soustraction

Table de 1 Table de 2 Table de 3 Table de 4 Table de 5 1 + 0 = 1 1 + 1 = 2 1 + 2 = 3 1 + 3 = 4 1 + 4 = 5 1 + 5 = 6 1 + 6 = 7 1 + 7 = 8 1 + 8 = 9 1 + 9 = 10 1 + 10 = 11 2 + 0 = 2 2 + 1 = 3 2 + 2 = 4 2 + 3 = 5 2 + 4 = 6 2 + 5 = 7 2 + 6 = 8 2 + 7 = 9 2 + 8 = 10 2 + 9 = 11 2 + 10 = 12 3 + 0 = 3 3 + 1 = 4 3 + 2 = 5 3 + 3 = 6 3 + 4 = 7 3 + 5 = 8 3 + 6 = 9 3 + 7 = 10 3 + 8 = 11 3 + 9 = 12 3 + 10 = 13 4 + 0 = 4 4 + 1 = 5 4 + 2 = 6 4 + 3 = 7 4 + 4 = 8 4 + 5 = 9 4 + 6 = 10 4 + 7 = 11 4 + 8 = 12 4 + 9 = 13 4 + 10 = 14 5 + 0 = 5 5 + 1 = 6 5 + 2 = 7 5 + 3 = 8 5 + 4 = 9 5 + 5 = 10 5 + 6 = 11 5 + 7 = 12 5 + 8 = 13 5 + 9 = 14 5 + 10 = 15 Table de 6 Table de 7 Table de 8 Table de 9 Table de 10 6 + 0 = 6 6 + 1 = 7 6 + 2 = 8 6 + 3 = 9 6 + 4 = 10 6 + 5 = 11 6 + 6 = 12 6 + 7 = 13 6 + 8 = 14 6 + 9 = 15 6 + 10 = 16 7 + 0 = 7 7 + 1 = 8 7 + 2 = 9 7 + 3 = 10 7 + 4 = 11 7 + 5 = 12 7 + 6 = 13 7 + 7 = 14 7 + 8 = 15 7 + 9 = 16 7 + 10 = 17 8 + 0 = 8 8 + 1 = 9 8 + 2 = 10 8 + 3 = 11 8 + 4 = 12 8 + 5 = 13 8 + 6 = 14 8 + 7 = 15 8 + 8 = 16 8 + 9 = 17 8 + 10 = 18 9 + 0 = 9 9 + 1 = 10 9 + 2 = 11 9 + 3 = 12 9 + 4 = 13 9 + 5 = 14 9 + 6 = 15 9 + 7 = 16 9 + 8 = 17 9 + 9 = 18 9 + 10 = 19 10 + 0 = 10 10 + 1 = 11 10 + 2 = 12 10 + 3 = 13 10 + 4 = 14 10 + 5 = 15 10 + 6 = 16 10 + 7 = 17 10 + 8 = 18 10 + 9 = 19 10 + 10 = 20

Table de 1 Table de 2 Table de 3 Table de 4 Table de 5 1 – 1 = 0 2 – 1 = 1 3 – 1 = 2 4 – 1 = 3 5 – 1 = 4 6 – 1 = 5 7 – 1 = 6 8 – 1 = 7 9 – 1 = 8 10 – 1 = 9 11 – 1 = 10 2 – 2 = 0 3 – 2 = 1 4 – 2 = 2 5 – 2 = 3 6 – 2 = 4 7 – 2 = 5 8 – 2 = 6 9 – 2 = 7 10 – 2 = 8 11 – 2 = 9 12 – 2 = 10 3 – 3 = 0 4 – 3 = 1 5 – 3 = 2 6 – 3 = 3 7 – 3 = 4 8 – 3 = 5 9 – 3 = 6 10 – 3 = 7 11 – 3 = 8 12 – 3 = 9 13 – 3 = 10 4 – 4 = 0 5 – 4 = 1 6 – 4 = 2 7 – 4 = 3 8 – 4 = 4 9 – 4 = 5 10 – 4 = 6 11 – 4 = 7 12 – 4 = 8 13 – 4 = 9 14 – 4 = 10 5 – 5 = 0 6 – 5 = 1 7 – 5 = 2 8 – 5 = 3 9 – 5 = 4 10 – 5 = 5 11 – 5 = 6 12 – 5 = 7 13 – 5 = 8 14 – 5 = 9 15 – 5 = 10 Table de 6 Table de 7 Table de 8 Table de 9 Table de 10 6 – 6 = 0 7 – 6 = 1 8 – 6 = 2 9 – 6 = 3 10 – 6 = 4 11 – 6 = 5 12 – 6 = 6 13 – 6 = 7 14 – 6 = 8 15 – 6 = 9 16 – 6 = 10 7 – 7 = 0 8 – 7 = 1 9 – 7 = 2 10 – 7 = 3 11 – 7 = 4 12 – 7 = 5 13 – 7 = 6 14 – 7 = 7 15 – 7 = 8 16 – 7 = 9 17 – 7 = 10 8 – 8 = 0 9 – 8 = 1 10 – 8 = 2 11 – 8 = 3 12 – 8 = 4 13 – 8 = 5 14 – 8 = 6 15 – 8 = 7 16 – 8 = 8 17 – 8 = 9 18 – 8 = 10 9 – 9 = 0 10 – 9 = 1 11 – 9 = 2 12 – 9 = 3 13 – 9 = 4 14 – 9 = 5 15 – 9 = 6 16 – 9 = 7 17 – 9 = 8 18 – 9 = 9 19 – 9 = 10 10 – 10 = 0 11 – 10 = 1 12 – 10 = 2 13 – 10 = 3 14 – 10 = 4 15 – 10 = 5 16 – 10 = 6 17 – 10 = 7 18 – 10 = 8 19 – 10 = 9 20 – 10 = 10

Le carnet de savoirs : un

essentiel pour l’apprentissage !

Ce carnet de savoirs a été conçu pour faire des mathématiques de façon autonome.

Ce carnet contient :

toutes les notions de 3e année expliquées simplement et accompagnées d’exemples ; des exercices pour valider la compréhension de certaines notions ;

la définition de tous les mots de vocabulaire et symboles mathématiques à maîtriser au 2e cycle du primaire ; les tables d’addition, de soustraction, de multiplication et de division.

Un contenu numérique riche et varié

Sur maZoneCEC, accédez aux cahiers et aux guides en format numérique (PC, MAC, Chromebook et iPad), ainsi qu’à de nombreux enrichissements, dont :

✓ des animations amusantes sur les notions et la manipulation ;

✓ des exercices interactifs autocorrectifs stimulants ;

✓ des causeries mathématiques numériques avec de la manipulation au TNI pour chaque notion ;

✓ des joggings interactifs ;

J’apporte toujours mon carnet de savoirs à la maison pour faire des maths !

✓ une trousse numérique complète d’ateliers et de jeux

Pour en savoir plus, consultez le site Web www.editionscec.com