GRAFOS DIRIGIDOS Y NO
DIRIGIDOS
MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN SUPERIOR
UNIVERSIDAD BICENTENARIA DE ARAGUA
VICERRECTORADO ACADÉMICO FACULTAD DE INGENIERÍA
SISTEMAS EXPERTOS Y LOGICA DIFUSA
SAN CRISTOBAL – EDO. TACHIRA
GRAFOS
Localidad Rubio, Edo. Táchira
JUNIO 2024
AUTOR: DOUGLAS MANUEL MORA JAIMES
C.I.: 31181014
SECCIÓN T1
TUTOR(A): PROF. YUSBELIS PEREZ
REPÚBLICA BOLIVARIANA DE VENEZUELA
EDITORIAL
Los grafos son una buena herramienta para modelar, analizar y resolver problemas en diversas disciplinas. Su capacidad para representar relaciones, su aplicabilidad en el análisis de redes, su uso en algoritmos y optimización, su estudio en teoría de grafos y su utilidad en la visualización de datos los convierten en una herramienta muy valiosa para comprender y abordar desafíos complejos en campos científicos, tecnológicos y sociales.
EDITORIAL........................................
INTRODUCCION..............................
DEFINICION.....................................
LAS
GRAFOS
INDICE
3PAG
5PAG
6PAG
ARISTAS.................................... 7PAG
DIRIGIDOS........................ 8PAG GRAFOS NO DIRIGIDOS................. 9PAG LOS NODOS.................................... 11PAG ORDENACION................................ 14PAG EJEMPLOS ALGORITMOS.............. 15PAG
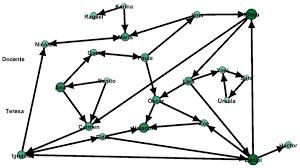
Introduccion
Un grafo dirigido es un conjunto de nodos o vértices conectados por arcos unidireccionales. Cada arco representa una relación o conexión entre dos nodos, y tiene una dirección que indica la dirección en la que se puede seguir para llegar de un nodo al otro. Estos grafos son usados para modelar situaciones en las que la dirección de la relación entre los nodos es importante, como por ejemplo en una red de transporte o en un diagrama de flujo. También se les conoce como digrafos.
Los grafos dirigidos, también conocidos como digrafos, son una estructura matemática que consiste en un conjunto de elementos, llamados "nodos" o "vértices", conectados por "arcos" o "aristas" unidireccionales. Cada arista tiene una dirección específica que indica la relación de un nodo origen a un nodo destino. Estos grafos son útiles para modelar situaciones en las que hay una relación de un punto a otro que no es recíproca.
En los grafos dirigidos, se pueden encontrar conceptos importantes como: nodos adyacentes, camino, ciclo, componente fuertemente conexa, entre otros. Son muy utilizados en la teoría de grafos, algoritmos de búsqueda y en aplicaciones informáticas como redes de computadoras, rutas de navegación, representación de flujos de información, entre otros.
Definición
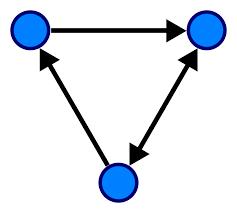
Las aristas
Las aristas en un grafo dirigido son los elementos que representan la relación direccional entre dos nodos o vértices. Cada arista tiene un nodo origen y un nodo destino, indicando la dirección del flujo de la relación. Por ejemplo, si consideramos un grafo dirigido que modela las conexiones de vuelo entre ciudades, las aristas representarían los trayectos unidireccionales de una ciudad a otra.
Aquí tienes un ejemplo de aristas en un grafo dirigido que representa conexiones de vuelos entre ciudades:
- Arista de "A" a "B": indica que hay un vuelo directo de la ciudad "A" a la ciudad "B".
- Arista de "B" a "C": representa un vuelo directo de la ciudad "B" a la ciudad "C".
- Arista de "C" a "A": muestra un vuelo directo de la ciudad "C" a la ciudad "A".
En este ejemplo, cada arista conecta dos ciudades en una dirección específica, re
Grafos Dirigidos
Los grafos dirigidos, también conocidos como digrafos, son estructuras matemáticas que consisten en un conjunto de nodos (vértices) conectados por aristas (arcos) unidireccionales. Cada arista tiene una dirección asociada que indica la relación de un nodo origen hacia un nodo destino. Estos grafos son útiles para representar situaciones donde la relación entre los elementos no es simétrica.
Aquí tienes dos ejemplos de grafos dirigidos:
1. Red de autopistas: Imagina un grafo dirigido que representa la red de autopistas de una ciudad. Cada nodo sería una intersección o una salida, y las aristas representarían los segmentos de autopista que conectan esas ubicaciones. Las aristas indicarían la dirección del flujo de tráfico en cada autopista.
2. Relaciones laborales: Supongamos un grafo dirigido que modela las relaciones de supervisión en una empresa. Cada nodo sería un empleado, y las aristas representarían la dirección de supervisión de un empleado a otro.
Grafos no Dirigidos
Un grafo no dirigido es un conjunto de nodos unidos por aristas sin ninguna dirección específica. En un grafo no dirigido, las aristas no tienen un punto de inicio ni de fin designado.
Aquí tienes dos ejemplos
1. *Grafo Social:* En un grafo no dirigido que representa una red social, cada nodo representa a una persona y las aristas representan la amistad entre ellas. Por ejemplo, si Alicia es amiga de Juan y Juan es amigo de Pedro, el grafo no dirigido tendría nodos para Alicia, Juan y Pedro, con aristas que los conectan entre sí.
2. *Red de Carreteras:* En un grafo no dirigido que representa una red de carreteras, los nodos representan ciudades y las aristas representan las carreteras que las conectan. Por ejemplo, si las ciudades A, B y C están conectadas por carreteras, el grafo no dirigido tendría nodos para A, B y C, con aristas que representan las carreteras entre ellas.
Los Nodos
En informática, un nodo se refiere a un dispositivo individual en una red informática que puede enviar, recibir, o retransmitir datos. Los nodos pueden ser computadoras, servidores, enrutadores, conmutadores u otros dispositivos de red. Cada nodo en una red tiene una dirección única que le permite ser identificado dentro de la red. Los nodos se comunican entre sí a través de la red para intercambiar información y servicios. Los nodos también pueden ser parte de una estructura
jerárquica en una red, con nodos de mayor nivel actuando como controladores o servidores y nodos de menor nivel actuando como dispositivos finales o clientes.
Los Nodos
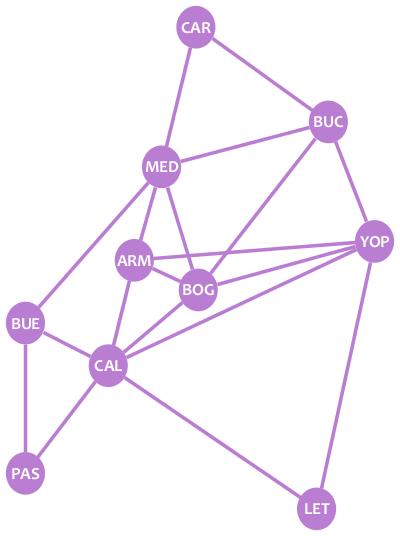
Los Nodos- ejemplos
1. Nodo en red de computadoras: En una red de computadoras, un nodo es un dispositivo o punto de conexión que puede enviar, recibir, almacenar o procesar datos. Por ejemplo, una computadora, una impresora, un servidor, un enrutador, un switch, etc., son todos ejemplos de nodos en una red de computadoras.
2. Nodo en árbol de directorios: En un árbol de directorios de un sistema operativo, un nodo es un punto de la estructura jerárquica que representa un directorio, subdirectorio o archivo. Cada nodo puede tener varios hijos que son subdirectorios o archivos que están contenidos en él. Por ejemplo, en un árbol de directorios de Windows, el nodo raíz suele ser el disco principal (C:), y debajo de él puede haber varios nodos que representan carpetas y archivos.
3. Nodo en estructuras de datos: En programación y en el campo de la informática, un nodo es un elemento básico de una estructura de datos que almacena información y enlaces a otros nodos. Por ejemplo, un nodo en una lista enlazada contiene un valor (dato) y un puntero que apunta al siguiente nodo en la lista. Otro ejemplo son los nodos en un árbol binario, donde cada nodo tiene un valor y enlaces a sus nodos hijos izquierdo y derecho.
Ordenación
La ordenación se refiere al proceso de organizar elementos o datos en un determinado orden, de acuerdo a algún criterio específico. Este criterio puede variar dependiendo de la naturaleza de los elementos a ordenar, como por ejemplo, orden alfabético, numérico o cronológico.
Ejemplos de algoritmos
infinito = 1e10
def bellman _ford(grafo, inicio, fin):
num _ vertices = grafo.get_ num _vertices()
aristas = grafo.get edges()
distancia = [infinito for vértice in range(num vertices)]
previo = [ninguno para vértice en range(num vertices)]
distancia[inicio] = 0
for i in range(fin + 1): for (u, v) in aristas:
if distancia[v] > distancia[u] + grafo.get weight(u, v):
distancia[v] = distancia[u] + grafo.get weight(u, v)
previo[v] = u
for (u, v) in aristas: if distancia[v] > distancia[u] + grafo.get_weight(u, v):
raise ErrorCicloPesoNegativo()
return distancia, previo
Ejemplos de algoritmos
#include <iostream>
#include <vector>
using namespace std;
class Grafo { int v; // número de vértices
vector<int> *adj; // puntero a un vector que contiene listas de adyacencia
public:
Grafo(int v); // Constructor
void add edge(int u, int v); // función para añadir una arista al grafo
void DFS(int nodo _actual, vector<bool> &visitado); };
// Implementación de DFS
void Grafo::DFS(int nodo actual, vector<bool> &visitado) {
visitado[nodo actual] = true; cout << nodo actual << " " ; for (int sucesor : adj[nodo actual]) { if (!visitado[sucesor]) { DFS(sucesor, visitado); } } }
CONCLUSION
Los grafos dirigidos son una herramienta fundamental en la teoría de grafos y en diferentes campos de estudio y aplicación. A través de ellos, es posible representar y analizar relaciones y conexiones direcionales entre elementos de un conjunto.
Estos grafos son especialmente útiles en el análisis de redes complejas como las redes de transporte, las redes sociales, los circuitos eléctricos, entre otros, ya que permiten modelar la dirección y el sentido de las diferentes conexiones. Además, son ampliamente utilizados en la programación y en la teoría de algoritmos, ya que permiten representar problemas complejos de una manera estructurada y eficiente.
La importancia de los grafos dirigidos radica en su capacidad para modelar relaciones asimétricas entre elementos, lo cual es fundamental en situaciones donde la dirección de la conexión es relevante. Además, permiten analizar y comprender de manera más profunda el comportamiento de sistemas complejos, facilitando la identificación de patrones y la toma de decisiones informadas.
En resumen, los grafos dirigidos son una herramienta poderosa y versátil que se utiliza en una amplia variedad de campos y disciplinas. Su capacidad para representar y analizar relaciones direcionales los convierte en una herramienta indispensable en la resolución de problemas complejos y en el estudio de sistemas dinámicos.
AUTOR
