WISKUNDE (DEEL 2

KAARTEN IN DE LES WISKUNDE (DEEL 2*)

DIDIER DESES * Voor deel 1 en referenties : zie Wiskunde & Onderwijs, nr. 163, 245-251.

4. DRIEHOEK VAN PASCAL 4.1 Definitie en gebruik De driehoek van Pascal is een gekend onderwerp in de lessen wiskunde. De driehoek van Pascal is volgende getallendriehoek.

De getallen worden als volgt berekend. Op elke zijde van de driehoek staat telkens 1. De getallen in de driehoek zijn de som van de twee getallen erboven. • In de combinatoriek wordt het aantal keuzen van p objecten geteld dat gemaakt kan worden uit een totaal van n verschillende objecten, zonder welbepaalde volgorde en zonder herhaling. Het aantal keuzen wordt gegeven door middel van combinaties of binomiaal coëfficiënten.

Voor de combinaties geldt volgende formule:

Deze driehoek heeft zeer vele eigenschappen. We geven hier enkele van de meest gekende. • De getallen in de nde rij van deze driehoek zijn de coëfficiënten van de uitwerking van

Deze formule is equivalent met de formule die de driehoek van Pascal genereert. De combinaties zijn dus de getallen uit de driehoek van Pascal. • Indien we beide vorige punten samenzetten, bekomen we de stelling die bekend staat onder de naam Binomium van Newton. Het bewijs ervan toont dat een stelling uit de analyse (het uitwerken van veeltermen) soms een combinatorisch bewijs kan hebben.

Bewijs.

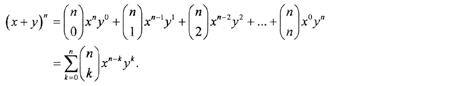
Bij de uitwerking moet je in elke van de factoren ofwel ofwel kiezen. De term wordt bekomen door keer een te kiezen (en dus keer een . Dit kan op manieren. Aldus telt de term .keer mee in de uitwerking

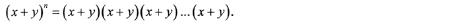
en bekom je dus een bijdrage van

aan de totale som.

• Pascal bestudeerde de driehoek in zijn "Traité du Triangle Arithmétique", maar hij was zeker niet de eerste die hem opschreef. De getallendriehoek kwam reeds voor in een Chinees handboek uit de 14de eeuw. Pascal was wel de eerste die het verband legde met de binomiaalcoëfficiënten. Ook andere fractalen zitten verborgen in de driehoek van Pascal. Laat je bijvoorbeeld de 3-vouden of de 5-vouden weg, dan krijg je volgende resultaten.

• Indien je de even getallen uit de driehoek van Pascal weglaat en de andere zwart kleurt, bekom je een figuur die reeds op een andere plaats in dit artikel is opgedoken, de zeef van Sierpinksi.

In het algemeen krijg je altijd een fractaal indien je de p-vouden weglaat, waarbij p priem is.

4.2 Kaartspel Volgend solitaire kaartspel is gebaseerd op dezelfde regel als die voor de driehoek van Pascal. Je begint met tien kaarten te leggen in driehoek-

vorm. Daarnaast heb je een reserve van drie plaatsen waar je telkens één kaart opzij kan leggen. De bedoeling van het spel is om de tien lege plaatsen op te vullen aan de hand van de regel uit de driehoek van Pascal.

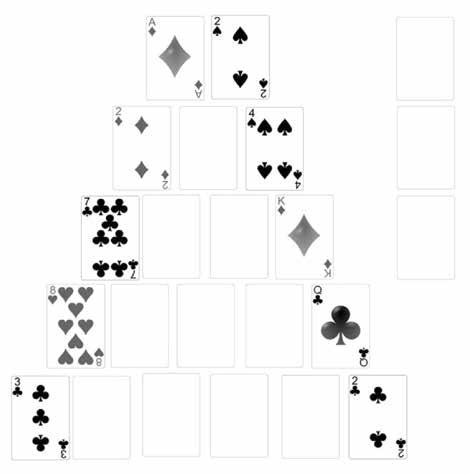
De nieuwe kaart kan ergens op de juiste plaats worden gelegd, ofwel wordt ze op één van de drie reserveplaatsen bewaard, ofwel wordt ze weggelegd en kan ze niet meer gebruikt worden. • Het spel wordt gewonnen als de volledige driehoek af is. • Soms is het onmogelijk om de driehoek af te werken. Wanneer bijvoorbeeld de bovenste twee kaarten azen zijn en alle 2's op de zijkanten staan, is het spel onmogelijk. Deze gevallen komen echter tamelijk zelden voor. • De beste strategie is om op voorhand in gedachten uit te rekenen welke kaarten je nodig hebt, zodat je de gepaste kaarten opzij kan houden. Gezien het om tien kaarten gaat, is dit een goede geheugentraining.

• Een open plaats wordt opgevuld met een kaart met een waarde die gelijk is aan de som van de waarden van de twee kaarten erboven. De eerste kaart bovenaan zou dus een 3 moeten zijn. • De waarden van de kaarten zijn als volgt : A , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , J , Q , K komt overeen met 1 , 2 , 3 , 4, 5 , 6, 7, 8, 9, 10, 11 , 12, 13. Indien een som groter is dan 13, wordt er 13 afgetrokken. We geven een voorbeeld.

5. REKENEN MET KAARTEN 5.1 Een groepvan kaarten In de vorige paragraaf werd een manier gegeven om waarden van kaarten op te tellen. We herhalen dat de waarden als volgt zijn : A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K komt overeen met 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13. Indien een som groter is dan 13, wordt er 13 afgetrokken.

Dit is eigenlijk wiskundig niet helemaal correct. Beschouw de volgende sommen :

• Een kaart mag slechts geplaatst worden indien de twee kaarten erboven aanwezig zijn. De tweede rij kan dus pas worden opgevuld als eerst de bovenstaande 3 geplaatst werd. • De kaarten uit de overblijvende stapel worden één voor één omgedraaid. Het is eenvoudig na te gaan dat dit ook geldt voor alle andere kaarten

i.p.v. 5. We herkennen hierin de eigenschap van het neutraal element voor de optelling. We kunnen dus beter stellen dat K = 0 i.p.v. 13. We zetten eventjes hetgeen we weten op een rijtje. • Elke twee kaarten kunnen worden opgeteld en de uitkomst zal een waarde zijn in {0 , 1 , 2 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12}. De som is dus overal gedefinieerd en inwendig. • De K is het neutraal element voor de optelling. • Elke kaart kan worden aangevuld tot een waarde 13 door een andere kaart, deze laatste is het symmetrisch element van de eerste.

• Je kan ook gemakkelijk zien dat de volgorde waarin drie kaarten opgeteld worden geen belang heeft, dit levert de associativiteit. • Ten slotte is deze optelling ook commutatief.

We concluderen dat { A , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , J , Q , K } met deze optelling een (eindige) commutatieve groep is met dertien elementen.

5.2 Piramide-solitaire Bij dit spel wordt eerst een piramide gelegd van 28 overlappende kaarten.

Nu is de vrij en kan je die weghalen samen met omdat deze ook elkaars tegengestelde zijn.

• Wanneer geen kaarten meer weggehaald kunnen worden mag je de bovenste kaart van de overgebleven stapel omdraaien. Indien deze je niet verder helpt, moet je ze weggooien en neem je de volgende. Anders gebruik je ze om een kaart van de piramide weg te halen. • Je wint het spel als je de volledige piramide kan wegwerken.

5.3 Het spelCalculation Onze groep van kaarten wordt voortgebracht door A in die zin dat :

• Twee kaarten kunnen verwijderd worden indien hun som 13 is, d.w.z. indien ze elkaars tegengestelde zijn in onze groep. • Indien een kaart onder een andere zit, mag je ze nog niet verwijderen. • Met bovenstaande kaarten begin je door te verwijderen, deze heeft sowieso een waarde 13. Daarna neem je en weg want

Een groep die voortgebracht wordt door één enkel element heet een cyclische groep. Voor elk positief geheel getal is er precies één cyclische groep (op een isomorfisme na), waarvan de grootte is, en is er precies één oneindige cyclische groep (de gehele getallen onder optelling). Vandaar dat de cyclische groepen de eenvoudigste groepen zijn en zij ook volledig zijn geclassificeerd. Onze groep is dus isomorf me t ,+ (de gehele getallen modulo 13).

We hebben net getoond dat A een voortbrenger is van onze groep. Wat met de andere elementen? Elk element brengt op zich een deelgroep

voort. De stelling van Lagrange zegt dat het aantal elementen van een deelgroep een deler moet zijn van het totaal aantal elementen van de groep. Omdat onze groep 13 elementen telt en dit een priemgetal is, zijn de enige deelgroepen en de groep zelf. Hieruit volgt dat elk element de ganse groep voortbrengt. De volgorde waarin dit gebeurt, is steeds anders. We geven de voorbeelden met A, 2, 3 en 4.

Dit is de basis van het solitaire spel calculation. Eerst haalt men een aas, een twee, een drie en een vier uit het kaartspel. Dit zijn de voortbrengers. Naast deze kaarten moeten in juiste volgorde (zie hierboven) de andere kaarten geplaatst worden tijdens het spel. Daarnaast heb je plaats voor vijf reservestapels.

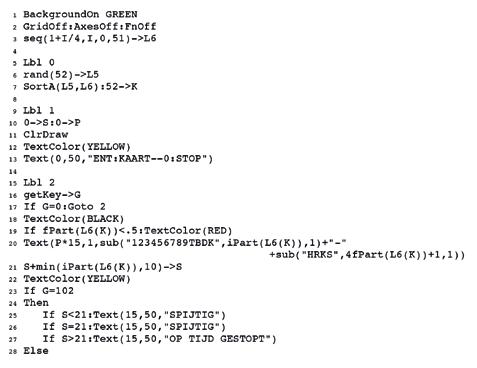
6. BLACKJACK OP DE TI-84 COLOR PLUS Onderstaand programma simuleert het kaartspel Blackjack op een TI-84 Color Plus. Het spelletje werd doelbewust eenvoudig gehouden, zodat de programmeertechnieken duidelijk zichtbaar zijn.

die er al is. Anders moet de kaart geplaatst worden op één van de reservestapels. • De bovenste kaart van een reservestapel mag altijd verhuisd worden naar een voortbrengerstapel indien het haar beurt is. • Men wint het spel indien men alle vier voortbrengerstapels kan afwerken tot K. • Dit spel is niet alleen een spel van geluk, een goede speler zal bijna twee keer op drie het spel kunnen winnen. • Kleine tip : gebruik een aparte reservestapel om alle K weg te bergen.

Leg deze nooit op een andere kaart want dan moet je eerst een volledige voortbrenger afwerken alvorens aan de onderste kaart te kunnen.

• De kaarten uit de overgebleven stapel worden één voor één getrokken. • Een kaart mag op één van de vier voortbrengerstapels gelegd worden indien ze volgt op de kaart

We overlopen het programma. 1-2 Het grafisch scherm wordt ingesteld. We gebruiken een groene achtergrond om een casinolook te bekomen. 3 Een pakje kaarten wordt in lijst L 6 geplaatst. Elke kaart heeft een waarde (1 - 13) en een soort (Harten, Ruiten, Klaveren, Schoppen). Om deze beide elementen in één enkel getal te plaatsen gebruiken we volgende truc. De soorten komen overeen met de getallen na de komma (0,00 ; 0,25 ; 0,50 ; 0,75). Zo komt het laatste getal (13,75) overeen met . 5-7 Nu worden de kaarten gemengd. Dit gebeurt door een tweede lijst van willekeurige getallen te plaatsen in L 5 . Beide lijsten worden dan geordend afhankelijk van de waarden in L 5 , de kaarten in L 6 staan daarna in een willekeurige volgorde. De variabele K

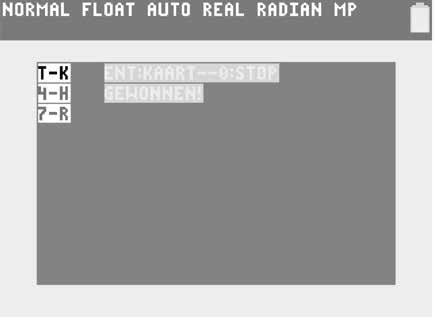
is de bovenste kaart, voorlopig de 52ste. 9-13 Het spel begint hier. De som S wordt op 0 gezet en het aantal kaarten P van de speler ook. Het grafisch scherm wordt leeggemaakt en de instructies verschijnen. 15-17 Deze drie regels zijn een trucje om te wachten tot de gebruiker een toets heeft ingedrukt. 18-20 Eenmaal een toets ingedrukt, wordt de kleur op zwart gezet. Indien echter het deel na de komma (fPart) van de bovenste kaart (K) kleiner is dan 0,50 gaat het om een rode kaart en wordt de tekstkleur aangepast. Hierna wordt met i Part de waarde van de kaart bepaald. Deze gebruikt men dan om het juiste symbool uit 123456789TBDK te selecteren (we schrijven hier T voor 10 zodat elke kaart juist één symbool nodig heeft). Op analoge wijze wordt fPart gebruikt om de soort voor te stellen HRKS (Harten, Ruiten, Klaveren, Schoppen). De speler heeft P kaarten en elke lijn tekst is 15 pixels hoog, dus de kaart wordt weggeschreven op hoogte van het scherm. 21 De nieuwe som wordt bepaald. Door gebruik te maken van tellen alle beeldjes voor 10, de azen tellen in deze versie voor 1. 23-27 Indien de speler op de toets O heeft gedrukt (toetscode 102) wil hij stoppen. Naar gelang de som S wordt een boodschap afgedrukt die aangeeft of dit de juiste beslissing was. 28-33 Indien de speler niet wenst te stoppen, krijgt hij de kaart. Er is nu één kaart minder op de stapel en de speler heeft een kaart meer . Indien de som minder dan 21 bedraagt, wordt er verder gespeeld. Indien niet, heeft de speler gewonnen of verloren en krijgt hij de passende boodschap. 35-37 Opnieuw een wachtlus. 38-40 Indien er nog meer dan tien kaarten over zijn, wordt een volgend spel begonnen, anders worden de kaarten opnieuw gemengd.

Deze versie van Blackjack is verschillend van de versie in casino's, toch is een Hi-Lo count mogelijk. Als je speelt, wil je weten of je moet stoppen of niet. Indien er nog veel kleine kaarten zijn, loont het risico om verder te gaan. De count kan je dus als volgt beschrijven.

Indien de count positief is, zijn er al vele grote kaarten gevallen en blijven er dus kleine kaarten over. Het is dan in je voordeel om niet te snel te stoppen. Natuurlijk garandeert dit geen winst! Let wel dat je de count terug op nul zet als de kaarten worden gemengd.

UIT PYTHAGORAS

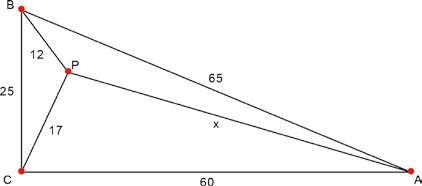
Hieronder staat een rechthoekige driehoek met zijden 25, 60 en 65. Verder ligt er in de driehoek een punt P met afstand 17 tot de rechte hoek en afstand 12 tot een ander hoekpunt. Bepaal de afstand tot het derde hoekpunt.

DIDIER DESES DIDDESEN@GMAIL.COM, MUILENSTRAAT 239, 1770 LIEDERKERKE. KA KOEKELBERG, FELIX VANDE SANDESTRAAT 17, 1081 BRUSSEL.

'Wiskunde & Onderwijs' is het tijdschrift van de Vlaamse Vereniging Wiskundeleraars (VVWL). Meer info vind je op de website www.vvwl.be.

OEFENING 1

In deel 1 kwam het volgende aan bod 1. Kaarten mengen. 2. Hi-Lo count. 3. Torens van Hanoi.