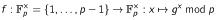
21 minute read
CRYPTOGRAFIE
CRYPTOGRAFIE: VAN BROWSER TOT EID
FREDERIK VERCAUTEREN I S P RO F E S S O R I N D E O N D E R ZO E K S G RO E P CO S I C (CO M P U T E R S EC U R I T Y A N D I N D U S T R I A L C RY P TO G R A P H Y ) VA N H E T D E PA RT E M E N T E SAT A A N D E K U L E U V E N . H I J D O E T O N D E R ZO E K N A A R TO E PAS S I N G E N VA N G E TA LT H EO R I E E N A LG E B R A I S C H E M E E T K U N D E I N P U B L I E K E S L E U T E L C RY P TO G R A F I E . FREDERIK.VERCAUTEREN@ESAT.KULEUVEN.BE
Cryptografie (afgeleid van het griekse kryptòs “verborgen” en graphein “schrijven”) is de wetenschap die zich bezighoudt met het beveiligen van informatie en communicatie. Het meest bekende voorbeeld van cryptografie is ongetwijfeld encryptie, waarbij een klaartekst onleesbaar wordt gemaakt door deze om te zetten in een cijfertekst. De invoer van het encryptie-algoritme is niet enkel de klaartekst maar ook een (encryptie)sleutel. Het omgekeerde proces waarbij een cijfertekst wordt omgezet in een klaartekst heet decryptie; en het decryptie-algoritme neemt als invoer een cijfertekst en een (decryptie)sleutel. De beschrijving van de algoritmes zelf is in moderne cryptografie nooit geheim, enkel de sleutel(s). Dit is het zogeheten principe van Kerckhoffs, een Nederlandse cryptograaf die dit principe al in 1883 formuleerde.
Encryptie is maar een zeer klein onderdeel van de moderne cryptografie, waar behalve geheimhouding, ook andere toepassingen bestudeerd worden, zoals data-integriteit, authenticiteit van zowel gebruikers als data en onweerlegbaarheid, bv. door gebruik te maken van digitale handtekeningen. Cryptografie heeft een zeer lange en boeiende geschiedenis, zie bv. “The Codebreakers – The Story of Secret Writing” van David Kahn (2) of “The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography” van Simon Singh (4). Vóór 1976 bestonden er enkel symmetrische sleutelalgoritmen: hierbij is de encryptiesleutel gelijk aan de decryptiesleutel en deze ene sleutel moet gekend zijn (en geheim gehouden worden) door zowel de afzender als ontvanger van het bericht. Het meest gebruikte symmetrische sleutel encryptiesysteem is ongetwijfeld AES (Advanced Encryption Standard). AES heette oorspronkelijk Rijndael en werd in 1998 ontworpen door twee Belgische cryptografen, Joan Daemen en Vincent Rijmen, beide toen verbonden aan de onderzoeksgroep Cosic van KU Leuven. AES wordt werkelijk overal gebruikt zoals voor internetbankieren en online winkelen, beveiliging van wifi, versleutelen van bestanden …
Het grote probleem van symmetrische cryptografie is sleutelovereenkomst: hoe kunnen de afzender en ontvanger de geheime sleutel met elkaar overeenkomen, zonder dat een derde partij (een aanvaller) deze sleutel ook te weten kan komen. Dit probleem werd zeer elegant opgelost in 1976 door Diffie en Hellman door de uitvinding van publieke sleutel cryptografie (1) Dit algoritme is nu gekend als Diffie-Hellman sleutelovereenkomst en vormt nog steeds de basis van beveiligde communicatie over het internet; het zit bv. ingebakken in alle browsers (zie verder). In publieke sleutel cryptografie heeft elke gebruiker een sleutelpaar, bestaande uit een publieke sleutel voor encryptie en een private sleutel voor decryptie. Dit systeem kan best geïllustreerd worden aan de hand van de normale brievenpost: iedereen die het adres van de ontvanger weet (de publieke sleutel) kan deze een brief sturen, maar enkel de eigenaar van de sleutel van de postbus (de private sleutel), kan de brieven uit de postbus halen. (zie figuur 1)
SLEUTELOVEREENKOMST Diffie en Hellman maken gebruik van elementaire algebra om commuterende éénwegsfuncties te construeren, waaruit hun algoritme voor sleutelovereenkomst volgt. Een éénwegsfunctie is een functie die makkelijk te evalueren is, maar moeilijk te inverteren, i.e. gegeven is het heel moeilijk om
Figuur 1 Diffie-Hellman sleutelovereenkomst
te berekenen. De éénwegsfunctie die Diffie en Hellman gebruiken is machtsverheffing in een eindig veld 1 : gegeven een groot priemgetal p (in de huidige systemen is ) en een vaste generator van (een deelgroep van) de multiplicatieve groep van het eindig veld , is de functie gegeven door .
Het inverteren van deze functie f is gekend als het discreet logaritme probleem (DLP). Figuur 1 geeft een gedetailleerde beschrijving van de resulterende Diffie-Hellman sleutelovereenkomst tussen twee partijen Alice en Bob. Elk van hen kiest een geheime exponent en berekent de éénwegsfunctie resulterend in en respectievelijk. Het paar is het private-publieke sleutelpaar van Alice en dat van Bob. De publieke sleutels worden uitgewisseld over een onbeveiligd kanaal. De gemeenschappelijke geheime sleutel is dan gegeven door

, die zowel door Alice als Bob kan berekend worden. In deze laatste stap wordt gebruikgemaakt van het feit dat de éénwegsfuncties commuteren. De gemeenschappelijke sleutel , kan dan gebruikt worden in combinatie met AES om alle verdere communicatie tussen Alice en Bob te beveiligen. een probleem: hoe weet Bob dat het bericht A dat hij ontvangt wel degelijk van Alice afkomstig is? Dit probleem kan opgelost worden aan de hand van een digitale handtekening (zie verder), die de authenticiteit van het bericht van Alice garandeert. In de praktijk gebruikt men dus altijd een combinatie van Diffie-Hellman en een digitaal handtekeningschema.
Het Diffie-Hellman protocol zoals beschreven in Figuur 1 heeft echter
Alhoewel de multiplicatieve groep van een eindig veld nog steeds vaak gebruikt wordt voor sleutelovereenkomst, zien we recent een duidelijke verschuiving naar het gebruik van een ander type groep, nl. de groep van punten op een elliptische kromme over een eindig veld. Uit de beschrijving van het Diffie-Hellman protocol kan men inderdaad makkelijk zien dat elke eindige commutatieve groep waarin het discreet logaritme probleem moeilijk is, kan gebruikt worden.
Een elliptische kromme bestaat uit alle oplossingen van
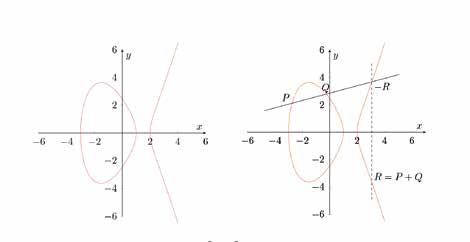
een vergelijking van de vorm waarbij constanten zijn in een bepaald veld. Figuur 2 (links) toont de kromme over het veld van de reële getallen .
Verrassend genoeg kan men de verzameling van de punten op een elliptische kromme de structuur van een commutatieve groep geven! Hiervoor is er wel 1 extra punt nodig, dat we met 0 noteren en “het punt op oneindig” noemen. En natuurlijk is er een bewerking nodig. Vaak wordt die als een “optelling” (of som) ( ) genoteerd. Per definitie stellen we de som van de 3 snijpunten van een rechte met de kromme gelijk aan het neutraal element (“0”) van de groep. Hieruit volgt direct de constructie van de groepswet (" ") zoals beschreven in Figuur 2 (rechts), nl. startende van twee punten en , trekken we de rechte door en , die de kromme in een derde punt zal snijden. Na spiegeling ten opzichte van de x -as verkrijgen we dan het punt dat we de som van de punten en noemen; we noteren . Het derde snijpunt van de rechte door en met de kromme noteren we als . De rechte door de punten en is een verticale rechte en snijdt de elliptische kromme niet zichtbaar in een derde punt, maar dat zien we als “het punt op oneindig” zodat . Het neutraal element kan men zich dus inbeelden als het punt dat oneindig ver op de y-as ligt.
Hoe tel je dan een punt bij zichzelf op? Door de limiet te nemen voor wordt de rechte door en uiteindelijk de raaklijn aan de kromme in het punt . Die raaklijn snijdt de kromme in een derde punt en dat is dan het punt , tenzij de raaklijn verticaal zou zijn, maar dan is
Als we een punt een aantal keer (bv. keer) bij zichzelf optellen bekomen we een ander punt . Deze operatie heet scalaire vermenigvuldiging en is het analogon van machtsverheffiing voor eindige velden. Het berekenen van de scalar gegeven de punten en . wordt dan ook het elliptische kromme discreet logaritme probleem (ECDLP) genoemd.
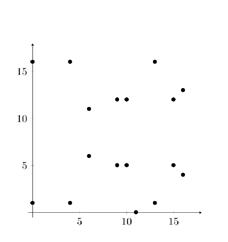
In cryptografie werkt men niet met elliptische krommen over het veld maar met elliptische krommen over een eindig veld . De groep van de punten op de elliptische kromme is dan ook eindig en elk element kan efficiënt en exact voorgesteld worden als een koppel elementen uit . In Figuur 3 is de elliptische kromme weergegeven over het eindig veld . In dit geval bestaat de kromme, die we noteren als , uit een eindige verzameling punten; de formules voor de groepswet, afgeleid voor het reële geval, blijven echter onverkort gelden over omdat deze breuken van veeltermen zijn. (zie figuur 3)
Het grote voordeel van elliptische krommen is dat het ECDLP op een kromme veel moeilijker is dan het DLP in ; zo zal bv. het ECDLP voor met p een 256-bit priemgetal ongeveer even moeilijk zijn als het DLP in met q een
Figuur 3 Elliptische kromme over
3072-bit priemgetal. Dit verschil in grootte heeft ook een impact op de efficiëntie: voor de gegeven parameters zal de groepswet in bijna tien keer sneller te berekenen zijn dan die in .
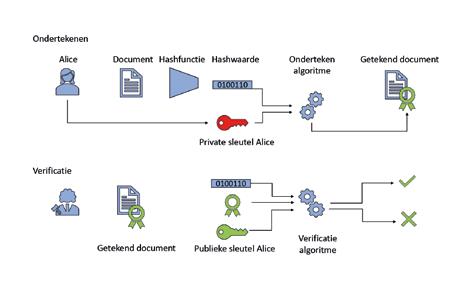
DIGITALE HANDTEKENING Een digitaal handtekeningschema wordt gebruikt om de authenticiteit en integriteit van een digitaal document te garanderen, en omvat twee algoritmes: het digitaal (onder) tekenen van een document en het verifiëren van de digitale handtekening. Zoals in Figuur 4 aangegeven, is het onderteken-algoritme een functie van het document dat getekend moet worden en de private sleutel van de ondertekenaar (in dit geval Alice). In praktijk wordt niet het document zelf getekend (wegens te groot), maar wel de zgn. hashwaarde van het document, een soort vingerafdruk van het document van beperkte lengte bv. 256 bits. Iedereen die in het bezit is van de publieke sleutel van Alice, is in staat om de digitale handtekening te
verifiëren. Een geldige digitale handtekening garandeert de volgende eigenschappen:
• de handtekening kan enkel gezet worden door de eigenaar van de private sleutel; • het document dat getekend werd, werd niet aangepast; • de persoon die de digitale handtekening gezet heeft kan niet ontkennen dat hij dat gedaan heeft, wat ervoor zorgt dat een digitale handtekening bindend is.
Net zoals bij sleutelovereenkomst is er een subtiel probleem: bij verificatie van een handtekening moet men 100% zeker weten dat de publieke sleutel echt die van Alice is. In praktijk wordt dit probleem opgelost aan de hand van certificaten en een publieke sleutel infrastructuur. Een certificaat is een document waarin de identiteit van een bepaalde partij (bv. Alice) gekoppeld wordt aan de publieke sleutel van die partij. Dit document wordt op zijn beurt digitaal ondertekend door een zogeheten CA (certificaat authoriteit), een bedrijf dat effectief verifieert dat de identiteit en publieke sleutel bij elkaar horen.
Een vaak gebruikt digitaal handtekeningschema is RSA, ontworpen in 1977 door Ron Rivest, Adi Shamir and Leonard Adleman (3). RSA maakt gebruik van het feit dat het makkelijk is om twee grote priemgetallen en met elkaar te vermenigvuldigen, maar gegeven het product het zeer moeilijk is om de priemfactorisatie te berekenen. Een publieke sleutel in RSA bestaat uit een product van twee grote priemgetallen
Figuur 4 Zetten en verifiëren van een digitale handtekening
en een encryptie-exponent e die onderling ondeelbaar gekozen wordt met . De private sleutel bestaat uit de decryptie-exponent .
Om een document m te ondertekenen, zal Alice eerst de hashwaarde berekenen en dan de digitale handtekening . Iedereen die de publieke sleutel van Alice weet, kan dan de handtekening verifiëren door eerst te berekenen en deze waarde te vergelijken met de hashwaarde . Indien beide gelijk zijn, is de digitale handtekening een geldige handtekening. In de praktijk gebruikt men tegenwoordig priemgetallen van 1024 bits en dus .
Een ander vaak gebruikt digitaal handtekeningschema maakt opnieuw gebruik van elliptische krommen over eindige velden en heet ECDSA: Elliptic Curve Digital Signature Algorithm. Ook hier zijn de sleutelgroottes voor ECDSA veel kleiner dan voor RSA, bv. net als voordien komt 256-bits ECDSA ongeveer overeen met 3072-bit RSA.
TOEPASSINGEN Iedere dag gebruikt iedereen, vaak zonder het te weten, cryptografie bv. om een beveiligde verbinding, een zogeheten HTTPS-verbinding, op te zetten met een webserver over het internet. Achter de schermen wordt de communicatie geëncrypteerd met het TLS-protocol (Transport Layer Security). Om een concreet voorbeeld te geven doorlopen we de verschillende stappen wanneer een klant naar https://www.coolblue.be/ surft. Nadat de verbinding met de webserver van Cooblue tot stand komt, start de server een Diffie-Hellman sleutelovereenkomst (gebruikmakende van eindige velden of elliptische krommen), en waarbij de input van de server (de A in Figuur 1) digitaal getekend wordt (met RSA of met ECDSA). De server stuurt dan de
Figuur 5 Beveiligde verbinding met Coolblue
volgende data door naar de browser van de klant: de Diffie-Hellman data, de handtekening op deze data en een certificaat dat de publieke sleutel van de server bevat. Bij ontvangst verifieert de browser van de klant het certificaat en de handtekening en genereert zelf input (de in Figuur 1) voor het Diffie-Hellman protocol, die naar de server wordt gestuurd. Op het einde van het Diffie-Hellman protocol wordt de gemeenschappelijke geheime sleutel K berekend die dan gebruikt wordt om alle verdere communicatie tussen de browser en de server te encrypteren met AES.
Figuur 5 bevat een screenshot die de details van zo'n verbinding weergeeft als men surft met Mozilla Firefox. Indien men klikt op het hangslot naast de link ziet men dat de verbinding beveiligd is, en na klikken op > naast secure connection ziet men alle details van de verbinding. Deze verbinding is dus beveiligd met TLS en maakt gebruik van Elliptic Curve
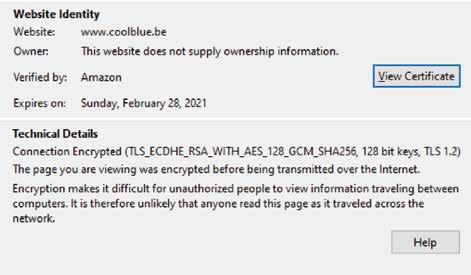
Diffie-Hellman (ECDH) waarbij de input van de server digitaal ondertekend wordt met RSA, en waarbij nadien alle communicatie geëncrypteerd wordt met AES met sleutellengte 128 bits (dit is enkel de sleutellengte voor AES, niet voor ECDH noch RSA). Het is ook mogelijk om de details van het certificaat van de webserver van Coolblue te bekijken, zoals weergegeven in Figuur 6. Daaruit blijkt dat Coolblue een RSA publieke sleutel gebruikt van 2048 bits en dat de encryptie-exponent gelijk is aan . Bovendien is dit certificaat digitaal getekend door de CA van Amazon, wiens publieke sleutel opnieuw in een certificaat zit. Dit is op zijn beurt getekend door de Amazon Root CA 1, wat een certificaat is dat standaard in Mozilla Firefox zit ingebouwd. Om de authenticiteit van een publieke sleutel te verifiëren is het dus nodig om de ganse keten van certificaten te verifiëren tot men uitkomt bij het ingebouwde certificaat.
Een tweede veel gebruikte toepassing zijn de Belgische elektronische identiteitskaarten (eID). De eID bevat naast de gebruikelijke data zoals naam en voornaam, geboorteplaats

en -datum etc., een cryptografische chip die twee types sleutelparen bevat: een sleutelpaar voor authenticatie, dat bv. gebruikt wordt om in te loggen op een bepaalde website, en een sleutelpaar om digitale handtekeningen te zetten. Een digitale handtekening die gezet wordt met een eID is wettelijk gezien equivalent aan een handgeschreven handtekening en kan dus bv. gebruikt worden om een contract (of de belastingsaangifte) te ondertekenen. Beide sleutelparen zijn op de huidige eID's, RSA-sleutels die 2048 bits lang zijn en een levensduur hebben van 10 jaar. De sleutels worden bij initialisatie van de eID door de cryptografische chip zelf gegenereerd, en de private sleutels verlaten nooit het beveiligde geheugen van de chip. Met een eID-kaartlezer en de eID-viewer is het bovendien makkelijk om deze sleutelparen te bekijken. Vanaf 2021 zal er overgeschakeld worden op het ECDSA handtekeningschema, omwille van de eerder genoemde voordelen, nl. kortere sleutels en meer efficiënte algoritmen.
REFERENTIES 1 Diffie, Whitfield and Hellman, Martin New Directions in Cryptography, IEEE Transactions on In- formation Theory, 22 (6), pp. 644-654, 1976 2 Kahn, David The Codebreakers - The Story of Secret Writing, 1967 3 Rivest, Ron and Shamir, Adi and Adleman, Leonard A Method for Obtaining Digital Signatures and Public-Key Cryptosystems, Communications of the ACM. 21 (2), pp. 120-126, 1978 4 Singh, Simon The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography, Bantam Doubleday Dell Publishing Group Inc., 1999
WAT IS EEN (EINDIG) VELD? Onder een veld (Engels: Field) verstaan we in de algebra een verzameling uitgerust met twee bewerkingen: een som (“ ”) en een product (“ ”). Elke bewerking zorgt voor een voldoend goede structuur, met name de structuur van een groep. Voor de som is dat de commutatieve groep ( ). Er is een neutraal element (“0”) en elk element heeft een tegengesteld element. Voor het product is dat de commutatieve groep ( . Deze groep wordt ook wel genoteerd om te wijzen op het multiplicatieve aspect. Hier is het neutraal element “1”, en elk nietnul element van heeft een multiplicatief invers. Voorts zijn er de gewone distributiviteiten die rekenen met producten van sommen in goede banen leiden.
De meest bekende voorbeelden van velden zijn het veld van de reële getallen ( ), maar ook de rationale getallen ( ) en de complexe getallen ( ) zijn velden. Minder gewoon, maar even praktisch is de verzameling van de gehele getallen modulo een priem . De elementen in die verzameling noteren we met 0, 1, 2, … , en we hanteren de afspraak dat , … Het is rekenen als op een klok, met uren.
Zo kun je verifiëren dat ( ) ook een veld vormt. Als bv. , dan geldt in dat en dat ook . Typisch wordt geschreven dat en . Het past dus om te schrijven dat in dit veld . Er zijn oneindig veel priemgetallen, en dus oneindig veel eindige velden. Meer zelfs, bij elk priemgetal zijn er oneindig veel eindige velden waarin = 0. Een structuureigenschap van eindige velden zorgt ervoor dat ze erg makkelijk in een computer kunnen voorgesteld worden, onafgezien van hun aantal elementen.
Let wel: ook in , met kan men rekenen. Deze verzameling vormt ook een optelgroep. Als niet priem is, is er echter geen multiplicatieve groep. Zo geldt bv. in dat .
Algebra wordt zoveel leuker als je eens een vraagstukje mag oplossen voor de elementen van een eindig veld!
Paul Igodt
HET DRAAIEND STOKJE
MICHEL ROELENS REDACTIE UITWISKELING
Ben je het filmpje ‘Straight pole, curved hole’ ook tegengekomen? Een stokje draait rond een as en passeert bij elke omwenteling door een gleuf (figuur 1).
In onze lessen ruimtemeetkunde van de derde graad lijkt het vaak alsof de ruimte enkel bewoond wordt door punten, rechten, vlakken en bollen. Het lijkt me een goed idee om ook – heel eventjes maar – een ander oppervlak te bespreken. Een bijzonder boeiend oppervlak is de (een–bladige) hyperboloïde. Dit filmpje, of het hebbeding zelf, is een prima vertrekpunt om het over die koeltorenvormige figuur te hebben. Je kunt het speelgoedje maken met een 3D-printer (zie Myminifactory) of bestellen bij iemand die het ge-3D-print heeft (Devinmontes). Ik beperk mij tot het filmpje.
Met de lesactiviteit hieronder laat ik zien hoe de hyperboloïde naar aanleiding van het filmpje in de klas kan worden besproken. Je kunt hierbij een GeoGebrafiguur of bordtekening maken die geleidelijk aan meegroeit met de stappen van de afleiding. We gaan ervan uit dat de leerlingen vertrouwd zijn met ruimtemeetkunde (vergelijkingen van rechten en vlakken) en met de as-vergelijking van een hyperbool. Een aanpak gebaseerd op goniometrie vind je in van Hoven e.a. (2017).

Figuur 1 Beeld uit het filmpje Straight pole, curved hole
DE VORM VAN DE GLEUF Het stokje draait rond een verticale as. Het stokje is kruisend met de as, en schuin (niet loodrecht kruisend). De wentelas is een rand van een vlak schermpje waar een gleuf in uitgesneden is. In de opdrachten hieronder ga je uitzoeken welke vorm de gleuf precies moet hebben zodat de stok er bij het voorbijdraaien juist in past. In het filmpje zijn het stokje en de gleuf nogal breed; in het wiskundig model werken we met een lijnstuk en een flinterdunne kromme gleuf.

We kiezen een assenstelsel zodat de wentelas samenvalt met de -as en het scherm een deel is van het -vlak.
De gleuf is symmetrisch ten opzichte van een vlak op halve hoogte; daarom plaatsen we de oorsprong op halve hoogte. Verder gaan we ervan uit dat de hoogte van het speelgoedje gelijk is aan 2 (zodat we op de -as van -1 tot 1 gaan).
Om te beginnen draaien we het stokje naar frontale stand, aan de voorkant van de wentelas (zie foto en GeoGebrafiguur).
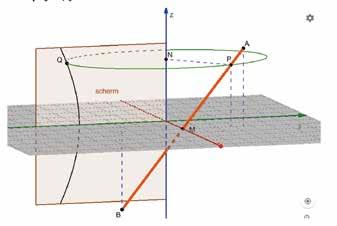

1. Als het bovenste punt van het stokje in deze stand coördinaten heeft, wat zijn dan de coördinaten van het onderste punt en die van het midden van het stokje?
2. Neem een willekeurig punt van het stokje, op hoogte . Het stokje is nog steeds in dezelfde frontale stand. Wat zijn de coördinaten van ?
3. Als de stok ronddraait, welke baan volgt het punt dan? (Geef een concreet antwoord: niet enkel de vorm van de baan maar ook de afmetingen.)
Een cirkelvormige baan in het horizontaal vlak . Het middelpunt van de cirkel is en de straal is .
4. Noem het punt van het scherm waar het punt P terechtkomt wanneer het door het scherm passeert. Wat zijn de coördinaten van ?
Het scherm is (een stuk van) het halfvlak . Het punt van de cirkelvormige baan dat in dit halfvlak ligt, is .
5. Als we laten variëren, dan beschrijft een kromme op het scherm. Geef parametervergelijkingen van deze kromme.
6. Geef cartesiaanse vergelijkingen van deze kromme.
Hiervoor moet de parameter geëlimineerd worden. Dit geeft:
7. Bewijs dat deze kromme een hyperbooltak is.
We werken vanaf nu in het vlak de vergelijkingen te vermelden:
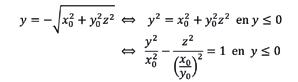
zonder dit nog in
Dit is een hyperbooltak in het -vlak.
8. Wat is het verband tussen deze kromme en de gleuf?
De gleuf moet de vorm hebben van het stuk van deze hyperbooltak, voor . En natuurlijk moet de gleuf een bepaalde ‘dikte’ hebben om de stok, die geen wiskundig lijnstuk is, door te laten.
9. Als de rechte waar het stokje een stuk van is bij het wentelen een ‘spoor’ zou nalaten in de ruimte, dan ontstaat een oppervlak dat ‘eenbladige hyperboloïde’ heet. Verklaar de naam.
Hyperboloïde omdat de doorsnede met het -vlak, en evengoed met elk ander vlak door de wentelas, een hyperbool is. Of nog: omdat dit het omwentelings lichaam is dat ontstaat wanneer je in plaats van de kruisende rechte deze hyperbool laat wentelen rond dezelfde wentelas. Eenbladig omdat je de hyperbool ook rond de -as zou kunnen laten wentelen en in dat geval een oppervlak uit twee stukken krijgt, een ‘tweebladige hyperboloïde’.
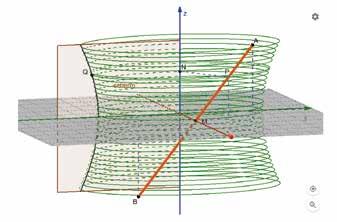
De volledige hyperboloïde stopt niet waar het wentelende stokje eindigt. Het omwentelingslichaam (het ‘spoor’ in de ruimte) van een rechte die wentelt rond een as vormt een (eenbladige) hyperboloïde wanneer de wentelende rechte de wentelas kruist maar niet loodrecht kruist. De naam hyperboloïde heeft te maken met de vorm van de gleuf in het filmpje: een hyperbool. Je kunt de hyperboloïde ook verkrijgen door deze hyperbool te wentelen rond de as.
Het is maar een kleine stap om een vergelijking van de hyperboloïde te bepalen. Met de notaties van de vorige werktekst: op hoogte hebben we een cirkel met middelpunt en straal . Dit levert meteen een parametervoorstelling van de hyperboloïde op:
Door te elimineren, vinden we een cartesiaanse vergelijking van de hyperboloïde: .
Een dergelijke vergelijking kun je niet zondermeer in GeoGebra ingeven, maar wel in het gratis programma Surfer, bekend van de Imaginary-tentoonstelling die in 2015-2016 door Vlaanderen reisde. Voor de parameters en (die ik gewoon als en heb ingetypt) maakt het programma dan schuifbalken aan. Merk op: als heb je een cilinder en als een kegel. Als beide parameters nul zijn, dan krijg je de wentelas. Als beide parameters niet nul zijn, heb je een hyperboloïde. Uiteraard wordt ook hier maar een begrensd stuk van de hyperboloïde getekend.

Dat er eventueel nog meer over de hyperboloïde te vertellen valt, kun je (her)lezen in Roelens, 2002.
BRONNEN Devinmontes. https://www.devinmontes.com/store/straightpole-curved-hole (Hier is het te koop voor 30 dollar). Kircher, M. (2017). Allow Us to Explain How This Straight Pole Fits Through a Curved Hole. NYMag. https://nymag.com/intelligencer/2017/01/straight-pole-curved-hole-optical-illusionexplanation.html (Eenvoudige uitleg hoe het kan dat een rechte door een krom gat passeert). Myminifactory. https://www.myminifactory.com/object/3dprint-30750 (Bestanden om het voorwerp 3D te printen). Roelens, M. (2002). Wentelende lichamen en de hyperboloïde. Uitwiskeling 19/1, 9-14. Straight pole, curved hole. https://imgur.com/gkp04Gc (Het filmpje). Surfer. https://imaginary.org/program/surfer. van Hoven, M., Klok, M., Soto y Koelemeijer, G. (2017). Past precies. Euclides 93, 22-24.
Dit artikel verscheen in Uitwiskeling 34/2. Benieuwd naar meer? Op www.uitwiskeling.be vind je alle info. Daar kun je ook de werkteksten uit het artikel downloaden.