Analyse 4 i Integraalrekening
D-finaliteit gevorderde wiskunde
Philip Bogaert
Filip Geeurickx
Marc Muylaert
Roger Van Nieuwenhuyze
Erik Willockx
CARTOONS
Dave Vanroye
Hoe gebruik je VBTL ?
Dit boek bevat vier hoofdstukken. Elk hoofdstuk is opgebouwd uit verschillende paragrafen met aan het einde een handige samenvatting.
Definities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond.
Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt.


1 2 *
De nummers van de oefeningen hebben een gele kleur. Een sterretje duidt op een extra uitdaging. Maak ook kennis met voorbeeldvragen uit ijkingstoetsen en toelatingsexamens.
Achteraan in dit boek vind je de oplossingen
Oplossingen
ICT is een ideaal hulpmiddel.
Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets. Die vind je terug via www.polpo.be.
Wat moet je kennen en kunnen ?
Op het einde van elk hoofdstuk zie je een handig overzicht van wat je moet kennen en kunnen


Tussen 1665 en 1685 vonden Isaac Newton (1642 – 1727) en Gottfried Wilhelm Leibniz (1646 – 1716) onafhankelijk van elkaar de differentiaalrekening uit. Hiermee konden ze raaklijnen aan krommen en grafieken van functies bepalen. Daarover leerde je al in de vorige boeken.
Newton ontdekte kort daarna dat het omgekeerde van differentiëren kon worden toegepast op het berekenen van oppervlakten en volumes van figuren (vlakke en ruimtelijke) die worden begrensd door krommen of gekromde oppervlakken.
Al vanaf de oudheid probeerden wiskundigen de oppervlakte onder een kromme te berekenen. Voor de oppervlakte van een cirkelschijf werkte de geniale Griek Archimedes (3e eeuw v.Chr.) met ingeschreven regelmatige veelhoeken en leidde hij zo de formule πr 2 af. In dit boek leer je zelf een methode om de oppervlakte onder een kromme te benaderen met rechthoekjes. Ook maak je kennis met een manier om de oppervlakte exact te berekenen. Daarbij ga je functies integreren. Je zult merken dat er een eenvoudig verband bestaat tussen integreren en differentiëren.
Als je ooit oppervlakten moet berekenen in Parc Güell (Barcelona), neem dan zeker dit boek mee als hulp.



INKIJKEXEMPLAARDIEKEURE









Inhoud
INKIJKEXEMPLAARDIEKEURE





1
Bepaalde integralen
1.1 Het ontstaan van de integraalrekening – het integraalbegrip 9
1.2 Riemannsommen 13
1.3 Definitie van de bepaalde integraal 16
1.4 Oppervlakten met een toestandsteken (of georiënteerde oppervlakten) 17
1.5 Praktische werkwijze voor het berekenen van een bepaalde integraal 19
1.6 Optelbaarheid van de bepaalde integraal 24
1.7 Oppervlakte van het gebied begrensd door de grafiek van een functie en de x-as 26
1.8 Oppervlakte van het gebied begrensd door de grafieken van twee functies 28
1.9 Hoofdstelling van de integraalrekening 30
1.10 Toepassingen op oppervlakteberekening 37
1.11 Oneigenlijke integralen 42
3
Toepassingen van de integraalrekening
3.1 Oppervlakte van bijzondere vlakke figuren 119
3.2 Zwaartepunt van een vlakke figuur 127
3.3 Volume van omwentelingslichamen 132
3.4 Booglengte van een vlakke kromme 158
3.5 Manteloppervlakte van een omwentelingslichaam 165
Analyse 4 i Integraalrekening INKIJKEXEMPLAARDIEKEURE
2
Integratiemethoden
2.1 Fundamentele integralen 69
2.2 Integratie door substitutie 77
2.3 Integratie van elementaire rationale functies – splitsen in partieelbreuken 91
2.4 Partiële integratie 99
4
Toepassingen van integralen in andere disciplines
4.1 Snelheid en afgelegde weg 179
4.2 Versnelling en snelheid 181
4.3 Kracht en arbeid 183
4.4 Marginale kostprijs 186
4.5 Gini-coëfficiënt en Lorenzcurve van de inkomensverdeling 188
4.6 Elasticiteit van de vraag 190



Bepaalde integralen
1 INKIJKEXEMPLAARDIEKEURE







Deze fiets- en wandelbrug, die meer dan 20 miljoen euro heeft gekost, kun je in haar volle glorie bezichtigen in het Engelse Stockton-on-Tees. Ze werd de infinity bridge genoemd omdat ze (samen met de weerspiegeling in het water) het symbool voor oneindigheid vormt.
Als het wandel- en fietsplatform mooi horizontaal is en je kent de functie om de bogen te beschrijven, dan kun je de oppervlakte tussen kromme en rechte berekenen (en daarbij heb je integralen nodig …).
In Dubai (Verenigde Arabische Emiraten) is er trouwens een brug met dezelfde naam die we hier ook hadden kunnen plaatsen, zoek die gerust eens op.


Bepaalde integralen
1 Het ontstaan van de integraalrekening – het integraalbegrip 9
2 Riemannsommen 13
3 Definitie van de bepaalde integraal 16
4 Oppervlakten met een toestandsteken (of georiënteerde oppervlakten) 17
5 Praktische werkwijze voor het berekenen van een bepaalde integraal 19
6 Optelbaarheid van de bepaalde integraal 24
7 Oppervlakte van het gebied begrensd door de grafiek van een functie en de x-as 26
8 Oppervlakte van het gebied begrensd door de grafieken van twee functies 28
9 Hoofdstelling van de integraalrekening 30
10 Toepassingen op oppervlakteberekening 37
11 Oneigenlijke integralen 42
12
Wat moet je kennen en kunnen? 66
1 Het ontstaan van de integraalrekening – het integraalbegrip






Enkele voorbeelden :
De grootste wiskundige van de hele oudheid was ongetwijfeld de Griek Archimedes (287 – 212), die in Syracuse op Sicilië woonde als adviseur van koning Heroon.
Zijn belangrijkste prestatie is de uitvinding van de integraalrekening, tweeduizend jaar voordat Newton en Leibniz de differentiaalrekening ontdekten.
Hij leverde belangrijke bijdragen die behoren tot het gebied dat we nu de integraalrekening noemen : de bepaling van de oppervlakte van vlakke figuren en het volume van lichamen.
INKIJKEXEMPLAARDIEKEURE
In Archimedes’ boek ‘De kwadratuur van een parabool’ vinden we de volgende stelling : de oppervlakte van een parabolisch segment met de koorde a als basis is gelijk aan 4 3 maal de oppervlakte van de ingeschreven driehoek met basis a en top in dat punt van de parabool waar de raaklijn evenwijdig is aan a
a
oppervlakteparaboolsegmentOAB = 4 3 maaloppervlakte ∆OAB
Een bewijs m.b.v. integralen vind je op blz. 37.
In het boek ‘Over de bol en de cilinder’ vinden we de volgende uitdrukkingen:
De oppervlakte van een bol is het viervoud van de oppervlakte van een grote cirkel ( A bol = 4πr 2 )
Het volume van een bol is gelijk aan 2 3 van het volume van de omgeschreven cilinder
Een bewijs van die eigenschappen m.b.v. integralen vind je op blz. 139.
De aanpak van de oude Grieken had echter een belangrijke beperking: voor de berekening van de oppervlakte van elke nieuwe figuur was een nieuwe aanpak nodig, meestal gebaseerd op de meetkunde van die tijd. Ze hadden geen algemene methode waarmee de berekeningen konden worden uitgevoerd.




Pas in de zeventiende eeuw ontwikkelden Newton en Leibniz, onafhankelijk van elkaar, een algemene methode om oppervlakten van kromlijnige figuren te berekenen : de integraalrekening. Newton vond namelijk, kort nadat hij de differentiaalrekening had bedacht, dat de omgekeerde bewerking van differentiëren de methode van de integraalrekening is.
We geven eerst enkele voorbeelden van grootheden die als oppervlakten voorgesteld kunnen worden. Newton
a Oppervlakten
In de vlakke meetkunde heb je al de oppervlakte van een aantal figuren bestudeerd. We frissen je geheugen even op.
INKIJKEXEMPLAARDIEKEURE
b Afgelegde weg
In de volgende grafiek wordt de snelheid die een sprinter ontwikkelt, uitgezet in functie van de tijd.
(m/s)

– Kun je berekenen hoeveel afstand hij heeft afgelegd in 10 seconden?
De afstand kun je op de grafiek zichtbaar maken in de vorm van een oppervlakte. Welke ?
c Nitraatgehalte in water
Een bedrijf, gelegen aan een rivier die uitmondt in de Schelde, loost regelmatig nitraatafval. Het heeft een vergunning gekregen van de overheid voor het lozen van 1 ton per week.
De stroomsnelheid van de rivier wordt verondersteld constant te zijn met een debiet van 40 000 m3 water per dag. Stroomafwaarts wordt eenmaal per dag (op de middag) een watermonster gemeten. Voor deze week geeft dit :






Via deze meetresultaten kun je de hoeveelheid nitraten schatten die het meetstation passeert. Met een debiet D = 40 000 m3/dag en de gemeten concentratie c is de totale hoeveelheid nitraten n die gedurende een dag (een tijdsinterval ∆t ) passeert, te schatten met de formule : n = D · c · ∆t
Voor de hele week ( ∆t = 1) wordt dat :

INKIJKEXEMPLAARDIEKEURE

D ( c 2 + + c 7) · ∆t = 40 000 m3 · 21,9729 g/m3 = 878,916 kg.
Wegens het grote debiet is er ook een snelle verandering in concentratie. De enige manier om nauwkeuriger de lozing van de fabriek te controleren is vaker meten. In plaats van eenmaal per dag besluit men viermaal daags (0.00 u., 6.00 u., 12.00 u. en 18.00 u.) te meten. Dat geeft het volgende resultaat.
















In een week tijd zijn dat dus 28 metingen (c1 to c 28). Vooral tijdens de weekdagen zijn de resultaten van de metingen in de voormiddag opvallend hoger dan in de namiddag.
Voor de totale hoeveelheid nitraten in de loop van deze week geldt ∆ t = 1 4 : n = D ( c 1 + c 2 + ... + c 28 ) 1 4 = 40000m3 92,0332g/m3 1 4 = 920,332kg
Het verschil van meer dan 40 kg nitraat gemeten bij een nauwkeurige waarneming leidde tot de plaatsing van een sensor in het water, die continu stalen neemt. De sensor geeft een signaal dat wordt doorgegeven aan een penschrijver, die een directe grafische weergave levert van het gemeten signaal. De uitvoer van de penschrijver is een grafiek van het gemeten nitraatgehalte (in g/m3) als functie van de tijd (in dagen).
INKIJKEXEMPLAARDIEKEURE
De totale hoeveelheid nitraat in een week is evenredig met de oppervlakte onder de grafiek.
Oplossing :
De oppervlakte bedraagt 23,0085 eenheden. Dat resulteert in 920,34 kg nitraat per week.
In veel situaties waarbij je met grafieken werkt, heeft de oppervlakte tussen de grafiek en de x -as een betekenis. De gezochte oppervlakte kun je schatten door het gebied op te delen in rechthoekjes en de oppervlakte van die laatste op te tellen.
In dit boek leer je hoe je zo’n oppervlakte nauwkeurig kunt verkrijgen als de vergelijking van de grafiek bekend is. Je berekent dan een bepaalde integraal.
2 Riemannsommen
We vragen ons af wat de oppervlakte is van het gebied in het eerste kwadrant dat ingesloten wordt door de grafiek van de functie f met f ( x ) = –x 2 + 2x + 3, de x -as en de y -as.
Hiertoe verdelen we het interval [ 0, 3] in 3 gelijke deelintervallen met breedte ∆x = 1. We beschouwen nu twee soorten rechthoeken.
De ondersom s3 van de oppervlakten van de eerste soort rechthoeken is kleiner dan de gevraagde oppervlakte.
s 3 = 1 3 + 1 3 + 1 0 = 6
De bovensom S3 van de oppervlakten van de tweede soort rechthoeken is groter dan de gevraagde oppervlakte.
S 3 = 1 4 + 1 4 + 1 3 = 11
Hoe meer deelintervallen, hoe fijner de rechthoeken (Riemannfrietjes genaamd), en hoe dichter de ondersom en bovensom de werkelijke oppervlakte benaderen.
voor n = 6 (∆x = 0,5) krijgen we :
INKIJKEXEMPLAARDIEKEURE
Om de oppervlakte exact te bepalen, berekenen we s n en S n voor steeds groter wordende waarden van n en proberen we de limieten te berekenen voor n → +∞
We vermoeden dat lim n → +∞ sn = lim n → +∞ Sn = 9, zodat de exacte oppervlakte van het gebied 9 (oppervlakte-eenheden) groot is. Later zullen we berekenen dat dat inderdaad zo is.

Bernhard Riemann (1826–1866)
Georg Friedrich Bernhard Riemann werd op 17 september 1826 geboren in Breselenz (niet ver van Hannover) als tweede kind in een gezin met zes kinderen.
Zijn vader, een lutherse dominee, onderwees zijn kinderen zelf, maar toen Bernhard 10 was, ging hij naar de school in het dorp.
In 1840, hij was toen 14, ging hij naar het lyceum in Hannover. Hij woonde in die tijd bij zijn grootmoeder, die hem financieel steunde. Toen die in 1842 overleed, ging hij naar het gymnasium van Lüneburg. Hij was een zeer verlegen en teruggetrokken jongen met een zwakke gezondheid, waar hij heel zijn leven de gevolgen van droeg.
INKIJKEXEMPLAARDIEKEURE
De schooldirecteur merkte snel het wiskundige talent van Riemann op en gaf hem het boek ‘Théorie des nombres’ van Legendre. Nauwelijks 6 dagen later had de jonge Riemann dit bijna 900 bladzijden tellende leerboek over getaltheorie ingestudeerd. Zijn commentaar: “Dit was een prachtig boek, ik heb het onder de knie.”
In 1846 schreef hij zich in als student aan de universiteit van Göttingen. Aanvankelijk volgde hij les aan de faculteit theologie om te voldoen aan het verlangen van zijn vader, die van hem een dominee had willen maken. Vrij vlug gaf hij die richting op om zich toe te leggen op de wiskunde.
Na een jaar verhuisde hij naar de universiteit van Berlijn, waar hij les kreeg van Jacobi, Steiner, Dirichlet en Eisenstein. Het was Dirichlet die Riemann het meest beïnvloedde en hem vroeg om zijn medewerker te worden. In 1849 keerde Riemann naar Göttingen terug om zijn doctoraat voor te bereiden. In 1851 promoveerde hij onder Gauss met zijn proefschrift ‘Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse’. In 1854 moest Riemann nog een proefschrift schrijven, een zogenaamd Habilitationsschrift, om een aanstelling te krijgen aan de universiteit van Göttingen. In dat proefschrift gaf hij een precieze definitie van integreerbaarheid, die tegenwoordig bekendstaat als de Riemannintegraal en een verbetering was van de definitie van Cauchy en Dirichlet. Pas in 1902 ontwikkelde de Franse wiskundige Henri Lebesgue (1875 – 1941) de zogenaamde Lebesgue-integraal, een nog ruimer begrip, dat voor veel doeleinden beter bleek.
In 1857 werd Riemann assistent-professor aan de universiteit van Göttingen. In 1859 overleed Dirichlet, die Gauss had opgevolgd. Riemann werd benoemd tot zijn opvolger. In datzelfde jaar werd hij ook verkozen tot corresponderend lid van de Berlijnse academie van wetenschappen. Hij was door zijn ontdekkingen beroemd geworden in Europa.
Dankzij zijn baan als professor ging het Riemann op financieel gebied een stuk beter en in 1862 huwde hij met Elise Koch. Nauwelijks een maand later kreeg hij pleuritis en werd hij ernstig ziek.
Hij reisde regelmatig naar Italië om te herstellen. In 1863 werd zijn dochter Ida geboren in Pisa. Bernhard Riemann stierf op 20 juli 1866 aan het Lago Maggiore ten gevolge van tuberculose.




3 Definitie van de bepaalde integraal
Op dezelfde manier kun je de oppervlakte van het gebied tussen de grafiek van een positieve, continue functie f en de x -as in het interval [ a , b ] bepalen.
1 Verdeel [ a , b ] in n gelijke deelintervallen met breedte ∆ x = b a n .
2 Bereken in elk ( i -de) deelinterval het minimum van de functiewaarden ( f min( x i ) = m i ) en het maximum van de functiewaarden ( f max( x i ) = M i ). Aangezien f continu is in [ a , b ] zijn dat minimum en dat maximum steeds te vinden (stelling van Weierstrass).
3 Bereken de ondersom sn
en de bovensom Sn
4 Bereken lim n → +∞ sn enlim n → +∞ Sn
We kunnen bewijzen dat voor functies die continu zijn in [ a , b ] de limieten bestaan en gelijk zijn.
5 De gemeenschappelijke waarde van de limieten noemen we de bepaalde integraal van a tot b van de functie f
We noteren : lim n → +
Opmerking :
De Duitse wiskundige Bernhard Riemann heeft aangetoond dat het niet nodig is om het maximum of het minimum van de functiewaarden te nemen. Je krijgt ook hetzelfde resultaat als je de breedte vermenigvuldigt met een willekeurige functiewaarde f ( xi) die in het deelinterval aangenomen wordt.
De Riemannsom noteer je dan als
INKIJKEXEMPLAARDIEKEURE
Kiezen we nu in elk deelinterval een willekeurige x i , dan geldt : m i f ( x i ) M i
i -dedeelinterval metbreedte x
De Riemannsom ligt dus altijd tussen de ondersom en de bovensom. Laat je nu n oneindig groot worden, dus Dx → 0, dan benaderen de ondersom, de bovensom en de bovenstaande Riemannsom elkaar.
Immers : lim
Volgens de insluitstelling van de limieten geldt dus (zie VBTL 5 Analyse 2) :
INKIJKEXEMPLAARDIEKEURE
4
Oppervlakten
met een toestandsteken (of georiënteerde oppervlakten)
Een buitenhuisje wordt van energie voorzien door een accumulator, verbonden met een tiental zonnepanelen. Anderzijds wordt er ook heel wat energie verbruikt door allerlei toestellen. Het nettoresultaat van deze toe- en afname van energie (gisteren) wordt weergegeven door de volgende grafiek.
Oppervlakten van de gebieden boven de x -as betekenen een toename van energie. Oppervlakten van gebieden onder de x -as betekenen een afname van energie.
Het is dus zinvol om aan de oppervlakte van een gebied een teken toe te kennen. We maken de volgende afspraak. Oppervlakten van gebieden boven de x -as hebben een positieve waarde en die onder de x -as hebben een negatieve waarde.
Het nettoresultaat van de energietoename/-afname is de som van de oppervlakten met hun teken. We definiëren de bepaalde integraal voor de energiefunctie f over [ 0, 24] als de som van de (georiënteerde) oppervlakten van de gebieden tussen : – de grafiek van de energiefunctie f ; – de x -as ; – de rechten x = 0 en x = 24.
Notatie :
We beschouwen de tekentabel van de functie f in [ 0, 24]
Hieruit volgt dat :
INKIJKEXEMPLAARDIEKEURE
Als de functiewaarden negatief zijn, wordt ook de integraal van de functie negatief. We moeten dan rekenen met de tegengestelden van die functiewaarden.
Bijgevolg geldt :
Meetkundige betekenis van de bepaalde integraal
Gegeven is de functie f , die continu is in het interval [ a , b ].
De bepaalde integraal van a tot b van de functie f is de som van de oppervlakten met teken (georiënteerde oppervlakten) van de gebieden tussen : – de grafiek van f ; – de x -as ; – de rechten x = a en x = b (evenwijdig met de y -as).
Notatie : b a f ( x ) dx
Merk op dat de bepaalde integraal enkel bepaald wordt door de functie f en de grenswaarden a (beneden- of ondergrens) en b (bovengrens).
Voorbeeld :
Opmerkingen : ① De naam van de variabele speelt geen rol. Dus
② Als f ( x ) zowel positieve als negatieve waarden aanneemt in [ a , b ], dan moet je dat interval zo splitsen dat er gebieden ontstaan waarin f ( x ) uitsluitend positief (of 0) of uitsluitend negatief (of 0) is.
③ Uit het voorgaande blijkt dat de functies die continu zijn in een gesloten interval, in dat interval ook integreerbaar zijn.
5 Praktische werkwijze voor het berekenen van een bepaalde integraal
Om bepaalde integralen te berekenen, volgen we de werkwijze die gegeven werd op blz. 16.
De integraal van een functie f over het interval [ a , b ] is het getal dat je als volgt bekomt :
1 Verdeel [ a , b ] in n gelijke deelintervallen met breedte ∆ x = b a n .
2 Bereken de functiewaarde f ( x ) van een willekeurig getal x i uit elk deelinterval.
3 Bepaal de som : ∆
( x 1 )+
4 Bereken de limiet van die som voor n → +∞ , dat is voor Dx → 0.
In symbolen :
Voorbeelden :
Dat is de oppervlakte van een rechthoek met afmetingen
en 1.
b Integraal van x
We verdelen [ a , b ] in n deelintervallen met breedte ∆ x = b a n . Als x i nemen we de linkergrens van elk interval. INTERVAL
[
INKIJKEXEMPLAARDIEKEURE
We nemen a < b .
desomvandeeerste n termen vaneenrekenkundigerijis: s = u 1 + u n 2 n
Dat is de oppervlakte van een rechthoekig trapezium met als grote basis b , als kleine basis a en als hoogte b – a
Integraal
De benaming ‘integraal’ komt van het Latijnse ‘integrare’, wat ‘volledig maken’ betekent. Die benaming werd door Leibniz vermoedelijk gekozen om uit te drukken dat het getal de ‘integratie’ of volledige oppervlakte weergaf tussen de kromme en de x-as.
De notatie van de bepaalde integraal is als volgt ontstaan. De plaats van het somteken (∑) werd ingenomen door een ouderwetse S, de eerste letter van ‘summa’ (Latijn voor som). a is de ondergrens en b is de bovengrens van het hele interval. f(x) is de integrand, d.w.z. het voorschrift van de te integreren functie. De notatie dx zegt dat je de lengte van een deelinterval zo klein kunt kiezen als je zelf wilt : D x → 0.
c Integraal van x 2
over het interval [ 0, b ] met b > 0
We verdelen [ 0, b ] in n deelintervallen met breedte ∆ x = b a n . Als xi nemen we de rechtergrens van elk interval.
[
INKIJKEXEMPLAARDIEKEURE
[
[



(*) Stelindeformule (k + 1)3 = 1 + 3k + 3k 2 + k 3 k achtereenvolgensgelijkaan1,2,..., n .Danbekomje:
23 = 1 + 3 1 + 3 12 + 13
33 = 1 + 3 2 + 3 22 + 23
43 = 1 + 3 · 3 + 3 · 32 + 33
(1 + n )3 = 1 + 3n + 3n 2 + n 3
Tellenwerespectievelijkderechterledenendelinkerledenbijelkaarop,enschrappenwelinksen rechtsdegelijketermen(= gelijkederdemachten),dankrijgenwe:
Taak : bewijs deze eigenschap opnieuw door volledige inductie. over het interval [
b a x 2 dx = 0 a x 2 dx + b 0 x 2 dx = a 0 x 2 dx + b 0 x 2 dx symmetrie = ( a )3 3 + b 3 3 = b 3 a 3 3
over het interval [ a , b ] met a < b ⩽ 0
b a x 2 dx = a b x 2 dx symmetrie = ( a )3 3 ( b )3 3 = b 3 a 3 3 y –b b –a a O y = x 2 x
Besluit :
b a x 2 dx = b 3 a 3 3
Opmerking :
Je merkt vast de regelmaat in de 3 formules die we tot nu toe gezien hebben. We kunnen dus vermoeden dat algemeen geldt :
b a x n dx = b n +1 n + 1 a n +1 n + 1 n ∈ N
INKIJKEXEMPLAARDIEKEURE
Het algemeen bewijs geven we later. Het is duidelijk dat deze methode alleen maar voor zeer eenvoudige functies snel tot een resultaat leidt. Voor de andere gevallen is het nodig dieper in te gaan op de eigenschappen van bepaalde integralen.
Aanvullende definities (uitbreiding van het integraalbegrip) :
In b a f ( x )dx noemen we a de ondergrens en b de bovengrens.
De definitie van blz. 17 geldt alleen voor a < b
• a = b Voor een functie f die integreerbaar is in a geldt : a a f ( x )dx = 0
We kunnen die integraal dus opvatten als een grensgeval in de formule. Als we in de Riemannsom aannemen dat Dx = 0, dan zijn de som zelf en haar limiet gelijk aan nul.
• a > b Voor een functie f die integreerbaar is over [ b , a ] geldt : b a f ( x )dx = a b f ( x )dx
Die definitie wordt aannemelijk als we in de Riemannsom van blz. 17 aanvaarden dat Dx < 0. Het teken van de som en van haar limiet wordt dan gewijzigd.
6 Optelbaarheid van de bepaalde integraal
Op de bovenstaande tekening lezen we af :
c
b
)dx = A 1 A 2 + A 3
Hieruit blijkt de eigenschap
Als a , b en c behoren tot een interval waarin f integreerbaar is, dan hebben we voor elke ligging van a , b en c :
Bewijs :
We zullen ervan uitgaan dat a , b en c drie verschillende getallen zijn. Gerangschikt in stijgende orde zijn er dan 6 mogelijkheden voor a , b en c : abc , acb , bac , bca , cab , cba . We geven voor het geval abc een bewijs. We nemen een verdeling van [ a , b ] en een verdeling van [ b , c ]. De vereniging van beide is dan de verdeling van [ a , c ]. Voor de Riemannsommen horend bij die verdelingen schrijven we de grenzen bij het somteken.
Dus :
Als we deze verdelingen onbeperkt verfijnen, dan krijgen we door een limietovergang : c a f ( x )dx =
)
)
f ( x )dx +
)dx
)
)dx
Merk de gelijkenis op met de bekende formule van Chasles-Möbius voor vectoren in het vlak of in de ruimte.
Taak: ➀ Bewijs de stelling als twee van de drie getallen a , b en c aan elkaar gelijk zijn.
➁ Bewijs de stelling als alle drie de getallen a , b en c gelijk zijn.
➂ Geef een bewijs van de stelling voor het geval bac
Enkele verdere eigenschappen :
1 Lineariteit
Als f en g integreerbaar zijn over een interval en als k een gegeven reëel getal is, dan zijn ook f + g en k · f integreerbaar over dit interval en dan geldt :
Bewijs van (1) :
Taak: geef een analoog bewijs van eigenschap 2.
Opmerking :
De eigenschappen (1) en (2) kunnen we als volgt samenvatten.
Alsdefuncties f en g integreerbaarzijnin [
in woorden: de integraal van een lineaire combinatie van functies is een lineaire combinatie van de integralen.
Voorbeeld :
2 Ongelijkheden
Als f en g integreerbaarzijnin [a , b ],dangeldt:
Bewijs : We veronderstellen dat
7 Oppervlakte van het gebied begrensd door de grafiek van een functie en de x-as
Inhetvoorbeeldvanvorigeblz.vondenwedat
Meetkundiggezienbetekentditdat 4 3 degeoriënteerdeoppervlakteisvanhetgebiedbegrensddoordegrafiek
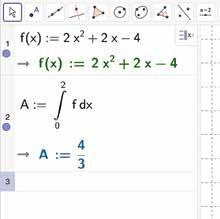








Willen we de werkelijke oppervlakte van gebieden I en II samen berekenen, dan moeten we de twee opper vlakten apart berekenen.
– We onderzoeken eerst waar de grafiek van f boven of onder de x -as ligt. x
grafiek onder de
INKIJKEXEMPLAARDIEKEURE
– In [ 0, 1] ligt de grafiek van f onder de x -as. Hier is de georiënteerde oppervlakte negatief en dus gelijk aan het tegengestelde van de gevraagde oppervlakte.
– In [ 1, 2] ligt de grafiek van f boven de x -as. De georiënteerde oppervlakte is positief en dus gelijk aan de gevraagde oppervlakte.
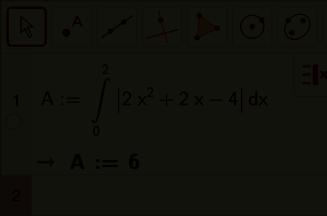
– De totale (werkelijke) oppervlakte bedraagt dus :
Opmerking :
We kunnen ook zeggen dat de gevraagde oppervlakte A gelijk is aan
Geef hiervoor een verklaring.
Dus : A = A I + A II =
0 | 2 x 2 + 2 x 4 | dx = 6
Regel :
Om de oppervlakte te bepalen van het gebied begrensd door de grafiek van de functie f en de x -as in het interval [ a , b ] op de x -as, ga je als volgt te werk.
1 Bereken de nulwaarden van f die in [ a , b ] gelegen zijn en bepaal het teken van f in elk deelinterval.
2 Bepaal de oppervlakte in elk deelinterval.
Is f ( x ) ⩾ 0, dan is de oppervlakte over dat deelinterval gelijk aan de integraal van f over dat interval. Is f ( x ) ⩽ 0, dan is de oppervlakte over dat deelinterval het tegengestelde van de integraal van f over dat deelinterval.
3 Tel de bekomen oppervlakten op.
Opmerking :
We kunnen ook zeggen dat de gevraagde oppervlakte gelijk is aan
| f ( x ) | dx
Door de absolute waarde van f ( x ) als integrand te nemen, worden de gebieden die bij f onder de x -as liggen, gespiegeld om de x -as, zodat ze boven de x -as liggen.
Taak : toon aan dat de oppervlakte van het gebied dat ingesloten wordt door de grafiek van f met f ( x ) = –x 2 + 2x + 3, de x -as en de y -as, gelijk is aan 9.
8 Oppervlakte van het gebied begrensd door de grafieken van twee functies
Voorbeeld :
Bereken de oppervlakte A van het gebied tussen de grafieken van de functies f en g met
in het interval [ –3, 2]
– We onderzoeken eerst waar de grafiek van f of de grafiek van g het meest naar boven ligt.
Hiertoe onderzoeken we het teken van v






• In [ 3, 2] geldt:


In [ 2,0] geldt:
• In [0,2] geldt: v ( x ) 0of f ( x ) g ( x )=
Opmerking :
We kunnen ook zeggen dat A
Geef een verklaring.
Toegepastophetvoorbeeldwordt A =
) |

Regel :
Om de oppervlakte te bepalen van het gebied begrensd door de grafieken van twee functies f en g in het interval [ a , b ] gaan we als volgt te werk.
1 We berekenen de nulwaarden van v = f – g die in [ a , b ] gelegen zijn en bepalen het teken van v ( x ) = f ( x ) – g ( x ) in elk deelinterval.
2 We bepalen de oppervlakte in elk deelinterval. Is v ( x ) ⩾ 0, dan is de oppervlakte over dat deelinterval gelijk aan
v ( x ) dx . Is v ( x ) ⩽ 0, dan is de oppervlakte over dat deelinterval gelijk aan
3 We tellen de bekomen oppervlakten op.
Opmerking :
We kunnen zeggen dat de gevraagde oppervlakte gelijk is aan b a | v ( x ) | dx of b a | f ( x ) g ( x ) | dx
9 Hoofdstelling van de integraalrekening
1 Integraalfuncties
Uit (5) volgt : b 1 x 2 dx = b 3 3 13 3 = b 3 3 1 3
INKIJKEXEMPLAARDIEKEURE
Met elke bovengrens b stemt een b 1 x 2 dx overeen.
Zoontstaateenfunctie I 1 ,met I 1 ( x )= x 3 3 1 3
We noemen ze de integraalfunctie van f met f ( x ) = x 2 en ondergrens 1.
schrijven we I a ( x )= x a f ( t ) dt . x y 1 O1 x f ( x ) = x 2 I 1( x )
De functie I 1 laat met elke x de oppervlakte I ( x ) overeenstemmen onder de grafiek van f in het interval [ 1, x ]
Algemeen zouden we door I a met I a ( x )= x a f ( x ) dx de integraalfunctie van f met ondergrens a kunnen voorstellen.
Omdat in die notatie x in twee betekenissen voorkomt,
Volgens opmerking 1 (blz. 18) speelt de naam van de variabele geen rol.
Er geldt dus : b a f ( x ) dx = b a f ( t ) dt = b a f ( u ) du = ...
integraalfunctie
Defunctie I a met I a ( x )= x a f ( t )dt
noemen we de integraalfunctie van f met ondergrens a I a ( x ) stelt de veranderlijke oppervlakte voor onder de grafiek van f in [ a , x ] x y y = f (x) 0 a x Ia(x)
Voorbeelden :
INKIJKEXEMPLAARDIEKEURE
We kunnen dus vermoeden dat algemeen geldt : D ( I a ( x ))= D
Met andere woorden : de afgeleide van een integraalfunctie is opnieuw de oorspronkelijke functie.
Die eigenschap noemen we de hoofdstelling van de integraalrekening. Om de stelling te bewijzen, hebben we eerst een hulpstelling nodig.
2 Middelwaardestelling van de integraalrekening middelwaardestelling
Als f continuisin [a , b ],danbestaatereen c ∈ [a , b ] : b a f (
Bewijs :
1 a < b
We verdelen [a , b ] in n gelijke deelintervallen met lengte ∆ x = b a n xi is een willekeurig getal in het i -de deelinterval.
Stellen we nu m = inf[ f [ a , b ]] dan geldt : M = sup[ f [ a , b ]] y x M m O a r xi s b y = f ( x ) i -dedeelinterval m f ( x i ) M ∆ x > 0
( x ) dx M
n deelintervallen
Aangezien f continu is, bestaat er in [ a , b ] een r zodat f ( r ) = m en een s zodat f ( s ) = M (stelling van Weierstrass).
Volgens de tussenwaardestelling bereikt f ( x ) in [ r , s ] alle waarden tussen m en M Dus bestaat er in [ r , s ] en bijgevolg in [ a , b ] minstens één c zodat
f ( c )= 1 b a · b a f ( x ) dx ,waaruitvolgt: ∃
2 a = b
Danis b a f ( x )dx = 0 =( b a ) f ( c )
3 a > b
Uit 1 volgtdan:
INKIJKEXEMPLAARDIEKEURE
)
Meetkundige betekenis van de middelwaardestelling Is f continu in [ a , b ], dan bestaat er een c in [ a , b ] zodat de oppervlakte van de rechthoek met b – a als basis en f ( c ) als hoogte gelijk is aan de oppervlakte onder de grafiek van f in [ a , b ]
( b a ) · f ( c )= b a f ( x ) dx of f ( c )= 1 b a
gemiddelde waarde
Het getal 1 b a b a f ( x ) dx noemen we de gemiddelde waarde van f over [ a , b ]
Opmerking :
f ( c )= 1 b a b a f ( x ) dx met c ∈ ]a , b [ kunnenweookschrijvenals
( c )=
We kunnen dit interpreteren als de uitbreiding van het rekenkundig gemiddelde van de functiewaarden f ( x 1), f ( x 2), …, f ( x n ).
Daarom noemen we f ( c ) de gemiddelde waarde van f in [ a , b ]
Voorbeeld :
3 Hoofdstelling van de integraalrekening hoofdstelling integraalrekening
Bewijs :
4
Primitieve functies
De integraalfunctie I a met I a ( x )= x a f ( t ) dt is een primitieve functie van f , want volgens de hoofdstelling is DIa( x ) = f ( x )
primitieve functie
F iseen primitievefunctie van f
DF = f of F = f f ( x ) f ′( x )
Voorbeelden :
differentiëren primitiveren
• F met F ( x )= x 3 iseenprimitievefunctievan f met f ( x )= 3 x 2 want Dx 3 = 3 x 2 .
Andereprimitievefunctiesvan f hebbenalsvoorschrift x 3 1, x 3 + 2, x 3 + 8 3 ,...
Wezullenaantonendatalleprimitievefunctiesvan f eenvoorschrifthebbenvandevorm x 3 + C ,met C eenwillekeurigreëelgetal.
• F met F ( x )= sin x iseenprimitievefunctievan f met f ( x )= cos x want D (sin x )= cos x .
Andereprimitievefunctiesvan f hebbenalsvoorschriftsin x 1 2 ,sin x + 1,sin x + 5 3
Wezullenaantonendatalleprimitievefunctiesvan f eenvoorschrifthebbenvandevormsin x + C ,met C eenwillekeurigreëelgetal.
stelling
Twee primitieve functies F 1 en F 2 van f verschillen slechts in een constante term.
Bewijs :
F 1 is een primitieve functie van f
F 2 is een primitieve functie van f
DF 1 = f en DF 2 = f
DF 2 = DF 1
DF 2 DF 1 = 0
D ( F 2 F 1 )= 0
INKIJKEXEMPLAARDIEKEURE
F 2 F 1 = C met C ∈ R
Besluit :
F 2 = F 1 + C met C ∈ R
Een functie heeft oneindig veel verschillende primitieve functies, die onderling slechts een constante verschillen. Daarom wordt vaak de volgende notatie gebruikt.
Als f een functie is met f ( x ) = 3x 2, dan is F met F ( x ) = x 3 + C een primitieve functie van f
Bij het bepalen van een primitieve functie van f ga je dus op zoek naar een functie F waarvan de afgeleide f is.
Voorbeelden :
• Deprimitievefunctiesvan f met f ( x )= sin x zijndefuncties F met F ( x )= cos x + C
want D ( cos x )= sin x
• Deprimitievefunctiesvan f met f ( x )= x 2 zijndefuncties F met F ( x )= x 3 3 + C
want D x 3 3 = x 2
• Deprimitievefunctiesvan f met f ( x )= 1 x 2 zijndefuncties F met F ( x )= 1 x + C
want D 1 x = 1 x 2
• Meeralgemeenzijndeprimitievefunctiesvan f met f ( x )= x n met n = 1defuncties F met F ( x )= x n +1 n + 1 + C
want D x n +1 n + 1 = (n + 1) · x n n + 1 = x n
• Deprimitievefunctiesvan f met f ( x )= 1 x zijndefuncties F met F ( x )= ln | x | + C
want D ln | x | = 1 x
• Deprimitievefunctiesvan f met f ( x )= a x zijndefuncties F met F ( x )= a x ln a + C
• Deprimitievefunctiesvansinhzijndefunctiescosh + C
want D (cosh x )= sinh x
• Deprimitievefunctiesvan f met f ( x )= 1 √ x 2 + k zijndefuncties F met F ( x )= ln | x + √
want D (ln | x +
INKIJKEXEMPLAARDIEKEURE
(k
R ) zieanalyse3
Taak : Vul nu zelf de volgende tabel aan. Raadpleeg de rekenregels van afgeleiden in het boek Analyse 3. functie f met f
5 Berekenen van bepaalde integralen d.m.v. primitieve functies
We zoeken nu een methode om de integraal b a f ( x ) dx te berekenen van een willekeurige continue functie f
We weten dat I a met I a ( x )= x a f ( t ) dt een primitieve functie van f is. Als F een willekeurige primitieve functie
van f is, dan hebben we I a ( x )= x a f (
INKIJKEXEMPLAARDIEKEURE
)+ C
• Stellen we x = a , dan vinden we : a a f ( t ) dt = F (a )+ C
0 = F (a )+ C C = F (a ) endus: I
• Stellen we x = b , dan vinden we : I a ( b )= b
) dt = F ( b ) F (a )
Het verschil F ( b ) – F ( a ) wordt kort genoteerd als [ F ( x )] b a
We hebben nu volgende eigenschap bewezen :
Als f continu is in [ a , b ] en F is een willekeurige primitieve functie van f in [ a , b ], dan geldt : b a f ( x ) dx =[ F ( x )] b a = F (
Praktische berekening : Om een bepaalde integraal b a f ( x ) dx te berekenen, gaan we als volgt te werk.
1 We berekenen een willekeurige primitieve functie F van f
2 We berekenen F ( a ) en F ( b ).
3 We berekenen F ( b ) – F ( a )
Voorbeelden :
x
We vinden hier de formule terug van blz. 23.
10 Toepassingen op oppervlakteberekening
1 Oppervlakte van een paraboolsegment
We zoeken de oppervlakte A van het deel van het vlak begrensd door de parabool met vergelijking y 2 = 2px en de rechte met vergelijking x = a Uit de symmetrie van deze figuur om de x -as volgt :
INKIJKEXEMPLAARDIEKEURE
Hieruit volgt dat
Dit laatste resultaat was al door Archimedes gekend (zie blz. 9).
Opmerking : Uit het vorige volgt ook dat
2 Oppervlakte van een hyperboolsegment
We zoeken de oppervlakte A van het deel van het vlak begrensd door de hyperbool met vergelijking xy = k , de x -as en de rechten met vergelijking x = a en x = b ( a , b > 0)
We vinden :
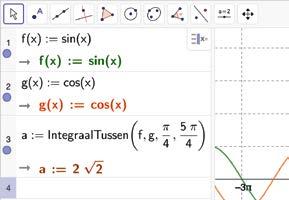
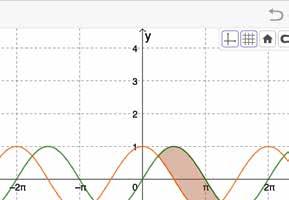
3 Oppervlakte van het gebied tussen de grafieken van f met f ( x) = sin x en g met g( x) = cos x in π
We onderzoeken eerst het teken van v ( x )= sin x cos x in
De gevraagde oppervlakte :



4 Oppervlakteberekening met y als onafhankelijke variabele


Voorbeeld : Bereken de oppervlakte A van het gebied begrensd door de parabool met vergelijking y 2 = 4x en de rechte met vergelijking y = 2x – 4.
We zoeken eerst de snijpunten :
De snijpunten zijn dus S1 (1, –2) en S2 (4, 4).
De oppervlakte A is eenvoudiger te berekenen door y in plaats van x te beschouwen als onafhankelijke variabele.
y 2 = 4 x ⇐⇒ x = y 2 4 = f ( y )
y = 2 x 4 ⇐⇒ x = y + 4 2 = g ( y )
)=
INKIJKEXEMPLAARDIEKEURE
5 Praktische toepassing
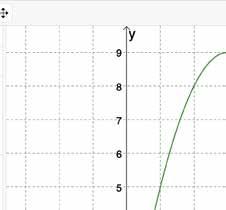
Een poort is parabolisch van vorm en kan beschreven worden door de vergelijking y = 6x – x 2
De poort is de oppervlakte van het gebied begrensd door de kromme met vergelijking y = 6x – x 2 en de x -as.
• Hoe breed is de poort (breedste punt) ?
Hoe hoog is de poort ? (1 eenheid = 1 meter)
• De poort is dringend aan een likje verf toe. Eén liter verf kost € 15. Met 1 liter verf schilder je 4 m2. Hoeveel verf heb je nodig en wat kost je dat, als je weet dat de verf steeds per liter wordt verkocht ?
• Tijdens het schilderen ben je van plan tweemaal te pauzeren.
Je doet dat telkens nadat je 1 3 van de poort hebt geverfd.
Als je van links naar rechts schildert, op hoeveel meter van de linkerkant pauzeer je dan telkens ?

Oplossing :
• Snijpunten van de parabool met de x -as : A( 0, 0) en B( 6, 0)
• Top van de parabool : C( 3, 9)
Breedte van de poort : ( 6 – 0) m = 6 m
Hoogte van de poort : 9 m




INKIJKEXEMPLAARDIEKEURE
• Oppervlakte van de poort : A = 6
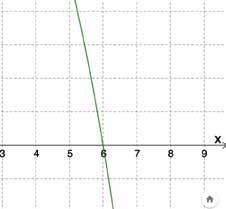


De oppervlakte van de poort bedraagt 36 m2. Je hebt dus 9 liter verf nodig en dat kost je € 135.
• Eerste pauze.
Je pauzeert de eerste maal nadat je 1 3 van de oppervlakte hebt geverfd.
De vraag is nu : bij welke bovengrens is het resultaat van de bepaalde integraal gelijk aan 12 ?
Stellen we die bovengrens gelijk aan a , dan krijgen we de volgende ‘integraalvergelijking’. a 0 (6 x x 2 )dx = 12
3 x 2 x 3 3 a 0 = 12
3a 2 a 3 3 = 12
a 3 9a 2 + 36 = 0
Die laatste vergelijking in a lossen we op met behulp van ICT.
Antwoord :
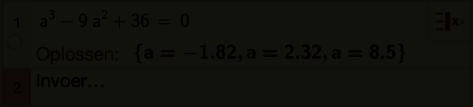
Op 2,32 meter van de linkerkant pauzeer je een eerste maal.
• Tweede pauze.
Je pauzeert een tweede maal nadat je 2 3 van de oppervlakte hebt geverfd. Dat is nadat je 24 m2 hebt geverfd.
Een analoge redenering als de vorige geeft : a 0 (6 x x 2 )dx = 24
3 x 2 x 3 3 a 0 = 24
3a 2 a 3 3 = 24
a 3 9a 2 + 72 = 0
INKIJKEXEMPLAARDIEKEURE
Met behulp van ICT :

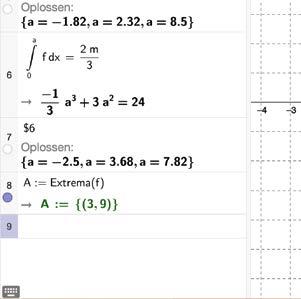
Antwoord :


Je pauzeert een tweede maal op 3,68 m van de linkerkant.
Opmerking :


Na het berekenen van de grens van de eerste pauze kun je de grens van de tweede pauze ook als volgt vinden :
6 – 2,32 = 3,68
11 Oneigenlijke integralen
Bij de definitie van de bepaalde integraal b a f ( x ) dx hebben we verondersteld dat de integratiegrenzen
reële getallen zijn en dat de integrand binnen het interval [ a , b ] begrensd is.
Wanneer we de definitie uitbreiden tot het geval waarbij minstens een van de grenzen oneindig groot wordt, spreken we van een oneigenlijke integraal van de eerste soort.
Wanneer we de definitie uitbreiden tot het geval waarbij de integrand niet begrensd is binnen de integratiegrenzen, spreken we van een oneigenlijke integraal van de tweede soort.
Oneigenlijke integralen van de eerste soort
Een oneigenlijke integraal van de eerste soort is een integraal waarvan minstens een van de grenzen oneindig groot wordt.
Notaties :
INKIJKEXEMPLAARDIEKEURE
Voorbeeld 1 :
Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f met f ( x )= 1 x en de x -as rechts van de rechte met vergelijking x = 1.
M.a.w.bereken
Oplossing :
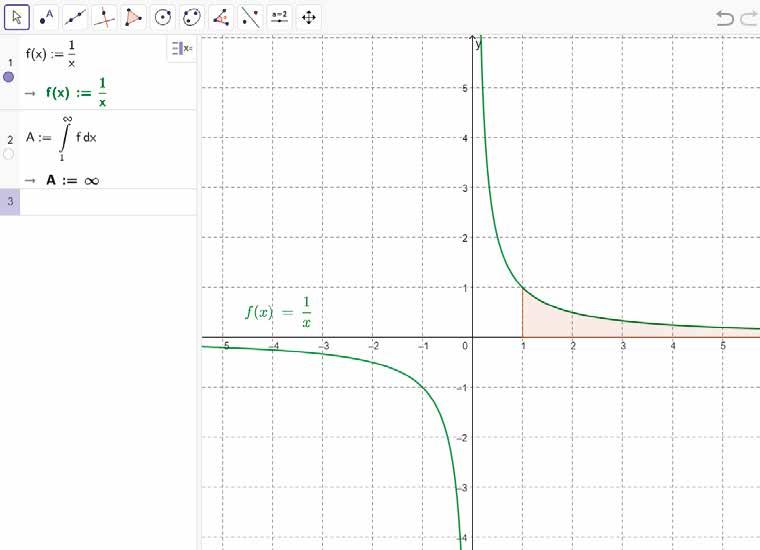



De oppervlakte van het onbegrensde gebied G is dus oneindig. We zeggen dat de oneigenlijke integraal divergent is.
Voorbeeld 2 :
Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f met f ( x )= 1 x 2 en de x -as links van de rechte met vergelijking x = –1.
M.a.w.:bereken
INKIJKEXEMPLAARDIEKEURE
Oplossing :

Ondanks het feit dat het gebied G onbegrensd is, is de oppervlakte eindig ( = 1) We zeggen dat de oneigenlijke integraal convergent is.
Voorbeeld 3 :
Bereken de oppervlakte van het deel van het vlak begrensd door de grafiek van de functie f met f ( x )= 1 1 + x 2 en de x -as.
M.a.w.:bereken
INKIJKEXEMPLAARDIEKEURE
Oplossing :
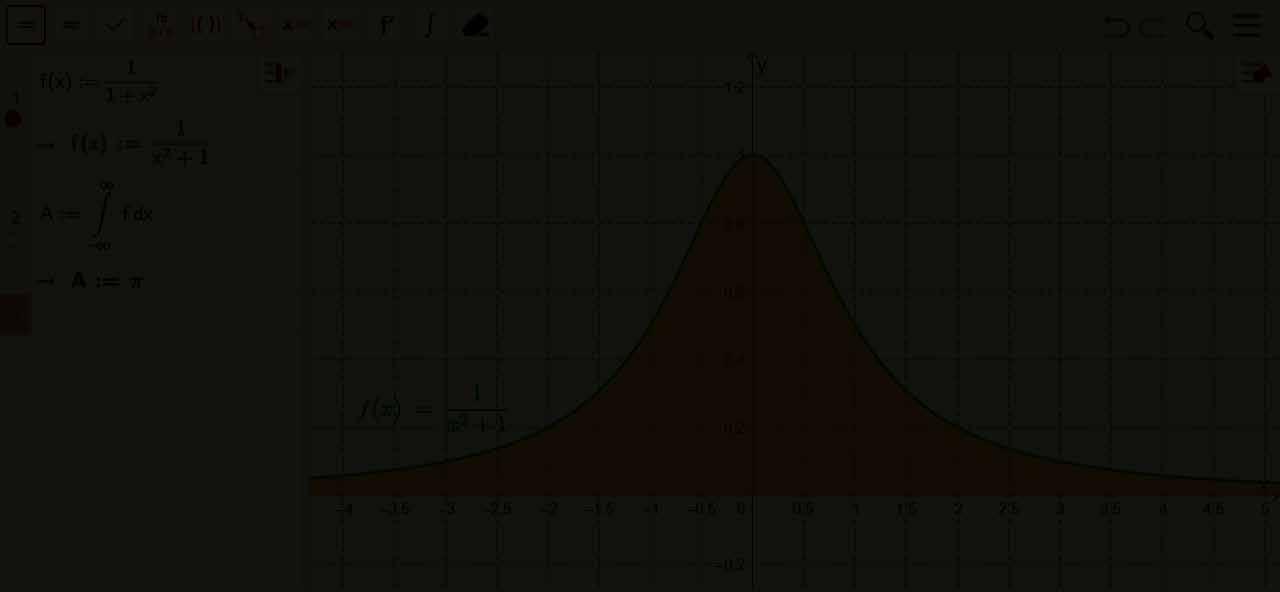
zodat
Algemeen
Op voorwaarde dat deze limieten bestaan.
Is deze limiet eindig, dan noemen we de oneigenlijke integraal convergent; is deze limiet oneindig, dan noemen we de oneigenlijke integraal divergent
Oneigenlijke integralen van de tweede soort
Een oneigenlijke integraal van de tweede soort is een integraal waarbij de integrand niet begrensd is binnen de integratiegrenzen.
Voorbeeld 1 :
Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f met f ( x )= 1 x 2 en de x -as, en dat voor x ∈ [ 0, 1].
M.a.w.:bereken 1 0 1 x 2 dx .
Oplossing :
INKIJKEXEMPLAARDIEKEURE

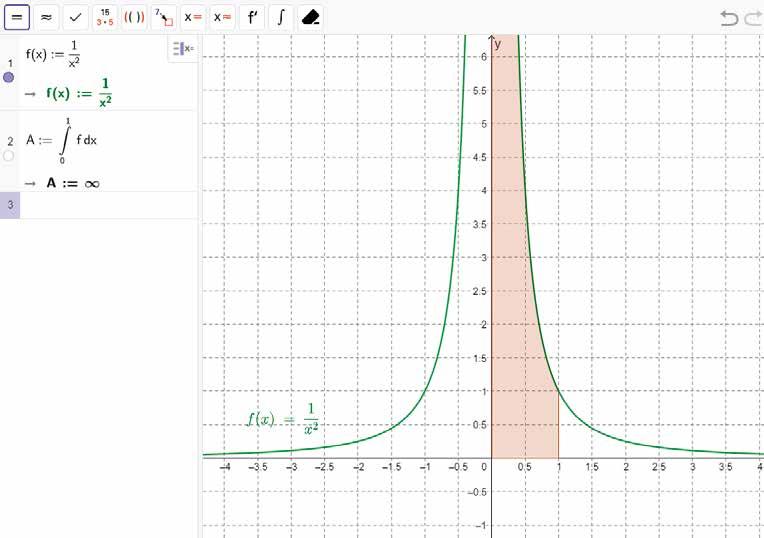


Omdat lim x →0 > 1 x 2 =+∞ is de functie f niet begrensd in [ 0, 1]. Merk op dat 0 een pool is van f We definiëren de gevraagde integraal als volgt:
De oppervlakte van het onbegrensde gebied G is dus oneindig. De oneigenlijke integraal is divergent.
Voorbeeld 2 :
Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f met f ( x )= 1 2√ x en de x -as, en dat voor x ∈ [ 0, 4]
M.a.w.:bereken 4 0 1 2√ x dx
Oplossing :
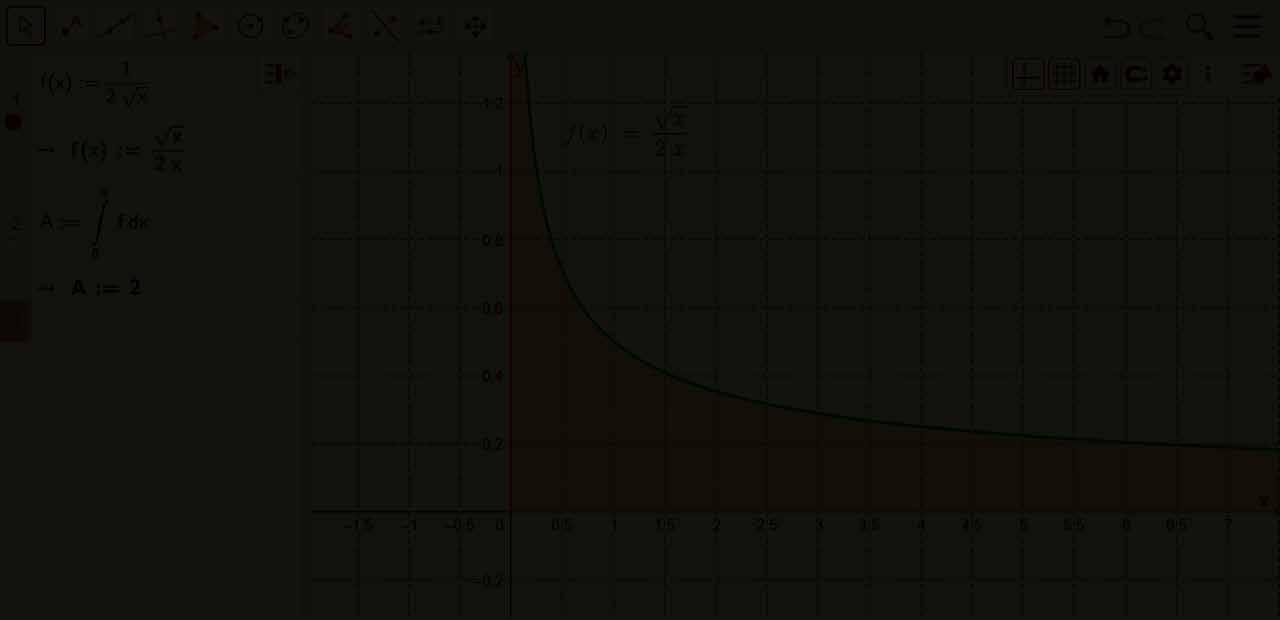
Omdatlim
INKIJKEXEMPLAARDIEKEURE
∞ is f nietbegrensdin [0,4].Wedefiniërendegevraagdeintegraalalsvolgt:
Ondanks het feit dat het gebied G onbegrensd is, is de oppervlakte eindig. De oneigenlijke integraal is convergent.
Voorbeeld 3 :
Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f met f ( x )= 1 3 √ x 2 en de x -as, en dat voor x ∈ [ –1, 1]
M.a.w.:bereken 1
Oplossing :

Omdatlim
INKIJKEXEMPLAARDIEKEURE
.Wedefiniërendegevraagdeintegraalalsvolgt:
Algemeen :
Is f nietbegrensdin a enis f integreerbaarover ]a , b ],danis b a f ( x ) dx = lim t →a > b t f ( x ) dx
Is f nietbegrensdin b enis f integreerbaarover [a , b [,danis
b a f ( x ) dx = lim
t a f ( x ) dx
Is f nietbegrensdin c ∈ ]a , b [ enis f integreerbaarover [a , c [ ∪ ] c , b ],danis
b a f ( x ) dx = lim t → c < t a f ( x ) dx + lim t → c > b t f ( x ) dx .
Is deze limiet eindig, dan noemen we de oneigenlijke integraal convergent ; is deze limiet oneindig, dan noemen we de oneigenlijke integraal divergent.
12
Samenvatting
• Je kent de definitie van een bepaalde integraal.
– De gemeenschappelijke waarde van de limieten van de bovensom S n en de ondersom s n noemen we de bepaalde integraal van a tot b van de continue functie f :
: integraalteken
a : ondergrens
– Riemanndefinitie :
b : bovengrens
f ( x ): integrand
dx : lengte van een deelinterval
• Je kent de meetkundige betekenis van de bepaalde integraal.
De bepaalde integraal van a tot b van een functie f die continu is in [ a , b ] is de som van de georiënteerde oppervlakten van de gebieden tussen de grafiek van f , de x -as en de rechten met vergelijking x = a en x = b
Oppervlakten van gebieden boven de x -as hebben een positieve waarde en die onder de x -as hebben een negatieve waarde.
• Je kent de volgende eigenschappen van de bepaalde integraal.
a f ( x ) dx = 0
• Je kent de methode om de oppervlakte te bepalen van het gebied begrensd door de grafiek van een functie f en de x -as in het interval [ a, b ] op de x -as.
( x ) | dx
• Je kent de methode om de oppervlakte te bepalen van het gebied begrensd door de grafieken van de functies f en g in het interval [ a, b ].
A =
a | f ( x ) g ( x ) | dx
• Je weet wat een integraalfunctie is.
De functie Ia met I a ( x )= x a f ( t ) dt noemen we de integraalfunctie van f met ondergrens a .
• Je kent de middelwaardestelling van de integraalrekening en je kunt ze bewijzen.
f iscontinuin [a , b ]=⇒∃ c ∈ [a , b ] : b a f ( x ) dx =( b a ) f ( c )
Hetgetal 1 b a b a f ( x ) dx noemenwedegemiddeldewaardevan f over [a , b ]
• Je kent de hoofdstelling van de integraalrekening en je kunt ze bewijzen.
Als f continuisin [a , b ],dangeldtin [a , b ] : I a ( x )= D
• Je weet wat een primitieve functie is.
F is een primitieve functie van f ⟺ DF = f of F ′ = f
INKIJKEXEMPLAARDIEKEURE
x a f ( t ) dt
= f ( x )
Twee primitieve functies van f verschillen slechts in een constante term.
• Je kunt een bepaalde integraal berekenen met behulp van primitieve functies.
Als f continu is in [ a , b ] en F is een willekeurige primitieve functie van f , dan is : b a f ( x ) dx =[ F ( x )] b a = F ( b ) F (a )
• Je weet wat oneigenlijke integralen van de eerste soort en van de tweede soort zijn en je kunt ze berekenen.
– Een oneigenlijke integraal van de eerste soort is een integraal waarvan minstens een van de grenzen naar oneindig nadert. +
)
x ) dx
f ( x ) dx = lim t →−∞ b t f ( x ) dx
f ( x ) dx = lim
f ( x ) dx
op voorwaarde dat die limieten bestaan.
Is de limiet eindig, dan noemen we de oneigenlijke integraal convergent. Is de limiet oneindig, dan noemen we de oneigenlijke integraal divergent.
– Een oneigenlijke integraal van de tweede soort is een integraal waarbij de integrand niet begrensd is binnen de integratiegrenzen.
Is f nietbegrensdin a enis f integreerbaarover ]a , b ],danis
( x ) dx .
Is f nietbegrensdin b enis f integreerbaarover [a , b [,danis
f ( x ) dx = lim
f ( x ) dx
Is f nietbegrensdin c ∈ ]a , b [ enis f integreerbaarover [a , c [ ∪ ] c , b ],danis
Is de limiet eindig, dan noemen we de oneigenlijke integraal convergent. Is de limiet oneindig, dan noemen we de oneigenlijke integraal divergent.
13 Oefeningen
Beschouw de functie f met functievoorschrift f ( x )= x 1 2
a Bereken de ondersom van deze functie over het interval [ 1, 8] bij zeven (gelijke) deelintervallen.
0 b Bereken de bovensom van deze functie over het interval [ 1, 8] bij zeven (gelijke) deelintervallen.
c Bereken met behulp van oppervlakteformules de exacte oppervlakte van het vlakdeel begrensd door de grafiek van deze functie en de x -as over het interval [ 1, 8]
Gegeven is de functie g met functievoorschrift g ( x ) = x + 1.
a Bereken de ondersom en de bovensom van de functie over het interval [ –4, 4] bij acht (gelijke) deelintervallen.
b Bereken met behulp van oppervlakteformules de exacte oppervlakte van het gebied tussen de grafiek van de functie en de x -as over het interval [ –4, 4]
Gegeven is de functie h met functievoorschrift h ( x ) = 4 – 2x.
a Bereken de ondersom en de bovensom van de functie over het interval [ –4, 1] bij tien (gelijke) deelintervallen.
b Bereken met behulp van oppervlakteformules de exacte oppervlakte van het gebied tussen de grafiek van deze functie en de x -as over het interval [ –4, 1]
Gegeven is de functie f met functievoorschrift f ( x )= 3 8 ( x 3 8 x 2 + 16 x )
Bereken de ondersom en de bovensom van de functie over het interval [ 0, 4] bij respectievelijk 4, 8 en 16 (gelijke) deelintervallen.
Toon aan dat b a x 3 dx = b 4 4 a
4 met behulp van Riemannsommen (zie blz. 16).
Tip : n i =1 i 3 = n 2 (n + 1)2 4 (bewijs deze formule met volledige inductie.) Bereken 6 0 f ( x ) dx
Bereken de oppervlakte van het gebied onder de parabool met vergelijking y = x 2 en boven het interval [ 0, 3] op de x -as als volgt :
a Verdeel het interval [ 0, 3] in 6 ( = n ) gelijke deelintervallen met lengte ∆ x = 1 2 en bereken de ondersom sn en de bovensom Sn
INKIJKEXEMPLAARDIEKEURE
b Bereken met ICT de ondersom en de bovensom voor n = 20, 50, 100, 500 en 999.
Leid hieruit lim n →+∞ sn enlim n →+∞ Sn af.
c Toon aan dat voor een willekeurige n (met n Dx = 3) geldt : sn = 3(3 ∆ x )(
Bepaallim n →+∞ (∆ x →0) sn enlim n →+∞ (∆ x →0) Sn .
Aanwijzing: n i =1 i 2 = n (n + 1)(2n + 1) 6
d Bereken nu de gevraagde oppervlakte. Controleer je antwoord met ICT.


Bereken volgende bepaalde integralen. a 4 0 f ( x ) dx met f ( x )= 2als0 x 2 1als2 < x 4
x als0 x < 3
)=
f ( x ) dx met f ( x )=
3als x 1 2 x + 5als1 < x < 3 x 4als3 x 4
0als x > 4
3als3 x < 6 x 3als6 x 8
De debietgrafiek van de wekelijkse wasbeurt van de heer Albert E. ziet er ongeveer uit zoals op onderstaande figuur.

a Bedenk een voorschrift bij het debiet D in functie van de tijd t
b Hoeveel liter is er in de badkuip na 5, 10, 20, 25 en 30 minuten ? c Beschrijf het watervolume in de badkuip in functie van de tijd en teken de bijbehorende volumegrafiek. d Bereken de afgeleide van de volumefunctie. Vergelijk met de debietfunctie en formuleer je bevindingen.
In de volgende grafiek wordt de snelheid van een jogger in meter per minuut uitgezet in functie van de tijd. tijd(min.) snelheid(m/min.)
a Bereken de afgelegde afstand na 30 minuten. b Bereken de gemiddelde snelheid (in km/h).
Bereken de volgende integralen.
Bereken de oppervlakte van het lichtgroen gekleurde gebied.
Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f , de x -as en de gegeven verticale lijnen als :
a f ( x )= 2 x 4 x = 1, x = 1
b f ( x )= x 2 + 2 x + 3 x = 0, x = 3
c f ( x )= x 2 4 x = 2, x = 3
d f ( x )= x 3 + 4 xx = √3, x = √2
e f ( x )=( x 2)( x 2 1) x = 1, x = 2
Bereken de oppervlakte van het gebied ingesloten tussen de grafiek van de functie f en de x -as (tussen de snijpunten met de x -as) als :
a f ( x )= x 2 + 4 x
b f ( x )= x 2 + 5 x 4e f ( x )= x 4 10 x 2 + 9
c f ( x )= x 3 3 x + 2
Bereken de oppervlakte van het blauw gekleurde gebied.
f ( x ) = 5x – x 2
g ( x ) = x 2 – 3x + 6 x y
Bereken de oppervlakte van het gebied begrensd door de grafieken van f en g met onderstaande voorschriften en de gegeven verticale lijnen.
a f ( x )= 2 x 2
b f ( x )= x 2
( x )= x 2 + 1, x = 0, x = 1
( x )= 2 x , x = 0, x = 2
c f ( x )= x 3 3 x 2 + 2 g ( x )= x 1, x = 2, x = 3
d f ( x )= x 3 + 2 x 2 4 g ( x )= x 2 + 4 x , x = 3, x = 2
Bereken de oppervlakte van het gebied begrensd door de grafieken van f en g als :
a f ( x )= 2 x x 2 g ( x )= x
b f ( x )= x 2 2 g ( x )= x 2 7 x + 12
c f ( x )= 6 x x 2 g ( x )= x 2 2 x
d f ( x )= x 3 3 x 2 + 3 x 1 g ( x )= x 1
e f ( x )= x 3 + 8 g ( x )= x 2 + 2 x + 8
Bepaal de oppervlakte van het gekleurde gebied.
k 1 ↔ y = x 2 6 x + 5
k 2 ↔ y = x 2 + 6 x 5
↔ y = 5
Bepaal de oppervlakte van het gebied ingesloten door de grafiek van de functie f met f ( x ) = 3x 2 – x 4 en de rechte met vergelijking y = –4
Gegeven zijn de functies f en g met f ( x ) = ( x + 2)3 en g ( x ) = 8 + 4x . a Bereken de oppervlakte van het gebied ingesloten door de grafieken van f en g b Bereken de oppervlakte van het gebied ingesloten door de grafieken van f en g en de rechte met vergelijking x = 1.
c Bereken de oppervlakte van het gebied ingesloten door de grafieken van f en g en de rechte met vergelijking y = 27
Bepaal de oppervlakte van het gebied begrensd door de parabool met vergelijking y 2 = 4x en de rechte door de punten P( 1, 2) en Q( 4, –4).
Bereken de oppervlakte van het gebied ingesloten door de grafiek van f met f ( x ) = x 4 – 12x 2 en de verticale lijnen door de buigpunten van de grafiek.
Bereken de oppervlakte van het gebied ingesloten door de parabool met vergelijking 4y = x 2 en de rechten met vergelijking 2y = x en y = x
De grafiek van f met f ( x ) = x 3 + 3x 2 sluit met de raaklijn in P( 2, f ( 2)) en de x -as een gebied in. Bereken de oppervlakte van dat gebied.
Een poort is parabolisch van vorm en kan beschreven worden door de vergelijking y = 3( 4 – x 2) (de poort is de oppervlakte van het gebied tussen de parabool en de x -as).
Gevraagd :
a Bereken de oppervlakte van de poort.
b Hoeveel hoger moet je de poort maken (zelfde breedte op de x -as en nog steeds parabolisch van vorm) opdat de oppervlakte zou verdubbelen ?
c Hoeveel breder moet je de poort maken (zelfde hoogte en nog steeds parabolisch van vorm) opdat de oppervlakte zou verdubbelen ?
De spanten van deze sporthal hebben de vorm van een parabool met vergelijking y = x x 2 25 .
De vloer is een rechthoek van 25 bij 35 meter.
Bereken het volume van de hal.
Bepaal k ( ∈ R) zodat :
Los de volgende vergelijkingen op.
a x 2 tdt + 1 x dt = 0
b 1 x (5 u 4 16) du + x 1 (5 u 4 16) du = 0
De oppervlakte van het gebied ingesloten door de grafiek van f met f ( x ) = x 3, de x -as en de rechte met vergelijking x = k ( k > 0) is 324. Bereken k .
De oppervlakte van het vlakdeel ingesloten door de grafiek van f met f ( x ) = x 2 – 4x + 3, de x -as, de y -as en de rechte met vergelijking x = k ( k ∈ R+) is 4. Bereken k .
Bepaal de oppervlakte van het gebied ingesloten door de grafiek van de functie f met f ( x ) = –5x 4 + 10x 3 + 14x 2 + 2x + 3 en de x -as.
Bepaal nu k (nauwkeurigheid 3 decimalen) zodat de rechte met vergelijking x = k die oppervlakte in twee gelijke delen verdeelt.
Als f continu is in [ a , b ], bewijs dan :
b a f ( x ) dx b a | f ( x ) | dx
Hint : bewijs eerst dat voor elke x ∈ dom f geldt : – |
Verklaar waarom a a f ( x ) dx = 0 (a > 0) als de functie f een oneven functie is.
Bepaal de integraalfunctie I a met I a ( x ) = y = x x 2 25 van de functies met onderstaande voorschriften.
Toon telkens aan dat I ′ a ( x ) = f ( x )
a f ( t )= 5
b f ( t )= 2 t + 1
Bepaal een primitieve functie van de functies met onderstaande voorschriften.
a f ( x )= 4 3 x 3 + 2 3 x
b f ( x )= 1 x 2 1 + 2 x 2
c f ( x )= 1 √ x + 2
d f ( x )= 2 x · ln2 e f ( x )= 2sin x 3cos x
Gegeven zijn de functies f , g en h met f ( x ) = sin 2
, g ( x ) = –cos 2x en h ( x ) = 2sin x cos x
a Toon aan dat f en g beide primitieve functies van h zijn.
b Toon aan dat f en g slechts een constante verschillen en geef die constante.
Bereken de volgende bepaalde integralen.
Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f , de x -as en de gegeven verticale lijnen als :
a f ( x )= 3 √ xx = 0, x = 8c f ( x )= 1 x 2 x = 1, x = 2
b f ( x )= e x x = 2, x = 2d
Gegeven is de functie f met f ( x )= 1 2 x
A ( p ) is de oppervlakte van het gebied ingesloten door de grafiek van f , de x -as, de y -as en de rechte met vergelijking x = p met p > 0.
a Bereken A ( p ).
b Bereken de waarde van p waarvoor geldt : A (p )= 3 4ln2
Gegeven is de functie f met f ( x )= 2√ x
De rechte t raakt aan de grafiek van f in het punt P( …, 4)
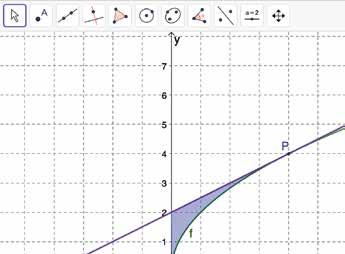

a Geef een vergelijking van t .

b Bereken de blauw gekleurde oppervlakte.
Bereken de oppervlakte van het gebied begrepen tussen de krommen met vergelijking :
a y = 8 x 6 x 2 ; y = 2 x
b y = x 2 ; y = 16 x 2 ; x = 4; y = 0
c y = 1 + cos x ; y = 1 sin x ; x = 3π 4 ; x = 7π 4
d y = x 2 2 ; y = 1 x 2 + 1
e y 2 = 2 x ; x 2 = 2 y
f y 2 = x ; y = x 2
g y 2 = 8 x ; y = x
h y 2 = 4 x ; x = 0; y = 2
i y 2 = 2 x 1; y = x 2
j y = ln x ; x = 0; y = 1; y = 2


Hint: Neem y als onafhankelijke variabele (zietoepassing4 blz.38-39)
Bereken in het aangeduide integratie-interval het getal c , waarvan sprake in de middelwaardestelling, voor de volgende integralen.
2 1 ( x + 1) dx b
Bereken de gemiddelde waarde van de functie f over het interval [ a , b ] als :
Bereken de volgende oneigenlijke integralen van de eerste soort.
Bereken de volgende oneigenlijke integralen van de tweede soort.
Is de volgende uitspraak juist ? Verklaar.
Kun je de volgende integraal berekenen ? Verklaar.
Bepaalde integralen
De parabool in deze figuur heeft vergelijking y = x 2. De waarden a en b op de y -as voldoen aan 0 < a < b
y a b
Toelatingsexamen arts 2023, vraag 8 50
De gearceerde oppervlakte wordt gegeven door
Toelatingsexamen arts 2021, vraag 7
Op bijgaande figuur worden de parabolen met vergelijking y = ( x – 1)2 en y = ( x + 1)2 en de rechte met vergelijking y = 9 afgebeeld. Bepaal de oppervlakte van het ingekleurde deel in de figuur.

IJkingstoets burgerlijk ingenieur september 2019, oefening 30
De figuur toont de grafiek van een oneven functie f
Welke van de onderstaande integralen geeft de oppervlakte van het gekleurde gebied als resultaat ?
Waaraan is de oppervlakte van het gekleurde gebied op de figuur gelijk ?
INKIJKEXEMPLAARDIEKEURE
IJkingstoets basiskennis wiskunde handelsingenieur 2022, vraag 36
Wat is de oppervlakte van het gebied begrensd door de y -as, de kromme y = e x en de rechte y = 2 ?
IJkingstoets basiskennis wiskunde handelsingenieur 2023, vraag 36
Op bijgaande figuur zijn de parabool met vergelijking y = x 2 en het punt A( 2, 4) afgebeeld. Wat is de vergelijking van de rechte door de oorsprong die het ingekleurde gebied begrensd door de y -as, de parabool en de horizontale rechte y = 4 in twee even grote delen verdeelt ?
Oefenmodules ijkingstoets 2022-2023, faculteit ingenieurswetenschappen KU Leuven, oefening 7.12
Bepaalde integralen
Beschouw het gebied tussen de parabool met vergelijking y = x 2 – 2x + 2, de raaklijn aan de parabool in het punt ( 3, 5) en de coördinaatassen. De oppervlakte van dit gebied is gelijk aan :
Oefenmodules ijkingstoets 2022-2023, faculteit ingenieurswetenschappen KU Leuven, oefening 7.14
Gegeven de functie : R → R : x → x = max{m ∈ Z : m x }. Dat is de functie die elk reëel getal x afbeeldt op het grootste geheel getal kleiner of gelijk aan x , bijvoorbeeld π = 3. Wat is de waarde van de bepaalde integraal
x dx ?
IJkingstoets burgerlijk ingenieur juli 2022, oefening 28
Veronderstel dat f : R → R een continue functie is die voldoet aan f ( x ) = f ( –x ) voor alle x ∈ R. Er is gegeven dat 1
IJkingstoets burgerlijk ingenieur augustus 2020, oefening 22
De oppervlakte van het gebied ingesloten door de krommen met vergelijking y = x 2 en y = √ x is gelijk aan :
Typevragen ijkingstoets industrieel ingenieur, standaardvragen oefening 9
Ik kan een oppervlakte onder de grafiek van een functie benaderen met behulp van een ondersom of bovensom van rechthoeken. 13
Ik ken de definitie van de bepaalde integraal als limiet van een som.
Ik ken de betekenis van de bepaalde integraal als georiënteerde oppervlakte tussen de grafiek en de horizontale as in een bepaald interval.
Ik kan een bepaalde integraal berekenen.
Ik ken de optelbaarheid en lineariteit van de bepaalde integraal.
Ik kan met behulp van een bepaalde integraal de oppervlakte berekenen die begrensd is door de grafieken van twee functies.
Ik ken de middelwaardestelling en kan ze bewijzen.
Ik ken de hoofdstelling van de integraalrekening en kan ze bewijzen.
Ik ken de betekenis van een primitieve functie.
Ik kan de oppervlakte berekenen van een gebied met y als onafhankelijke veranderlijke.
Ik ken de definitie van oneigenlijke integralen en weet hoe ik die moet berekenen.
16
17
19
24
28
31
33
34
37
42
