
MIJN WISKUNDE
PORTFOLIO VAARDIGHEDEN ICT
TWEEDE JAAR


MIJN WISKUNDE
PORTFOLIO VAARDIGHEDEN ICT
TWEEDE JAAR
ICT kan ingeschakeld worden om berekeningen uit te voeren, maar ook om grafische voorstellingen te maken en eigenschappen te analyseren.
Transformaties van het vlak met GeoGebra - GGB
Een translatie over een vector, een spiegeling om een as (of om een punt) en een rotatie rond een centrum over een hoek? Het kan perfect uitgevoerd worden met GeoGebra. Analyseer de eigenschappen en leg het verband met congruentie.
Van pagina 4 tot en met pagina 13 kun je GeoGebra terugvinden. We starten met een herhaling van de basisleerstof, die je in je eerste jaar aangeboden kreeg. Daarna leer je met teksten werken en komen de verschillende transformaties van het vlak aan bod.
Computationeel denken
Vanaf pagina 14 leer je doelgericht algoritmes begrijpen en maken volgens de principes van computationeel denken. Je maakt kennis met verschillende bouwstenen en legt de link met de geziene leerstofonderdelen uit de lessen wiskunde.
We werken met de programmeertaal Scratch. Die vind je terug via https://scratch.mit.edu.
© CC-BY SA 2.0. Scratch is een project van de Scratch Foundation, in samenwerking met de Lifelong Kindergarten Group van het MIT Media Lab. Het is gratis beschikbaar op https://scratch.mit.edu.
Als extraatje vind je drie opgaven terug van de Bebraswedstrijd, waarin leerlingen uitgedaagd worden tot computationeel en probleemoplossend denken.
© 2023 Bebras – International Challenge on Informatics and Computational Thinking. This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Op de achterflap vind je een overzicht van de verschillende onderwerpen en vaardigheden. Evalueer jezelf. Dit doe je door jezelf minimaal één en maximaal vijf sterren te geven. Ook je leerkracht kan je werk beoordelen. In de laatste kolom komt dan de eindbeoordeling door het correcte duimpje in te kleuren.
Auteurs
Björn Carreyn
Filip Geeurickx
Roger Van Nieuwenhuyze

Dit portfolio hoort bij het leerwerkboek VBTL 2 Meetkunde.
Eerste editie
Verantwoordelijke uitgever die Keure
Niets uit deze uitgave mag verveelvoudigd en / of in het openbaar gemaakt worden door middel van druk, fotokopie, microfilm of op welke wijze dan ook zonder voorafgaande schriftelijke toestemming van de uitgever. No part of this book may be reproduced in any form by print, microfilm of any other means without written permission from the publisher.

MIJN WISKUNDE
PORTFOLIO VAARDIGHEDEN ICT
TWEEDE JAAR
ook verkrijgbaar voor het tweede jaar


















Hoeken
Opdracht 1:
Teken een willekeurige hoek α
Teken de twee benen (halfrechten) van deze hoek.
Teken de bissectrice van α. Dit doe je door te kiezen voor ‘Bissectrice’ en te klikken op de twee benen. Als je deze methode kiest, laat GeoGebra twee bissectrices zien: de binnenbissectrice en de buitenbissectrice.
In het hoekpunt merk je nu zes hoeken die per twee aan elkaar gelijk zijn.
Hoe groot zijn deze hoeken?
Druk de grootte uit in functie van α
Driehoeken
Opdracht 2:
Teken een driehoek ABC.
Teken de drie middelloodlijnen.
Noem het snijpunt van de drie middelloodlijnen O.
Teken de cirkel die O als middelpunt heeft en | OA | als straal.
Kleur deze cirkelschijf geel.
Deze cirkel noemen we de omgeschreven cirkel van driehoek ABC.
Dit is de cirkel die door de drie hoekpunten van een driehoek gaat.
Opdracht 3:
Teken een driehoek ABC.
Teken de drie bissectrices.
Noem het snijpunt van de drie bissectrices O.
Teken de loodlijn door O op lijnstuk [ AB].
Het snijpunt van de loodlijn met het lijnstuk noem je E.
Teken de cirkel met O als middelpunt en | OE | als straal.
Kleur deze cirkelschijf rood.


Deze cirkel noemen we de ingeschreven cirkel van driehoek ABC.
Dit is de grootste cirkel die je kunt tekenen in een driehoek.
Opdracht 4:
Teken een willekeurige vierhoek en laat de oppervlakte verschijnen. Verbind de opeenvolgende middens van de zijden. Kleur de figuur die je zo bekomt rood.
Wat is de naam van deze figuur?
Laat ook de oppervlakte hiervan verschijnen.
Wat kun je besluiten in verband met de oppervlakte van de eerste en de tweede vierhoek?
Opdracht 5:
Teken een parallellogram ABCD met co( A) = ( –1, 3), co( B) = ( 2, 5) en co( C) = ( –1, –3) Kleur de figuur ondoorzichtig groen.
Wat is de coördinaat van D?
Opdracht 6:
Teken een parallellogram ABCD en laat alle hoekgroottes verschijnen.
Dit lukt makkelijk door te kiezen voor 'Hoek' en dan te klikken in het parallellogram.
A en B zijn opeenvolgende hoeken, net als B en C.
Ook C en D noemen we opeenvolgende hoeken, net als D en A .
Wat kun je besluiten in verband met twee opeenvolgende hoeken in een parallellogram?
Cirkels
Opdracht 7:
Teken het logo van de Olympische Spelen.

Omtrek van een driehoek weergeven als tekst
Teken een driehoek ABC.
De zijden krijgen als naam a, b en c.
In het algebravenster links zal je nu de omtrek laten berekenen met de instructie ‘som’. In dat venster typ je: ‘som=a+b+c’.

Kies voor het icoontje en vervolgens voor . Klik ergens in het tekenvenster en typ: ‘Omtrek van driehoek ABC is ’.
Klik daarna op Geavanceerd en dan op het
GeoGebra-icoontje. Hier zie je alles wat in algebravenster staat. Kies voor som en druk op OK. De tekst verschijnt in het tekenvenster.
Verplaats even één van de hoekpunten.

Teken een driehoek ABC.

Kies voor het icoontje en klik ergens binnen de driehoek. De hoeken krijgen als naam α, b en g.
In het algebravenster links typ je: ‘som = ’.
Als je al eerder som hebt gedefinieerd, kies dan voor som2. Dan typ je: ‘som2= ’. Je definieert deze som als α + b + g. Je vindt de Griekse letters onderaan je scherm op het klavier. Kies er voor letters. Onderaan links zie je de knop voor Griekse letters.

Kies voor het icoontje . Klik ergens in het tekenvenster en typ: ‘De hoekensom is ’. Klik daarna op Geavanceerd en dan op het GeoGebra-icoontje. Kies voor som2 en druk op OK.

Opdracht 1:
Teken een willekeurige vierhoek en geef de som van de hoeken als tekst weer.
Wat is de hoekensom van een vierhoek?
Opdracht 2:
Teken een willekeurige vijfhoek en geef de som van de hoeken als tekst weer.
Wat is de hoekensom van een vijfhoek?
Opdracht 3:
Teken een regelmatige vijfhoek, zeshoek en zevenhoek. Laat de hoeken van elke veelhoek verschijnen alsook de hoekensom van de veelhoek. Vul de tabel in en zoek de formule om de grootte van een hoek in een regelmatige veelhoek te bepalen.
regelmatige vierhoek
regelmatige vijfhoek
regelmatige zeshoek
regelmatige zevenhoek
regelmatige n-hoek
Opdracht 4:
Wat is de hoekensom van een twaalfhoek?
Hoe groot is elke hoek van een regelmatige twaalfhoek?
Een punt spiegelen
Teken vier punten A, B, C en D in het vlak.
Teken een willekeurige rechte a door A. Er wordt dan ook een punt E getekend.
Spiegel nu de punten A, B, C en D om de as a.
Dit doe je door te kiezen voor het icoontje van lijnspiegeling

Klik nu eerst op het te spiegelen punt A en daarna ergens op de spiegelas a.
Doe hetzelfde voor de punten B, C en D.
Opdracht 1:
Ga na dat a de middelloodlijn is van [ BB′] als volgt.
Teken de rechte BB′
Noem M het snijpunt van BB′ met a.
Ga na dat M het midden is van [ BB′] en laat dit zien op het scherm.
Ga na dat a loodrecht staat op BB′ en laat dit zien op het scherm.
Teken een driehoek ABC.
Teken een willekeurige rechte a.
Ga naar de werkbalk en kies voor het

icoontje .
Klik nu eerst op de getekende driehoek (ergens middenin) en daarna ergens op a

Versleep het punt A. Verandert het spiegelbeeld?
Versleep de rechte a. Veranderen de twee driehoeken?
Kun je de punten A′, B′ en C′ verslepen? JA / NEEN
Opdracht 2:
Een spiegeling behoudt de - lengte van een lijnstuk - loodrechte stand - evenwijdigheid - grootte van een hoek - oppervlakte van een figuur - collineariteit
Illustreer deze eigenschappen op je scherm.
Denk goed na met welke figuur je zult werken, zodat deze opdracht eenvoudiger wordt.
In het vlak heeft elk punt een coördinaat. Deze coördinaat bestaat uit twee coördinaatgetallen. Het eerste coördinaatgetal lees je op de x-as af, het tweede op de y-as.
Om het rooster en de assen te zien, kun je op het tekenveld met de rechtermuisknop klikken.
Vink de assen en het rooster aan.
Opdracht 3:
Geef in het algebravenster het volgende in: A = ( 4, 8) en B = ( 10, –7) en C = ( –10, –4).
Als je coördinaten wil weergeven op het scherm, klik dan op de punten met de rechtermuisknop.
Ga naar Instellingen en vink Label tonen aan. Kies voor Naam & Waarde. Teken de driehoek ABC.
Spiegel de driehoek om de x-as. Bepaal de coördinaten van deze drie beeldpunten.
De coördinaten zijn:
Wat kun je besluiten in verband met de coördinaatgetallen na spiegeling om de x-as?
Spiegel nu de oorspronkelijke driehoek ABC om de y-as.
Bepaal de coördinaten van deze driebeeldpunten.
De coördinaten zijn:
Wat kun je besluiten in verband met de coördinaatgetallen na spiegeling om de y-as?
Opdracht 4:
Teken de rechte AB als co( A) = ( 2, 2) en co ( B) = ( –5, –5). Die rechte noemen we de eerste bissectrice van het assenkruis. Teken een willekeurige driehoek CDE en spiegel die om de rechte AB. Wat kun je besluiten over de coördinaatgetallen na spiegeling om de eerste bissectrice?
Besluit:
Een punt verschuiven
Teken vier punten in het vlak en noem ze A, B, C en D.
Ga naar de werkbalk en kies voor het icoontje .

Klik op twee plaatsen in het tekenvenster en een vector −→ EF wordt getekend.
Ga dan naar de werkbalk en kies voor het icoontje

Klik eerst op A en daarna op de vector −→ EF. Doe hetzelfde voor B, C en D.
Teken de vectoren −→ AA , −→ BB , −→ CC en −→ DD .
Wat valt er op als je de vectoren −→ AA , −→ BB , −→ CC en −→ DD met elkaar vergelijkt?
Een figuur verschuiven
Teken een vierhoek ABCD en een vector −→ EF
Zoek het beeld van de vierhoek over vector −→ EF.
Eigenschappen onderzoeken en ontdekken
Opdracht 1:
Teken een lijstuk [ AB]. Meet dit lijnstuk.
Teken een vector. Verschuif [ AB] over de vector.
Bepaal nu de lengte van het schuifbeeld.
Welke eigenschap wordt hier toegepast?
Opdracht 2:
Teken een driehoek ABC. Meet de grootte van de hoek A .
Teken een vector −→ DE. Verschuif de driehoek ABC over die vector.
Meet de grootte van de hoek A . Versleep A en hou de grootte van de hoeken A en A in het oog.
Welke eigenschap zie je hier toegepast?
Opdracht 3:
Teken een parallellogram ABCD.
Geef de oppervlakte van ABCD op het scherm weer.
Teken −→ AC.
Zoek t −→ AC (ABCD).
Ook de figuur A′B′C′D′ is een parallellogram.
Wat kun je besluiten over de oppervlakte van dit parallellogram?
Opdracht 4:
Teken een rechthoek ABCD.
Geef de oppervlakte van ABCD op het scherm weer.
Zoek t −→ DA (ABCD).
Welke figuur is A′B′C′D′? Wat kun je besluiten over de oppervlakte van deze figuur?
Opdracht 5:
Teken een driehoek ABC.
Teken de hoogtelijn AH, waarbij H het snijpunt is van de hoogtelijn met BC.
Teken een vector −→ DE.
Zoek t −→ DE (AH), t −→ DE (∆ABC) en t −→ DE (H)
Verklaar dat A′H′ een hoogtelijn is in de driehoek A′B′C′ .
Opdracht 6:
Teken een ruit ABCD.
We gaan de ruit ABCD drie keer verschuiven en op een andere manier inkleuren.
Zoek t −→ AB (ABCD). Kleur de figuur geel in.
Zoek t −→ AC (ABCD). Kleur de figuur groen in.
Zoek t −→ AD (ABCD). Kleur de figuur blauw in.
Wat kun je besluiten over de figuur die bepaald wordt door de vier ruiten?
Een figuur roteren
Teken een willekeurige veelhoek.
Teken een centrum O en een hoek α
Ga dan naar de werkbalk en kies voor het icoontje
Klik nu eerst op de getekende veelhoek, daarna op het centrum O en vul in het venster dat zich opent α in.
Probeer volgende figuur te tekenen (dus ook de cirkelbogen!).
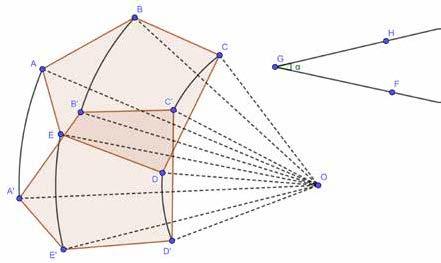
Om een cirkelboog van A naar A′ te tekenen, kies je voor het icoontje

Klik daarna achtereenvolgens op O, op A en op A′ .
Teken nu ook cirkelbogen tussen de andere punten en de nodige stippellijnen.
Je kunt nu het centrum verslepen, de draaiingshoek vergroten of verkleinen en/of een punt of de volledige veelhoek verslepen.
Probeer dit uit en kijk wat er gebeurt.
Teken een driehoek ABC.
Teken een willekeurig punt O.
Ga naar de werkbalk en kies voor het icoontje

Klik nu eerst op de getekende driehoek (ergens middenin) en daarna op O. Het beeld van driehoek ABC door de puntspiegeling wordt getekend.
Teken nu ook de lijnstukken [ AA′], [ BB′] en [ CC′]
Geef die lijnstukken weer in stippellijn.
Opdracht 1:
Teken een vierkant ABCD. Kleur de figuur blauw in.
Roteer het vierkant ABCD vier keer. Doe dit volgens volgende rotatie en kleur het resultaat telkens blauw in: r(A, 180°), r(B, –180°), r(C, 180°), r(D, –180°)
Om een groot vierkant te bekomen, moet je nog vier ruimtes opvullen.
Welke transformaties zal ABCD nog moeten ondergaan om het volledige vierkant te bekomen?
Opdracht 2:
Teken een rechthoekige gelijkbenige driehoek ABC met rechte hoek in A. Kleur de figuur groen in.
Kleur ook de volgende beelden groen in: r(A, 90°)( ΔABC)
r(A, –90°)( ΔABC)
sA( ΔABC)
Welke figuur verkrijg je? Verklaar.
Kleur ook de volgende beelden lichtgroen in: r(B, –90°)( ΔABC)
r(C, 90°)( ΔABC)
sBC( ΔABC)
Verschuif ten slotte driehoek ABC zodat de grote figuur een vierkant wordt.
Wat is de verhouding van de oppervlakte van het grote vierkant tot de oppervlakte van driehoek ABC?
Opdracht 3:
Geef in het algebravenster het volgende in: A = ( 4, 8) en B = ( 10, –7) en C = ( –10, –4) en O = ( 0, 0) en teken de driehoek ABC.
Spiegel de driehoek ten opzichte van O, de oorsprong van het assenstelsel.
Bepaal de coördinaten van die drie punten.
De coördinaten zijn:
Wat kun je besluiten in verband met de coördinaatgetallen na een puntspiegeling om O?
In deze code in Scratch is ‘getal’ een variabele. Schrijf uit wat er precies gebeurt als je deze code uitvoert. Illustreer met een getallenvoorbeeld.

a Welke blokjes van de code moet je aanpassen zodat de getalwaarde berekend wordt van –3x + 1?
b Wat zal je aan de code moeten aanpassen zodat de getalwaarde berekend wordt van x2 – 5x + 4?
c Gebruik een herhalingsstructuur zodat de getalwaarde berekend wordt voor vijf getallen ingevoerd door de gebruiker.
d Gebruik een herhalingsstructuur zodat de getalwaarde berekend wordt voor vijfopeenvolgende getallen, startend vanaf het ingevoerde getal van de gebruiker.
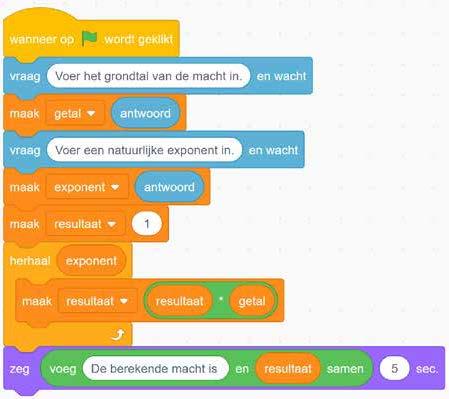
aVoer de code uit. Wat gebeurt er precies?
bIn wiskunde is 00 niet gedefinieerd. Zorg dat je deze melding krijgt als je dit wil berekenen.
cPas de code aan zodat die ook werkt voor negatieve exponenten.
dSchrijf een nieuwe code die op basis van een ingevoerd grondtal en een ingevoerde exponent aangeeft of de uitgerekende macht negatief of positief zal zijn.
aWelke transformatie is hier gebeurd?
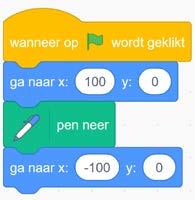
bSchrijf een code die start in het punt P( –50, 50) en eindigt in het beeldpunt P′ dat ontstaat door het punt te spiegelen om de x-as.
cSchrijf een code die start in het punt P( 150, 0) en eindigt in het beeldpunt P′ dat ontstaat door het punt te spiegelen om de eerste bissectrice.
dSchrijf een code die start in het punt P( 0, 0) en eindigt in het beeldpunt P′ dat ontstaat door het punt te verschuiven naar onder over een verticale vector van 100 lang.
e Schrijf een code die start in het punt P( –40, 90) en eindigt in het beeldpunt P′ dat ontstaat door het punt te verschuiven naar links over een horizontale vector van 300 lang.
g Schrijf een code die start in het punt P( –300, 100) en eindigt in het beeldpunt P′ dat ontstaat door het punt te roteren rond de oorsprong over 90° in tegenwijzerzin.
f Schrijf een code die start in een door de code willekeurig bepaald punt P en eindigt in het beeldpunt P′ dat ontstaat door het punt te spiegelen om de oorsprong.
h Schrijf een code die start in het door de code willekeurig bepaald punt P en eindigt in het beeldpunt P′ dat ontstaat door eerst het punt te spiegelen om de y-as, daarna te verschuiven naar rechts over een horizontale vector van 100 lang om tot slot te spiegelen om de oorsprong.
a Herinner je je de code nog voor een vierkant? Wijzig deze code zodat je een ruit verkrijgt waarvan één van de hoeken 30° is.

Wijzig de oorspronkelijke code zodat je een gelijkzijdige driehoek krijgt. Zorg ervoor dat de draaiingshoek die je nodig hebt in de herhaling berekend wordt.
b Wijzig de code zodat je ook een regelmatige vijfhoek en zeshoek kunt tekenen.
c Wijzig de code zodat de gebruiker met een getal kan aangeven welke regelmatige veelhoek hij getekend wil zien.
d Teken met Scratch één van deze spiraaltekeningen.


aTeken in Scratch een patroon van vijf congruente vierkanten waar telkens eenzelfde ruimte tussen is.
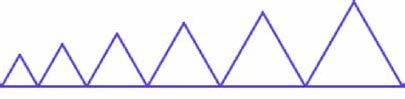
bTeken in Scratch deze opeenvolging van gelijkzijdige driehoeken.
cTeken in Scratch een rechthoek met lengte 100 en breedte 25. Teken een tweede rechthoek waarvan de oppervlakte vier keer groter is dan de eerste rechthoek.

Bebras is een internationale denkwedstrijd voor jongeren die het computationeel denken bevordert. Bebras is Litouws voor bever. De universiteit van Vilnius (die aan de oorsprong lag van Bebras) koos voor de bever vanwege de ijver en het probleemoplossend vermogen van dit dier. In België ligt de coördinatie van de wedstrijd bij de Universiteit Gent. Via bebras.be vind je meer info.
Bever Sawya zaagt houtblokken van verschillende lengtes en verkoopt ze vervolgens. Als ze klaar is met zagen, legt ze de boomstammen achter elkaar neer langs de 18 meter lange, smalle weg.
Als Sawya een boomstam neerlegt, plaatst ze deze op de eerste beschikbare en passende plek vanaf links. Wanneer ze een boomstam verkoopt, wordt deze eenvoudigweg verwijderd van de plek waar deze ligt.
Sawya heeft, in deze volgorde, boomstammen met de lengtes 2, 5, 3, 6 en 1 meter gemaakt. Dit leidt tot deze opstelling langs de weg:

Nu verkoopt ze de stammen van 6, 2 en 5 meter. Daarna zaagt ze een nieuwe boomstam van 4meter. Omdat ze deze op de eerste, passende plek vanaf links legt, ziet de weg er nu zo uit:

Nu moet Sawya stammen van 1, 2, 3 en 4 meter zagen. Welke volgorde van zagen maakt het mogelijk om alle stammen langs de weg neer te kunnen leggen (met als startpunt de prent hier onmiddellijk boven)?
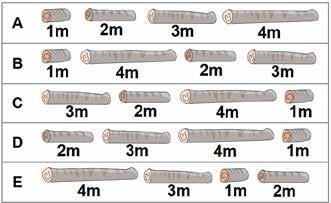
© 2023-CH-05
Auteurs tekst: Jean-Philippe Pellet (Zwitserland) Alieke Stijf (Nederland) - vertaling
Auteurs afbeeldingen: Susanne Datzko (Zwitserland) Darija Dasovic´ (Kroatië)
Vertaling: Kris Coolsaet (België)
Hieronder zie je een afbeelding die bestaat uit witte en rode vierkantjes in een raster van zes rijen en vijf kolommen.
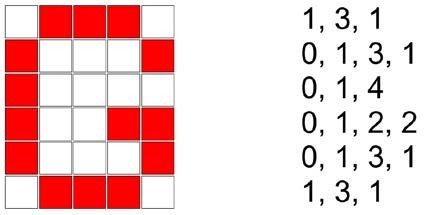
Je kunt deze afbeelding beschrijven met behulp van getallen door voor elke lijn op te sommen hoeveel opeenvolgende witte vierkantjes er zijn, dan hoeveel rode vierkantjes er zijn, dan hoeveel witte, enz., totdat je alle vierkantjes in de rij hebt behandeld. (Je ziet die getallenreeksen rechts in de figuur.) Opgelet! Het eerste getal in elke rij komt altijd overeen met het eerste aantal witte vierkantjes!
Tot slot voegen we alle getallen van boven naar onder samen tot één enkele reeks. Bij dit voorbeeld krijgen we dan 1, 3, 1, 0, 1, 3, 1, 0, 1, 4, 0, 1, 2, 2, 0, 1, 3, 1, 1, 3, 1.
Welke getallenreeks beschrijft de onderstaande afbeelding?

A0, 1, 3, 4, 1, 1, 3, 1, 0, 2, 2, 1, 0, 1, 3, 1, 2, 2, 1
B1, 3, 1, 4, 1, 1, 4, 0, 1, 3, 1, 0, 1, 3, 1, 1, 3, 1
C1, 3, 1, 0, 1, 4, 1, 4, 0, 1, 3, 1, 0, 1, 3, 1, 1, 3, 1
D1 , 3, 1, 4, 1, 1, 4, 1, 3, 1, 1, 3, 1, 1, 3, 1
© 2022-BR-05
Auteurs tekst: Leonardo Barichello (Brazilië) Anna Morpurgo (Italië) Evgenia Sendova (Bulgarije) Victor Koleszar (Uruguay) Kris Coolsaet (België) - vertaling
Auteur afbeeldingen: Leonardo Barichello (Brazilië)
Vertaling: Kris Coolsaet (België)
Tina start met één cirkel en één vierkant:

Daarna maakt zij met deze vormen een hart:

Tina kan alleen de volgende stappen uitvoeren:
• Draaien: Draai de vorm rond (zo ver of zo weinig ver als je wil).
• Verplaatsen: Verschuif de vorm naar een andere plaats.
• Kopiëren: Maak een kopie van de vorm op dezelfde plaats.
Welke stappen heeft Tina gebruikt om het hart te maken?
AKopieer cirkel. Draai vierkant. Verplaats cirkel. Verplaats cirkel.
BKopieer vierkant. Draai vierkant. Verplaats vierkant. Verplaats cirkel.
CKopieer cirkel. Draai cirkel. Verplaats cirkel. Verplaats vierkant.
DVerplaats cirkel. Verplaats cirkel. Kopieer cirkel. Verplaats vierkant.
© 2022-DE-02
Auteurs tekst: Michael Weigend (Duitsland) J.P. Pretti (Canada) Goran Sukovic (Montenegro) Alieke Stijf (Nederland) - vertaling
Auteurs afbeeldingen: Michael Weigend (Duitsland) Justina Dauksaite (VS)
Vertaling: Kris Coolsaet (België)
1GGB Herhaling
2GGB Werken met tekst
3GGB Spiegelingen
4GGB Translaties
5GGB Rotaties
6SCRATCH Getalwaarde
7SCRATCH Machten
8SCRATCH Transformaties
Vaardigheid Mijn evaluatie Oordeel leerkracht Gekend of niet?
- P
9SCRATCH Veelhoeken en spiraaltekeningen
10SCRATCH Congruentie en schaal C - P
11 EXTRA Drie BREBAS-opgaven C - P
Vaardigheden C = Computationeel denken – P = Probleemoplossende vaardigheid
Die Keure wil het milieu beschermen. Daarom kiezen wij bewust voor papier dat het keurmerk van de Forest Stewardship Council® (FSC®) draagt. Dit product is gemaakt van materiaal afkomstig uit goed beheerde, FSC®-gecertificeerde bossen en andere gecontroleerde bronnen.