MEETKUNDE
& METEND REKENEN
01 Transformaties van het vlak en symmetrie
wat je al kunt
–spiegelbeelden ontdekken in vlakke figuren en daarbij de termen spiegeling, beeld en spiegelas gebruiken –symmetrie ontdekken in reële situaties
– vlakke figuren tekenen met behulp van meetkundesoftware –gebruik maken van coördinaten om vlakke figuren te tekenen
wat je leert in deze module
–beeld van een vlakke figuur verklaren (translatie over een vector, spiegeling om een as, spiegeling om een punt, rotatie rond een centrum over een hoek) –eigenschappen van transformaties onderzoeken en toepassen
–ICT gebruiken om transformaties voor te stellen –het verband leggen tussen congruentie, symmetrie bij vlakke figuren enerzijds en transformaties anderzijds –symmetrie in ruimtefiguren herkennen
Inhoud
Instap
1 Transformaties van het vlak
2 Eigenschappen van transformaties
3 Symmetrie
Signaaloefeningen
Differentiatietraject
Studiewijzer
in de kijker
Je gebruikt ICT om transformaties voor te stellen.
wiskundetaal
–beeld –congruente figuren –spiegelen om een as –spiegeling – as –dekpunt –verschuiven –verschuiving –translatie –vector –roteren –rotatie –centrum –spiegelen om een punt –symmetrie –spiegelsymmetrisch om een as –lijnsymmetrisch –spiegelsymmetrisch om een punt –puntsymmetrisch
Instap
Opdracht 1
Teken het spiegelbeeld van het vierkant ABCD ten opzichte van de as a
Hoe wordt de rechte a genoemd bij deze spiegeling ?
Opdracht 2
Bij deze spiegeling is b een bijzondere spiegelas. De figuur links is het spiegelbeeld van de figuur rechts, en omgekeerd. Teken nu nauwgezet de ontbrekende delen.
Opdracht 3
Start bij de peper waar geen nummer bij staat.
Deze peper werd in het vlak op een bepaalde manier verplaatst. Hoe werd de peper verplaatst ?
Noteer onder elk vak het nummer van de peper waar je terechtkomt.
De peper werd verschoven over een afstand van 4 cm.
De peper werd gespiegeld ten opzichte van een verticale spiegelas.
De peper werd gedraaid om het punt O over een hoek van 70 °.
Opdracht 4
a) Het eerste vierkant wordt gespiegeld om de as a en komt terecht op het tweede vierkant.
Teken (in blauw) de spiegelas a
b) Het eerste vierkant wordt verschoven en komt terecht op het tweede vierkant.
Over welke afstand werd het eerste vierkant verschoven ?
c) Het vierkant wordt gedraaid over een hoek van 180 ° en komt terecht op het tweede vierkant. Om welk punt gebeurde deze draaiing ?
d) Teken dit punt en noem het O.
1 Transformaties van het vlak
Een transformatie van het vlak beeldt elk punt uit dat vlak af, op juist één ander punt in dat vlak.
Zo kan het beeld van een punt ontstaan door één van de onderstaande transformaties uit te voeren :
• het punt te spiegelen om een as
• het punt te verschuiven over een vector
• het punt te roteren rond een centrum over een hoek
• het punt te spiegelen om een punt
•
1.1 Spiegelen om een as
In de tekening hieronder zie je dat er meetkundige objecten (een punt, een driehoek, een vierhoek, een cirkel …) gespiegeld worden om een as. Deze as is een rechte a , de spiegelas . Met behulp van meetkundesoftware kun je het beeld tekenen van meetkundige objecten door een spiegeling om een as.
in symbolen lees je als
sa ( A) = A′ A′ is het beeld van het punt A door spiegeling om de as a sa ( ΔBCD) = ΔB′C′D′ ΔB′C′D′ is het beeld van ΔBCD door spiegeling om de as a
In het differentiatietraject vind je een stappenplan hoe je op papier zelf een spiegeling kan tekenen. Je kan ook ICT hiervoor gebruiken.
Merk op
• De afstand van A tot de spiegelas is gelijk aan de afstand van A′ tot de spiegelas.
• S is in de tekening een bijzonder punt. Het heeft zichzelf als beeld. Dit komt omdat het punt op de spiegelas ligt. We noemen dit een dekpunt .
• Twee vlakke figuren die dezelfde vorm en dezelfde grootte hebben, noemen we congruente figuren . We stellen vast dat een vlakke figuur en zijn beeld door een spiegeling ten opzichte van een rechte congruente figuren zijn.
1.2 Translatie over een vector
In de tekening hieronder zie je dat er meetkundige objecten (een punt, een driehoek, een vierhoek, een cirkel …) verschoven worden over een vector
De vector bepaalt …
• de richting van de translatie (evenwijdig met de drager van de vector)
• de zin van de translatie (volgens de pijl)
• de grootte van de translatie (de afstand)
in symbolen lees je als
# –XY de vector # –XY
t #–XY (A)= A′ A′ is het beeld van het punt A door een translatie over de vector # –XY
t #–XY (ΔBCD)= ΔB′ C′ D′ ΔB′C′D′ is het beeld van ΔBCD door een translatie over de vector # –XY
Met behulp van meetkundesoftware kun je het beeld tekenen van meetkundige objecten door een translatie over een vector. In het differentiatietraject vind je ook een stappenplan om dit op papier te doen.
Merk op
• Een ander woord voor translatie is verschuiving.
• | XY | = | AA′| = | BB′| = en XY ⫽ AA′ ⫽ BB′ ⫽
• # –XY = # –AA′ Hetzijngelijkevectoren.
• # –XY ≠ # –YXDitzijngeengelijkevectoren.Zehebbeneenanderezin.Wenoemenzetegengesteldevectoren.
• We stellen vast dat een vlakke figuur en zijn beeld door een translatie over een vector congruente figuren zijn.
1.3 Rotatie rond een centrum over een hoek
In de tekening hieronder zie je dat er meetkundige objecten (een punt, een driehoek, een vierhoek …) geroteerd (gedraaid) worden over een hoek
Het punt P, de driehoek ABC en de vierhoek DEFG worden geroteerd (gedraaid) rond het centrum O
P′ is het beeld van het punt P door een rotatie rond het centrum O over een hoek van 150 ° in tegenwijzerzin.
Driehoek A′B′C′ is het beeld van driehoek ABC door een rotatie rond het centrum O over een hoek van 60 ° in tegenwijzerzin.
Vierhoek D′E′F′G′ is het beeld van vierhoek DEFG door een rotatie rond het centrum O over een hoek van 105 ° in wijzerzin.
Met behulp van meetkundesoftware kun je het beeld tekenen van meetkundige objecten door een rotatie rond een centrum over een hoek.
in symbolen lees je als
r(O, α) een rotatie met centrum O over α
Dit lees je als ‘een rotatie met centrum O over α’.
Om aan de hand van de notatie te weten of er geroteerd wordt in wijzerzin of tegenwijzerzin, maken we volgende afspraak.
r( O, 60 °) α = 60 ° een rotatie rond het centrum O over 60 ° in tegenwijzerzin. +
r( O, -150 °) α = -150 ° een rotatie rond het centrum O over 150 ° in wijzerzin. -
in symbolen lees je als
r( O, 150 °) ( P) = P′ P′ is het beeld van het punt P door een rotatie rond het centrum O over 150 ° in tegenwijzerzin
r( O, -105 °) ( DEFG) = D′E′F′G′ D′E′F′G′ is het beeld van DEFG door een rotatie rond het centrum O over 105 ° in wijzerzin
In het differentiatietraject vind je een stappenplan hoe je op papier zelf een rotatie kan tekenen. Je kan ook ICT hiervoor gebruiken.
Merk op r( O, -210 °) ( P) = r( O, 150 °) ( P)
1.4 Spiegeling om een punt
In de tekening hiernaast zie je dat er meetkundige objecten (een punt, een driehoek, een vierhoek …) gespiegeld worden om een punt
Het punt P, de driehoek ABC en de vierhoek DEFG worden gespiegeld (gedraaid) rond het centrum O .
Met behulp van meetkundesoftware kun je het beeld tekenen van meetkundige objecten door een spiegeling om een punt.
in symbolen lees je als
sO een spiegeling om het punt O
sO ( P) = P′ P′ is het beeld van het punt P door een spiegeling om het punt O
sO ( DEFG) = D′E′F′G′ D′E′F′G′ is het beeld van DEFG door een spiegeling om het punt O
Merk op Spiegelen om een punt O is eigenlijk hetzelfde als roteren om het punt O over 180°.
1.5 Andere transformaties
De transformaties die je dit schooljaar bestudeert zijn bijzonder omdat het beeld van de vlakke figuur steeds een figuur is die congruent is met de oorspronkelijke figuur. Ook bij een samenstelling van meerdere van deze transformaties is het beeld van een vlakke figuur een congruente figuur.
Als je bijvoorbeeld een parallellogram eerst spiegelt om een as en daarna verschuift over een vector, dan is het beeld opnieuw een parallellogram dat congruent is met het oorspronkelijke parallellogram.
Er bestaan ook andere transformaties waarvan het beeld van een vlakke figuur niet congruent is met de oorspronkelijke figuur zoals bijvoorbeeld een projectie, een homothetie …
Verwerkingsopdrachten
Verklaar in deze realistische contexten het beeld door een transformatie.
a) Welke transformatie moet je met de witte bal uitvoeren om op de plaats van de groene bal terecht te komen ?
b) Welke transformatie is geïllustreerd door de waaier ?
c) Welke transformatie gebruikte de grafisch ontwerper van het logo van Airbnb?
d) Welke transformatie wordt geïllustreerd met de volgende schaakbeweging?
Noteer een transformatie die de paarse figuur afbeeldt op de oranje figuur.
a) Door welke transformatie is de vierhoek EFGH het beeld van de vierhoek ABCD ?
b) Door welke transformatie is de vierhoek IJKL het beeld van de vierhoek ABCD ?
c) Door welke transformatie is de vierhoek MNPQ het beeld van de vierhoek ABCD ?
d) Door welke transformatie is de vierhoek RSTU het beeld van de vierhoek ABCD ?
e) Teken het beeld van de rechthoek MNPQ door een rotatie rond het centrum O over een hoek van 90° in tegenwijzerzin.
f) Het beeld van P volgens spiegeling om de y-as is .
g) is het beeld van H volgens rotatie rond het centrum O over een hoek van 90°.
h) is het beeld van K volgens een translatie over de vector # –VW # –AG
i) A is het beeld van het punt volgens een spiegeling om de x-as.
j) is het beeld van het punt L volgens een spiegeling om het punt O.
k) L is het beeld van volgens een translatie over de vector # –VW # –AG
l) Noteer in symbolen.
T is het beeld van P door spiegeling om de y-as.
N is het beeld van S door rotatie rond het centrum O over 90 ° in wijzerzin.
a) Een rotatie rond het centrum O beeldt het punt P af op R. Wat is de hoek van deze rotatie?
b) De puntspiegeling met centrum M beeldt R af op S. Teken M.
c) Teken een vector zodat P het beeld is van S door translatie over die vector.
Door welke van volgende transformaties is de oranje zeshoek het beeld van de blauwe zeshoek? Vink aan.
□ spiegeling om a
□ translatie over # –AB
□ rotatie over -120° rond centrum M
□ puntspiegeling om M
□ geen van bovenstaande
a) In een restaurant worden volgende tafelschikkingen opgesteld. Verklaar telkens over welke hoek je een rotatie rond het centrum van de tafel moet uitvoeren om van zitplaats A naar zitplaats B te komen.
b) Er worden verschillende opstellingen uitgeprobeerd in een bureauruimte voor 4 personen. Verklaar telkens met één transformatie hoe persoon B op de tekening het beeld is van persoon A.
2 Eigenschappen van transformaties
2.1 Onderzoeken
Voer de volgende onderzoeken uit met behulp van ICT of door gebruik te maken van de pagina hiernaast..
Onderzoek 1
Bij welke transformaties is het beeld van drie collineaire punten ook collineair ?
Wat stel je vast op de tekening ? Vul de tabel verder aan.
een as
Onderzoek 2
Bij welke transformaties blijft de evenwijdigheid behouden?
Wat stel je vast op de tekening? Vul de tabel verder aan.
as
Onderzoek 3
Is het beeld van een rechte door een transformatie een evenwijdige aan die rechte ?
Wat stel je vast op de tekening ? Vul de tabel verder aan.
spiegeling om een as
translatie over een vector
rotatie rond een centrum over een hoek spiegeling om een punt
Onderzoek 4
Bij welke transformatie(s) wordt de lengte van een lijnstuk behouden ?
Wat stel je vast op de tekening ? Vul de tabel verder aan.
spiegeling om een as
translatie over een vector
rotatie rond een centrum over een hoek
spiegeling om een punt
|CD|
|C′D′|
Onderzoek 5
Bij welke transformatie(s) blijft de hoekgrootte behouden ?
Wat stel je vast op de tekening ? Vul de tabel verder aan.
spiegeling om een as
translatie over een vector
rotatie rond een centrum over een hoek
spiegeling om een punt
Om beter inzicht te verwerven in transformaties van het vlak gaan we op zoek naar eigenschappen. We vertrekken telkens van een rechthoekig trapezium ABCD. een spiegeling om as a
Spiegelingen, translaties en rotaties zijn bijzondere transformaties die afstanden en hoekgroottes behouden. De vorm en grootte van de figuur blijven daarbij onveranderd; alleen de positie verandert en soms de oriëntatie verandert. Zo'n transformatie noemen we een isometrie .
Niet alle transformaties hebben deze eigenschappen. Volgend jaar bestudeer je zo'n transformatie: een homothetie. De trapezium die wordt afgebeeld is een schaalmodel van de trapezium die de transformatie ondergaat.
eigenschappen
2.2 Eigenschappen
A) Eigenschappen in verband met collineariteit
Als drie punten collineair zijn, dan zijn de beeldpunten door een spiegeling om een as ook collineair.
Als drie punten collineair zijn, dan zijn de beeldpunten door een translatie over een vector ook collineair.
Als drie punten collineair zijn, dan zijn de beeldpunten door een rotatie rond een centrum over een hoek ook collineair.
Als drie punten collineair zijn, dan zijn de beeldpunten door een spiegeling om een punt ook collineair.
We stellen ook vast dat het beeld van een rechte door een spiegeling om een as, een verschuiving over een vector, een rotatie rond een centrum over een hoek of een spiegeling om een punt ook een rechte is.
B) Eigenschappen in verband met evenwijdigheid
eigenschappen
Een spiegeling om een as bewaart de evenwijdigheid.
Een translatie over een vector bewaart de evenwijdigheid.
Een rotatie rond een centrum over een hoek bewaart de evenwijdigheid.
Een spiegeling om een punt bewaart de evenwijdigheid.
Bij twee transformaties stellen we nog iets bijzonder vast: eigenschappen
Het beeld van een rechte door een translatie over een vector is een rechte die evenwijdig is met de oorspronkelijke rechte.
Het beeld van een rechte door een spiegeling om een punt is een rechte die evenwijdig is met de oorspronkelijke rechte.
C) Eigenschappen in verband met behoud van lengte eigenschappen
Een spiegeling om een as bewaart de lengte van een lijnstuk.
Een translatie over een vector bewaart de lengte van een lijnstuk.
Een rotatie rond een centrum over een hoek bewaart de lengte van een lijnstuk.
Een spiegeling om een punt bewaart de lengte van een lijnstuk.
Merk op
Het is eigenlijk logisch dat de lengte van een lijnstuk behouden blijft omdat we al konden vaststellen dat het beeld door een spiegeling om een as, een translatie over een vector, een rotatie rond een centrum over een hoek of een spiegeling om een punt een congruente figuur is met de oorspronkelijke figuur. Doordat het beeld congruent is met de oorspronkelijke figuur, blijft ook de oppervlakte behouden.
D) Eigenschappen in verband met het behoud van hoekgrootte eigenschappen
Een spiegeling om een as bewaart de grootte van een hoek.
Een translatie over een vector bewaart de grootte van een hoek.
Een rotatie rond een centrum over een hoek bewaart de grootte van een hoek.
Een spiegeling om een punt bewaart de grootte van een hoek.
Merk op
• Het is eigenlijk logisch dat de grootte van een hoek behouden blijft omdat we al konden vaststellen dat het beeld door een spiegeling om een as, een translatie over een vector, een rotatie rond een centrum over een hoek of een spiegeling om een punt een congruente figuur is met de oorspronkelijke figuur.
• De loodrechte stand van twee rechten blijft ook behouden bij een spiegeling om een as, een translatie over een vector, een rotatie rond een centrum over een hoek of een spiegeling om een punt.
Verwerkingsopdrachten
Elke tekening is een illustratie van een eigenschap. Noteer telkens de eigenschap in een volledige zin.
De vierhoek KLMN is het beeld van een parallellogram ABCD door een spiegeling om O. Welke uitspraken zijn juist? Vink aan.
□ Er bestaat een spiegeling om een rechte die het parallellogram ABCD afbeeldt op de vierhoek KLMN.
□ De vierhoeken KLMN en ABCD zijn congruent.
□ A, O en K zijn collineair.
□ AC ⫽ KM
Noteer telkens jouw werkwijze op basis van de gebruikte eigenschappen.
a) Gegeven: ABCD is een rechthoek.
N( 3, -1) is het beeld van het snijpunt van de diagonalen van de rechthoek ABCD door een translatie t
Gevraagd: Teken het beeld van de rechthoek ABCD door dezelfde translatie.
b) Gegeven: A( 3, 2) , B( -4, 2) en C( 0, 2) r is een rotatie rond de oorsprong over een hoek van 90°.
A′ is het draaibeeld van A
B′ is het draaibeeld van B
C′ is het draaibeeld van C
Gevraagd: Geef de coördinaat van A′, B′ en C′ en formuleer een besluit.
c) Gegeven: O en P zijn punten op de cirkel cM,r Bovendien zijn O( 0, 0) en P( 2, 2) dekpunten bij de spiegeling sa. M′ is het beeld van M door spiegeling om de as a.
Gevraagd: Bepaal de coördinaat van M′ en teken het beeld van de cirkel c
3 Symmetrie
3.1 Spiegelsymmetrie bij vlakke figuren
Sommige vlakke figuren hebben zichzelf als beeld als je een transformatie uitvoert. We zeggen dat vlakke figuren symmetrisch zijn als er een (bestudeerde) transformatie bestaat die de figuur op zichzelf afbeeldt.
A) Spiegelsymmetrisch om een as
definitie Een vlakke figuur is spiegelsymmetrisch om een as als het zichzelf als beeld heeft bij spiegeling om die as.
We noemen een as een symmetrieas als de vlakke figuur zichzelf als beeld heeft bij spiegeling om die as. De symmetrieas verdeelt de vlakke figuur in twee congruente vlakke figuren.
Merk op Vlakke figuren die spiegelsymmetrisch zijn om een as noemen we ook wel lijnsymmetrische figuren
Voorbeelden
In deze figuren werden de symmetrieassen aangeduid.
Driehoeken kunnen 0, 1 of 3 symmetrieassen hebben.
heeft geen symmetrieas
driehoeken ongelijkbenige driehoek gelijkbenige driehoek gelijkzijdige driehoek
voorbeeld
De symmetrieas bij de gelijkbenige driehoek is een merkwaardige lijn van die driehoek. eigenschap De hoogtelijn uit de top (of bissectrice van de tophoek, of zwaartelijn uit de top, of middelloodlijn van de basis) is de symmetrieas van een gelijkbenige driehoek.
Merk op Een gelijkzijdige driehoek is een bijzonder geval van een gelijkbenige driehoek. Je zou elke hoek als ‘tophoek’ kunnen beschouwen. Een gelijkzijdige driehoek heeft dus drie symmetrieassen.
Ook sommige vierhoeken hebben symmetrieassen.
Vierhoeken kunnen 0, 1, 2 of 4 symmetrieassen hebben.
vierhoeken
voorbeeld
B) Spiegelsymmetrisch om een punt definitie Een vlakke figuur is spiegelsymmetrisch om een punt als het zichzelf als beeld heeft bij spiegeling om dat punt.
We noemen het centrum een symmetriemiddelpunt als de vlakke figuur zichzelf als beeld heeft bij spiegeling om dat punt.
Merk op
Vlakke figuren die spiegelsymmetrisch zijn om een punt noemen we ook wel puntsymmetrische figuren .
Driehoeken hebben geen symmetriemiddelpunt.
Bij de vierhoeken zijn alle parallellogrammen (en dus ook ruiten, rechthoeken en vierkanten) spiegelsymmetrisch om een punt. Het symmetriemiddelpunt is het snijpunt van de diagonalen.
3.2 Spiegelsymmetrie in ruimtefiguren
A) Spiegelsymmetrisch om een vlak
definitie Een ruimtefiguur is spiegelsymmetrisch om een vlak als het zichzelf als beeld heeft bij spiegeling om dat vlak.
We noemen een vlak een symmetrievlak als een ruimtefiguur zichzelf als beeld heeft bij spiegeling om dat vlak. Het symmetrievlak verdeelt de ruimtefiguur in twee congruente ruimtefiguren.
Voorbeeld
De kubus heeft 9 symmetrievlakken.
B) Spiegelsymmetrisch om een punt
definitie Een ruimtefiguur is spiegelsymmetrisch om een punt als het zichzelf als beeld heeft bij spiegeling om dat punt.
In een kubus en een balk is het snijpunt van de ruimtediagonalen het symmetriemiddelpunt van de ruimtefiguur.
Verwerkingsopdrachten
a) Teken in een groene kleur alle symmetrieassen.
b) Plaats een rood symmetriemiddelpunt als de figuur spiegelsymmetrisch is om een punt.
a) Teken in een groene kleur alle symmetrieassen.
b) Plaats een rood symmetriemiddelpunt als de figuur spiegelsymmetrisch is om een punt.
a) Hoeveel symmetrievlakken heeft deze balk ?
b) Hebben alle balken zoveel symmetrievlakken ?
c) Bepaal het symmetriemiddelpunt.
Signaaloefeningen
Gegeven : ΔABC
a) Door welke transformatie is de driehoek DEF het beeld van de driehoek ABC ?
b) Door welke transformatie is de driehoek KLM het beeld van de driehoek ABC ?
c) Door welke transformatie is de driehoek GHI het beeld van de driehoek ABC ?
d) Waarom heeft het punt A zichzelf als beeld bij spiegeling om de rechte a?
e) E is het beeld van door een translatie over de vector # –VW # –AG
f) is het beeld van het punt B door rotatie rond centrum O over een hoek van -90°.
g) is het beeld van het punt V door een translatie over de vector # –VW # –AG
h) is het beeld van het punt G volgens een spiegeling om het punt O.
i) is het beeld van het punt E volgens een spiegeling om de x-as.
j) B′ is het beeld van het punt volgens een spiegeling om het punt A.
k) H is het beeld van door een translatie over de vector # –VW # –AG
l) Bepaal het centrum T zodat W het beeld is van L door puntspiegeling om het centrum T.
>>> Verder oefenen : D1 t.e.m. D32
a) r( O, 40 °)
b) sb ( R) = S
c) tAB ( U) = V
d) sO ( ΔKLM) = ΔK′L′M′
Noteer de geïllustreerde eigenschap.
⫽
a) Duid de symmetrieassen aan in deze logo's.
b) Als een figuur een symmetriemiddelpunt heeft, duid dan dit punt in het rood aan.
Bekijk aandachtig de volgende ruimtefiguren.
a) Hoeveel symmetrievlakken hebben deze ruimtefiguren ?
b) Indien er symmetrievlakken zijn, teken er één.
c) Duid – indien mogelijk – het symmetriemiddelpunt aan.
>>> Verder oefenen : D39 t.e.m. D48
Differentiatietraject
Welke transformatie wordt er geïllustreerd?
4
d) ΔMNP is … van ΔABC door een … om … O. 1 2 3
Welke transformaties herken je op dit antiek aardenwerk ?
Bij de werking van een viertaktmotor kun je enkele transformaties herkennen. Hiernaast zie je de vier posities van een viertaktmotor. Welke transformaties herken je ?
Bekijk aandachtig de tekening en vul aan met de juiste begrippen. Kies uit : de as, congruente figuren, het beeld, centrum, hoek, het punt, rotatie, spiegeling, tegenwijzerzin, de vector, translatie of wijzerzin.
a) ΔDEF is … van ΔABC door een … rond … O over een … van 80 ° in … .
b) ΔGHI is … van ΔABC door een … over … # –XY .
c) ΔJKL is … van ΔABC door een … om … a.
Inlaat Compressie Arbeid Uitlaat
Bepaal telkens over welke hoek wordt gedraaid zodat B het beeld is van A.
Is de paarse figuur f ′ het beeld van de rode figuur f door een spiegeling, translatie of rotatie ?
Wees volledig in je antwoord.
Geef telkens een transformatie of een samenstelling van transformaties zodat ...
a) blokje 2 het beeld is van blokje 1.
b) blokje 4 het beeld is van blokje 3.
c) blokje 6 het beeld is van blokje 5.
d) blokje 8 het beeld is van blokje 7.
methode
Je kan spiegelingen om een as op papier tekenen door gebruik te maken van dit stappenplan.
Om een vlakke figuur te spiegelen, kan je elk hoekpunt spiegelen of, als je de eigenschappen kent, gebruikmaken van de eigenschappen.
Hoe het beeld tekenen van A door te spiegelen ten opzichte van a?
STAP 1: Teken door A een stippellijn loodrecht op de spiegelas a.
STAP 2: Noem S het snijpunt van de loodlijn met a
STAP 3: Teken het beeld A′ zodat |AS| = |SA′|.
a) Teken het beeld van A, B en C door te spiegelen om de as a A
b) Teken het beeld van de driehoek en de vierhoek door te spiegelen om de as a.
Je kan translaties over een vector op papier tekenen door gebruik te maken van dit stappenplan. Om een vlakke figuur te verschuiven, kan je elk hoekpunt verschuiven of, als je de eigenschappen kent, gebruikmaken van de eigenschappen.
Hoe het beeld tekenen van A door een translatie over vector # –XY ? methode
STAP 1: Teken door A een evenwijdige aan XY.
STAP 2: Bepaal A′ op die evenwijdige zodat |AA′ | = |XY| en # –AA′ = # –XY.
STAP 3: Duid op [ AA′] dezelfde doorloopzin aan als op [ XY]
a) Teken het beeld van X, Y en Z door de translatie bepaald door # –AB
b) Teken het beeld van de vierhoek door de translatie over # –PQ # –RS
c) Teken het beeld van de driehoek door de translatie over # –PQ
–RS
methode
Je kan rotaties rond een centrum over een gegeven hoek op papier tekenen door gebruik te maken van dit stappenplan. Om een vlakke figuur te roteren, kan je elk hoekpunt roteren, of als je de eigenschappen kent, gebruikmaken van de eigenschappen.
Hoe het beeld tekenen van A door een rotatie om O over 75°?
STAP 1: Teken [ OA in stippellijn.
STAP 2: Zet je passerpunt in O en teken in tegenwijzerzin een cirkelboog door A.
STAP 3: Teken AOA′ = 75°.
a) Teken het beeld van A door een rotatie rond O over 120°.
c) Teken het beeld van B door een rotatie rond M over -75°.
b) Teken het beeld van driehoek XYZ door een rotatie rond O over 75°.
d) Teken het beeld van vlieger ABCD door een rotatie rond O over -100°.
methode
Je kan puntspiegelingen op papier tekenen door gebruik te maken van dit stappenplan.
Om een vlakke figuur spiegelen om een punt, kan je elk hoekpunt spiegelen om het centrum of, als je de eigenschappen kent, gebruikmaken van de eigenschappen.
Hoe het beeld tekenen van A door te puntspiegelen om het punt O?
STAP 1: Teken de rechte AO.
STAP 2: Teken A’ zodat O het midden is van [AA’].
a) Teken het beeld van A door te spiegelen om O. b) Teken het beeld van K door te spiegelen om L.
c) Teken het beeld van driehoek ABC door te spiegelen om O.
d) Teken het beeld van MNPQ door te spiegelen om M.
Open meetkundesoftware en voer de volgende opdrachten uit.
a) Teken een rechthoek ABCD. Spiegel deze rechthoek om de rechte AC.
b) Teken een ongelijkzijdige driehoek ABC. Teken de bissectrice b van A . Spiegel driehoek ABC om de rechte b
Open meetkundesoftware en voer de volgende opdrachten uit.
a) Teken een cirkel c met middelpunt M en straal 3. PQ is een middellijn van de cirkel c. Verschuif de cirkel c over de vector # –MQ
b) Teken een rechthoekige driehoek ABC met rechte hoek in A. Verschuif de driehoek over de vector # –BC
Open meetkundesoftware en voer de volgende opdrachten uit.
a) Teken een gelijkzijdige driehoek KLM. Roteer de driehoek KLM om K over 60 ° in tegenwijzerzin.
b) Teken een ruit ABCD. Het snijpunt van de diagonalen is E. Roteer de ruit ABCD om E over 90 ° in wijzerzin.
Open meetkundesoftware en voer de volgende opdrachten uit.
a) Teken een parallellogram ABCD. Spiegel het parallellogram om het punt A.
b) Teken een gelijkbenige driehoek KLM met top L. Spiegel de driehoek KLM om L.
Voer in Scratch de volgende code in :
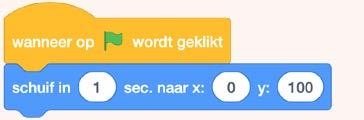
a) Welke transformatie in het vlak voert deze code uit ?
b) Wijzig de code zodat de sprite start in ( 0, 0) en daarna maar half zo ver komt als in de vorige code.
c) Waarom beweegt de sprite trager in het vlak bij de code uit opgave b ?
d) Wat moet je veranderen aan de code om de sprite meer rechts in het scherm te laten komen ?
e) Schrijf een code zodat de sprite twee transformaties uitvoert, daarna even wacht en dan in omgekeerde volgorde terugkeert naar zijn beginpositie.
Hoe lees je volgende notaties ?
a) sO ( P) = R c) t #–KL (M)= N
b) r( O, -120 °) ( A) = B d) st ( F) = G
Noteer in symbolen.
a) K is het beeld van L door een rotatie rond centrum O over een hoek van 70 ° in tegenwijzerzin.
b) B is het beeld van A door een translatie over de vector # –CD .
c) T is het beeld van S door spiegeling om de as d.
d) V is het beeld van W door spiegeling om het punt U.
Vul in.
a) ... is het beeld van V na spiegeling om de as b
b) ... is het beeld van P na translatie over de vector # –VT # –NP .
c) ... is het beeld van het punt T na spiegeling om het punt Q.
d) is het beeld van Q na spiegeling om de as PT.
e) M is het beeld van het punt ... na spiegeling om de as p
f) R is het beeld van het punt ... na translatie over de vector # –VT # –NP .
g) U is het beeld van het punt na spiegeling om het punt R.
h) N is het beeld van het punt ... na spiegeling om de as VM.
Gegeven: een vlakvulling van gelijkzijdige driehoeken en vierkanten
Gevraagd: Vul passend in.
a) E is het beeld van het punt … door rotatie rond D over 60°.
b) K is het beeld van … door een translatie over vector # –DG # –FH
c) P is het beeld van … door een spiegeling om de as AB.
d) K is het beeld van C door een rotatie rond … over … .
e) is het beeld van G door spiegeling om DK.
f) ΔDEF is het beeld van ΔDKB door rotatie rond … over …
g) … is het beeld van [BD] door een translatie over vector # –DG # –FH
h) … is het beeld van J door een rotatie rond K over 240°.
a) Welke transformatie in het vlak voert deze code uit ?
b) Wat moet je veranderen aan de code om dubbel zoveel lijntjes te hebben ?
c) Wijzig de code zodat de gebruiker kan invoeren hoeveel lijntjes hij wil hebben.
d) Is de getekende figuur altijd spiegelsymmetrisch om een punt ?
e) Is de getekende figuur altijd spiegelsymmetrisch om een as ?
Vul aan.
a) sb (Q)= … k) t # –MN (Q)= …
b) sb (U)= … l) t
QR (U)= …
c)
f) sq (P) = … p) tRS ([MN])= …
g) sq (∆NPS) = … q) tPR ([PN])= …
h) s … (P)= M r) t #–VU (c)= …
i) s … (P)= V s) t #–SN ([VR])=
j) s … (P)= V t) t (M)= U
Vul aan.
a) r(O, 30 °) ( F) = … f) r(O, …) ( P) = T
b) r(O, 210 °) ( J) = … g) r(O, …) ( X) = P
c) r(O, -60 °) ( A) = h) r(O, …) ( W) = S
d) r(O, 90 °) ( D) = … i) r(O, 270 °) ( … ) = W
e) r(O, -90 °) ( H) = … j) r(O, 120 °) ( … ) = S
Vul aan.
a) sH ( B) = f) sG ( ) = A
b) sM ( K) = g) sI ( ) = E
c) sI ( E) = … h) s ( A) = P
d) sG ( C) = … i) s ( BD) = NL
e) sH ( P) = … j) s ( EP) = KA
a) Teken sx ( A) , sx ( B) , sx ( C) , sx ( D) en noteer alle coördinaten.
25 y 1 1 0 x C( -3, 2) A( 2, 3)
Wat kan je besluiten over de coördinaten na spiegeling ten opzichte van de x-as ?
b) Teken sy ( A) , sy ( B) , sy ( C) , sy ( D) en noteer alle coördinaten.
Wat kan je besluiten over de coördinaten na spiegeling ten opzichte van de y-as ?
D( 3, -4)
B( 6, 5)
Los op zonder een tekening te maken.
a) A′ = sx ( A) co( A) = ( -4, -7) , dus is co( A′) = …
b) B′ = sx ( B) co( B) = ( 2, -3) , dus is co( B′) = …
c) C′ = sy ( C) co( C) = ( -4, -7) , dus is co( C′) = …
d) D′ = sy ( D) co( D) = ( 2, -3) , dus is co( D′) = …
Gegeven : A( 2, 3) ; B( 5, -2) ; C( -3, -4) ; P( 5, 4) en Q( 5, 7)
Gevraagd : Teken t #–PQ ( ΔABC) en noteer de coördinaten van de beeldpunten.
Teken een willekeurige driehoek ABC in een assenstelsel. Noteer de coördinaat van elk hoekpunt.
a) Draai de driehoek ABC om O over een hoek van 90 °.
b) Welk verband is er tussen de coördinaat van een hoekpunt en de coördinaat van het beeld van dat punt ?
c) Draai de driehoek ABC om O over een hoek van -90 °.
d) Welk verband is er tussen de coördinaat van een hoekpunt en de coördinaat van het beeld van dat punt ?
De punten A( -2, 4) , B( 1, 3) , C( 2, 0) en O( 0, 0) zijn gegeven. Teken ΔABC in een assenstelsel.
a) Teken sO ( ΔABC) .
b) Noteer de coördinaten van A′, B′ en C′. Wat kan je besluiten ?
De punten A( 2, 4) , B( 1, -3) en C( -4, 3) zijn gegeven.
a) Spiegel de punten A, B en C om de bissectrice van het eerste kwadrant.
b) Wat stel je vast in verband met de coördinaten van de gegeven punten en hun beelden ?
a)TekeneenrechthoekigedriehoekABCmet A = 90°.Tekendaarna r(A,90°) (ΔABC)en tBA (ΔABC).
b)TekeneenparallellogramABCD.Tekendaarna sAC (ABCD)en r(A,180°) (ABCD).
c)TekeneenruitABCDwaarbijMhetsnijpuntisvandediagonalen.
Tekendan r(M,90°) (ABCD)en t #–AC (ABCD).
a)Bepaaleenvector # –ABeneenas a zodat
b)BepaaleenpuntOeneenas b zodat sO (sb (E)) = F.
a)Bepaaleenas a en b zodat sb (sa (A)) = B.
b)Bepaaleenvector # –XYenpuntOzodat s0 (tXY (C)) = D.
Een translatie over een vector bewaart de loodrechte stand.
Een spiegeling om een as bewaart de lengte van een lijnstuk.
Welke eigenschap wordt hier geïllustreerd ?
Een spiegeling om een punt bewaart de grootte van een hoek.
Een rotatie rond een centrum over een hoek bewaart de oppervlakte.
Eigenschappen van transformaties kunnen tekenopdrachten makkelijker maken.
a) Zoek het draaibeeld van deze ruit, rond het centrum B over -160°, door zo weinig mogelijk punten te draaien.
b) Op welke eigenschap(pen) steun je ?
Eigenschappen van transformaties kunnen tekenopdrachten makkelijker maken.
a) Zoek het schuifbeeld van deze figuur over vector # –PQ door zo weinig mogelijk punten te verschuiven.
b) Op welke eigenschap(pen) steun je ?
Gegeven : A ∈ a, B ∈ a en C ∈ a | AB| = 9 en | AC| = 12 sA ([ BC]) = [ B′C′]
Gevraagd: Bepaal de mogelijke waarden voor | B′C′| .
Vervolledig de figuur zodat de rechte a een symmetrieas is.
a) Welke van deze speelkaarten zijn spiegelsymmetrisch om een as ?
b) Welke van deze speelkaarten zijn spiegelsymmetrisch om een punt ?
a) Duid – indien mogelijk – in deze tekeningen de symmetrieassen aan in het rood.
b) Duid – indien mogelijk – het symmetriemiddelpunt aan in het groen.
Teken een symmetrievlak bij deze ruimtefiguren.
Bepaal – indien mogelijk – het symmetriemiddelpunt van deze figuren.
a) c)
b) d)
Bepaal het aantal symmetrievlakken in deze ruimtefiguur.
Waar of niet waar ?
a) Elke driehoek heeft minstens één symmetrieas.
b) Als een vlakke figuur spiegelsymmetrisch is om een punt, dan is ze ook spiegelsymmetrisch om een as.
c) Een cirkel heeft oneindig veel symmetrieassen.
d) Een regelmatige n-hoek is spiegelsymmetrisch om een punt.
e) Een regelmatige n-hoek heeft n symmetrieassen.
f) Een vlakke figuur met minstens 2 symmetrieassen is ook spiegelsymmetrisch om een punt.
vlak geen symmetrievlak kan zijn van deze ruimtefiguur.
Waar of niet waar ?
a) Een bol heeft oneindig veel symmetrievlakken.
b) Een balk heeft minstens drie symmetrievlakken.
c) Een kubus heeft zes symmetrievlakken.
d) Een cilinder heeft een symmetrievlak dat evenwijdig is met het grondvlak.
In de wetenschappen gebruikt men structuurformules en chemische modellen om moleculen voor te stellen. Welke symmetrie herken je in deze voorstellingen ?
Ook in de ruimte wordt gebruik gemaakt van coördinaten. Een coördinaat bevat dan een x-coördinaat, een y-coördinaat en een z-coördinaat. Op de figuur zijn al vier coördinaten geplaatst.
Bepaal de coördinaten van de andere hoekpunten van de kubus als je weet dat de oorsprong van het assenstelsel het symmetriemiddelpunt is van deze kubus.
Studiewijzer
Differentiatietraject
Doelen
Ik kan het beeld verklaren van een vlakke figuur dat het resultaat is van een transformatie van het vlak.
Ik onderzoek eigenschappen van transformaties van het vlak en kan die aanwenden bij het uitvoeren van transformaties.
Ik kan spiegelsymmetrie herkennen in vlakke figuren en in ruimtefiguren.
Doelstellingen pagina in module pagina in vademecum
Ik kan het beeld verklaren van een vlakke figuur dat het resultaat is van een transformatie van het vlak. 4
Gebruik ICT om beter inzicht te krijgen in de verschillende soorten transformaties van het vlak. De transformaties : spiegeling om een as, spiegeling om een punt, translatie over een vector en rotatie rond een centrum over een hoek zorgen ervoor dat het beeld van een vlakke figuur een congruente figuur is.
verwerking : 1, 2, 3, 4, 5, 6 signaal : 1, 2 differentiatie : 1 t.e.m. 33
Ik kan de eigenschappen van transformaties herkennen en gebruiken.
De eigenschappen kunnen ervoor zorgen dat je niet elk beeldpunt moet tekenen. Niet elke eigenschap is geldig voor alle transformaties.
verwerking : 7, 8, 9 signaal : 3 differentiatie : 34 t.e.m. 38
Ik kan spiegelsymmetrie herkennen in vlakke figuren en in ruimtefiguren.
Spiegelsymmetrie om een as bij vlakke figuren zorgt ervoor dat de vlakke figuur in twee congruente figuren wordt verdeeld.
verwerking : 10, 11, 12 signaal : 4, 5 differentiatie : 39 t.e.m. 48
11
16
Auteurs Björn Carreyn, Filip Geeurickx en Roger Van Nieuwenhuyze
Eerste editie - Bestelnummer 94 606 0022 (module 01 van 17)
ISBN 978 90 4865 092 7 - KB D/2025/0147/6 - NUR 126 - Thema YPMF
Illustrator Jona Jamart - Design en lay-out Die Keure
Verantwoordelijke uitgever die Keure, Kleine Pathoekeweg 3, 8000 Brugge
RPR 0405 108 325 - © Copyright die Keure, Brugge