MEETKUNDE
02 Meetkundige objecten in het vlak

wat je al kunt
–punten, lijnen en vlakken herkennen
–lijnstukken meten en tekenen –het midden van een lijnstuk bepalen
–de soorten hoeken herkennen
wat je leert in deze module
–de begrippen ruimte, vlak, rechte, halfrechte, drager, lijnstuk en punt gebruiken
–de notatie van een vlak, rechte, halfrechte, drager, lijnstuk en punt lezen en gebruiken
–lijnstukken tot op 1 mm nauwkeurig meten en tekenen
–hoeken tot op 1 graad nauwkeurig meten en tekenen
–even grote hoeken tekenen
–de bissectrice van een hoek tekenen
–verbanden leggen tussen hoeken

Inhoud
Instap
1Punt, rechte, lijnstuk en halfrechte
2Lijnstukken meten
3Hoeken
4Hoeken meten en tekenen
5Bissectrice van een hoek
6Verbanden tussen twee hoeken
Signaaloefeningen
Differentiatietraject
Studiewijzer
in de kijker
Je controleert bij het maken van je boekentas of je voor elke les je passer, liniaal, geodriehoek en potlood bij hebt.
wiskundetaal
–ruimte
–vlak
–punt
–rechte
–halfrechte
–lijnstuk
–midden van een lijnstuk
–hoek
–bissectrice van een hoek
–overstaande hoeken
–constructie
–aanliggende hoeken
–nevenhoeken
–complementaire hoeken
–supplementaire hoeken
Instap
Opdracht 1
In the Dome of the Rock in Jerusalem kun je heel wat meetkundige figuren ontdekken. Probeer in de woordspin zo veel mogelijk wiskundige begrippen uit de meetkunde te noteren. Je kent vast nog heel wat zaken uit de basisschool, maar je kunt je ook laten inspireren door de foto’s.


https://commons.wikimedia.org
Opdracht 2
Welke hoeken herken je in de benen van volgende dansposes?


MEETKUNDE
INKIJKEXEMPLAARDIEKEURE




Opdracht 3
Kan de chauffeur de fietser zien? Duid met behulp van twee kijklijnen aan wat de chauffeur door de voorruit kan zien.


Opdracht 4
In opdracht 3 merkte je een onveilige situatie op. Er zijn echter nog meer plaatsen rond een vrachtwagen die gevaarlijk zijn. Als je je in de ‘dode hoek’ bevindt, dan ben je voor de chauffeur niet zichtbaar. Alle personen met een oranje of rode pet bevinden zich in de ‘dode hoek’ van deze vrachtwagen. Arceer dit gebied en zorg ervoor dat je je hier nooit in bevindt.
INKIJKEXEMPLAARDIEKEURE

1 Punt, rechte, lijnstuk en halfrechte
1.1 Vlak
Stel je voor dat de tegelvloer op de figuur blijft doorlopen, in welke richting je ook zou stappen. In de wiskunde noemen we die tegelvloer een vlak

het vlak alfa
het vlak bèta
Een vlak is een verzameling van oneindig veel punten. We noteren een vlak met een Griekse letter: α, β, π, …
symboollees je als
α alfa
β bèta
δ gamma
π pi
1.2Punt
Het vlak is een verzameling van oneindig veel punten. Een punt heeft geen afmetingen en stellen we door een stip voor. We benoemen een punt met een hoofdletter.
Een punt ligt altijd in een vlak. Je kunt dit in symbolen noteren.
in symbolenlees je als
A ∈ π A ligt in het vlak π of A is een element van het vlak π

Als we in onze lessen maar in twee dimensies werken, spreken we over vlakke meetkunde . Werken we in drie dimensies, dan spreken we over ruimtemeetkunde
Deze module gaat over de basisbegrippen van de vlakke meetkunde.
Merk op Twee punten kunnen verschillend zijn van elkaar, zoals A, B, C, D, E en F. Twee punten kunnen samenvallen, zoals F en G.
1.3Rechte
notatie a = AD = DE = EF = AB =
We benoemen een rechte door een kleine letter of door twee verschillende punten die op de rechte liggen.
in symbolenlees je als
B ∈ a B ligt op de rechte a of B is een element van de rechte a.
G ∉ a G ligt niet op de rechte a of G is geen element van de rechte a.
a ⊂ π De rechte a ligt in het vlak π of a is een deelverzameling van π.
eigenschapDoor twee verschillende punten kun je slechts één rechte tekenen. We zeggen ook dat een rechte bepaald wordt door twee verschillende punten.
definitie Collineaire punten zijn drie of meer verschillende punten die op eenzelfde rechte liggen.

Merk op
Door drie verschillende punten gaat niet altijd een rechte.
Zo liggen de punten A, B en C op eenzelfde rechte, maar de punten A, D en E niet.
eigenschapDoor één punt gaan oneindig veel verschillende rechten.
De rechten a, b, c, d en e gaan allemaal door het punt E. We zeggen dat a, b, c, d en e concurrente rechten zijn. Je kan bovendien nog oneindig veel andere rechten tekenen die ook door het punt E gaan. E e d c b a
INKIJKEXEMPLAARDIEKEURE
Je kan bijvoorbeeld in symbolen noteren dat E het enige gemeenschappelijke punt is van de rechten a en b
in symbolenlees je als
a ∩ b = { E} De doorsnede van rechte a en rechte b is de verzameling met het punt E.
1.4 Halfrechte
Als we de rechte r zouden ‘doorknippen’ in het punt A, dan krijgen we twee halfrechten.
Een halfrechte is aan één kant begrensd.
definitie Een halfrechte is een deelverzameling van een rechte die aan één kant begrensd is. grenspunt
We noemen A het grenspunt van [AB en van [AC.
notatie [AB of a [AC of b

Merk op In deze figuur is [AB ≠ [AC
in symbolenlees je als [AB ⊂ r alle punten van de halfrechte [AB liggen ook op de rechte r of [AB is een deelverzameling van de rechte r
Een halfrechte is een deelverzameling van een rechte. We noemen deze rechte de drager van de halfrechte.
[PQ is een halfrechte, r is de drager van [PQ.
[PS is een halfrechte, r is de drager van [PS.
[PQ = [PS
[PQ, [QP en [QS zijn halfrechten.

Merk op [VT ≠ [TV
V
1.5Lijnstuk
Een lijnstuk is langs twee kanten begrensd. Daarom gebruiken we in de notatie twee blokhaakjes.
Ook de grenspunten A en B behoren tot het lijnstuk.
B
notatie[AB]
definitie Een lijnstuk is een deelverzameling van een rechte die aan twee kanten begrensd is.
Een lijnstuk is een deelverzameling van een rechte. We noemen deze rechte de drager van het lijnstuk.
notatie[AB] ⊂ a a A B

INKIJKEXEMPLAARDIEKEURE
Merk op [AB] = [BA]
Verwerkingsopdrachten
Verbind elke omschrijving uit de eerste kolom met de bijbehorende notatie uit de tweede kolom.
lijnstuk met grenspunten A en B • • AB
halfrechte door A begrensd in B • • | AB|
rechte door de punten A en B • • [AB
halfrechte c • • [BA • c • [AB]
1, 2
drager van de halfrechte [IJ e
INKIJKEXEMPLAARDIEKEURE
drager van het lijnstuk [EF] d
Vervolledig de tekening.
• rechte r = RT
• halfrechte door A begrensd in C
• lijnstuk [TC]
• punt D op halfrechte [AT
Gegeven: P, Q, R en S de rechte z
Vul aan met ∈, ∉, ⊂, ⊄ of =
a)P z
b)Q [PR
c)R [QP
d)S RS
a)Teken een tennisbal G op de rechte a
[PR]
z
RS
[QR
[PQ z
[PQ PQ k) [PQ [PR l) [RS z m) [QR] z n) [SQ] SQ o) [PR] [RP] p)PQ z
b)Plaats een tennisbal H zodat A, C en H collineair zijn.
c)Plaats tennisbal I zodat AD ∩ BE = { I}

2 Lijnstukken meten
2.1 De lengte van een lijnstuk bepalen
Omdat een lijnstuk aan twee kanten begrensd is, kunnen we het meten.
Hoe meet je de lengte van een lijnstuk ?
methodeSTAP 1:Plaats eerst de tekenzijde van de geodriehoek op het lijnstuk.
STAP 2: Verschuif dan de geodriehoek zodat het nulpunt samenvalt met een van de grenspunten van het lijnstuk.
STAP 3:Lees de lengte af.
notatie | AB|
Voorbeeld :
• Om de afstand tussen twee punten A en B te bepalen, teken je het lijnstuk [AB].
• Meet de lengte van het lijnstuk [AB].
Of ook: bepaal | AB| | AB| = 5,7 cm

Conclusie: De lengte van het lijnstuk [AB] is 5,7 cm.
Merk op
• 5,7 cm = 57 mm
Met deze tabel kan je herleidingen uitvoeren.
Voorbeelden
• Lijnstukken die even lang zijn, kan je voorzien van eenzelfde merkteken.
2.2Even lange lijnstukken construeren
We kunnen meetkundige tekeningen schetsen, tekenen en soms construeren.
Wanneer we met de vrije hand en zonder geodriehoek of passer tekenen, dan spreken we over schetsen
Met tekenen bedoelen we dat we gebruikmaken van de geodriehoek (en passer) en mogen meten.
Bij construeren wordt er nooit gemeten. Je gebruikt je passer om afstanden af te passen en je liniaal om een rechte lijn te tekenen.
Constructie
Je kunt twee even lange lijnstukken tekenen zonder te meten. Dit doe je door gebruik te maken van een passer en een liniaal.





































Hoe construeer je even lange lijnstukken ?







methodeSTAP 1: Plaats eerst het passerpunt in C en het potloodpunt in D. Behoud deze passeropening.
STAP 2: Plaats dan het passerpunt in E. Teken een cirkelboogje.
Neem een willekeurig punt op de cirkelboog en noem het F.
STAP 3: Teken tot slot het lijnstuk [EF].
2.3Het midden van een lijnstuk
definitiein woorden
Het midden van een lijnstuk is een punt van dat lijnstuk dat even ver ligt van de grenspunten van dat lijnstuk.
in symbolen:
M is het midden van [AB] ⟺ M ∈ [AB]en | AM| = | MB|

Merk op
Om even lange lijnstukken aan te duiden, wordt gebruikgemaakt van dezelfde merktekens.
Verwerkingsopdrachten
Teken nauwkeurig de lijnstukken met de gegeven lengte.
[GH] met | GH| = 5,5 cm
INKIJKEXEMPLAARDIEKEURE
7 8 9
[MN] met | MN| = 0,7 dm
Construeer [KL] zodat | KL| = | GH| zonder [GH] te meten.
Teken een lijnstuk [RT] met | RT| = 6 cm.
Duid het midden U aan.
Teken een lijnstuk [AB] zodat | AB| = | RU|
Schrijf in symbolen:
a)[KP] en [LM] zijn even lange lijnstukken.
b)[PQ] , [RS] en [TU] zijn even lang.
c)[UX] en [YZ] zijn niet even lang.
notatie
3 Hoeken
3.1 Hoeken rondom ons
Een vrachtwagenchauffeur ziet niet alles. Als je je als fietser in de ‘dode hoek’ bevindt, dan ben je niet zichtbaar voor de chauffeur.

Als je naar de sterren kijkt, dan plaats je de sterrenkijker onder een bepaalde hoek.

3.2Benamingen en notatie
Een hoek bestaat uit twee benen en een hoekpunt. De benen zijn halfrechten, in dit geval [HA en [HB. De halfrechten hebben een gemeenschappelijk punt, namelijk het hoekpunt H.
H,A HB,BHAof α
Voor hoeken worden soms ook Griekse letters zoals α, β, ... gebruikt.
3.3De hoekgrootte
In de basisschool leerde je al dat je hoeken meet in graden. D = 45° lees je als ‘de hoek D meet 45 graden’. 45 noemen we het maatgetal, ° (graden) stelt de eenheid voor.
notatiein woorden
één graad = 60 minuten
in symbolen
1° = 60′
De architect van dit gebouw zal op het plan verschillende hoekgroottes genoteerd hebben.
INKIJKEXEMPLAARDIEKEURE
Een hoek van 22,5° kan je dus ook noteren als 22°30′
notatiein woorden
één minuut = 60 seconden
in symbolen
1′ = 60″

3.4 Soorten hoeken
definitie Een nulhoek is een hoek van 0°.
A A = 0°
definitie Een scherpe hoek is een hoek waarvan de hoekgrootte tussen 0° en 90° ligt.
0° < A < 90°
definitie Een rechte hoek is een hoek van 90°.
A A = 90°
Gebruik het symbool ∟ om de loodrechte stand aan te duiden.
definitie Een stompe hoek is een hoek waarvan de hoekgrootte tussen 90° en 180° ligt.
90° < A < 180°
definitie Een gestrekte hoek is een hoek van 180°. A A = 180°
definitie Een volle hoek is een hoek van 360°.
A A = 360°
Verwerkingsopdrachten
Vul de tabel aan.
naam
hoekgrootte 0° < A < 90° A = 90°
gestrekte hoek
Bepaal door te redeneren de grootte van de kleinste hoek gevormd door de wijzers en geef de benaming voor deze hoek.
hoekgrootte benaming
Bepaal de grootte van de hoeken zonder te meten. a)
4 Hoeken meten en tekenen
4.1 Hoeken meten
Hoeken meten doe je met een gradenboog.
Op je geodriehoek is een gradenboog tot op één graad nauwkeurig afgebeeld.
Hoe meet je een hoek met een geodriehoek ?
methodeSTAP 1: Plaats eerst het nulpunt van de geodriehoek op het hoekpunt.
STAP 2: Plaats de tekenzijde van de geodriehoek op één been van de hoek.
STAP 3: Lees het getal af dat op de geodriehoek bij het tweede been staat.
a)Bij een scherpe hoek kies je het kleinste getal.
b)Bij een stompe hoek kies je het grootste getal.

Merk op Je kunt de hoekgrootte ook bepalen met ICT.
4.2 Hoeken met een gegeven grootte grafisch voorstellen
Hoe teken je een hoek van 60 °?
methodeSTAP 1: Leg het nulpunt van de geodriehoek op het hoekpunt en de tekenzijde op de halfrechte.
Plaats een hulppunt bij 60°.
STAP 2:Teken een halfrechte door het hulppunt met het hoekpunt als grenspunt.
STAP 3:Duid de hoek aan met een boogje.
Noteer er het aantal graden bij.
Verwerkingsopdrachten
Schat eerst de hoekgrootte. Meet vervolgens de hoekgrootte. Noteer de antwoorden.
schatting:
schatting: schatting: meting: meting: meting:
Teken volgende hoeken.
5 Bissectrice van een hoek
5.1 Definitie
A = 60°
A1 = 30°
A2 = 30°
De rechte b deelt de hoek A in twee even grote hoeken.
definitiein woorden
Een bissectrice (of deellijn ) van een hoek is de rechte door het hoekpunt die deze hoek in twee even grote hoeken deelt.
in symbolen
b is de bissectrice (of deellijn) van de hoek A ⟺ A1 = A2 enA ∈ b
5.2Bissectrice van een hoek grafisch voorstellen
INKIJKEXEMPLAARDIEKEURE
Hoe teken je een bissectrice van een hoek ?
methodeSTAP 1: Meet de grootte van de hoek.
STAP 2:Bereken de grootte van de halve hoek.
Plaats een hulppunt bij de halve hoek.
STAP 3:Teken een rechte door dit hulppunt en het hoekpunt.
Benoem de rechte.
Duid de even grote hoeken aan met merktekens.
Teken de bissectrice b van de volgende hoeken.
a)Tekendebissectricesvandehoeken Aen B.
b)Tekendebissectricesvandehoeken C1 en C2
1 2
6 Verbanden tussen twee hoeken
6.1 Overstaande hoeken
M 2 1
M1 en M2 zijn overstaandehoeken.
definitie Overstaande hoeken zijn twee hoeken waarvan de benen in elkaars verlengde liggen. eigenschapOverstaande hoeken zijn even groot.
6.2Complementaire hoeken
α = 60° β = 30°
α + β = 60° + 30° = 90°
α en β zijn complementaire hoeken.
definitie Complementaire hoeken zijn twee hoeken waarvan de som 90° is.
Voorbeeld
60° is het complement van 30°.
30° is het complement van 60°.
Algemeen
Het complement van α is 90° - α
INKIJKEXEMPLAARDIEKEURE
β beta γ gamma δ delta TIP
Een hoek wordt dikwijls aangeduid met een Griekse letter.
α alfa

6.3Supplementaire hoeken
γ = 140°
δ = 40°
γ + δ = 140° + 40° = 180°
γ en δ zijn supplementaire hoeken.
definitie Supplementaire hoeken zijn twee hoeken waarvan de som 180° is.
Voorbeeld
140° is het supplement van 40°.
40° is het supplement van 140°.
Algemeen
Het supplement van α is 180° - α.
6.4 Aanliggende hoeken
α en β zijn aanliggende hoeken .
definitie Aanliggende hoeken zijn twee hoeken met een gemeenschappelijk been waarbij de andere benen langs beide zijden van het gemeenschappelijk been liggen.
6.5Nevenhoeken
INKIJKEXEMPLAARDIEKEURE
γ en δ zijn nevenhoeken
definitie Nevenhoeken zijn twee hoeken die aanliggend en supplementair zijn.
Verwerkingsopdrachten
Vul de meest geschikte naam in. Kies uit: overstaande hoeken, aanliggende hoeken en nevenhoeken.
a)
a)Welke hoeken uit oefening 18 zijn complementair?
b)Welke hoeken uit oefening 18 zijn supplementair?
A1 en A2
A1 en A3
A2 en A4
Hoeveel graden meet de hoek die …
a)complementair is met een hoek van 53°?
b)supplementair is met een hoek van 38°?
c)complementair is met het supplement van 140°?
Noteer in elke cirkel de hoekgrootte.
Signaaloefeningen
Hieronder zie je vijf meetkundige begrippen voorgesteld. Geef de notatie en de benaming.
notatie: notatie: benaming: benaming: d A
notatie: notatie: benaming: benaming:
notatie: benaming:
Schrijf in symbolen.
•Het lijnstuk [MN] meet 35 cm.
•De lijnstukken [AB] en [CD] zijn even lang.
•De lijnstukken [XY] en [AB] zijn niet even lang.
INKIJKEXEMPLAARDIEKEURE
Verder
Teken het midden van volgende lijnstukken.
Construeer de lijnstukken [CD] en [EF] als je weet dat
>>> Verder oefenen: D10 t.e.m. D23 >>> Verder oefenen: D10 t.e.m. D23
Schrijf in symbolen.
a)De grootte van de hoek D is 30°.
b)De hoek E is even groot als de hoek F
Gegeven: de tekening van enkele soorten hoeken
Gevraagd: Geef de benaming van de hoek en noteer de hoekgrootte.
INKIJKEXEMPLAARDIEKEURE
tekening: tekening: A A
benaming: benaming: hoekgrootte: hoekgrootte:
tekening: tekening:
benaming: benaming: hoekgrootte: hoekgrootte:
Bepaal de grootte van de hoek α zonder te meten.
a) b)
Meet de volgende hoeken en schrijf de correcte benaming op. Kies uit: nulhoek, scherpe hoek, rechte hoek, stompe hoek of gestrekte hoek.
grootte: grootte: benaming: benaming:
grootte: grootte: benaming: benaming:
A = 48°
B = 110°
Verder oefenen: D34
Teken met een geodriehoek het tweede been van de hoeken A, B, Cen D zodat ze de gegeven grootte krijgt.
A = 48°
B = 110°
C = 75°
D = 245°
A = 48°
B = 110°
C = 75°
D = 245°
C = 75° D = 245°
A = 48°
B = 110°
C = 75°
= 245°
Gegeven is een hoek α
a)Hoe groot is α ?
b)Hoe groot is het complement van α ?
c)Hoe groot is het supplement van α ?
d)Teken zowel het complement als het supplement van α
a)Hoe noem je de volgende hoeken? A 1 2 3 4 5
A1 en A4 zijn hoeken.
A1 en A2 zijn hoeken.
A1 en A5 zijn hoeken.
A3 en A4 zijn hoeken.
A4 en A5 zijn hoeken.
b)Tekenopdefiguurhierboveneenhalfrechteenduid A6 aanzodat A4 en A6 zowelcomplementair alsaanliggendzijn.
14
Teken een aanliggende hoek van α en een nevenhoek van β
>>> Verder oefenen: D46 t.e.m. D61
>>> Verder oefenen: D46 t.e.m. D61
INKIJKEXEMPLAARDIEKEURE
Differentiatietraject
AB IJ [NC] [DK [FH [OE] 1 2 3 4
Welke meetkundige begrippen staan hier afgebeeld?
Gegeven: twee verschillende punten D en M Gevraagd: Hoe lees je volgende notaties?
a) [DM b)[DM] c) | DM| d) DM
Schrijf voluit. Maak ook een tekening.
a)K ∈ m
b)P ∉ g , P ∈ s
c)EB ⊂ α
Teken de volgende rechten in het blauw, halfrechten in het zwart en lijnstukken in het groen:
Juist of fout?
a) | AB| = | BA|
b)[AB] = [BA]
c)AB = BA
d)[AB = [BA
Vul aan met het correcte symbool. Kies uit: ∈, ∉, ⊂, ⊄ of =.
INKIJKEXEMPLAARDIEKEURE
x y
a)B y
b)[DC DC
c)[AB] … x
d)AB … x
e)D x
f) y π
g)D … π
h)[AD] … AC
Teken vier collineaire punten U, X, Y en Z.
π
i)[BC CB]
j)C … y
k)[AB … π
l)AB … BA
a)Teken de drager van [ AB]
b)Plaats een punt G dat collineair is met D en C.

c)Duid [ BC] aan.
d)Vul in: FB ∩ ED = { … }
Lijnstukken
e)823 mm = 0,823 … f) 0,7 km = 70 000 … 9 10 11 12 13
Drie of meer rechten die één snijpunt gemeenschappelijk hebben, noemen we concurrente rechten.
Teken vier concurrente rechten g, h, i en j
Herleid.
INKIJKEXEMPLAARDIEKEURE
a)5 dm = … cm
b)326 mm = … cm
c) 37 m = … km
d)0,58 mm = … cm
e)3012,5 m = … km
f) 89,5 cm = … m
g)96,4 mm = … m
h)438,01 cm = … m
Noteer de lengte van volgende lijnstukken. Werk op 1 mm nauwkeurig.
Zorg voor de juiste notatie.
Teken een lijnstuk [AB] zodat | AB| = 6 cm.
Teken nadien [BC] en [CD] zodat | BC| = 4 cm en | CD| = 8 cm.
Vul de ontbrekende lengte-eenheid in.
a)3200 m = 3,2 …
b)2,02 cm = 20,2 …
c)15 km = 15 000 …
d)0,03 km = 300 …
Teken de lijnstukken [AB], [CD], [EF] en [FG] als je weet dat | AB| = 5,8 cm; | CD| = 33 mm; | EF| = 0,19 dm; | FG| = 6,1 cm.
Voer volgende opdrachten uit.
a)Teken een lijnstuk [MN] van 6 cm. Duid het midden H aan.
b)Teken een lijnstuk [RS] van 3,6 cm. Duid het midden I aan.
Construeer de gegeven driehoek zonder te meten.
Zes vrienden staan op een speelveld en spelen met een bal. Allison (A) schopt de bal naar Els (E) en Els naar Chadia (C). Chadia past de bal naar Franky (F) , die op zijn beurt de bal naar Dennis (D) trapt.
a)Welke afstand heeft de bal afgelegd als je weet dat er getekend is op schaal 1 :100?
b)Noteer je werkwijze.


Voeg in Scratch via de uitbreiding ‘pen’ toe. Met deze uitbreiding kun je tekenen. Start altijd met het commando ‘wis alles’, zo begin je met een blanco scherm. Plaats de sprite in de oorsprong. Gebruik vervolgens deze code.
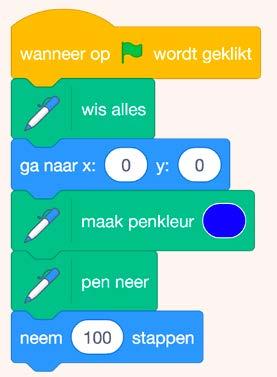
a)Wat doet deze code?
Gebruik nu volgende code.
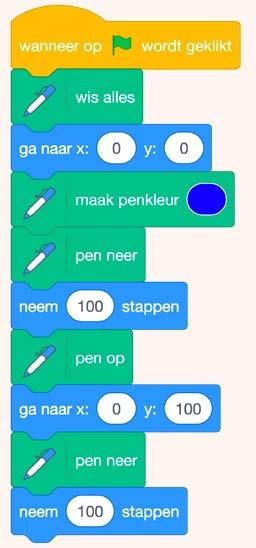
b)Wat doet deze code?
c)Pas de code aan zodat er nu een lijnstuk getekend wordt van 200 stappen.
INKIJKEXEMPLAARDIEKEURE
d) Verander de code zodat de gebruiker de lengte van het lijnstuk kan invoeren. Gebruik hiervoor onderstaande blokje.
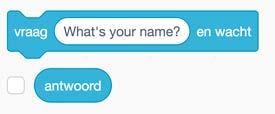
e) Pas de code aan zodat er twee lijnstukken getekend worden. Zorg ervoor dat het tweede lijnstuk drie keer zo lang is als het eerste.
a)Teken een willekeurige driehoek ABC.
b)Verbind de middens van de driehoek ABC. Benoem deze middens met D, E en F.
c)Teken nu driehoek DEF en verbind ook hierin de middens van die zijden. Noem die K, L en M.
d)Wat kan je besluiten over de oppervlakte van ∆DEF?
20 21 22 23
Vervolledig de driehoek, zonder te meten, zodat F het snijpunt is van [EF] en [FD] en zodat | DE| = | EF| = | FD| . Maak gebruik van een passer.
D E
INKIJKEXEMPLAARDIEKEURE
Construeer een driehoek XYZ zodat | XY| = 5 cm, | XZ| = 7 cm en | YZ| = 6 cm.
De punten A, B, C en D zijn collineair. | AB| = 4 cm, | BC| = 3 cm en | CD| = 6 cm.
Hoe lang is [BD]? Teken twee mogelijke situaties.
| AB| = 6 cm en | AC| = 4 cm P is het midden van [ AB] en Q is het midden van [ AC] . Wat kan je besluiten over de lengte van [ PQ] ?
Geef de juiste benaming van de getekende hoek.
INKIJKEXEMPLAARDIEKEURE
Geef de juiste benaming van de aangeduide hoeken.
a)Welke hoeken vormen samen een gestrekte hoek?
b)Welke hoeken zijn even groot?
Bepaal de grootte van de hoek. F
Benoem de aangeduide hoeken.
Geef de notatie.
Noteer de hoekgrootte erbij.
scherpe hoek
Bepaal alle hoekgroottes zonder te meten. Verklaar hoe je aan de uitkomst komt.



a)Bepaal de grootte van de aangeduide hoeken als je weet dat elk stuk even groot is.
b)In hoeveel gelijke stukken moet je de pizza verdelen zodat elke hoek in het midden van de pizza 24° zou zijn?
Voer in Scratch de volgende code in:

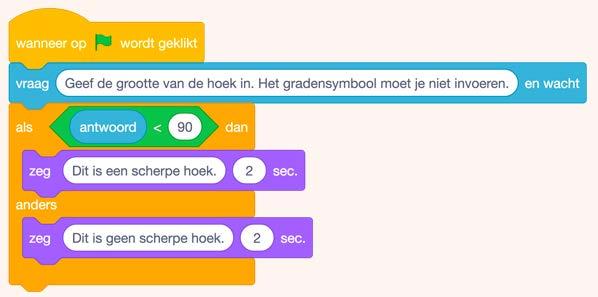
a)Wat doet deze code? Leg elke stap uit met een voorbeeld.
b)Pas de code aan zodat het controleert of de hoek recht is.
c)Pas de code aan zodat het controleert of de hoek gestrekt is.
d)Wat doet de onderstaande code? Leg elke stap uit met een voorbeeld.

e)Maak nu zelf een code die controleert of een hoek scherp, recht of stomp is.
Gegeven: C3 = 28°en C5 = 58°
Gevraagd:Berekenallehoekenzondertemeten. Verklaarhoejeaandeuitkomstkomt.
Bereken de gevraagde hoeken. Verklaar hoe je aan de uitkomst komt.
a)Gegeven:K CN = 164°
Gevraagd:BepaalN CMenK CL.
INKIJKEXEMPLAARDIEKEURE
b)Gegeven:F GI = 164°
Gevraagd:BepaalI GH,E GJ,I GEenF GJ.

Tekendehoeken Aen Calséénbeenendehoekgroottetelkensgegevenzijn. A = 25° C = 175°
INKIJKEXEMPLAARDIEKEURE
Tekentelkenseenhoek Ozodat A= O.
TekenmetICTtweeoverstaandehoeken B1 en B2 waarvan B1 = 50°.
TekenmetICTtweehoeken A1 en A2 dieéénbeengemeenschappelijkhebben zodat A1 = 35°en A2 = 76°.
TekenmetICTtweehoeken C1 en C2 diesamen180°vormenenwaarbij C1 = 76°.
Bissectrice van een hoek
Tekendegevraagdehoeken.
a)Teken Azodat A = F + G.
b)Teken Ezodat E = G F.
G
Teken met ICT of met je geodriehoek een driehoek AOE met | OE| = 6 cm, Oevengrootals Men Eevengrootals P. M
Duidhetvakjeaanals b debissectriceisvan A.
42
Teken de bissectrice van de volgende hoeken.
U X Y
Tekendebissectricevan A1 envan A2 Watvaltjeop?
TekeneenwillekeurigedriehoekABC.Tekendebissectricevan A, Ben C. Watvaltjeop?
De rechte b is de bissectrice van de aangeduide hoek. Bereken alle hoeken zonder te meten.

Verbanden
INKIJKEXEMPLAARDIEKEURE
Bereken telkens het complement en het supplement van de gegeven hoek.
Als je weet dat α + β = 180°, mag je dan besluiten dat …
a) α en β supplementair zijn?
b) α en β nevenhoeken zijn?
Vul aan.
a)Het complement van een hoek van 56° is een hoek van …
b)De complementaire hoek van een hoek van 35° is een hoek van …
c)Het supplement van een hoek van 48° is een hoek van …
d)De supplementaire hoek van een hoek van 95° is een hoek van …
e)Het complement van α is …
f) Het supplement van α is … .
a) α is het complement van β. Hoe groot is β ?
α
INKIJKEXEMPLAARDIEKEURE
b) α is het supplement van β. Hoe groot is β ?
Bereken telkens het complement en het supplement van de gegeven hoek.
complement van α supplement van α
Teken zonder te meten…
b)twee hoeken
Aen B C1 en C2 die elkaars supplement zijn.
a)twee hoeken Aen B C1 en C2 die elkaars complement zijn.
Teken een aanliggende hoek β van α zodat α + β = 90°.
Welke twee namen kun je geven aan α en β ?

Kies in Scratch bij code voor variabelen.
Een variabele is een ‘container’ waarin een waarde wordt opgeslagen. Deze waarde is bij het opstellen van de code niet gegeven en wordt vrij bepaald door de gebruiker van de code.
Je kunt containers dus gebruiken wanneer de waarden in een programma veranderlijk zijn. Containers zijn nuttig voor programmeurs als ze een code willen schrijven met veranderlijke waarden.
• Maak een eerste variabele en geef die de naam ‘hoek’.
• Maak een tweede variabele en geef die de naam ‘complement’.
• Gebruik onderstaande code.
INKIJKEXEMPLAARDIEKEURE


a)Wat doet deze code?
b)Pas de code aan zodat ook het supplement wordt gegeven.

Voeg in Scratch via de uitbreiding ‘pen’ toe.
Met deze uitbreiding kun je tekenen. Start altijd met het commando ‘wis alles’, zo begin je altijd met een blanco scherm.
Gebruik vervolgens deze code.

a)Wat doet deze code? Leg elke stap uit met een voorbeeld.
b) Teken een hoek van 30°. Van welk wiskundig begrip moet je hiervoor gebruikmaken?
c) Pas de code aan zodat een gebruiker een willekeurige hoek kan invoeren die vervolgens getekend wordt.
58
Waar of niet waar?
a)Een hoek van 60° is het complement van een hoek van 30°.
b)Het supplement van een hoek van 50°50′ is een hoek van 129°10′
c)Twee supplementaire hoeken kunnen even groot zijn.
d)Aanliggende hoeken kunnen complementair zijn.
e)Supplementaire hoeken kunnen aanliggend zijn.
f) Overstaande hoeken kunnen supplementair zijn.
INKIJKEXEMPLAARDIEKEURE
Bepaal telkens α
Vul aan.
a)Het complement van een hoek van 10° is een hoek van … .
b)De complementaire hoek van een hoek van 20°30′40″ is een hoek van … .
c)Het complement van het supplement van een hoek van 120° is een hoek van … .
d)De supplementaire hoek van een hoek van 100° is een hoek van … .
e)Het supplement van het supplement van een hoek van 111° is een hoek van …
f) Het complement van een hoek is deze hoek zelf, namelijk een hoek van
g)Het supplement van een hoek is de hoek zelf, namelijk een hoek van …
Teken de gevraagde hoek.
a) α is het complement van β. Teken β
INKIJKEXEMPLAARDIEKEURE
b) α is het supplement van β Teken het complement van β.
Zoek telkens de gevraagde hoek.
a)Een hoek is het dubbel van zijn complement. Hoe groot is deze hoek?
b)Een hoek is elf keer zo groot als zijn supplement. Hoe groot is deze hoek?
c)Het supplement van een hoek is 58° groter dan de hoek zelf. Hoe groot is deze hoek?
Het supplement van een hoek is vijf keer zo groot als het complement van deze hoek.
Hoe groot is de hoek?
INKIJKEXEMPLAARDIEKEURE
HANDIGE HOEKEN KAARTJES
Aanliggende hoeken zijn twee hoeken met een gemeenschappelijk been waarbij de andere benen langs beide zijden van het gemeenschappelijk been liggen.
een stompe hoek
Een hoek tussen 0° en 90°. A
comple- mentaire hoeken
Een hoek van 90° A
Twee hoeken die aanliggend en supplementair zijn.
gestrekte hoek
supple- mentaire hoeken
een volle hoek
Hoeken waarvan de benen in elkaars verlengde liggen.
Een hoek van 180° A neven- hoeken
aanliggende hoeken een rechte hoek
HANDIGE HOEKEN KAARTJES
INKIJKEXEMPLAARDIEKEURE
Een hoek tussen 90° en 180°. A
Een hoek van 360° A overstaande hoeken
Twee hoeken waarvan de som 180° is.
Een hoek van 0° A
scherpe hoek
een
Twee hoeken waarvan de som 90° is.
Studiewijzer
Differentiatietraject
Ik kan de benaming en notatie van meetkundige begrippen vlot gebruiken.
Ik kan lijnstukken nauwkeurig meten en tekenen.
INKIJKEXEMPLAARDIEKEURE
Ik ken de bijzondere hoeken en hun groottes.
Ik kan hoeken nauwkeurig meten en tekenen.
Ik kan de bissectrice van een hoek tekenen.
Ik ken de betekenis van overstaande, complementaire, supplementaire, nevenen aanliggende hoeken.
Doelstellingen pagina in module
Ik ken de definities en notaties van de meetkundige begrippen. 4
Zoek de definities van deze begrippen, lees ze aandachtig en schrijf ze eventueel een keer over.
verwerking: 1 t.e.m. 5 signaal: 1, 2 differentiatie: 1 t.e.m. 9
Ik kan de lengte van lijnstukken bepalen en de juiste notatie vlot gebruiken. Ik kan lijnstukken tot op 1 mm nauwkeurig tekenen en het midden van een lijnstuk bepalen. 10
Met een geodriehoek en met ICT kan je lijnstukken tekenen. Wees voldoende kritisch voor jezelf. Bekijk en controleer je eigen werk.
verwerking: 6 t.e.m. 9 signaal: 3, 4, 5 differentiatie: 10 t.e.m. 23
Ik weet hoe een hoek voorgesteld wordt en ken de benamingen van de verschillende soorten hoeken en hun hoekgroottes. 13
Met een geodriehoek en ICT kan je de grootte van een hoek bepalen.
verwerking: 10, 11, 12 signaal: 6, 7, 8 differentiatie: 24 t.e.m. 33
Ik kan de grootte van een hoek bepalen en een hoek met een geodriehoek en ICT tekenen. 16
Wees voldoende kritisch voor jezelf. Bekijk en controleer je eigen werk.
verwerking: 13, 14, 15 signaal: 9, 10 differentiatie: 34 t.e.m. 40
Ik ken de definitie van de bissectrice van een hoek en kan ze toepassen. 18 Maak gebruik van de definitie. Duid de twee even grote hoeken aan die ontstaan als je de bissectrice tekent.
verwerking: 16, 17 signaal : 11 differentiatie: 41 t.e.m. 45
Ik ken de betekenis van overstaande hoeken en weet dat deze steeds even groot zijn. Ik weet wat complementaire, supplementaire, neven- en aanliggende hoeken zijn. 20
Het begrip 'overstaande hoeken' komt vaak in de meetkunde voor. Kijk dus goed naar de gegevens en naar een (eventuele) tekening.
verwerking: 18 t.e.m. 21 signaal: 12, 13, 14 differentiatie: 46 t.e.m. 61
INKIJKEXEMPLAARDIEKEURE
Auteurs Björn Carreyn, Filip Geeurickx en Roger Van Nieuwenhuyze
Eerste editie - Bestelnummer 94 606 0012 (module 02 van 17)
ISBN 978 90 4865 054 5 - KB D/2025/0147/100 - NUR 126 - Thema YMPF
Illustrator Jona Jamart - Design en lay-out die Keure
Verantwoordelijke uitgever die Keure, Kleine Pathoekeweg 3, 8000 Brugge
RPR 0405 108 325 - © Copyright die Keure, Brugge
