04 Consolidatie

Inhoud (elk onderdeel behandelt de leerstof van module 01 t.e.m. 03)
blz. 02 – 05 Ken je de theorie?
blz. 06 – 07 Heuristiek in de kijker
blz. 08 – 13 Oefeningenreeks 1 peper
blz. 14 Problemen oplossen met heuristieken
blz. 15 – 18 Oefeningenreeks 2 pepers
blz. 19 – 24 Oefeningenreeks 3 pepers
blz. 25 Problemen oplossen met heuristieken
blz. 26 – 29 Oefeningenreeks 4 pepers
blz. 30 – 31 Oefeningenreeks 5 pepers
blz. 32 Problemen oplossen met heuristieken
blz. 33 – 34 Computationeel denken
blz. 35 Wiskunde in de economie
blz. 36 Overzicht oefenmateriaal
In deze consol I dat I emodule v I nd je theor I evragen en herhal I ngsvragen I n versch I llende pepercategor I eën over volgende modules :
– Module 01 : Inzicht in getallen
– Module 02 : Meetkundige objecten in het vlak
– Module 03: Data en onzekerheid
Consolidatie betekent :
– Hoe zet ik de leerstof – verspreid over vele gehelen – vast in mijn brein ?
– Ik wens mijn kennis te onderhouden en vast te houden.
– Ik wil beter weten waar we wat hebben gezien en geleerd.
– Om dit alles nog te versterken, staan de oefeningen van alle modules (verschillende onderwerpen) kriskras door elkaar.
TIP
• Verdeel je tijd goed over de verschillende onderdelen.
• Kies wijs.
• Als je twijfelt over wat je best eerst aanpakt, vraag raad aan je leerkracht.
Net als in studentenhaver zitten in deze module naast lekkere gedroogde vruchten ook gezonde zachte en harde noten.

Ken je de theorie ?
Noteer het ontbrekende woord, getal of symbool uit onderstaande zinnen.
a) Een geheel getal is een natuurlijk getal met een … , + of.
b) Een … hoek is 180° groot.
c) Om een geheel getal af te trekken van een ander geheel getal tellen we zijn … op bij dat geheel getal.
d) Bij een … maak je alleen gebruik van een passer en een liniaal.
e) Het … van een lijnstuk is het punt van dat lijnstuk dat even ver ligt van de grenspunten van dat lijnstuk.
f) … zijn twee hoeken die supplementair zijn.
g) Een veelhoek is een vlakke figuur begrensd door … .
h) Een rechte is drager van een lijnstuk of van een …
a)
Noteer het ontbrekende woord, getal of symbool uit onderstaande zinnen.
a) Een … is een rechte waarop een positieve zin door middel van een pijl is aangeduid.
b) n is de verzameling van de … getallen.
c) … is het symbool voor ‘niet groter dan’.
d) 100 is … % van 1000.
e) De … is de verhouding tussen een afstand op een tekening en de afstand in werkelijkheid.
f) Als een factor van een product (≠ 0) gelijk is aan het product van twee factoren, dan is de andere factor het … element.
a)
c)
Schrijf de zinnen in symbolen.
a) p is een natuurlijk getal.
b) De rechte s staat loodrecht op de rechte b.
c) 1,5 is geen geheel getal.
d) Het punt A ligt op de rechte p
e) De rechten p en q zijn samenvallend.
f) De rechten f en g snijden elkaar.
g) -5 is een geheel getal.
h) De lijnstukken [VW] en [PT] zijn even lang.
i) De lengte van het lijnstuk [HF] is 17 mm.
j) De punten C en F vallen samen.
k) De verzameling van de natuurlijke getallen is een deelverzameling van de verzameling van de gehele getallen.
l) Het punt P ligt niet op de rechte a
m) Het punt Q ligt in het vlak π
n) 3 is een deler van 12.
in symbolen
Ken je de wiskundige woordenschat ? Los het kruiswoordraadsel op. Je noteert IJ in 1 vakje.
Ga op zoek naar het verborgen begrip in de zacht ingekleurde vakjes.
HORIZONTAAL
2 Een hoek met hoekgrootte tussen 90° en 180° is … .
3 Bij halfrechte [AB noemen we A het ... .
6 De afstand tussen A en B noemen we ook de … van [AB] .
7 Een hoek met hoekgrootte tussen 0° en 90° is ...
10 Twee hoeken waarvan de benen in elkaars verlengde liggen zijn ...
11 Geheel getal dat zowel positief als negatief is.
12 60° is het ... van 30°.
13 ⊂
16 ∈
19 Bij 50 : 5 = 10 noem je het getal 5 de …
20 Resultaat van een vermenigvuldiging.
INKIJKEXEMPLAARDIEKEURE
VERTICAAL
1 Bij 5 + 3 = 8 noem je het getal 5 een …
2 60° is het … van 120°.
4 Natuurlijk getal dat exact twee verschillende delers heeft.
5 Resultaat van een deling.
8 Rechte die een hoek in twee even grote hoeken verdeelt.
13 ∩
9 Drie punten die op eenzelfde rechte liggen zijn ...
14 Eenheid van hoekgrootte.
15 ∪
17 Waar of vals? |AB| = |BA|
18 Bij 5 · 3 = 15 noem je het getal 5 een … .











Heuristiek in de kijker
Je kunt problemen op verschillende manieren oplossen. Soms kan het helpen door stap voor stap terug te denken. Je redeneert op een logische manier achteruit. We noemen deze heuristiek ook wel van achteren naar voor werken.
Voorbeeld
Remi denkt aan een getal, telt er 3 bij, vermenigvuldigt het resultaat met 2, trekt er dan 4 van af om tot het resultaat te delen door 7. Het resultaat dat Remi verkrijgt is 2. Aan welk getal dacht Remi? ?
Oefening 1
De gemiddelde massa van 4 zakken is 8 kg. Drie van de zakken hebben respectievelijk een massa van 10 kg, 12 kg en 8 kg. Wat is de massa van de vierde zak?
Oefening 2
Voor een priemgetallenspel zitten zeven leerlingen in een cirkel. Om de beurt zegt elke leerling, met de klok mee, een priemgetal. De eerste leerling zegt 2, de volgende 3, … De leerling die 97 zegt is de winnaar. Welke leerling moet starten zodat Elli wint?
INKIJKEXEMPLAARDIEKEURE
Oefening 3
Aan het station nemen een aatal passagiers de bus. Bij de eerste bushalte stapten 5 passagiers uit en kwamen er 8 passagiers aan boord. Bij de tweede halte stapten 6 passagiers uit, waardoor er nog 70 passagiers op de bus zaten. Hoeveel passagiers zaten er bij het vertrek aan het station op de bus?
INKIJKEXEMPLAARDIEKEURE
Oefening 4
In de kast staan kopjes gestapeld die dezelfde vorm en grootte hebben. Bepaal de hoogte van 1 kopje.


Oefening 5
Van een vierkant grasveld worden twee zijden uitgebreid met 5 meter zoals weergegeven op de tekening. Hierdoor is de oppervlakte van het veld toegenomen met 245 m2. Hoe groot was het originele veld?
Oefeningenreeks 1 peper
a) Plaats n , z en q bij dit venndiagram.
b) Noteer de onderstaande getallen op een correcte plaats in het diagram.
4; 4;4,4; 4,4; 4 1 ; 1 4 ; 4 4 en 4 4
2 3 4
In kranten en tijdschriften vind je geregeld schema’s, figuren, tabellen en diagrammen die bepaalde gegevens mooi voorstellen. Hieronder vind je een aantal voorstellingsvormen.
Verbind elke voorstellingsvormen met de correcte naam.
Gegeven : het getal 2731,08
a) Wat is de waarde van het cijfer 7 in dat getal ?
b) Welk getal is 4 tienden kleiner dan dat getal ?
c) Welk getal is 4 honderdsten groter dan dat getal ?
d) Hoeveel is 10% van dat getal ?
a) Geef 7 en 13 een correcte plaats op de getallenas.
b) Welke waarde hebben de letters A en B op deze getallenas ?
a) In een doos zitten 13 rijen met 9 potloden per rij. Hoeveel potloden zitten er in de doos?
b) Emma had 145 stickers. Ze geeft er 68 aan haar vriendin. Hoeveel stickers heeft Emma nog?
INKIJKEXEMPLAARDIEKEURE
c) Tom spaart voor een game. In januari spaart hij € 35, in februari € 42 en in maart € 50. Hoeveel heeft hij in totaal gespaard?
d) Er zijn 84 knikkers die eerlijk verdeeld moeten worden over 6 kinderen. Hoeveel knikkers krijgt elk kind?
e) In de sporthal worden 24 rijen met 15 stoelen per rij klaargezet voor een optreden. Hoeveel stoelen zijn er in totaal?
f) Lisa heeft 92 euro gespaard. Ze koopt een rugzak van 57 euro. Hoeveel geld houdt ze over?
g) Er zijn 96 stoelen in een zaal. Tijdens een evenement zijn er nog 38 plaatsen beschikbaar. Hoeveel stoelen zijn er bezet?
h) Er zijn 128 boeken die verdeeld worden over 8 planken. Hoeveel boeken liggen er op elke plank?
Maak de correcte verbindingen.
rechte AR ⬤
halfrechte [AR ⬤
⬤ [AR]
⬤ AR
⬤ [RA
⬤ [AR lijnstuk [AR] ⬤
⬤ | AR |
⬤ [RA]
⬤ RA
Als de maatbeker met 1 liter water gevuld is, zeggen we dat de maatbeker voor 100% gevuld is.
a) Kleur telkens de hoeveelheid water in de beker.
b) Vervolledig de ontbrekende notaties.
Plaats de getallen die hetzelfde resultaat hebben bij afronding op 0,1 nauwkeurig in eenzelfde kleur.
9,11 9,129,139,149,159,169,179,189,199,20
a) Teken een hoek D = 35°. b) Meet de onderstaande hoek E .
E
Bereken en schrijf je antwoord als een onvereenvoudigbare breuk.
a) 1 4 + 3 8 =
b) 2 6 + 1 3 =
c) 1 2 1 5 =
d) 2 15 + 2 3 =
e) 3 2 2 3 =
f)1 3 5 =
g) 10 8 + 3 4 = Geef door opsomming.
a) del 36 = c) del 63 =
b)8n =
a) Bepaal de coördinaat van A.
b) Kleur het gebied van het tweede kwadrant groen.
c) Plaats een punt P in het assenstelsel zodat elk coördinaatgetal negatief is.
d) Geef de coördinaat van P.
d)9n =
Het punt A heeft als coördinaat ( 2, 3) .
Hierbij is de x-coördinaat en de y-coördinaat.
Het punt B heeft als coördinaat ( -3, 1)
Hierbij is -3 de -coördinaat en 1 de -coördinaat.
Geef de coördinaat van de punten C, D en E.
Hoe noem je de hoeken α en β ?
Bereken. a) 2% van 3000 b) 20% van 140 c) 25% van 864 d) 50% van 49
17 18 19
Opa Lazlo heeft 12 875 euro gewonnen.
Hij verdeelt dit gelijk onder zijn 5 kleinkinderen.
Hoeveel euro krijgt elk kleinkind ?

Elke maand kan Emiel wat geld sparen. Het bedrag dat hij maandelijks op zijn spaarboekje stort, vind je in deze tabel terug. Bereken het bedrag dat hij gemiddeld per maand aan zijn spaarboekje toevoegt.
Mohamed koopt zeven T-shirts van 13 euro.
Hoeveel moet Mohamed betalen ?
Caro heeft 84 apps op haar tablet. Ze besluit om een derde ervan te verwijderen.
Hoeveel apps zullen nadien nog op haar tablet staan ?

Problemen oplossen met heuristieken
Hieronder vind je twee problemen. Je moet zelf een oplossingsstrategie kiezen en nagaan welke wiskundekennis je kunt gebruiken om het probleem op te lossen.
• Raadpleeg je vademecum om een gepaste heuristiek te kiezen en denk soms out of the box.
• Schrijf jouw oplossing netjes uit zodat je die kunt presenteren voor andere leerlingen.
• Vergelijk jouw oplossing met die van een andere leerling.
• Werk samen en kom tot nieuwe inzichten bij het oplossen van problemen.
Probleem 1
Op een tafel staan een grote en een kleine bokaal samen met drie pepers. Plaats de pepers in de bokalen zodat er in elke bokaal een oneven aantal pepers zit.
Gekozen heuristiek :

Probleem 2
Een getal van 3 cijfers wordt voorgesteld als + Bepaal met behulp van de gegeven som de waarde van elke peper en noteer het getal.
Gekozen heuristiek : +
Oefeningenreeks 2 pepers
a) Noteer alle mogelijke natuurlijke getallen van 2 cijfers als je alleen de cijfers 4 en 6 mag gebruiken.
b) Rangschik die getallen van groot naar klein.
c) Zoek het gemiddelde van die reeks getallen.
Maak een berekening. Vink aan wat past.
3 m + 9 mm =
a) Noteer het grootste natuurlijk getal met 3 verschillende cijfers.
b) Noteer het kleinste geheel getal met 4 verschillende cijfers.
A = {x ∣ x iseenlettervanhetwoordGETAL}
B = {x ∣ x iseenlettervanhetwoordCIJFER}
a) Noteer alle elementen van A en B in het venndiagram.
b) Bepaal door opsomming:
a) Geef 10 en 20 een correcte plaats op de getallenas.
b) Welke waarde hebben de letters A en B op deze getallenas ?
Gegeven : het punt A en de lijnstukken [ PQ] en [ KL]
Gevraagd : Construeer het lijnstuk [ AB] zodat | AB| = | PQ| en het lijnstuk [ BC] zodat | BC| = | KL|
Bepaal uit het hoofd.
a)ggd ( 8, 24) =
b)kgv ( 8, 24) =
P: de verzameling van de priemgetallen
c)ggd ( 7, 8) =
d)kgv ( 7, 8) =
R: de verzameling van de natuurlijke getallen kleiner dan 20
a) Wat betekent P ∩ R?
b) Geef P ∩ R door opsomming. P ∩ R =
Op dit staafdiagram vind je het aantal uren zonneschijn in een bepaalde week terug.
Aantal uren AANTAL UREN ZONNESCHIJN
a) Hoeveel uren scheen de zon op dinsdag ?
b) Op welke dagen was er een even groot aantal uren zonneschijn ?
c) Bereken het gemiddeld aantal uren zonneschijn per dag voor deze gegeven week.
d) Op welke dag scheen de zon het meest ?
e) Maak een staafdiagram voor de zonneschijnduur van afgelopen week in Ukkel met ICT.
Gegeven:
p1: Het cijfer van de eenheden is even.
p2: Het getal is deelbaar door 4.
a) Noteer indien mogelijk een implicatie of equivalentie.
b) Verklaar jouw antwoord.
Tekeneenhoek A1 = 65°. Teken vervolgens een tweede hoek A2 zodat hun som 110° bedraagt.
De figuur hiernaast is getekend op schaal 1 : 500. Bereken de omtrek in werkelijkheid.
Orden de getallen van klein naar groot. Noteer je antwoord door gebruik te maken van het symbool <.
a) 5656 ; 6566 ; 6656 ; 6565 ; 5565 en 5666
b)
De grafiek geeft het temperatuurverloop tussen 0 en 24 uur op een zonnige zomerdag in Geel weer.
a) Wat is de temperatuur om 8.00 uur ?
b) Wat is de temperatuur om 19.00 uur ?
c) Wat is het verschil tussen de hoogste en de laagste temperatuur ?
d) Stel een grafiek op voor het temperatuurverloop op een willekeurige dag in jouw gemeente en beantwoord de vragen opnieuw.
Temperatuurverloop in Geel
Temperatuur (°C)
Tijd (uur)
Oefeningenreeks 3 pepers
a) Noteer alle mogelijke natuurlijke getallen van 3 cijfers als je alleen de cijfers 3 en 7 mag gebruiken.
b) Zoek het gemiddelde van die reeks getallen.
c) Wat is de kans dat het getal begint met het cijfer 7 ?
d) Hoeveel procent van die getallen eindigt op het cijfer 3 ?
Bepaal de gemiddelde verkoop per week en de mediaan op basis van deze voorstellingswijze.
Verkoop bakkerij Bert
Aantal Week 1Week 2Week 3Week 4
a) Noteer het grootste negatief geheel getal met 4 verschillende cijfers.
b) Noteer het kleinste negatief geheel getal met 4 verschillende cijfers.
Op een kaartenapp zien we dat twee wegen een hoek vormen van 50°. Bepaal de andere aangeduide hoeken.
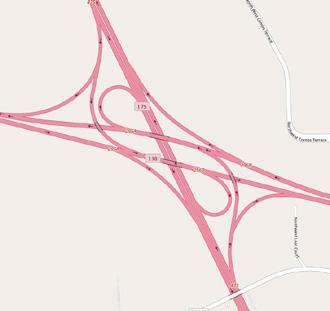
a) Geef 0 en 333 een correcte plaats op de getallenas.
b) Welke waarde hebben de letters A en B op de getallenas ?
a) Noteer de verzameling door opsomming.
A = { x ∈ n | x is een deler van 18} =
B = { x ∈ n | x is een veelvoud van 3} =
C = { x ∈ n | x is een priemgetal kleiner dan 10} =
b) Stel de verzamelingen voor in een klaverbladdiagram.
c) Geef door opsomming:
A ∩ B ∩ C =
d) Kleur de ware uitspraken.
a) Plaats de punten A( -4, 3) , B( 2, 0) en C( 1, -5) in het assenstelsel.
b) Bepaal de coördinaat van D zodat ABCD een parallellogram is.
Voor een toets wiskunde behaalden de leerlingen uit klas 1B de volgende resultaten op 20. 1413 11 10121791416 14121615199171420
Bereken het klasgemiddelde.
Antwoord : Het klasgemiddelde op de toets wiskunde is op .
Bepaal de grootte van elke hoek zonder te meten. Verklaar hoe je aan de uitkomst komt.
Mijn klantenkaart in Boekhandel Raaklijn is vol. Na tien aankopen krijg ik volgende keer 15% van het totaalbedrag om nieuwe boeken te kopen.
a) Hoeveel korting krijg ik bij mijn volgende aankoop ?
b) Hoeveel heb ik in de voorbije maanden gemiddeld per aankoop betaald ?
Celine rijdt met haar fiets aan gemiddeld 15 km per uur.
a) Welke afstand in meter legt ze af in één minuut ?

b) Hoelang fietst Celine als ze aan de gegeven snelheid 20 km heeft afgelegd?
Bekijk het fragment uit onderzoek rond schermtijd bij jongeren.
Antwoorden van 5788 jongeren op stellingen rond schermtijd
Mijn ouders besteden te veel tijd aan schermen.
Ik besteed te veel tijd aan schermen.
Niet akkoord Eerder niet akkoord
Eerder akkoord Akkoord Noch akkoord, noch niet akkoord
Bron: https://appstublieft.be/nieuwe-apenstaartjaren-cijfers-tonen-hoe-vlaamse-jongeren-met-digitale-media-omgaan/
a) Formuleer 2 vaststellingen.
b) Hoeveel jongeren vulden de bevraging in?
c) Hoeveel procent van de jongeren gaan ‘helemaal akkoord’ dat ze te veel tijd aan schermen besteden?
d) Wat is het aantal jongeren dat ‘helemaal akkoord’ gaat dat ze te veel tijd aan schermen besteden? Gebruik hiervoor de antwoorden uit b) en c).
Hoe groot is de kleinste hoek die de grote en de kleine wijzer maken om …
a) 19.00 uur ?
b) 16.00 uur ?
c) 16.30 uur ?
d) 10.30 uur ?

49
Noteer door opsomming de natuurlijke getallen met twee cijfers die een priemgetal zijn en waarbij zowel het cijfer van die eenheden als de tientallen ook priemgetallen zijn.
INKIJKEXEMPLAARDIEKEURE
Aan een aantal mensen werd gevraagd om een puzzel op te lossen. Er werd bijgehouden hoeveel minuten ze hiervoor nodig hadden.
Puzzeltijd
a) Aan hoeveel mensen werd dit gevraagd ?
b) Bereken de gemiddelde tijd om deze puzzel op te lossen.
c) Wat is de betekenis van de modus in deze context ?
Tijd (in min.)

Problemen oplossen met heuristieken
Hieronder vind je twee problemen. Je moet zelf een oplossingsstrategie kiezen en nagaan welke wiskundekennis je kunt gebruiken om het probleem op te lossen.
• Raadpleeg je vademecum om een gepaste heuristiek te kiezen en denk soms out of the box.
• Schrijf jouw oplossing netjes uit zodat je die kunt presenteren voor andere leerlingen.
• Vergelijk jouw oplossing met die van een andere leerling.
• Werk samen en kom tot nieuwe inzichten bij het oplossen van problemen.
Probleem 3
Vicky gooit met drie bijzondere dobbelstenen. Op de zijvlakken van de eerste dobbelsteen staan de getallen 1, 1, 3, 3, 5 en 5. Op zijvlakken van de tweede dobbelsteen staan de getallen 2, 2, 4, 4, 6 en 6. Op de zijvlakken van de derde dobbelsteen staan de getallen 2, 2, 3, 3, 4 en 4. Hoe groot is de kans dat de som van de getallen op de door Vicky gegooide dobbelstenen oneven is ?
Gekozen heuristiek :


2 4 3 13 246

Probleem 4
Teken 4 lijnstukken zonder je potlood op te heffen zodat de 9 punten met elkaar verbonden zijn.
Gekozen heuristiek :
Oefeningenreeks 4 pepers
Gegeven: een orthonormaal assenstelsel
a) Geef de coördinaat van A, B, C en D.
b) Bepaal de waarde van a als de oppervlakte van de rechthoek ABCD 35 is.
c) De oppervlakte van ABCD is even. Geef door opsomming alle mogelijke waarden van a.
In een kast zitten 6 groene en 8 rode T-shirts. Hoeveel T-shirts moet je minstens uit de kast halen om zeker te zijn dat er twee van dezelfde kleur bij zijn ?
Je mag niet kijken.
Arwèn stort 50% van haar zakgeld op haar spaarrekening. Daarna heeft ze 1/4 van het resterend bedrag nodig om een broodje van 5 euro te kopen. Hoeveel zakgeld had Arwèn in het begin?
Yarno fietst elke dag naar school. Hij houdt bij hoeveel tijd hij hiervoor nodig heeft.
Bij de afgelopen 10 tijdsmetingen doet hij volgende vaststellingen :
• de gemiddelde tijd is 14 min ;
• de modus is 12 min ;
• de mediaan is 13 min ;
• de variatiebreedte is 9 min.
a) Geef een mogelijke dataset zodat deze centrum- en spreidingsmaten kloppen.
INKIJKEXEMPLAARDIEKEURE
b) Houd gedurende 10 dagen je verplaatsingstijd naar school bij en bereken de modus, het gemiddelde, de mediaan en de variatiebreedte van je metingen.
54 mand 1mand 2
Op tafel staan twee manden met appels. De gemiddelde massa van een appel in de eerste mand bedraagt 200 gram, in de tweede mand 160 gram. Er wordt één appel uit mand 1 overgebracht naar mand 2 en één appel uit mand 2 overgebracht naar mand 1. Onder welke voorwaarden kan je met zekerheid zeggen dat de gemiddelde massa van een appel in beide manden is toegenomen?

We willen het verband onderzoeken tussen de grootte van een hoek A en de grootte van het complement B van deze hoek.
a) Vervolledig de tabel en teken een lijngrafiek die het verband weergeeft tussen deze groottes.
b) Onderzoek het verband voor twee supplementaire hoeken. Maak een tabel en teken de lijngrafiek.
Messi (M), Ronaldo (R) en Ibrahimovic (I) zijn de keeper en de verdedigers al voorbij.
Ze staan dus voor een leeg doel, maar de ene staat veel dichter bij het doel dan de andere. Wie van de drie heeft de grootste kans om te scoren ? Wie heeft de kleinste kans ?
Verklaar je antwoord. DOEL I M R
Welke getallen voldoen aan alle voorwaarden?
x ∈ ,6 < x ⩽ 24én x ∈ del48
Geef door opsomming alle mogelijke waarden van a, met a ∈ n en 0 < a < 11 …
a) zodat ggd ( a, 15) = 1 a =
b) zodat ggd ( a, 18) = 1 a =
c) zodat ggd ( a, 12) = 2 a =
Gegeven: b is de bissectrice van APB
Gevraagd:
a) Teken het complement van APB .
b) Teken een nevenhoek van APB .
Oefeningenreeks 5 pepers
Verklaar je antwoord. 60
Het Chinees en Japans talstelsel gebruiken volgende symbolen.
Voorbeeld
四千九百八十三
4 1000 + 9 100 + 8 10 + 3 = 4983
a) Zet volgende getallen om naar ons tiendelig talstelsel.
• 九九九九 千百十
• 三二四八 千百十
• 七百六十五
b) Schrijf de volgende getallen in het Chinees talstelsel.
• 873
• 2591
• 7200
Maak een passende tekening.
• POJenJOMzijnnevenhoeken.
KOMishetcomplementvanPOJ.
• Bij een proef worden 10 temperatuurmetingen uitgevoerd. De gemiddelde temperatuur is 18°C, de mediaan is ook 18°C en de variatiebreedte bedraagt 5°C. De proef wordt herhaald met een nieuwe reeks van 10 metingen. In deze tweede reeks blijft het gemiddelde 18°C, maar de variatiebreedte is nu 6°C. Is het volgende besluit correct? “Bij de tweede proef ligt de minimumtemperatuur lager én de maximumtemperatuur hoger dan bij de eerste proef.”
WAAR/NIET WAAR
Gegeven:
A: de delers van 48
B: de priemgetallen kleiner dan 20
C: de deler van 60
D: de natuurlijk veelvouden van 3
TIP
Noteer verzamelingen door opsomming.
a) Plaats de elementen in het venndiagram.
b) Arceer de gebieden die leeg zijn in het rood.
c) Omschrijf telkens het leeg gebied.
Gebied 1: In symbolen:
In woorden:
Gebied 2: In symbolen:
In woorden:

Problemen oplossen met heuristieken
Hieronder vind je twee problemen. Je moet zelf een oplossingsstrategie kiezen en nagaan welke wiskundekennis je kunt gebruiken om het probleem op te lossen.
• Raadpleeg je vademecum om een gepaste heuristiek te kiezen en denk soms out of the box.
• Schrijf jouw oplossing netjes uit zodat je die kunt presenteren voor andere leerlingen.
• Vergelijk jouw oplossing met die van een andere leerling.
• Werk samen en kom tot nieuwe inzichten bij het oplossen van problemen.
Probleem 5
Kies zeven verschillende getallen uit -4, -3, -2, -1, 0, 1, 2, 3, 4 en 5.
Maak een gedurige som van deze getallen.
Hoeveel verschillende uitkomsten zijn er mogelijk ?
Gekozen heuristiek :
Probleem 6
Naomi en Tristan maken samen lekkere pizza’s klaar. Om te bepalen wie straks de afwas zal doen, beslissen ze om een spelletje te spelen. Op tafel liggen 11 rode pepers. Naomi en Tristan mogen om beurt 1, 2 of 3 pepers nemen. Wie als laatste een of meerdere pepers moet nemen, verliest en doet de afwas. Hoe moet Naomi haar pepers nemen om zeker te zijn dat ze het spelletje zal winnen ?
Gekozen heuristiek :


Computationeel denken
Flowchart
Een flowchart helpt je om stap voor stap na te denken over een probleem, net zoals een computer dat doet. In een flowchart wordt er vaak pseudocode, geen echte programmeercode, gebruikt.
Bij wiskunde kun je flowcharts gebruiken om berekeningen of redeneringen op een logische manier uit te voeren. Je volgt dan de spelregels van de wiskunde en je kunt gebruik maken van definities, eigenschappen… om geen fouten te maken. Dit maakt moeilijke problemen overzichtelijk en makkelijker op te lossen. Zo weet je altijd welke stap je eerst moet doen en wat daarna komt!
a) Welke handelingen worden uitgevoerd in de flowchart hiernaast?
Maak: de variabelen a, b en som aan.
Voer een waarde in voor a en b
som = a + b
Toon(“De som van”, a, “en”, b, “is”, som, “.”)
Start Stop
b) Ken aan de variabele a de waarde 7 toe en aan de variabele b de waarde 11. Welke uitvoer verkrijg je?
Merk op
Een variabele is van een bepaald type. Wanneer je tekstueel programmeert kun je aangeven van welk type de variabelen a, b en som zijn. Wanneer je dan een invoer doet, wordt er een geheel getal als invoer verwacht.
Opdracht 1: Maak een flowchart zodat de opdracht kan worden uitgevoerd.
a) Het product van twee getallen laten berekenen en uitvoeren.
b) Het gemiddelde van drie getallen laten berekenen en uitvoeren.
Opdracht 2: Bekijk aandachtig de flowchart en beantwoord de vragen.
a) Voer voor a het getal 6 in en b het getal 3 in. Kleur jouw weg in de flowchart.
b) Leg uit wat er gebeurt bij de eerste ruitvormige pseudocode.
Start
Maak de variabelen a en b.
Voer een waarde in voor a en b.
Toon(“Het grootste getal is” a)
Toon(“De getallen zijn gelijk.”) Toon(“Het kleinste getal is b.”) a > b a = b
INKIJKEXEMPLAARDIEKEURE
Stop
c) Wat zal er gebeuren als je “nul” en “twee” invoert?
Opdracht 3: Maak een flowchart zodat de opdracht kan worden uitgevoerd.
a) Bepaal of het getal deelbaar is door 10.
b) Bepaal of het getal deelbaar is door 6.
Wiskunde in economie
A) Procenten
De laatste dag van de solden krijg je bovenop de kortingsprijs nog eens 10% extra korting. Bereken voor elke kortingsbol hoeveel korting je uiteindelijk krijgt.
INKIJKEXEMPLAARDIEKEURE
B) Wisselkoers
Dollar Euro Koers
Euro
a) Zoek de wisselkoers op en vul het schema aan.
b) Hoeveel Amerikaanse dollar is 1000 euro waard ?

c) Hoeveel euro is $ 500 ?
C) Data en lijndiagram
De BEL20–index is een Belgische aandelenindex waarin twintig aandelen noteren van bedrijven die actief zijn in België.
a) Welke informatie haal je uit deze lijngrafiek ?
b) Is dit een eerlijke grafiek ? Verklaar je antwoord.
c) Welke trend stel je vast voor deze maand ?
Waarde in euro
BEL20-index
Overzicht oefenmateriaal
•
•
Auteurs Björn Carreyn, Filip Geeurickx en Roger Van Nieuwenhuyze
Eerste editie - Bestelnummer 94 606 0012 (module 04 van 17)
ISBN 978 90 4865 054 5 - KB D/2025/0147/100 - NUR 126 - Thema YPMF
Illustrator Jona Jamart - Design en lay-out die Keure
Verantwoordelijke uitgever die Keure, Kleine Pathoekeweg 3, 8000 Brugge
RPR 0405 108 325 - © Copyright die Keure, Brugge
