Primary Maths for Scotland - Overview by Collins

The first maths mastery programme developed specifically for Scotland to plan routes through the Es and Os and help raise attainment for maths in Scotland

NEW Problem Solving Packs

Primary Maths for Scotland Teacher Guides

Primary Maths for Scotland

1st Level Maths

2nd Level Maths

Teacher Guide

Primary Maths for Scotland Aligned to CfE benchmarks

Teacher Guide Covers.indd 4

Aligned to CfE benchmarks

Teacher Guides 27/02/2019 10:47

978000834895 • 10th Sept • £100 9780008348946 • 26th Dec • £100 Teacher Guide Covers.indd 7

27/02/2019 10:47

Planning and teaching support manuals to accompany Primary Maths for Scotland Textbooks Primary Maths for Scotland

Primary Maths for Scotland

1st Level Maths 2nd Level Maths ensure pupils develop conceptual understanding alongside 2nd Level Maths Teacher Guide procedural

Teacher Guide fluency

Assessment Pack

provide ideas for active learning identify potential misconceptions and how to address them save time, with key vocabulary and resource lists included Aligned to CfE benchmarks

Aligned to CfE benchmarks

match the textbooks and their teaching to the CfE benchmarks

Teacher Guide Covers.indd 4

Aligned to CfE benchmarks

27/02/2019 10:47

978000834895 • 10th Sept • £100 9780008348946 • 26th Dec • £100 Teacher Guide Covers.indd 7

27/02/2019 10:47

Contact your local rep today to find out more:

Planning and teaching support to 188 154 • claire.mcauley@harpercollins.co.uk Claire • Eastmanuals Scotland • 07557 accompany Primary Maths for• West Scotland Christine Scotland •Textbooks 07825 116 401 • christine.stein@harpercollins.co.uk PMfS flyer_update oct-21_hi-res.indd 1

ensure pupils develop conceptual understanding alongside procedural fluency

Order from www.kelvinbooks.co.uk

22/02/2022 13:07

Textbooks

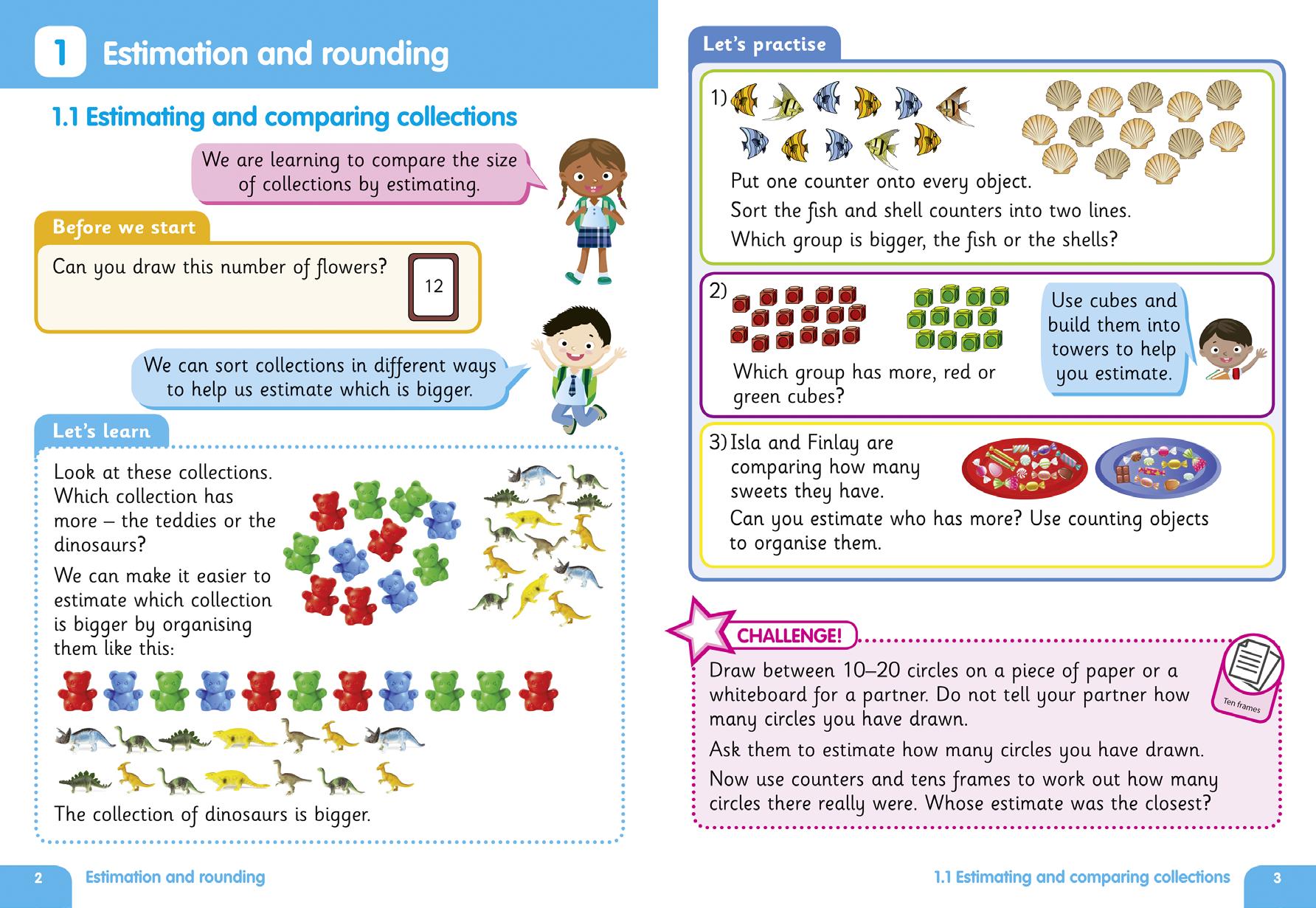
There are three textbooks at First Level and three at Second Level, each helping pupils to master maths at their own pace.

Let’s practise sections provide opportunities to consolidate conceptual learning and develop procedural fluency

Characters introduce learning outcomes and lead pupils through the maths

Each unit is tightly focused on one objective, following small steps of progression

Challenge questions give every child the chance to develop their problem solving and investigation skills

PMfS flyer_update oct-21_hi-res.indd 2

22/02/2022 13:07

Teacher Guides

Teacher Guides support teachers to plan and teach the CfE maths syllabus.

Provides an explanation of the key content of the topic, and the conceptual learning which should Estimation and rounding 2A and rounding 2A takeEstimation place

Shows the coverage of the CfE 1 Estimation and rounding 1 Estimation and rounding and Benchmarks within this section Estimation and rounding 2A Estimation and rounding 2A

ConceptualConceptual content content

Section overview Section overview Textbook 2A units

Textbook 2A Review units units

Prior learning Review units

Unit 1.1 Rounding whole numbers to the nearest 10

1C Unit 1.1 units 1.1, 1.2whole Rounding and 1.6 to the numbers

2-01a • 1C I can read and write numbers withand upwrite MNU • I can read numbers with

nearest 10

to 4 digits units 1.1, 1.2

1C Unit 1.2 units 1.1, 1.2whole Rounding and 1.6 to the numbers nearest 100

• • •

Unit 1.3 Rounding decimal fractions to the nearest whole number

1C Unit 1.3 units 1.1, 1.2 Rounding and 1.6 fractions decimal to the nearest whole number

• • • •

Unit 1.4 Estimating the answer using rounding

1C Unit 1.4 units 1.1, 1.2 the Estimating and 1.6 using answer rounding

to 4 digits

numbers to the within a number showswithin its value a number shows its value nearest 1000, I know the meaning •of Ieach digit know thein meaning of10 each 000digit and in the ones, tens, hundreds theand ones, tens, hundreds 100and 000. thousands columns thousands columns • Rounds decimal fractions to the I can read and write numbers withand up write numbers 1C • I can read with up nearest whole to 4 digits units 1.1, 1.2 to 4 digits number, to one and 1.6 I understand that the• place of a digit I understand that the place of aplace digit decimal within a number showswithin its value a number showsand its two value decimal I know the meaning •of Ieach digit know thein meaning ofplaces. each digit in the ones, tens, hundreds theand ones, tens, hundreds and thousands columns thousands columns • Applies knowledge I can read and write decimal fractions 1C of rounding to • I can read and write decimal fractions to one decimal units 1.1, 1.2 place to one decimal place give an estimate and to a calculation I can1.6 count in decimal amounts to one • I can count in decimal appropriate amounts to one to decimal place forwardsdecimal and backwards place forwards and backwards the context. I understand the value each digit the value of each digit • Iofunderstand in decimal fractions up in todecimal one decimal fractions up to one decimal place place

Benchmarks/ Es&Os MNU 2-01a

•

Rounds whole numbers to the nearest 1000, 10 000 and 100 000.

•

Rounds decimal fractions to the nearest whole number, to one decimal place and two decimal places.

•

Applies knowledge of rounding to give an estimate to a calculation appropriate to the context.

I can round whole numbers the whole numbers to the • I can to round nearest ten and the nearest hundred nearest ten and the nearest hundred

• 1C I can read and write numbers withand up write numbers with up • I can read • • •

Benchmarks/ Es&Os

1.6 • place Rounds whole • and I understand that the• place of a digitthat the I understand of a digit

•

Unit 1.2 Rounding whole numbers to the nearest 100

Prior learning

to 4 digits units 1.1, 1.2 to 4 digits and 1.6 I understand that the• place of a digitthat the place of a digit I understand within a number showswithin its value a number shows its value I know the meaning •of Ieach digit know thein meaning of each digit in the ones, tens, hundreds theand ones, tens, hundreds and thousands columns thousands columns I can round numbers•toI the can nearest round numbers to the nearest ten or hundred ten or hundred

In daily life we oftenInround to allow usnumbers to easily to work with andwork to check daily numbers life we often round allow us them to easily with them and to check answers. It is important that pupils have a clear of theunderstanding numerals theyofare answers. It is important thatunderstanding pupils have a clear the numerals they are working with and their value to be and abletheir to estimate They also need to They also need to working with value toand be round able toeffectively. estimate and round effectively. understand why we round and estimate through a wide rangethrough of contexts relevant understand why weproblems round and estimate problems a wide range of contexts relevant to daily life. to daily life. It is important that the children to use number lines, (as wellnumber as a range of other materials to of other materials to It is important that the children to use lines, (as well as a range represent numbers visually if needed) to visually allow them to explore howthem and why we round represent numbers if needed) to allow to explore howupand why we round up or down. In this way, or they can In also learn visualise these materials to help them make an down. this way,tothey can also learn to visualise these materials to help them make an active decision on rounding for themselves, ratherfor than simply following a rule. active decision on rounding themselves, rather than simply following a rule. For example, if we want round 382 towant the nearest hundred: Forto example, if we to round 382 to the nearest hundred: ________________________________________________________382________________ ________________________________________________________382________________ Children need to learnChildren to identify multiples on either of side, find theonhalfway pointfind the halfway point need to learnof tohundred identify multiples hundred either side, between them and use this understanding decide whether toto round up whether or down.to round up or down. between them and usetothis understanding decide

Resources Resources

• • • • •

Numeral cards 0 -• 100 Numeral cards 0 - 100

•

Money - £10, £100 and • notes Money - £10, £100 notes and £1 coins £1 coins

Round

•

Estimate

• Decimats • Arrow cards Physical materials• toPhysical represent materials to represent Arrow cards

numbers such as cubes or place numbers such as cubes or place value sticks value sticks

Promotes use of 3 3 mathematical language and provides definitions in the online glossary

A wide range of resources are provided online Estimation and rounding

Estimation

Misconceptions Potential misconception

Addressing the misconception

The pupil might not understand which digit in the number to look at to determine whether to round up or down.

•

e.g. 829 rounded to the nearest 100 is 900 (pupil is using last digit to round incorrectly)

Show number on a number line and ask them which multiple of 10 the number is between and how they decide which multiple is nearer to the number. Ask them which digit helps them decide.

• • • • • •

•

Use materials to represent the amounts. This could be cubes, arrow cards, counters or money.

•

Refer back to Place Value Units

•

The pupil might not understand the convention for rounding up if a digit is five or more.

•

Show number on a number line and allow them to explore which multiple is nearer on either side. Explain that we usually round up when the digit is five or more.

•

The pupil always rounds up, e.g. 62 rounded to the nearest ten is 70.

•

Show number on a number line and ask them which multiples the number is between and how they decide which multiple is nearer to the number. Ask them which digit helps them decide.

The pupil thinks rounding is just changing the numbers to zero, e.g. 587 rounded to the nearest 100 is 500

•

Show number on a number line and ask them which multiples the number is between and how they decide which multiple is nearer to the number. Ask them which digit helps them decide.

The pupil might not understand what each digit in a number represents

Lists the pre-requisite knowledge required to embark on the unit

Helps you identify and address misconceptions associated with the units

•

Decimats

Signposts units to review if children do not possess pre-requisite knowledge and skills

Key vocabulary Key vocabulary

Number lines 0 -100, 0 - 1000lines in 0 -100, 0 - 1000 • in Round • Number a range of increments – ones, a range of increments – ones, • Estimate tens, hundreds, tenths tens, hundreds, tenths

Teaching ideas Unit 1. Rounding whole numbers to the nearest 10 • • • • • •

Take a pack of numeral cards to 100 and shuffle them. Ask a child to pick one and tell you the number. Find the numeral on a number line to 100. Then ask what multiples are on either side of the number – can they find them on the number line? For example, if you picked 32, the multiples of 30 and 40 are the multiples of ten either side. Which is nearer to the number?

In this case 32 is nearer to 30, so we round down. Repeat with lots of different examples, rounding up and down. Discuss what happens if we have a number ending with 5 – explain that we u in this case, although it depends on the particular context. For instance if we were measuring materials to build a fence there may b we would always round down to make sure the length would not be between posts. Or if we wanted to buy tickets that cost £10 each and a group had £65, we round down to the nearest ten because we can’t use the £5 to buy anothe So there may be some particular contexts where we would always round d up, but otherwise the rule is that for numbers 5 and over we round up. Ask for examples why we might round to the nearest ten in daily money, directions. Extend to 3 digit and 4 digit numbers once confident.

Unit 2. Rounding whole numbers to the nearest 100 • •

Check understanding of rounding to the nearest 10 for a range of number Ask questions such as “What is 88 rounded to the nearest ten? How about 739 do I look at to decide? If I think of a number and round it up to 50 – what could numbers be?” Draw an empty number line on the whiteboard, e.g._______________379 Ask children what the multiples of 100 on either side would be. Ask them to write them in on the number line. Which multiple of 100 is nearer to 379? Discuss how they know. Explain that we round to the nearest 100 by finding the closest multiple o Repeat with different examples. Discuss what happens when a number ends in 50 – explain that we usua this case, although it depends on the particular context. Extend to 4 digit numbers once confident.

• Each unit offers ideas, • advice and guidance • for•• teaching the topic • • • •

PMfS flyer_update oct-21_hi-res.indd 3

22/02/2022 13:07

Early level

Early Level Record Book The record book can be used to assess achievement of the early level benchmarks and to demonstrate mastery of early level.

More or fewer?

Contents Curriculum organiser

Curriculum coverage

Page name

Page

Estimation and rounding

MNU 0-01a

More or fewer?

Colour match

Regular patterns

MNU 0-02a

Join me up

MNU 0-04

Me first!

Higher and faster

Collections

How many?

Party time

Colour the facts

Finding totals

Something is missing

Double up

Farm calculations

The bigger half?

Fair sharing

Number and number processes

Tick box contents page to easily identify what has been mastered

Fractions, decimal fractions and percentages

MNU 0-07a

Money

MNU 0-09a

Show me the money

Time

MNU 0-10a

What is going on?

Tick tock

Measurement

MNU 0-11a

Patterns and relationships MTH 0-13a

Measure me

How many?

Dancing patterns

Carry on please

Properties of 2D shapes and 3D objects

MTH 0-16a

Shape shift

Angle, symmetry and transformation

MTH 0-17a

This way

MTH 0-19a

Symmetry

Data and analysis

MNU 0-20a

Sorting toys

MNU 0-20b

Data drop

MNU 0-20c

Data drop

Completed

Date completed

Objective

I have developed a sense of comparing collections.

Coloured question boxes for easy navigation

Teacher’s notes 1) Tick which collection has the most in it. 2) Are there more bananas or apples? 3) Circle which collection has ‘fewer than’ the other collection?

Early Level Record Book V2b.indd 2

16/12/2019 15:06

Early Level Record Book V2b.indd 3

16/12/2019 15:06

Early Level Digital Pack The Digital Pack can be used with the whole class to demonstrate concepts, to embed knowledge and to practice key skills or can be set up on tablets, computers or whiteboards for group work, as invitations to play or as part of a learning carousel.

26 maths tools to support teachers in demonstrating tricky mathematical concepts

9 maths games that can be played at different levels

6 animated maths songs to embed key skills, such as counting back from 10 The primary maths mastery programme for Scotland

PMfS flyer_update oct-21_hi-res.indd 4



22/02/2022 13:07

Assessment Packs

Assessment packs are photocopiable resources that can be used both as a diagnostic tool to identify children requiring more support or challenge and to record and report children’s attainment. Supporting resources are available to download online.

Yearly progress checks help identify areas for improvement

Yearly progress check 2: end of P1 Teacher instructions Context

End of early level assessment 1

Explain to the children they are going on a space adventure with lots of maths problems to solve. The questions can be done in the suggested groupings or all together. Work with a small group of children at a time so that you can observe the strategies each child uses. Questions 7, 8 and 10 need to be done one-to-one and recorded on the child’s answer sheet. Resource sheets are provided.

Dinosaurs

Suggested grouping of questions

Context

1–7 • 8–12 • 13–16 • 17–18 • 19–20 • 21–23 • 24–26 • 27–29

Investigating Dinosaurs is a very popular topic in the Early Years. This assessment is suitable for use with children who have carried out class-based topic work relating to dinosaurs. Resources and materials previously used within the topic (concrete, pictorial and in story form) will provide familiar contexts and enable children to demonstrate their understanding and apply their knowledge. However, some of the tasks could be used without prior knowledge of dinosaurs.

Resources Resources provided online: Dot cards 1–10 Alien pictures • Gem resource sheet

Resources Resources provided online: A range of 2D shapes • Pictures of dinosaurs • Dinosaur wrapping paper Resources needed and available in the setting: 3D toy dinosaurs • Selection of fiction and non-fiction books pertaining to dinosaurs • Word bank of dinosaur names

Questions 1. Look at the numbers in the rockets. Write in the missing numbers. 2. Look at the numbers in the spaceships. Write in the missing numbers. 3. Write the following numbers in the moons – thirteen, zero, twenty, twelve, eight.

Tasks

Es & Os

Benchmarks

4. Look at the numbers on the aliens. Rewrite the numbers in order from the biggest to the smallest.

Task 1 Dinosaur sort

MNU 0-20b I can match objects, and sort using my own criteria, sharing my ideas with others.

•

Uses knowledge of colour, shape, size and other properties to match and sort items in a variety of different ways.

5. Look at the planets. Write in the missing numbers before, after or in-between the given numbers.

Task 2 Describe and design a dinosaur

MNU 0-02a I have explored numbers, understanding that they repesent quantities, and I can use them to count, create sequences and describe order.

•

Uses one-to-one correspondence to count a given number of objects to 20. Asks simple questions to collect data for a specific purpose. Collects and organises objects for a specific purpose. Applies counting skills to ask and answer questions and make relevant choices and decisions based on the data. Contributes to concrete or pictorial displays where one object or drawing represents one data value, using digital technologies as appropriate. Recognises, describes and sorts common 2D shapes and 3D objects according to various criteria; for example, straight, round, flat and curved.

7. The astronaut can count up to thirty. Can you count up to thirty? Please start at fourteen.

• •

MNU 0-16a I enjoy investigating objects and shapes • and can sort, describe and be creative with them. •

•

End-of-level assessments check that pupils have mastered one level before moving to another

6. Count how many aliens there are, write the total in the box.

8. a Give the child 18 aliens (toys or cut outs from the resources bank). Count the aliens. How many aliens are there? Now write the total in the box. b Now move the aliens into a circle. How many aliens are there? 9. Count each alien’s treasure and write the total in the box. Discuss why the third alien might be looking glum. Can the child explain that zero means there are none? 10. Show the children some dot cards to 10; regular dot patterns (five-wise ten-frames; pair-wise ten-frames; domino patterns) and irregular dot patterns (see resource pack). Show each card for a couple of seconds and ask How many dots are there? How do you know? How did you see the 7? etc. 11. Ask the child Look at the space coins here. Point to pile A. How many coins do you think there are (without counting)? Now look at these space coins. Point to pile B. Do you think there are more coins or less coins? Circle the correct answer. Ask the child to explain their thinking. Now count the coins in each pile to check your guess. Discuss how accurate their estimates were.

279623 Primary Maths for Scotland Early Level AP_Pg-00i_62.indd 4

279623 Primary Maths for Scotland Early Level AP_Pg-00i_62.indd 39

Early level yearly progress check 2: record sheet

24/07/20 6:53 PM

•

Add the names of the children in the group/class to the top of columns 3-12. Use multiple sheets depending on the size of your class. Mark each child as they complete their early level yearly progress check. Suggested coding is: A. Chose an appropriate strategy/method and used it correctly

•

Yearly progress check 2: marking guidance Topic benchmarks/ Es & Os

Question Answers and marking guidance

Number – order and place value MNU 0-02a

Answers and marking guidance is given 279623 Primary Maths for Scotland Early Level AP_Pg-00i_62.indd 29

PMfS flyer_update oct-21_hi-res.indd 5

24/07/20 6:52 PM

B. Chose an appropriate strategy/method but used it incorrectly or made an error in calculation C. Chose an inappropriate strategy/method or did not attempt the question

Answer: 5, 6, 7, 8, 9, 10, 11, 12 and 22, 23, 24, 25, 26, 27, 28, 29 On track • The child writes each missing number correctly and completes the forward sequence accurately and confidently. Further learning required • The child omits a number or numbers, especially when crossing a decade or in the early teens. • They mix up the number sequence. • They reverse the digits when writing some numbers from 12 to 30; for example, the child writes 15 as 51. • They require a visual support – for example, a number track – to help them complete the task. On track • The child writes each missing number correctly and completes the backwards sequence accurately and confidently. Further learning required • The child omits a number or numbers, for example when bridging 10. • They mix up the number sequence. • They reverse the digits when writing some numbers from 20–10; for example, the child writes 15 as 51. • They require a visual support – for example, a number track – to complete the task. On track • The child will immediately link each oral number word with its corresponding numeral and write it correctly. Further learning required • The child may be able to connect the oral number word with its symbol for one-digit numbers but find two-digit numbers more challenging, most commonly reversing digits; for example, writing 13 as 31. • They require a visual support – for example, a number track – to complete the task. On track • The child understands that the numbers symbolise quantities and can use this knowledge to confidently order the numbers. Further learning required • The child regards each digit in the numbers 12 and 19 as separate and so orders the numbers as follows: 1, 1, 2, 5, 8, 9. • They disregard the ‘ones’ digit in 2-digit numbers and so believe that 12 and 19 have the same value and are both ‘the smallest number’. • They need to use the 0–20 counting sequence to order the numbers. • They require a visual support – for example, a number track – to complete the task.

Question

Domain

MNU 0-02a

MNU 0-01a

MNU 0-03a

15a

MNU 0-07a

15b

MNU 0-07a

MNU 0-03a

MNU 0-13a

MNU 0-02a

MNU 0-03a

MNU 0-16a

22a

MNU 0-09a

22b

Record sheets allow teachers to monitor progress

MNU 0-09a

MNU 0-10a

24a

MNU 0-11a

24b

MNU 0-11a

24c

MNU 0-11a

25a,b,c

MNU 0-17a MNU 0-19a

MNU 0-20a MNU 0-20b

29a, b, c

MNU 0-20a MNU 0-20b

279623 Primary Maths for Scotland Early Level AP_Pg-00i_62.indd 38

24/07/20 6:53 PM

22/02/2022 13:07

Problem Solving Packs

Flexible resources that can be used to teach problem solving strategies and provide a readymade bank of rich problem solving activities

Number, Money and Measure

Cuttings

Let’s go!

Experiences and Outcomes •

I can use my knowledge of the sizes of familiar objects or places to assist me when making an estimate of measure. (MNU 2-11a)

•

I can use the common units of measure, convert between related units of the metric system and carry out calculations when solving problems. (MNU 2-11b)

•

I can explain how different methods can be used to find the perimeter and area of a simple 2D shape or volume of a simple 3D object. (MNU 2-11c)

Before they start...

Resources •

Centimetre square paper and scissors

•

Some pre-cut 6 cm by 4 cm rectangles and the outline of a 22 cm by 10 cm rectangle drawn on centimetre square paper.

•

Pupils need to be able to work with dimensions given in centimetres.

•

Pupils need to know how to calculate the area of a rectangle.

4 cm

10 cm

6 cm

4 cm

6 cm

Let’s Go give pupils working below agerelated expectations an What is the maximum number of 6 cm by 4 cm rectangles that can be cut from the 22 cm by 10 cm piece of plastic? Show how this can be done. enabling prompt. There Enabling prompt is an extension activity Pupils who are struggling to make a start on the problem may be encouraged to draw a 22 cm by 10 cm rectangle, or be given the rectangle already drawn on centimetre square paper. They can also be givenfor those working above some pre-cut 6 cm by 4 cm rectangles. The following prompts will help pupils to get started on the problem, with the teacher pointing to pupils’ diagrams as appropriate: age-related expectations • I wonder how many of these small rectangles can be fitted into the large one? 4 cm

22 cm

6 cm

• •

If we turn these ones around I wonder if we can fit in any more? Can you fit any more rectangles into this space?

Extension activity Let’s go!

Amman and Isla have a different rectangular piece of plastic. It measures 28 cm by 22 cm. They are going to cut out smaller rectangles measuring 10 cm by 6 cm from their piece of plastic so that some larger rips can be repaired.

When introducing the problem, the teacher can pose the question “Why do Findlay and Nuria want to cut the maximum number of rectangles?”. This will generate some discussion of reducing waste.

6 cm

Finlay and Nuria are repairing some small rips in the plastic covering of the school polytunnel. They have a rectangular piece of plastic measuring 22 cm by 10 cm which they intend to cut into smaller rectangles to use as patches. The smaller rectangles will each measure 6 cm by 4 cm. Finlay and Nuria want to cut the maximum number of 6 cm by 4 cm rectangles from the larger 22 cm by 10 cm rectangle.

10 cm

22 cm

6 cm

10 cm

6 cm

10 cm

28 cm

What is the maximum number of 10 cm by 6 cm rectangles that can be cut from the 28 cm by 22 cm piece of plastic? Show how this can be done.

Before They Start sections ensure pupils have the prerequisitie knowledge and skills they need before completing the problem

Second Level samples.indd 64-65

21/09/2021 14:09

Number, Money and Measure

Let’s discuss!

Let’s check!

When a range of solutions have been offered, the teacher should begin to facilitate discussion of these using prompts like: • Do all of the rectangles need to be lying the same way? •

Let’s Check gives solutions to the problem

✔

9 smaller rectangles can be cut out in this way:

If you arrange the rectangles in a different way, can you cut more out?

Using a visualiser, or similar, to display different solutions for discussion will be useful. The teacher can use a number of pre-cut 6 cm by 4 cm rectangles and the outline of a 22 cm by 10 cm rectangle to model different solutions and to demonstrate how moving the smaller rectangles around within the outline of the larger rectangle can result in different solutions. Some pupils may see the relationship between the dimensions of the smaller rectangle and the larger rectangle and use this as they decide where to place the smaller rectangles within the larger rectangle. Some pupils may work with areas immediately, using number facts to calculate the area of the large rectangle and the area of the small rectangle then dividing. This would provide an opportunity to discuss the real-life context and emphasise the importance of showing how the smaller rectangles can be cut out.

Note that rotations of this solution might be offered. Two examples are shown below. This provides valuable opportunities to discuss the real-life context.

If the most efficient solution (fig. 1) is not reached, it is likely that solutions like fig. 2 will be offered as the ‘best’ way to cut out the rectangles.

Let’s Discuss gives pupils different strategies to solve the problem independently, in pairs or groups. There are prompts for teachers as well as methods pupils may use

In the extension activity, 10 smaller rectangles can be cut out as shown here. Note that this is the same solution rotated.

Fig. 1

Fig. 2

For some pupils this might be a reasonable conclusion to the problem. For others though the teacher might direct the discussion towards the area ‘left over’ to encourage pupils to see that there may be a more efficient solution. Prompts like these may be useful: •

Do you think there is enough plastic left over to make another rectangle? How can you check this?

•

It is interesting that 6 cm and 4 cm added together make 10 cm (and/or 6 cm + 6 cm + 6 cm + 4 cm makes 22 cm and/or 6 cm + 4 cm + 4 cm + 4 cm + 4 cm makes 22 cm)

Some pupils might ask if the unused pieces of plastic can be collected and used to repair a rip. The teacher might use this as an opportunity to ask the pupils to consider how strong the smaller pieces might be and also how efficient this would be in terms of the work involved.

Let’s reflect! After pupils have had an opportunity to grapple with the problem they should be brought together and given an opportunity to share their strategies and discuss their progress towards a solution. It is likely that pupils will share approaches that involve them ‘having a go’, evaluating their solution, breaking down one attempt in order to look for a better solution, and so on.

Teacher Guide Reference • •

Second Level samples.indd 66-67

PMfS flyer_update oct-21_hi-res.indd 6

Let’s Reflect offers an opportunity to discuss different strategies and methods as a class, to consolidate learning

Unit 8, 1st Level Teacher Guide Unit 9, 2nd Level Teacher Guide

21/09/2021 14:09

22/02/2022 13:07

Maths wipe clean templates These ringbound templates: • allow teachers to work more efficiently with children during class • are flexible and can be tailored to each class • support active learning and engagement • reduce the need for photocopying and printing

Maths dictionary The Collins maths dictionary gives simple definitions of key maths terms, linked to full times table charts, weight measurements and geometry. Each concept is clearly laid out and illustrated, making this dictionary a fun and easy way for pupils to learn maths. array arr

algebra g gebra

B C D E F

algebra Algebra is a branch of mathematics that uses letters or symbols to represent numbers. It is used to help solve problems and investigate number patterns. The multiplication sign isn't used in algebra in case it is confused with the letter x. So 3 times n is written as 3n.

If y + 3 = 5, what is the value of y?

y=2

I J K L M N O P

D See equation, formula

a.m. The short way of writing ‘ante meridiem’ is a.m., which means before midday or noon. The lessons started at 9.15 a.m.

D See midday, p.m. -See Time in the Maths Wizard

analogue clock An analogue clock measures time using hands moving around a dial.

angle

approximate

The amount by which something turns is an angle. It is a measure of rotation, measured in degrees (°).

The approximate answer to 19 × 31 is 600. 19 × 31 ≈ 600

angle

D See acute angle, degree, obtuse angle, reﬂex angle, right angle, straight angle -See Geometry in the Maths Wizard

annual An annual event is one that happens once a year.

V W

When something turns anticlockwise, it goes round in the opposite direction to the hands on a clock.

The apex of a solid shape is the highest point from the base. The apex of a pyramid is the vertex at which the triangular faces meet.

The area of this rectangle is 12 squares.

An array is a regular arrangement of numbers or objects. It has rows and columns, usually in the form of a rectangle.

a b c d e f g h i j k l m n o p q r s t

-See Multiplication and division in the Maths Wizard

u v w

vertex

x y

PMfS flyer_update oct-21_hi-res.indd 7

array

The area of a rectangle can be calculated by multiplying its length by its width. Area = length x width

CG_Maths_Dictionary_2ndPROOF_A-Z_LIVE_27-11-17.indd 2

D See addition, division, multiplication, subtraction

The area of a surface is a measure of how much space is covered by that surface. It is usually measured in square units such as square centimetres (cm2) or square metres (m2)..

Mental arithmetic is calculating in your head.

area

apex D See digital clock, time -See Time in the Maths Wizard

Arithmetic is the branch of mathematics that involves numbers and calculating. It includes addition, subtraction, multiplication and division.

D See chord, circle, circumference -See Geometry in the Maths Wizard

anticlockwise

D See clockwise, rotate

An arc is a curved line that would make a complete circle if you continued it. A rainbow is an arc of colour in the sky.

arithmetic

Arrays can help you work out a multiplication. This array shows that 3x4 is the same as 4x3 and they both equal 12.

D See estimate, round

arc

Your birthday is an annual event. Unfortunately you can only celebrate it once a year.

Q S

An approximate answer is very close to the right answer, but not exact. The sign ≈ means ‘is approximately equal to’.

D See square centimetre

D See pyramid, vertex

z 3

27/11/2017 11:36

CG_Maths_Dictionary_2ndPROOF_A-Z_LIVE_27-11-17.indd 3

27/11/2017 11:36

22/02/2022 13:07

Order form Title

Qty

FREE sample

ISBN

RRP

Primary Maths for Scotland Early Level Record Book

978-0-00-835970-6

£3.99

Primary Maths for Scotland Early Level Teacher Guide

978-0-00-835969-0

£120.00

Primary Maths for Scotland Early Level digital pack (1 year subscription)

978-0-00-835968-3

£125.00

Primary Maths for Scotland Early Level Assessment Pack

978-0-00-839246-8

£75.00

Primary Maths for Scotland Textbook 1A

978-0-00-831395-1

£9.99

Primary Maths for Scotland Textbook 1B

978-0-00-831396-8

£9.99

Primary Maths for Scotland Textbook 1C

978-0-00-831397-5

£9.99

Primary Maths for Scotland First Level Teacher Guide

978-0-00-834894-6

£120.00

N/A

Primary Maths for Scotland First Level Assessment Pack

978-0-00-839247-5

£90.00

N/A

Primary Maths for Scotland Textbook 2A

978-0-00-831398-2

£11.99

Primary Maths for Scotland Textbook 2B

978-0-00-831399-9

£11.99

Primary Maths for Scotland Textbook 2C

978-0-00-831400-2

£11.99

Primary Maths for Scotland Second Level Teacher Guide

978-0-00-834895-3

£120.00

N/A

Primary Maths for Scotland Second Level Assessment Pack

978-0-00-839248-2

£90.00

N/A

Early Level Problem Solving Pack • July 2022

978-0-00-850866-1

£75.00

N/A

First Level Problem Solving Pack • July 2022

978-0-00-850867-8

£90.00

N/A

Second Level Problem Solving Pack • July 2022

978-0-00-850868-5

£90.00

N/A

First Level Wipe-Clean Maths Templates for CfE Primary Maths

978-0-00-832033-1

£4.99

Second Level Wipe-Clean Maths Templates for CfE Primary Maths

978-0-00-832034-8

£4.99

Early Level Wipe-Clean Maths Templates for CfE Primary Maths

978-0-00-836445-8

£4.99

Collins Maths Dictionary

978-0-00-821237-7

£9.99

N/A

Name: Position: School: Address:

Postcode:

Email: Phone number:

Fax:

Find out more or request sample material by contacting your local rep  01484 668 148

 leckiescotland.co.uk

 leckiescotland@harpercollins.co.uk

 LeckieforScotland

 Claire McAuley (East Scotland) 07557 188 154 • claire.mcauley@harpercollins.co.uk

 @LeckieScotland

 Christine Stein (West Scotland) 07825 116 401 • christine.stein@harpercollins.co.uk

PMfS flyer_update oct-21_hi-res.indd 8

 Freepost RTKB-SGZT-ZYJL Honley

22/02/2022 13:07