| Funciones polinomiales y sus gráficas 259
S E C C I Ó N 3.2
A continuación veamos algunos ejemplos más de funciones polinomiales.
P1x2
3
Grado 0
Q1x 2
4x 2 7
Grado 1
R1x2
x2
Grado 2
x 3
2
2x 2 6x 2 10
S1x2
Grado 3
Si un polinomio está formado por un solo término, entonces se llama monomio. Por ejemplo, P1x2 x3 y Q1x2 6x5 son monomios.
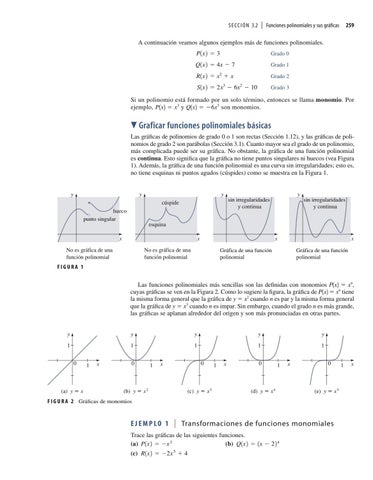
▼ Graficar funciones polinomiales básicas Las gráficas de polinomios de grado 0 o 1 son rectas (Sección 1.12), y las gráficas de polinomios de grado 2 son parábolas (Sección 3.1). Cuanto mayor sea el grado de un polinomio, más complicada puede ser su gráfica. No obstante, la gráfica de una función polinomial es continua. Esto significa que la gráfica no tiene puntos singulares ni huecos (vea Figura 1). Además, la gráfica de una función polinomial es una curva sin irregularidades; esto es, no tiene esquinas ni puntos agudos (cúspides) como se muestra en la Figura 1.
y
y
y
y sin irregularidades y continua
cúspide hueco punto singular
sin irregularidades y continua
esquina x
x
x
No es gráfica de una función polinomial
No es gráfica de una función polinomial
x Gráfica de una función polinomial
Gráfica de una función polinomial
FIGURA 1
Las funciones polinomiales más sencillas son las definidas con monomios P1x2 xn, cuyas gráficas se ven en la Figura 2. Como lo sugiere la figura, la gráfica de P1x2 xn tiene la misma forma general que la gráfica de y x2 cuando n es par y la misma forma general que la gráfica de y x3 cuando n es impar. Sin embargo, cuando el grado n es más grande, las gráficas se aplanan alrededor del origen y son más pronunciadas en otras partes. y
y
y
y
y
1
1
1
1
1
0
(a) y=x
1
x
0
1
x
(b) y=≈
0
1
x
(c) y=x£
0
1
(d) y=x¢
x
0
(e) y=x∞
F I G U R A 2 Gráficas de monomios
E J E M P LO 1
Transformaciones de funciones monomiales
Trace las gráficas de las siguientes funciones. (a) P1x2 x3 (b) Q1x2 5 (c) R1x2 2x 4
1x
22 4
1
x