3.1 y
Cresta (0, 0)
x
1
2
−2 −3
163
Extremos relativos y números críticos
f(x) = x 3 − 3x 2
−1
Extremos en un intervalo
Valle (2, −4)
−4
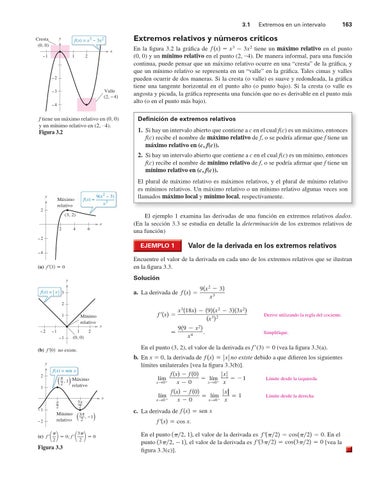
f tiene un máximo relativo en (0, 0) y un mínimo relativo en (2, –4). Figura 3.2
En la figura 3.2 la gráfica de f x x 3 3x 2 tiene un máximo relativo en el punto (0, 0) y un mínimo relativo en el punto (2, –4). De manera informal, para una función continua, puede pensar que un máximo relativo ocurre en una “cresta” de la gráfica, y que un mínimo relativo se representa en un “valle” en la gráfica. Tales cimas y valles pueden ocurrir de dos maneras. Si la cresta (o valle) es suave y redondeada, la gráfica tiene una tangente horizontal en el punto alto (o punto bajo). Si la cresta (o valle es angosta y picuda, la gráfica representa una función que no es derivable en el punto más alto (o en el punto más bajo). Definición de extremos relativos 1. Si hay un intervalo abierto que contiene a c en el cual f(c) es un máximo, entonces f(c) recibe el nombre de máximo relativo de f, o se podría afirmar que f tiene un máximo relativo en (c, f(c)). 2. Si hay un intervalo abierto que contiene a c en el cual f(c) es un mínimo, entonces f(c) recibe el nombre de mínimo relativo de f, o se podría afirmar que f tiene un mínimo relativo en (c, f(c)).
y
Máximo relativo
f(x) =
9(x 2 − 3) x3
El plural de máximo relativo es máximos relativos, y el plural de mínimo relativo es mínimos relativos. Un máximo relativo o un mínimo relativo algunas veces son llamados máximo local y mínimo local, respectivamente.
2
(3, 2) x
2
6
4
El ejemplo 1 examina las derivadas de una función en extremos relativos dados. (En la sección 3.3 se estudia en detalle la determinación de los extremos relativos de una función)
−2
Valor de la derivada en los extremos relativos
EJEMPLO 1 −4
(a) f 3
Encuentre el valor de la derivada en cada uno de los extremos relativos que se ilustran en la figura 3.3.
0
Solución
y
f(x) = ⏐x⏐ 3
a. La derivada de f x
9 x2 3 x3
2 1 −2
Mínimo relativo
−1
1 −1
f x x
x4
(0, 0)
f(x) = sen x
( π2 , 1( Máximo relativo
−1 −2
(c) f
x
π 2
3π 2
Mínimo relativo
(32π , − 1(
2
Figura 3.3
0; f
3 3x 2
.
Derive utilizando la regla del cociente.
Simplifique.
En el punto (3, 2), el valor de la derivada es f ′(3) = 0 (vea la figura 3.3(a).
y
1
9 x2 x3 2 x2
99
2
(b) f 0 no existe.
2
x 3 18x
3 2
0
x no existe debido a que difieren los siguientes b. En x = 0, la derivada de f x límites unilaterales [vea la figura 3.3(b)]. f x f 0 x lím lím 1 Límite desde la izquierda x→0 x→0 x 0 x f x f 0 x lím lím 1 Límite desde la derecha x→0 x→0 x 0 x c. La derivada de f x f x
sen x
cos x.
2, 1 , el valor de la derivada es f En el punto punto 3 2, 1 , el valor de la derivada es f 3 figura 3.3(c)].
2 2
cos cos 3
2 2
0. En el 0 [vea la