884
CAPÍTULO 14
DERIVADAS PARCIALES
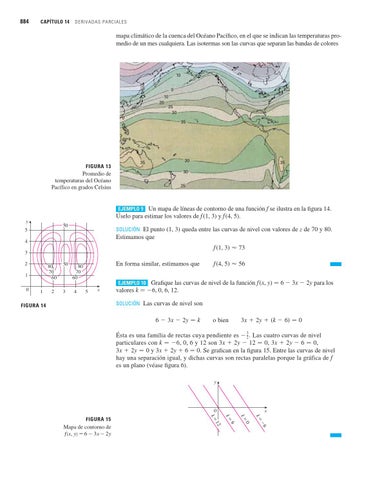
mapa climático de la cuenca del Océano Pacífico, en el que se indican las temperaturas promedio de un mes cualquiera. Las isotermas son las curvas que separan las bandas de colores
10 0 10 20 25 30 35
FIGURA 13
35
30 30
Promedio de temperaturas del Océano Pacífico en grados Celsius
25
EJEMPLO 9 Un mapa de líneas de contorno de una función f se ilustra en la figura 14. Úselo para estimar los valores de f (1, 3) y f (4, 5).
y
50
5
SOLUCIÓN El punto (1, 3) queda entre las curvas de nivel con valores de z de 70 y 80.
Estimamos que
4
f 共1, 3兲 ⬇ 73
3 2
80 70 60
1 0
35
1
2
50
3
En forma similar, estimamos que
80 70 60 4
5
x
f 共4, 5兲 ⬇ 56
EJEMPLO 10 Grafique las curvas de nivel de la función f (x, y) 6 3x 2y para los valores k 6, 0, 6, 12. SOLUCIÓN Las curvas de nivel son
FIGURA 14
6 3x 2y k
o bien
3x 2y 共k 6兲 0
3 Ésta es una familia de rectas cuya pendiente es 2 . Las cuatro curvas de nivel particulares con k 6, 0, 6 y 12 son 3x 2y 12 0, 3x 2y 6 0, 3x 2y 0 y 3x 2y 6 0. Se grafican en la figura 15. Entre las curvas de nivel hay una separación igual, y dichas curvas son rectas paralelas porque la gráfica de f es un plano (véase figura 6).
y
0
_6 k=
0 k=
6 k=
12 k=
FIGURA 15
Mapa de contorno de f(x, y)=6-3x-2y
x