SECCIÓN 7.1
INTEGRACIÓN POR PARTES
467
Si combinamos la fórmula para la integración por partes con la parte 2 del teorema fundamental del cálculo, podemos evaluar integrales definidas por partes. Evaluando ambos lados de la fórmula 1 entre a y b, suponiendo que f y J son continuas, y utilizando el teorema fundamental del cálculo, obtenemos
y
6
EJEMPLO 5
b
a
f x t x dx
f x tx
y
b
]
a
b
a
t x f x dx
Calcule y tan 1x dx. 1
0
SOLUCIÓN Sea
tan 1x
u
dx
du
Entonces
dv
x
v
x2
1
dx
Así que la fórmula 6 da
y
1
0
y
1
]
tan 1x dx
x tan 1x
0
1 tan 1 1 p 4
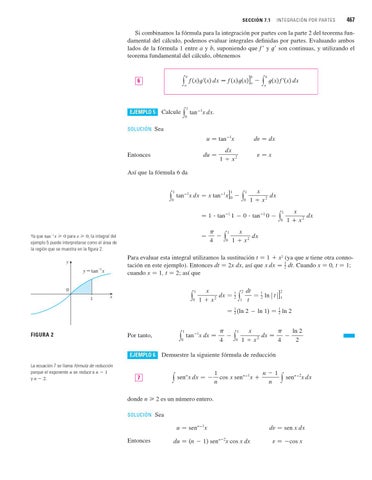
Ya que tan 1x 0 para x 0, la integral del ejemplo 5 puede interpretarse como el área de la región que se muestra en la figura 2.
y
0 tan 1 0 x
1
0
dx
x2
1
x2
1
x
1
0
x2
1
dx
dx
Para evaluar esta integral utilizamos la sustitución t m 1 x2 (ya que u tiene otra connotación en este ejemplo). Entonces dt m 2x dx, así que x dx 12 dt. Cuando x m 0, t m 1; cuando x m 1, t m 2; así que
y
y=tan–!x
0 1
y
x
1
0
y
x
x
1
0
x2
1
dx
y
1 2 1 2
FIGURA 2
EJEMPLO 6 La ecuación 7 se llama fórmula de reducción porque el exponente n se reduce a n 1 y n 2.
y
Por tanto,
1
0
tan 1x dx
p 4
y
2
1
dt t
1 2
ln 2
0
1
1 2
ln 1 x
1
2
]
ln t
1
x
2
ln 2
p 4
dx
ln 2 2
Demuestre la siguiente fórmula de reducción
7
1 cos x sen n 1x n
y sen x dx n
n
1 n
y sen
n 2
x dx
donde n 2 es un número entero. SOLUCIÓN Sea
u Entonces
du
senn 1x n
1 senn 2x cos x dx
dv
sen x dx
v
cos x