3.1
InterpolaciĂłn y el polinomio de Lagrange
79
primeros seis polinomios de Taylor alrededor de x0 5 0 para f (x) 5 e x. Ya que las derivadas de f (x) son todas ex, que evaluadas en x0 5 0 dan 1, los polinomios de Taylor son Se publicĂł muy poco del trabajo de Weierstrass durante su vida; no obstante, sus conferencias, en especial sobre la teorĂa de las IXQFLRQHV LQĂ X\HURQ GH PDQHUD VLJQLĂ€FDWLYD HQ XQD JHQHUDFLyQ completa de estudiantes.
P0 (x) = 1,
P1 (x) = 1 + x,
P4 (x) = 1 + x +
x2 , 2
P2 (x) = 1 + x +
x3 x4 x2 + + , 2 6 24
P3 (x) = 1 + x +
P5 (x) = 1 + x +
y
x3 x2 + , 2 6
x3 x4 x5 x2 + + + . 2 6 24 120
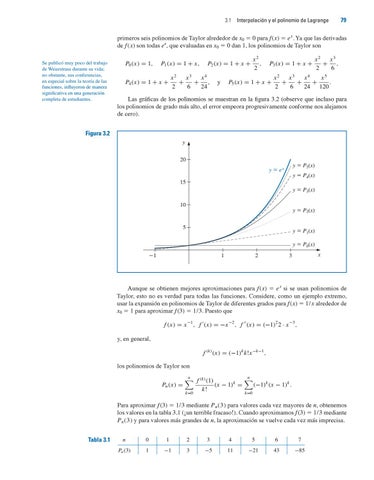
/DV JUiÀFDV GH ORV SROLQRPLRV VH PXHVWUDQ HQ OD ÀJXUD REVHUYH TXH LQFOXVR SDUD los polinomios de grado mås alto, el error empeora progresivamente conforme nos alejamos de cero).
Figura 3.2 y 20
y 5 P5(x)
y 5 ex
y 5 P4(x)
15
y 5 P3(x) 10
y 5 P2(x)
5
y 5 P1(x) y 5 P0(x)
21
2
1
x
3
Aunque se obtienen mejores aproximaciones para f (x) 5 e x si se usan polinomios de Taylor, esto no es verdad para todas las funciones. Considere, como un ejemplo extremo, usar la expansiĂłn en polinomios de Taylor de diferentes grados para f (x) 5 1/ x alrededor de x0 5 1 para aproximar f (3) 5 1/3. Puesto que
f (x) = x −1 , f (x) = −x −2 , f (x) = (−1)2 2 ¡ x −3 , y, en general,
f (k) (x) = (−1)k k!x −k−1 , los polinomios de Taylor son n
Pn (x) = k=0
f (k) (1) (x − 1)k = k!
n
(−1)k (x − 1)k .
k=0
Para aproximar f (3) 5 1/3 mediante P n (3) para valores cada vez mayores de n, obtenemos los valores en la tabla 3.1 (ÂĄun terrible fracaso!). Cuando aproximamos f (3) 5 1/3 mediante P n (3) y para valores mĂĄs grandes de n, la aproximaciĂłn se vuelve cada vez mĂĄs imprecisa.
Tabla 3.1
n
0
1
2
3
4
5
6
7
Pn (3)
1
−1
3
−5
11
−21
43
−85