Essential Maths Core for the Australian Curriculum 2ed 10 - final pages by cambridge_aused

TEXTBOOK ADVANCE COPY

March 2025

This textbook advance is provided as a sample for course preparation, planning and for use by teachers until the final products is available.

It should not be:

• made available in any other form

• uploaded to any website not affiliated to or authorised by Cambridge University Press & Assessment

• sold, reproduced or otherwise exploited for financial gain

• used in whole or in part to create a derivative work

• edited in any way (this includes the removal or modification of any branding, photographs or illustrations)

These advanced chapters have been provided for use by your school prior to publication of the textbook. The PDF supplied and all downloaded or printed excerpts must be destroyed once the textbook has been released.

For questions related to these instructions, please email copyright@cambridge.org

ShaftesburyRoad,CambridgeCB28EA,UnitedKingdom

OneLibertyPlaza,20thFloor,NewYork,NY10006,USA

477WilliamstownRoad,PortMelbourne,VIC3207,Australia

314–321,3rdFloor,Plot3,SplendorForum,JasolaDistrictCentre,NewDelhi–110025,India

103PenangRoad,#05–06/07,VisioncrestCommercial,Singapore238467

CambridgeUniversityPress&AssessmentisadepartmentoftheUniversityofCambridge.

WesharetheUniversity’smissiontocontributetosocietythroughthepursuitofeducation,learningandresearch atthehighestinternationallevelsofexcellence. www.cambridge.org

©DavidGreenwood,SaraWoolley,JennyGoodmanandJenniferVaughan2021,2025

Thispublicationisincopyright.Subjecttostatutoryexceptionandtotheprovisionsofrelevantcollective licensingagreements,noreproductionofanypartmaytakeplacewithoutthewrittenpermissionof CambridgeUniversityPress&Assessment.

Firstpublished2021 SecondEdition2025 2019181716151413121110987654321

CoverandtextdesignedbySardineDesign TypesetbydiacriTech PrintedinChinabyC&COffsetPrintingCo.,Ltd.

AcataloguerecordforthisbookisavailablefromtheNationalLibraryofAustraliaat www.nla.gov.au

ISBN978-1-009-593-861

Additionalresourcesforthispublicationatwww.cambridge.edu.au/GO

ReproductionandCommunicationforeducationalpurposes

TheAustralian CopyrightAct1968 (theAct)allowsamaximumofonechapteror10% ofthepagesofthispublication,whicheveristhe greater,tobereproducedand/orcommunicatedbyanyeducationalinstitutionforitseducationalpurposesprovidedthattheeducational institution(orthebodythatadministersit)hasgivenaremunerationnoticetoCopyrightAgencyLimited(CAL)undertheAct.

FordetailsoftheCALlicenceforeducationalinstitutionscontact:

CopyrightAgencyLimited Level12,66GoulburnStreet

SydneyNSW2000

Telephone:(02)93947600

Facsimile:(02)93947601

Email:memberservices@copyright.com.au

ReproductionandCommunicationforotherpurposes

ExceptaspermittedundertheAct(forexampleafairdealingforthepurposesofstudy,research,criticismorreview)nopart ofthispublicationmaybereproduced,storedinaretrievalsystem,communicatedortransmittedinanyformorbyanymeans withoutpriorwrittenpermission.Allinquiriesshouldbemadetothepublisherattheaddressabove.

CambridgeUniversityPress&AssessmenthasnoresponsibilityforthepersistenceoraccuracyofURLSforexternalorthird-party internetwebsitesreferredtointhispublicationanddoesnotguaranteethatanycontentonsuchwebsitesis,orwillremain,accurateor appropriate.Informationregardingprices,traveltimetablesandotherfactualinformationgiveninthisworkiscorrectatthetimeofﬁrst printingbutCambridgeUniversityPress&Assessmentdoesnotguaranteetheaccuracyofsuchinformationthereafter.

PleasebeawarethatthispublicationmaycontainimagesofAboriginalandTorresStraitIslanderpeoplewhoarenowdeceased.Several variationsofAboriginalandTorresStraitIslandertermsandspellingsmayalsoappear;nodisrespectisintended.Pleasenotethattheterms ‘IndigenousAustralians’and‘AboriginalandTorresStraitIslanderpeoples’maybeusedinterchangeablyinthispublication.

CambridgeUniversityPress&AssessmentacknowledgestheAboriginalandTorresStraitIslanderpeoplesofthisnation.Weacknowledgethe traditionalcustodiansofthelandsonwhichourcompanyislocatedandwhereweconductourbusiness.Wepayourrespectstoancestors andElders,pastandpresent.CambridgeUniversityPress&AssessmentiscommittedtohonouringAboriginalandTorresStraitIslander peoples’uniqueculturalandspiritualrelationshipstotheland,watersandseasandtheirrichcontributiontosociety.

5A Collectingdata

5B Frequencytables,columngraphsand histograms CONSOLIDATING

5C Dotplotsandstem-and-leafplots CONSOLIDATING

5D Rangeandmeasuresofcentre

5E Quartilesandoutliers

5F Boxplots 330 Progressquiz

5G Time-seriesdata

5H Bivariatedataandscatterplots

5I Lineofbestﬁtbyeye 349 Maths@Work:Projectmanageronabuildingsite

6A Interpretationofstraight-linegraphs CONSOLIDATING 382

6B Distance–timegraphs

6C Plottingstraightlines CONSOLIDATING 396

6D Midpointandlengthofalinesegment 403

6E Exploringgradient

6F Ratesfromgraphs

6G y = mx + c andspeciallines

6H Parallelandperpendicularlines

6I Sketchingwith x-and y-intercepts 442

6J Linearmodelling 448

6K Solvingsimultaneousequationsgraphically 456

6L RegionsontheCartesianplane 462

6M Directproportion 468

6N Inverseproportion 477 Maths@Work:Accountantorsmallbusinessowner 482

Algebra

7 Geometryandnetworks 500

Warm-upquiz 502

7A Parallellines CONSOLIDATING 504

7B Triangles CONSOLIDATING 509

7C Quadrilaterals 515

7D Polygons 520

7E Congruenttriangles 525

7F Similartriangles 532

7G Applyingsimilartriangles 538 Progressquiz 543

7H Applicationsofsimilarityinmeasurement 545

7I Introductiontonetworks 551

7J Isomorphicandplanargraphs 557

7K Trails,pathandEuleriancircuits 564

7L Shortestpathproblems 572

Maths@Work:Poolbuilder 577

Modelling 579

Technologyandcomputationalthinking 581

Puzzlesandgames 583

Chaptersummaryandchecklist 584

8 Indices,exponentialsandlogarithms 598

Warm-upquiz 600

8A Indexnotationandindexlawsfor multiplicationanddivision 601

8B Moreindexlawsandthezeroindex 606

8C Negativeindices 612

8D Scientiﬁcnotation 617

8E Graphsofexponentials 622 Progressquiz 626

8F Exponentialgrowthanddecay 627

8G Introducinglogarithms 633

8H Logarithmicscales 637

Maths@Work:Electricaltrades 646

Modelling 648

Technologyandcomputationalthinking 650

Puzzlesandgames 652

Chaptersummaryandchecklist 653

Chapterreview 656

Algebra,Measurement

9 Pythagoras’theoremandtrigonometry

9A ReviewingPythagoras’theorem CONSOLIDATING 661

9B Findingthelengthofashorterside 668

9C ApplicationsofPythagoras’theorem 673

9D Trigonometricratios CONSOLIDATING 679

9E Findingsidelengths 685

9F Solvingforthedenominator 690

Progressquiz 696

9G Findingangles 698

9H Anglesofelevationanddepression 704

9I Directionandbearings 713

Warm-upquiz 738 10A Expandingbinomialproducts 739

10B Factorisingadifferenceoftwosquares 745

10C Factorisingtrinomialsoftheform x2 + bx + c 749

10D Solvingequationsoftheform ax2 = c 753

10E Solvingequationsusingthenullfactorlaw 759 Progressquiz 765

10F Solvingequationsbycompletingthesquare 766

10G Applicationsofquadratics 771

10H Exploringparabolas 775

10I Graphsofcirclesandhyperbolas 786

Maths@Work:Drivinginstructor 794 Modelling 796

Technologyandcomputationalthinking 798

AbouttheAuthors

DavidGreenwood istheHeadofMathematicsatTrinityGrammarSchoolinMelbourneand has30+ yearsteachingmathematicsfromYear7to12.Heistheleadauthorforthe CambridgeEssentialseriesandhasauthoredmorethan80titlesfortheAustralian Curriculumandforthesyllabusesofthestatesandterritories.Hespecialisesinanalysing curriculumandthesequencingofcoursecontentforschoolmathematicscourses. Healsohasaninterestintheuseoftechnologyfortheteachingofmathematics.

SaraWoolley wasbornandeducatedinTasmania.ShecompletedanHonoursdegreein MathematicsattheUniversityofTasmaniabeforecompletinghereducationtraining attheUniversityofMelbourne.ShehastaughtmathematicsfromYears7to12since 2006andiscurrentlyaHeadofMathematics.Shespecialisesinlessondesignand creatingresourcesthatdevelopandbuildunderstandingofmathematicsforallstudents.

JenniferVaughan hastaughtsecondarymathematicsforover30yearsinNewSouthWales, WesternAustralia,QueenslandandNewZealandandhastutoredandlecturedinmathematics atQueenslandUniversityofTechnology.Sheispassionateaboutprovidingstudentsofallability levelswithopportunitiestounderstandandtohavesuccessinusingmathematics.Shehas hadextensiveexperienceindevelopingresourcesthatmakemathematicalconceptsmore accessible;hence,facilitatingstudentconﬁdence,achievementandanenjoymentofmaths.

JennyGoodman hastaughtinschoolsforover28yearsandiscurrentlyteachingataselective highschoolinSydney.Jennyhasaninterestintheimportanceofliteracyinmathematics education,andinteachingstudentsofdifferingabilitylevels.ShewasawardedtheJonesMedal foreducationatSydneyUniversityandtheBourkePrizeforMathematics.Shehaswritten for CambridgeMATHSNSW andwasinvolvedinthe Spectrum and SpectrumGold series.

StuartPalmer wasbornandeducatedinNewSouthWales.Heisafullyqualiﬁedhigh schoolmathematicsteacherwithmorethan25years’experienceteachingstudents fromallwalksoflifeinavarietyofschools.HehasbeenHeadofMathematicsintwo schools.Heisverywellknownbyteachersthroughoutthestatefortheprofessional learningworkshopshedelivers.StuartalsoassiststhousandsofYear12studentsevery yearastheypreparefortheirHSCExaminations.AttheUniversityofSydney,Stuart spentmorethanadecaderunningtutorialsforpre-servicemathematicsteachers.

Acknowledgements

Theauthorandpublisherwishtothankthefollowingsourcesforpermissiontoreproducematerial: Cover: © GettyImages/Westend61.

Images: © GettyImages/HappyKikky,Chapter1Opener/Vevchic86,p.10/CreativeCrop,p.13/alvarez,p.16/shapecharge, p.18/Cecilie Arcurs,p.24/martin-dm,p.25/ThomasBarwick,p.29/SDIProductions,p.30/clubfoto,p.32/Mikolette,p.33/ manusaponkasosod,p.36/djgunner,p.38/JennerImages,p.41/TrevorWilliams,p.42/AlpamayoPhoto,p.47/alicat,p.52/ GuidoMieth,p.56/DEVIMAGES,p.58/OscarWong,p.65/ZU 09,Chapter2Opener/AzmanL,p.71/GlobalP,p.75/ PhotographcopyrightEricMeola,p.81(1)/GlasshouseImages,p.81(2)/Joe Potato,p.82/AndreSchoenherr,p.85/ South agency,p.86/CTAylward,p.88/MartinBarraud,p.91/SergioAmiti,p.97/Opla,p.102/ZoranKolundzija,p.103/ nicolamargaret,p.106/xxmmxx,p.107/SolStock,p.110/PeterCade,p.111/ChuckSchugPhotography,p.112/EyeEmMobile GmbH,p.114/EyeEmMobileGmbH,p.115/IrynaMelnyk,p.127/Nastasic,p.132/MintImages,Chapter3Opener/JoseLuis PelaezInc,p.145/davidf,p.149/cjp,p.155/Matt Brown,p.181/TomMerton,p.190/Boy Anupong,p.199/ pamelasphotopoetry,p.200/Maskot,p.202/dusanpetkovic,p.208/FatCamera,p.215/Hispanolistic,p.233/BorisSV,p.235/ LumiNola,Chapter4Opener/victorass88,p.240/MontyRakusen,p.243/IsabelPavia,p.244/SENLI,p.249/Photo Concepts, p.259(1)/baranozdemir,p.259(2)/wragg,p.260/luoman,p.273/byFrankOlsen,Norway,p.281/AJ Watt,p.282/wepix,p.288 /pidjoe,p.291/MassimilianoFinzi,Chapter5Opener/LiveLifeTraveling,p.298/ti-ja,p.306/97,p.328/fcafotodigital,p.335(1)/ HalfpointImages,p.335(2)/Oleh Slobodeniuk,p.337/HelenAnne,p.342/marcoventuriniautieri,p.354/JohnCrux Photography,p.361/945ontwerp,p.369(1)/97,p.369(2)/AzmanJaka,p.383/HaitongYu,p.386(1)/ZoomPetPhotography, p.386(2)/slobo,p.389(1)/StocktrekImages,p.389(2)/sandrastandbridge,p.393/TJBlackwell,p.395/RalucaHotupan,p.401/ Westend61,p.402/emicristea,p.412/JGI/JamieGrill,p.420/HeritageImages/Contributor,p.433/GaryJohnNorman,p.440/ GraceCary,p.447/EzraBailey,p.454/AnnabelleBreakey,p.460/Henrik5000,p.461/Dhoxax,p.473/RungruedeeMalasri, p.481/RubberBallProductions,p.487/NealPritchardPhotography,Chapter7Opener/StefanoGi,p.504/AleksandrRybalko, p.520/Westend61,p.525/skegbydave,p.551/ROBERTBROOK/SCIENCEPHOTOLIBRARY,p.563/ManfredGottschalk,p.580/ NataliaSokko,p.582/MikeWewerka,p.593/sanjeri,Chapter8Opener/RapidEye,p.608/photovideostock,p.617/MPI/ Stringer,p.621/PepeLaguarda,p.627/AndreasReh,p.631/sengkuiLim/500px,p.645/schlol,p.648/ConstantineJohnny, p.652/Sjo,p.657/AntonPetrus,p.666/Klubovy,p.667/SeanJustice,p.671/Prasitphoto,p.698/GaryJohnNorman,p.717/ NickBrundlePhotography,p.726/ManuelSulzer,Chapter10Opener/Ascent/PKSMediaInc.,p.747/TimRobberts,p.748/ RafaelBen-Ari,p.758/KeiUesugi,p.763/Westend61,p.766/sturti,p.794/JohnerImages,p.805/RosmarieWirz,p.819. Everyefforthasbeenmadetotraceandacknowledgecopyright.Thepublisherapologisesforanyaccidentalinfringement andwelcomesinformationthatwouldredressthissituation.

© AustralianCurriculum,AssessmentandReportingAuthority(ACARA)2009topresent,unlessotherwiseindicated.Thismaterial wasaccessedfromtheACARAwebsite(www.acara.edu.au).ThematerialislicensedunderCCBY4.0(https://creativecommons.org/ licenses/by/4.0/).ACARAdoesnotendorseanyproductthatusesACARAmaterialormakeanyrepresentationsastothequalityof suchproducts.AnyproductthatusesmaterialpublishedonthiswebsiteshouldnotbetakentobeafﬁliatedwithACARAorhave thesponsorshiporapprovalofACARA.Itisuptoeachpersontomaketheirownassessmentoftheproduct.

Introduction

Thesecondeditionof EssentialMathematicsCOREfortheAustralianCurriculum hasbeensigniﬁcantlyrevisedandupdatedtosuit theteachingandlearningofVersion9.0oftheAustralianCurriculum.Manyoftheestablishedfeaturesoftheserieshavebeen retained,buttherehavebeensomesubstantialrevisions,improvementsandnewelementsintroducedforthiseditionacrossthe print,digitalandteacherresources.

Newcontentandsomerestructuring

Newcontenthasbeenaddedatallyearlevels.In Year7,thereisnewcontentonratiosandproportions,volumeoftriangular prisms,netsofsolidsandmeasurementrelatingtocircles.Allgeometrytopicsarenowcontainedinasinglechapter(Chapter7).In Year8,thereisnewcontentonorderofoperations,3D-coordinates,operationswithnegativefractions,areasofsectorsand compositeshapes,Pythagoras’theorem,inequalities,similarﬁgures,two-stepexperimentsandtreediagrams.For Year9,thereis newcontentonerrorsinmeasurement,inequalities,factorisation,samplingandproportion,quadraticsexpressionsandparabolas. In Year10,thereisnewcontentoncompositesolids,errorsinmeasurement,networksandlogarithmicscales.

Version9.0placesincreasedemphasison investigations and modelling,andthisiscoveredwithrevisedModellingactivitiesat theendofchaptersanddownloadableInvestigations.Therearealsomanynewelaborationscovering FirstNationsPeoples’ perspectives onmathematics,rangingacrossallsixcontentstrandsofthecurriculum.Thesearecoveredinasuiteofspecialised investigationsprovidedintheOnlineTeachingSuite.

Othernewfeatures

• Technologyandcomputationalthinking activitieshavebeenaddedtotheendofeverychaptertoaddressthecurriculum’s increasedfocusontheuseoftechnologyandtheunderstandingandapplicationofalgorithms.

• Targetedskillsheets –downloadableandprintable–havebeenwrittenforeverylessonintheseries,withtheintentionof providingadditionalpracticeforstudentswhoneedsupportatthebasicskillscoveredinthelesson,withquestionslinkedto workedexamplesinthebook.

• EditablePowerPointlessonsummaries arealsoprovidedforeachlessonintheseries,withtheintentionofsavingthetime ofteacherswhowerepreviouslycreatingthesethemselves.

Diagnosticassessmenttool

Alsonewforthiseditionisaﬂexible,comprehensivediagnosticassessmenttool,availablethroughtheOnlineTeachingSuite.This tool,featuringaround 10, 000 newquestions,allowsteacherstosetdiagnosticteststhatarecloselyalignedwiththetextbook content,viewstudentperformanceandgrowthviaarangeofreports,setfollow-upworkwithaviewtohelpingstudents improve,andexportdataasneeded.

Guidetotheworkingprograms

EssentialMathematicsCOREfortheAustralianCurriculum9.0 containsworkingprogramsthataresubtlyembeddedinthe exercises.ThesuggestedworkingprogramsprovidetwopathwaysthroughthebooktoallowdifferentiationforBuildingand Progressingstudents.

EachexerciseisstructuredinsubsectionsthatmatchtheAustralianCurriculum9.0proﬁciencystrands(withProblem-solving andReasoningcombinedintoonesectiontoreduceexerciselength),aswellas‘Goldstar’( ).Thequestions* suggestedforeach pathwayarelistedintwocolumnsatthetopofeachsubsection.

• Theleftcolumn(lightestshade)showsthequestionsintheBuildingworkingprogram.

• Therightcolumn(darkestshade)showsthequestionsintheProgressingworkingprogram.

Gradientswithinexercisesandproﬁciencystrands

Theworkingprogramsmakeuseoftwo gradientsthathavebeencarefullyintegrated intotheexercises.Agradientrunsthrough theoverallstructureofeachexercise–where there’sanincreasinglevelofsophistication requiredasastudentprogressesthrough theproficiencystrandsandthenontothe ‘GoldStar’question(s)–butalsowithineach proficiencystrand;thefirstfewquestions inFluencyareeasierthanthelastfew,for example,andthefirstfewProblem-solvingand reasoningquestionsareeasierthanthelastfew.

Therightmixofquestions

Questionsintheworkingprogramshavebeenselectedtogivethemostappropriatemixoftypesofquestionsforeachlearning pathway.StudentsgoingthroughtheBuildingpathwayaregivenextrapracticeattheUnderstandingandbasicFluencyquestions andonlytheeasiestProblem-solvingandreasoningquestions.TheProgressingpathway,whilenotchallenging,spendsalittleless timeonbasicUnderstandingquestionsandalittlemoreonFluencyandProblem-solvingandreasoningquestions.TheProgressing pathwayalsoincludesthe‘Goldstar’question(s).

Choosingapathway

Thereareavarietyofwaysofdeterminingtheappropriatepathwayforstudentsthroughthecourse.Schoolsandindividual teachersshouldfollowthemethodthatworksbestforthem.Ifrequired,theWarm-upquizatthestartofeachchaptercanbe usedasadiagnostictool.Thefollowingarerecommendedguidelines:

• Astudentwhogets 40% orlowershouldheavilyrevisecoreconceptsbeforedoingtheBuildingquestions,andmayrequire furtherassistance.

• Astudentwhogetsbetween 40% and 75% shoulddotheBuildingquestions.

• Astudentwhogets 75% andhighershoulddotheProgressingquestions.

Forschoolsthathaveclassesgroupedaccordingtoability,teachersmaywishtoseteithertheBuildingorProgressingpathwaysas thedefaultpathwayforanentireclassandthenmakeindividualalterationsdependingonstudentneed.Forschoolsthathave mixed-abilityclasses,teachersmaywishtosetanumberofpathwayswithintheoneclass,dependingonpreviousperformance andotherfactors.

* Thenomenclatureusedtolistquestionsisasfollows:

3,4:completeallpartsofquestions3and4

• 1–4:completeallpartsofquestions1,2,3and4

• 10(½):completehalfofthepartsfromquestion 10(a,c,e,.....orb,d,f,.....)

• 2–4(½):completehalfofthepartsofquestions2,3and4

• –:completenoneofthequestionsinthissection.

• 4(½),5:completehalfofthepartsofquestion4 andallpartsofquestion5

•

Guidetothisresource

PRINTTEXTBOOKFEATURES

1 NEW Newlessons: authoritativecoverageofnewtopicsintheAustralianCurriculum9.0intheformofnew,road-tested lessonsthroughouteachbook.

2 AustralianCurriculum9.0: contentstrands,sub-strandsandcontentdescriptionsarelistedatthebeginningofthechapter (seetheteachingprogramformoredetailedcurriculumdocuments)

3 Inthischapter: anoverviewofthechaptercontents

4 NEW Quickreference: Multiplication,primenumber,fractionwallanddivisibilityrulestablesatthebackofthebook

5 Chapterintroduction: setscontextforstudentsabouthowthetopicconnectswiththerealworldandthehistoryof mathematics

6 Warm-upquiz: aquizforstudentsonthepriorknowledgeandessentialskillsrequiredbeforebeginningeachchapter

7 Sectionslabelledtoaidplanning: Allnon-coresectionsarelabelledas‘Consolidating’(indicatingarevisionsection)or withagoldstar(indicatingatopicthatcouldbeconsideredchallenging)tohelpteachersdecideonthemostsuitablewayof approachingthecoursefortheirclassorforindividualstudents.

8 Learningintentions: setsoutwhatastudentwillbeexpectedtolearninthelesson

9 Lessonstarter: anactivity,whichcanoftenbedoneingroups,tostartthelesson

10 Keyideas: summarisestheknowledgeandskillsforthesection

11 Workedexamples: solutionsandexplanationsofeachlineofworking,alongwithadescriptionthatclearlydescribesthe mathematicscoveredbytheexample.Workedexamplesareplacedwithintheexercisesotheycanbereferencedquickly, witheachexamplefollowedbythequestionsthatdirectlyrelatetoit.

12 Nowyoutry: try-it-yourselfquestionsprovidedaftereveryworkedexampleinexactlythesamestyleastheworkedexample togivestudentsimmediatepractice

Workingprograms: differentiatedquestionsetsfortwoabilitylevelsinexercises

14 Puzzlesandgames: ineachchapterprovideproblem-solvingpracticeinthecontextofpuzzlesandgamesconnectedwith thetopic

15 Gentlestarttoexercises: theexercisebeginsatUnderstandingandthenFluency,withtheﬁrstquestionalwayslinkedto theﬁrstworkedexampleinthelesson

16 Chapterchecklist: achecklistofthelearningintentionsforthechapter,withexamplequestions

17 Chapterreviews: withshort-answer,multiple-choiceandextended-responsequestions;questionsthatare‘GoldStar’are clearlysignposted

18 Maths@Work: asetofextendedquestionsacrosstwopagesthatgivepracticeatapplyingthemathematicsofthechapter toreal-lifecontexts

19 NEW Technologyandcomputationalthinking activityineachchapteraddressesthecurriculum’sincreasedfocusonthe useofdifferentformsoftechnology,andtheunderstandingandimplementationofalgorithms

20 Modellingactivities: anactivityineachchaptergivesstudentstheopportunitytolearnandapplythemathematicalmodelling processtosolverealisticproblems

INTERACTIVETEXTBOOKFEATURES

21 NEW TargetedSkillsheets,oneforeachlesson,focusonasmallsetofrelatedFluency-styleskillsforstudentswhoneed extrasupport,withquestionslinkedtoworkedexamples

22 Workspaces: almosteverytextbookquestion–including allworking-out–canbecompletedinsidetheInteractive Textbookbyusingeitherastylus,akeyboardandsymbol palette,oruploadinganimageofthework

23 Self-assessment: studentscanthenself-assesstheir ownworkandsendalertstotheteacher.Seethe Introductiononpagexformoreinformation

24 Interactivequestiontabs canbeclickedonsothat onlyquestionsincludedinthatworkingprogramare shownonthescreen

25 HOTmathsresources: ahugecateredlibraryofwidgets, HOTsheetsandwalkthroughsseamlesslyblendedwith thedigitaltextbook

26 Desmosgraphingcalculator,scientiﬁccalculatorand geometrytoolarealwaysavailabletoopenwithinevery lesson

27 Scorcher: thepopularcompetitivegame

28 Workedexamplevideos: everyworkedexampleis linkedtoahigh-qualityvideodemonstration,supporting bothin-classlearningandtheﬂippedclassroom

29 Arevisedsetof differentiatedauto-marked practicequizzes perlessonwithsavedscores

30 Auto-markedmaths literacyactivitiesteststudents ontheirabilitytounderstandandusethekey mathematicallanguageusedinthechapter 29

31 Auto-markedpriorknowledgepre-test (the‘Warm-upquiz’oftheprintbook)fortestingtheknowledgethatstudents willneedbeforestartingthechapter

32 Auto-markedprogressquizzesandchapterreviewquestions inthechapterreviewscanbecompletedonline

DOWNLOADABLEPDFTEXTBOOK

33 InadditiontotheInteractiveTextbook,a PDFversionofthetextbook hasbeenretainedfortimeswhenuserscannotgo online.PDFsearchandcommentingtoolsareenabled.

ONLINETEACHINGSUITE

34 NEW DiagnosticAssessmentTool included withtheOnlineTeachingSuiteallowsforﬂexible diagnostictesting,reportingandrecommendations forfollow-upworktoassistyoutohelpyour studentstoimprove

35 NEW PowerPointlesson summariescontainthe mainelementsofeachlessoninaformthatcanbe annotatedandprojectedinfrontofclass

36 LearningManagementSystem withclass andstudentanalytics,includingreportsand communicationtools

37 Teacherviewofstudents’workand self-assessment allowstheteachertoseetheir class’sworkout,howstudentsintheclassassessed theirownwork,andany‘redﬂags’thattheclass hassubmittedtotheteacher

38 Powerfultestgenerator withahugebankof levelledquestionsaswellasready-madetests

39 Revampedtaskmanager allowsteachersto incorporatemanyoftheactivitiesandtoolslisted aboveintoteacher-controlledlearningpathways thatcanbebuiltforindividualstudents,groupsof studentsandwholeclasses

40 Worksheets,Skillanddrill,mathsliteracy worksheets,and twodifferentiatedchapter testsineverychapter,providedineditableWord documents

41 Moreprintableresources: allPre-tests andProgressquizzesandApplicationsand problem-solvingtasksareprovidedinprintable worksheetversions

1 Consumer arithmetic

Essentialmathematics:whyskillswithpercentagesand consumerarithmeticareimportant

Masteringmoneymanagementskillsareanessentialfoundationforyoutoachievepersonal ﬁnancialindependenceandhavesuccessinyourbusinessventures.

Essentialskillsusingpercentagesincludecalculationsofproﬁts,discounts,costprice,sellingprice andGST.Bycomparingdiscountedsellingprices,thebestdealcanbefound.

Incometaxcalculationshelpworkersandbusinessestobeawareoflegaltaxobligations,keep recordsforeligibledeductions,andnotbefacedwithunexpectedandcostlytaxdebtsattheend ofaﬁnancialyear.

Whenyoujointheworkforceandearnawage,itisimportanttoprepareapersonalbudget.This includesasavingsplantopayﬁxedandvariablecost-of-livingexpensesandmoneyputasidefor personaluse.

Calculationsusingsimpleandcompoundinterestratesenableapersontocomputeandcompare thefullcostofloans,debtrepayments,andthepotentialfuturevalueofinvestments.

Inthischapter

1AReviewofpercentages (Consolidating)

1BApplicationsofpercentages

1CIncome

1DIncometaxation

1EBudgeting

1FSimpleinterest

1GCompoundinterest

1HInvestmentsandloans

1IComparinginterestusing technology

AustralianCurriculum9.0

ALGEBRA

Usemathematicalmodellingtosolve appliedproblemsinvolvinggrowthand decay,includingﬁnancialcontexts; formulateproblems,choosingtoapply linear,quadraticorexponentialmodels; interpretsolutionsintermsofthe situation;evaluateandmodifymodels asnecessaryandreportassumptions, methodsandﬁndings(AC9M10A04) ©ACARA

Onlineresources

Ahostofadditionalonlineresources areincludedaspartofyourInteractive Textbook,includingHOTmathscontent, videodemonstrationsofallworked examples,auto-markedquizzesand muchmore.

1 Findthefollowingtotals.

$87560 ÷ 52 (tothenearestcent) e

2 Expressthefollowingfractionswithdenominatorsof 100.

3 Writeeachofthefollowingfractionsasdecimals.

4 Roundthefollowingdecimalstotwodecimalplaces.

5 Givethevaluesofthepronumeralsinthefollowingtable.

6 Calculatethefollowingannualincomesforeachofthesepeople.Use 52 weeksinayear. Tom: $1256 perweek a Sally: $15600 permonth b Anthony: $1911 perfortnight c Crystal: $17.90 perhour,for 40 hoursperweek,for 50 weeksperyear d

7 Withoutacalculator,ﬁnd:

8 Findthesimpleinterestonthefollowingamounts.

$400 at 5% p.a.for 1 year a $5000 at 6% p.a.for 1 year b $800 at 4% p.a.for 2 years c

9 Completethefollowingtable,givingthevaluesofthepronumerals.

10 Thefollowingamountsincludethe 10% GST.Bydividingeachoneby 1.1,ﬁndtheoriginal costsbeforetheGSTwasaddedtoeach.

$55 a $61.60 b $605 c

1A 1A Reviewofpercentages

Learningintentions

• Tounderstandthatapercentageisanumberoutof 100

• Tobeabletoconvertdecimalsandfractionstopercentagesandviceversa

• Tobeableto ndthepercentageofaquantity

Keyvocabulary: percentage,denominator

Itisimportantthatweareabletoworkwith percentagesinoureverydaylives.Banks,retailers andgovernmentsusepercentageseverydaytowork outfeesandprices.

Lessonstarter:Whichoptionshould Jamiechoose?

Jamiecurrentlyearns $68460 p.a.(peryear)andisgiven achoiceoftwodifferentpayrises.Whichshouldshe chooseandwhy?

ChoiceA:Increaseof $25 perweek

ChoiceB:Increaseof 2% onperannumsalary

Keyideas

Bankswillusepercentagestoworkoutaccountfees andhowmuchinteresttocharge.

A percentage means‘outof 100’.Itcanbewrittenusingthesymbol %,orasafractionor adecimal.

Forexample: 75 percent = 75%= 75 100 or 3 4 or 0.75

Toconvertafractionoradecimaltoapercentage,multiplyby 100

Toconvertapercentagetoafraction,writeitwitha denominator of 100 andsimplify.

15%= 15 100 = 3 20

Toconvertapercentagetoadecimal,divideby 100 15%= 15 ÷ 100 = 0.15

Toﬁndapercentageofaquantity,writethepercentageasafractionora decimal,thenmultiplybythequantity,i.e. x% of P = x 100 × P

Exercise1A

Und er stand ing

1 Completethefollowingusingthewords multiply or divide

a Toconvertadecimaltoapercentage by 100

b Toconvertapercentagetoadecimal by 100

c Toconvertafractiontoapercentage by 100

d Toconvertapercentagetoafraction by 100.

2 Completethefollowingtoexpressasafractioninpart a andadecimalinpart b.

a 7%= 7 i 23%= ii

b 18%= i 5%= ii

3 Completethefollowing

HintforQ3:Cancelanyfractions beforemultiplying.

Example1Convertingtoapercentage

Writeeachofthefollowingasapercentage.

Explanation

Writeusingadenominatorof 100 bymultiplying numeratoranddenominatorby 5 Alternatively,multiplythefractionby 100

Multiplythefractionby 100 Cancelcommonfactors,thensimplify.

c 0.07 ×

So 0.07 = 7%

Nowyoutry

Multiplythedecimalby 100 Movethedecimalpointtwoplacestotheright.

Writeeachofthefollowingasapercentage.

Converteachfractiontoapercentage.

HintforQ4:Firstwriteusinga denominatorof 100 or, alternatively,multiplyby 100

Writethesedecimalsaspercentages.

HintforQ5:Tomultiplyby 100, movethedecimalpointtwoplaces totheright.

Example2Writingpercentagesassimpliﬁedfractions

Writeeachofthefollowingpercentagesasasimpliﬁedfraction.

Solution

a 37%= 37 100

b 58%= 58 100 = 29 50

Explanation

Writethepercentagewithadenominatorof 100

Simplify 58 100 bycancelling,usingtheHCFof 58 and 100, whichis 2

= 29 50 c 6 1 2 %= 6 1 2 100 = 13 200

Writethepercentagewithadenominatorof 100

Doublethenumerator (6 1 2 ) andthedenominator(100) sothatthenumeratorisawholenumber.

Nowyoutry

Writeeachofthefollowingpercentagesasasimpliﬁedfraction.

Writeeachpercentageasasimpliﬁedfraction.

HintforQ6:Write withadenominator of 100,thensimplify ifpossible.

Example3Writingapercentageasadecimal

Convertthesepercentagestodecimals.

Solution

a 93%= 93 ÷ 100 = 0.93

b 7%= 7 ÷ 100 = 0.07

c 30%= 30 ÷ 100 = 0.3

Nowyoutry

Convertthesepercentagestodecimals.

Explanation

Dividethepercentageby 100.Thisisthesameasmoving thedecimalpointtwoplacestotheleft.

Dividethepercentageby 100

Dividethepercentageby 100 Write 0.30 as 0.3

7 Convertthesepercentagestodecimals.

Example4Findingapercentageofaquantity

Find 42% of $1800

Solution

42% of $1800 = 0.42 × 1800 = $756

Explanation

Rememberthat‘of’meanstomultiply.

Write 42% asadecimalorafraction: 42%= 42 100 = 0.42

Thenmultiplybytheamount.

Ifusingacalculator,enter 0.42 × 1800.

Withoutacalculator: 42 ✟✟ 100 1 × 18✚✚ 00 = 42 × 18 = 756

Nowyoutry

Find 36% of $2300

8 Useacalculatortoﬁndthefollowing.

Problem-solving and reasoning

9 A 300 gpiecontains 15 gofsaturatedfat.

a Whatfractionofthepieissaturatedfat?

b Whatpercentageofthepieissaturatedfat?

HintforQ9: 15 goutof 300 g.

10 About 80% ofthemassofahumanbodyiswater.IfHugois 85 kg,howmanykilogramsofwaterare inhisbody?

11 Remaspends 12% ofthe 6.6 hourschooldayinmaths.Howmanyminutesarespentinthe mathsclassroom?

12 Inacricketmatch,Brettspent 35 minutesbowling.

Histeam’stotalﬁeldingtimewas 3 1 2 hours. Whatpercentageoftheﬁeldingtime,correcttotwo decimalplaces,didBrettspendbowling?

HintforQ12:Firstconvert hourstominutes,andthen writeafractioncomparing times.

13 Malcolmlost 8 kg,andnowweighs 64 kg.Whatpercentageofhisoriginalweightdidhelose?

14 47.9% ofalocalcouncil’sbudgetisspentongarbagecollection.Ifaratepayerpays $107.50 per quarterintotalratecharges,howmuchdotheycontributeinayeartogarbagecollection?

15 BelowisthepreliminarydataonAustralia’spopulationgrowth,asgatheredbytheAustralianBureau ofStatisticsforagivenyear.

a Calculatethepercentagechangeforeachstateandterritoryshown usingthepreviousyear’spopulation,andcompletethetable.

b WhatpercentageofAustralia’soverallpopulation,correctto onedecimalplace,islivingin: NSW? i Vic? ii WA? iii

c Useaspreadsheettodrawapiechart(i.e.sectorgraph) showingthepopulationsoftheeightstatesandterritoriesinthetable.Whatpercentageof thetotalisrepresentedbyeachstate/territory?Roundyouranswertothenearestpercent.

d Inyourpiechartforpart c,whatistheanglesizeofthesectorrepresentingVictoria?

1B Applicationsofpercentages

Learningintentions

• Tounderstandwhatapercentageincreaseordecreaseofaquantityrepresents

• Tobeabletoincreaseanddecreaseanamountbyagivenpercentage

• Tobeabletousepercentageincreaseanddecreasetocalculateasellingpriceoradiscountedprice

• Tobeabletodeterminethepro tmadeonanitemandcalculatethisasapercentagepro t

Keyvocabulary: discount,pro t,sellingprice,costprice

Therearemanyapplicationsofpercentages.Pricesare oftenincreasedbyapercentagetocreateaproﬁtor decreasedbyapercentagewhenonsale.

Whengoodsarepurchasedbyastore,thecost totheowneriscalledthecostprice.Thepriceofthe goodssoldtothecustomeriscalledthesellingprice. Thispricewillvaryaccordingtowhetherthestoreis havingasaleordecidestomakeacertainpercentage proﬁt.

Lessonstarter:Discounts

Discussasaclass:

• Whichisbetter: 20% offora $20 discount?

Duringasale,aretailshopwilloftenofferapercentage discount,whereapercentageofthesellingpriceis subtractedtoformanewdiscountedsellingprice.

• Ifadiscountof 20% or $20 resultedinthesameprice,whatwastheoriginalprice?

• Whyarepercentagesusedtoshowdiscounts,ratherthanadollaramount?

Keyideas

Toincreasebyagivenpercentage,multiplybythesumof 100% andthegivenpercentage. Forexample:Toincreaseby 12%,multiplyby 112% or 1.12

Todecreasebyagivenpercentage,multiplyby 100% minusthegivenpercentage. Forexample:Todecreaseby 20%,multiplyby 80% or 0.8.

Proﬁtsanddiscounts:

• Thenormalpriceofthegoodsrecommendedbythemanufactureriscalledtheretailprice.

• Whenthereisasaleandthegoodsarepricedlessthantheretailprice,theyaresaid tobe discounted.

• Proﬁt istheamountofmoneymadebysellinganitemorserviceformorethanitscost.

• Proﬁt = sellingprice costprice,where sellingprice istheamounttheitemissold forand costprice istheoriginalcosttotheseller.

• Percentageproﬁt = proﬁt costprice × 100

• Percentagediscount = discount costprice × 100

Exercise1B

1 Bywhatnumberdoyoumultiplytoincreaseanamountby:

2 Bywhatnumberdoyoumultiplytodecreaseanamountby:

3 Usethewords sellingprice or costprice tocompletethefollowing.

a Aproﬁtismadewhenthe ismorethanthe

b Adiscountinastorereducesthe

c Proﬁt =

4 Decidehowmuchproﬁtorlossismadeineachofthefollowingsituations.

a sellingprice = $20

costprice = $15

costprice = $17.50

b sellingprice = $20

costprice = $250

c sellingprice = $234

Example5Increasingbyagivenpercentage

Increase $370 by 8%

Solution

$370 × 1.08 = $399.60

Nowyoutry

Increase $650 by 12%

Increase $90 by 5% a

Increase $400 by 10%

Increase $55 by 20%

Increase $490 by 8%. d

Increase $50 by 12% e

Increase $7000 by 3% f

Increase $49.50 by 14% g

Increase $1.50 by 140% h

Explanation

100%+ 8%= 108%

Write 108% asadecimal(orfraction)andmultiply bytheamount.

Showtwodecimalplacestorepresentthecents.

Example6Decreasingbyagivenpercentage

Decrease $8900 by 7%.

Solution

$8900 × 0.93 = $8277.00

Explanation

100% −7%= 93%

Write 93% asadecimal(orfraction)andmultiplyby theamount.

Remembertoputtheunitsinyouranswer.

Nowyoutry

Decrease $2700 by 18%

Decrease $1500 by 5%

Decrease $400 by 10%

6 HintforQ6:Todecreaseby

Decrease $470 by 20%. c Decrease $80 by 15%.

Decrease $550 by 25%

Decrease $119.50 by 15%

Decrease $49.50 by 5%

Decrease $47.10 by 24% h

Example7Calculatingproﬁtandpercentageproﬁt

Thecostpriceforanewcaris $24780 anditissoldfor $27600 Calculatetheproﬁt. a Calculatethepercentageproﬁt,totwodecimalplaces.

Solution

Explanation

a Proﬁt = sellingprice costprice Writetherule. = $27600−$24780

Substitutethevaluesandevaluate. = $2820

b Percentageproﬁt = proﬁt costprice × 100 Writetherule. = 2820 24780 × 100

Substitutethevaluesandevaluate. = 11.38% Roundyouranswerasinstructed.

Nowyoutry

Thecostpriceforanewrefrigeratoris $888 anditissoldfor $997 Calculatetheproﬁt. a Calculatethepercentageproﬁt,totwodecimalplaces. b

7 Copyandcompletethetableonproﬁtsandpercentageproﬁt.

Costprice Sellingprice Proﬁt Percentageproﬁt

a $10 $16

b $240 $300

c $15 $18

d $250 $257.50

e $3100 $5425

f $5.50 $6.49

HintforQ7: Percentageproﬁt = proﬁt costprice × 100

Example8Findingthesellingprice

Aretailerbuyssomecalicomaterialfor $43.60 aroll.Hewishestomakea 35% proﬁt.

Whatwillbethesellingpriceperroll?

a Ifhesells 13 rolls,whatproﬁtwillhemake? b

Solution

a Sellingprice = 135% of $43.60

= 1.35 × $43.60

= $58.86 perroll

b Proﬁtperroll = $58.86−$43.60

Explanation

Fora 35% proﬁttheunitpriceis 135%

Write 135% asadecimal (1.35) andevaluate.

Sellingprice costprice = $15.26

Totalproﬁt = $15.26 × 13

Thereare 13 rollsat $15.26 proﬁtperroll. = $198.38

Nowyoutry

Aretailerbuysswimsuitsfor $32 persuit.Shewishestomakea 30% proﬁt.

Whatwillbethesellingpriceofeachswimsuit? a Ifshesells 20 swimsuits,whatproﬁtwillshemake? b

8 Aretailerbuyssomechristmassnowglobesfor $41.80 each. Shewishestomakea 25% proﬁt.

a Whatwillbethesellingpricepersnowglobe?

b Ifshesellsaboxof 25 snowglobes,whatproﬁtwill shemake?

9 Asecond-handcardealerboughtatrade-incarfor $1200 andwishestoresellitfora 28% proﬁt.What istheresaleprice?

Example9Findingthediscountedprice

Ashirtworth $25 isdiscountedby 15%. Whatisthesellingprice? a Howmuchisthesaving? b

Solution

Explanation

a Sellingprice = 85% of $2515% discountmeanstheremustbe 85% left (100% −15%) = 0.85 × $25 Convert 85% to 0.85 andmultiplybytheamount. = $21.25

b Saving = 15% of $25

Yousave 15% oftheoriginalprice. = 0.15 × $25

Convert 15% to 0.15 andmultiplybytheoriginal price. = $3.75

orsaving = $25−$21.25 = $3.75

Nowyoutry

Saving = originalprice discountedprice

Asuitcaseworth $220 isdiscountedby 35%. Whatisthesellingprice? a Howmuchisthesaving? b

10 Samanthabuysawetsuitfromthesportsstorewheresheworks.Itsoriginalpricewas $79.95 Employeesreceivea 15% discount. Whatisthesellingprice? a HowmuchwillSamanthasave? b

11 Atravelagentoffersa 12.5% discountonairfaresifyoutravel duringMayorJune. ThenormalfaretoLondon(return trip)is $2446 a Whatisthesellingprice? b Howmuchisthesaving?

12 Astoresellssecond-handgoodsat 40% offtherecommendedretail price.Alawnmowerisvalued at $369

Whatisthesellingprice? a Howmuchwouldyousave? b

Problem-solving and reasoning

13–1615–18

13 Skijacketsaredeliveredtoashopinpacksof 50 for $3500.Theshopownerwishestomakea 35% proﬁt.

a Whatwillbethetotalproﬁtmadeonapack?

b Whatistheproﬁtoneachjacket?

14 Apairofsportsshoesisdiscountedby 47%.Therecommendedpricewas $179

a Whatistheamountofthediscount?

b Whatwillbethediscountedprice?

15 JeansarepricedataMaysalefor $89.Ifthisisasavingof 15% offthesellingprice,whatdothejeansnormallysellfor?

16 Discountedtyresarereducedinpriceby 35%.Theynowsellfor $69 each.Determine:

a thenormalpriceofonetyre

b thesavingifyoubuyonetyre.

17 Thelocalshoppurchasesacartonofcontainersfor $54.Eachcontainerissoldfor $4 Ifthecartonhad 30 containers,determine: theprofitpercontainer a thepercentageprofitpercontainer,totwodecimalplaces b theoverallprofitpercarton

c theoverallpercentageproﬁt,totwodecimalplaces.

18 Aretailerbuysabookfor $50 andwantstosellitfora 26% proﬁt.The 10% GSTmustthenbeaddedontothecostofthebook.

a Calculatetheproﬁtonthebook.

b HowmuchGSTisaddedtothecostofthebook?

c Whatistheadvertisedpriceofthebook,includingtheGST?

d Findtheoverallpercentageincreaseoftheﬁnalsellingprice comparedtothe $50 costprice.

Buildingagazebo — 19

19 Christopherdesignsagazeboforanewhouse.Hebuysthetimberfromaretailer,whosourcesitat wholesalepriceandthenmarksitupbeforesellingtoChristopheratretailprice.Thetablebelow showsthewholesalepricesaswellasthemark-upforeachtypeoftimber.

DetermineChristopher’soverallcostforthematerial,includingthemark-up. a Determinetheprofitmadebytheretailer. b Determinetheretailer’soverallpercentageprofit,totwodecimalplaces. c Iftheretailerpays 27% ofhisprofitsintax,howmuchtaxdoeshepayonthissale? d

1C 1C Income

Learningintentions

• Tounderstandarangeofdifferentwaysinwhichemployeescanbepaid

• Toknowhownetincomeiscalculatedfromgrossincomeanddeductions

• Tobeabletocalculatewagesforovertimeandshiftwork

• Tobeabletocalculatecommission

Keyvocabulary: wages,commission,salary,fees,grossincome,overtime,deductions,netincome,timeandahalf, doubletime,deductions

Youmayhaveearnedmoneyforbaby-sittingor deliveringnewspapersorhaveapart-timejob.As youmoveintotheworkforceitisimportantthatyou understandhowyouarepaid.

Lessonstarter:Whoearnswhat?

Asaclass,discussthedifferenttypesofjobsheldby differentmembersofeachperson’sfamily,anddiscuss howtheyarepaid.

• Whatarethedifferentwaysthatpeoplecanbe paid?

• Whatdoesitmeanwhenyouworkfewerthan full-timehours?

• Whatdoesitmeanwhenyouworklongerthan full-timehours?

Whatothertypesofincomecanpeopleintheclassthinkof?

Keyideas

Methodsofpayment

Employeescanbepaidindifferentways,according totheirtypeofwork.Forexample,employeescanbe paidanhourlyrate,asalary,acommission,orafee.

Hourly wages:Youarepaidacertainamountperhourworked.

Commission:Youarepaidapercentageofthetotalamountofsales.

Salary:Youarepaidasetamountperyear,regardlessofhowmanyhoursyouwork.

Fees:Youarepaidaccordingtothechargesyouset,e.g.doctors,lawyers,contractors.

Sometermsyoushouldbefamiliarwithinclude:

• Grossincome:thetotalamountofmoneyyouearnbeforetaxesandotherdeductions

• Deductions:moneytakenfromyourincomebeforeyouarepaid,e.g.taxation,union fees,superannuation

• Netincome:theamountofmoneyyouactuallyreceiveafterthedeductionsaretaken fromyourgrossincome

Netincome = grossincome deductions

Paymentsbyhourlyrate

Ifyouarepaidbythehouryouwillbepaidanamountperhourforyournormalworkingtime. Ifyouwork overtime (hoursbeyondthenormalworkinghours),theratesmaybedifferent.

Usually,normalworkingtimeis 38 hoursperweek.

Normal: 1.0 × normalrate

Timeandahalf: 1.5 × normalrate

Doubletime: 2.0 × normalrate

Ifyouworkshiftworkthehourlyratesmaydifferfromshifttoshift.

Forexample:

6 a.m.– 2 p.m.

2 p.m.– 10 p.m.

10 p.m.– 6 a.m.

Exercise1C

Und er stand ing

$24.00/hour (regularrate)

$27.30/hour (afternoonshiftrate)

$36.80/hour (nightshiftrate)

1 Matchthejobdescriptionontheleftwiththemethodofpayment ontheright.

Jennieispaid $85600 peryear a hourlywage A

Danielleearns 3% ofallthesalesshemakes b fee B

Jettearns $18.90 perhourworked c commission C

Stuartcharges $450 foraconsultation d salary D

2 Callumearns $1090 aweekandhasannualdeductionsof $19838

HintforQ2: Net = total deductions WhatisCallum’snetincomefortheyear?Assume 52 weeks inayear.

3 IfTaoearns $15.20 perhour,calculatehis:

time-and-a-halfrate a double-timerate b

Example10Findinggrossandnetincome(includingovertime)

Paulineispaid $13.20 perhouratthelocalstockyardtomuckoutthestalls.Hernormalhoursof workare 38 hoursperweek.Shereceivestimeandahalfforthenext 4 hoursworkedanddouble timeafterthat.

Whatwillbehergrossincomeifsheworks 50 hours? a Ifshepays $220 perweekintaxationand $4.75 inunionfees,whatwillbeherweekly netincome?

b Solution

a Grossincome = 38 × $13.20 + 4 × 1.5 × $13.20 + 8 × 2 × $13.20 = $792

b Netincome = $792− ($220 + $4.75) = $567.25

Nowyoutry

Explanation

Normal 38 hours

Overtimeratefornext 4 hours:timeanda half = 1.5 × normal

Overtimeratefornext 8 hours:double time = 2 × normal

Netincome = grossincome deductions

Tobyispaid $17.50 perhourathissupermarketjob.Hisnormalhoursofworkare 38 hoursperweek. Hereceivestimeandahalfforthenext 6 hoursworkedanddoubletimeafterthat.

Whatwillbehisgrossincomeifheworks 48 hoursinaweek? a

Ifhepays $240 perweekintaxationand $6.50 inunionfees,whatwillbehisweeklynetincome?

4 Jackispaid $14.70 perhour.Hisnormalhoursofworkare 38 hoursperweek.Hereceivestimeand ahalfforthenext 2 hoursworkedanddoubletimeafterthat.

a Whatwillbehisgrossincomeifheworks 43 hours?

b Ifhehas $207.20 ofdeductions,whatwillbehisweeklynetincome?

5 Copyandcompletethistable.

Example11Calculatingshiftwork

Michaelisashiftworkerandispaid $31.80 perhourforthemorningshift, $37.02 perhourforthe afternoonshiftand $50.34 perhourforthenightshift.Eachshiftis 8 hours.Inagivenfortnighthe worksfourmorning,twoafternoonandthreenightshifts.Calculatehisgrossincome.

Solution Explanation

Grossincome = 4 × 31.80 × 84 morningshiftsat $31.80 perhourfor 8 hours

+ 2 × 37.02 × 82 afternoonshiftsat $37.02 perhourfor 8 hours

+ 3 × 50.34 × 83 nightshiftsat $50.34 perhourfor 8 hours

= $2818.08

Nowyoutry

Grossincomebecausetaxhasnotbeenpaid.

Kateisashiftworkerandispaid $26.20 perhourforthemorningshift, $32.40 perhourforthe afternoonshiftand $54.25 perhourforthenightshift.Eachshiftis 8 hours.Inagivenfortnightshe worksﬁvemorning,threeafternoonandtwonightshifts.Calculatehergrossincome.

6 Gregworksshiftsataprocessingplant.Inagivenrostered fortnightheworks:

• 3 dayshifts($31.80 perhour)

• 4 afternoonshifts($37.02 perhour)

• 4 nightshifts($50.34 perhour).

a Ifeachshiftis 8 hourslong,determineGreg’sgross incomeforthefortnight.

b Iftheanswertopart a isGreg’saveragefortnightly income,whatwillbehisgrossincomefora year(i.e. 52 weeks)?

HintforQ6: Afortnight = 2 weeks

Manyhospitalworkersworkshiftwork.

Example12Calculatingincomeinvolvingcommission

Jeffsellsmembershipstoagymandreceives $225 perweekplus 5.5% commissiononhissales. Calculatehisgrossincomeaftera 5-dayweek.

Solution

Totalsales = $4630

Commission = 5.5% of $4630 = 0.055 × $4630 = $254.65

Grossincome = $225 + $254.65 = $479.65

Nowyoutry

Explanation

Determinethetotalsales: 680 + 450 + 925 + 1200 + 1375

Determinethecommissiononthetotalsalesat 5.5% by multiplying 0.055 bythetotalsales.

Grossincomeis $225 pluscommission.

Jinsellsvacuumcleanersandreceives $250 perweekplus 4.3% commissiononhersales.

Calculatehergrossincomeaftera 5-dayweek.

7 Acarsalesmanearns $5000 amonthplus 3.5% commissiononallsales.InthemonthofJanuary hissalestotalwas $56000.Calculate: hiscommissionforJanuary a hisgrossincomeforJanuary b

8 Arealestateagentreceives 2.75% commissiononthesaleofahousevaluedat $1250000 Findthecommissionearned.

9 Sarahearnsanannualsalaryof $77000 plus 2% commissiononallsales.Find: a herweeklybasesalarybeforesales

b hercommissionforaweekwhenhersalestotalled $7500

c hergrossweeklyincomefortheweekinpart b

d herannualgrossincomeifovertheyearhersalestotalled $571250

Problem-solving and reasoning

10 IfSimonereceives $10000 onthesaleofapropertyworth $800000,calculateherrateofcommission.

11 Jonahearnsacommissiononhissalesoffashionitems.Forgoods tothevalueof $2000 hereceives 6% andforsalesover $2000 he receives 9% ontheamountinexcessof $2000.Inagivenweek hesold $4730 worthofgoods.Findthecommissionearned.

12 Williamearns 1.75% commissiononallsalesattheelectrical goodsstorewhereheworks.IfWilliamearns $35 incommission onthesaleofonetelevision,howmuchdidtheTVsellfor?

13 Refertothepayslipbelowtoanswerthefollowingquestions.

KugerIncorporated

EmployeeID: 75403A

Name:ElmoRodriguez

PayMethod:EFT

Bankaccountname:E.Rodriguez

Bank:MathsvilleCreditUnion

BSB: 102-196 AccountNo: 00754031

Page: 1

PayPeriod: 21/05/2016

TaxStatus:GenExempt

a WhichcompanydoesElmoworkfor?

b WhatisthenameofElmo’sbankandwhatishisaccountnumber?

c HowmuchgrosspaydoesElmoearnin 1 year?

d HowoftendoesElmogetpaid?

e Howmuch,peryear,doesElmosalarysacriﬁce?

f HowmuchisElmo’shealthfundcontributioneachweek?

g Calculate 1 year’sunionfees.

h Usingtheinformationonthispayslip,calculateElmo’sannualtaxandalsohisannualnetincome.

i IfElmoworksMondaytoFridayfrom 9 a.m.to 5 p.m.eachdayforanentireyear,calculatehis effectivehourlyrateofpay.UseElmo’sfortnightlypaymentasastartingpoint.

1D 1D Incometaxation

Learningintentions

• TounderstandhowthekeycomponentsoftheAustraliantaxationsystemwork

• Tobeabletocalculateaperson’staxableincome

• Tobeabletocalculateaperson’staxpayableusingAustraliantaxbrackets Keyvocabulary: taxation,employer,employee,taxreturn,taxableincome,taxbracket,levy,deductions, p.a.(perannum)

Ithasbeensaidthatthereareonlytwo surethingsinlife:deathandtaxes!The AustralianTaxationOfﬁce(ATO)collects taxesonbehalfofthegovernmenttopay foreducation,hospitals,roads,railways, airportsandservices,suchasthepolice andﬁrebrigades.

InAustralia,theﬁnancialyearruns fromJuly 1 toJune 30 thefollowingyear. Peopleengagedinpaidemploymentare normallypaidweeklyorfortnightly.Most ofthempaysomeincometaxeverytime theyarepaidfortheirwork.Thisis knownasthePay-As-You-Gosystem (PAYG).

Attheendoftheﬁnancialyear (June 30),peoplewhoearnedanincome

Theamountofincometaxanemployeemustpayeachﬁnancialyear willdependonsettaxratesestablishedbytheATO.

completeanincometaxreturntodetermineiftheyhavepaidthecorrectamountofincometaxduring theyear.

Iftheypaidtoomuch,theywillreceivearefund.Iftheydidnotpayenough,theywillberequiredto paymore.

TheAustraliantaxsystemisverycomplexandthelawschangefrequently.Thissectioncoversthemain aspectsonly.

Lessonstarter:TheATOwebsite

TheAustralianTaxationOfﬁcewebsitehassomeincometaxcalculators.Useonetoﬁndouthowmuch incometaxyouwouldneedtopayifyourtaxableincomeis:

$10400 perannum(i.e. $200 perweek)

$20800 perannum(i.e. $400 perweek)

$31200 perannum(i.e. $600 perweek)

$41600 perannum(i.e. $800 perweek)

Doesapersonearning $1000 perweekpaytwiceasmuchtaxasapersonearning $500 perweek?

Doesapersonearning $2000 perweekpaytwiceasmuchtaxasapersonearning $1000 perweek?

Keyideas

The Employee You (the employee and taxpayer)

The Employer

The boss (your employer)

ThePAYGtaxsystemworksinthefollowingway.

The ATO

The Australian Taxation Ofﬁce

• Theemployeeworksforandgetspaidbytheemployereveryweek,fortnightormonth.

• Theemployercalculatesthetaxthattheemployeeshouldpayfortheamountearned bytheemployee.

• TheemployersendsthattaxtotheATOeverytimetheemployeegetspaid.

• TheATOpassestheincometaxtothefederalgovernment.

• OnJune 30,theemployergivestheemployeeapaymentsummarytoconﬁrmtheamount oftaxthathasbeenpaidtotheATOonbehalfoftheemployee.

• BetweenJuly 1 andOctober 31,theemployeecompletesa taxreturn andsendsittothe ATO.Somepeoplepayaregisteredtaxagenttodothisreturnforthem.

• Onthistaxreturn,theemployeeliststhefollowing.

– All formsofincome,includinginterestfrominvestments.

– Legitimatedeductionsshownonreceiptsandinvoices,suchaswork-relatedexpenses anddonations.

• Taxableincome iscalculatedusingtheformula: Taxableincome = grossincome deductions

• TherearetablesandcalculatorsontheATOwebsite,suchasthefollowing. Taxableincome

0−$18200 Nil

$18201−$45000 16cforeach $1 over $18200

$45001−$135000

$135001−$190000

$190001 andover

$4288 plus 30cforeach $1 over $45000

$31288 plus 37cforeach $1 over $135000

$51638 plus 45cforeach $1 over $190000

Thistablecanbeusedtocalculatetheamountoftaxyou shouldhave paid(i.e.thetax payable),asopposedtothetaxyou did payduringtheyear(i.e.thetaxwithheld).Each rowinthetableiscalleda taxbracket

• YoumayalsoneedtopaytheMedicare levy.ThisisaschemeinwhichallAustralian taxpayersshareinthecostofrunningthemedicalsystem.Formanypeoplethisiscurrently 2% oftheirtaxableincome.

• Itispossiblethatyoumayhavepaidtoomuchtaxduringtheyearandwillreceivea taxrefund.

• ItisalsopossiblethatyoumayhavepaidtoolittletaxandwillreceivealetterfromtheATO askingforthetaxliabilitytobepaid.

Exercise1D

Und er stand ing

Note:Thequestionsinthisexerciserelatetothetaxtablegiveninthe Keyideas,unlessstatedotherwise.

1 Completethisstatement:Taxableincome = incomeminus

2 Basedonthetableinthe Keyideas,determineifthefollowingstatementsaretrueorfalse?

a Ataxableincomeof $10400 requiresnotaxtobepaid.

b ThehighestincomeearnersinAustraliapay 45 centstaxforeverydollartheyearn.

3 Inthe2024/2025ﬁnancialyear,Ann’staxableincomewas $135000,whichputsherattheverytopof themiddletaxbracketinthetaxtable.Ben’staxableincomewas $190000,whichputshiminahigher taxbracket.IgnoringtheMedicarelevy,howmuchextrataxdidBenpaycomparedtoAnn?

Fluency

Example13Calculatingincometaxpayable

Duringthe2024/2025ﬁnancialyear,Richardearned $1050 perweek($54600 perannum)fromhis employerandothersources,suchasinterestoninvestments.Hehasreceiptsfor $375 for work-relatedexpensesanddonations.

CalculateRichard’staxableincome. a UsethistaxtabletocalculateRichard’staxpayableamount.

Taxableincome

0−$18200 Nil

Taxonthisincome

$18201−$45000 16cforeach $1 over $18200

$45001−$135000

$135001−$190000

$4288 plus 30cforeach $1 over $45000

$31288 plus 37cforeach $1 over $135000

$190001 andover $51638 plus 45cforeach $1 over $190000

RichardmustalsopaytheMedicarelevyof 2% ofhistaxableincome.Howmuchisthe Medicarelevy?

AddthetaxpayableandtheMedicarelevyamounts. d Expressthetotaltaxinpart d asapercentageofRichard’staxableincome,toonedecimalplace. e Duringtheﬁnancialyear,Richard’semployersentatotalof $6000 intaxtotheATO.HasRichard paidtoomuchtaxornotenough?Calculatehisrefundorliability.

f Solution

a Grossincome = $54600

Deductions = $375

Taxableincome = $54225

b Taxpayable:

$4288 + 0.3 × ($54225−$45000)

= $7055.50

Explanation

Taxableincome = grossincome deductions

Richardisinthemiddletaxbracketinthetable, inwhichitsays:

$4288 plus 30cforeach $1 over $45000

Note: 30 centsis $0.30. Continuedonnextpage

c 2 100 × 54225 = $1084.50

d $7055.50 + $1084.50 = $8140

e 8140 54225 × 100 = 15.0% (to 1 d.p.)

f Richardpaid $6000 intaxduringtheyear. Heshouldhavepaid $8140.Richardhas notpaidenoughtax.Hemustpayanother $2140 intax.

Nowyoutry

Medicarelevyis 2% ofthetaxableincome.

ThisisthetotalamountoftaxthatRichard shouldhavepaid.

ThisimpliesthatRichardpaidapproximately 15.0% taxoneverydollar.Thisissometimes readas‘15 centsinthedollar’.

Thisisknownasashortfalloraliability.He willreceivealetterfromtheATOrequesting paymentofthedifference.

$8140−$6000 = $2140

Duringthe2024/2025ﬁnancialyear,Francescaearned $82300 perannumfromheremployerand othersources,suchasinterestoninvestments.Shehasreceiptsfor $530 forwork-relatedexpenses anddonations.

CalculateFrancesca’staxableincome. a Usethetaxtablefromthe Keyideas tocalculateFrancesca’staxpayableamount.

b FrancescamustalsopaytheMedicarelevyof 2% ofhertaxableincome.Howmuchisthe Medicarelevy?

c AddthetaxpayableandtheMedicarelevyamounts. d Expressthetotaltaxinpart d asapercentageofFrancesca’staxableincome,toonedecimal place.

Duringtheﬁnancialyear,Francesca’semployersentatotalof $15000 intaxtotheATO. HasFrancescapaidtoomuchtaxornotenough?Calculateherrefundorliability.

f 4 Duringthe2024/2025ﬁnancialyear,Liamearned $94220 perannumfromhisemployerandother sources,suchasinterestoninvestments.Hehasreceiptsfor $615 forwork-relatedexpensesanddonations. CalculateLiam’staxableincome. a Usethetaxtablefromthe Keyideas tocalculateLiam’staxpayableamount. b LiammustalsopaytheMedicarelevyof 2% ofhistaxableincome.HowmuchistheMedicare levy?

AddthetaxpayableandtheMedicarelevyamounts. d

e Expressthetotaltaxinpart d asapercentageof Liam’staxableincome,toonedecimalplace.

f Duringtheﬁnancialyear,Liam’semployersenta totalof $21000 intaxtotheATO.HasLiampaid toomuchtaxornotenough?Calculatehisrefund orliability.

5 Usethetaxtableinthe Keyideas tocalculatetheincometaxpayableonthesetaxableincomes. $30000 a $60000 b $150000 c $200000 d

6 Leehascometotheendofherfirstfinancialyearemployedasawebsitedeveloper. OnJune 30 shemadethefollowingnotesaboutthefinancialyear.

Grossincomefromemployer

Grossincomefromcasualjob

Interestoninvestments

Donations

Work-relatedexpenses

$58725

$7500

$75

$250

$425

Taxpaidduringtheﬁnancialyear $11000

HintforQ6:Taxableincome = allincomes deductions

CalculateLee’staxableincome. a Usethetaxtableshowninthe Keyideas tocalculateLee’staxpayableamount. b LeemustalsopaytheMedicarelevyof 2% ofhertaxableincome.HowmuchistheMedicarelevy?

c AddthetaxpayableandtheMedicarelevy. d Expressthetotaltaxinpart d asapercentageofLee’staxableincome,toonedecimalplace. e HasLeepaidtoomuchtaxornotenough?Calculateherrefundorliability. f

Problem-solving and reasoning

7,8,10,117,9,11–13

7 Alec’sMedicarelevyis $1750.Thisis 2% ofhistaxableincome.WhatisAlec’staxableincome?

Taraissavingforanoverseastrip.Hertaxableincomeis usuallyabout $20000.Sheestimatesthatshewillneed $5000 forthetrip,sosheisgoingtodosomeextrawork toraisethemoney.HowmuchextrawillTaraneedtoearn inordertosavetheextra $5000 aftertax?

HintforQ8:Usethetaxtableinthe Keyideas toconsiderhowmuch extrataxshewillpay.

WhenSaledusedthetaxtabletocalculatehisincome taxpayable,itturnedouttobe $19288.Whatis histaxableincome?

10 Explainthedifferencebetweenataxrefundandataxliability.

HintforQ9:Usethetaxtablegiven inthe Keyideas todeterminein whichtaxbracketSaledfalls.

11 Gordanalookedatthelastrowofthetaxtableandsaid,‘Itissounfairthatpeopleinthattaxbracket mustpay 45 centsineverydollarintax.’ExplainwhyGordanaisincorrect.

12 Themostrecentsignificantchangeto Australianincometaxrateswasfirst appliedinthe2024/2025financial year.Considerthetaxtablesfor thetwoconsecutivefinancialyears 2023/2024and2024/2025.Notethat theamountslistedfirstineachtable areoftencalledthetax-freethreshold (i.e.theamountthatapersoncan earnbeforetheymustpaytax).

a Therearesomesigniﬁcantchanges betweentheﬁnancialyears 2023/2024and2024/2025. Describethreeofthem.

Taxableincome

0−$18200 Nil

2023/2024

Taxonthisincome

$18201−$37000 19cforeach $1 over $18200

$37001−$80000

$80001−$180000

$180001 andover

Taxableincome

$3572 plus 32.5cforeach $1 over $37000

$17547 plus 37cforeach $1 over $80000

$54547 plus 45cforeach $1 over $180000 2024/2025

Taxonthisincome

0−$18200 Nil

$18201−$45000 16cforeach $1 over $18200

$45001−$135000

$4288 plus 30cforeach $1 over $45000

$135001−$190000 $31288 plus 37cforeach $1 over $135000

$190001 andover

$51638 plus 45cforeach $1 over $190000

b Thefollowingpeoplehadthesametaxableincomeduringbothﬁnancialyears.Findthe differenceintheirtaxpayableamountsandstatewhethertheywereadvantagedor disadvantagedbythechanges,ornotaffectedatall?

Ali:Taxableincome = $5000 i

Charlotte:Taxableincome = $50000 iii

Xi:Taxableincome = $25000 ii

Diego:Taxableincome = $80000 iv

13 BelowisthetaxtableforpeoplewhoarenotresidentsofAustraliabutareworkinginAustralia.

Taxableincome

Taxonthisincome

$0−$135000 30cforeach $1

$135001−$190000 $40500 plus 37cforeach $1 over $135000

$190001 andover $60850 plus 45cforeach $1 over $190000

ComparethistabletotheoneintheexampleforAustralianresidents. Whatdifferencewoulditmaketotheamountoftaxpaidbythesepeopleiftheywerenon-residents ratherthanresidents?

Bill:Taxableincome = $5000 a

Jen:Taxableincome = $25000 b

Scott:Taxableincome = $100000 c

Melinda:Taxableincome = $200000 d

14a Chooseanoccupationorcareerinwhichyouareinterested.Imaginethatyouareworkinginthat job.Duringtheyearyouwillneedtokeepreceiptsforitemsyouhaveboughtthatarelegitimate work-relatedexpenses.Dosomeresearchontheinternetandwritedownsomeofthethingsthat youwillbeabletoclaimaswork-relatedexpensesinyourchosenoccupation.

bi Imagineyourtaxableincomeis $80000.Whatisyourtaxpayableamount?

ii Youjustfoundareceiptfora $100 donationtoaregisteredcharity.Thisdecreasesyourtaxable incomeby $100.Byhowmuchdoesitdecreaseyourtaxpayableamount?

1E 1E Budgeting

Learningintentions

• Toknowthetypesofexpensesthatareincludedinabudget

• Tounderstandhowabudgetisaffectedby xedandvariableexpenses

• Tobeabletocalculatesavingsandotherexpensesbasedontheinformationinabudget

• Tobeabletocalculatethebestbuy(cheapestdeal)fromarangeofoptions

Keyvocabulary: budget, xedexpenses,variableexpenses

Oncepeoplehavebeenpaidtheirincomefortheweek,fortnightormonth,theymustplanhowto spendit.Mostfamiliesworkonabudget,allocatingmoneyforﬁxedexpensessuchasthemortgageor rentandthevarying(i.e.changing)expensesofpetrol,foodandclothing.

Lessonstarter:Expensesforthemonth

Writedowneverythingthatyouthinkyourfamilywouldspendmoneyonfortheweekandthemonth, andestimatehowmuchthosethingsmightcostfortheentireyear.Wheredoyouthinksavingscouldbe made?Whatwouldbesomeadditionalannualexpenses?

Keyideas

A budget isanestimateofincomeandexpensesforaperiodoftime.

Managingmoneyforanindividualissimilartooperatingasmallbusiness.Expensescanbe dividedintotwoareas:

• Fixedexpenses (thesedonotchangeduringatimeperiod):paymentofloans,mortgages, regularbillsetc.

• Variableexpenses (thesecostschangeoveratimeperiod):clothing,entertainment,food etc.(theseareestimates)

Whenyourbudgetiscompletedyoushouldalwayscheckthatyourﬁguresare reasonableestimates.

Bylookingatthebudgetyoushouldbeabletoseehowmuchmoneyisremaining;thiscanbe usedassavingsortobuynon-essentialitems.

Exercise1E

1 Classifyeachexpenselistedbelowasmostlikelyaﬁxedexpenseoravariableexpense.

a monthlyrent

b monthlyphonebillpaymentplan

c takeawayfood

d stationerysuppliesforwork

2 Binhhasanincomeof $956 aweek.Hisexpenses,bothﬁxedandvariable,total $831.72 ofhis income.HowmuchmoneycanBinhsaveeachweek?

3 Roslynhasthefollowingmonthlyexpenses.Mortgage = $1458,mobilephone = $49,internet = $60, councilrates = $350,water = $55,electricity = $190.WhatisthetotalofRoslyn’smonthlyexpenses?

Example14Budgetingusingpercentages

Fionahasanetannualincomeof $36000 afterdeductions.Sheallocatesherbudgetona percentagebasis. Mortgage

a HowmuchshouldFionasave?

Determinetheamountofﬁxedexpenses,includingthemortgage,carloanandeducation.

b Istheamountallocatedforfoodreasonable?

Solution

Explanation

a Fixedexpenses = 55% of $36000 Themortgage,carloanandeducationare 55% intotal.

= 0.55 × $36000 Change 55% toadecimalandmultiplybythenetincome.

= $19800

b Savings = 10% of $36000

Savingsare 10% ofthebudget.

= 0.1 × $36000 Change 10% toadecimalandmultiplybythenetincome.

= $3600

c Food = 25% of $36000

Foodis 25% ofthebudget.

= 0.25 × $36000 Change 25% toadecimalandcalculate.

= $9000 peryear,or

Dividetheyearlyexpenditureby 52 tomakea $173 perweek decisiononthereasonablenessofyouranswer. Thisseemsreasonable.

Nowyoutry

Kylehasanetannualincomeof $64200 afterdeductions.Heallocateshisbudgetonapercentage basis.

Determinetheamountofﬁxedexpensesincludingtherentandbills. a HowmuchshouldKylesave? b Istheamountallocatedfortransportreasonable? c

4 Paulhasanannualincomeof $75000 afterdeductions.Heallocateshisbudgetonapercentagebasis.

a Determinetheamountofﬁxedexpenses,includingthemortgageandloans.

b HowmuchshouldPaulhaveleftoverafterpayingforhismortgage,carloanandpersonalloan?

c Istheamountallocatedforfoodreasonable?

5 Lachlanhasanincomeof $2120 permonth.Ifhe budgets 5% forclothes,howmuchwillheactually havetospendonclotheseachmonth?

Example15Budgetingusingﬁxedvalues

Runningacertaintypeofcarinvolvesyearly,monthlyandweeklyexpenditure.Considerthefollowing vehicle’scosts.

lease

• $210 permonth

registration

• $475 peryear

insurance

• $145 perquarter

servicing

• $1800 peryear

• $37 perweek

petrol

Determinetheoverallcosttorunthiscarforayear.

Whatpercentageofa $70000 salarywouldthisbe,correcttoonedecimalplace?

Solution

a Overallcost = 210 × 12

+ 475

+ 145 × 4

+ 1800

+ 37 × 52

= $7299

Theoverallcosttorunthecaris $7299

b % ofsalary = 7299 70000 × 100

= 10.4% (to 1 d.p.)

Nowyoutry

Explanation

Leasingcost: 12 monthsinayear

Registrationcost

Insurancecost: 4 quartersinayear

Servicingcost

Petrolcost: 52 weeksinayear

Theoverallcostisfoundbyaddingthe individualtotals.

Percentage = carcost totalsalary × 100 Roundasrequired.

Runningaboatinvolvesyearly,monthlyandweeklyexpenditure.Considerthefollowing boat’scosts.

registration

• $342 peryear

insurance

• $120 perquarter

servicing

• $360 peryear

fuel

• $300 permonth

• $2400 peryear

storingboat

Determinetheoverallcosttorunthisboatforayear.

Whatpercentageofa $82000 salarywouldthisbe,correcttoonedecimalplace?

6 Elianaisastudentandhasthefollowingexpensesinherbudget.

• rent $270 perweek

• electricity $550 perquarter

• phoneandinternet $109 permonth

• car $90 perweek

• food $170 perweek

• insurance $2000 ayear

DetermineEliana’scostsforayear. a

HintforQ6:Use 52 weeksina year, 12 monthsinayearand 4 quartersinayear.

WhatpercentageofEliana’snetannualsalaryof $45000 wouldthisbe,correctto onedecimalplace? b

7 ThecostsofsendingastudenttoModkinPrivate Collegeareasfollows.

• feesperterm(4 terms) $1270

• subjectleviesperyear $489

• buildingfundperweek $35

• uniformsandbooksperyear $367

Determinetheoverallcostperyear. a Iftheschoolbillstwiceayear,coveringallthe itemsabove,whatwouldbetheamountof eachpayment?

Howmuchshouldbesavedperweektomake thebiannualpayments?

8 Asmallbusinessownerhasthefollowingexpensestobudgetfor.

• rent $1400 amonth

• phoneline $59 amonth

• wages $1200 aweek

• electricity $430 aquarter

• water $120 aquarter

• insurance $50 amonth

Whatistheannualbudgetforthesmallbusiness? a

Howmuchdoesthebusinessownerneedtomakeeachweekjusttobreakeven? b Ifthebusinessearns $5000 aweek,whatpercentageofthisneedstobespentonwages?

Problem-solving and reasoning

9 Francine’spetrolbudgetis $47 fromherweeklyincomeof $350 Whatpercentageofherbudgetisthis?Giveyouranswertotwodecimalplaces. a Ifpetrolcosts $1.59 perlitre,howmanylitresofpetrol,correcttotwodecimalplaces,isFrancine budgetingforinaweek?

10 Grantworksa 34-hourweekat $15.50 perhour.Hisnetincomeis 65% ofhisgrossincome. Determinehisnetweeklyincome. a IfGrantspends 12% ofhisnetincomeonentertainment,determinetheamountheactuallyspends peryearonentertainment.

b Grantsaves $40 perweek.Whatpercentageofhisnetincomeisthis(totwodecimalplaces)?

11 Darioearns $432 perfortnightatatake-awaypizzashop.Hebudgets 20% forfood, 10% forrecreation, 13% fortransport, 20% forsavings, 25% fortaxationand 12% forclothing. Determinetheactualamountbudgetedforeachcategoryeveryfortnight.

Dario’swageincreasesby 30%

a Determinehowmuchhewouldnowsaveeachweek. b Whatpercentageincreaseistheanswertopart b ontheoriginalamountsaved?

c DeterminetheextraamountofmoneyDariosavesperyearafterhiswageincrease.

d Iftransportisaﬁxedexpense,itspercentageofDario’sbudgetwillchange.Determinethenew percentage.

Example16Calculatingbestbuys

Softdrinkissoldinthreeconvenientpacksatthelocalstore.

• cartonof 36 (375 mL) cansat $22.50

• asix-packof (375 mL) cansat $5.00

• 2-litrebottlesat $2.80

Determinethecheapestwaytobuythesoftdrink.

Solution Explanation

Buyingbythecarton:

Cost = $22.50 ÷ (36 × 375)

TotalmL = 36 × 375 = $0.0017 permL

DividetoworkoutthecostpermL.

Buyingbythesix-pack:

Cost = $5 ÷ (6 × 375)

TotalmL = 6 × 375 = $0.0022 permL

Buyingbythebottle:

Cost = $2.80 ÷ 2000

= $0.0014 permL

Â Thecheapestwaytobuythe softdrinkistobuythe 2-litrebottle.

Nowyoutry

TotalmL = 2 × 1000,since 1 L = 1000 mL.

ComparethethreecostspermL.

Abrandoftoiletrollsaresoldinthreepacktypesatthesupermarket.

• apackof 18 rollsfor $8.82

• apackof 6 rollsfor $3.30

• apackof 4 doublelengthrollsfor $3.68

Determinethecheapestwaytobuythetoiletrolls.

Teabagscanbepurchasedfromthesupermarketinthreeforms.

• 25 teabagsat $2.36

• 50 bagsat $4.80

• 200 bagsat $15.00 Whatisthecheapestwaytobuyteabags?

HintforQ12:Calculatethecost perteabagineachcase.

13 Aweeklytrainconcessionticketcosts $16.Adayticketcosts $3.60.Ifyouaregoingtoschoolonly 4 daysnextweek,isitcheapertobuyoneticketperdayoraweeklyticket?

14 Aholidaycaravanparkoffersitscabinsatthefollowingrates.

$87 pernight • (Sunday–Thursday)

$187 foraweekend • (FridayandSaturday)

$500 perweek •

a Determinethenightlyrateineachcase.

b Whichpriceisthebestvalue?

15 Tomatosauceispricedat:

200 mLbottle $2.35 • 500 mLbottle $5.24 •

a FindthecostpermLofthetomatosauceineachcase.

b Whichisthecheapestwaytobuytomatosauce?

c Whatwouldbethecostof 200 mLatthe 500 mLrate?

d Howmuchwouldbesavedbybuyingthe 200 mLbottleatthisrate?

e Suggestwhythe 200 mLbottleisnotsoldatthisprice.

16 Safeservehasasaleontennisballsforonemonth. Whenyoubuy:

• 1 container,itcosts $5

• 6 containers,itcosts $28

• 12 containers,itcosts $40

• 24 containers,itcosts $60

Youneed 90 containersforyourclubtohaveenoughforaseason.

a Determinetheminimumcostifyoubuyexactly 90 containers.

b Determinetheoverallminimumcost,andthenumberofextracontainersyouwillhaveinthis situation.

1F 1F Simpleinterest

Learningintentions

• Tounderstandhowsimpleinterestiscalculated

• Tobeabletocalculateinterestusingthesimpleinterestformula

• Tobeabletodeterminetherateofinterestbasedontheinterestearned

• Tobeabletocalculatetheamountowingonaloanandcalculaterepayments

Keyvocabulary: principal,rateofinterest,simpleinterest,annual,invest,borrow

Borrowedorinvestedmoneyusuallyhasanassociatedinterestrate.Theconsumerneedstoestablishthe typeofinteresttheyarepayingandtheeffectsithasontheamountborrowedorinvestedovertime. Someloansorinvestmentsdeliverthefullamountofinterestusingonlytheinitialloanorinvestment amountintheinterestcalculations.Thesetypesaresaidtousesimpleinterest.

Whenchoosingahome loan,youneedto considerthetypeand amountofinterestyou willbepaying.

Lessonstarter:Howlongtoinvest?

MarcusandBrittneyeachhave $200 intheirbankaccounts.Marcusearns $10 ayearininterest.Brittney earns 10% p.a.simpleinterest.

Forhowlongmusteachoftheminvesttheirmoneyforittodoubleinvalue?

Keyideas

Simpleinterest isatypeofinterestthatiscalculatedontheamount invested or borrowed.

Thetermsneededtounderstandsimpleinterestare:

• Principal(P):theamountofmoneyborrowedorinvested

• Rateofinterest(r):the annual (yearly)percentagerateofinterest(e.g. 3% p.a.)

• Time (t):thenumberofyearsforwhichtheprincipalisborrowedorinvested

• Interest (I ):theamountofinterestaccruedoveragiventime.

Theformulaforcalculatingsimpleinterestis:

I = principal × rate × time

I = Prt 100 (Sincetherateisapercentage)

Totalrepaid = amountborrowed + interest

Exercise1F

Und er stand ing

1 Intheformula I = Prt 100:

I isthe a P isthe b r isthe c t isthe d

2 Calculateinterestearned (I ) if: P = 1000, r = 4, t = 5

Fluency

Example17Usingthesimpleinterestformula

Usethesimpleinterestformula, I = Prt 100,toﬁnd:

theinterest (I ) when $600 isinvestedat 8% p.a.for 18 months a theannualinterestrate (r) when $5000 earns $150 interestin 2 years. b

Solution

a P = 600

r = 8

t = 18 months = 18 12 = 1.5 years I = Prt 100

= 600 × 8 × 1.5 100

Explanation

Writeouttheinformationthatyouknowandthe formula.

Substituteintotheformulausingyearsfor t = 72

Theinterestis $72 in 18 months.

b P = 5000 I = 150 t = 2 years

I = Prt 100

150 = 5000 × r × 2 100

150 = 100 × r r = 1.5

Writetheformulaandtheinformationknown. Substitutethevaluesintotheformulaandsolve theequationtoﬁnd r.

Dividebothsidesby 100.

Thesimpleinterestrateis 1.5% peryear.Writetherateasapercentage.

Nowyoutry

Usethesimpleinterestformula, I = Prt 100,toﬁnd:

theinterest (I ) when $450 isinvestedat 5% p.a.for 30 months a theannualinterestrate (r) when $3500 earns $210 interestin 3 years b

3 Usethesimpleinterestformula, I = Prt 100,toﬁnd:

a theinterest (I ) when $500 isinvestedat 6% p.a.for 24 months

b theannualinterestrate (r) when $3000 earns $270 interestin 3 years

4 Copyandcompletethistableofvaluesfor I , P, r and t.

a $700 5% p.a. 4 years

b $2000 7% p.a. 3 years

c $3500 3% p.a. 22 months

d $750 2 1 2 % p.a. 30 months

e $22500 3 years

f $1770 5 years

HintforQ4:Use I = Prt 100

$2025

$354

Example18Calculatingrepaymentswithsimpleinterest

$3000 isborrowedat 12% p.a.simpleinterestfor 2 years.

Whatisthetotalamountowedoverthe 2 years? a Ifrepaymentsoftheloanaremademonthly,howmuchwouldeachpaymentneedtobe? b

Solution Explanation

a P = $3000, r = 12, t = 2 I = Prt 100 = 3000 × 12 × 2 100 = $720

Totalamount = $3000 + $720 = $3720

Listtheinformationyouknow. Writetheformula.

Substitutethevaluesandevaluate.

Totalamountistheoriginalamount plus theinterest.

b Amountofeachpayment = $3720 ÷ 24 2 years = 24 months = $155 permonth Thereare 24 paymentstobemade. Dividethetotalby 24.

Nowyoutry

$5400 isborrowedat 9% p.a.simpleinterestfor 4 years. Whatisthetotalamountowedoverthe 4 years? a

Ifrepaymentsoftheloanaremademonthly,howmuchwouldeachpaymentneedtobe?

5 $5000 isborrowedat 11% p.a.simpleinterestfor 3 years.

a Whatisthetotalamountowedoverthe 3 years?

b Ifrepaymentsoftheloanaremademonthly,howmuchwould eachpaymentneedtobe?

HintforQ5:Calculatetheinterest ﬁrst.

6 Underhirepurchase,Johnboughtasecond-handcarfor $11500.Hepaidnodepositanddecidedto paytheloanoffin 7 years.Ifthesimpleinterestis 6.45%,determine: thetotalinterestpaid a thetotalamountoftherepayment b thepaymentspermonth. c

7 $10000 isborrowedtobuyasecond-handBMW.Theinterestiscalculatedatasimpleinterestrateof 19% p.a.over 4 years.

Whatisthetotalinterestontheloan? a Howmuchistoberepaid? b Whatisthemonthlyrepaymentonthisloan? c

Problem-solving and reasoning

8 HowmuchinterestwillGiorgioreceiveifheinvests $7000 instocksat 3.6% p.a.simpleinterestfor 4 years?

9 Rebeccainvests $4000 for 3 yearsat 5.7% p.a.simpleinterestpaid yearly.

Howmuchinterestwillshereceiveintheﬁrstyear? a

WhatisthetotalamountofinterestRebeccawillreceiveoverthe 3 years? b

HowmuchmoneywillRebeccahaveafterthe 3-yearinvestment? c

Hint:Substituteintothe formula I = Prt 100 andsolve theresultingequation. Aninvestmentof $15000 receivesaninterestpaymentover 3 yearsof $7200.Whatwastherateofsimpleinterest perannum?

11 Jonathonwishestoinvest $3000 at 8% perannum.How longwillheneedtoinvestforhistotalinvestmenttodouble?

12 Ivanwishestoinvestsomemoneyfor 5 yearsat 4.5% p.a.paidyearly.Ifhewishestoreceive $3000 ininterestpaymentsperyear,howmuchshouldheinvest?Roundyouranswertothenearest dollar.

13 Gretta’sinterestpaymentonherloantotalled $1875.Iftheinterestratewas 5% p.a.andtheloanhad alifeof 5 years,whatamountdidsheborrow?

14 Ashedmanufactureroffersﬁnancewitharateof 3.5% p.a.paidattheendof 5 yearswithadeposit of 10%,orarateof 6.4% repaidover 3 yearswithadepositof 20%. Melaniedecidestopurchaseafullyerectedfour-squareshedfor $12500 Howmuchdepositwillsheneedtopayineachcase? a Whatisthetotalinterestshewillincurineachcase? b Ifshedecidedtopaypermonth,whatwouldbethemonthlyrepayment? c Discussthebeneﬁtsofthedifferenttypesofpurchasingmethods. d

2 1A Ginaputs 36% ofher $6000 monthlysalaryinasavingsaccount.Howmuchdoesshe haveleftover? 3 1B Completethefollowing.

5 1B Anillegalscalperbuysaconcertticketfor $150 andsellsitfor $210.Whatisthepercentage proﬁt?

6 1C Findthegrossincomeforaparticularweekinthefollowingworksituations. Pippaisadoor-to-doorsalesrepresentativeforanairconditioningcompany.Sheearns $300 perweekplus 8% commissiononhersales.Inaparticularweekshemakes $8200 worthofsales.

a Ariispaid $15.70 perhourinhisjobasashopassistant.Theﬁrst 36 hoursheworksinaweek arepaidatthenormalhourlyrate,thenext 4 hoursattimeandahalfandthen doubletimeafterthat.Ariworks 42 hoursinaparticularweek.

7 1D Duringthe2024/2025ﬁnancial year,Cameronearned $76300 per annum.Hehadreceiptsfor $425 fordonationsandwork-related expenses.

CalculateCameron’staxable income.

$45001−$135000

$190001 andover $51638 plus 45cforeach $1 over $190000

UsethistaxtabletocalculateCameron’staxpayableamount,tothenearestcent. b CameronalsomustpaytheMedicarelevyof 2% ofhistaxableincome.Howmuchisthelevy, tothenearestcent?

Duringtheﬁnancialyear,Cameron’semployersentatotalof $14500 intaxtotheATOonhis behalf.Byaddingtogetheryouranswersfromparts b and c,calculatetheamountCameron mustpayorwillberefundedonhistaxreturn.

8 1E Charlihasthefollowingexpensesinherhouseholdbudget.

rent $320 perweek

• phoneandinternet $119 permonth

• electricity $72 perquarter

• carregistration $700 peryear

• othercarcosts $120 permonth

• food $110 perweek

•

• clothing $260 permonth

• medicalandotherinsurance $160 per month

Determinetheoverallcostforrunningthehouseholdfortheyear.(Use 52 weeksinayear.) a Whatpercentageofan $82000 annualsalarydoesyouranswertopart a represent?Round youranswertoonedecimalplace.

9 1F Usethesimpleinterestformula I = Prt 100 toﬁnd: theamountowedwhen $4000 isborrowedat 6% p.a.for 3 years

a theinvestmentperiod,inyears,ifaninvestmentof $2500 at 4% p.a.earns $450 ininterest

1G 1G Compoundinterest

Learningintentions

• Tounderstandhowcompoundinterestiscalculated

• Tobeabletoapplythecompoundinterestformulatocalculatethetotalamount

• Tobeabletousethecompoundinterestformulawithdifferenttimeperiodssuchasmonths

Keyvocabulary: compoundinterest,principal,rateofinterest

Forsimpleinterest,theinterestisalwayscalculatedontheprincipal amount.Sometimes,however,interestiscalculatedontheactual amountpresentinanaccountateachtimeperiodthatinterestis calculated.Thismeansthattheinterestisaddedtotheamount, thenthenextlotofinterestiscalculatedagainusingthisnew amount.Thisprocessiscalledcompoundinterest.

Compoundinterestcanbecalculatedusingupdatedapplications ofthesimpleinterestformulaorbyusingthecompoundinterest formula.

Lessonstarter:Investingusingupdated simpleinterest

Compoundinterestiscalculatedby addinginteresttotheinitialprincipal, thencalculatingthenextinterest amountbasedonthenewtotal,and repeatingthisprocess.

Considerinvesting $400 at 12% perannum.Whatisthebalanceat theendof 4 yearsifinterestisaddedtotheamountattheendofeachyear? Copyandcompletethetabletoﬁndout.

Time Amount(A

3rdyear

4thyear

Asyoucansee,theamountfromwhichinterestiscalculatediscontinuallychanging.

Keyideas

Compoundinterest isatypeofinterestthatispaidonaloanorearnedonaninvestment,which iscalculatednotonlyontheinitialprincipalbutalsoontheinterestaccumulatedduring theloan/investmentperiod.

Compoundinterestcanbefoundbyusingupdatedapplicationsofthesimpleinterestformula. Forexample, $100 compoundedat 10% p.a.for 2 years.

Year 1: 100 + 10% of 100 = $110

Year 2: 110 + 10% of 110 = $121,socompoundinterest = $21.

Thetotalamountinanaccountusingcompoundinterestforagivennumberoftimeperiods isgivenby:

A = P(1 + r 100)n ,where:

• Principal (P) = theamountofmoneyborrowedorinvested

• Rateofinterest (r) = thepercentageappliedtotheprincipalperperiodofinvestment

• Periods (n) = thenumberoftimeperiodstheprincipalisinvested

• Amount (A) = thetotalamountofyourinvestment

Interest = amount (A) principal (P)

Exercise1G

Und er stand ing

1 Consider $500 investedat 10% p.a.compoundedannually.

Howmuchinterestisearnedintheﬁrstyear?

Whatisthebalanceoftheaccountoncetheﬁrstyear’s interestisadded?

c Whatisthebalanceoftheaccountattheendof thesecondyear?

Howmuchinterestisearnedinthesecondyear?

HintforQ1:Forthesecond year,youneedtouse $500 plustheinterestfromtheﬁrst year.

2 $1200 isinvestedat 4% p.a.compoundedannuallyfor 3 years.Completethefollowing.

a Thevalueoftheprincipal P is b 4% isthe , r

c Thenumberoftimeperiodsthemoneyisinvestedis

3 Fillinthemissingnumbers.

a $700 investedat 8% p.a.compoundedannuallyfor 2 years.

A = (1.08)

b $1000 investedat 15% p.a.compoundedannually for 6 years.

A = 1000 ( )6

c $850 investedat 6% p.a.compoundedannuallyfor 4 years.

A = 850 ( )

Fluency

Example19Usingthecompoundinterestformula

HintforQ3:Forcompound interest, A = P(1 + r 100 )n

Determinetheamountafter 5 yearswhen $4000 iscompoundedannuallyat 8%

Solution

Explanation

P = 4000, n = 5, r = 8 Listthevaluesforthetermsyouknow.

A = P(1 + r 100 )n Writetheformula.

= 4000(1 + 8 100 )5 Substitutethevalues.

= 4000(1.08)5

Simplifyandevaluate.

= $5877.31 Writeyouranswertotwodecimalplaces, (nearestcent).

Nowyoutry

Determinetheamountafter 4 yearswhen $3000 iscompoundedannuallyat 6%

4 Determinetheamountafter 5 yearswhen:

$4000 iscompoundedannuallyat 5% a

$8000 iscompoundedannuallyat 8.35% b

$6500 iscompoundedannuallyat 16% c

$6500 iscompoundedannuallyat 8% d

HintforQ4: A = P(1 + r 100 )n

5 Determinetheamountwhen $100000 iscompoundedannuallyat 6% for: 1 year a 2 years b 3 years c 5 years d 10 years e 15 years f

Example20Convertingratesandtimeperiods

Calculatethenumberofperiodsandtheratesofinterestofferedperperiodforeachof thefollowing.

6% p.a.over 4 yearspaidmonthly a 18% p.a.over 3 yearspaidquarterly b

Solution

a n = 4 × 12 = 48 r = 6 ÷ 12 = 0.5

Explanation

4 yearsisthesameas 48 months, as 12 months = 1 year.

6% p.a. = 6% inoneyear. Divideby 12 toﬁndthemonthlyrate.

b n = 3 × 4 = 12 r = 18 ÷ 4

Therearefourquartersin 1 year. = 4.5

Nowyoutry

Calculatethenumberofperiodsandtheratesofinterestofferedperperiodforeach ofthefollowing.

3% p.a.over 2 yearspaidmonthly a 7% p.a.over 4 yearspaidbi-annually(twiceyearly) b

6 Calculatethenumberofperiods (n) andtheratesofinterest (r) offeredperperiodforthefollowing. (Roundtheinterestratetothreedecimalplaceswherenecessary.)

6% p.a.over 3 yearspaidbiannually a 12% p.a.over 5 yearspaidmonthly b

4.5% p.a.over 2 yearspaidfortnightly c

10.5% p.a.over 3.5 yearspaidquarterly d 15% p.a.over 8 yearspaidquarterly e 9.6% p.a.over 10 yearspaidmonthly f

HintforQ6:‘Bi-annually’ means‘twiceayear’. 26 fortnights = 1 year

Example21Findingcompoundedamountsusingmonths

Tony’sinvestmentof $4000 iscompoundedat 8.4% p.a.over 5 years.Determinetheamounthewill haveafter 5 yearsiftheinterestispaidmonthly.

Solution Explanation

P = 4000

n = 5 × 12

= 60

r = 8.4 ÷ 12

Listthevaluesofthetermsyouknow.

Convertthetimeinyearstothenumberofperiods(inthis question,months),i.e. 60 months = 5 years.

Converttherateperyeartotherateperperiod(i.e.months) bydividingby 12 = 0.7

A = P(1 + r 100 )n Writetheformula.

= 4000(1 + 0.007)60

Substitutethevalues 0.7 ÷ 100 = 0.007

= 4000(1.007)60 Simplifyandevaluate.

= $6078.95

Nowyoutry

Sally’sinvestmentof $6000 iscompoundedat 4.8% p.a.over 4 years.Determinetheamountshewill haveafter 4 yearsiftheinterestispaidmonthly.

7 Aninvestmentof $8000 iscompoundedat 12% p.a.over 3 years.Determinetheamounttheinvestor willhaveafter 3 yearsiftheinterestiscompoundedmonthly.

8 Calculatethevalueofthefollowinginvestmentsifinterestiscompoundedmonthly.

a $2000 at 6% p.a.for 2 years

b $34000 at 24% p.a.for 4 years

c $350 at 18% p.a.for 8 years

d $670 at 6.6% p.a.for 2 1 2 years

e $250 at 7.2% p.a.for 12 years

HintforQ8:Convertyearsto monthsandtheannualrate tothemonthlyrate.

9 Shaﬁqinvests $5000 compoundedmonthlyat 18% p.a.Determinethevalueoftheinvestmentafter:

10a Calculatetheamountofcompoundinterestpaidon $8000 attheendof 3 yearsforeachratebelow.

12% compoundedannually i

12% compoundedbiannually(twiceayear) ii

12% compoundedmonthly iii

12% compoundedweekly iv

12% compoundeddaily v

HintforQ10: 1 year = 12 months

1 year = 52 weeks

1 year = 365 days

b Whatisthedifferenceintheinterestpaidbetweenannualanddailycompoundinginthiscase?

11 Thefollowingareexpressionsrelatingtocompoundinterestcalculations.Determine theprincipal (P),numberofperiods (n),rateofinterestperperiod (r),annualrateofinterest (R) andtheoveralltime (t)

300(1.07)12,biannually a 5000(1.025)24,monthly b

1000(1.00036)65,fortnightly c

3500(1.000053)30,daily d 10000(1.078)10,annually e

HintforQ11:For 12 time periodswithinterestpaid twiceayear,thisis 6 years.

12 Ellenneedstodecidewhethertoinvesther $13500 for 6 yearsat 4.2% p.a.compoundedmonthlyor 5.3% compoundedbiannually.DecidewhichinvestmentwouldbethebestforEllen.

13 Youhave $100000 toinvestandwishtodoublethatamount.Usetrialanderrorinthefollowing.

a Determine,tothenearestwholenumberofyears,thelengthoftimeitwilltaketodothisusingthe compoundinterestformulaatratesof:

b Iftheamountofinvestmentis $200000 andyouwishtodoubleit,determinethetimeitwilltake usingthesameinterestratesasabove.

c Arethelengthsoftimetodoubleyourinvestmentthesameinpart a andpart b?

1H 1H Investmentsandloans

Learningintentions

• Tounderstandthataloancanberepaidininstalmentsthatincludeinterest

• Tobeabletocalculatethetotalpaymentforapurchaseorloaninvolvingrepayments

• Tobeabletocalculatebankinterestusingtheminimummonthlybalance

Keyvocabulary: investment,loan,repayment,interest,deposit,debit

Whenyouborrowmoney,interestischarged,andwhenyou investmoney,interestisearned.Whenyouinvestmoney,the institutioninwhichyouinvest(e.g.bankorcreditunion)pays youinterest.However,whenyouborrowmoney,theinstitution fromwhichyouborrowchargesyouinterest,sothatyoumust paybackthemoneyyouinitiallyborrowed,plustheinterest.

Lessonstarter:Creditcardstatements

RefertoAllan’screditcardstatementbelow.

a Howmanydaysweretherebetweentheclosingbalanceand theduedate?

b Whatistheminimumpaymentdue?

Ifyouareapprovedforabankloan,you willneedtorepaytheborrowedamount plusanyinterestchargedbythebank.

c IfAllanpaysonlytheminimum,onwhatbalanceistheinterestcharged?

d HowmuchinterestischargedifAllanpays $475.23 on 25/5?

Keyideas

Interestratesareassociatedwithmanyloanandsavingsaccounts.

Bankaccounts:

• accrueinteresteachmonthontheminimummonthlybalance

• mayincuraccount-keepingfeeseachmonth

Investments areamountsputintoabankaccountorsimilarwiththeaimofearninginterest onthemoney.

Loans (moneyborrowed)haveinterestchargedtothemontheamountleftowing(i.e. thebalance).

Repayments areamountspaidtothebank,usuallyeachmonth,torepayaloanplusinterest withinanagreedtimeperiod.

Exercise1H

Und er stand ing

1 Stateifthefollowingareexamplesofinvestments,loansorrepayments.

a Karapays $160 permonthtopayoffherholidayloan.

b Samdepositsa $2000 prizeinanaccountwith 3% p.a.interest.

c Georgiaborrows $6500 fromthebanktoﬁnancesettinguphersmallbusiness.

2 Donnacanaffordtorepay $220 amonth.Howmuchcansherepayover: 1 year? a 18 months? b 5 years? c

3 Saraﬁnabuysanewbedona‘buynow,paylater’offer.Nointerestischargedifshepaysforthebed in 2 years.Saraﬁna’sbedcosts $2490 andshepaysitbackoveraperiodof 20 monthsin 20 equal instalments.Howmuchiseachinstalment?

Fluency

Example22Repayingaloan

Wendytakesoutapersonalloanof $7000 tofundhertriptoSouthAfrica.Repaymentsaremade monthlyfor 3 yearsat $275 amonth.Find: thetotalcostofWendy’strip a theinterestchargedontheloan. b

Solution

a Totalcost = $275 × 36 = $9900

Explanation

3 years = 3 × 12 = 36 months

Cost = 36 lotsof $275

b Interest = $9900−$7000 = $2900 Interest = totalpaid amountborrowed

Nowyoutry

Jacobtakesoutapersonalloanof $13000 tobuyacar.Hemakesrepaymentsmonthlyfor 2 yearsat $680 amonth.Find: thetotalcostofthecar a theinterestchargedontheloan. b

4 Jasonhasapersonalloanof $10000.Heisrepayingtheloanover 5 years.Themonthlyrepaymentis $310

CalculatethetotalamountJasonrepaysoverthe 5 yearloan. a Howmuchinterestishecharged? b

5 Robertborrows $5500 tobuyasecond-handmotorbike.Herepays theloanin 36 equalmonthlyinstalmentsof $155. Calculatethetotalcostoftheloan. a HowmuchinterestdoesRobertpay? b

HintforQ4:Howmanymonthly repaymentsin 5 years?

6 Almaborrows $250000 tobuyahouse.Therepaymentsare $1736 amonthfor 30 years.

HowmanyrepaymentsdoesAlmamake? a WhatisthetotalamountAlmapaysforthehouse? b Howmuchinterestispaidoverthe 30 years? c

Example23Payingoffapurchase

Harrybuysanew $2100 computeronthefollowingterms: 20% deposit

•

• monthlyrepaymentsof $90 for 2 years.

Find:

thedepositpaid a thetotalpaidforthecomputer b theinterestcharged.

Solution

a Deposit = 0.2 × 2100 = $420

b Repayments = $90 × 24 = $2160

Totalpaid = $2160 + $420 = $2580

Explanation

Find 20% of 2100

2 years = 24 months Repay 24 lotsof $90 Repay = deposit + repayments

c Interest = $2580−$2100 Interest = totalpaid originalprice = $480

Nowyoutry

Sophiepays $3180 foraholidayapartmentrentalonthefollowingterms: 30% deposit

•

• monthlyrepaymentsof $195 for 1 year.

Find: thedepositpaid a thetotalpaidfortheapartment b theinterestcharged. c

7 Georgebuysacarfor $12750 onthefollowingterms: 20% depositandmonthlyrepayments of $295 for 3 years.

Calculatethedeposit. a Findthetotalofalltherepayments. b Findthecostofbuyingthecarontheseterms. c FindtheinterestGeorgepaysontheseterms. d

Example24Calculatinginterest

Anaccounthasaminimummonthlybalanceof $200 andinterestiscreditedmonthlyonthisamount at 1.5%

Determinetheamountofinteresttobecreditedattheendofthemonth. a Ifthebankchargesaﬁxedadministrationfeeof $5 permonthandotherfeestotalling $1.07, whatwillbethenetamountcreditedordebitedtotheaccountattheendofthemonth?

b Solution

Explanation

a Interest = 1.5% of $200 = 0.015 × $200 = $3 Interestis 1.5% permonth. Change 1.5% toadecimalandcalculate.

b Netamount = 3− (5 + 1.07) = −3.07

$3.07 willbedebitedfromtheaccount.

Nowyoutry

Subtractthedeductionsfromtheinterest.

Anegativeamountiscalledadebit.

Anaccounthasaminimummonthlybalanceof $180 andinterestiscreditedmonthlyonthisamount at 2.2%

Determinetheamountofinteresttobecreditedattheendofthemonth. a Ifthebankchargesaﬁxedadministrationfeeof $4.50 permonthandotherfeestotalling $1.18, whatwillbethenetamountcreditedordebitedtotheaccountattheendofthemonth?

b 8 Abankaccounthasaminimummonthly balanceof $300 andinterestiscredited monthlyat 1.5%

Determinetheamountofinteresttobe creditedeachmonth. a

Ifthebankchargesaﬁxedadministration feeof $3 permonthandfeesof $0.24, whatwillbethenetamountcreditedto theaccountattheendofthemonth?

9 Anaccounthasnoadministrationfee.The monthlybalancesforMay–Octoberareinthe tablebelow.Iftheinterestpayableonthe minimummonthlybalanceis 1%,howmuch interestwillbeadded: foreachseparatemonth? a overthe 6-monthperiod? b

Problem-solving and reasoning

10 Supersoundoffersthefollowingtwodealsonasoundsystemworth $7500

DealA:nodeposit,interestfreeandnothingtopayfor 18 months.

DealB: 15% offforcash.

a NickchoosesdealA.Find: thedeposithemustpay i theinterestcharged ii thetotalcostifNickpaysthesystemoffwithin 18 months. iii

b PhilchoosesdealB.WhatdoesPhilpayforthesamesound system?

c HowmuchdoesPhilsavebypayingcash?

11 CamdenFinanceCompanycharges 35% ﬂatinterestonallloans.

a Meiborrows $15000 fromCamdenFinanceover 6 years. Calculatetheinterestontheloan. i Whatisthetotalrepaid (i.e.loan + interest)? ii Whatisthevalueofeachmonthlyrepayment? iii

b Lancelleborrows $24000 fromthesamecompanyover 10 years. Calculatetheinterestonherloan. i Whatisthetotalrepaid? ii Whatisthevalueofeachmonthlyinstalment? iii

HintforQ10: 15% offis 85% oftheoriginalamount.

AlistoftransactionsthatEmmamadeovera 1-monthperiodisshown.Thebankcalculatesinterest daily at 0.01% andaddsthetotaltotheaccountbalanceattheendofthisperiod.Ithasan administrativefeeof $7 permonthandotherfeesoverthistimetotal $0.35. Copyandcompletethebalancecolumnofthetable.

HintforQ12:Inpart b, interestiscalculatedonthe end-of-the-daybalance.

Determinetheamountofinterestaddedoverthismonth. b Determinetheﬁnalbalanceafterallcalculationshavebeenmade.

c Suggestwhattheregulardepositsmightbefor. d

13 Thetablebelowshowstheinterestandmonthlyrepaymentsonloanswhenthesimpleinterestrateis 8.5% p.a.

a Usethetabletoﬁndthemonthlyrepaymentsforaloanof:

$1500 over 2 years i $2000 over 3 years ii $1200 over 18 months. iii

b DamienandLisacanaffordmonthlyrepaymentsof $60.Whatisthemosttheycanborrow andonwhatterms?

14 Partofacreditcardstatementisshownhere.

Understanding your account

CLOSING BALANCE

MINIMUM PAYMENT DUE

PAYABLE TO MINIMISE FURTHER INTEREST CHARGES

Whatistheclosingbalance?

CLOSING BALANCE

This is the amount you owe at the end of the statement period

MINIMUM PAYMENT DUE

This is the minimum payment that must be made towards this account

PAYABLE TO MINIMISE FURTHER INTEREST CHARGES

This amount you must pay to minimise interest charges for the next statement period

Whatisdueonthecardifonlytheminimumpaymentismadeontheduedate?

Thiscardcharges 21.9% p.a.interestcalculateddailyontheunpaidbalance.Toﬁndthedailyinterest amount,thecompanymultipliesthisbalanceby 0.0006.Whatdoesitcostininterestperdayifonly theminimumpaymentismade? c

15 Whenyoutakeoutaloanfromalendinginstitutionyouwillbeaskedtomakeregularpayments(usually monthly)foracertainperiodoftimetorepaytheloancompletely.Thelargertherepayment,theshorter thetermoftheloan.

Loansworkmostlyonareducingbalanceandyoucanﬁndouthowmuchbalanceisowingat theendofeachmonthfromastatement,whichisissuedonaregularbasis.

Let’slookatanexampleofhowthebalanceisreducing.

Ifyouborrow $15000 at 17% p.a.andmakerepaymentsof $260 permonth,attheendoftheﬁrst monthyourstatementwouldbecalculatedasshown.

Interestdue = 15000 × 0.17 12

= $212.50

Repayment = $260

Amountowing = $15000 + $212.50−$260

= $14952.50

Thisprocesswouldberepeatedforthenextmonth:

Interestdue = 14952.50 × 0.17 12

= $211.83

Repayment = $260

Amountowing = $14952.50 + $211.83−$260

= $14904.33

Asyoucansee,theamountowing isdecreasingandsoistheinterest owedeachmonth.Meanwhile,more ofyourrepaymentisactuallyreducing thebalanceoftheloan.

Astatementmightlooklikethis:

Checktoseethatallthecalculationsarecorrectonthestatementabove.

Asthisprocessisrepetitive,thecalculationsarebestdonebymeansofaspreadsheet.Tocreatea spreadsheetfortheprocess,copythefollowing,extendingyoursheettocover 5 years.

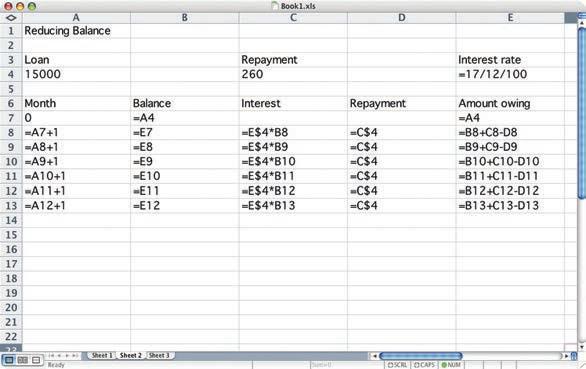
1I 1I Comparinginterestusingtechnology

Learningintentions

• Tounderstandhowtechnologycanbeusedtoef cientlycompareinterestcalculations

• Tobeabletousetechnologytocalculateinterestand nalamountsandcompareinterestplans

Keyvocabulary: simpleinterest,compoundinterest

Bothcompoundinterestandsimpleinterestcalculations involveformulas.TechnologyincludingscientiﬁcandCAS calculators,spreadsheetsorevencomputerprograms canbeusedtomakesimpleandcompoundinterest calculations.

Theseallowforquick,repeatedcalculationswhere valuescanbeadjustedandtheinterestfromdifferent accountscompared.

Lessonstarter:Whoearnsthe most?

• Ceannainvests $500 at 8% p.a.compoundedmonthly over 3 years.

Theuseoftechnologycanhelpperformrepeated compoundinterestandsimpleinterestcalculations quickly.

• Huxleyinvests $500 at 10% p.a.compoundedannuallyover 3 years.

• Loreliinvests $500 at 15% p.a.simpleinterestover 3 years.

– Howmuchdoeseachpersonhaveattheendofthe 3 years?

– Whoearnedthemost?

Keyideas

Youcancalculatethetotalamountofyourinvestmentforeitherformofinterestusingtechnology. Usingformulasincalculators

• Simpleinterest I = Prt 100

• Compoundinterest A = P(1 + r 100 )n

Simplecode

Tocreateprogramsforthetwotypesofinterest, enterthedatashownatright.

Thiswillallowyoutocalculatebothtypesofinterest foragiventimeperiod.Ifyouinvest $100000 at 8% p.a.paidmonthlyfor 2 years,youwillbeaskedfor P, R = r 100, t or n andthecalculatorwilldotheworkfor you.

Note: SomemodiﬁcationsmaybeneededfortheCAS orothercalculatorsorothertechnology.

Spreadsheet

Thespreadsheetsshownbelowcanbecompletedtocompileasimpleinterestandcompound interestsheet.

FillintheprincipalinB3 andtherateperperiodinD3.Forexample,for $4000 invested at 5.4% monthly,B3 willbe 4000 andD3 willbe 0.054 12 .

Exercise1I

Und er stand ing

1 Writedownthevaluesof P, r and n foraninvestmentof $750 at 7.5% p.a.,compoundedannually for 5 years.

2 Writedownthevaluesof P, r and t foraninvestment of $300 at 3% p.a.simpleinterestover 300 months.

3 Whichisbetteronaninvestmentof $100 for 2 years: HintforQ3:Forsimpleinterest

A simpleinterestcalculatedat 20% p.a.? B compoundinterestcalculatedat 20% p.a.and paidannually?

Example25Usingtechnology

Findthetotalamountofthefollowinginvestments,usingtechnology. $5000 at 5% p.a.compoundedannuallyfor 3 years. a $5000 at 5% p.a.simpleinterestfor 3 years. b

Solution

a $5788.13

Explanation

Use A = P(1 + r 100 )n oraspreadsheet(see Keyideas).

b $5750 Use I = Prt 100 withyourchosentechnology.

Nowyoutry

Findthetotalamountofthefollowinginvestments,usingtechnology. $6000 at 4% p.a.compoundedannuallyfor 5 years. a $6000 at 4% p.a.simpleinterestfor 5 years. b

4 a Findthetotalamountofthefollowinginvestments,usingtechnology.

$6000 at 6% p.a.compoundedannuallyfor 3 years. i

$6000 at 3% p.a.compoundedannuallyfor 5 years. ii

$6000 at 3.4% p.a.compoundedannuallyfor 4 years. iii

$6000 at 10% p.a.compoundedannuallyfor 2 years. iv

$6000 at 5.7% p.a.compoundedannuallyfor 5 years. v

b Whichoftheaboveyieldsthemostinterest?

5 a Findthetotalamountofthefollowinginvestments,using technologywherepossible.

$6000 at 6% p.a.simpleinterestfor 3 years. i

$6000 at 3% p.a.simpleinterestfor 6 years. ii

$6000 at 3.4% p.a.simpleinterestfor 7 years. iii

$6000 at 10% p.a.simpleinterestfor 2 years. iv

$6000 at 5.7% p.a.simpleinterestfor 5 years. v

b Whichoftheaboveyieldsthemostinterest?

6 a Determinethetotalsimpleandcompoundinterestaccumulated onthefollowing.

i $4000 at 6% p.a.payableannuallyfor: 1 year

ii $4000 at 6% p.a.payablebiannuallyfor: 1 year I 2 years II 5 years III 10 years IV

iii $4000 at 6% p.a.payablemonthlyfor: 1 year I 2 years II 5 years III 10 years IV

b Wouldyoupreferthesamerateofcompoundinterestor simpleinterestifyouwereinvestingmoneyandpayingofftheloanininstalments?

c Wouldyoupreferthesamerateofcompoundinterestorsimpleinterestifyouwere borrowingmoney?

7 a Copyandcompletethefollowingtableifsimpleinterestisapplied.

$18000 8% 2 years

b Explaintheeffectontheinterestwhenwedoublethe: rate i period ii overalltime. iii

8 Copyandcompletethefollowingtableifcompoundinterestisapplied.Youmayneedtouseacalculator andtrialanderrortoﬁndsomeofthemissingvalues.

Changingtheparameters

9 Ifyouinvest $5000,determinetheinterestrateperannum(totwodecimalplaces)ifthetotalamount isapproximately $7500 after 5 yearsandifinterestis: compoundedannually a compoundedquarterly b compoundedweekly.

c Commentontheeffectofchangingtheperiodforeachpaymentontherateneededtoachieve thesametotalamountinagiventime.

10 a Determine,toonedecimalplace,theequivalentsimpleinterestrateforthefollowinginvestments over 3 years.

$8000 at 4% compoundedannually. i

$8000 at 8% compoundedannually. ii

b Ifyoudoubleortriplethecompoundinterestrate,howisthesimpleinterestrateaffected?

Financemanager

Abookkeeperandanaccountsmanagerare bothoccupationsthatdealwithnumbersand budgets.Theyrequireemployeestohavegood communicationandmathematicalskills.

Employeesalsoneedacommitmenttodetail andtobehonest,astheydealwithother people’smoney.

Excellentnumberskillsareessentialinthese ﬁelds.Bookkeepersneedtoworkwith spreadsheets,percentages,taxsystemsand businessplans.

Completethesequestionsthataﬁnancemanager mayfaceintheirday-to-dayjob.

1 Considertheinformationsuppliedina sectionofabusinessbudgetfora 3-month period.

Roundallanswerstotwodecimalplaces. Calculatethetotalincomeforthemonth ofJuly.

(with 25% reduction)

b Calculatethetotalincomeforthemonth ofSeptember.

Calculatethetotalincomeforthemonth ofAugust.

c Whichmonthhadthehighestincome andbyhowmuch?

d Whatcontributedtothisincreasein income?

e Whatpercentageofthetotalincome forthe 3 monthsshowncamefroma ﬁxedfee?

f Whatwasthemonthlyﬁxedfeebefore the 25% reductionoccurred?

2 Theofﬁceexpensesforthesamecompanyforthesame 3-monthperiodaregiveninthetable.

a Calculatethepercentage ofthetotalofﬁce expensesforJulyspent onrent.

b Whatisthecostof electricityshowninthe table,andinwhatmonth isitshown?

c Whydoestheelectricity notappearintheother twomonths?

d Whatistheprojectedcostofelectricityfortheyear?

3 TheemploymentexpensesforthethreemonthsofOctober,NovemberandDecemberareshown.

a Calculatethetotalemploymentexpensesforthemonthof December.

b WhatisthewholenumberpercentageincreaseofNovember’s totalemploymentexpensesfromNovembertoDecember? Whatwasthecauseofthisincrease?

c Thecompanyhas 11 full-timeemployees.Whatisan employee’saverage: salarypermonth? i annualsalary? ii

d ThecompanyhastotalexpensesforthemonthofNovemberof $92117.Whatpercentageofthe totalexpensesforNovembercomesfromtheemploymentexpenses?

Usingtechnology

4 Atruckingbusinesshasinvestedinanewprimemoverforhaulingcattlebyroadtrain.Ithasabank loanof $230000 at 9% perannumchargedmonthly.ThebusinessrequiresanExcelspreadsheetto showtheprogressofthedebtrepayment.

a DevelopthefollowingtableinanExcelspreadsheetbyenteringformulasintotheyellowshaded cellstocalculatetheirvalues.Usethenotesbelowtohelpyou.

Notes:

HintforQ4:Afterentering yourformulas,checkspeciﬁc resultswithacalculator.

• Theinterestduepermonthis 1 12 of 9% ofthestartingbalanceforthatmonth.

• Theprincipal(i.e.debt)paidwillbethescheduledpaymentminustheinterestdue.

• Theendingbalanceswillequalthestartingbalanceminustheprincipalpaid.

• Thenextmonth’sstartingbalanceequalsthepreviousmonth’sendingbalance.

b Extendthetablefor 12 paymentsandanswerthefollowingquestions. WhatistheamountofdebtremainingonJuly 1? i WhatistheinterestpaidinOctober? ii UseanExcelformulatoﬁndthedifferencebetweentheprincipalpaidinDecemberandthe principalpaidinJanuary. iii Enter‘sum’formulastodeterminethetotalinterestpaidintheyearandthetotalprincipalpaid offintheyear. iv

Investinginart

Matildaisakeenartinvestorandhastheopportunitytopurchaseanewworkfromanauctionhouse. Theauctioneerissayingthattheestimatedvalueofthepaintingis $10000.Matilda’smaininvestment goalisforeachofherinvestmentstoatleastdoubleinvalueevery 10 years. Presentareportforthefollowingtasksandensurethatyoushowclearmathematicalworkings, explanationsanddiagramswhereappropriate.

1Preliminarytask

a IfMatildapurchasesthepaintingfor $10000 andassumesagrowthrateof 5% p.a.,calculate thevalueoftheinvestmentafter: 1 year i 2 years ii 3 years. iii

b Theruleconnectingthevalueofthe $10000 investment($A)growingat 5% p.a.after t years

isgivenby A = 10000 1 + 5 100 t

Checkyouranswerstopart a bysubstituting t = 1, t = 2 and t = 3 intothegivenrule andevaluatingthevalueof A usingyourcalculator,oraspreadsheet.

Constructasimilarruleforaninvestmentvalueof $12000 andagrowthrateof 3% ii

Constructasimilarruleforaninvestmentvalueof $8000 andagrowthrateof 8% iii

c Using A = 10000 1 + 5 100 t ﬁndthevalueofa $10000 investmentat 5% p.a.after 10 years.

i.e.Calculatethevalueof A if t = 10

2Modellingtask

TheproblemistodetermineaninvestmentgrowthratethatdeliversatleastadoublingofMatilda’s initialinvestmentamountafter 10 years.

a Writedownalltherelevantinformationthatwillhelpsolvethisproblem.Whatformulaneedsto beappliedinthistask?

b Explainwhatthenumbers 10000 and 5 meanintherule A = 10000 1 + 5 100 t inrelationto Matilda’sinvestment.

c Usetherule A = 10000 1 + r 100 t todeterminethevalueofMatilda’s $10000 investmentafter 10 yearsforthefollowinggrowthrates(r%).

r = 4 i r = 7 ii

r = 10 iii

d Chooseyourownvaluesof r usingonedecimalplaceaccuracyanddeterminethegrowthrate forwhichtheinvestmentdoublesinvalueafter 10 years.

e Byconsideringvaluesof r eithersideofyourchosenvaluefoundinpart d demonstratethatyour answeriscorrecttoonedecimalplace.

f Reﬁneyouranswersothatitiscorrecttotwodecimalplaces.

g Summariseyourﬁndingsanddescribeanykeyﬁndings.Youmightliketoshowyourresultsina spreadsheetsimilartotheonebelow.

3Extensionquestion

a Decideifchangingtheinitialinvestmentvaluechangesthetotalpercentageincreaseinvalue afterthesamenumberofyears.Justifyyouranswer.

b IfMatildaonlypaid $8000 fortheartworkbutstillwantedittobevaluedat $20000 after 10 years,determinethegrowthratethatshewillneedtheworktohave?Roundtotwodecimal places.

Formulate

Evaluate and verify

Communicate

Comparingsimpleandcompoundinterest

Keytechnology:Graphingandspreadsheets

Intheworldofﬁnance,itisimportanttoknowthe differencebetweensimpleandcompoundinterest. Thedifferencesinthevalueofinvestmentsandloans canbeverysigniﬁcantoverthelongterm.

Youwillrecalltheserulesfortheamount A:

• Simpleinterest: A = P

• Compoundinterest: A = P 1

1Gettingstarted

Imagineinvesting $100000

a Calculatethetotalvalueoftheinvestmentusingthefollowingsimpleinterestterms. 4% p.a.for 5 years. i 5% p.a.for 10 years. ii

b Calculatethetotalvalueoftheinvestmentusingthefollowingcompoundinterestterms. 4% p.a.for 5 years. i 5% p.a.for 10 years. ii

c Compareyouranswersfromparts a and b aboveanddescribewhatyounotice.Canyouexplain whythecompoundinterestreturnsarehigherthansimpleinterestreturns?

2Usingtechnology

Twopeopleinvest $100000 inthefollowingways:

• A:Simpleinterestat r1% for t years

• B:Compoundinterestat r2% for t years

a UsegraphingsoftwarelikeDesmostoconstructagraphofthetotalvalueoftheinvestments A and B onthesamesetofaxes.Useslidersfor r1 and r2 asshown.

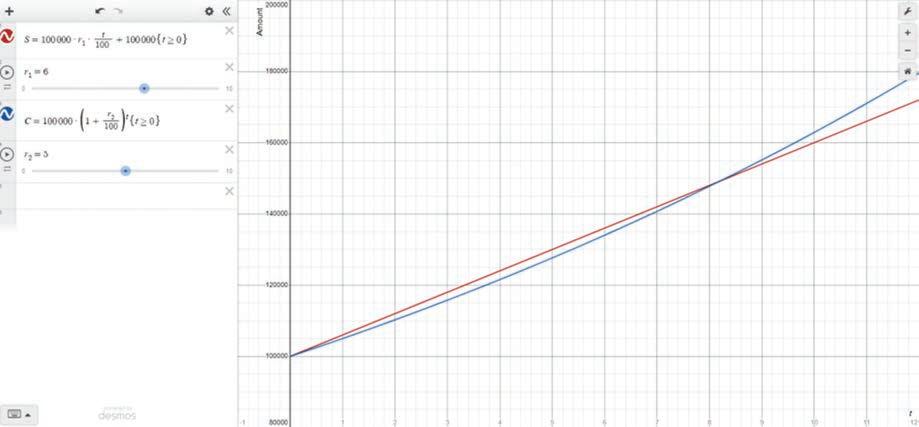
b Noteinthepreviousexamplethat r1 iscurrently 6 and r2 iscurrently 5.Dragthesliderstochange thevalueoftheinterestratesandnotethechangesinthegraphs.

c Chooseacombinationof r1 and r2 sothatthevaluesoftheinvestmentsareroughlyequalnear thefollowingnumberofyears.

5 i 10 ii

d Setthecompoundinterestrate r2 at 4%.Dragthe r1 slidertoﬁndasimpleinterestratesothatthe valuesoftheinvestmentsareapproximatelyequalafter 10 years.

3Applyinganalgorithm

Asimpleinterestratewhichisequivalenttoacompoundinterest ratecanbefoundusinganalgorithmicapproachinsidea spreadsheet.

a Considerthisﬂowchartwhichﬁndsthevalueofasimple interestinvestmentover t years.Bychoosing t = 4, runthroughthealgorithmandcompletethistablefor eachpass. n A 0 100000 1

= 100000, A = 100000, r = 5, n = 0

b Writeasimilarﬂowchartbutthistimeforthe compoundingcase.

c Applythesealgorithmsbysettingupaspreadsheetlike thefollowingtocomparethetotalvalueofasimpleand compoundinterestinvestmentof $100000 over t years.

d Afterﬁllingdownfromcellsinrow 6 comparethevaluesoftheinvestmentsovera 12-yearperiod. Experimentwiththenumbersinrow 2 changingtheinitialinvestmentamountandtheinterest rates.

e Usinga $100000 investmentandacompoundinterestrateof 5%,useyourspreadsheettoﬁndan equivalentsimpleinterestratethatdeliversanequalinvestmentvalueafter 10 years.

Puzzles and games

1 Findanddeﬁnethe 10 termsrelatedtoconsumerarithmeticandpercentageshiddeninthis wordﬁnd.

2 Howdoyoustopabullchargingyou?Answerthefollowingproblemsandmatchtheletterstothe answersbelowtoﬁndout.

3 Howmanyyearsdoesittake $1000 todoubleifitisinvestedat 10% p.a.compoundedannually?

4 ThechanceofJaydenwinningagameofcardsissaidtobe 5%.Howmanyconsecutivegames shouldJaydenplaytobe 95% certainhehaswonatleastoneofthegamesplayed?

Percentages

Simple (ﬂat rate) interest

I = simple interest

P = principal ($ invested)

r = rate per year, as a percentage

t = number of years

Compound interest

A = ﬁnal balance

P = principal ($ invested)

r = rate per time period, as a percentage

n = number of time periods money is invested for

Spreadsheets can be used to manage money or compare loans.

Increase 20 by 8% = or 0.15 × 459 = 20 × 108%

= 20 × 1.08

Decrease 20 by 8%

= 20 × 92%

= 20 × 0.92 15

Income

Hourly rate = $/h

Time and a half = 1 × hourly rate 1 2

Double time = 2 × hourly rate

Commissionis % of total sales

Gross income = total of all money earned

Net income = gross income deductions

Budgets

Deciding how income is spent on ﬁxed and variable expenses.

Money given from wages (income tax) to the government (Refer to the income tax table on page 22.)

Loans

Balance owing = amount left to repay

Repayment = money given each month to repay the loan amount and the interest

Chapterchecklist

AversionofthischecklistthatyoucanprintoutandcompletecanbedownloadedfromyourInteractiveTextbook.

1A 1

Icanconverttoapercentage.

e.g.Writeeachofthefollowingasapercentage.

a 7 40 b 0.24

1A 2

Icanwritepercentagesassimpliﬁedfractionsanddecimals.

e.g.Writeeachofthefollowingpercentagesasbothasimpliﬁedfractionandadecimal. a 53% b 4% c 10.5%

1A 3

1B 4

1B 5

Icanﬁndthepercentageofaquantity.

e.g.Find 64% of $1400.

Icanincreaseanddecreasebyagivenpercentage.

e.g.Fortheamountof $800: a increase $800 by 6% b decrease $800 by 15%

Icancalculatepercentageproﬁt.

e.g.Jimmybuysasecond-handdeskfor $145 andrestoresittoagoodcondition.Ifhesellsiffor $210, calculatehisproﬁtandthepercentageproﬁt,correcttoonedecimalplace.

1B 6

Icanﬁndthesellingprice.

e.g.Jobuyst-shirtsfor $24 eachandwishestomakea 28% proﬁtonthepurchase.Whatshouldbeher sellingpriceandwhatwillbetheproﬁtonthesaleof 20 t-shirts?

1B 7

1C 8

Icancalculateadiscount.

e.g.A $849 televisionisdiscountedby 18%.Whatisthesellingpriceofthetelevision?

Icanﬁndgrossandnetincomeinvolvingovertime.

e.g.Anikaearns $21.40 perhourandhasnormalworkinghoursof 38 hoursperweek.Sheearnstime andahalfforthenext 4 hoursworkedanddoubletimeafterthat.Shepays $190 perweekintaxand otherdeductions.

Calculatehergrossandnetincomeforaweekinwhichsheworks 45 hours.

1C 9 Icancalculateincomeinvolvingcommission.

e.g.Tiaearns $300 perweekplusacommissionof 6% onhersalesofsolarpanels.Ifshesells $8200 worthofsolarpanelsinaweek,whatishergrossincomefortheweek?

1D 10

Icancalculateincometaxpayable.

e.g.Noahearns $78406 peryear,includinginterestoninvestments.Hehasreceiptsfordonationsand workrelatedexpensesof $445

a CalculateNoah’staxableincome.

b UsethetaxtableintheKeyideasonpage 22 tocalculateNoah’staxpayableamount,tothenearest cent.

c IfNoahalsohastopay $1559 fortheMedicarelevy,calculatehistaxrefundifhisemployersent $16000 totheATO.

1E 11 Icanbudgetusingpercentages.

e.g.Ashhasanetannualincomeof $54800 afterdeductions.Sheallocatesherbudgetonapercentage basis.

) 25

a Determinetheamountofﬁxedexpenses(rentandtheloan).

b Determinehowmuchshebudgetstosaveeachmonth.

1E 12 Icanbudgetfromﬁxedvalues.

e.g.Runningacertaintypeofmotorbikeinvolvesthefollowingcosts:

• registration $520 peryear

• insurance $120 perquarter

• servicing $310 peryear

• petrol $64 permonth

Determinetheoverallcosttorunthebikeforayearandwhatpercentageofan $80000 salarythis wouldbe,correcttoonedecimalplace.

1E 13 Icancalculateabestbuy.

e.g.Packetsofchipscanbeboughtinthefollowingwaysatthestore:

• 20 packs(20 gramseach)for $5.50

• 6 packs(20 gramseach)for $3.35

• 2 sharebags(60 gramseach)for $4

Determinethecheapestwaytobuythechips.

1F 14 Icanusethesimpleinterestformulatoﬁndinterest.

e.g.Usethesimpleinterestformulatocalculatetheinterestwhen $800 isinvestedat 5% p.a.for 3 years.

1F 15 Icancalculaterepaymentsusingsimpleinterest.

e.g.Ifasimpleinterestloanof $4000 isborrowedfor 2 yearsatasimpleinterestrateof 4% p.a.,what isthetotalamountowedoverthe 2 yearsandifrepaymentsaremademonthly,howmuchwouldeach paymentneedtobe?

1F 16 Icanusethesimpleinterestformulatoﬁndtherateofinterest.

e.g.Usethesimpleinterestformulatocalculatetherateofinterestwhen $2800 earns $294 interestin 3 years.

1G 17 Icanusethecompoundinterestformula.

e.g.Determinetheamountafter 6 yearswhen $8000 iscompoundedannuallyat 3%

1G 18 Icanusecompoundinterestwithdifferenttimeperiods.

e.g.Aninvestmentof $5500 iscompoundedat 6% p.a.over 4 years.Determinetheamounthewillhave after 4 yearsifinterestispaidmonthly.

Chapter checklist

1H 19 Icanworkwithrepaymentstocalculateapurchasecost.

e.g.Vanessapaysfora $8600 travelpackagewithatravelagentwitha 30% depositandmonthly repaymentsof $300 for 2 years.

Calculate: a thedepositpaid, b thetotalamountpaidforthetravelpackageandhencetheinterestpaid.

1H 20 Icancalculateinterestearnedonanaccount.

e.g.Anaccounthasaminimummonthlybalanceof $140 andinterestiscreditedmonthlyonthis amountat 1.8%.Determinetheamountofinteresttobecreditedattheendofthemonthandthetotal amountcreditedordebitedifthebankcharges $5 permonthinaccountkeepingfees.

1I 21 Icanusetechnologytocalculateinterestandﬁnalamounts. e.g.Usetechnologytoﬁndthetotalamountonthefollowinginvestments.

a $7000 at 4% p.a.compoundedannuallyfor 5 years.

b $7000 at 4% p.a.simpleinterestfor 5 years.

Short-answerquestions

1 1A Convertthefollowing: 11 20 toapercentage a 0.12 toapercentage b 36% toasimpliﬁedfraction c 3.5% toadecimal. d

2 1A Find 16% of $9000 3 1B Increase $968 by 12%

Decrease $4900 by 7%

4 1B Thecostpriceofanitemis $7.60.Ifthisisincreasedby 50%,determine: theretailprice a theproﬁtmade. b

5 1B Anairfareof $7000 isdiscounted 40% ifyouﬂyoff-peak. Whatwouldbethediscountedprice?

6 1E Josephinebudgets 20% ofherincomefor entertainment.Ifheryearlyincomeis $37000, howmuchcouldbespentonentertainmentin: ayear? a amonth? b aweek(taking 52 weeksinayear)? c

7 1C

Mariahworksa 34-hourweekat $25.43 perhour.Hernetincomeis 62% ofherwage. Workoutherweeklynetincome. a If 15% isspentonclothing,determinetheamountshecanspendeachweek. b Ifshesaves $100,whatpercentage(totwodecimalplaces)ofhergrossweeklyincome isthis? c

8 1E Frankhasthefollowingexpensestorunhiscar: hirepurchasepayment

• $350 permonth registration

• $885 peryear insurance

• $315 perquarter servicing

• $90 perweek

• $1700 peryear petrol

a Findthetotalcostofrunninghisvehiclefor 1 year.

b Whatpercentage(tothenearestpercentage)oftheoverallcosttorunthecaristhecostofthe petrol?

9 1D Ronanworks 36 hoursinaweekat $39.20 perhour.Hepays $310 intaxand $20.50 in superannuationintheweek.Determine: hisgrosswageinaweek a hisnetpayinaweek. b

10 1D Lilreceivesanannualtaxableincomeof $90000. Usingthetaxtableshown,calculatetheamountoftaxshepaysovertheyear.

0−$18200 Nil

$18201−$45000 16cforeach $1 over $18200

$45001−$135000 $4288 plus 30cforeach $1 over $45000

$135001−$190000 $31288 plus 37cforeach $1 over $135000

$190001 andover $51638 plus 45cforeach $1 over $190000

IfLilpaysthe 2% Medicarelevyonhertaxableincome,ﬁndthisamount. b

11 1C Zanereceives 4.5% commissiononsalesof $790.Determinetheamountofhiscommission.

12 1F Findtheinterestpaidona $5000 loanunderthefollowingconditions.

8% p.a.simpleinterestover 4 years a 7% p.a.simpleinterestover 3 yearsand 4 months b

13 1G Findtheinterestpaidona $5000 loanunderthefollowingconditions. 4% p.a.compoundedannuallyover 3 years a 9.75% p.a.compoundedannuallyover 2 years b 6% p.a.compoundedmonthlyover 2 years c

1H Avehicleworth $7000 ispurchasedonaﬁnancepackage.Thepurchaserpays 15% deposit and $250 permonthover 4 years. Howmuchdepositispaid? a Whatarethetotalrepayments? b

Howmuchinterestispaidoverthetermoftheloan? c

Multiple-choicequestions

5 1C IfSimonreceives $2874 onthesaleofapropertyworth $195800,hisrateofcommission, toonedecimalplace,is:

6 1C Inagivenrosteredfortnight,Bilalworksthefollowingnumberof 8-hourshifts:

• threedayshifts($10.60 perhour)

• threeafternoonshifts($12.34 perhour)

• ﬁvenightshifts($16.78 perhour).

Histotalincomeforthefortnightis:

Acomputertabletisdiscountedby 26%.Whatisthepriceifitwasoriginally $329?

8 1H A $5000 loanisrepaidbymonthlyinstalmentsof $200 for 5 years.Theamountofinterest chargedis:

Extended-responsequestions

1 $5000 isinvestedat 4% p.a.compoundingannuallyfor 3 years. Whatisthevalueoftheinvestmentafterthe 3 years? a Howmuchinterestisearnedinthe 3 years? b Using r = 100I Pt ,whatsimpleinterestrateresultsinthesameamount? c Howmuchinterestisearnedontheinvestmentifitiscompoundedmonthlyat 4% p.a.forthe 3 years? d

2 YourbankaccounthasanopeningJulymonthlybalanceof $217.63.Youhavethefollowing transactionsoverthemonth.

Designastatementofyourrecordsif $0.51 istakenoutasafeeon 15 July. a Findtheminimumbalance. b Ifinterestiscreditedmonthlyontheminimumbalanceat 0.05%,determinetheinterestforJuly, roundedtothenearestcent. c

2 Measurement

Essentialmathematics:whymeasurementskillsare important

Accuratemeasurementskillsandcalculationsareessentialforyourhomeimprovementprojects andalsoforsafeindustrialoperationsandastablebuiltenvironment.

Spatialdesignersrelyonaccuratemeasurements.Forexample,interiordesignersplanfurniture layoutandlightingselections;digitalgamedesignerscreateimmersiveenvironmentswith proportionalaccuracy;farmersoptimizecroplayoutsandirrigationsystems;andeventplanners arrangeseating,staging,lightingandsoundsystems.

HVACtechniciansdesigneffectiveheatingandcoolingsystemsandcalculateperimeters,surface areas,andvolumesofairinroomsandducts,includinginofﬁces,restaurants,kitchens,hospitals, schoolsandmovietheatres.

Windturbinesrequireprecisemeasurementssothateachblade’scylindricaljoining-piececonnects perfectlytothehubandthentothecylindricalshaftandcirculargearsthatdrivetheelectric generator.Windpower P iscalculatedusingtheformula P = 1 2 qAv3 where q isairdensity, A isthe sweptcircularareaoftheblades,and v thewindspeed.

Inthischapter

2AConversionofunits (Consolidating)

2BPerimeter (Consolidating)

2CCircumference (Consolidating)

2DArea

2EAreaofcirclesandsectors

2FMeasurementerrorsandaccuracy

2GSurfaceareaofprisms

2HSurfaceareaofacylinder

2IVolumeofsolids

2JFurtherproblemsinvolvingprisms andcylinders

AustralianCurriculum9.0

MEASUREMENT

Solveproblemsinvolvingthesurfaceareaand volumeofcompositeobjectsusing appropriateunits(AC9M10M01)

SolvepracticalproblemsapplyingPythagoras’ theoremandtrigonometryofright-angled triangles,includingproblemsinvolving directionandanglesofelevationand depression(AC9M10M03)

Identifytheimpactofmeasurementerrorson theaccuracyofresultsinpracticalcontexts (AC9M10M04)

Usemathematicalmodellingtosolvepractical problemsinvolvingproportionandscalingof objects;formulateproblemsandinterpret solutionsintermsofthesituation;evaluate andmodifymodelsasnecessary,andreport assumptions,methodsandﬁndings (AC9M10M05)

NUMBER

Recognisetheeffectofusingapproximations ofrealnumbersinrepeatedcalculationsand comparetheresultswhenusingexact representations(AC9M10N01)

©ACARA

Onlineresources

Ahostofadditionalonlineresourcesare includedaspartofyourInteractiveTextbook, includingHOTmathscontent,video demonstrationsofallworkedexamples, auto-markedquizzesandmuchmore.

Warm-up

1 Nametheseshapes.Choosefromthewords trapezium, triangle, circle, rectangle, square, semicircle, parallelogram and rhombus a b c d e f g h

2 Writethemissingnumber.

3 Findtheperimeteroftheseshapes.

4 Findtheareaoftheseshapes.

5 Findtheareaofthesetrianglesusing A = 1 2 bh

6 Use C =p d and A =p r2 toﬁndthecircumferenceandareaofthiscircle.Roundyouranswerto twodecimalplaces.

2A 2A Conversionofunits

Learningintentions

• Toreviewthemetricunitsofmeasurement

CONSOLIDATING

• Tobeabletoconvertbetweenmetricunitsforlength,areaandvolume

Keyvocabulary: unit,length,area,volume

Toworkwithlength,areaorvolumemeasurements,itis importanttobeabletoconvertbetweendifferentunits. Forexample,timberiswidelyusedinbuildingsforframes, rooftrussesandwindows,thereforeitisimportantto orderthecorrectamountsothatthecostofthehouse isminimised.Althoughplansgivemeasurementsin millimetresandcentimetres,timberisorderedinmetres (oftenreferredtoaslinealmetres),sowehavetoconvertall ourmeasurementstometres.

Buildingahousealsoinvolvesmanyareaandvolume calculationsandunitconversions.

Beingabletocovertbetweenunitsof measurementisanimportantskillforabuilder.

Lessonstarter:Houseplans

Allhomesstartfromaplan,whichisusuallydesignedbyanarchitectandshowsmostofthebasic featuresandmeasurementsthatareneededtobuildthehouse.Measurementsaregiveninmillimetres.

• Howmanybedroomsarethere?

• Whatarethedimensionsofthemasterbedroom(i.e.BED 1)?

• Whatarethedimensionsofthemasterbedroom,inmetres?

• Willtherumpusroomﬁtapooltablethatmeasures 2.5 m × 1.2 m,andstillhaveroomtoplay?

• Howmanycarsdoyouthinkwillﬁtinthegarage?

Keyideas

Toconvertunits,drawanappropriatediagramanduseittoﬁndtheconversionfactor.

Forexample:

Conversions:

Area

Tomultiplyby 10, 100, 1000 etc.move thedecimalpointoneplacetotherightfor eachzero, e.g. 3.425 × 100 = 342.5

Todivideby 10, 100, 1000 etc.movethe decimalpointoneplacetotheleft foreachzero, e.g. 4.10 ÷ 1000 = 0.0041

3 = 100 × 100 × 100 = 1000000 10003 = 1000 × 1000 × 1000 = 1000000000

1 Writethemissingnumbersinthesesentencesinvolvinglength.

a Thereare min 1 km.

b Thereare mmin 1 cm.

c Thereare cmin 1 m.

2 Writethemissingnumbersinthesesentencesinvolvingareaunits.

a Thereare mm2 in 1 cm2

b Thereare cm2 in 1 m2

c Thereare m2 in 1 km2 .

3 Writethemissingnumbersinthesesentencesinvolvingvolumeunits.

a Thereare mm3 in 1 cm3

b Thereare m3 in 1 km3

c Thereare cm3 in 1 m3

Fluency

Example1Convertinglengthmeasurements

Converttheselengthmeasurementstotheunitsshowninthebrackets.

Explanation

Multiplywhenconvertingtoasmallerunit.

b 45 mm = 45 ÷ 10 = 4.5 cm

Nowyoutry

Dividewhenconvertingtoalargerunit.

Converttheselengthmeasurementstotheunitsshowninthebrackets. 4.6

4 Convertthefollowingmeasurementsoflengthtotheunitsgivenin thebrackets.

HintforQ4:Whenconverting toasmallerunit,multiply. Otherwise,divide.

Example2Convertingareameasurements

Converttheseareameasurementstotheunitsshowninthebrackets.

Explanation

Whendividingby 10000,movethedecimalpoint 4 placestotheleft. Continuedonnextpage

b 0.4 cm2 = 0.4 × 102 = 0.4 × 100 = 40 mm2

Nowyoutry

Converttheseareameasurementstotheunitsshowninthebrackets. 320 mm2 (cm2) a

mm2

km2 (m2) b

5 Convertthefollowingareameasurementstotheunitsgiveninthe brackets.

cm2 (mm2)

m2 (cm2) b 5 km2 (m2) c 2980000 mm2 (cm2) d 537 cm2 (mm2) e 0.023 m2 (cm2) f

Example3Convertingvolumemeasurements

Convertthesevolumemeasurementstotheunitsshowninthebrackets. 3.72 cm3 (mm3) a

) b

Solution Explanation a 3.72 cm3 = 3.72 × 103 = 3.72 × 1000 = 3720 mm3

b 4300 cm3 = 4300 ÷ 1003 = 4300 ÷ 1000000 = 0.0043 m3

Nowyoutry

Convertthesevolumemeasurementstotheunitsshowninthebrackets.

0.21 m3 (cm3) a 94000 mm3 (cm3) b

6 Convertthesevolumemeasurementstotheunitsgiveninthe brackets.

2 cm3 (mm3) a 0.2 m3 (cm3) b 5700 mm3 (cm3) c 0.015 km3 (m3) d

28300000 m3 (km3) e 762000 cm3 (m3) f

Problem-solving and reasoning

7 Anathletehascompleteda 5.5 kmrun.Howmanymetresdidtheathleterun?

8 Determinethemetresoftimberneededtoconstructthefollowingframes.

9 Findthetotalsumofthemeasurementsgiven,expressingyour answerintheunitsgiveninthebrackets.

10 cm, 18 mm (mm)

HintforQ9:Converttotheunitsin brackets.Adduptoﬁndthesum. a 1.2 m, 19 cm, 83 mm (cm) b

km, 258 m (km) c

10 Asnailismovingatarateof 43 mmeveryminute.Howmanycentimetres willthesnailmovein 5 minutes?

11 Whydoyouthinkthatbuildersmeasuremanyoftheirlengthsusingonly millimetres,eventheirlonglengths? Specialunits

12 Manyunitsofmeasurementapartfromthoserelatingtomm,cm,mandkmareusedinoursociety. Someofthesearedescribedhere.

(ha)

(

Convertthesespecialmeasurementstotheunitsgiveninthebrackets.Usetheconversion informationgivenabovetohelp.

2B 2B Perimeter CONSOLIDATING

Learningintentions

• Tobeabletocalculatetheperimeterofashape

• Tobeableto ndanunknownlengthgiventheperimeter

Keyvocabulary: perimeter

Perimeterisameasureoflengtharoundtheoutsideofashape.Wecalculateperimeterwhenordering ceilingcornicesforaroomormaterialsforfencingapaddockorwhendesigningahouse.

Farmersneedtomeasuretheperimeterofpaddockswhenbuildinga fencesotheyorderthecorrectamountofmaterials.

Lessonstarter:L-shapedperimeters

TheL-shapedﬁgureontherightincludesonlyright (90°) angles.Onlytwo measurementsaregiven.

• Canyouﬁgureoutanyothersidelengths?

• Isitpossibletoﬁnditsperimeter?Why?

Keyideas

Perimeter isthedistancearoundtheoutsideofatwo-dimensionalshape.

• Toﬁndtheperimeter,weaddallthelengthsofthesidesinthesameunits.

• Whentwosidesofashapearethesamelengththeyarelabelledwiththesamemarkings.

Exercise2B

Und er stand ing 1,2 2

1 Writethemissingword:Thedistancearoundtheoutsideofashapeiscalledthe

2 Writedownthevalueof x fortheseshapes.

Fluency

Example4Findingperimetersofbasicshapes

Findtheperimeteroftheseshapes.

Solution

a Perimeter = 3 + 2 + 4 + 3.5 = 12.5 cm

b Perimeter = 5 + 5.2 + 3 × 3 = 19.2 m

Nowyoutry

Findtheperimeteroftheseshapes.

Explanation

Addallthelengthsofthesidestogether.

Threelengthshavethesamemarkingsand thereforearethesamelength.

3 Findtheperimeteroftheseshapes.

HintforQ3c–f:Sideswiththe samemarkingsarethesame length.

4 Findtheperimeteroftheseshapes.

Problem-solving and reasoning

Example5Findingamissingsidelength

Findthevalueof x forthisshapewiththegivenperimeter.

5–7 6–10

Solution

4.5 + 2.1 + 3.4 + x = 11.9 10 + x = 11.9 x = 1.9

Nowyoutry

Explanation

Allthesidesaddto 11.9 inlength. Simplify.

Subtract 10 frombothsidestoﬁndthevalueof x

Findthevalueof x forthisshapewiththegivenperimeter.

5 Findthevalueof x fortheseshapeswiththegivenperimeters.

6 Findthevalueof x fortheseshapeswiththegivenperimeters.

HintforQ5:Addupallthesides andthendeterminethevalueof x tosuitthegivenperimeters.

= 17 m

= 22.9 cm

= 0.8 mm

Example6Workingwithperimeterwiththreedimensions

Aconcreteslabhasthemeasurementsshown.Allanglesare 90° Drawanewdiagram,showingallthemeasurementsinmetres. a Determinethelinealmetresoftimberneededtosurroundit. b

Solution

b Perimeter = 18.5 + 16.8 + 3.5 + 2.7 + 15 + 14.1 = 70.6 m

Thelinealmetresoftimberneededis 70.6 m.

Nowyoutry

Explanation

Convertyourmeasurementsand placethemallonthediagram.

1 m = 100 × 10 = 1000 mm

Addorsubtracttoﬁndthemissing measurements.

Addallthemeasurements.

Writeyouranswerinwords.

Aconcreteslabhasthemeasurementsshown.Allanglesare 90° Drawanewdiagramshowingallthemeasurementsinmetres. a Determinethelinealmetresoftimberneededtosurroundit. b

7 Sixconcreteslabsareshownbelow.Allanglesare 90° i Drawanewdiagramforeachwiththemeasurementsinmetres. ii Determinethelinealmetresoftimberneededforeachtosurroundit.

8 Arectangularpaddockhasperimeter 100 m.

Findthewidthofthepaddockifitslength is 30 m.

9 Theequilateraltriangleshownhasperimeter 45 cm.Finditssidelength. x cm

10 Writeformulasfortheperimeteroftheseshapes,usingthepronumeralsgiven.

HintforQ10:Aformulafor perimetercouldbe P = l + 2w or P = a + b + c

Howmanydifferenttables? 11,12

11 Alargediningtableisadvertisedwithaperimeterof 12 m.Thelengthandwidthareawholenumberof metres(e.g. 1 m, 2 m, ).Howmanydifferent-sized tablesarepossible?

12 Howmanyrectangles(usingwholenumbermetrelengths)haveperimetersbetween 16 mand 20 m, inclusive?

2C 2C Circumference

Learningintentions

CONSOLIDATING

• Toknowtheformulaforthecircumferenceofacircle

• Tobeableto ndthecircumferenceofacircle

• Tobeableto ndthecircumferenceofcircleportionsandsimplecompositeshapes

Keyvocabulary: circumference,pi,radius,diameter,circle

Toﬁndthedistancearoundtheoutsideofacircle–thecircumference–weusethespecialnumbercalled pi (p ).Piprovidesadirectlinkbetweenthediameter ofacircleandthecircumferenceofthatcircle.

Thewheelisoneofthemostusefulcomponentsin manyformsofmachineryanditsshape,ofcourse,is acircle.Onerevolutionofavehicle’swheelmovesthe vehicleadistanceequaltothewheel’scircumference.

Thecircumferenceofawheel,tellsyouhowfaravehicle movesforwardafteronefullrevolution.

Lessonstarter:Whencircumference = height

Hereisanexampleofacylinder.

• Trydrawingyourowncylindersothatitsheightisequaltothecircumferenceof thecirculartop.

• Howwouldyoucheckthatyouhavedrawnacylinderwiththecorrect dimensions?Discuss. height

Keyideas

The radius(r) isthedistancefromthecentreofa circle toapointonthecircle.

The diameter(d) isthedistanceacrossacirclethroughitscentre.

– Radius = 1 2 diameterordiameter = 2 × radius

Circumference(C) isthedistancearoundacircle.

– C = 2p× radius = 2p r or C =p× diameter =p d

– p (pi) isaspecialnumberandcanbefoundonyourcalculator. Itcanbeapproximatedby p¥ 3.142 C r d

Exercise2C

Und er stand ing 1–3 3

1a Thedistancefromthecentreofacircletoitsoutsideedgeiscalledthe b Thedistanceacrossacircle,throughitscentreiscalledthe c Thedistancearoundacircleiscalledthe

2 Writetheformulaforthecircumferenceofacircleusing: d fordiameter a r forradius. b

3 Whatfractionofacircleisshownhere?

Fluency

Example7Findingthecircumferenceofacircle

Findthecircumferenceofthesecirclestotwodecimalplaces. 2 cm a 2.65 mm b

Solution

a C = 2p r

= 2p (2)

= 12.57 cm (to 2 d.p.)

b C =p d

=p (2.65)

= 8.33 mm (to 2 d.p.)

Nowyoutry

Explanation

Writetheformulainvolvingtheradius, r Substitute r = 2

Roundyouranswertotwodecimalplaces.

Writetheformulainvolvingdiameter. Substitute d = 2.65

Roundyouranswertotwodecimalplaces.

Findthecircumferenceofthesecirclestotwodecimalplaces. 5 m a 4.85cm b

4 Findthecircumferenceofthesecircles,totwodecimalplaces.

Example8Findingperimetersofcompositeshapes

Findtheperimeterofthiscompositeshape,totwodecimalplaces. 3

HintforQ4:Use C = 2p r or C =p d.

Solution

P = 3 + 5 + 1 2 × 2p (2)

Explanation

= 8 + 2p Simplify.

= 14.28 m (to 2 d.p.) Roundyouranswerasinstructed. Addallthesides,includinghalfacircle.

Nowyoutry

Findtheperimeterofthiscompositeshape,totwodecimalplaces. 3 cm

Findtheperimeterofthesecompositeshapes,correcttotwodecimalplaces.

HintforQ5:Don’tforgettoaddthe straightsidestothefraction ( 1 4 , 1 2 or 3 4 ) ofthecircumference.

Problem-solving and reasoning

6 Davidwishestobuildacircularﬁshpond.Thediameterofthepondistobe 3 m.

a Howmanylinealmetresofbricksareneededtosurroundit?Roundyouranswertotwo decimalplaces.

b Whatisthecostifthebricksare $45 permetre?(Useyouranswerfrompart a.)

Thewheelsofabikehaveadiameterof 1 m.

a Howmanymetreswillthebiketravel(totwodecimalplaces)after: onefullturnofthewheels? i 15 fullturnsofthewheels? ii

HintforQ7:Foronerevolution, use C =p d

b Howmanykilometreswillthebiketravelafter 1000 fullturns ofthewheels?(Giveyouranswercorrecttotwodecimalplaces.)

8 Whatistheminimumnumberoftimesawheelofdiameter 1 mneedstospintocoveradistance of 1 km?Youwillneedtoﬁndthecircumferenceofthewheelﬁrst.Giveyouranswerasa wholenumber.

Findtheperimeterofthesecompositeshapes,correcttotwodecimalplaces.

HintforQ9:Makesureyouknowthe radiusordiameterofthecircle(s) youareworkingwith.

10a Rearrangetheformulaforthecircumferenceofacircle, C = 2p r,towrite r intermsof C.

b Find,totwodecimalplaces,theradiusofacirclewiththegivencircumference.

35 cm i 1.85 m ii 0.27 km iii Targetpractice

11 Atargetismadeupofthreerings,asshown.

a Findtheradiusofthesmallestring.

b Find,totwodecimalplaces,thecircumferenceofthe: smallestring i middlering ii outsidering. iii

HintforQ10:Towrite r interms of C dividebothsidesby 2p

c Ifthecircumferenceofadifferentringis 80 cm,whatwouldbeits radius,correcttotwodecimalplaces?

2D 2D Area

Learningintentions

• Toknowtheformulasfortheareasofsimpleshapes

• Tobeableto ndtheareaofsimpleshapes

Keyvocabulary: area,square,rectangle,triangle,rhombus,parallelogram,trapezium,perpendicular

Inthissimplediagram,arectangle,withsidelengths 2 mand 3 m,hasan areaof 6 squaremetresor 6 m2.Thisiscalculatedbycountingthenumber ofsquares(eachmeasuringasquaremetre)thatmakeuptherectangle.

Weuseformulastohelpusquicklycountthenumberofsquareunits containedwithinashape.Forthisrectangle,forexample,theformula A = lw simplytellsustomultiplythelengthbythewidthtoﬁndthearea.

Lessonstarter:Howdoes

Lookatthistriangle,includingitsrectangularreddashedlines.

• Howdoestheshapeofthetrianglerelatetotheshapeofthe outsiderectangle?

• Howcanyouusetheformulaforarectangletohelpﬁndtheareaofthe triangle(orpartsofthetriangle)?

• Whyistherulefortheareaofatrianglegivenby A = 1 2 bh?

Keyideas

The area ofatwo-dimensionalshapeisthenumberofsquareunitscontainedwithinitsboundaries. Someofthecommonareaformulasareasfollows.

The‘height’inatriangle,parallelogramortrapeziumshouldbe perpendicular (at 90°)to thebase.

Exercise2D

Und er stand ing

1 Matcheachshape(a–f)withitsareaformula(A–F).

2 Theseshapesshowthebaseandaheightlength.Writedownthegivenheightofeachshape.

Example9Usingareaformulas

Findtheareaofthesebasicshapes.

Solution

a Area = lw

= 7 × 3

Explanation

Writetheformulafortheareaofarectangle.

Substitutethelengths l = 7 and w = 3 = 21 cm2

b Area = 1 2 (a + b)h

= 1 2 (3 + 5) × 2

Simplifyandincludetheunits.

Writetheformulafortheareaofatrapezium.

Substitutethelengths a = 3, b = 5 and h = 2 = 8 cm2

c Area = 1 2 bh

= 1 2 × 5.8 × 3.3

Simplifyandincludetheunits.

Writetheformulafortheareaofatriangle.

Substitutethelengths b = 5.8 and h = 3.3 = 9.57 m2

Nowyoutry

Findtheareaofthesebasicshapes.

Simplifyandincludetheunits.

HintforQ3:First,choosethe correctformulaandsubstitute foreachpronumeral(letter).

4 Findtheareaofthesebasicshapes.

Problem-solving and reasoning

Arectangulartabletopis 1.2 mlongand 80 cmwide. Findtheareaofthetabletopusing: squaremetres (m2) a squarecentimetres (cm2) b

6 Twotriangularsailshavesidelengthsasshown.Findthetotalarea ofthetwosails.

Example10Applyingareaformulas

Christinedecidestousecarpettocovertheﬂoorofherrectangular bedroom,shownatright.Determine:

theareaofﬂoortobecovered a thetotalcostifthecarpetcosts $32 persquaremetre. b

HintforQ5:Firstconverttothe unitsthatyouwanttoworkwith.

a Areaofﬂoor = l × w = 3.5 × 2.6 = 9.1 m2

b Costofcarpet = 9.1 × 32 = $291.20

Nowyoutry

Theroomisarectangle,souse A = l × w tocalculatethe totalﬂoorspace.

Everysquaremetreofcarpetcosts $32

Richodecidestolaylawnonhistriangularbackyard,shownatright. Determine:

theareaoflawntobelaid a thetotalcostiflawncosts $11 persquaremetre. b

7 Jack’sshedistohaveaﬂatrectangularroof,whichhedecidestocover withmetalsheets.

a Determinethetotalareaoftheroof.

b Ifthemetalrooﬁngcosts $11 asquaremetre,howmuchwillitcost intotal?

8 Aslidingdoorhastwoglasspanels.Eachoftheseis 2.1 mhighand 1.8 mwide.

a Howmanysquaremetresofglassareneeded?

b Whatisthetotalcostoftheglassifthepriceis $65 per squaremetre?

9 Arectangularwindowhasawholenumbermeasurementforitslengthandwidthanditsareais 24 m2 Writedownthepossiblelengthsandwidthsforthewindow.

Determinetheareaofthehousesshown(ifallanglesarerightangles),insquaremetres(correcttotwo decimalplaces).

Findthevalueofthepronumeralintheseshapes,roundingyouranswertotwodecimalplaces eachtime.

HintforQ11:First,writethe appropriateformulaandsubstitute fortheareaandlengthpronumerals. Thensolvefortheunknown.

Fourwaystoﬁndtheareaofatrapezium

12 Findtheareaofthistrapeziumusingeachofthesuggestedmethods.

2E 2E Areaofcirclesandsectors

Learningintentions

• Toknowtheformulafortheareaofacircle

• Tobeabletocalculatewhatfractionofacircleisrepresentedbyasector

• Tobeableto ndtheareaofcirclesandsectors

Keyvocabulary: sector,circle,radius,diameter,pi

Likeitscircumference,acircle’sareaislinkedtothespecialnumberpi (p ).Theareaistheproductofpi andthesquareoftheradius,so A =p r2

Knowingtheformulafortheareaofacirclehelpsusbuildcircularobjects,planwatersprinklersystems andestimatethedamagecausedbyanoilslickfromashipincalmseas.

Lessonstarter:Whatfractionisthat?

Whenﬁndingareasofsectors,weﬁrstneedtodecidewhatfractionofacircleweare dealingwith.Thissector,forexample,hasaradiusof 4 cmanda 45° angle.

• Whatfractionofafullcircleisshowninthissector?

• Howcanyouusethisfractiontohelpﬁndtheareaofthissector?

• Howwouldyousetoutyourworkingtoﬁnditsarea?

Keyideas

Theformulaforﬁndingthearea (A) ofacircleofradius r isgivenbythe equation: A =p r2

Whenthediameter (d) ofthecircleisgiven,determinetheradiusbefore calculatingtheareaofthecircle: r = d ÷ 2.

A sector isaportionofacircleincludingtworadii.

Theangleofasectorofacircledeterminesthefractionofthecircle.Afullcircleis 360° .

• Thissectoris h 360 ofacircle.

• Theareaofasectorisgivenby A = h 360 ×p r2

Exercise2E

1 Whichisthecorrectworkingstepfortheareaofthiscircle?

2 Whichisthecorrectworkingstepfortheareaofthiscircle?

=p (10)2 A A = (p 10)2 B

=p (5)2 C

= 5p E

3 Whatfractionofacircleisshownbythesesectors?Simplifyyourfraction.

Example11Findingareasofcircles

Findtheareaofthesecircles,correcttotwodecimalplaces.

3 m a 1.06 km b

Solution

a A =p r 2

=p (3)2

=p× 9

= 28.27 m2 (to 2 d.p.)

b Radius r = 1.06 ÷ 2 = 0.53 km

A =p r 2

=p (0.53)2

= 0.88 km2 (to 2 d.p.)

Nowyoutry

Explanation

Writetheformula.

Substitute r = 3

Evaluate 32 = 9 andthenmultiplyby p

Findtheradius,giventhediameterof 1.06

Writetheformula.

Substitute r = 0.53

Writeyouranswertotwodecimalplaces withunits.

Findtheareaofthesecircles,correcttotwodecimalplaces.

5 m a 3.92cm b

Findtheareaofthesecircles,correcttotwodecimalplaces.

Example12Findingareasofsectors

Findtheareaofthissector,correcttotwodecimalplaces.

HintforQ4: r = d ÷ 2

Solution

Fractionofcircle = 60 360 = 1 6

Area = 1 6 ×p r 2

Explanation

Thesectoruses 60° outofthe 360° ina wholecircle.

Writetheformula,includingthefraction. = 1 6 ×p (10)2

Substitute r = 10 = 52.36 m2 (to 2 d.p.)

Writeyouranswertotwodecimalplaces.

Nowyoutry

Findtheareaofthissector,correcttotwodecimalplaces.

Findtheareaofthesesectors,correcttotwodecimalplaces.

HintforQ5:Firstdetermine thefractionofafullcircle thatyouareworkingwith.

Problem-solving and reasoning

6–87,8,9(½)

6 Apizzawith 40 cmdiameterisdividedintoeightequalparts.Findtheareaofeachportion,correctto onedecimalplace.

Example13Findingareasofcompositeshapes

Findtheareaofthiscompositeshape,correcttotwodecimalplaces.

Solution

Explanation

Theshapeismadeupofasemicircleandatriangle.Writethe formulasforbothshapes.

Substitute

= 1.5707...

= 3.57 cm2 (to 2 d.p.) Writeyouranswertotwodecimalplaceswithunits.

Nowyoutry

Findtheareaofthiscompositeshape,correcttotwodecimalplaces.

Findtheareaofthesecompositeshapes,correcttotwo decimalplaces.

HintforQ7:ForQuestion 7,ﬁndthe areaofeachshapethatmakesup thelargershape,thenaddthem. Forexample,triangle + semicircle.

8 Thelawnareainabackyardismadeupofasemicircularregionwithdiameter 6.5 manda right-angledtriangularregionoflength 8.2 m,asshown.Findthetotalareaoflawninthebackyard, correcttotwodecimalplaces.

9 Findtheareaofthesecompositeshapes,correcttoonedecimalplace.

HintforQ9:Useadditionor subtraction,depending ontheshapegiven.

Circularpastries

10 Arectangularpieceofpastryisusedtocreatesmallcircular pastrydiscsforthebaseofChristmastarts.Therectangularpiece ofpastryis 30 cmlongand 24 cmwide,andeachcircularpiece hasadiameterof 6 cm.

Howmanycircularpiecesofpastrycanberemovedfromthe rectangleinthisarrangement?

Findthetotalarearemovedfromtheoriginalrectangle, correcttotwodecimalplaces.

Findthetotalareaofpastryremaining,correcttotwodecimalplaces.

c Iftheremainingpastrywascollectedandre-rolledtothesamethickness,howmanycircularpieces couldbecut?(Assumethatthepastrycanbere-rolledandcutmanytimes.)

2F 2F Measurementerrorsandaccuracy

Learningintentions

• Tounderstandthedif cultyinobtainingexactmeasurements

• Toknowhowto ndtheupperandlowerboundaries(limitsofaccuracy)forthetruemeasurement

• Tounderstandthatroundingoffinintermediatecalculationsleadstoanaccumulatederror Keyvocabulary: accuracy,precision,rounding,accumulatederror,limitsofaccuracy

Humansandmachinesmeasuremanydifferentthings, suchasthetimetakentoswimarace,thelength oftimberneededforabuildingandthevolume ofcementneededtolayaconcretepatharound aswimmingpool.Thedegreeorlevelofaccuracy requiredusuallydependsontheintendedpurposeof themeasurement.

Allmeasurementsareapproximate.Errorscan happenasaresultoftheequipmentbeingusedorthe personusingthemeasuringdevice.

Accuracyisameasureofhowclosearecorded measurementistotheexactmeasurement.Precision istheabilitytoobtainthesameresultoverandover again.

millisecondandroundedtohundredths.Anelectronic beephasreplacedthepistolsoundthattook 0.15 secondstoreachthefarthestathlete.Acamera scanstheﬁnishline 2000 times/secondandsignalsthe timerasathletesﬁnish.

Lessonstarter:Roundingadecimal

• Apieceoftimberismeasuredtobe 86 cm,correcttothenearestcentimetre. Whatisthesmallestmeasurementpossiblethatroundsto 86 cmwhenroundedtothenearestcm?

a Whatisthelargestmeasurementpossiblethatroundsto 86 cmwhenroundedtothenearestcm? b

• Ameasurementisrecordedas 6.0 cm,correcttothenearestmillimetre. Whatunitswereusedwhenmeasuring? a Whatisthesmallestdecimalthatcouldberoundedtothisvalue? b Whatisthelargestdecimalthatwouldhaveresultedin 6.0 cm? c

• Considerasquarewithsidelength 7.8941 cm.Whatistheperimeterofthesquareifthesidelengthis: usedwiththefourdecimalplaces? a roundedtoonedecimalplace? b truncatedatonedecimalplace(i.e. 7.8)? c

Keyideas

The limitsofaccuracy tellyouwhattheupperandlowerboundariesareforthetrue measurement.

• Usually,itis ± 0.5 × thesmallestunitofmeasurement. Forexample,whenmeasuringtothenearestcentimetre, 86 cmhaslimitsfrom 85.5 cmupto (butnotincluding) 86.5 cm.

Majortrackeventsareelectronicallytimedtothe

• Whenmeasuringtothenearestmillimetre,thelimitsofaccuracyfor

86.05 cm.

Errorscanalsooccurinmeasurementcalculationsthatinvolveanumberofsteps.

• Itisimportanttouseexactvaluesoralargenumberofdecimalplacesthroughoutcalculations toavoidanaccumulatederror.

Exercise2F

1 Stateadecimalthatgives 3.4 whenroundedfromtwo decimalplaces.

2 Stateameasurementof 3467 mm,correcttothenearest: centimetre a metre b

3 Whatisthesmallestdecimalthatcouldresultinananswerof 6.7 whenroundedtoonedecimalplace?

4 Completethesecalculations.

a 8.7 × 3.56 roundedtoonedecimalplace i Takeyourroundedanswerfrompart ai,multiplyitby 1.8 androundtoonedecimalplace. ii

b 8.7 × 3.56 answeringwiththreedecimalplaces i Takeyourexactanswerfrompart bi,multiplyitby 1.8 androundtoonedecimalplace. ii

c Compareyouranswersfromparts aii and bii.Whatdoyounotice?Whichanswerismoreaccurate?

Example14Avoidingaccumulatederrors

Considertheshapeshown.

a Findtheareaofthesemicircle,roundingtoonedecimalplace.

b Findtheareaofthetriangleintheshape,roundingtoonedecimalplace.

c Hence,ﬁndthetotalareausingyouranswertoparts a and b

d Nowrecalculatethetotalareabyretainingmorepreciseanswersforthe calculationstoparts a and b above.Roundyourﬁnalanswercorrecttoone decimalplace.

e Compareyouranswerstoparts c and d above.Howcanyouexplainthe difference?

Continuedonnextpage

Solution

a Areasemicircle = 1 2 ×p× 12.49 2 2 = 61.261 = 61.3 m2 (to 1 d.p.)

b Areatriangle = 1 2 × 12.49 × 7.84 = 49.0 m2 (to 1 d.p.)

c Totalarea = 61.3 + 49.0 = 110.3 m2

d Areasemicircle = 61.2610 m2 Areatriangle = 48.9608 m2

Totalarea = 61.2610…+ 48.9608 = 110.2218 m2

Totalareais 110.2 m2 (to 1 d.p.)

e Theanswersdifferby 0.1 m2 whenrounded toonedecimalplace.

Theerrorresultsinpart c fromtherounding inintermediatestepsinparts a and b

Nowyoutry

Considertheshapeshown.

Explanation

Areaofasemicircle = 1 2 p r2 where r isthe diameter ÷ 2

Roundtoonedecimalplace.

Trianglearea = 1 2 bh

Combineroundedareasofsemicircleand triangle.

Retainanumberofdecimalplacesforboththe semicircleandtriangleareas.

Combinetheareastocalculatethetotalarea.

Roundﬁnalanswertoonedecimalplace.

Compare 110.3 m2 and 110.2 m2

Roundingerrorshaveaccumulatedtogivea differenceof 0.1 m2 .

Findtheareaofthesemicircle,roundingtoonedecimalplace. a

Findtheareaofthetriangleintheshape,roundingtoonedecimalplace. b Hence,ﬁndthetotalareausingyouranswertoparts a and b. c

10.82 m 6.24m

Nowrecalculatethetotalareabyretainingmorepreciseanswersforthe calculationstoparts a and b above.Roundyourﬁnalanswercorrectto onedecimalplace.

d Compareyouranswerstoparts c and d above.Howcanyouexplainthe difference? e

5 Considertheshapeshown.

Findtheareaofthesemicircle,roundingtoonedecimalplace. a Findtheareaofthetriangleintheshape,roundingtoonedecimalplace. b

Hence,ﬁndthetotalareausingyouranswertoparts a and b c Nowrecalculatethetotalareabyretainingmorepreciseanswersforthe calculationstoparts a and b above.Roundyourﬁnalanswercorrecttoone decimalplace.

Compareyouranswerstoparts c and d above.Howcanyouexplainthe difference?

6 Considertheshapeshown.

Findtheareaofthequartercircle,roundingtoonedecimalplace. a

Findtheareaofthetriangleintheshape,roundingtoonedecimalplace. b Hence,ﬁndthetotalareausingyouranswertoparts a and b c Nowrecalculatethetotalareabyretainingmorepreciseanswersforthe calculationstoparts a and b above.Roundyourﬁnalanswercorrectto onedecimalplace.

Compareyouranswerstoparts c and d above.Howcanyouexplainthe difference?

Example15Findinglimitsofaccuracy

Givethelimitsofaccuracyforthesemeasurements.

72 cm a 86.6 mm b

Solution

a 72 ± 0.5 × 1 cm

= 72−0.5 cmto 72 + 0.5 cm

= 71.5 cmto 72.5 cm

b 86.6 ± 0.5 × 0.1 mm

= 86.6 ± 0.05 mm

= 86.6−0.05 mmto 86.6 + 0.05 mm

= 86.55 mmto 86.65 mm

Nowyoutry

Explanation

Smallestunitofmeasurementisonewholecm.

Error = 0.5 × 1 cm

Thiserrorissubtractedandaddedtothegiven measurementtoﬁndthelimitsofaccuracy.

Smallestunitofmeasurementis 0.1 mm.

Error = 0.5 × 0.1 mm = 0.05 mm

Thiserrorissubtractedandaddedtothegiven measurementtoﬁndthelimitsofaccuracy.

Givethelimitsofaccuracyforthesemeasurements.

45 cm a 15.7 mm b

7 Foreachofthefollowing:

Givethesmallestunitofmeasurement(e.g. 0.1 cmisthesmallestunitin 43.4 cm). i Givethelimitsofaccuracy. ii

HintforQ7:Use ± 0.5 × smallestunitofmeasurement. l

8 Whatarethelimitsofaccuracyfortheamount$4500 whenitiswritten:

HintforQ8:Forsignificantfigures startcountingfromthefirst non-zerodigit. totwosignificantfigures? a tothreesignificantfigures? b tofoursignificantfigures? c

Problem-solving and reasoning

9 Writethefollowingasameasurement,giventhatthelowerandupperlimitsofthese measurementsareasfollows.

29.5

HintforQ9:Findthemiddleof theseintervals. f

10 Marthawritesdownthelengthofherfabricas 150 cm.AsMarthadoesnotgiveherlevelofaccuracy, givethelimitsofaccuracyofherfabricifitwasmeasuredcorrecttothenearest: centimetre a 10 centimetres b millimetre. c

11 Alengthofcopperpipeisgivenas 25 cm,correcttothenearestcentimetre.

a Whatarethelimitsofaccuracyforthismeasurement?

b If 10 piecesofcopper,eachwithagivenlengthof 25 cm,arejoinedendtoend,whatistheminimum lengththatitcouldbe?

c Whatisthemaximumlengthforthe 10 piecesofpipeinpart b?

Example16Applyingthelimitsofaccuracy

Janismeasureseachsideofasquareas 6 cm.Find:

a theupperandlowerlimitsforthesidesofthesquare

b theupperandlowerlimitsfortheperimeterofthesquare

c theupperandlowerlimitsforthesquare’sarea.

Solution

a 6 ± 0.5 × 1 cm

= 6−0.5 cmto 6 + 0.5 cm

= 5.5 cmto 6.5 cm

b Lowerlimit P = 4 × 5.5 = 22 cm

Upperlimit P = 4 × 6.5 = 26 cm

c Lowerlimit A = 5.52 = 30.25 cm2

Upperlimit A = 6.52 = 42.25 cm2

Nowyoutry

Explanation

Smallestunitofmeasurementisonewholecm.

Error = 0.5 × 1 cm

Thelowerlimitfortheperimeterusesthelower limitforthemeasurementtakenandtheupper limitfortheperimeterusestheupperlimit of 6.5 cm.

Thelowerlimitfortheareais 5.52,whereasthe upperlimitwillbe 6.52

Janismeasureseachsideofasquareas 9 cm.Find: theupperandlowerlimitsforthesidesofthesquare a theupperandlowerlimitsfortheperimeterofthesquare b theupperandlowerlimitsforthesquare’sarea.

12 Thesideofasquareisrecordedas 9.2 cm,correcttotwosigniﬁcantﬁgures. Whatistheminimumlengththatthesideofthissquarecouldbe? a Whatisthemaximumlengththatthesideofthissquarecouldbe?

b Findtheupperandlowerlimitsforthissquare’sperimeter.

c Findtheupperandlowerlimitsfortheareaofthissquare.

HintforQ12:Use theminimumand maximumlengths forparts c and d

13 Thesideofasquareisrecordedas 9.20 cm,correcttothreesigniﬁcantﬁgures. Whatistheminimumlengththatthesideofthissquarecouldbe? a Whatisthemaximumlengththatthesideofthissquarecouldbe? b

Findtheupperandlowerlimitsforthissquare’sperimeter.

Findtheupperandlowerlimitsfortheareaofthissquare. d

Howhaschangingthelevelofaccuracyfrom 9.2 cm(seeQuestion 12)to 9.20 cmaffectedthe calculationofthesquare’sperimeterandarea?

14 Codymeasuresthemassofababytobe 6 kg.Jacintasaysthesamebabyis 5.8 kgandLukegiveshis answeras 5.85 kg.

a Explainhowallthreepeoplecouldhavedifferentanswersforthesamemeasurement.

b Writedownthelevelofaccuracybeingusedbyeachperson.

c Arealltheiranswerscorrect?Discuss.

Percentageerror

15 Tocalculatethepercentageerrorofanymeasurement,theerror(i.e. ± thesmallestunitofmeasurement) iscomparedtothegivenorrecordedmeasurementandthenconvertedtoapercentage.

Forexample: 5.6 cm

Error =± 0.5 × 0.1 =± 0.05

Percentageerror = ± 0.05 5.6 × 100% =± 0.89%(totwosigniﬁcantﬁgures)

Findthepercentageerrorforeachofthefollowing.Roundtotwosigniﬁcantﬁgures.

28 m a 9 km b

8.9 km c 8.90 km d

178 mm e $8.96 f

$4.25 g 701 mL h

15(½)

1 2A Convertthegivenmeasurementstotheunitsshowninbrackets.

2 2B Findtheperimeteroftheseshapes.

3 2B Aconcreteslabisshownbelow.Allanglesare 90°

a Drawanewdiagram,showingallthemeasurementsinmetres.

b Determinethelinealmetresoftimberneededtosurroundit.

4 2C/E Findthecircumference (C) andarea (A) ofthesecircles,correcttotwodecimalplaces.

5 2D/E Findtheareaoftheseshapes.Roundyouranswertoonedecimalplaceinpart d

6 2D Arectangularkitchenflooristobereplacedwithwoodenfloorboards.Ifthefloorboards cost $46 persquaremetre,determinethecosttocoverthekitchenfloorifits dimensionsare 4.4 mby 3 m.

7 2C/E Findthearea (A) andperimeter (P) ofthecompositeshapeshown.Roundeachanswerto onedecimalplace.

8 2F Thesidelengthofasquareismeasuredtobe 9 cm.

Givethelimitsofaccuracyforthismeasurement. a Calculatetheareaofthesquareusingthe 9 cmmeasurement. b Amoreprecisesidelengthofthesquareis 8.5 cm.Calculatethedifferenceintheareaof thesquarecalculationusingasidelengthof 8.5 cmcomparedto 9 cm.

2G 2G Surfaceareaofprisms

Learningintentions

• Toknowthatthesurfaceareaofasolidcanberepresentedusinganet

• Tobeabletocalculatethesurfaceareaofaprism

Keyvocabulary: surfacearea,prism,net,cross-section

Thesurfaceareaofathree-dimensional objectcanbefoundbyﬁndingthe sumoftheareasofeachoftheshapes thatmakeupthesurfaceoftheobject.

Theminimum amountofwrapping paperrequiredto completelycovera giftisequaltothe surfacearea.

Lessonstarter:Whichnet?

Thesolidbelowisatriangularprismwitharight-angledtriangleasitscross-section.

• Howmanydifferenttypesofshapesmakeupitsoutsidesurface?

• Whatisapossiblenetforthesolid?Istheremorethanone?

• Howwouldyouﬁndthesurfacearea?

Keyideas

A prism isasolidwithaconstant cross-section shape.

Tocalculatethe surfacearea ofasolidorprism:

• Drawa net (i.e.atwo-dimensionaldrawingthatincludesallthesurfaces).

• Determinetheareaofeachshapeinsidethenet.

• Addtheareasofeachshapetogether.

Solid Net

Exercise2G

Und er stand ing

1 Atwo-dimensionaldrawingofallthefacesofasolidiscalleda

2 Forarectangularprism,answerthefollowing.

a Howmanyfacesdoestheprismhave?

b Howmany different rectanglesformthesurfaceoftheprism?

3 Forthistriangularprism,answerthefollowing.

a Whatistheareaofthelargestsurfacerectangle?

b Whatistheareaofthesmallestsurfacerectangle?

c Whatisthecombinedareaofthetwotriangles?

d Whatisthetotalsurfacearea?

Example17Findingthesurfaceareaofarectangularprism

Findthesurfaceareaofthisrectangularprismbyﬁrstdrawingitsnet.

Drawthenetofthesolid, labellingthelengthsandshapes ofequalareas.

A = 2 × areaofA + 2 × areaofB + 2 × areaofC = 2 × (8 × 3) + 2 × (5 × 3) + 2 × (8 × 5)

Substitutethecorrectlengths. = 158 cm2 Simplifyandincludeunits. Describeeacharea.

Nowyoutry

Findthesurfaceareaofthisrectangularprismbyﬁrstdrawingitsnet.

4 Findthesurfaceareaoftheserectangularprismsbyﬁrstdrawingtheirnets.

Example18Findingthesurfaceareaofatriangularprism

Findthesurfaceareaofthetriangularprismshown.

Solution

Surfacearea

= 2 × area A + area B + area C + area D

Explanation

Drawanetoftheobjectwithallthe measurementsandlabelthesectionsto becalculated.

Therearetwotriangleswiththesame areaandthreedifferentrectangles.

= 2 × ( 1 2 × 3 × 4) + (3 × 10) + (4 × 10) + (5 × 10) Substitutethecorrectlengths.

= 12 + 30 + 40 + 50

Calculatetheareaofeachshape. = 132 m2 Addtheareastogether.

Nowyoutry

Findthesurfaceareaofthetriangularprismshown.

Findthesurfaceareaofthefollowingprisms.

6 Findthesurfaceareaoftheseobjectsbyﬁrstdrawinganet.

HintforQ5:Triangularprismshave threerectanglesandtwoidentical triangles.

Problem-solving and reasoning

7 Acubewithsidelengthsof 8 cmistobepaintedalloverwithbrightredpaint.Whatisthetotal surfaceareathatistobepainted?

8 Whatistheminimumamountofpaperrequiredtowrapa boxwithdimensions 25 cmwide, 32 cmlongand 20 cmhigh?

Anopen-toppedboxistobecoveredinsideandoutwithaspecial material.Iftheboxis 40 cmlong, 20 cmwideand 8 cmhigh,ﬁnd theminimumamountofmaterialrequiredtocoverthebox.

10 Davidwantstopainthisbedroom.Theceilingandwallsaretobe thesamecolour.Iftheroommeasures 3.3 m × 4 mandtheceilingis 2.6 mhigh,ﬁndtheamountofpaintneededif: a eachlitrecovers 10 squaremetres b eachlitrecovers 5 squaremetres.

HintforQ9:Countbothinside andoutsidebutdonotinclude thetop.

11 AskirampintheshapeofatriangularprismneedstobepaintedbeforetheMoombaClassic waterskiingcompetitioninMelbourneisheld.Thebaseandsidesoftheramprequireafully waterproofpaint,whichcovers 2.5 squaremetresperlitre.Thetopneedsspecialsmoothpaint,which coversonly 0.7 squaremetresperlitre.

a Determinetheamountofeachtypeofpaintrequired.Roundyouranswerstotwodecimalplaces wherenecessary.

b Ifthewaterproofpaintis $7 perlitreandthespecialsmoothpaintis $20 perlitre,calculatethe totalcostofpaintingtheramp,tothenearestcent.(Usetheexactanswersfrompart a tohelp.)

Findthetotalsurfaceareaoftheserightsquare-basedpyramids.

13 Ihave 6 litresofpaintandon thetinitsaysthatthecoverage is 5.5 m2 perlitre.Iwishto paintthefouroutsidewalls ofashedandtheroof,which hasfouridenticaltriangular sections.WillIhaveenough painttocompletethejob?

HintforQ12:Squarepyramidshave onesquareandfouridentical triangles.

2H 2H Surfaceareaofacylinder

Learningintentions

• Tounderstandhowthenetofacylindercanbedrawntoshowthesurfacearea

• Toknowtheformulaforthesurfaceareaofacylinder

• Tobeabletocalculatethesurfaceareaofacylinder

Keyvocabulary: cylinder,area,prism,circumference,net,cross-section

Likeaprism,acylinderhasauniform cross-sectionwithidenticalcirclesas itstwoends.Thecurvedsurfaceofa cylindercanberolledouttoforma rectanglethathasalengthequaltothe circumferenceofthecircle.

Acanisagoodexampleofa cylinder.Weneedtoknowtheareaof theendsandthecurvedsurfacearea inordertocutsectionsfromasheetof aluminiumtomanufacturethecan.

Tinnedfoodmanufacturersusethesurfaceareaofacylindertoworkout howmuchmaterialisneeded.

Lessonstarter:Why 2p rh?

Wecanseefromthenetofacylinder(seethediagrambelowin Keyideas)thatthetotalareaofthetwo circularendsis 2 ×p r2 or 2p r2.Forthecurvedpart,though,considerthefollowing.

• Whycanitbedrawnasarectangle?Canyouexplainthisusingapieceofpaper?

• Whyarethedimensionsofthisrectangle h and 2p r?

• Wheredoestheformula A = 2p r2 + 2p rh comefrom?

Keyideas

A cylinder isasolidwithacircular cross-section

• Thenetcontainstwoequalcirclesandarectangle.The rectanglehasonesidelengthequaltothecircumference ofthecircle.

• A = 2 circles + 1 rectangle

= 2p r 2 + 2p rh

• Anotherwayofwriting 2p r2 + 2p rh is 2p r(r + h)

Exercise2H

Und er stand ing

1 Writethemissingword/expression.

a Theshapeofthecross-sectionofacylinderisa

b Thesurfaceareaofacylinderis A = 2p r2 +

2 Acylinderanditsnetareshownhere.

a Whatisthevalueof: r? ii h? i

b Findthevalueof 2p r,correcttotwodecimalplaces.

c Use A = 2p r2 + 2p rh toﬁndthesurfacearea,correcttotwo decimalplaces.

Example19Findingthesurfaceareaofacylinder

Byﬁrstdrawinganet,ﬁndthesurfaceareaofthiscylinder,correcttotwo decimalplaces.

Solution

Explanation

Drawthenetandlabeltheappropriatelengths.

A = 2 circles + 1 rectangle

= 2p r 2 + 2p rh

= 2p (1.7)2 + 2p (1.7)(5.3)

= 74.77 m2 (to 2 d.p.)

Nowyoutry

Writewhatyouneedtocalculate.

Writetheformula.

Substitutethecorrectvalues: r = 1.7 and h = 5.3

Roundyouranswertotwodecimalplaces.

Byﬁrstdrawinganet,ﬁndthesurfaceareaofthiscylinder,correctto twodecimalplaces.

Byﬁrstdrawinganet,ﬁndthesurfaceareaofthesecylinders,totwodecimalplaces.

HintforQ3:Rememberthat radius = diameter ÷ 2

4 Usetheformula A = 2p r2 + 2p rh toﬁndthesurfaceareaofthesecylinders,to onedecimalplace.

Findtheareaofonlythecurvedsurfaceofthesecylinders, toonedecimalplace.

HintforQ5:Findonlytherectangular partofthenet,souse A = 2p rh. Becarefulwiththeunitsinpart b!

Problem-solving and reasoning 6,7

6 Findtheoutsidesurfaceareaofapipeofradius 85 cmandlength 4.5 m,toonedecimalplace. Giveyouranswerinm2

7 Thebaseandsidesofacircularcaketinaretobelinedontheinsidewithbakingpaper.Thetinhasa basediameterof 20 cmandis 5 cmhigh.Whatistheminimumamountofbakingpaper required,toonedecimalplace?

Theinsideandoutsideofanopen-toppedcylindricalconcretetank istobecoatedwithaspecialwaterprooﬁngpaint.Thetankhas diameter 4 mandheight 2 m.Findthetotalareatobecoated withthepaint.Roundyouranswertoonedecimalplace.

Findthesurfaceareaofthesecylindricalportions,toonedecimalplace.

HintforQ8:Includethebase butnotthetop.

HintforQ9:Carefullyconsiderthe fractionofacirclemadeupbythe ends,andthefractionofafull cylindermadeupbythecurvedpart.

10 Asteamrollerhasalarge,heavycylindricalbarrelthatis 4 mwideandhasadiameterof 2 m.

a Findtheareaofthecurvedsurfaceofthebarrel,totwodecimalplaces.

b After 10 completeturnsofthebarrel,howmuchgroundwouldbecovered,totwodecimalplaces?

c Findthecircumferenceofoneendofthebarrel,totwodecimalplaces.

d Howmanytimeswouldthebarrelturnafter 1 kmofdistance,totwodecimalplaces?

e Whatareaofgroundwouldbecoveredifthesteamrollertravels 1 km?

2I 2I Volumeofsolids

Learningintentions

• Tounderstandhowthevolumeofsolidsrelatestoitsconstantcross-sectionandheight

• Toknowthecommonunitsforcapacity

• Toknowtheformulaforthevolumeofasolidwithauniformcross-section

• Tobeabletocalculatethevolumeofasolidwithauniformcross-section

Keyvocabulary: solid,volume,cross-section,uniform,prism,cylinder,perpendicular,capacity

Thevolumeofasolidistheamountofspaceitoccupies withinitsoutsidesurface.Itismeasuredincubicunits.

Forsolidswithauniformcross-section,theareaofthe cross-sectionmultipliedbytheperpendicularheightgives thevolume.Considertherectangularprismbelow.

4 6 3

Numberofcubicunits(base) = 4 × 6 = 24

Area(base) = 4 × 6 = 24 units2

Volume = area(base) × 3 = 24 × 3 = 72 units3

Knowinghowtocalculatethevolumeofa containerortoolboxisusefulforunderstanding howmuchitcanstore.

Lessonstarter:Volumeofatriangularprism

Thisprismhasatriangularcross-section.

• Whatistheareaofthecross-section?

• Whatisthe‘height’oftheprism?

• Howcan V = A × h beappliedtothisprism, where A istheareaofthecross-section?

Keyideas

Volume istheamountofthree-dimensionalspacewithinanobject.

Thevolumeofasolidwithauniformcross-sectionisgivenby V = A × h,where:

• A istheareaofthecross-section.

• h istheperpendicular(at 90°)height.

Rectangularprism Cylinder l w h V = lwh r h V =p r2h

Capacity isthevolumeofagivenobjectmeasuredinlitresormillilitres.

Unitsforcapacityinclude:

Exercise2I

Und er stand ing

1 Matchthesolid(a–c)withthevolumeformula(A–C). cylinder a V = lwh A rectangularprism b V = 1 2 bh × length B triangularprism c V =p r2h C

2 Writethemissingnumber.

a Thereare mLin 1 L.

b Thereare cm3 in 1 L.

3 Theareaofthecross-sectionofthissolidisgiven.Findthe solid’svolume,using V = A × h

Example20Findingthevolumeofarectangularprism

Findthevolumeofthisrectangularprism. 4 m 5 m 6 m

Solution

Explanation

V = A × h Writethegeneralformula.

= l × w × h l = 6, w = 5 and h = 4. = 6 × 5 × 4 Simplifyandincludeunits. = 120 m3

Nowyoutry

Findthevolumeofthisrectangularprism.

4 Findthevolumeoftheserectangularprisms. HintforQ4:Use V = lwh

Example21Findingthevolumeofacylinder

Findthevolumeofthiscylinder,correcttotwodecimalplaces.

Solution

Explanation

V = A × h Writethegeneralformula.

=p r 2 × h Thecross-sectionisacircle.

=p (2)2 × 6

Substitute r = 2 and h = 6

= 75.40 cm3 (to 2 d.p.) Simplifyandwriteyouranswerasrequired,withunits.

Nowyoutry

Findthevolumeofthiscylinder,correcttotwodecimalplaces. 9 m 3 m

5 Findthevolumeofthesecylinders,correcttotwodecimalplaces.

HintforQ5:Foracylinder: V

6 Atrianglewithbase 8 cmandheight 5 cmformsthebaseofaprism,as shown.Iftheprismstands 4.5 cmhigh,ﬁnd: a theareaofthetriangularbase b thevolumeoftheprism. 4.5 cm

7 Findthevolumeofthesetriangularprisms.

HintforQ7:Use V = A × h, where A isthearea ofatriangle.

Problem-solving and reasoning

8 Acylindricaldrumstandsononeendwithadiameterof 25 cmandwaterisﬁlledtoaheightof 12 cm. Findthevolumeofwaterinthedrum,incm3,correcttotwodecimalplaces.

Example22Workingwithcapacity

Findthenumberoflitresofwaterthatthiscontainercanhold.

Solution

Explanation

V = 30 × 40 × 20 Firstworkoutthevolumeincm3 = 24000 cm3 Thendivideby 1000 toconverttolitres,since 1 cm3 = 1 mL = 24 L andthereare 1000 mLin 1 litre.

Nowyoutry

Findthenumberoflitresofwaterthatthiscontainercanhold.

Findthenumberoflitresofwaterthatthesecontainerscanhold.

10 Findthevolumeofthesesolids,roundingyouranswerstotwodecimalplaces wherenecessary.

HintforQ10:Find theareaofthe cross-sectionﬁrst.

11 100 cm3 ofwateristobepouredintothiscontainer.

a Findtheareaofthebaseofthecontainer.

b Findthedepthofwaterinthecontainer.

12 Inascientiﬁcexperiment,solidcylindersoficeareremovedfroma solidblockcarvedoutofaglacier.Theicecylindershavediameter 7 cm andlength 10 cm.Thedimensionsofthesolidblockareshown inthediagram.

a Findthevolumeoficeintheoriginaliceblock.

b Findthevolumeoficeinoneicecylinder,totwodecimalplaces.

c Findthenumberoficecylindersthatcanberemovedfromtheice block,usingtheconﬁgurationshown.

d Findthevolumeoficeremainingaftertheicecylindersareremoved fromtheblock,totwodecimalplaces.

13 Thevolumeofapyramidorconeisexactlyone-thirdthevolumeoftheprismwiththesamebase areaandheight,i.e. V = 1 3 × A × h

Findthevolumeofthesepyramidsandcones.Roundyouranswertoonedecimalplacewhere necessary.

2J 2J Furtherproblemsinvolvingprisms andcylinders

Learningintentions

• Tobeabletocalculatethesurfaceareaandvolumeofacompositesolid

• Tobeabletosolveproblemsinvolvingcompositesolids

Keyvocabulary: compositesolid,prism,cylinder,net,Pythagoras’theorem,capacity

Recallthatwhenworkingwithcompositeshapeswecan ﬁndperimetersandareasbyconsideringthecombination ofthemorebasicshapesthat,together,formthecomposite shape.Similarly,wecanworkwithcompositesolidsby lookingatthecombinationofmorebasicsolids,likeprisms andcylinders.Thisleadstoﬁndingsurfaceareas,volumes andcapacityofsolids.

Thewell-knownEuropeanartistsChristoand Jeanne-Claudehadtheirhandsfullwithcomposite objectswhentheywrappedtheReichstag(Parliament building),Berlinin1995.Theyusedmorethan 100000 squaremetresoffabricand 15 kmofrope.

Lessonstarter:Whichsolids?

Lookatthesecompositesolids.

• Whatarethebasicsolidsthatmakeupeachcompositesolid?

• Explainamethodforﬁndingthevolumeofeachsolid.

• Explainamethodforﬁndingthesurfaceareaofeachsolid.

• Isthereenoughinformationprovidedineachdiagramtoﬁndthevolumeandsurfacearea?Discuss.

Keyideas

Compositesolidsaremadeupofmorethanonebasicsolid.

Volumesandsurfaceareasofcompositesolidscanbefoundbyconsideringthevolumesand surfaceareas(orpartthere-of)ofthebasicsolidscontainedwithin.

TheGermanparliament,theReichstag,was wrappedinfabricin1995tocreateatemporary workofart.

Pythagoras’theoremmaybeusedtohelpﬁndparticularlengths,providedthataright-angled triangleisgiven.

Recallthesecommonunitconversionsforcapacity.

Exercise2J

1 Namethetwobasicsolidsthatmakeupeachofthesecompositeshapes.

2 UsePythagoras’theoremtoﬁndthelengthofthehypotenuseintheseright-angledtriangles.

Example23UsingPythagoras’theoremtohelpﬁndthesurfaceareaofa triangularprism

Findthesurfaceareaofthistriangularprism.

Solution

c2 = a2 + b2

= 62 + 82

= 100

c = √100 = 10

Surfacearea = 2 × 1 2 × 8 × 6 + (8 × 12)

+ (6 × 12) + (10 × 12)

= 48 + 96 + 72 + 120 = 336 m2

Nowyoutry

Findthesurfaceareaofthistriangularprism.

Explanation

UsePythagoras’theoremtoﬁndthe lengthoftheslantingedge. 8 m 6 m c m

Thesurfaceareaismadeupoftwo congruenttriangularendsandthree differentrectangles.

3 UsePythagoras’theoremtohelpﬁndthesurfaceareaofthesetriangularprisms.

Example24Findingthesurfaceareaandvolumeofacompositesolid

Findthesurfaceareaandvolumeofthiscompositesolid,correcttotwodecimalplaces.

Solution

Surfacearea = 6 × 22 + 2p (1)(3) = 24 + 6p = 42.85 cm2 (to 2 d p )

Explanation

Thesurfaceareaismadeupof 5 squarefacesplusone more,whichismadeupoftheremainingpartoftheright sidefaceandtheendofthecylinder.

Thecurvedsurfaceofthecylinder (2p rh) isalsoincluded. Theradiusishalfthediameter,i.e. r = 1

Continuedonnextpage

Volume = 23 +p (1)2(3) = 8 + 3p = 17.42 cm3 (to 2 d.p.)

Nowyoutry

Thevolumeconsistsofthesumofacube(l3) andacylinder(p r2h).

Findthesurfaceareaandvolumeofthissolid,correcttotwodecimal places.

4 Forthesecompositesolids,ﬁnd: thesurfacearea i thevolume. ii Giveyouranswercorrecttotwodecimalplaces.

HintforQ4:Includeonlyexposed surfacesinthesurfacearea.

5 Findthecapacityofthesecompositesolids,inlitres.Roundyouranswertotwodecimalplaces wherenecessary. HintforQ5:Recall:

Problem-solving and reasoning

6 Hereisthedesignofaglasstennistrophy.Thebaseandthe cylindricalpartarebothmadeofglass.

Findthesurfaceareaofthetrophy,tothe nearestsquarecentimetre.

Findthevolumeofglass,tothenearestcubiccentimetre, requiredtomakethetrophy.

7 Whensolidsarepainted,theoutersurfaceareaneedstobeconsideredtohelpﬁndtheamountof paintrequiredforthejob.Assumethat 1 Lofpaintcovers 10 m2 Completeforeachoftheseobjects.

i Findthesurfaceareainsquaremetres,roundingyouranswertotwodecimalplaces wherenecessary.

ii Findtheamountofpaintthatmustbepurchased,assumingthatyoucanbuyonlyawhole numberoflitres.

8 Whensolidsarehollow,theinsidesurfaceareasareexposedtotheair.Findthesurfacearea(i.e.inner andoutercombined)ofapipeofdiameter 0.3 mandlength 3 m.Assumethattheinnerandouter diametersarethesame.(Roundyouranswertoonedecimalplace.)

9 Thisnutisasquare-basedprismwithacylindricalholeremovedfrom thecentre.Theholehasadiameterof 1 cm.Thenutiscoatedwith anti-rustpaint.Whatareaispainted,includingtheinnercylindrical surface?(Roundyouranswertoonedecimalplace.)

10 Thesesolidshaveapproximatelythesamevolume.

Whichhasthelargersurfacearea?Dosomecalculationstoﬁndout.

11 Acompanywishestodesignacontainerforpackagingandsellinglollies.Thetwodesignsare shownhere.

a Completesomecalculationstoshowthatthetwocontainershaveapproximatelythesamevolume.

b Whichdesignhastheleastsurfacearea?Justifyyouranswer.

12 Imaginethatacompanyasksyoutomakeatrayoutofasquarepieceofcard,measuring 10 cmby 10 cm,bycuttingoutfourcornersquaresandfoldingthemtoformatray,asshown. 10 cm 10 cm

a Whatwillbethevolumeofthetrayifthesidelengthofthesquarecut-outsis: 1 cm? i 2 cm? ii 3 cm? iii The 2 cmcut-outsareshownbelow. 2 cm 6 cm

b Whichsquarecut-outfrompart a givesthelargesttrayvolume?

c Canyouﬁndanothersizedcut-outthatgivesalargervolumethananyofthoseinpart a?

d Whatsizedcut-outgivesthemaximumvolume?

Bricklayer

Abricklayerhasaphysicallychallengingjob thatrequiresstaminaandstrengthandalso goodcommunicationskills,astheyoftenwork aspartofateam.

Bricklayersmusthaveasolidunderstandingof howtheconstructionprocessworksandthe abilitytoreadplansandblueprints.

Mathematicalskillsareessentialinthistrade.

Bricklayersmustunderstandratiosformixing mortarandcement.Goodmeasurementskills arealsoimportant,asbricklayersmustbeable toworkoutthenumberofbricksrequiredfor ajob,convertbetweendifferentunitsandtake accuratemeasurementsattheworksite,using themostappropriatetool.Anunderstanding ofgeometryandtrigonometryisalsorequired.

Completethesequestionsthatabricklayermayfaceintheirday-to-dayjob.

1 Astandardhousebrickhasdimensions l × w × h = 230 mm × 76 mm × 110 mm andthestandardthicknessofmortarwhenlayingbricksis 10 mm. Thebricksarelaidsothat l × h istheouterface.

a Whatisthelengthandheightofeachbrickincentimetres andmetres?

b Determinetheareaincm2 andm2 oftheouterfaceofonebrick.

c Determinethevolumeincubiccentimetresofeachbrick.

d Calculatethelength,inmetres(totwodecimalplaces), whenlayingthefollowingnumberofbricksinaline withmortarbetweeneachjoin. 10 bricks i 100 bricks ii

HintforQ1d:For 10 bricks,there wouldbe 9 mortarjoins.

e Calculatetheheight,inmillimetres,ofawallof 25 rowsofstandardhousebricks. Remembertoconsiderthethicknessofthemortar.

f Estimatehowmanystandardhousebricksareneededtobuildawall 4 mby 1.5 m,bydividing theareaofthewallbytheareaofabrick’sface.

HintforQ1b,c:

2 Ready-mixmortarcomesin 20 kgbagsthatcost $7.95 perbag.Onebagofmortarisusedtolay 20 standardhousebricks.

Usingstandardhousebricks(seedimensiondetailsinQuestion 1),abrickwallistobebuiltthathasa ﬁnishedlengthof 8630 mm,aheightof 2750 mmandisonebrickdeep.

a Calculatetheexactnumberofstandardhousebricksneededtobuildthiswall.Rememberto considerthethicknessofthemortar.

b HowmanyReady-mixmortarbagsmustbepurchasedforthiswall?

c Ifeachhousebrickcosts 60 cents,ﬁndthetotalcost,tothenearestdollar,ofthematerialsneeded forthiswall.

3 Atypeoflargebrickischosenforanoutsideretainingwall.These bricksaresoldonlyinwholepacksandeachpackcovers 12.5 square metreswhenlaid.Howmanywholepacksofthesebricksmust beboughttobuildawallwithdimensions:

a 6 mby 1.5 m?

b 9 mby 2 m?

HintforQ3:Youcan’tbuyhalf apack,sorounduptothe nextwholenumber.

4 Fastwallhousebricksarelargerandlighterthanstandardbricksandcanbeusedforsingle-storey constructions.Theyaresoldinpalletsof 1000 for $1258.21,includingdeliveryandGST.EachFastwall brickhasdimensions l × w × h = 305 mm × 90 mm × 162 mmandthestandardthicknessofmortar is 10 mm.

a Ifapallethas 125 bricksperlayer,howmanylayersdoeseachpallethave?

b Ifthewoodenbaseofthepallethasaheightof 30 cm,whatisthetotalheightofthepallet, incm,whenloadedwithbricks?

c Findtheexactnumberofbricksneededtobuildawallthatis 20.15 mlongand 6.87 mhigh. Remembertoconsiderthethicknessofthemortar.

d Determinethecostofthebricks,tothenearestdollar,requiredtobeboughtforbuildingthewall inpart c

Usingtechnology

5 Copythefollowingtableintoaspreadsheet.Thenenter formulasintotheshadedcellsand,hence,determinethe missingvalues.

HintforQ5:ForE5theformula wouldbe = G5 × A5 + (G5−1) × D5 ForG6theformulawould be = (

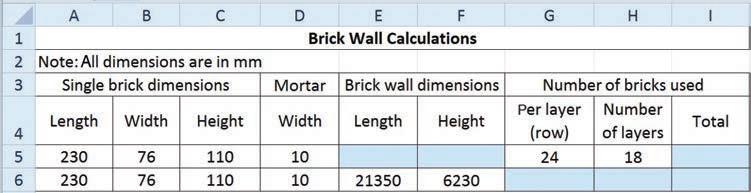
6 Copythefollowingtableintoyourspreadsheetunderneaththetable fromQuestion 5.Entertheformulasintotheshadedcellsand,hence, determinethemissingvalues.Assumethereare 1000 bricksper palletandthatonebagofmortarisusedper 20 brickslaid.

)

HintforQ6:Copythetotal numberofbricksused fromtheﬁrsttable.

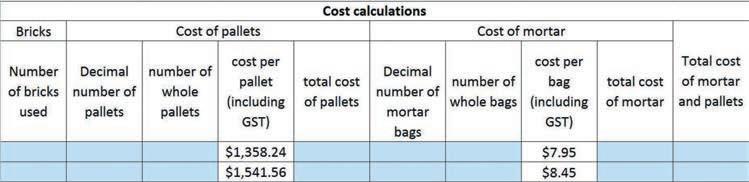
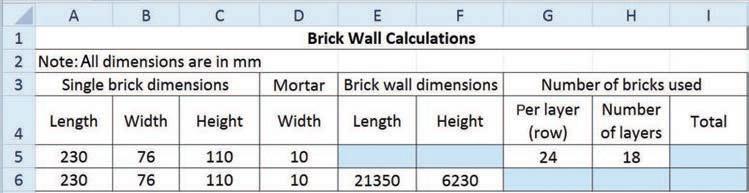
IncellB13 enter = ROUNDUP(B12, 0),whichwillroundthenumberfromcellB12 uptothenearest wholenumber;e.g. 1.3 willberoundedupto 2

7 Useyourspreadsheettablestoﬁndthetotalcostofmaterialsforthefollowingbrickwallsmadefrom Fastwallbricks.(SeeQuestion 4 forFastwallbrickdimensions.)Thespreadsheetformulaswillnotneed tobechanged.

a Awallof 44 bricksperlayer(row)and 30 layers(rows)ifpalletscost $1258.36,includingGST,and mortaris $7.55 perbag.

b Awall 20.15 mlongby 8.59 mhighifpalletscost $1364.32,includingGST,andmortaris $9.25 perbag.

Buildingplaygroundequipment

Agroupofhighschoolstudentshaveraisedsomemoneyforavolunteercommunityserviceproject. Thestudentsdecidetoaskthecounciliftheycanimprovethechildren’splaygroundequipmentinthe localpark.

Presentareportforthefollowingtasksandensurethatyoushowclearmathematicalworkings, explanationsanddiagramswhereappropriate.

1Preliminarytask

Calculatethefollowingareas,roundingtheanswerstoonedecimalplace.

a Calculatetheareaofacirclewithdiameter 3.5 m.

b Determinetheareaofthefollowingtriangles.Inpart ii youwillneedtoapplyPythagoras’ theoremtocalculatethetriangle’sheight.

c Determinethetotalsurfaceareaincm2 andm2 ofacylindricalbalancingbeamwithradius 12 cmandlength 3 m.

2Modellingtask

Formulate Youaretoprepareaproposalfortwoimprovementstothepark’splaygroundequipment: constructingasetoflowconcretecylindersthatchildrencanuseassteps,and

•

• therepaintingofanoldplaygroundroundabout.

Theproblemistodeterminethevolumeofconcreteandpaintneededandtoﬁndoutifthecostof theprojectiswithinabudgetof $200.

a Withtheaidofdiagrams,writedownalltherelevantmathematicalformulasthatareneeded tocalculate:

thevolumeandsurfaceareaofacylinder i theareaofanisoscelestriangle. ii

Concretecylinders

b Nineconcretecylindersofradius 20 cmare tobeconstructedhavingabove-ground heightsof:

15 cm, 30 cm, 45 cm, 60 cm, 75 cm, 60 cm, 45 cm, 30 cm, 15 cm.

Eachcylinderalsoextends 30 cmbelow groundforstability.

Copythefollowingtableintoanexcelspreadsheetandenterformulasintotheshadedcells. FormatcellstoNumber/onedecimalplace.Usepi()forentering p

ExtendtheExceltabletoincludeallninecylindersandthetotalsurfaceareaandvolumeusingunits ofcmandm.

Theroundabout

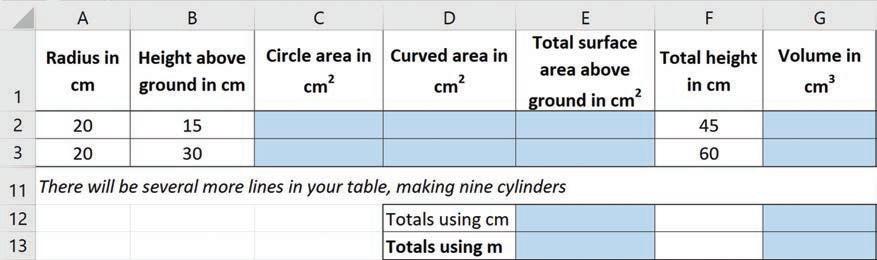
Theoldroundabouthasanoctagonshapedtopwith 8 isoscelestriangles;eachtrianglehasa 1 m baseandtwoequalsidesof 130 cm.Theroundabout’srectangularverticalsidesareeach 50 cmhigh and 1 minlength.

Determinetheareaofoneisoscelestriangleandonerectangleincm2.Youwillneedtoapply Pythagoras’theoremtocalculatethetriangle’sheight.

c Determinetheroundabout’ssurfacearea,includingthetopandsides,inm2 toonedecimalplace.

Thecouncilhasofferedtopourtheconcretecylinderssothestudentvolunteerswillonlybe responsibleforthepaintingjobs,includingthecylindersandtheroundabout.Onlythepaintingwill beincludedinthebudget.

Ifonlyonecolourisusedand 3 coatsareapplied,ﬁndthetotalareatobepainted.

Ifnon-slippaintcovers 8 m2/litredeterminethevolumeofpaintrequired.

Ifnon-slippaintcomesin 2 Lcansat $75 eachand 4 Lcansat $110 each,calculatetheminimum costofpaint,assumingthreecoatsarerequired,anddetermineiftheprojectiswithinbudget.

h Summariseyourﬁndingsstating:

thevolumeofconcreteneededforthecylinders i theoverallareatobepainted ii thedetailsofwhatcansofpainttobuyandthecost. iii

3Extensionquestion

a Inadifferentplaygroundthestepsarehalfcylinderswithradius 30 cmandallareofheight 50 cm.Theystandupwithoneverticalﬂatside,acurvedsideandasemicirculartop.The octagonalroundaboutismadeupof 8 isoscelestriangles,eachwithbaselength 1.4 mandtwo equalsidesof 1.83 m.Theroundabout’sverticalsidesarestill 50 cmhigh.Findthesurfaceareas andvolumesoftheplaygroundobjectsandcalculatethecostofpaintforthisplaygroundusing thesamecostsasinpart g

Evaluate and verify

Communicate

Technology and computational

Maximisingandminimisingwithsolids Keytechnology:Spreadsheets

Whenworkingwithsolidslikeprismsandcylinders, youmightbeinterestedineitherofthefollowing:

• minimisingthesurfaceareaforaﬁxedvolume

• maximisingthevolumeforaﬁxedsurfacearea.

Youwillrecalltheserulesforthesurface areaandvolumeofcylinders.

1Gettingstarted

Acompanyismakingdrumstoholdchemicalsandrequireseachcylindricaldrumtobe 50 litresin volumewhichis 50000 cm3 .

a Usethevolumeformulaforacylindertoshowthat h = 50000 p r2

b Findtheheightofthecylindercorrecttotwodecimalplacesiftheradiusis: 20 cm i 10 cm ii

c Findthesurfaceareaofthecylindercorrecttotwodecimalplacesiftheradiusis: 20 cm i 10 cm ii

d Findaradiusthatgivesasmallersurfaceareacomparedtotheexamplesinpart c above.

2Usingtechnology

a Constructaspreadsheettoﬁndtheheightandsurfaceareaforacylinderwithﬁxedvolume 50000 cm3.Usearadiusof 1 cmtostartandincreaseby 1 cmeachtimeasshown.

b Filldownfromcells A5, B4 and C4 toﬁndtheheightsandsurfaceareasforcylindricaldrumsof volume 50000 cm3.Locatetheintegerradiusvaluewhichprovidestheminimumsurfacearea.

c Doyouthinkthattheintegervalueoftheradiusgivesthetrueminimumvalueofthesurface area?Givereasons.

3Applyinganalgorithm

Wewillnowsystematicallyaltertheincrementmadetotheradiusvalueinourspreadsheettoﬁnda moreaccuratesolution.

a Applythisalgorithmtoyourspreadsheetandcontinueuntilyouaresatisﬁedthatyouhavefound theradiusvaluethatminimisesthesurfaceareacorrecttotwodecimalplaces.

• Step 1:Altertheformulaincell A5 sothattheincrementissmaller.e.g. 0.1 ratherthan 1

• Step 2:Filldownuntilyouhavelocatedtheradiusvaluethatminimisesthesurfacearea.

• Step 3:Adjustcell A4 toahighervaluesoyoudon’tneedtoscrollthroughsomanycells.

• Step 4:RepeatfromStep 1 butusesmallerandsmallerincrements(0.01 and 0.001)untilyou havefoundtheradiusvaluewhichminimisesthesurfaceareacorrecttotwodecimalplaces.

b Writedownthevaluefor r, h and A correcttotwodecimalplaceswhichgivestheminimum surfaceareaofacylindricaldrum.

c Nowaltertheﬁxedvolumeofthecylinderandrepeattheabovealgorithm.

d Whatdoyounoticeabouttherelationshipbetween r and h atthepointwherethereisaminimum surfacearea?Experimentwithdifferentvolumestoconﬁrmyourconjecture.

Puzzles and games

1 ‘Iamthesameshapeallthewaythrough.WhatamI?’Findtheareaofeachshape. Matchtheletterstotheanswersbelowtosolvetheriddle.

2 Onelitreofwaterispouredintoacontainerintheshapeofarectangularprism.The dimensionsoftheprismare 8 cmby 12 cmby 11 cm.Willthewateroverﬂow?

3 Acircularpieceofpastryisremovedfromasquaresheetwithsidelength 30 cm. Whatpercentageofpastryremains?

4 Howmanydifferentnetsarethereforacube?Donotcountreﬂectionsorrotationsof thesamenet.Hereisoneexample.

5 Givetheradiusofacirclewhosevalueforthecircumferenceisequaltothevaluefor thearea.

6 Findtheareaofthisspecialshape.

7 Acube’ssurfaceareais 54 cm2.Whatisitsvolume?

Conversion of units

Surface area

Perimeter

The distance around the outside of a shape.

Draw a net and add the surface areas.

Triangular prism

Cylinder

= 2 r 2 + 2 rh

2 endscurved part 4 m 3 m A = 2 ×× 4 × 3 + 6 × 4 + 6 × 3 + 6 × 5 = 84 m2

Circumference

The distance around the outside of a circle.

Area of basic shapes

Square: A = l 2

Rectangle: A = lw

Triangle: A = bh1 2

Measurement

The volume and surface area of composite solids (made up of more than one solid) can be found by combining the volume and surface area (or parts of) the individual solids.

Composite solids associated with the measuring instruments and how they are used.

Accuracy depends on any error

Limits of accuracy are usually

Parallelogram: A = bh

Trapezium: A = (a + b)h

Rhombus: A = xy1 2 1 2

For any prism, V = Ah where A is the area of the cross-section. ± 0.5 × the smallest unit. Area of a circle

It is important to use exact values or a large number of decimal places to avoid accumulating errors in calculations.

Chapter checklist

Chapterchecklist

AversionofthischecklistthatyoucanprintoutandcompletecanbedownloadedfromyourInteractiveTextbook.

2A 1

Icanconvertbetweenmetricunitsoflength. e.g.Convertthesemeasurementstotheunitsshowninthebrackets. a 2.3 m(cm) b 270000 cm(km)

2A 2 Icanconvertbetweenmetricunitsofarea. e.g.Convertthesemeasurementstotheunitsshowninthebrackets. a 32000 m2 (km2) b 7.12 cm2 (mm2)

2A 3 Icanconvertbetweenmetricunitsofvolume. e.g.Convertthesemeasurementstotheunitsshowninthebrackets. a 3.7 cm3 (mm3) b 5900000 cm3 (m3)

2B 4 Icanﬁndtheperimeterofbasicshapes. e.g.Findtheperimeterofthisshape.

2B 5 Icanﬁndamissingsidelengthgiventheperimeter. e.g.Findthevalueof x forthisshapewiththegivenperimeter.

2C 6 Icanﬁndthecircumferenceofacircle.

e.g.Findthecircumferenceofacirclewithadiameterof 5 m,correcttotwodecimalplaces.

2C 7 Icanﬁndtheperimeterofsimplecomposite shapes.

e.g.Findtheperimeterofthiscompositeshape,correctto twodecimalplaces.

2D 8 Icanﬁndtheareaofsquares,rectanglesand triangles.

e.g.Findtheareaofthistriangle.

2D 9 Icanﬁndtheareaofrhombuses,parallelogramsand trapeziums.

e.g.Findtheareaofthistrapezium.

2E 10 Icanﬁndtheareaofacircle.

e.g.Findtheareaofthiscircle,correcttotwodecimalplaces.

2E 11 Icanﬁndtheareaofasector.

e.g.Findtheareaofthissector,correcttotwodecimalplaces.

2E 12 Icanﬁndtheareaofsimplecomposite shapesinvolvingsectors.

e.g.Findtheareaofthiscompositeshape,correctto twodecimalplaces.

2F 13 Icanunderstandandavoidaccumulatingerrors. e.g.Findthetotalareaofthisshapebyﬁndingtheareaofthesemicircle andtriangleeachtoonedecimalplacethenaddingandthenbyusingno intermediaterounding.Explainwhichanswerismoreaccurate.

2F 14 Icanstatethesmallestunitforagivenmeasurement.

e.g.Writedownthesmallestunitofmeasurementfor 27.3 cm.

2F 15 Icanﬁndthelimitsofaccuracyforagivenmeasurement. e.g.Givethelimitsofaccuracyforthemeasurement 65.3 m.

2G 16 Icanﬁndthesurfaceareaofarectangular prismusinganet.

e.g.Findthesurfaceareaofthisrectangularprism.

2G 17 Icanﬁndthesurfaceareaofatriangular prismusinganet.

e.g.Findthesurfaceareaofthistriangularprism.

2H 18 Icanﬁndthesurfaceareaofacylinder.

e.g.Findthesurfaceareaofthiscylinder,correcttotwodecimal places.

2I 19 Icanﬁndthevolumeofaprism. e.g.Findthevolumeofthistriangularprism.

Chapter checklist

2I 20 Icanﬁndthevolumeofacylinder.

e.g.Findthevolumeofthiscylinder,correcttotwodecimalplaces.

2I 21 Icanﬁndthevolumeofaprism,givingananswer inLormL.

e.g.Findthevolumeofthisrectangularprisminlitres.

2J 22 Icanﬁndthesurfaceareaandvolumeofacomposite solid.

e.g.Findthesurfaceareaandvolumeofthiscompositesolidcorrectto twodecimalplaces.

Short-answerquestions

1 2A Convertthesemeasurementstotheunitsshowninthebrackets. 5.3 km (m) a 27000 cm2 (m2) b 0.04 cm3 (mm3) c

2 2B Findtheperimeteroftheseshapes.

3 1C/E Forthecircleshown,ﬁnd,totwodecimalplaces: thecircumference a thearea b

4 2E Forthesecompositeshapes,ﬁnd,totwodecimalplaces: theperimeter i thearea ii

5 2D Findtheareaoftheseshapes.

2G Findthesurfaceareaoftheseprisms.

7 2H Determinethesurfaceareaofthiscylinder,totwodecimal places.

8 2I Findthevolumeofthesesolids,totwodecimalplaceswherenecessary.

Chapter

9 2F Givethelimitsofaccuracyforthesemeasurements.

10 2J Findthesurfaceareaandvolumeofthiscompositesolid correcttotwodecimalplaces.

Multiple-choicequestions

1 2A

Thenumberofcentimetresinakilometreis:

2 2B Theperimeterofasquarewithsidelengths 2 cmis:

3 2B Theperimeteroftheshapeshownisgivenbytheformula:

4 2C Acorrectexpressionfordeterminingthecircumferenceofacirclewithdiameter 6 cmis:

5 2D Theareaofarectanglewithsidelengths 3 cmand 4 cmis:

6 2D Thecorrectexpressionforcalculatingtheareaofthistrapeziumis:

7 2E Asector’scentreanglemeasures 90°.Thisisequivalentto:

2I Thevolumeofacubeofsidelength 3 cmis:

10 2H Thecurvedsurfaceareaforthiscylinderisclosestto:

Extended-responsequestions

1 Anewplaygroundisbeingbuiltwiththeshapeanddimensionsas shown.

a Theplaygroundwillbesurroundedbywoodenplanks. Determinetheperimeteroftheplaygroundcorrecttotwo decimalplaces. i Ifthewoodtobeusedcosts $16.50/m,whatwillbethecostof surroundingtheplayareatothenearestdollar? ii

b Theplaygroundareaistobecoveredwithalayerofwoodchips. Findtheareaoftheplaygroundcorrecttoonedecimalplace.

c Ifabagofwoodchipsfromthehardwarestorecovers 7.5 m2,how manybagswouldberequiredtocovertheplaygroundarea?

d Arectangularsandpitistobeincludedasshown.Ifsandistobe spreadﬂatandﬁlledtoaheightof 40 cm,determinethevolume ofsandrequiredinm3

2 Acylindricaltankhasdiameter 8 mandheight 2 m.

a Findthetotalvolumeofthetank,totwodecimalplaces.

b Findthetotalvolumeofthetankinlitres,totwodecimalplaces. Note:Thereare 1000 litresin 1 m3

c Findthesurfaceareaofthecurvedpartofthetank,totwodecimalplaces.

d Findthesurfacearea,includingthetopandthebase,totwodecimalplaces.

3 Algebraand equations

Essentialmathematics:whyskillswithalgebraand equationsareimportant

Byknowinghowtousealgebraicformulas,solveequationsandmanageExcelspreadsheet formulasyouwillhaveimportantskillswidelyusedinbusinesses,tradesandprofessions.

Nursesﬁnddriprate R = V t where V isvolumeinmland t ishours.Amechaniccalculatesengine pistonvolume V = p D2S 4 where D isborediameterand S isstrokelength.

Boatbuildersusemanyalgebraicformulasincludingtocalculateweightandbuoyancy,centreof gravity(G),andthemetacentre(M),whichisthepivotheightofatiltedboat.Boatswithagreater distancebetweenMandGaremorestable.

Tradeworkerssolveequationsforcostofmaterials,jobtimesandproﬁt;businessessolve equationstodetermineaffordablestockandstafflevels.

Simultaneousequationscansolveyourpersonalﬁnancequestionssuchas:ﬁndingthebestdeal forbuyingandmaintainingacar;identifyingthejobwiththebestearningsovertime;and discoveringthebestinvestmentaccount.

Inthischapter

3AAlgebraicexpressions (Consolidating)

3BSimplifyingalgebraicexpressions

3CExpandingalgebraicexpressions

3DFactorisingalgebraicexpressions

3EMultiplyinganddividingalgebraicfractions

3FAddingandsubtractingalgebraicfractions

3GSolvinglinearequations (Consolidating)

3HSolvingmoredifﬁcultlinearequations

3IUsingformulas

3JLinearinequalities

3KSolvingsimultaneousequationsusing substitution

3LSolvingsimultaneousequationsusing elimination

ALGEBRA

Expand,factoriseandsimplifyexpressionsandsolve equationsalgebraically,applyingexponentlawsinvolving products,quotientsandpowersofvariables,andthe distributiveproperty(AC9M10A01)

Solvelinearinequalitiesandsimultaneouslinearequations in2variables;interpretsolutionsgraphicallyand communicatesolutionsintermsofthesituation (AC9M10A02)

Usemathematicalmodellingtosolveappliedproblems involvinggrowthanddecay,includingﬁnancialcontexts; formulateproblems,choosingtoapplylinear,quadraticor exponentialmodels;interpretsolutionsintermsofthe situation;evaluateandmodifymodelsasnecessaryand reportassumptions,methodsandﬁndings(AC9M10A04)

©ACARA

Onlineresources

Ahostofadditionalonlineresourcesareincludedaspart ofyourInteractiveTextbook,includingHOTmathscontent, videodemonstrationsofallworkedexamples, auto-markedquizzesandmuchmore.

AustralianCurriculum9.0

Warm-up

1 Writealgebraicexpressionsforthefollowing.

3 lotsof x a onemorethan a b 5 lessthan 2m c 4 timesthesumof x and y d

2 Findthevalueofthefollowingwhen x = 4 and y = 7

5x a 2y + 3 b xy −5 c 2(x + y) d

3 Decidewhetherthefollowingpairsoftermsareliketerms.

6x and 8 a 3a and 7a b 4xy and 2yx c 3x2 and 10x d

4 Simplify: 3m + 5m a

b 4x + 3y + 2x + 5y c 2 × 4 × x d 5 × a × 3 × b e 6y ÷ 2 f

5 Expand:

2(x + 5) a 3(y −2) b 4(2x −3) c x(3x + 1) d

6 FindtheHCF(highestcommonfactor)ofthesepairsofterms.

8, 12 a 18, 30 b 7a, 14a c 2xy and 8xz d 5x and 8x2 e 7x2y and 21xy2 f

7 Simplify: 3 8 + 2 5 a 6 7 1 3 b 5

8 Statetrue(T)orfalse(F)forwhetherthefollowingareequations.

9 Completethefollowing.

10 Writeanexpressionforeachofthefollowing. thesumof x and 3 a sixmorethan n b double w c halfof x d sixmorethandouble x e sevenlessthan x f threemorethan x andthendoubled g onemorethantriple x h

11 Solvethefollowingsimpleequations.

12 Answertrue(T)orfalse(F)tothefollowing.

3A 3A Algebraicexpressions CONSOLIDATING

Learningintentions

• Toknowthenamesofthepartsofanalgebraicexpression

• Tobeabletoformalgebraicexpressionsfromsimplewordproblems

• Tobeabletoevaluateexpressionsbysubstitutinggivenvalues

Keyvocabulary: expression,pronumeral,variable,term,constantterm,coef cient,substitute,evaluate

Algebrainvolvestheuseofpronumerals(alsocalledvariables), whicharelettersthatrepresentnumbers.Numbersandpronumerals connectedbymultiplicationordivisionform terms,and expressions areoneormoretermsconnectedbyadditionorsubtraction.

Ifatickettoanartgallerycosts $12,thenthecostfor y visitorsis theexpression 12 × y = 12y.Bysubstitutingvaluesfor y wecanﬁnd thecostsfordifferentnumbersofvisitors.Forexample,ifthereare ﬁvevisitors,then y = 5 and 12y = 12 × 5 = 60.Sototalcost = $60

It’sfreetovisitTheNationalGallery ofAustraliabutsomespecial exhibitionsrequirepaidentry.Using algebra,youcancalculatethecost ofmultipletickets.

Lessonstarter:Expressionsatthegallery

Ben,AleaandVictoriaarevisitingtheartgallery.Thethreeofthemcombinedhave $c betweenthem.Drinks cost $d andBenhasbought x postcardsinthegiftshop. Writeexpressionsforthefollowing.

• Thecostoftwodrinks.

• Theamountofmoneyeachpersonhasifthemoneyissharedequally.

• ThenumberofpostcardsAleaandVictoriaboughtifAleaboughtthreemorethanBenandVictoria boughtﬁvelessthantwicethenumberBenbought.

Keyideas

A pronumeral (or variable)isaletterusedtorepresentanunknownnumber.

Algebraic expressions aremadeupofoneormoretermsconnectedbyadditionorsubtraction, e.g. 3a + 7b, x 2 + 3y, 3x −4

• A term isagroupofnumbersandpronumeralsconnectedbymultiplicationanddivision, e.g. 2x, y 4, 5x2

• A constantterm isanumberwithnoattachedpronumerals,e.g. 7, −3

• The coefﬁcient isthenumbermultipliedbythepronumeralsintheterm; e.g. 3 isthecoefﬁcientof y in 2x + 3y.

−4 isthecoefﬁcientof x in 5−4x.

1 isthecoefﬁcientof x2 in 2x + x 2

Thisexpressionhas 3 terms: 3x, 2y and 4 3x 2y + 4

3 is the coefﬁcient of x

2 is the coefﬁcient of y 4 is the constant term

Operationsinalgebraicexpressions.

• Theoperationsforadditionandsubtractionarewrittenwith‘+’and‘ ’.

• Multiplicationiswrittenwithoutthesign,e.g. 3 × y = 3y

• Divisioniswrittenasafraction,e.g. y ÷ 4 = y 4 or 1 4 y

Toﬁndthevalueofanexpression(orto evaluate), substitute avalueforeachpronumeral.The orderofoperations(BODMAS)isfollowed.Forexample,if x = 2 and y = 3: 4xy y 2 = 4 × 2 × 3−32 = 24−9 = 15

Exercise3A

Und er stand ing 1–3 1

1 Fillinthemissingword(s)inthesentences,usingthewords expression,term,constantterm or coefﬁcient

a Analgebraic ismadeupofoneormoretermsconnectedbyaddition andsubtraction.

b Atermwithoutapronumeralpartisa

c Anumbermultipliedbythepronumeralsinatermisa

d Numbersandpronumeralsconnectedbymultiplicationanddivisionforma

2 Expressthefollowinginsimpliﬁedmathematicalform.

x plus 3 a 5 × y b a ÷

3 Substitutethevalue 3 forthepronumeral x inthefollowingandevaluate.

Example1Namingpartsofanexpression

Considertheexpression xy 2 −4x + 3y2 −2.Determine: thenumberofterms a theconstantterm b thecoefﬁcientof: c y2 i x ii

SolutionExplanation

a 4 Therearefourtermswithdifferentcombinationsofpronumeralsand numbers,separatedby + or

b −2 Thetermwithnopronumeralsis −2.Thenegativeisincluded.

ci 3 ii −4

Thenumbermultipliedby y2 in 3y2 is 3

Thenumbermultipliedby x in −4x is −4.Thenegativesignbelongstothe termthatfollows.

Nowyoutry

Considertheexpression 4y x 3 −2x2 + 1.Determine:

thenumberofterms a theconstantterm. b thecoefﬁcientof: c

y i x2 ii

4 Forthesealgebraicexpressions,determine:

thenumberofterms i theconstantterm ii thecoefﬁcientof y iii

4xy + 5y + 8 a

2xy + 1 2 y2 −3y + 2 b

2x2 −4 + y c

Example2Writingalgebraicexpressions

Writealgebraicexpressionsforthefollowing.

threemorethan x a

HintforQ4:Thecoefﬁcientisthe numbermultipliedbythe pronumeralsineachterm.The constanttermhasnopronumerals.

4 lessthan 5 times y b thesumof c and d isdividedby 3 c theproductof a andthesquareof b d

Solution

a x + 3

b 5y −4

c c + d 3

d ab2

Nowyoutry

Explanation

Morethanmeansadd (+).

Timesmeansmultiply (5 × y = 5y) andlessthanmeanssubtract ( )

Add c and d ﬁrst (+),thendivideby 3 (÷) Divisioniswrittenasafraction.

‘Product’means‘multiply’.Thesquareof b is b2 (i.e. b × b) a × b2 = ab2

Writealgebraicexpressionsforthefollowing.

ﬁvemorethan y a 7 lessthan 3 times x b thesumof a and b isdividedby 5 c theproductof x andthesquareof y d

5 Writeanexpressionforthefollowing.

twomorethan x a fourlessthan y b thesumof ab and y

HintforQ5:Quotientmeans ÷ Productmeans × 1 3 y = y 3 c threelessthan 2 lotsof x d theproductof x and 5 e twice m f threetimesthevalueof r g halfof x h three-quartersof m i thequotientof x and y j thesumof a and b is dividedby 4 k theproductofthesquareof x and y l

Example3Substitutingvalues

Findthevalueoftheseexpressionswhen x = 2, y = 3 and z = −5 xy + 3y a y2 8 x b 2x yz c

Solution

a xy + 3y = 2 × 3 + 3 × 3 = 6 + 9 = 15

b y 2 8 x = 32 8 2 = 9−4 = 5

c 2x yz = 2 × 2−3 × (−5) = 4− (−15) = 4 + 15 = 19

Nowyoutry

Explanation

Substituteforeachpronumeral: x = 2 and y = 3

Recallthat xy = x × y and 3y = 3 × y

Simplify,followingorderofoperations,bymultiplyingﬁrst.

Substitute y = 3 and x = 2 32 = 3 × 3 and 8 2 = 8 ÷ 2

Dosubtractionlast.

Substituteforeachpronumeral.

3 × (−5) = −15

Tosubtractanegativenumber,additsopposite.

Findthevalueoftheseexpressionswhen x =

, y = −2 and

6 Findthevalueoftheseexpressionswhen a = 4, b =

HintforQ6: 12 + (−2) = 12−2

Problem-solving and reasoning 7–9 8–11

7 Writeanexpressionforthefollowing.

a Thecostof 5 pencilsat x centseach.

b Thecostof y applesat 35 centseach.

c Oneperson’ssharewhen $500 isdividedamong n people.

d Thecostofapizza ($11) equallysharedbetween m people.

e Parvinda’sagein x years’timeifheis 11 yearsoldnow.

HintforQ7:Considerwhatyou woulddoifanumberwasin placeofthepronumeral.

8 AtaxiinSydneyhasapick-upcharge(i.e.ﬂagfall)of $3.40 andcharges $2 perkm.

a Writeanexpressionforthetaxifareforatripof d kilometres.

b Useyourexpressioninpart a toﬁndthecostofatripthatis: 10 km i 22 km ii

HintforQ8:Thetaxifarehas initialcost + costperkm × numberofkm.

9 a Yethinksofanumber,whichwewillcall x Nowwriteanexpressionforeachofthefollowingstages. Hedoublesthenumber. i Hedecreasestheresultby 3 ii Hemultipliestheresultby 3 iii

b If x = 5,useyouranswertopart aiii toﬁndtheﬁnalnumber.

10 Asquarewithsidelength x ischangedtoarectanglebyincreasing thelengthby 1 anddecreasingthewidthby 1

a Writeanexpressionforthenewlengthandwidthof therectangle.

b Isthereanychangeintheperimeteroftheshape?

HintforQ10:Perimeteristhe sumofthesidelengths. Areaformulas:

c Writeanexpressionfortheareaoftherectangle. i Usetrialanderrortodeterminewhethertheareaoftherectangleismoreorlessthantheoriginal square.Byhowmuch? ii

11 Theareaofatriangleisgivenby A = 1 2 bh h

a If b = 6 and h = 7,whatisthearea?

b Iftheareais 9,whatarethepossiblewholenumbervaluesfor b if h isalsoawholenumber?

Areaandperimeter 12

12 Fortheshapesshown,writeanexpressionfor: theperimeter i thearea. ii

3B 3B Simplifyingalgebraicexpressions

Learningintentions

• Tobeabletoidentifyliketerms

• Toknowthatonlyliketermscanbecombinedunderadditionandsubtraction

• Tobeabletosimplifyalgebraicexpressionsusingthefouroperations: +, , × and ÷

Keyvocabulary: liketerms,pronumeral

Manyareasofﬁnanceandindustryinvolvecomplexalgebraic expressions.Oftentheseexpressionscanbemadesimplerby applyingtherulesofaddition,subtraction,multiplicationand division.

Justaswewouldwrite 3 + 3 + 3 + 3 as 4 × 3,wewrite

x + x + x + x as 4 × x or 4x.Similarly, 3x + 2x = 5x and 3x −2x = 1x (1x iswrittenas x).

Wealsoknowthat 2 ×

3 × 4 × 2 etc.,so 2

and (

.Bywritingadivision asafractionwecanalsocancelcommonfactors.Forexample, 9x ÷ 3 = 9x 3 = 3x

Lessonstarter:Equivalentexpressions

Alotoftheappsusedbysitemanagers havealgebraicexpressionsrunninginthe background.

Splittheseexpressionsintotwogroupsthatareequivalentbysimplifyingthemﬁrst.

3x +

Keyideas

Liketerms havetheexactsamepronumeralfactors,includingpowers;e.g. 3x and 7x,and 4x2y and −3x2y

• Since x × y = y × x, 3xy and 2yx areliketerms.

Additionandsubtractionapplytoliketermsonly.

Forexample, 5x + 7x = 12x 7ab −6ab = 1ab = ab 3x + 2y cannotbesimpliﬁed

Multiplicationanddivisionapplytoallterms.

• Inmultiplication,dealwithnumeralsandpronumeralsseparately: 2 × 8a = 2 × 8 × a = 16a

6x × 3y = 6 × 3 × x × y = 18xy

Whendividing,writeasafractionandcancelcommonfactors: ✁ 84x ✁ 21 = 4x

6x2 ÷ (3x) = 6x2 3x = ✁ 62 × ✚ x 1 × x ✁ 31 × ✚ x 1 = 2x

Exercise3B

Und er stand ing

1 Arethefollowingsetsoftermsliketerms?Answeryes(Y)orno(N).

2 Simplifythefollowing.

8g + 2g

3 Simplifythefollowing.

4 Simplifythesefractionsbycancelling. 4 8 a 12 3

1–4 4

HintforQ2:Addorsubtractthe pronumeralsinliketerms.

HintforQ4:Choosethehighest

Fluency

Example4Identifyingliketerms

Writedowntheliketermsinthefollowinglists.

Solution

a 6a and 3a

5xa and 2ax

b 3x2a and −5x2a

Nowyoutry

Writedowntheliketermsinthefollowinglists.

5 Writedowntheliketermsinthefollowinglists.

Explanation

Bothtermscontain a

Bothtermscontain ax: x × a = a × x

Bothtermscontain x2a

HintforQ5:Liketermshave thesamepronumeralfactors.

and 5yx areliketerms.

Example5Collectingliketerms

Simplifythefollowing.

4a + 5a + 3 a

3x + 2y + 5x −3y b

5xy + 2xy2 −2xy + xy2 c

Solution

a 4a + 5a + 3 = 9a + 3

b 3x + 2y + 5x −3y = 3x + 5x + 2y −3y = 8x y

c 5xy + 2xy 2 −2xy + xy 2

= 5xy −2xy + 2xy 2 + xy 2

= 3xy + 3xy 2

Nowyoutry

Simplifythefollowing.

7x + 3x + 2 a

2a + 4b + 3a −2b b

4mn + 3m2n mn + 2m2n c

6 Simplifythefollowingbycollectingliketerms.

Explanation

Collectliketerms (4a and 5a) andadd coefﬁcients.

Collectliketermsin x (3 + 5 = 8) and y (2−3 = −1).Note: −1y iswrittenas y

Collectliketerms.In xy,thenegativebelongs to 2xy.In xy2,recallthat xy2 is 1xy2 .

4t + 3t + 10 a 5g g + 1 b

3x −5 + 4x c 4m + 2−3m d

2x + 3y + x e 3x + 4y x + 2y f

8a + 4b −3a −6b g 2m −3n −5m + n h

3de + 3de2 + 2de + 4de2 i 6kl −4k2l −6k2l −3kl j 3x2y + 2xy2 xy2 + 4x2

Example6Multiplyingalgebraicterms

Simplifythefollowing.

2a × 7d a −3m × 8mn b

Solution

a 2a × 7d = 2 × 7 × a × d = 14ad

b −3m × 8mn = −3 × 8 × m × m × n = −24m 2 n

Nowyoutry

Simplifythefollowing.

4x × 5w a

−2a × 6ac b

Explanation

Multiplycoefﬁcientsandcollectthepronumerals: 2 × a × 7 × d = 2 × 7 × a × d Multiplicationcanbedoneinanyorder.

Multiplycoefﬁcients (−3 × 8 = −24) and pronumerals.Recall: m × m canbewrittenas m2

7 Simplifythefollowing.

HintforQ7:Multiplythe numeralsandcollectthe pronumerals. a × b = ab

Example7Dividingalgebraicterms

Simplifythefollowing.

Solution Explanation a

Cancelhighestcommonfactorofnumerals, i.e. 6

Writedivisionasafraction.

Cancelthehighestcommonfactorof 12 and 8 andcancelan a and b

Nowyoutry

Simplifythefollowing.

8 Simplifybycancellingcommonfactors.

HintforQ8:Write eachdivisionasa fractionﬁrstwhere necessary.

Problem-solving and reasoning

9 Arectangle’slengthisthreetimesitswidth, x.Writea simpliﬁedexpressionfor: therectangle’sperimeter a therectangle’sarea.

HintforQ9:Drawarectangle andlabelthewidth x and thelength 3 × x = 3x. b

10 Fillinthemissingtermtomakethefollowingtrue.

8x + 4− = 3x + 4 a

3x + 2y + 4y = 3x −2y b

3b × = 12ab c

4xy × ( ) = −24x2y d

12xy ÷ ( ) = 6y e ÷ (15ab) = 2a 3 f

11 Findexpressionsinsimplestformfortheperimeter (P) andarea (A) oftheseshapes.

HintforQ11:Perimeteristhesumof allthesides. Area = l × w l w c

12 Arectangulargardenbedhaslengthgivenby 6x andarea 18x2 Whatisthewidthofthegardenbed? A = 18x2 6x

HintforQ12:Theopposite of × is ÷

Orderofoperations 13

13 Simplifythefollowingexpressions,usingorderofoperations.

3C 3C Expandingalgebraicexpressions

Learningintentions

• Tounderstandthedistributivelawforexpandingbrackets

• Tobeabletoexpandexpressionsinvolvingbrackets

Keyvocabulary: distributivelaw,expand

Whenanexpressionismultipliedbyaterm,eachtermintheexpressionmustbemultipliedbytheterm. Bracketsareusedtoshowthis.Forexample,todouble 4 + 3 wewrite 2 × (4 + 3),andeachtermwithinthe brackets(both 4 and 3)mustbedoubled.Theexpandedversionofthisexpressionis 2 × 4 + 2 × 3 Similarly,todoubletheexpression x + 1,wewrite 2(x + 1) = 2 × x + 2 × 1.Thisexpansionofbracketsuses thedistributivelaw.

Inthisdiagram, 7 blueblocksaredoubledingroupsof 4 and 3

Lessonstarter:Rectanglebrackets

Considerthediagramshown.

• Writeanexpressionfortherectanglearea A1

• Writeanexpressionfortherectanglearea A2

• Addyourresultsfor A1 and A2 togivetheareaoftherectangle.

• Writeanexpressionforthetotallengthoftherectangle.

• Usingthetotallength,writeanexpressionfortheareaofthe rectangle.

• Combineyourresultstocompletethisstatement: 4(x + 2) =

Keyideas

The distributivelaw isusedto expand andremovebrackets: • Thetermsinsidethebracketsaremultipliedbythetermoutsidethebrackets.

(b c) = ab ac a(b + c) = ab + ac

Forexample, 2(x + 4) = 2 × x + 2 × 4 = 2x + 8

Exercise3C

Und er stand ing 1,2 2

1 Thedistributivelawsaysthateachterminsidethe ismultipliedbytheterm thebrackets.

2 Completethefollowing.

3(x + 4) = 3 × + 3 × = 3x + a 2(x −5) = 2 × + × (−5) = −10 b 2(4x + 3) = 2 × + × 3 = + 6 c

Example8Expandingexpressionswithbrackets

Expandthefollowing.

2(x + 5) a 3(2x −3) b 3y(2x + 4y) c

Solution

a 2(x + 5) = 2 × x + 2 × 5 = 2x + 10

Explanation

Multiplyeachterminsidethebracketsby 2 b 3(2x 3) = 3 × 2x + 3 × ( 3) = 6x 9

c 3y(2x + 4y) = 3y × 2x + 3y × 4y = 6xy + 12y2

Nowyoutry

Multiply 2x and −3 by 3 3 × 2x = 3 × 2 × x = 6x.

Multiply 2x and 4y by 3y 3y × 2x = 3 × 2 × x × y and 3y × 4y = 3 × 4 × y × y

Recall: y × y iswrittenas y2

Expandthefollowing. 3(x + 4) a 5(3x −2) b

3 Expandthefollowing.

2(x + 4) a 3(x + 7) b

4(y −3) c 5(y −2) d

2(3x + 2) e 4(2x + 5) f

3(3a −4) g 7(2y −5) h

5(2a + b) i 3(4a −3b) j

2x(x + 5) k 3x(x −4) l

2a(3a + 2b) m 2y(3x −4y) n

3b(2a −5b) o 4m(3m n) p

a(2a + 5b) c

HintforQ3:Usethedistributive law:

a(b + c) = a × b + a × c = ab + ac

a(b c) = a × b + a × ( c) = ab ac

Example9Expandingexpressionswithanegativeoutthefront

Expandthefollowing.

−3(x −4) a −2x(3x −2y) b

Solution

a 3(x 4) = 3 × x + ( 3) × ( 4) = 3x + 12

b 2x(3x 2y) = 2x × 3x + ( 2x) × ( 2y) = 6x2 + 4xy

Nowyoutry

Expandthefollowing.

Explanation

Multiplyeachterminsidethebracketsby −3

−3 × (−4) =+12 Ifthereisanegativesignoutsidethebracket,the signofeachterminsidethebracketsischanged whenexpanded.

−2x × 3x = −2 × 3 × x × x and −2x × (−2y) = −2 × (−2) × x × y

−4(x −5) a −3y(2x −4y) b

4 Expandthefollowing.

−2(x + 3) a −5(m + 2) b

−3(w + 4) c −4(x −3) d

−2(m −7) e −7(w −5) f

(x + y) g (x y)

−2x(3x + 4) i

−3x(2x + 5) j

Note: (x + y) = −1(x + y) h

HintforQ4:Anegativeoutthefrontwill changethesignofeachterminthebrackets whenexpanded. −2(x −3) = −2x + 6

−4x(2x −2) k −3y(2y −9) l

−2x(3x −5y) m −3x(3x + 2y) n

−6y(2x + 3y) o

Example10Simplifyingexpressionsbyremovingbrackets

Expandandsimplifythefollowing.

8 + 3(2x −3) a 3(2x + 2) −4(x + 4) b

Solution

a 8 + 3(2x 3) = 8 + 6x 9 = 6x 1

Explanation

Expandthebracketsﬁrst: 3 × 2x + 3 × (−3) = 6x −9

Collectliketerms: 8−9 = −1 b 3(2x + 2) − 4(x + 4) = 6x + 6 − 4x 16 = 2x 10

Expandthebracketsﬁrst.Notethat

−4(x + 4) = −4 × x + (−4) × 4 = −4x −16

Collectliketerms: 6x −4x = 2x and 6−16 = −10

Nowyoutry

Expandandsimplifythefollowing.

5 + 2(4a −3) a

5(y + 3) −2(2y + 5) b

5 Expandandsimplifythefollowing.

HintforQ5:Expand ﬁrst,thencollect liketerms.

Problem-solving and reasoning

6 Fillinthemissingterm/numbertomakeeachstatementtrue.

7 Fourrectangularroomsinahousehaveﬂoorsidelengthslistedbelow. Findanexpressionfortheareaofeachﬂoorinexpandedform.

HintforQ7: Areaofarectangle = l × w andremembertousebrackets.

8 Thedeckonahouseisconstructedintheshapeshown.Findtheareaofthedeckinexpandedform. (Alllinesmeetat 90°.)

9 Viratearns $x butdoesnothavetopaytaxontheﬁrst $18200

a WriteanexpressionfortheamountofmoneyViratistaxedon.

b Viratistaxed 10% ofhisearningsinpart a.Writeanexpanded expressionforhowmuchtaxhepays.

Expandingbinomialproducts

HintforQ9:Toﬁnd 10% of anamount,multiplyby 10 100 = 0.1

10 Arectanglehasdimensions (x + 2) by (x + 3),asshown.Theareacanbefoundby summingtheindividualareas:

(x + 2)(x + 3) =

Thiscanalsobedoneusingthedistributivelaw: (x + 2)(x + 3) = x(x + 3) + 2(x + 3) = x 2 + 3x + 2x + 6

= x 2 + 5x + 6

Expandandsimplifythesebinomialproductsusingthismethod.

3D 3D Factorisingalgebraicexpressions

Learningintentions

• Tobeabletoidentifythehighestcommonfactorofterms

• Toknowtheformofafactorisedexpression

• Tounderstandthatfactorisingandexpandingarereverseprocesses

• Tobeabletofactorisealgebraicexpressionsinvolvingacommonfactor

Keyvocabulary: highestcommonfactor,factorise,term

Factorisingisanimportantstepinsolvingmanytypesofequationsandinsimplifyingalgebraicexpressions. Justas 15 canbeexpandedandwrittenas 3 × 5,wecanfactorisetowriteanalgebraicexpressionasthe productofitsfactors.Factorisingisthereforetheoppositeofexpanding.

Lessonstarter:Productsoffactors

• Expandtheproduct 6(2x + 4)

Therearesome commonformulas thatcanbeappliedto quicklyexpandbrackets, suchasthedifferenceof squaresrule.

• Writeasmanyproductsasyoucan(usingwholenumbers)thatgivethesameresultas 6(2x + 4) when expanded.

• Whichofyourproductshasthehighestnumberinfrontofthebrackets?Whatisthisnumber?

• Howdoesthisnumberrelatetothetwotermsintheexpandedform?

• Writeaproductoffactorsthatexpandto 18x + 24,usingthehighestcommonfactor.

Keyideas

Factorising involveswritinganexpressionasaproduct.

Factorisationistheoppositeprocessofexpansion.

Tofactoriseanexpression,takeoutthe highestcommonfactor (HCF) ofeachoftheterms.The highestcommonfactoristhelargestnumber,pronumeralorproductofthesethatdividesinto eachterm.

• DivideeachtermbytheHCFandleavetheexpressioninthebrackets.

• Afactorisedexpressioncanbecheckedbyexpandingtogettheoriginalexpression.

• IftheHCFhasbeenremoved,thetermsinthebracketsshouldhavenocommonfactors;e.g. 2(x + 3) isfullyfactorised,but 2(4x + 6) isnotbecause 2 canstillbedividedintoboth 4 and 6 withinthebrackets.

Forexample: 3x + 12 = 3(x + 4) HCF: 3 2x 2 + 8x = 2x(x + 4) HCF: 2x

Exercise3D

Und er stand ing

1 Writedownthehighestcommonfactor (HCF) ofthesepairofnumbers. 10 and 16 a 9 and 27 b 14 and 35 c 36 and 48 d

1–3 3

2 Statetrue(T)orfalse(F)iftheﬁrstexpressionisthefactorisedformofthesecondexpression.Conﬁrm byexpanding.

3(x + 2), 3x + 6 a −2(x −4), −2x −8 b

3 Considertheexpression 4x2 + 8x

a WhichofthefollowingfactorisedformsusestheHCF?

2(2x2 + 4x) A 4(x2 + 8x) B 4x(x + 2) C 2x(2x + 4) D

b WhatcanbesaidaboutthetermsinsidethebracketsoncetheHCFisremoved,whichisnotthe casefortheotherforms?

Fluency

Example11Findingthehighestcommonfactor(HCF)

DeterminetheHCFofthefollowing.

8a and 20 a 3x and 6x b 10a2 and 15ab c

Solution

a HCFof 8a and 20 is 4

Explanation

Comparenumeralsandpronumeralsseparately. Thehighestcommonfactor (HCF) of 8 and 20 is 4 a isnotacommonfactor.

b HCFof 3x and 6x is 3x.HCFof 3 and 6 is 3 x isalsoacommonfactor.

c HCFof 10a2 and 15ab is 5a.HCFof 10 and 15 is 5 HCFof a2 and ab is a.

Nowyoutry

DeterminetheHCFofthefollowing.

10x and 25 a 7x and 14x b

4 DeterminetheHCFofthefollowing.

6x and 12 a 10 and 15y

8a and 12b c 9x and 18y d

5a and 20a e 10m and 22m f

14x and 21x g 8a and 40ab h

3a2 and 9ab i 4x2 and 10x j

HintforQ4:Findthe HCFofthenumeral andvariablefactors. b

16y and 24xy k 15x2y and 25xy l

Example12Factorisingsimpleexpressions

Factorisethefollowing.

4x + 20 a 6a −15b b

Solution

a 4x + 20 = 4(x + 5)

b 6a −15b = 3(2a −5b)

Nowyoutry

Factorisethefollowing.

Explanation

HCFof 4x and 20 is 4.Place 4 infrontofthe bracketsanddivideeachtermby 4

Expandtocheck: 4(x + 5) = 4x + 20

HCFof 6a and 15b is 3.Place 3 infrontofthe bracketsanddivideeachtermby 3

3x + 15 a 12m −18n b

5 Factorisethefollowing.

3x + 9 a 4x −8 b 10y −20 c

6a + 30 d 5x + 5y e 12a + 4b f

18m −27n g 36x −48y h 8x + 44y i 24a −18b j 121m + 55n k 14k −63l

HintforQ5:Checkyour answerbyexpanding. 3(x + 3) = 3x + 9 l

Example13Factorisingexpressionswithpronumeralcommonfactors

Factorisethefollowing.

8y + 12xy a 4x2 −10x b

Solution

Explanation

a 8y + 12xy = 4y(2 + 3x) HCFof 8 and 12 is 4,HCFof y and xy is y Place 4y infrontofthebracketsanddivideeachtermby 4y

Checkthat 4y(2 + 3x) = 8y + 12xy

b 4x2 −10x = 2x(2x −5) HCFof 4x2 and 10x is 2x.Place 2x infrontofthe bracketsanddivideeachtermby 2x

Recall: x2 = x × x

Nowyoutry

Factorisethefollowing.

9a + 24ab a 15x2 −35x b

6 Factorisethefollowing. 14x + 21xy a 6ab −15b b 32y −40xy c

5x2 −5x d x2 + 7x

HintforQ6:PlacetheHCFin frontofthebracketsand divideeachtermbytheHCF: 14x + 21xy = 7x( + ) e 2a2 + 8a f 12a2 + 42ab g 9y2 −63y h 6x2 + 14x i 9x2 −6x j 16y2 + 40y k 10m −40m2 l

Example14Factorisingexpressionsbyremovingacommonnegative

Factorise −10x2 −18x

Solution

−10x2 −18x = −2x(5x + 9)

Explanation

TheHCFof −10x2 and −18x is −2x,including thecommonnegative.Place −2x infrontof thebracketsanddivideeachtermby −2x Dividingbyanegativechangesthesignof eachterm.

Nowyoutry

Factorise −8y2 −36y

7 Factorisethefollowing,includingthecommonnegative.

x −6 a −4a −8

Problem-solving

and reasoning

8 Factorisethesemixedexpressions.

9 Givetheperimeteroftheseshapesinfactorisedform.

HintforQ7:Dividing byanegative changesthesign oftheterm.

8,98(½),9–11

HintforQ8:Besuretoﬁndthe highestcommonfactorﬁrst.

HintforQ9:Findtheperimeter ﬁrst,thenfactorise.

10 Asquaresandpithasperimeter (4x + 12) metres.Whatisthesidelengthofthesquare?

11 Commonfactorsfromexpressionsinvolvingmorethantwotermscanberemoved inasimilarway.FactorisethesebytakingouttheHCF.

Takingoutabinomialfactor

12 Acommonfactormaybeabinomialterm,suchas (x + 1) Forexample, 3(x + 1) + x(x + 1) hasHCF = (x + 1),so 3(x + 1) + x(

,where (3 +

) is whatremainswhen 3(x + 1) and x(x + 1) aredividedby (x + 1) Usethemethodabovetofactorisethefollowing.

3E 3E Multiplyinganddividingalgebraic fractions

Learningintentions

• Toknowthatexpressionsmustbefactorisedbeforecommonfactorscanbecancelled

• Tobeabletosimplifyalgebraicfractionsbycancellingcommonfactors

• Tobeabletomultiplyanddividealgebraicfractions

Keyvocabulary: algebraicfraction,commonfactor,factorise,numerator,denominator,reciprocal

Sincepronumeralsrepresentnumbers,therulesforalgebraicfractionsarethesameasthoseforsimple numericalfractions.Thisincludesprocessessuchascancellingcommonfactorstosimplifythecalculation anddividingbymultiplyingbythereciprocalofafraction.

Theprocessofcancellingrequirescancellingoffactors,forexample:

Foralgebraicfractions,youneedtofactorisetheexpressionstoidentifyandcancelcommonfactors.

Lessonstarter:Expressionsasproductsoftheirfactors

• Factorisetheseexpressionstowritethemasaproductoftheirfactors.Fillintheblanksandsimplify.

• Describetheerrorsmadeinthesefactorisations. 1

Keyideas

An algebraicfraction isafractioncontainingpronumeralsaswellasnumbers.

Simplifyalgebraicfractionsbycancellingcommonfactorsinfactorisedform.

Forexample, 4x + 6

Tomultiplyalgebraicfractions:

• Factoriseexpressionsifpossible.

• Cancelcommonfactorsbetweenanynumeratorand denominator.

• Multiplyremainingnumeratorsanddenominators together.

Todividealgebraicfractions:

• Multiplybythe reciprocal ofthefractionfollowingthedivision sign e.g.thereciprocalof 6 is 1 6,thereciprocalof a b is b a .

• Followtherulesformultiplication.

Exercise3E

Und er stand

1 Writethesefractionsinsimplestformbycancellingcommonfactors.

21 a 9 12

2 Writethereciprocalofthesefractions. 3

3 Followtherulesformultiplicationanddivisiontosimplifythese numericfractions.Cancelcommonfactorsbeforemultiplying.

HintforQ2:The reciprocalof a b is b a

Example15Cancellingcommonfactors

Simplifybycancellingcommonfactors.

Solution Explanation

Cancelthehighestcommonfactorof 8 and 12 (i.e. 4) andcancelthe x

Nowyoutry

Simplifybycancellingcommonfactors. 18

Cancelthehighestcommonfactors: 3 and (x + 2)

4 Simplifybycancellingcommonfactors.

HintforQ4:Cancel theHCFofthe numeralsand pronumerals. g

4(x + 1) 8

Example16Simplifyingbyfactorising

Simplifythesefractionsbyfactorisingﬁrst.

Explanation

Factorisetheexpressioninthenumerator, whichhasHCF = 3.Thencancelthecommon factorof 3

4 istheHCFinthenumerator. Afterfactorising, (x + 2) canbeseenasa commonfactorandcanbecancelled.

Nowyoutry

Simplifythesefractionsbyfactorisingﬁrst.

16x −8 8 a

3x −6 x −2

b 5 Simplifythesefractionsbyfactorisingﬁrst. 4x + 8 4 a 6a −30 6 b 8y −12 4 c 14b −21 7 d 3x + 9 x + 3 e

x −20 x −5 f 6x + 9 2x + 3 g

HintforQ5:Cancelafteryou havefactorisedthenumerator.

Example17Multiplyingalgebraicfractions

Simplifytheseproducts.

12 5x × 10x 9 a

3(x −1) 10 × 15 x −1 b Solution

Explanation a

12 4

Cancelcommonfactorsbetweennumeratorsand denominators: 5x and 3 Thenmultiplythenumeratorsandthedenominators. b 3

x −1 1 = 9 2 ( = 4 1 2 )

Nowyoutry Simplifytheseproducts. 20 3x × 6x 25 a

6 Simplifytheseproducts.

Cancelthecommonfactors,whichare (x −1) and 5 Multiplynumeratorsanddenominators.

HintforQ6:Cancelany commonfactorsbetween numeratorsanddenominators beforemultiplying.

Example18Dividingalgebraicfractions

Simplifythefollowing.

Solution

Nowyoutry

Simplifythefollowing.

7 Simplifythefollowing.

Explanation

Multiplybythereciprocalofthesecond fraction.

Thereciprocalof 9x 4 is 4 9x

Cancelcommonfactors: 3x and 4

Note: 3x2 9x =

31 × x × ✚ x 1 3 ✁ 9 × ✚ x 1 Multiplythenumeratorsandthedenominators.

Thereciprocalof x −2 6 is 6 x −2

Cancelthecommonfactors (x −2) and 3,and multiply.Recall: 4 1 = 4

HintforQ7:Todivide,multiplybythe reciprocalofthefractionfollowing thedivisionsign. x 5 ÷ x 15 = x 5 × 15 x

Problem-solving and reasoning

8 Findtheerrorinthesimplifyingofthesefractionsandcorrectit.

HintforQ8:Rememberthat commonfactorscanbeeasily identiﬁedwhenexpressionsarein factorisedform.

9 Simplifythesealgebraicfractionsbyfactorisingexpressionsﬁrstinthenumeratorand/ordenominator.

10 Byremovinganegativefactor,furthersimplifyingissometimespossible.

Forexample, −2x −4 x + 2 = −2✘✘✘✘

Usethisideatosimplifythefollowing.

2 −4x x + 4

HintforQ10:Takingouta negativefactorchangesthe signofeachterminsidethe brackets. c

Cancellingofpowers 11

11 Justas x✁ 21 ✚ x 1 = x, (x + 1)✁ 21 ✘✘✘ x + 1 1 = x + 1.Usethisideatosimplifythesealgebraicfractions.

Somewillneedfactorisingﬁrst.

(x −3)2 9x × 3x 4x −12 e

3F 3F Addingandsubtractingalgebraic fractions

Learningintentions

• Toknowthatthestepsforaddingandsubtractingalgebraicfractionsarethesameasfornumericalfractions

• Tobeableto ndthelowestcommondenominatoroffractions

• Tobeabletoaddandsubtractalgebraicfractions

Keyvocabulary: lowestcommondenominator,equivalentfraction,algebraicfraction,numerator,denominator

Aswithmultiplyinganddividing,thestepsforaddingandsubtractingnumericalfractionscanbe appliedtoalgebraicfractions.Alowestcommondenominatorisrequiredbeforethefractionscanbe combined.

Lessonstarter:Stepsforaddingfractions

• Writeoutthelistofstepsyouwouldgivetosomeonetoshowthemhowtoadd 3 5 and 2 7

• Followyourstepstoaddthefractions 3x 5 and 2x 7

• Whatisdifferentwhenthesestepsareappliedto x + 2 5 and x 7 ?

Keyideas

Toaddorsubtract algebraicfractions:

• Determinethe lowestcommondenominator(LCD) –thesmallestcommonmultipleofthe denominators.

Forexample,theLCDof 3 and 5 is 15 andtheLCDof 4 and 12 is 12

• Writeeachfractionasanequivalentfractionbymultiplyingthedenominator(s)toequalthe LCD.Whendenominatorsaremultiplied,numeratorsshouldalsobemultiplied.

Forexample, x 3 + 2x 5 (LCDof 3 and 5 is 15.)

= x(× 5) 3(× 5) + 2x(× 3) 5(× 3)

= 5x 15 + 6x 15 and 2x 4 x 12 (LCDof 4 and 12 is 12.)

= 2x(× 3) 4(× 3) x 12

= 6x 12 x 12

• Addorsubtractthenumerators.

Forexample, 5x 15 + 6x 15 = 11x 15 and 6x 12 x 12 = 5x 12

Toexpress x + 1 3 withadenominatorof 12,boththenumeratoranddenominatormustbemultiplied by 4 withbracketsrequiredtomultiplythenumerator:

(x + 1)(× 4) 3(× 4) = 4x + 4 12

Exercise3F

Und er stand ing

1 Writedownthelowestcommondenominator (LCD) for thesepairsoffractions. 2x 5 , x 4

2 Completetheseequivalentfractionsbygivingthe missingterm.

x 4 = 12 a 2x 5 = 15

3 Completethefollowingbyﬁllingintheboxes.

x 4 + x

1–3 3

HintforQ1:TheLCDisnotalways thetwodenominatorsmultiplied together;e.g. 3 × 6 = 18 butthe LCDof 3 and 6 is 6

HintforQ2:Forequivalentfractions, whateverthedenominatoris multipliedby,thenumeratormust bemultipliedbythesameamount. b x −1 4 = (x −1) 20 c

Example19Addingandsubtractingalgebraicfractions

Simplifythefollowing.

x 2 + x 3 a 4x 5 x 2 b x 2 5 6 c

Solution

a x(× 3)

2(× 3) + x(× 2) 3(× 2) = 3x 6 + 2x 6 = 5x 6

b 4x(× 2) 5(× 2) x(× 5) 2(× 5) = 8x 10 5x 10 = 3x 10

c x(× 3) 2(× 3) 5 6 = 3x 6 5 6 = 3x −5 6

Explanation

TheLCDof 2 and 3 is 6 Expresseachfractionwithadenominatorof 6 andaddnumerators.

TheLCDof 5 and 2 is 10. Expresseachfractionwithadenominatorof 10 andsubtract 5x from 8x

TheLCDof 2 and 6 is 6.Multiplythenumerator anddenominatorof x 2 by 3 toexpresswitha denominatorof 6 Writeasasinglefraction; 3x −5 cannotbe simpliﬁed.

Nowyoutry

Simplifythefollowing.

x 4 + x 5 a 3x 2 x 7 b x 3 + 7 9 c

4 Simplifythefollowing.

x 3 + x 4 a x 5 + x 2

HintforQ4:Expresseachfraction withacommondenominatorusing theLCD,thenaddorsubtract numerators. b x 3 x 9

5 Simplifythefollowing.

Example20Addingandsubtractingwithbinomialnumerators

Simplifythefollowingalgebraicexpressions.

Solution

b (x + 3)(× 7) 3(× 7) + (x −4)(× 3)

Explanation

TheLCDof 4 and 6 is 12. Expresseachfractionwithadenominator of 12

Whenmultiplying (x + 2) by 3,bracketsare required.

Expandthebracketsandcollecttheterms: 3x + 6−2x = 3x −2x + 6

TheLCDof 3 and 7 is 21 Expresseachfractionwithadenominator of 21

Expandeachpairofbracketsﬁrstandaddby collectingliketerms.

Nowyoutry

Simplifythefollowingalgebraicexpressions.

6 Simplifythesealgebraicexpressions.

Problem-solving and reasoning

7 Findtheerrorineachofthefollowingandthencorrectit. 2

8 Recallthattheexpansionof −5(x −2) is −5x + 10, so 6(x + 1) −5(x −2) = 6x + 6−5x + 10 = x + 16

Usethismethodtosimplifythesesubtractions.

9 TheLCDofthefractions 4 x + 2 3 is 3 × x = 3x

UsethistoﬁndtheLCDandsimplifythesefractions.

4 x + 2 3

Pronumeralsinthedenominator 10

10 AsseeninQuestion 9,pronumeralsmayformpartoftheLCD. Thefractions 5 2x and 3 4 wouldhaveaLCDof 4x,whereasthefractions 3 x and 5 x2 wouldhaveaLCD of x2

ByﬁrstﬁndingtheLCD,simplifythesealgebraicfractions. 3 4 + 5 2x a

4 x + 1 x2 e

3 2x + 2 x2 g

3G 3G Solvinglinearequations

Learningintentions

• Toknowwhatasolutiontoanequationmeans

• Tobeabletosolveasimplelinearequation

• Tobeabletoverifyasolutiontoanequation

CONSOLIDATING

Keyvocabulary: equation,linearequation,solve,variable,pronumeral,backtracking,verify,substitute,solution

Acricketbatsmanwillputonsocks,thencricketshoesand,finally,padsinthatorder.Whenthegameis over,theseitemsareremovedinreverseorder:firstthepads,thentheshoesandfinallythesocks.Nobody takestheirsocksoffbeforetheirshoes.Asimilarreversaloccurswhensolvingequations.

Wecanundotheoperationsaround x bydoingtheoppositeoperationinthereverseordertohowthey havebeenappliedto x.Tokeepeachequationbalanced,wealwaysapplythesameoperationtobothsides ofanequation.

Forexample:

Applyingoperationsto x = 7 Undoingtheoperationsaround x

Thiscricketerhasputonhiswhitesﬁrst,followedbyhis protectivepads.Attheendofhisinnings,hewillneedto removethepadsbeforetakingoffhiswhites,reversingthe orderinwhichheputthemon.

Lessonstarter:Keepingitbalanced

Threeweighingscalesareeachbalancedwithvariousweightsontheleftandrightpans.

Whatweighthasbeenremovedfromeachsideofscales 1 togettoscales 2?

• Whathasbeendonetoboththeleftandrightsidesofscales 2 togettoscales 3?

• Whatequationsarerepresentedineachofthebalancedscalesshownabove?

• Whatmethodscanyourecallforsolvingequations? •

Keyideas

An equation isamathematicalstatementthatincludesanequalssign.Theequationwillbe trueonlyforcertainvalue(s)ofthepronumeral(s)thatmaketheleft-handsideequaltothe right-handside.

Forexample: 5x 6 = −2, 3p + 2t = 6 areequations; 6x −13 isnotanequation.

A linearequation containsavariable(e.g. x)tothepowerof 1 andnootherpowers.

Forexample: 3x −5 = 7, 4(m −3) = m + 6 arelinearequations; x2 = 49 isnotlinear.

To solve anequation,undotheoperationsbuiltaround x bydoingtheoppositeoperationin thereverseorder.

• Alwaysperformthesameoperationtobothsidesofanequationsoitremainsbalanced.

Forexample:

For 5x + 2 = 17,weobserveoperationsthathavebeenappliedto x: x 5x 5x + 2 × 5 + 2

Sowesolvetheequationby‘undoing’theminreverseorderonbothsidesoftheequation: 5x + 25x x 2 ÷ 5 and 17153 2 ÷ 5

Thisgivesthesolution:

• Alternatively,asolutionneednotshowtheoperationsappliedtoeachside.Thesecanbe donementally.Forexample: 5x + 2 = 17 5x = 15 x = 3

Aﬂowchartcanbeusedtosolveequations.First,theequationisbuiltupfollowingtheorder ofoperationsappliedto x andthenthesolutionfor x isfoundbyundoingtheseoperations inthereverseorder.

Forexample,hereisaﬂowchartsolutionto 5x + 2 = 17

Solution x = 3

• Backtracking istheprocessofundoingtheoperationsappliedto x

To verify ananswermeanstocheckthatthesolutioniscorrectbysubstitutingtheanswerto seeifitmakestheequationtrue.

e.g.Verifythat x = 3 isasolutionto 5x + 2 = 17

LHS = 5x + 2 RHS = 17

= 5(3) + 2

= 17 Â x = 3 isasolution.

Usingcalculatorstosolveequations

Solvetheequation 5x −4 3 = 12.

UsingtheTI-Nspire:

Ina Calculator pageuse menu >Algebra>Solve andtypetheequation asshown.

Hint: usethefractiontemplate( ctrl ÷ )

UsingtheClassPad:

Tap solve(,then andtypetheequationas shown.

Exercise3G

Und er stand ing 1–3 3

1 Statethemissingwordornumber.

a Anequationisastatementthatcontainsan sign.

b Alinearequationcontainsavariabletothepowerof

2 Considertheequation 2x + 3 = 7

a Completethistablebyevaluating 2x + 3 forthegivenvaluesof x x 0 1 2 3

2x + 3

b Bylookingatyourtableofvalues,whichvalueof x isthesolutionto 2x + 3 = 7?

3 Decidewhether x = 2 isasolutiontotheseequations.

x + 3 = 5 a 2x = 7 b

x −1 = 4

c 2x −1 = 10 d 3x + 2 = 8 e 2− x = 0 f

HintforQ3:Substitute x = 2 to seewhetherLHS = RHS.

Fluency

Example21Solvingone-stepequations

Solve: x + 7 = 12 a x −9 = 3 b 3x = 12 c x 4 = 20 d

Solution

a x + 7 = 12

x = 5

Verify:LHS = 5 + 7 RHS = 12 = 12

b x −9 = 3

x = 12

Verify:LHS = 12−9 RHS = 3 = 3

c 3x = 12

x = 4

Verify:LHS = 3 × 4 RHS = 12 = 12

d x 4 = 20

x = 80

Nowyoutry

Verify:LHS = 80 4 RHS = 20 = 20

Solve:

4 Solvethefollowing.

Explanation

Writetheequation.Theoppositeof + 7 is −7. Subtract 7 frombothsides. Checkthatyouransweriscorrect.

Writetheequation.Theoppositeof −9 is + 9 Add 9 tobothsides. Checkthatyouransweriscorrect.

Writetheequation.Theoppositeof × 3 is ÷ 3

Dividebothsidesby 3. Checkthatyouransweriscorrect.

Writetheequation.Theoppositeof ÷ 4 is × 4

Multiplybothsidesby 4

Checkthatyouransweriscorrect.

HintforQ4: 8 + x = 14 isthesameas x + 8 = 14 16 = m + 1 isthesameas m + 1 = 16

5 Solvethefollowing.

3 × 1 2 = 3 1 × 1 2 = 3 2 c 15p = 15 d 6m = −42 e −10 = 20p f x 5 = 10 g m 3 = 7 h a 6 = −2 i

6 Solvethefollowingequations.

x + 9 = 12 a x + 3 = 12 b x + 15 = 4 c

x −7 = 3 d x −2 = 12

3x = 9 g 4x = 16 h 2x = 100 i

x 5 = 4 j x 3 = 7 k x 7 = 1 l

HintforQ6:Carry outthe‘opposite’ operationtosolve for x e x −5 = 5 f

Example22Solvingtwo-stepequations

Solve 4x + 5 = 17

Solution

4x + 5 = 17

4x = 12 x = 12 4 x = 3

Verify:LHS = 4(3) + 5 RHS = 17 = 17

Nowyoutry

Solve 5x −1 = 19

7 Solvethefollowingequations.

Explanation

Writetheequation. Subtract 5 frombothsidesﬁrst.

Dividebothsidesby 4 Simplify.

Checkyouranswer.

2x + 5 = 7 a 3x + 2 = 11 b 4x −3 = 9 c 6x + 13 = 1 d 8x + 16 = 8

HintforQ7:Firstchooseto addorsubtractanumberfrom bothsidesandthendivideby thecoefﬁcientof x e 10x + 92 = 2 f 3x −4 = 8 g 2x −7 = 9 h 5x −4 = 36 i 2x −6 = −10 j 7x −3 = −24 k 6x −3 = 27 l

Example23Solvingtwo-stepequationsinvolvingsimplefractions

Solve x 5 −3 = 4

Solution

x 5 −3 = 4

x 5 = 7 x = 35

Verify:LHS = 35 5 −3 RHS = 4 = 4

Explanation

Writetheequation.

Add 3 tobothsides.

Multiplybothsidesby 5.

Checkthatyouransweriscorrect.

Nowyoutry

Solve x 7 + 2 = 6

8 Solvethefollowingequations.

x 3 + 2 = 5 a x 6 + 3 = 3 b x 7 + 4 = 12 c

x 4 −3 = 2

Example24Solvingmoretwo-stepequations

Solve x + 4 2 = 6

Solution

x + 4 2 = 6 x + 4 = 12 x = 8

Verify:LHS = 8 + 4 2 RHS = 6 = 6

Nowyoutry

Solve x −3 4 = 1. 9 Solvethefollowingequations. m + 1 2 = 3 a

= 3 c x + 5 3 = 2 d n −4 5 = 1

Explanation

HintforQ8:Whensolving equations,theorderof stepsisimportant.For x 3 −5,undothe −5 ﬁrst, thenundothe ÷3

Writetheequation. In x + 4 2 weﬁrstadd 4 andthendivideby 2.Sotoundowe ﬁrstmultiplybothsidesby 2 Thensubtract 4 frombothsides.

Checkthatyouransweriscorrect.

HintforQ9:Whensolvingequations,the orderofstepsisimportant.For x + 7 3 , undothe ÷3 ﬁrst,thenundothe +7 Nevercancelanumberjoinedby + or toan x.In x + 8 4 ,youcannot cancelthe 4 intothe 8.

Problem-solving and reasoning

Example25Writingequationsfromwordproblems

Foreachofthefollowingstatements,writeanequationandsolveforthepronumeral.

When 7 issubtractedfrom x,theresultis 12 a

When x isdividedby 5 andthen 6 isadded,theresultis 10 b

When 4 issubtractedfrom x andthatanswerisdividedby 2,theresultis 9 c

Solution

a x −7 = 12

x = 19

b x 5 + 6 = 10 x 5 = 4 x = 20

c x −4 2 = 9 x −4 = 18 x = 22

Nowyoutry

Explanation

Subtract 7 from x meanstostartwith x andthensubtract 7 ‘Theresult’means‘=’. Remembertocheckyouranswer.

Divide x by 5,thenadd 6 andmakeitequalto 10 Solvetheequationbysubtracting 6 frombothsidesﬁrst.

Subtracting 4 from x gives x −4,anddividethatanswerby 2. Undo ÷ 2 bymultiplyingbothsidesby 2,thenadd 4 tobothsides.

Foreachofthefollowingstatements,writeanequationandsolveforthepronumeral.

When 3 isaddedto x,theresultis 9 a

When x isdividedby 3 then 7 issubtracted,theresultis 0. b

When 6 issubtractedfrom x andthatanswerisdividedby 3,theresultis 10 c

10 Foreachofthefollowingstatements,writeanequationandsolveforthepronumeral.

When 4 isaddedto x,theresultis 6 a

When x isaddedto 12,theresultis 8 b

When 5 issubtractedfrom x,theresultis 5

When x isdividedby 3 andthen 2 isadded,theresultis 8. d

HintforQ10: 5 subtracted from x is x −5 c

Twicethevalueof x isaddedto 3 andtheresultis 9 e

(x −3) isdividedby 5 andtheresultis 6 f

3 times x plus 4 isequalto 16 g

11 Writeanequationandsolveitforeachofthesequestions. Theperimeterofasquareis 52 cm.Determinethelengthoftheside.

P = 52 cm a

HintforQ11:Drawadiagramand chooseapronumeraltorepresent theunknownside.Thenwritean equationandsolveit. ? cm

Theperimeterofanisoscelestriangleis 32 mm.Iftheequalsidesareboth 10 mm,determinethe lengthoftheotherside.

P = 32 mm 10 mm

12 Convertthefollowingintoequations,thensolvethemfor theunknownnumber.

n ismultipliedby 2,then 5 isadded.Theresultis 11

a Fourtimesacertainnumberisaddedto 9 andtheresult is 29.Whatisthenumber?

c Anumberplus 6 hasbeendividedby 4.Theresultis 12 Whatisthenumber?

Halfofanumberless 2 equals 12.Whatisthenumber?

d 12 issubtractedfromacertainnumberandtheresult isdividedby 5.Iftheansweris 14,whatisthenumber?

13 Writeanequationandsolveitforeachofthesequestions. Thesumoftwoconsecutivewholenumbersis 23 Whatarethenumbers?

b Threelessthanﬁvetimesanumberis 12.Whatis thenumber?

IfIadd 5 totwiceanumber,theresultis 17.Whatis thenumber?

HintforQ12:Chooseapronumeralto representtheunknownnumber,then writeanequationusingthepronumeral. 1 2 of x canbewrittenas x 2.

HintforQ13:Consecutivewhole numbersareonenumberapart; e.g. 3, 4, 5, 6 etc.Thenextconsecutivenumberafter x is x + 1

Onepersonis 19 yearsolderthananotherperson.Theiragesumis 69.Whataretheirages?

d Andrewthrewtheshot-put 3 mmorethantwicethedistanceBarrythrewit.IfAndrewthrewthe shot-put 19 m,howfardidBarrythrowit?

14 Aservicetechniciancharges $40 upfrontand $60 foreachhoursheworks. Findalinearequationforthetotalcharge, $C,ofanyjobfor h hoursworked. a Whatwilla 4-hourjobcost? b Ifthetechnicianworksonajobfor 3 daysandaverages 6 hoursperday,whatwillbethe overallcost?

c Ifacustomerischarged $400,howlongdidthejobtake?

15 Apetroltankholds 71 litresoffuel.Itoriginallycontained 5 litres.Ifapetrolpumpfillsitat 6 litres perminute,find: alinearequationfortheamountoffuel(V litres)inthetankattime t minutes a howlongitwilltaketofillthetankto 23 litres b howlongitwilltaketofillthetank. c

1 3A Fortheexpression 2x + y 2 −3x2 + 5,determine: a thenumberofterms b theconstantterm c thecoefﬁcientof: x2 i y ii

2 3A Findthevalueofthefollowingexpressionsif a = 2, b = −5 and c = 8.

3 3B Simplifythefollowingbycollectingliketerms.

4 3B Simplifythefollowing.

5 3C Expandthefollowing.

6 3C Expandandsimplifythefollowing.

7 3D Factorisethefollowingbyﬁrstidentifyingthehighestcommonfactor.(Include anycommonnegatives.)

8 3E Simplifybycancellingcommonfactors.Youwillneedtofactoriseﬁrstinparts b and c

9 3E Simplifythefollowingalgebraicfractions.

10 3F Simplifythefollowingalgebraicfractions.

11 3F Simplify

12 3G Solvethefollowingequations

13 3G Fourmorethantwolotsofanumberis 22.Writeanequationandsolveittoﬁndthenumber.

3H 3H Solvingmoredifﬁcultlinearequations

Learningintentions

• Tobeabletoexpandbracketsandcollectliketermswhensolvingalinearequation

• Tobeabletocollectpronumeralstoonesideinordertosolvealinearequation

• Tobeabletosolveasimplewordproblembysettingupandsolvingalinearequation

Keyvocabulary: expand,liketerms,product,equivalent

Morecomplexlinearequationsmayhavevariablesonbothsidesoftheequationand/orbrackets.Examples are 6x = 2x −8 or 5(x + 3) = 12x + 4.

Bracketscanberemovedbyexpanding.Equationswithvariablesonbothsidescanbesolvedbycollecting variablestooneside,usingadditionorsubtractionofaterm.

Morecomplexlinearequationsofthistypeareusedwhenconstructingbuildingsandinscience andengineering.

Lessonstarter:Stepsinthewrongorder

Thestepstosolve 8(x + 2) = 2(3x + 12) arelistedhereintheincorrectorder.

8(x + 2) = 2(3x + 12) x = 4

2x + 16 = 24

8x + 16 = 6x + 24 2x = 8

Arrangetheminthecorrectorder,workingfromtheproblemtothesolution.

•

• Byconsideringallthestepsinthecorrectorder,writewhathashappenedineachstep.

Keyideas

Whensolvingcomplicatedlinearequations:

1 First, expand anybrackets. Inthisexample,multiplythe 3 intotheﬁrstbracketandthe −2 intothesecondbracket.

3(2x − 1) − 2(x 2) = 22 6x − 3 − 2x + 4 = 22

2 Collectany liketerms ontheLHSandanyliketermsontheRHS. Collectingliketermsoneachsideofthisexample: 2x − 13 = 3x + 5

5x − 4 − 3x 9 = x − 5 + 2x + 10

5x −3x = 2x, −4−9 = −13, x + 2x = 3x and −5 + 10 = 5

3 Ifanequationhasvariablesonbothsides,collecttoonesidebyaddingorsubtractingoneof theterms.

Forexample,whensolvingtheequation 12x + 7 = 5x + 19,ﬁrstsubtract 5x frombothsides: LHS: 12x + 7−5x = 7x + 7,RHS: 5x + 19−5x = 19: 12x + 7 = 5x + 19

7x + 7 = 19 5x 5x

4 Starttoperformtheoppositeoperationtobothsidesoftheequation.

5 RepeatStep 4 untiltheequationissolved.

6 Verifythattheansweriscorrect.

Tosolveawordproblemusingalgebra:

• Readtheproblemandﬁndoutwhatthequestionisaskingfor.

• Deﬁneapronumeralandwriteastatementsuchas:‘Let x bethenumberof …’.The pronumeralisoftenwhatyouhavebeenaskedtoﬁndinthequestion.

• Writeanequationusingyourdeﬁnedpronumeral.

• Solvetheequation.

• Answerthequestioninwords.

Exercise3H

Und er stand ing

1 Choosefromthewords collect, expand and one tocompletethefollowingwhensolvinglinear equations.

First anybrackets. a anyliketerms. b

Ifvariablesareonbothsides,collectto side. c

2 When −2(x −1) isexpanded,theresultis: HintforQ2:takecarewith

x −2 A

x + 2 D

3 When 2x issubtractedfrombothsides, 5x + 1 = 2x −3 becomes: 3x −1 = 3 A 7x + 1 = −3 B 7

Example26Solvingequationswithbrackets

Solve 4(x −1) = 16

Solution

4(x −1) = 16

Explanation

Expandthebrackets: 4 × x and 4 × (−1). 4x −4 = 16 Add 4 tobothsides.

4x = 20 Dividebothsidesby 4 x = 5 Alternatively,since 4 isafactorof 16,youcoulddivideboth sidesby 4 ﬁrst.

Nowyoutry

Solve 3(x + 1) = 15

4 Solveeachofthefollowingequationsbyﬁrstexpandingthebrackets.

3(x + 2) = 9 a 4(x −1) = 16 b

3(x + 5) = 12 c 4(a −2) = 12 d

5(a + 1) = 10 e 2(x −10) = 10 f

6(m −3) = 6 g 3(d + 4) = 15 h

7(a −8) = 14 i 10(a + 2) = 20 j

5(3 + x) = 15 k 2(a −3) = 0 l

Example27Solvingequationswithtwosetsofbrackets

Solve 3(2x + 4) + 2(3x −2) = 20

Solution

3(2x + 4) + 2(3x 2) = 20

6x + 12 + 6x −4 = 20

12x + 8 = 20

Nowyoutry

Explanation

Usethedistributivelawtoexpandeachsetof brackets.

CollectliketermsontheLHS. 12x = 12

Subtract 8 frombothsides. x = 1

Dividebothsidesby 12

Solve 2(3x −1) −3(x −4) = 16

5 Solvethefollowingequations.

3(2x + 3) + 2(x + 4) = 25

2(2x + 3) + 3(4x −1) = 51 c 3(2x −2) + 5(x + 4) = 36 d

4(2x −3) + 2(x −4) = 10 e 2(3x −1) + 3(2x −3) = 13 f 2(x −4) + 3(x −1) = −21 g 4(2x −1) + 2(2x −3) = −22 h

HintforQ5:Expandeachpairof bracketsandcollectliketerms beforesolving. a 2(2x + 3) + 4(3x + 1) = 42 b

6 Solvethefollowingequations.

3(2x + 4) −4(x + 2) = 6

8(x −1) −2(3x −2) = 2 e 5(2x −3) −2(3x −1) = −9 f 5(2x + 1) −3(x −3) = 35 g 4(2x −3) −2(3x −1) = −14 h

HintforQ6: −4(x + 2) = −4x −8 −4(x −2) = −4x + 8 a 2(5x + 4) −3(2x + 1) = 9 b 2(3x −2) −3(x + 1) = −7 c 2(x + 1) −3(x −2) = 8 d

Example28Solvingequationswithvariablesonbothsides

Solve 7x + 9 = 2x −11 for x

Solution

7x + 9 = 2x −11

5x + 9 = −11

5x = −20

Explanation

Subtract 2x frombothsides.

Subtract 9 frombothsides. x = −4

Dividebothsidesby 5.

Nowyoutry

Solve 10x + 3 = 8x −1 for x

7 Findthevalueof x inthefollowing.

7x = 2x + 10 a 10x = 9x + 12 b

8x = 4x −12 c 6x = 2x + 80 d

2x = 12− x

e 2x = 8 + x f

3x + 4 = x + 12 g 4x + 9 = x −3 h

2x −9 = x −10 i 6x −10 = 12 + 4x j

9x = 10− x k 1− x = x + 3 l

HintforQ7:Removetheterm containing x ontheRHS.Forparts e, k and l,youwillneedtoadd x to bothsides.

Example29Solvingequationswithfractions

Solve 2x + 3 4 = 2 for x

Solution

2x + 3 4 = 2

2x + 3 = 8

2x = 5

x = 2.5

Nowyoutry

Solve 4x −3 2 = 4

8 Solvethefollowingequations.

Explanation

Multiplybothsidesby 4

Subtract 3 frombothsides.

Dividebothsidesby 2

Example30Solvingequationswithmoredifﬁcultfractions

Solve 3x 2 −4 = 2 for x.

Solution

3x 2 −4 = 2

3x 2 = 6

3x = 12

Explanation

Add 4 tobothsides.

Multiplybothsidesby 2 x = 4

Nowyoutry

Solve 5x 3 + 1 = 6 for x

9 Solvethefollowingequations.

x 3 + 1 = 5 a x 3 + 1 = 7

Dividebothsidesby 3

HintforQ8:Firstmultiplyby thedenominator.

HintforQ9:Firstaddorsubtract anumberfrombothsides.

Problem-solving and reasoning

10 Foreachofthesequestions,writeanequationandsolveitfor x (x + 3) cm

+ 4)

10–1311–14

= 52 cm

= 22 cm

11 Solvethefollowingequationsusingtrialanderror(guess,checkand reﬁne).Substituteyourchosenvaluesof x untilyouhavefoundavalue thatmakestheequationtrue.

x + 22 3 = 4x a

5(3− x) = 2(x + 7.5) b 2x −1 4 = 2− x c

Example31Solvingawordproblem

Findthevalueof x iftheareaofrectangle ABCD shownis 24 cm2

Solution

A = l × w

24 = (x + 3) × 4

24 = 4x + 12

HintforQ10:ForQuestion 10c, verticallyoppositeanglesare equal.

Explanation

Writeanequationforarea.

Substitute: l = (x + 3), w = 4, A = 24

Expandthebrackets: (x + 3) × 4 = 4(x + 3)

12 = 4x Subtract 12 frombothsides.

3 = x Dividebothsidesby 4 x = 3 Writetheanswer.

Nowyoutry

Findthevalueof x iftheareaofrectangle ABCD shownis 40 m2

Findthevalueof x iftheareais 35 cm2 5 cm (x + 4) cm

Findthevalueof x iftheareais 42 cm2

6 cm (x + 4) cm

Findthevalueof x 2x + 3 3x 4 e

Findthevalueof x iftheareais 27 cm2 3 cm (2x 1) cm

Verticallyoppositeangles areequal.Findthevalue of x

13 Using x fortheunknownnumber,writedownanequation andthensolveittoﬁndthenumber.

Theproductof 5 and 1 morethananumberis 40 a Theproductof 5 and 6 lessthananumberis −15 b When 6 lessthan 3 lotsofanumberisdoubled, theresultis 18 c

When 8 morethan 2 lotsofanumberistripled, theresultis 36

10 morethan 4 lotsofanumberisequivalentto 6 lotsofthenumber. e

5 morethan 4 timesanumberisequivalentto 1 lessthan 5 timesthenumber.

6 morethanadoublednumberisequivalentto 5 lessthan 3 lotsofthenumber. g

HintforQ12:Formthearea equationﬁrst.

HintforQ13:

• ‘Product’means‘to multiply’

• Theproductof 5 and 1 morethananumber means 5(x + 1)

• ‘6 lessthan 3 lotsofa numberisdoubled’will requirebrackets.

• ‘Tripled’meansthree timesanumber.

• ‘Equivalent’means ‘equalto’.

14 ValentinaandHarrisonareplanningtohireacarfortheirweddingday.‘VehiclesForYou’havethe followingdeal: $850 hiringfeeplusachargeof $156 perhour.

Writeanequationforthecost ($C) ofhiringacarfor h hours.

IfValentinaandHarrisonhavebudgetedforthecartocostamaximumof $2000,ﬁndthemaximum numberoffullhourstheycanhirethecar.

Ifthecarpicksupthebrideat 1:15 p.m.,atwhattimemusttheeventﬁnishifthecostistoremain withinbudget?

Morethanonefraction — 15

15 Consider:

4x −2 3 = 3x −1 2

2 ✁ 6(4x −2) ✁ 31 = 3 ✁ 6(3x −1) ✁ 21 (Multiplybothsidesby 6 (LCMof 2 and 3)togetridofthefractions.)

2(4x −2) = 3(3x −1) (Simplify.)

8x −4 = 9x −3 (Expandbothsides.)

−4 = x −3 (Subtract 8x frombothsides.)

−1 = x (Add 3 tobothsides.)

Â x = −1

Solvethefollowingequationsusingthemethodshownabove.

Usingtechnology3H:Solvinglinearequations

ThisactivityisavailableonthecompanionwebsiteasaprintablePDF.

3I 3I Usingformulas

Learningintentions

• Tounderstandthatarelationshipbetweenvariablescanbedescribedusingformulas

• Tobeabletosubstituteintoaformulaandevaluate

• Tobeabletosolveanequationaftersubstitutionintoaformula

Keyvocabulary: subject,formula,variable,substitute,evaluate

Aformula(orrule)isanequationthatrelatestwo ormorevariables.Youcanﬁndthevalueofoneof thevariablesifyouaregiventhevalueofallother unknowns.

Youwillalreadybefamiliarwithmanyformulas. Forexample, C = 2p r istheformulaforﬁndingthe circumference, C,ofacirclewhengivenitsradius, r

F = 9 5 C + 32 istheformulaforconvertingdegrees Celsius, C,todegreesFahrenheit, F

s = d t istheformulaforﬁndingthespeed, s,when giventhedistance, d,andtime, t

ThisthermometerdisplaysbothdegreesCelsiusand degreesFahrenheit.Itshows 14°Candapproximately 57°F,accuratelyreﬂectingtheconversionformula.

C, F and s aresaidtobethesubjectsoftheformulasgivenabove.

Lessonstarter:Jumbledsolution

Problem:Theformulafortheareaofatrapeziumcanbewrittenas A = h 2 (a + b)

Xavierwasaskedtoﬁnd a,giventhat A = 126, b = 10 and h = 14,andtowritetheexplanationbeside eachstepofthesolution.

Xavier’ssolutionandexplanationarebelow.Hissolutioniscorrectbuthehasjumbledupthesteps intheexplanation.CopyXavier’ssolutionandwritethecorrectinstruction(s)besideeachstep. Example1

Solution Jumbledexplanation

A = h 2 (a + b)

126 = 14 2 (a + 10)

126 = 7(a + 10)

126 = 7a + 70

56 = 7a

a = 8

Subtract 70 frombothsides. Dividebothsidesby 7 Substitutethegivenvalues. Copytheformula.

Simplify 14 2 . Expandthebrackets.

Keyideas

A formula isanequationthatrelatestwoormorevariables.

The subject ofaformulaisavariablethatusuallysitsonitsownontheleft-handside.Forexample, the C in C = 2p r isthesubjectoftheformula.

Avariableinaformulacanbeevaluatedbysubstitutingnumbersforallothervariables.

Aformulacanberearrangedtomakeanothervariablethesubject. C = 2p r canberearranged togive r = C 2p Notethat

Exercise3I

Und er stand ing

1 Statetheletterthatisthesubjectintheseformulas.

I = Prt 100

2 Substitutethegivenvaluesintoeachofthefollowingformulas toﬁndthevalueofeachsubject.Roundtheanswerto onedecimalplacewhereappropriate.

m = F a ,when F = 180 and a = 3

HintforQ1:Thesubjectofa formulaistheletteronits own,ontheleft-handside.

HintforQ2:Copyeach formula,substitutethegiven valuesandthencalculate theanswer. a A = lw,when l = 6 and w = 8 b A = 1 2 (

Fluency

Example32Substitutingvaluesandsolvingequations

If v = u + at,ﬁnd t when v = 16, u = 4 and a = 3

Solution

v = u + at

16 = 4 + 3t

12 = 3t

4 = t

t = 4

Nowyoutry

Explanation

Substituteeachvalueintotheformula. v = 16, u = 4, a = 3

Anequationnowexists.Solvethisequationfor t

Subtract 4 frombothsides.

Dividebothsidesby 3

Answerwiththepronumeralontheleft-handside.

If A = 1 2 xy,ﬁnd y when A = 12 and x = 4

3 If v = u + at,ﬁnd t when:

v = 16, u = 8 and a = 2 a v = 20, u = 8 and a = 3 b

v = 100, u = 10 and a = 9 c v = 84, u = 4 and a = 10 d

4 If P = 2(l + 2b),ﬁnd b when:

P = 60 and l = 10

a P = 48 and l = 6 b

P = 96 and l = 14 c P = 12.4 and l = 3.6 d

5 If V = lwh,ﬁnd h when:

V = 100, l = 5 and w = 4 a V = 144, l = 3 and w = 4 b

V = 108, l = 3 and w = 12 c V = 280, l = 8 and w = 5 d

6 If A = 1 2 bh,ﬁnd b when:

HintforQ3:Firstcopythe formula.Thensubstitutethe givenvalues.Thensolve theequation.

A = 90 and h = 12

a A = 72 and h = 9 b

A = 108 and h = 18 c A = 96 and h = 6 d

7 If A = h 2 (a + b),ﬁnd h when:

a A = 20, a = 4 and b = 1

b A = 48, a = 5 and b = 7

c A = 108, a = 9 and b = 9

d A = 196, a = 9 and b = 5

8 E = mc2.Find m when:

E = 100 and c = 5

a E = 4000 and c = 10 b E = 72 and c = 1 c E = 144 and c = 6 d

9 If V =p r2h,ﬁnd h (toonedecimalplace)when:

V = 160 and r = 3

a V = 400 and r = 5 b V = 1460 and r = 9 c V = 314 and r = 2.5 d

Problem-solving and reasoning

10 Theformula F = 9C 5 + 32 isusedtoconverttemperaturefrom degreesCelsius (°C) (whichisusedinAustralia)todegrees Fahrenheit (°F ) (whichisusedintheUSA).

a Whenitis 30°C inSydney,whatisthetemperature inFahrenheit?

HintforQ6:For 90 = 1 2 × b × 12, 1 2 × b × 12 = 1 2 × 12 × b = 6b

So, 90 = 6b Solvefor b

HintforQ7:Whensolvingthe equationﬁrstundothedivisionby 2 bymultiplyingbothsidesby 2

HintforQ8:Squarethe c value beforesolvingtheequation.

HintforQ9:For 160 = 9p h,dividebothsidesby 9p toﬁnd h: h = 160 9p

Thenevaluateona calculator.

10–1210,12–14

b HowmanydegreesCelsiusis 30° Fahrenheit?Answertoonedecimal place.

c Waterboilsat 100°C.WhatisthistemperatureindegreesFahrenheit?

d Whatis 0°F indegreesCelsius?Answertoonedecimalplace.

HintforQ10:When ﬁnding C,youwill haveanequation tosolve.

11 Thecost,indollars,ofataxiis C = 3 + 1.45d,where d isthedistancetravelled,inkilometres.

a Whatisthecostofa 20 kmtrip?

b Howmanykilometrescanbetravelledfor $90?

12 I = Prt 100 calculatesinterestonaninvestment.Find:

a P when I = 60, r = 8 and t = 1

b t when I = 125, r = 5 and P = 800

c r when I = 337.50, P = 1500 and t = 3

13 Thenumberoftabletsanursemustgiveapatientisfoundusingtheformula: Tablets = strengthrequired tabletstrength

a 750 milligramsofadrugmustbeadministeredtoapatient.Howmany 500 milligramtabletsshould thenursegivethepatient?

b Ifthenurseadministers 2.5 ofthesetabletstoanotherpatient,howmuchofthedrugdidthe patienttake?

14 Adripisawayofpumpingaliquiddrugintoapatient’sblood.Theﬂowrateofthepump,inmillilitres perhour,iscalculatedusingtheformula:Rate = volume(mL) time(h)

a Apatientneeds 300 mLofthedrugadministeredover 4 hours.Calculatetherate,inmL/h,which needstobedeliveredbythepump.

b Apatientwasadministered 100 mLofthedrugatarateof 300 mL/h.Howlongwasthe pumprunning?

Calculationchallenges

15–17

15 Ataxagentcharges $680 foran 8-hourday.Theagentusestheformula F = 680x 8 tocalculateafeeto aclient,indollars.

a Whatdoesthe x represent?

b Ifthefeechargedtoaclientis $637.50,howmanyhours,toonedecimalplace,didtheagentspend workingontheclient’sbehalf?

Findtheareaandperimeteroftriangle ABC,shown.

x) cm

HintforQ16:UsePythagoras’ theoremtoﬁnd x

17 Iqrais 10 yearsolderthanUrek.In 3 years’time,shewillbetwiceasoldasUrek.Howoldare theynow?

3J 3J Linearinequalities

Learningintentions

• Toknowthefourinequalitysymbolsandwhattheymean: <, >, ≤, ≥

• Tobeabletoillustrateaninequalityusinganumberline

• Toknowwhentoreverseaninequalitysymbol

Keyvocabulary: inequality,inequalitysymbol,linearinequality

Therearemanysituationsinwhichasolutiontothe problemisbestdescribedusingoneofthesymbols <, Ä, > or Å.Forexample,amedicalcompanywillpublishthe lowestandhighestamountsforasafedoseofaparticular medicine;e.g. 20 mg/day Ä dose Ä 55 mg/day,meaning thatthedoseshouldbebetween 20 and 55 mg/day. Aninequalityisamathematicalstatementthatuses an‘islessthan’ (<),an‘islessthanorequalto’ (Ä),an ‘isgreaterthan’ (>) oran‘isgreaterthanorequalto’ (Å) symbol.Inequalitiesmayresultinaninﬁnitenumberof solutions.Thesecanbeillustratedusinganumberline. Youcansolveinequalitiesinasimilarwaytosolving equations.

Lessonstarter:Whatdoesitmeanfor x ?

Apharmacistwillexplainthesaferangeoftablets youcantakeeachdaytoensureyougetthe beneﬁtwithoutharm.

Thefollowinginequalitiesprovidesomeinformationaboutthenumber

• Canyoudescribethepossiblevaluesfor x thatsatisfyeachinequality?

• Testsomevaluestocheck.

• Howwouldyouwritethesolutionfor x?Illustrateeachonanumberline.

Keyideas

Thefour inequalitysymbols are <, Ä, > and Å

• x > a means x isgreaterthan a

• x Å a means x isgreaterthanorequalto a

• x < a means x islessthan a

• x Ä a means x islessthanorequalto a

Onthenumberline,aclosedcircle(•)indicatesthatthenumberisincluded.Anopencircle(°) indicatesthatthenumberisnotincluded.

Solving linearinequalities followsthesamerulesassolvinglinearequations,except:

• Wereverseaninequalitysymbolifwemultiplyordividebyanegativenumber.

Forexample, −5 < −3 and 5 > 3,andif −2x < 4 then x > −2

• Wereversetheinequalitysymbolifthesidesareswitched. Forexample,if 2 Å x,then x Ä 2.

Usingcalculatorstosolveinequalities

Solvetheinequality 5 < 3−2x 3 .

UsingtheTI-Nspire:

Ina Calculator pageuse menu >Algebra>Solve andtypetheinequalityas shown.

Hint: theinequalitysymbols(e.g. <)are accessedusing ctrl =

Hint: usethefractiontemplate( ctrl ÷ )

UsingtheClassPad:

Tap solve(,andtypetheinequalityasshown.

Exercise3J

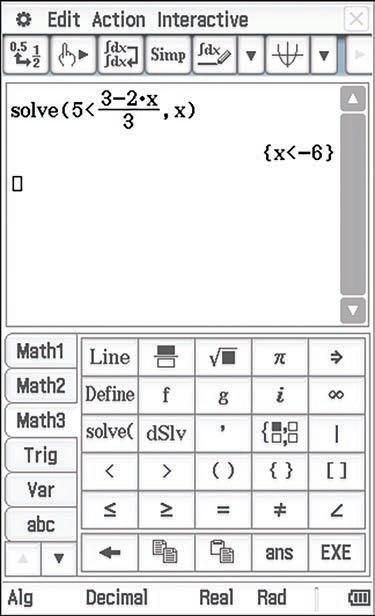
1 Matcheachinequalitygivenwiththecorrectnumberline.

HintforQ1:Lookbackatthe Keyideas. Thedirectionofthe arrowheadisthesameasthe directionoftheinequalitysymbol.

2 Matcheachinequalitywiththecorrectdescription.

x < 2 a x isgreaterthan 2 A x Å 2 b x islessthanorequalto 2 B x Ä 2 c x islessthan 2 C

x > 2 d x isgreaterthanorequalto 2 D

Fluency

Example33Writinginequalitiesfromnumberlines

Writeeachnumberlineasaninequality.

Solution

a x > 2

b x Ä −1

Nowyoutry

Explanation

Anopencirclemeans 2 isnotincluded.

Aclosedcirclemeans −1 isincluded.

Writeeachnumberlineasaninequality. x 2 1 3 4 a 78910 x b

3 Writeeachgraphasaninequality. 012 3 x

4 Showeachofthefollowingonseparatenumberlines. x Å 7 a x > 1 b x < 1

HintforQ3:Theinequality symbolwillhavethesame directionasthearrow.

HintforQ4:For x Å 7,drawanumber lineshowingsomenumbersaround 7 x 6897

Useaclosedcircle(•)for Å and Ä

Useanopencircle(°)for > and <.

5 Writeaninequalitytodescribewhatisshownoneachofthefollowingnumberlines.

HintforQ5:Thepronumeralis attheendofthenumberline. b 6 a 4 2 0 2 4 c

Example34Writingandgraphinginequalities

Writeeachofthefollowingasaninequalityandthenshoweachsolutiononanumberline. x islessthanorequalto 3 a x isgreaterthan 1 b x islessthan 0 c x isgreaterthanorequalto −2 d

Solution

a x Ä 3

b x > 1

c x < 0

d x Å −2

Explanation

Lessthanorequalto, Ä,closedcircle

Greaterthan, >,opencircle

Lessthan, <,opencircle

Greaterthanorequalto, Å,closedcircle

Nowyoutry

Writeeachofthefollowingasaninequalityandthenshoweachsolutiononanumberline. x isgreaterthan −4 a x islessthanorequalto 6 b

6 Writeeachofthefollowingasaninequalityandthenshoweachsolutiononanumberline. x islessthanorequalto 6 a x isgreaterthan 4 b x islessthan 2 c x isgreaterthanorequalto 5 d

7 Writeeachofthefollowingasaninequality,usingthepronumeral n.

ThenumberofpeoplewhovisittheSydneyOperaHouse eachyearismorethan 100000 a

Thenumberoflolliesinabagshouldbeatleast 50. b Afactoryworkermustpackmorethanthree boxesaminute. c

HintforQ7:‘Atleast 50’means ‘50 ormore’.

Morethan 100 penguinstakepartinthenightlyparadeonPhillipIsland.

Theweightofasuitcaseis 30 kgorless. e

8 Writeeachofthefollowingstatementsasaninequality anddeterminewhichofthenumbersbelowmakeeach inequalitytrue.

−6, −2, 1 2 , 0, 2, 5, 7, 10, 15, 24

HintforQ8:Writethe inequality,thenlistthegiven numbersthatmakeittrue.

a x isgreaterthan 10 b

x islessthanzero

x isgreaterthanorequalto 10

c x islessthanorequaltozero d

x isgreaterthanorequalto −1 e x islessthan 10 f

Problem-solving and reasoning

Example35Solvingandgraphinginequalities

Solvethefollowingandshowyoursolutiononanumberline.

2x −1 > 17 a x 3 Ä −2 b

Solution

a 2x −1 > 17

Explanation

Add 1 tobothsides. 2x > 18

Dividebothsidesby 2 x > 9 1112 x 10 89 7 > usesanopencircle.

b x 3 Ä −2

Multiplybothsidesby 3. x Ä −6

6 5 x 7 9 8 10

Ä usesaclosedcircle.

Nowyoutry

Solvethefollowingandshowyoursolutiononanumberline.

9 Solveeachofthefollowinginequalitiesandshowyoursolutiononanumberline. 2

HintforQ9:Keeptheinequalitysymbol thesamewhen:

• addingorsubtractinganumberfrom bothsides

• multiplyingordividingbothsidesby apositivenumber.

10 Solvethefollowing. 2

11 Givethesolutionsetforeachofthefollowing.

3 + 7 > 2

HintforQ11:For x + 2 4 Ä 1, ﬁrstmultiplybothsides by 4.For x 4 −1 Å 6,ﬁrst add 1 tobothsides.

12 Foreachofthefollowing,writeaninequalityandsolveittoﬁndthepossiblevaluesof x Whenanumber, x,ismultipliedby 3,theresultislessthan 9. a Whenanumber, x,ismultipliedby 3 andtheresultdividedby 4,itcreatesananswerlessthan 6 b Whenanumber, x,isdoubledandthen 15 isadded,theresultisgreaterthan 20 c Thuongis x yearsoldandGaryis 4 yearsolder.Thesumoftheiragesislessthan 24 d Kaitlynhas x ridesontheFerriswheelat $4 arideandspends $7 onfood.Thetotalamountshe spendsislessthanorequalto $27.

Example36Solvinginequalitieswhenthepronumeralhasanegativecoefﬁcient

Solve 4− x Å 6

Solution

4− x Å 6

x Å 2

x Ä −2

Alternativesolution:

4− x Å 6

4 Å 6 + x

−2 Å x

x Ä −2

Nowyoutry

Solve 5−2x < 17

Explanation

Subtract 4 frombothsides.

Dividebothsidesby −1.

Whenwedividebothsidesbya negative number,theinequality symbolisreversed.

Addthe x tobothsidessothatitispositive.

Subtract 6 frombothsides.

Switchthesidestohavethe x ontheleft-handside.

Reversetheinequalitysymbol.Notethattheinequalitysymbolstill ‘points’tothe x

13 Choosean appropriatestrategy tosolvethefollowing.

x <

HintforQ13:Rememberto reversetheinequalitysymbol whenmultiplyingordividing byanegativenumber. e.g.

Investigatinginequalities 14

14a Letusstartwiththenumbers 4 and 6 andthetruerelationship 4 < 6.Copyandcompletethe followingtable. Trueorfalse?

Multiplyby 2

Divideby 2 Multiplyby −2

b Copyandcompletethefollowing. Whensolvinganinequality,youcanaddor anumberfrombothsidesandtheinequality remainstrue.Youcanmultiplyor bya numberandthe alsoremainstrue. However,ifyou or byanegative theinequalitysymbolmustbereversed fortheinequalitytoremain

3K 3K Solvingsimultaneousequationsusing substitution

Learningintentions

• Tounderstandthatasolutiontoapairofsimultaneousequationscanbefoundalgebraically

• Tobeabletousethemethodofsubstitutionto ndasolutiontoapairofsimultaneousequations

• Tobeabletoapplythemethodofsubstitutiontosolvesimultaneousequationsinarealcontext

Keyvocabulary: substitute,subject,de ne

Apairofsimultaneousequationsisformedwhentherearetwounknownquantities(i.e.variables)and twopiecesofinformationrelatingthesequantities.Thesolutiontothesesimultaneousequationsgivesthe variablevaluesthatmakebothequationstrue.

Anexampleoftwovariablesisthecostofaweddingreceptionandthenumberofinvitedguests.Two simultaneousequationscouldbemadefromtwodifferentcateringcompanies.Thesolutionwillbethe numberofgueststhatmakethecostsequalforthetwocompanies.Usingequationshelpstoaccurately comparethetwodeals.

Lessonstarter:Equationsandsolutions

Knowingtheaverage costofcateringper personhelpsyou determinehowmany peopleyoucanaffordto invitetoyourevent.

Albertis 11 yearsolderthanJennyandthesumoftheiragesis 69.WhataretheagesofAlbertandJenny? Herearethestepstosolvethisproblembuttheyareinthewrongorder.Decideonthecorrectorder.

A x + (x + 11) = 69

2x + 11 = 69

2x = 58 x = 29

B Let x = Jenny’sage Let y = Albert’sage

C Jennyis 29 yearsold. Albertis 40 yearsold.

D x + y = 69

y = x + 11

Keyideas

Thealgebraicmethodof substitution isgenerallyusedwhenatleastoneofthelinearequations has x or y asthesubject; e.g. y = 3x + 4 and 3x + y = 2 or y = −2x + 6 and y = x −1 or x = 2 and 2x y = 5

Themethodinvolves:

• substitutingoneequationintotheother

• solvingfortheremainingvariable

• substitutingtoﬁndthevalueofthesecondvariable.

Whenproblem-solvingwithsimultaneouslinearequations,followthesesteps.

• Deﬁne/describetwounknownsusingpronumerals.

• Writedowntwoequationsusingyourpronumerals.

• Solvetheequationsusingthemethodofsubstitution.

• Answertheoriginalquestioninwords.

Usingcalculatorstosolvesimultaneousequations

Solve y = 3x −1 and y = 2− x simultaneously.

UsingtheTI-Nspire: UsingtheClassPad:

Theequationscanbesolvedsimultaneously. Select menu >Algebra>SolveSystemof Equations>SolveSystemofEquations Enterthenumberofequationsandthe variables,thentypetheequationsasshown.

Exercise3K

Und er stand ing 1,2 2

1 Writethemissingwordstocompleteeachstatement.Choosefrom substituted, simultaneous and substitution.

a equationsinvolveatleasttwoequationsandtwovariables.

b If x (or y)isreplacedwithanumber,thenwehave thatnumberfor x

c If x (or y)isreplacedwithanalgebraicexpression,thenwehave thatexpressionfor x (or y).

d Whenwealgebraicallysubstituteoneequationintoanother,thisiscalledsolving simultaneousequationsbythemethodof .

2 Choosethecorrectoption.

a When y = x −1 issubstitutedinto 2x + y = 6,theresultis:

2x + (x −1) = 6 A

2x −1 = 6 B

x −1 = 6 C

2x x + 1 = 6 D

3x = 6 E

b When y = 2x + 3 issubstitutedinto x −3y = 1,theresultis:

x + 3(2x + 3) = 1 A 3(2x + 3) = 1 B

x −3(2x + 3) = 1 C x (2x + 3) = 1 D

2x −3 = 1 E Fluency

HintforQ1:Inpart a,replace y in 2x + y = 6 with x + 1

Example37Usingthesubstitutionmethodtosolvesimultaneousequations

Solvethepairofsimultaneousequations y = 5x and y = 2x + 6

Solution

y = 5x [1]

y = 2x + 6 [2]

Substitute[1]into[2]:

5x = 2x + 6

3x = 6

x = 2

Substitute x = 2 into[1]:

y = 5(2)

y = 10

Solutionis x = 2, y = 10

Check: 10 = 2(2) + 6

Nowyoutry

Explanation

Labelthetwoequations.

Explainhowyouaresubstitutingtheequations. Replace y inthesecondequationwith 5x Subtract 2x frombothsides. Dividebothsidesby 3.

Alternatively,substituteintoequation[2].

Replace x withthenumber 2. Simplify.

Writethesolution.

Substituteyoursolutionintotheotherequationto check.

Solvethepairofsimultaneousequations y = 7x and y = 2x + 5

3 Solvethefollowingpairsofsimultaneousequations

y = 5x y = 3x + 4

= 4x

= −3x + 7

HintforQ3: y = 5x y = 3x + 4 ∴ 5x = 3x + 4

Example38Solvingsimultaneousequationswiththesubstitutionmethod

Solvethesesimultaneousequationsusingthesubstitutionmethod.

2x + y = −7 and y = x + 2 a y = x + 3 and 2x + 3y = 19 b

Solution

a 2x + y = −7 [1]

y = x + 2 [2]

Substituteequation[2]intoequation[1].

2x + (x + 2) = −7

3x + 2 = −7

3x = −9 x = −3

Substitute x = −3 intoequation[2].

y = (−3) + 2 = −1

Solutionis x = −3, y = −1

b y = x + 3 [1]

2x + 3y = 19 [2]

Substitute[1]into[2]:

2x + 3(x + 3) = 19

2x + 3x + 9 = 19

5x + 9 = 19

5x = 10 x = 2

Substitute x = 2 into[1]:

y = (2) + 3 y = 5

Thesolutionis x = 2, y = 5

Check: 2(2) + 3(5) = 19

Explanation

Labelthetwoequations.

Substituteequation[2]intoequation[1]since equation[2]hasapronumeralasthesubject.

Solvetheresultingequationfor x

Substitutetoﬁnd y

Explainhowyouaresubstitutingtheequations.

Replace y inthesecondequationwith (x + 3) Expandthebrackets.

Simplify.

Subtract 9 frombothsides.

Dividebothsidesby 5.

Alternatively,substituteintoequation(2).

Replace x withthenumber 2

Simplify.

Writethesolution.

Substituteyoursolutionintotheotherequation tocheck.

Nowyoutry

Solvethesesimultaneousequationsusingthesubstitutionmethod.

3x + y = 4 and y = x −4 a y = x −1 and 3x + 2y = −12 b

4 Solvethefollowingpairsofsimultaneousequationsusing thesubstitutionmethod.

y = x + 2 and 3x + y = 6 a

y = x + 3 and 2x + y = 18

y = x −1 and 3x + y = 11 c

y = x −1 and 3x + 5y = 27 d

y = x + 2 and 2x + 3y = −19 e

y = x + 5 and 5x y = −1 f

y = x −3 and 5x −2y = 18 g

y = x −4 and 3x y = 2 h

5 Solvethefollowingpairsofsimultaneousequations.

y = 2

y = 2x + 4

y = 4

2x + 3y = 20 c

= −1 y = 2x −7

HintforQ4:Inpart d, replace y inthesecond equationwith (x −1).Itisimportant tousebrackets.

3x + 5 y = 27

Remember that

y = x – 1 5(x – 1) = 5x – 5

HintforQ5:Replace y inthesecondequation with 2 y = 2 y = 2x + 4

6 Solvethefollowingpairsofsimultaneousequations.

x = 2

3x + 2y = 14

x = 7

4x −3y = 31 c

Rememberthat 3x means 3 × x a x = −3 y = −2x −4 b

HintforQ6:Replace x inthe secondequationwith 2. x = 2

3 x + 2y = 14

7 Solvethefollowingpairsofsimultaneousequations usingthesubstitutionmethod.

y = 2x + 3

11x −5y = −14

y = 3x −5

3x + 5y = 11 c y = 4x + 1 2x −3y = −23 d

HintforQ7:Becareful withsignswhen expandingbrackets.

5 × (+ 3) = −15

11x − 5(2x + 3) = 11x − 10x 15

Whenmultiplying numberswithdifferent signs,theansweris negative. a y = 3x −2 7x −2y = 8 b

Problem-solving and reasoning

8,9 8,10,11

Example39Solvingwordproblemswithsimultaneousequations(substitution)

Jadeis 5 yearsolderthanMarian.Iftheircombinedageis 33,ﬁndtheirages.

Solution

Let j beJade’sageand m be Marian’sage.

j = m + 5 [1]

j + m = 33 [2]

(m + 5) + m = 33

2m + 5 = 33

2m = 28

m = 14

j = m + 5 [1]

j = 14 + 5

j = 19

Jadeis 19 yearsoldandMarian is 14 yearsold.

Nowyoutry

Explanation

Deﬁnetwopronumeralsusingwords.

TheﬁrstpieceofinformationisthatJadeis 5 yearsolder thanMarian.

Thesecondpieceofinformationisthattheircombined ageis 33

Substitute m + 5 for j inthesecondequation.

Collectanyliketerms,so m + m = 2m

Subtract 5 frombothsides.

Dividebothsidesby 2.

Usetheﬁrstequation, j = m + 5,toﬁnd j

Answertheoriginalquestioninwords.

Arectangle’slengthis 3 cmmorethanitswidth.Ifitsperimeteris 32 cm,determineitsdimensions.

8 Kyeis 5 yearsolderthanViviana.Iftheircombinedage is 81,determinetheirages.

9 Thelengthofarectangleisthreetimesthewidth.Ifthe perimeteroftherectangleis 48 cm,determineitsdimensions.

10 Avanillathickshakeis $2 morethanafruitytwirl.Ifthree vanillathickshakesandﬁvefruitytwirlscost $30,determine theirindividualprices.

11 Carlosis 3 morethantwiceElla’sage.Ifthesumoftheirages is 54 years,determinetheirages.

HintforQ8:FirstdeﬁneapronumeralforKye’sageandanother pronumeralforViviana’sage.Then writetwoequationsbeforesolving.

HintforQ9:Drawadiagramto helpformtheperimeterequation.

HintforQ10:Ifafruitytwirl costs $x,then 5 willcost $5x

Rentals

12 ThegivengraphrepresentstherentalcostofanewcarfromtwocarrentalﬁrmscalledPaul’sMotor MartandJoe’sCarRental.

Joe’s (1000, 260)

Paul’s (1000, 250)

driven (km)

a Determine: theinitialrentalcostfromeachcompany i thecostperkilometrewhenrentingfromeachcompany ii thelinearequationsforthetotalcostfromeachcompany iii thenumberofkilometresatwhichthetotalcostisthesameforbothrentalﬁrms,usingthe methodofsubstitution.

b DescribewhenyouwoulduseJoe’sorPaul’srentalﬁrm.

Distance

3L 3L Solvingsimultaneousequationsusing elimination

Learningintentions

• Tobeabletousethemethodofeliminationto ndasolutiontoapairofsimultaneousequations

• Tobeabletoapplythemethodofeliminationtosolvesimultaneousequationsinarealcontext

Keyvocabulary: elimination,simultaneous,multiple

Asecondmethodforsolvingsimultaneousequations,called elimination,cansometimesbemoreefﬁcient,dependingonhowthe equationsarestructuredintheﬁrstplace.

Whensettingupequationsforrealsituations,weshoulddeﬁnethe unknownquantitiesusingpronumerals.Whensolvingsimultaneous linearequationsthereshouldbeonlytwounknownquantitiesfortwo equationsformedfromthegiveninformation.

Forexample,tworelatedvariablesarethecostofowningacarand thenumberofkilometresdriven.Fortwodifferentcars,twoequations couldbemaderelatingthesevariables.Thesimultaneoussolution givesthenumberofkilometresthatmakesthetotalrunningcostsof eachcarequal.Solvingsimultaneousequationsprovidesinformation foranaccuratecomparisonofcostsbetweentwovehicles.

Lessonstarter:Eliminatingavariable

Simultaneousequationscanbeused tocomparecarinsuranceproviders bysolvingforvariableslikepremium costsandcoveragelimits.

Onestepintheeliminationmethodinvolvesaddingorsubtractingtwoequationsinordertoeliminateone ofthevariables.Whenadding,wewrite [1]+[2];whensubtracting,wewrite [1] [2] Astudenthaseitheraddedorsubtractedpairsofequations,buthasmanyincorrectanswers.

•

• Determinewhichanswersareincorrectandwritethecorrectanswerforthese.(Note:Donotsolve theequationsfor x or y.)

5x + 3y = 34 [1]

7x −3y = 26 [2]

[1]+[2] gives:

12x + 0 = 60

2x −2y = 8 [1]

4x −2y = 24 [2]

[1] [2] gives:

2x −4y = 16

5x + 3y = 31 [1]

5x −3y = 19 [2]

[1]+[2] gives:

0 + 0 = 12

Keyideas

3x + 2y = 18 [1] 2x −2y = 2 [2] [1]+[2] gives:

x −4y = 20

x + 3y = 16 [1]

x + 2y = 3 [2] [1]+[2] gives:

+ y = 19

x + 3y = 15 [1]

+ 2y = 12 [2]

1] [2] gives:

x + y = 3

x −3y = 9 [1] 2x −3y = 4 [2] [1] [2] gives: 5x + 0 = 5

3x + 2y = 25 [1] 2x + 2y = 18 [2]

[1] [2] gives: x + 0 = 43

x y = 5 [1] 3x y = −2 [2] [1] [2] gives: 4x = 3 I

Elimination isgenerallyusedtosolvesimultaneousequationswhenbothequationsare intheform ax + by = d

e.g. 2x y = 6 and 3x + y = 10 or −5x + y = −2 and 6x + 3y = 5

Addingorsubtractingmultiplesofthesetwoequationsallowsoneofthevariablesto beeliminated.

• Add x y = 10 and 3x + y = 34 toeliminate y

• Subtract 5x + 2y = 7 and 5x + y = 6 toeliminatethe x

• Formamatchingpairbymultiplyingbyachosenfactor.

Forexample, 2

Whenproblem-solvingwithsimultaneouslinearequations,followthesesteps.

• Deﬁne/describetwovariablesusingletters.

• Writedowntwoequationsusingyourvariables.

• Solvetheequationsusingthemethodofelimination.

• Answertheoriginalquestioninwords.

Exercise3L

1 Whatoperation (i.e. + or ) willmaketheseequationstrue?

2 Multiplybothsidesoftheequation 3x −2y = −1 bythefollowingnumbers.Writethenewequations. 2 a 3 b 4 c

3 Choosethecorrectoption.

a When 2x + y = 3 isaddedto 5x y = 11 theresultis: 7x = 11 A 7x = 14 B 3x = 14 C

b When x + y = 5 issubtractedfrom 3x + y = 7 theresultis:

Fluency

(½)

Example40Eliminatingavariablebyadditionofequationsthensolving

Addequation[1]toequation[2]andthensolvefor x and y

x + 2y = 10 [1]

x −2y = 2 [2]

Solution

x + 2y = 10 [1]

x −2y = 2 [2]

[1]+[2] gives:

2x + 0 = 12

2x = 12

x = 6

Explanation

Copyequationswiththelabels [1] and [2].

Writetheinstructiontoadd: [1]+[2]

Addthe x column: x + x = 2x

Addthe y column: 2y + (−2y) = 0.

AddtheRHS: 10 + 2 = 12 andthendividebothsidesby 2

(½)

Substitute x = 6 into [1]:

6 + 2y = 10

2y = 4 y = 2

Inequation [1],replace x with 6.Equation [2] couldalso havebeenused.

Subtract 6 frombothsides. Dividebothsidesby 2

Solutionis x = 6, y = 2. Writethesolution.

Check: [2] 6−2 × (2) = 2,true

Nowyoutry

Checkthatthesolutionsatisﬁesequation [2].

Addequation[1]toequation[2]thensolvefor x and y

3x + y = 11 [1]

x y = 5 [2]

4 Copyeachpairofequations,addequation [1] to [2], thensolvefor x and y

x + y = 7 [1]

x y = 5 [2]

[1]+[2]

3x + 2y = 20 [1]

−3x + y = 1 [2]

[1]+[2]

+ 2y = 11 [1] x −2y = −5 [2] [1]+[2]

5 Copyeachpairofequations,subtractequation [2] from equation [1] andthensolvefor x and y,showingallsteps.

2x + y = 16 [1]

x + y = 9 [2]

[1] [2]

3x + 5y = 49 [1]

3x + 2y = 25 [2]

[1] [2]

[1] [2] c

5x −4y = 16 [1]

2x −4y = 4 [2]

6 Determinethesolutionofthefollowingsimultaneous equationsusingtheeliminationmethod.

a x + y = 7 and 5x y = 5

b x + y = 5 and 3x y = 3

c x y = 2 and 2x + y = 10

d x y = 0 and 4x + y = 10

HintforQ5: [1] [2] 5x 4y 2x 4y 16 4 4y (−4y) =−4y + 4

HintforQ6:Labelthetwoequations,one undertheother,anddecidewhetherto eliminate x or y;i.e.eliminatewhichever variablehasthesamenumberineach equation.Rememberthat +y + ( y) = 0.

7 Solvethefollowingpairsofsimultaneousequations,usingthe eliminationmethod.Youwillneedtosubtracttheequationsto eliminateoneofthevariables.

3x + 4y = 7

2x + 4y = 6

Example41Formingamatchingpair

HintforQ7:Alwayslabel theequationsandwritethe instruction;e.g. [1] [2] or [2] [1]

Determinethesolutionofthesimultaneousequations x + y = 6 and 3x + 2y = 14,usingthe eliminationmethod.

Solution

x + y = 6 [1]

3x + 2y = 14 [2]

[1]× 2 : 2x + 2y = 12 [3]

[2] : 3x + 2y = 14 [2]

[2] [3]: x = 2

Substitute x = 2 into [1]:

2 + y = 6 y = 4

Solutionis x = 2, y = 4

Check: 3(2) + 2(4) = 14 true

Nowyoutry

Explanation

Labelthetwoequationsanddecidehowtoforma matchingpair.

Create 2y ineachequationbymultiplying[1]by 2

Subtractthetwoequationsbecause 2y −2y = 0, 3x −2x = x and 14−12 = 2

Alternatively,substituteintoequation [2]

Replace x withthenumber 2

Subtract 2 frombothsides.

Writethesolution.

Checkthatthesolutionsatisﬁestheotherequation.

Determinethesolutionofthesimultaneousequations x + y = 4 and 5x + 2y = 11,usingthe eliminationmethod.

8 Solvethesesimultaneousequationsbyﬁrstforminga matchingpair.

−3y = 1 2x + y = 9

+ 2y = 10

HintforQ8:Multiplyone equationbyanumberto formamatchingpair.

Example42Formingamatchingpairbymultiplyingbothequations

Solvethesimultaneousequations 3x + 2y = 6 and 5x + 3y = 11,usingtheeliminationmethod.

Solution Explanation 3x + 2y = 6 [1] 5x + 3y = 11 [2] [1]× 3 : 9x + 6y = 18 [3] [2]× 2 : 10x + 6

[4] [3] : x = 4

Labelthetwoequationsanddecidewhetherto eliminate x or y

Multiplyingtheﬁrstequationby 3 andthe secondby 2 resultsinamatchingpair 6y ineach equation.

Subtracttheequationssince 6y −6y = 0.

Substitute x = 4 into [1]:

3(4) + 2y = 6

2y = −6 y = −3

Solutionis x = 4, y = −3

Check: 5(4) + 3(−3) = 11

Nowyoutry

Alternatively,substituteintoequation [2]

Replace x withthenumber 4

Subtract 12 frombothsides,since 3 × 4 = 12

Dividebothsidesby 2.

Writethesolution.

Checkthesolutionwiththeotherequation.

Solvethesimultaneousequations 5x + 3y = 1 and 2x + 5y = 8,usingtheeliminationmethod.

9 Solvethefollowingpairsofsimultaneousequations, usingtheeliminationmethod.

3x + 2y = 6 and 5x + 3y = 11

3x + 2y = 5 and 2x + 3y = 5 b

2x + y = 4 and 5x + 2y = 10 c

2x + 5y = 7 and x + 3y = 4 d

HintforQ9:Whenmultiplyinganequation byanumber,multiplyeverytermonthe LHSandRHSbythatnumber.Always writetheinstructionformultiplying, e.g. [2]× 4. a

10 Solvethefollowingpairsofsimultaneousequations, usingtheeliminationmethod.

3x + 5y = 8 x −2y = −1

4x −3y = 0

3x + 4y = 25 c

HintforQ10:Choosetoeliminate x or y. Thecoefﬁcientsneedtobethesame size(with + or );e.g. −4x and 4x or −5y and 5y.Choosetoaddorsubtract theequationstoeliminateonevariable. a 2x + y = 10 3x −2y = 8 b

11 Solvethefollowingpairsofsimultaneousequations.

5x + 3y = 18 and 3y x = 0 a 3x y = 13 and x + y = −9 b

2x + 7y = −25 and 5x + 7y = −31 c 2x + 6y = 6 and 3x −2y = −2 d 4x −5y = −14 and 7x + y = −5 e 7x −3y = 41 and 3x y = 17 f

Problem-solving and reasoning

12–1512,13,16–18

Example43Solvingwordproblemswithsimultaneousequations(elimination) KathyisolderthanBlake.Thesumoftheiragesis 17 yearsandthedifferenceis 5 years.FindKathy andBlake’sages.

Solution

Explanation

Let k beKathy’sageand b beBlake’sage.Deﬁnetwovariables.

k + b = 17 [1]

k b = 5 [2]

Theﬁrstpieceofinformationis‘thesumoftheir agesis 17’.

Thesecondis‘thedifferenceis 5 andKathyis olderthanBlake’.

Continuedonnextpage

[1]+[2]: 2k = 22 k = 11

Substitute k = 11 into [1]: 11 + b = 17 b = 6

Addthetwoequationstoeliminate b or, alternatively,subtracttoeliminate k

Alternatively,substituteinto [2] Subtract 11 frombothsides. Kathyis 11 yearsoldandBlakeis 6 Answertheoriginalquestioninwords.

Nowyoutry

Thesumoftwonumbersis 97 andtheirdifferenceis 13.Findthetwonumbers.

12 AydenisolderthanTamara.Thesumoftheiragesis 56 yearsandthedifferenceis 16 years. UsesimultaneousequationstoﬁndAydenandTamara’sages.

Example44Problemsolvingwithsimultaneousequations

Reesepurchasesthreedaffodilsandﬁvepetuniasfromthelocalnurseryandthecostis $25 Giulianabuysfourdaffodilsandthreepetuniasandthecostis $26 Determinethecostofeachtypeofﬂower.

Solution

Let $d bethecostofadaffodiland $p bethecostofapetunia.

3d + 5p = 25 [1]

4d + 3p = 26 [2]

[1]× 4 : 12d + 20p = 100 [3]

[2]× 3 : 12d + 9p = 78 [4]

[3] [4] : 11p = 22 p = 2

Substitute p = 2 into [1]:

3d + 5(2) = 25

3d + 10 = 25 3d = 15 d = 5

Check: 4(5) + 3(2) = 26 true

Daffodilscost $5 andpetuniascost $2 each.

Nowyoutry

Explanation

Deﬁneyourvariables.

Threedaffodilsandﬁvepetuniasfromthelocal nurserycost $25 Fourdaffodilsandthreepetuniascost $26

Multiply [1] by 4 and [2] by 3 toobtaina matchingpair(12d and 12d).

Subtracttheequationstoeliminate d. Dividebothsidesby 2

Alternatively,substituteinto [2] Replace p withthenumber 2. Simplify.

Subtract 10 frombothsides. Dividebothsidesby 3

Checkyoursolutionsbysubstitutingintothe secondequation.

Answerthequestioninwords.

Jesspurchases 4 bucketsofchipsand 3 drinksfor $23.50,whileNigelpurchases 3 bucketsofchipsand 4 drinksfor $22.Findthepriceofabucketofchipsandadrink.

13 Amarketstallsellstwofruitpacks:

Pack 1 : 10 applesand 5 mangoes ($12.50)

Pack 2 : 15 applesand 4 mangoes ($13.50)

Deﬁnetwopronumeralsandsetupapairoflinear equationstoeventuallyﬁndthecostofeachfruit.

a Solvethetwosimultaneousequationstodeterminethe individualpricesofeachpieceoffruit.

b Determinethecostofoneappleandﬁvemangoes.

Ticketstoabasketballgamecost $3 forchildrenand $7 foradults.If 5000 peopleattendedthegameandthe

totaltakingsatthedoorwas $25000,determinethe numberofchildrenandadultswhoattendedthegame.

HintforQ14:Whatyouare beingaskedtoﬁndisoften howyoudeﬁneyourvariables.

AMathstestcontainsmultiple-choicequestionsworth 2 markseachand short-answerquestionsworth 3 markseach.Thetestisoutof 50 marks andthereare 22 questions.

a Deﬁnetwopronumeralstorepresentthenumberofeachquestiontype.

b Setuptwolinearequations.

c Solvethetwoequationssimultaneouslytodeterminethe numberofmultiple-choicequestions.

HintforQ15:Totalmarksis 50 Numberofquestionsis 22.

16 Let x and y betwonumbersthatsatisfythefollowingstatements.Setuptwolinear equationsaccordingtotheinformationandsolvethemsimultaneouslyto determinethenumbersineachcase.

a Theirsumis 16 buttheirdifferenceis 2

b Theirsumis 30 buttheirdifferenceis 10

c Twicethelargernumberplusthesmalleris 12 andtheirsumis 7

17 Findthevalueof x and y inthefollowingrectangles.Youwillneedtowritetwo equationsandsolveusingtheeliminationmethod.

3 5 x + 2y x + y

10 6 4x y 2x + 3y b

HintforQ17:Oppositesides ofrectanglesareequal.

18 Gordoniscurrently 31 yearsolderthanhisdaughter.In 30 years’timehewillbetwicehis daughter’sage.Using g forGordon’scurrentageand d forGordon’sdaughter’scurrentage, completethefollowing.

a Writedownexpressionsfor:

Gordon’sagein 30 years’time. i Gordon’sdaughter’sagein 30 years’time. ii

b Writedowntwolinearequations,usingtheinformationatthestart.

c SolvetheequationstoﬁndthecurrentagesofGordonandhisdaughter.

19 Usetechnologytosolvethesesimultaneousequations.

3x + 2y = 6 and 5x + 3y = 11 a

3x + 2y = 5 and 2x + 3y = 5 b

4x −3y = 0 and 3x + 4y = 25 c

2x + 3y = 10 and 3x −4y = −2 d

−2y −4x = 0 and 3y + 2x = −2 e

−7x + 3y = 22 and 3x −6y = −11 f

Nurse

Nursingisacareerthatisbothchallengingand rewarding.Itrequiresapersontobecaring andempathetic.Goodcommunicationskills,as wellasanunderstandingofmathematicsand science,arealsoimportant.

Nursesneedtobecompetentinmany mathematicalareas,includingfractions, ratios,convertingunitsofmeasurementand equations.Theymustbeabletocalculate medicaldosages,substituteintoequationsand alsoknowhowtoprogramthecorrectﬂow rateforintravenous(IV)drips.

Completethesequestionsthataretypicalofanurse’sjobadministeringmedication.

1 Usetheseformulastoanswereachofthefollowingquestions.

Volumerequired = strengthneeded strengthinstock × volumeofstocksolution

Numberoftablets = strengthrequired strengthpertabletinstock

Whatvolume,inmL,ofPethidineshouldbegivenifthepatientisprescribed

existingstockcontains 100 mgin 2 mL?

b Pethidine 50 mghasbeenorderedtoalleviateapatient’spain.Thestockstrengthis 75 mg/ 1.5 mL.HowmuchPethidineshouldbegiven?

Calculatethevolume,inmL,ofinsulinthatisrequiredforapatientwhohasbeenprescribed 60 unitsofthedrug,ifthestockis 100 units/1 mL.

Howmanytabletsdoesanurseneedtogiveforaprescriptionof 500 mgofamoxicillinperday, ifthestockavailableinthewardis 250 mgpercapsule?

Howmanytabletsareneededforadosageof 125 mg,ifthestockavailableislabelled 25 mg pertablet?

2 Paediatricsisabranchofmedicinedealingwithyoung children.Differentformulasareusedtocalculatethe dosessuitableforchildren.Applytherulesgivenbelow tocompletethefollowingcalculationsandstateeach answertothenearestmg.

Clarke’sbodyweightrule:

Child’sdose = weightofchild (kg) averageadultweight (70 kg) × adultdose

Clarke’sbodysurfacearearule:

Child’sdose = surfaceareaofchild (m2) averageadultsurfacearea (1.7 m2) × adultdose

Fried’srule(usedforinfantsunder 1 yearold):

Child’sdose = ageinmonths 150 × adultdose

Young’srule(usedforchildrenaged 2 to 12 years):

Child’sdose = ageinyears age + 12 × adultdose

UseYoung’sruletocalculatetheAmoxildoseneededfora 10-year-oldboy,iftheadultdoseofthe drugAmoxilis 250 mg.

UseClarke’sbodyweightruletoﬁndachild’sdoseforthedrugAmpicillin,giventhechild’sweight is 15 kgandanadult’sdoseis 500 mg.

UseFried’sruletocalculatethedoserequiredforan 8-month-oldbabygirlfor thedrugamoxicillan,giventhatanadult’sdoseis 500 mg.

UseClarke’sbodysurfaceareaformulatoﬁndthe doseofpenicillin,inmg,requiredforachildwhosesurface areais 8000 cm2,giventhattheadultdoseis 1 gram.

Hintforpart d: Recall 1 m2 = 10000 cm2

3 Drugsthataregivenwithanintravenous(IV)dripuseadifferentsetofequationstocalculatethetime neededorthedroprateperminute.

Time(inminutes) = volume(mL) ﬂowrate(drops/min) × dripfactor

Flowrate(drops/minute) = volume(mL) time(mins) × dripfactor

UsetheequationsabovetoanswerthesequestionsaboutIVdrugdosage.Thedripfactorisin drops/mL.Stateallanswersroundedtoonedecimalplace.

Findtheﬂowrate,indropsperminute,whena 1 2 litre

bagofsalinesolutionisrunover 4 hourswiththeIVmachine setatadripfactorof 20 dropspermL.

Hintforpart a:Recall 1 L = 1000 mL

a AnIVdripofsalinesolutionstartedat 4:15 p.m.Tuesday.Themachinehas 700 mLtorunandisset at 40 drops/minwithadripfactorof 18 dropspermL.AtwhattimewilltheIVbeﬁnished?

b Howlongwillittake 180 mLofzeronegativebloodtoﬂowthroughanIVat 36 drops/minute whenthebloodsupplymachineissetatadripfactorof 15 drops/mL?

Usingtechnology

4 SetupthisExcelworksheettocalculatetheendingtimesofintravenousdripsforvariouspatients.You willneedtocopythegivendataandenterformulasintotheshadedcells.

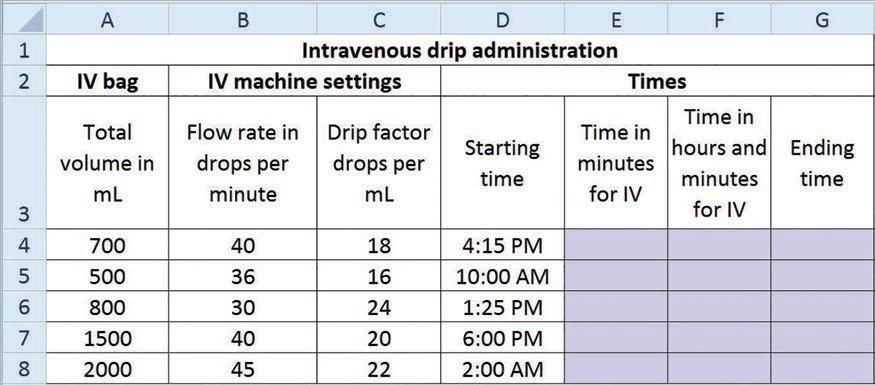
HintforQ4:

• Formatstartingandendingtimesas Number Category:Custom,Type:h:mmAM/PM

• Tocalculatetimeinhoursandminutes,divide thetimeinminutesbythenumberofminutes in 24 hours,andformatcellsas NumberCategory: CustomandType:h:mm

Movietheatrepricing

Asmallboutiquemovietheatreisopeningsoonandwillbepublishingadultandchildticketpriceson itswebsite.Aftersomeanalysis,theownerdecidestomakethefollowingassumptions:

• Thesumofthecostofachildticketandanadultticketwillbe $30

• 40 childrenand 25 adultsareexpectedtoattendeachevening. Presentareportforthefollowingtasksandensurethatyoushowclearmathematicalworkings, explanationsanddiagramswhereappropriate.

1Preliminarytask

a Ifthecostofachildmovieticketis $6,ﬁndthecostofanadultticket.

b Findtherevenue(totalamountearned)forthemovietheatreononeparticulareveningusing theassumptionthat 40 childrenand 25 adultsattendandachildticketis $6

c Solvethefollowingsimultaneousequations.

Usetheeliminationmethod,orrewritetheﬁrstequationandusethesubstitutionmethod.

2Modellingtask

Formulate Theproblemistodetermineasuitablepricefortheadultandchildticketstoachievearevenueofat least $1000

a Writedownalltherelevantinformationthatwillhelpsolvethisproblem.

b Using $a forthecostofanadultticketand $c forthecostofachildticket.Determinethe equationsfor,

Thesumofthecostofachildticketandanadultticketwillbe $30 i Therevenue($R)if 40 childrenand 25 adultsattendononeparticularevening. ii Ifthetotalrevenue, R,fortheeveningis $900,substitutethisintotheequationaboveto formanewequation,relating a and c iii

c Solvethetwosimultaneousequationsinpart b toﬁndthecostofoneadultticketandone childticket.

d Bychangingthevalueof R intheequationforrevenueinpart bii,solvetwosimultaneous equations,and,ﬁndthecostofanadultticketandachildticketiftherevenueis:

$825 i $960 ii $984 iii $1086 iv

e Explorethefollowingspecialcasesforthetotalrevenueearnedanddecideiftheyrepresent reasonablepricingstructures.Writeasentencedetailingifyouthinkthateachrevenueresults inagoodpricingstructure.

$975 i $765 ii

Evaluate and verify

f Explorethepossibilityoftherevenuebeing $1200 basedontheassumptionsmadebythe company.Explainwhyyoureachedyourconclusion

g Isitreasonableforthecompanytoassumetheycanearnover $1000 eacheveningwiththeir otherassumptions?

h Summariseyourresultsbycompletingatablesuchastheonebelow.

Equation 1 Equation 2

3Extensionquestion

a Considerusinganonlinegraphingtool,suchasDesmosorGeogebra,toshowhowgraphscan beusedtosolvetheproblemreplacingthe a with x andthe c with y

b Ifthesumofthecostofachildticketandanadultticketischangedto $40,doyouthinkitwould bereasonabletoexpectthatmorethan $1000 revenuecanbeearnedeachevening?Explainyour choicesandcalculationstojustifyyouranswer.

Solvingequationsnumerically

Keytechnology:Graphingsoftwareandspreadsheets

Weknowthatwecanusealgebraictechniquestosolve linear,quadraticandevenexponentialequations;however, inmanysituationssuchtechniquesdonotworkorare toocumbersometodealwith.Insuchcasesanumerical techniquecanbeusedwherewerepeatedlymovecloser andclosertothesolutionuntiladesiredlevelofaccuracy isreached.Technologycanhelpusachievethesenumerical stepsandﬁndaccuratesolutions.

1Gettingstarted

Wewillstartbylookingatthesolutiontothelinearequation 7(2x −1) −5 = 0.Byhand,wecould solvethisbyexpandingandusingthebalancemethod;however,inthiscasewewilluseanumerical approachby‘zoomingin’tothesolution.

a Findthevalueof 7(2x −1) −5 forthefollowingvaluesof x x = 0 i x = 0.5 ii

b Whichvalueof x frompart a givesavalueof 7(2x −1) −5 whichisclosestto 0?

c Tryothervaluesof x between 0 and 1 andtrytoﬁndasolutiontotheequation 7(2x −1) −5 = 0 correcttoonedecimalplace.

d Tryothervaluesof x between 0 and 1 andtrytoﬁndasolutiontotheequation 7(2x −1) −5 = 0 correcttotwodecimalplaces.

2Usingtechnology

a Constructaspreadsheetwhichevaluates 7(2x −1) −5 forvariousvaluesof x.Useincrementsof 0.1 as shown.

b FilldownfromthecellsA4 andB3.Forwhichvalueof x is 7(2x −1) −5 closesttozero?

c Anothermethodforzoomingin onasolutionistouseagraphof y = 7(2x −1) −5 andlookatwhere y = 0.Usegraphingsoftwarelike Desmostosetupagraphwhich focusesonthepointswhere y = 0

d Placepointsattheplacewhere y = 0 Bylookingatthegraphyoucan seethatthesolutionisbetween 0.8 and 0.9

3Applyinganalgorithm

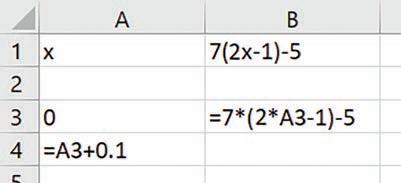
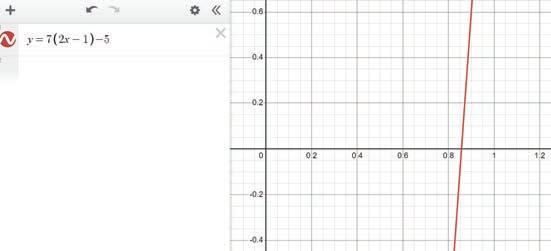
Toobtainevenmoreaccuratesolutionstothepreviouslinearequationwecanzoomincloserusingthe spreadsheetorgraph.

a Usethisalgorithmwithyourspreadsheettoﬁndthesolutionofthelinearequation.

• Step 1:AltertheformulaincellA4 sothattheincrementissmaller.e.g. 0.01 ratherthan 0.1

• Step 2:Filldownuntilyouhavelocatedthevalueof x forwhich 7(2x −1) −5 isclosesttozero.

• Step 3:AdjustcellA3 toadifferentvaluesoyoudon’tneedtoscrollthroughsomanycells.

• Step 4:RepeatfromStep 1 butusesmallerandsmallerincrements(0.001 and 0.0001)untilyou havefoundthevalueof x forwhich 7(2x −1) −5 isclosesttozero,correcttothreedecimal places.

b Usethefunctionsofyourgraphingsoftwaretozoomintothepoint where y = 0.Usethescaletohelpﬁndthesolutiontotheequation. Keepzoominginuntilyouaresatisﬁedthatyoursolutioniscorrect tothreedecimalplaces.

0.8570.858

Puzzles and games

1 Inthismagicsquare,eachrowandcolumnaddstoasumthatisanalgebraicexpression.Complete thesquaretoﬁndthesum.

2 Theanswerstotheseequationswillformamagicsquare,whereeachrow,columnanddiagonal willaddtothesamenumber.Drawa 4 by 4 squareforyouranswersandcheckthattheydomake amagicsquare.

3 Writeanequationandsolveittohelpyouﬁndeachunknownnumberinthesepuzzles.

a Three-quartersofanumberplus 16 isequalto 64

b Anumberisincreasedby 6,thenthatanswerisdoubledandtheresultisfourmorethantriple thenumber.

c Theaverageofanumberanditstripleisequalto 58.6

d In 4 years’time,Ahmed’sagewillbedoubletheagehewas 7 yearsago.Howoldis Ahmednow?

4 Byapplyingatleasttwooperationsto x,writethreedifferentequationssothateachequationhas thesolution x = −2.Verifythat x = −2 makeseachequationtrue. Forexample, 3 × (−2) + 10 = 4,soonepossibleequationwouldbe 3x + 10 = 4

5 Writetwosetsofsimultaneousequationssothateachpairhasthesolution x = 3, y = −2

6 WhichAustraliancityhasitscentreontheintersectionoftheWarregoHighwayandtheNew EnglandHighway?

Todecodethispuzzle,solvetheinequalitiesandsimultaneousequationsbelow,andmatchthem toanumberlineorsolution.Placethecorrespondinglettersabovethematchingnumberstoﬁnd theanswer.

Solvetheseinequalitiesandmatchthesolutiontoanumberline(1 3).

Solvethesesimultaneousequationsandmatchtothesolution(4 6). 3

7 JulesandEnzoareparticipatinginalong-distancebikerace.Julesridesat 18 km/handhasa 2 hourheadstart.Enzotravelsat 26 km/h.

a HowlongdoesittakeforEnzotocatchuptoJules?(Use:Distance = speed × time.)

b HowfardidtheybothridebeforeEnzocaughtuptoJules?

8 Emilytravelledadistanceof 138 kmbyjoggingfor 2 hoursandcyclingfor 5 hours.Shecould havetravelledthesamedistancebyjoggingfor 4 hoursandcyclingfor 4 hours.Findthespeed atwhichshewasjoggingandthespeedatwhichshewascycling.

Puzzles and games

Expanding

a (b + c ) = ab + ac

a (b c ) = ab ac

e.g. 2(4x + 3) = 8x + 6 3x (2x y ) =−6x 2 + 3xy

Simplifying expressions

Add/subtract like terms only. Like terms have the same pronumeral factors.

e.g. 3x and 7x, 2xy and 4yx , not 2x and x 2 or 3y and 4xy For example, 3x + 2y x + 7y = 3

Multiply/Divide

Algebraic expressions

Algebra

Adding/subtracting algebraic fractions

Find the lowest common denominator and combine.

e.g.LCD is 6.

Factorising

This is the opposite of expanding Factorised form Expanded form = 2x Look for highest common

2x 2 6x = −2x (x + 3)

7 is the coefﬁcient of 4 is the coefﬁcient of

4 terms 3 is the constant term. x y.

Multiplying/dividing algebraic fractions

Multiply: Cancel common factors in factorised form and then multiply.

e.g.

Divide: Multiply by the reciprocal of the fraction following the ÷ sign.

Reciprocal of is . a b b a = 12x 3(x + 4) 2 8x x + 4 × 1 1 1 4 3xy + 7x 4y + 3

Solving linear equations that have brackets and pronumerals on both sides

• Expand all brackets.

Solving linear equations

the value that makes an Solving involves ﬁnding equation true.

Equations with fractions

e.g.

2 = 7 3x 4

3x 4

• Collect like terms on each side of the equation.

• Collect terms with a pronumeral to one side (usually the LHS).

• Solve for unknown.

e.g.

12(x + 1) 2(3x 3) = 4(x + 10)

12x + 12 6x + 6 = 4x + 40

6x + 18 = 4x + 40

2x + 18 = 40 2x = 22 x = 11

e.g. 2x + 5 = 9 2x = 4 (subtract 5) x = 2 (divide by 2)

Equations

Formulas

e.g. A = πr , C = 2πr

An unknown value can be found by substituting values for the other variables.

3x = 36 (× 4 both sides)

x = 12 (÷ 3 both sides)

e.g. = 7

2x 5 3

2x 5 =× 3 to both sides)

=+ 2 to both sides) 9 (ﬁrst 21 (ﬁrst

2x = 26 (+ 5 to both sides)

x = 13 (÷ 2 to both sides)

A formula can be rearranged to make a different variable the subject; i.e. the variable is out the front on its own.

e.g. E = mc 2 m when , ﬁnd E = 320 and c = 4.

320 = m × 4 2 (substitute values)

320 = 16 m

20 = m (divide both sides by 16)

m = 20 (Write the answer with m on the left.)

Inequalities

These are represented using >, <, ≥, ≤ rather than =

e.g. x > 2

2 not included

34 x 2 01 1

e.g. x ≥ 2 2 is included

34 x 2 01 1

Solving inequalities uses the same steps as solving equations, except when multiplying or dividing by a negative number. In this case, the inequality symbol must be reversed.

e.g. 4 2x > 10 ( 4)

2x > 6 (÷ 2) x < 3 (reverse symbol)

Solving word problems

Deﬁne variable(s).

2 Set up equation(s).

3 Solve equation(s).

4 Check each answer and write in words.

Simultaneous equations

Use substitution or elimination to ﬁnd the solution that satisﬁes two equations.

Substitution

e.g. 2x + y = 12 [1] y = x + 3 [2]

In [1] replace y with [2]: 2x + (x + 3) = 12 3x + 3 = 12 3x = 9 x = 3

Sub. 3 to ﬁnd y x = In [2] y = 3 + 3 = 6

Solution is x = 3, y = 6

Elimination

Ensure both equations

have a matching pair. Add two equations if matching pair has different sign; subtract if same sign.

e.g. x + 2y = 2 [1] 2x + 3y = 5 [2] [1] × 2: 2x + 4y = 4 [3] [3] [2]: y =−1

In [1]: x + 2( 1) = 2 x 2 = 2 x = 4

Solution is x = 4, y = −1

Chapterchecklist

AversionofthischecklistthatyoucanprintoutandcompletecanbedownloadedfromyourInteractiveTextbook.

3A 1 Icanidentifythepartsofanalgebraicexpression.

e.g.Fortheexpression 4a + 3b −7,statethe: a numberofterms b constantterm c coefﬁcientof b

3A 2 Icanformanalgebraicexpression. e.g.Writeanalgebraicexpressionfor:

a 3 morethan 2 lotsof a b theproductof x and y,dividedby 2

3A 3 Icanevaluateanalgebraicexpressionusingsubstitution.

e.g.If x = 2, y = 5 and z = −3,evaluate: a xy + 2z b y2 xz

3B 4 Icanidentifyliketerms.

e.g.Writedowntheliketermsinthefollowinglist:

3B 5 Icancollectliketerms.

e.g.Simplify:

a 5b + 4b −2 b 4xy + 3x −5xy + 3x

3B 6 Icanmultiplyanddividealgebraicterms.

e.g.Simplify:

a 3a × 5ab b 9xy ÷ (18x)

3C 7 Icanexpandexpressionswithbrackets. e.g.Expandthefollowing.

a 4(3x −2) b −2y(5x −7y)

3C 8 Icansimplifyexpressionsbyremovingbrackets.

e.g.Expandandsimplify 3(2x + 5) −2(x + 2)

3D 9 IcandeterminetheHCF. e.g.DeterminetheHCFofthefollowing.

a 6x and 24x b 8ab and 20b2

3D 10 Icanfactoriseexpressionswithcommonfactors. e.g.Factorisethefollowing. a 8a + 12 b 6

3E 11 Icansimplifyalgebraicfractions.

e.g.Simplifythisfractionbyfactorisingﬁrst: 4x −12 x −3

3E 12 Icanmultiplyalgebraicfractions.

e.g.Simplifythisproduct: 3(x −2) 4x × 10x x −2.

(includingcommonnegative)

3E 13 Icandividealgebraicfractions.

e.g.Simplify 5x2 9 ÷ 10x 3 .

3F 14 Icanaddandsubtractsimplealgebraicfractions.

e.g.Simplify 3x 4 x 16

3F 15 Icanaddandsubtractwithbinomialnumerators.

e.g.Simplify x + 2 4 x 10

3G 16 Icansolvesimplelinearequations. e.g.Solvetheselinearequations. 2x −1 = 7 a x + 4 2 = 12 b

3G 17 Icansetupandsolvewordedproblemsusinglinearequations. e.g. 5 lessthantwiceanumberisequalto 31.Findthenumber.

3H 18 Icansolveequationswithbrackets.

e.g.Solve 3(x −2) = 21

3H 19 Icansolveequationswithvariablesonbothsides.

e.g.Solve 5x −2 = 3x + 6.

3H 20 Icansolvemorecomplexequationswithfractions.

e.g.Solve 2x −1 4 = −1

3H 21 Icansetupandsolveanequationwithbracketsfromarealsituation. e.g.Findthevalueof x iftheareaofthistriangleis 32 m2 4 m (x – 2) m

3I 22 Icansubstituteintoaformulaandsolveforavariable.

e.g.If A = h 2 (a + b) and A = 20, h = 4 and b = 3 ﬁndthevalueof a

3J 23 Icanillustrateaninequalityonanumberline.

e.g.Represent x > −2 onanumberline.

3J 24 Icansolveasimpleinequality.

e.g.Solve 3x −2 > 7

Chapter checklist

3J 25 Icansolveaninequalitywhenthepronumeralhasanegativecoefﬁcient. e.g.Solve 6−3x Å 18

3K 26 Icanusethemethodofsubstitutiontoﬁndthesolutiontoapairof simultaneousequations.

e.g.Solvethesimultaneousequations y = x −2 and 2x + 3y = −1 usingthesubstitutionmethod.

3K 27 Icanusethemethodofsubstitutiontoﬁndasolutiontoarealproblem involvingsimultaneousequations.

e.g.Jonahis 9 yearsolderthenPennyandtheircombinedagesis 47.Findtheirages.

3L 28 Icanusethemethodofeliminationtoﬁndthesolutiontoapairof simultaneousequations.

e.g.Solvethesimultaneousequations x + y = 1 and 4x + 3y = 5 usingtheeliminationmethod.

3L 29 Icanusethemethodofeliminationtoﬁndasolutiontoarealproblem involvingsimultaneousequations.

e.g.Jillbuys 5 pensand 2 pencilsfromherfavouritestorefor$13,whileMichaelbuys 4 ofthe samepensand 3 ofthesamepencilsfromthesamestorefor$12.50.Findthecostofthispenand pencilfromthisstore.

Short-answerquestions

1 3A Considertheexpression 3xy −3b + 4x2 + 5

a Howmanytermsareintheexpression?

b Whatistheconstantterm?

c Statethecoefﬁcientof: x2 i b ii

2 3A Writeanalgebraicexpressionforthefollowing.

a 3 morethan y

b 5 lessthantheproductof x and y

c thesumof a and b isdividedby 4

3 3A Evaluatethefollowingif x = 3,

4 3B Simplifythefollowingexpressions.

5 3C Expandthefollowingandcollectliketermswherenecessary.

6 3D Factorisethefollowingexpressions.

(includethecommonnegative) d

7 3F Simplifythefollowingalgebraicfractionsinvolvingadditionandsubtraction.

8 3E Simplifythesealgebraicfractionsbyﬁrstcancellingcommonfactorsinfactorisedform.

9 3G Solvethefollowing.

4a = 32 a m 5 = −6 b

x +

10 3H Solvethefollowingbyﬁrstexpandingthebrackets.

) =

11 3H Findthevalueof p inthefollowing.

12 3H Writeanequationforthefollowingandthensolveit. Sixtimesanumberequals 420.Whatisthenumber? a Eightmorethananumberequals 5.Whatisthenumber? b Anumberdividedby 9 gives 12.Whatisthenumber? c Sevenmorethananumbergives 3.Whatisthenumber? d

13 3I

Thesumofanumberand 2.3 equals 7.Whatisthenumber? e

For A = 1 2 hb,ﬁnd b when A = 24 and h = 6 a

For V = lwh,ﬁnd w when V = 84, l = 6 and h = 4. b

For A = x + y 2 ,ﬁnd x when A = 3.2 and y = 4 c

For E = mc2,ﬁnd m when E = 40 and c = 2 d For F = 9 5 C + 32,ﬁnd C when F = 95 e

14 3J Writetheinequalitydisplayedoneachofthefollowingnumberlines.

15 3J Solvethefollowing.

x + 8 Å −10 a 2x + 6 > 10 b m −6 Å 4 c −6x Ä 12 d 8− x Ä 10 e 5− x 3 > 2 f

16 3K Solvethesimultaneousequationsusingthesubstitutionmethod.

y = 5x −13

2x + 3y = 12 a

y = x −1

y = 3x −11 b

17 3L Determinethesolutionofthefollowingsimultaneousequations,usingtheelimination method.

2x + 7y = −25

5x + 7y = −31 a

x −2y = 0 b

3x + 2y = 8

x + 3y = 8

4x + 5y = 11 c

18 3L Thesumoftwonumbersis 15 andtheirdifferenceis 7.Usesimultaneousequationstoﬁnd thetwonumbers.

19 3L Amoneyboxcontains 20 centand 50 centcoins. Theamountinthemoneyboxis $50 andthereare 160 coins.

a Deﬁnetwovariablesandsetupapairoflinear equations.

b Solvethetwosimultaneousequationsto determinethenumberof 20 centand 50 cent coins.

20 3K Therearetwiceasmanyadultsaschildrenatalocalgrandﬁnalfootballmatch.Itcosts $10 foradultsand $2 forchildrentoattendthematch.Ifthefootballclubcollected $1100 attheentrancegates,howmanychildrenwenttoseethematch?

Multiple-choicequestions

1 3A Thecoefﬁcientof x in 3xy −4x + 7 is:

2 3B Thesimpliﬁedformof

3 3C Theexpandedformof

4 3D Thefullyfactorisedformof

5 3E Thesimpliﬁedformof 2(x + 1)

is:

6 3F Thesumofthealgebraicfractions 3x 8 + x 12 is: x 5 A x

7 3H Tosolvetheequation 3(2x + 4) −4(x + 2) = 6,youwouldﬁrst:

dividebothsidesby 12 A expandthebrackets B subtract 6 frombothsides C multiplybothsidesby 6 D add 4(x + 2) tobothsides E

8 3G Anumberisincreasedby 6 andthendoubled.Theresultis 36.Thistranslatestotheequation: 6x + 2 = 36 A 2x + 6 = 36 B 2(x + 6) = 36 C 2(x −6) = 36 D x + 12 = 36 E

9 3H If 4a −6 = 2a,then a equals: −1 A 1 B 6 C 3 D −3 E

10 3J x Ä 4 isasolutionto:

x + 1 < 3 A 3x −1 Ä 11 B x 2 −1 Å 0 C x −1 Å 1 D x Ä −4 E

11 3J Whichnumberlineshows x + 4 < 6?

12 3H Thesolutionto 5x 9 −4 = 1 is: x = 6 A x = −9 B x = −5 C

x = 9 D x = 5 E

13 3H Thesolutionto 3(x −1) = 12 is:

x = −1 A x = 2 B x = 0 C

x = 5 D x = 4 E

14 3K Thesimultaneousequations y = 3x and x + y = 4 havethesolution:

x = 1, y = 3 A

x = 3, y = 1 B

x = 2, y = 6 C

x = 2, y = 2 D

x = −1, y = 5 E

15 3K Substituting y = x −1 into x + 2y = 3 gives: x −2x −2 = 3 A x + 2y −2 = 3 B x x −1 = 3 C x + 2x −1 = 3 D x + 2(x −1) = 3 E

16 3L Adding x + y = 3 to x y = 4 gives: 2x −2y = 7 A 2x = 7 B x = 7 C y = 7 D 2y = 7 E

Extended-responsequestions

1 Aroominahousehastheshapeanddimensions,inmetres,shown.All linesmeetat 90°

a Findtheperimeteroftheroom,infactorisedform.

b If x = 3,whatistheroom’sperimeter?

c Iftheperimeteris 27 m,whatisthevalueof x? Theﬂooroftheroomistoberecarpeted.

d Givetheareaoftheﬂoorintermsof x andinexpandedform.

e Ifthecarpetcosts $20 persquaremetreand x = 3,whatisthecostoflayingthecarpet?

2 Twocomputerconsultantshaveanup-frontfeeplusanhourlyrate.Rhyscharges $50 plus $70 per hour,whereasAgnescharges $100 plus $60 perhour.

a Using $C forthecostand t hoursforthetime,writearuleforthecostofhiring: Rhys i Agnes ii

b IfAgnescharges $280,solveanequationtoﬁndhowlongshewashiredfor.

c Usethealgebraicmethodofsubstitutiontosolvethesimultaneousequationsandﬁndthe numberofhoursforwhichthecostisthesameandwhatthiscostis.