13. Multiplicación de polinomio por polinomio

Multiplicaciónde polinomio por polinomio

Información del libro: Para multiplicar dos polinomios se multiplica casa uno de los términos del primer polinomio por cada uno de los términos del segundo polinomio, aplicando la leyes para multiplicación de monomios. Finalmente se reducen los términos semejantes.

Información de google: Multiplicar polinomios implica aplicar las reglas de los exponentes y la Propiedad Distributiva para simplificar el producto. Esta multiplicación también puede ilustrarse con un modelo en área y puede ser útil al modelar situaciones del mundo real. Entender los productos de polinomios es un paso importante para factorizar y resolver ecuaciones algebraicas.

El Producto de un Monomio y un Polinomio Otra forma de efectuar {productos entre ´polinomios es colocado uno debajo del otro después de ordenarlos. Luego se multiplica términos a términos, se escribe cada producto de tal manera que queden columnas de términos semejantes, por último se reduce dichos términos.

La Propiedad Distributiva puede ser usada para multiplicar un polinomio por un monomio Sólo recuerda que el

monomio debe ser multiplicado por cada término en el polinomio.

Considera la expresión 2x(2x 2 + 5x + 10).

Esta expresión puede ser modelada con un esquema como el mostrado abajo. Este modelo se llama modelo de área porque las piezas rectangulares representan el área

2x

4x 3

10x 2

20x

Podemos ver que el producto del ancho, 2x, y el largo, 2x 2 + 5x + 10,

es el área de toda la región sombreada. El área puede dividirse en tres piezas más pequeñas. Cada una de esas piezas tiene un ancho de 2x y el largo está representado por uno de los términos del polinomio.

Los modelos de área son una manera útil de visualizar un problema de multiplicación. Pero también podemos encontrar el producto de dos polinomios algebraicamente, Ejemplos míos:

Vamos a multiplicar el binomio 2x+32x+3 por el monomio 4x4x. Para ello, multiplicamos 2x2x por 4x4x y 33 por 4x4x:

El producto 2x⋅4x2x⋅4x se simplifica multiplicado sus coeficientes y sumando los

Que la Propiedad Distributiva dice que multiplicar una suma por un número es lo mismo que multiplicar cada sumando por el número y luego sumarlos: a(b + c) = ab + ac. No

Importa cuántos términos haya: a(b + c + d) = ab + ac + ad.

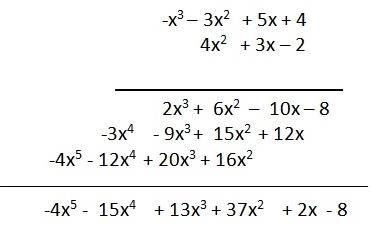
Ejemplo:

exponentes de sus partes literales (1 y 1):

Hacemos lo mismo con el producto 3⋅4x3⋅4x (ahora los exponentes son 0 y 1):

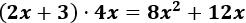
Por tanto, el producto calculado