11. Sustracción de polinomios

Información del libro:

La sustracción de polinomios se realiza escribiendo la suma del primer polinomio y el opuesto del segundo polinomio. Luego se reducen términos semejantes. Información de google: Para realizar una resta de polinomios, es necesario

Ejemplos:

La sustracción es la operación inversa de la suma. Si se tiene:

a __ b = a + __ b Apliquemos este concepto al siguiente ejercicio en el cual hay una sustracción o resta.

p(x) = 3 x 2 + 2 x 5 –5 x p(x) –q(x) = p(x) + –q(x)

q(x) = 6 x 5 –8 x + 4 x 2

agrupar los monomios (las expresiones de un único término) de acuerdo a sus características y proceder a la simplificación de aquellos que resultan semejantes. La operación en sí se realiza sumando el opuesto del sustraendo al minuendo.

El primer paso consiste en reemplazar los polinomios en la operación dada. p(x) __ q(x) = 3 x 2 + 2 x 5 __ 5 x __ [ 6 x 5 __ 8 x + 4 x 2 ] A continuación se aplica la propiedad de la operación inversa de la adición y, eliminando el paréntesis, se cambian los signos del polinomio que está a la derecha del signo menos.

3 x 2 + 2 x 5 __ 5 x __ [ 6 x 5 __ 8 x + 4 x 2 ]

3 x 2 + 2 x 5 __ 5 x + __ [ 6 x 5 __ 8 x + 4 x 2 ] 3 x 2 + 2 x 5 __ 5 x + __ 6 x 5 + 8 x __ 4 x 2

El tercer paso consiste en ordenar los polinomios de acuerdo a su grado decreciente o creciente y reducir los términos semejantes. Si hay una resta se procede a utilizar la propiedad anteriormente citada (en este

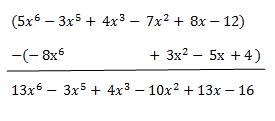
Caso hay que cambiar el

Ejemplos míos:

Signo de resta que está delante del 4 x).

2 x 5 + __ 6 x 5 + 3 x 2 __ 4 x 2 + __ 5 x + 8 x 2 x 5 + __ 6 x 5 + 3 x 2 + __ 4 x 2 + __ 5 x + 8 x Podemos comprobar que:

2 + __ 6 = __ 4, Que

3 + __ 4 = __ 1 y que

__ 5 + 8 = 3, Para quedar:

= __ 4 x 5 __ x 2 + 3 x