1.8.4 - Relativistic Mechanics and the Unified Field
The form defining the Unified Field yields powerful physics right out of the gate. For instance, physics struggles to explain the location of the antimatter from the universe’s birth, where antimatter has the property of being opposite in charge to its matter partner. If antimatter and matter were to collide, they would mutually annihilate, producing intense energy in the process. Far-fetched explanations have been proposed, e.g., it has been said that an asymmetry existed at the moment of the universe’s birth, favoring the numbers of matter versus antimatter. These kinds of explanations are a direct affront to the net-zero principle, and, for this reason, they are in no way valid. Examples of matter/antimatter pairs are the electron/positron (�, �), and the proton/antiproton (�, �), where we use the bar convention over the particle to denote antimatter. Mathematically, antimatter rotates in the opposite direction on the infinite sphere of tangent spaces comprising the Unified Field, which are the vacuum singularities at the Planck scale. Matter and antimatter share a mutual boundary on these infinite spheres of tangent spaces, but move around in opposite directions, accounting for the dynamics of the virtual particles of the vacuum. Exponentiation yields a radial extension away from the boundary of the singularity that can move inward or outward depending on the magnitude of the real-valued component. We present generalized mathematical terms for form as �, and � as its anti-form partner. In �-dimensions, the Lie algebra for the form is defined as �(�) = �(� + ��), and the anti-form
Exponentiation of the Lie algebra of the form yields
and for the anti-form
and for � ≠ 0, the radial component of ���5�(�)6 will be less than one, while the radial component of
greater than one. The pair represents the symmetric splitting of the identity element, and mutual annihilation occurs if the form/anti-form pair collides, given the result of their product
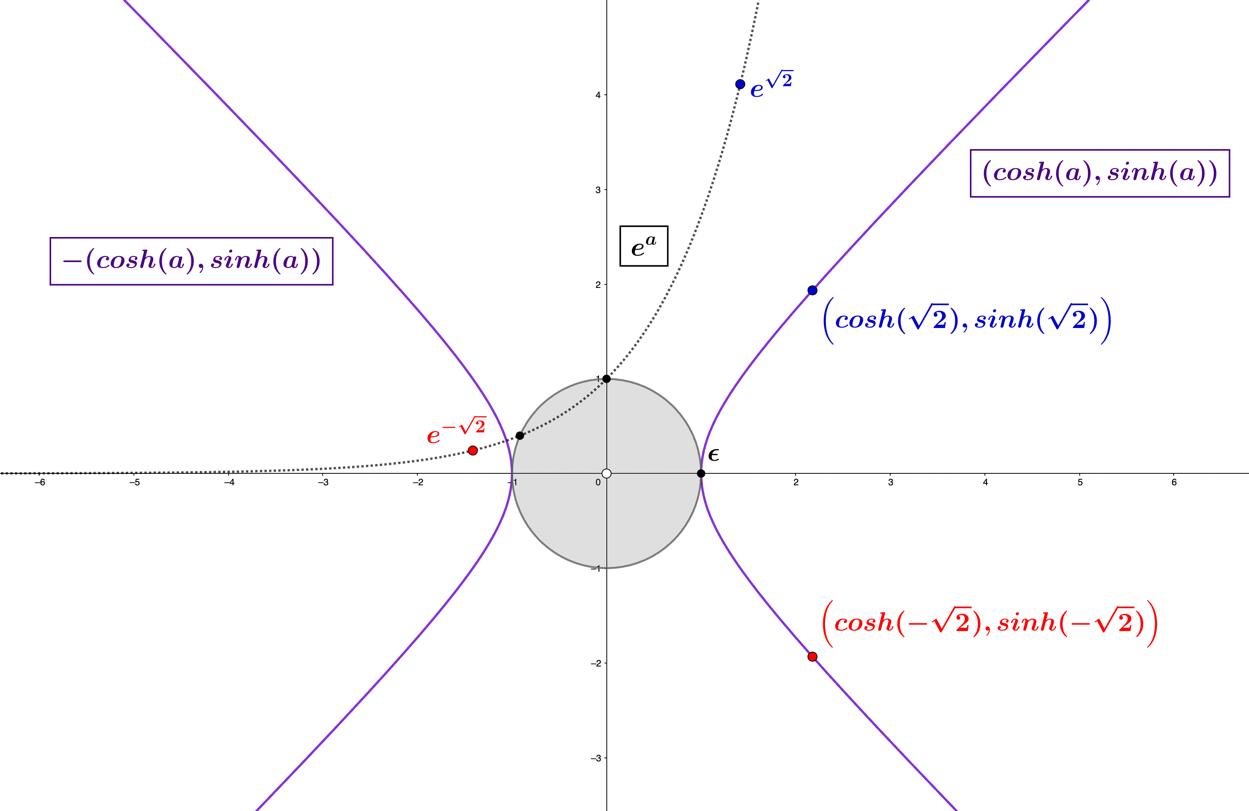
Mathematically, the answer to the question of antimatter’s whereabouts is that it is present in the Unified Field; only it exists at radial distances of the Plank length and below. Important to realize is that the distance from zero to the Plank length holds just as much information as the distance of the Plank length to infinity does. Depicted in the following figure, we show a plot of the function � % for � ∈ ℝ, which adheres to the net-zero principle given that it is a symmetric split of the zerodimensional identity, unitary in volume and located at the function’s vertical intercept.
The real exponential portion � % of the anti-form expression
= � $ = � % � &' is inversely proportional to its form counterpart � % . But it is critical to envision that when bound to the spacetime geometry of the hyperbolae, the magnitude of the radial extension from the origin is equal in the parametric representation (���ℎ(�) , ���ℎ(�)), � ∈ ℝ, depicted in Figure 1.8.6, for � = ±√2. Limiting this concept to only matter and antimatter obscures the true nature of mathematics at work. Extending the terminology to form and anti-form is the appropriate conceptual treatment, given that matter and antimatter are one manifestation of the multi-faceted Unified Field Antimatter must have all the accouterments that matter does, including the geometric space it sits in, forces, and relativistic implications of its mass, to name just a few. So, the mathematical framework which defines anti-form is as complete and flawless as its form counterpart.
Next, we consider a form in the guise of a flowing point in spacetime as the expression, ���5�(�)6 = � � = � , � &, (1 8 74) where � &- represents the form’s wave properties, and � , represents the radial extension beyond the Plank distance of the unit singularity’s boundary and encodes its relativistic properties. Lie algebras that are not axis-based, meaning solely real or imaginary, will cease to be located on the unit singularity’s boundary once exponentiated.
We define the following Lie algebra, Α, as
, representing the hyperbolic Lie algebra, and
as
, representing the imaginary spherical Lie algebra. Given that the algebras commute,
=
the following expressions are equal
which represents the product of two generators, one hyperbolic and the other complex spherical. The product
be expressed in terms of hyperbolic functions
or the circular trigonometric functions
The energy-momentum relation in physics is defined as
which holds for a system or a body, for the momentum �, the speed of light �
mass In spacetime, all massive bodies must have some motion, but with the ideological case of a massive body at rest, the energy-momentum relation reduces to the well-known energy-mass equivalence
and for massless particles, the relation simplifies to
The energy-momentum relation of a massive object is related to the Lorentz factor by the expression
and the scalar momentum, |�|, is defined as
Using the hyperbolic Lorentz factor equivalence, we find
The scalar momentum, |�|, is related to the hyperbolic
Considering how the two hyperbolic functions relate to relativistic mechanics leads to the following relativistic equivalence for the exponential function
and solving for energy, we find
We again consider the idealistic case for a massive object at the rest ideal (� = 0), where the energy relation becomes � = �* � 0 . After substituting this relation into the expression above, we find
and given that � = 0, we have that
Returning to the hyperbolic generator, � . , from our generator product,
we substitute our relativistic equivalences, yielding
� (�* � 0 ) ⁄ term out, gives us
The matrix product above is a form representing a flowing point in spacetime and will have an inverse anti-form counterpart, representing a flowing anti-point in anti-spacetime, found by the evaluation of the following inverse
The result above can be expressed as the matrix product � . � &/ , and by substituting the relativistic terms into the product, we arrive at the inverse matrix � (.!&/)
where the anti-form counterpart contains the inverse and hyperbolically derived relativistic factor
With matrix representations for
With this result, the relativistic energy of our generator product simplifies to
which given �1 � 0 is a scalar value, it can be moved to the left-hand side of the �-matrix, ultimately, we find a result consistent with our initial relativistic energy equivalence � =
generator product, the energy of an idealized massive object system, for
which is consistent with the expected result from relativistic mechanics.
To consider the relativistic energy-momentum for the generator product of a system comprised of a massless object, we first take the � = ���ℎ(�) function identity
Next, we multiply the matrix by the scalar-valued
terms will cancel, leading to the energy matrix, �,
For a system comprised of a massless object, the invariant mass will be equal to zero, �
= 0, and solving each entry in the � matrix above for our massless object system
we find the previously defined result energy-momentum identity
the energy matrix result has the consistent form
The matrix solution above for � is the result of the energy-momentum relationship � = p(��)0 + (�* � 0)0 , and taking (solely) this approach obscures the fundamental relationship that exists between energy and the spherical and hyperbolic geometries. For this reason, we start by considering the �
matrix
As we have seen previously, an isolated generator-coordinate system will evolve in time due to the generator operating on itself through its successive powers. We define a spherical time variable � to represent a mathematical calculative progression. Then, we can express the evolution of the calculative/spherical time-dependent generator system as
which will have the following matrix form
� is the wavenumber and � is the speed of light This equivalence can be seen by starting with the
identity
where the product of the wavelength � and the frequency � equals � The angular frequency, �, is related to frequency as
the wavenumber, �, to the wavelength, as
and the speed of light is related to the angular frequency and the wavenumber as the following identity equivalence
Solving this equivalence for � and �, we find the following
which establishes that � &/6 = � &785
As already stated, the relativistic energy for a massless object is equal to
where the momentum can be expressed in terms of the wavenumber as
and in terms of the angular frequency
leading to the energy equivalence
We recall that the time-dependent Schrödinger’s equation we presented for our generator was
which expresses the energy equivalence between the time-derivative for
of ℏ0
�(�, �), representing a massive object in space. The energy of the system of the �
generator will take the same form of the left-hand side of the time-dependent Schrödinger’s equation, which can be appreciated after defining our generator to be the wavefunction
The negative sign for the above results from our choice of a positive-valued angular frequency � Calculating the time derivative for the wavefunction gives us the result
found using the relativistic energy-momentum relationship
When the velocity in space is positive and less than the speed of light, the Lorentz factor related terms
for which the coordinates in hyperbolic space are related to the object’s velocity in spacetime. Our massless object system represents axial light, with a purely spherical generator geometry, meaning it does not have a velocity in spacetime. Solving the Lorentz factor related terms � and � for � = 0, we find
and taking the Lorentz factor matrix representation for
we plug into it our null-velocity Lorentz factor results, finding the result
which is consistent with the system we are describing.
