La importancia de las matematicas y las aportaciones de Isaac Newton en la

LA IMPORTANCIA DE LAS MATEMATICAS Y LAS APORTACIONES DE ISAAC NEWTON WN LA ACTUALIDAD

El pensamiento Lógico-Matemático está relacionado con la habilidad de trabajar y pensar en términos de números y la capacidad de emplear el razonamiento lógico. El desarrollo de este pensamiento es clave para el desarrollo de la inteligencia matemática y es fundamental para el bienestar de los niños, niñas y su desarrollo, ya que este tipo de inteligencia va mucho más allá de las capacidades numéricas, aporta importantes beneficios como la capacidad de entender conceptos y establecer relaciones basadas en la lógica de forma esquemática y técnica. Implica la capacidad de utilizar de manera casi natural el cálculo, las cuantificaciones, proposiciones o hipótesis. Todos nacemos con la capacidad de desarrollar este tipo de inteligencia.

El pensamiento lógico matemático es fundamental para comprender conceptos abstractos, razonamiento y comprensión de relaciones. Capacidad de solucionar problemas en diferentes ámbitos de la vida, formulando hipótesis y estableciendo predicciones. Fomenta la capacidad de razonar, sobre las metas y la forma de planificar para conseguirlo.

La influencia e importancia de las matemáticas en la sociedad, ha ido en constante crecimiento, en buena parte, debido al espectacular aumento de sus aplicaciones.

La influencia e importancia de las matemáticas en la sociedad ha ido en constante crecimiento, en buena parte debido al espectacular aumento de sus aplicaciones.

4

No es concebible la innovación tecnológica, en el sentido actual de Investigación y Desarrollo, sin la presencia preeminente de las matemáticas y sus métodos. De ahí que la enseñanza de las matemáticas con la del español ocupen un lugar estratégico en la formación diseñada por los currículos de diversos países, incluyendo una participación sustancial en la carga horaria semanal.

Los sistemas educativos actuales están orientando sus procesos para que los estudiantes, no sólo accedan al conocimiento, sino a que también lo entiendan, critiquen y transformen.

Frecuentemente se escucha decir que la lógica representa la base fundamental para el desarrollo de las matemáticas. Afirmamos también que, a su vez, las matemáticas permiten el desarrollo de una lógica de pensamiento, o de un pensamiento lógico. Esta última afirmación requiere distinguir el tipo de lógica de la que hablamos. Si se piensa en una lógica formal, como tradicionalmente la conocemos, donde el cumplimiento de formas y reglas para dar validez a las conclusiones es irrestricto, los caminos construidos mediante las matemáticas pueden volverse camisas de fuerza para el desarrollo libre del pensamiento y de la capacidad de aprender a aprender.

Por el contrario, consideramos que la lógica que sustenta el propósito de las matemáticas como instrumento para el desarrollo del aprendizaje reflexivo es la lógica dialéctica, en la que los conceptos que parecen contrapuestos y contradictorios, como concreto–abstracto, análisis–síntesis, inducción–deducción, entre otros, no son uno la negación del otro sino más bien los elementos duales, los polos entre los cuales se desplaza el pensamiento.

El proceso de enseñanza aprendizaje de las matemáticas apunta al uso de una lógica dialéctica, en la que intervienen no sólo los conocimientos y habilidades sino

5

la movilización de actitudes de descubrimiento y diálogo interno que construyen un espíritu crítico, un análisis reflexivo y un pensamiento creativo.

Para el desarrollo de competencias metacognitivas, tan importantes son los contenidos matemáticos como la forma en que se desarrolla el proceso de enseñanza aprendizaje de ellos mismos, al mostrar aplicaciones dentro de la disciplina en la que se inscribe el proceso y la reflexión sobre ello.

Por la forma como construyen las soluciones a los problemas, las matemáticas apoyan el desarrollo de una "comunidad nutritiva" que se sustenta en el entendimiento mutuo por el diálogo logrado a partir de la creación de un lenguaje con significados puestos en común.

Las matemáticas permiten, a partir del desarrollo del pensamiento lógico dialéctico, el desarrollo de competencias metacognitivas, base fundamental para la capacidad de aprender a aprender. ISAAC NEWTON EL HOMBRE CONECTADO CON EL UNIVERSO

Isaac Newton vivió como un científico reconocido durante toda su vida, mantuvo una cercanía con la clase política, por esto mismo en 1689 fue elegido miembro del Parlamento, fue encargado de la custodia de la Casa de la Moneda en 1969 y recibió de la Reina Ana el título de Sir.

Isaac Newton es sin duda un antes y un después por su obra científica, por su entregada dedicación al estudio, a la observación y al conocimiento.

La imagen de Isaac Newton y una manzana son una escena que hemos visto y, sin embargo, su trabajo en teología y en la alquimia le darían una sensibilidad única, que muy seguramente con ella pudo percibir al mundo de una forma distinta.

6

Se sabe que Newton fue reacio a los conflictos y por lo mismo, a publicar sus artículos.

Lo cierto es que Newton «estaba conectado con el Universo» de una forma impresionante, a la vez que su legado científico también lo es. Por eso es el mismísimo Neil De Grese Tyson lo elige como el más grande físico de la historia.

Así pues, cómo explican las mismas Leyes de Newton, la ciencia al tenerlo en sus terrenos, esto provocaría un movimiento proporcional en el conocimiento a lo que se considera como la Revolución científica, todo debido a su trabajo centrado en el descubrimiento de la Ley de la gravitación universal, uno de los más reconocidos descubrimientos de Newton la ley de gravitación que consiste en que una masa atrae otra masa por la gravedad, y a esto hizo una fórmula: F= G x m1 x m2/d2 y está la usó para explicar el recorrido de cometas, mareas, equinoccios, etc.

APORTES A LAS MATEMÁTICAS

La constitución de una teoría coherente, el cálculo infinitesimal, cuyos elementos habían sido progresivamente elaborados sobre todo a partir de comienzos del S. Uniéndose en lo que él llamó el método de las fluxiones, Newton desarrolló en el otoño de 1666 lo que se conoce hoy como cálculo, un método nuevo y poderoso que situó a las matemáticas modernas por encima del nivel de la geometría griega.

En su teoría de la gravitación universal explicó los movimientos celestes, a partir de la existencia de una fuerza; la fuerza de la gravedad, que actuando a distancia produce una atracción entre masas. Esta fuerza de gravedad es la misma fuerza que en la superficie de la Tierra denominamos peso. Es una fuerza directamente proporcional al producto de las masas que interactúan e inversamente proporcional a la distancia que las separa. Newton consiguió explicar con su fuerza de gravedad el movimiento elíptico de los planetas.

APLICACIONES DE SUS DESCUBRIMIENTOS A OTROS CAMPOS

La óptica fue otra área por la que Newton demostró interés muy pronto. Newton en el campo de la física postuló las Leyes de Newton, en las que explicaba el movimiento de los cuerpos, así como sus efectos y causas.

Las tres leyes de Newton

Las tres leyes de Newton o las leyes de la dinámica asentaron las bases de la física, pues permitían explicar las fuerzas que regían el comportamiento mecánico de los objetos.

Primera ley: Ley de la Inercia

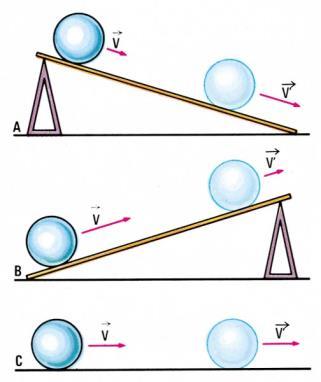
Esta ley postula que todo cuerpo permanece en estado de reposo (sin movimiento) de forma indefinida

a no ser que otro objeto ejerza una fuerza sobre él.

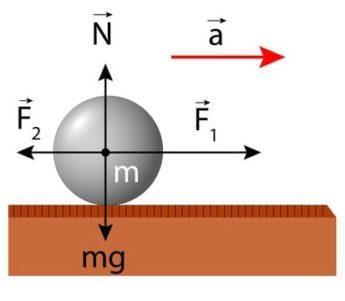
Segunda ley: Ley fundamental de la Dinámica

Esta ley afirma que la aceleración que adquiere un cuerpo es directamente proporcional a la fuerza que otro cuerpo ejerce sobre él.

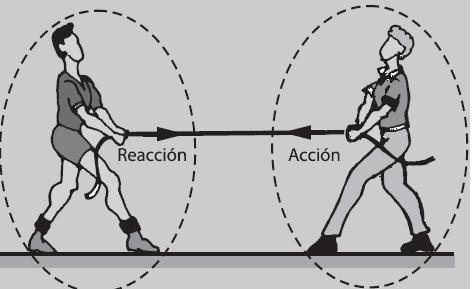
Tercera ley: Ley de Acción y Reacción

Esta ley establece que cuando un objeto ejerce una fuerza sobre un segundo cuerpo, éste ejerce sobre el primero una fuerza de igual magnitud, pero en sentido opuesto a la que ha recibido.

En conclusión, sabemos que el razonamiento lógico matemático a veces puede ser complicado, sin embargo, se pueden descubrir cosas impresionantes que aportan algo a la sociedad actual como lo hizo Isaac Newton quien hizo aportaciones en su época y que sirvieron para la actualidad. Su madre lo sacó de la escuela para darle el trabajo de

8

agricultor a quien Newton no le interesaba mucho.

Aunque la vida le sonrió y su antiguo maestro convenció a su madre para que lo dejara entrar a la Universidad de Cambridge. Posteriormente se graduó en 1665.

Tomemos de ejemplo la aportación más popular de Newton, hablamos de la Ley De Gravedad «Estaba en un huerto, observando cómo caían las manzanas». En ese momento descubrió la fuerza de atracción a la que estaba sujetada la manzana, a la que denominó “La ley de la gravedad''. Ahora entendamos que con una sola aportación cambió demasiado el pensamiento lógico como la famosa frase «Todo lo que sube tiene que bajar.» aunque no logremos verlo, está frase significa mucho y más en nuestra época actual donde jóvenes están siendo formados para descubrir cosas nuevas y aportarlas en la vida actual, veamos las matemáticas actuales no como una cosa aburrida, sino como una oportunidad de descubrir y aportar algo nuevo para que el mundo sea más avanzado y mejor cada día. 9