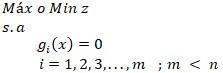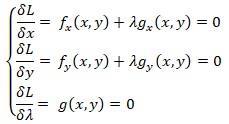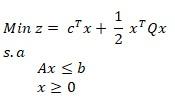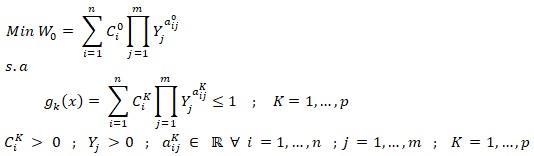MÉTODOS DE LA PROGRAMACIÓN NO LINEAL.
YeffersonGuerrero.
TITULO ORIGINAL.
MÉTODOS DE LAPROGRAMACIÓN NO LINEAL.
© UNIVERSIDAD BICENTENARIA DE ARAGUA.
© ESCUELADE INGENIERÍADE SISTEMAS.
© ANGEL PORRAS.
NÚMERO DE REGISTRO
4.989 – 55
Autor:
Porras, Z. Ángel, Y de J
C.I – V: 30.841.084
Unidad Curricular: Investigación de Operaciones II
Sección: T1
Trimestre: VIII

EDITORIAL FORYUL
SanCristóbal,Marzode2024


ÍNDICE. CONTENIDO N° PÁGINA. 1) Introducción…………………………………………………………………...........1 2) Exportación e Importación Continua de Productos………………..………...2 3) Multiplicadores de Lagrange………………..…………...………………..……...2 4) Programación Cuadrática……………..…………………………………...……...3 5) Cadenasde Markov………………………..……..………………………….…..…4 6) Programación Geométrica………………..……..………………………….…..…5 7) Conclusiones……………….…………………………………….…………..……….7 8) ReferenciasBibliográficas…….……………..………………..……………………8

INTRODUCCIÓN

La programación no lineal cuenta con una cantidad de modelos matemáticos los cuales sirven de gran ayuda para determinar una solución en problemas que se presentan dentro de las empresas, es decir, en base a la problemática que se evalué, se puede decidir que modelo matemático de programación sirve para la obtención de la resolución correspondiente, para el caso de la programación no lineal se tiene una alta variedad de herramientas encargadas de formular dichas soluciones.
Existen diversos tipos de programación que trabajan por medio de estas técnicas, la programación cuadrática se enfoca en poder minimizar ecuaciones cuadráticas a fin de analizar la complejidad de las restricciones que poseen las variables asociadas, ésta programación se conforma de una serie de métodos matemáticos; por otra parte, está la programación geométrica, destinada a encontrar soluciones en base a problemas representados por polinomios generalizados.
Es por ello que la diversidad de métodos es inmensa siendo ejecutados para casos específicos, como lo es la exportación e importación continua de productos, un área en donde es vital llevar a cabo todas sus actividades de manera planificada y satisfactoria, por lo que si se presentan problemas hay que resolverlos lo más rápido posible, de lo contrario sólo se generarán pérdidas y retrasos en el tiempo de entrega.

N° PÁG 1
.

EXPORTACIÓN E IMPORTACIÓN CONTINUA DE PRODUCTOS.


Se toma como base para la ejecución de los métodos de la programación no lineal a un pequeño emprendimiento cuya misión es completar procesos de exportación e importación de manera continua de una cantidad variada de productos, los cuales se transportan mediante diversas vías.
MULTIPLICADORES DE LAGRANGE.
Son herramientas matemáticas que permiten saber como solucionar problemas de maximización o minimización, tomando en cuenta el valor de la variables que se tienen así como sus restricciones, estas deben estar en forma de igualdad.
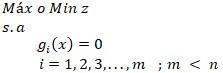
El objetivo de los multiplicadores es formular un nuevo problema en donde no existan restricciones que perjudiquen directamente a la función objetivo, por lo tanto, estos crean una nueva función objetivo, cuyo nombre es función Lagrangiana, la misma se encarga de habilitar más espacios paraposibles soluciones, esta sedefine mediante:
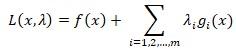
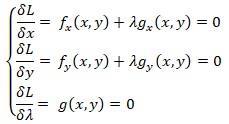
Luego de ello, se procede a derivarla parcialmente, creando consigo un sistema de ecuaciones, el cual al ser resuelto se obtienen todos los elementos del sistema, mediante puntosde evaluación.
N° PÁG 2

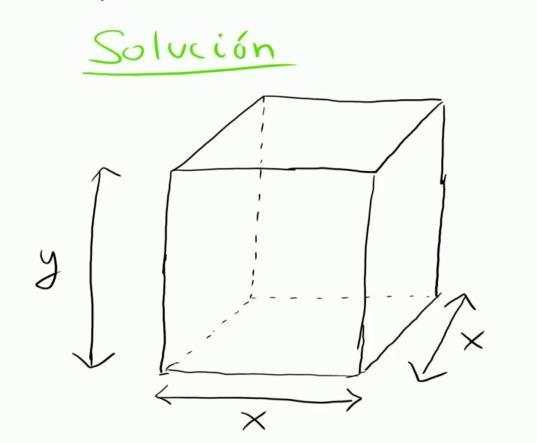
Un ejemplo de los multiplicadores de Lagrange también conocidos como Optimización, pudiendo ser linealmente restringida o no restringida; es para el caso de minimizar costos por medio de la maximización de cajas con la finalidad de presentar una mayor capacidad de almacenar productos, transportando altas cantidades de productos enmenor tiempo y menos viajes

PROGRAMACIÓN CUADRÁTICA.
Al igual que en la programación lineal esta se busca minimizar funciones cuadráticas conformadas de variables que se encuentran sujetas a restricciones lineales de desigualdad e igualdad, sin embargo, en la programación no lineal sus métodos se expanden, teniendo entonces las metodologías de Beale, HildrethD"Esopo, Zheil-Van de Panne, BarankinDorgman, Graves – Winston, entre otros.
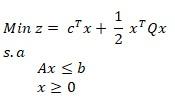

Aunque la herramienta más utilizada en este tipo de programación es el Método de Wolfe, elcual obtiene los primeros valores de las derivadas parciales a través de los multiplicadores de Lagrange, para redefinir la función objetivo actual a una función de problemas lineales, sumando cada vez más las restricciones que serán trabajadas con el método simplex, realizando una serie de iteraciones hasta hallar la solución óptima.
N° PÁG 3

Para la exportación e importación estos métodos sirven de ayuda en el mismo caso de la maximización de las cajas, sólo que esta vez se toma en cuenta el espacio que ocupan de maneral general en el área donde serán trasladadas, por lo que, se necesita encontrar una solución en donde se puedan maximizar las cajas ampliando la cantidad de productos sin que sepierda espacio vital.


CADENAS DE MARKOV.
Se conforman de un conjunto de series en donde se tienen distintos eventos, enfocadas en la determinación de la probabilidad que ocurra un evento, esta es totalmente dependiente de lo que ocurra en el evento anterior, es decir, la probabilidad de que algo suceda es relativo a lo que sucede con anterioridad. Dichas cadenas se plasman de manera gráfica, pero se resuelven a través de matrices detransición, cuya forma matemática viene dadapor:

Matricesde Transición.


Las matrices de transición son aquellas matrices cuadradas que no poseen elementos negativos, además la suma de los elementos de cada fila debe ser igual a 1, es por ello que resultan útiles al momento de estudiar las cadenas de Markov, puesto que evalúan los valores de las variables en todos los estados de los eventos desdeel principio hasta el final, .
N° PÁG 4

Sin duda alguna en la exportación e importación continua de productos las cadenas de Markov pueden servir de gran ayuda, convirtiendo los procesos de transporte más eficientes, debido a que por medio de matrices de transición se determina la probabilidad de que los productos sean trasladados de un lugar a otra de forma más rápida sin que el medio de transporte se vea afectado en cuanto a recursoso costos.


PROGRAMACIÓN GEOMÉTRICA.
Se encarga de resolver problemas que contienen funciones conformadas por elementos matemáticos específicos denominados posinomios, los cuales son polinomios positivos generalizados, estos se encargan de minimizar la función objetivo, mediante otros modelos, entre ellos el modelo de Cauchy – Schwarz basadoen la desigualdad dela media aritmética – geométrica.
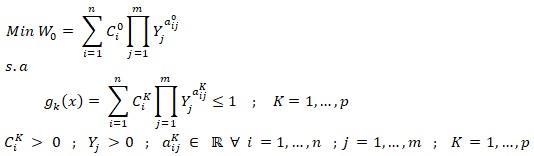
Se inicia el procedimiento para hallar la solución, comenzando con el cálculo de las derivadas parciales, sus resultados determinan la forma que tomará la función objetivo, finalmente se da resolución a los sistemas de ecuaciones formados con sus variables y restricciones, evaluando consigo si el problema tiene solución por medio de la programación geométrica asícomosu grado dedificultad
Forma de los Posinomios.
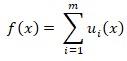
N° PÁG 5

Ahora bien, este método posee un alto nivel de complejidad, por lo que, resulta muy útil para resolver impedimentos que se presenten, para el caso de las exportaciones e importaciones funciona de gran ayuda para hallar una forma óptima de entregar pedidos de manera más rápida, utilizando diferentes medios de transporte, con la finalidad de reducir tiempo y aumentar el valor delas ganancias previstas.

No obstante, existe una variedad de métodos enfocadas a los problemas de la programación no lineal, los cuales también tienen su aporte a las óptimas soluciones que se tienen en los proyectos empresariales, algunas de dichas técnicas son:
- Programación Convexa
- Programación No Convexa.
- Programación Separable.
- Programación Fraccional.
- Método deBúsquedaDirecta.
- Método Dicótomo
- Método dela SecciónDorada.

N° PÁG 6



La programación no lineal está conformada por una serie de métodos matemáticos que ayudan a las empresas a optimizar sus actividades, consiguiendo resultados positivos al momento de ejecutar su trabajo y en las ganancias que la misma crea a nivel general, esto se evidencia a través de la Exportación e Importación Continua de Productos, donde se tienen retos que son superados gracias a la implementación correcta de dichas técnicas matemáticas que hallan soluciones para problemas puntuales.
Uno de los métodos más utilizados son los multiplicadores de Lagrange, estos estudian la mejor forma para solucionar problemas de maximización o eliminación de variables con restricciones de igualdad, sirviendo como apoyo para referenciar una óptima maximización en el tamaño de las cajas donde se transportan los productos, haciendo que las mismas sean más grandes y acaparen mayor cantidad de productos al aumentar el valor de la disponibilidad en su espacio.
Otros elementos de la programación lineal muy útiles para resolver percances dentro de la exportación o importación son los diversos tipos de programación, teniendo entonces cuadrática, convexa, no convexa, geométrica, separable, fraccional, así como también los métodos de la sección dorada, de búsqueda directa, entre otros. Todos ellos tienen como misión encontrar la solución óptima por medio del estudio de las variables junto con sus restricciones de desigualdad e igualdad.
N° PÁG 7
CONCLUSIÓN

REFERENCIAS BIBLIOGRÁFICAS

Álvarez, L. (2012). Programación No Lineal. Disponible en: http://itpn.mx/recursosisc/3semestre/investigaciondeoperaciones/Unidad% 20III Consultado: Marzo 19, 2024.
Bandala, K. (2010). Tipos de Problemas de Programación No Lineal. Disponible en:
https://karenbandala.wordpress.com/unidad-iii/3-3problemas-no-restringidos-programacion-no-lineal/ Consultado: Marzo 19, 2024.
García, J. (2017). Métodos de Programación No Lineal. Disponible en: https://www.calameo.com/books/001027554ec83072261a8
Consultado: Marzo 19, 2024.
Pérez, K. (2011). Programación No Lineal. Disponible en: https://www.aliat.click/BibliotecasDigitales/economico_administrativo/Inv estigacion_de_operaciones/Investigacion_de_operaciones_Parte_2.pdf Consultado: Marzo 19, 2024.
Rivero, R. (2017). Métodos de Programación No – Lineal. Disponible en: https://www.slideshare.net/RobertMilt/metodos-deprogramacion-nolineal Consultado: Marzo 19, 2024.
Suarez, F. (2016). Programación No Lineal. Disponible en: https://www.lifeder.com/programacion-no-lineal/ Consultado: Marzo 19, 2024.
Torres, M. (2018). ¿Qué es la Programación No Lineal? Disponible en: https://www.euroinnova.edu.es/blog/que-es-la-programacion-no-lineal Consultado: Marzo 19, 2024.
N° PÁG 8