Guandinango

ESTUDIANTILDE MATEMÁTICA

UNIVERSIDAD POLITÉCNICA ESTATAL DEL CARCHI

NIVELACION CARRERA DE TURISMO

Asignatura: Matemática

Nivel / Paralelo: Nivelación 0AM

Tema: Portafolio Estudiantil de Matemática

Alumna:

Leidy Stefania Guandinango Portilla

APRENDIZAJE AUTÓNOMO Y

APRENDIZAJE EN CONTACTO CONELDOCENTE-PARCIAL1

Talleres

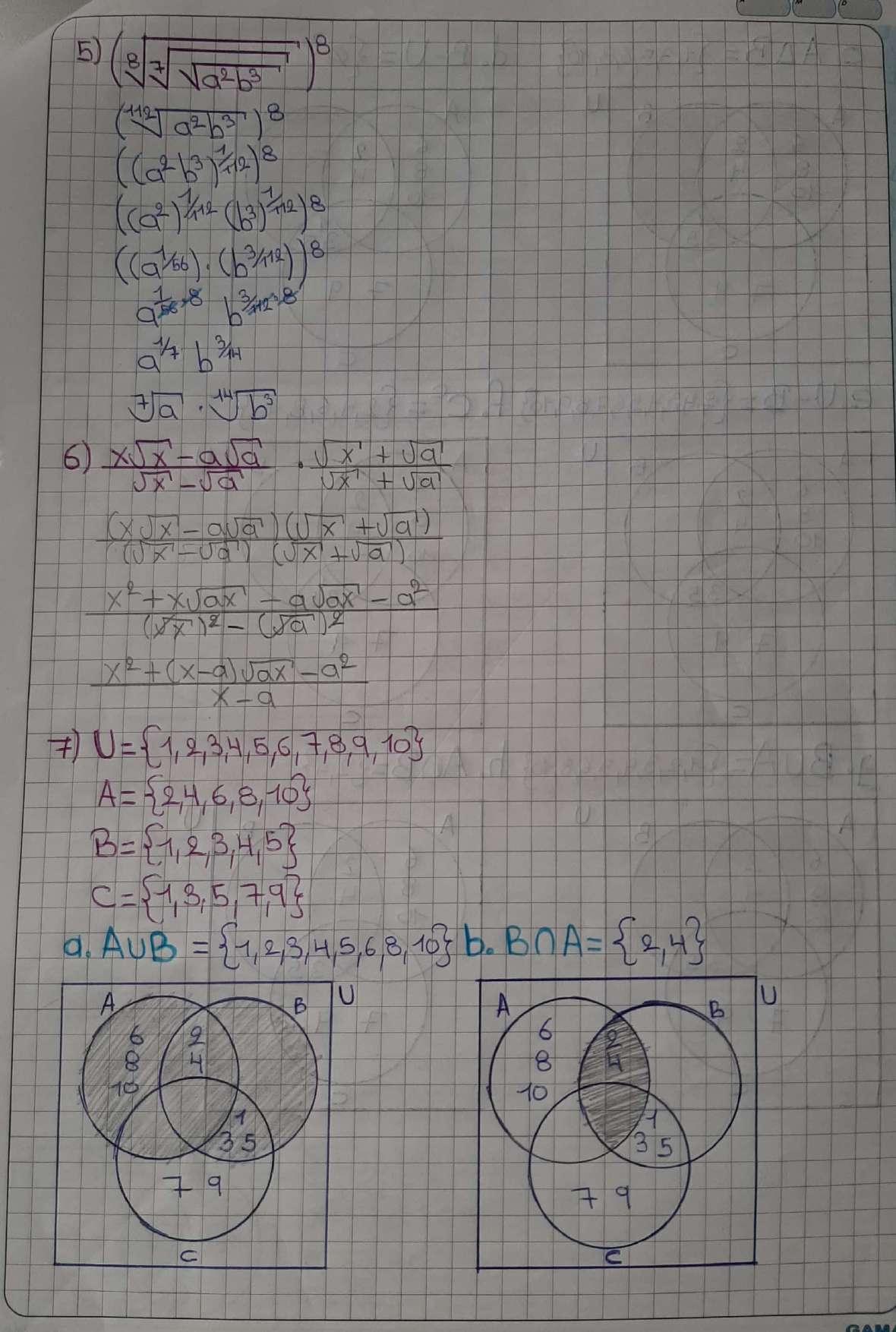
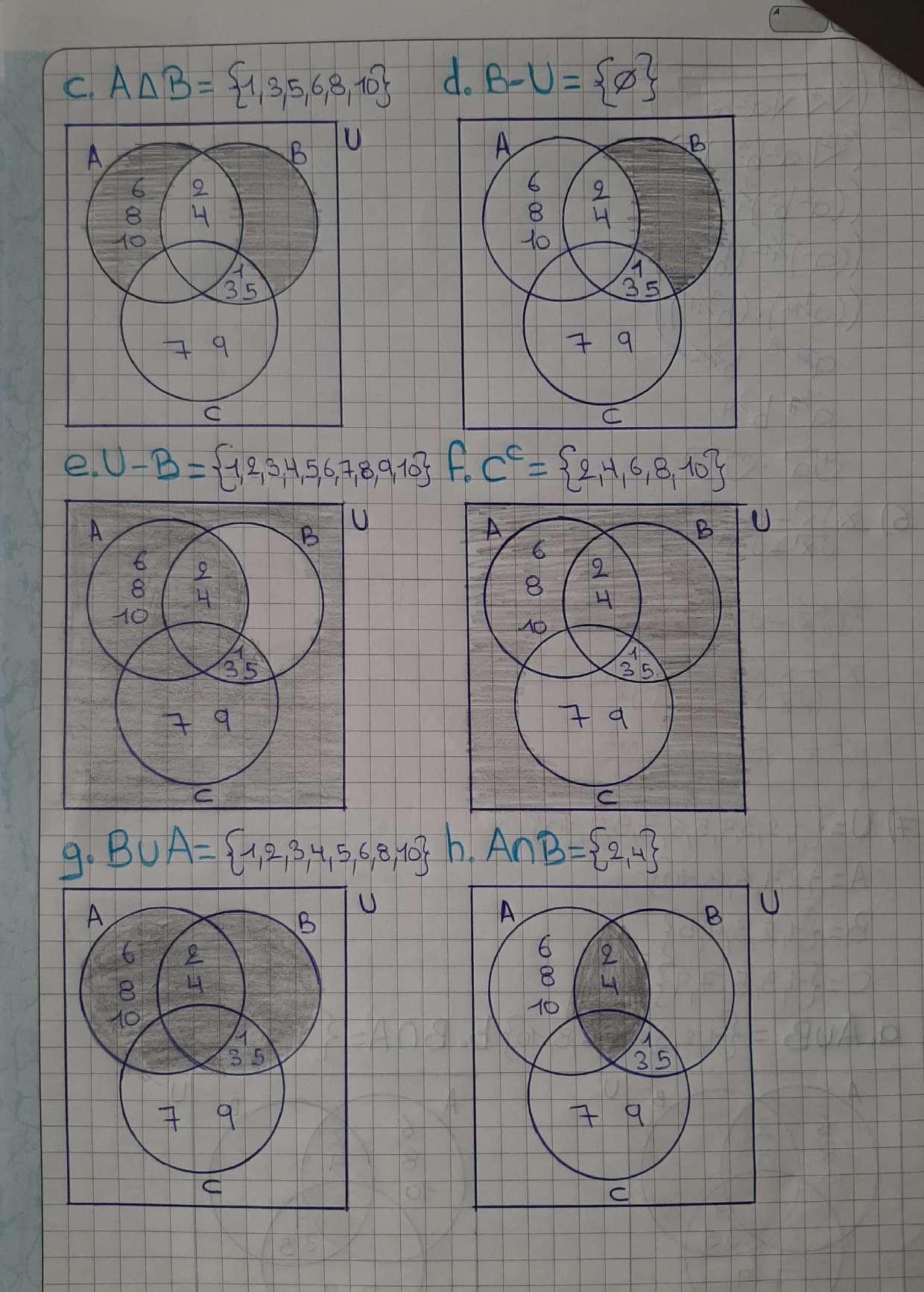
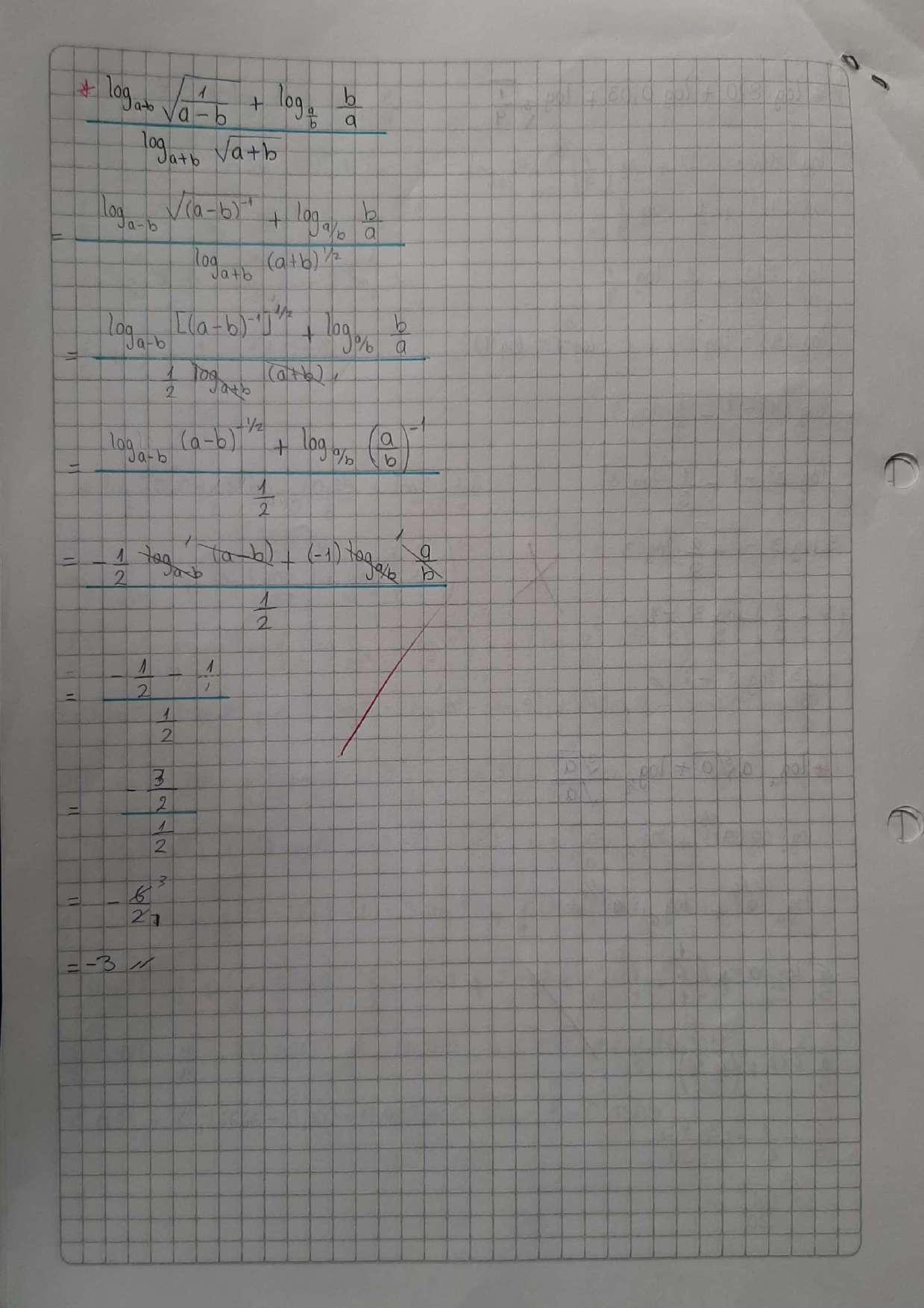
EXPOSICIÓN-PARCIAL1

ExposicióndeProductosyCocientesNotables

Productos y Cocientes Notables

Andrea Armijos

Emily Narváez

Leidy Guandinango

Adonis Mora

Dickerson Revelo

PRODUCTOS NOTABLES

Definición

Los productos notables son operaciones algebraicas, donde se expresan multiplicaciones de polinomios, que no necesitan ser resueltas tradicionalmente, sino que con la ayuda de ciertas reglas se pueden encontrar los resultados de las mismas.

Cuadrado de un binomio

Binomio al cuadrado

Es la multiplicación de un binomio por sí mismo, expresada en forma de potencia, donde los términos son sumados o restados:

a. Binomio de un cuadrado suma:

Es igual al cuadrado del primer término, más el doble del producto de los términos, más el cuadrado del segundo término. Se expresa de la siguiente manera:

(a+b)2 =(a+b) *(a+b).

b. Binomio de un cuadrado resta : se aplica la misma regla del binomio de una suma, solo que en este caso el segundo término es negativo. Su fórmula es la siguiente:

Ejemplos

Suma: (4a+2b)=(4a)2 +2(4a * 2b)+(2b)2

(4a+2b)=8a2 +2(8ab)+4b2

(4a+2b)=8a2+16ab+4b2 .

Resta:

Es decir, que el resultado de multiplicar la suma de dos números por su diferencia es el mismo que si restamos los cuadrados de ambos números Cuadrado de la suma por la diferencia de dos cantidades

(a+b)(a-b)=��2 −��2

a. Para el binomio al cubo de una

suma:

•El cubo del primer término, más el triple del cuadrado del primer término por el segundo.

•Más el triple del primer término, por el segundo al cuadrado.

•

Binomio al cubo

Binomio al Cubo

b. Para el binomio al cubo de una resta:

•El cubo del primer término, menos el triple del cuadrado del primer término por el segundo.

•Más el triple del primer término, por el segundo al cuadrado.

•Menos el cubo del segundo término.

(a–b)3 =(a–b) *(a–b)2

(a–b)3 =(a–b) * (a2 –2ab+b2)

(a–b)3 =a3 –2a2b+ab2 –ba2 +2ab2 –b3

(a–b)3 =a3 –3a2b+3ab2 –b3 .

Ejemplos

Suma: (a+3)3 =a3 +3(a)2 *(3)+3(a)*(3)2 +(3)3

(a+3)3 =a3+3(a)2 *(3)+3(a)*(9)+27

(a+3)3 =a3+9a2 +27a+27.

Resta: (b–5)3 =b3 +3(b)2 *(-5)+

(b–5)3 =b3 +3(b)2 *(-5)+3(b)*(25)-125

(b–5)3 =b3 –15b2 +75b–125

Producto de binomios con un término común

Es igual a la suma o resta:

• Producto de los términos comunes.

• Producto de la suma o resta de los términos no comunes por el término común.

• Producto de términos no comunes.

(x+a)(x+b)=��2 + ��+�� ��+(��∙��)

Producto de 2 binomios de la forma

(mx±a) (nx±b)

Es igual a la suma o resta:

• Producto de los primeros términos de los binomios.

• Producto del segundo término del primer binomio y el primer término del segundo binomio.

• Producto del primer término del primer binomio y el segundo término del segundo binomio.

• Producto de los segundos términos de los binomios.

Trinomio al cuadrado

Es igual a la suma o resta:

• Primer término al cuadrado.

• Segundo término al cuadrado.

• Tercer término al cuadrado.

• Dos veces el primero por el segundo.

• Dos veces el primero por el tercero.

• Dos veces el segundo por el tercero.

(a+��+��)=��2 +��2+��2 +2ab+2ac+2bc

Trinomio al Cubo

El primer termino elevado al cubo, mas el segundo termino elevando al cubo, mas el tercer termino elevado al cubo. Mas el triple producto del primer termino mas el segundo, por el primer termino mas el tercero por el segundo termino mas el tercero

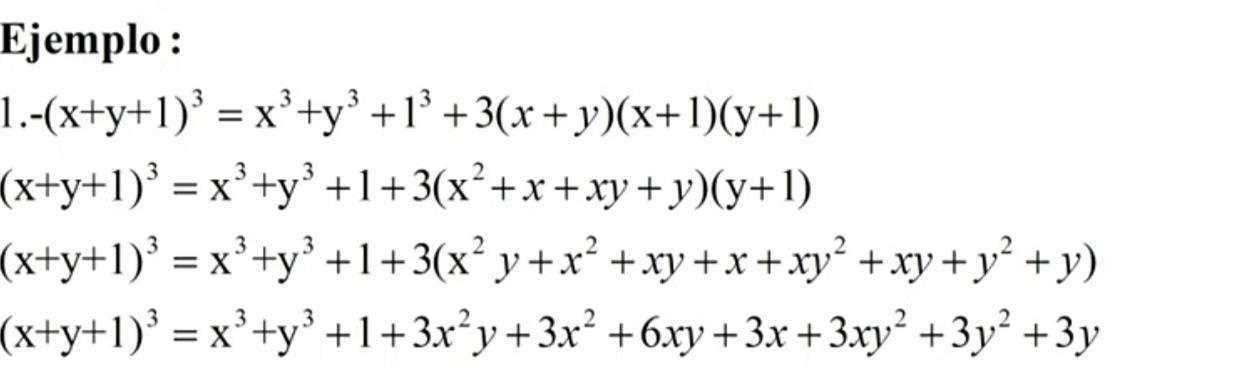
Definición de cocientes

Los cocientes notables son divisiones exactas entre expresiones algebraicas, que se usan con frecuencia en algebra y calculo. Al igual que ocurre con los productos notables, la división no se lleva a cabo, si no que el resultado de los cocientes se aplica directamente cuando es necesario

Cocientes de la diferencia de potencias iguales entre la diferencia de sus bases (-/-)

Se siguen los siguientes pasos:

1. Existirá un número de términos igual al exponente de los términos del dividendo y todos serán positivos.

2. En cada término se multiplica el término de la izquierda por el término de la derecha de la expresión dada.

3. En el primer término el factor de la izquierda tendrá un exponente igual al del dividendo disminuido en uno, y el factor de la izquierda tendrá un exponente de cero

4. Para los exponentes de los demás términos: El término de la izquierda disminuye una unidad, y los de la derecha aumentan también una unidad (si se suman los exponentes de los dos términos siempre será igual a n-1)

Ejemplos

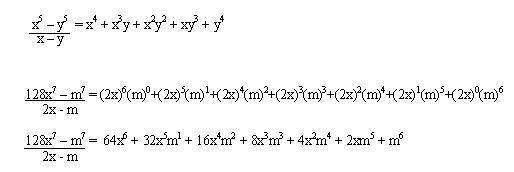
Sumas de potencias iguales, impares entre la suma de sus bases

La suma de potencias de exponentes iguales impares siempre es divisible exactamente entre la suma de sus bases. Se estructura igual que el anterior con la siguiente diferencia en el paso uno. El primer factor del resultado será positivo, el segundo negativo y así seguirán alternándose hasta el último término.

Diferencia de potencias iguales, pares entre las sumas de sus bases(-/+)

La diferencia de potencias de exponentes iguales pares siempre es divisible exactamente entre la suma de sus bases. Se estructura exactamente igual que el anterior sin diferencias.

IMPORTANTE: Si tenemos una suma de potencias iguales pares NUNCA será divisible exactamente entre la suma de sus bases, TAMPOCO lo será la diferencia de potencias iguales impares entre la suma de sus bases.

Caso 4 cuando no es un cociente notable

La siguiente división no es un cociente notable:

No importa si n es par o impar, simplemente no es una división exacta mires por donde la mires, si aplicamos al teorema del resto, el valor de x sería

x=a, reemplazando en el dividendo. El resto es diferente de cero para cualquier valor de n, por tanto el caso

4 no es un cociente notable

EVALUACIONES-PARCIAL1

PruebasSemanalesyPruebaParcial

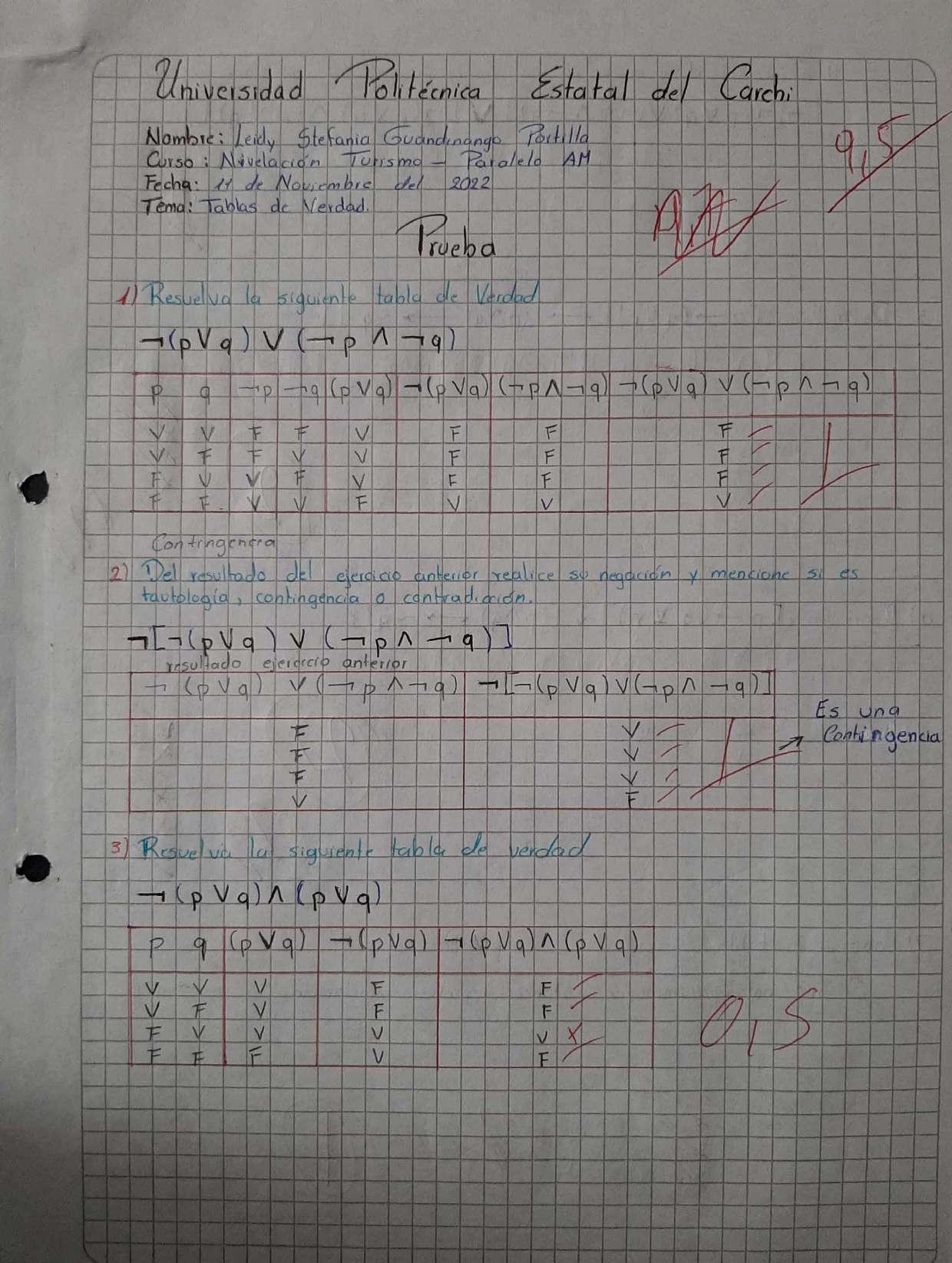
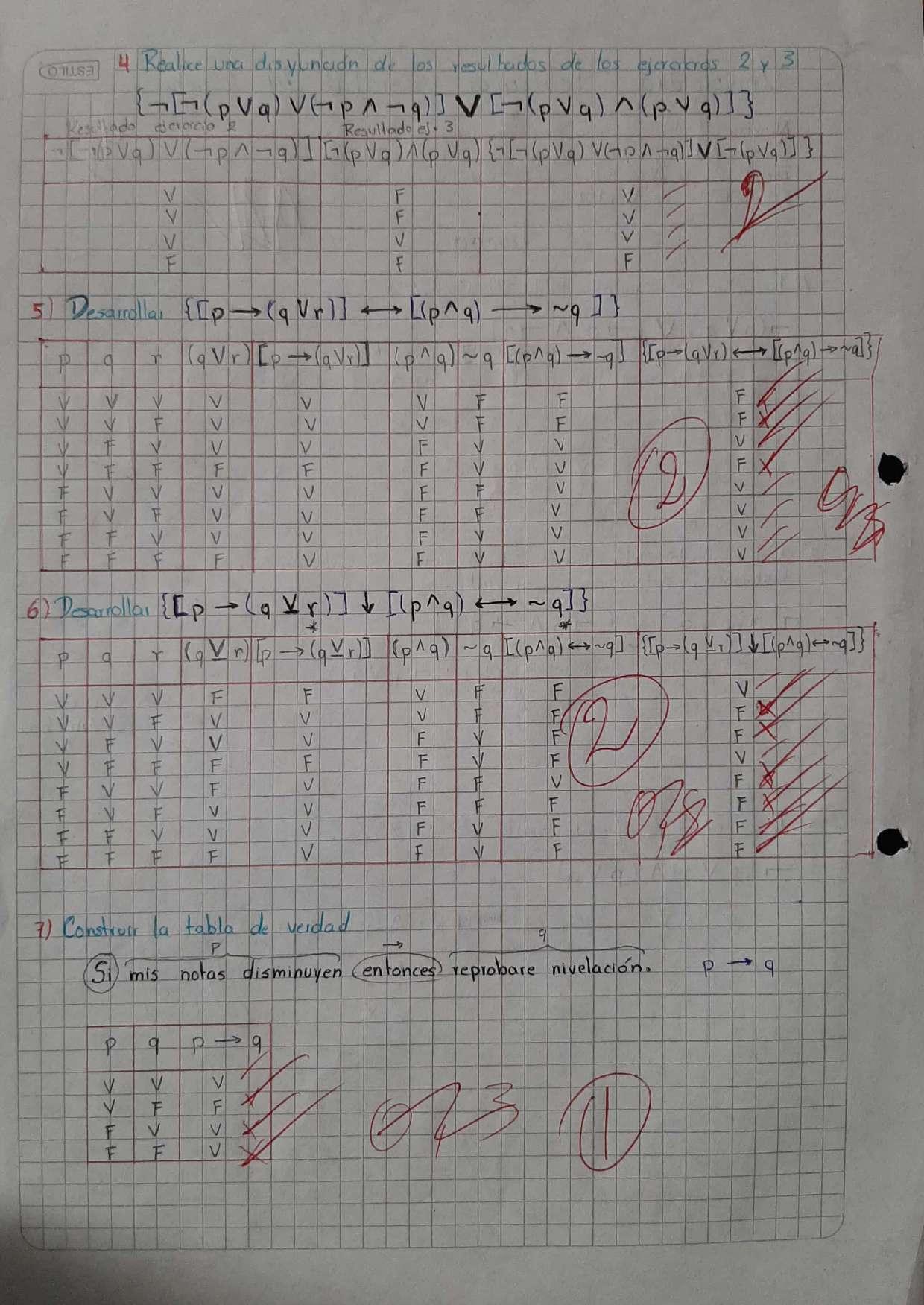
APRENDIZAJE AUTÓNOMO Y

APRENDIZAJE EN CONTACTO CONELDOCENTE-PARCIAL2

Talleres

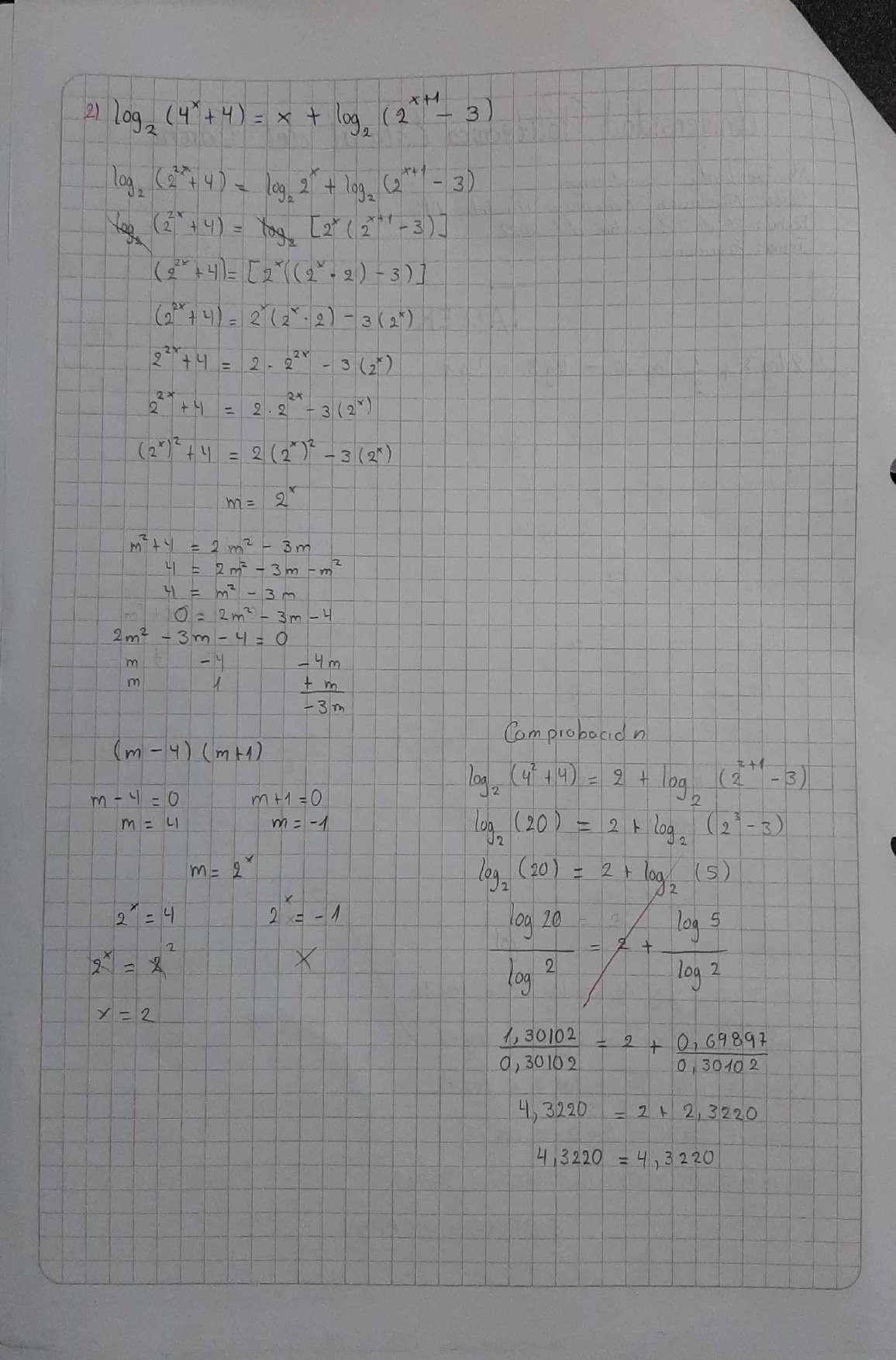
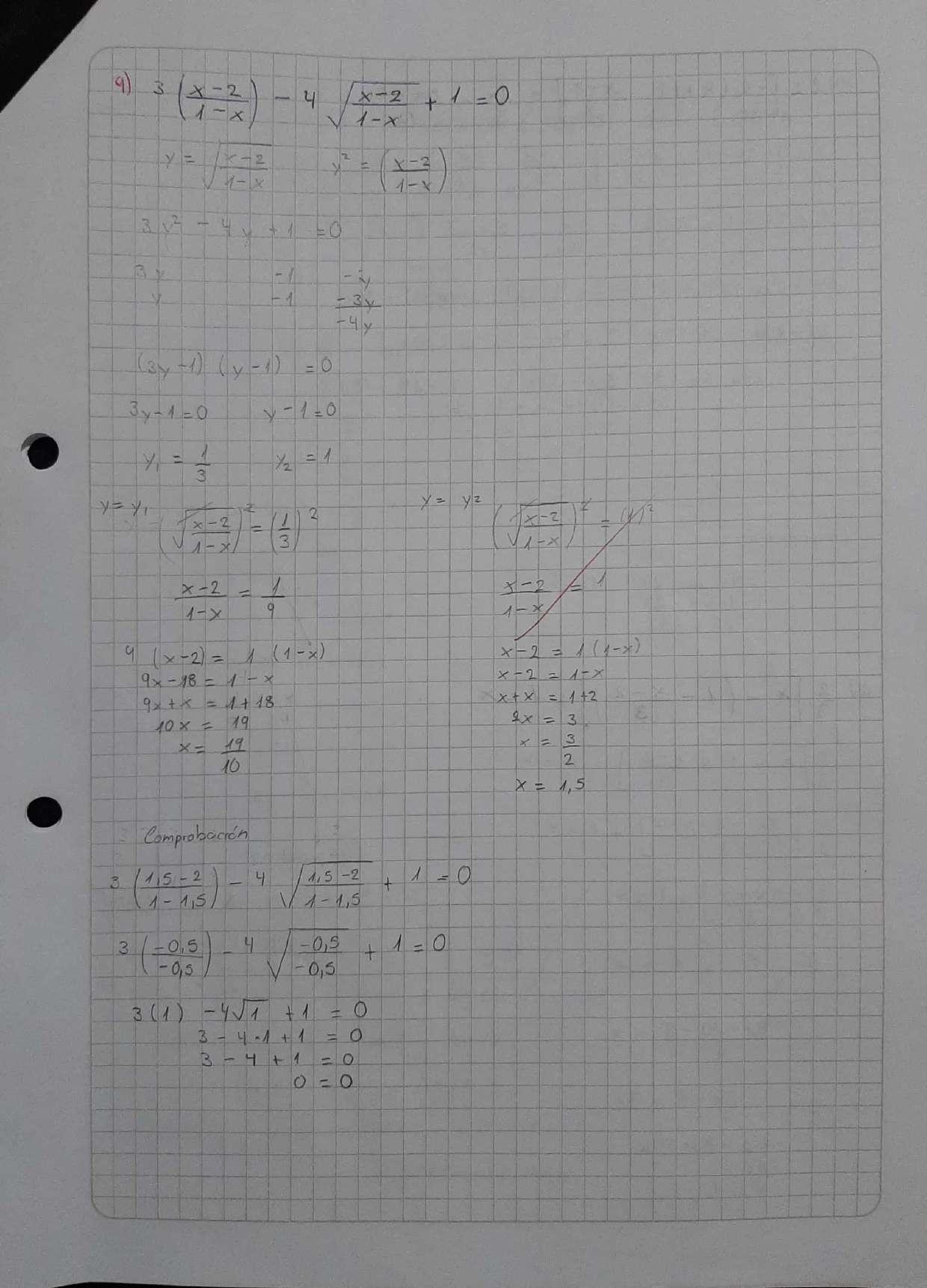
EXPOSICIÓN-PARCIAL2

ExposicióndeSistemasdeEcuaciones

UNIVERSIDADPOLITÉCNICAESTATALDELCARCHI

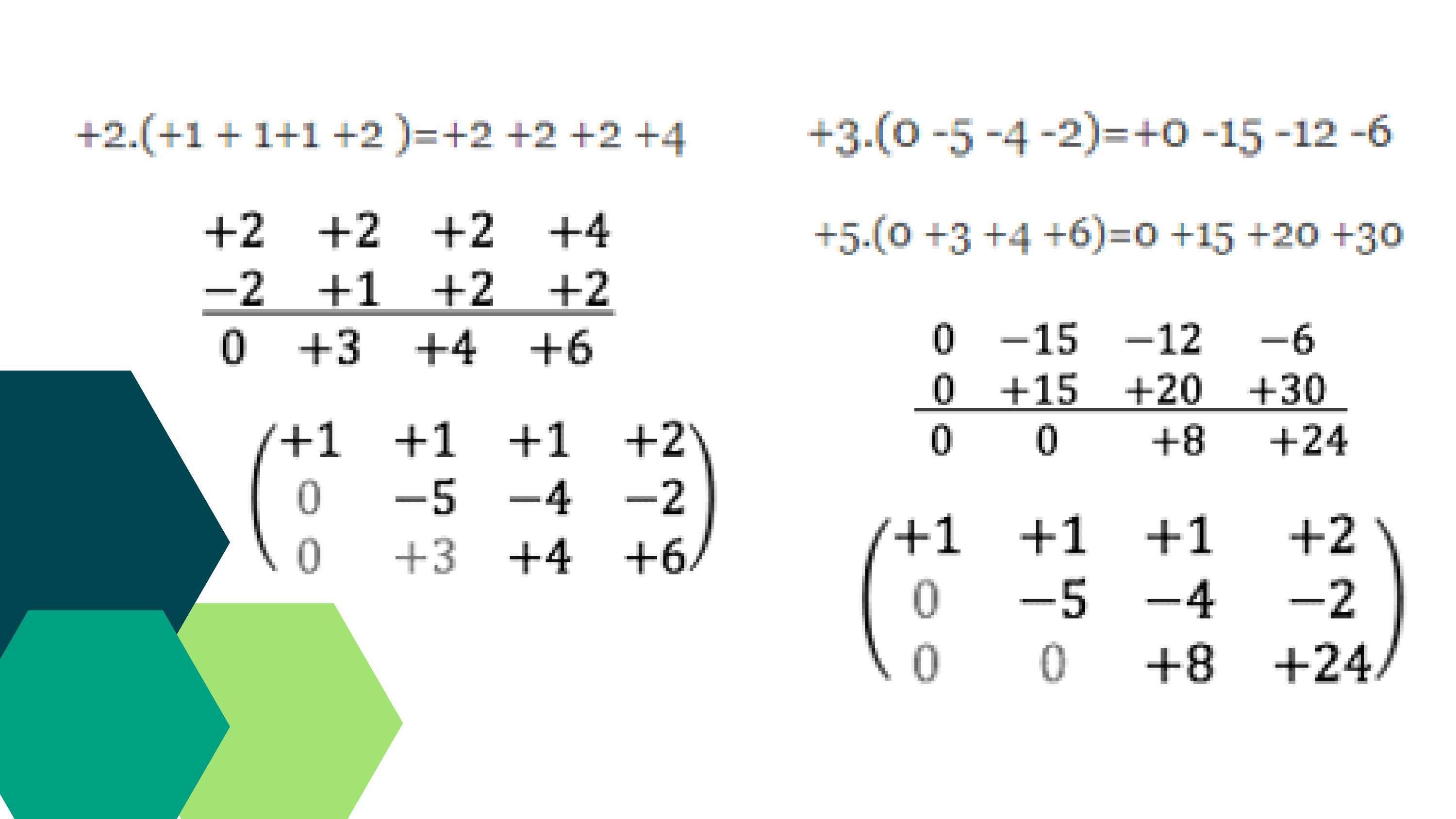
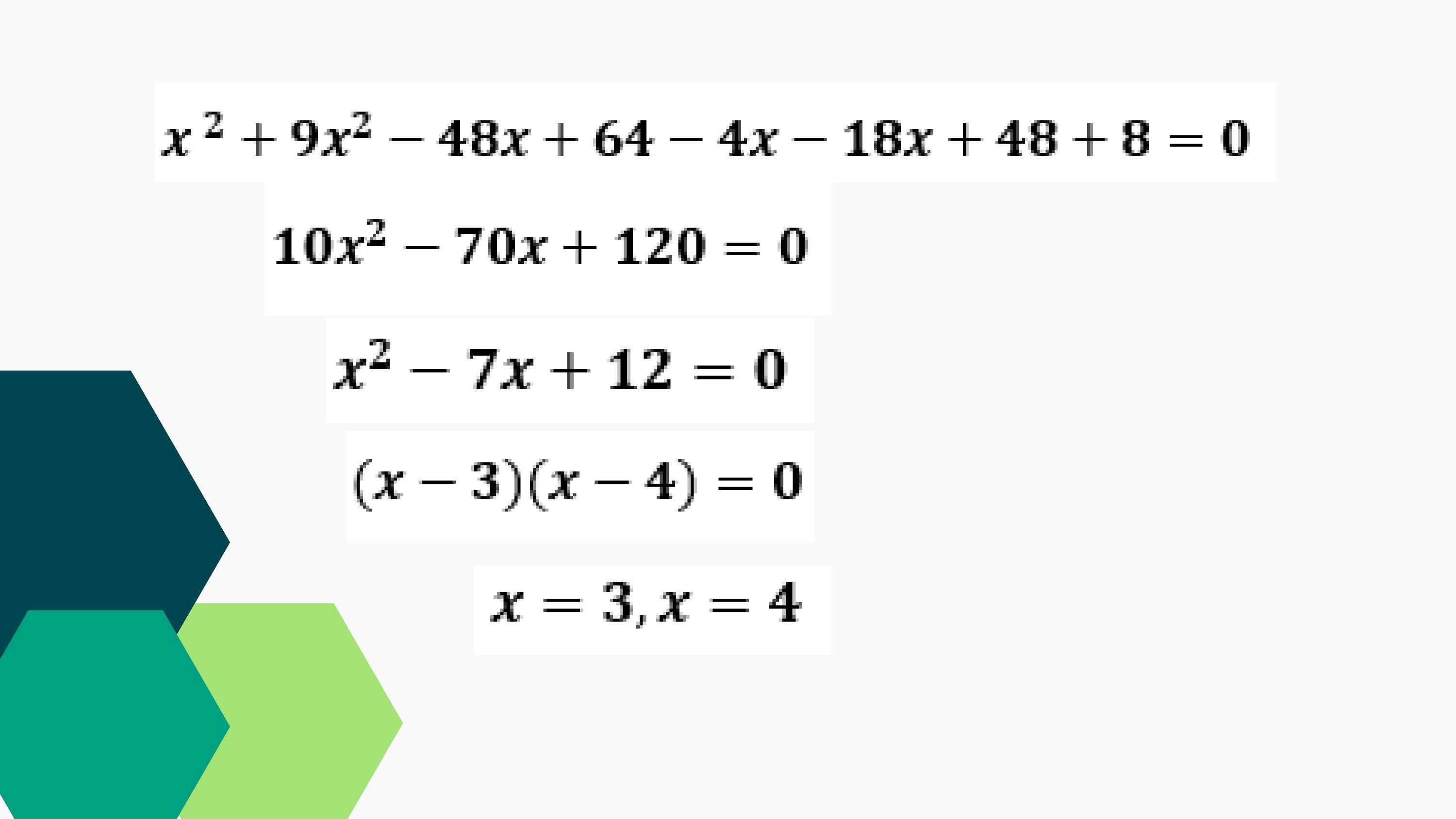
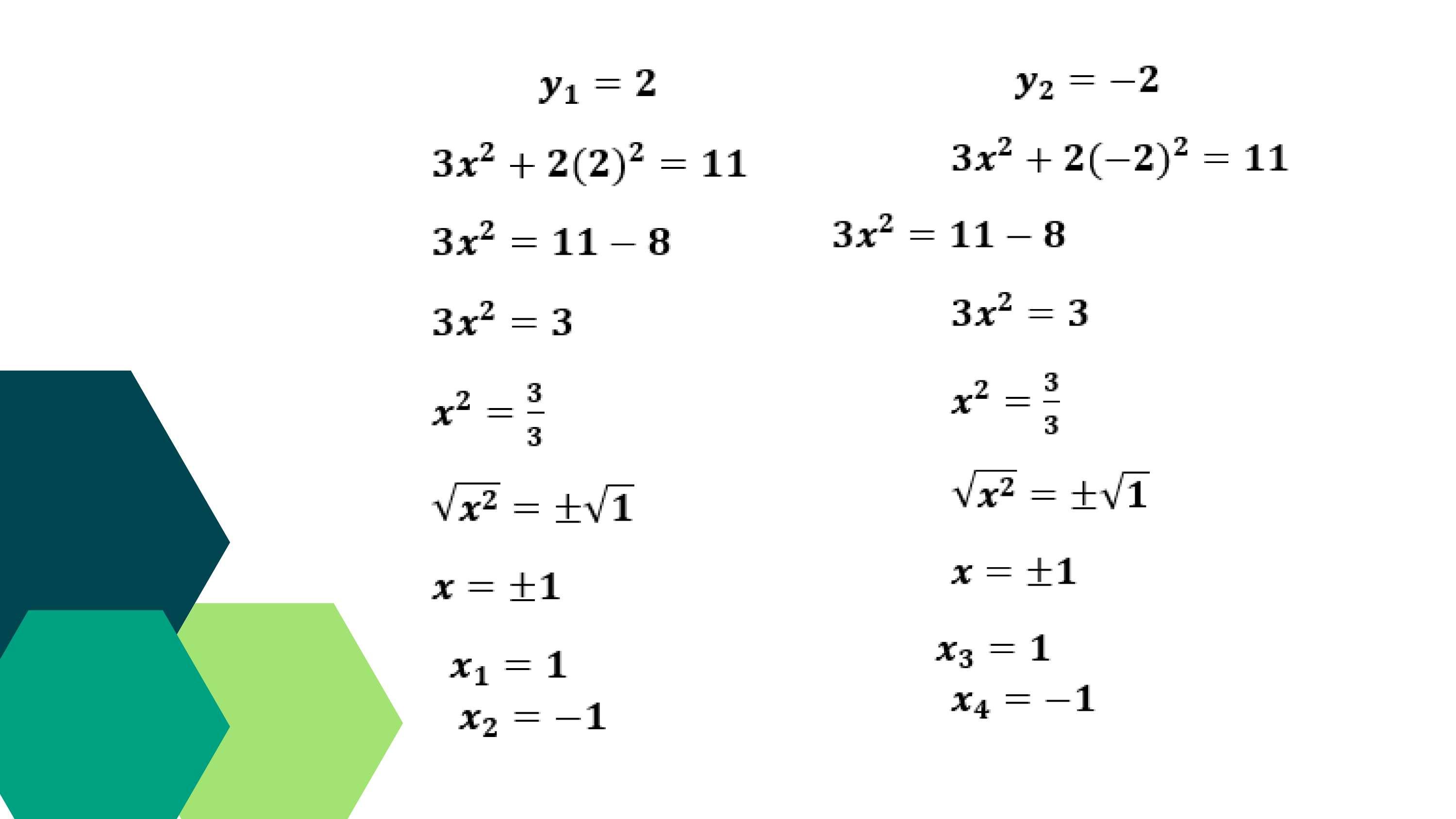
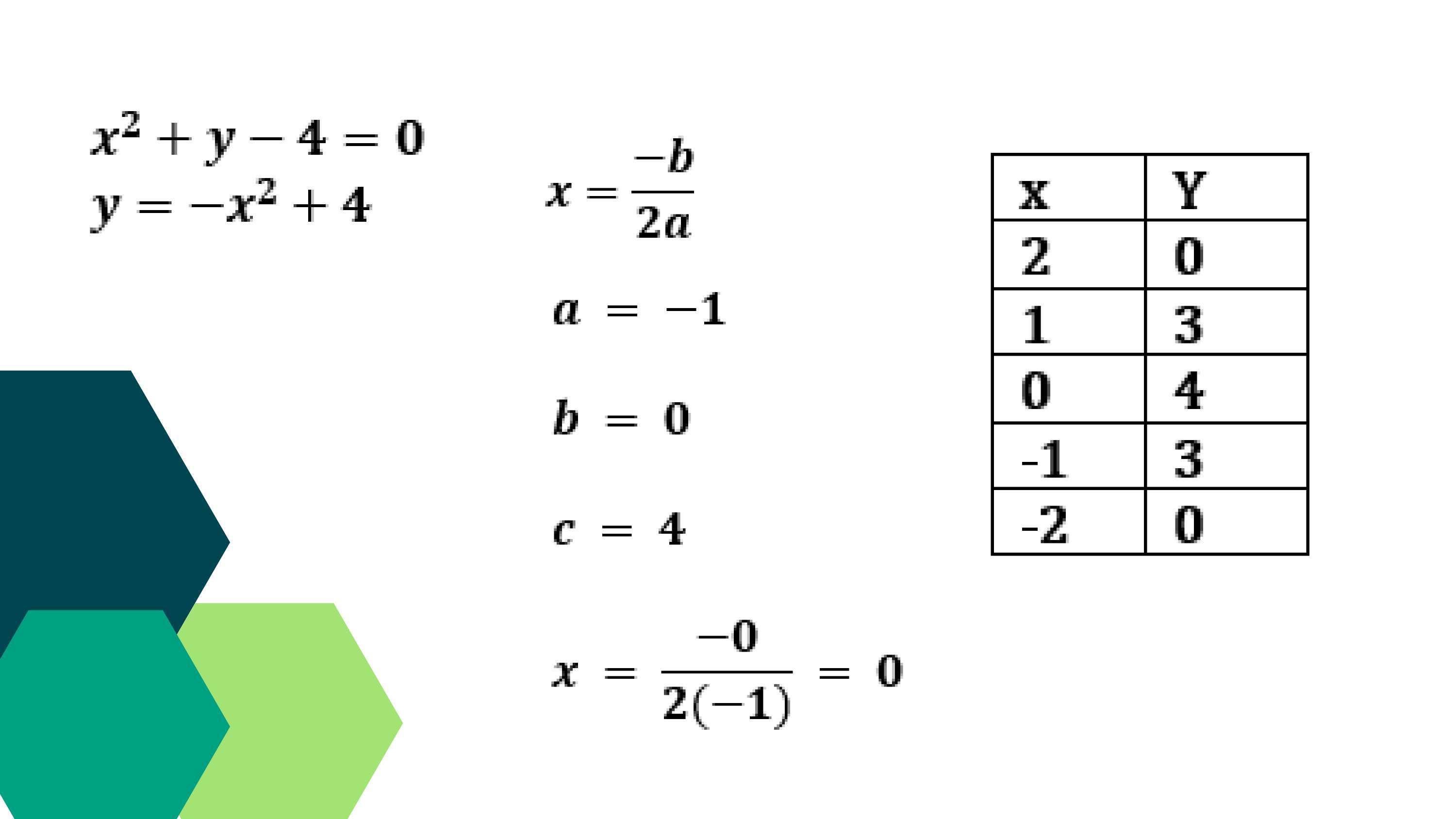
PORTADA

UNIVERSIDAD POLITÉCNICA ESTATAL DEL CARCHI NIVELACION CARRERA DE TURISMO

Asignatura: Matemática.

Nivel / Paralelo: Nivelación 0AM

Tema: Sistemas de ecuaciones lineales y cuadráticas

Nombre: Evelyn Puente

Brilly Rogel.

Karen Imbaquingo.

Dickerson Revelo.

Andrea Armijos.

Leidy Guandinango.

Fecha: 03/01/2023.

INTRODUCCION

El presente informe se realiza con la finalidad de aprender y posteriormente explicar lo concerniente al tema de sistemas de ecuaciones lineales y cuadráticos, definiciones y métodos más usados para su resolución. Realizamos este informe ante la falta o escaso conocimiento sobre los sistemas de ecuaciones en los estudiantes de Nivelación de la carrera de Turismo y la importancia que estos tienen para resolver problemas de diversas áreas y ciencias.

De esta manera, en nuestra investigación encontramos que los sistemas de ecuación son un conjunto de ecuaciones con varias incógnitas en la que deseamos encontrar una solución común. Además, estos sistemas se dividen principalmente en sistema de ecuaciones lineales y sistema de ecuaciones cuadráticas.

De esta manera se conoce como sistema de ecuación lineal al conjunto de dos o más ecuaciones de primer grado. Estos sistemas se resuelven por varios métodos, sin embargo, los más utilizados son métodos de eliminación o reducción, igualación, sustitución, el método de Gauss y el método grafico mismos que se detallan en el presente informe. Así también, determinamos que los sistemas de ecuaciones cuadráticas son el conjunto de dos o más ecuaciones donde al menos una de ellas es de segundo grado. Para resolver estos sistemas también se utilizan métodos como el de sustitución, eliminación y por cambio de variable.

OBJETIVOS

Objetivo general

Investigar los sistemas de ecuaciones lineales y cuadráticas para entender y practicar la solución de estos.

Objetivos específicos

1) Investigar sobre los sistemas de ecuaciones lineales y cuadráticas.

2) Identificar y reconocer los métodos más conocidos para resolver estos sistemas de ecuaciones.

3) Analizar los procesos de los métodos paso a paso para su correcta resolución.

DESARROLLO

Sistema De Ecuaciones Lineales Definición

Al hablar de este tema encontramos que:

Un sistema de ecuaciones lineales es un conjunto de ecuaciones que tiene más de una incógnita. Las incógnitas aparecen en varias de las ecuaciones, pero no necesariamente en todas. Lo que hacen estas ecuaciones es relacionar las incógnitas entre sí.

Ejemplo de un sistema de dos ecuaciones con dos ecuaciones:

=1

5�� =6

SOLUCION: x=1 y=-1

Resolver un sistema de ecuaciones consiste en encontrar el valor de cada incógnita para que se cumpla todas las ecuaciones del sistema. Pero no siempre existe solución, o bien, pueden existir infinitas soluciones. Si hay una única solución (un valor para cada incógnita como en el ejemplo anterior) se dice que el sistema es compatible determinado (Matesfacil, s.f.)

Método de Reducción o Eliminación

El método de reducción o eliminación es uno de los diversos métodos que existen para resolver ecuaciones, si el sistema es de dos ecuaciones lineales con dos incógnitas, este método consiste en procurar que una de las incógnitas tenga el mismo coeficiente en las dos ecuaciones para que, al restarlas miembro a miembro, se elimine dicha incógnita, dando lugar a una ecuación con una única incógnita (Matemáticas profe Alex, 2018).

Pasos para resolver una ecuación por método de reducción

1. Multiplicar la o las ecuaciones.

2. Sumar para eliminar (quedara una sola ecuación).

3. Resolver la ecuación.

4. Reemplazar el valor.

Ejemplo:

{4��+3�� =10

5�� 6�� = 7 (2)

{8��+6�� =20

5�� 6�� = 7

13x + 0 = 13

X=���� ����

X=1

Reemplazamos x=1

4x+3y=10

4(1)+3y=10

4+3y=10

3y=10-4

3y=6

Y=�� ��

Y=2

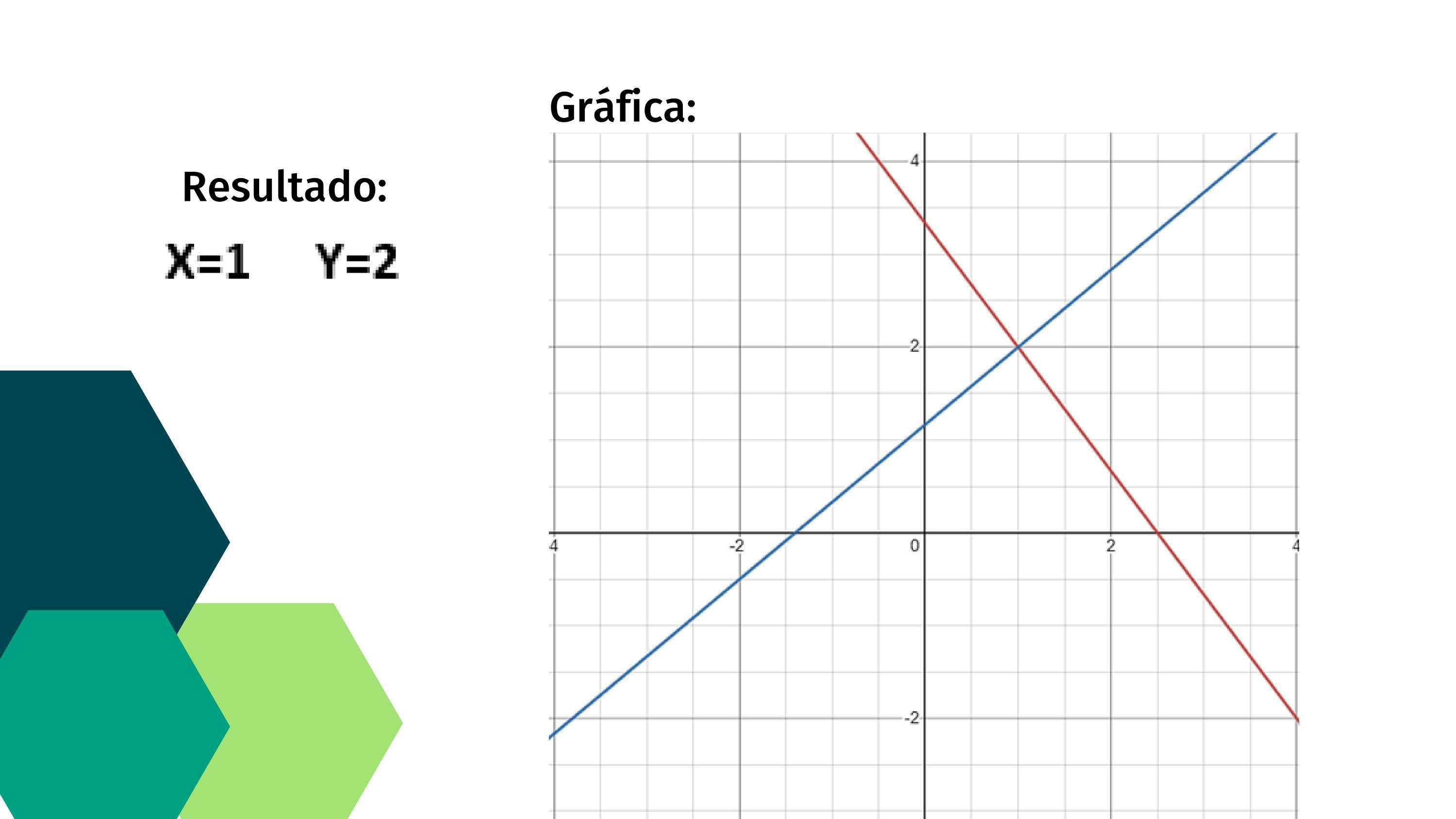
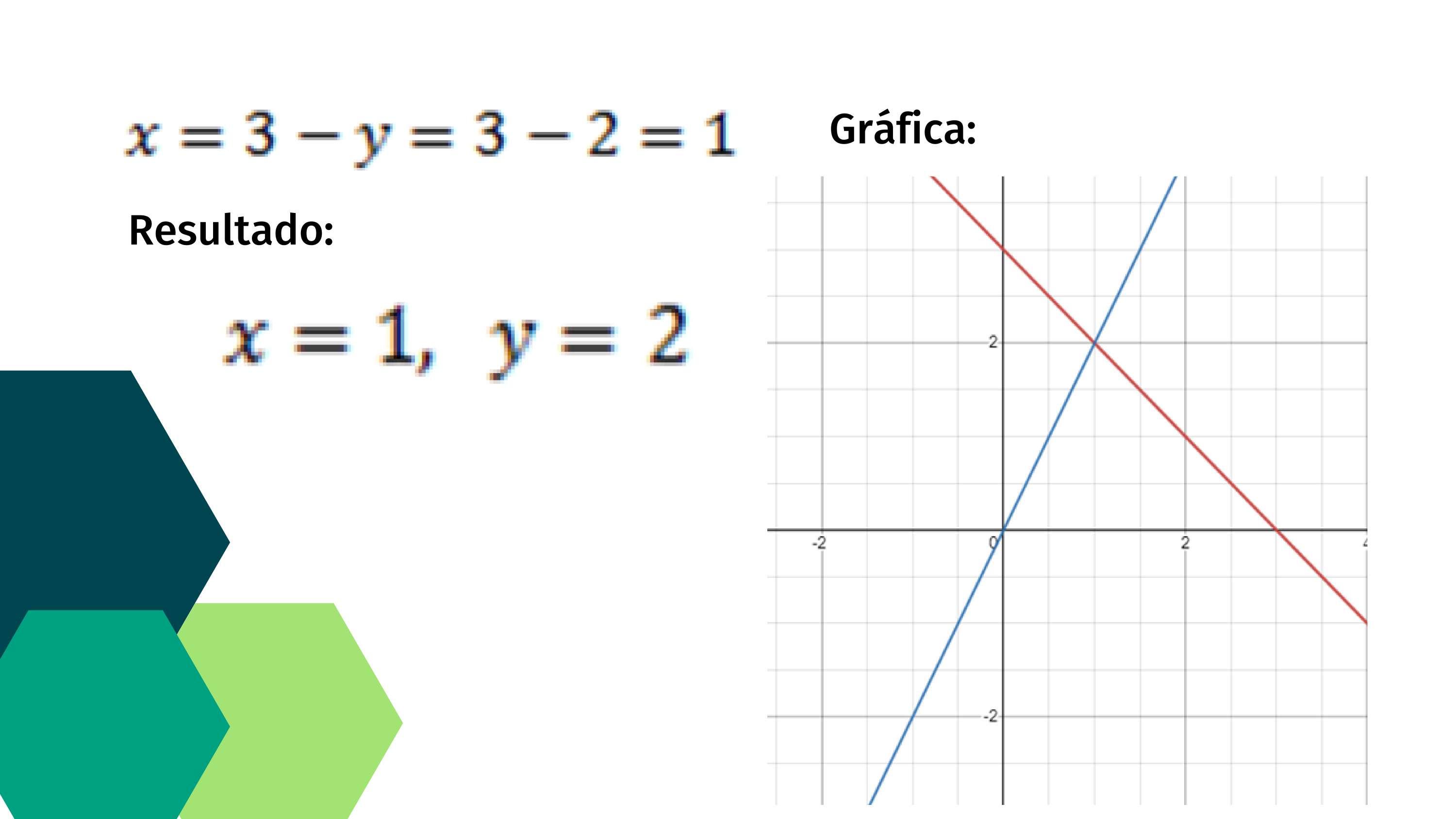
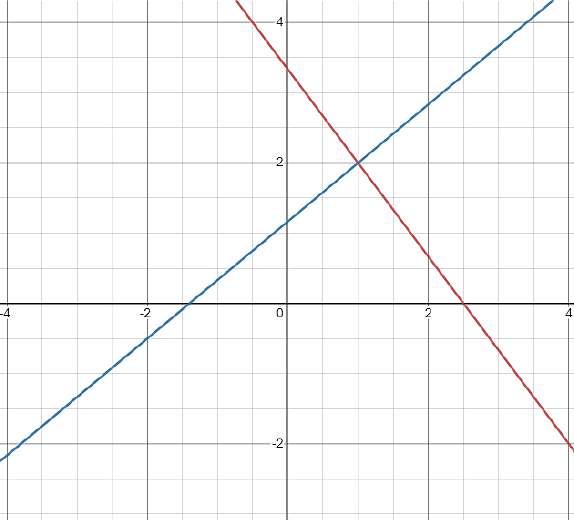
X=1 Y=2 Es la solución de este sistema de ecuaciones.

Gráfica Generada por Desmos

Método de igualación.

El método de igualación “consiste en aislar una incógnita en las dos ecuaciones para igualarlas” (Ramos, 2021).

Los pasos por seguir son los siguientes:

En primer lugar, elegimos la incógnita que deseamos despejar. En este caso, empezaremos por la «x» y despejo la misma en ambas ecuaciones.

Una vez hemos despejado, igualamos:

Por último, sustituimos el valor que hemos calculado despejando la otra incógnita en una de las ecuaciones iniciales.

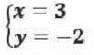
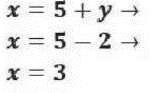
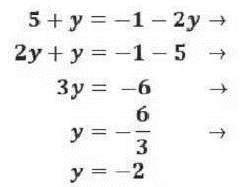
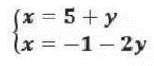
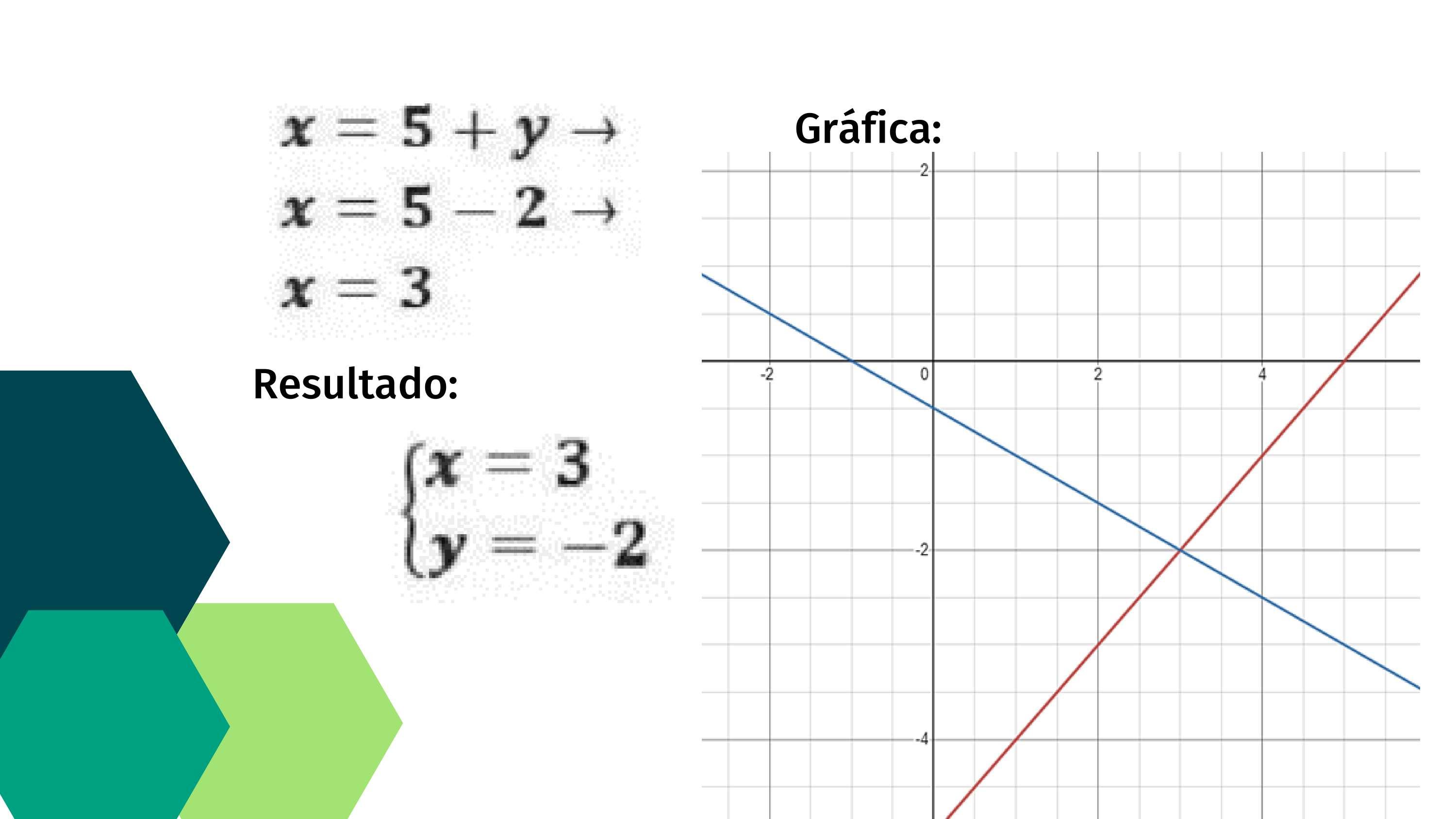
La solución del sistema es:

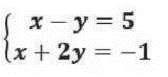
Gráfica Generada por Desmos.

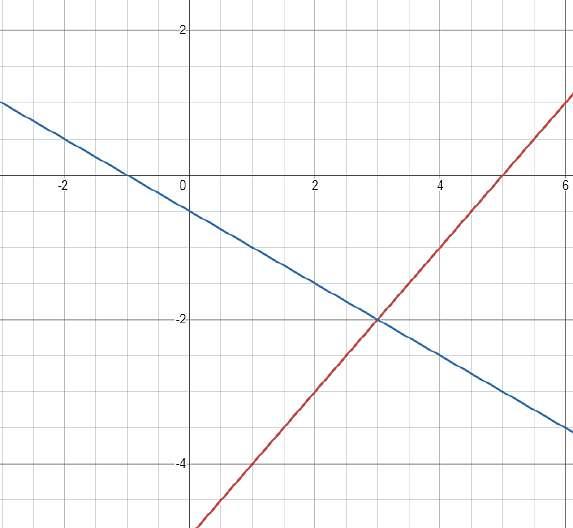
Método de sustitución.

El método de sustitución “consiste en aislar en una ecuación una de las dos incógnitas para sustituirla en la otra ecuación.” (Ramos, 2021). Obteniendo así una ecuación de primer grado con la otra incógnita, y. Una vez resuelta, calculamos el valor de X sustituyendo el valor de y que ya conocemos.

Los pasos para resolver son los siguientes:

Despejamos en la primera ecuación la x:

Y la sustituimos en la segunda:

Calculamos x sabiendo y=2:

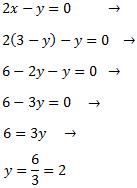
Por tanto, la solución del sistema es Gráfica Generada por Desmos

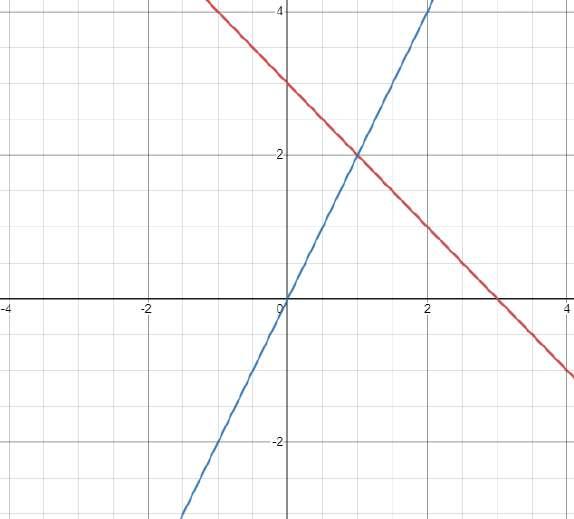
Método de Gauss

El método de Gauss se lo aplica para resolver sistemas de ecuaciones lineales 3x3, con 3 ecuaciones lineales y con 3 incógnitas o más, el objetivo es disminuir ecuaciones e incógnitas. Según lo investigado

El sistema de Gauss consiste en obtener un sistema equivalente al sistema original que tenemos que resolver, de manera que nos quede un sistema con una ecuación con una incógnita, otra ecuación con dos incógnitas, otra ecuación con tres incógnitas (Ekuatio, s.f.)

1. Separar los coeficientes.

2. Intercambiar fila 1 y fila 2.

3. Empezar convirtiendo los 2 números inferiores en 0.

4. Dividir el número superior con el fin de que salga 0, y a ese número lo multiplicamos con los números de la segunda fila.

5. Con el siguiente número hacemos lo mismo.

6. Con la nueva tabla copiamos las 2 filas y realizamos con el número que nos de 0 la multiplicación.

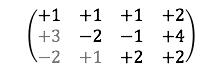
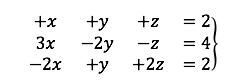
7. Copiamos como una ecuación.

8. Finalmente realizamos las ecuaciones y reemplazamos los valores, y para comprobar nos debe dar una igualdad.

Sistema De Ecuaciones Cuadráticas

Definición

Conocemos como sistemas de ecuaciones cuadráticas o sistemas de segundo grado a aquellos que están formados por al menos una ecuación cuadrática. Para resolverlos debemos aplicar los métodos revisados anteriormente sobre sistemas de ecuaciones lineales y otros métodos propios de los sistemas cuadráticos o de segundo grado (Alonso Borrego, Cabezón Ochoa , Fernández Rubio , García Cebrian, & Ruiz Gil, 2008).

Ejemplos

Sistema con 1 ecuación lineal y 1 ecuación cuadrática

El método idóneo para la solución de este sistema es:

El método de sustitución

“Este método utiliza la propiedad aditiva, multiplicativa y de sustitución; el procedimiento consiste en que despejes una de las variables de la ecuación lineal y luego sustituyas dicha variable en la ecuación cuadrática” (Universidad de Guanajuato,2021)

Ejemplo:

Identifica que la ecuación lineal del sistema y despeja la variable ��

Después sustituye �� =���� �� en la ecuación cuadrática

Desarrolla las operaciones

�� �� +������ ������+���� ���� ������+����+��=��

Suma los términos semejantes

�������� ������+������=��

Simplifica la ecuación dividiendo para 10 a toda la ecuación

���� ����+����=��

Factoriza

(�� ��)(�� ��)=��

Verifica la solución

��=��,��=��

Sustituye la solución de la variable �� en la ecuación �� = ���� ��

��=�� ��=��

��=��(��) �� ��=��(��) ��

��=�� ��=��

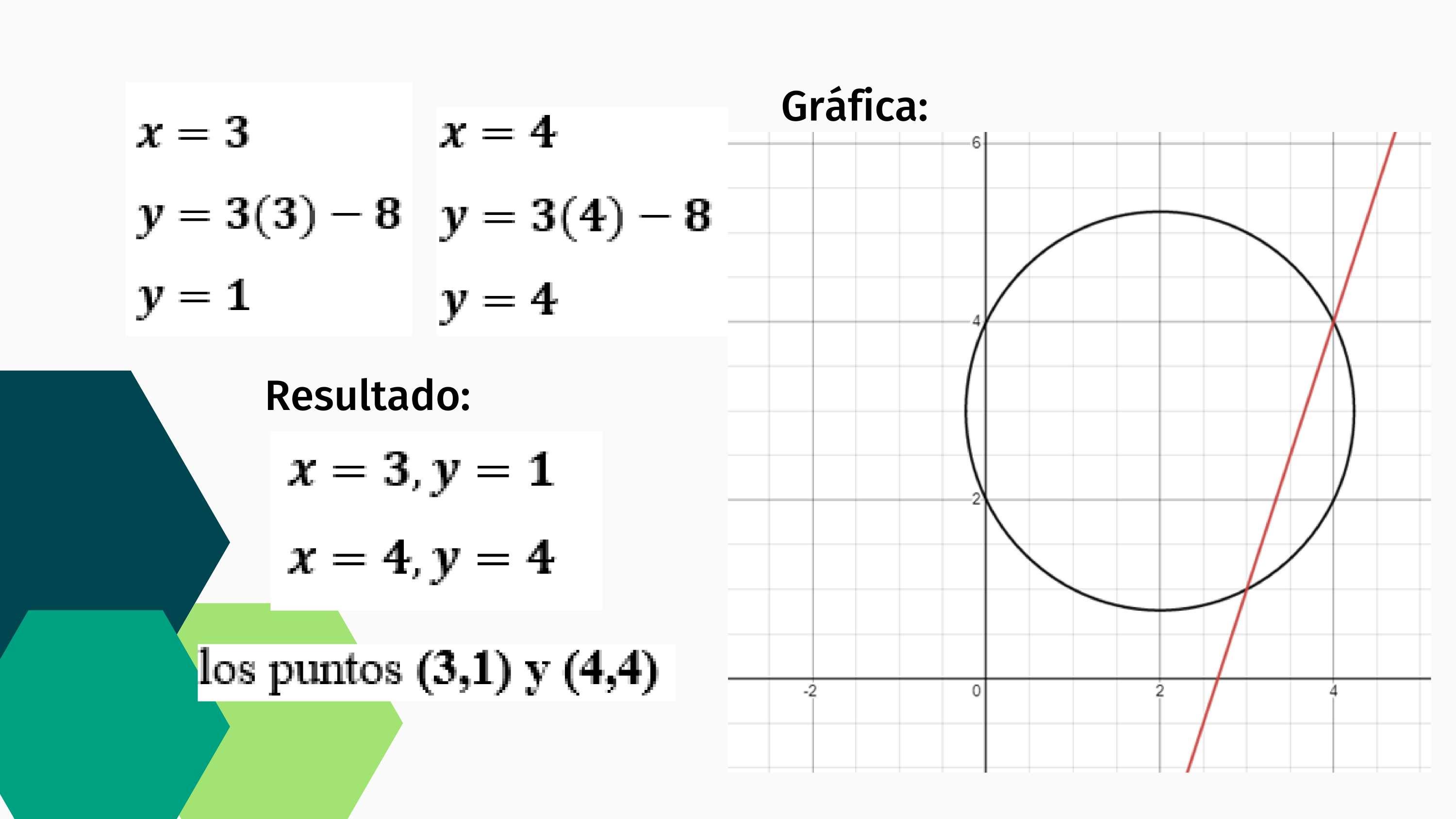
Concluye que la solución es:

��=��,��=��

��=��,��=��

o bien los puntos (3,1) y (4,4)

Gráfica Generada por Desmos Sistema con 2 ecuaciones cuadráticas

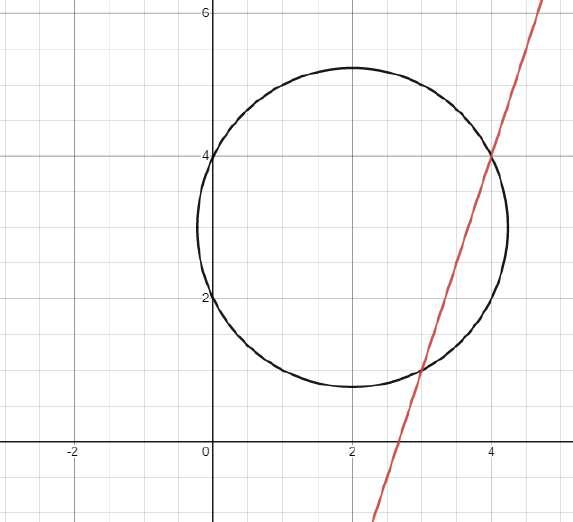
Por eliminación

Para resolver este tipo de sistemas de ecuaciones cuadráticas se puede realizar por algunos métodos de solución de los sistemas lineales. Sin embargo, uno de los métodos más sencillos para resolver sistemas cuadráticos resulta con el método de eliminación.

Así, y de acuerdo con la Universidad de Guanajuato (2021), se usa el método de eliminación para resolver sistemas de ecuaciones cuadráticos por su beneficiosa propiedad de multiplicación y suma, la cual usada con determinados números nos permite eliminar o anular variables y hacer más fácil la solución de dichos ejercicios.

Esto se refleja en el siguiente ejemplo

Iniciamos multiplicando la primera ecuación del sistema por el coeficiente de la variable a eliminar de la segunda ecuación con signo contrario. También multiplicamos la segunda ecuación del sistema por el coeficiente de la variable a eliminar de la primera ecuación manteniendo el mismo signo, así:

Sumamos las ecuaciones obtenidas anteriormente, eliminamos la variable y despejamos la variable restante.

Finalmente, sustituimos los valores de y en una ecuación del sistema original, sí:

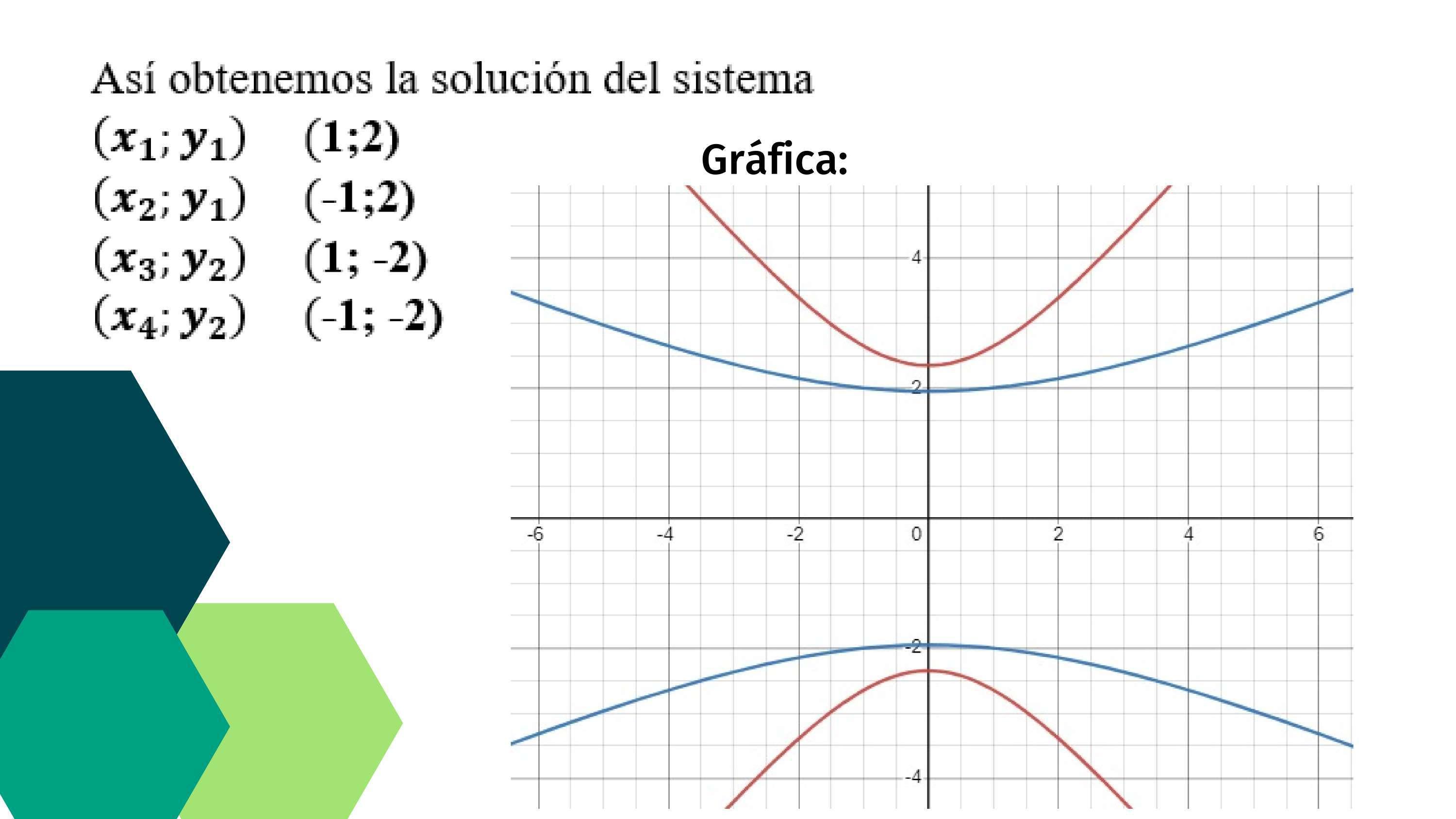
Así obtenemos la solución del sistema

(����;����) (1;2)

(����;����) (-1;2)

(����;����) (1; -2)

(����;����) (-1; -2)

Gráfica Generada por Desmos

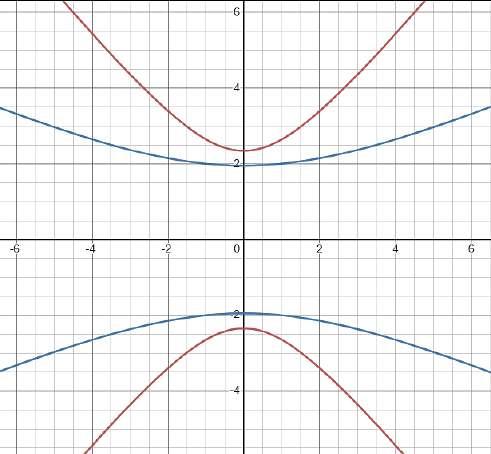
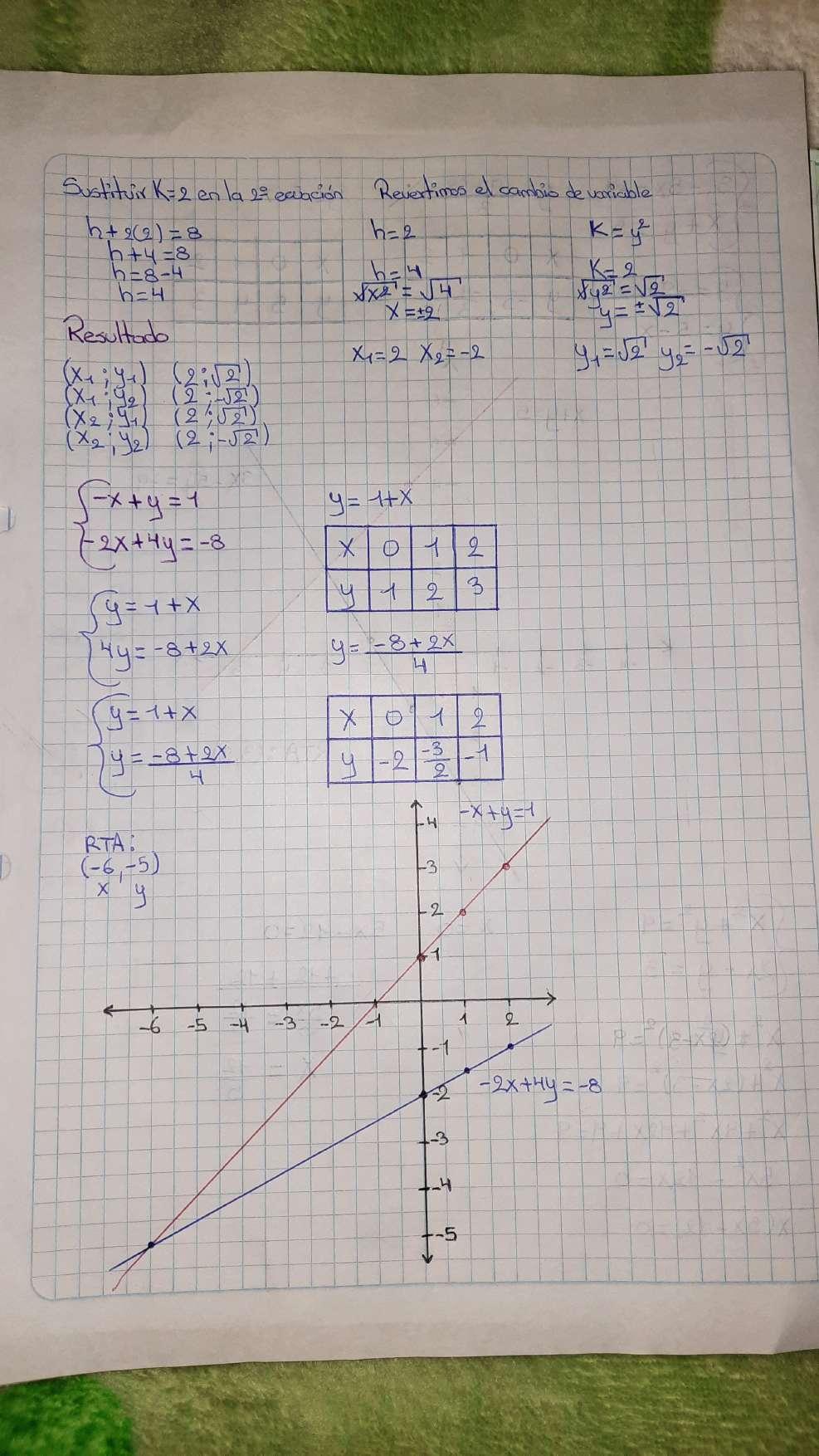
Por Cambio de Variable

Este método de cambio de variable es uno de los más conocidos y utilizados a la hora de resolver ecuaciones y sistemas de ecuaciones cuadráticas y exponenciales. Con la aplicación de esta técnica se permite pasar de una ecuación o sistema de ecuaciones complejo a uno más sencillo. En el caso de estos ejercicios se usa el cambio de variable para “convertir este sistema de segundo grado en uno de primero” (Javier Valdés Gómez, 2017, 2m16s).

El cambio de variable consiste en plantear una nueva variable para hacer más sencilla el desarrollo del problema, sin olvidar que al final se debe revertir este cambio, es decir, dejar la variable original (Jdm, 2011).

Para comprender mejor este método, se plantea el siguiente ejemplo:

Iniciamos realizando el cambio de variable

Así obtenemos el nuevo sistema:

Al pasar de tener un sistema de ecuación cuadráticas a uno lineal, que es el fin principal de este método, resolvemos el nuevo sistema por cualquier método de solución para sistemas de ecuaciones lineales. En este caso utilizaremos el método de sustitución.

Despejar n en la segunda ecuación Reemplazar n en la primera ecuación

Reemplazo el valor de m en el despeje de n

Para finalizar, revertimos el cambio de variable para obtener el resultado del sistema.

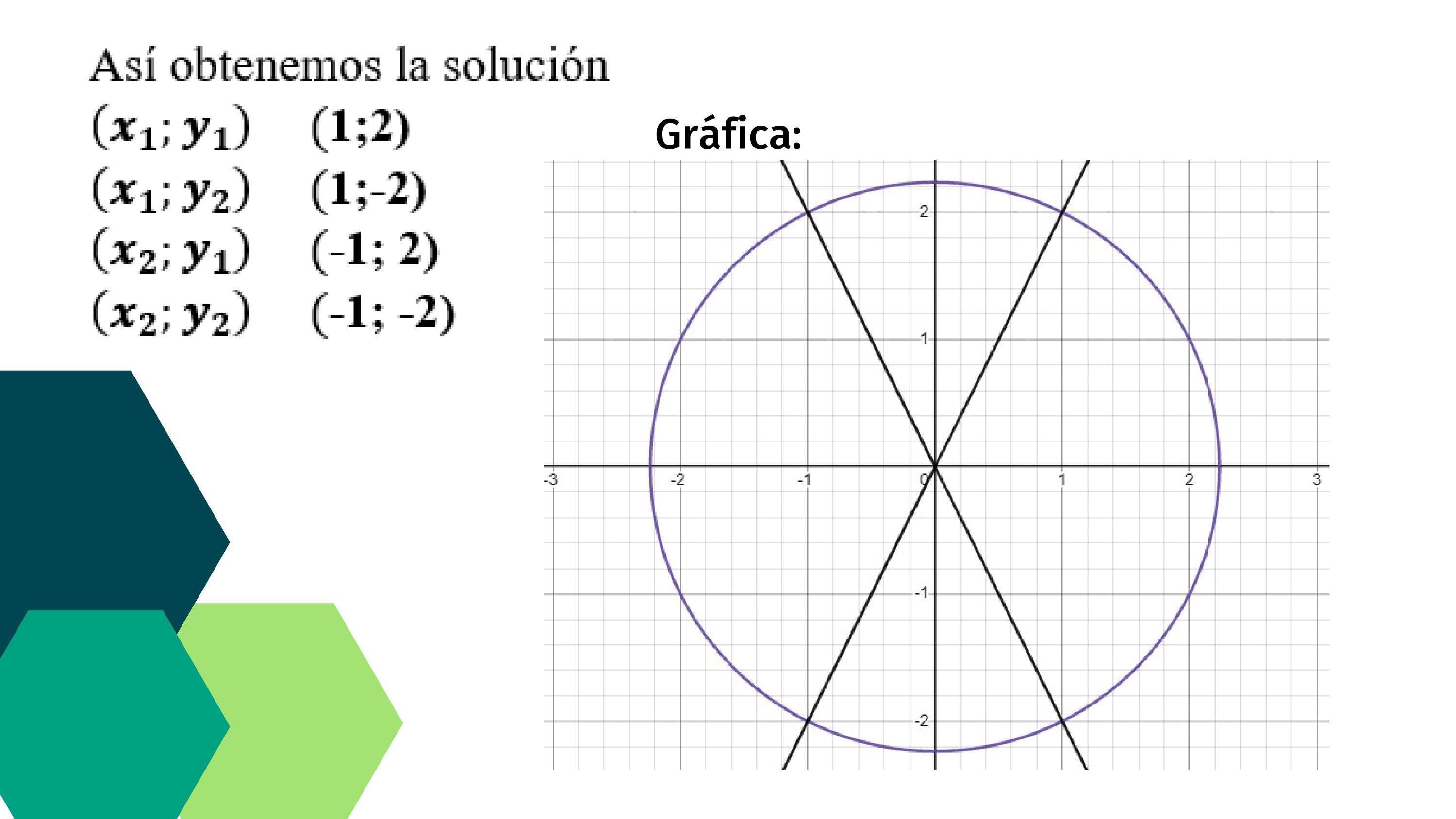
la solución del sistema

Gráfica Generada por Desmos

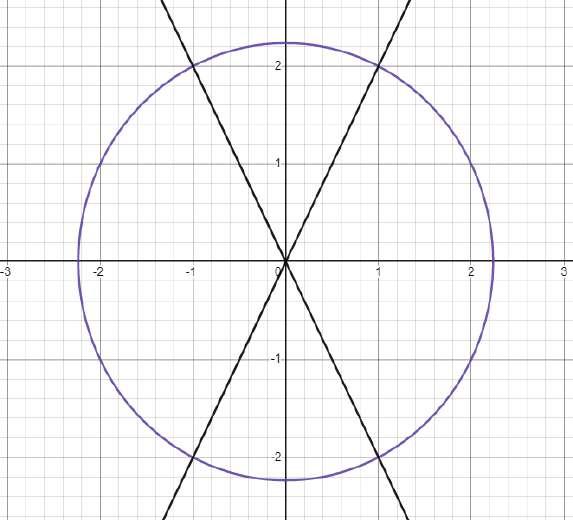
Método Gráfico

Sistemas de Ecuaciones Lineales

El método gráfico en los sistemas de ecuaciones lineales nos indica que:

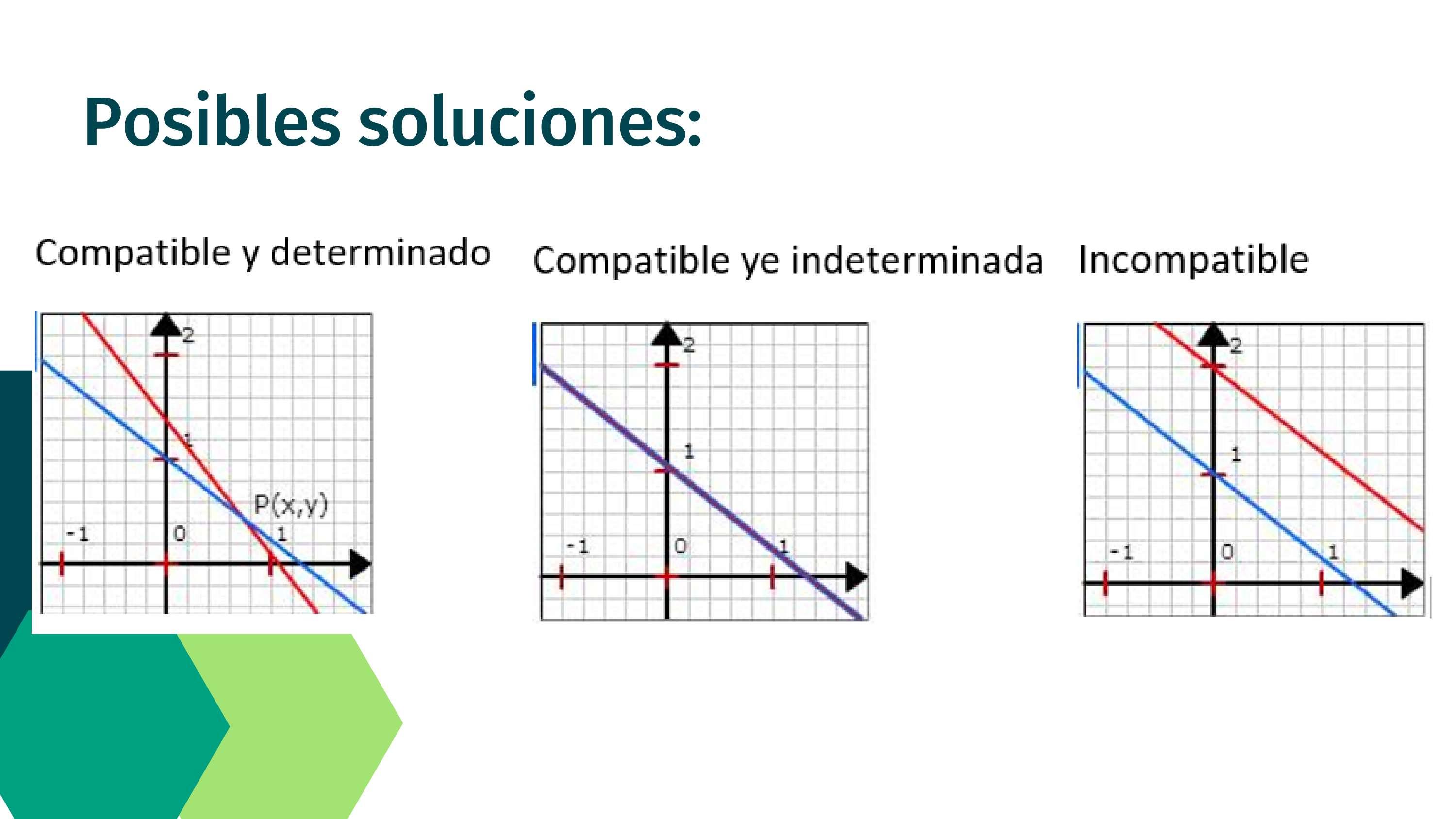
Cada una de las ecuaciones que forman un sistema lineal de dos ecuaciones con dos incógnitas es la de una función de primer grado, es decir, una recta. El método gráfico para resolver este tipo de sistemas consiste, por tanto, en representar en unos ejes cartesianos, o sistema de coordenadas, ambas rectas y comprobar si se cortan y, si es así, dónde. Esta última afirmación contiene la filosofía del proceso de discusión de un sistema por el método gráfico.

Hay que tener en cuenta, que, en el plano, dos rectas sólo pueden tener tres posiciones relativas (entre sí): se cortan en un punto, son paralelas o son coincidentes (la misma recta). Si las dos rectas se cortan en un punto, las coordenadas de éste son el par (x, y) que conforman la única solución del sistema, ya que son los únicos valores de ambas incógnitas que satisfacen las dos ecuaciones del sistema, por lo tanto, el mismo es compatible determinado. Si las dos rectas son paralelas, no tienen ningún punto en común,

por lo que no hay ningún par de números que representen a un punto que esté en ambas rectas, es decir, que satisfaga las dos ecuaciones del sistema a la vez, por lo que éste será incompatible, o sea sin solución.

Por último, si ambas rectas son coincidentes, hay infinitos puntos que pertenecen a ambas, lo cual nos indica que hay infinitas soluciones del sistema (todos los puntos de las rectas), luego éste será compatible indeterminado (Universidad Politécnica Estatal del Carchi [UPEC], 2022,p.105)

El proceso de resolución de un sistema de ecuaciones mediante el método gráfico se resume en las siguientes fases:

1. Se despeja la incógnita Y en ambas ecuaciones.

2. Se elabora una tabla de valores asociada a cada ecuación. Para cada tabla de valores se asignan a la incógnita X un par de valores (a conveniencia), y se calcula qué valor tomará la incógnita y en cada caso.

Ecuación I: Ecuación II:

X1 Y1

X2 Y2

X Y X1 Y1 X2 Y2

La recta asociada a la ecuación I pasará por los puntos (x1, y1), (x2, y2)y la asociada a la ecuación II pasará por los puntos (x′1, y′1), (x1′, y2′) Se representan en el plano los puntos (x1, y1), (x2,y2) se unen. Así queda representada la recta asociada a la ecuación

I. Se representan en el mismo plano los puntos (x′1, y′1), (x′2, y′2)y se unen. Así queda representada la recta asociada a la ecuación II. La solución gráfica del sistema es el punto de corte de ambas rectas.

3. Cada ecuación lineal tiene como representación gráfica una recta. Un punto de corte de ambas rectas será solución del sistema. Por lo tanto:

a. Si las rectas se cortan en un punto la solución del sistema es única.

b. Si las rectas son paralelas, el sistema no tiene solución.

c. Si las rectas son coincidentes, el sistema tiene infinitas soluciones.

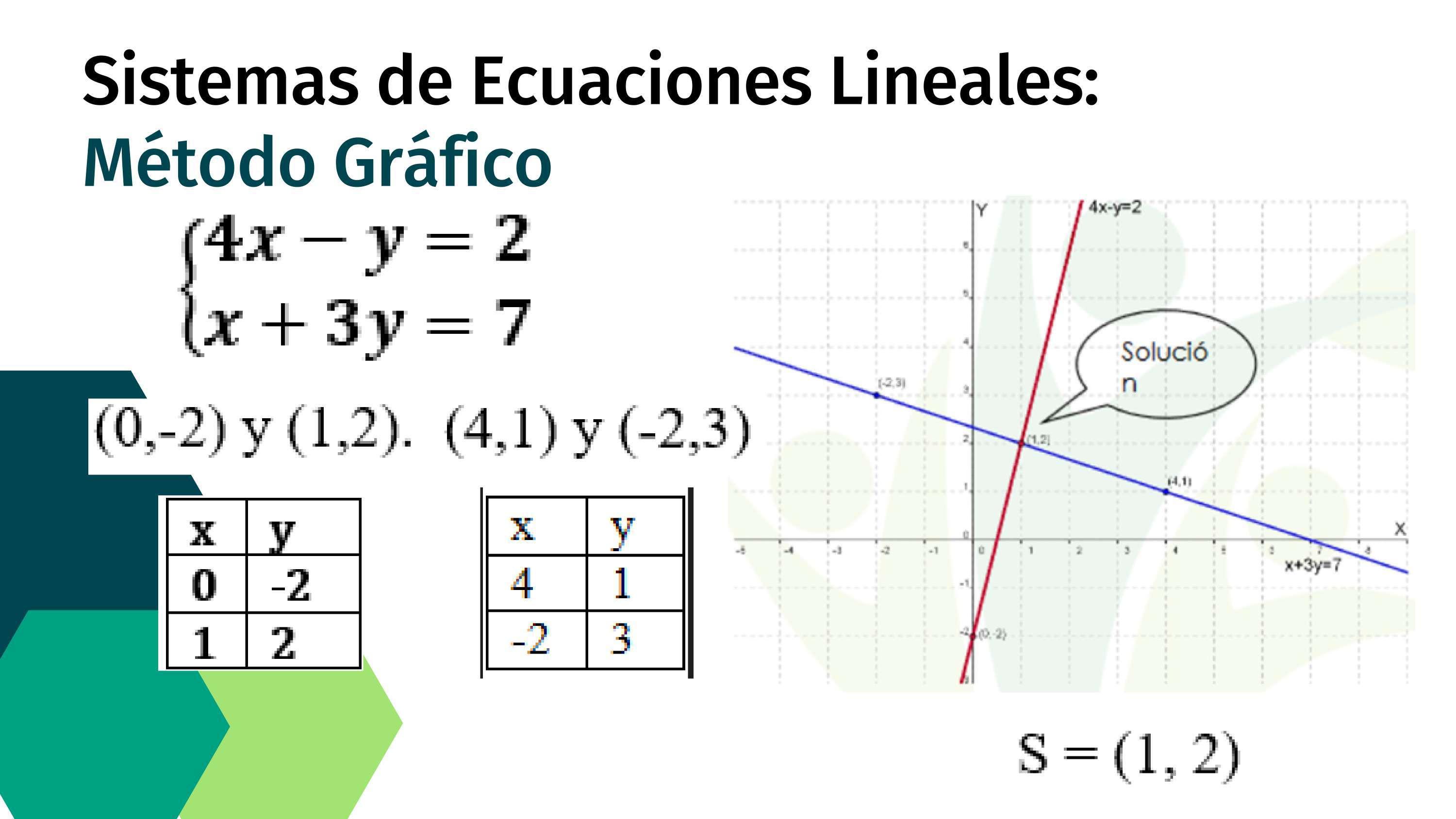
Ejemplo:

•Tabla de valores de la primera ecuación: La recta asociada a la primera ecuación pasa por (��, ��) y (��,��)

•Tabla de valores de la segunda ecuación: La recta asociada a la segunda ecuación pasa por (��,��) y ( ��,��)

•Representación gráfica: Gráfica

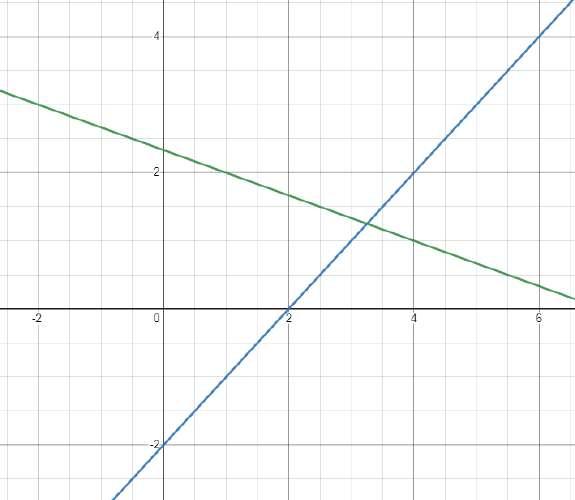
Solución del sistema es el par ordenado: (��,��)

Sistemas de Ecuaciones Cuadrática

Al hablar de sistemas de ecuaciones cuadráticas por el método gráfico, tenemos que: Los sistemas de ecuaciones de segundo grado son de tipo no lineal, y para su resolución se usan los procedimientos aplicados en los sistemas de primer grado o lineales. Considerando que el sistema estuviera formado por dos ecuaciones en donde debe tenerse en cuenta que

(Universidad Politécnica Estatal del Carchi [UPEC], 2022):

• Las ecuaciones cuadráticas son representativas de curvas cónicas, ya sean circunferencias, elipses, parábolas o hipérbolas. Así, cuando se representa gráficamente estas ecuaciones en un plano, es posible visualizar varios casos, tal como lo indica Universidad Politécnica Estatal del Carchi [UPEC] (2022, p. 110).

• Si las dos cónicas, o una cónica y una recta, del sistema se cortan en uno o dos puntos, el sistema es compatible determinado.

• Cuando se obtienen dos cónicas coincidentes, el sistema es compatible indeterminado.

• Si las dos cónicas, o la cónica y la recta, no se cortan en ningún punto del plano, el sistema es incompatible (carece de solución).

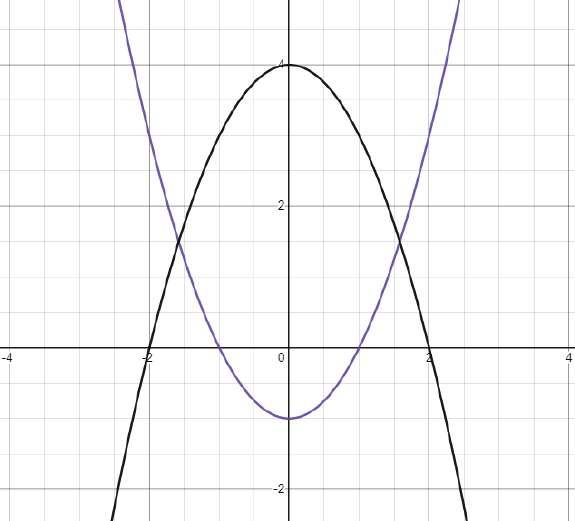
Ejemplo:

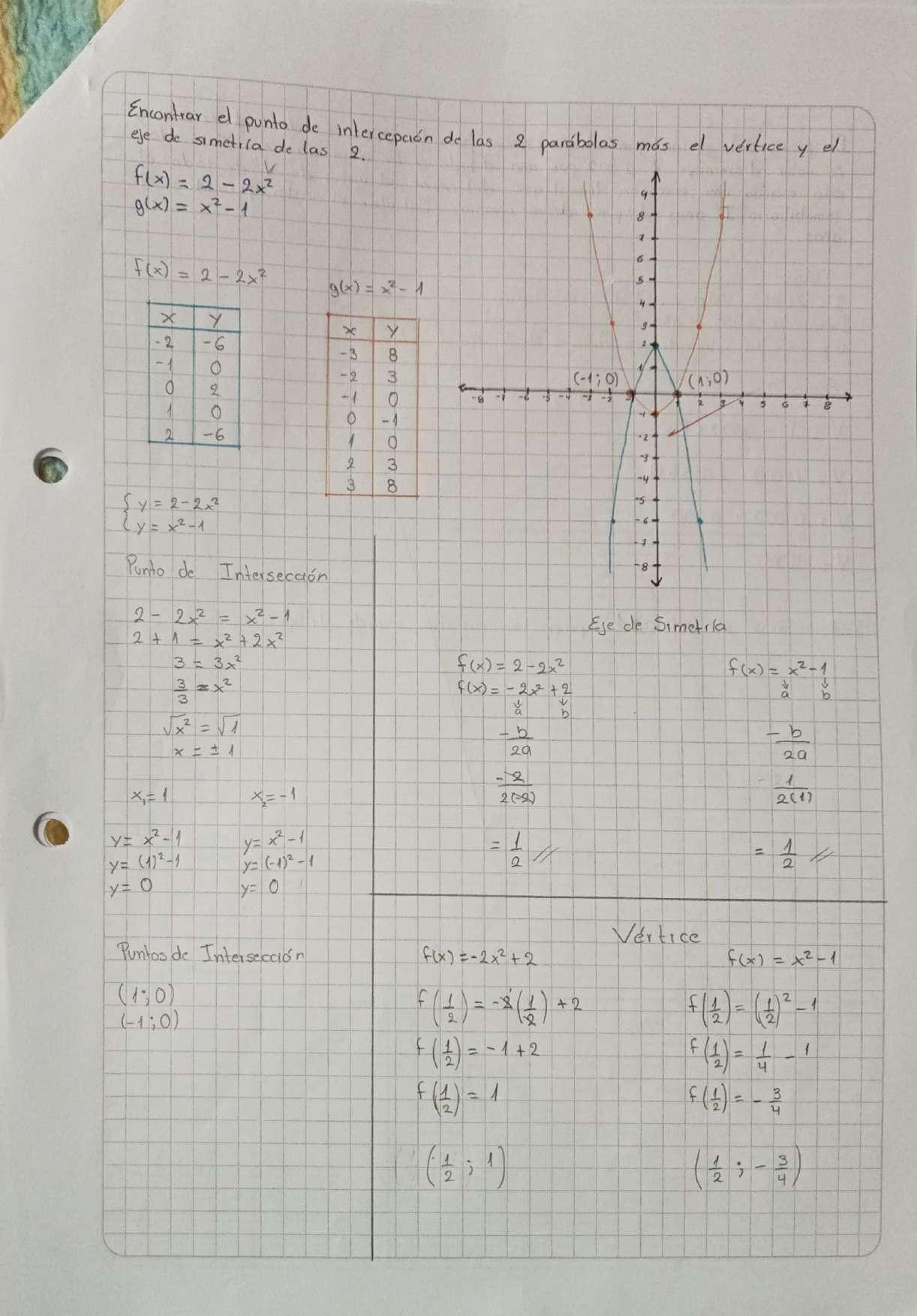
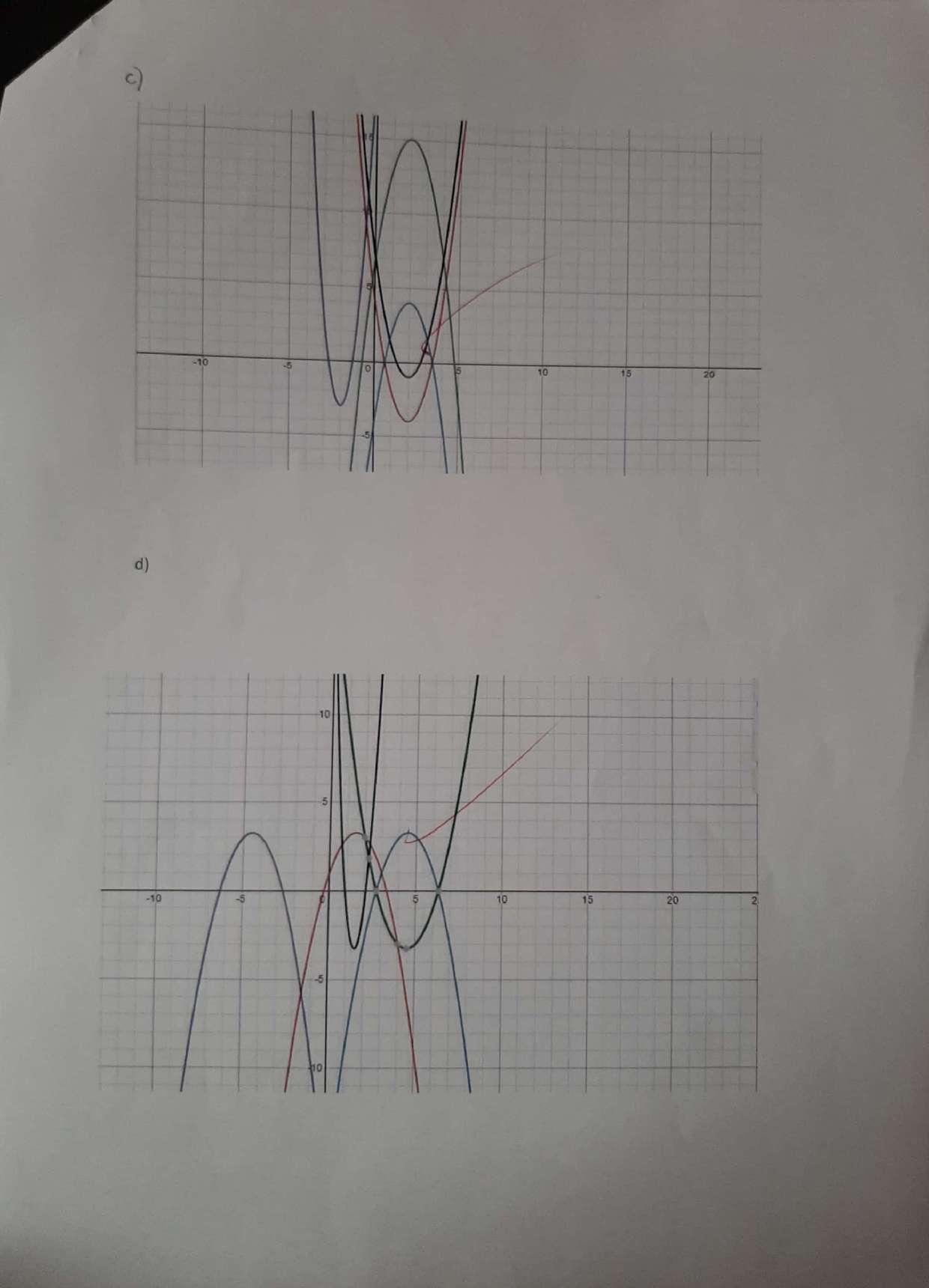
Podemos encontrar la solución del sistema de ecuación por el método grafico como negativa y positiva las parábolas.

Tomando la primera ecuación

Vértice: (��,��)

��= �� ���� �� = �� �� = �� �� = �� �� = �� ��(��) = �� x y 2 3 1 0 0 -1 -1 0 -2 3

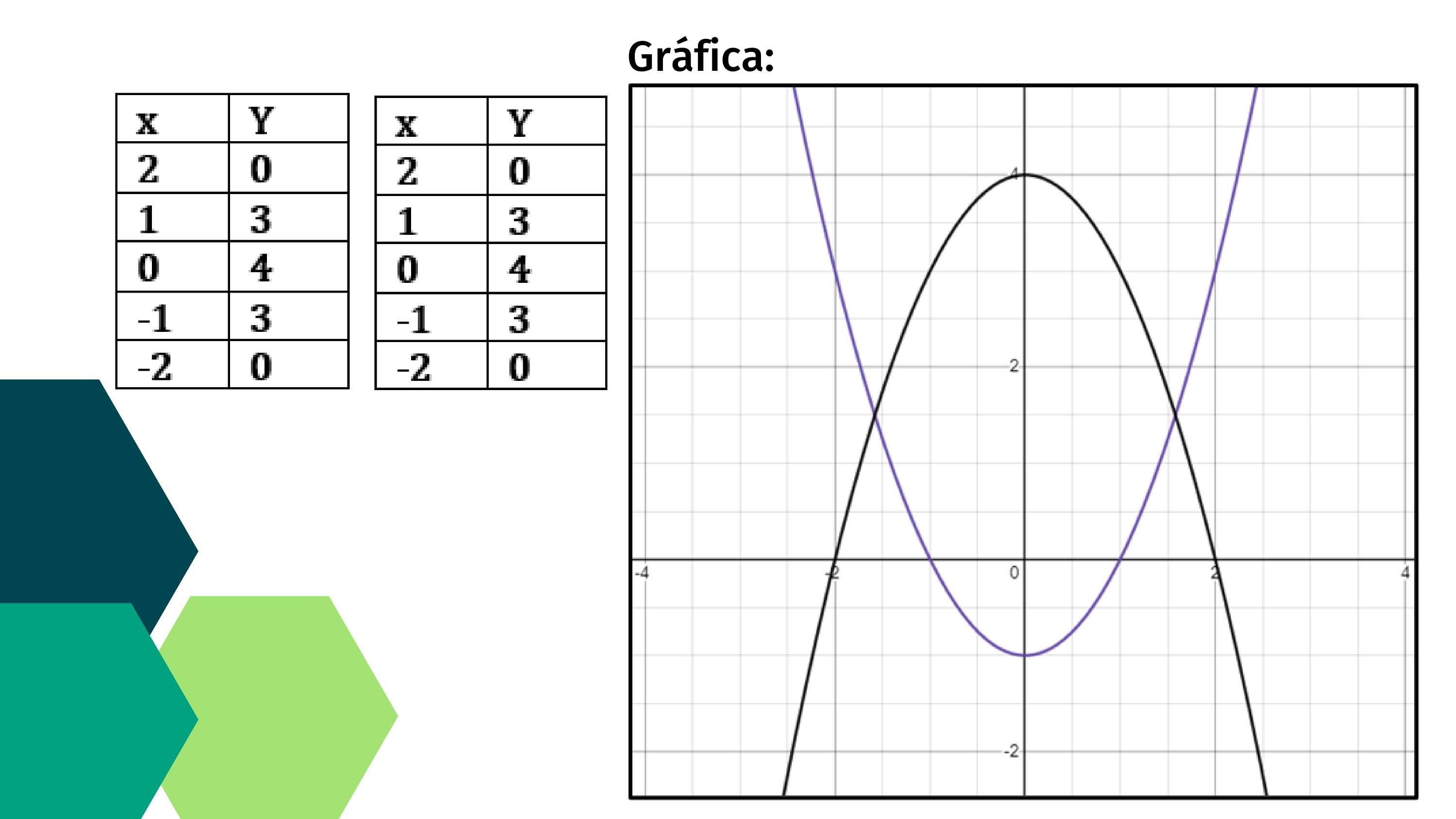
Tomando la segunda ecuación ���� +�� ��=��

��= ���� +��

Vértice: (��,��) ��= �� ���� �� = ��

•Representación gráfica:

Gráfica Generada por Desmos

CONCLUSIONES

Gracias a la investigación realizada obtuvimos un mejor conocimiento sobre qué son, para qué sirven y cuáles son los métodos más usados para resolver los sistemas de ecuaciones lineales y cuadráticas. Y así, al momento de buscar una solución, sea en problemas cotidianos ya que estos existen en el diario vivir o se nos plantean en diversas áreas y ciencias, las podremos predecir de una manera rápida y razonable. En fin, tener un conocimiento claro sobre la finalidad que tiene el sistema de ecuaciones es de gran importancia para los estudiantes de nivelación Turismo, pues será de gran ayuda en lo personal y también para poder ayudar a más personas que desconozcan estos métodos fundamentales para una correcta resolución.

Además, gracias a la investigación sobre los sistemas de ecuación lineal y cuadrática, podemos concluir que estos sistemas son de mucho valor y utilidad para resolver problemas de todo tipo, a la vez que logramos identificar y conocer los métodos de resolución más utilizados en los sistemas de ecuaciones. Esto es importante para que nosotros como estudiantes logremos desarrollar diferentes habilidades que por naturaleza llevamos dentro.

Para terminar, podemos decir que la investigación fue clave en nuestro proceso de estudio matemático, ya que de esta manera analizamos el proceso paso a paso de cada uno de los métodos más utilizados para resolver correctamente los sistemas de ecuaciones lineales y cuadráticas. A su vez, compartimos y socializamos el trabajo realizado para establecer comparaciones y llegar a acuerdos entre todos con el fin de seleccionar la información más relevante y así, generar un material que sea de ayuda a la hora de realizar una exposición.

REFERENCIAS

Alonso Borrego, J. L., Cabezón Ochoa , M. Á., Fernández Rubio , J. I., García Cebrian, M. J., & Ruiz Gil, C. (2008). Matemáticas B. Obtenido de Cide@d Centro para la Innovación y Desarrollo de la Educación a Distancia:

http://recursostic.educacion.es/secundaria/edad/4esomatematicasB/ecuaciones/impres os/quincena4.pdf

Desmos. Calculadora Gráfica. https://www.desmos.com/ calculator?lang=es

Ekuatio. (s.f.). Cómo resolver sistemas de ecuaciones lineales por el método de Gauss.

Obtenido de https://ekuatio.com/como-resolver-sistemas-de-ecuaciones-lineales-porel-metodo-de-gauss-ejercicios-resueltos/

Javier Valdés Gómez. (23 de febrero de 2017). Sistemas de ecuaciones de segundo grado.

[Archivo de video]. YouTube. https://www.youtube.com/watch?v=UkxYwar05VE

Jmd. (22 de abril de 2011). Cambio de Variable. Obtenido de Matetam.

http://www.matetam.com/glosario/definicion/cambio-variable

Matesfacil. (s.f.). Métodos para Sistemas de Ecuaciones: Sustitución, Igualación y Reducción. Obtenido de https://www.matesfacil.com/ESO/Ecuaciones/resueltossistemas-ecuaciones.html

Matemáticas profe Alex. (10 de mayo de 2018). Sistemas de ecuaciones 2x2 | Método de Reducción - Eliminación | Ejemplo 1. [Archivo de video]. YouTube.

https://www.youtube.com/watch?v=0ilTVp5uRz8

Ramos, L. (2021). Sistema de ecuaciones lineales. Santa Teresa del Tuy: Noria

C.I.15.040.809.

Universidad de Guanajuato. (2 de diciembre de 2021). Clase digital 9: Métodos de solución de sistemas de ecuaciones cuadráticas con dos variables. Obtenido de NODO Universitario Universidad de Guanajuato. https://blogs.ugto.mx/rea/clase-digital-9metodos-de-solucion-de-sistemas-de-ecuaciones-cuadraticas-con-dos-variables/ (Universidad Politécnica Estatal del Carchi [UPEC]. (2022). Guía Didáctica de Matemática

Tulcán: UPEC. https://upecedumy.sharepoint.com/personal/fernando_ortega_upec_edu_ec/_layouts/15/AccessDenie d.aspx?Source=https%3A%2F%2Fupecedu%2Dmy%2Esharepoint%2Ecom%2Fperso nal%2Ffernando%5Fortega%5Fupec%5Fedu%5Fec%2F%5Flayouts%2F15%2Foned rive%2Easpx%3Fid%3D%252Fpersonal%252Ffernando%255Fortega%255Fupec%2

55Fedu%255Fec%252FDocuments%252F2022B%252FGu%25C3%25ADas%252FG

u%25C3%25ADa%2520Did%25C3%25A1ctica%2520Matem%25C3%25A1ticas%2

520%252D%2520Unidad%2520II%2520%252D%2520CENIV%2520%252D%2520

2022B%252Epdf%26parent%3D%252Fpersonal%252Ffernando%255Fortega%255F

upec%255Fedu%255Fec%252FDocuments%252F2022B%252FGu%25C3%25ADas

%26ga%3D1&correlation=69cf86a0%2Db06b%2Dd000%2Dca46%2D17ab6bce2c86

&Type=item&name=4cc1677e%2De736%2D4b4c%2Da911%2D42e1858934fa&listI temId=90

EVALUACIONES-PARCIAL2

PruebasSemanalesyPruebaParcial

APRENDIZAJE AUTÓNOMO Y

APRENDIZAJE EN CONTACTO CONELDOCENTE-PARCIAL3

Talleres

UNIVERSIDAD POLITÉCNICA ESTATAL DEL CARCHI

Nombre: Leidy Guandinango Curso: Nivelación Turismo – Paralelo AM

Fecha: 16 de enero del 2022 Materia: Matemática

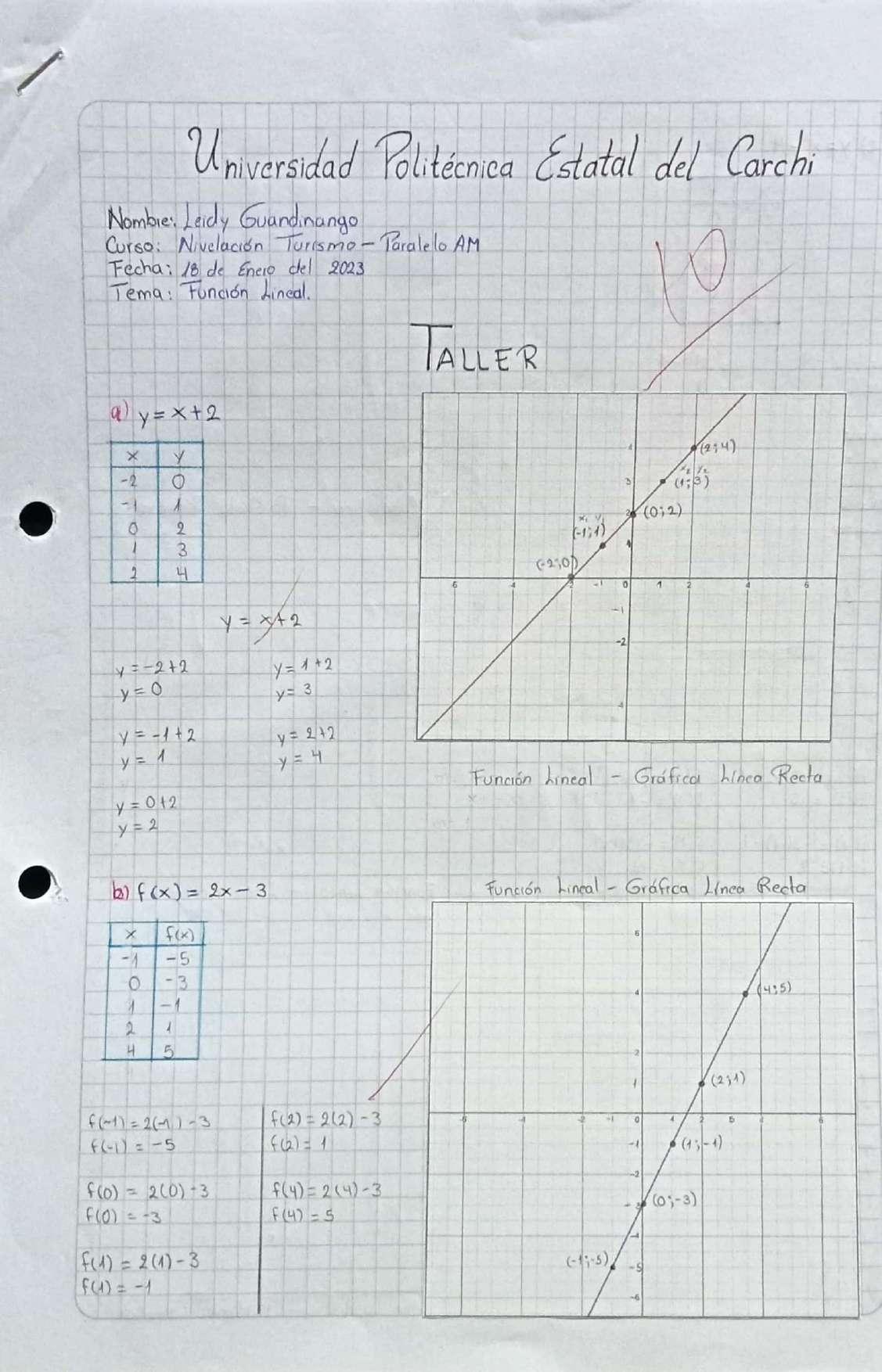
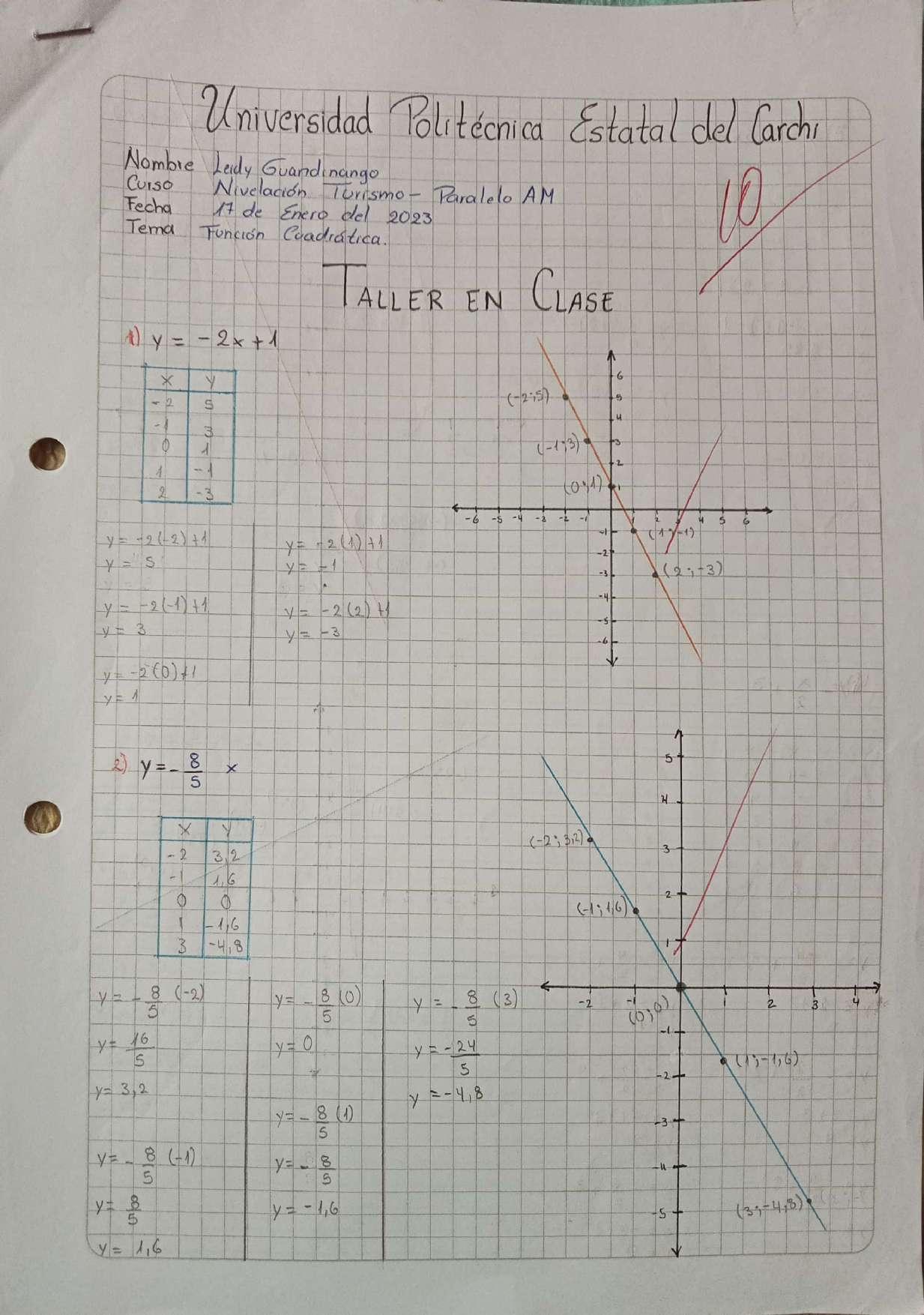
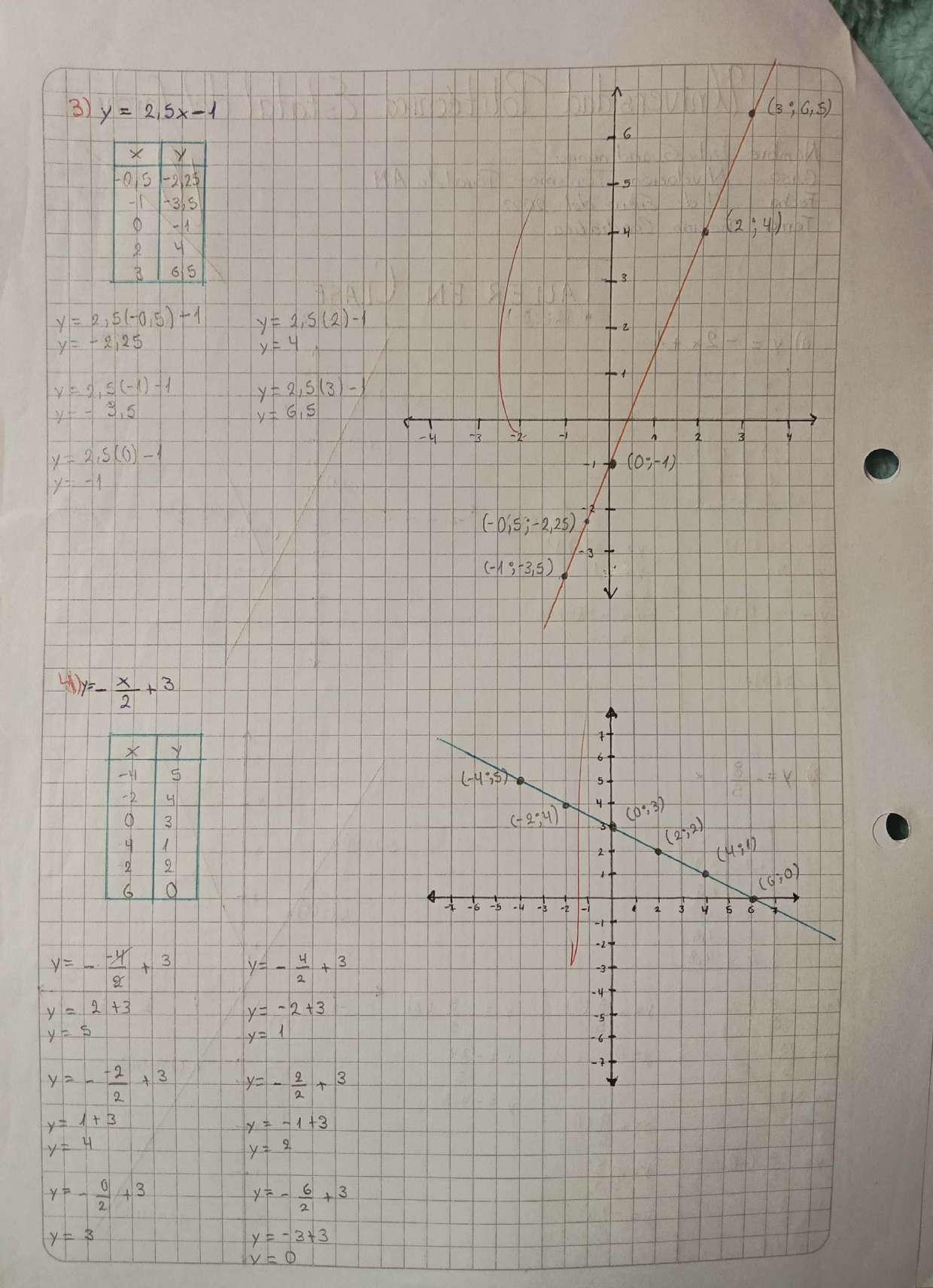
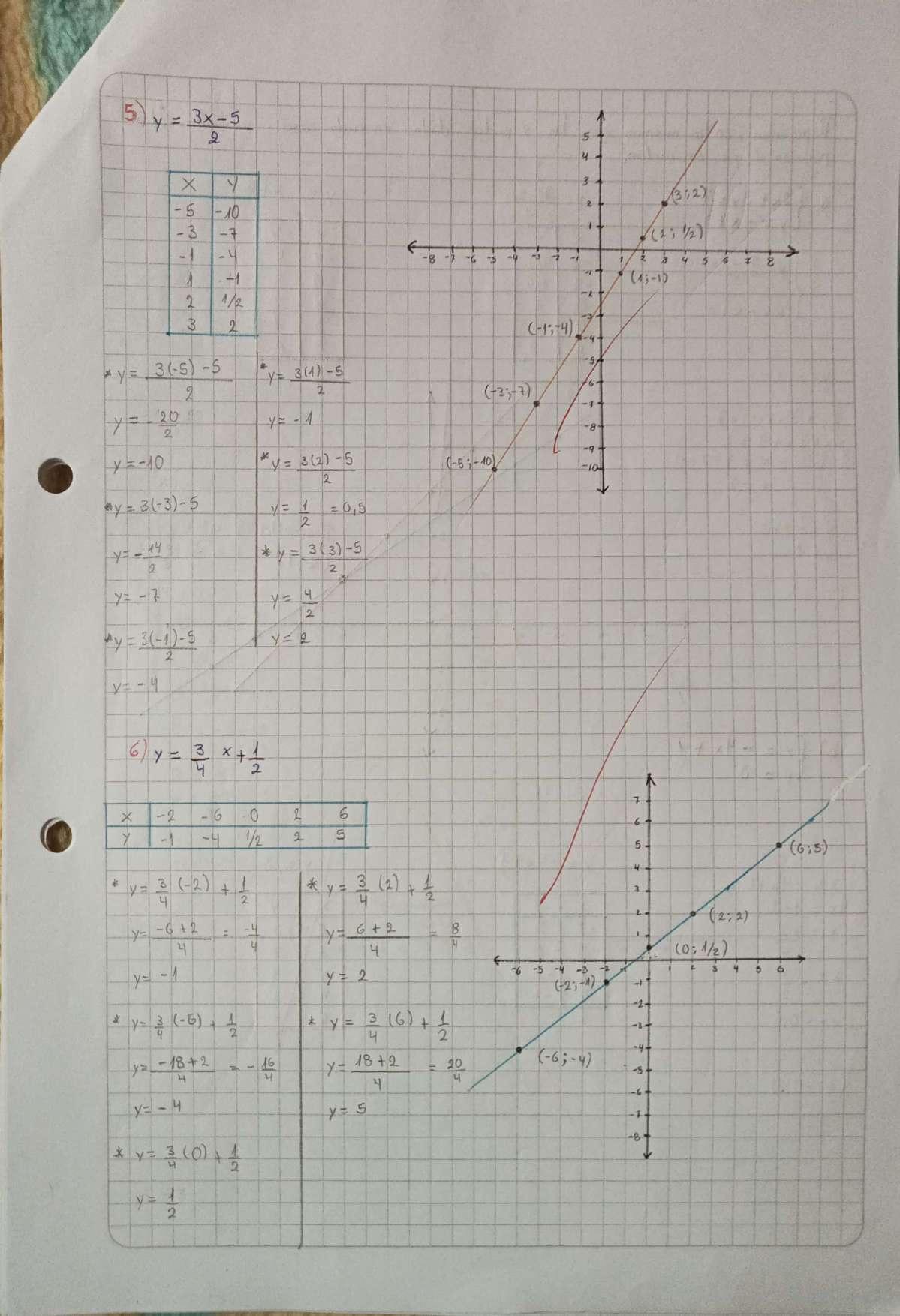
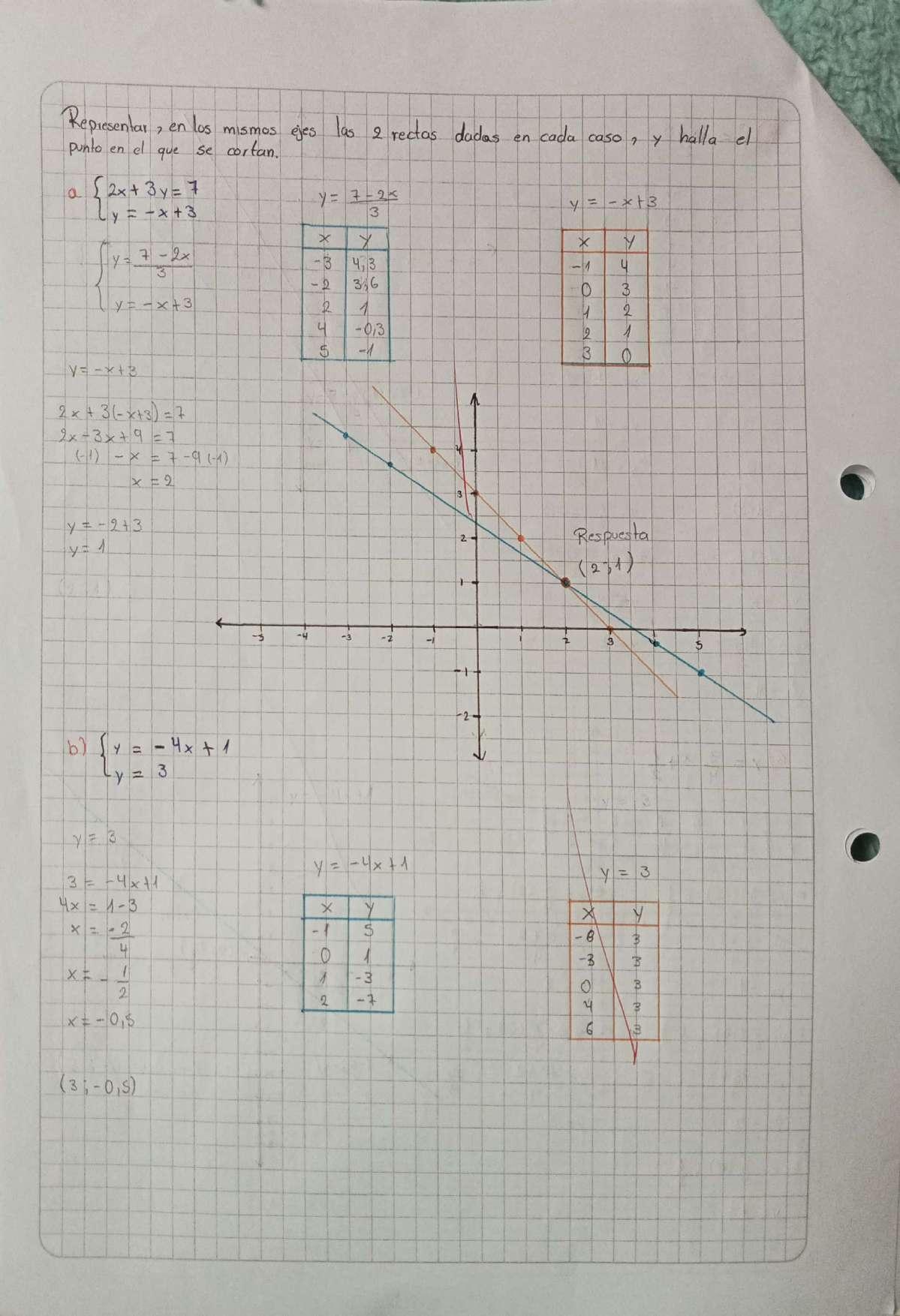
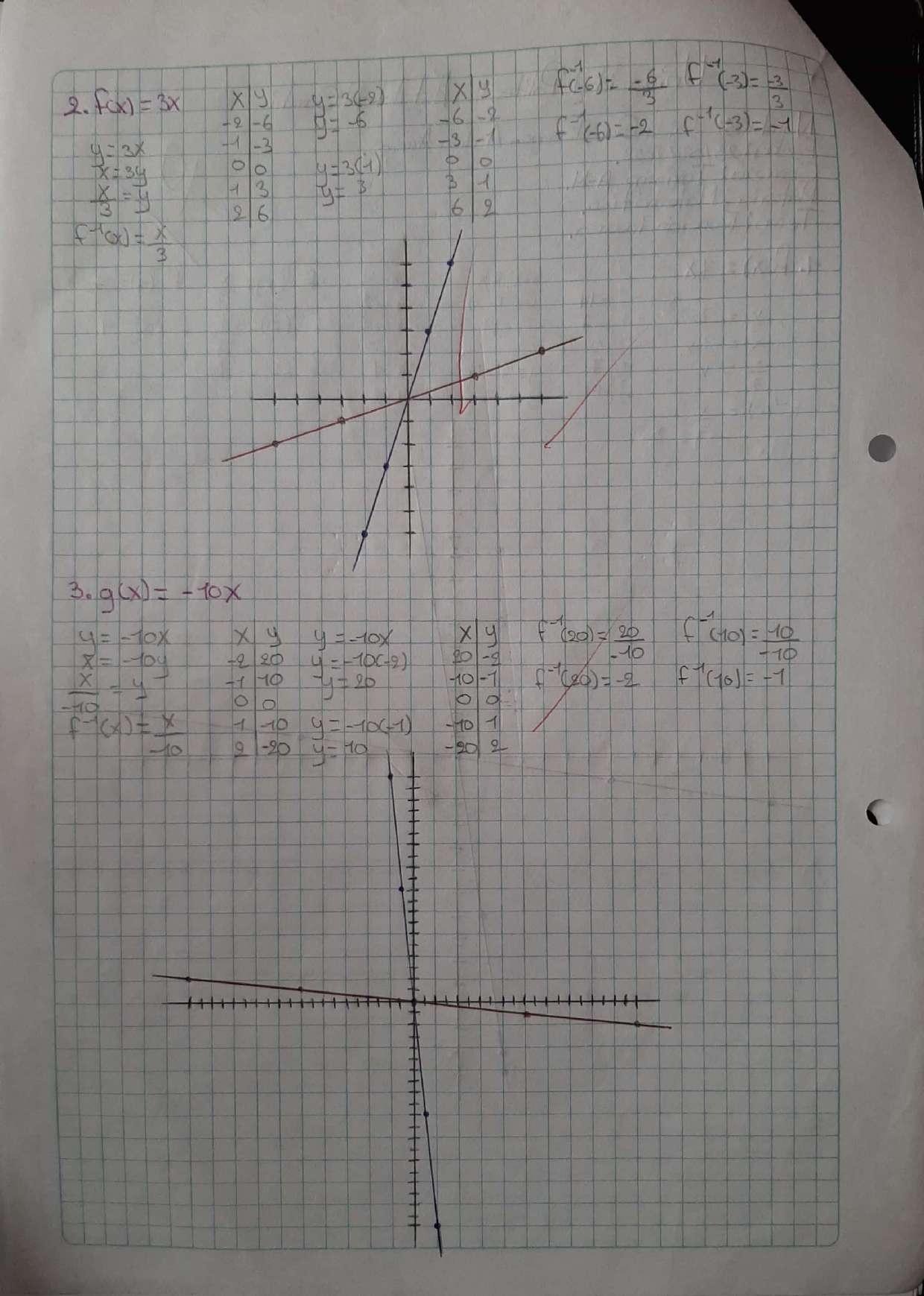
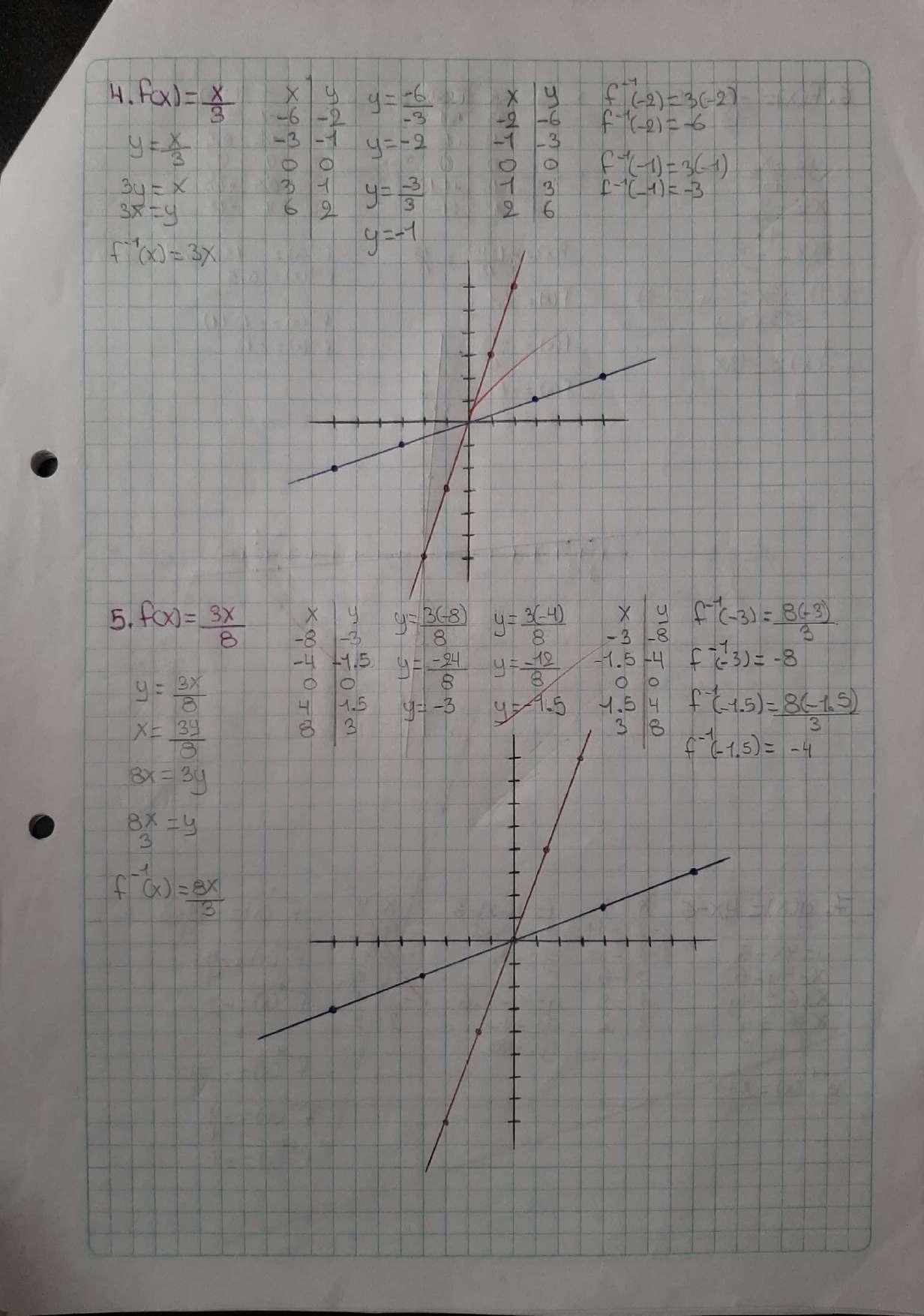
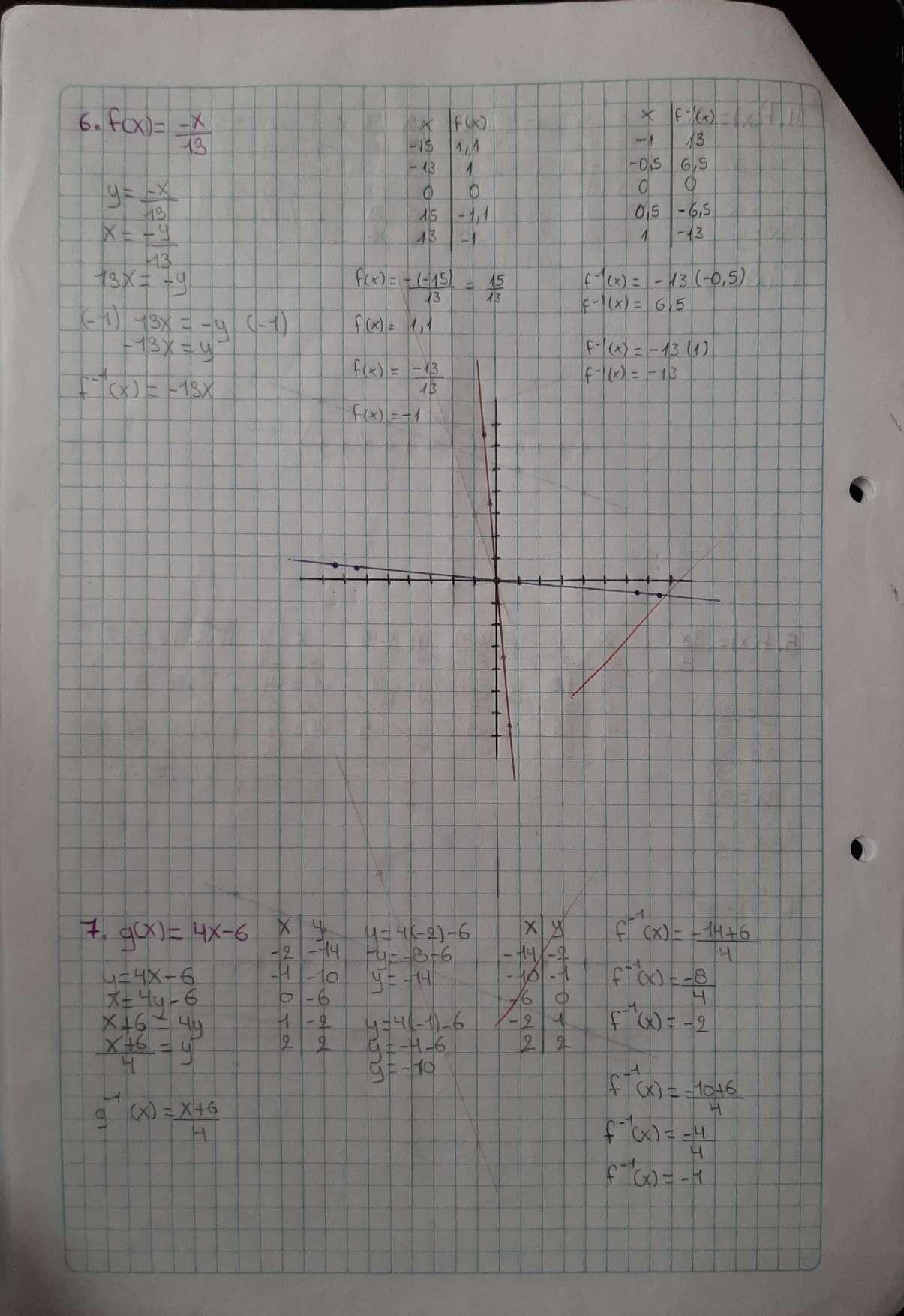
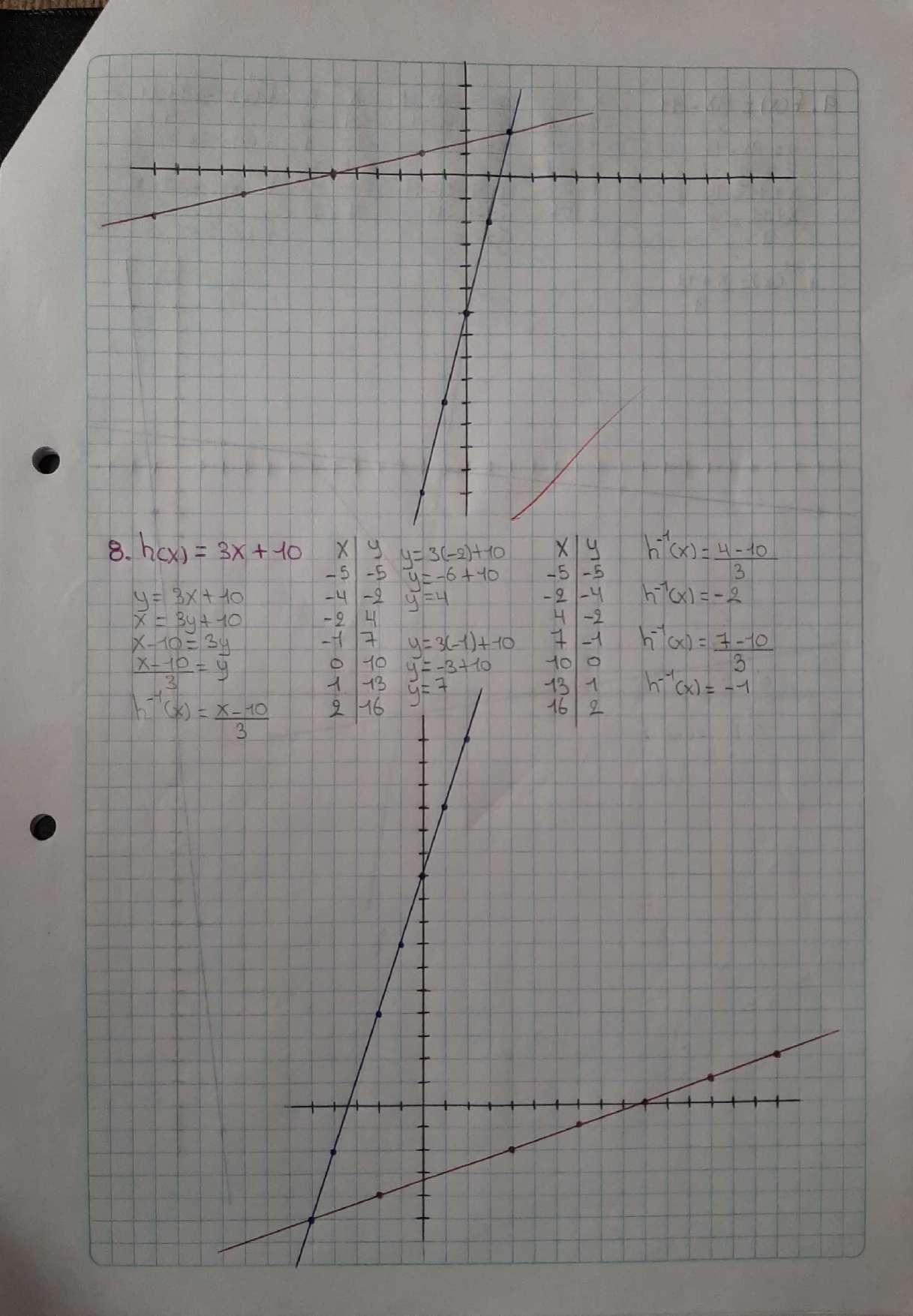
APLICACIÓN FUNCIONES LINEALES

1) Un motociclista transita por una autopista recta a una aceleración y velocidad constante. Su copiloto contabiliza las señales de tránsito que existen en la calzada:

• Cuando lleva 1 minuto, ha observado 3 señales.

• Cuando lleva 3 minutos, ha observado 15 señales.

• Obtener la función que proporciona el número de señales vistas en función del tiempo sabiendo que es una ecuación lineal.

¿Cuántas señales habrá visto en media hora?

Observará 177 señales.

Datos:

Obtenemos la Función: ��(��)=6�� 3

Entonces:

��(30)=6(30) 3

��(30)=180 3

��(30)=177

2) La UPEC realiza una inversión de 5.000$ para preparar libros de matemáticas El coste de fabricación y publicación por libro es de 4$. Además, se debe pagar al autor del libro 1$ por cada libro por derechos de autor. Se decide que el precio de venta del libro sea 15$.

Se pide:

a. La función de beneficios (ganancias menos gastos) de la universidad en función del número de libros vendidos. Representar su gráfica.

b. El número de libros que deben venderse para que la universidad tenga unas ganancias de 100.000$.

c. ¿Cuáles son los beneficios si se venden sólo 200 libros?

Datos:

Inversión=5000$

Costo x turista=4$

Reservación =1$

PVP =15$

Obtenemos la Función: ��(��)=15�� 4�� �� 5000≥0

a. ��(��)=10�� 5000

b. ��(��)=10�� 5000

100000 =10�� 5000

100000+5000 =10��

105000=10��

�� = 105000 10

�� =10500

c. ��(��)=10�� 5000

��(200)=10(200) 5000

��(200)= 3000

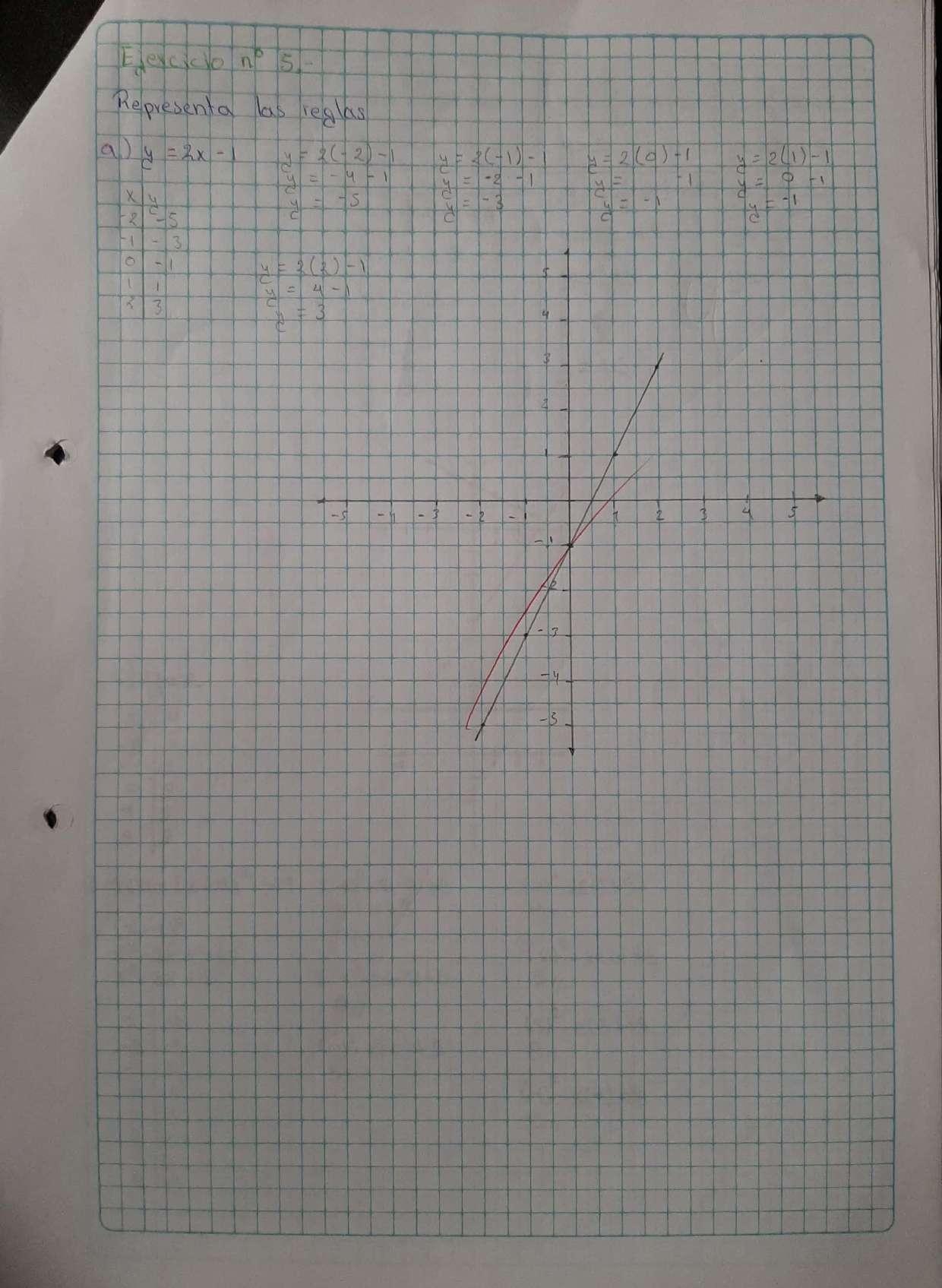
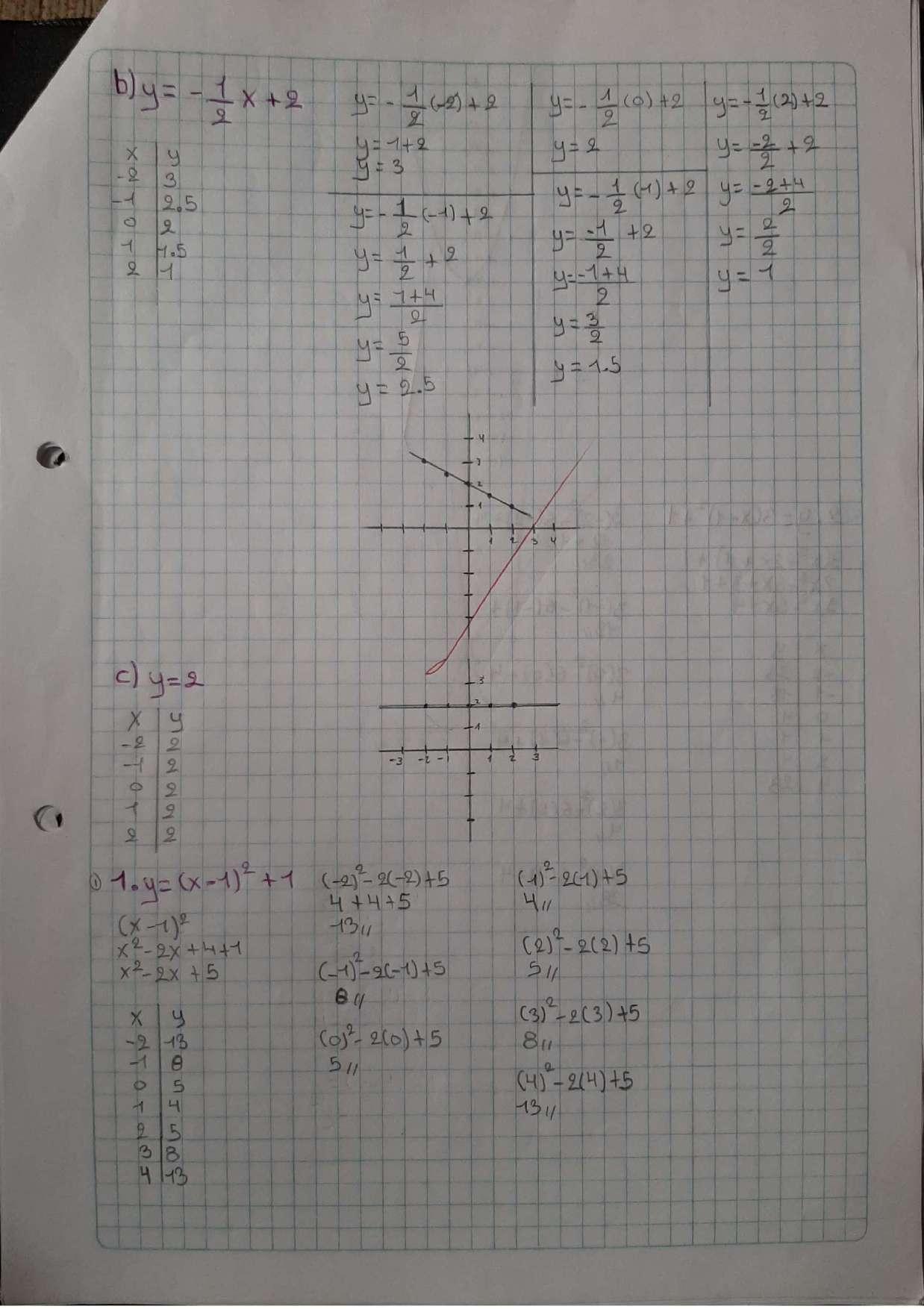
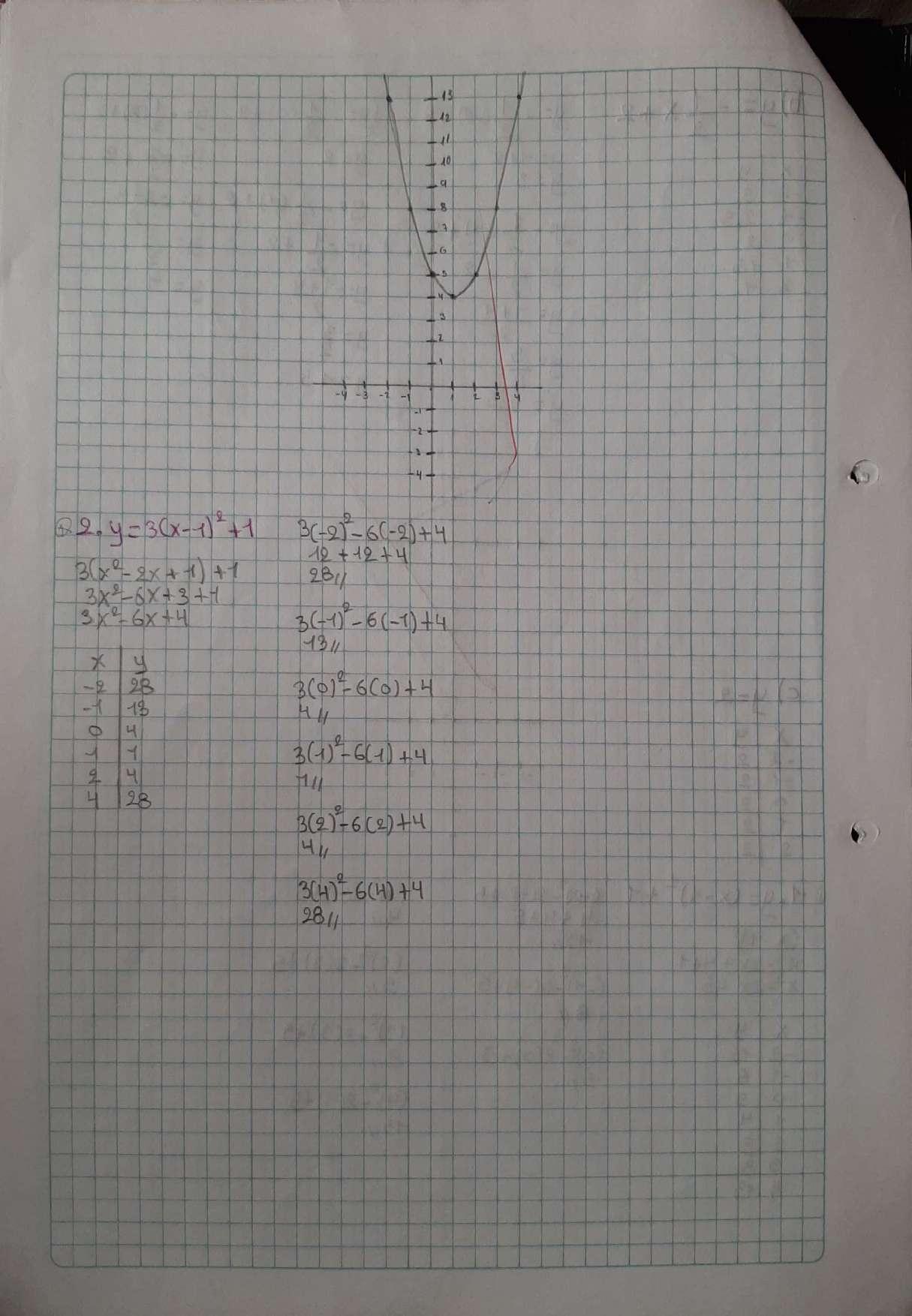
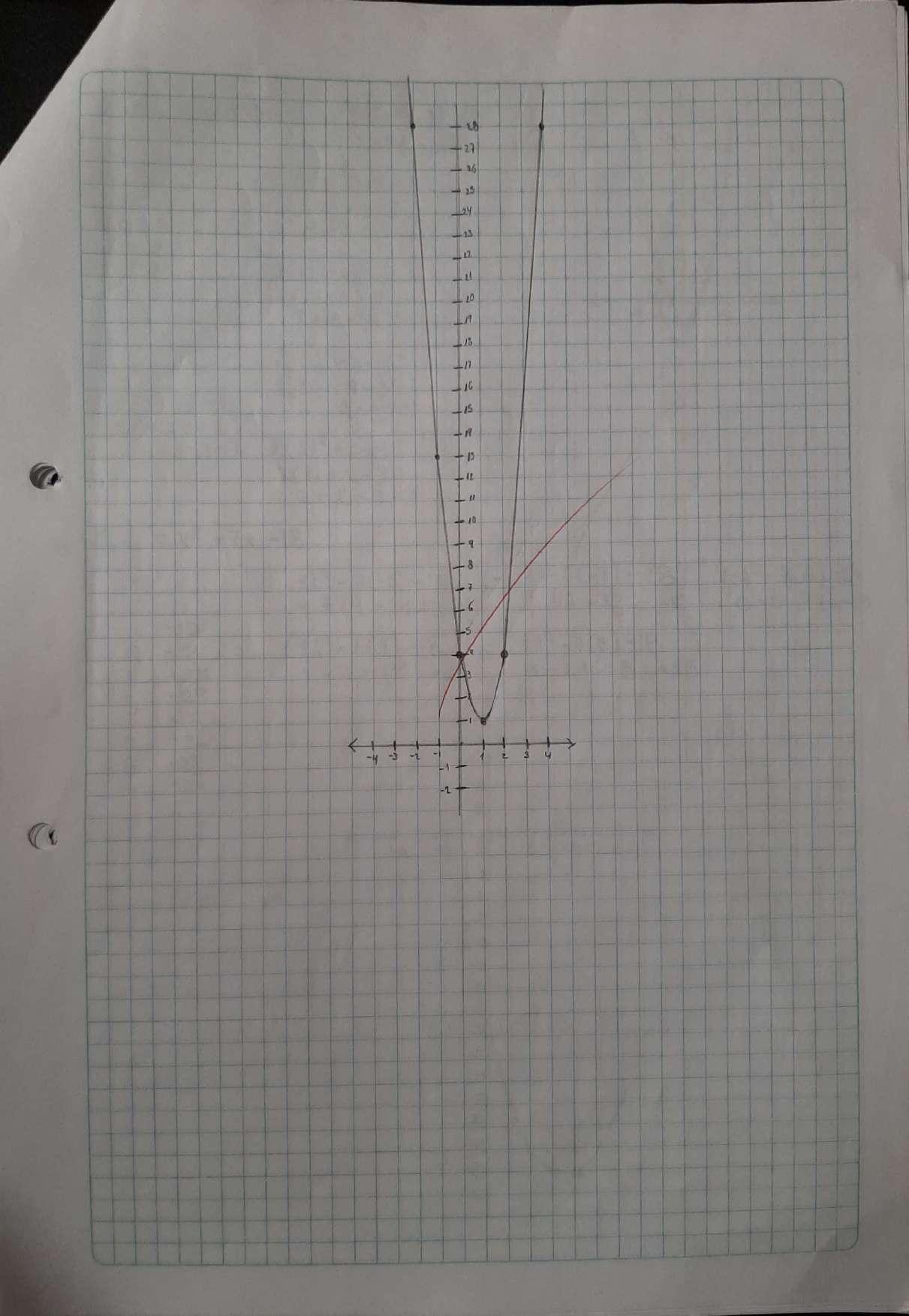
EVALUACIONES-PARCIAL3

PruebasSemanalesyPruebaParcial

UNIVERSIDADPOLITÉCNICAESTATALDELCARCHI NIVELACIÓNTURISMO